Gap-Filling of MODIS Time Series Land Surface Temperature (LST) Products Using Singular Spectrum Analysis (SSA)
Abstract
:1. Introduction
2. Study Area, Data
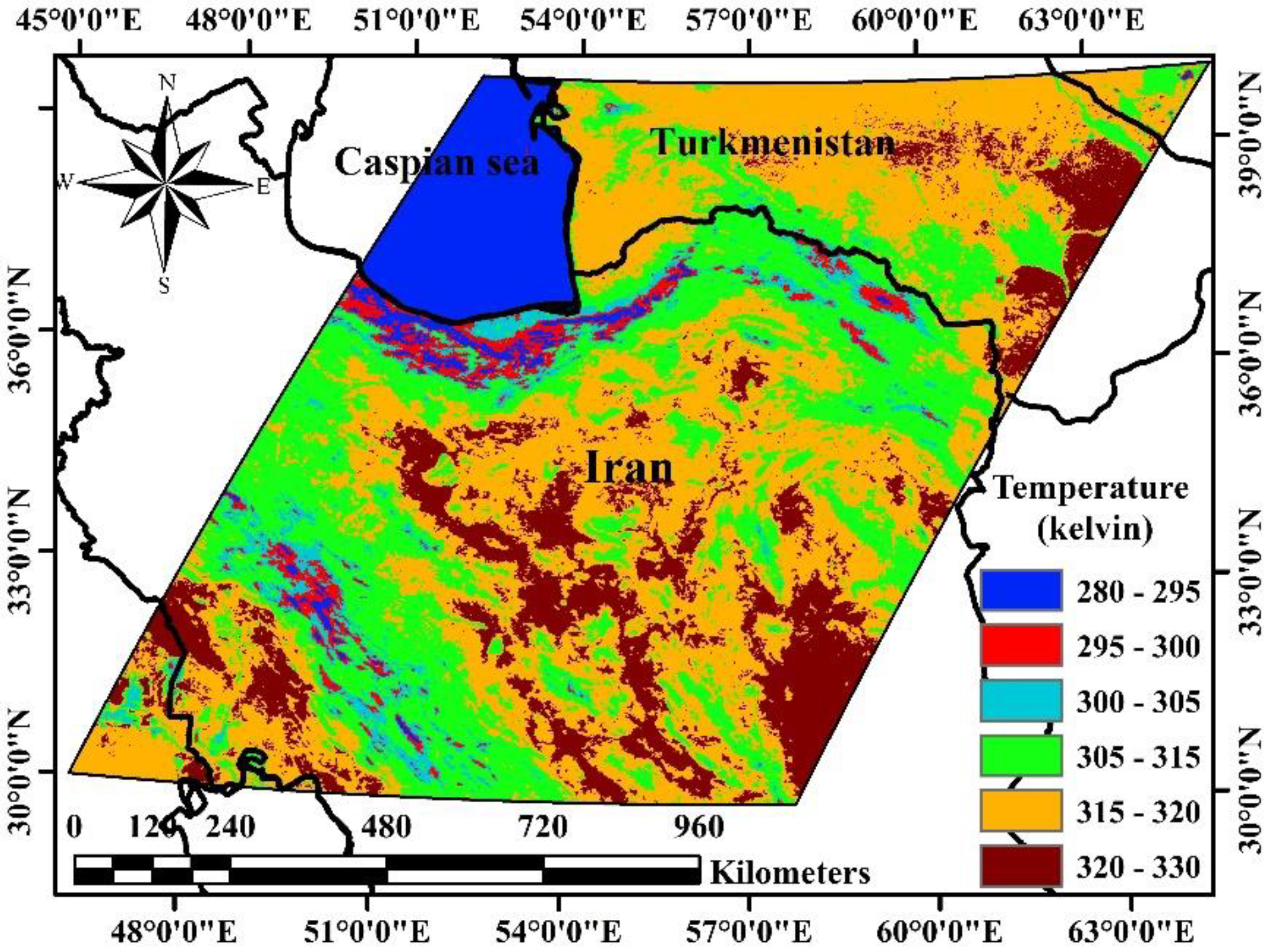
2.1. Study Area
2.2. Data (Satellite Time Series Images)
3. Methodology
Singular Spectrum Analysis (SSA)
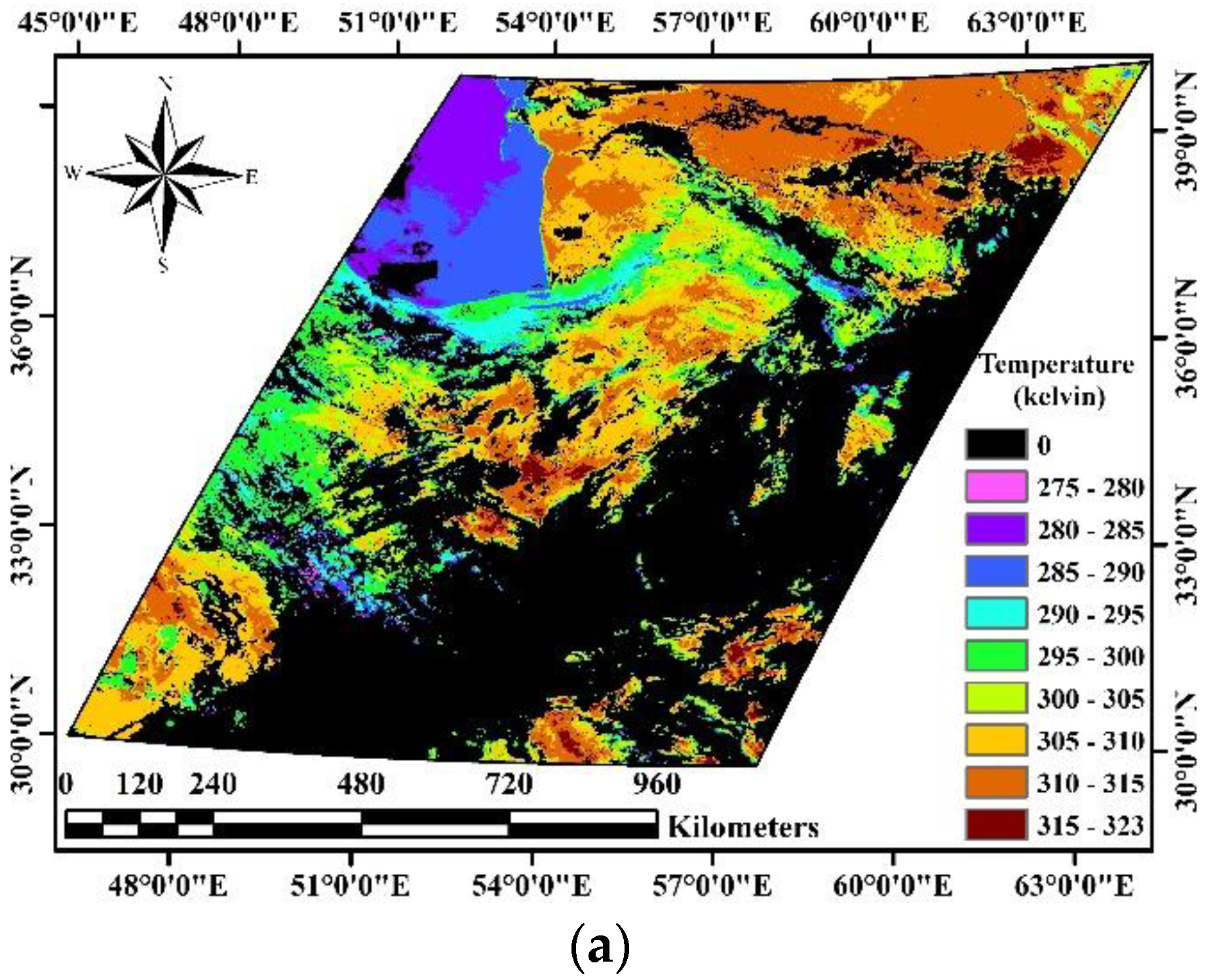
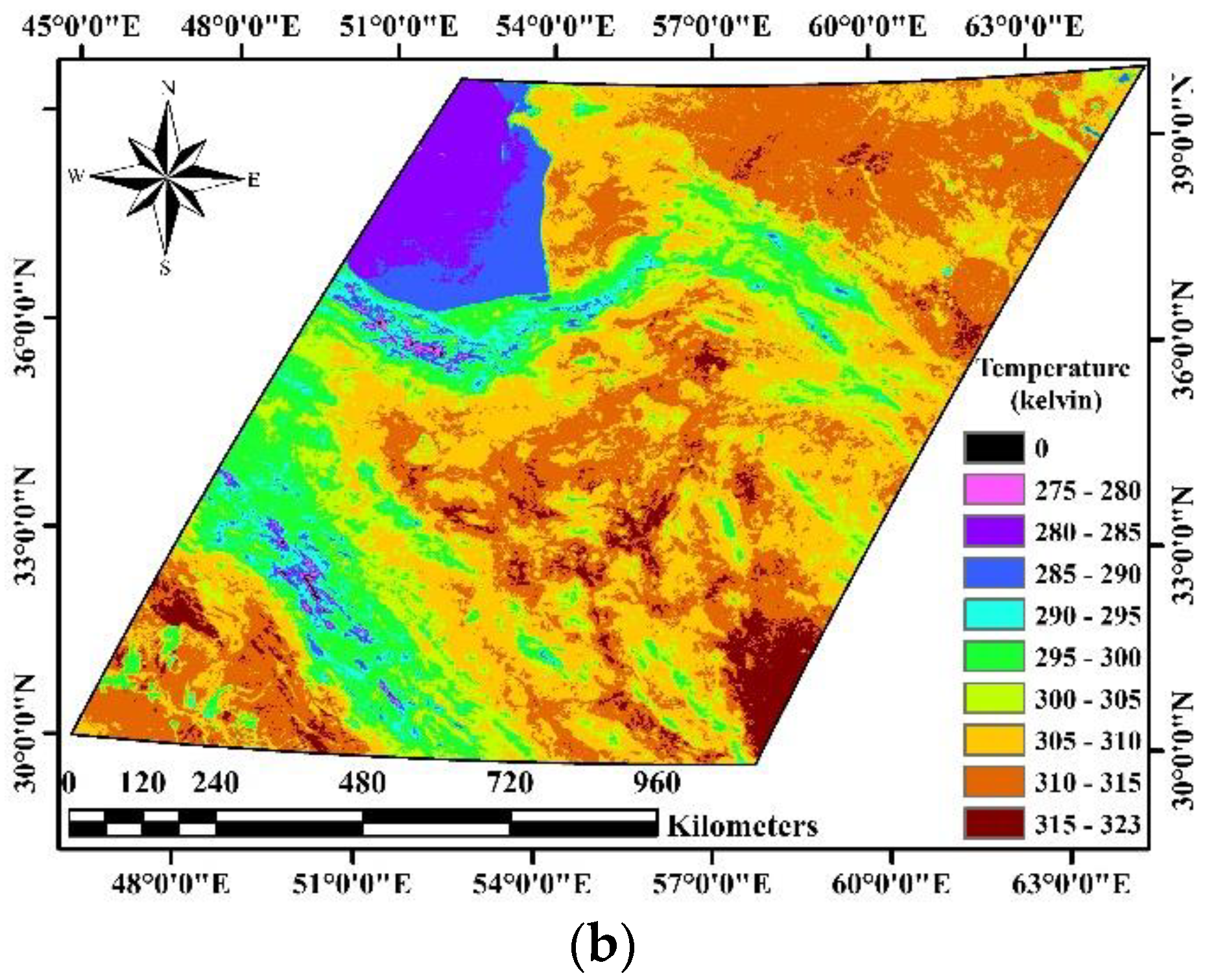
4. Results
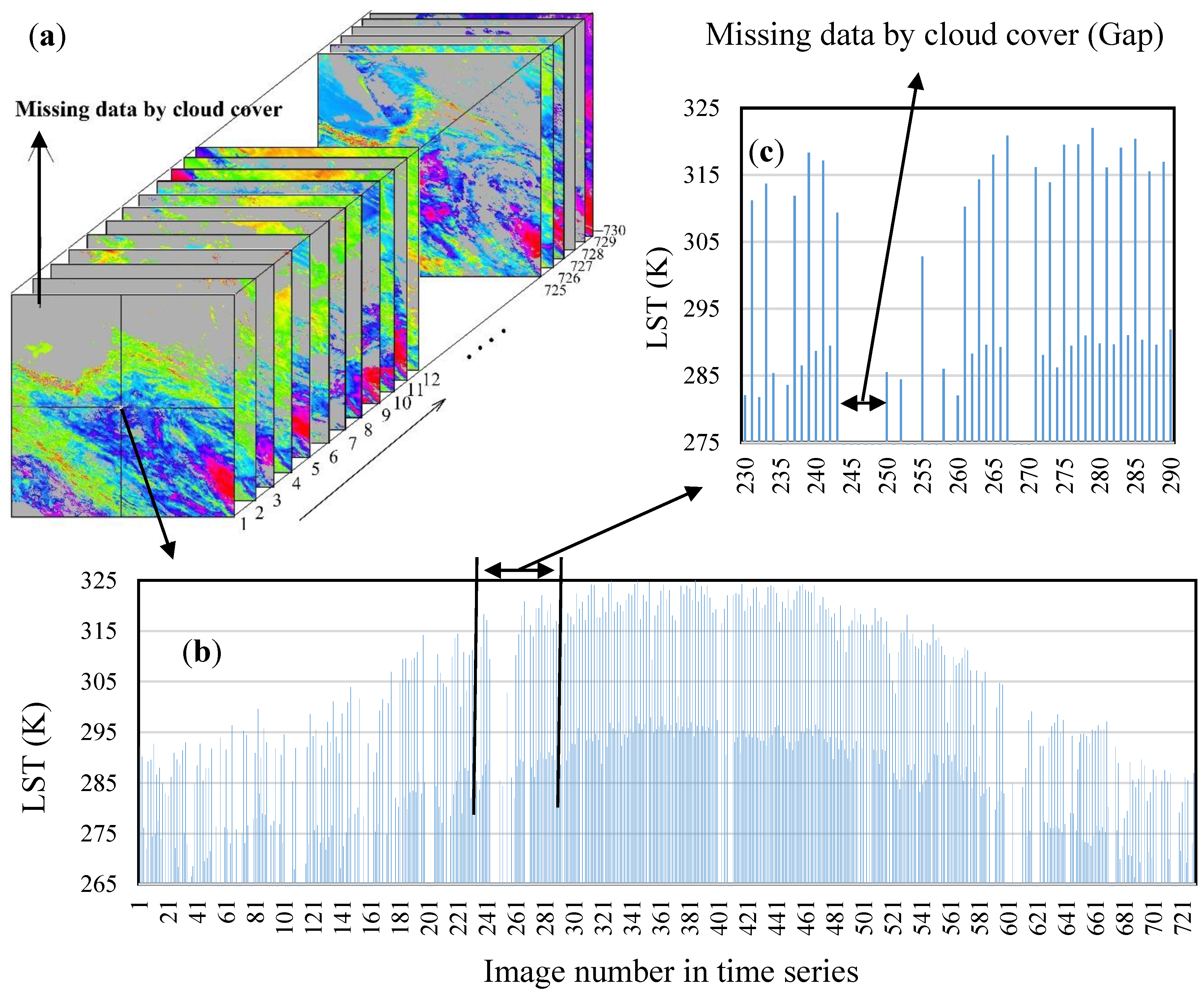
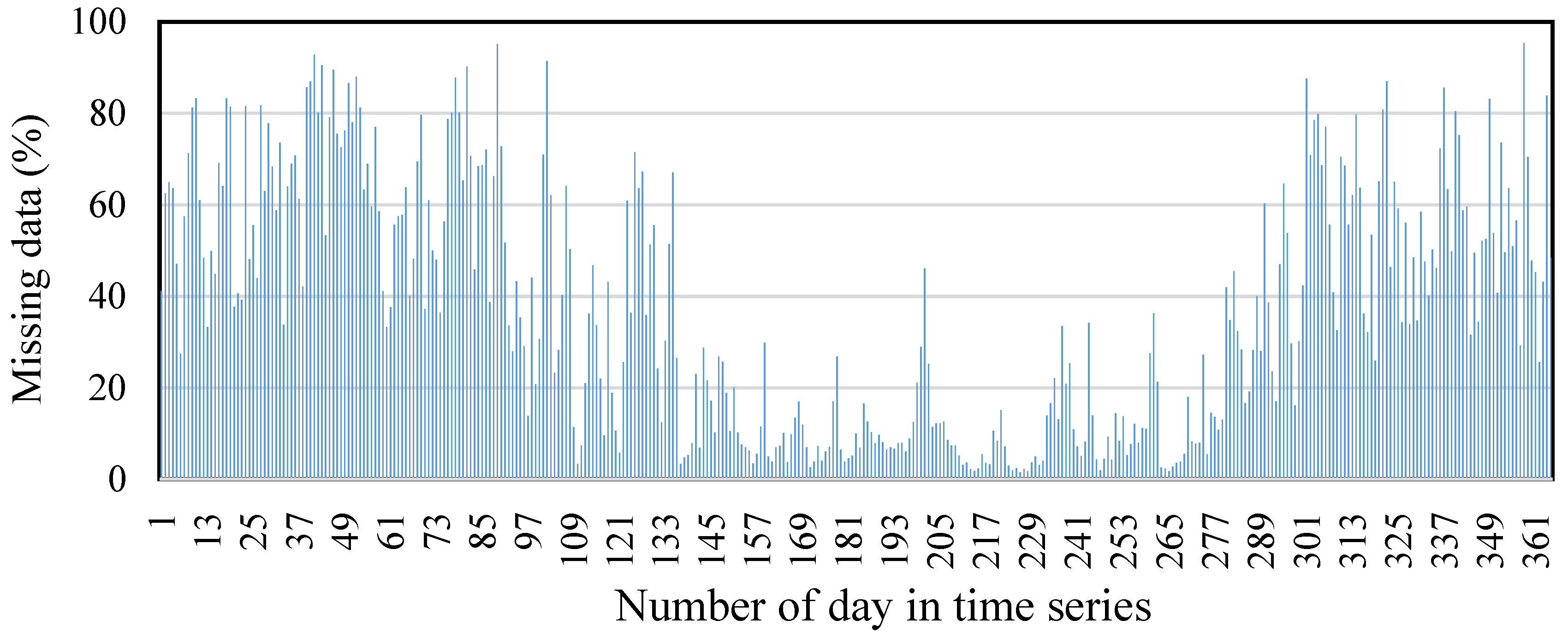
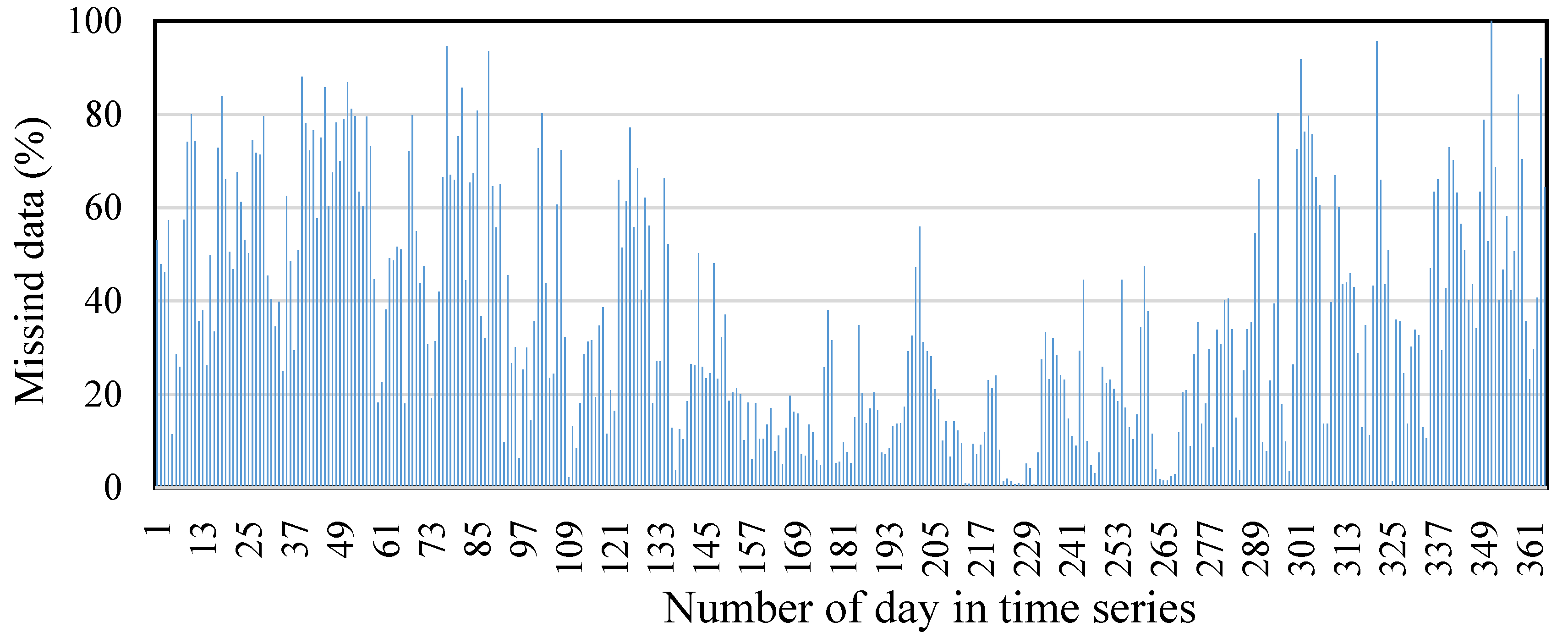
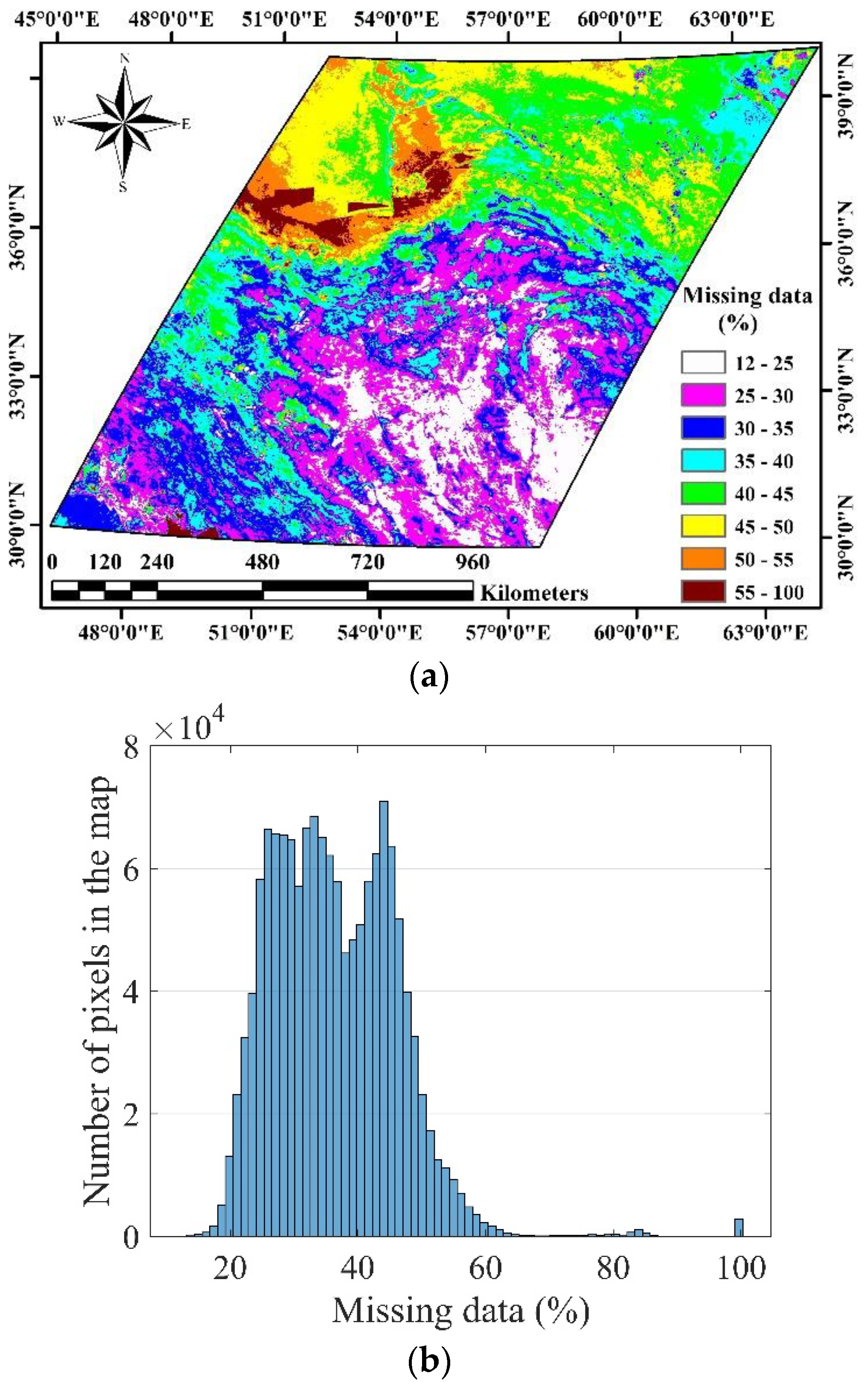
4.1. Spatio-Temporal Distribution of the Missing Data
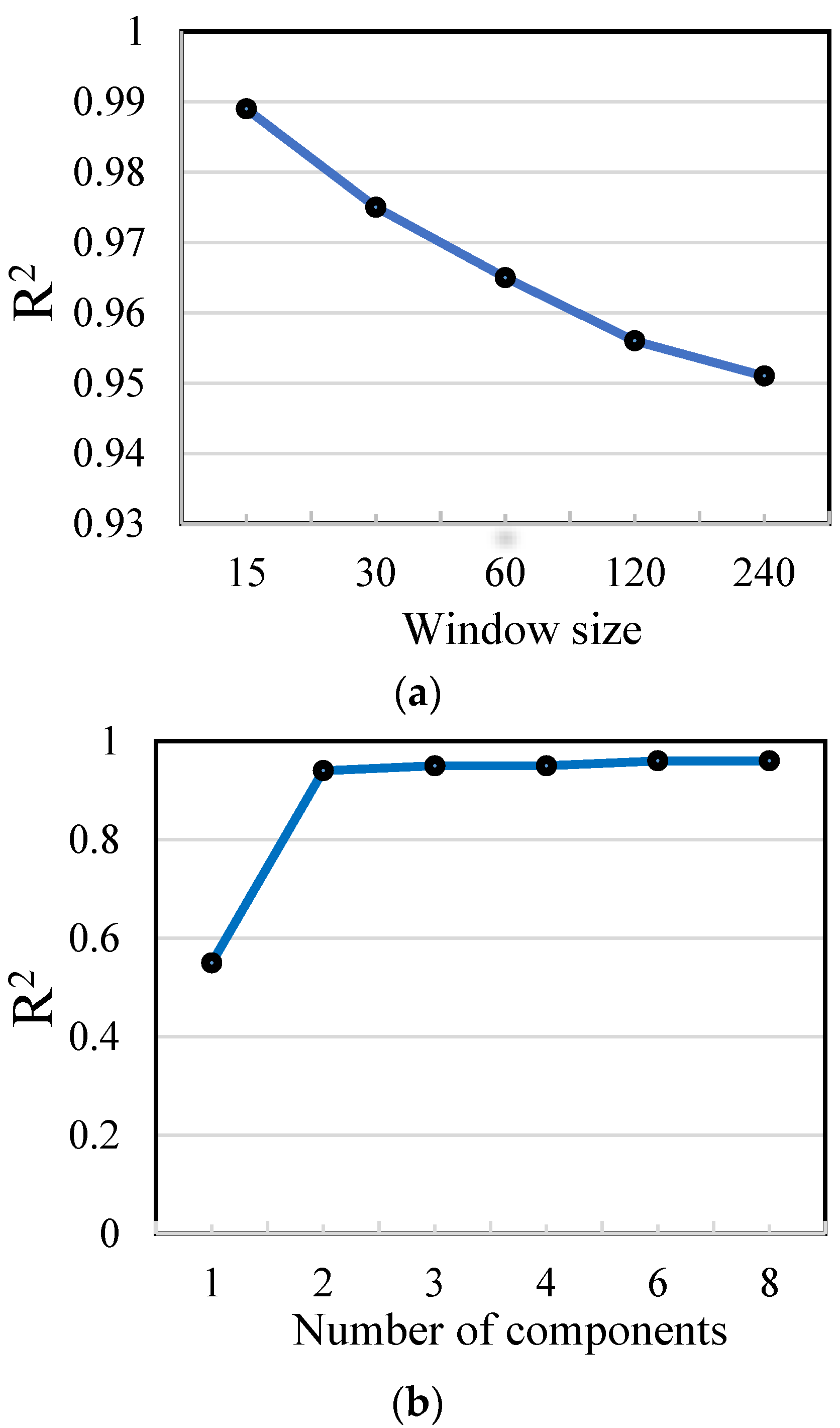
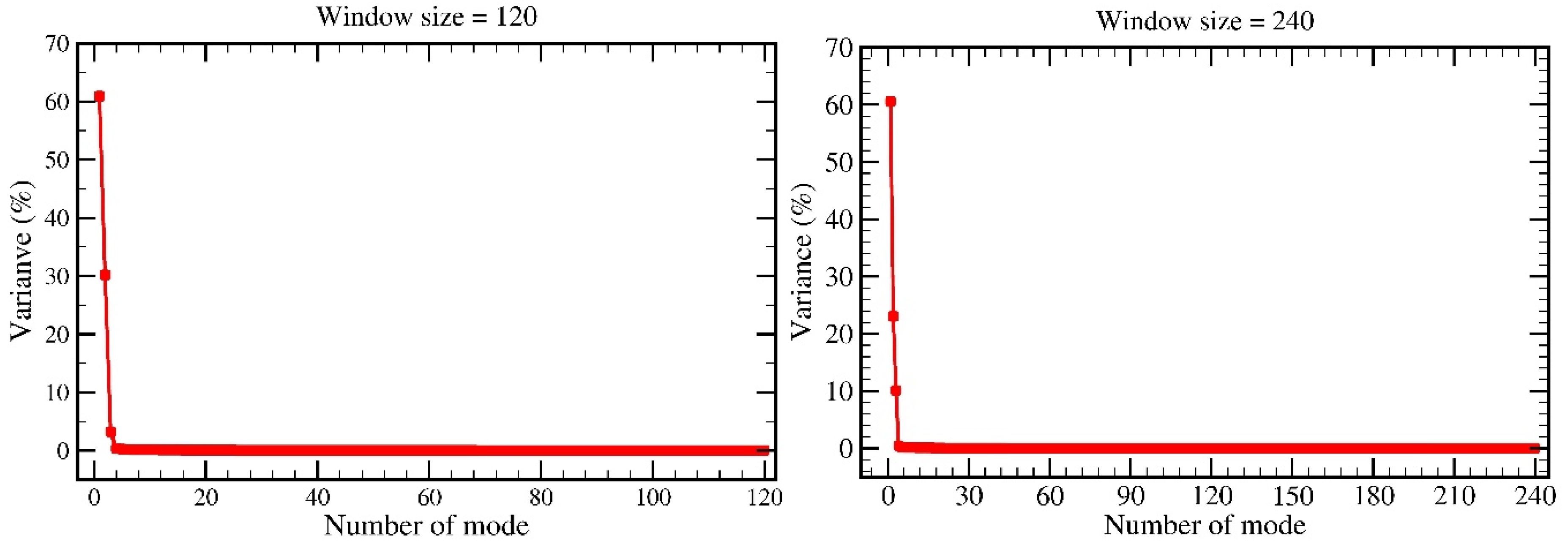
4.2. Determining the Parameters of SSA Algorithm
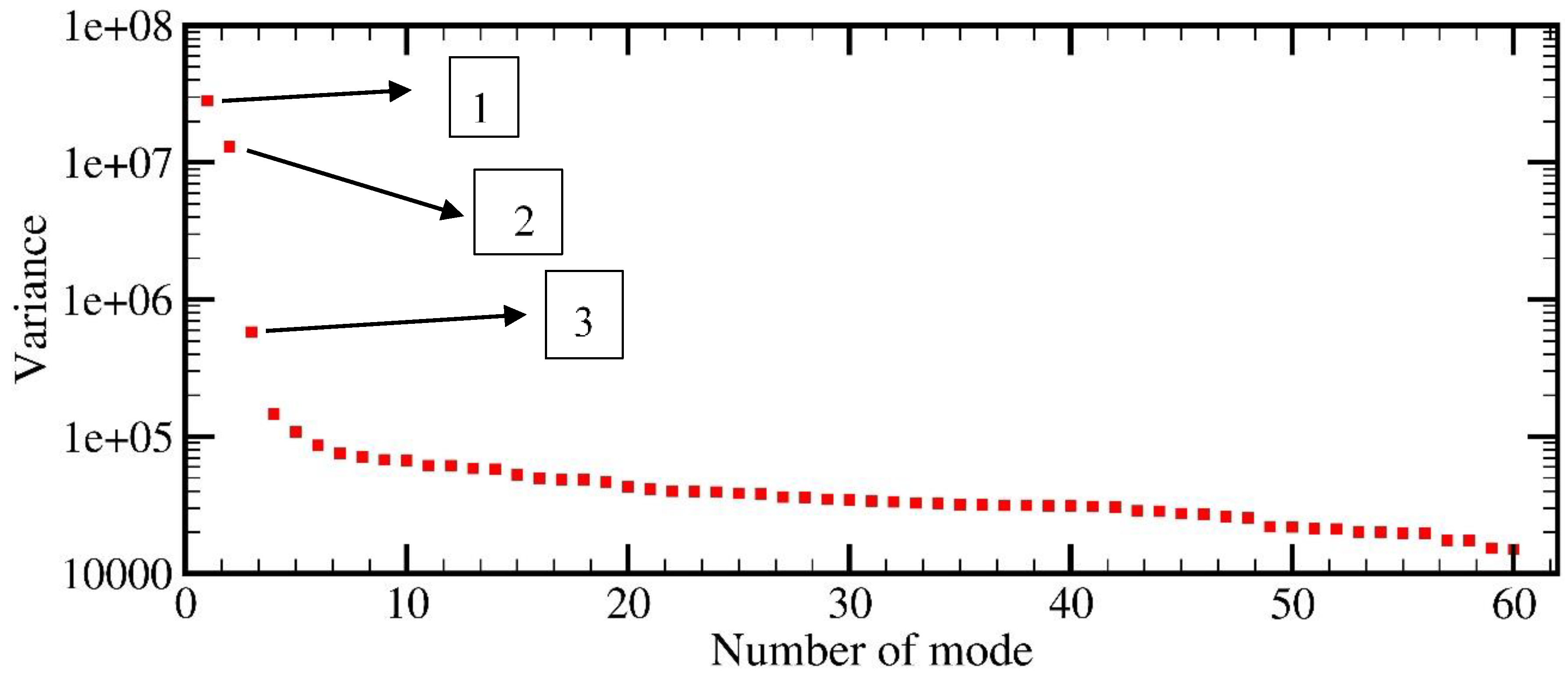
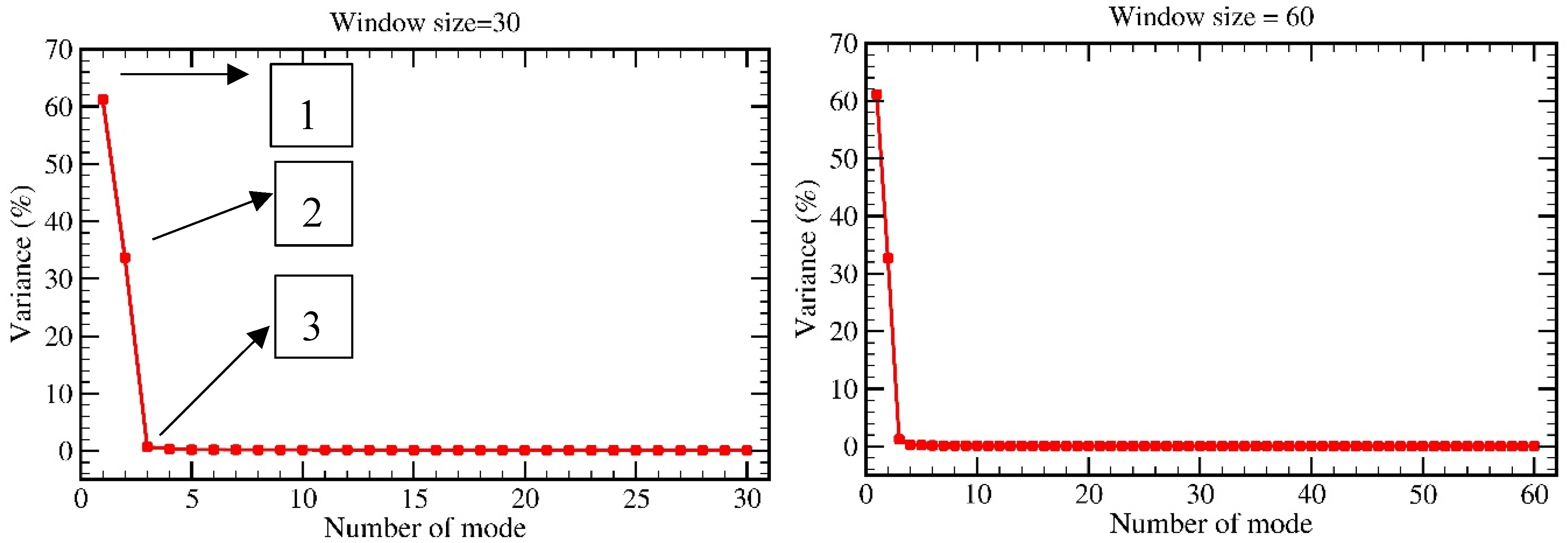
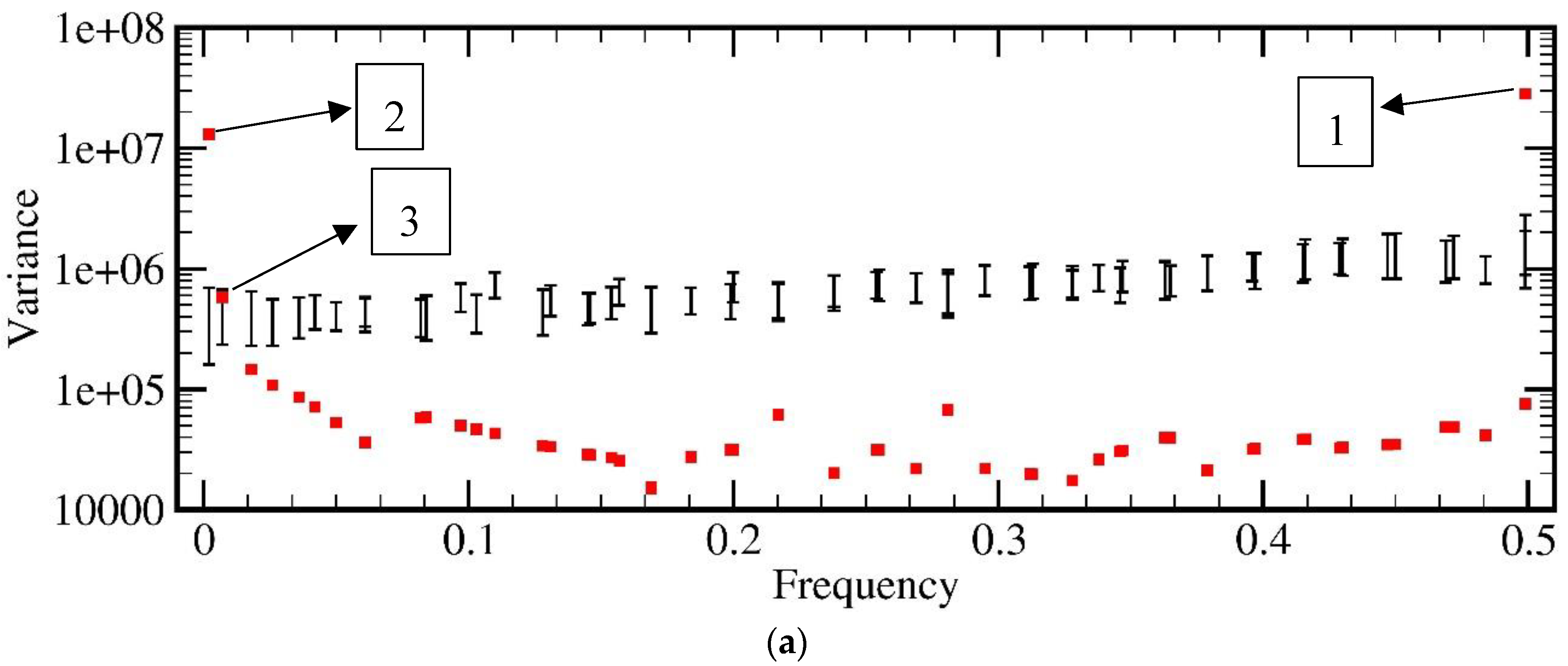
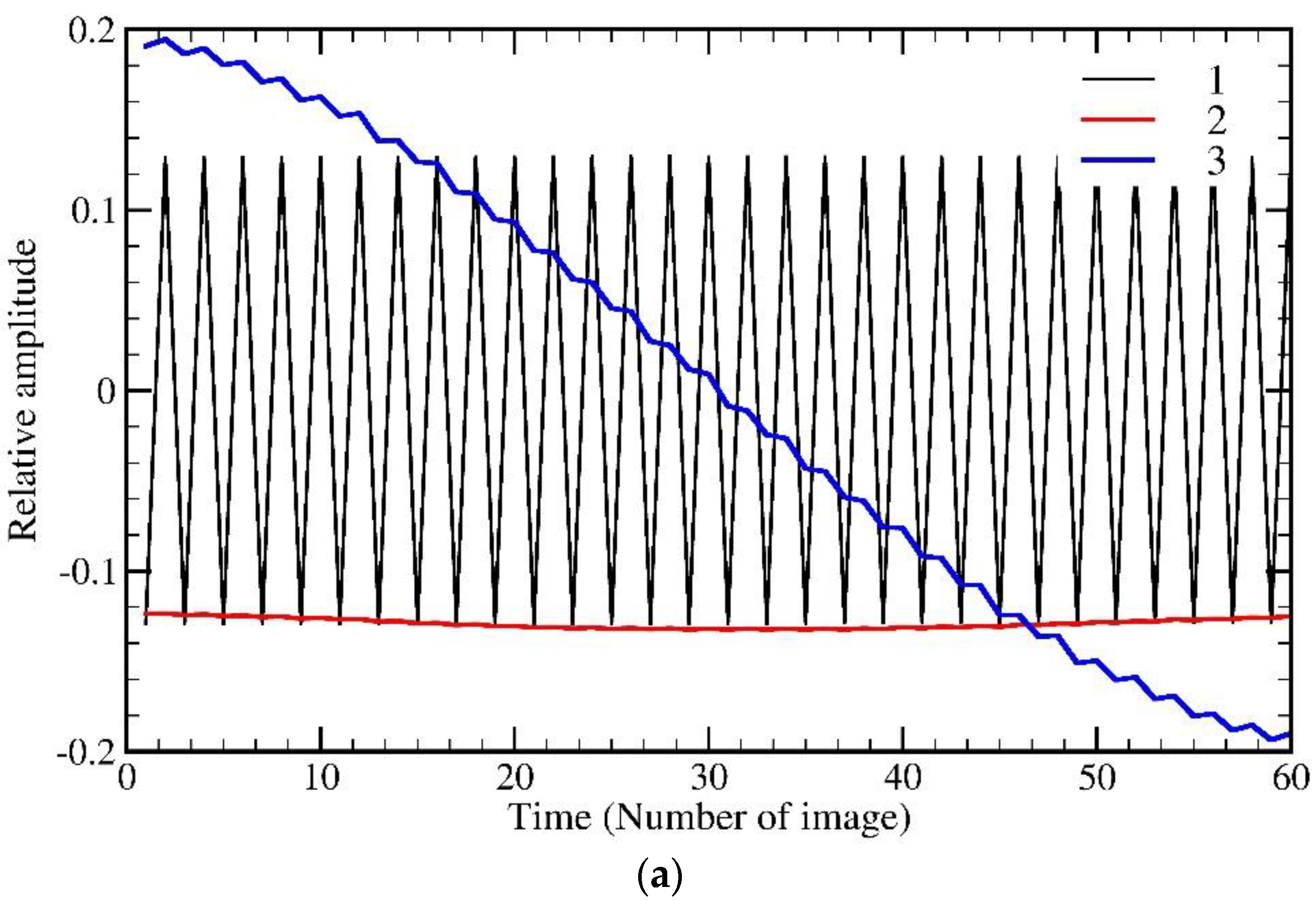
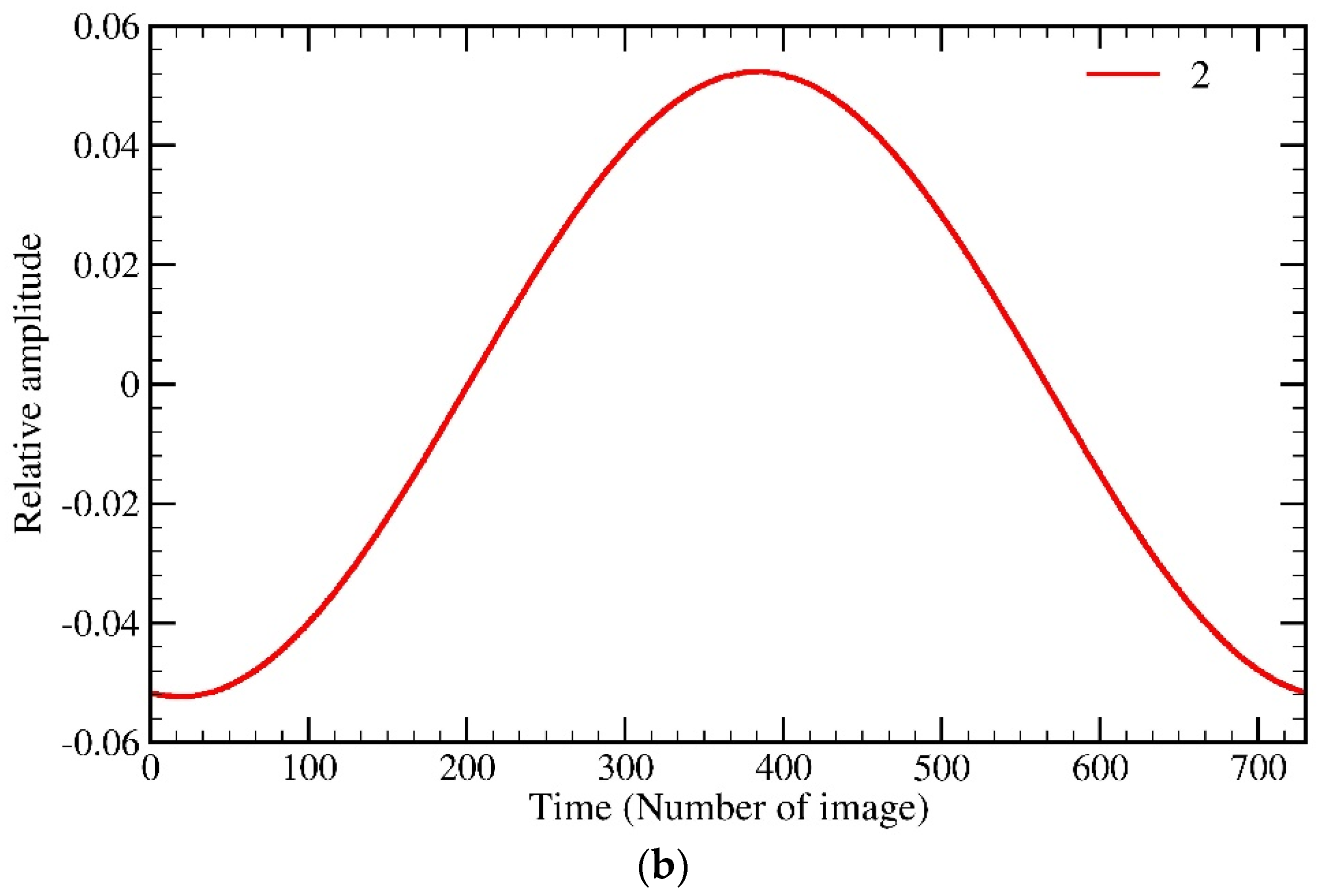
4.3. Determining the Significant Periodic Components in the SSA Algorithm
4.4. Data Basis and Null Hypothesis Basis Monte Carlo Test Results
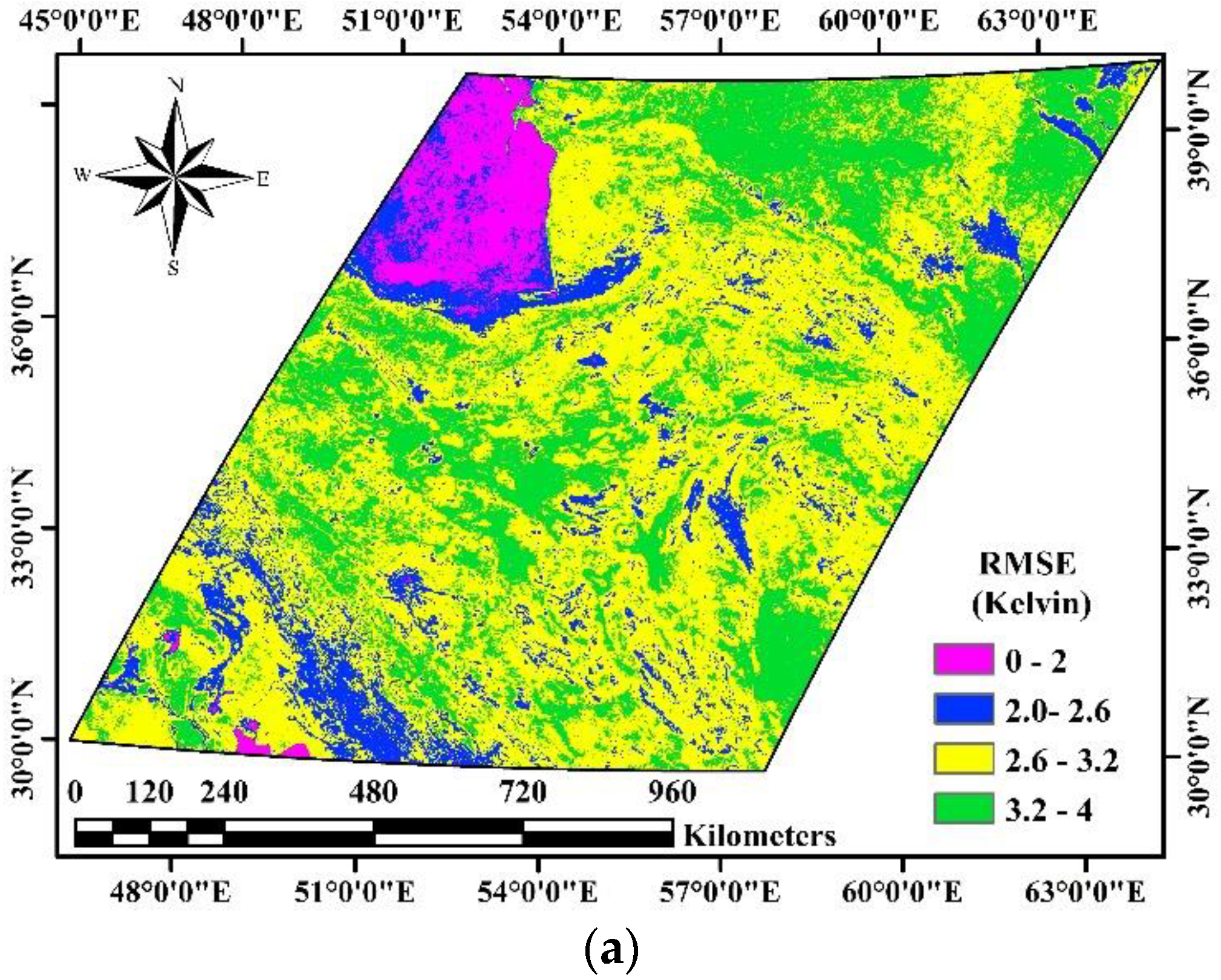
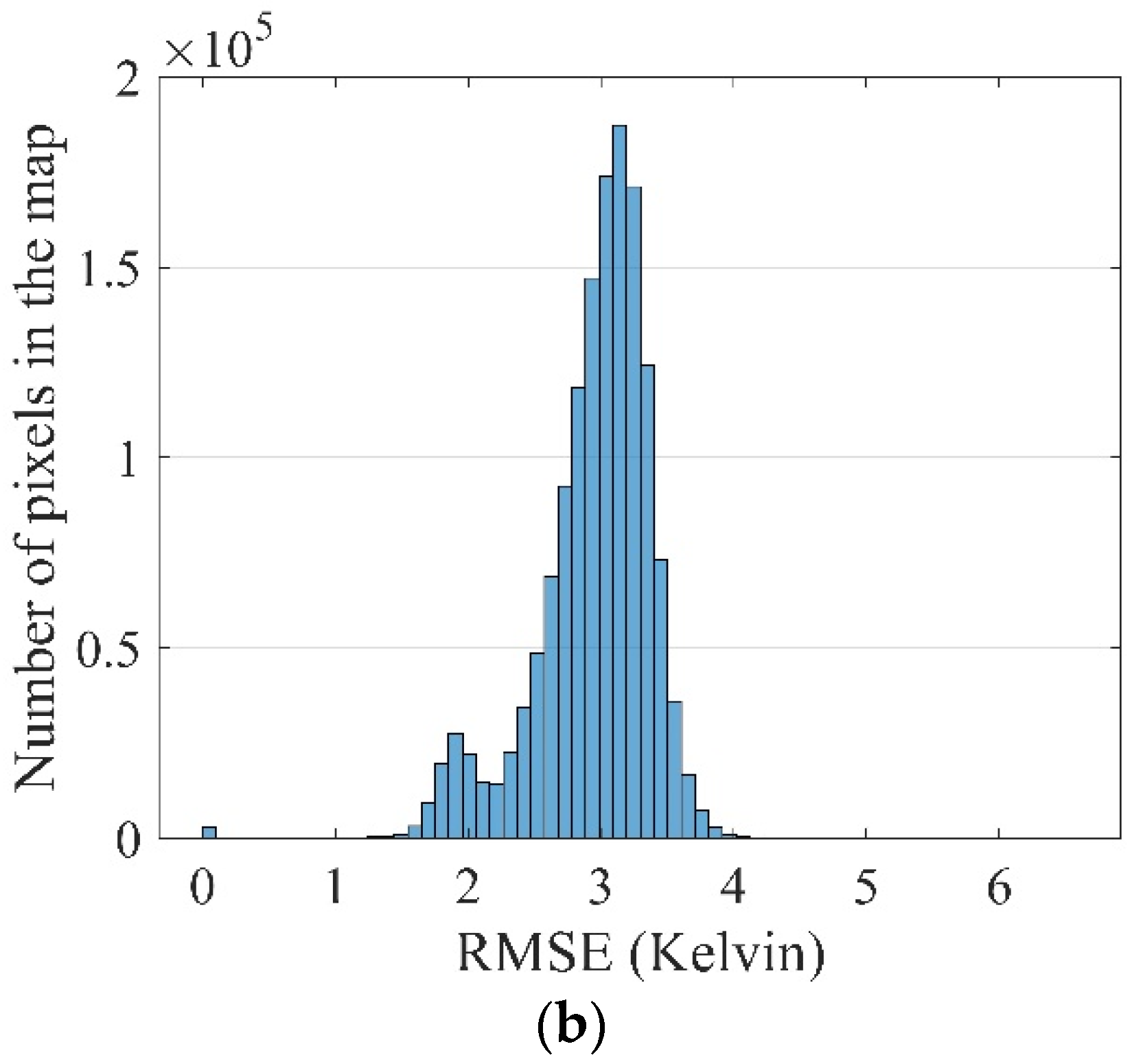
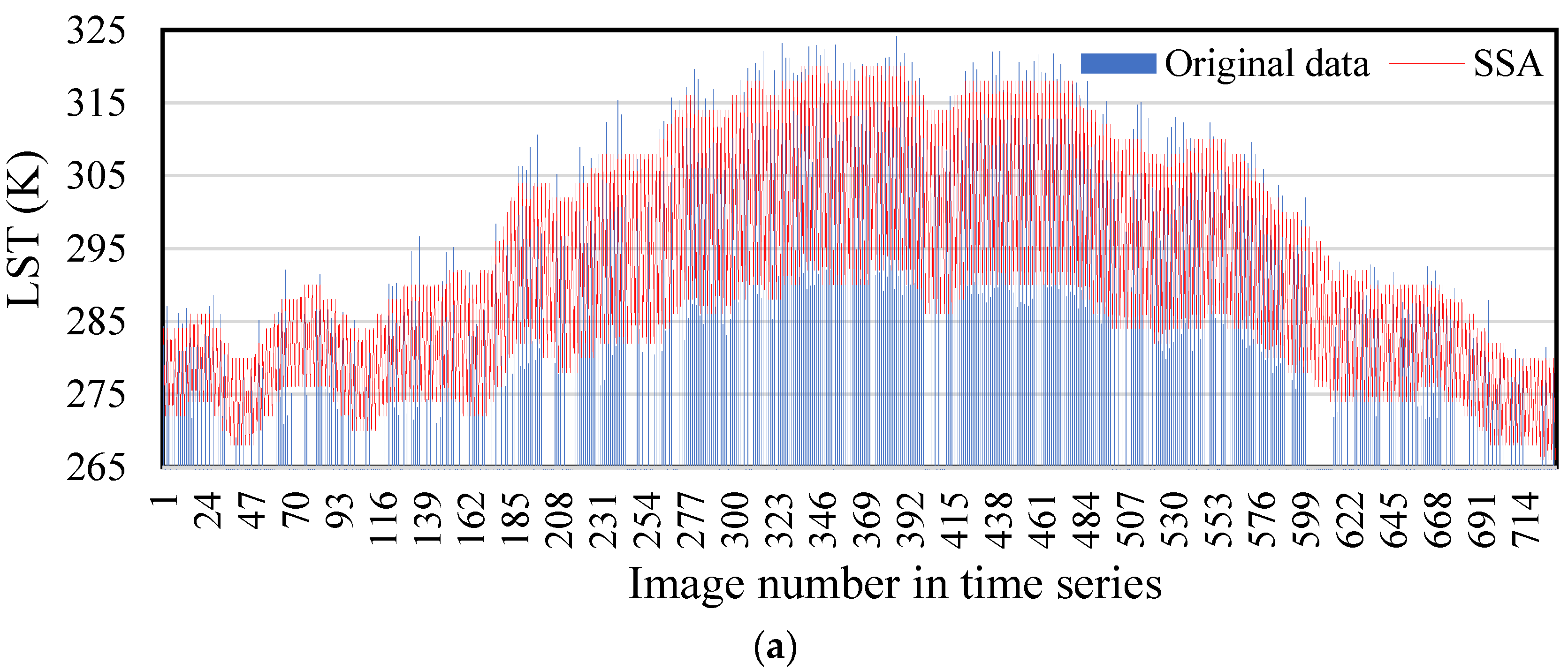
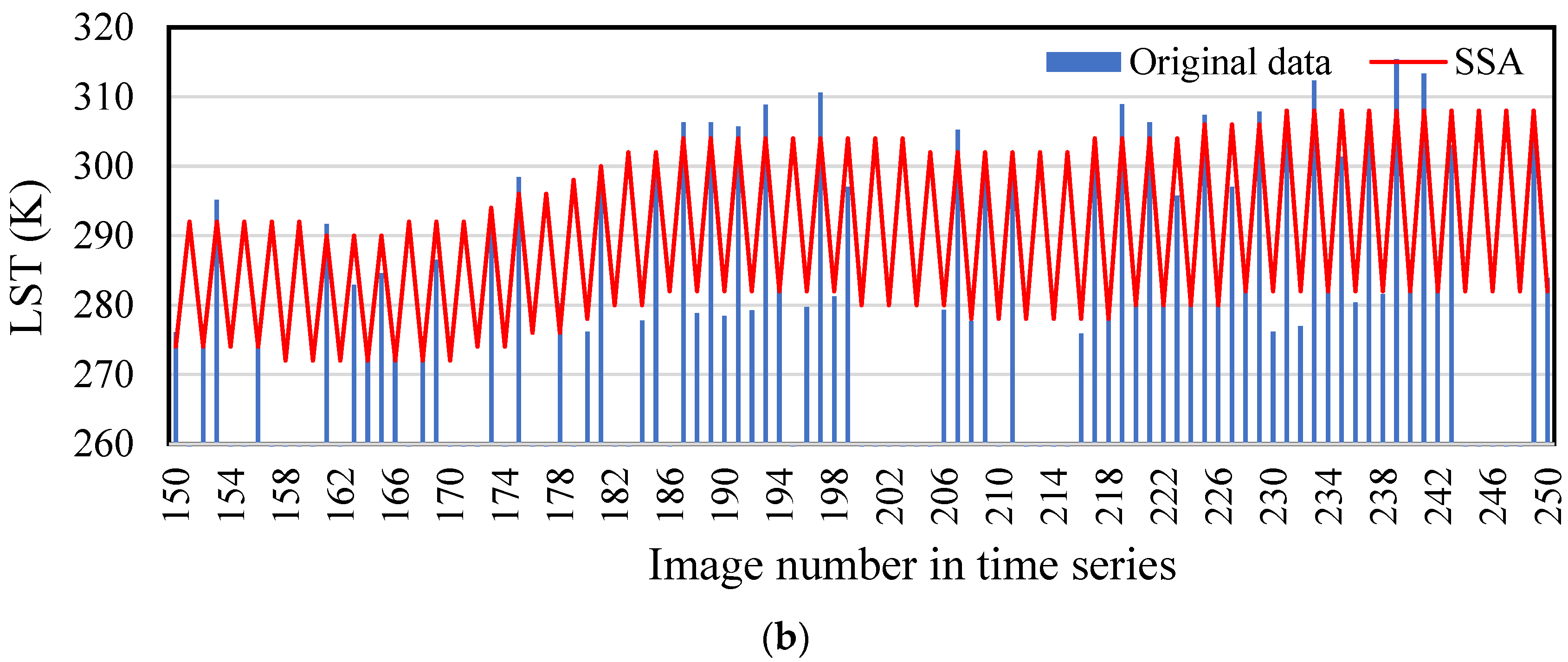
4.5. Assessment of Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ghafarian, H.R.; Menenti, M.; Jia, L.; den Ouden, H. Reconstruction of cloud-free time series satellite observations of land surface temperature. EARSel eProc. 2012, 11, 123–131. [Google Scholar]
- Xu, Y.; Shen, Y. Reconstruction of the land surface temperature time series using harmonic analysis. Comput. Geosci. 2013, 61, 126–132. [Google Scholar] [CrossRef]
- Sobrino, J.A.; El Kharraz, J.E.; Li, Z.-L. Surface temperature and water vapour retrieval from MODIS data. Int. J. Remote Sens. 2003, 24, 5161–5182. [Google Scholar] [CrossRef]
- Running, S.W.; Justice, C.O.; Salomonson, V.; Hall, D.; Barker, J.; Kaufmann, Y.J.; Strahler, A.H.; Huete, A.R.; Muller, J.P.; Vanderbilt, V.; et al. Terrestrial remote sensing science and algorithms planned for EOS/MODIS. Int. J. Remote Sens. 1994, 15, 3587–3620. [Google Scholar] [CrossRef]
- Wan, Z.; Zhang, Y.; Zhang, Q.; Li, Z.L. Validation of the land-surface temperature products retrieved from Terra Moderate Resolution Imaging Spectroradiometer data. Remote Sens. Environ. 2002, 83, 163–180. [Google Scholar] [CrossRef] [Green Version]
- Sun, D.; Pinker, R.T.; Basara, J.B. Land surface temperature estimation from the next generation of Geostationary Operational Environmental Satellites: GOES M–Q. J. Appl. Meteorol. 2004, 43, 363–372. [Google Scholar] [CrossRef]
- Estes, M.G., Jr.; Al-Hamdan, M.Z.; Crosson, W.; Estes, S.M.; Quattrochi, D.; Kent, S.; McClure, L.A. Use of remotely sensed data to evaluate the relationship between living environment and blood pressure. Environ. Health Perspect. 2009, 117, 1832. [Google Scholar] [CrossRef] [PubMed]
- Tatem, A.J.; Goetz, S.J.; Hay, S.I. Terra and Aqua: New data for epidemiology and public health. Int. J. Appl. Earth Obs. Geoinf. 2004, 6, 33–46. [Google Scholar] [CrossRef] [PubMed]
- Schmugge, T.; French, A.; Ritchie, J.C.; Rango, A.; Pelgrum, H. Temperature and emissivity separation from multispectral thermal infrared observations. Remote Sens. Environ. 2002, 79, 189–198. [Google Scholar] [CrossRef]
- Rousta, I.; Doostkamian, M.; Haghighi, E.; Mirzakhani, B. Statistical-Synoptic Analysis of the Atmosphere Thickness Pattern of Iran’s Pervasive Frosts. Climate 2016, 4, 41. [Google Scholar] [CrossRef]
- Soltani, M.; Laux, P.; Kunstmann, H.; Stan, K.; Sohrabi, M.M.; Molanejad, M.; Sabziparvar, A.A.; SaadatAbadi, A.R.; Ranjbar, F.; Rousta, I.; et al. Assessment of climate variations in temperature and precipitation extreme events over Iran. Theor. Appl. Climatol. 2016, 126, 775–795. [Google Scholar] [CrossRef]
- Soltani, M.; Zawar-Reza, P.; Khoshakhlagh, F.; Rousta, I. Mid-latitude Cyclones Climatology over Caspian Sea Southern Coasts–North of Iran. Available online: https://ams.confex.com/ams/21Applied17SMOI/webprogram/Paper246601.html (accessed on 20 June 2018).
- Rousta, I.; Soltani, M.; Zhou, W.; Cheung, H.H. Analysis of Extreme Precipitation Events over Central Plateau of Iran. Am. J. Clim. Chang. 2016, 5, 297. [Google Scholar] [CrossRef]
- Rousta, I.; Doostkamian, M.; Taherian, A.M.; Haghighi, E.; Ghafarian Malamiri, H.R.; Ólafsson, H. Investigation of the Spatio-Temporal Variations in Atmosphere Thickness Pattern of Iran and the Middle East with Special Focus on Precipitation in Iran. Climate 2017, 5, 82. [Google Scholar] [CrossRef]
- Rousta, I.; Javadizadeh, G.; Dargahian, F.; Ólafsson, H.; Shiri Karimvandi, A.; Vahedinejad, S.H.; Doostkamian, M.; Monroy Vargas, E.R.; Asadolahi, A. Investigation of Vorticity during Prevalent Winter Precipitation in Iran. Adv. Meteorol. 2018, in press. [Google Scholar]
- Julien, Y.; Sobrino, J.A. Comparison of cloud-reconstruction methods for time series of composite NDVI data. Remote Sens. Environ. 2010, 114, 618–625. [Google Scholar] [CrossRef]
- Zhou, J.; Jia, L.; Menenti, M. Reconstruction of global MODIS NDVI time series: Performance of harmonic analysis of time series (HANTS). Remote Sens. Environ 2015, 163, 217–228. [Google Scholar] [CrossRef]
- Ackerman, S.A.; Strabala, K.I.; Menzel, W.P.; Frey, R.A.; Moeller, C.C.; Gumley, L.E. Discriminating clear sky from clouds with MODIS. J. Geophys. Res. Atmos. 1998, 103, 32141–32157. [Google Scholar] [CrossRef] [Green Version]
- Ghafarian Malamiri, H.R. Reconstruction of Gap-Free Time Series Satellite Observations of Land Surface Temperature to Model Spectral Soil Thermal Admittance. Available online: https://repository.tudelft.nl/islandora/object/uuid:63dc3402-9fd6-4594-a00e-7aa5ae2501aa?collection=research (accessed on 20 June 2018).
- Jia, L.; Shang, H.; Hu, G.; Menenti, M. Phenological response of vegetation to upstream river flow in the Heihe Rive basin by time series analysis of MODIS data. Hydrol. Earth Syst. Sci. 2011, 15, 1047–1064. [Google Scholar] [CrossRef] [Green Version]
- Roerink, G.; Menenti, M.; Verhoef, W. Reconstructing cloudfree NDVI composites using Fourier analysis of time series. Int. J. Remote Sens. 2000, 21, 1911–1917. [Google Scholar] [CrossRef]
- Verhoef, W. Application of harmonic analysis of NDVI time series (HANTS). Fourier Anal. Temp. Am. Cont. 1996, 108, 19–24. [Google Scholar]
- Verhoef, W.; Menenti, M.; Azzali, S. Cover A colour composite of NOAA-AVHRR-NDVI based on time series analysis (1981–1992). Int. J. Remote Sens. 1996, 17, 231–235. [Google Scholar] [CrossRef]
- Menenti, M.; Azzali, S.; Verhoef, W.; Van Swol, R. Mapping agroecological zones and time lag in vegetation growth by means of Fourier analysis of time series of NDVI images. Adv. Space Res. 1993, 13, 233–237. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, D.; Tang, L.; Hu, J.; Xi, X. Analysing the vegetation cover variation of China from AVHRR-NDVI data. Int. J. Remote Sens. 2008, 29, 5301–5311. [Google Scholar] [CrossRef]
- Julien, Y.; Sobrino, J.A.; Verhoef, W. Changes in land surface temperatures and NDVI values over Europe between 1982 and 1999. Remote Sens. Environ. 2006, 103, 43–55. [Google Scholar] [CrossRef]
- Alfieri, S.M.; Lorenzi, F.D.; Menenti, M. Mapping air temperature using time series analysis of LST: The SINTESI approach. Nonlinear Proc. Geophys. 2013, 20, 513–527. [Google Scholar] [CrossRef]
- Broomhead, D.S.; King, G.P. Extracting qualitative dynamics from experimental data. Phys. D Nonlinear Phenom. 1986, 20, 217–236. [Google Scholar] [CrossRef]
- Kondrashov, D.; Ghil, M. Spatio-temporal filling of missing points in geophysical data sets. Nonlinear Proc. Geophys. 2006, 13, 151–159. [Google Scholar] [CrossRef] [Green Version]
- Vautard, R.; Yiou, P.; Ghil, M. Singular-spectrum analysis: A toolkit for short, noisy chaotic signals. Phys. D Nonlinear Phenom. 1992, 58, 95–126. [Google Scholar] [CrossRef]
- Golyandina, N.; Zhigljavsky, A. Singular Spectrum Analysis for Time Series; Springer Science & Business Media: Berlin, Germany, 2013; Available online: https://books.google.com.hk/books?hl=zh-TW&lr=&id=CUpEAAAAQBAJ&oi=fnd&pg=PP5&dq=Singular+Spectrum+Analysis+for+time+series.+&ots=zF6W4hag3S&sig=yuKb4t8umEUW2AQXkcGD28nfZC8&redir_esc=y#v=onepage&q=Singular%20Spectrum%20Analysis%20for%20time%20series.&f=false (accessed on 20 June 2018).
- Golyandina, N.; Nekrutkin, V.; Zhigljavsky, A.A. Analysis of Time Series Structure: SSA and Related Techniques; Chapman and Hall/CRC: Washington, DC, USA, 2001. [Google Scholar]
- Ghil, M.; Vautard, R. Interdecadal oscillations and the warming trend in global temperature time series. Nature 1991, 350, 324. [Google Scholar] [CrossRef]
- Vautard, R.; Ghil, M. Singular spectrum analysis in nonlinear dynamics, with applications to paleoclimatic time series. Phys. D Nonlinear Phenom. 1989, 35, 395–424. [Google Scholar] [CrossRef]
- Yiou, P.; Baert, E.; Loutre, M.F. Spectral analysis of climate data. Surv. Geophys. 1996, 17, 619–663. [Google Scholar] [CrossRef]
- Yiou, P.; Sornette, D.; Ghil, M. Data-adaptive wavelets and multi-scale singular-spectrum analysis. Phys. D Nonlinear Phenom. 2000, 142, 254–290. [Google Scholar] [CrossRef] [Green Version]
- Kondrashov, D.; Shprits, Y.; Ghil, M. Gap filling of solar wind data by singular spectrum analysis. Geophys. Res. Lett. 2010, 37, L15101. [Google Scholar] [CrossRef]
- Wang, D.; Liang, S. Singular Spectrum Analysis for Filling Gaps and Reducing Uncertainties of MODIS Land Products. 2008. Available online: https://ieeexplore.ieee.org/abstract/document/4780153/ (accessed on 20 June 2018).
- Marques, C.A.F.; Ferreira, J.A.; Rocha, A.; Castanheira, J.M.; Melo-Gonçalves, P.; Vaz, N.; Dias, J.M. Singular spectrum analysis and forecasting of hydrological time series. Phys. Chem. Earth 2006, 31, 1172–1179. [Google Scholar] [CrossRef]
- Wan, Z. MODIS Land-Surface Temperature Algorithm Theoretical Basis Document (LST ATBD). Available online: https://modis.gsfc.nasa.gov/data/atbd/atbd_mod11.pdf (accessed on 20 June 2018).
- Wan, Z. New refinements and validation of the collection-6 MODIS land-surface temperature/emissivity product. Remote Sens. Environ. 2014, 140, 36–45. [Google Scholar] [CrossRef]
- Musial, J.P.; Verstraete, M.M.; Gobron, N. Comparing the effectiveness of recent algorithms to fill and smooth incomplete and noisy time series. Atmos. Chem. Phys. 2011, 11, 7905–7923. [Google Scholar] [CrossRef] [Green Version]
- Elsner, J.B.; Tsonis, A.A. Singular Spectrum Analysis: A New Tool in Time Series Analysis; Springer Science & Business Media: New York, NY, USA, 1996. [Google Scholar]
- Allen, M.R.; Smith, L.A. Monte Carlo SSA: Detecting irregular oscillations in the presence of colored noise. J. Clim. 1996, 9, 3373–3404. [Google Scholar] [CrossRef]
- Schoellhamer, D.H. Singular spectrum analysis for time series with missing data. Geophys. Res. Lett. 2001, 28, 3187–3190. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.L.; Tang, B.H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef] [Green Version]
- Ghafarian Malamiri, H.R.; Khormizie, H.Z. Reconstruction of cloud-free time series satellite observations of land surface temperature (LST) using harmonic analysis of time series algorithm (HANTS). J. RS GIS Nat. Resour. 2017, 8, 37–55. [Google Scholar]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghafarian Malamiri, H.R.; Rousta, I.; Olafsson, H.; Zare, H.; Zhang, H. Gap-Filling of MODIS Time Series Land Surface Temperature (LST) Products Using Singular Spectrum Analysis (SSA). Atmosphere 2018, 9, 334. https://doi.org/10.3390/atmos9090334
Ghafarian Malamiri HR, Rousta I, Olafsson H, Zare H, Zhang H. Gap-Filling of MODIS Time Series Land Surface Temperature (LST) Products Using Singular Spectrum Analysis (SSA). Atmosphere. 2018; 9(9):334. https://doi.org/10.3390/atmos9090334
Chicago/Turabian StyleGhafarian Malamiri, Hamid Reza, Iman Rousta, Haraldur Olafsson, Hadi Zare, and Hao Zhang. 2018. "Gap-Filling of MODIS Time Series Land Surface Temperature (LST) Products Using Singular Spectrum Analysis (SSA)" Atmosphere 9, no. 9: 334. https://doi.org/10.3390/atmos9090334
APA StyleGhafarian Malamiri, H. R., Rousta, I., Olafsson, H., Zare, H., & Zhang, H. (2018). Gap-Filling of MODIS Time Series Land Surface Temperature (LST) Products Using Singular Spectrum Analysis (SSA). Atmosphere, 9(9), 334. https://doi.org/10.3390/atmos9090334







