The FuGas 2.3 Framework for Atmosphere–Ocean Coupling: Comparing Algorithms for the Estimation of Solubilities and Gas Fluxes
Abstract
1. Introduction
2. Methods
2.1. Solubility
2.2. Transfer Velocity
2.3. Validation with Field Data
2.4. Application within Geoscientific Models
3. Results and Discussion
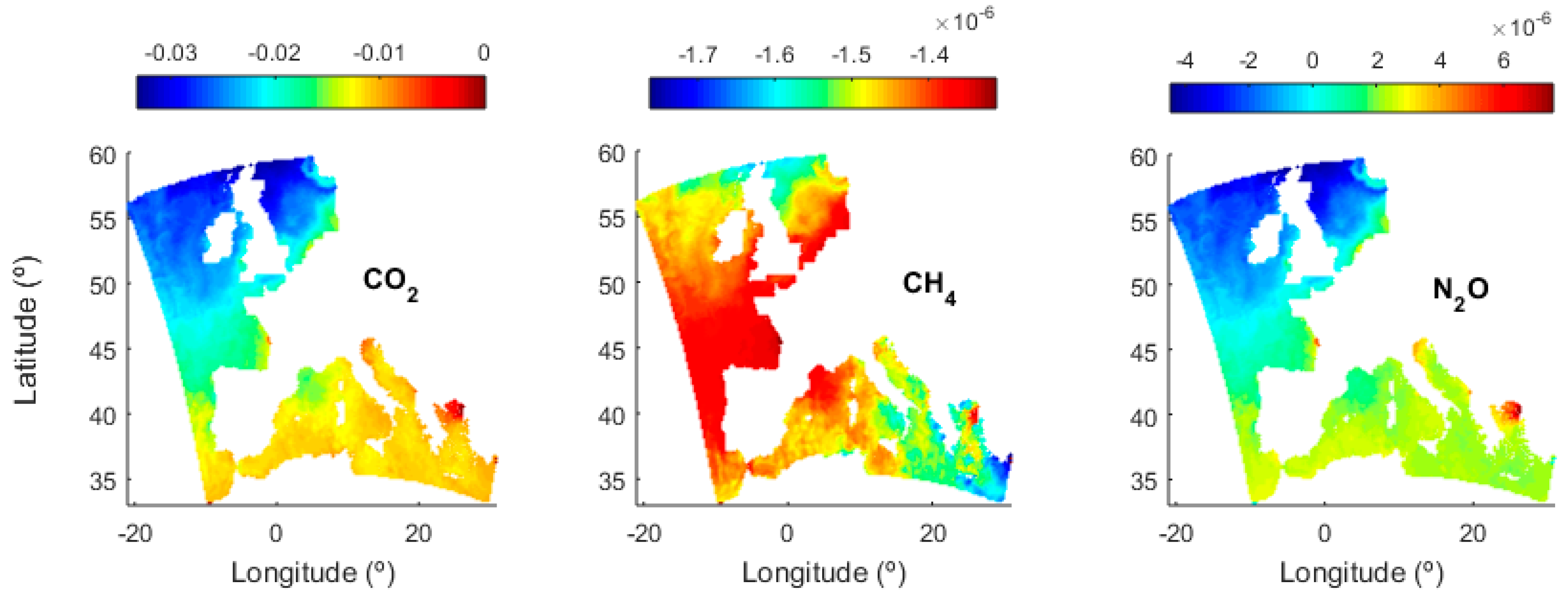
3.1. Solubility Estimates
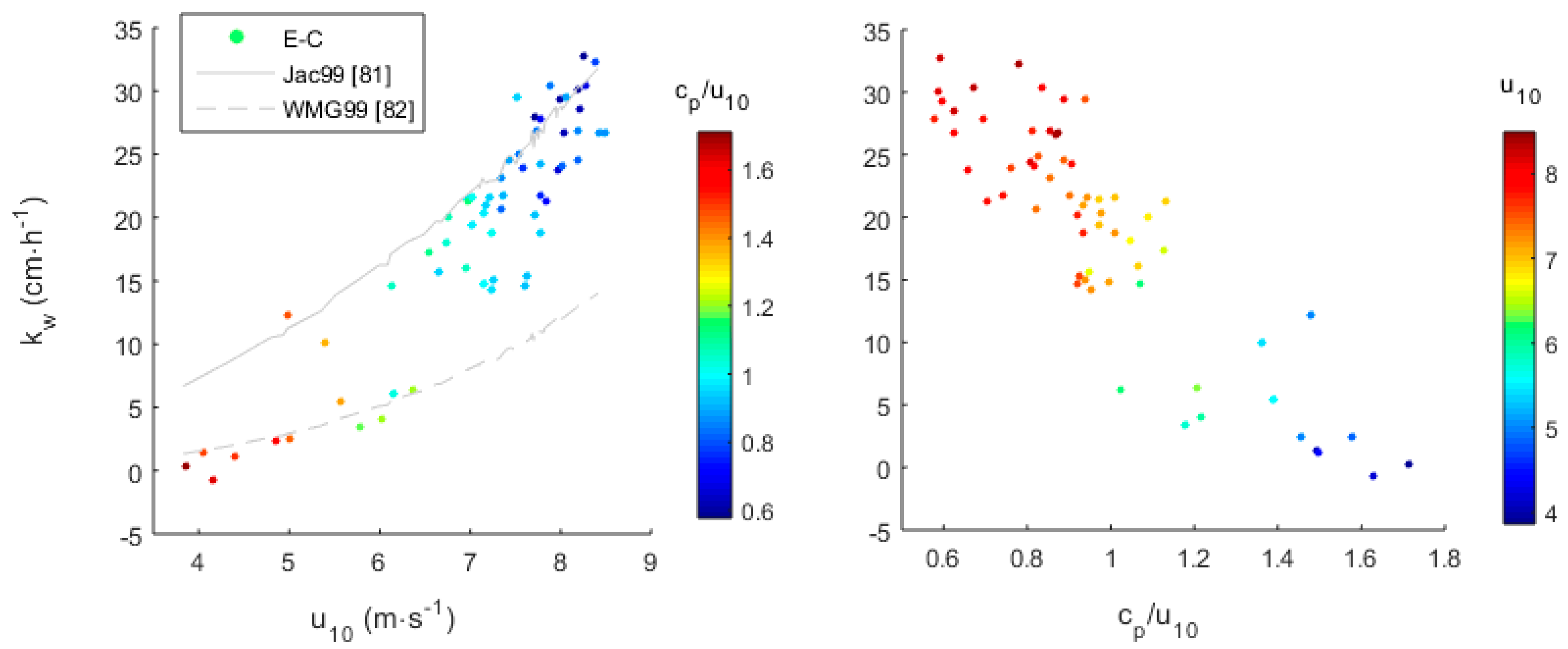
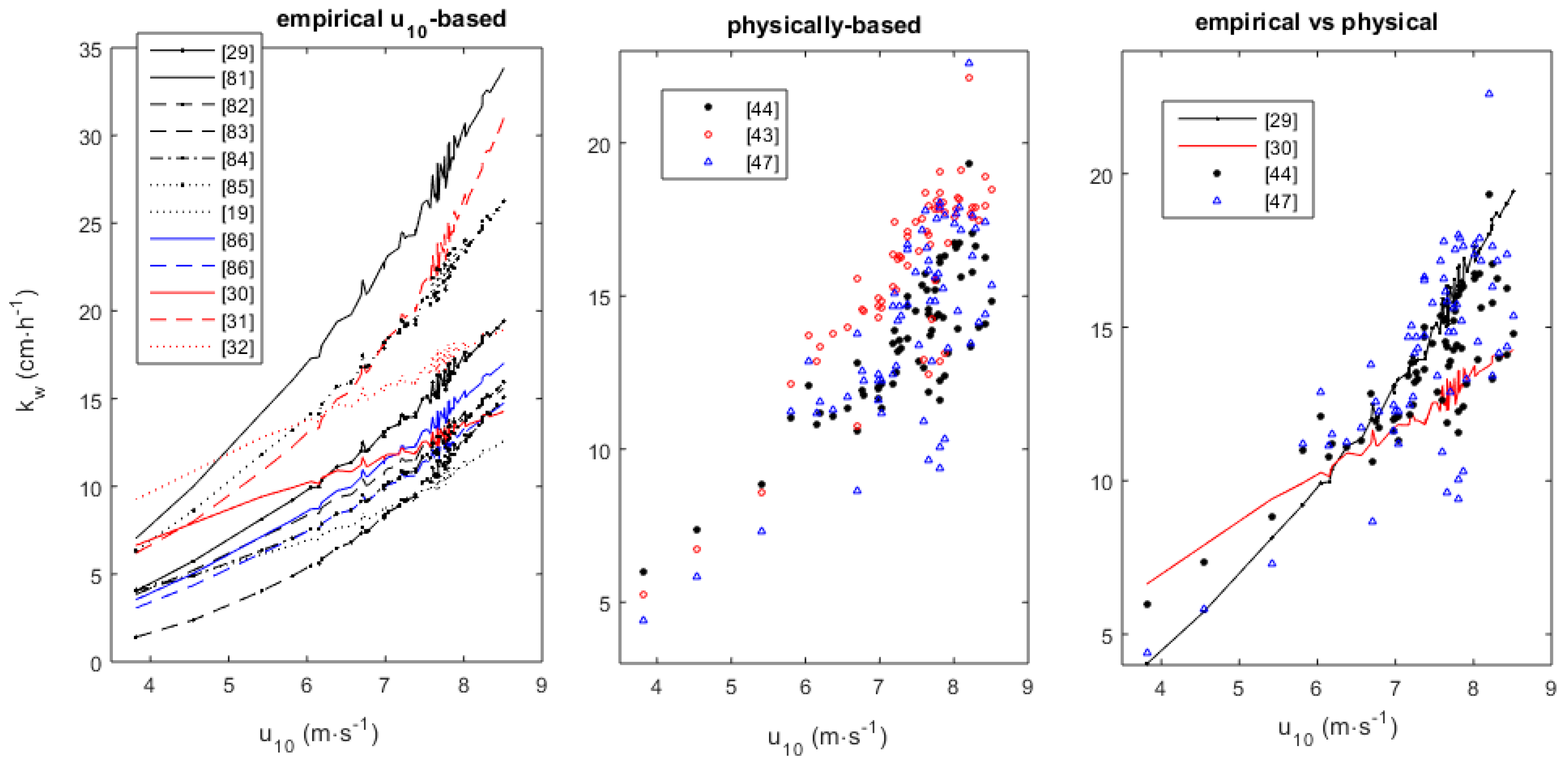
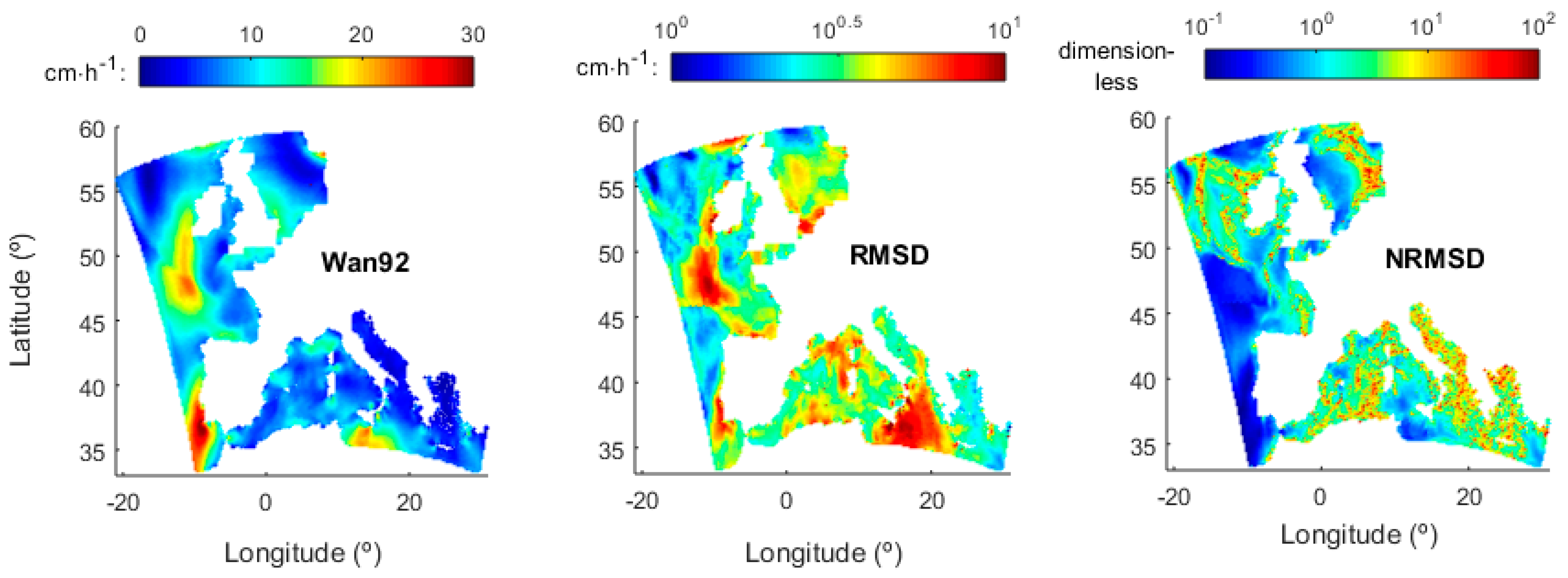
3.2. Transfer Velocity Estimates from Field Data
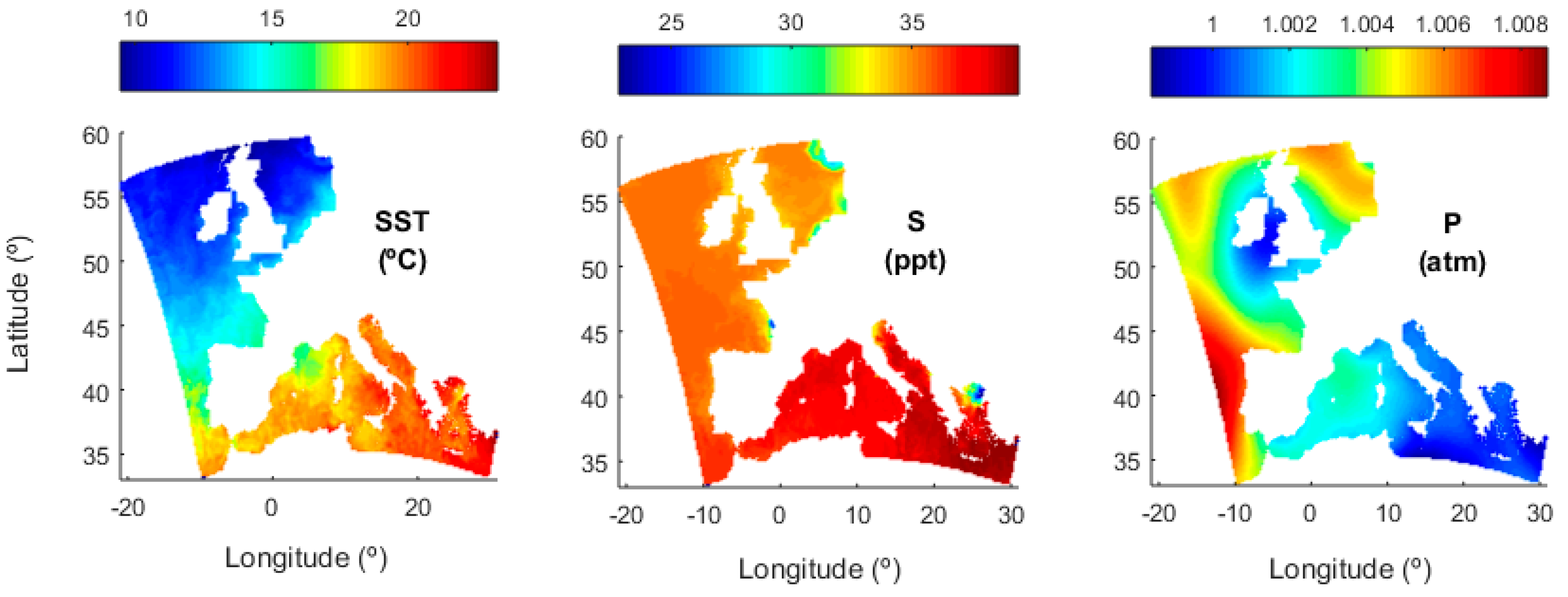
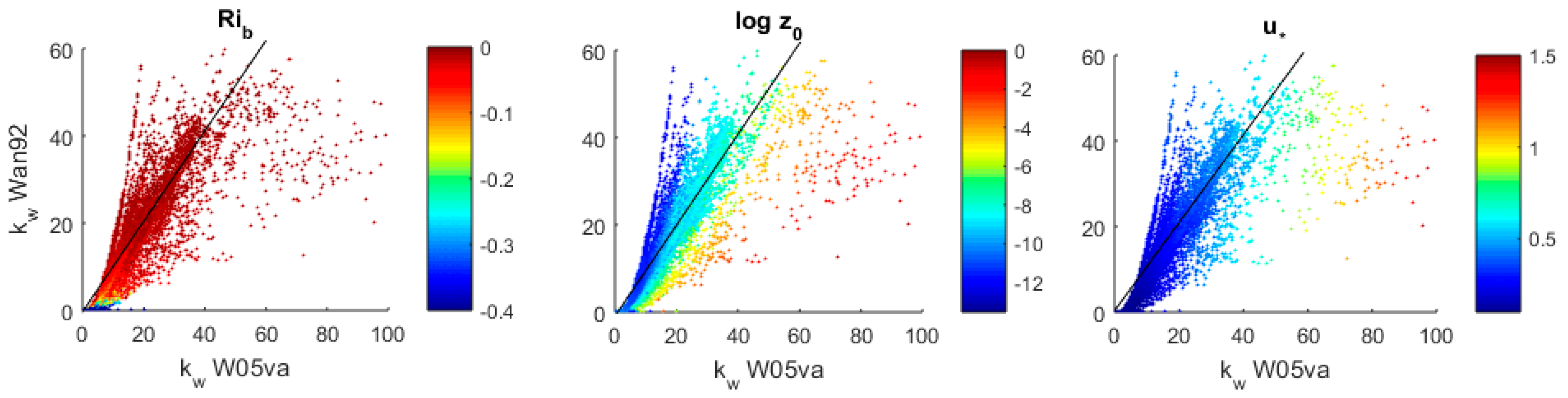
3.3. Transfer Velocity Estimates from Level 4 Data
3.3.1. Atmospheric Stability
3.3.2. Roughness Length
3.3.3. Transfer Velocities
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Takahashi, T.; Sutherland, S.C.; Sweeney, C.; Poisson, A.; Metzl, N.; Tilbrook, B.; Bates, N.; Wanninkhof, R.; Feely, R.A.; Sabine, C.; et al. Global sea-air CO2 flux based on climatological surface ocean pCO2, and seasonal biological and temperature effects. Deep Sea Res. Part II Top. Stud. Oceanogr. 2002, 49, 1601–1622. [Google Scholar] [CrossRef]
- Sarmiento, J.L.; Gruber, N. Ocean Biogeochemical Dynamics; Princeton University Press: Princeton, NJ, USA, 2013; pp. 73–100. [Google Scholar]
- Gypens, N.; Borges, A.V. Increase in dimethylsulfide (DMS) emissions due to eutrophication of coastal waters offsets their reduction due to ocean acidification. Front. Mar. Sci. 2015, 1. [Google Scholar] [CrossRef]
- Menzo, Z.M.; Elliott, S.; Hartin, C.A.; Hoffman, F.M.; Wang, S. Climate change impacts on natural sulfur production: Ocean acidification and community shifts. Atmosphere 2018, 9, 167. [Google Scholar] [CrossRef]
- Borges, A.V. Do we have enough pieces of the jigsaw to integrate CO2 fluxes in the coastal ocean? Estuaries 2005, 28, 3–27. [Google Scholar] [CrossRef]
- Cole, J.J.; Caraco, N.F. Atmospheric exchange of carbon dioxide in a low-wind oligotrophic lake measured by the addition of SF6. Limnol. Oceanogr. 1998, 43, 647–656. [Google Scholar] [CrossRef]
- Cole, J.J.; Caraco, N.F. Carbon in catchments: Connecting terrestrial carbon losses with aquatic metabolism. Mar. Freshw. Res. 2001, 52, 101–110. [Google Scholar] [CrossRef]
- Borges, A.V.; Delille, B.; Frankignoulle, M. Budgeting sinks and sources of CO2 in the coastal ocean: Diversity of ecosystems counts. Geophys. Res. Lett. 2005, 32, L14601. [Google Scholar] [CrossRef]
- Rutgersson, A.; Norman, M.; Schneider, B.; Petterson, H.; Sahlée, E. The annual cycle of carbon dioxide and parameters influencing the air–sea carbon exchange in the Baltic Proper. J. Mar. Syst. 2008, 74, 381–394. [Google Scholar] [CrossRef]
- Harley, J.F.; Carvalho, L.; Dudley, B.; Heal, K.V.; Rees, R.M.; Skiba, U. Spatial and seasonal fluxes of the greenhouse gases N2O, CO2 and CH4 in a UK macrotidal estuary. Estuar. Coast. Shelf Sci. 2015, 153, 62–73. [Google Scholar] [CrossRef]
- Lansø, A.S.; Bendtsen, J.; Christensen, J.H.; Sørensen, L.L.; Chen, H.; Meijer, H.A.J.; Geels, C. Sensitivity of the air–sea CO2 exchange in the Baltic Sea and Danish inner waters to atmospheric short-term variability. Biogeosciences 2015, 12, 2753–2772. [Google Scholar] [CrossRef]
- Dutta, M.K.; Mukherjee, R.; Jana, T.K.; Mukhopadhyay, S.K. Biogeochemical dynamics of exogenous methane in an estuary associated to a mangrove biosphere; The Sundarbans. NE coast of India. Mar. Chem. 2015, 170, 1–10. [Google Scholar] [CrossRef]
- Nevison, C.D.; Weiss, R.F.; Erickson, D.J., III. Global oceanic emissions of nitrous oxide. J. Geophys. Res. 1995, 100, 15809–15820. [Google Scholar] [CrossRef]
- Nevison, C.D.; Lueker, T.J.; Weiss, R.F. Quantifying the nitrous oxide source from coastal upwelling. Glob. Biogeochem. Cycles 2004, 18, GB1018. [Google Scholar] [CrossRef]
- Barnes, J.; Upstill-Goddard, R.C. N2O seasonal distributions and air-sea exchange in UK estuaries: Implications for the tropospheric N2O source from European coastal waters. J. Geophys. Res. 2011, 116, G01006. [Google Scholar] [CrossRef]
- Smith, S.V.; Hollibaugh, J.T. Coastal metabolism and the oceanic organic carbon balance. Rev. Geophys. 1993, 31, 75–89. [Google Scholar] [CrossRef]
- Liss, P.S.; Slater, P.G. Flux of gases across the air-sea interface. Nature 1974, 247, 181–184. [Google Scholar] [CrossRef]
- Upstill-Goddard, R.C. Air-sea gas exchange in the coastal zone. Estuar. Coast. Shelf Sci. 2006, 70, 388–404. [Google Scholar] [CrossRef]
- Wanninkhof, R.; Asher, W.E.; Ho, D.T.; Sweeney, C.S.; McGillis, W.R. Advances in quantifying air-sea gas exchange and environmental forcing. Annu. Rev. Mar. Sci. 2009, 1, 213–244. [Google Scholar] [CrossRef] [PubMed]
- Johnson, M.T. A numerical scheme to calculate temperature and salinity dependent air-water transfer velocities for any gas. Ocean Sci. 2010, 6, 913–932. [Google Scholar] [CrossRef]
- Vieira, V.M.N.C.S.; Martins, F.; Silva, J.; Santos, R. Numerical tools to estimate the flux of a gas across the air–water interface and assess the heterogeneity of its forcing functions. Ocean Sci. 2013, 9, 355–375. [Google Scholar] [CrossRef]
- Vieira, V.; Sahlée, E.; Jurus, P.; Clementi, E.; Pettersson, H.; Mateus, M. Improving estimates of atmosphere-ocean greenhouse gas fluxes for Earth-System modelling. In ESA SP, Proceedings of the Living Planet Symposium, Prague, Czeck Republic, 9–13 May 2016; European Space Agency: Paris, France, 2016; Volume 740. [Google Scholar]
- Weiss, R.F. Carbon dioxide in water and seawater: The solubility of a non-ideal gas. Mar. Chem. 1974, 2, 203–215. [Google Scholar] [CrossRef]
- Weiss, R.F.; Price, B.A. Nitrous oxide solubility in water and seawater. Mar. Chem. 1980, 8, 347–359. [Google Scholar] [CrossRef]
- Mackay, D.; Shiu, W.Y. A critical review of Henry’s law constants of environmental interest. J. Phys. Chem. Ref. Data 1981, 10, 1175–1197. [Google Scholar] [CrossRef]
- Copin-Montegut, C. A new formula for the effect of temperature on the partial pressure of CO2 in seawater. Mar. Chem. 1988, 25, 29–37. [Google Scholar] [CrossRef]
- Sander, R. Compilation of Henry’s law constants (Version 4.0) for water as solvent. Atmos. Chem. Phys. 2015, 15, 4399–4981. [Google Scholar] [CrossRef]
- Frew, N.M.; Bock, E.J.; Schimpf, U.; Hara, T.; Haubecker, H.; Edson, J.B.; McGillis, W.R.; Nelson, R.K.; McKenna, S.P.; Uz, B.M.; et al. Air-sea gas transfer: Its dependence on wind stress, small-scale roughness, and surface films. J. Geophys. Res. 2004, 109, C08S17. [Google Scholar] [CrossRef]
- Wanninkhof, R. Relationship between wind speed and gas exchange over the ocean. J. Geophys. Res. 1992, 97, 7373–7382. [Google Scholar] [CrossRef]
- Carini, S.; Weston, N.; Hopkinson, C.; Tucker, J.; Giblin, A.; Vallino, J. Gas exchange rates in the Parker River estuary, Massachusetts. Biol. Bull. 1996, 191, 333–334. [Google Scholar] [CrossRef] [PubMed]
- Raymond, P.A.; Cole, J.J. Gas exchange in rivers and estuaries: Choosing a gas transfer velocity. Estuaries 2001, 24, 312–317. [Google Scholar] [CrossRef]
- Borges, A.V.; Vanderborght, J.P.; Schiettecatte, L.S.; Gazeau, F.; Ferron-Smith, S.; Delille, B.; Frankignoulle, M. Variability of the Gas Transfer Velocity of CO2 in a Macrotidal Estuary (the Scheldt). Estuaries 2004, 27, 593–603. [Google Scholar] [CrossRef]
- Soloviev, A.V.; Schlüssel, P. Parameterization of the temperature difference across the cool skin of the ocean and of the air–ocean gas transfer on the basis of modelling surface renewal. J. Phys. Oceanogr. 1994, 24, 1339–1346. [Google Scholar] [CrossRef]
- Brunke, M.A.; Zeng, X.; Misra, V.; Beljaars, A. Integration of a prognostic sea surface skin temperature scheme into weather and climate models. J. Geophys. Res. 2008, 113, D21117. [Google Scholar] [CrossRef]
- Soloviev, A.; Schlüssel, P. Evolution of cool skin and direct air-sea gas transfer coefficient during daytime. Bound. Layer Meteorol. 1996, 77, 45–68. [Google Scholar] [CrossRef]
- Soloviev, A.V.; Lukas, R. Observation of spatial variability of diurnal thermocline and rain-formed halocline in the western Pacific warm pool. J. Phys. Oceanogr. 1996, 26, 2529–2538. [Google Scholar] [CrossRef]
- Fairall, C.W.; Bradley, E.F.; Godfrey, J.S.; Wick, G.A.; Edson, J.B.; Young, G.S. Cool-skin and warm-layer effects on sea surface temperature. J. Geophys. Res. 1996, 101, 1295–1308. [Google Scholar] [CrossRef]
- Zeng, X.; Beljaars, A. A prognostic scheme of sea surface skin temperature for modelling and data assimilation. Geophys. Res. Lett. 2005, 32, L14605. [Google Scholar] [CrossRef]
- Grachev, A.A.; Fairall, C.W. Dependence of the Monin–Obukhov Stability Parameter on the Bulk Richardson Number over the Ocean. J. Appl. Meteorol. 1997, 36, 406–414. [Google Scholar] [CrossRef]
- Fairall, C.W.; Hare, J.E.; Edson, J.B.; McGillis, W. Parameterization and micrometerological measurements of air-sea gas transfer. Bound. Layer Meteorol. 2000, 96, 63–105. [Google Scholar] [CrossRef]
- Asher, W.E.; Farley, P.J. Phase-Doppler anemometer measurement of bubble concentrations in laboratory-simulated breaking waves. J. Geophys. Res. 1995, 100, 7045–7056. [Google Scholar] [CrossRef]
- Woolf, D.K. Bubbles and their role in gas exchange. In The Sea Surface and Global Change; Duce, R.A., Liss, P.S., Eds.; Cambridge University Press: New York, NY, USA, 1997; pp. 173–205. [Google Scholar]
- Zhao, D.; Toba, Y.; Suzuki, Y.; Komori, S. Effect of wind waves on air-sea gas exchange: Proposal of an overall CO2 transfer velocity formula as a function of breaking-wave parameter. Tellus B Chem. Phys. Meteorol. 2003, 55, 478–487. [Google Scholar] [CrossRef]
- Woolf, D.K. Parameterization of gas transfer velocities and sea state-dependent wave breaking. Tellus B Chem. Phys. Meteorol. 2005, 57, 87–94. [Google Scholar] [CrossRef]
- Zhang, W.; Perrie, W.; Vagle, S. Impacts of winter storms on air-sea gas exchange. Geophys. Res. Lett. 2006, 33, L14803. [Google Scholar] [CrossRef]
- Jeffery, C.; Robinson, I.; Woolf, D. Tuning a physically-based model of the air-sea gas transfer velocity. Ocean Model. 2010, 31, 28–35. [Google Scholar] [CrossRef]
- Zhao, D.; Xie, L. A practical bi-parameter formula of gas transfer velocity depending on wave states. J. Oceanogr. 2010, 66, 663–671. [Google Scholar] [CrossRef]
- Goddijn-Murphy, L.; Woolf, D.K.; Callaghan, A.H. Parameterizations and algorithms for oceanic whitecap coverage. J. Phys. Oceanogr. 2011, 41, 742–756. [Google Scholar] [CrossRef]
- Shuiqing, L.; Dongliang, Z. Gas transfer velocity in the presence of wave breaking. Tellus B Chem. Phys. Meteorol. 2016, 68, 27034. [Google Scholar] [CrossRef]
- Gutiérrez-Loza, L.; Ocampo-Torres, F.J.; Nava, H.G. The effect of breaking waves on CO2 air-sea fluxes in the coastal zone. Bound. Layer Meteorol. 2018. [Google Scholar] [CrossRef]
- Clayson, C.A.; Fairall, C.W.; Curry, J.A. Evaluation of turbulent fluxes at the ocean surface using surface renewal theory. J. Geophys. Res. 1996, 101, 28503–28513. [Google Scholar] [CrossRef]
- Bock, E.J.; Edson, J.B.; Frew, N.M.; Hara, T.; Haussecker, H.; Jähne, B.; McGillis, W.R.; McKenna, S.P.; Nelson, R.K.; Schimpf, U.; et al. Overview of the CoOP experiment: Physical and chemical measurements parameterizing air-sea heat exchange. In Gas Transfer at Water Surfaces; Donelan, M.A., Drennan, W.M., Saltzman, E.S., Wanninkhof, R., Eds.; AGU: Washington, DC, USA, 2002; pp. 39–44. [Google Scholar]
- Zappa, C.J.; Asher, W.E.; Jessup, A.T.; Klinke, J.; Long, S.R. Microbreaking and the enhancement of air-water transfer velocity. J. Geophys. Res. Oceans 2004, 109. [Google Scholar] [CrossRef]
- Soloviev, A.; Donelan, M.; Graber, H.; Haus, B.; Schlüssel, P. An approach to estimation of near-surface turbulence and CO2 transfer velocity from remote sensing data. J. Mar. Syst. 2007, 66, 182–194. [Google Scholar] [CrossRef]
- Turney, D.E.; Banerjee, S. Air-water gas transfer and near-surface motions. J. Fluid Mech. 2013, 733, 588–624. [Google Scholar] [CrossRef]
- Wang, B.; Liao, Q.; Fillingham, J.; Bootsma, H.A. On the coefficients of small eddy and surface divergence models for the air-water gas transfer velocity. J. Geophys. Res. Oceans 2015, 120. [Google Scholar] [CrossRef]
- Bigdeli, A.; Hara, T.; Loose, B.; Nguyen, A.T. Wave attenuation and gas exchange velocity in marginal sea ice zone. J. Geophys. Res. Oceans 2018, 123. [Google Scholar] [CrossRef]
- Frew, N.M.; Nelson, R.K.; McGillis, W.R.; Edson, J.B.; Bock, E.J.; Hara, T. Spatial variations in surface micro-layer surfactants and their role in modulating air-sea exchange. In Gas Transfer at Water Surfaces; Donelan, M.A., Drennan, W.M., Saltzman, E.S., Wanninkhof, R., Eds.; AGU: Washington, DC, USA, 2002; pp. 153–159. [Google Scholar]
- McKenna, S.P.; McGillis, W.R. The role of free-surface turbulence and surfactants in air-water gas transfer. Int. J. Heat Mass Transf. 2004, 47, 539–553. [Google Scholar] [CrossRef]
- Pereira, R.; Schneider-Zapp, K.; Upstill-Goddard, R.C. Surfactant control of gas transfer velocity along an offshore coastal transect: Results from a laboratory gas exchange tank. Biogeosciences 2016, 13, 3981–3989. [Google Scholar] [CrossRef]
- Ho, D.T.; Bliven, L.F.; Wanninkhof, R. The effect of rain on air-water gas exchange. Tellus B Chem. Phys. Meteorol. 1997, 49, 149–158. [Google Scholar] [CrossRef]
- Ho, D.T.; Asher, W.E.; Bliven, L.F.; Schlosser, P.; Gordan, E.L. On mechanisms of rain-induced air-water gas exchange. J. Geophys. Res. 2000, 105, 24045–24057. [Google Scholar] [CrossRef]
- Frost, T.; Upstill-Goddard, R.C. Meteorological controls of gas exchange at a small English lake. Limnol. Oceanogr. 2002, 47, 1165–1174. [Google Scholar] [CrossRef]
- Zappa, C.J.; Ho, D.T.; McGillis, W.R.; Banner, M.L.; Dacey, J.W.H.; Bliven, L.F.; Ma, B.; Nystuen, J. Rain-induced turbulence and air-sea gas transfer. J. Geophys. Res. Oceans 2009, 114. [Google Scholar] [CrossRef]
- Zappa, C.J.; Asher, W.E.; Jessup, A.T.; Klinke, J.; Long, S.R. Effect of microscale wave breaking on air-water gas transfer. In Gas Transfer at Water Surfaces; Donelan, M.A., Drennan, W.M., Saltzman, E.S., Wanninkhof, R., Eds.; AGU: Washington, DC, USA, 2002; pp. 23–29. [Google Scholar]
- Jähne, B.; Munnich, K.O.; Bosinger, R.; Dutzi, A.; Huber, W.; Libner, P. On the parameters influencing air-water gas exchange. J. Geophys. Res. 1987, 92, 1937–1949. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988; pp. 151–195. [Google Scholar]
- Taylor, P.K.; Yelland, M.J. The dependence of sea surface roughness on the height and steepness of the waves. J. Phys. Oceanogr. 2001, 31, 572–590. [Google Scholar] [CrossRef]
- Fairall, C.W.; Bradley, E.F.; Hare, J.E.; Grachev, A.A.; Edson, J.B. Bulk parameterization of air-sea fluxes: Updates and verification for the COARE algorithm. J. Clim. 2003, 16, 571–591. [Google Scholar] [CrossRef]
- Smith, S.D.; Anderson, R.J.; Oost, W.A.; Kraan, C.; Maat, N.; DeCosmo, J.; Katsaros, K.B.; Davidson, K.L.; Bumke, K.; Hasse, L.; et al. Sea surface wind stress and drag coefficients: The HEXOS results. Bound. Layer Meteorol. 1992, 60, 109–142. [Google Scholar] [CrossRef]
- Johnson, H.K.; Hoejstrup, J.; Vested, H.J.; Larsen, S.E. Dependence of sea surface roughness on wind waves. J. Phys. Oceanogr. 1998, 28, 1702–1716. [Google Scholar] [CrossRef]
- Lange, B.; Johnson, H.K.; Larsen, S.; Hojstrup, J.; Kofoed-Hansen, H.; Yelland, M.J. On detection of a wave age dependency for the sea surface roughness. J. Phys. Oceanogr. 2004, 34, 1441–1458. [Google Scholar] [CrossRef]
- Hwang, P. Drag coefficient, dynamic roughness and reference wind speed. J. Oceanogr. 2005, 61, 399–413. [Google Scholar] [CrossRef]
- Pan, Y.; Sha, W.; Zhu, S.; Ge, S. A new parameterization for sea surface aerodynamic roughness. Prog. Nat. Sci. 2008, 18, 1365–1373. [Google Scholar] [CrossRef]
- Lee, H.N. Improvement of surface flux calculations in the atmospheric surface layer. J. Appl. Meteorol. 1997, 36, 1416–1423. [Google Scholar] [CrossRef]
- Högström, U.; Sahlée, E.; Drennan, W.M.; Kahma, K.K.; Smedman, A.-S.; Johansson, C.; Pettersson, H.; Rutgersson, A.; Tuomi, L.; Zhang, F.; et al. Momentum fluxes and wind gradients in the marine boundary layer—A multi-platform study. Boreal Environ. Res. 2008, 13, 475–502. [Google Scholar]
- Donelan, M.A.; Drennan, W.M.; Katsaros, K.B. The air-sea momentum flux in conditions of wind sea and swell. J. Phys. Oceanogr. 1997, 27, 2087–2099. [Google Scholar] [CrossRef]
- Webb, E.K.; Pearman, G.I.; Leuning, R. Correction of flux measurements for density effects due to heat and water vapour transfer. Quart. J. R. Meteorol. Soc. 1980, 106, 85–100. [Google Scholar] [CrossRef]
- Clementi, E.; Oddo, P.; Korres, G.; Drudi, M.; Pinardi, N. Coupled wave-ocean modelling system in the Mediterranean Sea. In Proceedings of the 13th International Workshop on Wave Hindcasting, Banff, AB, Canada, 27 October–1 November 2013. [Google Scholar]
- EPA United States Environmental Protection Agency. Climate Change Indicators in the United States—Atmospheric Concentrations of Greenhouse Gases. Available online: https://www.epa.gov/climate-indicators/climate-change-indicators-atmospheric-concentrations-greenhouse-gases (accessed on 29 April 2018).
- Jacobs, C.M.J.; Kohsiek, W.; Oost, W.A. Air–sea fluxes and transfer velocity of CO2 over the North Sea: Results from ASGAMAGE. Tellus B Chem. Phys. Meteorol. 1999, 51, 629–641. [Google Scholar] [CrossRef]
- Wanninkhof, R.; McGillis, W.R. A cubic relationship between air-sea CO2 exchange and wind speed. Geophys. Res. Lett. 1999, 26, 1889–1892. [Google Scholar] [CrossRef]
- Nightingale, P.D.; Malin, G.; Law, C.S.; Watson, A.J.; Liss, P.S.; Liddicoat, M.I.; Boutin, J.; Upstill-Goddard, R.C. In Situ evaluation of air-sea gas exchange parameterizations using novel conservative and volatile tracers. Glob. Biogeochem. Cycles 2000, 14, 373–387. [Google Scholar] [CrossRef]
- McGillis, W.R.; Edson, J.B.; Ware, J.D.; Dacey, J.W.H.; Hare, J.E.; Fairall, C.W.; Wanninkhof, R. Carbon dioxide flux techniques performed during GasEx-98. Mar. Chem. 2001, 75, 267–280. [Google Scholar] [CrossRef]
- Weiss, A.; Kuss, J.; Peters, G.; Schneider, B. Evaluating transfer velocity-wind speed relationship using a long-term series of direct eddy correlation CO2 flux measurements. J. Mar. Syst. 2007, 66, 130–139. [Google Scholar] [CrossRef]
- Ho, D.T.; Law, C.S.; Smith, M.J.; Schlosser, P.; Harvey, M.; Hill, P. Measurements of air-sea gas exchange at high wind speeds in the Southern Ocean: Implications for global parameterizations. Geophys. Res. Lett. 2006, 33, L16611. [Google Scholar] [CrossRef]
- Mackay, D.; Yeun, A.T.K. Mass transfer coefficient correlations for volatilization of organic solutes from water. Environ. Sci. Technol. 1983, 17, 211–217. [Google Scholar] [CrossRef] [PubMed]
- Jackson, D.L.; Wick, G.A.; Hare, J.E. A comparison of satellite-derived carbon dioxide transfer velocities from a physically based model with GasEx cruise observations. J. Geophys. Res. 2012, 117, G00F13. [Google Scholar] [CrossRef]
- Wanninkhof, R.; Knox, M. Chemical enhancement of CO2 exchange in natural waters. Limnol. Oceanogr. 1996, 41, 689–697. [Google Scholar] [CrossRef]
- Bade, D.L.; Cole, J.J. Impact of chemically enhanced diffusion on dissolved inorganic carbon stable isotopes in a fertilized lake. J. Geophys. Res. 2006, 111, C01014. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vieira, V.M.N.C.S.; Jurus, P.; Clementi, E.; Mateus, M. The FuGas 2.3 Framework for Atmosphere–Ocean Coupling: Comparing Algorithms for the Estimation of Solubilities and Gas Fluxes. Atmosphere 2018, 9, 310. https://doi.org/10.3390/atmos9080310
Vieira VMNCS, Jurus P, Clementi E, Mateus M. The FuGas 2.3 Framework for Atmosphere–Ocean Coupling: Comparing Algorithms for the Estimation of Solubilities and Gas Fluxes. Atmosphere. 2018; 9(8):310. https://doi.org/10.3390/atmos9080310
Chicago/Turabian StyleVieira, Vasco M. N. C. S., Pavel Jurus, Emanuela Clementi, and Marcos Mateus. 2018. "The FuGas 2.3 Framework for Atmosphere–Ocean Coupling: Comparing Algorithms for the Estimation of Solubilities and Gas Fluxes" Atmosphere 9, no. 8: 310. https://doi.org/10.3390/atmos9080310
APA StyleVieira, V. M. N. C. S., Jurus, P., Clementi, E., & Mateus, M. (2018). The FuGas 2.3 Framework for Atmosphere–Ocean Coupling: Comparing Algorithms for the Estimation of Solubilities and Gas Fluxes. Atmosphere, 9(8), 310. https://doi.org/10.3390/atmos9080310






