A Mechanism of the Interdecadal Changes of the Global Low-Frequency Oscillation
Abstract
1. Introduction
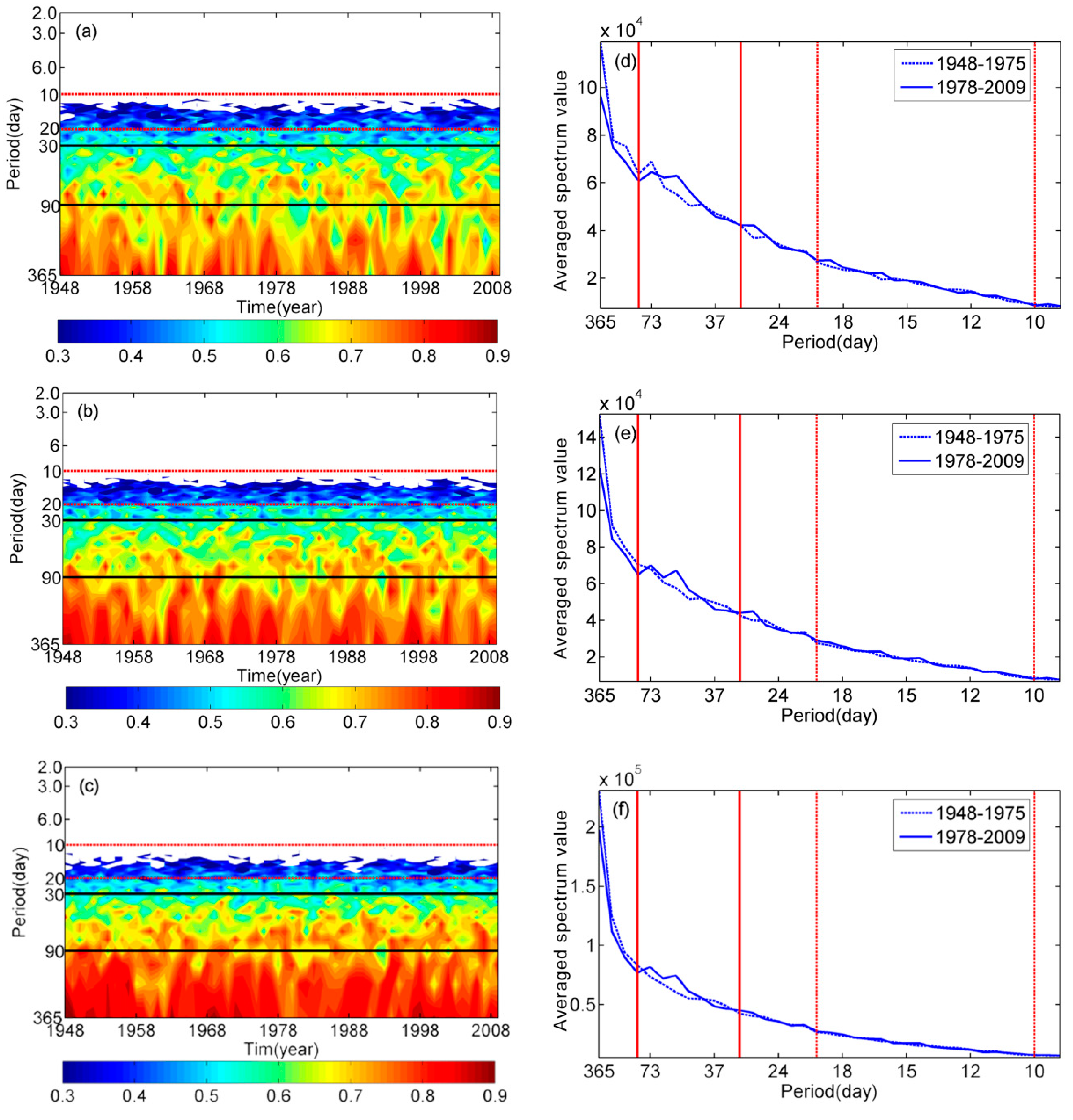
2. Observed Interdecadal Changes of the Global Low-Frequency Oscillation
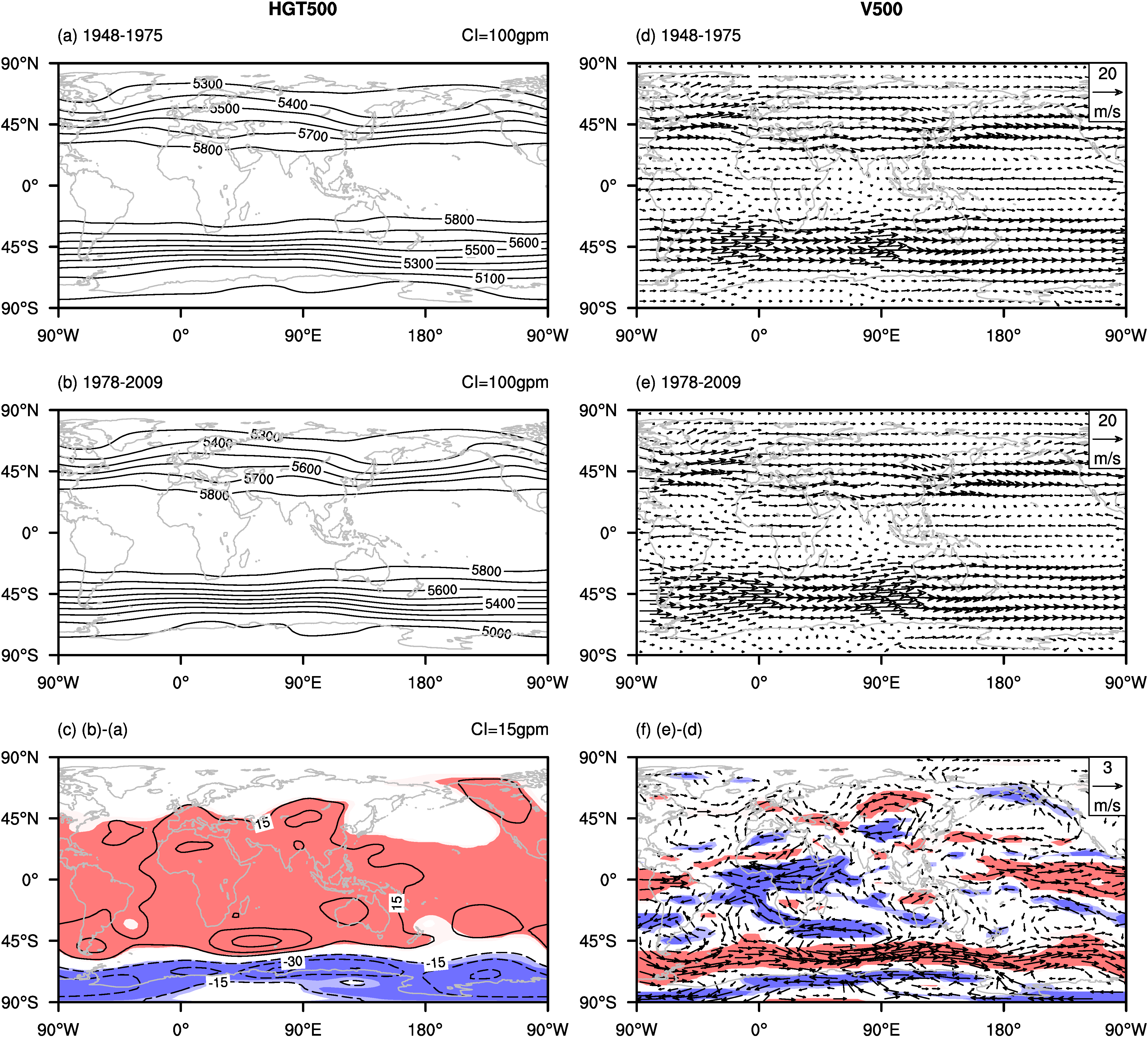
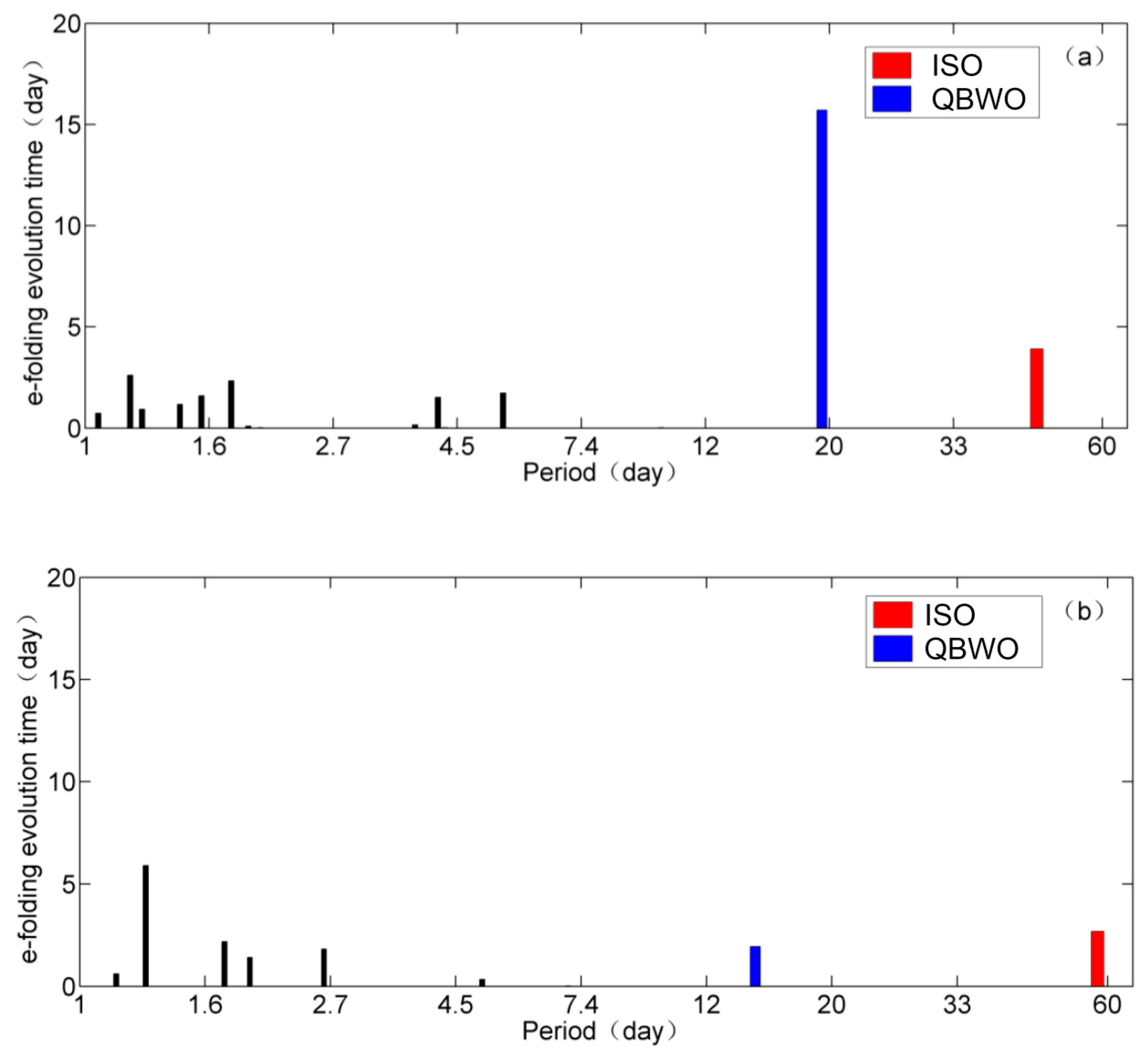
3. Possible Mechanism
4. Summary and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mao, J.Y.; Sun, Z.; Wu, G.X. 20–50-day oscillation of summer Yangtze rainfall in response to intraseasonal variations in the subtropical high over the western North Pacific and South China Sea. Clim. Dyn. 2010, 34, 747–761. [Google Scholar] [CrossRef]
- He, J.H.; Lin, H.; Wu, Z.W. Another look at influences of the Madden-Julian Oscillation on the wintertime East Asian weather. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Lu, R.Y.; Dong, H.L.; Su, Q.; Ding, H. The 30–60-day intraseasonal oscillations over the subtropical western North Pacific during the summer of 1998. Adv. Atmos. Sci. 2014, 31, 1–7. [Google Scholar] [CrossRef]
- Madden, R.A.; Julian, P.R. Description of Global-Scale Circulation Cells in the Tropics with a 40–50 Day Period. J. Atmos. Sci. 1972, 29, 1109–1123. [Google Scholar] [CrossRef]
- Madden, R.A.; Julian, P.R. Detection of a 40–50 Day Oscillation in the Zonal Wind in the Tropical Pacific. J. Atmos. Sci. 1971, 28, 702–708. [Google Scholar] [CrossRef]
- Murakami, M. Analysis of Summer Monsoon Fluctuations over India. J. Meteorol. Soc. Jpn. 1976, 54, 15–31. [Google Scholar] [CrossRef]
- Krishnamurti, T.N.; Bhalme, H.N. Oscillations of a Monsoon System. Part I. Observational Aspects. J. Atmos. Sci. 1976, 33, 1937–1954. [Google Scholar] [CrossRef]
- Ghil, M.; Mo, K. Intraseasonal Oscillations in the Global Atmosphere. Part I: Northern Hemisphere and Tropics. J. Atmos. Sci. 1991, 48, 752–779. [Google Scholar] [CrossRef]
- Madden, R.A.; Julian, P.R. Observations of the 40–50-day tropical oscillation—A review. Mon. Weather Rev. 1994, 122, 814–837. [Google Scholar] [CrossRef]
- Goswami, B.N.; Mohan, R.S.A. Intraseasonal oscillations and interannual variability of the Indian summer monsoon. J. Clim. 2001, 14, 1180–1198. [Google Scholar] [CrossRef]
- Foltz, G.R.; McPhaden, M.J. The 30–70 day oscillations in the tropical Atlantic. Geophys. Res. Lett. 2004, 31, 1–4. [Google Scholar] [CrossRef]
- Wang, B.; Webster, P.; Kikuchi, K.; Yasunari, T.; Qi, Y. Boreal summer quasi-monthly oscillation in the global tropics. Clim. Dyn. 2006, 27, 661–675. [Google Scholar] [CrossRef]
- Wen, M.; Li, T.; Zhang, R.; Qi, Y.J. Structure and Origin of the Quasi-Biweekly Oscillation over the Tropical Indian Ocean in Boreal Spring. J. Atmos. Sci. 2010, 67, 1965–1982. [Google Scholar] [CrossRef]
- Wen, M.; Zhang, R.H. Quasi-Biweekly Oscillation of the Convection around Sumatra and Low-Level Tropical Circulation in Boreal Spring. Mon. Weather Rev. 2008, 136, 189–205. [Google Scholar] [CrossRef]
- Sobel, A.H.; Maloney, E.D.; Bellon, G.; Frierson, D.M. The role of surface heat fluxes in tropical intraseasonal oscillations. Nat. Geosci. 2008, 1, 653–657. [Google Scholar] [CrossRef]
- Cao, J.; Wen, Z.P.; Chang, Y.L.; Li, X.R. Wavelet analysis of the convectively-coupled equatorial waves. Sci. China Earth Sci. 2012, 55, 675–684. [Google Scholar] [CrossRef]
- Wang, L.; Kodera, K.; Chen, W. Observed triggering of tropical convection by a cold surge: Implications for MJO initiation. Q. J. R. Meteorol. Soc. 2012, 138, 1740–1750. [Google Scholar] [CrossRef]
- Zhang, C.D. Madden-Julian oscillation. Rev. Geophys. 2005, 43, 1–36. [Google Scholar] [CrossRef]
- Li, T.; Wang, B. A review on the western north pacific monsoon: Synoptic-to-interannualvariabilities. Terr. Atmos. Ocean. Sci. 2005, 16, 285–314. [Google Scholar] [CrossRef]
- Ha, K.J.; Heo, K.Y.; Lee, S.S.; Yun, K.S.; Jhun, J.G. Variability in the East Asian monsoon: A review. Meteorol. Appl. 2012, 19, 200–215. [Google Scholar] [CrossRef]
- Lee, J.Y.; Fu, X.H.; Wang, B. Predictability and prediction of the Madden-Julian Oscillation: A review on progress and current status. In The Global Monsoon System: Research and Forecast, 3rd ed.; World Scientific: Singapore, 2017; pp. 147–159. [Google Scholar]
- Wheeler, M.C.; Kim, H.J.; Lee, J.Y.; Gottschalck, J.C. Real-time forecasting of modes of tropical intraseasonal variability: The Madden-Julian and boreal summer intraseasonal oscillations. In The Global Monsoon System: Research and Forecast, 3rd ed.; World Scientific: Singapore, 2017; pp. 131–138. [Google Scholar]
- Li, C.Y. Actions of summer monsoon troughs (ridges) and tropical cyclone over South Asia and moving CISK mode. Sci. Sin. Ser. B 1985, 28, 1197–1206. [Google Scholar] [CrossRef]
- Lau, K.M.; Peng, L. Origin of Low-Frequency (Intraseasonal) Oscillations in the Tropical Atmosphere. Part I: Basic Theory. J. Atmos. Sci. 1987, 44, 950–972. [Google Scholar] [CrossRef]
- Takahashi, M. A Theory of the Slow Phase Speed of the Intraseasonal Oscillation using the Wave-CISK. J. Meteorol. Soc. Jpn. Ser. II 1987, 65, 43–49. [Google Scholar] [CrossRef][Green Version]
- Chang, C.P.; Lim, H. Kelvin wave-CISK: A possible mechanism for the 30–50 day oscillations. J. Atmos. Sci. 1988, 45, 1709–1720. [Google Scholar] [CrossRef]
- Li, C.Y. Dynamical study on 30–50 day oscillation in the tropical atmosphere outside Equator. Chin. J. Atmos. Sci. 1990, 14, 83–92. (In Chinese) [Google Scholar] [CrossRef]
- Emanuel, K.A. An Air-Sea Interaction Model of Intraseasonal Oscillations in the Tropics. J. Atmos. Sci. 1987, 44, 2324–2340. [Google Scholar] [CrossRef]
- Neelin, J.D.; Held, I.M.; Cook, K.H. Evaporation-Wind Feedback and Low-Frequency Variability in the Tropical Atmosphere. J. Atmos. Sci. 1987, 44, 2341–2348. [Google Scholar] [CrossRef]
- Li, C.Y.; Xiao, Z.N. The 30–60 day oscillations in the global atmosphere excited by warming in the equatorial eastern Pacific. Chin. Sci. Bull. 1992, 37, 484–489. [Google Scholar]
- Li, W.B.; Ji, L.R. Mechanisms of the atmospheric Teleconnection Associated with the Activity of the Asian Summer Monsoon Part II: Optimal Forcing and Atmospheric Responses. Chin. J. Atmos. Sci. 1999, 23, 571–580. (In Chinese) [Google Scholar] [CrossRef]
- Li, W.B.; Ji, L.R. Mechanisms of the atmospheric teleconnection associated with activity of the Asian summer monsoon part I: Analyses of the normal modes and the finite Time unstable singular vectors. Chin. J. Atmos. Sci. 1999, 23, 477–486. (In Chinese) [Google Scholar] [CrossRef]
- Li, C.Y.; Liao, H.Q. Behaviour of coupled modes in a simple nonlinear air-sea interaction model. Adv. Atmos. Sci. 1996, 13, 183–195. [Google Scholar] [CrossRef]
- Wang, B.; Xie, X.S. Coupled modes of the warm pool climate system. Part I: The role of air-sea interaction in maintaining Madden-Julian oscillation. J. Clim. 1998, 11, 2116–2135. [Google Scholar] [CrossRef]
- Goswami, P.; Mathew, V. A Mechanism of Scale Selection in Tropical Circulation at Observed Intraseasonal Frequencies. J. Atmos. Sci. 1994, 51, 3155–3166. [Google Scholar] [CrossRef][Green Version]
- Chatterjee, P.; Goswami, B.N. Structure, genesis and scale selection of the tropical quasi-biweekly mode. Q. J. R. Meteorol. Soc. 2004, 130, 1171–1194. [Google Scholar] [CrossRef]
- Frederiksen, J.S.; Frederiksen, C.S. Monsoon disturbances, intraseasonal oscillations, teleconnection patterns, blocking, and storm tracks of the global atmosphere during January 1979: Linear theory. J. Atmos. Sci. 1993, 50, 1349–1372. [Google Scholar] [CrossRef]
- Frederiksen, J.S. A Unified Three-Dimensional Instability Theory of the Onset of Blocking and Cyclogenesis. II. Teleconnection Patterns. J. Atmos. Sci. 1983, 40, 2593–2609. [Google Scholar] [CrossRef]
- Frederiksen, J.S. A Unified Three-Dimensional Instability Theory of the Onset of Blocking and Cyclogenesis. J. Atmos. Sci. 1982, 39, 969–982. [Google Scholar] [CrossRef]
- Simmons, A.J.; Wallace, J.M.; Branstator, G.W. Barotropic Wave Propagation and Instability, and Atmospheric Teleconnection Patterns. J. Atmos. Sci. 1983, 40, 1363–1392. [Google Scholar] [CrossRef]
- Yang, D.S.; Cao, W.Z. A Possible Dynamic Mechanism of the Atmospheric 30–60 Day Period Oscillation in the Extratropical Latitude. Chin. J. Atmos. Sci. 1995, 19, 209–218. (In Chinese) [Google Scholar] [CrossRef]
- Li, C.Y.; Wu, P.L.; Zhang, Q. Some characters of the 30–60 day oscillation in the atmospheric circulation in North Hemisphere. Sci. China Ser. B Chem. Life Sci. Earth Sci. 1990, 20, 764–774. (In Chinese) [Google Scholar] [CrossRef]
- Li, C.Y.; Zhang, Q. Global atmospheric low-frequency teleconnection. Prog. Nat. Sci. Int. 1991, 1, 447–452. [Google Scholar]
- Li, C.Y.; Cao, W.Z.; Li, G.L. Effect of basic flow on triggering the instability of atmospheric intraseasonal oscillation in mid-high latitudes. Sci. China Ser. B Chem. Life Sci. Earth Sci. 1995, 25, 978–985. (In Chinese) [Google Scholar] [CrossRef]
- Chen, T.C.; Chen, J.M. The 10–20-Day Mode of the 1979 Indian Monsoon: Its Relation with the Time Variation of Monsoon Rainfall. Mon. Weather Rev. 1993, 121, 2465–2482. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Hurrell, J.W. Decadal atmosphere-ocean variations in the Pacific. Clim. Dyn. 1994, 9, 303–319. [Google Scholar] [CrossRef]
- Wang, L.; Chen, W.; Huang, R.H. Changes in the variability of north pacific oscillation around 1975/1976 and its relationship with East Asian winter climate. J. Geophys. Res. 2007, 112, 1–13. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Yu, Y.Q.; He, J.H.; Zhang, Z.G. Characteristics and numerical simulation of the tropical intraseasonal oscillations under global warming. Acta Meteorol. Sin. 2006, 64, 723–733. [Google Scholar]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
- Cao, J.; You, Y.L. New method for low order spectral model and its application. Appl. Math. Mech. 2006, 27, 477–484. [Google Scholar] [CrossRef]
- Li, C.Y. Excitation of the atmospheric unstable modes (chapter 4.3). In An Introduction to Climate Dynamics, 2nd ed.; China Meteorological Press: Beijing, China, 2000; pp. 136–149. (In Chinese) [Google Scholar]
- Wang, L.; Xu, P.Q.; Chen, W.; Liu, Y. Interdecadal variations of the Silk Road pattern. J. Clim. 2017, 30, 9915–9932. [Google Scholar] [CrossRef]
- Wang, L.; Chen, W. The East Asian winter monsoon: Re-amplification in the mid-2000s. Chin. Sci. Bull. 2014, 59, 430–436. [Google Scholar] [CrossRef]
- Byshev, V.I.; Neiman, V.G.; Anisimov, M.V.; Gusev, A.V.; Serykh, I.V.; Sidorova, A.N.; Figurkin, A.L.; Anisimov, I.M. Multi-decadal oscillations of the ocean active upper-layer heat content. Pure Appl. Geophys. 2017, 174, 2863–2878. [Google Scholar] [CrossRef]
- Ponomarev, V.I.; Dmitrieva, E.V.; Shkorba, S.P.; Karnaukhov, A.A. Change of the global climate region at the turn of the XX–XXI centuries. Vestnik MGTU 2018, 21, 160–169. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Wang, L.; Yang, S.; Chen, W.; Huangfu, J.L. Decadal changes of the wintertime tropical tropospheric temperature and their influences on the extratropical climate. Chin. Sci. Bull. 2016, 61, 737–744. [Google Scholar] [CrossRef]
- Gu, W.; Wang, L.; Hu, Z.Z.; Hu, K.M.; Li, Y. Interannual variations of the first rainy season precipitation over south China. J. Clim. 2017, 31, 623–640. [Google Scholar] [CrossRef]
- Zhang, R.H. Changes in East Asian summer monsoon and summer rainfall over eastern China during recent decades. Chin. Sci. Bull. 2015, 60, 1222–1224. [Google Scholar] [CrossRef]
| ISO | QBWO | |||||
|---|---|---|---|---|---|---|
| 850 hPa | 500 hPa | 200 hPa | 850 hPa | 500 hPa | 200 hPa | |
| 1948–1975 | 59,193 | 61,710 | 67,835 | 23,294 | 24,181 | 22,865 |
| 1978–2009 | 61,348 | 64,397 | 73,209 | 24,438 | 25,318 | 23,616 |
| confidence level of difference | 90% | 96% | 99.6% | 92% | 93% | 83% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, R.; Chen, Q.; Liu, Y.; Wang, L. A Mechanism of the Interdecadal Changes of the Global Low-Frequency Oscillation. Atmosphere 2018, 9, 292. https://doi.org/10.3390/atmos9080292
Yang R, Chen Q, Liu Y, Wang L. A Mechanism of the Interdecadal Changes of the Global Low-Frequency Oscillation. Atmosphere. 2018; 9(8):292. https://doi.org/10.3390/atmos9080292
Chicago/Turabian StyleYang, Ruowen, Quanliang Chen, Yuyun Liu, and Lin Wang. 2018. "A Mechanism of the Interdecadal Changes of the Global Low-Frequency Oscillation" Atmosphere 9, no. 8: 292. https://doi.org/10.3390/atmos9080292
APA StyleYang, R., Chen, Q., Liu, Y., & Wang, L. (2018). A Mechanism of the Interdecadal Changes of the Global Low-Frequency Oscillation. Atmosphere, 9(8), 292. https://doi.org/10.3390/atmos9080292






