1. Introduction
Although a natural process in most part of the world, wildland fires represent a constant threat wherever there exists a possible interface with human activities. A large number of tightly-coupled physical phenomena interact in the development of a large wildfire. Temperature increase in the fuel generates pyrolysis gases, the composition of which depends on the vegetation, and which can blaze. The intense heat release can dramatically modify the local meteorology, generating strong local convective motion and fire-induced winds, that in turn modify the fire front dynamics and drive the fire propagation [
1]. To simulate wildland fire, the fire front propagation must be solved at the scale of a few meters to precisely take into account wind, slope, humidity and obstacles (road, rocks). Eventually, fire-atmosphere interactions with the local motions need to be taken into account to properly represent the composition, density, structure and transport of the plume.
Nevertheless, simulating large wildland fires requires choosing between the complexity of the code, data availability, the speed at which the result must be obtained and the computational framework. The variety of models thus ranges from physically-detailed, fire/atmosphere coupled and computationally-intensive (and limited to relatively small fires) models such as FIRETEC [
2], WFDS [
3] or FIRESTAR [
4,
5] to empirical, uncoupled (forced wind field) models such as FARSITE [
6] that are adapted to provide rapid simulation of very large wildfires. As an intermediate trade-off, approaches coupling a 2D-surface fire propagation model with a mesoscale atmospheric model [
7,
8,
9] have shown their ability to capture some of the complex phenomena occurring in large fires while still being adapted to a real-time response.
This last approach is developed in this study, which focuses on testing the ability of these coupled fire-atmosphere models to represent micro-scale atmospheric and fire front effects on a real and large observed fire case. Numerical fire/atmosphere coupling has already undergone numerous studies, starting from the static fire simulations of [
10] to the pioneering works of [
7,
11] where a simplified model of [
12] fire spread was coupled to the atmospheric model of [
13]. More recently, the original Clark/Coen model evolved to the CAWFE model [
14], while efforts at extending the WRF weather forecasting model [
15] have resulted in the WRF/fire module [
8], widely used even at the scale of large fires (several square kilometers [
16,
17,
18,
19]).
A similar system is used here, based on the atmospheric Meso-NH model [
20,
21] interactively coupled with the ForeFire fire spread model [
22]. Specifically, the fire model is different from the [
23] model used in other approaches taking into account the effects of wind and slope through coefficients experimentally fitted to wind values “as if the fire was not there”. Moreover, although large wildfires remain an objective, specific numerical methods were developed so that all phenomena could be simulated at a resolution close to their characteristic scale.
The target case study is decomposed into four nested domains ranging from 2.4-km to 50-m resolution, allowing one to explore the local to the regional impact of a large wildfire in an interactive fire-atmosphere coupling. Fire front is integrated at the scale of thermal transfer (sub-meter), fuel consumption at the resolution of the vegetation database (5 m), local atmosphere and winds at the resolution of the convective structures above the fire front (50 m) and smoke tracer transport at the meso-scale (2 km).
The ForeFire fire front solver [
9,
24] has been developed to enable the use of several propagation models, as well as coupled with nested Meso-NH domains by defining fluxes for all the physical and chemical properties. Coupled with the Meso-NH atmospheric model [
21], it has already been the subject of several investigations on relatively small fires with encouraging results, such as simulating atmospheric feedbacks in agreement with other coupled numerical models [
25], and reproducing vertical wind velocities and temperatures in the range of what was observed during the controlled experiment FireFlux [
26].
The study proposed in this work is devoted to evaluating the ability of this code to scale up to large fires, about a hundred times the size of previous wildfires already simulated, and in extreme fire weather conditions (temperature over 40 degrees, very low air humidity, low to moderate winds). The case study here is the Aullene wildfire that burned more than 2000 ha in less than one day in July 2009. It aims to understand how the fire modifies the dynamical structure of the surrounding atmosphere, by characterizing the turbulence in the near-fire environment.
The second part of the article presents briefly the Meso-NH and ForeFire models, focusing on the way fire fluxes are integrated and coupled between both. The third part is devoted to the presentation of the simulations of the 2009 Aullene fire, and the fourth part validates subjectively the coupled simulation and focuses on the dynamical structure of the plume and the surrounding atmosphere at 50-m horizontal resolution. Elements of computational times are given at the end of this section. Conclusions are drawn in
Section 5.
2. Presentation of the Models and Coupling Methods
The simulation system is composed of two main components: the fire and the atmospheric codes. Both can be considered as solvers of numerous physical processes that are required to provide relevant forecast in a reasonable time. Major differences exist between both models, with the fire system being comparatively highly discontinuous and inhomogeneous, dealing with small scales. A consequence of this is that pertinent numerical methods and algorithms differ for the two models. The fire front solver uses a prognostic front velocity, or Rate Of Spread (ROS) model, that can analytically and directly provide this ROS, given fuel, atmosphere and current front state. These local parameters are interpolated at the front position in the atmospheric model with wind specifically taken as input in the ROS model [
22].
Feedback from the fire to the atmospheric model requires an aggregation of results made at the fire scale, as it will typically be solved at a much finer scale. Fire to atmosphere feedbacks may influence many other parameters, such as surface roughness, albedo and chemistry, but we only consider for the moment the main fields influencing atmosphere dynamics, i.e., water vapor, heat, wind and smoke tracer fluxes.
2.1. Meso-NH Atmospheric Model
The Meso-NH non-hydrostatic atmospheric model [
20,
21] is an open-source research model based on the anelastic assumption, allowing simultaneous simulation of several scales of motion, by an interactive grid-nesting technique. The meteorological variables (temperature, water substances and Turbulent Kinetic Energy (TKE)) and scalar variables (like tracers) are advected with a so-called monotonic piecewise parabolic method [
27] associated with a forward-in-time temporal scheme, while the wind is transported by a fourth order centered scheme associated with the Leap-Frog (LF) temporal scheme. The major asset of the fourth order centered scheme is its good accuracy (effective resolution on the order of 5–6
[
28]) with the LF scheme imposing a strong limit on the time step. Surface parametrizations are performed in the SURFEX model [
29] with the Interactions between Soil, Biosphere, and Atmosphere (ISBA) parameterization [
30] for the vegetation canopy, and integrated in Meso-NH as surface flux boundary conditions at each atmospheric time step.
The grid-nesting of Meso-NH allows the simultaneous running of models of different horizontal resolutions, sharing the same vertical grid. Only the highest resolution nested domain is coupled with the fire simulation, with wind, temperature, water vapor, pressure and scalar tracer exchanged at their common time step.
2.2. Wildfire Propagation
ForeFire is a so-called fire area simulator, with the fire font defined as the contour of the burning area. The main originalities of this code are the numerical method used and the modular and expandable software architecture, written in C++, open source and available at
https://github.com/forefireAPI/. The code can be run standalone, embedded as a software library or coupled with an atmospheric model, all with similar initialization procedures. Moreover, the front propagation is not tied to any particular velocity (ROS) or surface flux (for diagnostic/coupling) models and could be extended with user-defined models.
While several methods may be used to capture fire front evolution (see [
31] for a review of numerical interface tracking and capturing methods), the fire front advance is performed by an interface capturing Lagrangian markers method inspired by [
32] and similar to FarSite [
6,
7,
11,
13]. The specificities of this interface capturing method compared to [
6,
13] are the discrete event temporal scheme (based on a scheduler rather than on regular time steps) and markers’ motion, which are not tied to any underlying grid such as in [
13,
32] or the original Marker And Cell (MAC) method [
33]. A complete description and test of the code may be found in [
24,
34].
The appropriate level of accuracy of the discretization is specified through a maximum distance
d allowed between two consecutive markers and is called the perimeter resolution. A new marker is dynamically added if two markers are farther than
d and deleted if closer than
. The Discrete Event Simulation (DES) time scheme permits one to apply the Courant–Friedrichs–Lewy (CFL) constraint to each segment at each marker update and consequently updating more frequently areas where the interface is the most active (in an approach similar to [
35]). In DES, each simulation element, node, marker or sub-model must compute its optimal local time step and schedule its future update as events in a shared and time-sorted timetable. Simulation is driven by processing the most imminent event, updating an element that may re-schedule a new event.
Scheduling can be seen as the most aggressive automatic time stepping method and requires a time-consuming and relatively complex data structure for time sorting. This feature is therefore unlikely a major computational cost cutter in most multiphase fluid mechanics, as the continuity equation generally prevents the co-existence of wide interface velocity spread. In applications where a large inhomogeneity in the interface velocity field can be observed, such as in wildland fires, optimization may dramatically reduce computational cost as it focuses computation on fast moving elements. Here, front markers are by far the most frequently-updated element, and a key parameter for this integration scheme is the spatial increment that defines the maximum distance by which a marker may travel before being updated and topological checks performed at the marker location.
A high resolution matrix of Arrival Time (AT) is diagnosed from the front advance and used to keep track of the fire history to perform instantaneous surface diagnostics. This arrival time matrix is updated locally, marking the date at which the first marker burned a location using a polygon filling algorithm. The AT matrix resolution requires fixing a physical lower limit, making the hypothesis of a typically minimal propagative front depth . On large domains (tens of km), this two-dimensional matrix may contain millions of points at a typical resolution of m. Nevertheless, as the active burning area is a small fraction of the total domain extension, AT matrices are handled as a sparse matrix that may still be computed efficiently.
2.3. Fire Velocity (ROS) Model
The Balbi [
22] model, like the Rothermel model, can be classified as a quasi-physical model. Its formulation is based on the assumption that the front propagates as a radiating panel in the direction normal to the front. The model verifies that for a specific wind, terrain and fuel configuration, the absorbed energy equals the combustion energy directed toward the unburned fuel. This energy is the sum of a “radiant” part from the flame and a “conductive” part within the fuel layer. The assumption is also made that only a given portion
of the combustion energy is released as radiation because the flame is viewed as a wind tilted radiant panel with an angle
toward the unburned fuel.
A major assumption, also present in the Rothermel model and removed in the model formulation for this study, is that the fire is always traveling at a stationary speed that verifies , meaning that all energy is absorbed within the fuel bed for the computation of , a potential rate of spread. Because of this assumption, front velocity is only dependent on fuel, but not on the instantaneous fire state (previous intensity, front curvature, depth), so it cannot therefore accelerate or go to extinction.
By using the front tracking solver, local front depth
and curvature
are always available as numerical diagnostics of the front allowing one to take into account this instantaneous state of the front. The updated, non-stationary, formulation used in this study is available in [
34].
In a coupled configuration, the wind should be taken at mid-flame height and at the flame location. Flame height is not a direct prognostic variable in the model, and assuming a purely triangular flame of base length over the fuel (with E the fuel height), this mid-height may be roughly approximated with . Wind values that are used to drive the fire at the fire marker location are interpolated from the first grid level. If bilinear interpolation is used on the horizontal plane, vertical interpolation is the subject of several assumptions and parameterization. It is possible to either assume that the wind speed is valid over the whole level height or to interpolate it at the approximated mid-flame height. Both methods are arguable, with tests presenting no large differences between them as the ROS model already imposes little wind effect on slow propagation speed (small, flank or backfiring flames). Moreover, one of the major problems is the triangular flame hypothesis for the height computation and approximations of the surface vertical roughness that can be arguable at the scale at which a vertical approximation may be made. For this study, given the lack of appropriate high resolution data on local vegetation height, vertical wind velocity was not interpolated in large fire configurations in order to reduce overall computational cost.
2.4. Coupling Atmospheric and Wildfire Models
A two-way coupling is assumed between the fire and atmospheric model and performed at each atmospheric time step (typically sub-second). In the fire model, the atmospheric model is handled as one element with a constant update period equal to this atmospheric time step. Surface wind fields are sent to the fire model at the end of each atmospheric time step, while fire fluxes are updated at the start of next step. Two wind fields (start and end steps) are thus available in the fire simulation. Less frequent (typically hours) re-normalization steps are performed in real-cases’ reanalysis to take into account global meteorological forcing (temperature, humidity). Atmospheric grid geometry is also sent to the fire solver at initialization to compute local interpolations at the front position.
A bi-linear interpolation in space and time is performed to deduce the point wind value at each marker location. Forcing the atmospheric model with ground conditions stemming from the fire is simplified by Meso-NH’s ability to handle fluxes’ forcing at the ground level. There is a clear limitation to the level of the combustion process that can be resolved as Meso-NH is not designed for cells smaller than a few meters with combustion handled as a subgrid process.
Computation of the desired fluxes is carried out using a high resolution AT matrix with burning area determined at each atmospheric time step and for each ground atmospheric cell as the difference between the current time t and arrival time of the fire at the location .
Integration of local fluxes is performed by applying a flux model
on all the AT points
contained in an atmospheric cell:
and thus, the resolution of the burning map has to be much higher than the atmospheric one to ensure that averages over each atmospheric ground cell define well-posed boundary conditions forced by the fire on the atmosphere.
Flux models for heat
and water
are models that must provide ground forcing conditions during an atmospheric time step duration given a current time
t and the arrival time of the fire at the location
. While CAWFE and WRF/SFire make use of the BURNUP algorithm from Albini [
36], we approximate the flux models based on numerical studies from [
37]. Fluxes are here represented by a simple analytic gamma function that represents a more intense release at the early combustion stage. The gamma function has the advantage of being easily integrable, and for a total mass/energy
release for a duration
, the flux at the fire location
is given by:
Burning duration
is extrapolated from the [
38] model. Heat and vapor fluxes (resp.
and
) used throughout the domain are computed over the flaming area and for this burning duration. The total amount released during this process is induced from several assumptions. All the water content (
) is assumed to evaporate during the combustion phase. The fraction of radiant energy and combustion efficiency (portion of flaming energy) are assumed to take values
and
, with a total heat release forced at ground level given by
. A passive scalar injection is also set with a constant release of 1 per
in the burning area to act as a smoke tracer.
In the fire front solver, velocity models are user defined as single C++ class files with several already available in the standard distribution for speed (Rothermel, Balbi, isotropic, wind only) and may be extended by adding new classes. For use in a coupled configuration, the code architecture allows the same classes’ definitions for surface flux models for different chemical compounds, heat and vapor. The coupled simulation code was developed originally for ideal simulation cases [
25], extended for use in real cases at different resolutions [
9,
26], with this study the first to present this coupled system for use in large wildfires.
3. Presentation of the Simulation
3.1. Observations of the Fire Case
The Aullene fire occurred on 23 July 2009, lasted five days and burned more than 3000 ha of forest with 2000 ha during the first afternoon. The same day, two other major fires (Peri, Ortolo) occurred, bringing the total burnt area over 6000 ha.
Figure 1 shows the diurnal variation of temperature, relative humidity and wind speed measured at the Sartene weather station located 20 km away from the fire. The hours prior to the fire were characterized by extreme weather conditions with low relative humidity (10%), very high temperatures (more than 40
C) and low to moderate winds (up to 6
).
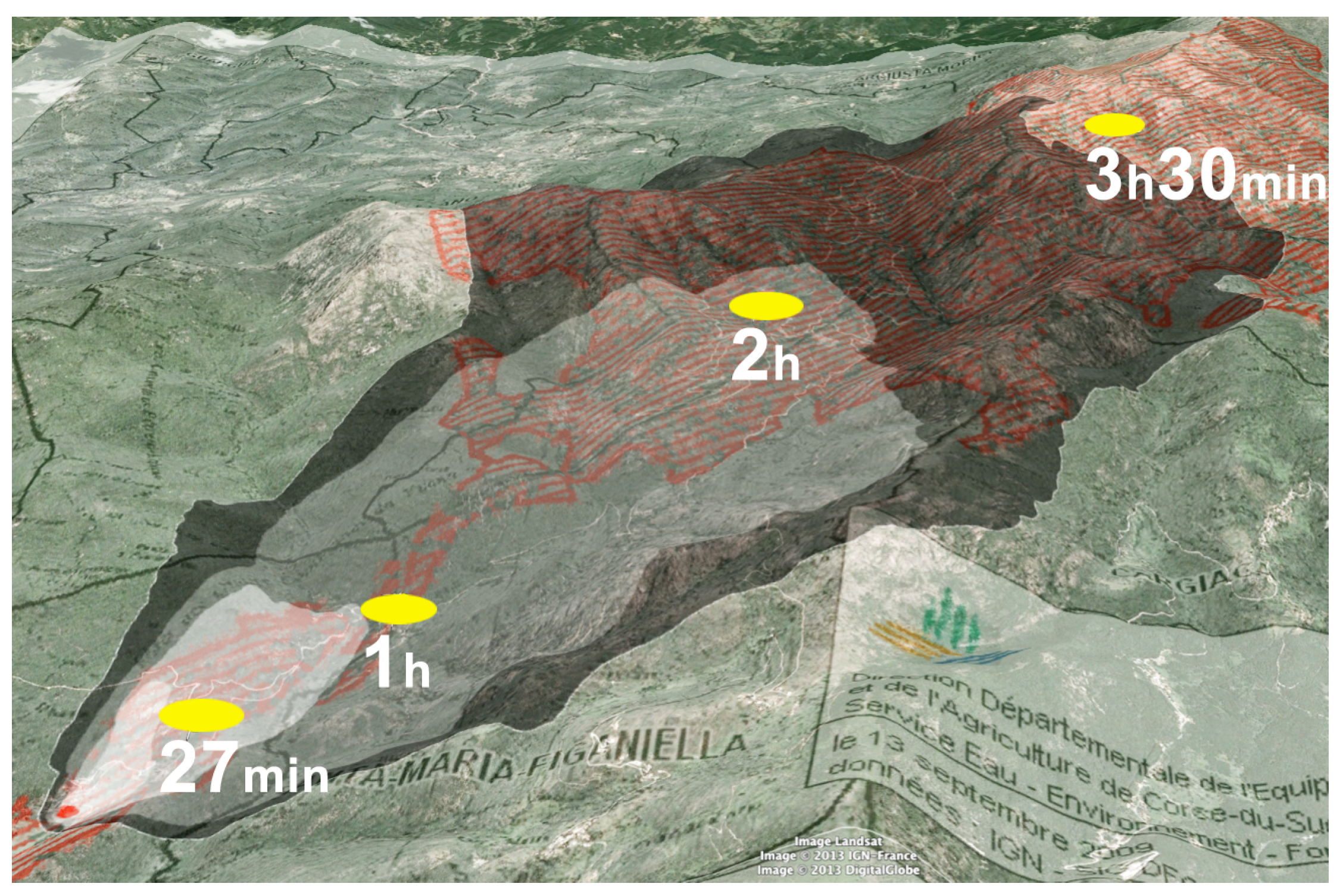
The landscape of the region is typical of the Corsican mountains with a 8 km-wide and 30 km-long valley starting at sea level with elevation rising to more than 2000 m. The fire started at 13:26 UTC and was very active during the first 6 h. Fire fighting actions and an increase in relative humidity slowed down the fire progression at around 19:00 UTC, stopping the propagation at sunset (21:00 UTC). Containment actions handled during the first hour were mainly unsuccessful. Then, during the most active propagation time, all the fire fighting actions were concentrated on the north flanks to prevent the fire from expanding to the next valley.
3.2. Numerical Configuration
In order to resolve the development of the fire/weather system from the fire front to the large-scale atmospheric transport of the fire plume, the two-way nesting capability of the Meso-NH model is applied with four nested domains (
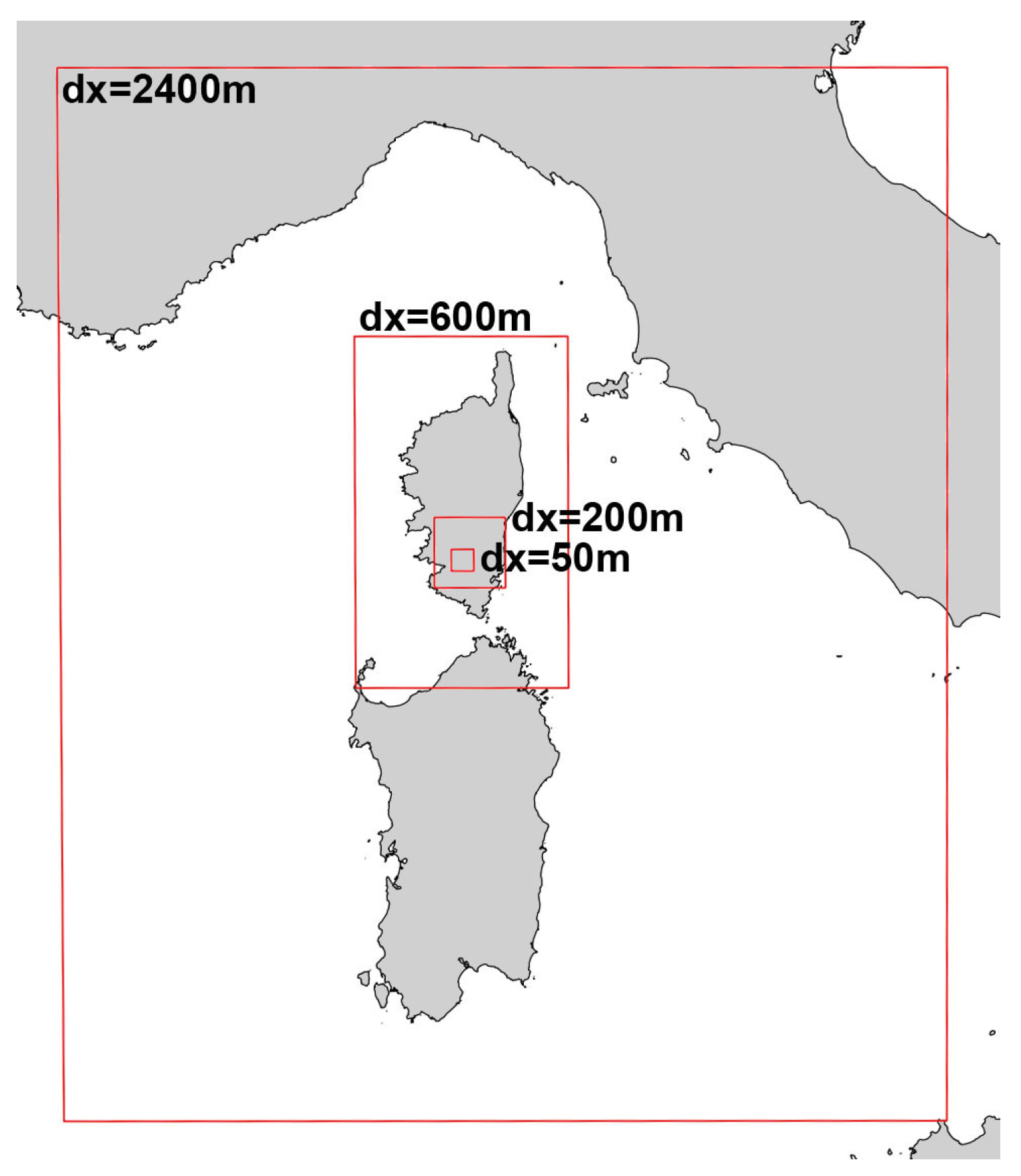
Figure 2). The horizontal grid size is 2400 m for the outer domain covering 600 km × 720 km. The inner computational grids have grid increments of respectively 600, 200 and 50 m, covering a total area of respectively 144 km × 240 km, 48 km × 48 km and 15 km × 15 km for the innermost model. The time step is 12 s for the outermost model and decreases to 6 s, 2 s and 0.5 s for the finer models.
Initial and lateral boundary conditions are provided by the Aladin limited-area model (10-km horizontal resolution) operational at Meteo-France in 2009, with updates of the coupling files every 6 h. The simulation with the coarsest resolution began on 23 July 2009 at 0000 UTC, with a progressive downscaling up to the finest resolution beginning at 1200 UTC.
The vertical resolution is identical for all the nested domains, with 66 levels up to 10 km and a first level above the ground at 10-m height. All the nested models use the one and a half order closure turbulence scheme of [
39] with a prognostic TKE: the three finest resolution domains use the 3D version of the scheme, while the first one only considers the 1D version, neglecting the horizontal turbulent fluxes. In addition, the 200-m and 50-m resolution domains consider the [
40] mixing length, while the first two use the one of [
41]. In the same way, only the coarsest model uses the [
42] mass flux scheme to parametrize the thermals in the atmospheric boundary layer while they are explicitly resolved at a finer scale.
The fire propagation resolution is
m, with perimeter and AT matrix resolution
m. Fire resolutions are illustrated in
Figure 3, which presents the successive scales from the front (markers) to combustion (arrival time matrix), integrated at the horizontal atmospheric resolution to provide fire fluxes forcing to Meso-NH. The resolution
m of the fire propagation model is limited by the actual resolution of the fuel distribution data.
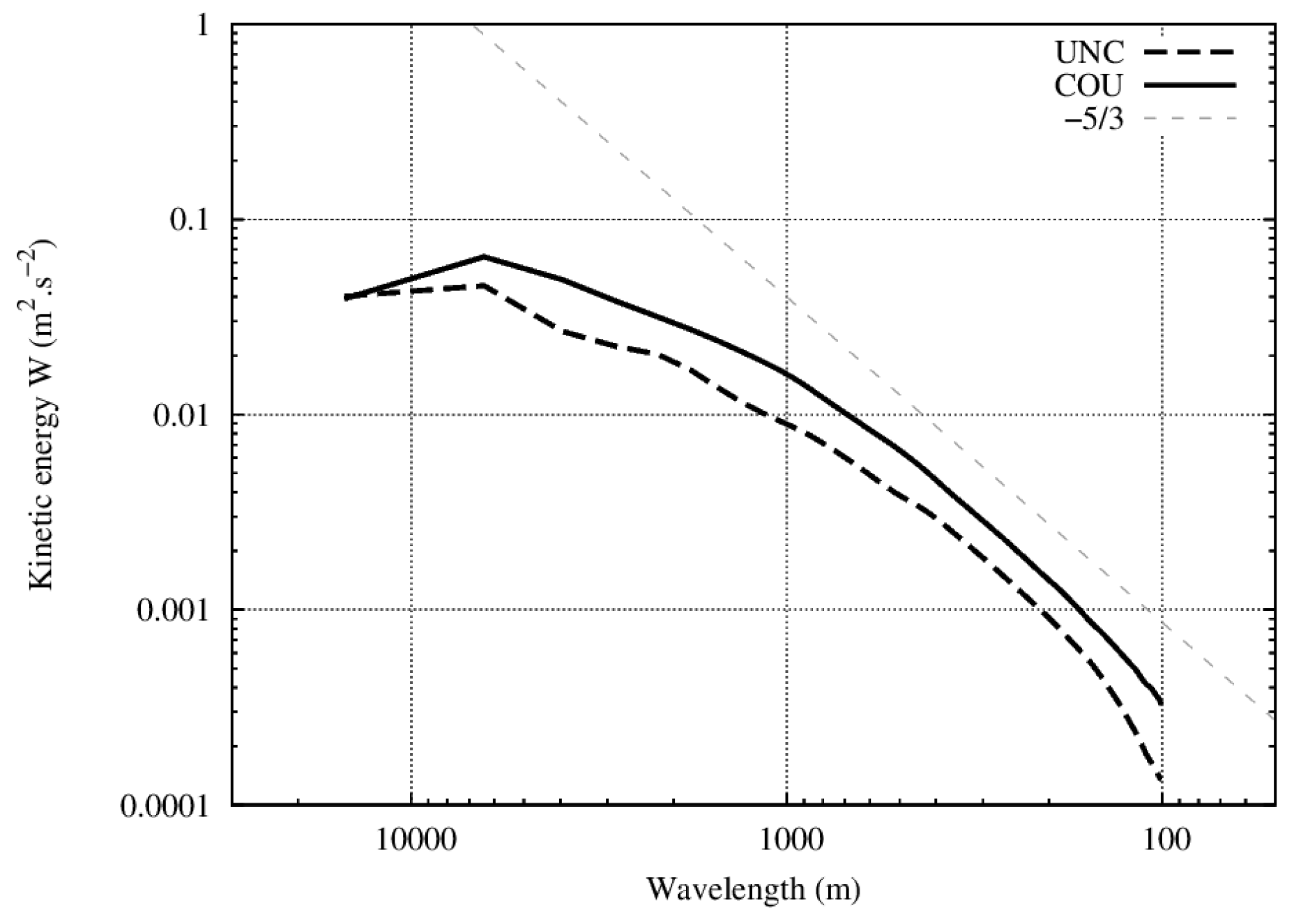
Three different simulations have been run to conduct a sensitivity study of the coupling method. The main simulation is the “coupled” coupling simulation, or “feedback-on”, where the interaction between the atmospheric and fire models is two-way, as described above. An “uncoupled” simulation was run, or “feedback-off”, where the atmospheric winds are provided to the fire model, but the fire model returns nothing to the atmosphere. The third simulation is the “fire-to-atm ” mode where Meso-NH wind fields are not used by ForeFire, so there is no fire-line propagation with the marker method. A pre-computed arrival time matrix is used to compute the fluxes at each atmospheric time step. This matrix is computed using a simulation of the fire with the integration of the modified fuel distribution to represent fire-fighting actions (massive air attack at the flanks and at the fire head around the end of the fire). The “feedback-off” wind field at 14 UTC was selected for this fire-to-atm arrival time matrix as it provided the best fit to match observed fire passing points and final shape. In return, ForeFire provides the modified surface fluxes to Meso-NH. “Feedback-off” simulations can be used if the forecast starts from an already developed fire (with an actual observed burning area), or to investigate a “what-if” scenario of a fire simulated without the overhead of the atmospheric model.
3.3. Data Sources
The fuel layer is derived from the National Forest Inventory and is coupled with data from the IGN BD TOPO
® for road and drainage networks. The Digital Elevation Model (DEM) is extracted from IGN BD ALTI
® 25-m resolution. IFN classes have been grouped according to the methodology developed in [
43] and use the proposed characterization of the vegetation.
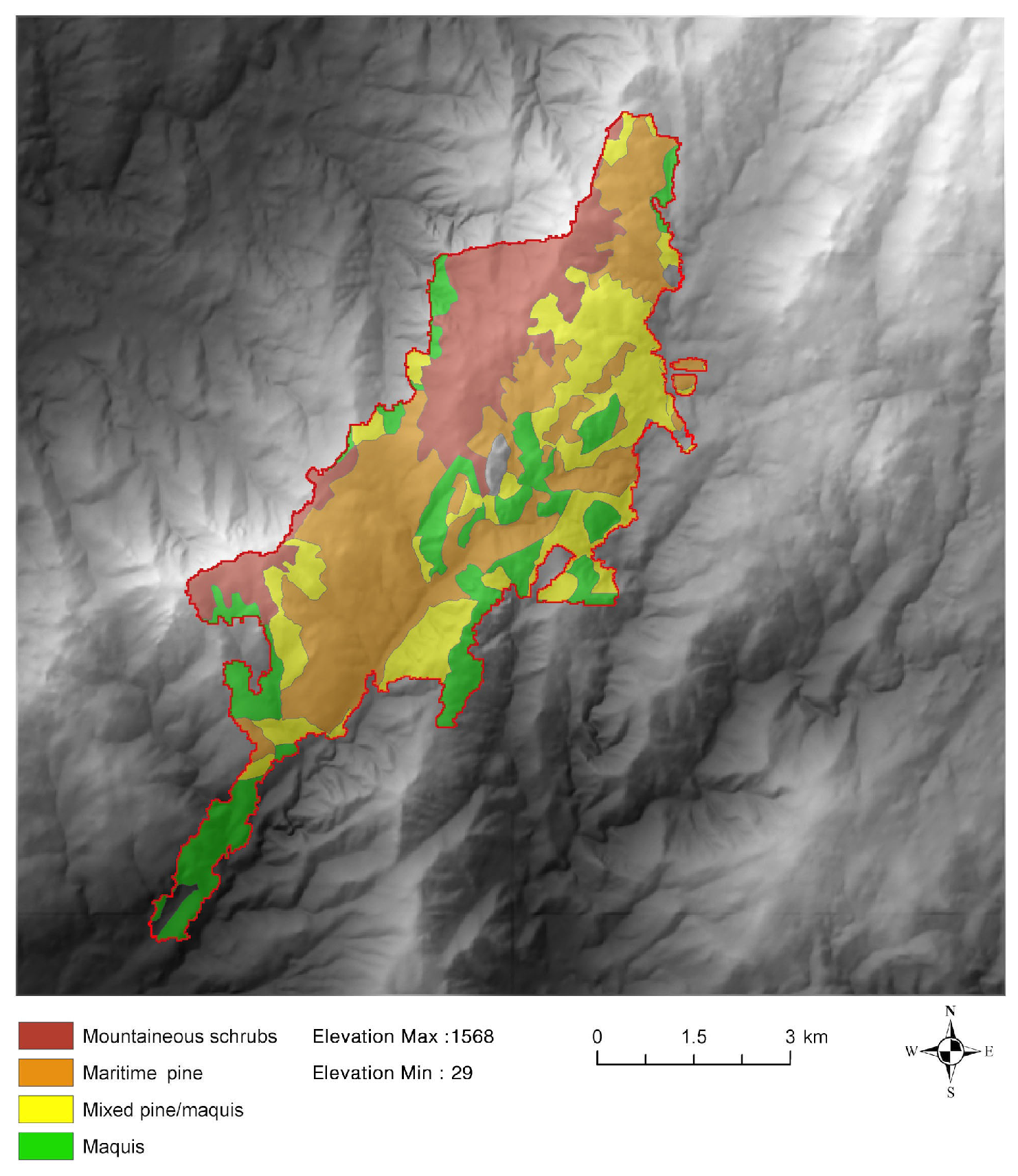
Figure 4 presents the fuel distribution over the final burnt area, with four main classes, as well as small non-burnable area providing fuel breaks. Vegetation heterogeneity, orography or small unreported older fires influence the fire propagation at small scales. These heterogeneities are not accounted for in this work, and the chosen fuel types are taken as the best guesses.
Fuel parameters (mass loading
, height
E (m), moisture content (m) and heat of combustion
) used in the front velocity model for these four major classes are presented in
Table 1. These values correspond to the dead fuel load of relatively small particles (branches with diameters less than
m) that are assumed to drive the flaming fire. Pine and mixed pines’ fuel estimates are equivalent fuel types that were given by foresters in charge of the area. Except from the maquis, where estimates of similar species are available from [
43], it was not possible to match with the foresters any relevant fuel characterization available in the literature. Moisture content was estimated to be very dry with values for the day reported well under 10% for shrubs. The same parameters were used for the fluxes’ models, with only the thin fuel contributing to heat injection, focusing the intense effects on the active fire area. Although the omission of larger fuel particle probably under-evaluates the contribution of the fire, it is consistent with the assumptions of the velocity model.
5. Conclusions
The coupled code Meso NH/ForeFire aims to be able to simulate large wildfires, solving complex fire-induced flow while implementing a high-resolution front advection method. The fire front velocity model can be parametrized with measurable properties of the fuel and is well adapted to coupled simulation, as it uses instantaneous wind speed just over the fire front to calculate the flame angle. The non-parallel version of the code has previously been used to perform simulations of real wildfires with results that qualitatively match observation in terms of fire dynamics [
9] and atmospheric chemistry [
53].
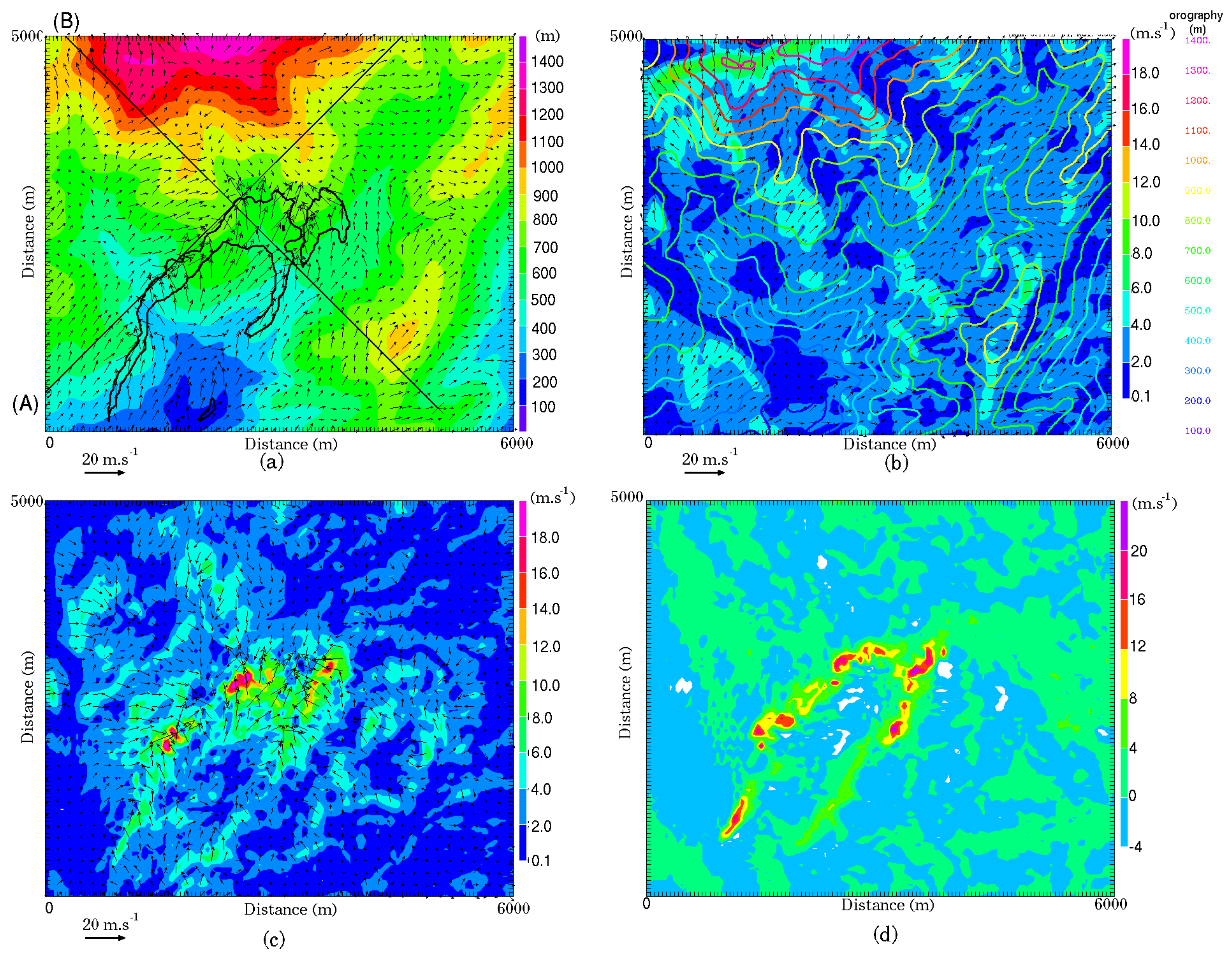
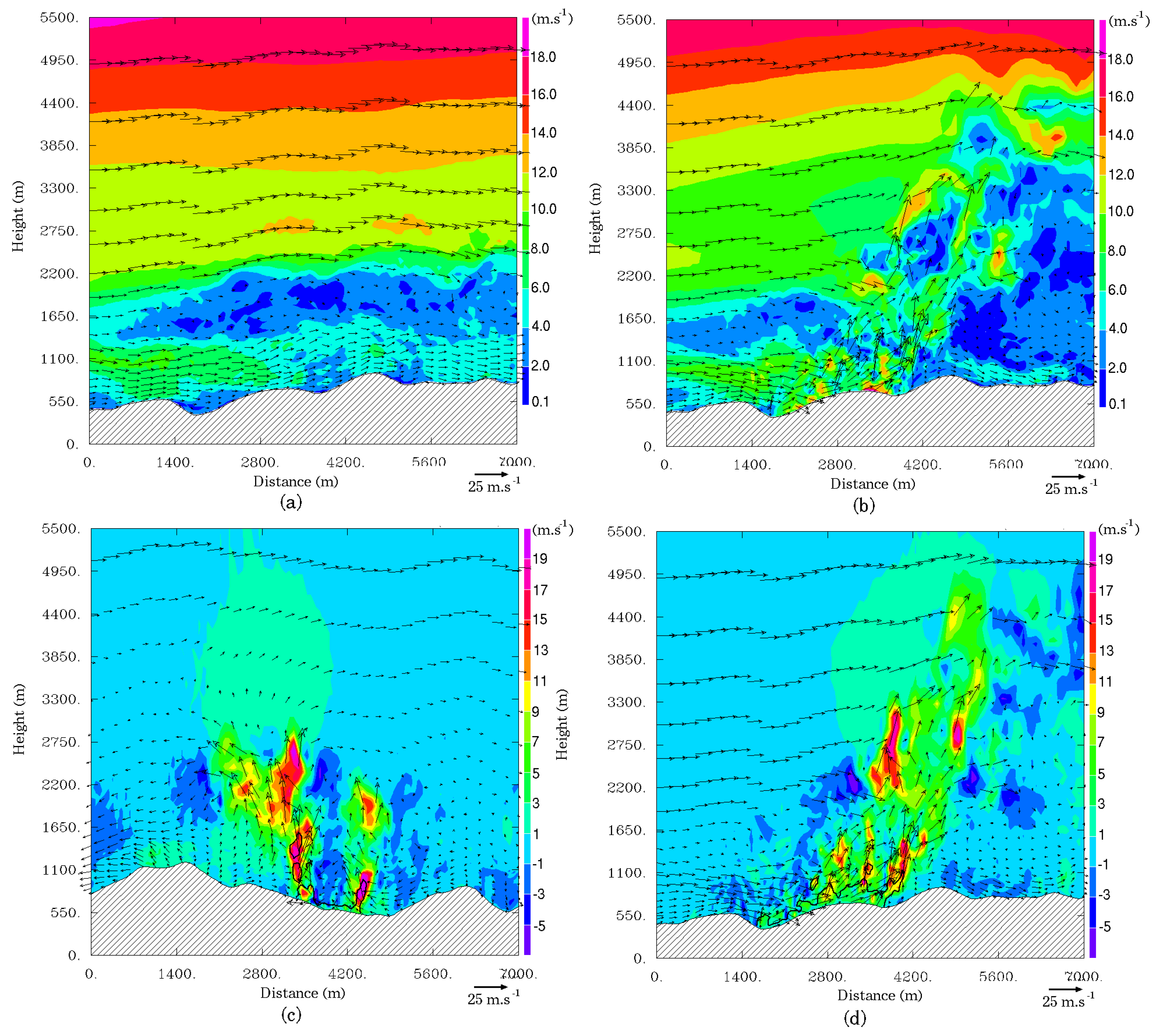
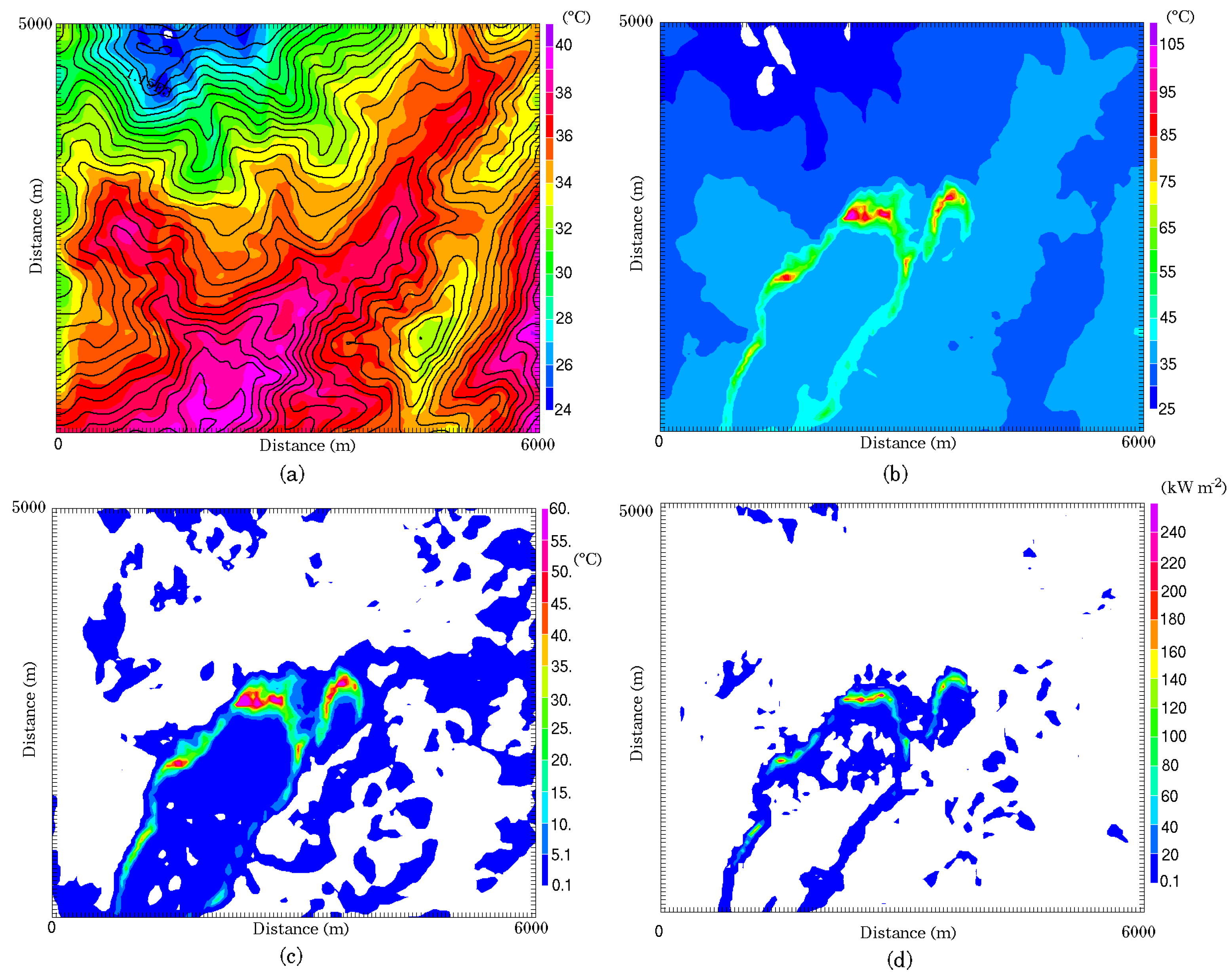
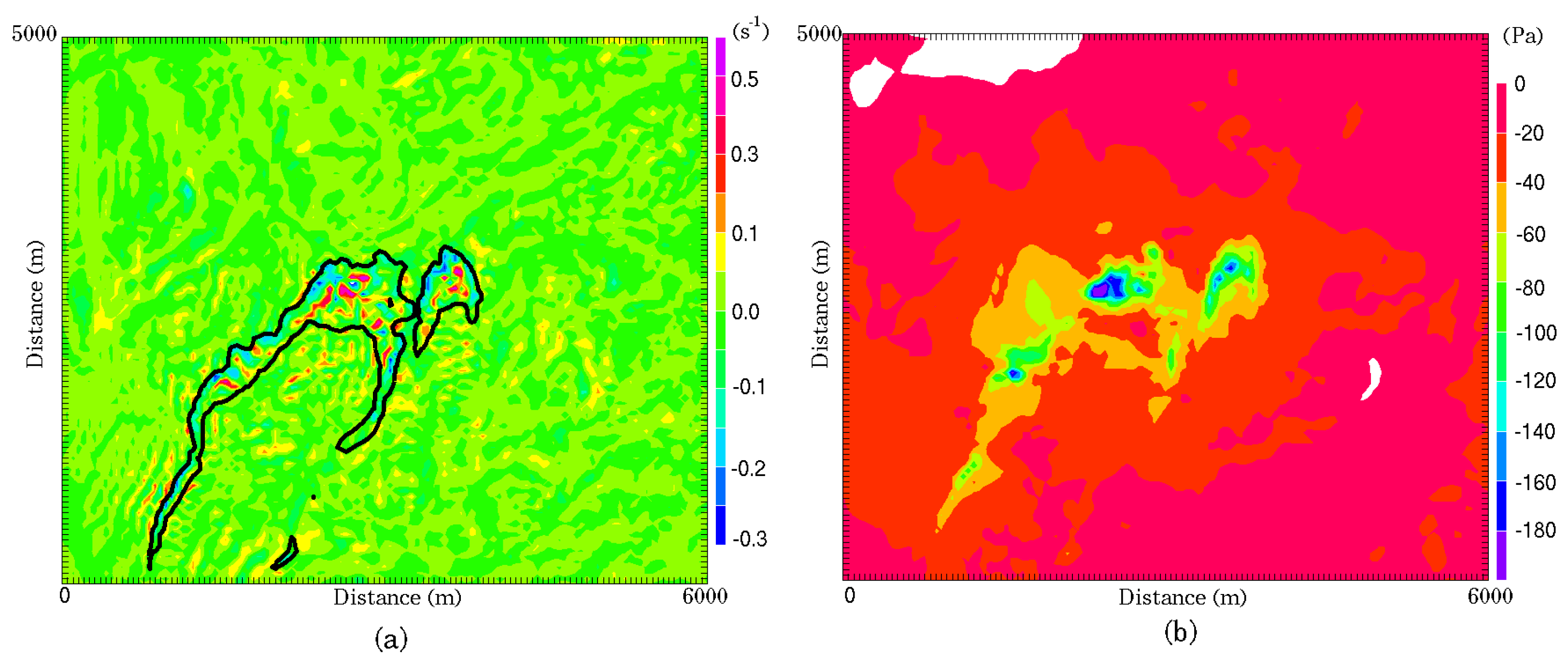
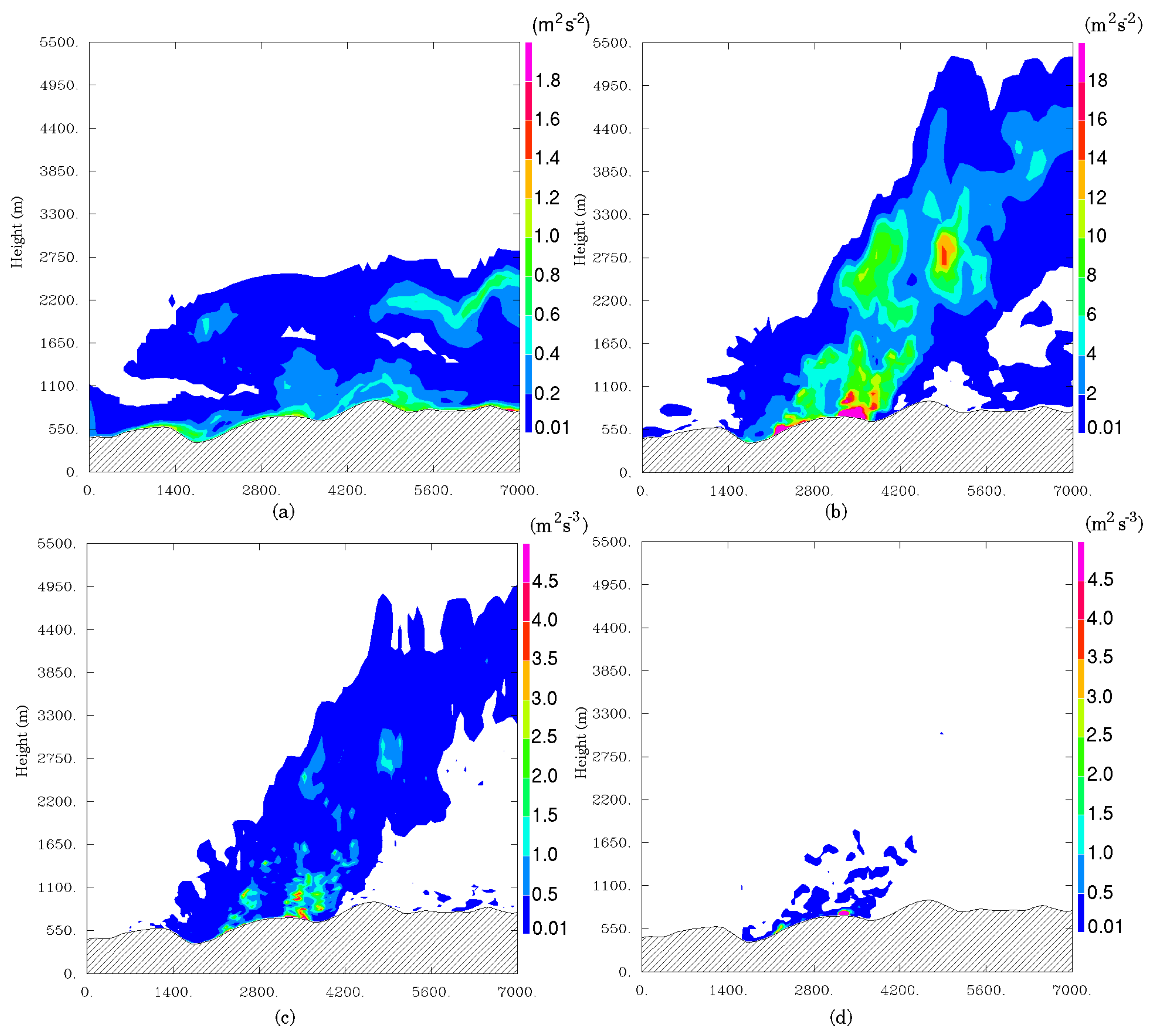
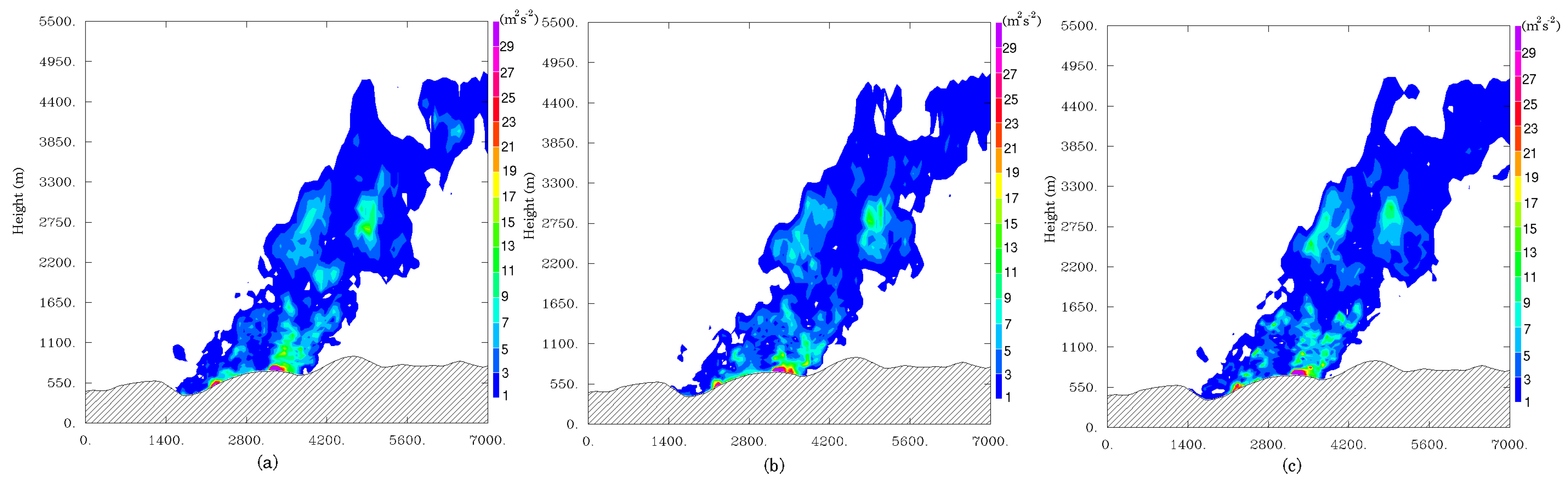
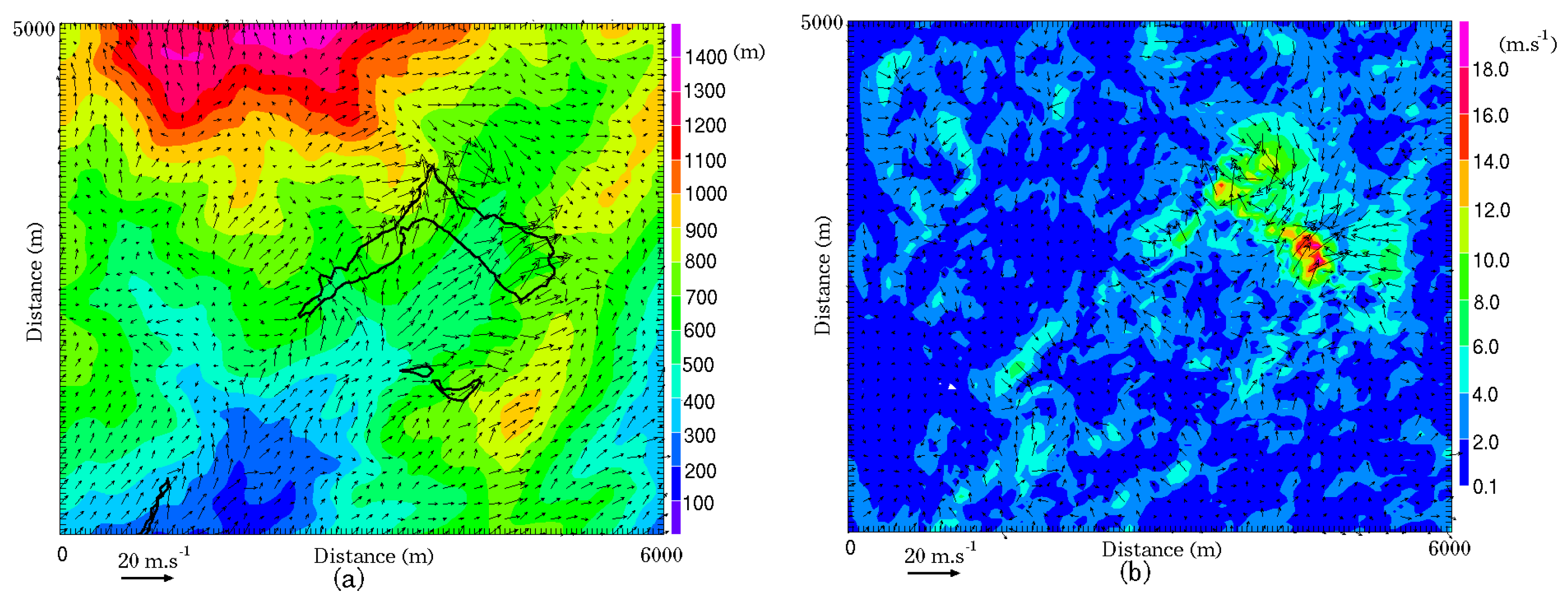
The embedded parallel strategy demonstrated in this study ensures that the coupled model will behave in the same way as the atmospheric model and thus will benefit from further improvements. The system proves to be able to simulate a large wildfire, although with some arguable simplifications of important processes and relatively raw parametrization given the complex landscape. It makes it possible to simulate both the fine-scale fire-atmosphere interactions occurring at tens of meters scales around the fire front and larger regional scales with a good degree of realism. The multiscale simulation allowed exploring the dynamical structure of the surrounding atmosphere. Wildland fire induced strong surface winds generating a few thousand meter convective column with pockets of updrafts, stronger at higher levels and following a multi-cell distribution, while strong downdrafts occurred behind the plume and the fire front. At 50-m resolution, subgrid motions as well as the resolved momentum were strongly enhanced by the fire. Shear had a larger contribution than buoyancy to the turbulence within the fire plume partly due to high sheared initial winds.
It is reasonable to think that such coupled models will run faster than real time on medium-sized clusters in the near future. This type of coupled simulation could then become a decision support tool, forecasting plume size, transport dispersion and smoke concentration at the ground (information of prime importance to protect the population) and anticipating the visibility loss for the fire fighters and civil transport in general. In terms of forecasting the fire-line location, it is unlikely that such models ever reach the ability and precision of very fast codes that can be tweaked and adapted in real time to fire observations and fighting scenarios. Nevertheless, such codes still require wind, temperature and more generally changing weather pattern forecasts. Fire to atmosphere numerical coupling appears to be a reasonable way of forecasting extreme weather events that can strongly affect local meteorological conditions.
The major point was to demonstrate and build the platform that may now receive enhancement from the community, as all codes are open source.
The main plan is to improve fuel models, as well as the fire velocity and surface flux models in order to better represent the combustion phase that will refine the diagnosis of turbulent fluxes at the ground level and the combustion phase of larger fuel particles. The simulation of more systematic very large wildfires at high resolution with a complex fuel structure is the current goal for model validation, along with the development of an operational tool chain for fire and fire-weather forecasting if sufficient performance can be achieved.