Microclimate Variation and Estimated Heat Stress of Runners in the 2020 Tokyo Olympic Marathon
Abstract
:1. Introduction
2. Methods
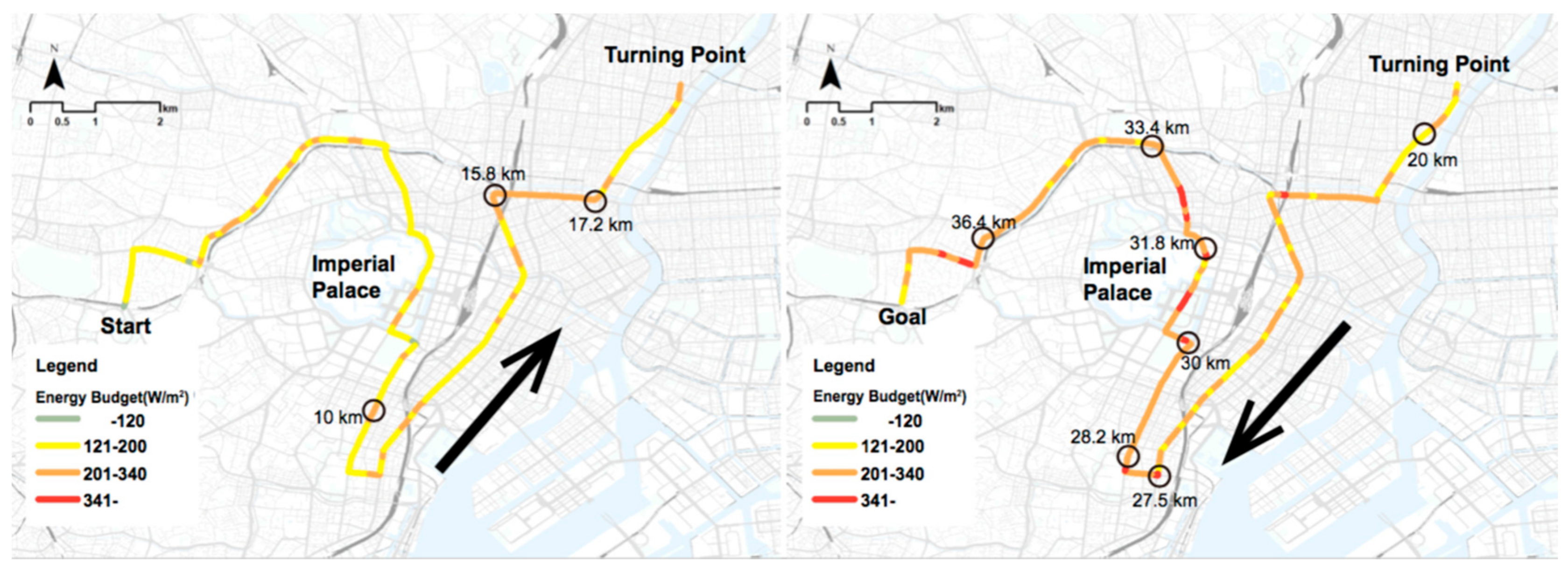
2.1. Study Area
2.2. Research Methodology
2.1.1. Thermal Environment Measurements along the Marathon Course
2.1.2. Estimated Heat Balance of Runners: Application of the COMFA Human Heat Balance Model
2.1.3. Identifying Hot Locations along the Marathon Course
2.1.4. Approaches to Mitigate Heat Stress
3. Results
3.1. Mean and Standard Deviation of Meteorological Variables
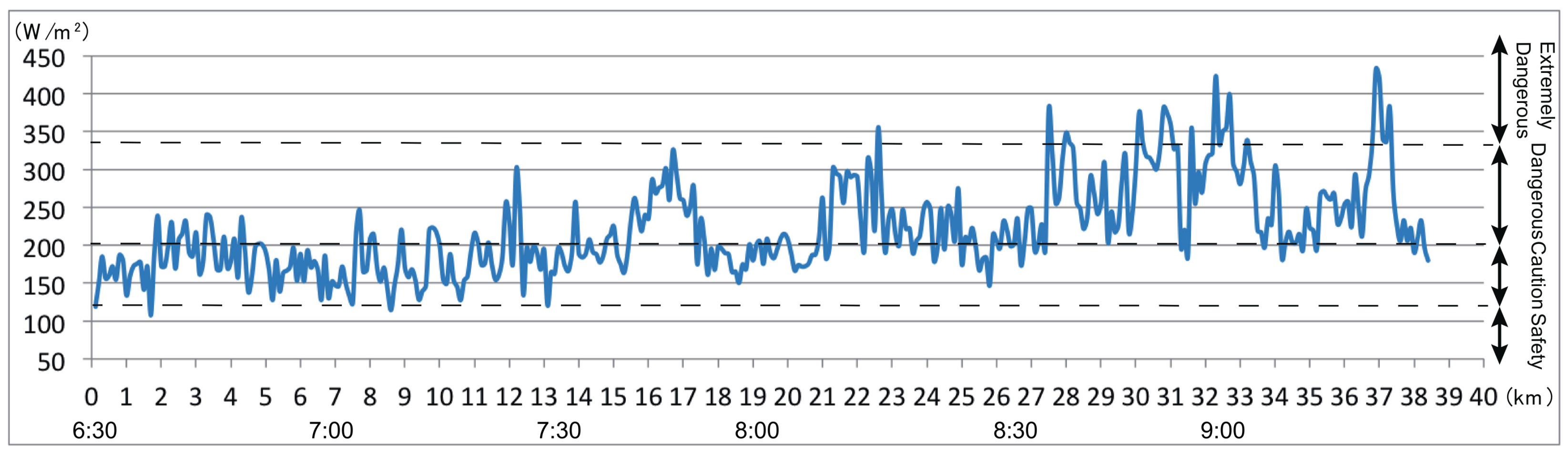
3.2. Maps and Graphs of Human Energy Budget
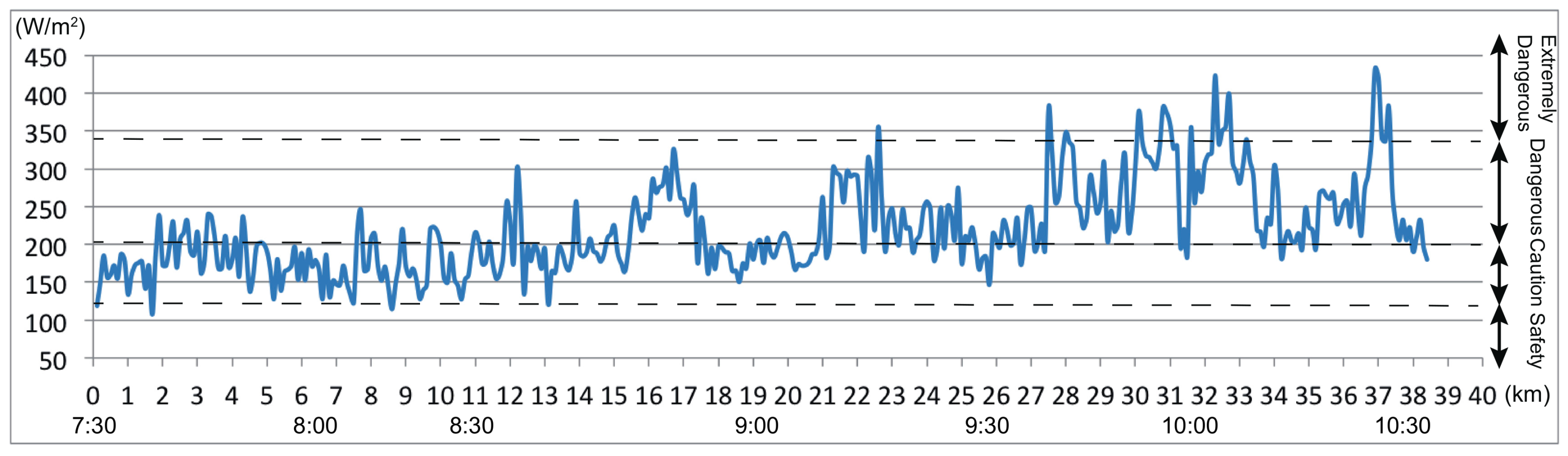
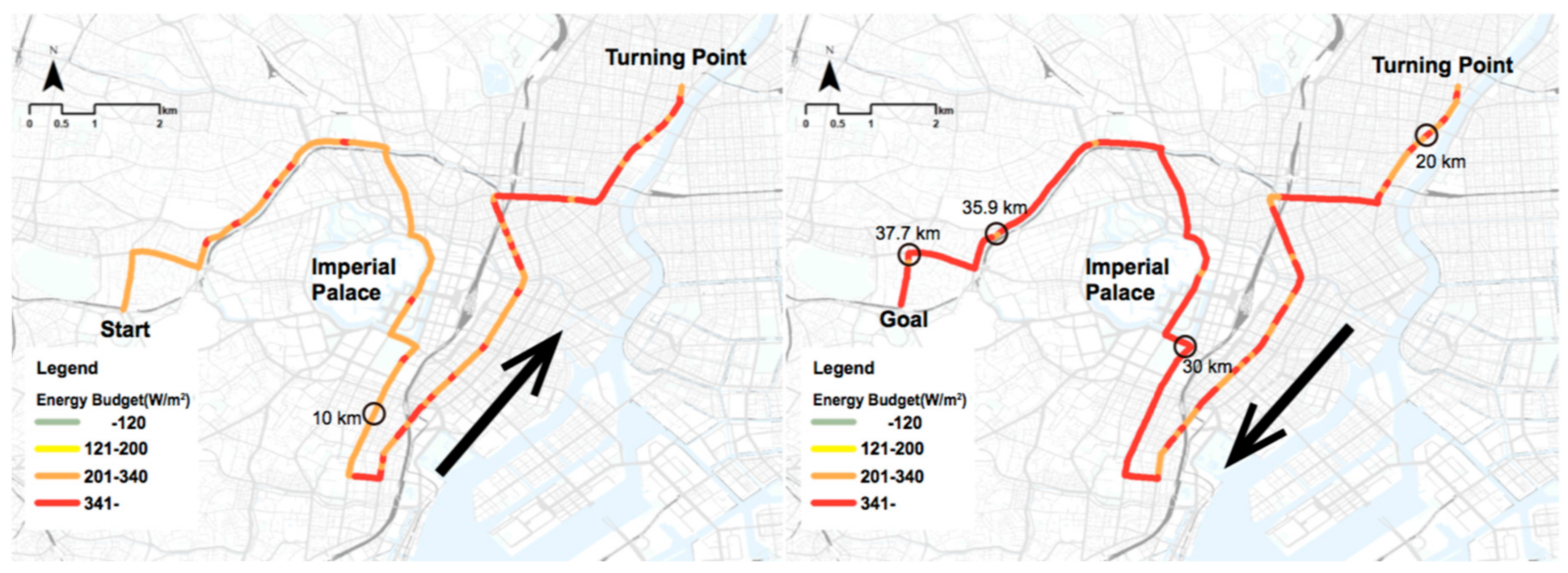
3.2.1. August 9, 2016
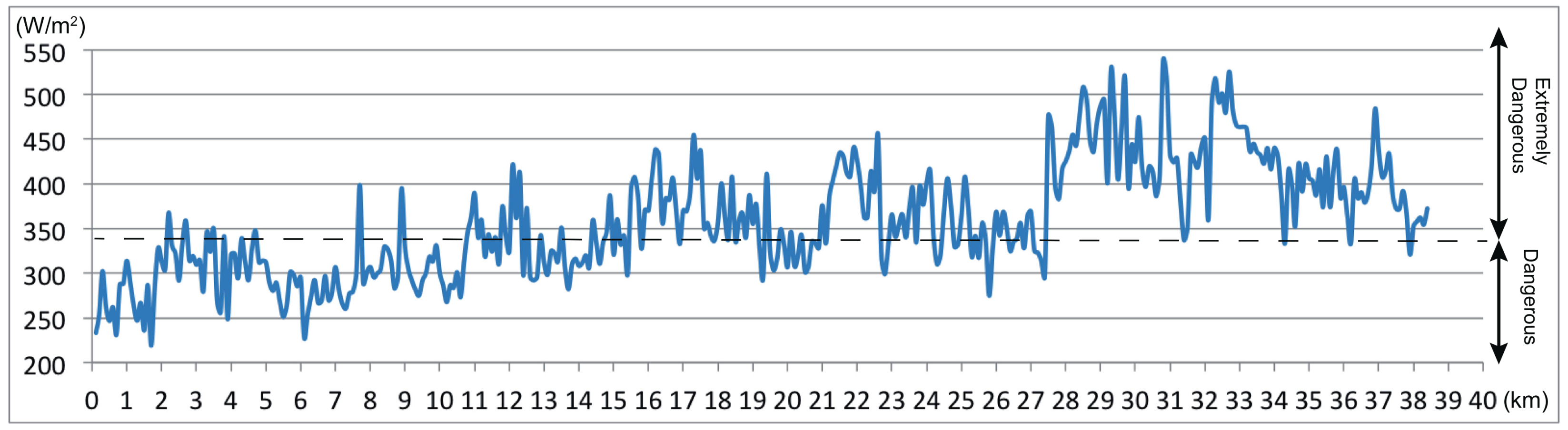
3.2.2. Worst-Case Scenario
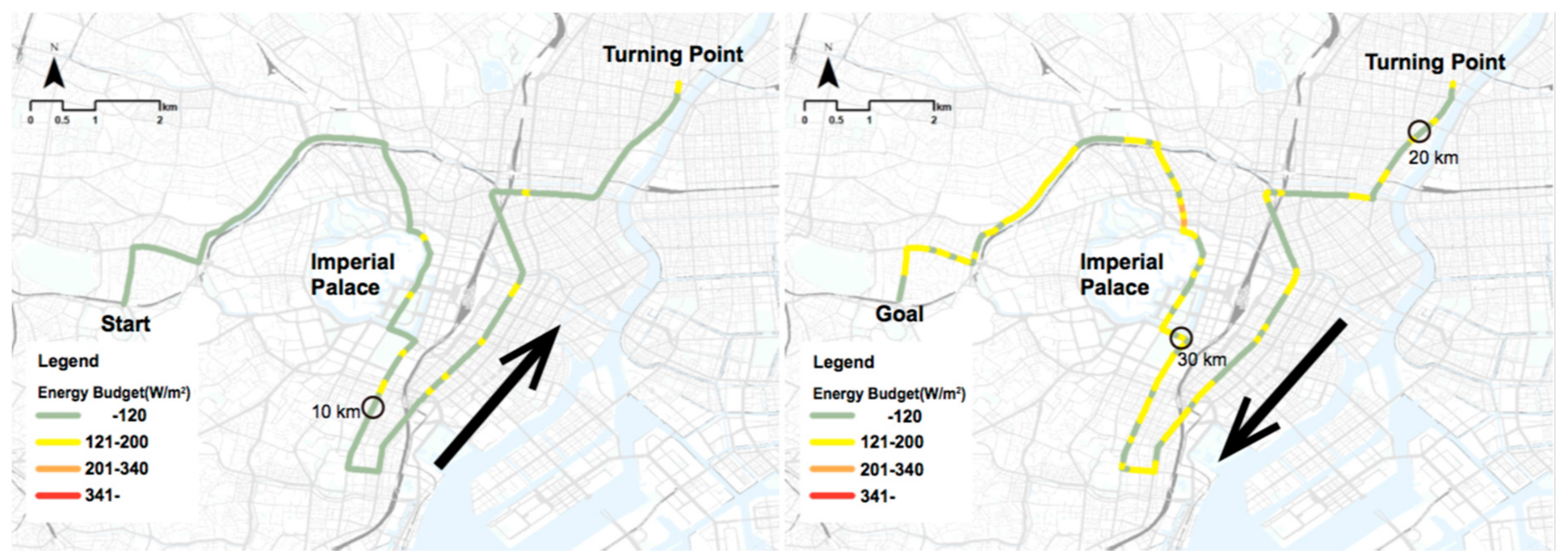
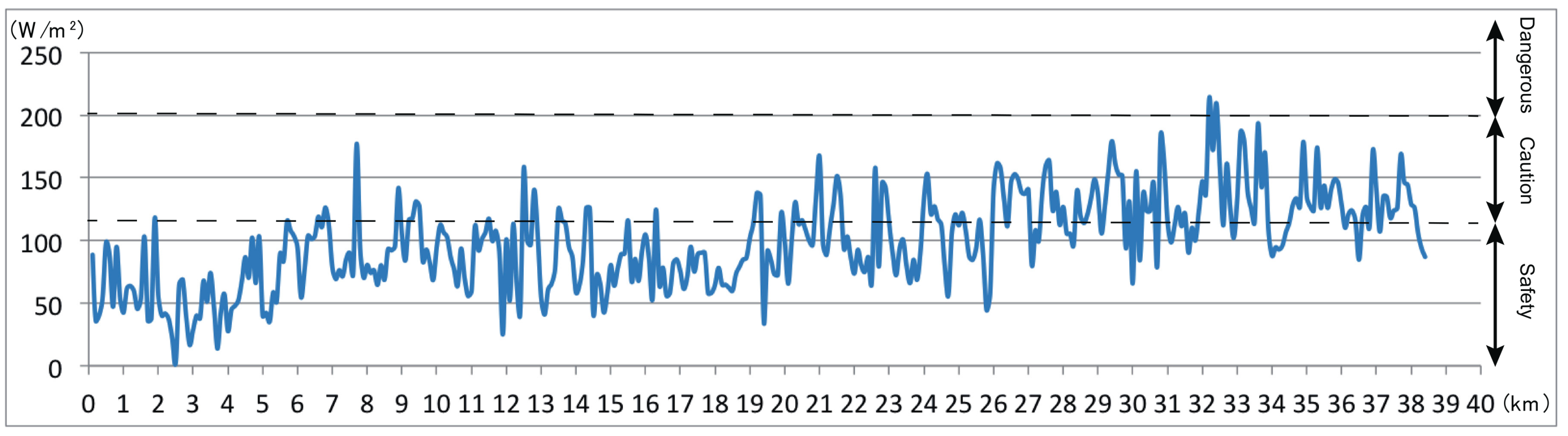
3.2.3. Best-Case Scenario
3.2.4. August 25, 2016: Early Start
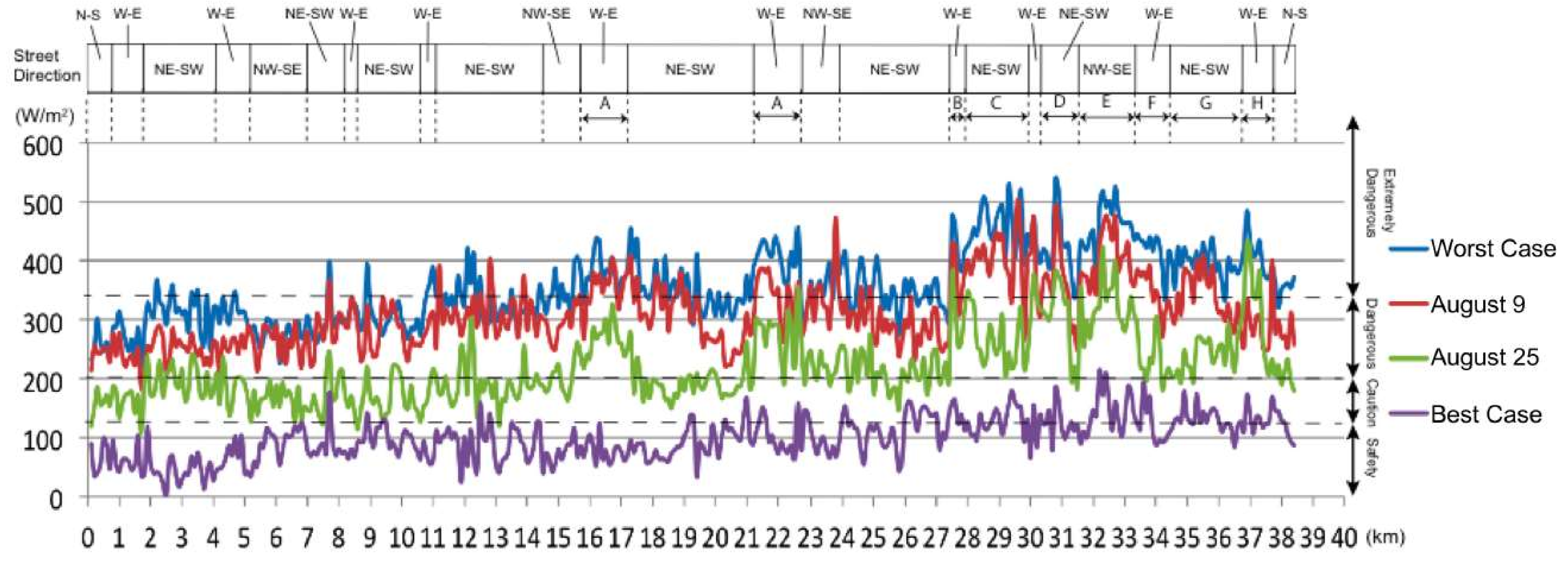
3.3. Comparison of the Results for Each Case
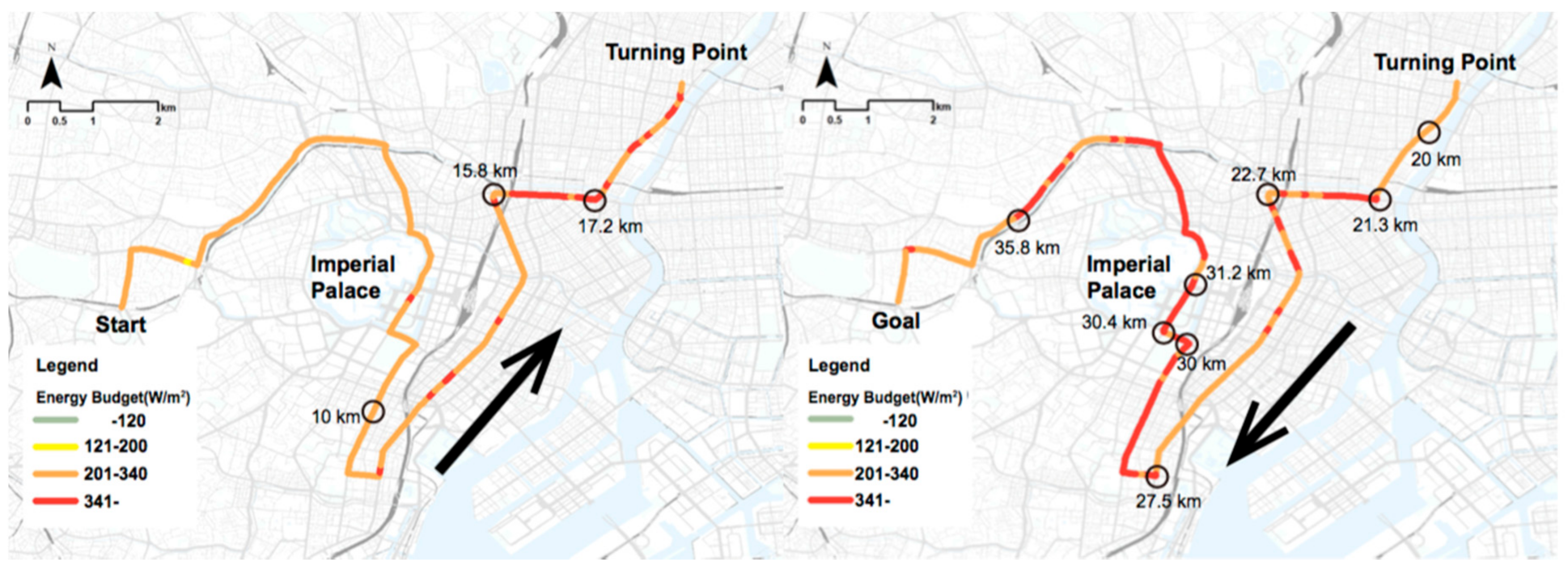
3.4. Characteristics of Sections Considered Dangerous
3.4.1. Individual Characteristics of Each Section
Section A (15.7–17.2 km, 21.3–22.7 km)
Section B (27.5–27.9 km)
Section C (28–29.9 km)
Section D (30.4–31.2 km)
Section E (31.3–33.3 km)
Section F (33.4–34.4 km)
Section G (34.5–36.7 km)
Section H (36.8–37.7 km)
3.4.2. Summary
4. Approaches to Heat Stress Mitigation
4.1. Group II
4.2. Group III
4.3. Group IV
4.4. Group V
5. Conclusions
- On clear sunny days (the worst-case scenario), many stretches along the course were rated as dangerous or extremely dangerous. In particular, the stretch from 27.5 km–37.7 km is dominated by race segments in direct sunlight and had near-continuous sections that significantly exceeded the extremely dangerous standard. This section is in particular need of measures to improve heat stress conditions.
- Under cloudy weather (the best-case scenario), from the start of the race, there were stretches that were rated as at the safe level. However, in the second half of the race, there were stretches rated as caution. Therefore, even under conditions that are the coolest for the given time of year, it is necessary to take measures against heat stress.
- Starting the race one hour earlier would decrease race temperatures and increase the number of shaded sections on the return route. These results suggest that starting the race one hour earlier would be an effective measure against heat stress by shortening the continuous stretches rated as extremely dangerous, as demonstrated by comparing data gathered using the race’s scheduled start time.
- Based on the classified sections along the course, we propose: (1) allowing runners to run in the shade of buildings, (2) making use of urban greenery, such as expanding the tree canopy, and (3) placing temporary tree planters and sunshades as three effective strategies for reducing the heat stress from the Sun and longwave radiation.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tokyo Metropolitan Government Environment Bureau. Available online: https://www.kankyo.metro.tokyo.jp/climate/other/countermeasure/suishinkaigi.html (accessed on 16 June 2017). (In Japanese).
- Golden, J.S. The built environment induced urban heat island effect in rapidly urbanizing arid regions—A sustainable urban engineering complexity. Environ. Sci. 2003, 1, 321–349. [Google Scholar] [CrossRef]
- Tan, J.; Zheng, Y.; Tang, X.; Guo, C.; Li, L.; Song, G.; Zhen, X.; Yuan, D.; Kalkstein, A.; Li, F.; et al. The urban heat island and its impact on heat waves and human health in Shanghai. Int. J. Biometeorol. 2010, 54, 75–84. [Google Scholar] [CrossRef] [PubMed]
- Patz, J.A.; Campbell-Lendrum, D.; Holloway, T.; Foley, J.A. Impact of regional climate change on human health. Nature 2005, 438, 310–317. [Google Scholar] [CrossRef] [PubMed]
- Nakai, S.; Itoh, T.; Morimoto, T. Deaths from heat-stroke in Japan: 1968–1994. Int. J. Biometeorol. 1999, 43, 124–127. [Google Scholar] [CrossRef] [PubMed]
- Wetterhall, S.F.; Coulombier, D.M.; Herndon, J.M.; Zaza, S.; Cantwell, J.D. Medical care delivery at the 1996 Olympic Games. J. Am. Med. Assoc. 1998, 279, 1463–1468. [Google Scholar] [CrossRef]
- Zhang, J.J.; Wang, L.D.; Chen, Z.; Ma, J.; Dai, J.P. Medical care delivery at the Beijing 2008 Olympic Games. World J. Emerg. Med. 2011, 2, 267–271. [Google Scholar] [CrossRef] [PubMed]
- Kakamu, T.; Wada, K.; Smith, D.R.; Endo, S.; Fukushima, T. Preventing heat illness in the anticipated hot climate of the Tokyo 2020 Summer Olympic Games. Environ. Health Prev. Med. 2017, 22, 68. [Google Scholar] [CrossRef] [PubMed]
- Smith, K.R.; Woodward, A.; Lemke, B.; Otto, M.; Chang, C.J.; Mance, A.A.; Balmes, J.; Kjellstrom, T. The last Summer Olympics? Climate change, health, and work outdoors. Lancet 2016, 388, 642–644. [Google Scholar] [CrossRef]
- Huang, L.; Li, J.; Zhao, D.; Zhu, J. A fieldwork study on the diurnal changes of urban microclimate in four types of ground cover and urban heat island of Nanjing, China. Build. Environ. 2008, 43, 7–17. [Google Scholar] [CrossRef]
- Miyazaki, H.; Moriyama, M.; Yoshida, A. Field study on green canopy as urban cool-spot. Nat. Hum. Act. 1996, 1, 51–56. [Google Scholar]
- Middel, A.; Häb, K.; Brazel, A.J.; Martin, C.; Guhathakurta, S. Impact of urban form and design on microclimate in Phoenix, AZ. Landsc. Urban Plan. 2014, 122, 16–28. [Google Scholar] [CrossRef]
- Middel, A.; Selover, N.; Hagen, B.; Chhetri, N. Impact of shade on outdoor thermal comfort—A seasonal field study in Tempe, Arizona. Int. J. Biometeorol. 2016, 60, 1849–1861. [Google Scholar] [CrossRef] [PubMed]
- Helou, N.E.; Tafflet, M.; Berthelot, G.; Tolaini, J.; Marc, A.; Guillaume, M.; Hausswirth, C.; Toussaint, J.F. Impact of environmental parameters on marathon running performance. PLoS ONE 2012, 7, e37407. [Google Scholar] [CrossRef] [PubMed]
- Hodder, S.G.; Parsons, K. The effects of solar radiation on thermal comfort. Int. J. Biometeorol. 2007, 51, 233–250. [Google Scholar] [CrossRef] [PubMed]
- Otani, H.; Kaya, M.; Tamaki, A.; Watson, P.; Maughan, R.J. Effects of solar radiation onendurance exercise capacity in a hot environment. Eur. J. Appl. Physiol. 2016, 116, 769–779. [Google Scholar] [CrossRef] [PubMed]
- Yamasaki, Y.; Tsunemattsu, N.; Yokohama, H.; Umeki, K.; Honjo, T. Prediction of Thermal Environment in Olympic Marathon Course by Thermal Comfort Map. Environ. Inf. Sci. 2016, 30, 43–48. (In Japanese) [Google Scholar]
- Kashimura, O.; Minami, K.; Hoshi, A. Prediction of WBGT for the Tokyo 2020 Olympic Marathon. Jpn. J. Biometeorol. 2016, 53, 139–144. [Google Scholar]
- Brown, R.D.; Gillespie, T.J. Microclimatic Landscape Design: Creating Thermal Comfort and Energy Efficiency; Wiley: Hoboken, NJ, USA, 1995; pp. 1–208. [Google Scholar]
- Vanos, J.K.; Warland, J.S.; Gillespie, T.J.; Kenny, N.A. Improved predictive ability of climate–human–behaviour interactions with modifications to the COMFA outdoor energy budget model. Int. J. Biometeorol. 2012, 56, 1065–1074. [Google Scholar] [CrossRef] [PubMed]
- Brown, R.D.; Gillespie, T.J. Estimating outdoor thermal comfort using a cylindrical radiation thermometer and an energy budget model. Int. J. Biometeorol. 1986, 30, 43–52. [Google Scholar] [CrossRef] [PubMed]
- d’Ambrosio Alfano, F.R.; Palella, B.I.; Riccio, G. The role of Measurement Accuracy on the Heat Stress Assessment according to ISO 7933: 2004. WIT Trans. Biomed. Health 2007, 11, 115–124. [Google Scholar]
- d’Ambrosio Alfano, F.R.; Dell’Isola, M.; Palella, B.I.; Riccio, G.; Russi, A. On the measurement of the mean radiant temperature and its influence on the indoor thermal environment assessment. Build. Environ. 2013, 63, 79–88. [Google Scholar] [CrossRef]
- Palella, B.I.; Quaranta, F.; Riccio, G. On the management and prevention of heat stress for crews onboard ships. Ocean Eng. 2016, 112, 277–286. [Google Scholar] [CrossRef]
- Tokura, H.; Nabeshima, M.; Nisioka, M.; Nakao, M. Mobile observation method for spatial variation of direction and velocity of wind on grand level. Proc. Res. Meet. Arch. Inst. Jpn. Kinki Branch (Environment) 2007, 47, 289–292. (In Japanese) [Google Scholar]
- ISO 9920: Ergonomics of the Thermal Environment: Estimation of Thermal Insulation and Water Vapour Resistance of a Clothing Ensemble; ISO: Geneva, Switzerland, 2007.
- Kenny, N.A.; Warland, J.S.; Brown, R.D.; Gillespie, T.G. Part A: Assessing the performance of the COMFA outdoor thermal comfort model on subjects performing physical activity. Int. J. Biometeorol. 2009, 53, 415–428. [Google Scholar] [CrossRef] [PubMed]
- Kenny, N.A.; Warland, J.S.; Brown, R.D.; Gillespie, T.G. Part B: Revisions to the COMFA outdoor thermal comfort model for application to subjects performing physical activity. Int. J. Biometeorol. 2009, 53, 429–441. [Google Scholar] [CrossRef] [PubMed]
- Vanos, J.K.; Warland, J.S.; Gillespie, T.J.; Slater, G.A.; Brown, R.D.; Kenny, N.A. Human energy budget modeling in urban parks in Toronto, ON and applications to emergency heat stress preparedness. J. Appl. Meteorol. Climatol. 2012, 51, 1639–1653. [Google Scholar] [CrossRef]
- De Freitas, C.R.; Dawson, N.J.; Young, A.A.; Mackey, W.J. Microclimate and heat stress of runners in mass participation events. J. Clim. Appl. Meteorol. 1985, 24, 184–191. [Google Scholar] [CrossRef]
- Ainsworth, B.E.; Haskell, W.L.; Herrmann, S.D.; Meckes, N.; Bassett, D.R., Jr.; Tudor-Locke, C.; Greer, J.L.; Vezina, J.; Whitt-Glover, M.C.; Leon, A.S. Compendium of Physical Activities: A second update of codes and MET values. Med. Sci. Sports Exerc. 2011, 43, 1575–1581. [Google Scholar] [CrossRef] [PubMed]
- Vanos, J.K.; Herdt, A.J.; Lochbaum, M.R. Effects of physical activity and shade on the heat balance and thermal perceptions of children in a playground microclimate. Build. Environ. 2017, 126, 119–131. [Google Scholar] [CrossRef]
- Hardin, A.W.; Vanos, J.K. The influence of surface type on the absorbed radiation by a human under hot, dry conditions. Int. J. Biometeorol. 2018, 62, 43–56. [Google Scholar] [CrossRef] [PubMed]
- Kenny, N.A.; Warland, J.S.; Brown, R.D.; Gillespie, T.G. Estimating the radiation absorbed by a human. Int. J. Biometeorol. 2008, 52, 491–503. [Google Scholar] [CrossRef] [PubMed]
- Middel, A.; Lukasczyk, J.; Maciejewski, R. Sky View Factors from synthetic fisheye photos for thermal comfort routing—A case study in phoenix, Arizona. Urban Plan 2017, 2, 19–31. [Google Scholar] [CrossRef]
- Middel, A.; Lukasczyk, J.; Maciejewski, R.; Demuzere, M.; Roth, M. Sky view factor footprints for urban climate modeling. Urban Clim. 2018. under review. [Google Scholar]
- Lukasczyk, J.; Middel, A.; Zakrzewski, S.; Arnold, M.; Maciejewski, R. Urban Form and Composition of Street Canyons: A Human-Centric Big Data and Deep Learning Approach. Landsc. Urban Plan. 2018. under review. [Google Scholar]
- Monteith, J.L.; Unsworth, M.H. Principles of Environmental Physics, 3rd ed.; Academic Press: New York, NY, USA, 2008; pp. 1–418. [Google Scholar]
- Harlan, S.L.; Brazel, A.J.; Prashad, L.; Stefanov, W.L.; Larsen, L. Neighborhood microclimates and vulnerability to heat stress. Soc. Sci. Med. 2006, 63, 2847–2863. [Google Scholar] [CrossRef] [PubMed]
- Vanos, J.K.; Warland, J.S.; Gillespie, T.J.; Kenny, N.A. Thermal comfort modelling of body temperature and psychological variations of a human exercising in an outdoor environment. Int. J. Biometeorol. 2012, 56, 21–32. [Google Scholar] [CrossRef] [PubMed]
- Havenith, G.; Holmer, I.; Parsons, K.C. Personal factors in thermal comfort assessment: Clothing properties and metabolic heat production. Energy Build. 2002, 34, 581–591. [Google Scholar] [CrossRef]
- Vanos, J.K.; Warland, J.S.; Gillespie, T.J.; Kenny, N.A. Review of the physiology of human thermal comfort while exercising in urban landscapes and implications for bioclimatic design. Int. J. Biometeorol. 2010, 54, 319–334. [Google Scholar] [CrossRef] [PubMed]
- Hosokawa, Y.; Grundstein, A.J.; Vanos, J.K.; Cooper, E.R. Environmental Condition and Monitoring. In Sport and Physical Activity in the Heat; Casa, D.J., Ed.; Springer: Cham, Switzerland, 2018; pp. 147–162. [Google Scholar]
- Höppe, P. Different aspects of assessing indoor and outdoor thermal comfort. Energy Build. 2002, 34, 661–665. [Google Scholar] [CrossRef]
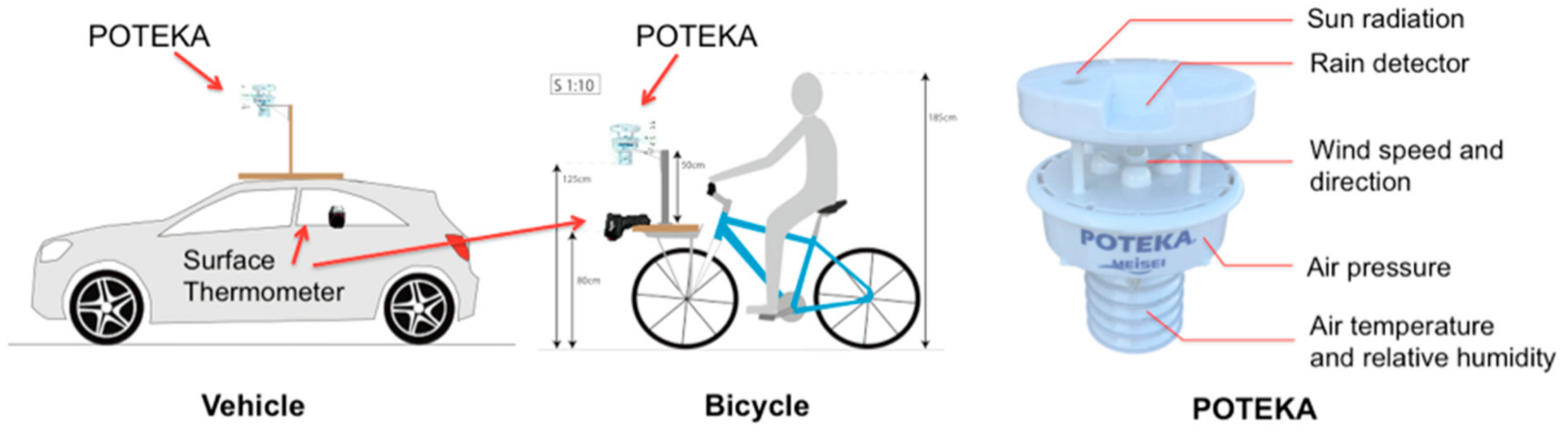
| Instrument | Parameter | Model | Accuracy | Interval |
|---|---|---|---|---|
| Thermometer | Air Temperature (°C) | POTEKA | ±0.3 °C | 1 s |
| Hygrometer | Relative Humidity (%) | POTEKA | ±5% | 1 s |
| Pyrometer | Solar Radiation (W/m2) | POTEKA | ±10% | 1 s |
| Surface thermometer | Surface Temperature (°C) | ThermoGEAR G100 | ±2 °C | 3 s |
| Anemometer | Wind + Activity Speed (m/s) | POTEKA | ±1.0 m/s | 1 s |
| GPS | Latitude and Longitude | eTrex30 | 3 to 6 m | 1 s |
| Date | Time | Sky Condition |
|---|---|---|
| Jul 29, 2016 | 7:30–10:29 | sunny |
| Aug 5, 2016 | 7:30–10:30 | sunny |
| Aug 6, 2016 | 7:30–10:31 | sunny |
| Aug 9, 2016 | 7:30–10:33 | sunny |
| Aug 11, 2016 | 7:30–9:57 | cloudy |
| Aug 12, 2016 | 7:30–10:15 | cloudy |
| Aug 13, 2016 | 7:30–10:16 | sunny |
| Aug 14, 2016 | 7:30–10:10 | cloudy |
| Aug 23, 2016 | 6:30–9:20 | cloudy |
| Aug 25, 2016 | 6:30–9:25 | sunny |
| Aug 26, 2016 | 7:30–10:25 | sunny |
| Day or Scenario | Ta (°C) | RH (%) | Wind Speed | Solar Radiation | Road Surface Temperature | |
|---|---|---|---|---|---|---|
| (m s−1) | (W m−2) | (°C) | ||||
| 29 July | Mean ± SD | 29.3 ± 1.26 | 58.9 ±4.59 | 2.0 ± 0.79 | 427.5 ± 317.76 | 35.3 ± 5.64 |
| Range | 27.0–32.8 | 49.1–66.4 | 0.5–4.4 | 46.9–1024.1 | 27.5–49.5 | |
| 5 August | Mean ± SD | 30.8 ±1.27 | 58.2 ± 4.65 | 2.0 ± 0.82 | 281.1 ± 215.59 | 36.4 ± 4.43 |
| Range | 28.7–33.9 | 48.1–65.6 | 0.5–5.7 | 51.7–1052.8 | 29.8–51.4 | |
| 6 August | Mean ± SD | 30.6 ±1.08 | 62.2 ± 3.35 | 1.9 ± 0.69 | 349.8 ± 238.76 | 37.7 ± 4.31 |
| Range | 28.2–32.7 | 55.5–69.8 | 0.7–4.5 | 56.1–999.6 | 30.9–49.0 | |
| 9 August | Mean ± SD | 34.3 ± 1.82 | 37.0 ± 5.87 | 2.0 ± 0.88 | 350.8 ± 249.13 | 38.6 ± 5.06 |
| Range | 29.6–37.6 | 29.5–50.3 | 0.6–8.3 | 43.2–949.1 | 27.8–54.8 | |
| 11 August | Mean ± SD | 28.2 ± 0.45 | 46.2 ± 1.86 | 1.9 ± 1.19 | 125.7 ± 95.83 | 33.4 ± 1.66 |
| Range | 27.1–29.5 | 42.9–51.2 | 0.4–10.4 | 28.3–375.4 | 30.5–39.4 | |
| 12 August | Mean± SD | 27.3 ± 0.82 | 59.0 ± 4.41 | 1.7 ± 0.87 | 231.7 ± 83.16 | 34.2 ± 2.24 |
| Range | 25.9–29.2 | 49.7–64.6 | 0.4–10.3 | 94.4–450.0 | 29.9–40.6 | |
| 13 August | Mean ± SD | 27.8 ± 0.90 | 53.5 ± 3.32 | 1.7 ± 0.82 | 347.4 ± 193.51 | 36.1 ± 4.05 |
| Range | 26.3–30.0 | 48.3–59.9 | 0.3–6.0 | 60.3–1066.4 | 29.5–50.4 | |
| 14 August | Mean ± SD | 26.3 ± 0.85 | 54.8 ± 3.19 | 1.7 ± 0.87 | 253.4 ± 119.17 | 34.3 ± 3.04 |
| Range | 24.7–28.2 | 49.1–59.9 | 0.4–10.7 | 61.3–727.8 | 29.0–43.9 | |
| 23 August | Mean ± SD | 27.8 ± 0.96 | 69.0 ± 3.79 | 1.9 ± 0.78 | 101.4 ± 70.31 | 27.7 ± 1.61 |
| Range | 26.0–29.5 | 62.2–75.2 | 0.5–5.0 | 12.7–399.4 | 25.1–32.3 | |
| 25 August | Mean ± SD | 29.0 ± 1.07 | 61.0 ± 4.88 | 2.0 ± 0.67 | 203.0 ± 190.22 | 31.0 ± 4.15 |
| Range | 26.9–31.6 | 50.4–70.1 | 0.5–5.4 | 14.6–824.0 | 25.4–45.3 | |
| 26 August | Mean ± SD | 30.1 ± 1.09 | 57.3 ± 3.55 | 2.0 ± 0.73 | 311.9 ± 227.17 | 35.5 ± 5.00 |
| Range | 27.4–32.6 | 51.0–65.8 | 0.6–5.1 | 27.3–1015.9 | 27.7–50.4 | |
| Worst | Reference day | August 9 | August 5 | August 5 | Max of each section | August 9 |
| Mean ± SD | 34.3 ± 1.82 | 47.4 ± 5.55 | 2.0 ± 0.82 | 514.4 ± 276.26 | 38.6 ± 5.06 | |
| Range | 29.6–37.6 | 38.5–62.1 | 0.5–5.7 | 109.8–1066.4 | 27.8–54.8 | |
| Best | Reference day | August 14 | August 11 | August 13 | Min of each section | August 11 |
| Mean ± SD | 26.3 ± 0.85 | 51.8 ± 3.35 | 2.0 ± 0.88 | 97.5 ± 62.94 | 33.4 ± 1.66 | |
| Range | 24.7–28.2 | 45.6–59.6 | 0.6–8.3 | 27.3–341.4 | 30.5–39.4 | |
| August 9, 2016 | Worst Case | BEST CASE | August 25, 2016 | |
|---|---|---|---|---|
| Safe | 0% | 0% | 70.8% | 0.8% |
| Caution | 0.3% | 0% | 28.6% | 44.8% |
| Dangerous | 70.3% | 45.1% | 0.6% | 50.5% |
| Extreme Dangerous | 29.4% | 54.9% | 0% | 3.9% |
| Both Trees and Buildings | Only Trees | Nothing | |
|---|---|---|---|
| W-E | A B F H (I) | ||
| NE-SW | C (II) | D G (III) | D (IV) |
| NW-SE | E (V) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kosaka, E.; Iida, A.; Vanos, J.; Middel, A.; Yokohari, M.; Brown, R. Microclimate Variation and Estimated Heat Stress of Runners in the 2020 Tokyo Olympic Marathon. Atmosphere 2018, 9, 192. https://doi.org/10.3390/atmos9050192
Kosaka E, Iida A, Vanos J, Middel A, Yokohari M, Brown R. Microclimate Variation and Estimated Heat Stress of Runners in the 2020 Tokyo Olympic Marathon. Atmosphere. 2018; 9(5):192. https://doi.org/10.3390/atmos9050192
Chicago/Turabian StyleKosaka, Eichi, Akiko Iida, Jennifer Vanos, Ariane Middel, Makoto Yokohari, and Robert Brown. 2018. "Microclimate Variation and Estimated Heat Stress of Runners in the 2020 Tokyo Olympic Marathon" Atmosphere 9, no. 5: 192. https://doi.org/10.3390/atmos9050192
APA StyleKosaka, E., Iida, A., Vanos, J., Middel, A., Yokohari, M., & Brown, R. (2018). Microclimate Variation and Estimated Heat Stress of Runners in the 2020 Tokyo Olympic Marathon. Atmosphere, 9(5), 192. https://doi.org/10.3390/atmos9050192





