3.1. Comparisons of COSMIC and IGRA
In order to compare the PW derived from radiosonde observations with COSMIC satellite data in details, we selected eight stations for the case study, with consideration of latitude, elevation and the distance to the ocean. The locations are shown in
Figure 1.
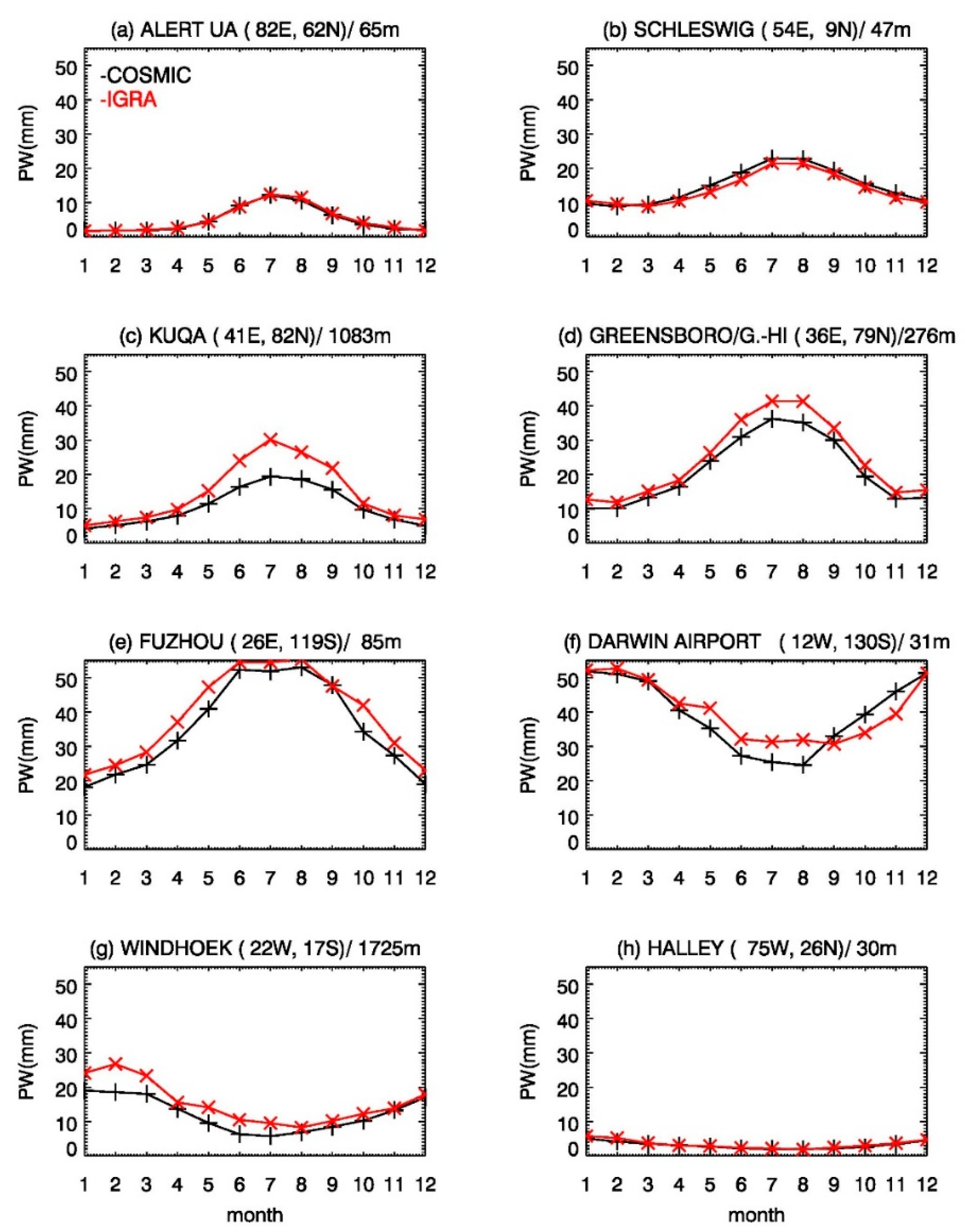
The variations of monthly averaged PW at selected stations are shown in
Figure 2. In general, PWs derived from two datasets show consistent patterns. PWs are larger in warm seasons and smaller in cold seasons for both hemispheres. In the polar regions, PWs are quite small (
Figure 2a,h) and the differences between two observations are relatively small. PWs at the Antarctic are below 10 mm throughout the whole year. In summer, stations in the Arctic (
Figure 2a) have relatively larger PWs than other seasons. Overall, PWs derived from COSMIC have smaller values in the middle and lower latitudes than the ones from radiosonde observations, except for two stations (
Figure 2b,f). The PWs from the satellite are relatively larger than the ones from the radiosonde observations at the European station Schleswig (
Figure 2b) throughout the year. For the Darwin Airport station (
Figure 2f), which is located in the Southern Hemisphere, the IGRA PWs are smaller than the COSMIC ones in springtime.
It is noteworthy that two stations with elevation over 1 km (
Figure 2c,g) have larger IGRA PWs, especially for the summertime, with differences larger than 5 mm or even higher. As presented in
Section 2, PW values are accumulated from the ground to the highest observing level for the COSMIC data. Because of the existence of the lowest perigee point, the void lower levels (from the surface to the lowest perigee point) are filled with PW value of the lowest water vapor observation of water vapor. This process might cause an averaged 2 mm or less bias of PW, as Teng et al. introduced in their research [
19]. This might bring the differences between COSMIC and IGRA PW closer over stations, especially for those with higher elevations.
According to
Figure 2, it is easily found that the PWs increase from the polar region to the tropical region. However, not all stations in the tropical area have larger PW values. PWs in summer at the tropics are usually about 50 mm (
Figure 2e,f). However, for station Windhoek (
Figure 2g), summer PWs have not reached 30 mm. This station might be influenced by Benguela Current, which is a cold current that constrains the evaporation of the sea surface and brings less water vapor to the coastal area. This implies that the coastal regions may not always be assumed to have sufficient water vapor supply and PWs at these areas may be impacted by the ocean current.
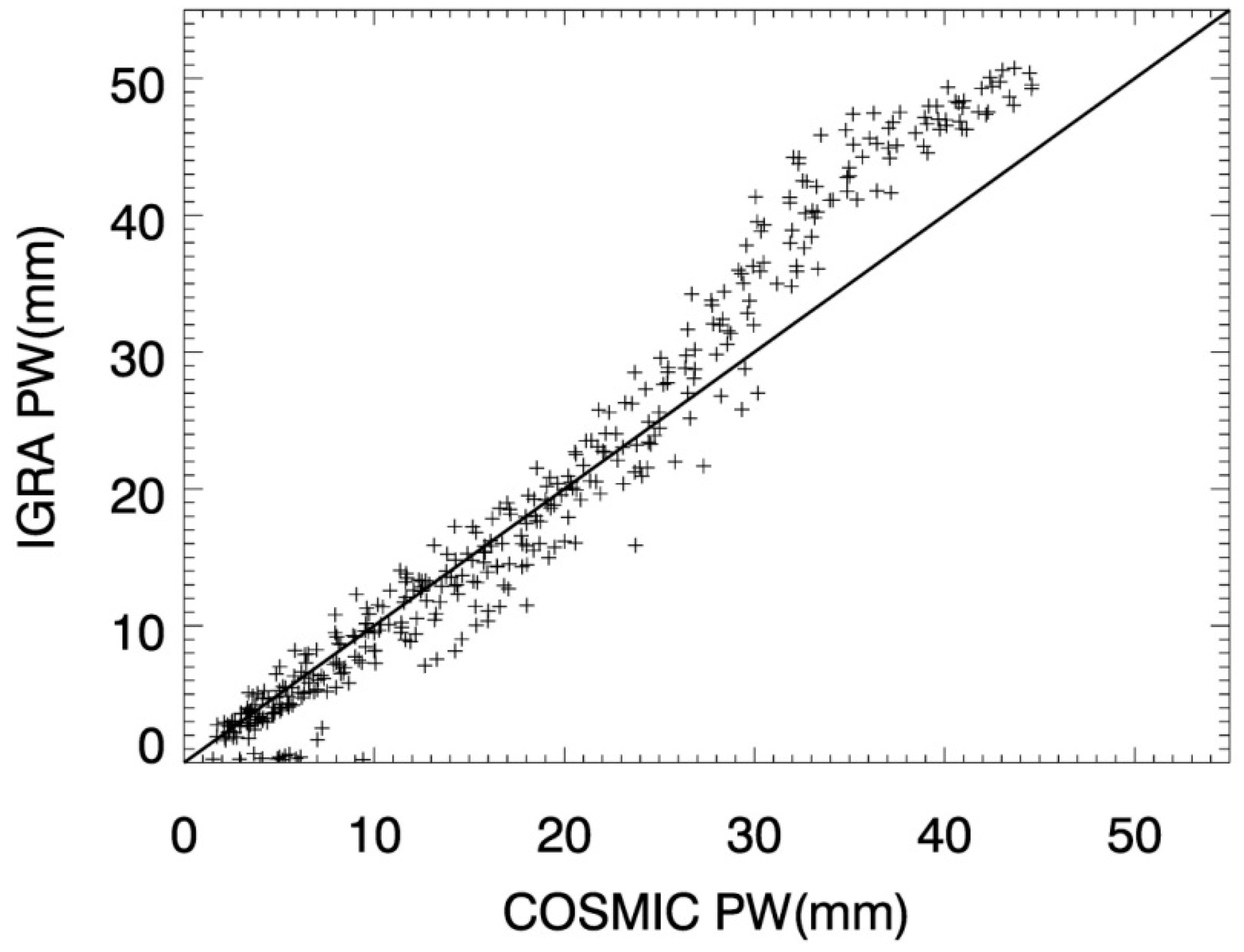
To further explore the differences in PW derived from COSMIC and radiosonde observations, the latitudinal monthly averaged PWs of both observations are compared in scatterplots (
Figure 3). Note that the latitudinal mean values are obtained by the averaged values in 5° latitude width (36 bins). Two observations show a good agreement, and Spearman’s correlation is 0.98 (significant). When the PW values are smaller than 30 mm, two observations scatter around the
y =
x line evenly. However, when the PWs are larger than 30 mm, COSMIC PWs are systematically smaller than the ones derived from IGRA. This difference will be further explored in the following sections. Interestingly, there are a few spots with very small IGRA PW values scattered above the
x-axis. This indicates that there are some areas with little atmospheric water vapor where radiosonde observations cannot fully capture the real circumstance of the water vapor content but COSMIC can.
3.2. Spatial and Seasonal Variations
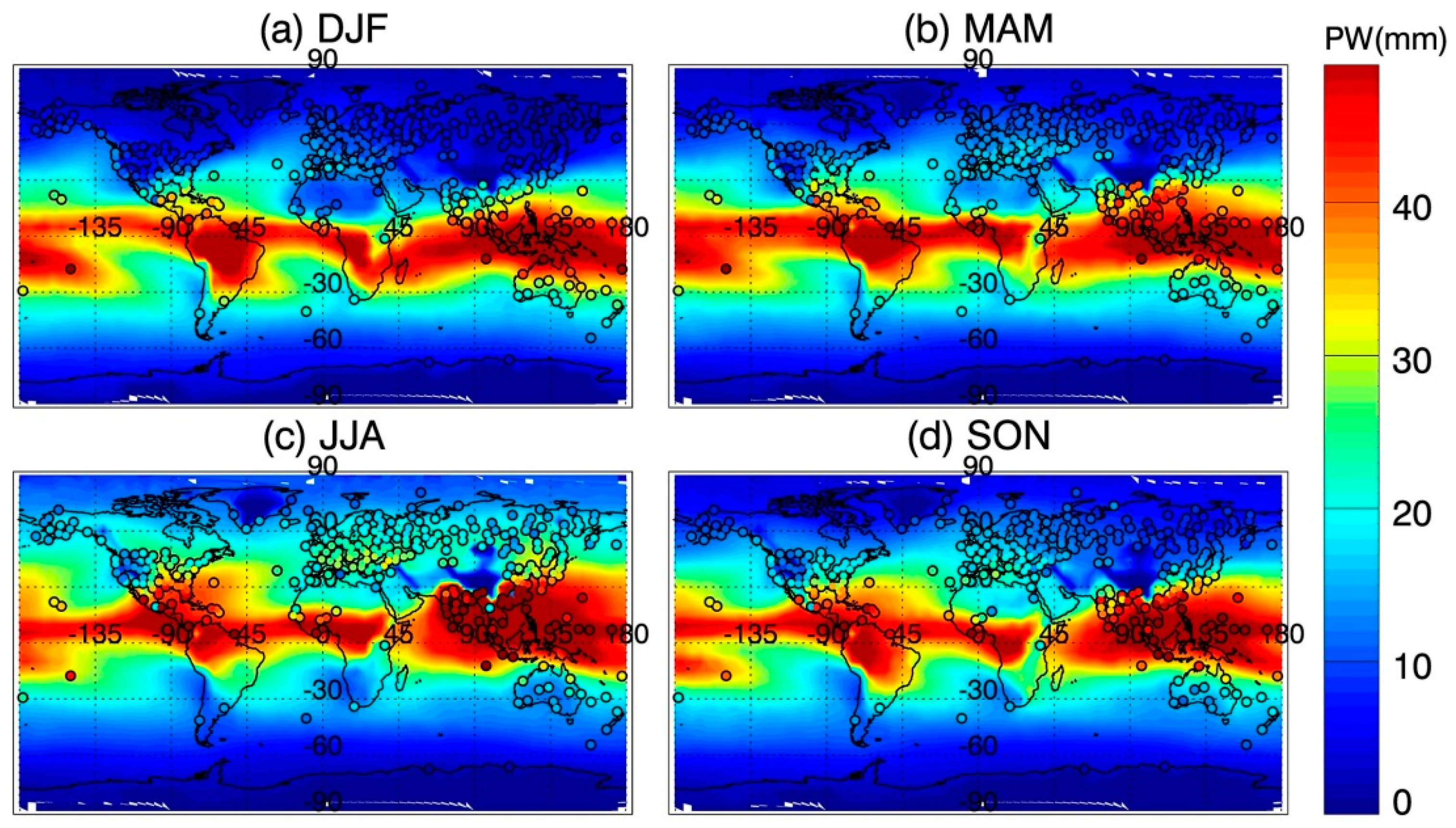
The comparison of global averaged PW between IGRA and COSMIC in four seasons during 2007–2016 is presented in
Figure 4. The colored dots denote the results from IGRA radiosonde observations. The radiosonde stations are distributed unevenly in the Northern and Southern Hemispheres, and over 80% of radiosonde stations are in the Northern Hemisphere. Meanwhile, in the Southern Hemisphere, most stations are located in the continent of Australia and equatorial regions to the north of Australia. The dominant seasonal variations of PW derived from two observations are similar.
PW peaks in the tropical area with average values of 40 mm. The larger differences shown in
Figure 3 are assumed to be in this region, where PWs are generally larger than 30 mm. The scatterplot in
Figure 3 shows the latitudinal averaged results. The COSMIC PWs contain the information of both ocean and lands, while the IGRA PWs mainly show the results on land. According to
Figure 4, the IGRA stations usually located in the hot spots in the tropical region. This may be the reason for the IGRA PWs being larger than the COSMIC PWs in the region with PWs larger than 30 mm.
There are 3 PW maxima regions in the tropical area. One is located in the Amazon Plain, the second in Southeast Asia and the last in Congo basin. For the first peak region, the river Amazon and the large cover of tropical rainforests supply the upper atmosphere with sufficient water vapor. In addition, under the control of the intertropical convergence zone (ITCZ), the continual upward flow makes the supply stronger. The second region is Southeast Asia, surrounded by ocean, having a great amount of water vapor sources to the upper atmosphere. The last and smallest region of peak PW value is Congo basin, which also has a large area of rainforest, providing abundant water vapor to the upper level. The pattern of variations in PW is similar to the distribution of annual mean precipitation presented by Good et al. [
25] and Kuo et al.’s [
26], and all PW maxima regions have larger precipitation. In Holloway and Neelin’s [
27] research of the temporal relations of column water vapor and precipitation in the tropical area, they found an autocorrelation time of PW compared to precipitation and that PW increases consistently with mesoscale convective activity. This indicates that changes in PW can be used as a predictor of precipitation. In addition, in Kuo et al.’s [
26] research, the two-way interaction between PW and convection is revealed. Most published results indicated the complicated relationships between PW and rainfall. The regions with large PWs may have a few amounts of rainfall or even no rain. The dynamical processes also play a role in determining whether it will rain. On the other side, the local PWs may be not enough to support one rainstorm and the water vapor transport is also important to the precipitation events.
For mid-latitudes, PW is much smaller than in the tropics and it varies obviously in four seasons. Summer PWs are generally larger than other seasons. However, there is a consistent low PW region in all four seasons, which is in the southwest of China. The elevations of this region are relatively high, at about 3000 m or even higher. Stations of
Figure 2c with high elevation are only in this region. This implies that the elevation also has some impact on the PWs and that higher elevation has smaller PW.
In the polar regions, PW values decrease to less than 10 mm and do not show any seasonal variations. However, the Northern Hemisphere has a much brighter color in summer over the mid-latitude area, even over the Arctic, than that in the Southern Hemisphere summer. This might be associated with higher temperatures or active circulations in the summer of the Northern Hemisphere.
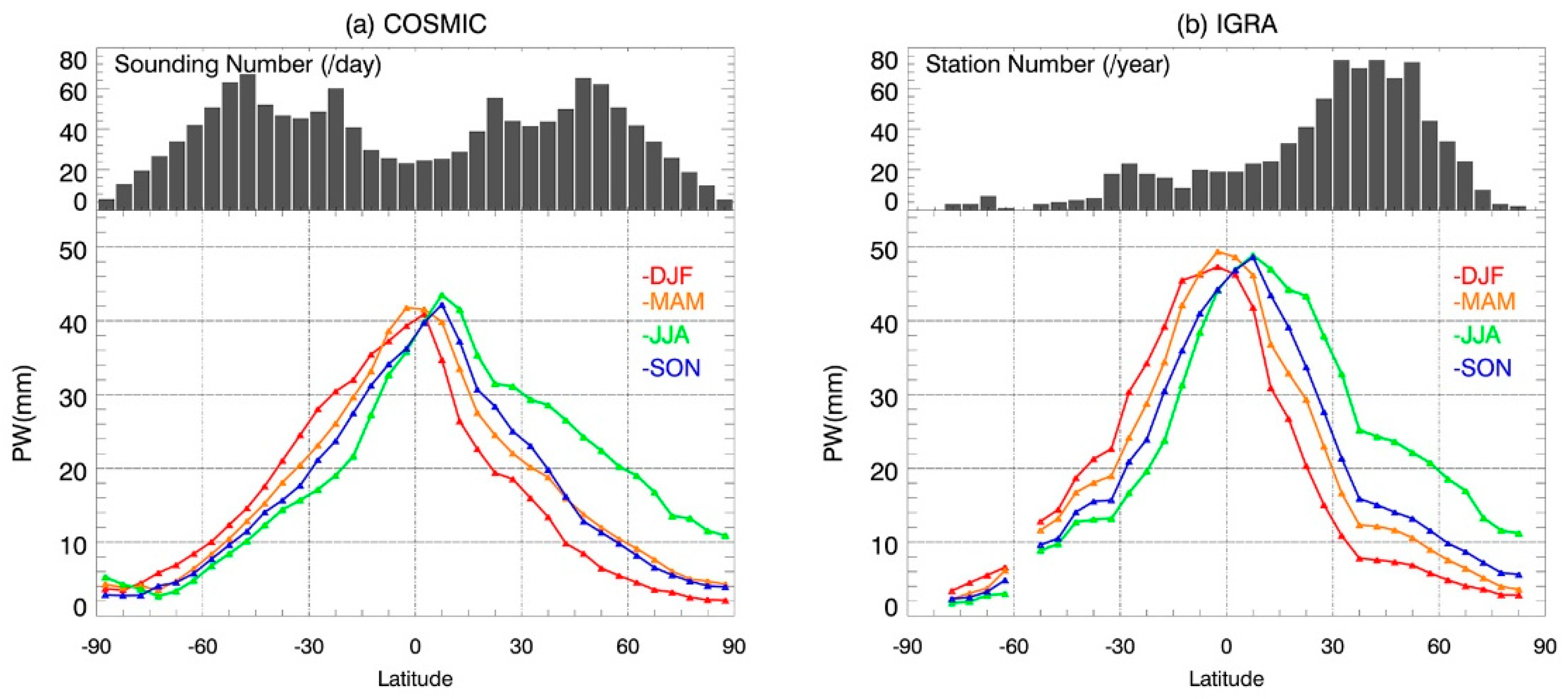
In order to investigate the detailed latitudinal variability of PW, zonal mean values are obtained in latitudinal bins. The numbers of soundings (COSMIC) and stations (IGRA) in each latitude bin are presented in
Figure 5. Note the sparse radiosonde station distribution in the southern hemisphere, which brings a larger uncertainty to the radiosonde results in this region (
Figure 5b). In general, the patterns of the latitudinal variation of two observational datasets are quite similar. These patterns are also consistent with the global precipitation variation decreasing from the tropics to two poles reported by Luo et al. [
28]. In the Southern Hemisphere, PWs are very similar in different seasons; while in the Northern Hemisphere, PWs in four seasons show larger differences in magnitude. For example, PW in the Northern Hemisphere summer is obviously larger than in the other three seasons, especially for the region with latitudes larger than 30° N. It is consistent that larger PW values occur in the summer of the Northern Hemisphere, as mentioned in
Figure 4.
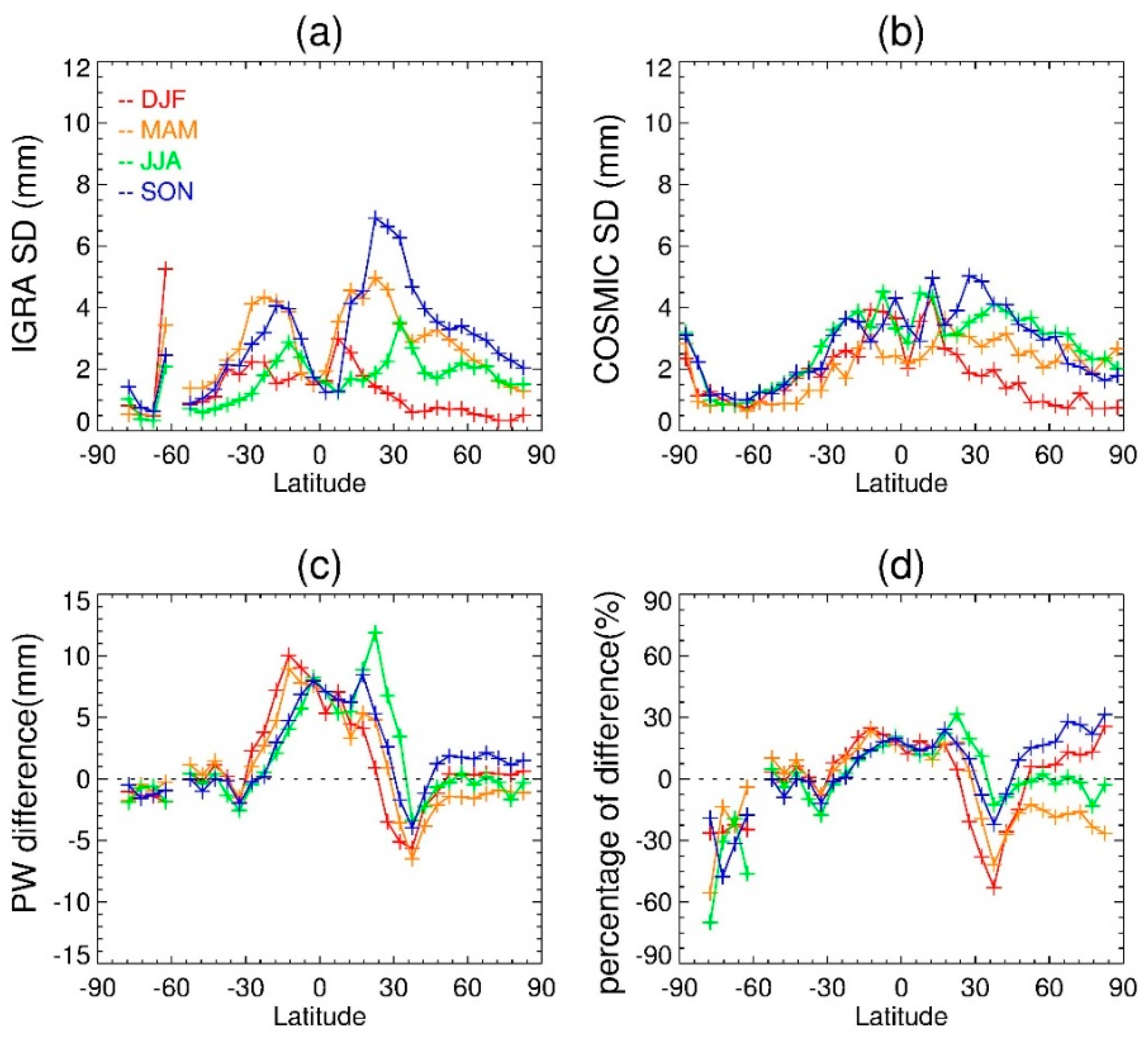
To quantify the differences between two observations, the PW differences of two observations in latitudinal variations are analyzed, along with the standard deviations of latitudinal seasonal results (
Figure 6). Regarding the standard deviations of two datasets, they are generally larger in the Northern Hemisphere. The larger standard deviations for the IGRA PWs may result from the inhomogeneous stations’ distribution. The differences range from −6 mm to 12 mm and vary in latitude (
Figure 6c). The distinct differences occur in the tropical area and they are generally more than 5 mm. The differences decrease linearly from the tropical region to the mid-latitudes. Overall, IGRA PW is larger than COSMIC PW. There are two exceptions. One is the high latitudes in the Southern Hemisphere, with a COSMIC PW 1 mm larger. The other one is the region around 30° N in the Northern Hemisphere: the COSMIC PWs are about 5 mm larger than the ones derived from radiosonde.
In addition, the different variations also show apparent seasonal features. For the 30° S to 30° N region, except for the equator region, differences in summer are usually greater than the ones in winter. No seasonal variations are found around the equator region. The seasonal differences are close there. Regarding the middle and high latitudes in the Southern Hemisphere, the differences do not show any seasonal variability either, and the values are around 0. On the other hand, for the middle and high latitudes in the Northern Hemisphere, the seasonal differences show a different pattern. The largest differences occur in autumn and spring, while differences in summer and winter are both close to 0. The IGRA PW is about 2 mm greater than the COSMIC PW in autumn, while it is the opposite situation for the spring. The PWs derived from COSMIC in autumn and spring are similar from about 40° N to 90° N (
Figure 5a). However, the IGRA PWs in autumn are generally greater than the ones in spring in this region (
Figure 5b), which may result in the different patterns in the seasonal differences (
Figure 6c).
In
Figure 6d, the percentage of PW differences of IGRA and COSMIC shows that large differences in magnitude do not equal large differences in percentage. Even though the differences in polar regions between two observations are small (
Figure 6c), the corresponding percentages of differences are relatively larger than the ones in the tropical region. For the regions from 60° S to 30° N, the differences in percentages are within 20%, with little seasonal variations. There are two latitudinal bins with percentages larger than 50%. One is the difference in winter and autumn over the Antarctic. For this region, the observation itself may have large uncertainties. The other one is the difference in winter in the region of about 35° N. As mentioned above, there is a consistent low PW region in all seasons in the southwest of China, which is around the 35° N latitude bin. The change points in four seasons in
Figure 5b may be related to this consistent low PW region, which results in the larger percentages in the differences between two data sets.
3.3. Trends in PW
Since the surface temperature has changed globally in recent decades, it is reasonable to ask whether PW has also changed in the past decades. Some earlier studies have reported PWs to have some significant changes regionally [
1,
6,
7,
8,
9,
13,
16]. We will pay more attention to the changes in global PWs, especially for the most recent decade.
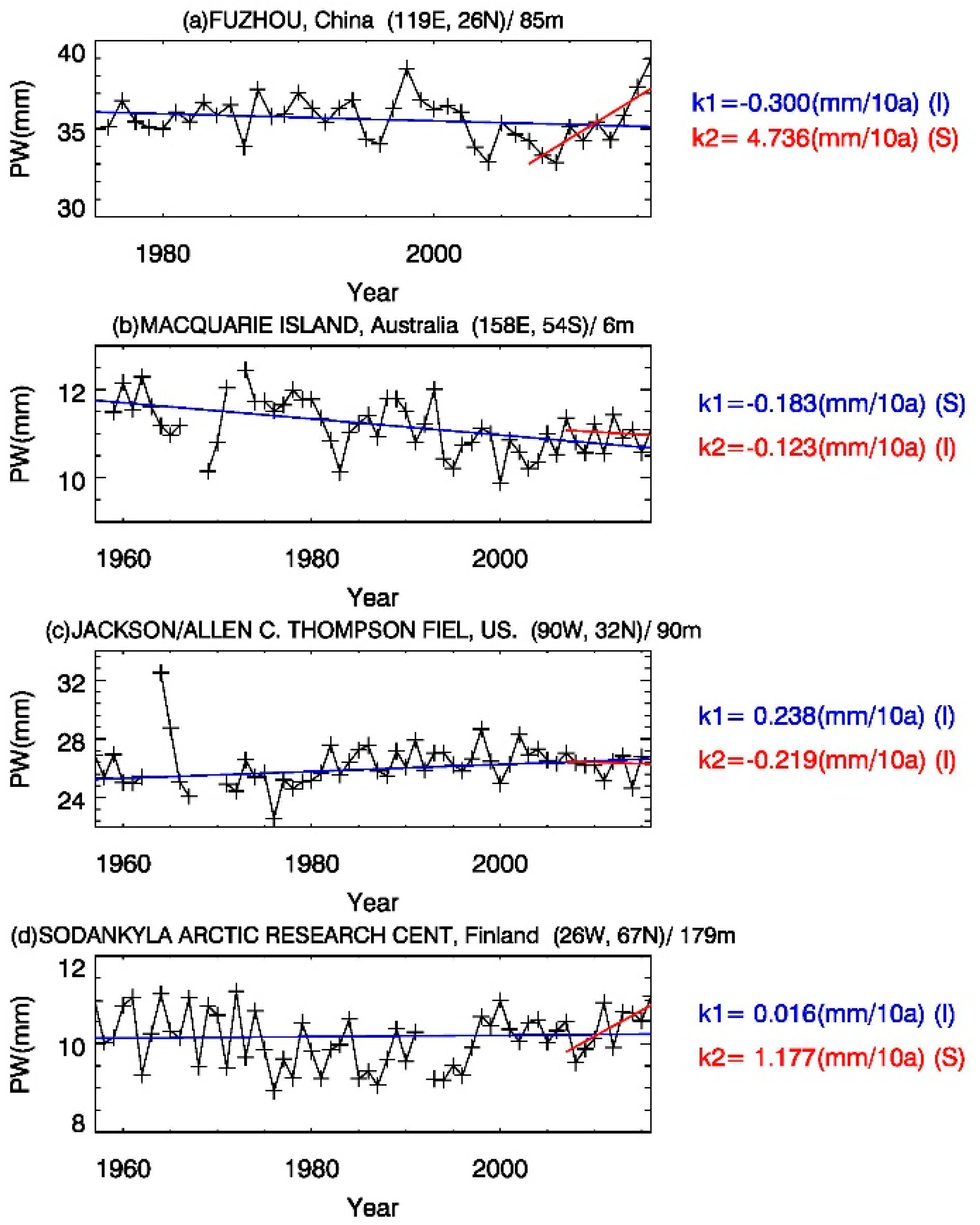
We firstly choose four stations from different countries (locations shown as blue triangles in
Figure 1) to investigate their PW trends in the last 60 years and in the most recent 10 years (
Figure 7). Different changes are found in the long-term periods and in the recent decade. For example, PWs at the station Fuzhou China (
Figure 7a) present an insignificant decreasing for the past several decades. However, it exhibits a statistically significant increasing trend in the past 10 years. The opposite situation is found at station Jackson/Allen C. Thompson Fiel, US, although both trends are not statistically significant. PWs in Australia show a consistent decrease in both periods, while PWs at the Finland station have not changed much in the long trend, but experienced a significant increasing trend in the most recent decade.
Since there are more than 60-year measurements from IGRA radiosonde observations, long-term changes in global PWs can be obtained. Stations with 60 complete years of PW observations are plotted and stations with significant trends are marked with bold black circles in
Figure 8. It can be found that most significant trends occur at those stations of the United States (US), Europe and Australia. PWs at all Australian stations present statistically significant decreasing trends in the last 60 years, while PWs at most stations in the US have increasing trends. Ross and Elliott [
6,
7] and Durre et al. [
8] both reported the increasing trends of PW in the US region during 1973–2006, which is consistent with our results.
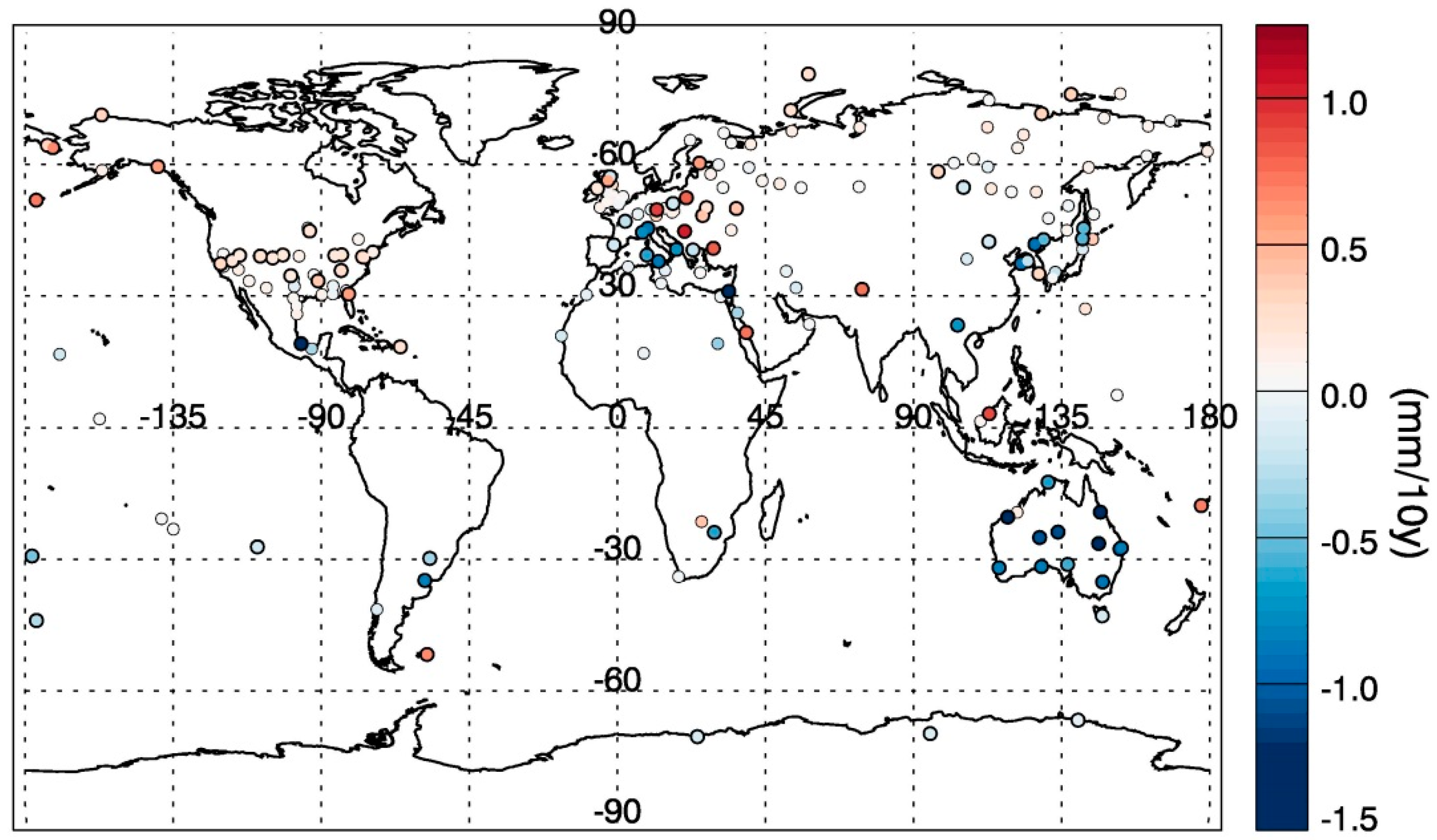
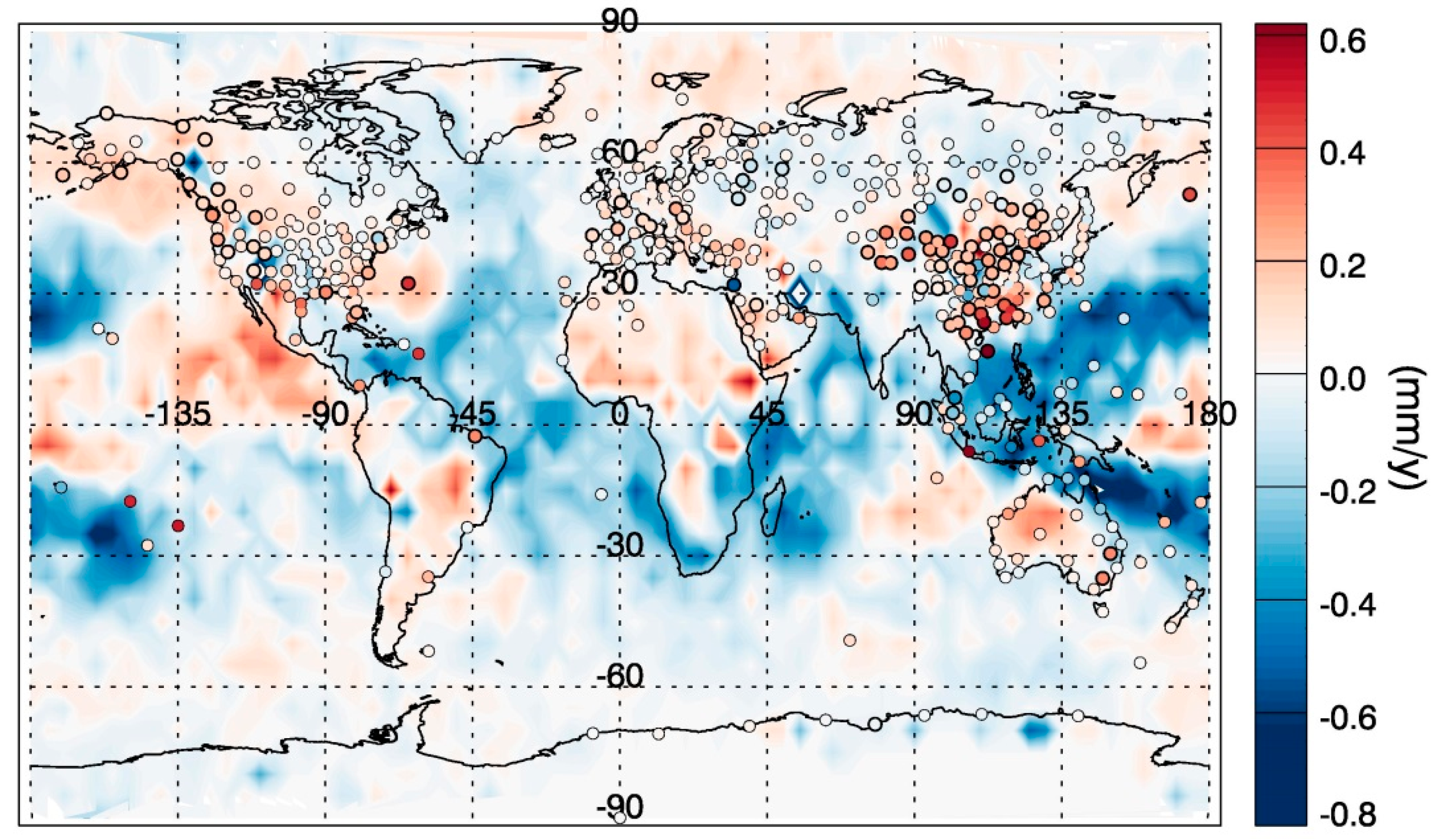
Besides the long-term trend in PW, we are more focused on PW changes in the recent 10 years. Since COSMIC observations perform quite well in comparison with radiosonde data and, more importantly, are covered globally and evenly, they can complement the limitation of IGRA observations. Based on COSMIC and radiosonde observations from 2007–2016,
Figure 9 presents the global changes in PW during the most recent decade. It shows an overall similar trend pattern in PW. For most ocean regions, PW has been decreasing in the last 10 years, especially in the tropical area. Except for the Antarctic and inland of the Eurasian continent lands, most land areas show a statistically significant increasing trend in PW. In addition, for North America and European region, PWs have been increasing for the last 10 years and also for last 60 years. On the other side, in Australia, Eastern Asia, and Mediterranean region, PW has been decreasing for last 60 years, but with increasing trend in the recent decade. Due to the lack of data accumulations, most Asian stations are not suitable for long-term trend analysis but show statistically significant increasing trends in the last decade.
Wang et al. [
23] analyzed the global PWs from 1988 to 2011 and found widespread positive trends of PW all over the world, including lands and oceans. However, according to
Figure 9, for the most recent 10 years, PWs have shown uptrends over land and downtrends over oceans, which means the widespread increase of water vapor in the troposphere over land. This rise of tropospheric water vapor might result in the increase of intensity and frequency of precipitation over land [
29,
30]. Zhai and Eskridge studied the relationship between PW and precipitation over China using the radiosonde observations from 1970 to 1990, and a positive correlation between these two variables is revealed [
16]. However, in recent research, more complicated relationships were reported between PW and precipitation. Wang et al. studied the variations in PWs and precipitation in mainland China during 1995–2012 and found that the regional trends in PW are not always consistent with the regional trends in precipitation [
1]. These imply that not all changes in precipitation can be explained by the changes in PW. The variation of PW might affect the global precipitation as PW is one of the sources of precipitation. But earlier researches on the relationships between precipitation and PW all show complicated associations of these two and the results vary from region to region. The global relationship of PW and precipitation needs to be further investigated in the future.