Multidecadal Variability in the Subseasonal Peak of Low-Level Convergence over the Pacific Warm Pool
Abstract
:1. Introduction
2. Data
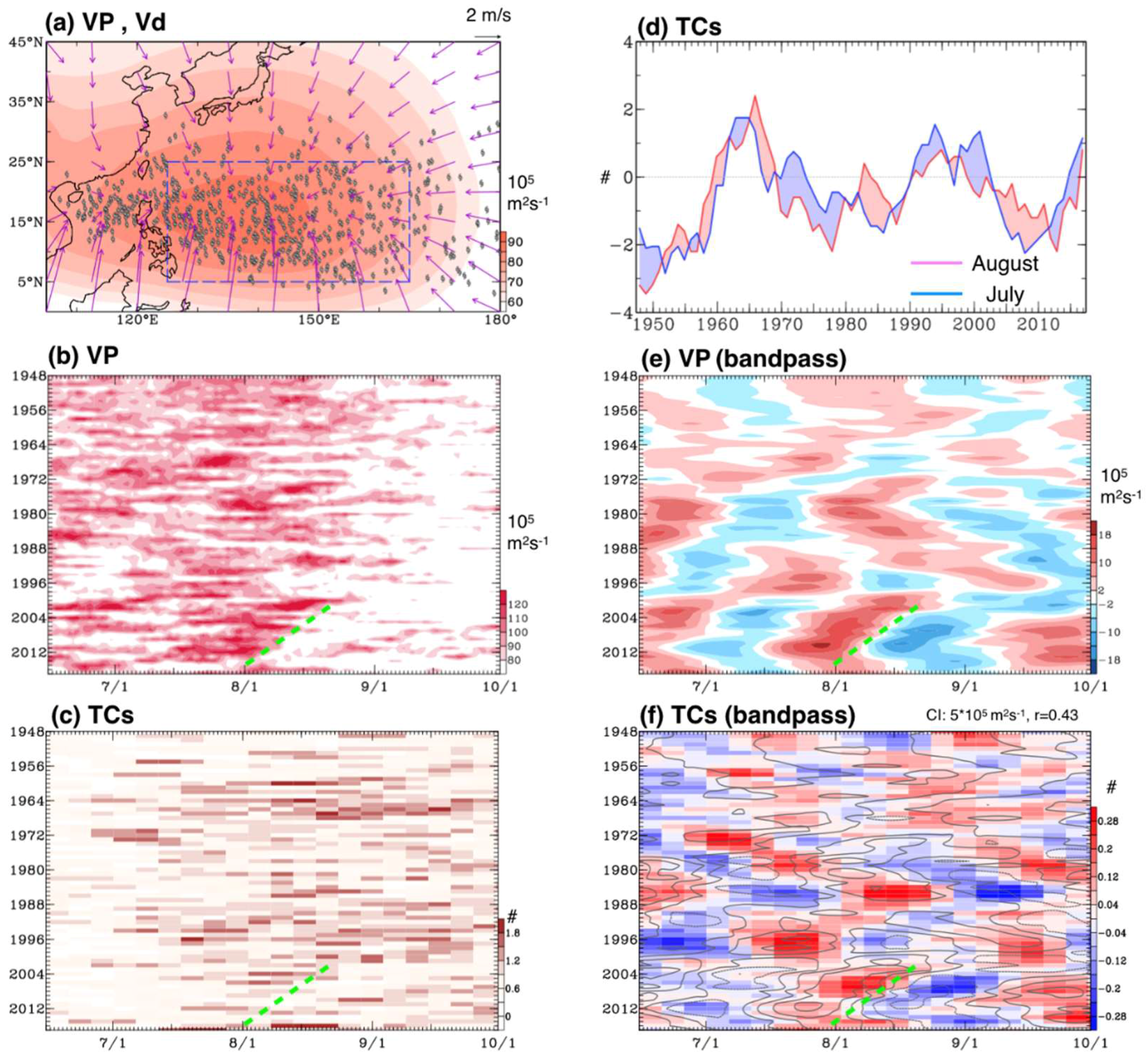
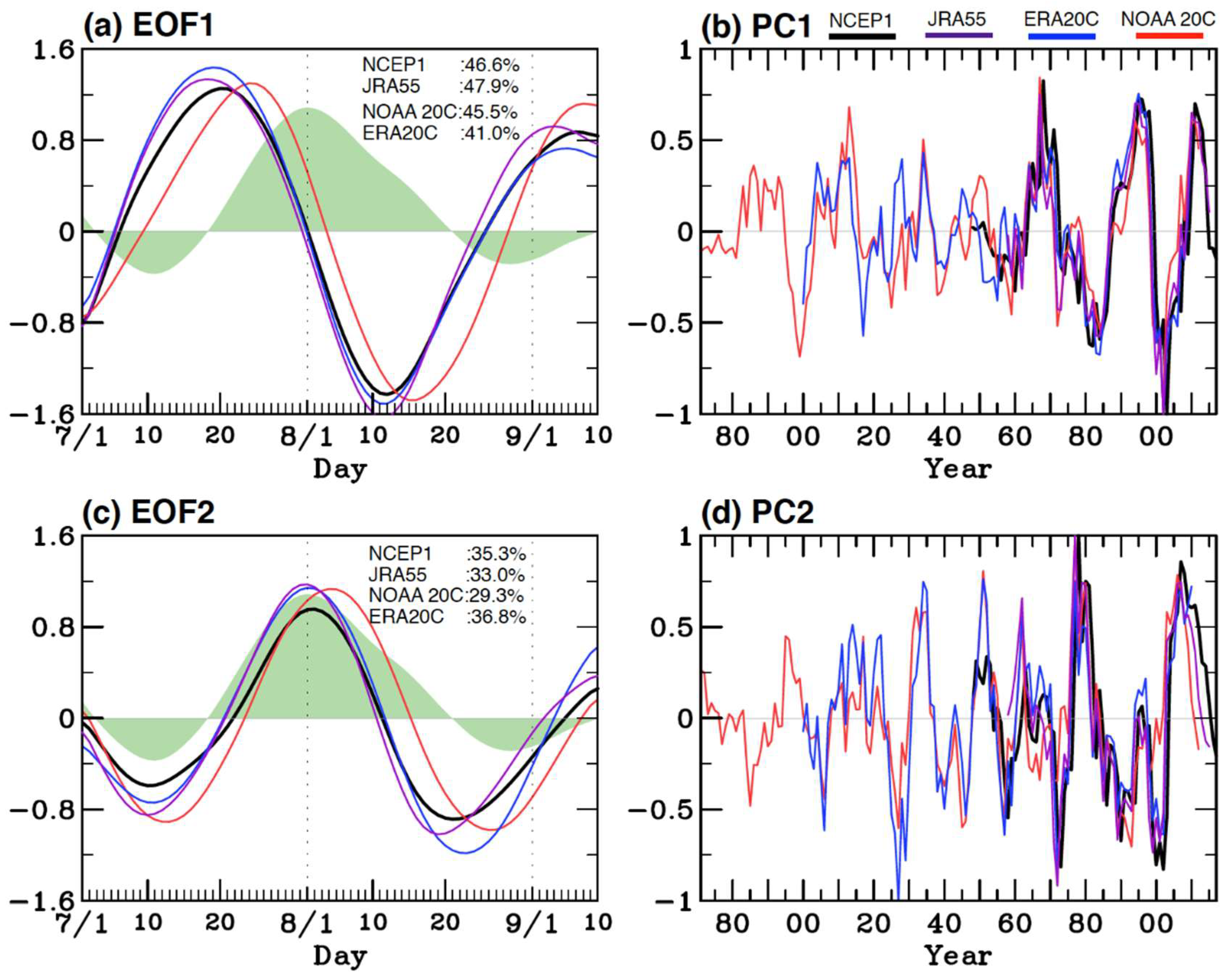
3. Empirical Analysis
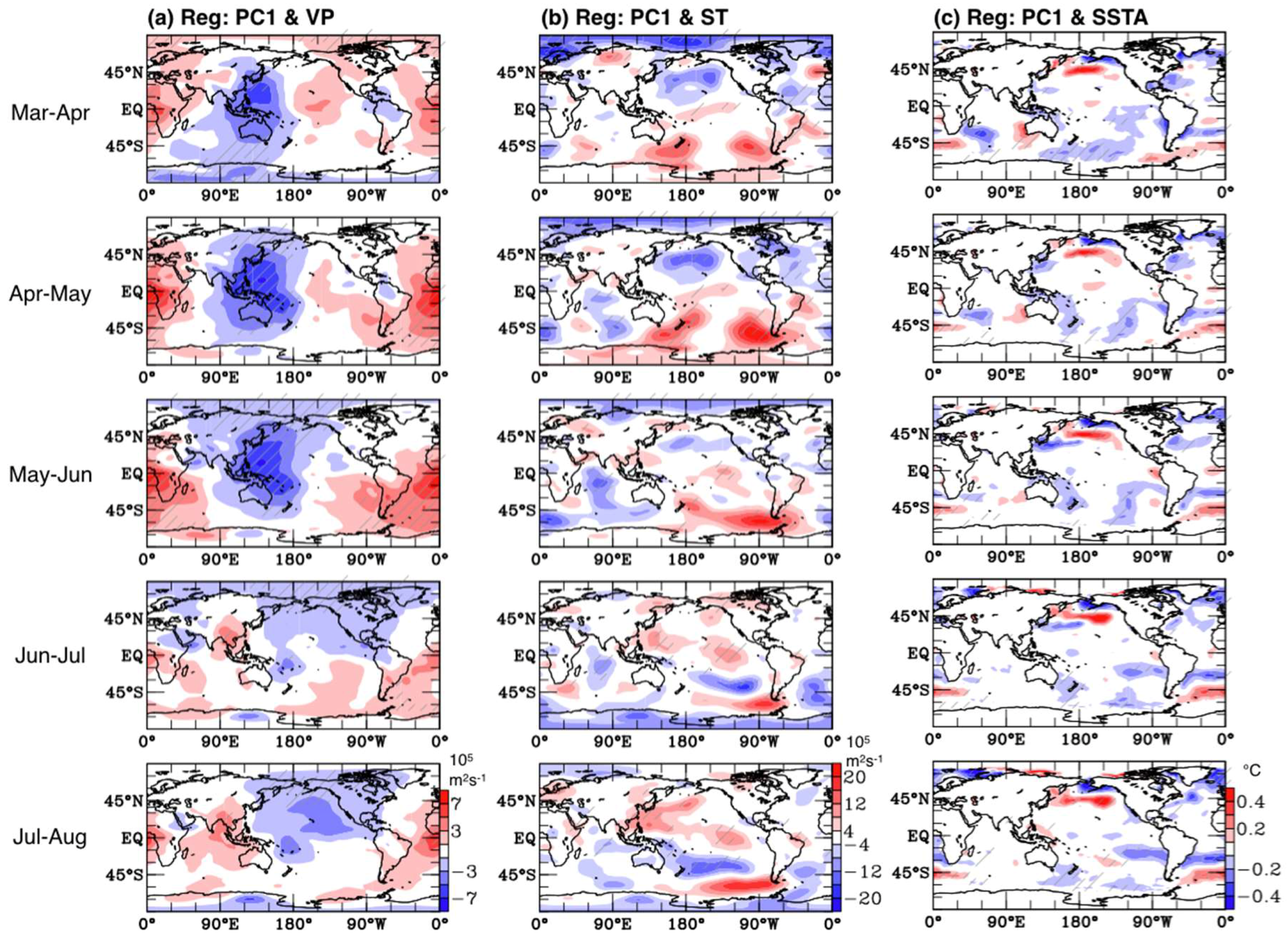
4. Possible Mechanisms
5. Summary
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Emanuel, K.; Sundararajan, R.; Williams, J. Hurricanes and global warming: Results from downscaling IPCC AR4 simulations. Bull. Am. Meteorol. Soc. 2008, 89, 347–367. [Google Scholar] [CrossRef]
- Chen, T.-C.; Wang, S.-Y.; Yen, M.-C.; Gallus, W.A., Jr. Role of the monsoon gyre in the interannual variation of tropical cyclone formation over the western North Pacific. Weather Forecast. 2004, 19, 776–785. [Google Scholar] [CrossRef]
- Liu, K.S.; Chan, J.C. Inactive Period of Western North Pacific Tropical Cyclone Activity in 1998–2011. J. Clim. 2013, 26, 2614–2630. [Google Scholar] [CrossRef]
- Yeh, S.-W.; Kang, S.-K.; Kirtman, B.P.; Kim, J.-H.; Kwon, M.-H.; Kim, C.-H. Decadal change in relationship between western North Pacific tropical cyclone frequency and the tropical Pacific SST. Meteorol. Atmos. Phys. 2010, 106, 179–189. [Google Scholar] [CrossRef]
- Jennings, R. Taiwan Aims to Rein in Water Use Amid Unusual Drought. Available online: http://www.latimes.com/world/asia/la-fg-taiwan-drought-20150510-story.html (accessed on 1 March 2018).
- Hong, C.-C.; Lee, M.-Y.; Hsu, H.-H.; Chang, T.-C. Compounding factors causing the unusual absence of tropical cyclones in the western North Pacific during August 2014. J. Geophys. Res. Atmos. 2016, 121, 9964–9976. [Google Scholar] [CrossRef]
- Harr, P.A.; Elsberry, R.L. Large-Scale Circulation Variability over the Tropical Western North Pacific. Part I: Spatial Patterns and Tropical Cyclone Characteristics. Mon. Weather Rev. 1995, 123, 1225–1246. [Google Scholar] [CrossRef]
- McBride, J.L. Tropical cyclone formation. In Global Perspective on Tropical Cyclones; WMO/TD-No. 693; World Meteorological Organization: Geneva, Switzerland, 1995; pp. 63–105. [Google Scholar]
- Sobel, A.H.; Maloney, E.D. Effect of ENSO and the MJO on western North Pacific tropical cyclones. Geophys. Res. Lett. 2000, 27, 1739–1742. [Google Scholar] [CrossRef]
- Maloney, E.D.; Dickinson, M.J. The Intraseasonal Oscillation and the Energetics of Summertime Tropical Western North Pacific Synoptic-Scale Disturbances. J. Atmos. Sci. 2003, 60, 2153–2168. [Google Scholar] [CrossRef]
- Chen, T.-C.; Wang, S.-Y.; Yen, M.-C.; Clark, A.J. Impact of the intraseasonal variability of the western North Pacific large-scale circulation on tropical cyclone tracks. Weather Forecast. 2009, 24, 646–666. [Google Scholar] [CrossRef]
- Huang, P.; Chou, C.; Huang, R. Seasonal modulation of tropical intraseasonal oscillations on tropical cyclone geneses in the western North Pacific. J. Clim. 2011, 24, 6339–6352. [Google Scholar] [CrossRef]
- Nakano, M.; Sawada, M.; Nasuno, T.; Satoh, M. Intraseasonal variability and tropical cyclogenesis in the western North Pacific simulated by a global nonhydrostatic atmospheric model. Geophys. Res. Lett. 2015, 42, 565–571. [Google Scholar] [CrossRef]
- Chen, T.-C.; Wang, S.-Y.; Yen, M.-C. Interannual variation of the tropical cyclone activity over the Western North Pacific. J. Clim. 2006, 19, 5709–5720. [Google Scholar] [CrossRef]
- Pohl, B.; Matthews, A.J. Observed changes in the lifetime and amplitude of the Madden–Julian Oscillation associated with interannual ENSO sea surface temperature anomalies. J. Clim. 2007, 20, 2659–2674. [Google Scholar] [CrossRef]
- Kim, J.; Ho, C.; Kim, H.; Sui, C.; Park, S.K. Systematic variation of summertime tropical cyclone activity in the western North Pacific in relation to the Madden–Julian oscillation. J. Clim. 2008, 21, 1171–1191. [Google Scholar] [CrossRef]
- Li, R.C.; Zhou, Y.W.; Chan, J.C.L.; Huang, P. Asymmetric modulation of western North Pacific cyclogenesis by the Madden–Julian oscillation under ENSO conditions. J. Clim. 2012, 25, 5374–5385. [Google Scholar] [CrossRef]
- Wang, B.; Chan, J.C.L. How Strong ENSO Events Affect Tropical Storm Activity over the Western North Pacific. J. Clim. 2002, 15, 1643–1658. [Google Scholar] [CrossRef]
- Camargo, S.J.; Emanuel, K.A.; Sobel, A.H. Use of a Genesis Potential Index to Diagnose ENSO Effects on Tropical Cyclone Genesis. J. Clim. 2010, 20, 4819–4834. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woolen, J.; et al. The NCEP/NCAR 40-Year Reanalysis Project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
- Huang, B.; Thorne, P.; Banzon, V.; Boyer, T.; Chepurin, G.; Lawrimore, J.; Menne, M.; Smith, T.; Vose, R.; Zhang, H. Extended Reconstructed Sea Surface Temperature version 5 (ERSSTv5): Upgrades, Validations, and Intercomparisons. J. Clim. 2017, 30, 8179–8205. [Google Scholar] [CrossRef]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H.; et al. The JRA-55 Reanalysis: General specifications and basic characteristics. J. Meteorol. Soc. Jpn. 2015, 93, 54–58. [Google Scholar] [CrossRef]
- Compo, G.P.; Whitaker, J.S.; Sardeshmukh, P.D.; Matsui, N.; Allan, R.J.; Yin, X.; Gleason, B.E.; Vose, R.S.; Rutledge, G.; Bessemoulin, P.; et al. The Twentieth Century Reanalysis Project. Q. J. R. Meteorol. Soc. 2011, 137, 12–18. [Google Scholar] [CrossRef]
- Compo, G.P.; Whitaker, J.S.; Sardeshmukh, P.D. Feasibility of a 100 year reanalysis using only surface pressure data. Bull. Am. Meteorol. Soc. 2006, 87, 175–190. [Google Scholar] [CrossRef]
- Whitaker, J.S.; Compo, G.P.; Wei, X.; Hamill, T.M. Reanalysis without radiosondes using ensemble data assimilation. Mon. Weather Rev. 2004, 132, 1190–1200. [Google Scholar] [CrossRef]
- Poli, P.; Hersbach, H.; Dee, D.P.; Berrisford, P.; Simmons, A.J.; Vitart, F.; Laloyaux, P.; Tan, D.G.H.; Peubey, C.; Thépaut, J.-N.; et al. ERA-20C: An atmospheric reanalysis of the twentieth century. J. Clim. 2016, 29, 4083–4097. [Google Scholar] [CrossRef]
- Wang, S.-Y.; Gillies, R.R.; Dool, H. On the yearly phase delay of winterintraseasonal mode in the western United States. Clim. Dyn. 2014, 42, 1649–1664. [Google Scholar] [CrossRef]
- Wang, S.-Y.S.; Lin, Y.-H.; Wu, C.-H. Interdecadal change of the active-phase summer monsoon in East Asia (Meiyu) since 1979. Atmos. Sci. Lett. 2016, 17, 128–134. [Google Scholar] [CrossRef]
- Madden, R.A.; Julian, P.R. Detection of a 40–50 day oscillation in the zonal wind in the tropical Pacific. J. Atmos. Sci. 1971, 28, 702–708. [Google Scholar] [CrossRef]
- Madden, R.A.; Julian, P.R. Description of global-scale circulation cells in the tropics with a 40–50 day period. J. Atmos. Sci. 1972, 29, 1109–1123. [Google Scholar] [CrossRef]
- Knutson, T.R.; Weickmann, K.M. 30–60 day atmospheric oscillations: Composite life cycles of convection and circulation anomalies. Mon. Weather Rev. 1987, 115, 1407–1436. [Google Scholar] [CrossRef]
- Hsu, H.-H.; Weng, C.-H. Northwestward Propagation of the Intraseasonal Oscillation in the Western North Pacific during the Boreal Summer: Structure and Mechanism. J. Clim. 2001, 14, 3834–3850. [Google Scholar] [CrossRef]
- Maloney, E.D.; Hartmann, D.L. The Madden–Julian oscillation, Barotropic dynamics, and North Pacific tropical cyclone formation. Part I: Observations. J. Atmos. Sci. 2001, 58, 2545–2558. [Google Scholar] [CrossRef]
- Wheeler, M.; Hendon, H.H. An all-season real-time multivariate MJO index: Development of an index for monitoring and prediction. Mon. Weather Rev. 2004, 132, 1917–1932. [Google Scholar] [CrossRef]
- Zhang, C.; Dong, M. Seasonality in the Madden–Julian oscillation. J. Clim. 2004, 17, 3169–3180. [Google Scholar] [CrossRef]
- Zhang, C. Madden-Julian Oscillation. Rev. Geophys. 2005, 43. [Google Scholar] [CrossRef]
- Miura, H.; Satoh, M.; Nasuno, T.; Noda, A.T.; Oouchi, K. A Madden–Julian Oscillation event realistically simulated by a global cloudresolving model. Science 2007, 318, 1763–1765. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.J.; Song, X. Interaction of deep and shallow convection is key to Madden-Julian Oscillation simulation. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Ling, J.; Zhang, C. Structural evolution in heating pro-files of the MJO in global reanalyses and TRMM retrievals. J. Clim. 2011, 24, 825–842. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.-H.; Wang, S.-Y.S. Multidecadal Variability in the Subseasonal Peak of Low-Level Convergence over the Pacific Warm Pool. Atmosphere 2018, 9, 158. https://doi.org/10.3390/atmos9050158
Lin Y-H, Wang S-YS. Multidecadal Variability in the Subseasonal Peak of Low-Level Convergence over the Pacific Warm Pool. Atmosphere. 2018; 9(5):158. https://doi.org/10.3390/atmos9050158
Chicago/Turabian StyleLin, Yen-Heng, and S.-Y. Simon Wang. 2018. "Multidecadal Variability in the Subseasonal Peak of Low-Level Convergence over the Pacific Warm Pool" Atmosphere 9, no. 5: 158. https://doi.org/10.3390/atmos9050158
APA StyleLin, Y.-H., & Wang, S.-Y. S. (2018). Multidecadal Variability in the Subseasonal Peak of Low-Level Convergence over the Pacific Warm Pool. Atmosphere, 9(5), 158. https://doi.org/10.3390/atmos9050158




