Next Article in Journal
Evaluating the Sensitivity of the Mass-Based Particle Removal Calculations for HVAC Filters in ISO 16890 to Assumptions for Aerosol Distributions
Next Article in Special Issue
Evaluations of WRF Sensitivities in Surface Simulations with an Ensemble Prediction System
Previous Article in Journal
Comprehensive Evaluation of Machine Learning Techniques for Estimating the Responses of Carbon Fluxes to Climatic Forces in Different Terrestrial Ecosystems
Previous Article in Special Issue
Improvement in the Modeled Representation of North American Monsoon Precipitation Using a Modified Kain–Fritsch Convective Parameterization Scheme
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 9
Issue 3
10.3390/atmos9030084
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Numerical Simulation of Heavy Rainfall in August 2014 over Japan and Analysis of Its Sensitivity to Sea Surface Temperature

by
Yuki Minamiguchi
*,
Hikari Shimadera
,
Tomohito Matsuo
and
Akira Kondo
Graduate School of Engineering, Osaka University, 2-1 Yamadaoka, Suita, Osaka 565-0871, Japan
*
Author to whom correspondence should be addressed.
Atmosphere 2018, 9(3), 84; https://doi.org/10.3390/atmos9030084
Submission received: 7 November 2017 / Revised: 22 February 2018 / Accepted: 23 February 2018 / Published: 26 February 2018
(This article belongs to the Special Issue WRF Simulations at the Mesoscale: From the Microscale to Macroscale)
Browse Figures
Versions Notes

Abstract

:
This study evaluated the performance of the Weather Research and Forecasting (WRF) model version 3.7 for simulating a series of rainfall events in August 2014 over Japan and investigated the impact of uncertainty in sea surface temperature (SST) on simulated rainfall in the record-high precipitation period. WRF simulations for the heavy rainfall were conducted for six different cases. The heavy rainfall events caused by typhoons and rain fronts were similarly accurately reproduced by three cases: the TQW_5km case with grid nudging for air temperature, humidity, and wind and with a horizontal resolution of 5 km; W_5km with wind nudging and 5-km resolution; and W_2.5km with wind nudging and 2.5-km resolution. Because the nudging for air temperature and humidity in TQW_5km suppresses the influence of SST change, and because W_2.5km requires larger computational load, W_5km was selected as the baseline case for a sensitivity analysis of SST. In the sensitivity analysis, SST around Japan was homogeneously changed by 1 K from the original SST data. The analysis showed that the SST increase led to a larger amount of precipitation in the study period in Japan, with the mean increase rate of precipitation being 13 ± 8% K−1. In addition, 99 percentile precipitation (100 mm d−1 in the baseline case) increased by 13% K−1 of SST warming. These results also indicate that an uncertainty of approximately 13% in the simulated heavy rainfall corresponds to an uncertainty of 1 K in SST data around Japan in the study period.

1. Introduction

In recent years, climate change has occurred as a consequence of global warming. The climate change results in severe precipitation events with more intense and more frequent rainfall, according to the Intergovernmental Panel on Climate Change (IPCC) Fifth Assessment Report [1]. This is because the saturation pressure of water vapor increases due to the air temperature rise under the global warming, and the amount of water vapor supplied from the sea increases due to the rise in sea surface temperature (SST). Based on the Clausius-Clapeyron (CC) relationship, the atmosphere can hold more moisture in warmer air temperatures with a rate of about 6–7% K−1, and extreme precipitation intensities can also increase by this rate because of global warming [2,3,4,5]. While daily extreme precipitation intensities typically increase with a warming atmosphere by within the rate expected from the CC relationship [6,7], changes in shorter duration precipitation extremes may well exceed the rate [6]. In terms of SST, it is virtually certain that the upper ocean (0–700 m) warmed from 1971 to 2010 [1], and SST around Japan will increase by about 0.6–2.1 K by 2100 [8]. According to the statistics over Japan for 1979 to 2013, annual maximum and 95 percentile precipitations have increased (2−4% per decade) with rising air temperature (0.29 K per decade) and SST (0.21 K per decade) [9].
A number of numerical studies on extreme weather events causing severe precipitation have been conducted [10,11,12,13,14,15]. Numerous previous studies have reported that global warming, including SST warming, can lead to intensifications of tropical cyclones [16,17,18,19,20] and extreme precipitation events [21,22,23,24]. For analyses of climate change impacts, although projections by general circulation models have been widely used [13,14,15,21,25], a number of recent studies have employed regional climate models with finer horizontal resolutions (1–10 km) [11,12,18,19,20,22,24], which better represent geographical characteristics and fine scale atmospheric dynamics. The Weather Research and Forecasting (WRF) model [26] has been the most frequently used as a regional model.
SST influences atmospheric circulation and precipitation processes [27,28,29], and its warming may increase heavy rainfall intensities. The impact of SST on precipitation in an actual weather event can be estimated by comparing precipitations simulated with realistic and changed SST boundary conditions. Several numerical studies focusing on actual weather events have investigated this impact with this method: Pepler et al. [30] estimated that the impact of local SST change by 1–2 K on precipitation was 8–12% on the east coast of Australia in rainfall events caused by local cyclones during 2007–2008; Takahashi et al. [31] examined the impact of SST in the Japan Sea in a typical winter heavy-snowfall season from December 2005 to February 2006, and reported that the calculated precipitation on the Japan Sea side of Japan increased by 6–12% K−1; and Manda et al. [22] revealed that the rapid seasonal SST rising in East China Sea caused torrential rainfall events over western Japan in early summer of 2012 by the Baiu (Meiyu) monsoon front.
As mentioned above, SST has a large impact on precipitation, and therefore, reliable SST data are required to accurately simulate heavy precipitation. SST data typically depend on observational or reanalyzed SST datasets, and the accuracy of SST data are limited by atmospheric water vapor and aerosols observed by satellite [32,33,34]. Previous studies [34,35,36,37] compared multiple SST dataset, and they indicated that there were uncertainties that affected the atmospheric circulation. Additionally, Fu and Wang [36] showed that tropical cyclone’s intensity depended on SST dataset. Therefore, it is essential to evaluate the impact of uncertainty in SST on simulated heavy precipitation.
In this study, we focused on a series of heavy rainfall events over Japan in August 2014 [38], when Typhoons Nakri and Halong attacked Japan, and rain fronts frequently passed over. The total precipitation of the month was the largest on record for August in western Japan. During this period, torrential rain and storms caused serious damage in Japan such as landslides, inundations, floods, and other disasters. Typhoon Nakri occurred in the east of the Philippines on 29 July 2014, and approached the Okinawa and Amami Islands from July 31 to August 1. The typhoon caused heavy rain in Japan even after it turned into a tropical depression in the Yellow Sea on August 3. Typhoon Halong, which occurred on the east of Guam on July 29, approached the Daito Islands on August 7. It approached and passed through the Shikoku and Kinki regions in western Japan from August 9 to 10, causing the highest peak precipitation in the series of events. In the last half of the month, rain fronts stagnated near Japan and led to frequent occurrence of intense rainfall events. On August 20, landslides occurred at Hiroshima city following an intense rain of more than 100 mm h−1. During these events, warm and humid air was continuously supplied from south of Japan.
There are the following two purposes in this study: one is to evaluate the performance of WRF for simulating the heavy rainfall events over Japan in August 2014, and the other is to investigate the impact of uncertainty in SST on the WRF simulation of the recent record-high summertime precipitation. This paper describes a set of numerical simulations of heavy rainfall and its sensitivity to SST using WRF version 3.7. First, WRF simulations were conducted with six different settings, and their performances for reproducing precipitation were evaluated. Then, a numerical experiment with an optimal setting selected based on the performance evaluation and with changed SST data was conducted in order to evaluate the impact of uncertainty in SST on simulated heavy precipitation.

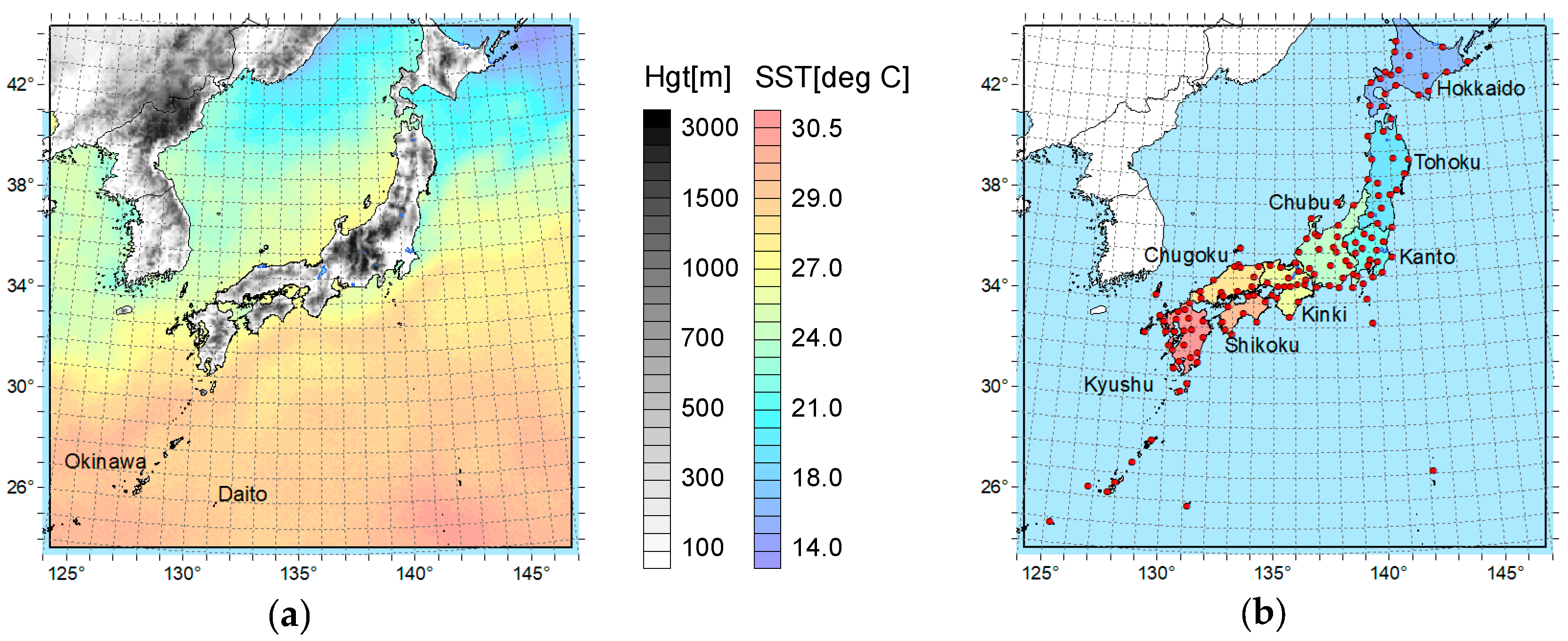
2. Methods

2.1. Common WRF Configurations

This study focused on the series of heavy rainfall events in August 2014. WRF simulations were conducted from 1 July to 31 August 2014 with July as a spin-up period. Figure 1 shows the WRF modeling domain on the Lambert conformal conic projection map, which has an area of 2250 km × 2250 km and covers almost all of Japan. The vertical layers consisted of 40 sigma-pressure coordinated layers from the surface to 100 hPa. Figure 1a also shows average SST in the study period, which tended to be higher than that in August of 1981–2010 according to the Japan Meteorological Agency (JMA) [39]. As shown in Figure 1b, there are 147 meteorological observatories for validation of WRF simulation in the domain. The area of Japan was divided into eight regions consisting of Hokkaido, Tohoku, Kanto, Chubu, Kinki, Chugoku, Shikoku, and Kyushu. The numbers of observatories in these regions are 18, 17, 17, 26, 15, 14, 9, and 31, respectively.
Static geographical data, objective analysis data, and physical parameterizations used in this study were similar to those used by Shimadera et al. [40]. Topography and land use were derived from the 30-s resolution data of the United States Geological Survey and the 100-m resolution National Land Numerical Information data of the Geospatial Information Authority of Japan, respectively. Initial and boundary conditions in the atmosphere were derived from the mesoscale model grid point value (MSM GPV) data produced by JMA [41]. Daily SST was derived from the high-resolution, real-time, global sea surface temperature analysis data (RTG_SST_HR) by the U.S. National Centers for Environmental Prediction (NCEP) [42] in order to conduct WRF simulations with time-varying SST. Initial conditions of variables on the ground surface and in soil layers were derived from the final operational global analysis (FNL) data by NCEP [43]. The MSM GPV data have spatial resolutions of 0.0625° (longitude) × 0.05° (latitude) for ground level data and 0.125° (longitude) × 0.1° (latitude) for pressure level data and a temporal resolution of 3 h. The RTG_SST_HR data have a spatial resolution of 0.0833° and a temporal resolution of 24 h. The FNL data have a spatial resolution of 1° and a temporal resolution of 6 h. The physical parameterizations used in this study include the Yonsei University scheme [44] for the planetary boundary layer parameterization, the WRF single-moment 6-class microphysics scheme [45], the Noah land surface model [46], the rapid radiative transfer model [47] for long wave radiation, and the Dudhia scheme [48] for the shortwave radiation. Previous studies [40,49] showed that WRF accurately reproduced meteorological fields in Japan with these physical parameterizations. However, because Shimadera et al. [40] also mentioned that there were difficulties in simulating summertime precipitation accurately at a certain time and location, this study evaluated the WRF results mainly by spatially integrated values. Further studies with different physical parameterizations may enable the improvement of the model performance for summertime precipitation.

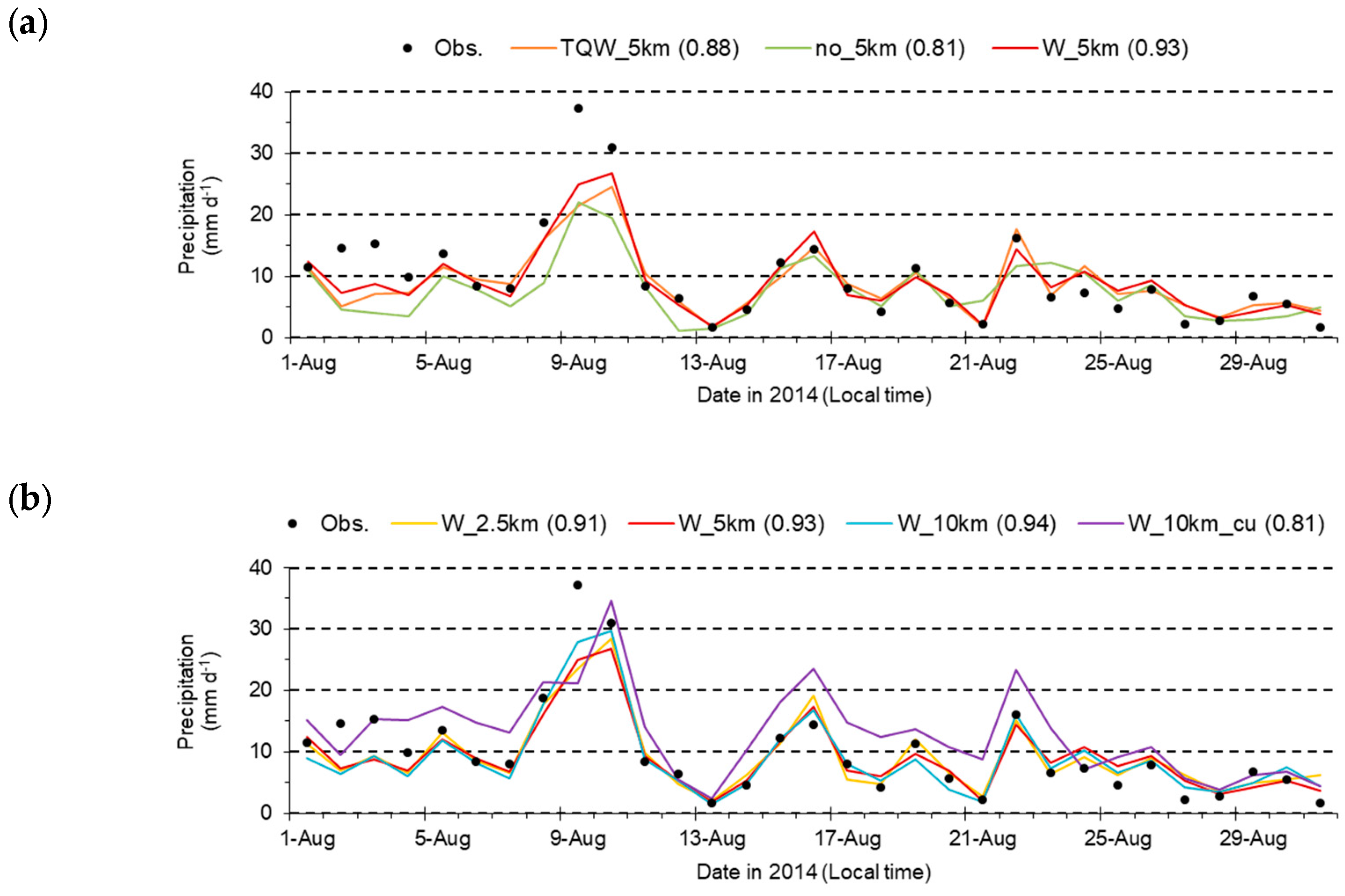
2.2. Selection of Optimal WRF Setting

In order to determine an optimal setting for examining the sensitivity of heavy precipitation to SST, WRF simulations were conducted for six cases summarized in Table 1. The six cases with the common configurations described in Section 2.1 have differences in configurations of the grid nudging, the horizontal grid resolution, and the cumulus parameterization.
Regarding the nudging, we compared the following three cases: TQW_5km with the nudging for potential temperature, mixing ratio and horizontal wind components, no_5km without the nudging, and W_5km with the nudging for horizontal wind components. The nudging may improve a long-term simulation in a large domain. However, since the nudging suppresses the influence of SST change, it is preferable not to apply the nudging, especially for air temperature and humidity that are strongly influenced by SST, in the sensitivity experiment. Therefore, the setting with the minimum nudging should be selected as an optimal setting after confirming its good reproducibility. The nudging for potential temperature, mixing ratio, and horizontal wind components was applied with nudging coefficients of 1.0 × 10−4 s−1, 1.0 × 10−5 s−1, and 1.0 × 10−4 s−1, respectively, in the entire simulation domain and period with the MSM GPV data.
W_2.5km, W_5km, and W_10km cases were conducted to evaluate the impact of the horizontal resolution on the model performance. These resolutions and the numbers of grid cells are 2.5, 5, 10 km, and 900 × 900, 450 × 450 and 225 × 225, respectively. A simulation with finer spatial resolution requires larger computational cost because of larger number of grid cells and shorter integration time step. Therefore, an optimal setting should reproduce meteorological fields accurately with as coarse resolution as possible. Additionally, in W_10km_cu case, the cumulus parameterization of Kain [50] was applied in order to investigate whether we should apply the cumulus scheme for representing sub-grid scale clouds in the case with relatively coarse resolution.
The results of the WRF simulation were compared with ground-level observation data of daily air temperature, humidity, wind speed, and precipitation derived from monthly datasets by JMA [51]. The model performance was evaluated using the Pearson’s correlation coefficient (r), the mean bias error (MBE), the mean absolute error (MAE), the root mean square error (RMSE), and the index of agreement (IA). IA is defined by
IA = 1 − ∑ i = 1 N ( M i − O i ) 2 ∑ i = 1 N ( | M i − O ¯ | + | O i − O ¯ | ) 2
in which M i and O i are simulated and observed value at a certain observation point and a time i , M ¯ and O ¯ are mean values of simulated and observed values at all the observation points and times, respectively, and N is the number of samples. IA was proposed by Willmott [52] and varies between 0 and 1. IA = 1 indicates a perfect match between observed and simulated variables. Emery et al. [53] set benchmarks with statistical measures for the performance of meteorological models: MBE ≤ ±0.5 °C, MAE ≤ 2 °C, and IA ≥ 0.8 for air temperature; MBE ≤ ±1 g kg−1, MAE ≤ 2 g kg−1, and IA ≥ 0.6 for specific humidity; MBE ≤ ±0.5 m s−1, RMSE ≤ 2 m s−1, and IA ≥ 0.6 for wind speed. There are many previous studies that use these benchmarks around the world, for example, Europe (Cartelle et al. [54]), China (Fu et al. [55]), and also Japan (Shimadera et al. [40,49]).

2.3. Sensitivity Analysis on SST

A numerical experiment was conducted in order to estimate the sensitivity of precipitation to SST in the heavy rainfall in August 2014. An optimal WRF setting determined through comparisons of the six cases described in Section 2.2 was used as the baseline case of the sensitivity analysis. In the sensitivity analysis, WRF simulations were performed for SST+1 and SST−1 cases, in which SST over the entire domain was homogeneously added and subtracted by 1 K from the original SST data, respectively, like a previous study [31]. Note that feedbacks from the atmosphere to the sea surface, such as SST decrease due to enhanced evaporation by strengthened wind, were not considered in this study, because the WRF simulations were conducted with external SST data.

3. Results and Discussion

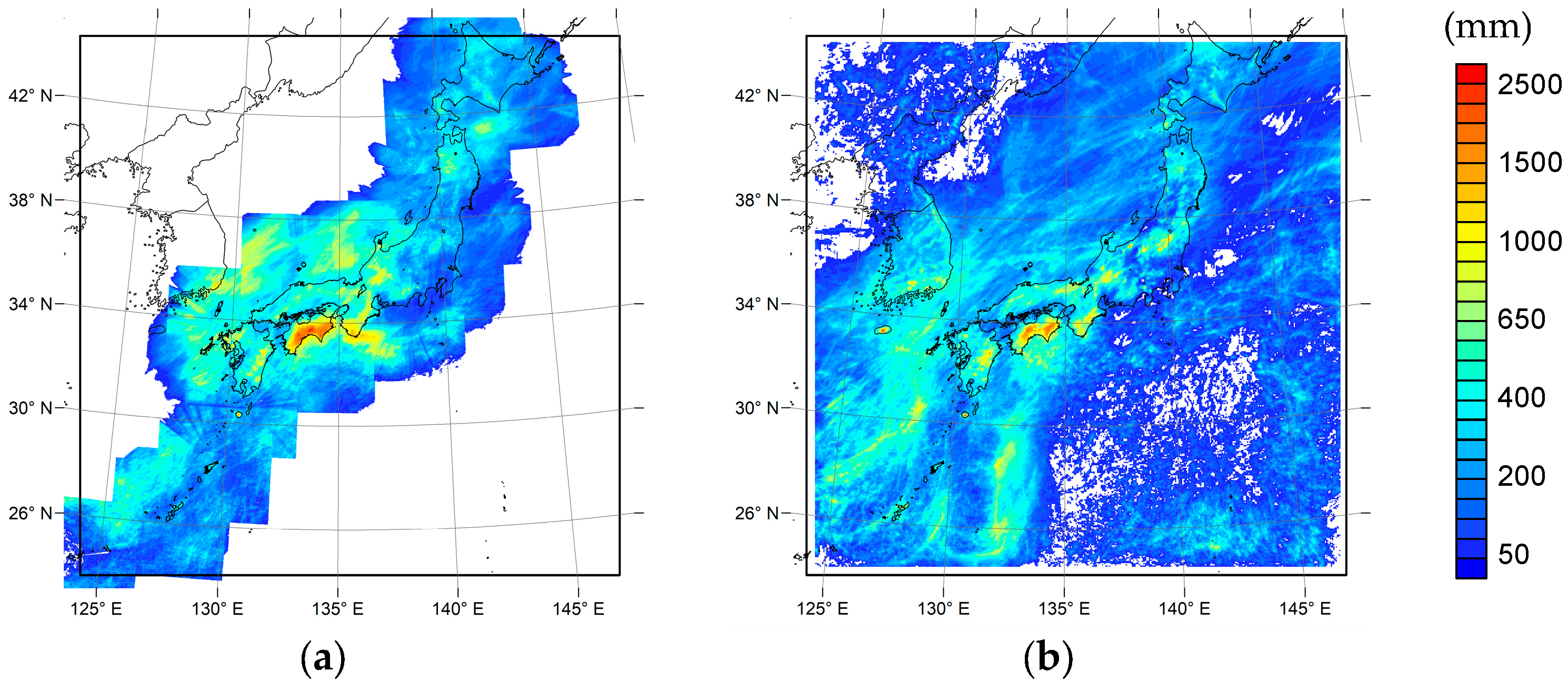
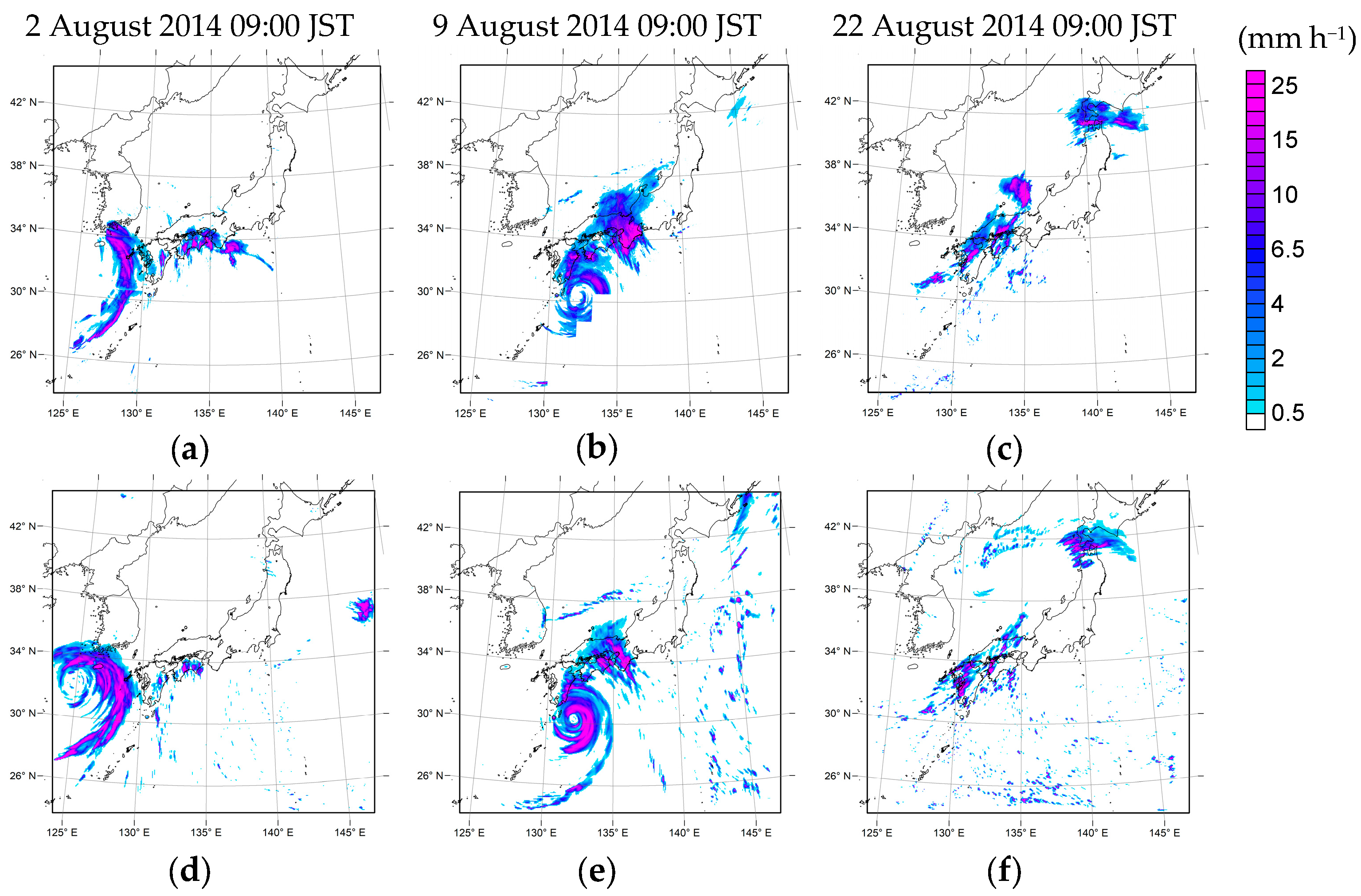
3.1. Reproducibility of the Heavy Rainfall

Table 2 summarizes statistical values for the WRF performance at the meteorological observatories in August 2014. The statistical comparisons indicated that simulated air temperature, specific humidity, and wind speed were all in good agreement with observed values. For air temperature and specific humidity, the model satisfied all the Emery’s benchmarks in all the six settings with high correlations between the observed and simulated values. For wind speed, the model tended to overestimate, but met the benchmarks for RMSE and IA in all simulations. For precipitation, the values of r and IA were not as high as those for the other three weather elements because of the difficulty in simulating precipitation at a specific location and/or time. However, there were relatively clear differences in the model performances. Among the six simulation cases, TQW_5km, W_5km, and W_2.5km cases better agreed with the observations according to r and IA.
Figure 2 shows time series comparisons of the observed and simulated daily precipitations averaged for all the meteorological observatories with corresponding r values. As mentioned in chapter 1, precipitation was predominantly caused by Typhoons Nakri and Halong in the first half of the study period (1–15 August), and by rain fronts in the last half (16–31 August). The peak precipitation from August 9–10 was associated with Typhoon Halong that approached and passed through the Shikoku and Kinki regions in the period. While WRF tended to underestimate this peak precipitation, the model approximately simulated the spatially averaged temporal variation patterns. Figure 3 shows mean daily precipitation averaged for the meteorological observatories in each of the eight regions (Figure 1b) for the first and last halves of August 2014. During the first half of the period characterized by the two typhoons, precipitation varied significantly by region, with especially large values in the Shikoku and Kinki regions as a result of Typhoon Halong. Although WRF tended to underestimate the amount of precipitation in the Shikoku and Kinki regions with large values, the amount was the largest in the Shikoku region followed by the Kinki, Kyushu, and Chugoku regions both in the observation and simulation, indicating that the model accurately captured the spatial variation pattern. Meanwhile, during the last half characterized by rain fronts, there was indistinct spatial variation in the temporal mean precipitation. WRF accurately reproduced the amount of precipitation in the period, except for the overestimation in W_10km_cu case.
The following paragraphs describe comparisons to determine each optimal setting for the sensitivity analysis of SST in terms of the grid nudging, the horizontal resolution, and the cumulus scheme.
First, according to a comparison of TQW_5km, W_5km, and no_5km cases in terms of the nudging, no_5km case showed the worst performance for simulating the heavy rainfall in August 2014, with the largest underestimation of precipitation, the lowest IA for daily precipitation (Table 2), and the least accurate temporal variation of daily precipitation (Figure 2a). In contrast, the performances of TQW_5km and W_5km cases were equivalently accurate. Since it is desirable to minimize the application of the nudging in SST change experiment, the optimal setting is the nudging only for horizontal wind components.
When comparing W_2.5km, W_5km, and W_10km in terms of the horizontal resolution, although the three cases similarly accurately captured the spatially averaged temporal variation of daily precipitation (Figure 2b), W_10km case showed slightly worse performance compared to W_2.5km and W_5km cases, with lower IA for daily precipitation (Table 2). Meanwhile, the performances of W_2.5km and W_5km cases were almost equivalent to each other. Therefore, the horizontal resolution of 5 km with a smaller computational load was selected as the optimal setting for the sensitivity analysis.
Concerning the cumulus parameterization, the reproducibility of precipitation in W_10km_cu case was inferior to that in W_10km case, with lower IA (Table 2) and almost consistent overestimations (Figure 2b and Figure 3) in W_10km_cu case. Therefore, the application of the cumulus scheme of Kain [50] is not acceptable in this study.
From these results, we decided to conduct the SST change experiment under the optimal setting with the nudging only for horizontal wind components, as well as the horizontal resolution of 5 km and without the cumulus scheme, namely W_5km case. The horizontal resolution of around 5 km has been widely used in previous studies [11,18,24,31,56]. The W_5km case captured the amount of precipitation in the extreme heavy rainfall due to typhoons in the Shikoku region being the best among all cases except for W_10km_cu case (Figure 3a), which clearly overestimated the amount of precipitation during the last half of the month (Figure 2b and Figure 3b).
Spatial distribution of simulated precipitation in W_5km case was compared with that of observed precipitation obtained from the Radar/Raingauge-Analyzed Precipitation data by JMA [57]. The Radar/Raingauge-Analyzed Precipitation data has a spatial resolution of 1 km and a temporal resolution of 30 minutes, and covers areas within a few hundred kilometers from the coastal lines of Japan. Figure 4 shows spatial distributions of the observed and simulated monthly precipitations in August 2014. Although W_5km case slightly underestimated the largest amount of monthly precipitation in the Shikoku region caused by Typhoons Nakri and Halong, it approximately reproduced the spatial variation pattern over the land area in Japan. Figure 5 illustrates spatial distributions of observed and simulated hourly precipitations at 09:00 JST on 2 August 2014 for Typhoon Nakri, on 9 August for Typhoon Halong and on 22 August for a rain front associated with an extratropical cyclone. Table 3 shows observed and simulated minimum surface pressures and their positions of Typhoon Nakri and Halong at these times. The W_5km case roughly captured distribution patterns of precipitation in the heavy rainfall events. It also captured their intensities and tracks of cyclones.

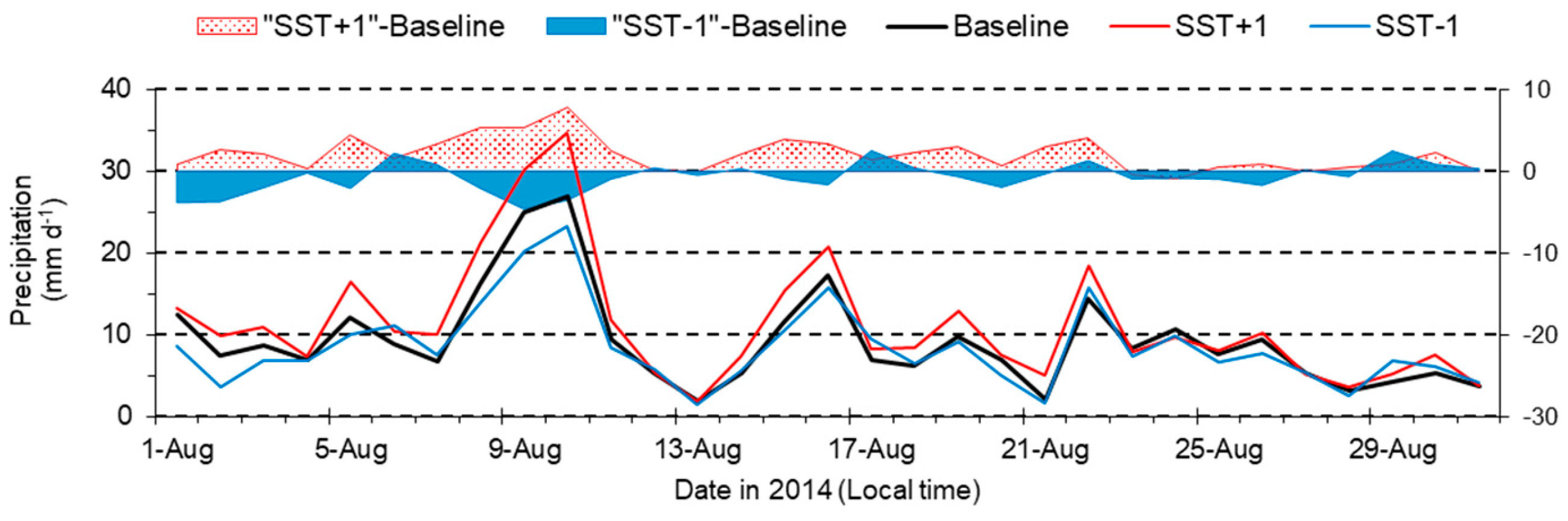
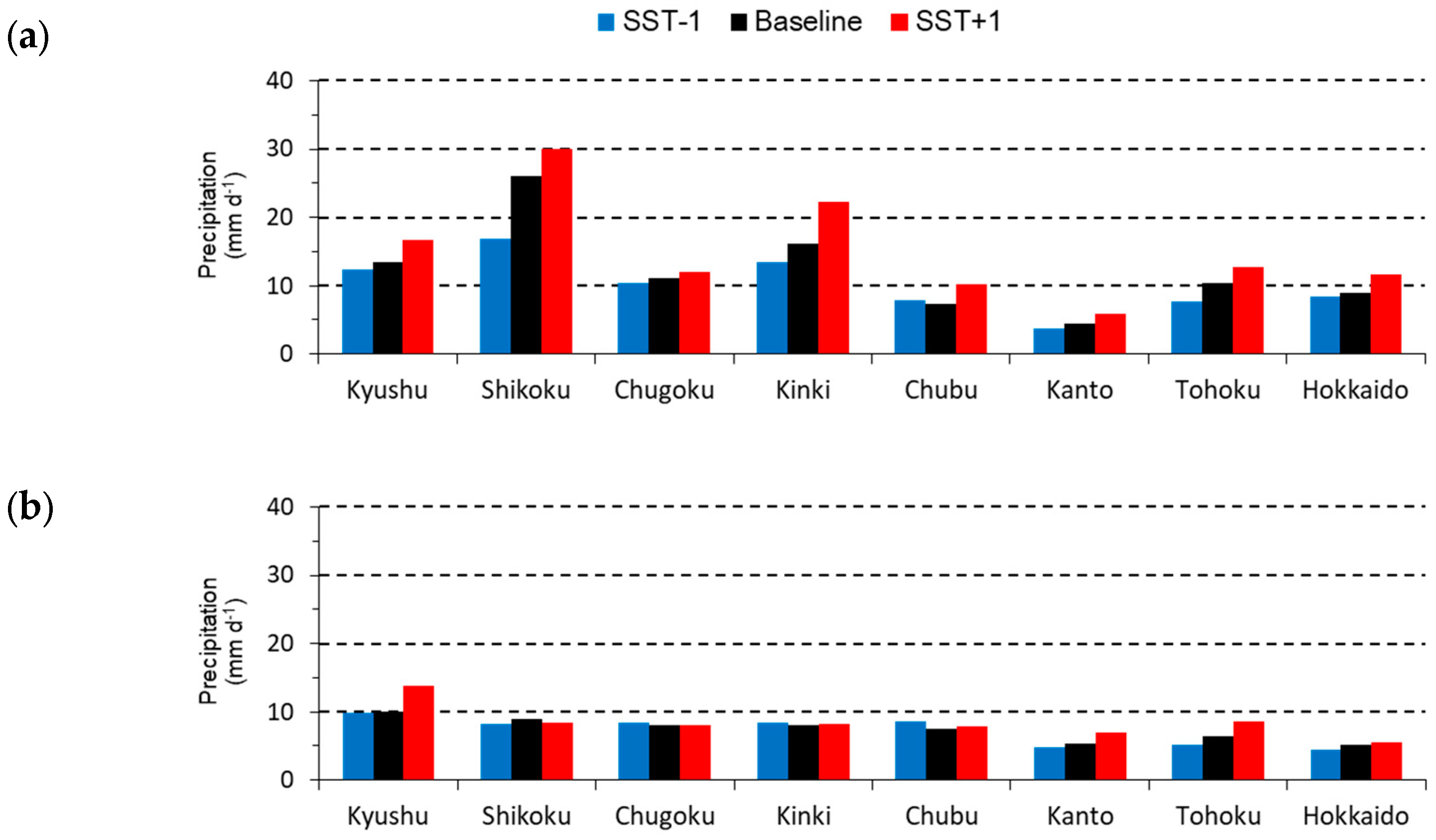
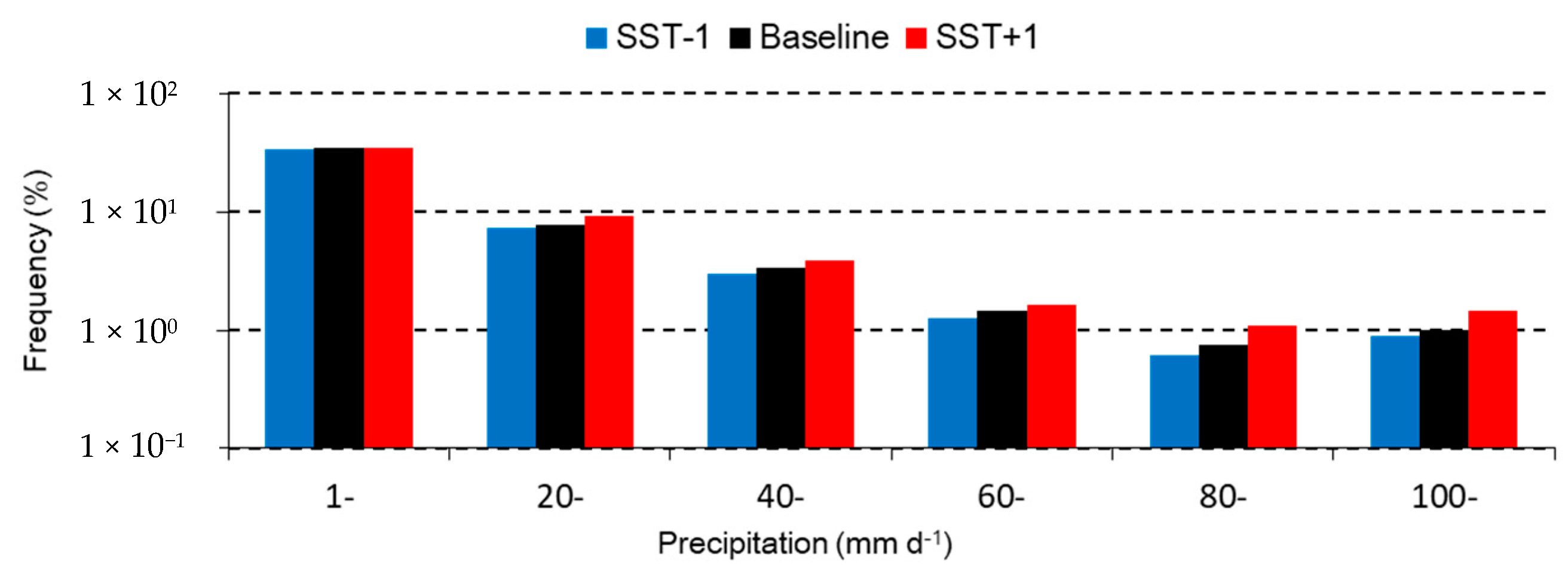
3.2. Sensitivity of Precipitation to SST

The sensitivity of the heavy rainfall in August 2014 to SST was analyzed by comparing W_5km as the baseline case with SST+1 and SST−1 cases, in which SST was homogeneously added and subtracted by 1 K from the original SST data, respectively. As the comprehensive results of the SST change the experiment, Table 4 shows monthly precipitation, monthly mean 2-m air temperature, and latent and sensible heat fluxes averaged over the land area of Japan, the sea area, and the entire area in the modeling domain. The results indicate that SST warming contributed to the increase in precipitation on the whole. SST warming increased the latent heat flux from the sea surface, namely the supply of water vapor to the atmosphere, which resulted in a larger amount of precipitable water. Meanwhile, SST warming also increased the sensible heat flux from the sea surface and increased the air temperature. Since the saturation pressure of water vapor increases with increasing air temperature, higher air temperature can prevent cloud formations. Although SST warming has both positive and negative impacts on the amount of precipitation, it is concluded that precipitation typically increases with SST warming within the range of SST in this study. The mean increase amount (rate) of precipitation by SST warming was 46 ± 30 mm month−1 K−1 (13 ± 8% K−1) over the land area of Japan. This result indicates that a 1 K uncertainty in SST corresponds to an approximately 13% uncertainty in the simulated heavy precipitation. Takahashi et al. [31] estimated that the impact of SST on winter precipitation on the Japan Sea side of Japan was by 6−12% K−1. Pepler et al. [30] estimated that the impact of local SST change by 1–2 K on rainfall was 8−12% on the east coast of Australia. The sensitivity of the heavy rainfall in August 2014 in Japan to SST estimated in this study was similar to those in the previous studies focusing on different meteorological conditions. In the SST change cases, the changes of air temperature from the baseline case were smaller than those of SST, because the lateral boundary conditions were the same as those of the baseline case. In addition, because air temperature near the sea surface was affected by SST, the atmosphere in SST+1 (SST−1) case was more unstable (stable) than that in the baseline case, which probably contributed to an enhancement (attenuation) of convection and an increase (decrease) of precipitation. As a result, the increase rate of precipitation to SST warming was higher than 7% K−1 due to atmospheric warming based on the CC relationship.
The SST sensitivity was also analyzed in terms of temporal and spatial variations. Figure 6 shows a time series comparison of daily precipitations averaged for all the meteorological observatories in the different SST cases. Figure 7 shows mean daily precipitation averaged for the meteorological observatories in each of the eight regions (Figure 1b) for the first half of August 2014 associated with the two typhoons and the last half associated with rain fronts. Figure 8 illustrates spatial distributions of daily precipitation difference from the baseline case in the SST change cases for the two periods. The increase in precipitation with warming SST was remarkable over southern to western Japan including the Kinki and Shikoku regions where there was a large amount of precipitation associated with Typhoons Nakri and Halong (Figure 4b and Figure 5d,e) during the first half of August 2014. By contrast, there were smaller changes in the amount of precipitation related to rain fronts during the last half of the month. As a result, the mean increase amounts of precipitation by SST warming were 2.2 ± 1.4 and 0.9 ± 1.2 mm d−1 K−1 over the land area of Japan in the first and last halves, respectively. The large difference between the two periods was probably due to the difference in the total precipitation (larger in the first half and smaller in the last), because the difference in the corresponding increase rates (15 ± 9 and 10 ± 13% K−1 for the first and last halves, respectively) was less clear. Although the amount of precipitation generally increased with warming SST, negative impacts of SST change on precipitation were also widely distributed (Figure 8). For example, in the Chubu region, the amount of precipitation in SST−1 case was larger than that in the baseline case for the two periods (Figure 7). These results reflect the non-linear relationship between SST and precipitation.
Figure 9 shows frequency distribution of daily precipitation at the meteorological observatories in August 2014 in SST−1, the baseline, and SST+1 cases. The frequencies of precipitation with an intensity of more than 1 mm d−1 were 47, 50, and 52% in SST−1, the baseline, and SST+1 cases, respectively. Among the three cases, the daily precipitation more than 20 mm was the most frequent in SST+1 case. These results indicate that SST warming contributed to increases in both precipitation duration and intensity. As a result, 99 percentile value of daily precipitation (100 mm d−1 in the baseline case) increased by 13% K−1 along with increasing SST.
The sensitivity analysis showed that the mean change of simulated precipitation caused by SST change in the heavy rainfall over Japan in August 2014 was approximately 13% K−1. This result indicates that an uncertainty of approximately 13% in the simulated heavy rainfall corresponds to an uncertainty of 1 K in SST data around Japan in the study period.

4. Conclusions

This study was conducted to evaluate the WRF performance for simulating the heavy rainfall events over Japan in August 2014, and to investigate the impact of uncertainty in SST on simulated precipitation fields in the period. First, WRF simulations were conducted with six different settings, and their performances for reproducing precipitation were evaluated. Then, a numerical experiment with an optimal setting selected based on the performance evaluation and with changed SST data was conducted for examining the sensitivity of simulated heavy precipitation to SST.
The six settings for the WRF simulations had different configurations of the grid nudging (with the nudging for air temperature, humidity, and horizontal wind components, without the nudging or with the wind nudging), the horizontal grid resolution (2.5, 5 or 10 km), and the cumulus parameterization (applied to the case with the wind nudging and 10-km resolution). Among the six settings, the following three similarly accurately reproduced the heavy rainfall: TQW_5km with the air temperature, humidity and wind nudging, and 5-km resolution; W_5km with the wind nudging and 5-km resolution; and W_2.5km with the wind nudging and 2.5-km resolution. Among these three settings, W_5km was decided as the optimal setting for the SST sensitivity study, because the nudging for air temperature and humidity in TQW_5km suppresses the influence of SST change, and W_2.5km requires larger computational load. In the first half of August 2014 characterized by Typhoons Nakri and Halong, although precipitation peaks tended to be underestimated, spatial and temporal variation patterns of precipitation were accurately captured in the W_5km case. Meanwhile, in the last half characterized by rain fronts, the amount of precipitation was accurately reproduced in W_5km case.
In the sensitivity analysis, SST was uniformly added and subtracted by 1 K. Although there were both positive and negative responses of precipitation to SST changes depending on time and region, precipitation generally increased with warming SST because of the increasing water supply to the atmosphere. As a result, the mean increase amounts (rates) in precipitation over the land area of Japan by SST warming were 46 ± 30 mm month−1 K−1 (13 ± 8% K−1), 2.2 ± 1.4 mm d−1 K−1 (15 ± 9 % K−1), and 0.9 ± 1.2 mm d−1 K−1 (10 ± 13% K−1) in the month and the first and last halves of the month, respectively. In addition, the increase rate of the 99 percentile value of daily precipitation (100 mm d−1 in the baseline case) by SST warming was 13% K−1. These results are interpreted as an uncertainty of approximately 13% in the simulated heavy rainfall over Japan in August 2014 that is associated with an uncertainty of 1 K in SST data around Japan during that period.

Acknowledgments

This research was supported by JSPS KAKENHI Grant Number 26420581 and 26740038. MSM GPV data were provided by the Japan Meteorological Business Support Center.

Author Contributions

Yuki Minamiguchi performed the numerical simulations, analyzed the data, and also wrote the paper. Hikari Shimadera prepared the numerical simulation system including analysis tools and designed the numerical experiments. Tomohito Matsuo and Akira Kondo provided significant suggestions on data analyses. All the authors have read and approved the final manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Intergovernmental Panel on Climate Change. CLIMATE CHANGE 2014 Synthesis Report; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2014. [Google Scholar]
  2. Boer, G.J. Climate change and the regulation of the surface moisture and energy budgets. Clim. Dyn. 1993, 8, 225–239. [Google Scholar] [CrossRef]
  3. Allen, M.R.; Ingram, W.J. Constraints on the future changes in climate and the hydrological cycle. Nature 2002, 419, 224–232. [Google Scholar] [CrossRef] [PubMed]
  4. Trenberth, K.E.; Dai, A.; Rasmussen, R.M.; Parsons, D.B. The changing character of precipitation. Bull. Am. Meteorol. Soc. 2003, 84, 1205–1217. [Google Scholar] [CrossRef]
  5. Pall, P.; Allen, M.R.; Stone, D.A. Testing the Clausius–Clapeyron constraint on changes in extreme precipitation under CO2 warming. Clim. Dyn. 2007, 28, 351–363. [Google Scholar] [CrossRef]
  6. Lenderink, G.; van Meijgaard, E. Increase in hourly precipitation extremes beyond expectations from temperature changes. Nat. Geosci. 2008, 1, 511–514. [Google Scholar] [CrossRef]
  7. Nayak, S.; Dairaku, K. Future changes in extreme precipitation intensities associated with temperature under SRES A1B scenario. Hydrol. Res. Lett. 2016, 10, 139–144. [Google Scholar] [CrossRef]
  8. Japan Meteorological Agency. Global Warming Projection Vol. 7; Japan Meteorological Agency: Chiyoda-ku, Japan, 2008. (In Japanese)
  9. Fujibe, F. Relationship between Interannual Variations of Extreme Hourly Precipitation and Air/Sea-Surface Temperature in Japan. SOLA 2015, 11, 5–9. [Google Scholar] [CrossRef]
  10. Cruz, F.T.; Narisma, G.T. WRF simulation of the heavy rainfall over Metropolitan Manila, Philippines during tropical cyclone Ketsana: A sensitivity study. Meteorol. Atmos. Phys. 2016, 128, 415–428. [Google Scholar] [CrossRef]
  11. Ishikawa, H.; Oku, Y.; Kim, S.; Takemi, T.; Yoshino, J. Estimation of a possible maximum flood event in the Tone River basin, Japan caused by a tropical cyclone. Hydrol. Processes 2013, 27, 3292–3300. [Google Scholar] [CrossRef]
  12. Nakamura, R.; Shibayama, T.; Esteban, M.; Iwamoto, T. Future typhoon and storm surges under different global warming scenarios: Case study of typhoon Haiyan (2013). Nat. Hazards 2016, 82, 1645–1681. [Google Scholar] [CrossRef]
  13. Yoshida, K.; Sugi, M.; Mizuta, R.; Murakami, H.; Ishii, M. Future Changes in Tropical Cyclone Activity in High-Resolution Large-Ensemble Simulations. Geophys. Res. Lett. 2017, 44, 9910–9917. [Google Scholar] [CrossRef]
  14. Brayshaw, D.J.; Hoskins, B.; Blackburn, M. The Basic Ingredients of the North Atlantic Storm Track. Part II: Sea Surface Temperature. J. Atmos. Sci. 2011, 68, 1784–1805. [Google Scholar] [CrossRef]
  15. Sugi, M.; Noda, A.; Sato, N. Influence of the Global Warming on Tropical Cyclone Climatology: An Experiment with the JMA Global Model. J. Meteorol. Soc. Japan 2002, 80, 249–272. [Google Scholar] [CrossRef]
  16. Knutson, T.R.; McBride, J.L.; Chan, J.; Emanuel, K.; Holland, G.; Landsea, C.; Held, I.; Kossin, J.P.; Srivastava, A.K.; Sugi, M. Tropical cyclones and climate change. Nat. Geosci. 2010, 3, 157–163. [Google Scholar] [CrossRef] [Green Version]
  17. Yamada, Y.; Satoh, M.; Sugi, M.; Kodama, C.; Noda, A.T.; Nakano, M.; Nasuno, T. Response of Tropical Cyclone Activity and Structure to Global Warming in a High-Resolution Global Nonhydrostatic Model. J. Clim. 2017, 30, 9703–9724. [Google Scholar] [CrossRef]
  18. Kanada, S.; Takemi, T.; Kato, M.; Yamasaki, S.; Fudeyasu, H.; Tsuboki, K.; Arakawa, O.; Takayabu, I. A Multimodel Intercomparison of an Intense Typhoon in Future, Warmer Climates by Four 5-km-Mesh Models. J. Clim. 2017, 30, 6017–6036. [Google Scholar] [CrossRef]
  19. Takayabu, I.; Hibino, K.; Sasaki, H.; Shiogama, H.; Mori, N.; Shibutani, Y.; Takemi, T. Climate change effects on the worst-case storm surge: A case study of Typhoon Haiyan. Environ. Res. Lett. 2015, 10, 064011. [Google Scholar] [CrossRef]
  20. Lackmann, G.M. Hurricane Sandy before 1900 and after 2100. Bull. Am. Meteorol. Soc. 2015, 96, 547–560. [Google Scholar] [CrossRef]
  21. Volosciuk, C.; Maraun, D.; Semenov, V.A.; Tilinia, N.; Gulev, S.K.; Latif, M. Rising Mediterranean Sea Surface Temperatures Amplify Extreme Summer Precipitation in Central Europe. Sci. Rep. 2016, 6, 32450. [Google Scholar] [CrossRef] [PubMed]
  22. Manda, A.; Nakamura, H.; Iizuka, S.; Miyama, T.; Moteki, Q.; Yoshioka, M.K.; Nishii, K.; Miyasaka, T. Impacts of a warming marginal sea on torrential rainfall organized under the Asian summer monsoon. Sci. Rep. 2014, 4, 5741. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  23. Lee, D.K.; Cha, D.H.; Kang, H.S. Regional climate simulation of the 1998 summer flood over East Asia. J. Meteorol. Soc. Japan 2004, 82, 1735–1753. [Google Scholar] [CrossRef]
  24. Lyra, A.; Tavares, P.; Chou, S.C.; Sueiro, G.; Dereczynski, C.; Sondermann, M.; Silva, A.; Marengo, J.; Giarolla, A. Climate change projections over three metropolitan regions in Southeast Brazil using the non-hydrostatic Eta regional climate model at 5-km resolution. Theor. Appl. Climatol. 2017, 1–20. [Google Scholar] [CrossRef]
  25. Zhang, X.; Zwiers, F.W.; Li, G.; Wan, H.; Cannon, A.J. Complexity in estimating past and future extreme short-duration rainfall. Nat. Geosci. 2017, 10, 255–259. [Google Scholar] [CrossRef]
  26. Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Baker, D.M.; Duda, M.G.; Huang, X.-Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; Technical Note TN-475+STR; NCAR: Boulder, CO, USA, 2008. [Google Scholar]
  27. Ting, M.; Wang, H. Summertime U.S. Precipitation Variability and Its Relation to Pacific Sea Surface Temperature. J. Clim. 1997, 10, 1853–1873. [Google Scholar] [CrossRef]
  28. Yamamoto, M.; Hirose, N. Influence of assimilated SST on regional atmospheric simulation: A case of a cold-air outbreak over the Japan Sea. Atmos. Res. 2008, 9, 13–17. [Google Scholar] [CrossRef]
  29. Iizuka, S. Simulations of wintertime precipitation in the vicinity of Japan: Sensitivity to fine-scale distributions of sea surface temperature. J. Geophys. Res. 2010, 115, D10107. [Google Scholar] [CrossRef]
  30. Pepler, A.S.; Alexander, L.V.; Evans, J.P.; Sherwood, S.C. The influence of local sea surface temperatures on Australian east coast cyclones. J. Geophys. Res. Atmos. 2016, 121, 352–363. [Google Scholar] [CrossRef]
  31. Takahashi, H.; Ishizaki, N.; Kawase, H.; Hara, M.; Yoshikane, T.; Ma, X.; Kimura, F. Potential Impact of Sea Surface Temperature on Winter Precipitation over the Japan Sea Side of Japan: A Regional Climate Modeling Study. J. Meteorol. Soc. Japan 2013, 91, 471–488. [Google Scholar] [CrossRef] [Green Version]
  32. Reynolds, W.R.; Folland, C.K.; Parker, D.E. Biases in satellite-derived sea-surface-temperature data. Nature 1989, 341, 728–731. [Google Scholar] [CrossRef]
  33. Reynolds, W.R. Impact of Mount Pinatubo aerosols on satellite-derived sea surface temperatures. J. Clim. 1993, 6, 768–774. [Google Scholar] [CrossRef]
  34. Chan, P.-K.; Gao, B.-C. A comparison of MODIS, NCEP, and TMI sea surface temperature datasets. IEEE Geosci. Remote Sens. Lett. 2005, 2, 270–274. [Google Scholar] [CrossRef]
  35. Reynolds, W.R.; Chelton, D.B. Comparisons of daily sea surface temperature analyses for 2007–2008. J. Clim. 2010, 23, 3545–3562. [Google Scholar] [CrossRef]
  36. Fu, H.; Wang, Y. Effect of uncertainties in sea surface temperature dataset on the simulation of typhoon Nangka (2015). Atmos. Sci. Lett. 2017. [Google Scholar] [CrossRef]
  37. Qingyuan, W.; Yanan, W.; Yiwei, L. Comparison of two Centennial-scale Sea Surface Temperature Datasets in the Regional Climate Change Studies of the China Seas. IOP Conf. Ser. Earth Environ. Sci. 2017, 81, 012077. [Google Scholar] [CrossRef]
  38. Japan Meteorological Agency. Prompt Report on Heavy Precipitation in August 2014; Japan Meteorological Agency: Chiyoda-ku, Japan, 2014. (In Japanese)
  39. Japan Meteorological Agency. Available online: http://www.data.jma.go.jp/kaiyou/shindan/index.html (accessed on 20 December 2017).
  40. Shimadera, H.; Kondo, A.; Shrestha, K.L.; Kitaoka, K.; Inoue, Y. Numerical Evaluation of the Impact of Urbanization on Summertime Precipitation in Osaka, Japan. Adv. Meteorol. 2015. [Google Scholar] [CrossRef]
  41. Japan Meteorological Business Support Center. Available online: http://www.jmbsc.or.jp/jp/online/file/f-online10200.html (accessed on 20 December 2017).
  42. Gemmill, W.; Katz, B.; Li, X. RTG SST High Res. SST, Daily real-time, global sea surface temperature-high-resolution analysis: RTG_SST_HR. NOAA/NCEP. NOAA/NWS/NCEP/MMAB Office Note 2007, 260, 39. Available online: http://polar.ncep.noaa.gov/sst/ (accessed on 20 December 2017).
  43. National Centers for Environmental Prediction/National Weather Service/NOAA/U.S. Department of Commerce. NCEP FNL Operational Model Global Tropospheric Analyses, Continuing from July 1999; Research Data Archive at the National Center for Atmospheric Research; Computational and Information Systems Laboratory: Boulder, CO, USA, 2000. [CrossRef]
  44. Hong, S.-Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
  45. Hong, S.-Y.; Lim, J.-O.J. The WRF Single-Moment 6-Class Microphysics Scheme (WSM6). J. Korean Meteorol. Soc. 2006, 42, 129–151. [Google Scholar]
  46. Chen, F.; Dudhia, J. Coupling an Advanced Land Surface-Hydrology Model with the Penn State-NCAR MM5 Modeling System. Part I: Model Implementation and Sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
  47. Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
  48. Dudhia, J. Numerical study of convection observed during the Winter Monsoon Experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
  49. Shimadera, H.; Kojima, T.; Kondo, A.; Inoue, Y. Performance comparison of CMAQ and CAMx for one-year PM2.5 simulation in Japan. Int. J. Environ. Pollut. 2015, 57, 146–161. [Google Scholar] [CrossRef]
  50. Kain, J.S. The Kain-Firtsch Convective Parameterization: An Update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
  51. Japan Meteorological Business Support Center. Available online: http://www.jmbsc.or.jp/jp/offline/cd0061.html (accessed on 10 January 2018).
  52. Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar]
  53. Emery, C.; Tai, E.; Yarwood, G. Enhanced Meteorological Modeling and Performance Evaluation for Two Texas Ozone Episodes; The Texas Natural Resource Conservation: Austin, TX, USA, 2001.
  54. Cartelle, D.; Vellon, J.M.; Rodriguez, A.; Valino, D.; Gonzalez, J.A.; Casas, C.; Carrera-Chapela, F. PrOlor: A Modelling Approach for Environmental Odor Forecast. Chem. Eng. Trans. 2016, 54, 229–234. [Google Scholar] [CrossRef]
  55. Fu, X.; Cheng, Z.; Wang, S.; Hua, Y.; Xing, J.; Hao, J. Local and Regional Contributions to Fine Particle Pollution in Winter of the Yangtze River Delta, China. Aerosol Air Qual. Res. 2016, 16, 1067–1080. [Google Scholar] [CrossRef]
  56. Gentry, M.S.; Lackman, G.M. Sensitivity of Simulated Tropical Cyclone Structure and Intensity to Horizontal Resolution. Mon. Weather Rev. 2010, 138, 688–704. [Google Scholar] [CrossRef]
  57. Japan Meteorological Business Support Center. Available online: http://www.jmbsc.or.jp/jp/offline/cd0100.html (accessed on 20 December 2017).
Atmosphere 09 00084 g001 550
Figure 1. Modeling domains showing (a) topography of land areas and average SST (sea surface temperature) of August 2014; (b) locations of meteorological observatories and division of regions for analyses of precipitation.
Figure 1. Modeling domains showing (a) topography of land areas and average SST (sea surface temperature) of August 2014; (b) locations of meteorological observatories and division of regions for analyses of precipitation.
Atmosphere 09 00084 g001
Atmosphere 09 00084 g002 550
Figure 2. Temporal variations of daily precipitation averaged for all the meteorological observatories in August 2014 for the comparison of (a) the grid nudging, and (b) the horizontal resolution and the cumulus scheme. Values in parentheses are the Pearson’s correlation coefficients between observed and simulated daily precipitations averaged for all the observatories.
Figure 2. Temporal variations of daily precipitation averaged for all the meteorological observatories in August 2014 for the comparison of (a) the grid nudging, and (b) the horizontal resolution and the cumulus scheme. Values in parentheses are the Pearson’s correlation coefficients between observed and simulated daily precipitations averaged for all the observatories.
Atmosphere 09 00084 g002
Atmosphere 09 00084 g003 550
Figure 3. Mean daily precipitations averaged for the meteorological observatories in each region during (a) 1 to 15 and (b) 16 to 31 August 2014 for the observation and six WRF settings.
Figure 3. Mean daily precipitations averaged for the meteorological observatories in each region during (a) 1 to 15 and (b) 16 to 31 August 2014 for the observation and six WRF settings.
Atmosphere 09 00084 g003
Atmosphere 09 00084 g004 550
Figure 4. Spatial distributions of monthly precipitation in August 2014 obtained from (a) Radar/Raingauge-Analyzed Precipitation data and (b) W_5km case. The Radar/Raingauge-Analyzed Precipitation data covers areas within a few hundred kilometers from the coastal lines of Japan.
Figure 4. Spatial distributions of monthly precipitation in August 2014 obtained from (a) Radar/Raingauge-Analyzed Precipitation data and (b) W_5km case. The Radar/Raingauge-Analyzed Precipitation data covers areas within a few hundred kilometers from the coastal lines of Japan.
Atmosphere 09 00084 g004
Atmosphere 09 00084 g005 550
Figure 5. Spatial distributions of hourly precipitation obtained from Radar/Raingauge-Analyzed Precipitation data at 09:00 JST on (a) 2 August 2014, (b) 9 August 2014, (c) 22 August 2014, and of hourly precipitation and wind fields obtained from W_5km case at 09:00 JST on (d) 2 August 2014, (e) 9 August 2014, and (f) 22 August 2014. The Radar/Raingauge-Analyzed Precipitation data covers areas within a few hundred kilometers from the coastal lines of Japan.
Figure 5. Spatial distributions of hourly precipitation obtained from Radar/Raingauge-Analyzed Precipitation data at 09:00 JST on (a) 2 August 2014, (b) 9 August 2014, (c) 22 August 2014, and of hourly precipitation and wind fields obtained from W_5km case at 09:00 JST on (d) 2 August 2014, (e) 9 August 2014, and (f) 22 August 2014. The Radar/Raingauge-Analyzed Precipitation data covers areas within a few hundred kilometers from the coastal lines of Japan.
Atmosphere 09 00084 g005
Atmosphere 09 00084 g006 550
Figure 6. Temporal variations of daily precipitation averaged for all the meteorological observatories in August 2014 for the comparison of the baseline, SST+1, and SST−1 cases. The second axis indicates the precipitation difference from the baseline condition (“SST+1”—Baseline, “SST−1”—Baseline).
Figure 6. Temporal variations of daily precipitation averaged for all the meteorological observatories in August 2014 for the comparison of the baseline, SST+1, and SST−1 cases. The second axis indicates the precipitation difference from the baseline condition (“SST+1”—Baseline, “SST−1”—Baseline).
Atmosphere 09 00084 g006
Atmosphere 09 00084 g007 550
Figure 7. Mean daily precipitations averaged for the meteorological observatories in each region during (a) 1 to 15 and (b) 16 to 31 August 2014 in the sensitivity study on SST.
Figure 7. Mean daily precipitations averaged for the meteorological observatories in each region during (a) 1 to 15 and (b) 16 to 31 August 2014 in the sensitivity study on SST.
Atmosphere 09 00084 g007
Atmosphere 09 00084 g008 550
Figure 8. Mean daily precipitation difference from the baseline condition in (a) SST−1 and (b) SST+1 conditions during the first half of August 2014, and (c) SST−1 and (d) SST+1 conditions during the last half of August 2014.
Figure 8. Mean daily precipitation difference from the baseline condition in (a) SST−1 and (b) SST+1 conditions during the first half of August 2014, and (c) SST−1 and (d) SST+1 conditions during the last half of August 2014.
Atmosphere 09 00084 g008
Atmosphere 09 00084 g009 550
Figure 9. Frequency distribution of daily precipitation at the meteorological observatories in August 2014 in SST−1, the baseline, and SST+1 cases.
Figure 9. Frequency distribution of daily precipitation at the meteorological observatories in August 2014 in SST−1, the baseline, and SST+1 cases.
Atmosphere 09 00084 g009
Table
Table 1. Condition settings of WRF simulations to determine the optimal setting for SST sensitivity analysis.
Table 1. Condition settings of WRF simulations to determine the optimal setting for SST sensitivity analysis.
CaseNudgingResolutionCumulus
TQW_5kmTQW5 kmOff
no_5kmOff5 kmOff
W_5kmW5 kmOff
W_2.5kmW2.5 kmOff
W_10kmW10 kmOff
W_10km_cuW10 kmOn
Note: T, Q, and W in the Nudging column indicate that the grid nudging for potential temperature, water vapor mixing ratio, and horizontal wind components is turned on, respectively.
Table
Table 2. Statistical evaluation of WRF performance for simulating daily meteorological variables at meteorological observatories in August 2014.
Table 2. Statistical evaluation of WRF performance for simulating daily meteorological variables at meteorological observatories in August 2014.
CaseNMeanrMBEMAERMSEIA
Temperature (°C) (°C)(°C)(°C)
Obs.455525.2
TQW_5km 25.40.9380.160.871.090.967
no_5km 25.40.8990.161.081.400.947
W_5km 25.30.9150.070.991.270.956
W_2.5km 25.70.9300.470.961.240.958
W_10km 24.80.893−0.391.191.510.940
W_10km_cu 24.90.882−0.331.261.570.935
Humidity (g kg−1) (g kg−1)(g kg−1)(g kg−1)
Obs.455217.0
TQW_5km 16.30.945−0.660.931.140.957
no_5km 16.10.913−0.861.151.440.932
W_5km 16.40.936−0.520.901.120.958
W_2.5km 16.30.937−0.660.951.180.953
W_10km 16.70.932−0.310.861.080.961
W_10km_cu 16.50.932−0.420.891.110.959
Wind Speed (m s−1) (m s−1)(m s−1)(m s−1)
Obs.45553.0
TQW_5km 3.60.8180.600.961.410.872
no_5km 3.90.7810.901.181.680.827
W_5km 3.60.8190.610.971.410.871
W_2.5km 3.50.8310.530.891.280.887
W_10km 3.70.7810.721.101.610.839
W_10km_cu 3.70.7780.711.111.620.837
Precipitation (mm d−1) (mm d−1)(mm d−1)(mm d−1)
Obs.453110.0
TQW_5km 9.10.605−0.938.3620.140.750
no_5km 7.70.453−2.339.8723.350.637
W_5km 9.20.630−0.758.4919.920.775
W_2.5km 9.40.628−0.648.3819.890.773
W_10km 9.20.559−0.859.1221.930.726
W_10km_cu 13.00.5333.0411.6822.730.709
Note: N, r, MBE, MAE, RMSE, and IA denote sample number, the Pearson’s correlation coefficient, the Mean Bias Error, the Mean Absolute Error, the Root Mean Square Error, and the Index of Agreement, respectively. The bold italic value indicates the best agreement with the observations for each statistical indicator.
Table
Table 3. Observed and simulated minimum surface pressures and their positions of typhoons at 09:00 JST on 2 and 9 August 2014.
Table 3. Observed and simulated minimum surface pressures and their positions of typhoons at 09:00 JST on 2 and 9 August 2014.
Indicator2 August 2014 09:00 JST9 August 2014 09:00 JST
Obs. [38]W_5kmObs. [38]W_5km
Minimum surface pressure980 hPa978 hPa955 hPa955 hPa
Latitude of the center31.9° N32.4° N30.4° N30.3° N
Longitude of the center124.9° E124.9° E132.3° E132.1° E
Table
Table 4. Monthly precipitation, 2-m air temperature, and heat fluxes averaged over land area of Japan, sea area, and entire area in the modeling domain in different SST conditions.
Table 4. Monthly precipitation, 2-m air temperature, and heat fluxes averaged over land area of Japan, sea area, and entire area in the modeling domain in different SST conditions.
AreaSST−1BaselineSST+1
Precipitation (mm month−1)
Japan335364425
Sea154188266
Domain163194263
2-m air temperature (°C)
Japan22.322.322.5
Sea25.525.726.4
Domain24.724.925.5
Upward latent heat flux (W m−2)
Japan858384
Sea77100133
Domain7998125
Upward sensible heat flux (W m−2)
Japan373634
Sea−1610
Domain81316

Share and Cite

MDPI and ACS Style

Minamiguchi, Y.; Shimadera, H.; Matsuo, T.; Kondo, A. Numerical Simulation of Heavy Rainfall in August 2014 over Japan and Analysis of Its Sensitivity to Sea Surface Temperature. Atmosphere 2018, 9, 84. https://doi.org/10.3390/atmos9030084

AMA Style

Minamiguchi Y, Shimadera H, Matsuo T, Kondo A. Numerical Simulation of Heavy Rainfall in August 2014 over Japan and Analysis of Its Sensitivity to Sea Surface Temperature. Atmosphere. 2018; 9(3):84. https://doi.org/10.3390/atmos9030084

Chicago/Turabian Style

Minamiguchi, Yuki, Hikari Shimadera, Tomohito Matsuo, and Akira Kondo. 2018. "Numerical Simulation of Heavy Rainfall in August 2014 over Japan and Analysis of Its Sensitivity to Sea Surface Temperature" Atmosphere 9, no. 3: 84. https://doi.org/10.3390/atmos9030084

APA Style

Minamiguchi, Y., Shimadera, H., Matsuo, T., & Kondo, A. (2018). Numerical Simulation of Heavy Rainfall in August 2014 over Japan and Analysis of Its Sensitivity to Sea Surface Temperature. Atmosphere, 9(3), 84. https://doi.org/10.3390/atmos9030084

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop