Geostatistical Merging of a Single-Polarized X-Band Weather Radar and a Sparse Rain Gauge Network over an Urban Catchment

Abstract

Optimal Quantitative Precipitation Estimation (QPE) of rainfall is crucial to the accuracy of hydrological models, especially over urban catchments. Small-to-medium size towns are often equipped with sparse rain gauge networks that struggle to capture the variability in rainfall over high spatiotemporal resolutions. X-band Local Area Weather Radars (LAWRs) provide a cost-effective solution to meet this challenge. The Clermont Auvergne metropolis monitors precipitation through a network of 13 rain gauges with a temporal resolution of 5 min. 5 additional rain gauges with a 6-minute temporal resolution are available in the region, and are operated by the national weather service Météo-France. The LaMP (Laboratoire de Météorologie Physique) laboratory’s X-band single-polarized weather radar monitors precipitation as well in the region. In this study, three geostatistical interpolation techniques—Ordinary kriging (OK), which was applied to rain gauge data with a variogram inferred from radar data, conditional merging (CM), and kriging with an external drift (KED)—are evaluated and compared through cross-validation. The performance of the inverse distance weighting interpolation technique (IDW), which was applied to rain gauge data only, was investigated as well, in order to evaluate the effect of incorporating radar data on the QPE’s quality. The dataset is comprised of rainfall events that occurred during the seasons of summer 2013 and winter 2015, and is exploited at three temporal resolutions: 5, 30, and 60 min. The investigation of the interpolation techniques performances is carried out for both seasons and for the three temporal resolutions using raw radar data, radar data corrected from attenuation, and the mean field bias, successively. The superiority of the geostatistical techniques compared to the inverse distance weighting method was verified with an average relative improvement of 54% and 31% in terms of bias reduction for kriging with an external drift and conditional merging, respectively (cross-validation). KED and OK performed similarly well, while CM lagged behind in terms of point measurement QPE accuracy, but was the best method in terms of preserving the observations’ variance. The correction schemes had mixed effects on the multivariate geostatistical methods. Indeed, while the attenuation correction improved KED across the board, the mean field bias correction effects were marginal. Both radar data correction schemes resulted in a decrease of the ability of CM to preserve the observations variance, while slightly improving its point measurement QPE accuracy.

1. Introduction

Reliable rainfall data is an essential prerequisite for hydrological models [1,2]. Weather services and towns throughout the world have implemented rain gauge networks with specific attention to urban catchments, where the socioeconomic consequences of hazardous precipitation events are high. Rain gauge networks provide point measurements with satisfying accuracy; however, they struggle to capture the spatial and temporal structure of rainfall events [3]. Studies, such as [4], recommend spatiotemporal resolutions of 100 m and 5 min for catchments smaller than 1 ha, which is not feasible with rain gauge networks. In order to obtain rainfall measurements with such a high resolution, the only viable option is the weather radar. C-band and S-band weather radars have a range of hundreds of kilometers with a typical spatial resolution of 250–1000 m and a temporal resolution of 5–10 min; however, these systems are quite expensive and do not deliver the high spatial resolution urban hydrology applications often need. X-band radars are economical alternative systems with an even higher spatiotemporal resolution for a range of tens of kilometers [5].

Several sources of error can affect the measurements delivered by a radar system. Calibration errors may introduce a drift in radar data. To tackle this issue, original and regularly updated calibration reports are often needed. A long-term comparison of the accumulated rainfall from the radar and the nearest gauge for a large number of events is an alternative method to detect a calibration drift in the radar data [6]. Moreover, ground clutter, which refers to non-precipitating echoes due to obstacles (birds, mountains, buildings…), blends with the precipitation radar images. One of the most widely used methods for ground clutter correction consists of creating a static clutter map on a polar grid: pixels where the reflectivity values exceed a certain threshold 90% (for example) of the time for dry events are identified as clutter, then an interpolation method, such as the nearest neighbor or inverse distance weighting, is applied to the clutter pixels using reflectivity values from clutter-free pixels [6]. In addition to that, attenuation by hydrometeors of the radar signal has been recognized as a major problem in weather radars since the inception of the technology [7,8]. X-band weather radars are especially vulnerable to attenuation, as its effects are inversely proportionate to the wavelength. Hitschfeld and Bordan developed a method capable of estimating the path-integrated attenuation factor along a radar beam [9]. This algorithm performs well for corrections under 10 dB; however, it becomes numerically unstable beyond this threshold. Delrieu et al. proposed a backward method using mountain returns as a constraint [10]. Others have used a C-band radar to correct X-band non-polarimetric radar data along each radial [11]. The recent emergence of polarimetric and/or Doppler X-band radars has rendered correcting attenuation a less challenging task [12,13,14] in contrast to non-polarimetric radars. Other sources of error include the reflectivity–rainfall rate power law that is dependent on hydrometeors’ drop size distribution, overestimation of reflectivity in the melting layer of the atmosphere (the bright band), etc.

Merging both radar and rain gauge network data seems to be the ideal way to obtain accurate rainfall fields. Most studies use the rain gauges as a “ground truth” of precipitation, and radar data as a complementary source of information. In reality, rain gauges suffer from a great number of errors that skew its measurements. A study showed that rain gauge biases can amount to 40% in strong thunderstorms [15]. In addition to these issues, the merging of radar and rain gauge data faces another hurdle: the sampling properties. Indeed, a radar sample’s volumetric precipitation is at an altitude that depends on its tilt as opposed to a point rain gauge measurement, and it is also a source of additional discrepancy between the two measuring instruments [16]. Despite these difficulties, many techniques to jointly use radar and rain gauge data have been developed over the decades. The first family of techniques consisted in finding multiplicative adjustment factors to correct radar data using rain gauges [17]. A second more elaborate set of techniques is based on a geostatistical approach. Krajewski used cokriging to combine radar and rain gauge data [18]. Comparison studies of geostatistical methods with other methods, such as the Thiessen polygon, inverse square distance, non-linear regression, mean field bias correction, range-dependent adjustment, static local bias correction, and the Brandes spatial adjustment, found that the geostatistical techniques performed the best [19,20]. Others compared Kriging with External Drift (KED), Conditional Merging (CM), and Indicator Kriging with External Drift (IKED) using the univariate method Ordinary Kriging (OK) with rain gauge data only as a reference for several scenarios of rain gauge stations’ density and temporal resolutions, and concluded that there is a benefit to using these methods even for very high temporal resolutions [21]. New approaches to merging radar and rain gauge data have been investigated in other studies, such as the use of Bayesian techniques [22] and Copula based methods [23].

The goal of this study is to investigate the performance of the merging techniques Kriging with External Drift and Conditional merging using data from a single-polarized non doppler X-band weather radar as well as the Clermont Auvergne metropolis and Météo France networks of rain gauges at three high resolutions: 5, 30, and 60 min. The effects of correcting the radar data for attenuation using the Hitschfeld–Bordan correction scheme and the correction of the mean field bias on the two interpolation techniques were assessed on a 1-year precipitation dataset (summer of 2013 and winter of 2015). The motivation of this study started with the PhD study [24], where the two techniques were used on one summer and one winter rainfall event. They showed promising results despite performing worse than the ordinary “kriged” rain gauge stations in terms of mean error. KED and CM performed marginally worse when attenuation-corrected data were used.

This paper is organized into five sections. The introduction is followed by the Methodology section, where the Hitschfeld–Bordan Attenuation scheme, the mean field bias of radar data according to the least squares method, the geostatistical approaches, and the interpolation performance metrics are described, and this section also provides the general steps undertaken for the analysis. The third section focuses on the study area and the datasets. Section 4 presents the results of the cross-validation that was carried out, and an analysis of the results ensues. Finally, Section 5 provides a summary, and the conclusions, of the study.

2. Methodology

2.1. The Hitschfeld–Bordan Attenuation Scheme

When an electromagnetic wave travels along its propagation path with an initial power $P$, a small amount of this power $dP$ is lost during the process, which is notably true at X-band frequencies when precipitation is encountered. In the context of radars, $dP$could be expressed as:

$$dP=-2kPdr$$

(1)

The factor of 2 is added in the second term of Equation (1) to refer to the fact that the radar signal travels from the radar to the target and back. $r$ is the distance to the radar and $k$ (dB Km⁻¹) is the specific attenuation coefficient. Integrating Equation (1) over distance $r>0$ becomes:

$$P\left(R\right)=\epsilon P_0\ast A\left(r\right)$$

(2)

with:

$$A\left(r\right)=\exp \left[-0.46{\int }_0^{r}k\left(s\right)ds\right]$$

(3)

where $\epsilon$ is the calibration error adjustment factor; it is assumed to be equal to 1 in this study. $A$ is the multiplicative path-integrated attenuation factor. It represents the ratio between the energy of the radar and the energy it would have had if there were no attenuation effects at gate$r$.

The mean power $\overline{P}$ received from hydrometeors at radar gate$r$ is according to radar theory [25]:

$$\overline{P}\left(r\right)=C\frac{K^2}{R^2}Z\left(r\right)$$

(4)

where $C$ is the radar constant, $\left|K\right|$ is the dielectric coefficient of water ($K^2=0.93$), and $Z$ is the measured, hence attenuated, reflectivity in mm⁶ m⁻³. Equation (2) could be written as:

$$Z\left(R\right)=\epsilon Z_0\ast A\left(r\right)$$

(5)

where $Z_0$ is the unattenuated reflectivity measure at gate $r$. Equation (5) could be developed into [26]:

$$\frac{d[A{\left(r\right)}^{\frac{1}{\beta }}]}{dr}=-\frac{0.46}{\beta }{\left[\frac{Z\left(r\right)}{\alpha }\right]}^{\frac{1}{\beta }}$$

(6)

Equation (6) was established using a power law between the measured reflectivity and the specific attenuation factor:

$$Z=\alpha k^{\beta }$$

(7)

where $\alpha$ and $\beta$ are coefficients depending on the operating frequency of the radar [11]. At the X-band frequency range, $\alpha =132 250$ and $\beta =1.2$are appropriate values for $\alpha$ and $\beta$ [27].

Integrating the specific attenuation factor over the two-way path between the radar and the target hydrometeor using Equation (7) is the Path Integrated Attenuation (PIA):

$$PIA=2{\int }_0^r{\left[\frac{Z\left(s\right)}{\alpha }\right]}^{\frac{1}{\beta }}ds$$

(8)

$PIA$maps could be easily computed using reflectivity maps on a polar grid, then the multiplicative path-integrated attenuation factors are calculated using a development of Equation (3):

$$A\left(r\right)={\left[1-\frac{0.23}{\beta }PIA\left(r\right)\right]}^{\beta }$$

(9)

A constraint of a 10-dB correction maximum is added to the correction scheme as a way to avoid numerical instabilities occurring beyond that threshold.

2.2. The Mean Field Bias Correction Scheme

The radar data field bias could fall into two categories: a mean field bias and a range-dependent one. The mean field bias can be corrected with a multiplicative adjustment factor using rain gauges, and the range-dependent bias can be corrected using the reflectivity profiles of a vertically pointing radar [28]. The unavailability of a vertically pointing radar means that no range-dependent bias correction method is applied to the radar data. In this study, we focus on the mean field bias as a method to improve the KED and CM geostatistical techniques’ performance. This stems from a vital assumption we make throughout this study: rain gauges are supposed to deliver the true values of precipitation rates. Rain gauge measurement errors were not accounted for in order to emulate a scenario where radar and rain gauge data are blended together in real time. The estimation of errors in rain gauges is more efficient in post-processing Quantitative Precipitation Estimation (QPE), where a large time-series of rain gauge measurements is available.

For N rain gauges located at the coordinates$x_1$, $x_2,x_N$with the observations $G_1,G_2,G_N$at a given time t and the radar rainfall values $R_1,R_2,R_N$ at time t. The mean field bias factor $MFB$ based on the least squares method is:

$$MFB=\frac{{\sum }_{i=1}^N{G}_i{R}_i}{{\sum }_{i=1}^N{R}_i{}^2}$$

(10)

Equation (10) is the $MFB$expression obtained from minimizing the sum of squared differences between the gauge and bias-corrected radar observations:

$${\displaystyle \sum }_{i=1}^N{\left[G_i-MFB\ast R_i\right]}^2=\min$$

(11)

Weights could be added to each term of the numerator and denominator of Equation (10) in order to account for differences in radar-rainfall accuracy (e.g., as a function of range or the number of gauges inside radar pixels) [29].

2.3. Interpolation and Geostatistical Merging Techniques for Radar and Rain Gauge Data

In order to obtain a rainfall estimate over the whole catchment from a sparse rain gauge network, an interpolation method is necessary. Geostatistical methods, such as ordinary kriging, have been recognized across many fields, including meteorology, as powerful methods for providing unbiased estimates with minimum variance. Multivariate methods include secondary variables, such as radar data, in our case in order to complement rain gauge data with the aim of obtaining an improved QPE. In this subsection, the univariate technique ordinary kriging (OK) is described, as well as the multivariate techniques Kriging with an External Drift (KED) and Conditional Merging (CM).

2.3.1. Univariate Interpolation Techniques

Precipitation is a complex process with different phenomena taking place at different scales. Such complexity means that establishing a deterministic or mathematical solution to infer precipitation rates at ungauged locations is unattainable with our current knowledge. In his seminal thesis in 1965 [30], Matheron circumvented this issue by treating the variation as if it were the product of a spatial random process. In this context, precipitation is regarded as a spatial random variable and a rainfall event as a realization of this process. In order to be able to compute statistics or draw inferences, either multiple realizations should be available, or we must assume the process is stationary [31].

Let $V$ be a spatial random variable. $V$ is stationary if for any finite number n of points$x_1,\dots ,x_n$, the joint distribution of $V\left(x_1\right),\dots ,V\left(x_n\right)$ is the same as the joint distribution of $V\left(x_1+h\right),\dots ,V\left(x_n+h\right)$ [32], where h is a distance vector in space; h is just a distance if isotropy is assumed.

$V$ can be represented at location $x$ as:

$$V\left(x\right)=\mu \left(x\right)+\epsilon \left(x\right)$$

(12)

where $\mu$ is the mean of the process and $\epsilon$ is a random quantity with a mean of zero and a covariance $C\left(h\right)$ given by:

$$C\left(h\right)=E\left[\epsilon \left(x\right)\epsilon \left(x+h\right)\right]$$

(13)

or:

$$C\left(h\right)=E\left[V\left(x\right)V\left(x+h\right)-{\mu }^2\right]$$

(14)

where $E$ is the mathematical expectation. Notice that if the mean $\mu$ is not constant, the covariance cannot exist [31].

Stationarity is too strong as an assumption in most applications; so, a weaker form of stationarity is required. Matheron assumed intrinsic stationarity. $V$ is intrinsically stationary if [33]:

$$\{\begin{array}{c}E\left[V\left(x+h\right)-V\left(x\right)\right]=0 for all x and h\\ \gamma \left(h\right)=\frac{1}{2}var\left[V\left(x+h\right)-V\left(x\right)\right] exists and depends only on h\end{array}$$

(15)

where $\gamma \left(h\right)$ is called the variogram. In order to estimate it, an experimental variogram is computed through the radar data at distance $h$ as follows:

$$\gamma (\overrightarrow{h})=\frac{1}{N(\overrightarrow{h})}{\displaystyle \sum }_{i=1}^{N\left(h\right)}[R\left(x_i\right)-R(x_i+\overrightarrow{h})]²$$

(16)

where $N(\overrightarrow{h})$ is the number of data pairs located at a distance vector $\overrightarrow{h}$of each other, although we will disregard anisotropy in this study considering that it only marginally affects the outcome of the kriging techniques; hence, $h$is just the distance between the pairs. $R\left(x_i\right)$and $R(x_i+\overrightarrow{h})$ is the precipitation rate at $x_i$ and$x_i+\overrightarrow{h}$, respectively.

Legorgeu [24] used a climatological approach described in [34] to infer the variogram using 100 time steps with a temporal resolution of 1 h over a period of 5 years (2006–2011). In this study, we examined the performance of geostatistical approaches at three temporal resolutions: 5, 30, and 60 min over time steps spanning over two seasons (summer 2013 and winter 2015). For each temporal resolution and for each season, an average variogram is computed, and each time step considered is standardized by the variance as shown in Equation (17):

$${\gamma }_{season}\left(h\right)=\frac{1}{n}{\displaystyle \sum }_{i=1}^n\frac{\gamma \left(h,i\right)}{var\left(i\right)}$$

(17)

where $n$ refers to the number of time steps considered to compute the standardized variogram ${\gamma }_{season}$, $\gamma \left(h,i\right)$refers to the value of the variogram of time step $i$ at distance $h$, and $var\left(i\right)$ is the variance of said time step. The fitting process to choose the best theoretical variogram is done both visually and with the help of the software “gstat” in the R environment. “Gstat” is an R package containing utility functions for variogram modelling; simple, ordinary, and universal point or block (co)kriging; spatiotemporal kriging; sequential Gaussian or indicator (co)simulation; and variogram and variogram map plotting. [35].

Both the spherical variogram model as in Equation (18) and the exponential variogram model as in Equation (19) model are considered for this study.

$${\gamma }_{\mathit{Spherical}}\left(h\right)=f\left(x\right)=\{\begin{array}{cc}{c}_0& if h=0\\ c_0+c\left[\frac{3}{2}\frac{h}{\beta }-\frac{1}{2}{\left(\frac{h}{\beta }\right)}^2\right] & if0<h\le \beta \\ c& if h>0\end{array}$$

(18)

$${\gamma }_{Exponential}\left(h\right)=f\left(x\right)=\{\begin{array}{cc}{c}_0& if h=0\\ c_0+c\left[1-\exp \left(-\frac{h}{\beta }\right)\right] & if h>0\end{array}$$

(19)

where $c_0$ is the nugget, $c$ is the sill, and β is the range.

A reliable variogram is critical to the OK method’s performance. In our study, only 18 gauges were available, which makes the number of pairs insufficient for the computation of the variogram. Hence, we use inverse distance weighting for the rain gauge data alone. We will still use OK to interpolate rain gauges over the study area; however, the variogram will be inferred from radar data. At each time step, 10% of the radar pixels are chosen randomly to infer the standardized variogram as in Equation (17).

2.3.2. Multivariate Geostatistical Interpolation Techniques

The aim of this study is to merge rain gauge and radar data in order to improve QPE. Therefore, radar data was the only secondary variable used as an additional source of information in order to complement the rain gauge network’s shortcomings, especially when it comes to capturing the spatiotemporal variability of rainfall. In fact, rain gauge data is regarded as the ground truth, since the measurements are direct (no reflectivity–rainfall rate conversion needed) at discrete locations on the ground level; thus, it is used as a primary source of information in the multivariate merging techniques applied in this study (Kriging with external drift and conditional merging).

Conditional Merging (CM)

This method was first introduced by Ehret [36], and has been used since then in several studies, such as Sinclair et al. [37], for rainfall field simulation. Berndt et al. [21] compared its performance to OK, KED, and IKED (Indicator Kriging with External Drift) for various rain gauge network densities and temporal resolutions, and found that it outperformed these methods and was less sensitive to poor radar quality compared to KED. Rabiei et al. [38] implemented the quantile mapping bias correction method on radar data, and then the radar data was merged with rainfall observations by CM and KED. CM showed greater sensitivity to radar data quality, but performed better than all other interpolation techniques when using bias-corrected radar data.

The main strength of CM is preserving the spatial structures detected by the weather radar while simultaneously keeping rain gauge observations intact in the final predicted rainfall field. This is achieved through a number of steps. First, the rain gauge observations are interpolated through OK on the radar grid, then the closest radar pixels to each rain gauge are selected and then interpolated by OK on the same grid. Step 3 is computing a deviation grid between the observed radar grid and the interpolated radar grid. Finally, the deviation grid is added to the rain gauge interpolation grid to obtain the final rainfall field.

Kriging with External Drift (KED)

KED diverges from OK in its use of a secondary variable to include a trend, such as radar data, satellite data, elevation, and distance to the radar; hence, the name of the method. The target variable $R$ (here, rainfall rates at ungauged locations) is assumed to be equal to a stochastic term $Y$ and a deterministic trend m [30]. At location x:

$$R\left(x\right)=Y\left(x\right)+m\left(x\right)$$

(20)

The trend $m$ should be a linear combination of the secondary variable $X_1$or more generally variables $X_1,X_2,X_N$with$N>1$:

$$m\left(x\right)=a+{\displaystyle \sum }_{i=1}^N{b}_k{X}_k$$

(21)

Implementing KED requires, in our case, performing a linear regression between rain gauge and radar data (the auxiliary variable) to determine the trend’s coefficients $a$ and$b_1$. This is often challenging, as many time steps record zero precipitation and do not vary smoothly in space [31]. This problem could be dealt with by increasing the number of gauges: an option that it is not feasible in this particular study. We apply KED according to the straightforward approach developed by Velasco-Forero et al. [39], which circumvents this challenge through the following steps:

• Rain gauges are interpolated using OK on the area on interest (The radar grid)
• The nearest radar pixels to the rain gauges are selected and interpolated by OK on the area of interest.
• A deviation map between the fields obtained in step a and b is calculated
• The experimental variogram of the deviation map (the residual variogram) is computed and then used to interpolate rain gauge data over the area of interest.

Although KED under this approach is quite similar to CM, Velasco-Forero et al. [39] pointed out that the results “might be more precise because the full map of radar values is included in the estimation process but in as unbiased a manner as possible”.

2.4. Quality and Performance Metrics

In this subsection, we describe two statistical metrics used to investigate the radar data’s quality for each season and at each rain gauge location, as well as three interpolation performance metrics applied to the cross-validation results with the aim of comparing the different univariate and multivariate interpolation techniques used in the study.

2.4.1. Quality Metrics

In order to evaluate the quality of radar data considering rain gauge data as the ground truth, the temporal root mean square error $(RMS{E}_{temp}$) is calculated for every station location as expressed in Equation (22). In fact, the squared deviation between the rain gauge and the corresponding radar pixel prevents underestimations and overestimations from compensating for each other. This statistical metric is temporal as it is calculated for all time steps selected in the study at each rain gauge. Our aim is to eventually identify locations where the error is noticeably higher than the rest of the study area.

$$RMS{E}_{temp}\left(x\right)=\sqrt{\frac{{\sum }_{i=1}^L\left[R_{Raingauge}\left(x,t_i\right)-R_{Radar}\left(x,t_i\right)\right]{}^2}{L}}$$

(22)

where $L$refers to the number of time steps considered per season, and $R_{Raingauge}$ and $R_{Radar}$ are the rainfall rate values derived from the rain gauge at location $x$ and the radar data pixel at the same location, respectively.

A high $RMS{E}_{temp}$ indicates an important discrepancy between the rain gauge and the radar.

Spatially, the radar/rain gauge RMSE is computed for every time step as an average along all rain gauge stations:

$$RMS{E}_{spatial}\left(t\right)=\sqrt{\frac{{\sum }_{i=1}^n\left[R_{Raingauge}\left(x_i,t\right)-R_{Radar}\left(x_i,t\right)\right]{}^2}{n}}.$$

(23)

$RMS{E}_{spatial}$ may help us highlight just how much impact the rain type has on radar data. Indeed, rain types change seasonally, with convective events characterizing the summers and stratiform events the winter.

2.4.2. Interpolation Performance Metrics

The accuracy of the interpolation methods (inverse distance weighting (IDW) using rain gauge data alone and OK, KED, and CM using radar data to infer the variograms) will be assessed with the leave-one-out cross-validation method. Indeed, for every time step, an estimation of the precipitation rate is carried out using one of the interpolation methods with all of the rain gauges but one. The resulting precipitation estimate R′ at the excluded rain gauge location is then compared to the true measurement R recorded by that same rain gauge. This operation is repeated for all gauges one at a time. At the end, we obtain an observation field comprised of the rain gauges and their measurements, and then a field with measurements obtained by cross-validation at each rain gauge location. We can apply statistical metrics at this point on both fields in order to investigate how close the cross-validation field is to the observation field for every interpolation method.

• The Bias criterion accounting for the overall difference between the values generated by cross-validation and the observed ones:

  $$Bias=\frac{1}{n}{\displaystyle \sum }_{i=1}^n\left[R^{\prime }\left(x\right)-R\left(x\right)\right].$$

  (24)
  A $Bias$ value close to zero is indicative of a good interpolation performance.
• The root mean square error normalized with the average of the observations $\langle R\rangle$:

  $$RMSE=\frac{1}{\langle R\rangle }\sqrt{\frac{1}{n}{\displaystyle \sum }_{i=1}^n\left[R^{\prime }\left(x\right)-R\left(x\right)\right]}².$$

  (25)
  The closer the $RMSE$ (the root mean square error) to zero, the better is the interpolation performance.
• The variance ratio coefficient $RVAR$:
  The closer the variance ratio coefficient $RVAR$ gets to one, the better preserves the variance of the observed data more.

  $$RVAR=\frac{Var\left[R^{\prime }\left(x\right)\right]}{Var\left[R\left(x\right)\right]}.$$

  (26)

2.5. General Scheme of the Study

The primary objective of this study is investigating the benefits of incorporating radar data in QPE products using geostatistical methods. Moreover, the Hitschfeld–Bordan scheme and the mean field bias correction method are applied to the radar data, and their effects on the merging techniques KED and CM are evaluated. In order to meet these objectives, the study is structured as follows:

• Selection of hourly time steps where precipitation is recorded in both seasons.
• Collection of Rain gauge data from the Météo-France rain gauge network at their 6 min native temporal resolution (for each hour of rain selected, each rain gauge provides 10 measurements).
• Aggregation of the rain gauge data at 30 and 60 min temporal resolutions (Météo-France rain gauge data is disaggregated from 6 to 5 min resolution).
• Collection of radar data corresponding to the selected time steps (step 1).
• Aggregation of radar data from their native 30 s temporal resolution to the three temporal resolutions of this study: 5, 30, and 60 min.
• Correction of radar data from clutter using a static clutter map.
• Computation of seasonal standardized variograms for each temporal resolution using radar data.
• Time steps with poor radar quality (using the spatial bias), a low average precipitation rate, or displaying a bright band in the radar field are excluded from the cross-validation procedure.
• The cross-validation procedure is applied using the deterministic inverse distance weighting method and the three geostatistical methods OK, KED, and CM for each season and temporal resolution.
• The interpolation performance metrics are computed for the four methods using the cross-validation procedure’s results.
• The cross-validation procedure is reapplied to the multivariate geostatistical methods KED and CM using radar data corrected from attenuation effects using the Hitschfeld–Bordan scheme. Interpolation metrics are computed again and compared to those obtained without this correction.
• The cross-validation procedure is reapplied to the multivariate geostatistical methods KED and CM using radar data corrected from the mean field bias (no attenuation correction in this step). Interpolation metrics are computed again and compared to those obtained without this correction.

3. Study Area and Data

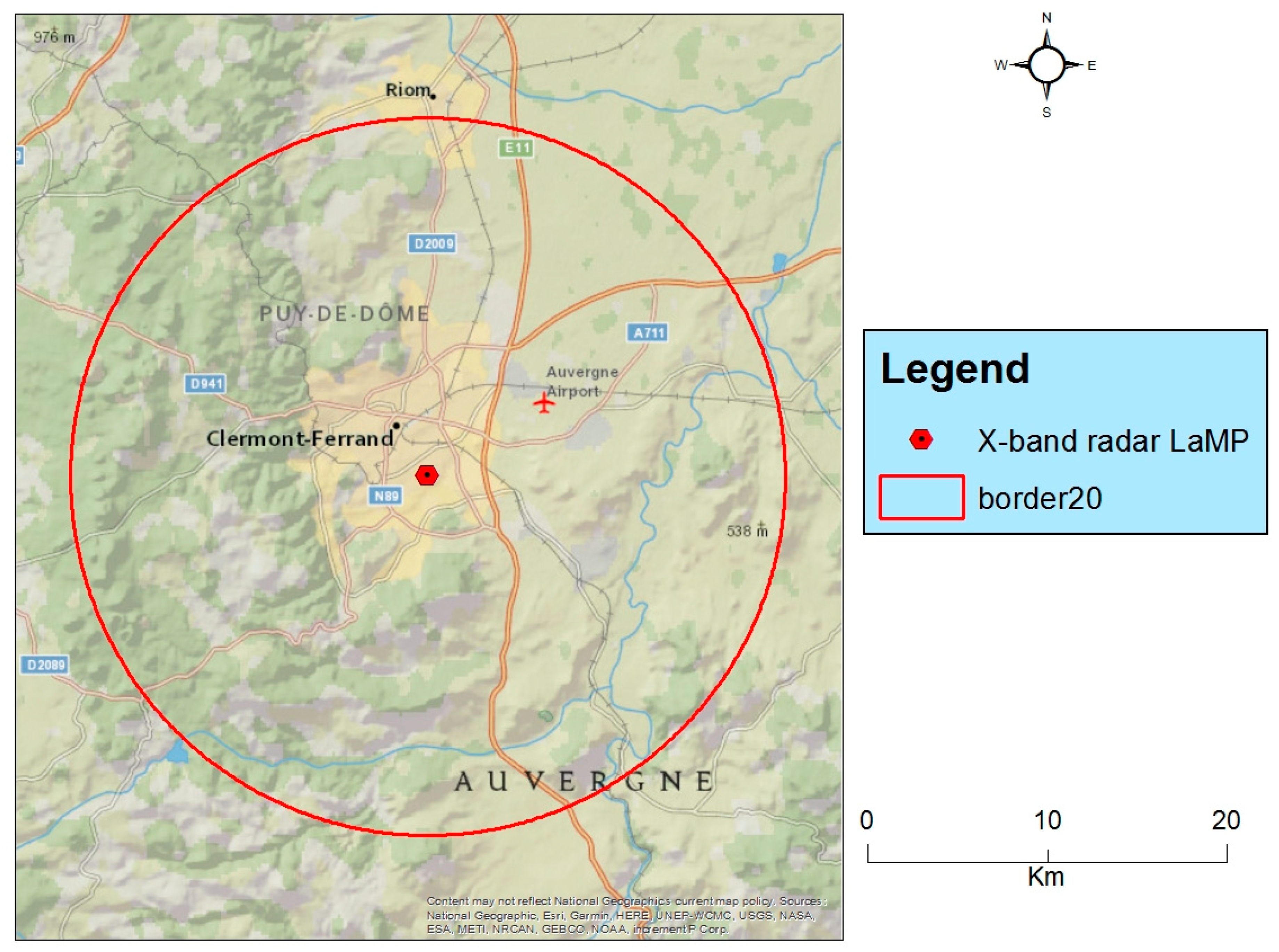
The study area is located within 20 km of the LaMP (Laboratoire de Météorologie Physique in French or Laboratory of Physical Meteorology) single-polarized non-Doppler X-band weather radar located in the Clermont Auvergne metropolis in central France. Figure 1, where the ESRI (Environmental Systems Research Institute) National Geographic World Map is used as a base map, shows the size of the 301 Km² metropolis, constituting approximately 24% of the area of interest (limited by the blue circle in Figure 1). The urban character of the region is accentuated by other small urban centers, such as Riom in the north and Veyre-Monton to the south of the area of interest.

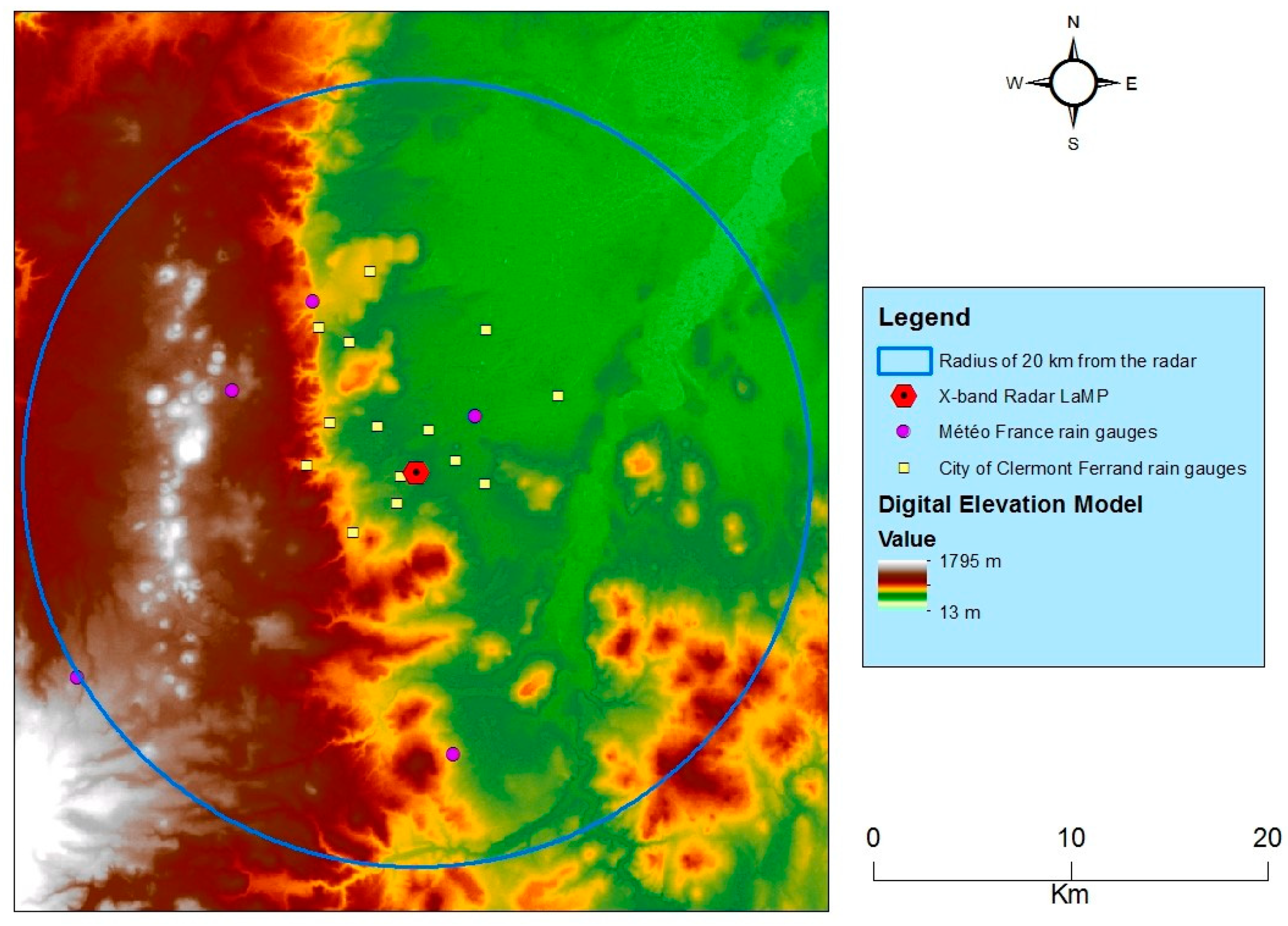
Figure 2 shows the rain gauge network as well as the Digital Elevation Model (DEM) of the terrain and the location of the X-band radar. The western part is dominated by the Puy mountain range with a local peak of 1465 m. The South West leads towards the Puy de Sancy Mountain (1885 m). In contrast, the eastern side of the study area is considerably flatter, as a sizeable portion of it is part of the Limagne plain with the Allier River going through it in the Northeast. The average annual precipitation is around 550 mm/year with the highest monthly rainfall averages occurring during the summer months.

The radar specifications are set up to 5° antenna elevation, and a maximum range at 20 km with 60 m radial resolution (Summer 2013) or at 36 km maximum range with a 90 m radial resolution (Winter 2015). We confine the study area to 20 km from the laboratory radar, as it sufficiently encompasses all the rain gauges without changing the radial resolutions. The specifications of the LaMP radar are shown in

Table 1. The technical characteristics of the LaMP X-band radar.

Parameters	Specifications
Transmitted frequency	9.41 GHz
Peak power	24 kW
Pulse length	80 ns
Pulse repetition frequency	2100 Hz
Antenna information	Parabolic with fixed elevation (5°), 2.5° power beam width at 3 dB

. The radar was originally a marine radar, but it was extensively modified to serve as a weather radar [5].

The rain gauge network used here is a combination of two independently operated networks: the Clermont Auvergne metropolis, which operates 13 gauges at 5 min resolution, and the National Weather Service Méteo-France, which operates 5 gauges at 6 min resolution. As we are interested in the following temporal resolution: 5, 30 and 60 min, the 6 min temporal resolution gauges were disaggregated to 5 min using a moving 6-hour window centered on the target time step. OK provides a precipitation estimate at the target time step with time replacing distance in variogram Equation (16) and precipitation data from the 6 h window. Both the 5 and 6 min rain gauges’ data were also aggregated to 30 and 60 min.

Table 2. The number of time steps considered in the study.

Temporal Resolution	Number of Time Steps
	Summer 2013	Winter 2015
5	629	992
30	117	182
60	62	101

shows the number of time steps considered for both seasons for each temporal resolution. The same rainfall events were used across the three temporal resolutions, which enabled us to see the effects of temporal aggregation on the investigated geostatistical techniques. Only two seasons were considered, as there have been periods where the radar was malfunctioning or transported to other regions for specific missions, such as the COPS (Convective and Orographically-induced Precipitation Study) campaign in the summer of 2007 [40], or the HYMEX (Hydrometeorological Cycle in the Mediterranean Experiment) campaign in the fall of 2012 [41,42].

Table 3. The distribution of hourly time steps across the two seasons of the dataset.

Summer 2013	March	April	Mai	June	July	August	September
	3	26	28	4	1	0	0
Winter 2015	September	October	November	December	January	February	March
	15	17	37	2	14	7	9

shows the distribution of the hourly time steps across the months of the two seasons (from 21 March 2013 to 21 September 2013 for the summer season and from 22 September 2014 to 20 March 2015 for the winter season). The hourly time steps belong to several rainfall events spanning over 18 days in the summer season and 17 days in the winter season.

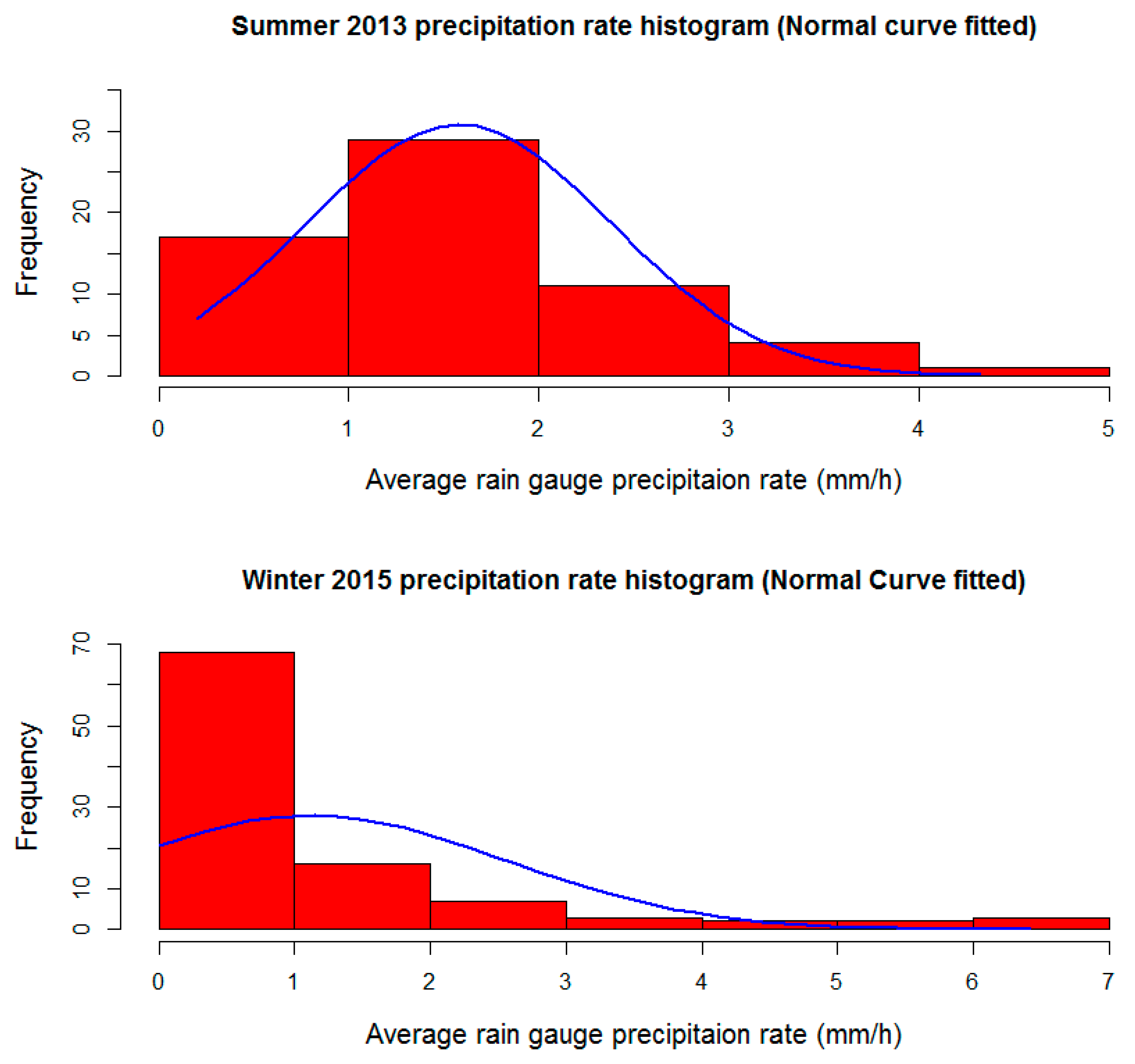
As far as precipitation rates are concerned, there is a stark difference between the two seasons. In fact, as Figure 3 shows, the winter season is dominated by very light rain with an average precipitation rate under 1 mm/h; on the other hand, the summer season has much tenser precipitations rates with most hourly averages between 1 and 2 mm/h but with lesser extremes (4.3 mm/h in summer and 6.5 mm/h in winter). This might be explained by the difference in the rain type between the two seasons. Section 4 reinforces this probability through an analysis of the standardized variograms for the two seasons for the three temporal resolutions.

3.1. Preprocessing of the Radar Data

Radar data suffers from a host of errors as shown in the Introduction, which makes them strongly biased [43]. As the radar does not measure rainfall directly, a Z-R power law relationship is necessary to convert the reflectivity Z into the precipitation rates R. In order to establish such a relationship, it is necessary to assume a certain raindrop distribution; however, that distribution changes depending on the rain type. The existence of frozen particles adds another layer of complexity [44].

The power law used in this study to retrieve rainfall rate was developed by Marshall and Palmer [45]:

$$Z=200\ast R^{1.6}$$

(27)

where $Z$ s in mm⁶ m⁻³ and $R$ is in mm/h. This $Z-R$ relationship is chosen because a specific one for the region of the study is not available to our knowledge.

In order to get rid of undesirable clutter, a static clutter map was realized by the laboratory during dry clear sky events to determine the location of ground clutter cells. It was determined that a threshold of 17.3 dBZ was adequate to isolate clutter cells. Although the process was visual, it succeeded in removing clutter properly. For each radar image, radar pixels located inside the identified clutter cells were removed, and the remaining pixels were then interpolated using the inverse distance weighting method over a 100 × 100 m Cartesian grid covering the study area. The passage from a polar to a Cartesian grid may lead to a loss of variance; however, it is considered to be marginal as small rain cells are conserved.

3.2. Radar Data’s Quality

The quality metrics introduced in Section 2.4.1 are computed for both seasons with each temporal resolution.

Comparing a rain gauge rainfall rate measurement to the one provided by the corresponding radar data pixel is not straightforward. In fact, the radar may detect rainfall rates inferior to the rain gauge’s QPE resolution (2.4 mm/h for the Clermont Auvergne rain gauges and 1 mm/h for the Météo-France rain gauges). In such a situation, it is difficult to determine if the reflectivity values measured by the radar correspond to false non-zeros due to the instrument’s limitations (detailed in the introduction), or if they correspond to actual light rain. Therefore, the temporal root mean square error $RMS{E}_{temp}$ is computed at every gauge location, but only for time steps when this specific rain gauge detected rainfall. $RMS{E}_{temp}$ values offer great insight into the radar quality at a specific location, and are, therefore, an appropriate tool to evaluate the radar point measurement QPE’s quality.

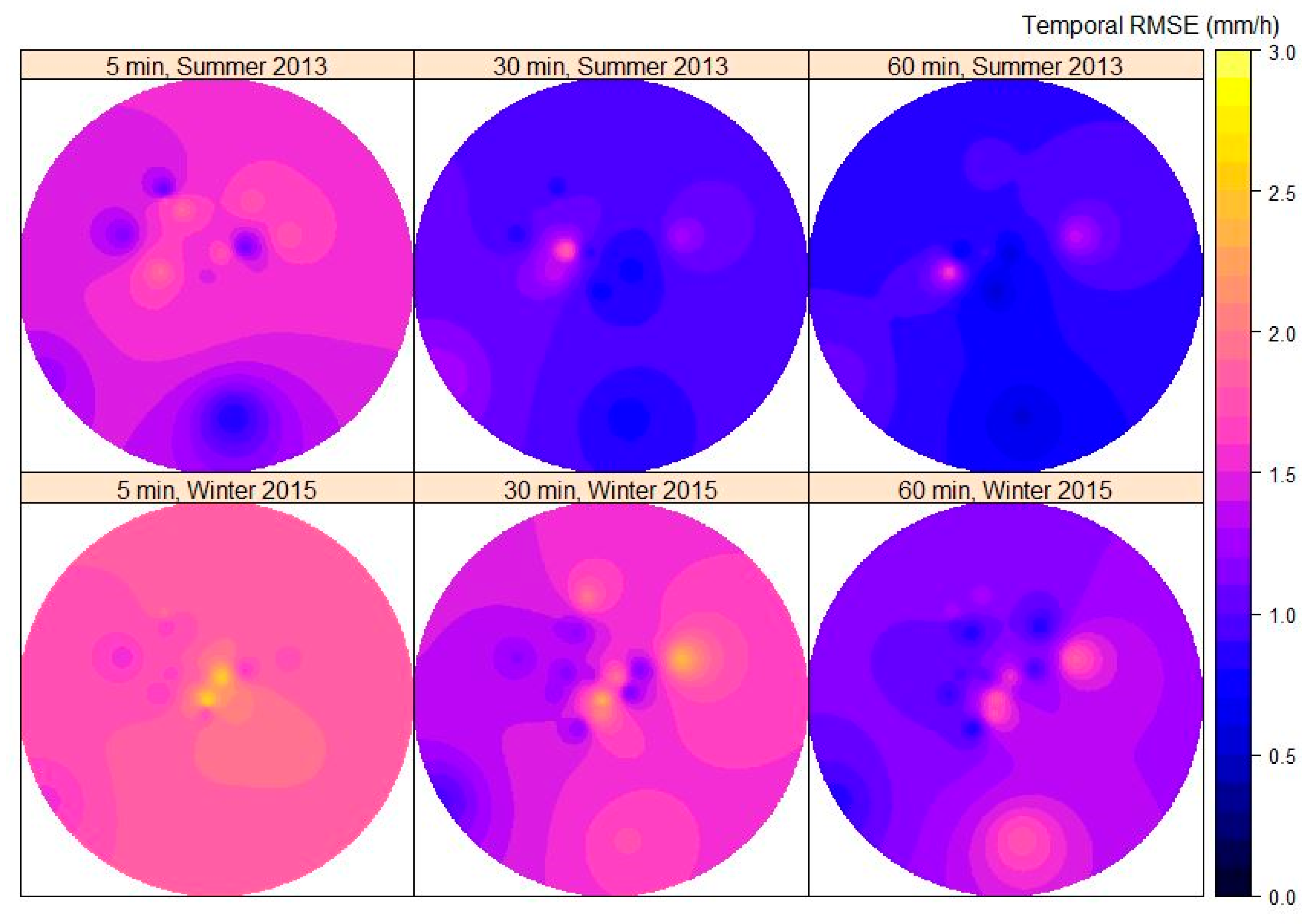
Figure 4 shows $RMS{E}_{temp}$ maps for each season and temporal resolution. The $RMS{E}_{temp}$values were interpolated over the area of interest using the inverse distance weighting interpolation technique. Overall, as Figure 4 clearly illustrates, averaging radar and rain gauge data over greater accumulation times decreases the temporal bias for both seasons. For example, the average $RMS{E}_{temp}$ decreases from 1.50 mm/h to 0.99 mm/h and from 1.84 mm/h to 1.50 mm/h for the summer and winter season, respectively, when the temporal resolution goes from 5 to 30 min. The averaging from 30 to 60 min yields the same results: the average $RMS{E}_{temp}$ decreases from 0.99 mm/h to 0.86 mm/h and from 1.50 mm/h to 1.19 mm/h for the summer and winter season, respectively, when the temporal resolution goes from 30 to 60 min.

The seasonal comparison indicates higher temporal biases in the winter season compared to the summer season for the three temporal resolutions. This is may be due to the difference in rain type and precipitation intensity between both seasons as shown in Figure 3. In particular, the summer season experienced stronger and highly convective events compared to the winter season, with the exception of a few thunderstorms taking place in the month of October (winter season). This leads us to conclude that the quality of radar data was better overall in the summer season of 2013 in terms of point measurement QPE.

The spatial bias $RMS{E}_{spatial}$is computed over all time steps where at least a single rain gauge detected precipitation. Contrary to $RMS{E}_{temp}$, this metric enables us to detect time steps with poor radar data (high $RMS{E}_{spatial}$) by taking all of the differences between radar and rain gauge data into account for every time step. Figure 5 shows the distribution density of $RMS{E}_{spatial}$ for both seasons at every temporal resolution. As for$RMS{E}_{temp}$, averaging reduces the spatial resolution significantly: the median $RMS{E}_{spatial}$ falls from 1.24 mm/h to 0.7 mm/h and from 1.09 mm/h to 0.6 mm/h for the summer and winter season, respectively, when averaging 5 min data to 30 min.

The seasonal comparison reveals that the winter season has better radar data quality compared to the summer season in terms of $RMS{E}_{spatial}$. We suspect the rain type to be the reason here again, as it is the only factor that changes seasonally (the radar setting and location stayed the same).

4. Results and Analysis

4.1. Variograms Inference and Analysis

In order to infer the variograms used in this study for every temporal resolution and for both seasons, all time steps with an average over 0.2 mm/h were used. This threshold corresponds to one of the Clermont-Ferrand gauges detecting rainfall at least once in an hour. Twelve thousand random pixels were picked up from the 100 × 100 m grid to compute the variograms, and then standardized by the variance of each time step as expressed in Equation (17). The six experimental inferred variograms following this method were then fitted to the corresponding theoretical ones using Equations (13) and (14) as shown in Figure 6 (

Table 4. The parameters of the theoretical models used in Ordinary Kriging (OK), Kriging with an External Drift (KED), and Conditional Merging (CM).

Season	Parameters	Temporal Resolution
		5 min	30 min	60 min
Summer 2013	Nugget	0.18	0.20	0.20
	Sill	1.06	1.09	1.07
	Range (Km)	10.68	12.62	13.17
	Model	Spherical	Spherical	Spherical
Winter 2015	Nugget	0.20	0.19	0.24
	Sill	1.12	1.19	1.16
	Range (Km)	14.83	18.22	17.37
	Model	Spherical	Spherical	Spherical

provides the features of every theoretical variogram). The spherical model was chosen to take into account the variance fluctuations at distances larger than the theoretical range. Indeed, the semivariance is constant beyond the range in the spherical model, as opposed to the exponential model where it keeps increasing.

Figure 3 contains the experimental variograms and their theoretical counterparts. Across the two seasons and three temporal resolutions of this study, a few realizations could be pointed out:

• The nugget or the nugget variance is the average halved squared difference between two measurements separated by an infinitesimally small distance, when h tends to zero in Equation (16). In this context, it means a distance inferior to the resolution of the radar grid of 100 m. As such, it represents the stochastic uncertainty of a single measurement. In this study, the nugget variance is around 0.2 (or 20% of the total variance of the rainfall fields measured by the radar) regardless of season and temporal resolution. This quite high nugget variance is naturally expected to influence the accuracy of the interpolation of rain gauges using OK with a variogram inferred from the radar.
• The experimental sills and ranges are larger in winter compared to summer, which is in line with the findings in [21,38]. This is probably attributed to the fact that stratiform rainfall events are more common in winter. Indeed, stratiform rainfall cells are more spread out over large areas; hence, a higher spatial continuity in precipitation results in a higher range and overall variance (sill).
• The average range is smaller for the 5 min temporal resolution compared with the remaining 30 and 60 temporal resolutions. This is due to the temporal smoothing effect with larger accumulation periods.

4.2. Cross-Validation Results

Section 3.2 demonstrated the existence of both a temporal and spatial bias in radar data. Temporal resolutions (30 and 60 min) exhibit less temporal and spatial bias (Figure 4 and Figure 5); however, this comes at the expense of the high spatiotemporal variability captured at the 5 min temporal resolution, which is very valuable for urban hydro-meteorological applications. Identifying those radar pixels that correspond to each rain gauge is a crucial step for both KED and CM. The nearest pixels to the gauges were utilized, and spatial mismatches were deemed negligible as they remained under the grid resolution of 100 m for the most part. The spatial mismatches refer to the distance between the rain gauge and the center of the nearest radar pixel projected vertically to the ground.

The number of remaining time steps, once the three criteria above were applied to the data, is listed in

Table 5. The number of time steps remaining for cross-validation.

Temporal Resolution	Number of Time Steps
	Summer 2013	Winter 2015
5	283	368
30	67	74
60	33	41

.

The radar data were used to infer the variograms for each time step. Indeed, the small size of the rain gauge network (18 rain gauges only) was not enough to build reliable experimental variograms with enough pairs at each distance to calculate the semivariance and identify the variogram features: the nugget, the sill, and the range. Inverse Distance weighting is the only method that uses the rain gauge data exclusively. All of the other methods use the variogram, and therefore radar data.

In order to compare the cross-validation results for the different interpolation techniques, we evaluate the relative improvement of method M₂ (Bias₂, RMSE₂, RVAR₂) in comparison with method M₁ (Bias₁, RMSE₁, RVAR₁). The relative change in terms of bias is$PBIAS$, and in terms of the root mean square error and the variance ratio coefficient is$PRMSE$, $PRVAR$ respectively. $PBIAS$, $PRMSE$ and $PRVAR$ are calculated thusly:

$$PBIAS=\{\begin{array}{c}\frac{|BIA{S}_2-BIA{S}_1|}{BIA{S}_1} if BIA{S}_2-BIA{S}_1\le 0\\ -\frac{|BIA{S}_2-BIA{S}_1|}{BIA{S}_1} if BIA{S}_2-BIA{S}_1>0\end{array}$$

(28)

$$PRMSE=\{\begin{array}{c}\frac{|RMS{E}_2-RMS{E}_1|}{RMS{E}_1} if RMS{E}_2-RMS{E}_1\le 0\\ -\frac{|RMS{E}_2-RMS{E}_1|}{RMS{E}_1} if RMS{E}_2-RMS{E}_1>0\end{array}$$

(29)

$$PRVAR=\{\begin{array}{c}|RVA{R}_1-1\left|-|RVA{R}_2-1\right| if |RVA{R}_1-1\left|\ge |RVA{R}_2-1\right|\\ |RVA{R}_2-1\left|-|RVA{R}_1-1\right| if |RVA{R}_1-1|\langle |RVA{R}_2-1|\end{array}$$

(30)

$PBIAS$, $PRMSE$ and $PRVAR$ are percentages. They are positive if there is an improvement in method M₂ compared with method M₁ (or if there is an improvement after correcting the radar data from the mean field bias or from attenuation effects using the same method interpolation method). This means that PBIAS and PRMSE are positive if the bias and RMSE decrease and RVAR becomes closer to 1.

Table 6. Interpolation Performance metrics results for IDW, OK, KED and CM (BIAS in mm/h, RMSE and Rvar are without unit).

Cross-Validation Results (No Radar Data Correction Is Applied)		5 min			30 min			60 min
		BIAS	RMSE	RVAR	BIAS	RMSE	RVAR	BIAS	RMSE	RVAR
Summer 2013	IDW	0.0771	0.7861	0.1186	0.0562	0.5122	0.1201	0.0406	0.3774	0.1075
	OK	0.0247	0.7810	0.2409	0.0213	0.4823	0.2746	0.0189	0.3603	0.2493
	KED	0.0335	0.8079	0.4406	0.0218	0.4828	0.4254	0.0194	0.3545	0.3758
	CM	0.0494	0.9863	0.4490	0.0492	0.7644	1.1681	0.0373	0.5525	0.8793
Winter 2015	IDW	−0.0411	1.4163	0.1169	−0.0405	0.7243	0.1193	−0.0221	0.5728	0.1164
	OK	−0.0172	1.4338	0.2269	−0.0165	0.7084	0.2504	−0.0086	0.5550	0.2486
	KED	−0.0291	1.5800	0.5296	−0.0205	0.7408	0.3936	−0.0057	0.5388	0.3955
	CM	−0.0283	1.6819	0.4879	−0.0222	1.0258	0.7662	−0.0106	0.8854	0.9832

shows the cross-validation results for the three interpolation performance metrics introduced in Section 2.4.2. Clutter removal was the only correction step applied to the radar data.

Despite introducing a quite high nugget variance at the observation locations, OK outperforms IDW for every temporal resolution and for both seasons. Across all temporal resolutions and both seasons, the bias was substantially reduced (PBIAS = 60%), the RMSE was improved by PRMSE = 3%, and the gain of variance was PRVAR= 13%. This result shows that it is better to use OK for time steps where radar data is not available but an already computed standardized seasonal variogram is. In this study, the standardized seasonal variogram was adjusted to each time step using the variance of the rain gauge observations.

KED and CM performed noticeably better than IDW but not OK.

Table 7. The average relative improvement when comparing IDW and OK with geostatistical techniques (KED and CM).

M1	M2	PBIAS	PRMSE	PRVAR
IDW	KED	54%	0%	31%
	CM	31%	−39%	62%
OK	KED	−17%	−2%	18%
	CM	−75%	−43%	48%

shows the relative improvement when comparing IDW and OK with the geostatistical techniques (KED and CM), respectively. PBIAS, PRMSE, and PRVAR are averaged over all temporal resolutions and both seasons. While the relative improvement is quite important when comparing KED and CM with IDW, OK performs noticeably better than CM (PBIAS = −75%, PRMSE = −43%, and PRVAR = 48%). KED performs better than OK in terms of RVAR (PRVAR = 17%), but fails to perform the same as OK in terms of point measurement QPE accuracy (PBIAS = −17%, PRMSE = −2%).

There seems to be a tradeoff to be made between obtaining the most accurate measurement point estimation (gauged by bias and RMSE) and the preservation of the observations’ variance (gauged by RVAR). This may be explained by the fact that the radar captures the variability of rainfall quite well, but struggles at point measurement QPE; thus, including the radar data as a second variable in KED and CM results in a higher RVAR but a lower RMSE and/or bias. Taking all metrics into account, KED is the better multivariate interpolation technique overall. In fact, across all temporal resolutions and both seasons, KED improved bias by 31% and RMSE by 27% compared to CM; however, CM outperformed KED at preserving the observations’ variance (PRVAR = 31%).

4.3. Effects of Mean Field Bias Correction on Geostatistical Merging Techniques

The Mean Field bias correction was performed on radar data for all time steps used in the cross-validation procedure in order to reduce the bias in the radar data and result in a better interpolation performance for KED and CM. However, this was not straightforward.

Table 8. The relative improvement in interpolation Performance metrics results for KED and CM when radar data is corrected from the mean field bias.

Cross-Validation Results (Radar Data Corrected from the Mean Field Bias)		5 min			30 min			60 min
		PBIAS	PRMSE	PRVAR	PBIAS	PRMSE	PRVAR	PBIAS	PRMSE	PRVAR
S13	KED	1%	0%	0%	0%	0%	0%	−2%	0%	0%
	CM	−1%	−1%	0%	−2%	5%	−11%	0%	5%	−22%
W15	KED	2%	0%	0%	−5%	22%	5%	−8%	0%	0%
	CM	2%	6%	−15%	−9%	29%	−30%	5%	19%	−53%

shows the relative improvement in the interpolation performance metrics for KED and CM compared with the metrics in Table 6 where no mean field bias correction was applied.

A sharp decrease in the PRVAR, when comparing the performance of CM before and after the MFB correction was applied, is the only significant change the MFB correction method had (e.g., PRVAR = −53% for the winter season at the 60 min temporal resolution). KED is mostly unaffected by the correction, with most relative improvement metrics under 2% (On average: PBIAS = −2%, PRMSE = 4%, and PRVAR = 1%), with the notable exception of the 30 min temporal resolution in the winter season, where a gain in PRMSE = 22% and RVAR = 5% is partially offset by a decrease in bias PBIAS = −5%.

The difference between the two geostatistical methods resides in the exploitation of the radar deviation map. CM adds the deviation field directly into the observation field (interpolated by OK). This means that applying the mean field bias correction to radar data reduces the value of the deviation map (as the radar pixels corresponding to the rain gauges have values closer to those of the rain gauges); consequently, the results of the CM interpolation become closer to those of OK. KED uses the deviation map indirectly via the residual variogram, which contains the deviation map effects.

4.4. Effects of Attenuation on the Geostatistical Merging Techniques

Table 9. The relative improvement in interpolation Performance metrics results for KED and CM when radar data is corrected from attenuation effects.

Cross-Validation Results (Radar Data Corrected from Attenuation Effects)		5 min			30 min			60 min
		PBIAS	PRMSE	PRVAR	PBIAS	PRMSE	PRVAR	PBIAS	PRMSE	PRVAR
S 2013	KED	4%	−1%	7%	−5%	0%	0%	10%	12%	7%
	CM	9%	8%	−13%	−2%	5%	−11%	11%	21%	−35%
W 2015	KED	3%	−2%	8%	53%	3%	11%	7%	3%	9%
	CM	−3%	8%	−7%	11%	13%	−33%	−8%	16%	−52%

shows the relative improvement in the KED and CM interpolation performance metrics when the radar data was corrected from attenuation effects using the Hitschfeld–Bordan scheme. KED’s performance was improved across the board (on average across the three temporal resolutions and both seasons: PBIAS = 12%, PRMSE = 2%, and PRVAR = 7% compared to when no attenuation scheme was applied). When it comes to CM, the results are more mixed. The loss of variance using attenuation-corrected data (on average PRVAR = −25%) is usually accompanied with a relative improvement in either bias or RMSE (on average PBIAS = 3% and PRMSE = 12%). Generally speaking, attenuation correction increases the point measurement accuracy at the gauge locations.

5. Summary and Conclusions

The aim of this work was to investigate the performance of geostatistical methods for merging radar and rain gauge data at high temporal resolutions. To our knowledge, previous studies used C-band radars that cover much larger areas and suffer less attenuation. In order to examine the influence of temporal resolution, time steps at 5, 30, and 60 min resolutions from two seasons (summer 2013 and winter 2015) were considered in the dataset. The radar data quality was assessed through the quantification of temporal bias at each rain gauge location and spatial bias for every time step. Three geostatistical techniques were used in this study: OK, KED, and CM as well as the deterministic method IDW. They were evaluated and compared through cross-validation.

We found that the X-band radar data suffers from greater temporal bias at gauge locations in the winter season compared to the summer season. Conversely, the spatial bias assessing the radar quality for each time step was smaller on average for the winter season compared to the summer season. Other differences between both seasons can be detected in the standardized variograms, where the sills and ranges are greater in winter, suggesting more stratiform rainfall events.

The Clermont Auvergne catchment suffers from a lack of rain gauges (18 rain gauges only). In this case, using Ordinary Kriging with a radar-inferred variogram achieves a better QPE than classic methods, such as IDW. This leads us to believe that computing a variogram using radar data from a local radar or the Météo-France nationwide C-band/S-band/X-band network for each season is better than using a deterministic method, such as IDW, especially with a sparse rain gauge network. OK with a radar-inferred variogram presents a unique advantage: it can be applied once the variogram is computed whether the radar is operational or not.

In the following, the relative improvement is given as an average across the three temporal resolutions and both seasons.

When it comes to geostatistical methods, KED was the best multivariate geostatistical QPE method overall. KED improved bias by 31% and RMSE by 27% compared to CM; however, CM generally excelled at preserving the observations’ variance better than all the other methods, including KED (PRVAR = 31%).

The Hitschfeld–Bordan attenuation correction scheme helped KED improve its performance noticeably (PBIAS = 12%, PRMSE = 2%, and PRVAR = 7% compared to when KED was applied without correcting radar data from attenuation effects), while the mean field bias correction method effects were marginal (PBIAS = −2%, PRMSE = 4%, and PRVAR = 1% compared to when KED was applied without correcting radar data from the mean field bias). Both correction schemes, however, affected the performance of CM in a more concrete way by reducing its capacity to recuperate the variance of the observations (PRVAR = −25% after the attenuation correction and PRVAR = −22% after the mean field bias correction), while slightly increasing its accuracy (a marginal increase in bias and/or RMSE values).

Merging radar and rain gauge data is an interesting research subject to pursue in order to develop better QPE products. In our study, OK and KED performed the best even though single-polarimetric X-band weather radars have a rather low quality compared to C-band and S-band weather radars that are far more popular despite being more expensive. OK of rain gauge data using a radar-data-inferred variogram proved to be a better alternative to the deterministic IDW method. This proves the importance of the weather radar as a complimentary source of information and encourages further work on the subject. The next step is to examine how the merging of X-band radar and rain gauge data compares to the nationwide QPE product provided by Météo-France through a number of C-, S-, and X-band radars covering the whole country. This will hopefully lead us to exploit both QPE products for rainfall nowcasting over the Clermont Auvergne catchment.