Next Article in Journal
The Impact of Divalent Cations on the Enrichment of Soluble Saccharides in Primary Sea Spray Aerosol
Previous Article in Journal
Impact of Atmospheric Circulation on the Occurrence of Hot Nights in Central Europe
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 9
Issue 12
10.3390/atmos9120475
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Comparative Study of Bin and Bulk Cloud Microphysics Schemes in Simulating a Heavy Precipitation Case

by
Hyunho Lee
1,2,* and
Jong-Jin Baik
1
1
School of Earth and Environmental Sciences, Seoul National University, Seoul 08826, Korea
2
Center for Climate Systems Research, Columbia University, New York, NY 10025, USA
*
Author to whom correspondence should be addressed.
Atmosphere 2018, 9(12), 475; https://doi.org/10.3390/atmos9120475
Submission received: 4 September 2018 / Revised: 30 November 2018 / Accepted: 30 November 2018 / Published: 3 December 2018
(This article belongs to the Section Meteorology)
Browse Figures
Versions Notes

Abstract

:
Comparisons between bin and bulk cloud microphysics schemes are conducted by simulating a heavy precipitation case using a bin microphysics scheme and four double-moment bulk microphysics schemes in the Weather Research and Forecasting (WRF) model. For this, we implemented an updated bin microphysics scheme in the WRF model. All of the microphysics schemes underestimate observed strong precipitation, but the bin microphysics scheme yields the result that is closest to observations. The differences among the schemes are more pronounced in terms of hydrometeor number concentration than in terms of hydrometeor mixing ratio. In this case, the bin scheme exhibits remarkably more latent heat release by deposition and riming than the bulk schemes. This causes stronger updrafts and more upward transport of water vapor, which leads to more deposition, and again, increases the latent heat release. An additional simulation using the bin scheme but excluding the riming of cloud droplets on ice crystals, which is not or poorly treated in the examined bulk schemes, shows that surface precipitation is slightly weakened and moved farther downwind compared to that of the control simulation. This implies that the more appropriate representation of microphysical processes in the bin microphysics scheme contributes to the more accurate prediction of precipitation in this case.

1. Introduction

There are two methods that are widely used to represent clouds and precipitation in numerical weather and climate models: bulk and bin microphysics schemes. Usually, bulk microphysics schemes parameterize size distributions of cloud particles using only a few parameters, and calculate microphysical processes by integrating analytic functions. For example, currently most widely used bulk microphysics schemes adopt a kind of gamma distribution with two independent variables (number concentration and mixing ratio) to express drop size distributions, and present the condensational growth rate of drops as a function of the two variables by integrating or approximating the vapor diffusion equation. This method has obvious drawbacks; any analytic function with a few independent variables cannot express arbitrary size distribution shapes. In contrast to bulk microphysics schemes, bin microphysics schemes explicitly express the distributions by dividing cloud particles into a few tens to hundreds of bins and evaluate microphysical processes of the particles in each bin. While bin microphysics schemes are believed to be useful to investigate the evolution of size distributions of particles in clouds, bulk microphysics schemes are widely used in operational weather forecasting, owing to their much lower computational cost than bin microphysics schemes.
Since Ogura and Takahashi [1] and Soong [2] developed bin microphysics schemes to represent cloud microphysical processes in numerical models, there has been a growing body of studies that develops and utilizes bin microphysics schemes to better understand clouds and precipitation [3,4,5,6,7,8,9,10,11,12]. Previous studies have reported that results obtained using bin microphysics schemes are generally closer to observations than those obtained using bulk microphysics schemes (e.g., mesoscale convection, [3,4]; mixed-phase cloud system, [5,6]; tropical cyclone, [7]). In addition, some studies have utilized bin microphysics schemes as a benchmark for evaluating or developing bulk microphysics schemes [13,14,15,16]. Khain et al. [17] provided a comprehensive comparison between bin and bulk microphysics schemes.
While many of the studies that compare bin and bulk microphysics schemes have focused on comparisons in idealized atmospheric conditions [18], a few studies have dealt with real cases. Fan et al. [6] compared the results of a bin microphysics scheme [19] to those of a double-moment bulk microphysics scheme [20] in simulating two precipitation cases that occurred in southern China, and examined aerosol effects on the precipitation cases. That study showed that the bin microphysics scheme better simulates deep convective clouds than the bulk microphysics scheme and that the opposite reaction to an increase in aerosol loading is a key mechanism to the differences. Iguchi et al. [5] compared the results of another bin microphysics scheme [9] to those of a single-moment bulk microphysics scheme [21,22] in simulating three precipitation cases, and showed that the bin microphysics scheme agrees better with observations than the bulk microphysics scheme. Iguchi et al. [5] suggested the fall velocity of hydrometeors as a key component.
Previous studies that focused on comparisons between bin and bulk microphysics schemes in simulating real cases have tended to choose just one bulk microphysics scheme for comparison, making it somewhat difficult to distinguish differences originating from the choice of a specific scheme and those originating from generic differences between bin and bulk microphysics schemes. Therefore, in this study, several double-moment bulk microphysics schemes are chosen and compared to one bin microphysics scheme. In addition, while previous studies have tended to focus on the expression of particle size distributions, this study investigates whether differences in the results of bin and bulk microphysics schemes can be caused by more appropriate representations on microphysical processes in the bin microphysics scheme. A plausible factor that partially explains differences in simulated surface precipitation is presented, and reliability of the factor is investigated with an additional simulation. The numerical model used in this study, experimental setup, and the selected case are described in Section 2. Simulation results are presented and discussed in Section 3 and Section 4. A summary and conclusions are provided in Section 5.

2. Model Description, Experimental Setup, and Case Description

The Weather Research and Forecasting (WRF) model v3.7.1 [23] is used for this study. The bin microphysics scheme of the Hebrew University Cloud Model is implemented in the WRF model [9,12,24]. This scheme evaluates nucleation, vapor diffusion processes (condensation, evaporation, deposition, and sublimation), collision, breakup, freezing, melting, ice crystal multiplication, and sedimentation. Seven hydrometeor types are considered: liquid drop, three ice crystals (column, plate, and dendrite), snow, graupel, and hail. A simplified version of this bin microphysics scheme that deals with warm microphysical processes only has also been used in combination with the WRF model to simulate idealized shallow convective clouds [25]. The spatiotemporal evolution of particle size distribution of each hydrometeor is evaluated by predicting number concentrations at 43 mass doubling bins, in which the ratio of masses between two adjacent bins is two. In addition to the number concentrations, liquid water fractions at mass grid points of snow, graupel, and hail are predicted to incorporate the gradual melting of large ice particles in the scheme. Rimed fractions of snow are also predicted to update the density and terminal velocity of snow particles. Note that the bin microphysics scheme used in this study is somewhat different from the publicly available version [12], in which the number of bins for each hydrometeor and aerosol is 33 and some microphysical processes (e.g., gradual melting), as well as liquid water fractions of large ice particles and rimed fractions of snow particles, are not predicted.
The number concentration of aerosols is calculated using 43 mass doubling bins, in which the maximum radius of aerosols is 2 μm. Aerosols are activated into liquid drops if their radii are larger than the critical radius determined by environmental supersaturation according to the Köhler theory. The radius of newly activated droplets is determined to be the larger of the smallest radius in the mass bin grid and five times the dry aerosol radius, to consider the effects of giant aerosols [26]. Ice crystals form by stochastic freezing of drops [27], or by deposition and condensation-freezing nucleation [28], or by ice crystal multiplication [29]. The mass of newly formed ice crystals is either that of frozen drop (via stochastic freezing) or the smallest mass in the mass bin grid (via nucleation or multiplication). Compared to Lee and Baik [24], the scheme is further improved by including the breakup of large snow particles following Khain et al. [9]. Turbulence-induced collision enhancement is not included.
For bulk microphysics schemes, the WRF Double-Moment 6-class (WDM6) scheme [30], Milbrandt scheme [31], Thompson–Eidhammer (or Thompson aerosol-aware) scheme [32], and National Severe Storms Laboratory (NSSL) scheme [33] are used. All of the selected bulk microphysics schemes predict cloud droplet number concentration and raindrop number concentration; in other words, they are double-moment for liquid drops. Note that although all of the bulk microphysics schemes are double-moment for liquid drops, there are noticeable differences among them. For example, the WDM6 scheme is single-moment for all ice particles [34], and the Thompson–Eidhammer scheme for snow and graupel. The Milbrandt scheme does not consider aerosol number concentration in the drop activation process and predicts the number of nucleated droplets using a hardwired method [35]. The Milbrandt and NSSL schemes consider explicit hail, whereas the WDM6 and Thompson–Eidhammer schemes predict graupel as the only rimed ice particle.
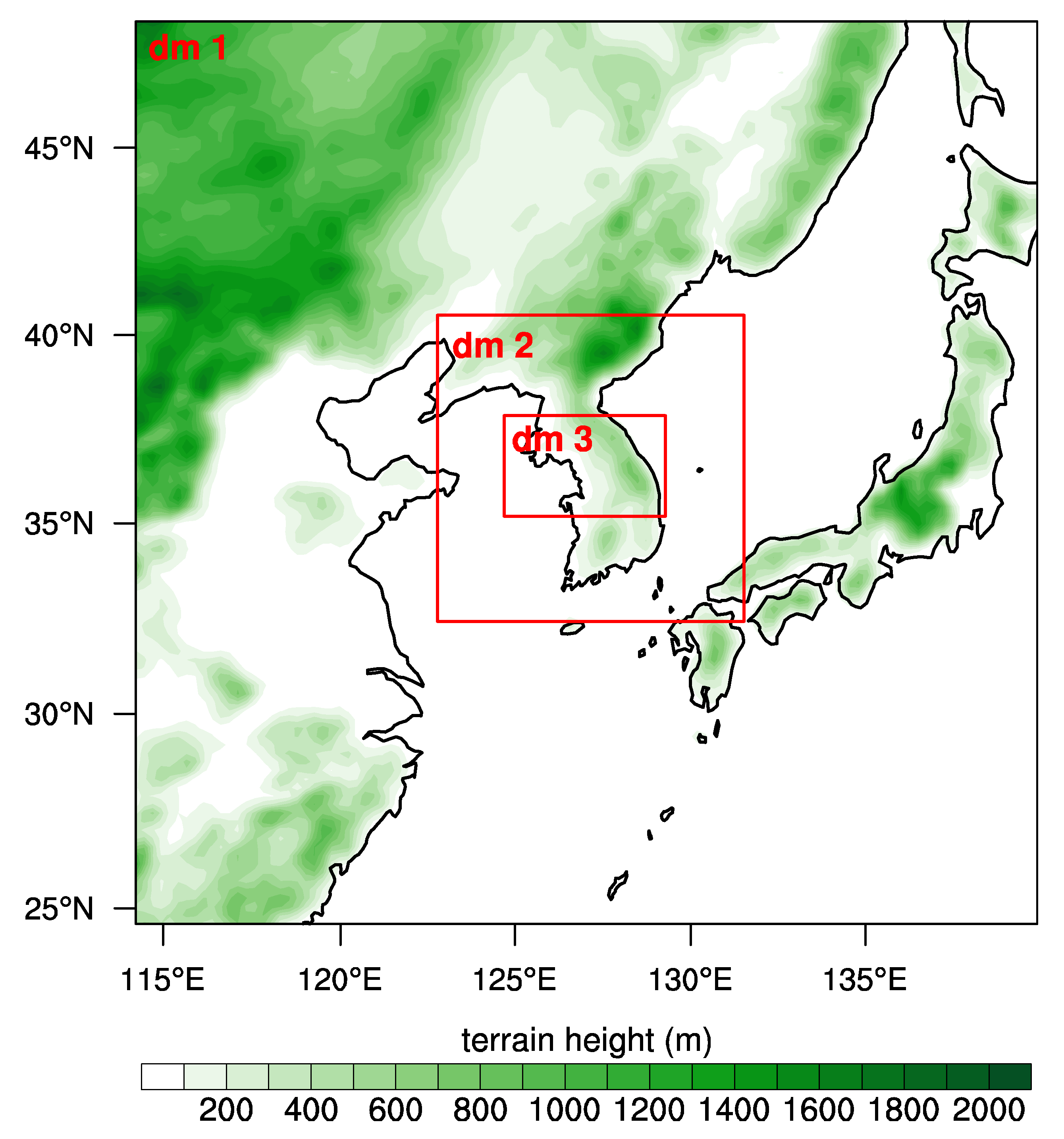
Three one-way nested domains are set for the model calculation. The numerical model setup including domain configuration is the same as in Lee and Baik [24], which is summarized and depicted in Figure 1, Table 1 and Table 2. The subgrid-scale cumulus scheme is applied only to domain 1. The model top is at 50 hPa (approximately 20 km). The domain is vertically divided into 33 layers. The vertical grid size is finest at the surface with ~30 m, and ~800 m in the free atmosphere. National Centers for Environmental Prediction (NCEP) Final (FNL) analysis data [36] that have a spatial resolution of 1° × 1° and a temporal resolution of 6 hr are used for the initial and boundary conditions of the outermost domain. In all simulations, the aerosol number concentration is set to be approximately 700 cm−3, which is similar to the hardwired value assumed in the polluted case of the Milbrandt scheme and supported by observations of long-term variations of aerosol concentration in and around the Korean Peninsula [37]. In the bin microphysics scheme, the initial aerosol size distribution is set to follow the Twomey equation [38], which is expressed as:
d N a d ln r a = 3 2 N 0 k ( 4 A 3 27 B r a 3 ) k / 2 ,
where ra is the radius of aerosol, N0 is the number concentration of activated aerosols at supersaturation of 1%, k is a constant that controls the slope of aerosol size distribution, and A and B are coefficients related to the curvature and solute effects, respectively [24].
A precipitation case that occurred on 21 September 2010 in the central region of the Korean Peninsula (roughly covered by domain 3 in Figure 1) is simulated. The maximum hourly precipitation rate and the maximum daily accumulated precipitation amount in this case reached approximately 100 mm hr−1 and 300 mm, respectively. In this case, the relatively cold and dry Siberian high was on the northwest side of the Korean Peninsula, and the relatively warm and moist western Pacific subtropical high was on the southeast side of the Korean Peninsula. A large amount of low-level moisture was supplied to the central Korean Peninsula by westerly winds along the edge of the western Pacific subtropical high. Precipitation occurred at a stationary front induced by the convergence of these two different air masses over the Korean Peninsula while thermodynamic instability (such as convective available potential energy) was low throughout the precipitation period. These features are common characteristics in heavy precipitation cases in the Korean Peninsula; hence, this case could be a representative of typical heavy precipitation in the Korean Peninsula. A detailed description of this case is given in Jung and Lee [44] and Lee and Baik [24]. The model is integrated for 24 hr from 21:00 LST (local standard time, UTC+09:00) 20 September. The first 6 hr is excluded from analysis considering the spin-up time of the model, and the remaining 18-hr data are used for analysis.

3. Comparison of Simulations to Observations

In this section, a simple comparison of simulation results to observations is presented. Because evaluations of the simulation results obtained using the bin microphysics scheme against observations are given in Lee and Baik [24] in more detail and the main purpose of this study is to compare bin microphysics scheme to bulk microphysics schemes, only a simple description focusing on performance comparison is given in this study.
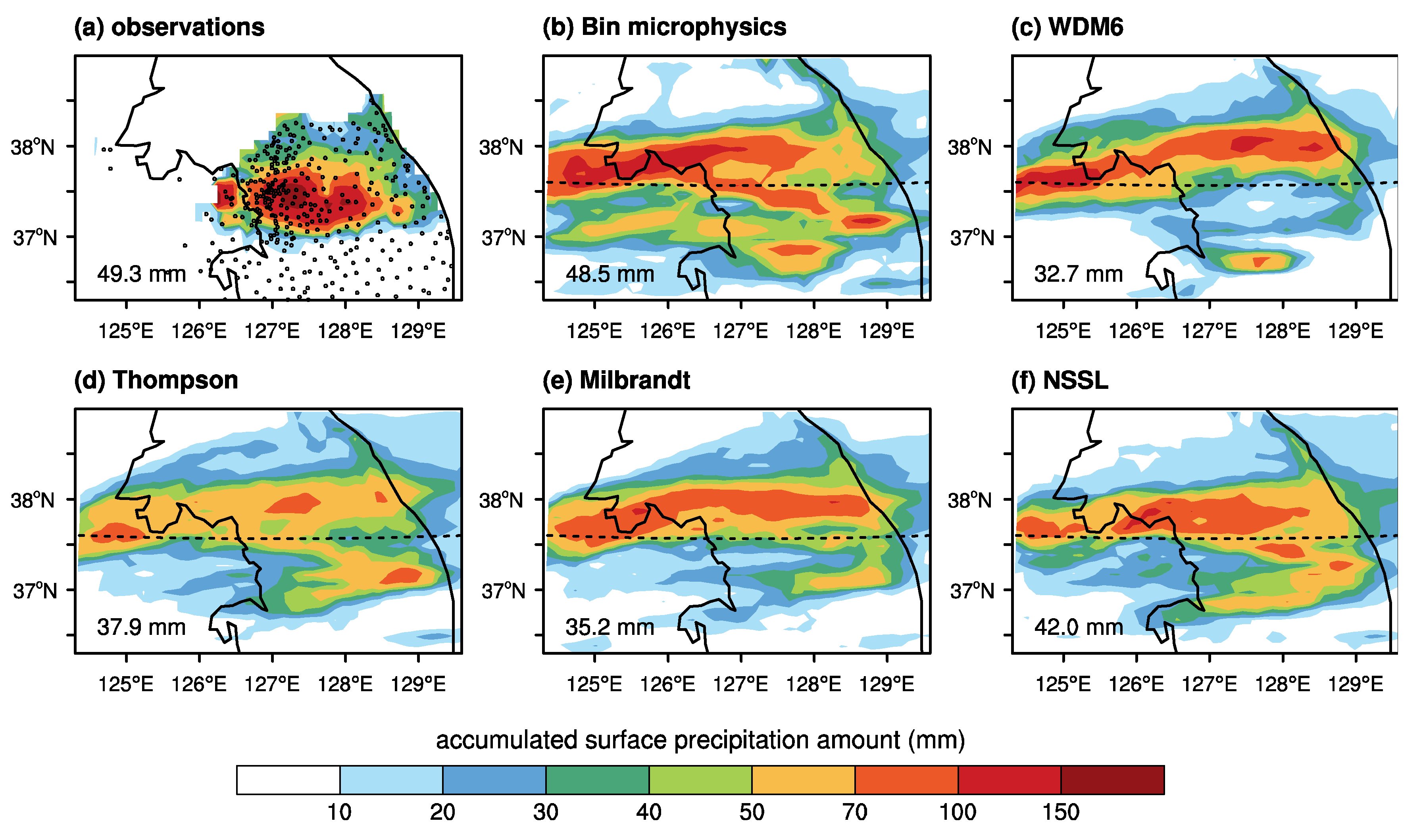
Figure 2 shows the 18-hr accumulated surface precipitation amounts observed by automatic weather systems (AWSs) and simulated by the model with different microphysics schemes. The number of AWSs is 346, whose locations are marked in Figure 2a. Surface precipitation amounts accumulated for every 15-min interval at each AWS are used. All of the simulations show two distinctly different precipitation bands: one north of ~37.6° N (the northern precipitation hereafter) and the other one south of ~37.6° N (the southern precipitation hereafter). The simulation results show the northern precipitation spreading across a relatively broad area with relatively uniform intensity compared to the southern precipitation. 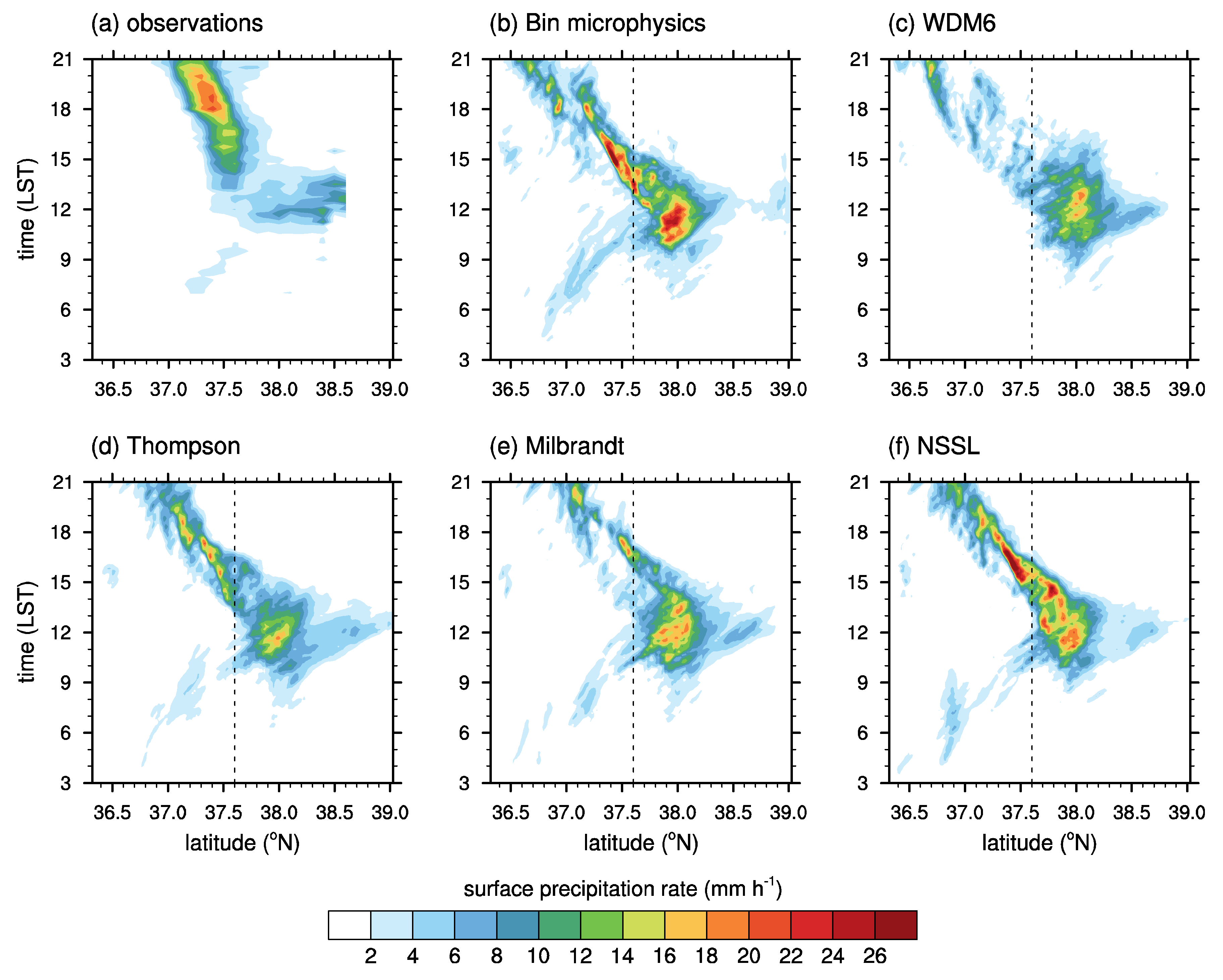The northern precipitation is not evident in Figure 2a, but radar observations show that the northern precipitation actually happened although the position and intensity are somewhat different from the simulation results [24]. The northern precipitation is not evident in the AWS observations because there are only a small number of AWSs in the region where the actual northern precipitation is concentrated. For the southern precipitation largely concentrated in the region of ~37.0° N—37.5° N and ~127° E—128° E, the bin microphysics scheme simulates strong precipitation that is underestimated and slightly northward biased compared to observations. However, the bin microphysics scheme simulates the location and propagation direction (southeastward) of the strong precipitation similar to observations. On the other hand, all of the bulk microphysics schemes simulate very small amounts of the southern precipitation compared to observations. Among the bulk microphysics schemes, the Thompson–Eidhammer and NSSL schemes simulate the largest amount of the southern precipitation, and the WDM6 scheme simulates the smallest amount of the southern precipitation. The latitude–time diagrams of surface precipitation rate averaged along the longitudinal direction are depicted in Figure 3. This figure also shows that this precipitation case can be separated into the northern precipitation propagating northward at a relatively fast speed before ~15 LST and the southern precipitation propagating southward at a relatively slow speed after ~15 LST. We note that the observed surface precipitation north of ~38°N seen in Figure 3a does not well represent real precipitation attributable to the lack of observation stations.
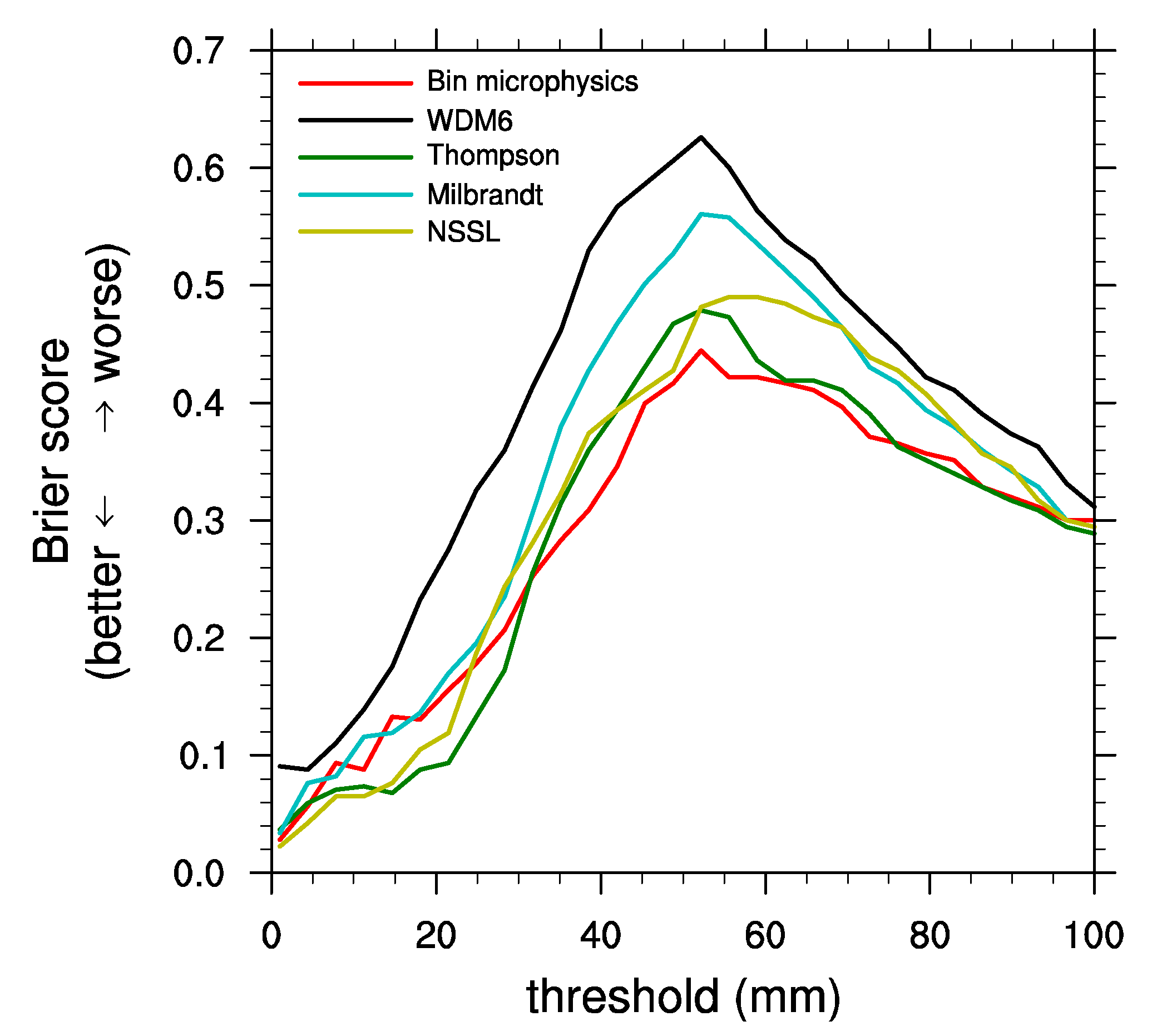
To evaluate the performance of each microphysics scheme in predicting surface precipitation amount more objectively, the Brier score [45,46] for the 18-hr accumulated surface precipitation amount is calculated across a range of thresholds (Figure 4). The Brier score (BS) is defined as:
BS = ∑ i = 1 N ( o i − f i ) 2 ,
where N is the number of comparison points, and oi and fi are observation values and forecasting values, respectively. Here, an observation value is defined as unity if the accumulated surface precipitation amount at a given point exceeds the threshold; zero otherwise. There are many methods to define forecasting values, but the same method as that of calculating the observation values is used. Note that different methods to define forecasting values could yield quantitatively different but qualitatively similar results. The Brier scores are low at small thresholds because of the widespread surface precipitation and low at large thresholds because of the limited area of strong surface precipitation. Figure 4 shows that the Brier score is generally highest (i.e., the model performance is worst) at thresholds of 40–80 mm in this case, and in that range, the bin microphysics scheme shows the best performance among the schemes.

4. Comparison of Bin Microphysics to Bulk Microphysics

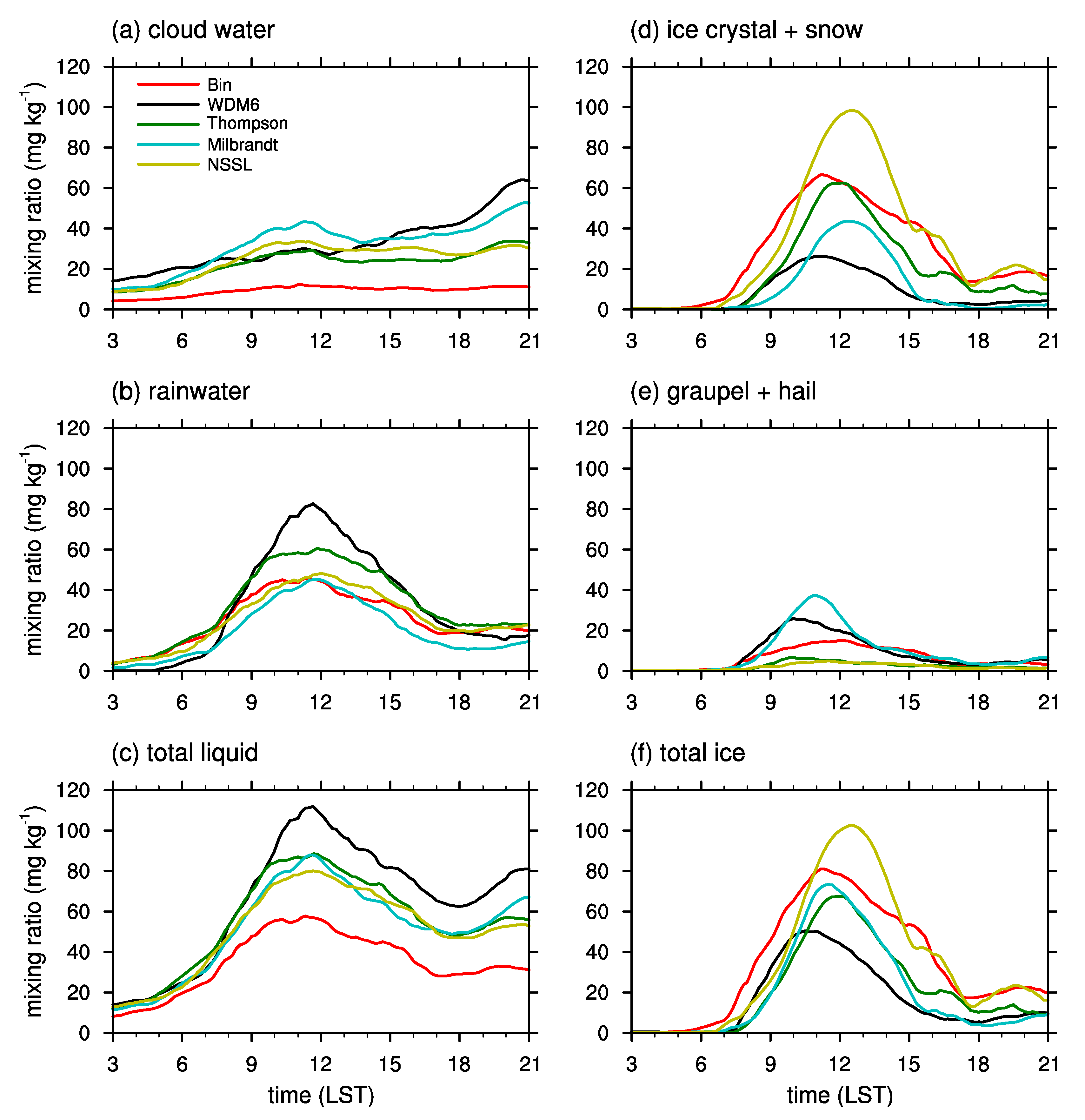
In this section, comparisons between the bin microphysics scheme and the four selected bulk microphysics schemes are described. Figure 5 shows the time series of mixing ratios of cloud water, rainwater, pristine and aggregated ice particles (ice crystal and snow), rimed ice particles (graupel and hail), the total liquid water, and the total ice particles. It should be noted that criteria to distinguish hydrometeor types are different depending on the schemes when comparing the mixing ratio of each hydrometeor type from different microphysics schemes.
Among the microphysics schemes, the bin microphysics scheme predicts the smallest cloud water mixing ratio and predicts the largest pristine and aggregated ice particle mixing ratio except the NSSL scheme, and it is one of the schemes that predict the smallest rainwater mixing ratio. In other words, all of the bulk microphysics schemes tend to predict a larger liquid water mixing ratio and a smaller ice particle mixing ratio than the bin microphysics scheme. This suggests that the ice microphysical processes are more active in the bin microphysics scheme than in the bulk microphysics schemes.
While all of the schemes generally predict a relatively smaller rimed ice particle mixing ratio than pristine and aggregated ice particle mixing ratio in this case, the bulk schemes that predict a larger pristine and aggregated ice particle mixing ratio (the NSSL and Thompson–Eidhammer schemes) generally tend to predict a smaller rimed ice particle mixing ratio, and vice versa (the WDM6 and Milbrandt schemes). This implies that the conversion rates from pristine and aggregated ice particles to rimed ice particles might differ greatly depending on the schemes. This so-called type conversion is known to have high uncertainties; even the bin microphysics scheme uses several ad hoc methods to consider the type conversion although it utilizes some additional information (e.g., rimed fractions of snow) to consider the type conversion. A recent alternative approach that predicts ice particle properties [47] is expected to reduce uncertainties in type conversion.
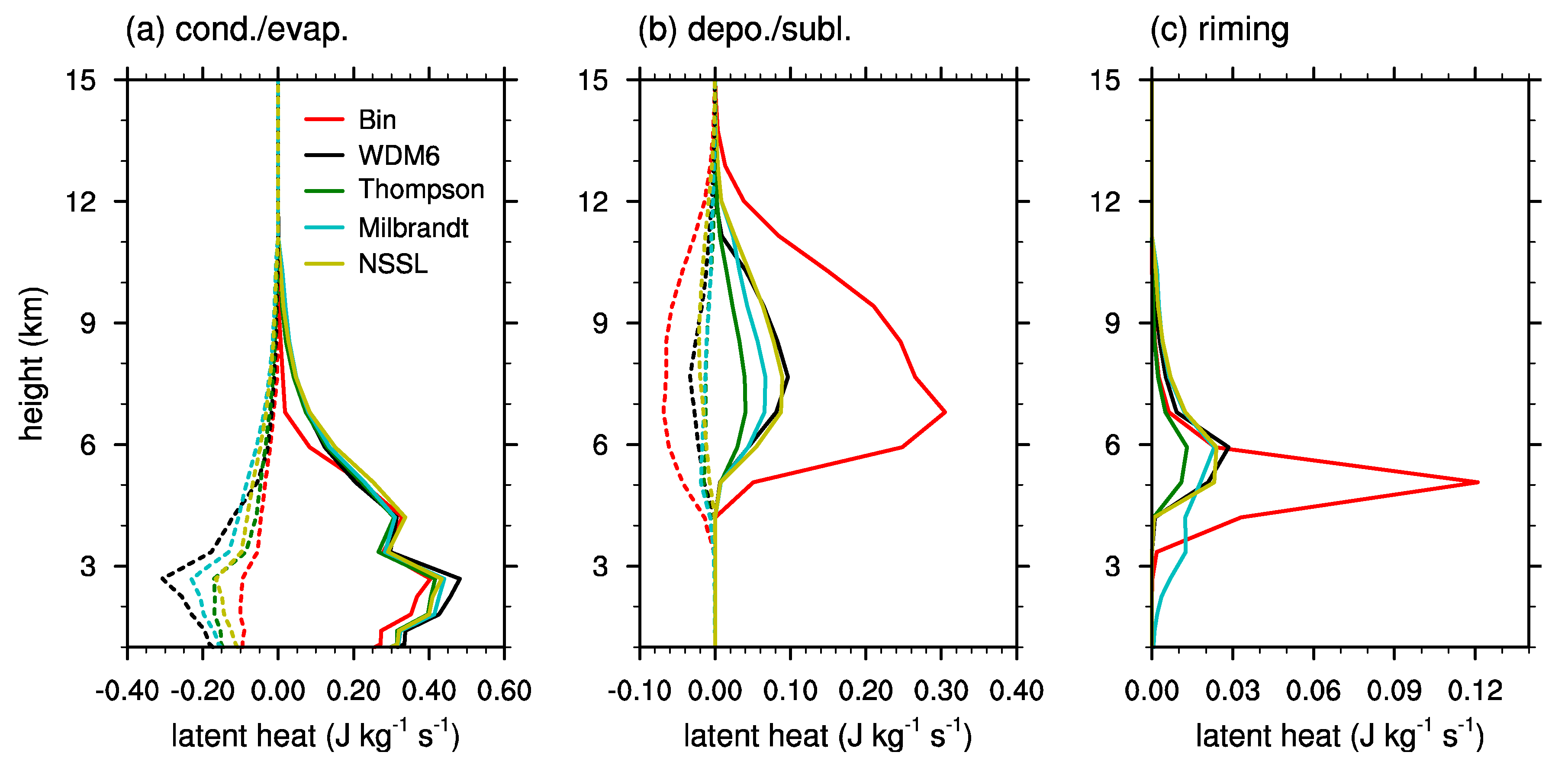
Figure 6 shows the vertical profiles of latent heat release and absorption rates by some selected microphysical processes. All of the examined schemes show similar vertical profiles of condensation and evaporation. The bin microphysics scheme shows the smallest condensation and evaporation below z ~ 3 km, which is presumably related to the result that the scheme predicts the lowest liquid water mixing ratio among the examined schemes (Figure 5c). Likewise, the WDM6 scheme, which predicts the largest liquid water mixing ratio, shows the largest condensation and evaporation below z ~ 3 km.
In contrast to condensation and evaporation, which show similar trends among the schemes, there are distinct differences in deposition, sublimation, and riming between the bin and bulk microphysics schemes. In particular, the bin microphysics scheme shows substantially larger deposition and riming compared to all of the examined bulk microphysics schemes. The latent heat release by deposition and riming in the bin microphysics scheme are more than three times those of the bulk microphysics schemes. The latent heat absorption by sublimation is also largest in the bin microphysics scheme among the examined schemes, but the heating by deposition is much larger than the cooling by sublimation in the bin microphysics scheme as well as in all of the bulk microphysics schemes. Note that the amounts of latent heat release and absorption by other microphysical processes (e.g., freezing and melting) are not large in all the schemes (not shown).
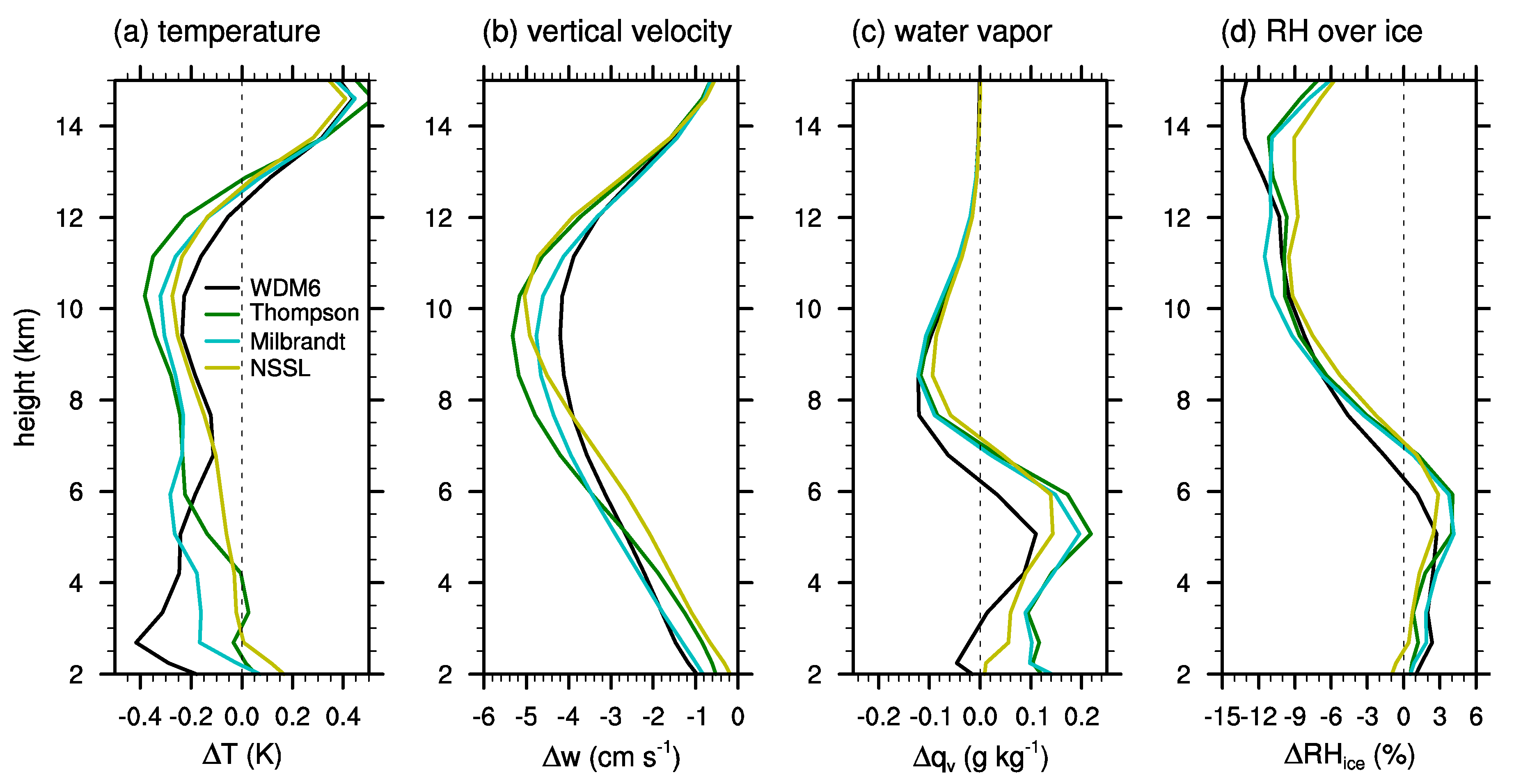
The differences in latent heat release by deposition and riming between the bin and bulk microphysics schemes are likely to alter the development of clouds and precipitation. Figure 7 shows the deviations of some selected atmospheric variables, which are temperature, vertical velocity, water vapor mixing ratio, and relative humidity with respect to ice, obtained using the bulk microphysics schemes from those obtained using the bin microphysics scheme. It is clearly seen that all of the bulk microphysics schemes show a lower temperature in the layer between ~4–12 km and weaker vertical velocity in all layers compared to the bin microphysics scheme. In addition, all of the bulk microphysics schemes generally show more water vapor in the lower layer (below ~6 or 7 km) but less water vapor in the upper layer than the bin microphysics scheme. Although the decrease in water vapor in the upper layer is similar in magnitude to the increase in the lower layer (Figure 7c), the decrease in relative humidity in the upper layer is more pronounced than the increase in the lower layer (Figure 7d). This is simply because the water vapor mixing ratio in the upper layer is much smaller than that in the lower layer.
The latent heat release, upward motion, and vapor diffusional growth are closely related to each other in cloud development. Once the temperature rises due to the latent heat release, the upward motion becomes stronger, and the stronger upward motions transport more water vapor from the lower layer to the upper layer. The transported water vapor prompts an increase in vapor diffusional growth of ice particles, which causes more latent heat release and a further rise in temperature. In this case, the bin microphysics scheme predicts a distinctly larger amount of latent heat release by deposition and riming compared to the bulk microphysics schemes (Figure 6). This larger latent heat release in the bin microphysics scheme causes the increases in temperature, vertical velocity, and upper-layer water vapor mixing ratio (Figure 7). The latent heat release is again amplified by the increased vapor diffusional growth in the upper layer. Note that the increased vertical velocity in the bin microphysics scheme might also affect the relatively small cloud water mixing ratio and relatively large pristine and aggregated ice particle mixing ratio (Figure 5a,d). The increased vertical velocity can transport more amount of cloud water from the lower layer, which can form more ice crystals in the upper layer.
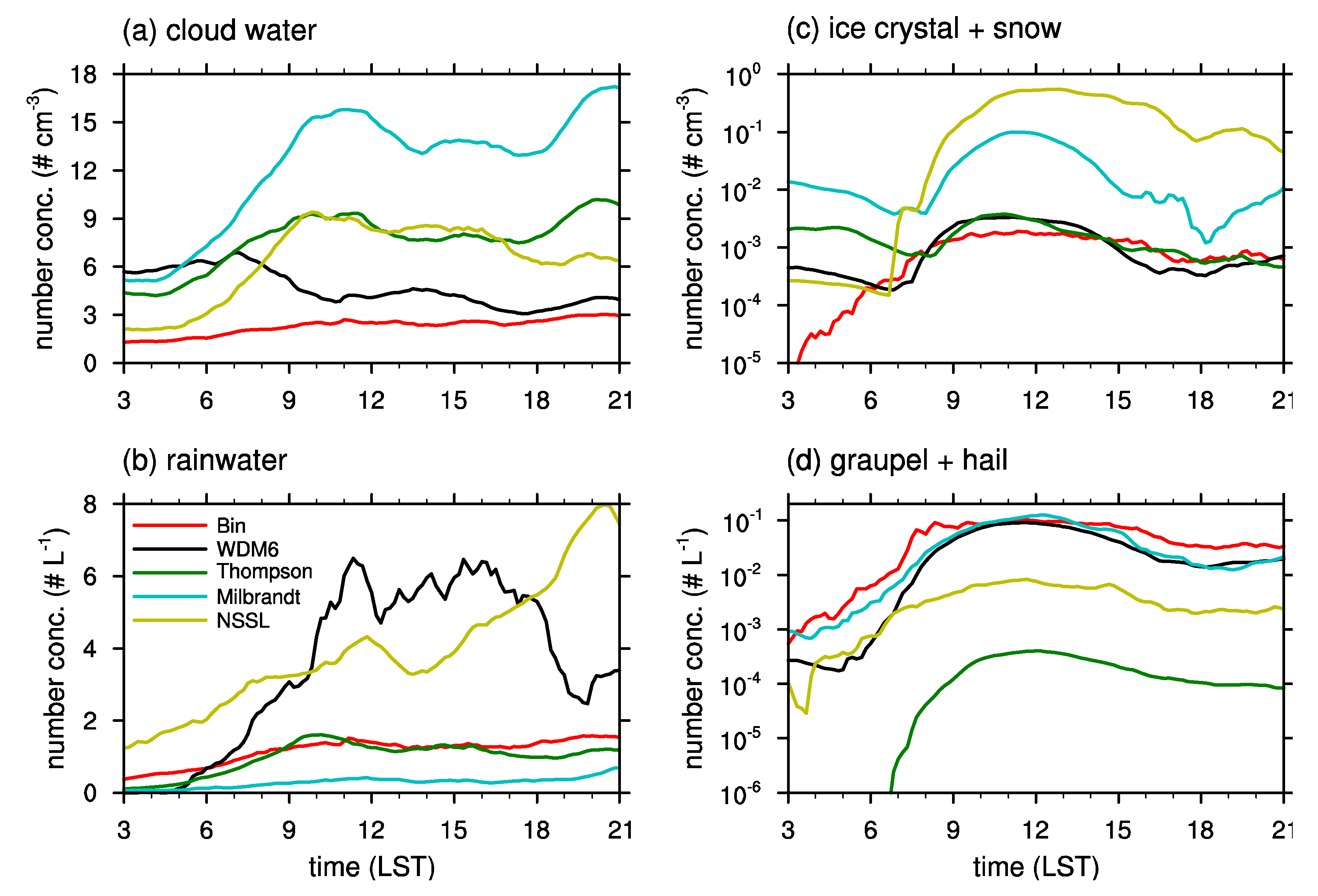
Figure 8 shows the time series of number concentrations of cloud water, rainwater, pristine and aggregated ice particles, and rimed ice particles. It is easily seen that the differences among the schemes are larger in terms of hydrometeor number concentration than in terms of hydrometeor mixing ratio (Figure 5). Moreover, the relative differences in ice particle number concentrations among the schemes are much larger than those of liquid particles. The NSSL and Milbrandt schemes yield the number concentrations of pristine and aggregated ice particles that are larger by several orders compared to those of the bin microphysics scheme, which would result in smaller ice particles. The Thompson–Eidhammer and NSSL schemes, which predict the smallest rimed ice particle mixing ratio among the schemes (Figure 5e), predict the significantly small number concentrations of rimed ice particles. These large differences in the hydrometeor number concentrations among the schemes simply show that uncertainties in predicting the number concentrations of hydrometeors, particularly of ice particles, are larger than those of the mixing ratios. There are relatively less studies that report reliable observational statistics on the hydrometeor number concentration. Because the hydrometeor number concentration is used to estimate a representative size of particles that is essential for calculating microphysical processes, these large uncertainties in predicting hydrometeor number concentration should be improved in future studies (e.g., [48]).
It was discussed in Figure 6 and Figure 7 that the bin microphysics scheme exhibits a larger latent heat release by deposition and riming compared to the examined bulk microphysics schemes and that this increased latent heat release enhances vertical motion. To investigate whether this enhanced convection is associated with the better performance in predicting the surface precipitation in the case considered in this study than that of the bulk microphysics schemes (Figure 2, Figure 3 and Figure 4), an additional simulation with a small modification of the bin microphysics scheme, which excludes the riming of cloud droplets onto ice crystals, is conducted. It is noted that the collision between ice crystals and cloud droplets is not considered in all the bulk microphysics schemes chosen in this study except the NSSL scheme, presumably because ice crystals and cloud droplets are generally regarded as non-sedimenting particles in bulk microphysics schemes. By excluding the riming of cloud droplets onto ice crystals, it is expected that the latent heat release attributable to riming would be decreased.
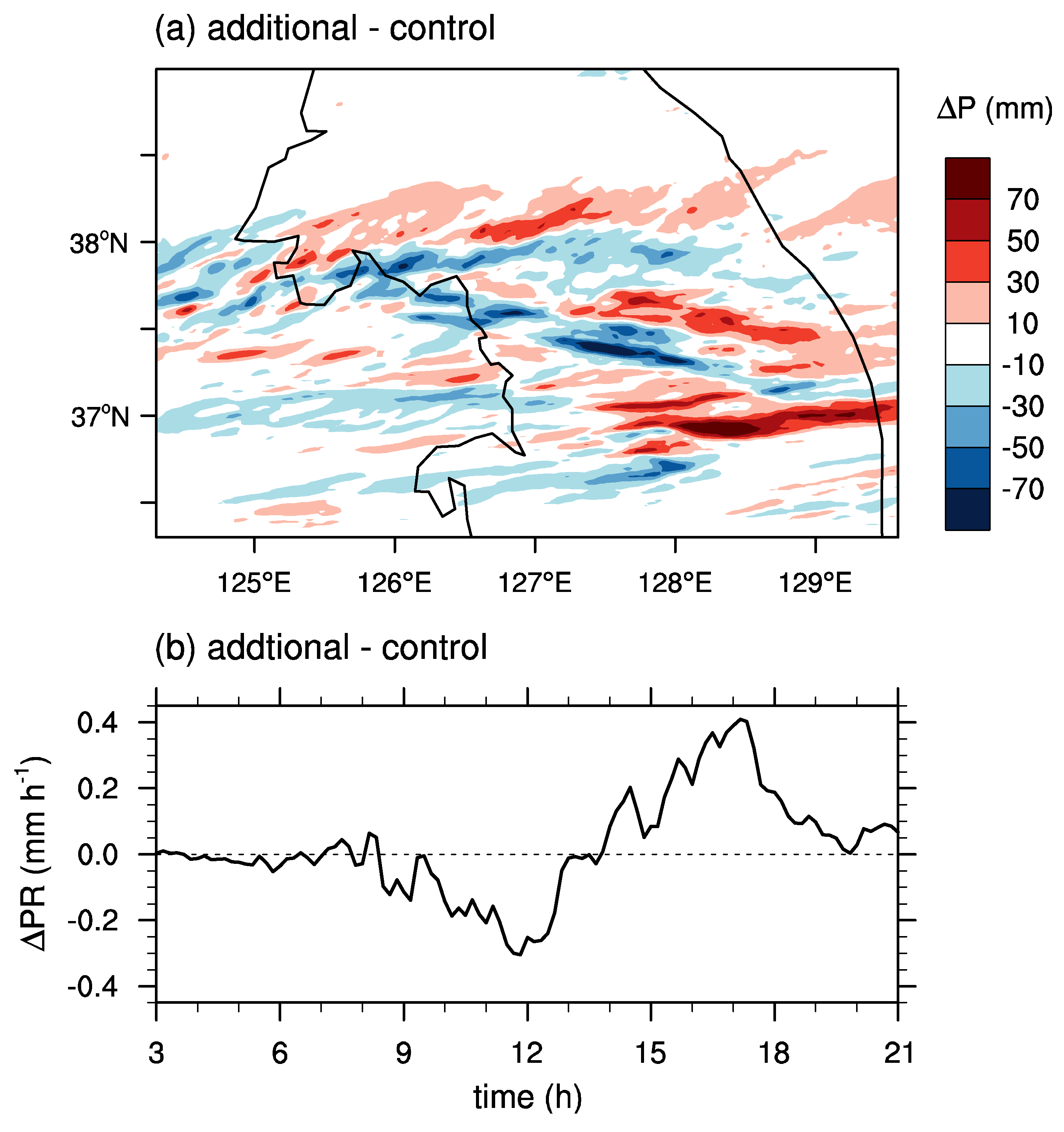
Figure 9 shows the differences in surface precipitation between the additional simulation and the control simulation (conducted using the original bin microphysics scheme). The southern precipitation in the region of ~37.0° N—37.6° N and ~126.5° E—129° E (see Figure 2b) is slightly weakened and shifted eastward. The time series of the difference in surface precipitation rate (Figure 9b) shows that the surface precipitation rate in the additional simulation is lower than that of the control simulation before ~13 LST.
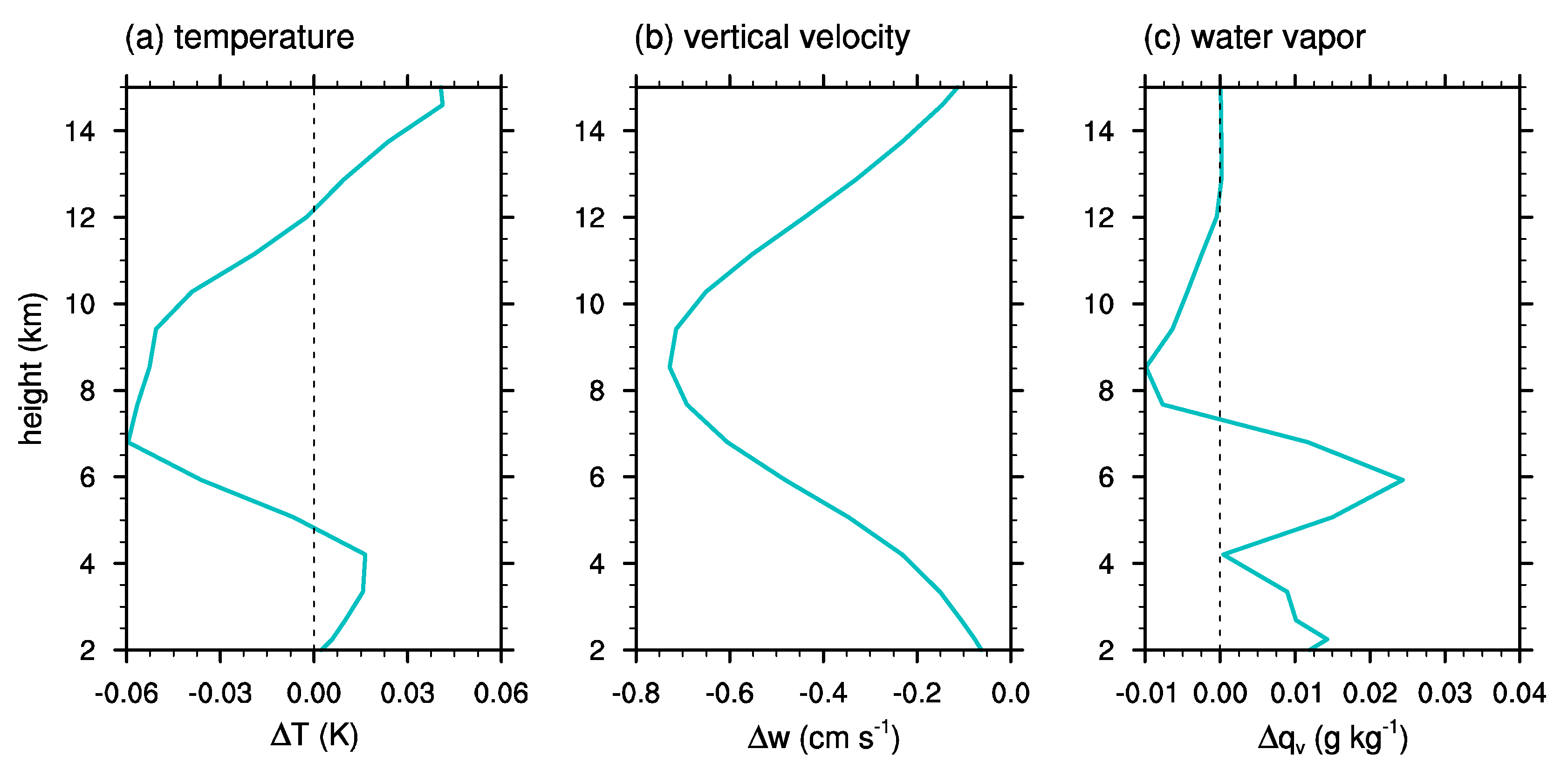
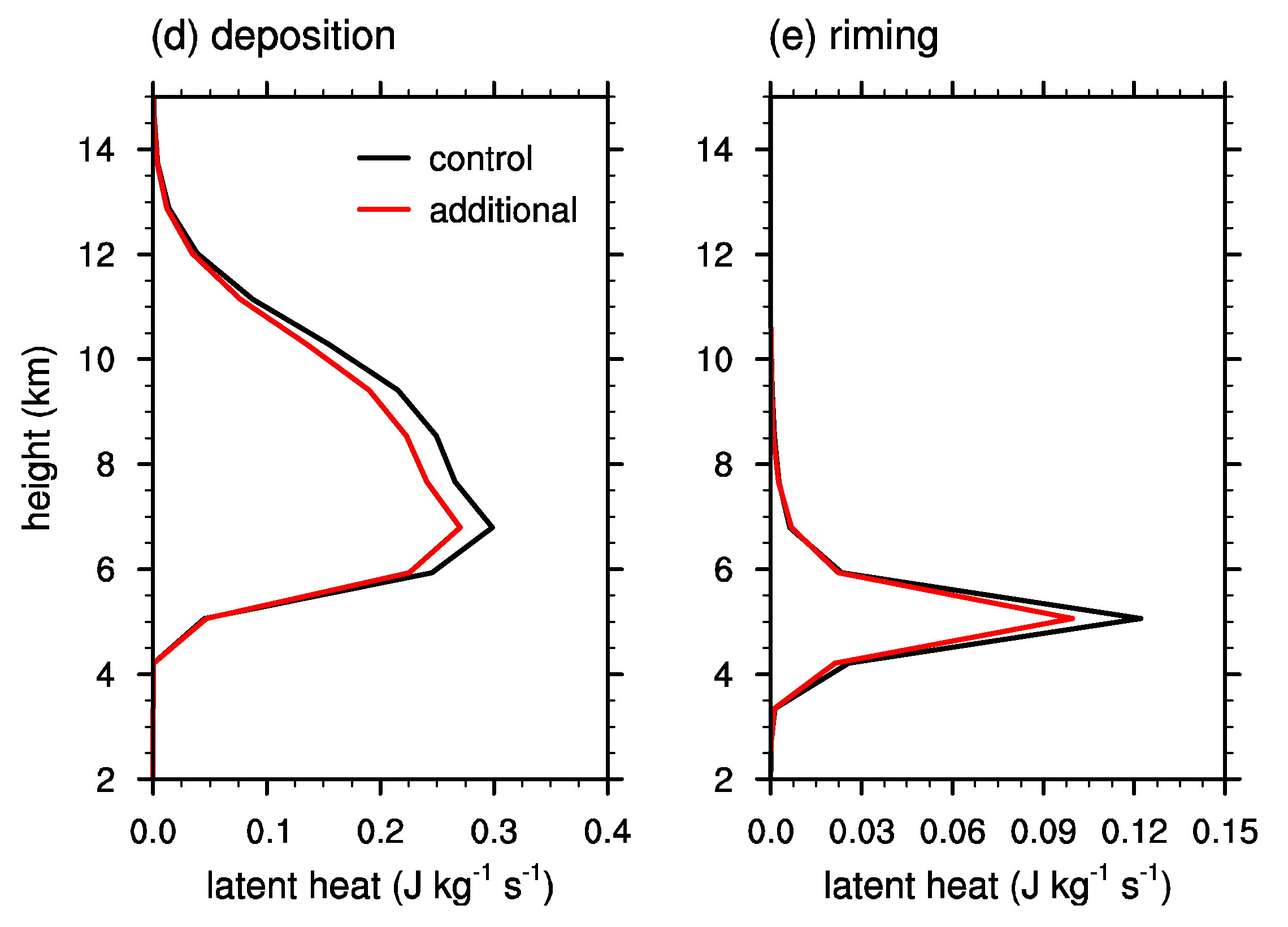
Figure 10 shows the vertical profiles of deviations in temperature, vertical velocity, and water vapor mixing ratio obtained in the additional simulation from those that are obtained in the control simulation, and the vertical profiles of latent heat release by deposition and riming. The profiles are obtained by averaging from 03 LST to 13 LST. It is clearly seen that the overall trends shown in Figure 10a–c are almost the same as shown in Figure 7a–c. In the additional simulation, the temperature in the upper level (~5–12 km) is decreased, the vertical velocity is decreased in the entire layer, and the upper-level (~7–12 km) water vapor mixing ratio is decreased. In addition, Figure 10d,e shows that deposition as well as riming is decreased in the additional simulation. Therefore, it can be concluded that by excluding the riming of cloud droplets onto ice crystals, latent heat release by riming and deposition is decreased, which causes the decreases in upper-level temperature, vertical velocity, and upper-level water vapor. These decreases seem to be associated with the slight decrease in surface precipitation amount and the shift of precipitation toward the downwind side (Figure 9), presumably attributable to the decrease in the convective activity and the growth of ice particles.
On the other hand, after ~14 LST, the surface precipitation rate increases in the additional simulation although the riming of cloud droplets on ice crystals is excluded. The accumulated surface precipitation amount is clearly increased in the region of ~37° N and ~128° E–129.5° E (Figure 9a). This can be explained by considering that the remaining small ice crystals and cloud droplets in clouds grow further by vapor diffusion, hence inducing an increase in vertical velocity and surface precipitation at the later stage. Our further analysis shows that latent heat releases by deposition and riming increase and upper-level temperature, vertical velocity, and upper-level water vapor mixing ratio are also enhanced in the additional simulation (not shown), contrary to the results before 13 LST. Therefore, the relationship between the surface precipitation and convective activity represented as latent heat release and vertical velocity remains similar even after ~14 LST.

5. Summary and Conclusions

This study compared the bin and bulk microphysics schemes by conducting numerical simulations for a real precipitation case using the WRF model. We implemented the bin microphysics scheme of the Hebrew University Cloud Model (somewhat different from the publicly available version) in the WRF model. Four bulk microphysics schemes in the WRF model (the WDM6 scheme, Thompson–Eidhammer scheme, Milbrandt scheme, and NSSL scheme), which are double-moment for liquid drops, were selected. Using the WRF model, the precipitation event that occurred on 21 September 2010 in the central Korean Peninsula was numerically simulated.
While all of the microphysics schemes underestimate the strong precipitation shown in the AWS observations, the bin microphysics scheme simulates the largest amount of the accumulated surface precipitation, which is the closest to observations. All of the bulk microphysics schemes tend to predict a larger liquid water mixing ratio and a smaller ice particle mixing ratio compared to the bin microphysics scheme, which might be partially contributed to by weaker vertical velocity in the bulk microphysics schemes. The bulk microphysics schemes that exhibit a larger rimed ice particle mixing ratio tend to exhibit a smaller pristine and aggregated ice particle mixing ratio, which implies that the conversion rates in the bulk microphysics schemes are substantially different depending on the schemes. In addition, the differences in hydrometeor number concentration among the schemes are larger than those of mixing ratio, which needs to be improved in future studies (e.g., [49]).
It was shown that all of the bulk microphysics schemes predict much smaller latent heat release by deposition and riming compared to the bin microphysics scheme. Also, they predict lower temperature, weaker vertical velocity, and smaller upper-level water vapor mixing ratio than the bin microphysics scheme in this case. The increased latent heat release can enhance itself again through the enhanced upward transport of moisture. It is found that no bulk microphysics schemes examined in this study, except the NSSL scheme, consider the growth of ice crystals by colliding with cloud droplets, presumably owing to their negligible fall velocities. The exclusion of this riming process in the bulk microphysics schemes might contribute to the underestimation of air temperature, vertical velocity, and upper-level water vapor mixing ratio compared to those of the bin microphysics scheme. An additional simulation with the bin microphysics scheme, in which the riming of cloud droplets onto ice crystals is excluded, revealed that the simulated surface precipitation is slightly decreased and moved to the downwind side compared to the control simulation conducted using the original bin microphysics scheme before a certain time instance. Before the time instance, the additional simulation exhibits the decreased deposition, riming, upper-level temperature, vertical velocity, and upper-level water vapor mixing ratio, which are very similar to those shown in the comparisons of the bulk and bin microphysics schemes. After the time instance, the results are reversed; deposition, riming, upper-level temperature, vertical velocity, and upper-level water vapor mixing ratio increase in the additional simulation compared to those of the control simulation, which is presumably attributable to the further vapor diffusional growth of small ice crystals aloft. The surface precipitation amount after the time instance is larger in the additional simulation, so the relationship between convective activity, which is represented as vertical velocity and vapor diffusion, and surface precipitation is still valid.
Previous studies have mainly focused on the fundamental differences between bin and bulk microphysics schemes in expressing the size distributions of cloud particles, and they have attempted to improve bulk microphysics schemes through a better representation of particle size distributions [30,50]. This study shows that a more appropriate representation of microphysical processes in bin microphysics scheme than in bulk microphysics schemes can contribute to more accurate prediction in this real precipitation case. Therefore, certain oversimplified assumptions in treating microphysical processes of traditional bulk microphysics schemes (e.g., ignoring the terminal velocities of cloud droplets and ice crystals and the collision between cloud droplets and ice crystals) need to be revised and constrained by detailed observations [48] to improve the performance of bulk microphysics schemes. This can help better understanding and prediction of precipitation.

Author Contributions

H.L. and J.-J.B. conceptualized this study and designed the methodology. H.L. performed numerical simulations, prepared figures, and wrote the manuscript. J.-J.B. supervised this study, and reviewed and edited the manuscript.

Funding

The authors were supported by the Korea Meteorological Administration Research and Development Program under grants KMIPA 2015-5190 and by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT (No. 2016R1A2B2013549).

Acknowledgments

The authors thank Ismail Gultepe and three anonymous reviewers for their valuable comments. The authors thank supercomputer management division of the Korea Meteorological Administration for providing us with the supercomputer resource. The source code of the bin microphysics scheme can be provided based upon request to the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ogura, Y.; Takahashi, T. The development of warm rain in a cumulus model. J. Atmos. Sci. 1973, 30, 262–277. [Google Scholar] [CrossRef]
  2. Soong, S.-T. Numerical simulation of warm rain development in an axisymmetric cloud model. J. Atmos. Sci. 1974, 31, 1262–1285. [Google Scholar] [CrossRef]
  3. Lynn, B.; Khain, A.; Dudhia, J.; Rosenfeld, D.; Pokrovsky, A.; Seifert, A. Spectral (bin) microphysics coupled with a mesoscale model (MM5). Part 1. Model description and first results. Mon. Weather Rev. 2005, 133, 44–58. [Google Scholar] [CrossRef]
  4. Lynn, B.; Khain, A. Utilization of spectral bin microphysics and bulk parameterization schemes to simulate the cloud structure and precipitation in a mesoscale rain event. J. Geophys. Res. 2007, 112, D22205. [Google Scholar] [CrossRef]
  5. Iguchi, T.; Nakajima, T.; Khain, A.; Saito, K.; Takemura, T.; Okamoto, H.; Nishizawa, T.; Tao, W.-K. Evaluation of cloud microphysics in JMA-NHM simulations using bin or bulk microphysical schemes through comparison with cloud radar observations. J. Atmos. Sci. 2012, 69, 2566–2586. [Google Scholar] [CrossRef]
  6. Fan, J.; Leung, L.R.; Li, Z.; Morrison, H.; Chen, H.; Zhou, Y.; Qian, Y.; Wang, Y. Aerosol impacts on clouds and precipitation in eastern China: Results from bin and bulk microphysics. J. Geophys. Res. 2012, 117, D00K36. [Google Scholar] [CrossRef]
  7. Khain, A.; Lynn, B.; Shpund, J. Simulation of intensity and structure of hurricane Irene: Effects of microphysics, aerosols and model resolution. In Proceedings of the Sixth Symposium on Aerosol-Cloud-Climate Interactions, Atlanta, GA, USA, 2–6 February 2014. [Google Scholar]
  8. Fan, J.; Leung, L.R.; Rosenfeld, D.; Chen, Q.; Li, Z.; Zhang, J.; Yan, H. Microphysical effects determine macrophysical response for aerosol impacts on deep convective clouds. Proc. Natl. Acad. Sci. USA 2013, 110, E4581–E4590. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  9. Khain, A.; Rosenfeld, D.; Pokrovsky, A.; Blahak, U.; Ryzhkov, A. The role of CCN in precipitation and hail in a mid-latitude storm as seen in simulations using a spectral (bin) microphysics model in a 2D dynamic frame. Atmos. Res. 2011, 99, 129–146. [Google Scholar] [CrossRef]
  10. Geresdi, I. Idealized simulation of the Colorado hailstorm case: Comparison of bulk and detailed microphysics. Atmos. Res. 1998, 45, 237–252. [Google Scholar] [CrossRef]
  11. Xue, L.; Teller, A.; Rasmussen, R.; Geresdi, I.; Pan, Z.; Liu, X. Effects of aerosol solubility and regeneration on mixed-phase orographic clouds and precipitation. J. Atmos. Sci. 2012, 69, 1994–2010. [Google Scholar] [CrossRef]
  12. Khain, A.; Pokrovsky, A.; Pinsky, M.; Seifert, A.; Phillips, V. Simulation of effects of atmospheric aerosols on deep turbulent convective clouds using a spectral microphysics mixed-phase cumulus cloud model. Part I: Model description and possible applications. J. Atmos. Sci. 2004, 61, 2963–2982. [Google Scholar] [CrossRef]
  13. Seifert, A.; Beheng, K.D. A double-moment parameterization for simulating autoconversion, accretion and selfcollection. Atmos. Res. 2001, 59–60, 265–281. [Google Scholar] [CrossRef]
  14. Shipway, B.J.; Hill, A.A. Diagnosis of systematic differences between multiple parameterizations of warm rain microphysics using a kinematic framework. Q. J. R. Meteorol. Soc. 2012, 138, 2196–2211. [Google Scholar] [CrossRef]
  15. Lee, J.; Baik, J.-J. A physically based autoconversion parameterization. J. Atmos. Sci. 2017, 74, 1599–1616. [Google Scholar] [CrossRef]
  16. Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.D. Explicit forecasts of winter precipitation using an improved bulk microphysics scheme. Part II: Implementation of a new snow parameterization. Mon. Weather Rev. 2008, 136, 5095–5115. [Google Scholar] [CrossRef]
  17. Khain, A.; Beheng, K.D.; Heymsfield, A.; Korolev, A.; Krichak, S.O.; Levin, Z.; Pinsky, M.; Phillips, V.; Prabhakaran, T.; Teller, A.; et al. Representation of microphysical processes in cloud-resolving models: Spectral (bin) microphysics versus bulk parameterization. Rev. Geophys. 2015, 53, 247–322. [Google Scholar] [CrossRef] [Green Version]
  18. Li, X.; Tao, W.-K.; Khain, A.P.; Simpson, J.; Johnson, D.E. Sensitivity of a cloud-resolving model to bulk and explicit bin microphysical schemes. Part I: Validation with a PRE-STORM case. J. Atmos. Sci. 2009, 66, 3–21. [Google Scholar] [CrossRef]
  19. Khain, A.; Leung, L.R.; Lynn, B.; Ghan, S. Effects of aerosols on the dynamics and microphysics of squall lines simulated by spectral bin and bulk parameterization schemes. J. Geophys. Res. 2009, 114, D22203. [Google Scholar] [CrossRef]
  20. Morrison, H.; Curry, J.A.; Khvorostyanov, V.I. A new double moment microphysics parameterization for application in cloud and climate models. Part I: Description. J. Atmos. Sci. 2005, 62, 1665–1677. [Google Scholar] [CrossRef]
  21. Lin, Y.-L.; Farley, R.D.; Orville, H.D. Bulk parameterization of the snow field in a cloud model. J. Clim. Appl. Meteorol. 1983, 22, 1065–1092. [Google Scholar] [CrossRef]
  22. Eito, H.; Aonashi, K. Verification of hydrometeor properties simulated by a cloud-resolving model using a passive microwave satellite and ground-based radar observations for a rainfall system associated with the Baiu front. J. Meteorol. Soc. Jpn. 2009, 87A, 425–446. [Google Scholar] [CrossRef]
  23. Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.-Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; Mesoscale and Microscale Meteorology Division in National Center for Atmospheric Research: Boulder, CO, USA, 2008. [Google Scholar] [CrossRef]
  24. Lee, H.; Baik, J.-J. Effects of turbulence-induced collision enhancement on heavy precipitation: The 21 September 2010 case over the Korean Peninsula. J. Geophy. Res. Atmos. 2016, 121, 12319–12342. [Google Scholar] [CrossRef]
  25. Lee, H.; Baik, J.-J.; Khain, A.P. Turbulence effects on precipitation and cloud radiative properties in shallow cumulus: An investigation using the WRF-LES model coupled with bin microphysics. Asia-Pac. J. Atmos. Sci. 2018, 54, 457–471. [Google Scholar] [CrossRef]
  26. Kogan, Y.L. The simulation of a convective cloud in a 3D model with explicit microphysics. Part I: Model description and sensitivity experiments. J. Atmos. Sci. 1991, 48, 1160–1188. [Google Scholar] [CrossRef]
  27. Biggs, E.K. The formation of atmospheric ice crystals by the freezing of droplets. Q. J. R. Meteorol. Soc. 1953, 79, 510–519. [Google Scholar] [CrossRef]
  28. Meyers, M.P.; DeMott, P.J.; Cotton, W.R. New primary ice-nucleation parameterization in an explicit cloud model. J. Appl. Meteorol. 1992, 31, 708–721. [Google Scholar] [CrossRef]
  29. Hallett, J.; Mossop, S.C. Production of secondary ice crystals during the riming process. Nature 1974, 249, 26–28. [Google Scholar] [CrossRef]
  30. Lim, K.-S.S.; Hong, S.-Y. Development of an effective double-moment cloud microphysics scheme with prognostic cloud condensation nuclei (CCN) for weather and climate models. Mon. Weather Rev. 2010, 138, 1587–1612. [Google Scholar] [CrossRef]
  31. Milbrandt, J.A.; Yau, M.K. A multimoment bulk microphysics parameterization. Part II: A proposed three-moment closure and scheme description. J. Atmos. Sci. 2005, 62, 3065–3081. [Google Scholar] [CrossRef]
  32. Thompson, G.; Eidhammer, T. A study of aerosol impacts on clouds and precipitation development in a large winter cyclone. J. Atmos. Sci. 2014, 71, 3636–3658. [Google Scholar] [CrossRef]
  33. Mansell, E.R.; Ziegler, C.L.; Bruning, E.C. Simulated electrification of a small thunderstorm with two-moment bulk microphysics. J. Atmos. Sci. 2010, 67, 171–194. [Google Scholar] [CrossRef]
  34. Hong, S.-Y.; Dudhia, J.; Chen, S.-H. A revised approach to ice microphysical processes for the bulk parameterization of clouds and precipitation. Mon. Weather Rev. 2004, 132, 103–120. [Google Scholar] [CrossRef]
  35. Cohard, J.-M.; Pinty, J.-P. A comprehensive two-moment warm microphysical bulk scheme. I: Description and tests. Q. J. R. Meteorol. Soc. 2000, 126, 1815–1842. [Google Scholar] [CrossRef]
  36. CISL RDA: NCEP FNL Operational Model Global Tropospheric Analyses, continuing from July 1999. Available online: https://rda.ucar.edu/datasets/ds083.2/ (accessed on 29 November 2018).
  37. Kim, J.H.; Yum, S.S.; Shim, S.; Kim, W.J.; Park, M.; Kim, J.-H.; Kim, M.-H.; Yoon, S.-C. On the submicron aerosol distributions and CCN number concentrations in and around the Korean Peninsula. Atmos. Chem. Phys. 2014, 14, 8763–8779. [Google Scholar] [CrossRef] [Green Version]
  38. Twomey, S. The nuclei of natural cloud formation. Part II: The supersaturation in natural clouds and the variation of cloud droplet concentration. Geofis. Pura Appl. 1959, 43, 243–249. [Google Scholar] [CrossRef]
  39. Janjic, Z.I. Nonsingular Implementation of the Mellor-Yamada Level 2.5 Scheme in the NCEP Meso Model; National Centers for Environmental Prediction: College Park, MD, USA, 2002.
  40. Dudhia, J. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
  41. Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmosphere: RRTM, a validated correlated-k model for the long-wave. J. Geophys. Res. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
  42. Kain, J.S. The Kain-Fritsch convective parameterization: An update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
  43. Chen, F.; Dudhia, J. Coupling an advanced land-surface/hydrology model with the Penn State/NCAR MM5 modeling system. Part I: Model description and implementation. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
  44. Jung, W.; Lee, T.-Y. Formation and evolution of mesoscale convective systems that brought the heavy rainfall over Seoul on September 21, 2010. Asia-Pac. J. Atmos. Sci. 2013, 49, 635–647. [Google Scholar] [CrossRef]
  45. Brier, G.W. Verification of forecasts expressed in terms of probabilities. Mon. Weather Rev. 1950, 78, 1–3. [Google Scholar] [CrossRef]
  46. Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 3rd ed.; Academic Press: Oxford, UK, 2011; ISBN 978-0-12-385022-5. [Google Scholar]
  47. Morrison, H.; Milbrandt, J.A. Parameterization of cloud microphysics based on the prediction of bulk ice particle properties. Part I: Scheme description and idealized tests. J. Atmos. Sci. 2015, 72, 287–311. [Google Scholar] [CrossRef]
  48. Gultepe, I.; Heymsfield, A.J.; Field, P.R.; Axisa, D. Ice-phase precipitation. In AMS Meteorological Monographs 58: Ice Formation and Evolution in Clouds and Precipitation: Measurement and Modeling Challenges; American Meteorological Society: Boston, MA, USA, 2017; Volume 58, pp. 6.1–6.36. [Google Scholar] [CrossRef]
  49. Gultepe, I.; Isaac, G.A. Scale effects on averaging of cloud droplet and aerosol number concentrations: Observations and models. J. Clim. 1999, 12, 1268–1279. [Google Scholar] [CrossRef]
  50. Igel, A.L.; van den Heever, S.C. The importance of the shape of cloud droplet size distributions in shallow cumulus clouds. Part I: Bin microphysics simulations. J. Atmos. Sci. 2017, 74, 249–258. [Google Scholar] [CrossRef]
Atmosphere 09 00475 g001 550
Figure 1. Three nested computational domains with terrain height.
Figure 1. Three nested computational domains with terrain height.
Atmosphere 09 00475 g001
Atmosphere 09 00475 g002 550
Figure 2. The 18-hr accumulated surface precipitation amount (a) observed by AWSs and simulated using the (b) bin microphysics scheme, (c) WRF Double-Moment 6-class (WDM6) scheme, (d) Thompson–Eidhammer scheme, (e) Milbrandt scheme, and (f) National Severe Storms Laboratory (NSSL) scheme. The fields of accumulated precipitation amount are obtained by averaging observed or simulated precipitation amounts in the 0.15° × 0.15° box centered at each grid point. Circles in (a) indicate the locations of AWSs. Dashed lines in (b–f) indicate the 37.6° N line, which “roughly” divides the northern precipitation and the southern precipitation. The accumulated surface precipitation amount averaged over the AWS locations are given in the bottom left corner of each panel.
Figure 2. The 18-hr accumulated surface precipitation amount (a) observed by AWSs and simulated using the (b) bin microphysics scheme, (c) WRF Double-Moment 6-class (WDM6) scheme, (d) Thompson–Eidhammer scheme, (e) Milbrandt scheme, and (f) National Severe Storms Laboratory (NSSL) scheme. The fields of accumulated precipitation amount are obtained by averaging observed or simulated precipitation amounts in the 0.15° × 0.15° box centered at each grid point. Circles in (a) indicate the locations of AWSs. Dashed lines in (b–f) indicate the 37.6° N line, which “roughly” divides the northern precipitation and the southern precipitation. The accumulated surface precipitation amount averaged over the AWS locations are given in the bottom left corner of each panel.
Atmosphere 09 00475 g002
Atmosphere 09 00475 g003 550
Figure 3. Latitude–time diagrams (Hovmöller diagrams) of surface precipitation rate averaged along the longitudinal direction (a) observed at AWSs and obtained using the (b) bin microphysics scheme, (c) WDM6 scheme, (d) Thompson–Eidhammer scheme, (e) Milbrandt scheme, and (f) NSSL scheme. Dashed lines in (b–f) are the rough dividers that divide the northern precipitation and the southern precipitation. Note that the observed surface precipitation north of ~38° N is not representative of real precipitation, attributable to the lack of AWSs.
Figure 3. Latitude–time diagrams (Hovmöller diagrams) of surface precipitation rate averaged along the longitudinal direction (a) observed at AWSs and obtained using the (b) bin microphysics scheme, (c) WDM6 scheme, (d) Thompson–Eidhammer scheme, (e) Milbrandt scheme, and (f) NSSL scheme. Dashed lines in (b–f) are the rough dividers that divide the northern precipitation and the southern precipitation. Note that the observed surface precipitation north of ~38° N is not representative of real precipitation, attributable to the lack of AWSs.
Atmosphere 09 00475 g003
Atmosphere 09 00475 g004 550
Figure 4. The Brier score for the 18-hr accumulated surface precipitation amount of each microphysics scheme across a range of thresholds. A lower Brier score indicates better model performance, and a higher Brier score worse model performance.
Figure 4. The Brier score for the 18-hr accumulated surface precipitation amount of each microphysics scheme across a range of thresholds. A lower Brier score indicates better model performance, and a higher Brier score worse model performance.
Atmosphere 09 00475 g004
Atmosphere 09 00475 g005 550
Figure 5. Time series of domain-averaged mixing ratios of (a) cloud water, (b) rainwater, (c) total liquid water (the sum of cloud water and rainwater), (d) pristine and aggregated ice particles (ice crystal and snow), (e) rimed ice particles (graupel and hail), and (f) total ice particles (the sum of pristine and aggregated and rimed ice particles). Note that the WDM6 and Thompson–Eidhammer schemes consider graupel as the only rimed ice particles.
Figure 5. Time series of domain-averaged mixing ratios of (a) cloud water, (b) rainwater, (c) total liquid water (the sum of cloud water and rainwater), (d) pristine and aggregated ice particles (ice crystal and snow), (e) rimed ice particles (graupel and hail), and (f) total ice particles (the sum of pristine and aggregated and rimed ice particles). Note that the WDM6 and Thompson–Eidhammer schemes consider graupel as the only rimed ice particles.
Atmosphere 09 00475 g005
Atmosphere 09 00475 g006 550
Figure 6. Vertical profiles of horizontally averaged latent heat release and absorption rates by (a) condensation and evaporation, (b) deposition and sublimation, and (c) riming. In (a), solid and dashed lines correspond to condensation and evaporation, respectively. In (b), solid and dashed lines correspond to deposition and sublimation, respectively.
Figure 6. Vertical profiles of horizontally averaged latent heat release and absorption rates by (a) condensation and evaporation, (b) deposition and sublimation, and (c) riming. In (a), solid and dashed lines correspond to condensation and evaporation, respectively. In (b), solid and dashed lines correspond to deposition and sublimation, respectively.
Atmosphere 09 00475 g006
Atmosphere 09 00475 g007 550
Figure 7. Vertical profiles of deviations in horizontally averaged (a) temperature, (b) vertical velocity, (c) water vapor mixing ratio, and (d) relative humidity with respect to ice obtained using the bulk microphysics schemes from those obtained using the bin microphysics scheme.
Figure 7. Vertical profiles of deviations in horizontally averaged (a) temperature, (b) vertical velocity, (c) water vapor mixing ratio, and (d) relative humidity with respect to ice obtained using the bulk microphysics schemes from those obtained using the bin microphysics scheme.
Atmosphere 09 00475 g007
Atmosphere 09 00475 g008 550
Figure 8. Time series of domain-averaged number concentrations of (a) cloud water, (b) rainwater, (c) pristine and aggregated ice particles (ice crystal and snow), and (d) rimed ice particles (graupel and hail). Note that each panel has its own unit and scale.
Figure 8. Time series of domain-averaged number concentrations of (a) cloud water, (b) rainwater, (c) pristine and aggregated ice particles (ice crystal and snow), and (d) rimed ice particles (graupel and hail). Note that each panel has its own unit and scale.
Atmosphere 09 00475 g008
Atmosphere 09 00475 g009 550
Figure 9. (a) Difference in the accumulated surface precipitation amount between the additional simulation that excludes the riming of cloud droplets onto ice crystals in the bin microphysics scheme and the control simulation (conducted using the original bin microphysics scheme). (b) Time series of difference in surface precipitation rate between the additional and control simulations.
Figure 9. (a) Difference in the accumulated surface precipitation amount between the additional simulation that excludes the riming of cloud droplets onto ice crystals in the bin microphysics scheme and the control simulation (conducted using the original bin microphysics scheme). (b) Time series of difference in surface precipitation rate between the additional and control simulations.
Atmosphere 09 00475 g009
Atmosphere 09 00475 g010a 550Atmosphere 09 00475 g010b 550
Figure 10. (Upper panels) Vertical profiles of deviations in horizontally averaged (a) temperature, (b) vertical velocity, and (c) water vapor mixing ratio obtained in the additional simulation from those in the control simulation. (Lower panels) Vertical profiles of horizontally averaged latent heat release by (d) deposition and (e) riming obtained in the control and the additional simulations. All the profiles are obtained by averaging from 03 LST to 13 LST.
Figure 10. (Upper panels) Vertical profiles of deviations in horizontally averaged (a) temperature, (b) vertical velocity, and (c) water vapor mixing ratio obtained in the additional simulation from those in the control simulation. (Lower panels) Vertical profiles of horizontally averaged latent heat release by (d) deposition and (e) riming obtained in the control and the additional simulations. All the profiles are obtained by averaging from 03 LST to 13 LST.
Atmosphere 09 00475 g010aAtmosphere 09 00475 g010b
Table
Table 1. Physics parameterizations used in this study.
Table 1. Physics parameterizations used in this study.
ProcessParameterization
Planetary boundary layerMellor–Yamada–Janjic [39]
Shortwave radiationMM5 [40]
Longwave radiationRapid Radiative Transfer Model [41]
Subgrid-scale cumulusKain–Fritsh [42]
Land surfaceNoah [43]
Surface layerEta Similarity [39]
Table
Table 2. Horizontal grid size, number of horizontal grid points, and time step in each computational domain.
Table 2. Horizontal grid size, number of horizontal grid points, and time step in each computational domain.
Domain 1Domain 2Domain 3
Horizontal grid size25 km5 km1.667 km
Number of horizontal grid points108 × 108181 × 181286 × 178
Time step60 s12 s4 s

Share and Cite

MDPI and ACS Style

Lee, H.; Baik, J.-J. A Comparative Study of Bin and Bulk Cloud Microphysics Schemes in Simulating a Heavy Precipitation Case. Atmosphere 2018, 9, 475. https://doi.org/10.3390/atmos9120475

AMA Style

Lee H, Baik J-J. A Comparative Study of Bin and Bulk Cloud Microphysics Schemes in Simulating a Heavy Precipitation Case. Atmosphere. 2018; 9(12):475. https://doi.org/10.3390/atmos9120475

Chicago/Turabian Style

Lee, Hyunho, and Jong-Jin Baik. 2018. "A Comparative Study of Bin and Bulk Cloud Microphysics Schemes in Simulating a Heavy Precipitation Case" Atmosphere 9, no. 12: 475. https://doi.org/10.3390/atmos9120475

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop