Numerical Investigation on the Effect of Avenue Trees on PM2.5 Dispersion in Urban Street Canyons
Abstract
1. Introduction
2. Methods
2.1. Simulation Model
2.1.1. Airflow Model
2.1.2. Revised Generalized Drift Flux Model
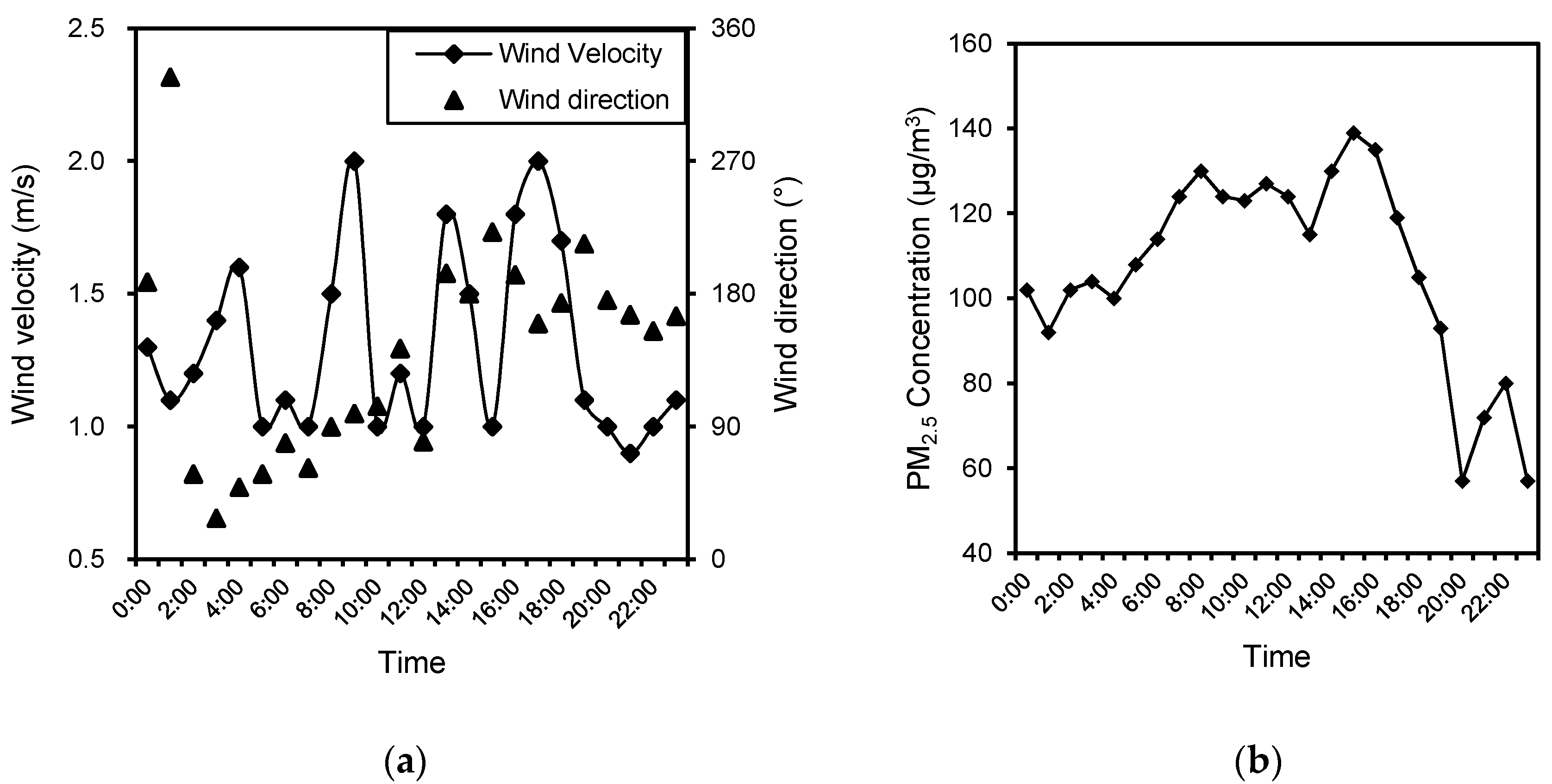
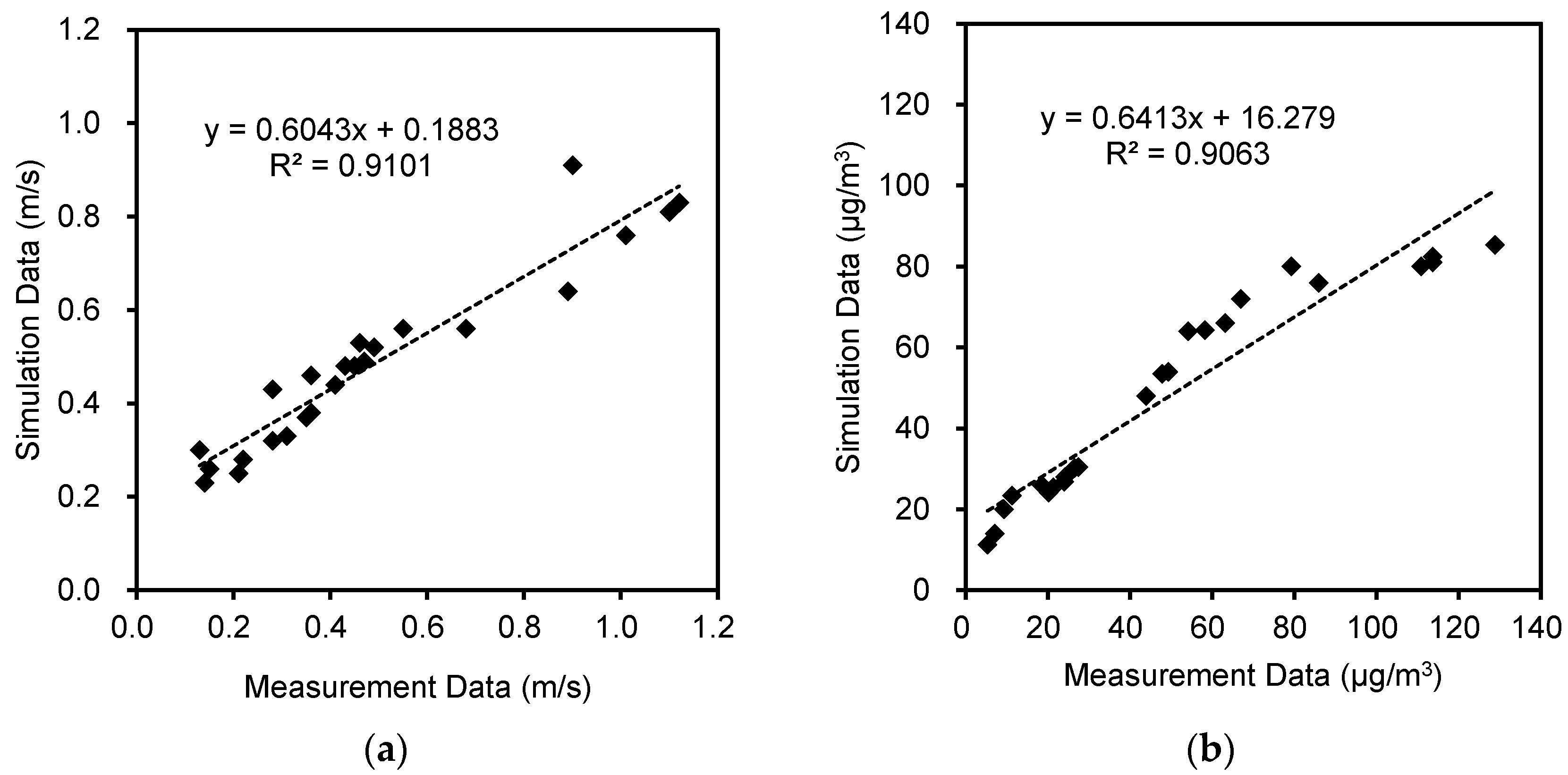
2.1.3. Validation Studies
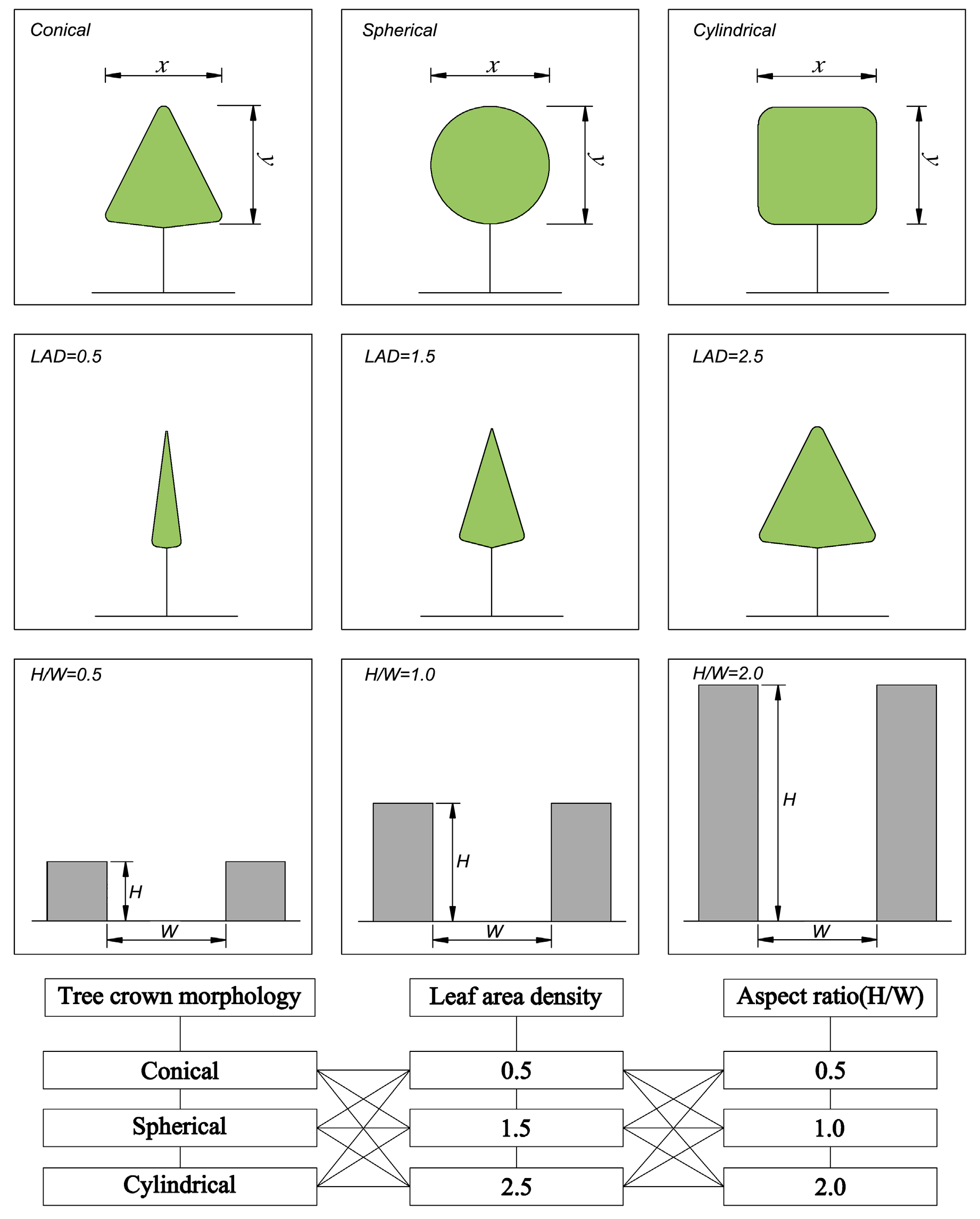
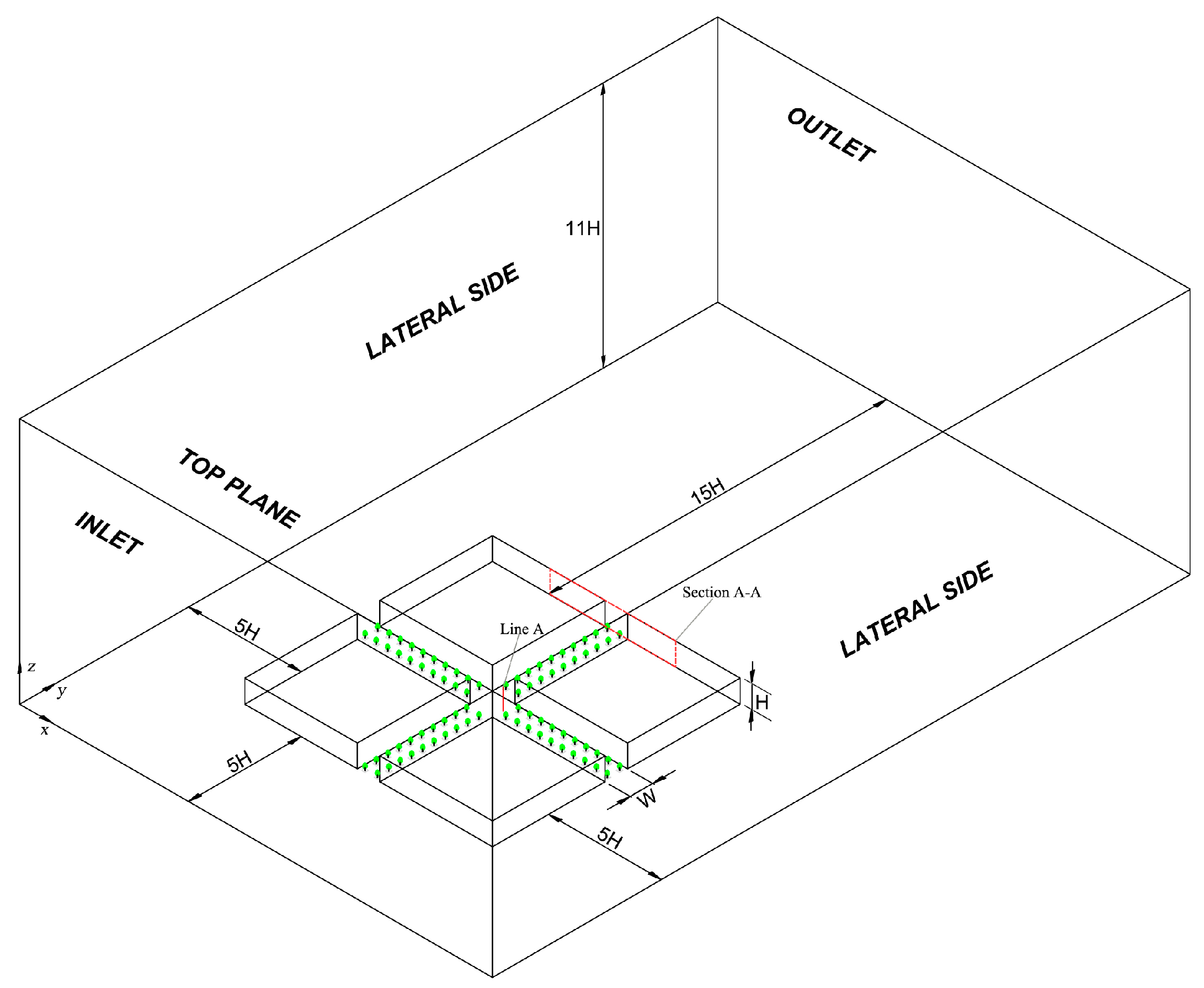
2.2. Numerical Simulation Setup
2.3. Boundary Conditions and Grid Independence Testing
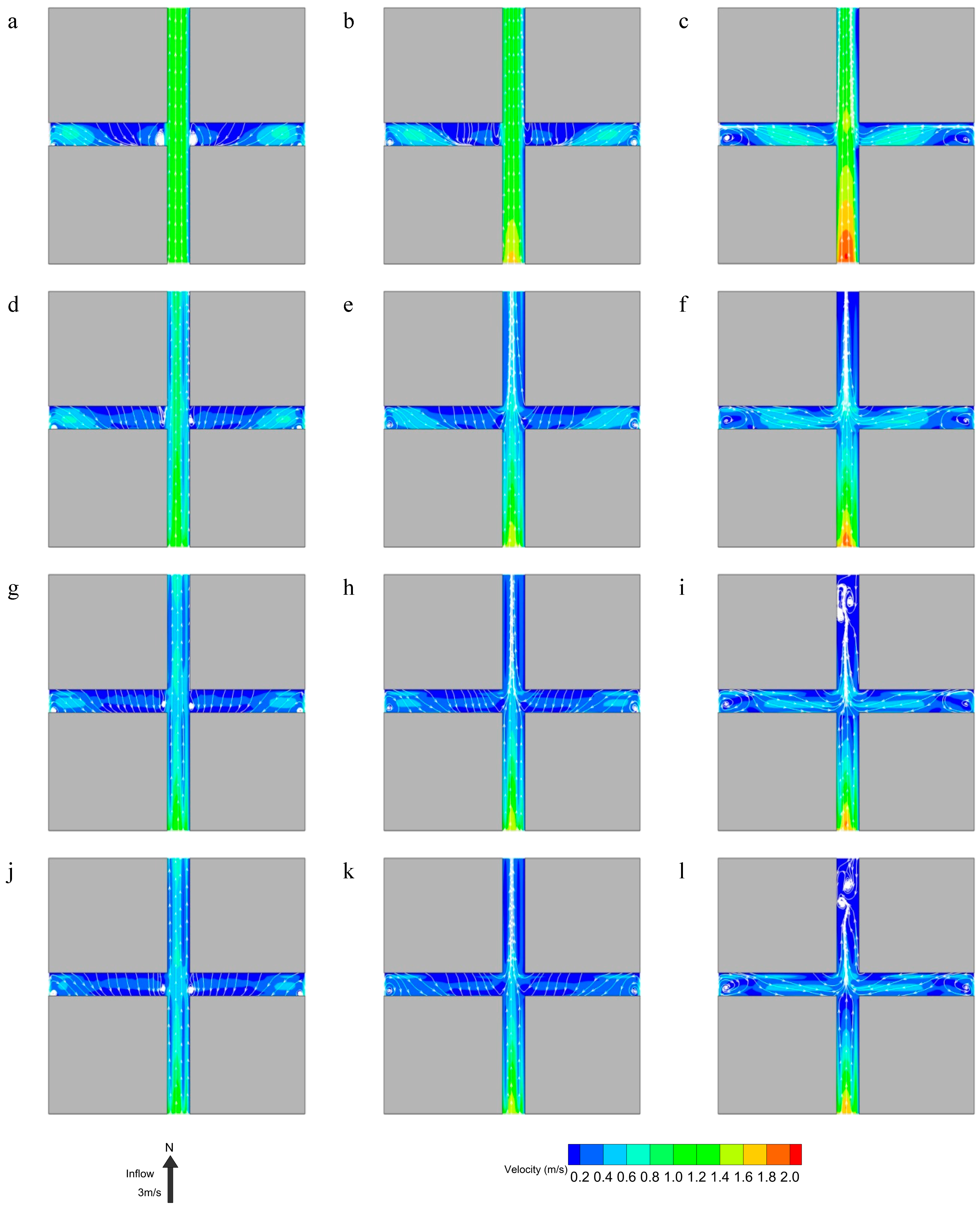
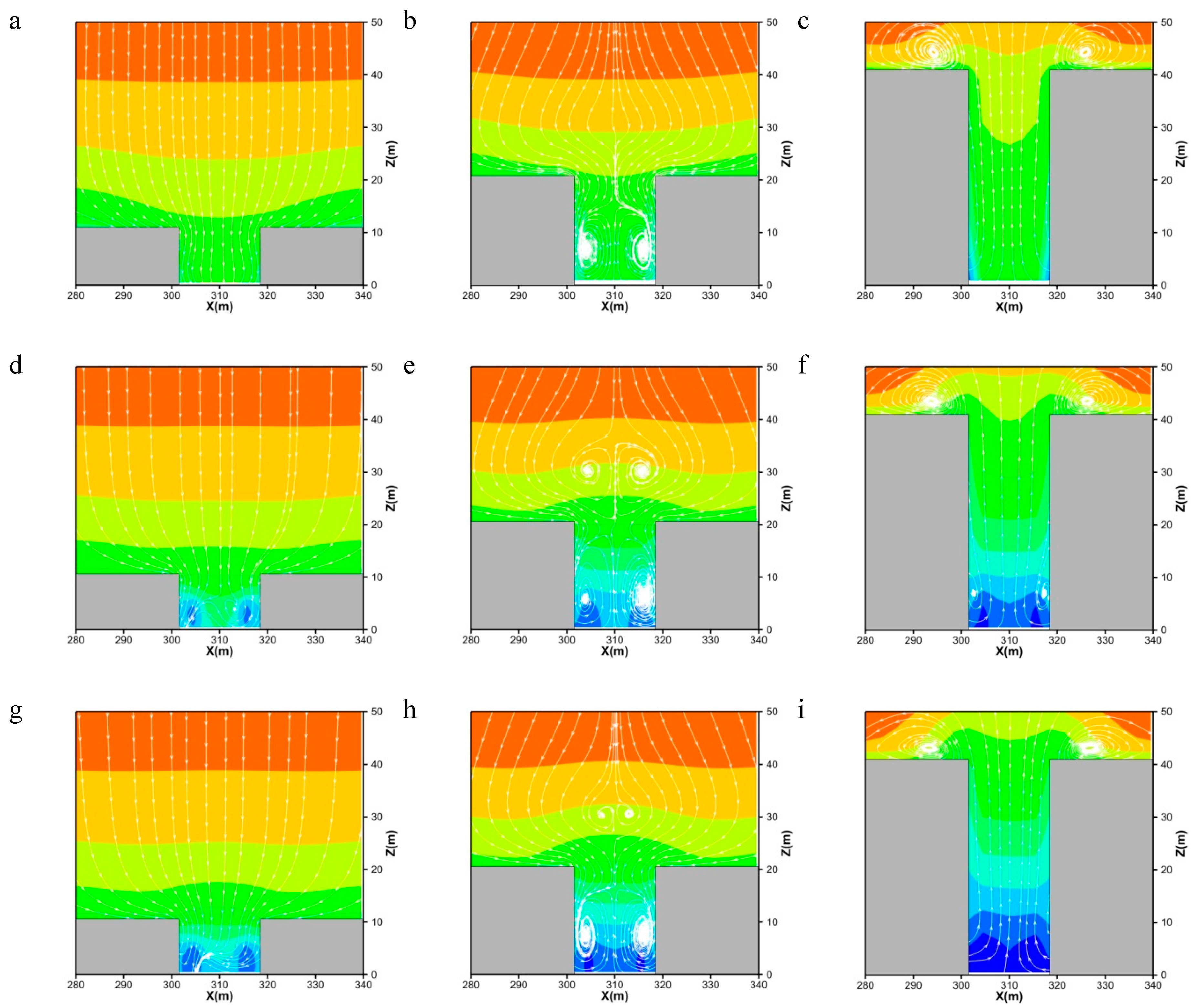
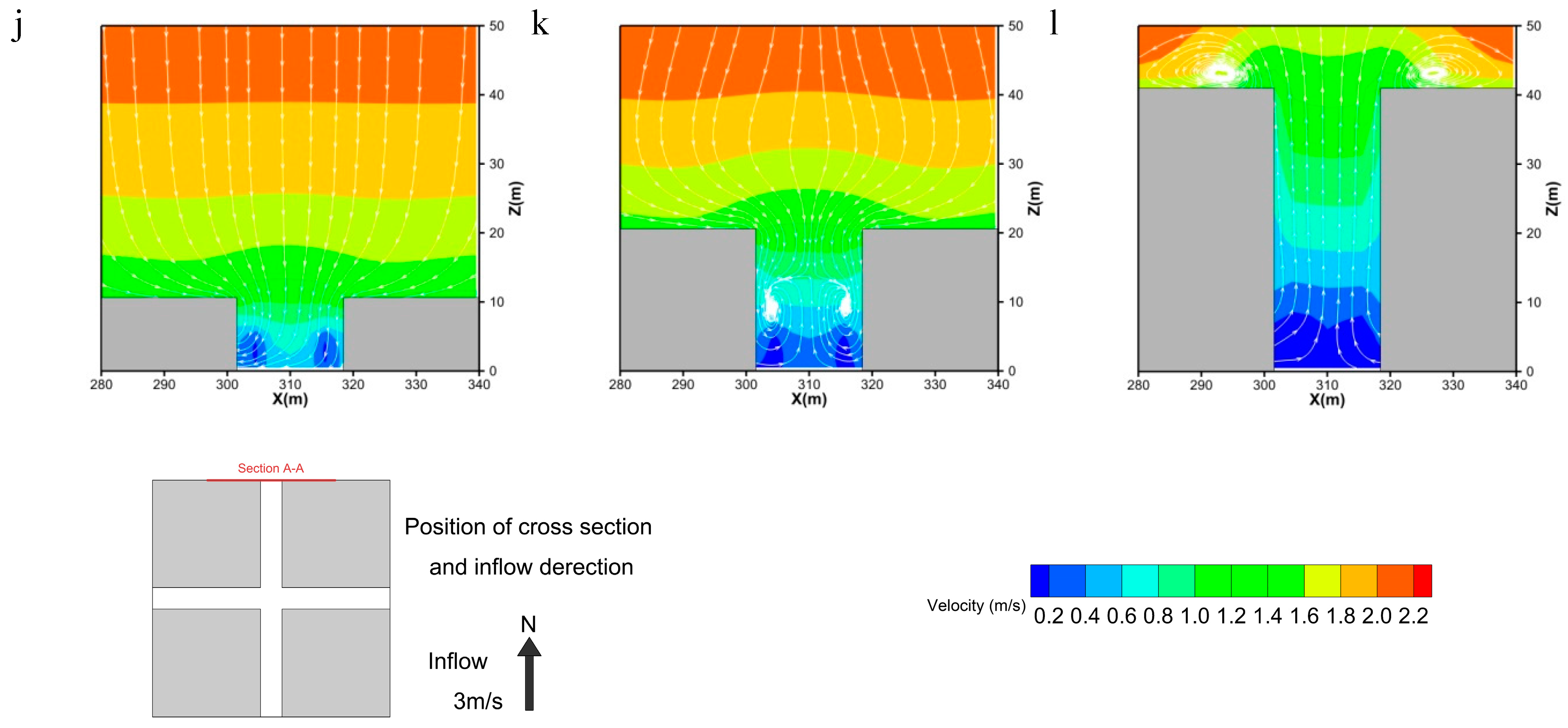
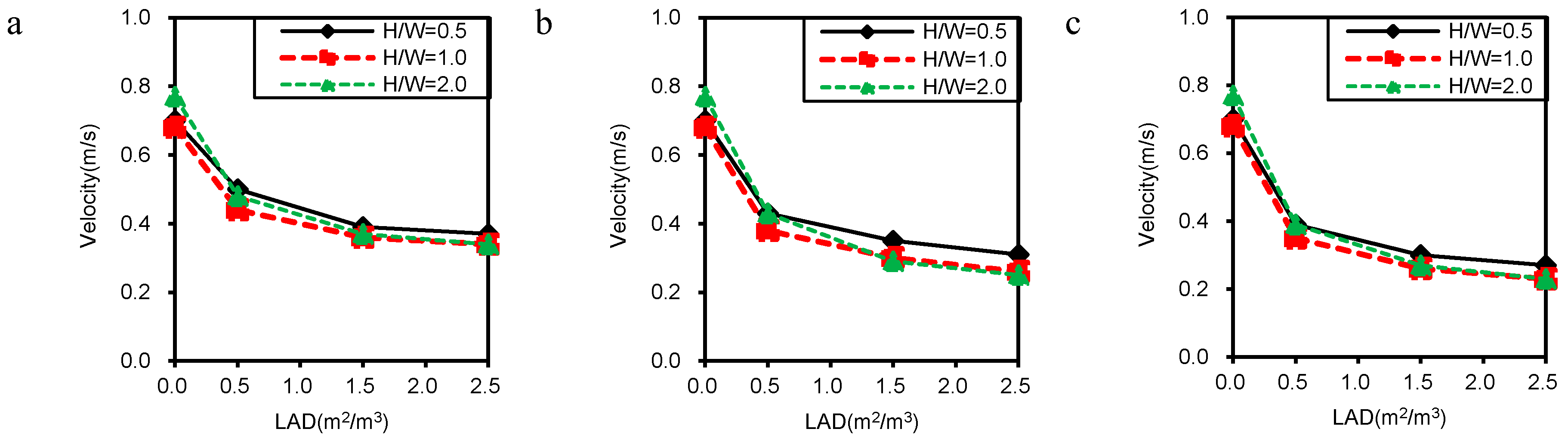
3. Results and Discussion
3.1. Airflow Field
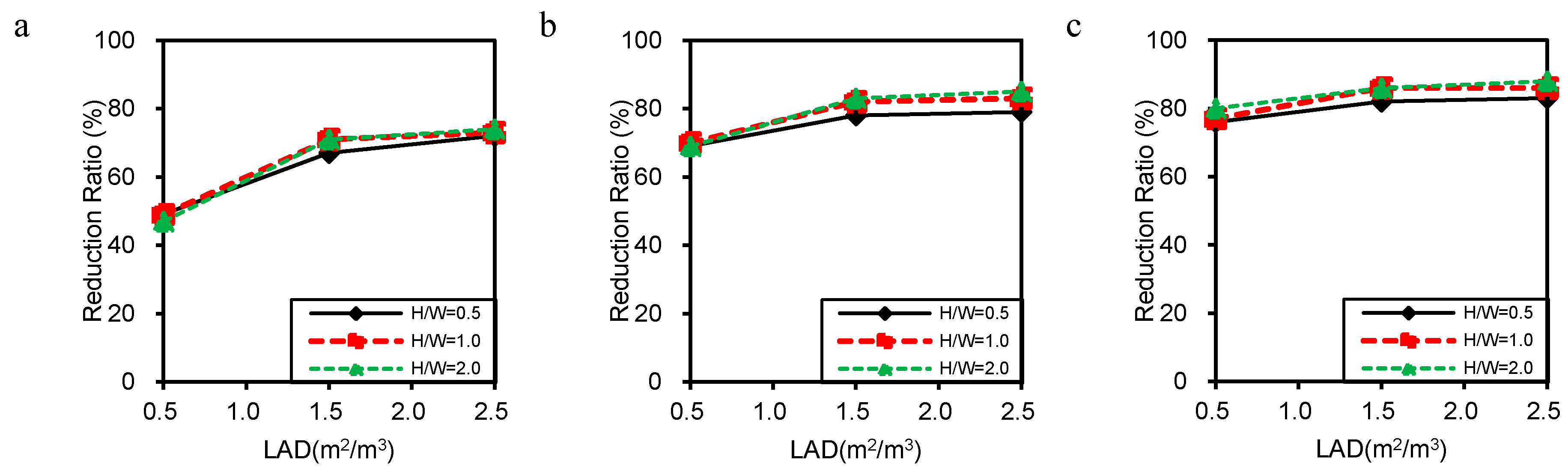
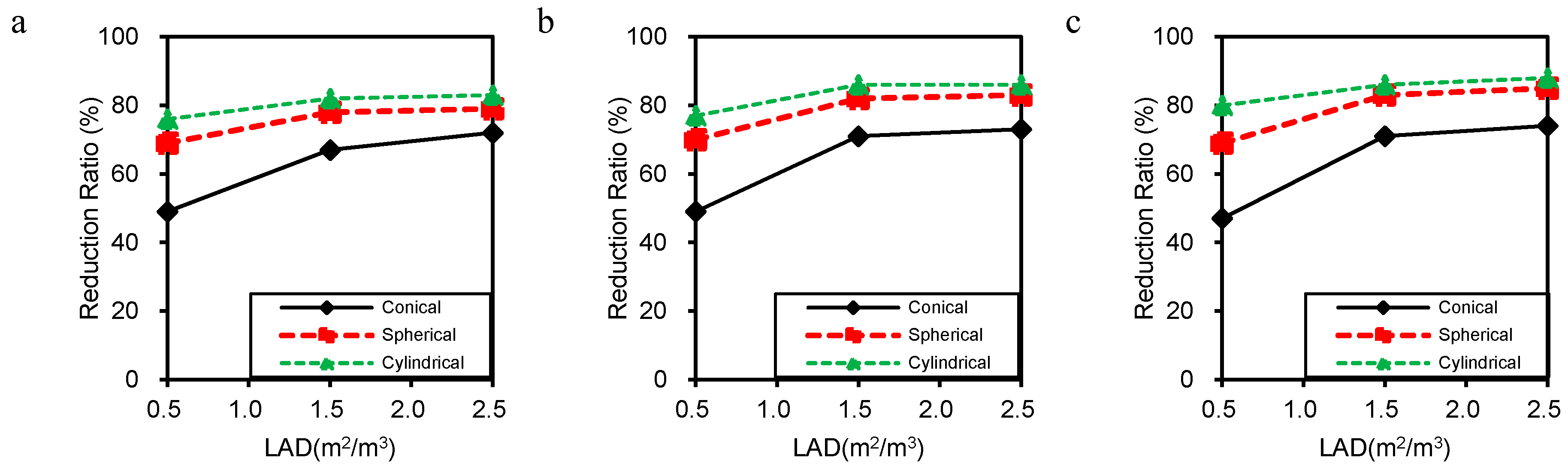
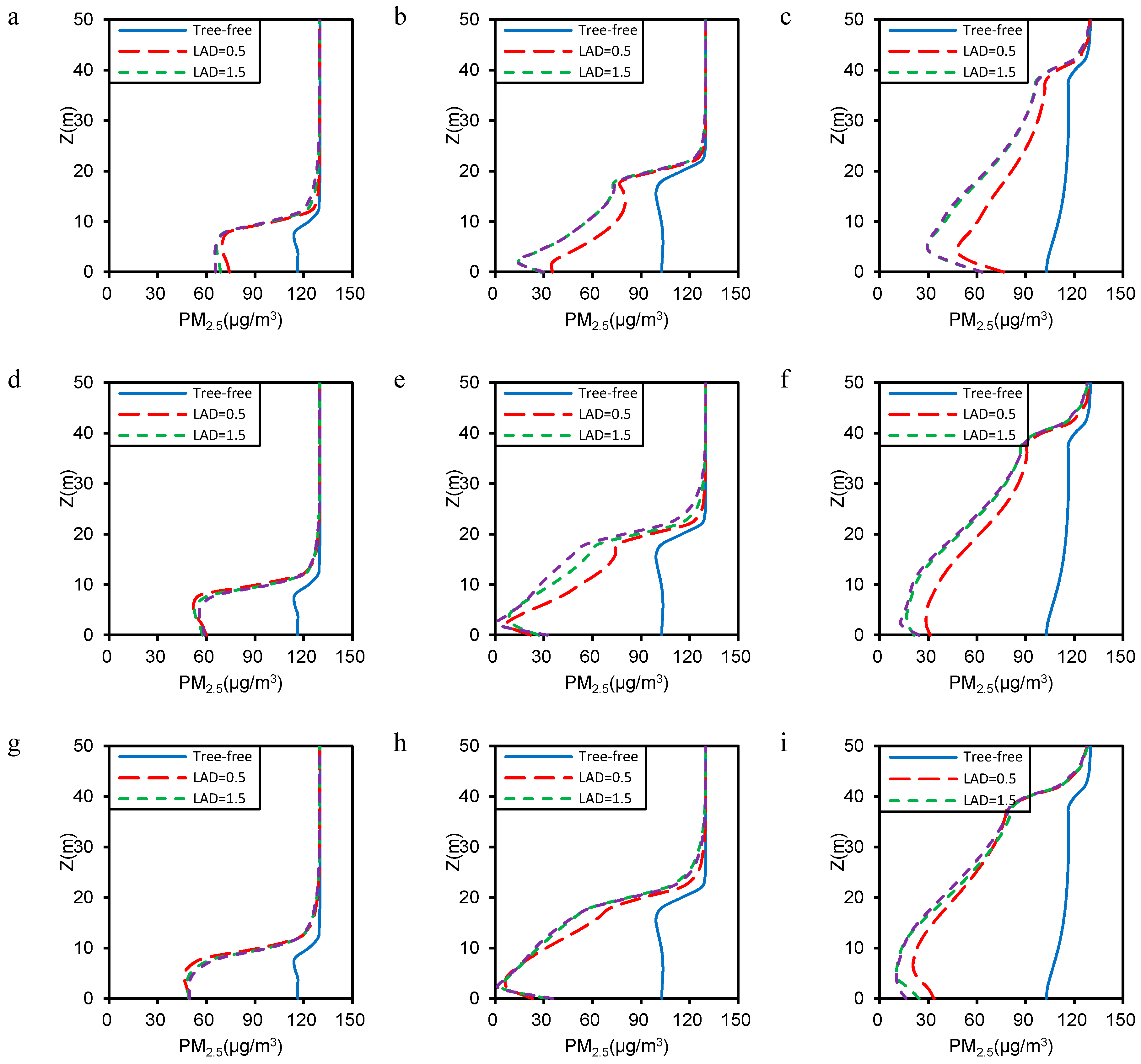
3.2. Particulate Matter Dispersion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, Y.; Ebenstein, A.; Greenstone, M.; Li, H. Evidence on the impact of sustained exposure to air pollution on life expectancy from China’s Huai River policy. Proc. Natl. Acad. Sci. USA 2013, 110, 12936–12941. [Google Scholar] [CrossRef] [PubMed]
- Ye, B.; Ji, X.; Yang, H.; Yao, X.; Chan, C.K.; Cadle, S.H.; Chan, T.; Mulawa, P.A. Concentration and chemical composition of PM2.5 in Shanghai for a 1-year period. Atmos. Environ. 2003, 37, 499–510. [Google Scholar] [CrossRef]
- Beijing Municipal Environmental Monitoring Center (BMEMC). Real-Time Air Quality in Beijing. Available online: http://www.bjmemc.com.cn (accessed on 25 January 2016).
- Beckett, K.P.; Freer-Smith, P.H.; Taylor, G. Urban woodlands: Their role in reducing the effects of particulate pollution. Environ. Pollut. 1998, 99, 347–360. [Google Scholar] [CrossRef]
- Beckett, K.P.; Freer-Smith, P.H.; Taylor, G. Particulate pollution capture by urban trees: Effect of species and wind speed. Glob. Chang. Biol. 2000, 6, 995–1003. [Google Scholar] [CrossRef]
- Ould-Dada, Z.; Baghini, N.M. Resuspension of small particles from tree surfaces. Atmos. Environ. 2001, 35, 3799–3809. [Google Scholar] [CrossRef]
- Ould-Dada, Z. Dry deposition profile of small particles within a model spruce canopy. Sci. Total Environ. 2002, 286, 83–96. [Google Scholar] [CrossRef]
- Freer-Smith, P.H.; Khatib-El, A.A.; Taylor, G. Capture of particulate pollution by trees: A comparison of species typical of semi-arid areas (Ficus nitida and Eucalyptus globulus) with European and North American species. Water Air Soil Pollut. 2004, 155, 173–187. [Google Scholar] [CrossRef]
- Freer-Smith, P.H.; Beckett, K.P.; Taylor, G. Deposition velocities to Sorbus aria, Acer campestre, Populus deltoids × trichocarpa ‘Beaupré’, Pinus nigra and × Cupressocyparis leylandii for coarse, fine and ultra-fine particles in the urban environment. Environ. Pollut. 2005, 133, 157–167. [Google Scholar] [CrossRef] [PubMed]
- Sæbø, A.; Popek, R.; Nawrot, B.; Hanslin, H.M.; Gawronska, H.; Gawronski, S.W. Plant species differences in particulate matter accumulation on leaf surfaces. Sci. Total Environ. 2012, 427–428, 347–354. [Google Scholar] [CrossRef] [PubMed]
- Moria, J.; Hanslinc, H.M.; Burchi, G.; Sæbø, A. Particulate matter and element accumulation on coniferous trees at different distances from a highway. Urban For. Urban Green. 2015, 14, 170–177. [Google Scholar] [CrossRef]
- Salmond, J.A.; Williams, D.E.; Laing, G.; Kingham, S.; Dirks, K.; Longley, I.; Henshaw, G.S. The influence of vegetation on the horizontal and vertical distribution of pollutants in a street canyon. Sci. Total Environ. 2013, 443, 287–298. [Google Scholar] [CrossRef] [PubMed]
- Jin, S.; Guo, J.; Wheeler, S.; Kan, L.; Che, S. Evaluation of impacts of trees on PM2.5 dispersion in urban streets. Atmos. Environ. 2014, 99, 277–287. [Google Scholar] [CrossRef]
- Przybysz, A.; Sæbø, A.; Hanslin, H.M.; Gawrońskia, S. Accumulation of particulate matter and trace elements on vegetation as affected by pollution level, rainfall and the passage of time. Sci. Total Environ. 2014, 481, 360–369. [Google Scholar] [CrossRef] [PubMed]
- Hwang, H.J.; Yook, S.J.; Ahn, K.H. Experimental investigation of submicron and ultrafine soot particle removal by tree leaves. Atmos. Environ. 2011, 45, 6987–6994. [Google Scholar] [CrossRef]
- Popek, R.; Gawrońska, H.; Wrochna, M.; Gawroński, S.W.; Sæbø, A. Particulate matter on foliage of 13 woody species: Deposition on surfaces and phytostabilisation in Waxes-a 3-Year Study. Int. J. Phytoremediat. 2013, 15, 245–256. [Google Scholar] [CrossRef] [PubMed]
- Terzaghi, E.; Wild, E.; Zacchello, G.; Cerabolini, B.E.L.; Jones, K.C.; Di Guardo, A. Forest filter effect: Role of leaves in capturing/releasing air particulate matter and its associated PAHs. Atmos. Environ. 2013, 74, 378–384. [Google Scholar] [CrossRef]
- Montazeri, H.; Blocken, B. CFD simulation of wind-induced pressure coefficients on buildings with and without balconies: Validation and sensitivity analysis. Build. Environ. 2013, 60, 137–149. [Google Scholar] [CrossRef]
- Schatzmann, M.; Leitl, B. Issues with validation of urban flow and dispersion CFD models. J. Wind Eng. Ind. Aerodyn. 2011, 99, 169–186. [Google Scholar] [CrossRef]
- Britter, R.; Schatzmann, M. Background and justification document to support the model evaluation guidance and protocol. Int. J. Environ. Pollut. 2007, 44, 139–146. [Google Scholar]
- Gousseau, P.; Blocken, B.; Stathopoulos, T.; Van-Heijst, G.J.F. CFD simulation of near-field pollutant dispersion on a high-resolution grid: A case study by LES and RANS for a building group in downtown Montreal. Atmos. Environ. 2011, 45, 428–438. [Google Scholar] [CrossRef]
- Gallagher, J.; Baldauf, R.; Fuller, C.H.; Kumar, P.; Gill, L.W.; McNabola, A. Passive methods for improving air quality in the built environment: A review of porous and solid barriers. Atmos. Environ. 2015, 120, 61–70. [Google Scholar] [CrossRef]
- Chan, T.L.; Dong, G.; Leung, C.W.; Cheung, C.S.; Hung, W.T. Validation of a two-dimensional pollutant dispersion model in an isolated street canyon. Atmos. Environ. 2002, 36, 861–872. [Google Scholar] [CrossRef]
- Gromke, C.; Ruck, B. Influence of trees on the dispersion of pollutants in an urban street canyon-Experimental investigation of the flow and concentration field. Atmos. Environ. 2007, 41, 3287–3302. [Google Scholar] [CrossRef]
- Buccolieri, R.; Gromke, C.; Sabatino, S.D.; Ruck, B. Aerodynamic effects of trees on pollutant concentration in street canyons. Sci. Total Environ. 2009, 407, 5247–5256. [Google Scholar] [CrossRef] [PubMed]
- Wania, A.; Bruse, M.; Blond, N.; Weber, C. Analysing the influence of different street vegetation on traffic-induced particle dispersion using microscale simulations. J. Environ. Manag. 2012, 94, 91–101. [Google Scholar] [CrossRef] [PubMed]
- Vos, P.E.J.; Maiheu, B.; Vankerkom, J.; Janssen, S. Improving local air quality in cities: To tree or not to tree? Environ. Pollut. 2013, 183, 113–122. [Google Scholar] [CrossRef] [PubMed]
- Buccolieri, R.; Salim, S.M.; Leo, L.S.; Sabatino, S.D.; Chan, A.; Ielpo, P.; Gennaro, G.; Gromke, C. Analysis of local scale tree-atmosphere interaction on pollutant concentration in idealized street canyons and application to a real urban junction. Atmos. Environ. 2011, 45, 1702–1713. [Google Scholar] [CrossRef]
- Zhang, Y.; Gu, Z.; Lee, S.; Fu, T.M.; Ho, K.F. Numerical simulation and in situ investigation of fine particle dispersion in an actual deep street canyon in Hong Kong. Indoor Built Environ. 2011, 20, 206–216. [Google Scholar] [CrossRef]
- Park, S.; Kim, J.; Kim, M.J.; Park, R.J.; Cheong, H. Characteristics of flow and reactive pollutant dispersion in urban street canyons. Atmos. Environ. 2015, 108, 20–31. [Google Scholar] [CrossRef]
- Scungio, M.; Arpino, F.; Cortellessa, G.; Buonanno, G. Detached eddy simulation of turbulent flow in isolated street canyons of different aspect ratios. Atmos. Pollut. Res. 2015, 6, 351–364. [Google Scholar] [CrossRef]
- Scungio, M.; Arpino, F.; Stabile, L.; Buonanno, G. Numerical simulation of ultrafine particle dispersion in urban street canyons with the Spalart-Allmaras turbulence model. Aerosol Air Qual. Res. 2013, 13, 1423–1437. [Google Scholar] [CrossRef]
- Jeanjean, A.P.R.; Buccolieri, R.; Eddy, J.; Monks, P.S.; Leigh, R.J. Air quality affected by trees in real street canyons: The case of Marylebone neighborhood in central London. Urban For. Urban Green. 2017, 22, 41–53. [Google Scholar] [CrossRef]
- Zhong, J.; Cai, X.; Bloss, W.J. Modelling the dispersion and transport of reactive pollutants in a deep urban street canyon: Using large-eddy simulation. Environ. Pollut. 2015, 200, 42–52. [Google Scholar] [CrossRef] [PubMed]
- Neft, I.; Scungio, M.; Culver, N.; Singh, S. Simulations of aerosol filtration by vegetation: Validation of existing models with available lab data and application to near-roadway scenario. Aerosol Sci. Technol. 2016, 50, 937–946. [Google Scholar] [CrossRef]
- Santiago, J.-L.; Martilli, A.; Martin, F. On dry deposition modelling of atmospheric pollutants on vegetation at the microscale: Application to the impact of street vegetation on air quality. Bound. Layer Meteorol. 2017, 162, 451–474. [Google Scholar] [CrossRef]
- Moradpour, M.; Afshin, H.; Farhanieh, B. A numerical investigation of reactive air pollutant dispersion in urban street canyons with tree planting. Atmos. Pollut. Res. 2017, 8, 253–266. [Google Scholar] [CrossRef]
- Hofmana, J.; Bartholomeus, H.; Janssen, S.; Calders, K.; Wuyts, K.; Wittenberghe, S.V.; Samson, R. Influence of tree crown characteristics on the local PM10 distribution inside an urban street canyon in Antwerp (Belgium): A model and experimental approach. Urban For. Urban Green. 2016, 20, 265–276. [Google Scholar] [CrossRef]
- Willis, K.J.; Petrokofsky, G. The natural capital of city trees. Science 2017, 356, 374–376. [Google Scholar] [CrossRef] [PubMed]
- Lin, B.; Li, X.; Zhu, Y.; Qin, Y. Numerical simulation studies of the different vegetation patterns’ effects on outdoor pedestrian thermal comfort. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1707–1718. [Google Scholar] [CrossRef]
- Amorim, J.H.; Rodrigues, V.; Tavares, R.; Valente, J.; Borrego, C. CFD modeling of the aerodynamic effect of trees on urban air pollution dispersion. Sci. Total Environ. 2013, 461–462, 541–551. [Google Scholar] [CrossRef] [PubMed]
- Katul, G.; Mahrt, L.; Poggi, D.; Sanz, C. One- and two-equation models for canopy turbulence. Bound. Layer Meteorol. 2004, 113, 81–109. [Google Scholar] [CrossRef]
- Kimura, A.; Iwata, T.; Mochida, A.; Yoshino, H.; Ooka, R.; Yoshida, S. Optimization of plant canopy model for reproducing aerodynamic effects of trees: (Part 1) Comparison between the canopy model optimized by the present authors and that proposed by Green. Archit. Inst. Jpn. 2003, 9, 721–722. [Google Scholar]
- Ji, W.; Zhao, B. Numerical study of the effects of trees on outdoor particle concentration distributions. Build. Simul. 2014, 7, 417–427. [Google Scholar] [CrossRef]
- Bell, J.N.B.; Treshow, M. Air Pollution and Plant Life, 2nd ed.; John Willey & Sons, Ltd.: Chichester, UK, 2003. [Google Scholar]
- Oke, T.R. Street design and urban canopy layer climate. Energy Build. 1988, 11, 103–113. [Google Scholar] [CrossRef]
- Zhang, N.; Dong, L.; Hao, P.; Yan, H.; Wang, K.; Luo, Y. Study on structure of street trees in central districts of Beijing. J. Cent. South Univ. For. Technol. 2014, 34, 101–106. [Google Scholar]
- Shi, X. Preliminary Study on Fixing Carbon Dioxide Releasing Oxygen and Retention of Dust of Street Trees in Beijing. Master’s Thesis, Beijing Forestry University, Beijing, China, 22 June 2010. [Google Scholar]
- Franke, J.; Hellsten, A.; Schlunzen, K.H.; Carissimo, B. The COST 732 Best Practice Guideline for CFD simulation of flows in the urban environment: A summary. Int. J. Environ. Pollut. 2011, 44, 419–427. [Google Scholar] [CrossRef]
- Tominaga, Y.; Mochida, A.; Yoshie, R.; Kataoka, H.; Nozu, T.; Yoshikawa, M.; Shirasawa, T. AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1749–1761. [Google Scholar] [CrossRef]
- Mochida, A.; Lun, I.Y.F. Prediction of wind environment and thermal comfort at pedestrian level in urban area. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1498–1527. [Google Scholar] [CrossRef]
- Zhao, B.; Chen, C.; Tan, Z. Modeling of ultrafine particle dispersion in indoor environments with an improved drift flux model. J. Aerosol Sci. 2009, 40, 29–43. [Google Scholar] [CrossRef]
- Barratt, R. Atmospheric Dispersion Modeling: An Introduction to Practical Applications; Earthscan Publications: London, UK, 2001. [Google Scholar]
- Roache, P.J. Perspective: A method for uniform reporting of grid refinement studies. J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Gromke, C.; Buccolieri, R.; Sabatino, S.D.; Ruck, B. Dispersion study in a street canyon with tree planting by means of wind tunnel and numerical investigations-Evaluation of CFD data with experimental data. Atmos. Environ. 2008, 42, 8640–8650. [Google Scholar] [CrossRef]


| Typical Plants | 3D Geometric Figure | Crown Volume Expressions | CH(y) (m) | CD(x) (m) | CBH (m) | LAD (m2/m3) | Vd (m/s) [9,10] |
|---|---|---|---|---|---|---|---|
| Picea wilsonii | Cone | πx2y/12 | 5 | 3 | 0.5 | 1.71 | 0.0252 |
| Pinus tabulaeformis | Cone | πx2y/12 | 6 | 3 | 1 | 1.69 | 0.0175 |
| Platycladus orientalis | Cone | πx2y/12 | 6 | 5 | 0.5 | 2.20 | 0.0407 |
| Ginkgo biloba | Cone | πx2y/12 | 7 | 3 | 2 | 1.26 | 0.0245 |
| Koelreuteria paniculata | Oval | πx2y/6 | 8.5 | 4 | 2.5 | 1.54 | 0.0081 |
| Acer truncatum | Oval | πx2y/6 | 6.5 | 4 | 1.5 | 0.92 | 0.0122 |
| Sabina chinensis | Cone | πx2y/12 | 3.5 | 3 | 0.5 | 0.83 | 0.0068 |
| Syringa oblata | Sphericity | πx2y/6 | 1 | 1.5 | 0 | 0.96 | 0.0075 |
| Comparison Criteria | Paired Differences | t | Significance Value (Two-Tailed) 1 | ||||
|---|---|---|---|---|---|---|---|
| Mean | Standard Deviation | Standard Error Mean | 95% Confidence Interval of the Difference | ||||
| Lower | Upper | ||||||
| PM2.5 | 1.80 | 15.63 | 3.19 | −4.80 | 8.40 | 0.56 | 0.578 |
| Air velocity | 0.0054 | 0.1331 | 0.0272 | −0.0508 | 0.0616 | 0.20 | 0.844 |
| Tree Crown Morphology | Typical Avenue Trees | Crown Volume Expression 1 | Vd |
|---|---|---|---|
| Conical | Fraxinus pennsylvanica × F. velutina | πx2y/12 | 0.0036 |
| Spherical | Sophora japonica | πx2y/6 | 0.0068 |
| Cylindrical | Populus tomentosa | πx2y/4 | 0.0075 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, B.; Lin, B.; Qin, H. Numerical Investigation on the Effect of Avenue Trees on PM2.5 Dispersion in Urban Street Canyons. Atmosphere 2017, 8, 129. https://doi.org/10.3390/atmos8070129
Hong B, Lin B, Qin H. Numerical Investigation on the Effect of Avenue Trees on PM2.5 Dispersion in Urban Street Canyons. Atmosphere. 2017; 8(7):129. https://doi.org/10.3390/atmos8070129
Chicago/Turabian StyleHong, Bo, Borong Lin, and Hongqiao Qin. 2017. "Numerical Investigation on the Effect of Avenue Trees on PM2.5 Dispersion in Urban Street Canyons" Atmosphere 8, no. 7: 129. https://doi.org/10.3390/atmos8070129
APA StyleHong, B., Lin, B., & Qin, H. (2017). Numerical Investigation on the Effect of Avenue Trees on PM2.5 Dispersion in Urban Street Canyons. Atmosphere, 8(7), 129. https://doi.org/10.3390/atmos8070129





