1. Introduction
Analysis of meteorological feature curves, including the analysis of contours, streamlines, trough lines, and frontal lines, is of great importance for weather forecasting. The rapid development of computer technology has allowed the development of models that automatically extract feature curves from meteorological data. At present, feature curves such as contours and streamlines are analyzed objectively in most meteorological analysis systems, including the American Advanced Weather Interactive Processing System (AWIPS) [
1] and the Chinese Meteorological Information Comprehensive Analysis and Processing System (MICAPS) [
2]. However, numerous synoptic constraints limit the processing of other feature curves, such as trough lines, to manual methods. Therefore, automatic identification of troughs has become a focus for researchers.
By definition, a trough is an elongated (extended) region of relatively low atmospheric pressure. Significant weather changes generally exist near these troughs; for instance, precipitation may occur due to the updraft ahead of a trough, while clearing may occur due to the downdraft behind a trough. Particularly, troughs are accompanied by significant and sometimes hazardous weather phenomena, such as hailstorms and thunderstorms, which necessitate the analysis of upper air charts. This makes the recognition and positioning of troughs an important problem. To identify these features, curves called trough lines are marked on a weather chart. Trough lines are usually identified by arrangements of isobars, which are concave towards areas of low pressure along an individual isobar’s maximum curvature. Subjective analysis has become the primary method of trough line identification, though this method suffers from two primary problems. First, it is difficult to obtain real-time processing results for synoptic analyses due to the amount of data and the inefficiencies inherent in manual work. Second, the subjectivity of the forecaster may lead to inaccurate, different, or missed identifications. Objective analysis and visualization methods should be developed to resolve these problems. Thus, the digital abstraction and representation of synoptic analysis principles has become the focus of research into objective trough line identification.
To the best of our knowledge, the objective identification of trough lines has not been a major focus of scholars. In the existing literature, Huang et al. [
3,
4] constructed a relation-based spatial aggregation framework to identify trough lines by connecting the maximum curvature points of isobar segments, and Wong [
5] used the genetic algorithm method to extract adjacent arc segments to detect a low-pressure system. These authors recognized trough lines using a fitness function that maximized changes in the pressure gradient perpendicular to the isobars. In addition, Li et al. [
6] extracted a trough line using an image-processing technique to distinguish geometric characteristics in the pressure field. Jann [
7] used gridded geopotential or pressure data to trace curvature and vorticity, thereby identifying trough lines using pattern recognition methods. Similarly, automated methods of front recognition have been heavily researched [
8]. These methods have been used as references for the present study, due to the similarities between trough line and frontal line analyses. For example, a framework for front identification has been developed and widely used in analyses of frontal behavior [
9,
10,
11,
12]. The model extracts areas with large thermal contrast from gridded thermal fields. Candidate frontal lines are extracted from the gridded thermal field as contour lines connecting zero values of a locating variable, and any spurious lines are filtered out using threshold-masking variables that represent the strength of the frontal lines.
In the field of geography, the extraction of valley (ridge) lines from terrain data is similar to trough recognition. For example, Ohtake et al. [
13] proposed a method for detecting view- and scale-independent ridge (valley) lines, in which first-order and second-order curvature derivatives of shapes were approximated by dense triangular meshes. Pang [
14] extracted valley-ridge lines from a point set model, in which the potential valley-ridge points were identified according to a large principal curvature in the algorithm. In other research [
15,
16], the method used to recognize trough lines was based on vertex curves that connect the points of maximum curvature in level sets.
The aforementioned methods of trough identification primarily rely on pressure field data. In actuality, forecasters prefer to analyze trough lines using wind field data because wind direction has a distinct distribution. The horizontal wind in geostrophic balance is parallel to an isobaric line; a sharp change in wind direction generally indicates the bending point of an isobar. Schultz [
17] studied different mechanisms of frontal troughs and noted that in most cases, pressure troughs consistently coincided with wind shifts; that is, the wind shear line and the trough line are nearly consistent.
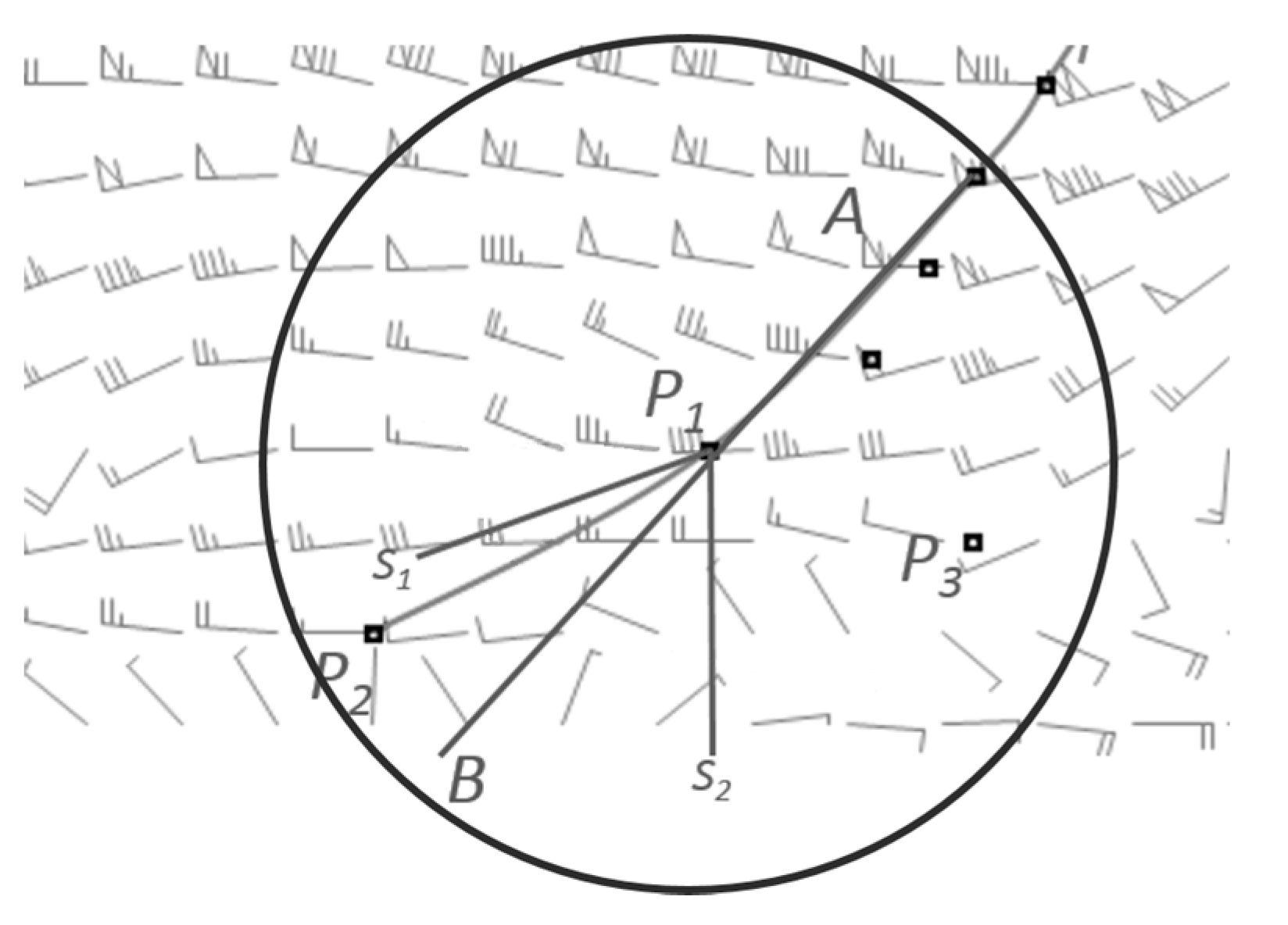
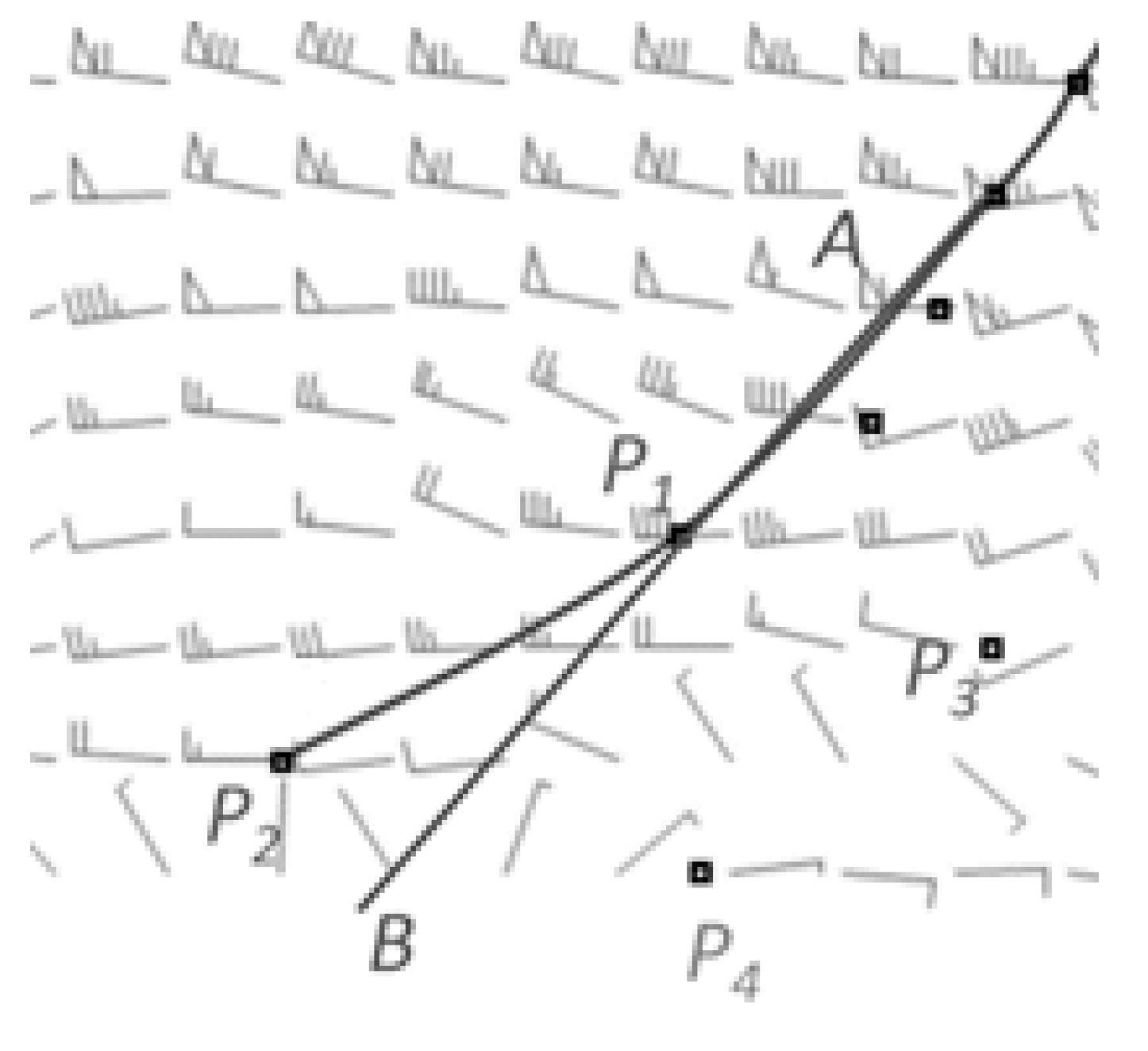
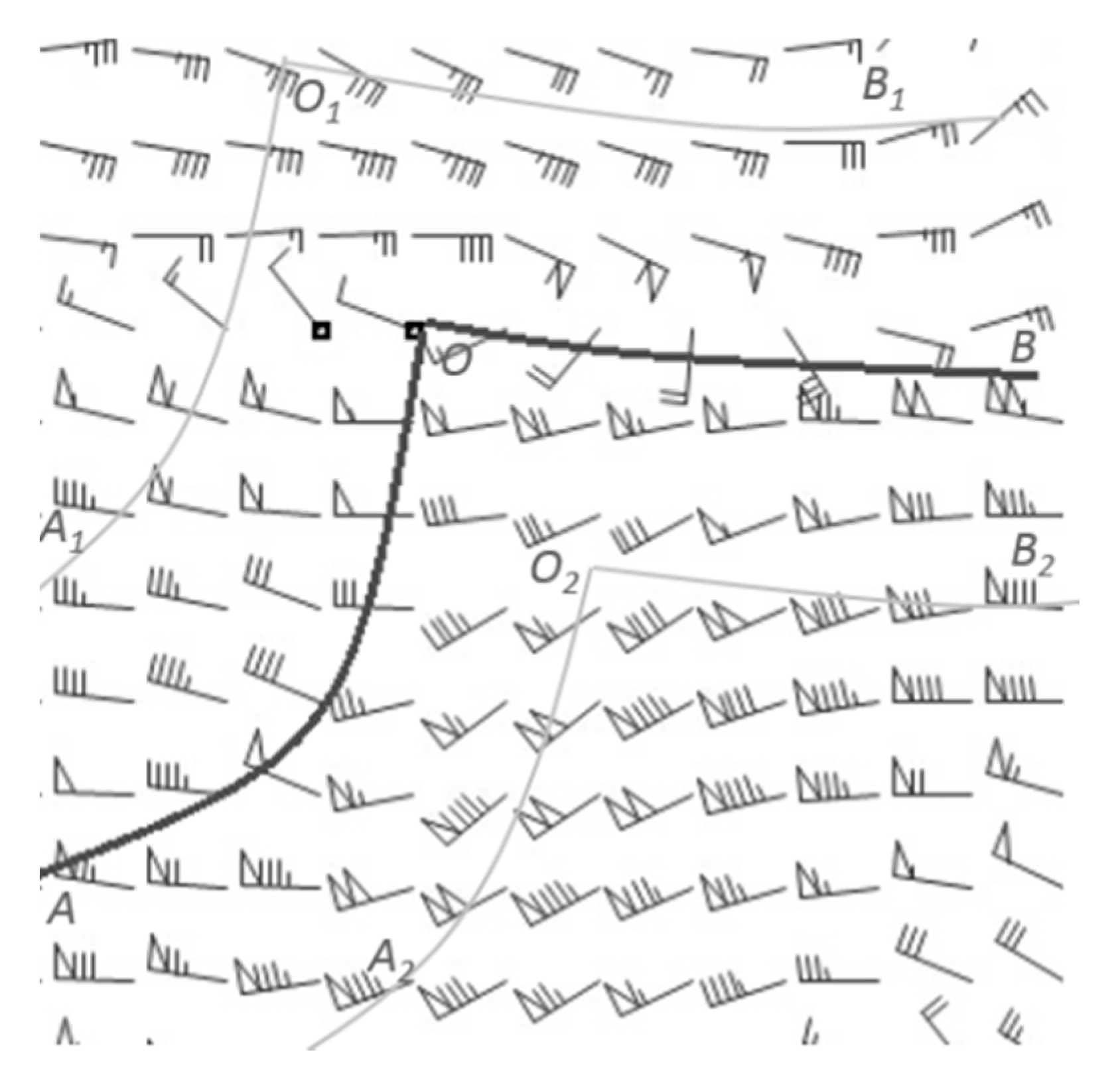
Thus, an objective method for identifying trough lines from wind field data is proposed. We seek to analyze longwave and shortwave trough lines. To analyze longwave trough lines, cyclonic centers are located, and candidate trough points are filtered simultaneously. Then, the longwave trough lines are identified according to the distance and angle between the candidate trough points. Next, the candidate shortwave trough points are extracted from the region in which longwave trough lines are infrequent, as determined by the angular deflection and vorticity of the grids, which are clustered and fitted to produce shortwave trough lines. The remainder of this paper is organized as follows:
Section 2 describes the proposed identification method by which the trough lines are categorized and analyzed;
Section 3 presents the experiment and results; and
Section 4 addresses our conclusions.
3. Results and Discussion
We implemented this approach on a personal computer and used wind field data from the National Centers for Environmental Prediction (NCEP) to test it.
Section 3.2 demonstrates this approach, and
Section 3.3 compares the automatic identification results in this paper to subjective analysis results, using recall ratio and precision ratio data to examine the accuracy and reliability of the method.
3.1. Parameters and Data
The approach was carried out on a PC with an Intel Core i7-3770 CPU, 3.40 GHz, 8 GB of RAM and a 64-bit Windows 7 operating system. In terms of the method’s parameters, considering that the troughs are generally without evident direction change, we set the desired tracing direction as a small angle. The angles from 3° to 10° were tested; when the tracing direction was set at a larger angle, such as 8° or 9°, the trough lines were more zigzaged, and if the angle was relatively small, such as 3° or 4°, there was not enough trough points to trace longwave trough lines. Thus, the fixed angle was set at 5°. In addition, the set of WeightA and WeightB were relatively simple, because the angle condition is often more important than the distance condition in tracing longwave trough lines. The weight values for distance () and angle () were set to 0.6 and 0.8, respectively. Lastly, during the shortwave trough line tracing process, the variable weights of angular deflection () and vorticity () were found to work best at an interval of 2–3. If the β and γ were larger than 3, fewer candidate shortwave trough points would be extracted, which might not obtain reasonable shortwave trough lines; if the β and γ were smaller than 2, it would add lots of noise point to influence the curve fitting of candidate trough points; thus, we tried to use and .
To examine our approach, six-hour re-analysis wind field grid data from NCEP were employed. The data included zonal and meridional wind speed components corresponding to latitude and longitude, and the spatial resolution of the data was 2.5° × 2.5°. We focused on the 500 hPa geopotential height for two reasons. First, the change and movement of air at this height is relatively steady, and the periodic change in the wind field is explicit. Second, most weather processes leave an imprint on the 500 hPa isobaric surface, which can be used to predict future weather changes more accurately. The region we chose for this experiment was 0°–60° N and 60°–180° E, which is widely used for synoptic chart analysis in East and South Asia.
3.2. Case Study
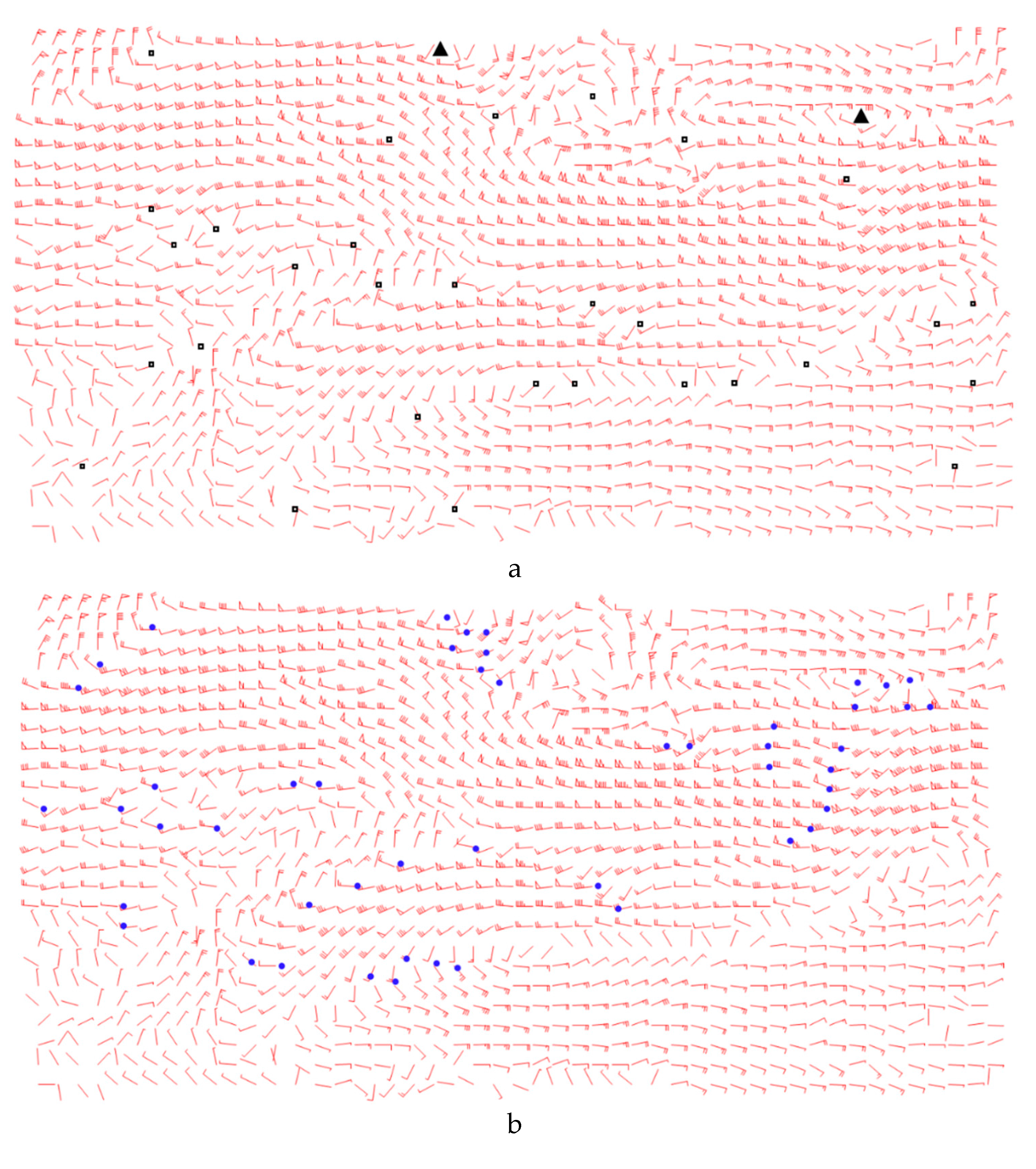
We used wind field data from 30 April 2009 at 1600 UTC to test the validity of the proposed method. The automatic identification results of each step in tracing longwave trough lines (including the extraction of cyclonic centers and candidate longwave trough points) are shown in
Figure 4. In
Figure 4a, dark spots represent the location of points with local minimum wind speed; the cyclonic centers are extracted from these points using the method proposed in
Section 2.2.1. All cyclonic centers were found precisely and were used as the starting points of trough lines. In
Figure 4b, the candidate points for longwave trough lines were extracted according to the wind direction of the grid points, as described in
Section 2.2.2. The final result of the longwave trough lines analysis is illustrated on a geographic background in
Figure 4c, with Lambert projection. Because the tracing direction is constrained to a given scope, few evident bending points can be seen in the trough lines. The evaluated function offers more reasonable trough points, which aids in the acquisition of accurate tracing results.
The experimental results from each step of the automatic shortwave trough line identification (including the extraction of candidate shortwave trough points, trough point clustering, and curve fitting) are shown in
Figure 5.
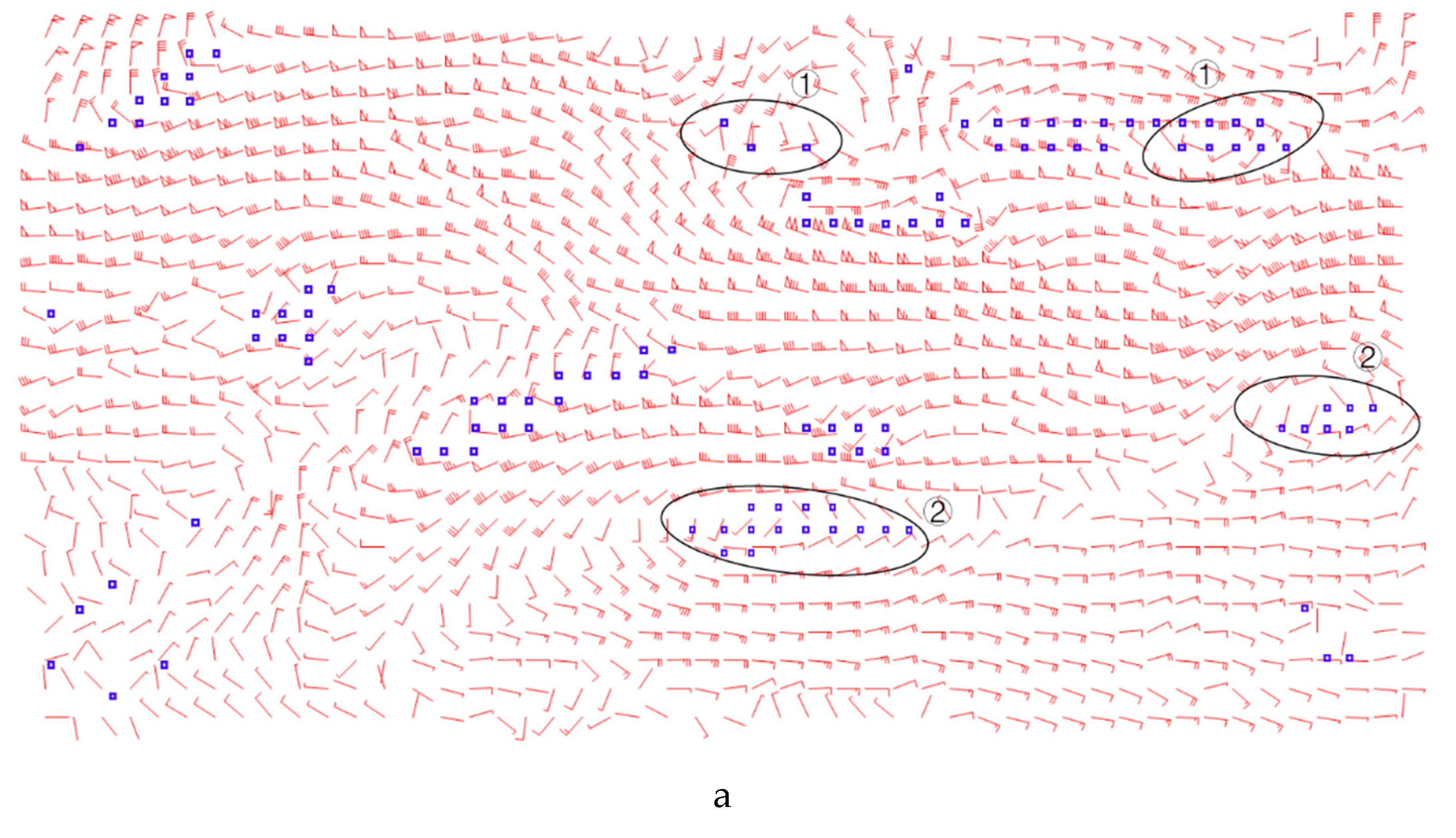
Figure 5a shows the candidate shortwave trough points that were extracted based on angular deflection and vorticity factors, with those candidates in the longwave trough regions (which are marked with symbol ①) removed, as described in
Section 2.3.2. A minimum spanning tree clustering algorithm was applied to obtain some of the shortwave trough point sets. Because trough lines generally appear near low-pressure areas, the candidates around anticyclonic (high-pressure) centers were removed even if the wind shear there was significant, which are marked with symbol ②.
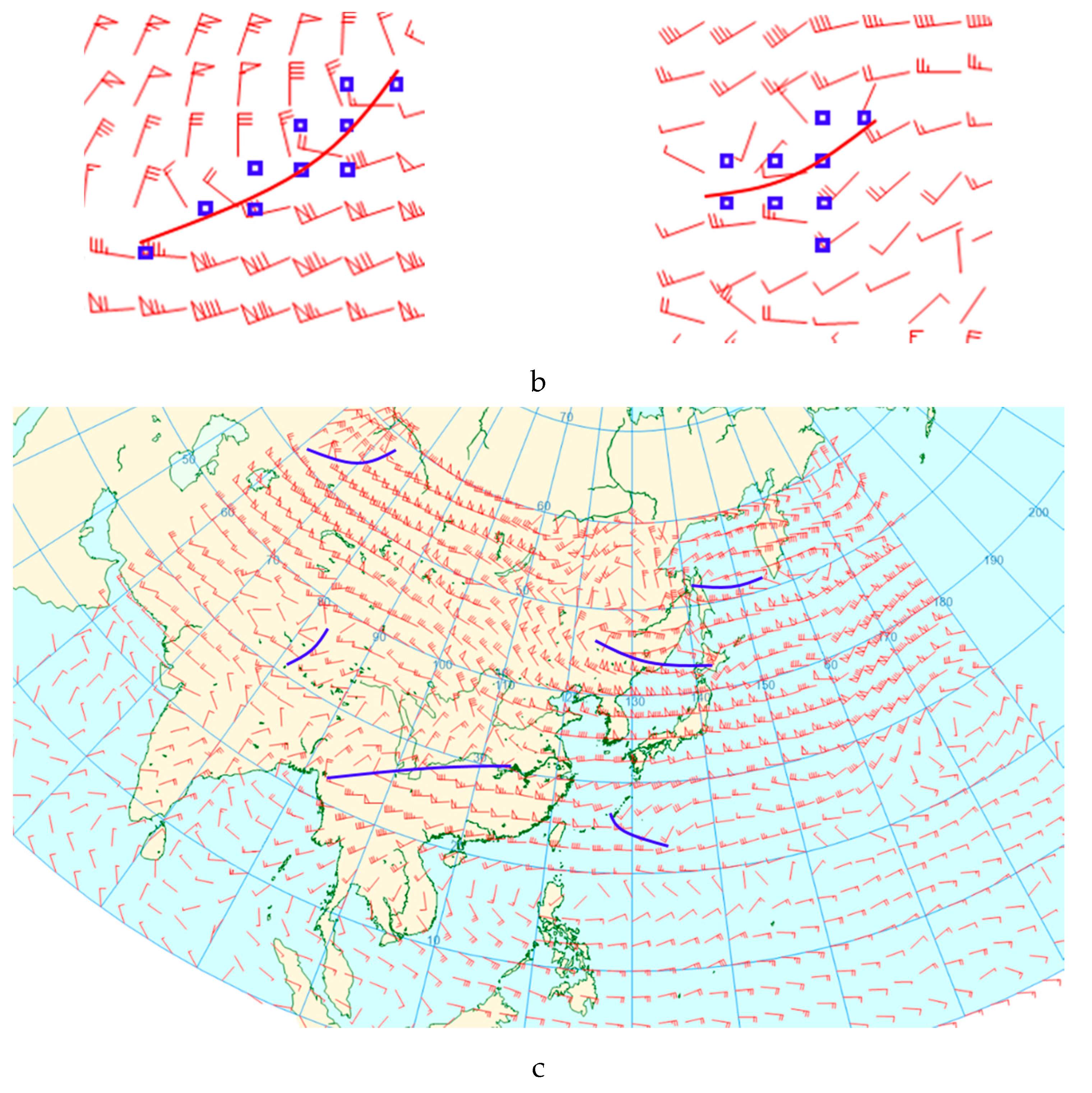
Figure 5b shows two examples of the curve fitting for shortwave trough points. In these examples, the quartic polynomial was used to achieve smooth shortwave trough lines from candidate shortwave trough point sets. The final shortwave trough lines produced by the automatic analysis are displayed on a geographic background map in
Figure 5c.
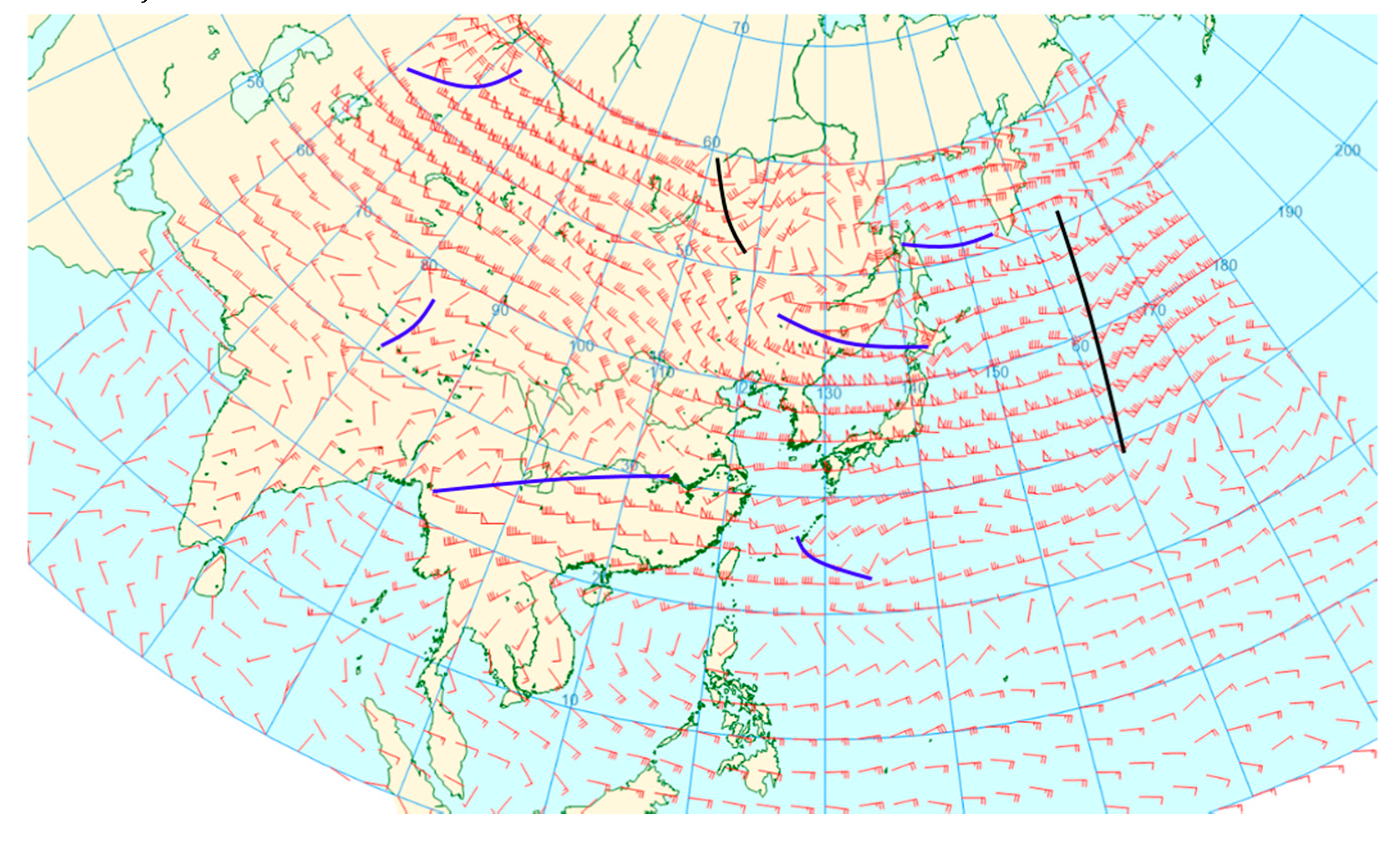
The identification result, combined with both longwave and shortwave trough lines, is shown in
Figure 6. Compared to the manual analysis performed by forecasters, our method produces results much closer to the subjective result.
Furthermore, 70 groups of wind field data at 500 hPa from 2009 to 2010 were analyzed using our method. Examples of the experimental results from this analysis are shown in
Figure 7.
3.3. Comparison and Evaluation
Several experiments were completed to compare our method to the subjective analysis of trough lines. To do so, two professional weather forecasters were invited to help conduct a manual analysis of trough lines using the same wind field data sets, which were taken as ground truth. The objective analysis results from our method were overlaid onto the subjective trough lines derived from the same wind field. We then delineated a rectangular region around each subjective trough line and visually identified whether a matching objective trough line was located within the rectangle of the subjective trough line. We then quantitatively assessed the matching pairs by adopting a quantification judgement method from previous research [
27]. The consistency degree was used to measure the location consistency and scope consistency between subjective and objective trough lines. The consistency degree is represented as follows:
Within the rectangular region of a matching pair,
is the number of grid points in the objective trough line,
is the number of grid points in the subjective trough line, and
represents the number of grid points in both trough lines. Particularly, if the subjective trough line crossed between two grid points and at least one of the two points is in the objective trough line, we assumed a coincident point was present, which was then added to
. The consistency degree range was set from 0 to 100; a larger degree corresponded to greater similarity between the two trough lines.
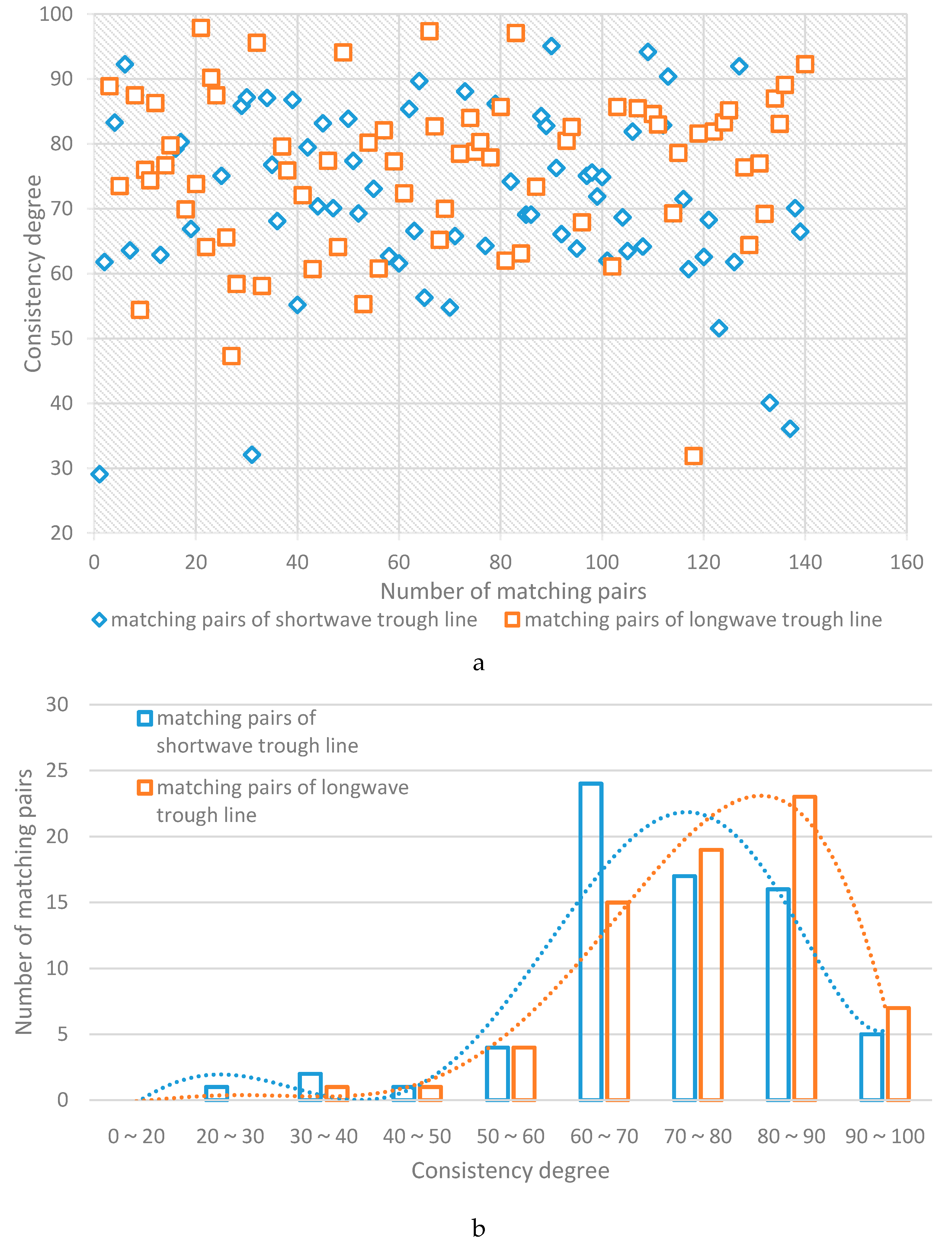
The consistency degrees for all matching pairs from wind field data were computed using the aforementioned quantification judgement method, and the partial results (a total of 140 samples, including 70 matching pairs of shortwave trough lines and 70 matching pairs of longwave trough lines, which were selected randomly from all matching pairs) are shown in
Figure 8.
Figure 8a indicates that most of the matching pairs’ consistency degrees exceeded 60, which means the objective analysis of the location and length of the trough lines is generally consistent with the subjective result. In addition, given the more obvious trends and greater lengths of longwave trough lines, they are identified more exactly than shortwave trough lines, as illustrated in
Figure 8b. The orange dotted line in
Figure 8b is the polynomial fitting curve about the statistical result of longwave matching pairs’ consistency degree, where the blue represents the polynomial fitting curve of shortwave matching pairs’ consistency degree. It can be seen that the average consistency degree of the major matching pairs of longwave trough lines is approximately 85, while that of shortwave trough lines is approximately 80. The result indicates that the objective identification of longwave trough lines is more exact than longwave trough lines.
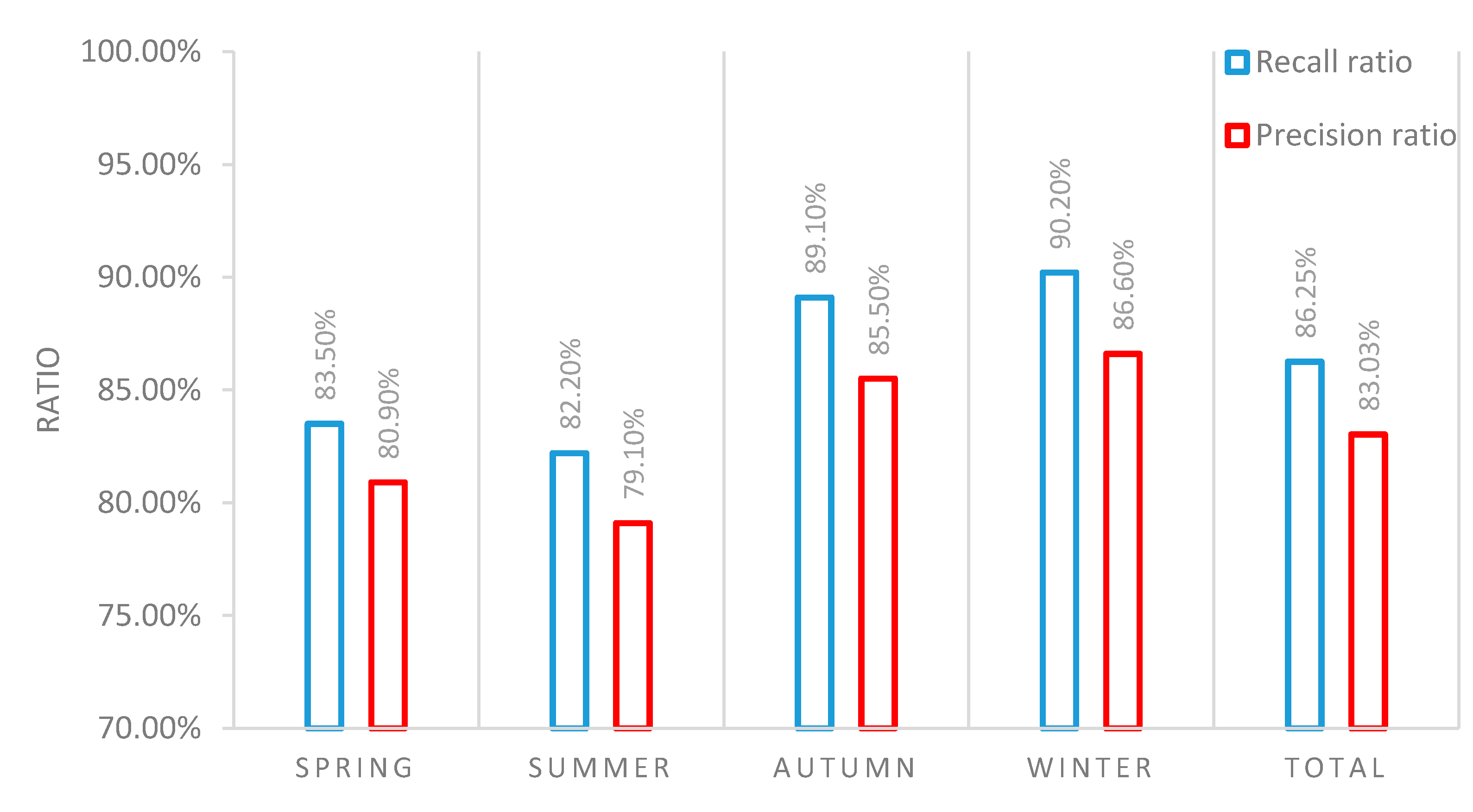
According to the advice of the forecasters, if the consistency degree was greater than 60, the trough line identification for a matching pair was viewed as a success. Evaluation criteria, including the recall ratio and precision ratio, were then proposed to examine the accuracy and reliability of our identification method:
where
is the number of successful matching pairs,
is the number of subjective trough lines, and
is the number of objective trough lines. All trough lines were assessed and the results shown in
Figure 9. Based on this analysis, we determined that a more accurate and effective trough line identification process was possible during the fall and winter than during the spring and summer. This may be because the synoptic system is comparatively steady during fall and winter, with evident trends in major troughs; that is, most troughs are longwave troughs, which may be easier to analyze. Nevertheless, the total recall ratio and precision ratio reached 86.25% and 83.03%, respectively, which may meet the practical demands of weather forecasters.
4. Conclusions
In this paper, an objective method for identifying trough lines using wind field data was proposed. Longwave and shortwave trough lines were analyzed in different ways. To analyze longwave trough lines, cyclonic centers were first located and candidate trough points were filtered according to wind direction. Candidate longwave trough points were traced starting from the cyclonic centers (based on distance and angle conditions). Next, shortwave trough candidate points were identified according to the angular deflection and vorticity of grid points, which were then clustered and fitted to a curve to define the shortwave trough lines. Compared to other methods (based on pressure field data), this approach conforms better to the experience and rules of the manual identification of trough lines. Moreover, from a global perspective, the wind direction has more distinct distribution than isolines extracted from pressure field data, which indicates that the method can be used more widely. The experimental results show that longwave trough lines can be more accurately determined than shortwave trough lines relative to manual analysis, because they have more obvious trends and greater lengths. Furthermore, by classifying the recall ratio and precision ratio of the identification results by season, we determined that trough line identification was more accurate and effective during the fall and winter than during the spring and summer. The reason is that synoptic systems during the fall and winter are steadier than those during the spring and summer, potentially resulting in more longwave trough lines; therefore, the analysis is comparatively easy and exact. In general, the method proposed here allows for the objective identification of trough lines and can cater to the practical demands of weather forecasting work.
However, the method might be less robust in areas with irregular wind fields, which may lead to the missed identification of trough lines, and more effort will be made in the future to improve the method. In addition, self-adaptive parameters, according to the different data resolution and wind field features, will be the focus of our future study to achieve better identification results.