Merging MODIS and Ground-Based Fine Mode Fraction of Aerosols Based on the Geostatistical Data Fusion Method
Abstract
:1. Introduction
2. Methods and Data
2.1. Comparison of Theretical FMFs
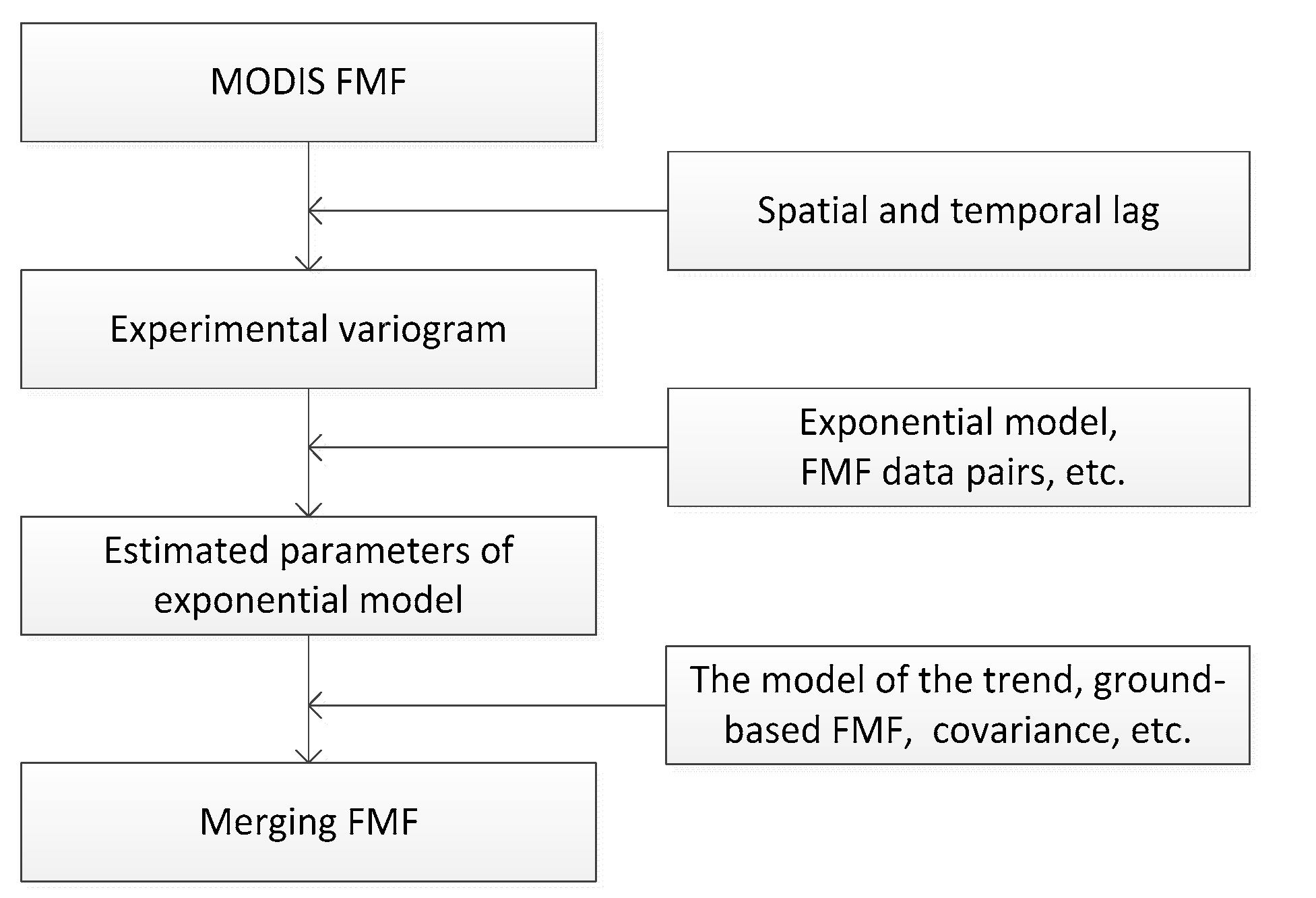
2.2. Fusion Method for Merging FMF
- (i)
- Analysis of the experimental variogram:
- (ii)
- Estimated parameters in the experimental variogram:
- (iii)
- Merging space-borne and ground-based FMF using the UK method:
2.3. PMRS Model
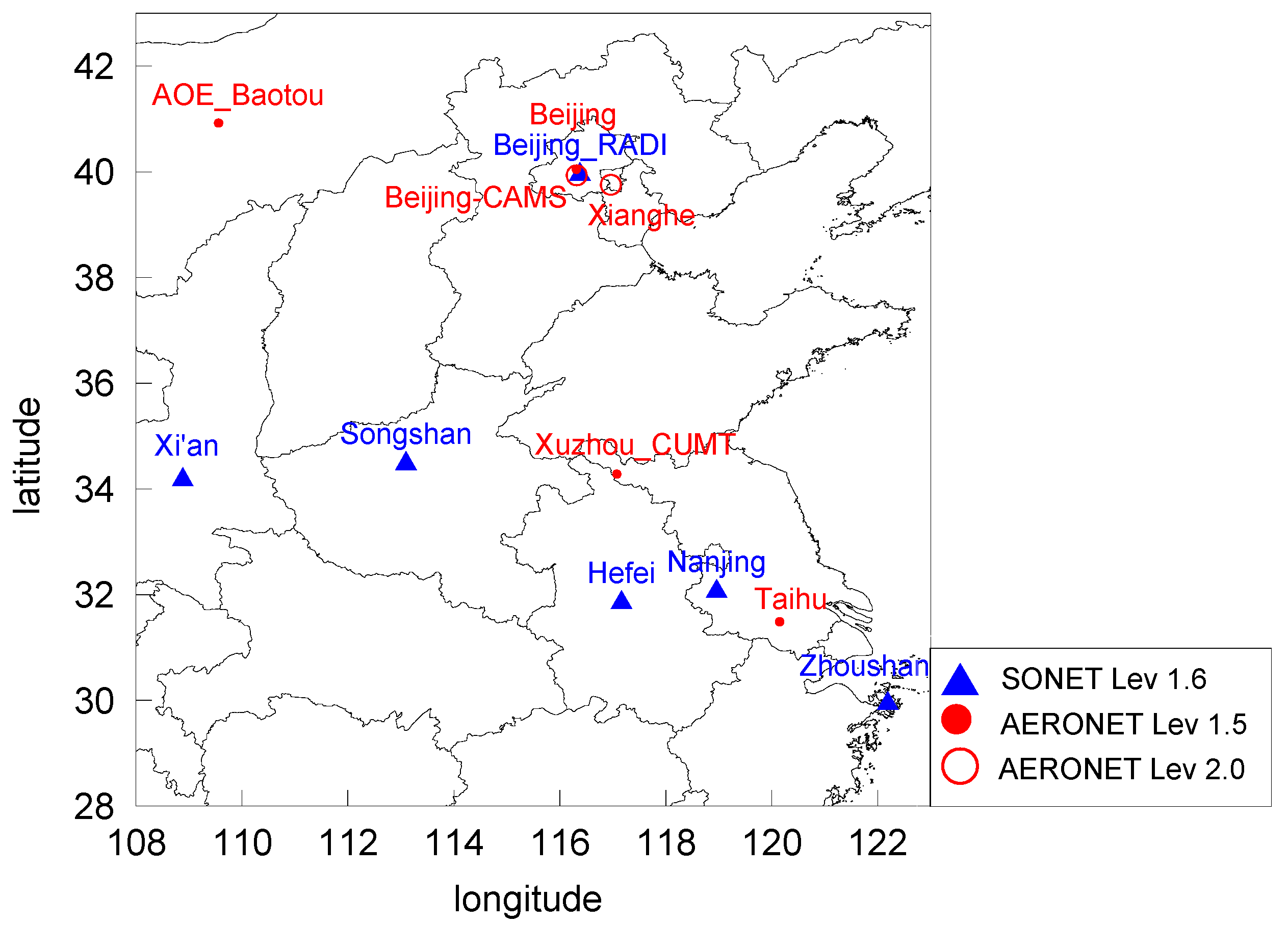
2.4. Data and Study Area
3. Results
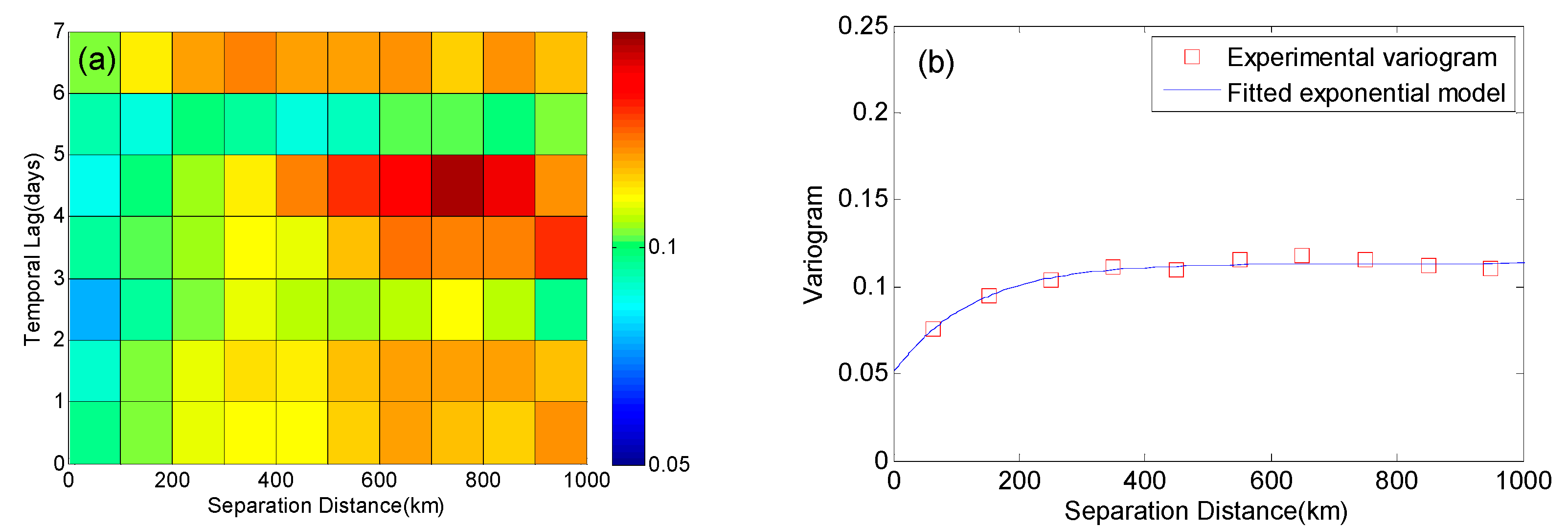
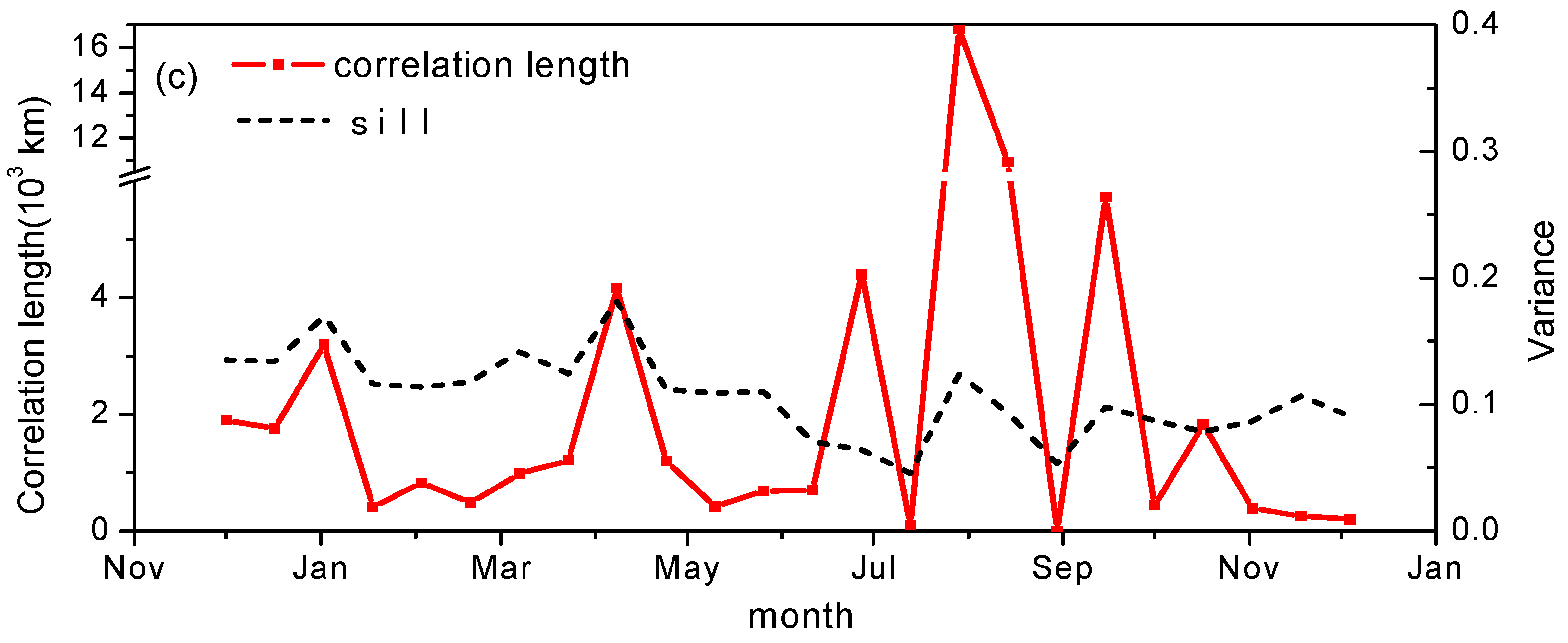
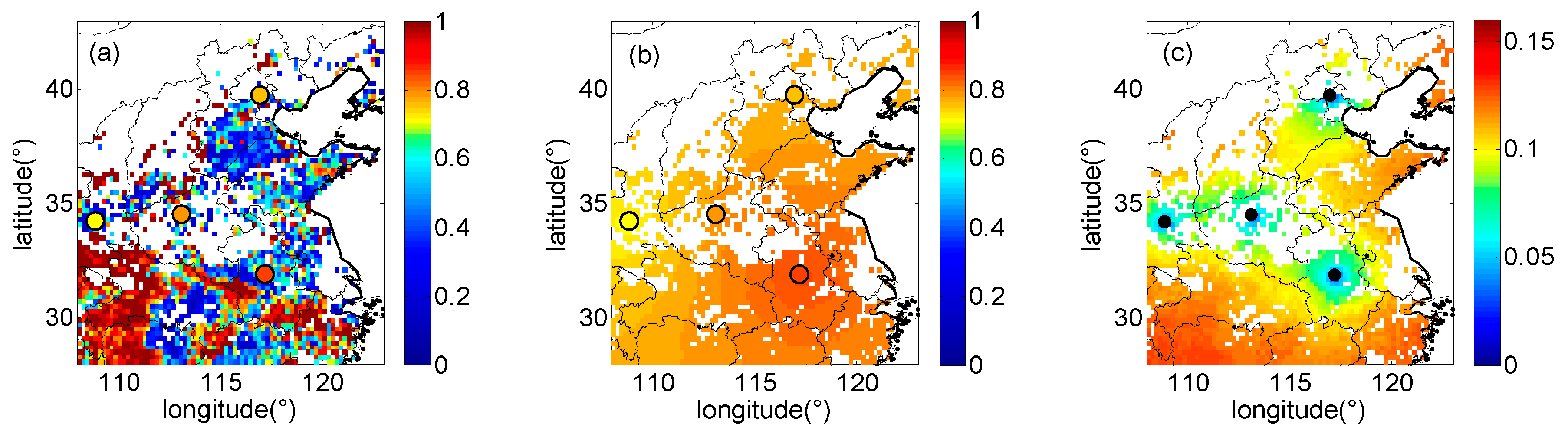
3.1. Spatiotemporal Variability Analysis
3.2. Fusion Results
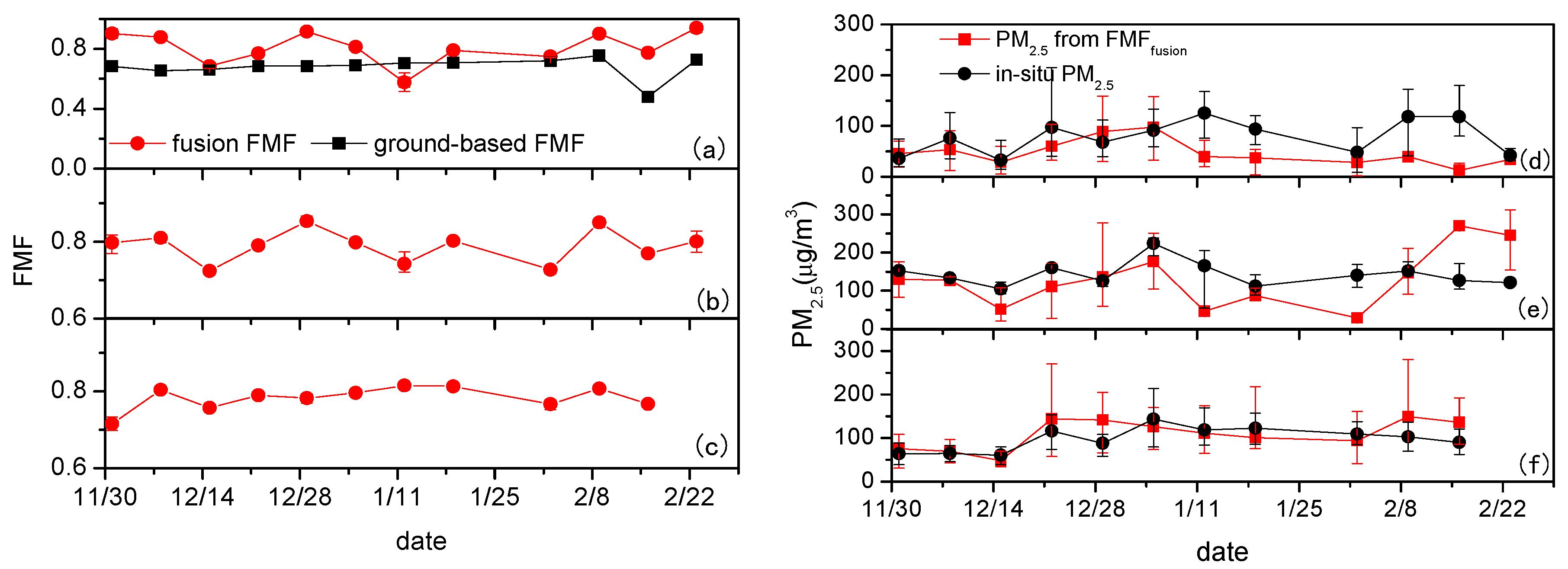
3.2.1. FMF Test Case
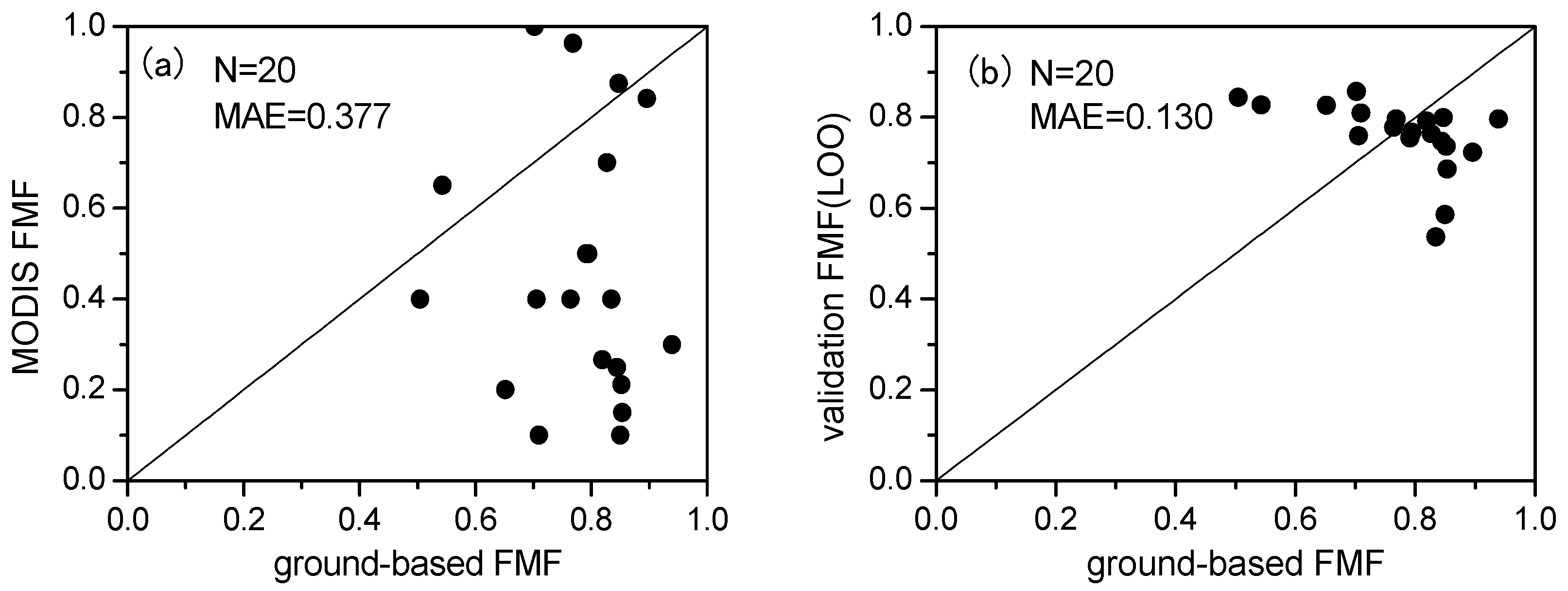
3.2.2. Comparison and Validation
3.3. PM2.5 Results
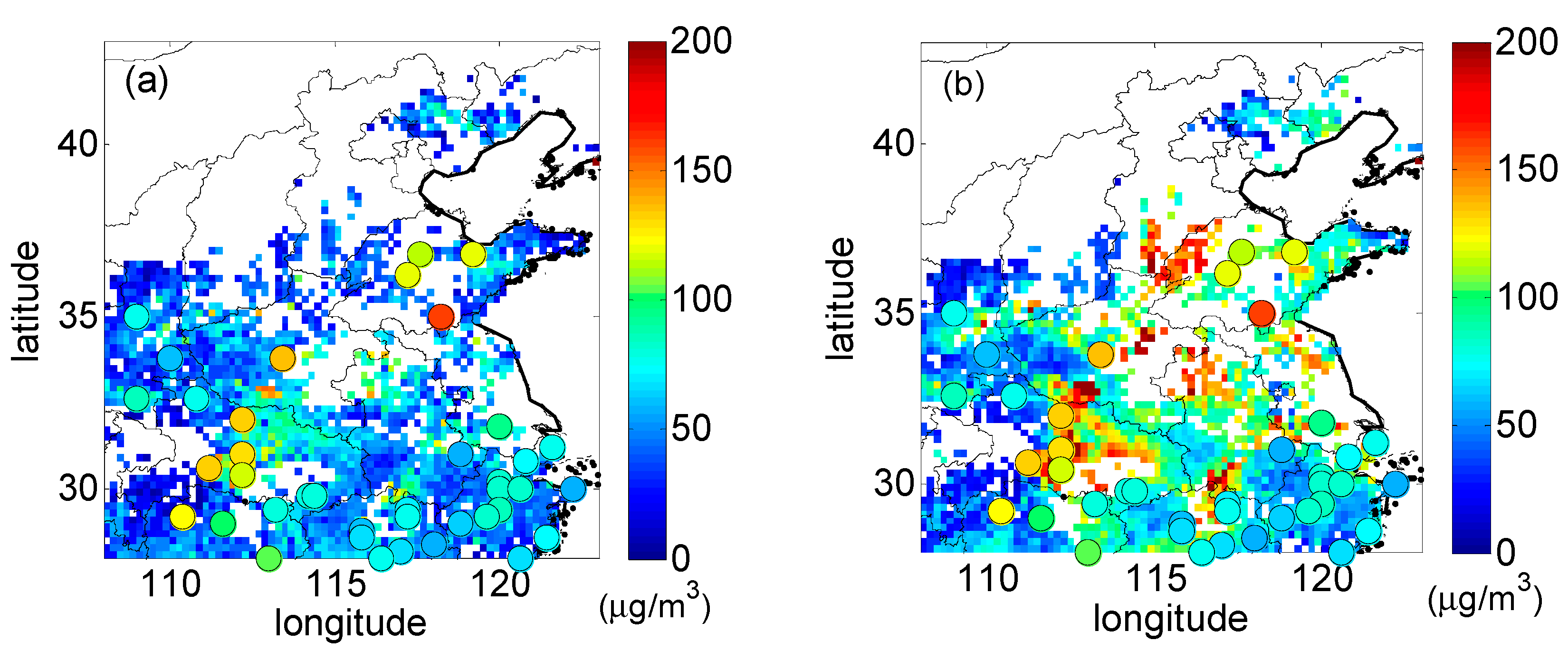
3.3.1. PM2.5 Test Case
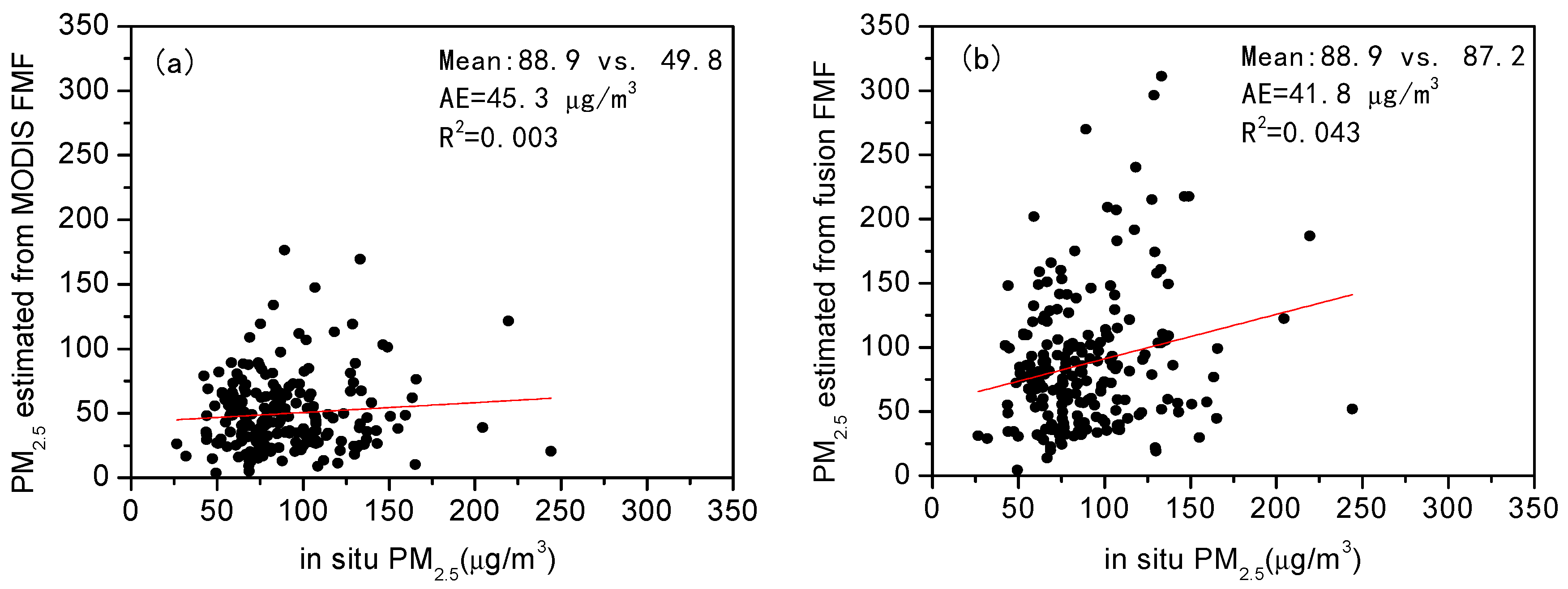
3.3.2. Validation of PM2.5
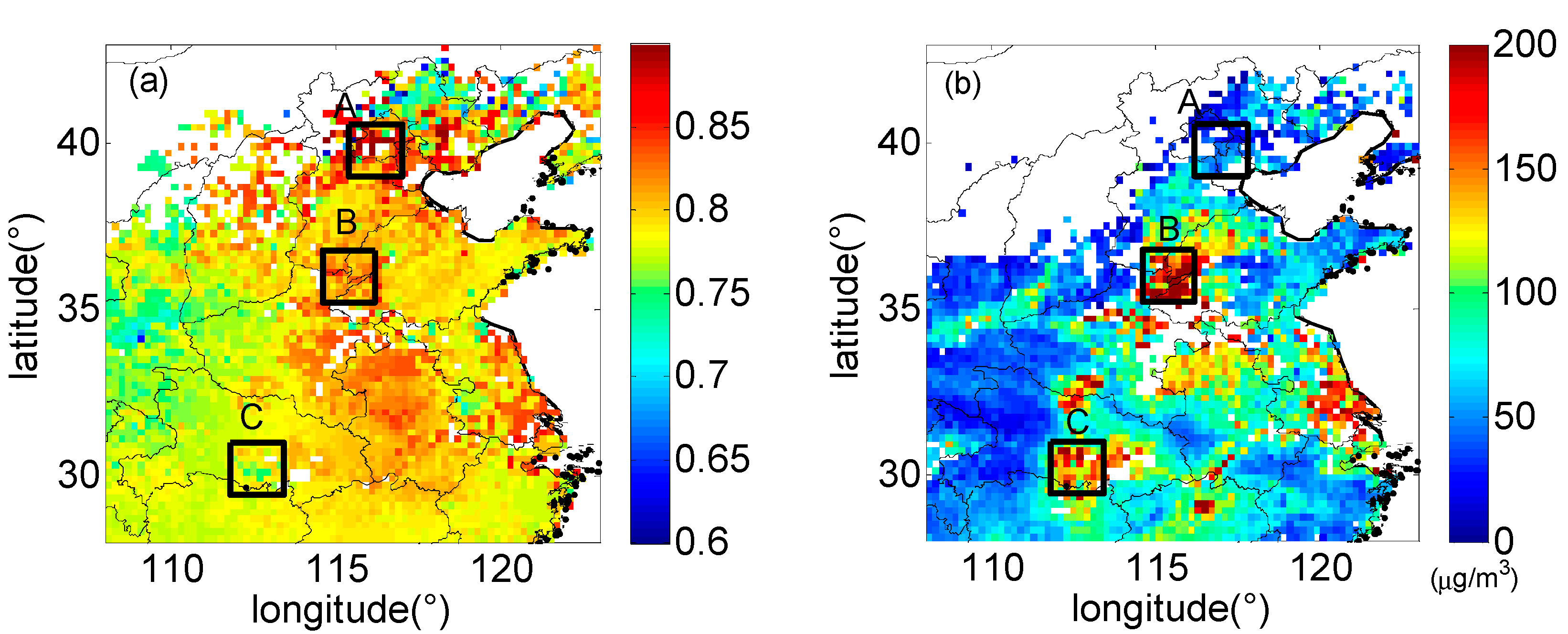
3.4. Spatio-Temporal Characteristics Analysis of FMF and PM2.5
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
A.1. UK Theory in Merging FMF
References
- Pope, C.A.; Burnett, R.T.; Thun, M.J.; Calle, E.E.; Krewski, D.; Ito, K.; Thurston, G.D. Lung cancer, cardiopulmonary mortality, and long-term exposure to fine particulate air pollution. JAMA 2002, 287, 1132–1141. [Google Scholar] [CrossRef]
- Kunzli, N.; Jerrett, M.; Mack, W.J.; Beckerman, B.; LaBree, L.; Gilliland, F.; Thomas, D.; Peters, J.; Hodis, H.N. Ambient air pollution and atherosclerosis in Los Angeles. Environ. Health Perspect. 2005, 113, 201–206. [Google Scholar] [CrossRef] [PubMed]
- Brook, R.D.; Rajagopalan, S.; Pope, C.A.; Brook, J.R.; Bhatnagar, A.; Diez-Roux, A.V.; Holguin, F.; Hong, Y.L.; Luepker, R.V.; Mittleman, M.A.; et al. Particulate matter air pollution and cardiovascular disease an update to the scientific statement from the American heart association. Circulation 2010, 121, 2331–2378. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Paciorek, C.J.; Koutrakis, P. Estimating regional spatial and temporal variability of PM2.5 concentrations using satellite data, meteorology, and land use information. Environ. Health Perspect. 2009, 117, 886–892. [Google Scholar] [CrossRef] [PubMed]
- Paciorek, C.J.; Liu, Y. Limitations of remotely sensed aerosol as a spatial proxy for fine particulate matter. Environ. Health Perspect. 2009, 117, 904–909. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Christopher, S.A. Intercomparison between satellite-derived aerosol optical thickness and PM2.5 mass: Implications for air quality studies. Geophys. Res. Lett. 2003, 30, 4. [Google Scholar] [CrossRef]
- Lee, H.J.; Coull, B.A.; Bell, M.L.; Koutrakis, P. Use of satellite-based aerosol optical depth and spatial clustering to predict ambient PM2.5 concentrations. Environ. Res. 2012, 118, 8–15. [Google Scholar] [CrossRef] [PubMed]
- Hutchison, K.D.; Smith, S.; Faruqui, S.J. Correlating MODIS aerosol optical thickness data with ground-based PM2.5 observations across Texas for use in a real-time air quality prediction system. Atmos. Environ. 2005, 39, 7190–7203. [Google Scholar] [CrossRef]
- Engel-Cox, J.A.; Young, G.S.; Hoff, R.M. Application of satellite remote-sensing data for source analysis of fine particulate matter transport events. J. Air Waste Manag. Assoc. 2005, 55, 1389–1397. [Google Scholar] [CrossRef] [PubMed]
- Drury, E.; Jacob, D.J.; Spurr, R.J.D.; Wang, J.; Shinozuka, Y.; Anderson, B.E.; Clarke, A.D.; Dibb, J.; McNaughton, C.; Weber, R. Synthesis of satellite (MODIS), aircraft (ICARTT), and surface (IMPROVE, EPA-AQS, AERONET) aerosol observations over eastern north America to improve MODIS aerosol retrievals and constrain surface aerosol concentrations and sources. J. Geophys. Res. Atmos. 2010, 115, 17. [Google Scholar] [CrossRef]
- Wang, J.; Xu, X.G.; Spurr, R.; Wang, Y.X.; Drury, E. Improved algorithm for MODIS satellite retrievals of aerosol optical thickness over land in dusty atmosphere: Implications for air quality monitoring in China. Remote Sens. Environ. 2010, 114, 2575–2583. [Google Scholar] [CrossRef]
- Xu, X.G.; Wang, J.; Henze, D.K.; Qu, W.J.; Kopacz, M. Constraints on aerosol sources using GEOS-Chem adjoint and MODIS radiances, and evaluation with multisensor (OMI, MISR) data. J. Geophys. Res. Atmos. 2013, 118, 6396–6413. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.Q. Remote sensing of atmospheric fine particulate matter (PM2.5) mass concentration near the ground from satellite observation. Remote Sens. Environ. 2015, 160, 252–262. [Google Scholar] [CrossRef]
- Xu, H.; Xue, Y.; Guang, J.; Li, Y.; Yang, L.; Hou, T.; He, X.; Dong, J.; Chen, Z. A semi-empirical optical data fusion technique for merging aerosol optical depth over China. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 2524–2527. [Google Scholar]
- Loeb, N.G.; Sun, W.; Miller, W.F.; Loukachine, K.; Davies, R. Fusion of CERES, MISR, and MODIS measurements for top-of-atmosphere radiative flux validation. J. Geophys. Res. Atmos. 2006, 111, D18209. [Google Scholar] [CrossRef]
- Singh, M.K.; Venkatachalam, P. Merging of aerosol optical depth data from multiple remote sensing sensors. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 4173–4175. [Google Scholar]
- Xu, Q.; Obradovic, Z.; Han, B.; Li, Y.; Braverman, A.; Vucetic, S. Improving Aerosol Retrieval Accuracy by Integrating AERONET, MISR and MODIS Data. In Proceedings of the 2015 7th International Conference on Information Fusion, Philadelphia, PA, USA, 25–28 July 2005. [Google Scholar]
- Chatterjee, A.; Michalak, A.M.; Kahn, R.A.; Paradise, S.R.; Braverman, A.J.; Miller, C.E. A geostatistical data fusion technique for merging remote sensing and ground-based observations of aerosol optical thickness. J. Geophys. Res. Atmos. 2010, 115, 12. [Google Scholar] [CrossRef]
- Jinnagara Puttaswamy, S.; Nguyen, H.M.; Braverman, A.; Hu, X.; Liu, Y. Statistical data fusion of multi-sensor AOD over the continental United States. Geocarto Int. 2014, 29, 48–64. [Google Scholar] [CrossRef]
- Guo, J.; Gu, X.; Yu, T.; Cheng, T.; Chen, H.; Xie, D. Trend Analysis of the Aerosol Optical Depth over China Using Fusion of MODIS and MISR Aerosol Products via Adaptive Weighted Estimate Algorithm; IOP Publishing Ltd.: Bristol, UK, 2013; p. 88661X. [Google Scholar]
- Xu, H.; Guang, J.; Xue, Y.; de Leeuw, G.; Che, Y.H.; Guo, J.; He, X.W.; Wang, T.K. A consistent aerosol optical depth (AOD) dataset over mainland China by integration of several aod products. Atmos. Environ. 2015, 114, 48–56. [Google Scholar] [CrossRef]
- Leptoukh, G.; Zubko, V.; Gopalan, A. Spatial Aspects of Multi-Sensor Data Fusion: Aerosol Optical Thickness. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Barcelona, Spain, 23–28 July 2007; Sensing and Understanding Our Planet. IEEE: New York, NY, USA, 2007; Volumes 1–12, pp. 3119–3122. [Google Scholar]
- Nirala, M. Technical note: Multi-sensor data fusion of aerosol optical thickness. Int. J. Remote Sens. 2008, 29, 2127–2136. [Google Scholar] [CrossRef]
- Zubko, V.; Leptoukh, G.G.; Gopalan, A. Study of data-merging and interpolation methods for use in an interactive online analysis system: MODIS Terra and Aqua daily aerosol case. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4219–4235. [Google Scholar] [CrossRef]
- Li, L.; Shi, R.; Zhang, L.; Zhang, J.; Gao, W. The Data Fusion of Aerosol Optical Thickness Using Universal Kriging and Stepwise Regression in East China. In Proceedings of SPIE; International Society for Optics and Photonics: San Diego, CA, USA, 2014; p. 922112. [Google Scholar]
- Nguyen, H.; Cressie, N.; Braverman, A. Spatial statistical data fusion for remote sensing applications. J. Am. Stat. Assoc. 2012, 107, 1004–1018. [Google Scholar] [CrossRef]
- Yang, G.; Zhang, G.; Li, S. Application of universal kriging interpolation in geomagnetic map. J. Chin. Inert. Technol. 2008, 8, 162–166. [Google Scholar]
- O’Neill, N.T.; Dubovik, O.; Eck, T.F. Modified Ångström exponent for the characterization of submicrometer aerosols. Appl. Opt. 2001, 40, 2368–2375. [Google Scholar] [CrossRef] [PubMed]
- O’Neill, N.T.; Eck, T.F.; Holben, B.N.; Smirnov, A.; Dubovik, O.; Royer, A. Bimodal size distribution influences on the variation of Ångström derivatives in spectral and optical depth space. J. Geophys. Res. Atmos. 2001, 106, 9787–9806. [Google Scholar] [CrossRef]
- O’Neill, N.T.; Eck, T.F.; Holben, B.N.; Smirnov, A.; Royer, A.; Li, Z. Optical properties of boreal forest fire smoke derived from sun photometry. J. Geophys. Res. Atmos. 2002, 107, 21. [Google Scholar] [CrossRef]
- O’Neill, N.T.; Eck, T.F.; Smirnov, A.; Holben, B.N.; Thulasiraman, S. Spectral discrimination of coarse and fine mode optical depth. J. Geophys. Res. Atmos. 2003, 108, 15. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.Q.; Wang, Y.; Li, K.T.; Li, D.H.; Zhang, Y.H.; Wei, P.; Wang, L.; Lu, Y. Improving accumulation-mode fraction based on spectral aerosol optical depth in Beijing. Spectrosc. Spectr. Anal. 2013, 33, 2795–2802. [Google Scholar]
- Armstrong, M. Problems with universal kriging. J. Int. Assoc. Math. Geol. 1984, 16, 101–108. [Google Scholar] [CrossRef]
- Stein, A.; Corsten, L.C.A. Universal kriging and cokriging as a regression procedure. Biometrics 1991, 47, 575–587. [Google Scholar] [CrossRef]
- Yan, H. The Development and Implementation of Spatial Interpolation Technology. Master’s Thesis, Southwest Petroleum University, Chengdu, China, April 2005. [Google Scholar]
- Levy, R.C.; Remer, L.A.; Tanré́, D.; Mattoo, S.; Kaufman, Y.J. Algorithm for Remote Sensing of Tropospheric Aerosol over Dark Targets from MODIS: Collections 005 and 051: Revision 2. 2009. Available online: http://modis.gsfc.nasa.gov/data/atbd/atbd_mod02.pdf (accessed on 3 July 2017).
- Holben, B.N.; Eck, T.F.; Slutsker, I.; Tanre, D.; Buis, J.P.; Setzer, A.; Vermote, E.; Reagan, J.A.; Kaufman, Y.J.; Nakajima, T.; et al. AERONET—A federated instrument network and data archive for aerosol characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
- Holben, B.N.; Tanre, D.; Smirnov, A.; Eck, T.F.; Slutsker, I.; Abuhassan, N.; Newcomb, W.W.; Schafer, J.S.; Chatenet, B.; Lavenu, F.; et al. An emerging ground-based aerosol climatology: Aerosol optical depth from AERONET. J. Geophys. Res. Atmos. 2001, 106, 12067–12097. [Google Scholar] [CrossRef]
- Li, Z.; Li, D.; Li, K.; Xu, H.; Chen, X.; Chen, C.; Xie, Y.; Li, L.; Li, L.; Li, W. A sun/sky-radiometer observation network with the extension of multi-wavelength polarization measurements. J. Remote Sens. 2015, 19, 495–519. [Google Scholar]
- Xie, Y.S.; Li, Z.Q.; Li, D.H.; Xu, H.; Li, K.T. Aerosol optical and microphysical properties of four typical sites of SONET in china based on remote sensing measurements. Remote Sens. 2015, 7, 9928–9953. [Google Scholar] [CrossRef]
- Li, Z.; Gu, X.; Wang, L.; Li, D.; Xie, Y.; Li, K.; Dubovik, O.; Schuster, G.; Goloub, P.; Zhang, Y.; et al. Aerosol physical and chemical properties retrieved from ground-based remote sensing measurements during heavy haze days in Beijing winter. Atmos. Chem. Phys. 2013, 13, 10171–10183. [Google Scholar] [CrossRef]
- National Centers for Environmental Prediction/National Weather Service/NOAA/U.S. Department of Commerce. 2000, updated daily. NCEP FNL Operational Model Global Tropospheric Analyses, continuing from July 1999. Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory. Available online: https://rda.ucar.edu/datasets/ds083.2/ (accessed on 30 July 1999).
| Type | rf/μm | rc/μm | lnσf | lnσc | Cf/Cc | n | k | FMFv |
|---|---|---|---|---|---|---|---|---|
| WS | 0.118 | 1.17 | 0.6 | 0.6 | 2 | 1.45 | 0.0035 | 0.65 |
| BB | 0.132 | 4.50 | 0.4 | 0.6 | 4 | 1.52 | 0.025 | 0.80 |
| DU | 0.100 | 3.40 | 0.6 | 0.8 | 0.066 | 1.53 | 0.008 | 0.06 |
| Type | FMF(MODIS) | FMF(SDA) | Error(MODIS-SDA) |
|---|---|---|---|
| WS | 0.82 | 0.78 | 0.04 |
| BB | 0.98 | 0.95 | 0.03 |
| DU | 0.31 | 0.32 | 0.01 |
| Value | Ground-Based FMF | MODIS FMF | FMF (LOO) | Δ (MODIS) | Δ (LOO) |
|---|---|---|---|---|---|
| Maximum | 0.94 | 1.00 | 0.86 | 0.75 | 0.34 |
| Minimum | 0.50 | 0.10 | 0.54 | 0.03 | 0.01 |
| Mean | 0.77 | 0.46 | 0.76 | 0.38 | 0.13 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, A.; Li, Z.; Zhang, Y.; Zhang, Y.; Li, D. Merging MODIS and Ground-Based Fine Mode Fraction of Aerosols Based on the Geostatistical Data Fusion Method. Atmosphere 2017, 8, 117. https://doi.org/10.3390/atmos8070117
Zhao A, Li Z, Zhang Y, Zhang Y, Li D. Merging MODIS and Ground-Based Fine Mode Fraction of Aerosols Based on the Geostatistical Data Fusion Method. Atmosphere. 2017; 8(7):117. https://doi.org/10.3390/atmos8070117
Chicago/Turabian StyleZhao, Aimei, Zhengqiang Li, Ying Zhang, Yang Zhang, and Donghui Li. 2017. "Merging MODIS and Ground-Based Fine Mode Fraction of Aerosols Based on the Geostatistical Data Fusion Method" Atmosphere 8, no. 7: 117. https://doi.org/10.3390/atmos8070117
APA StyleZhao, A., Li, Z., Zhang, Y., Zhang, Y., & Li, D. (2017). Merging MODIS and Ground-Based Fine Mode Fraction of Aerosols Based on the Geostatistical Data Fusion Method. Atmosphere, 8(7), 117. https://doi.org/10.3390/atmos8070117







