Evaluation and Parameter Optimization of Monthly Net Long-Wave Radiation Climatology Methods in China

Abstract

Based on surface radiation balance data and meteorological observations at 19 radiation stations in China from 1993 to 2012, we assessed the applicability of seven empirical formulas for the estimation of monthly surface net long-wave radiation (R_nl). We then established a revised method applicable to China by re-fitting the formula using new observational data. The iterative solution method and the multivariate regression analysis method with the minimum root mean square error (RMSE) were used as the objective functions in the revised method. Meanwhile, the accuracy of the CERES (Clouds and the Earth’s Radiant Energy System) estimated R_nl was also evaluated. Results show that monthly R_nl over China was underestimated by the seven formulas and the CERES data. The Tong Hongliang formula with lowest errors was the best among the seven formulas for estimating R_nl over China as a whole, followed by the Penman and the Deng Genyun formulas. The estimated R_nl based on the CERES data also showed relatively higher precision in accordance with the three formulas mentioned above. The FAO56-PM formula (Penman–Monteith formula recommended in the No. 56 report of the Food and Agriculture Organization) without calibration was not applicable to China due to its low accuracy. For individual stations, the Deng Genyun formula was the most accurate in the eastern plain area, while the Tong Hongliang formula was suitable for the plateau. Regional formulas were established based on the geographical distribution of water vapor pressure and elevation over China. The revised national and regional formulas were more accurate than the seven original formulas and the CERES data. Furthermore, the regional formulas produced smaller errors than the national formula at most of the stations. The regional formulas were clearly more accurate than the Deng Genyun formula at stations in Northwestern China and on the Tibetan Plateau. They were also more accurate than the Tong Hongliang formula at the stations located in the eastern area. Therefore, the regional formulas developed in this study are recommended as the standard climatology formulas to calculate monthly R_nl over China.

1. Introduction

Surface net long-wave radiation (R_nl) represents the difference between the upward long-wave radiation emitted from the surface and the downward long-wave radiation from the atmosphere [1]. It is the quantity of heat loss from the ground surface through R_nl exchange [2]. R_nl is one of the important components to the Earth’s surface radiation balance, and the energy exchange between the ground and the atmosphere. Knowing R_nl is necessary for many meteorological studies, e.g., the forecasting of diurnal temperature variations, minimum air temperatures, nocturnal frosts, and fog [3]. Compared with other components of the radiation balance, although R_nl is difficult to observe directly, which is mainly limited by the lack of sophisticated instrumentation, it still can be determined from components of the radiation balance observations using the surface radiation balance equation at a radiation station [2]. However, the stations with complete radiation balance observations are relatively rare, thus, large-scale and long-term R_nl is difficult to obtain in China. Using empirical or semi-empirical radiation formulas, estimating R_nl could complement the above limits of R_nl in time and space. Empirical formulas are the simplest methods to estimate R_nl, compared with, e.g., remote sensing, linear interpolation, and neural networks [4]. The estimated R_nl can be applied in several fields, such as calculating evapotranspiration.

The surface net long-wave radiation is influenced by surface temperature, air temperature, water vapor pressure, and cloud cover. Many different empirical or semi-empirical formulas have been proposed for R_nl using routine observations of these meteorological factors. The formula of Angstrom [5] estimated R_nl from air temperature, water vapor pressure, and cloud cover. From the 1930s to the 1950s, cloud cover was replaced by relative sunshine duration in the formulas of Brunt [6], Bepлянд [7], and Penman [8]. The formulas of Swinbank [9] and Idso [10] were based on air temperature and cloud cover. The Food and Agriculture Organization (FAO) of the United Nations proposed a revised formula based on the Penman method in the Irrigation and Drainage Papers No. 24 [11] (hereafter FAO24) and No. 56 [12] (hereafter FAO56-PM). The FAO56-PM formula has been applied extensively and globally. The accuracy of the common net long-wave radiation equations adopted in Penman-type evapotranspiration formulas was examined in Japan based on observations [13,14]. Regional formulas were established separately for plains and plateaus in China by Tong using measured air temperature, sunshine duration, and water vapor pressure [15]. The Penman method was improved by Deng based on observed data at the Beijing Radiation Station in China [16]. Formulas to estimate R_nl on the Tibetan Plateau were provided by Ji et al. [17] and Li et al. [18]. The variation characteristics and empirical formulas for estimating the net long-wave radiation flux over the oceans were also studied [19,20,21,22,23,24].

In recent years, less attention has been paid to the climatological estimation of R_nl compared with that of solar radiation. Furthermore, the empirical or semi-empirical formulas for R_nl have been rarely studied because of the lack of measured values, and the FAO56-PM formula has been applied in most studies over China [25,26,27,28,29,30,31,32,33] without calibration. However, the parameterization schemes of existing formulas characterized the atmospheric and surface conditions of certain spaces and periods, and are probably not appropriate to China based on the new observations. Thus, due to climate change and regional specificity, calibration must be carried out to improve empirical coefficients to estimate R_nl more accurately in China. Where measurements of the surface radiation balance are available, calibration of R_nl can be conducted. The objective of this study was to assess the applicability of the existing seven empirical formulas for estimating R_nl and make a regional calibration using radiation measurements over China to improve the performance of the method for estimating R_nl in China. The satellite estimated datasets of long-wave radiation of the Clouds and Earth’s Radiant Energy System (CERES) have been widely used in various applications. The accuracy of the surface net long-wave radiation fluxes from CERES Energy Balanced And Filled (EBAF)-Surface Edition 2.8 (National Aeronautics and Space Administration, Washington, DC, USA) is also evaluated along with others from the seven formulas mentioned above.

2. Data and Methods

2.1. Data

High-quality monthly observations of net radiation, solar radiation, reflected radiation, maximum and minimum air temperature, water vapor pressure, and sunshine duration were collected at 19 radiation stations in China during 1993–2012 (

Table 1. Radiation stations used in the study.

No.	Station	Latitude (°N)	Longitude (°E)	Elevation (m)	Observed Period	Standard Rnl (W/m2)
1	Beijing	39.80	116.47	31.3	1993–2012	76.0
2	Chengdu	30.67	104.02	506.1	1993–2003	40.4
3	Ejin Banner	41.95	101.07	940.5	1993–2012	121.5
4	Golmud	36.42	94.92	2807.6	1993–2012	106.4
5	Guangzhou	23.22	113.48	70.7	1993–2012	44.7
6	Harbin	45.75	126.77	142.3	1993–2012	73.9
7	Kashgar	39.47	75.98	1289.4	1993–2012	90.8
8	Kunming	25.00	102.65	1888.1	1993–2012	71.2
9	Lanzhou	36.05	103.88	1517.2	1993–2004	81.0
10	Lhasa	29.67	91.13	3648.9	1993–2012	116.1
11	Mohe	52.97	122.52	433.0	1993–2012	65.3
12	Sanya	18.22	109.58	419.4	1993–2012	64.6
13	Shanghai	31.40	121.45	5.5	1993–2012	55.0
14	Shenyang	41.73	123.52	49.0	1993–2012	74.0
15	Urumuqi	43.78	87.65	935.0	1993–2012	85.1
16	Wenjiang	30.75	103.87	547.7	2004–2012	40.3
17	Wuhan	30.60	114.05	23.6	1993–2012	48.6
18	Yuzhong	35.87	104.15	1874.4	2005–2012	86.9
19	Zhengzhou	34.72	113.65	110.4	1993–2012	64.2

). The 19 stations are nearly uniformly distributed across the whole country (Figure 1). The radiation data were measured using automatic thermoelectric pyranometers. The observed data, latitude, longitude, and elevation of the stations were provided by the National Meteorological Information Center (NMIC) of the China Meteorological Administration (CMA). Radiation and meteorological measurements made at the stations were carefully checked using quality control procedures, and quality control flags were supplied with the data by NMIC. In order to ensure the veracity of the evaluation, 4.56% of the total samples were removed if the radiation observation is missing. Some missing meteorological data were estimated by averaging the observed values over 1993–2012 at the same station.

As one of the highest priority scientific satellite instruments developed for NASA’s Earth Observing System (EOS), CERES sensors were placed onboard the Terra and Aqua satellites. EBAF-Surface Ed 2.8 is one of the CERES products, which provides monthly and climatological averages of computed fluxes of the Earth’s surface. CERES EBAF-Surface Ed 2.8 data of surface net long-wave radiation are available online from the CERES website [34]. The CERES data products use meteorological assimilation data from the Goddard Earth Observing System (GEOS-4 and 5) Data Assimilation System reanalysis to characterize the atmospheric state. GEOS-4 was used from March 2000 through December 2007, and GEOS-5 was used beginning in January 2008. The CERES EBAF-Surface Ed 2.8 data during the period of March 2000 to December 2012 were interpolated into the station points listed in Table 1 by bi-linear interpolation, so they could be compared with the standard R_nl over China.

Observations of the surface energy balance in China were initiated at the radiation stations in January 1993, however, observations of the R_nl were not made at that time. R_nl at a radiation station can be determined from components of the radiation balance observations using the surface radiation balance equation:

$$R_{\mathrm{nl}}=R_{\mathrm{s}}-R_{\mathrm{k}}-R_{\mathrm{n}}$$

(1)

where R_n is the net radiation, R_s is the solar radiation, R_k is the reflected radiation, and R_nl is the net long-wave radiation. R_s represents the incoming radiation energy, and R_k and R_nl are the short-wave and long-wave radiation energy loss, respectively. R_n, R_s, and R_k have been measured using automatic thermoelectric pyranometers in China since January 1993.

From Equation (1), we obtained monthly R_nl values based on the observations of R_n, R_s, and R_k at the 19 solar radiation stations from 1993 to 2012 as a standard to assess the applicability of the existing seven empirical formulas for computing R_nl, and to establish an optimum net long-wave radiation formula for China. Mean annual values of monthly standard R_nl for each station are listed in Table 1. The values of monthly standard R_nl ranged from 40.3 to 121.5 W/m² at the 19 stations. R_nl decreased, in general, from Southeast to Northwest China. Lower R_nl occurred in Sichuan Province (Chengdu and Wenjiang), and higher values occurred on the Tibetan Plateau (Golmud and Lhasa) and the northwestern part of Inner Mongolia (Ejin Banner). The range of values and the spatial distribution were similar to some previous studies [35,36,37] and NCEP (National Centers for Environmental Prediction) reanalysis data. Meanwhile, as shown in Table 1, the standard R_nl increased with the station altitude, especially when the altitude above 1000 m. The evolution of standard R_nl at some stations (e.g., Beijing and Ejin Banner) was shown in Figure 2, and it can be seen that the values increased during spring, reaching a maximum in summertime and a minimum in winter. Monthly minimum R_nl varied between 0 and 50.0 W/m², and the maximum values were between 200.0 and 250.0 W/m². The standard R_nl at Lhasa station, which were 116.4, 85.8, and 78.7 W/m² from June to August, respectively, agreed with the measured values of the first and second Tibetan Plateau Meteorology Scientific Experiment [38,39]. The standard R_nl at Wuhan station was 48.6 W/m², similar to that at the nearby Shouxian station, where the observed values were supported by the Atmospheric Radiation Measurement (ARM) Program. These comparisons showed that the standard monthly R_nl determined from the components of the radiation balance observations using the surface radiation balance equation were credible. In addition, this method was widely applied to calculate R_nl as a standard to establish a climatology formula and temporal-spatial distribution analysis in several studies [15,36,39,40,41] due to the lack of directly-observed data. This confirmed that the R_nl obtained in this study can be applied as the standard for the parameter evaluation and modification of the R_nl climatology formula.

2.2. Methods

2.2.1. Empirical Formulas

We tested the application of the seven existing empirical formulas for computing the monthly surface net long-wave radiation (R_nl). The magnitude of R_nl is influenced by air temperature, surface temperature, humidity, and cloud cover [42]. These formulas were derived on a physical basis and obtained by empirical correlations, and the R_nl was estimated from maximum and minimum air temperature, water vapor pressure, and relative sunshine duration. R_nl can be estimated using the following equation:

$$R_{\mathrm{nl}}=\sigma \left(\frac{{T_{\min }}^4+{T_{\max }}^4}{2}\right)\left(a_0+a_1\sqrt{e_{\mathrm{a}}}\right)\left(b_0+(1-b_0)\frac{n_{\mathrm{s}}}{N_{\mathrm{s}}}\right)$$

(2)

where R_nl is the net long-wave radiation (W/m²), σ is the Stefan–Boltzmann constant (5.67 × 10⁻⁸ W/(K⁴∙m²)), T_min is the minimum absolute temperature (K), T_max is the maximum absolute temperature (K), e_a is the water vapor pressure (kPa), n_s is the actual sunshine duration (hour), N_s is the maximum possible sunshine duration (hour), n_s/N_s is the relative sunshine duration, and a₀, a₁ (kPa⁻¹), and b₀ are the coefficients of the parameterization schemes. N_s was calculated based on latitude, elevation, and the number of the day of the year according to the FAO56 report [12].

In this study, the seven common formulas (

Table 2. The seven common formulas to calculate monthly net long-wave radiation.

Formulas		Equations	No.
Brunt		$R_{\mathrm{nl}}=\sigma \left(\frac{{T_{\min }}^4+{T_{\max }}^4}{2}\right)\left(0.56-0.291\sqrt{e_{\mathrm{a}}}\right)\left(0.1+0.9\frac{n_{\mathrm{s}}}{N_{\mathrm{s}}}\right)$	(3)
Penman		$R_{\mathrm{nl}}=\sigma \left(\frac{{T_{\min }}^4+{T_{\max }}^4}{2}\right)\left(0.56-0.250\sqrt{e_{\mathrm{a}}}\right)\left(0.1+0.9\frac{n_{\mathrm{s}}}{N_{\mathrm{s}}}\right)$	(4)
Bepлянд		$R_{\mathrm{nl}}=\sigma \left(\frac{{T_{\min }}^4+{T_{\max }}^4}{2}\right)\left(0.39-0.183\sqrt{e_{\mathrm{a}}}\right)\left(0.1+0.9\frac{n_{\mathrm{s}}}{N_{\mathrm{s}}}\right)$	(5)
FAO24		$R_{\mathrm{nl}}=\sigma \left(\frac{{T_{\min }}^4+{T_{\max }}^4}{2}\right)\left(0.34-0.139\sqrt{e_{\mathrm{a}}}\right)\left(0.1+0.9\frac{n_{\mathrm{s}}}{N_{\mathrm{s}}}\right)$	(6)
FAO56-PM		$R_{\mathrm{nl}}=\sigma \left(\frac{{T_{\min }}^4+{T_{\max }}^4}{2}\right)\left(0.34-0.139\sqrt{e_{\mathrm{a}}}\right)\left(1.35\frac{R_s}{R_{so}}-0.35\right)$	(7)
Deng Genyun		$R_{\mathrm{nl}}=\sigma \left(\frac{{T_{\min }}^4+{T_{\max }}^4}{2}\right)\left(0.32-0.082\sqrt{e_{\mathrm{a}}}\right)\left(0.3+0.7\frac{n_{\mathrm{s}}}{N_{\mathrm{s}}}\right)$	(8)
Tong Hongliang	Plain	$R_{\mathrm{nl}}=\sigma \left(\frac{{T_{\min }}^4+{T_{\max }}^4}{2}\right)\left(0.32-0.093\sqrt{W_{\infty }}\right)\left(0.43+0.57\frac{n_{\mathrm{s}}}{N_{\mathrm{s}}}\right)$	(9)
	Plateau	$R_{\mathrm{nl}}=\sigma \left(\frac{{T_{\min }}^4+{T_{\max }}^4}{2}\right)\left(0.304-0.021\sqrt{W_{\infty }}\right)\left(0.1+0.9\frac{n_{\mathrm{s}}}{N_{\mathrm{s}}}\right)\exp (0.00012z)$	(10)
		$W_{\infty }=(0.1054+1.513e_{\mathrm{a}})\exp (0.00006z)$	(11)

R_nl, σ, T_min, T_max, e_a, n_s, and N_s represent the same factors and constants as above. R_s is the solar radiation, R_so is the clear-sky solar radiation, and R_s and R_so in the FAO56-PM formula were calculated according to the FAO56 report [12]. W_∞ is the atmospheric moisture content calculated based on e_a and z using Equation (11). Z is the elevation (m).

) to estimate R_nl were collected from Brunt [6], Penman [8], Bepлянд [7], FAO24 [11], FAO56-PM [12], Deng Genyun [16], and Tong Hongliang [15]. The unit of e_a was converted to kPa, and the minimum and maximum temperatures were used for comparison.

2.2.2. Analytical Methods

The performance of the existing and refitted formulas reported here was judged based on the correlation coefficient (R), mean bias error (MBE), mean absolute bias error (MABE), mean absolute percentage error (MAPE), and root mean square error (RMSE) between the estimates and the standard values. The MBE reflects the estimation error, where a positive value means a higher estimate and a negative value means a lower estimate, and a smaller absolute MBE indicates a more accurate method [43,44,45]. RMSE reflects the estimated sensitivity and extreme effects of samples, with smaller values indicating better accuracy [46]. MBE, MABE, MAPE, and RMSE are calculated by:

$$\mathrm{MBE}=\frac{{\displaystyle \sum _{i=1}^n\left(y_i-x_i\right)}}{n}$$

(12)

$$\mathrm{MABE}=\frac{{\displaystyle \sum _{i=1}^n\left|y_i-x_i\right|}}{n}$$

(13)

$$\mathrm{MAPE}=\frac{{\displaystyle \sum _{i=1}^n\left(\left|\frac{y_i-x_i}{x_i}\right|\times 100\%\right)}}{n}$$

(14)

$$\mathrm{RMSE}=\sqrt{\frac{{\displaystyle \sum _{i=1}^n{\left(y_i-x_i\right)}^2}}{n}}$$

(15)

where x_i is the observation or standard value; y_i is the estimate; and n is the number of samples. For the amount of data in this study, 3894 monthly values of radiation and climate factors based on surface observations and 2459 monthly values of CERES EBAF-Surface Ed 2.8 R_nl data were used.

3. Results and Discussion

3.1. Assessment of the Existing R_nl Empirical Formulas

Based on the observed data during 1993–2012, the monthly R_nl at the 19 solar radiation stations in China was calculated using the seven formulas listed in Table 2. The average standard R_nl of the 19 stations was 75.4 W/m². The average estimated R_nl based on the Penman, Deng Genyun, and Tong Hongliang formulas and CERES data were 69.1, 61.0, 65.4 and 64.6 W/m², respectively. They were much closer to the average standard R_nl than those based on the other four formulas; Brunt, Bepлянд, FAO24, and FAO56-PM formulas produced estimated R_nl values of 60.3, 46.1, 44.7, and 42.6 W/m², respectively. 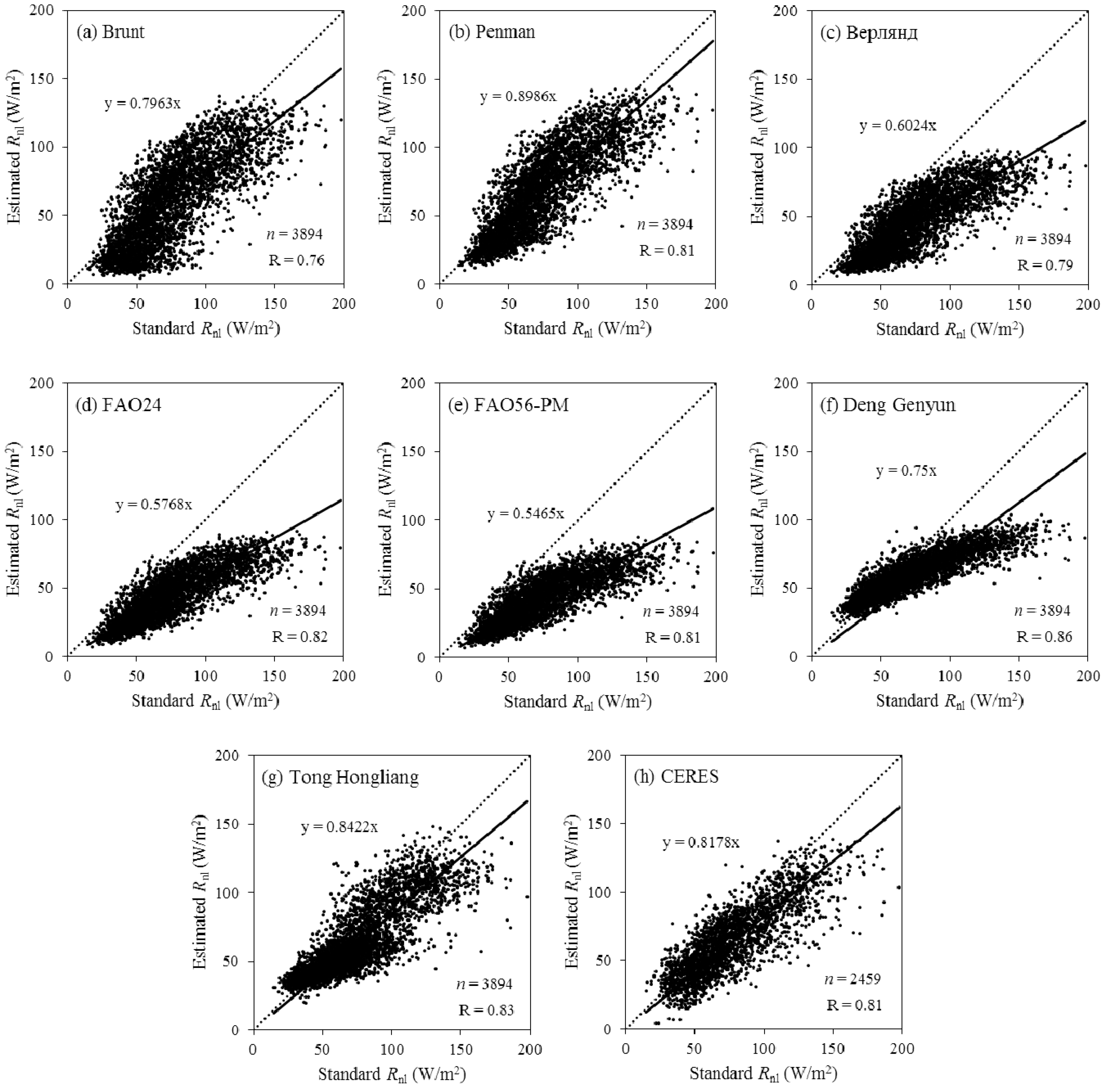We also compared the R, MBE, MABE, MAPE, and RMSE of the standard and estimated R_nl based on the seven tested formulas, as well as CERES data for the 19 stations (Figure 3 and

Table 3. Comparison of the standard and estimated monthly net long-wave radiation based on the seven existing empirical formulas and CERES data.

Formulas	R	MBE (W/m2)	MABE (W/m2)	MAPE (%)	RMSE (W/m2)
Brunt	0.762	–15.152	21.061	30.266	26.420
Penman	0.809	–6.280	15.662	22.068	19.972
Bepлянд	0.795	–29.302	29.707	39.294	34.967
FAO24	0.817	–30.733	30.913	39.826	36.116
FAO56-PM	0.809	–32.771	32.904	42.078	38.426
Deng Genyun	0.860	–14.441	17.871	20.965	24.606
Tong Hongliang	0.827	–10.027	15.107	19.562	20.092
CERES	0.814	–11.941	16.454	21.819	21.612

). This showed that the R_nl based on the empirical coefficients recommended in the Deng Genyun formula had the highest R compared with the standard values (Figure 3f), followed by the Tong Hongliang formula (Figure 3g). The R_nl based on the Brunt formula had the lowest R (Figure 3a). The MBE of the estimated R_nl was negative for the seven formulas and CERES data, suggesting that R_nl was underestimated by all of the formulas. In particular, the Bepлянд, FAO24, and FAO56-PM simulations were much lower than the standard values for most of the samples (Figure 3c–e) compared with those of the other four formulas.

In general, the Tong Hongliang formula had the highest accuracy with the lowest MABE, MAPE, and RMSE among the seven empirical formulas for estimating monthly R_nl over the whole of China, followed by the Penman and the Deng Genyun formulas. The estimated R_nl based on the CERES data also showed relatively higher precision in accordance with these three formulas mentioned above. The FAO56-PM formula with the lowest accuracy was not applicable to China. These results agreed with the research of Yin et al. [47]. For individual stations, the accuracy of the Deng Genyun formula was the highest on the eastern plains. Compared with the other six formulas, the Deng Genyun formula had the lowest MABE, MAPE, and RMSE at nine stations, including Beijing, Chengdu, Harbin, Mohe, Sanya, Shanghai, Shenyang, Wenjiang, and Zhengzhou (

Table 4. Order of formula precisions for calculating the monthly net long-wave radiation at nineteen radiation stations in China.

	Order	1	2	3	4	5	6	7
Station
Beijing		Deng	Penman	Tong	Brunt	Bepлянд	FAO24	FAO56
Chengdu		Deng	Tong	Penman	Brunt	FAO24	FAO56	Bepлянд
Ejin Banner		Penman	Brunt	Tong	Deng	Bepлянд	FAO24	FAO56
Golmud		Tong	Penman	Brunt	Deng	Bepлянд	FAO24	FAO56
Guangzhou		Tong	Deng	Penman	FAO24	FAO56	Brunt	Bepлянд
Harbin		Deng	Penman	Tong	Brunt	Bepлянд	FAO24	FAO56
Kashgar		Tong	Deng	Penman	Brunt	Bepлянд	FAO24	FAO56
Kunming		Tong	Deng	Penman	Brunt	Bepлянд	FAO24	FAO56
Lanzhou		Tong	Penman	Deng	Brunt	Bepлянд	FAO24	FAO56
Lhasa		Penman	Tong	Brunt	Deng	Bepлянд	FAO24	FAO56
Mohe		Deng	Tong	Penman	Bepлянд	Brunt	FAO24	FAO56
Sanya		Deng	Tong	Penman	FAO24	FAO56	Bepлянд	Brunt
Shanghai		Deng	Tong	Penman	Brunt	FAO24	FAO56	Bepлянд
Shenyang		Deng	Penman	Tong	Brunt	Bepлянд	FAO24	FAO56
Urumuqi		Tong	Penman	Brunt	Deng	Bepлянд	FAO24	FAO56
Wenjiang		Deng	Tong	Penman	Brunt	FAO24	Bepлянд	FAO56
Wuhan		Tong	Deng	Penman	Brunt	FAO24	FAO56	Bepлянд
Yuzhong		Tong	Penman	Brunt	Deng	Bepлянд	FAO24	FAO56
Zhengzhou		Deng	Tong	Penman	Brunt	Bepлянд	FAO24	FAO56

). The Deng Genyun formula was, therefore, suitable for stations located on the plain in Eastern China at an altitude of less than 600 m. This was most likely because the empirical constants of the relative sunshine duration (n_s/N_s) were different from those of the other formulas and correctly described the effect of cloud cover on R_nl. Furthermore, the empirical constants derived from the Beijing station data only using the Deng Genyun formula largely fit east China, suggesting that the coefficient was almost the same for this area. The Tong Hongliang formula was more accurate at stations with an elevation greater than 900 m, including Golmud, Kashgar, Kunming, Lanzhou, Urumuqi, and Yuzhong (Table 4). The Tong Hongliang formula was suitable for the plateau area because of the altitude correction that is applied when calculating the atmospheric moisture. The FAO24 and FAO56-PM formulas showed the lowest accuracy at most of the stations.

3.2. Establishment of Optimal R_nl Empirical Formulas

The partial correlation analysis showed that the estimated errors of the seven tested formulas were mainly related to water vapor pressure or elevation, except for FAO56-PM. Therefore, water vapor pressure and elevation were the two most critical factors affecting the R_nl estimate. In this paper, apart from revising the formula for the whole of China (hereafter, the national formula), we also established revised regional formulas for the eastern and northwestern areas and the Tibetan Plateau, according to the geographical distribution of water vapor pressure and elevation over China.

First, the monthly standard net long-wave radiation at the 19 stations was calculated based on the surface radiation balance equation using observations from 1993 to 2012. Second, the parameter b₀ in Equation (2) was iterated with a step of 0.01 from 0 to 1. The maximum and minimum air temperature, water vapor pressure, and relative sunshine duration were used as inputs to obtain a₀ and a₁ using multivariate regression for different b₀. Finally, the R_nl of different b₀, a₀, and a₁ was estimated. The best b₀, a₀, and a₁ was determined using the minimum RMSE between the estimate and standard values as the objective function. Considering the limited data, some samples from odd years (n = 1949) were used to calibrate the parameters, and the other samples from even years (n = 1945) were preserved to validate an optimum net long-wave radiation formula calibration, which is called the validated R_nl. The national and regional formulas are listed in

Table 5. Revised national and regional formulas to calculate net long-wave radiation in China.

Formulas	Stations Used to Modeling	Equations	Area Recommended to Use
National formula	The whole of 19 stations listed in Table 1	$R_{\mathrm{nl}}=\sigma \left(\frac{{T_{\min }}^4+{T_{\max }}^4}{2}\right)\left(0.47-0.13\sqrt{e_{\mathrm{a}}}\right)\left(0.11+0.89\frac{n_{\mathrm{s}}}{N_{\mathrm{s}}}\right)$	Entire China
Regional formulas	Beijing, Chengdu, Guangzhou, Harbin, Kunming, Mohe, Sanya, Shanghai, Shenyang, Wenjiang, Wuhan, Zhengzhou	$R_{\mathrm{nl}}=\sigma \left(\frac{{T_{\min }}^4+{T_{\max }}^4}{2}\right)\left(0.42-0.12\sqrt{e_{\mathrm{a}}}\right)\left(0.19+0.81\frac{n_{\mathrm{s}}}{N_{\mathrm{s}}}\right)$	Eastern area of China
	Ejin Banner, Kashgar, Lanzhou, Urumuqi, Yuzhong	$R_{\mathrm{nl}}=\sigma \left(\frac{{T_{\min }}^4+{T_{\max }}^4}{2}\right)\left(0.42-0.06\sqrt{e_{\mathrm{a}}}\right)\left(0.09+0.91\frac{n_{\mathrm{s}}}{N_{\mathrm{s}}}\right)$	Northwestern area of China
	Golmud, Lhasa	$R_{\mathrm{nl}}=\sigma \left(\frac{{T_{\min }}^4+{T_{\max }}^4}{2}\right)\left(0.46-0.12\sqrt{e_{\mathrm{a}}}\right)\left(0.32+0.68\frac{n_{\mathrm{s}}}{N_{\mathrm{s}}}\right)$	Tibetan Plateau

.

The correlation coefficient, R, between the validated and standard R_nl for national and regional formulas, were 0.85 and 0.87, respectively (Figure 4), which were both higher than those for most of the existing seven formulas evaluated in this study. Some discrepancies existed with R_nl values greater than 120 W/m². However, the two formulas provided a reasonable simulated R_nl, and the regression equation could adequately describe R_nl and can be used to analyze R_nl.

Table 6. Comparison of the standard and validated net long-wave radiation of the nineteen radiation stations based on the revised national and regional formulas.

	Errors	MBE (W/m2)		MABE (W/m2)		MAPE (%)		RMSE (W/m2)
Station		National Formula	Regional Formula	National Formula	Regional Formula	National Formula	Regional Formula	National Formula	Regional Formula
Beijing		6.062	1.667	10.999	9.451	16.468	13.755	13.351	11.810
Chengdu		–1.433	1.334	6.062	5.836	16.010	16.199	7.966	7.624
Ejin Banner		–12.760	–13.870	18.317	17.545	13.930	13.189	24.460	24.263
Golmud		–3.966	5.671	12.389	11.556	11.915	12.353	14.804	14.069
Guangzhou		5.987	5.674	8.893	7.633	20.530	18.814	11.586	9.817
Harbin		–3.596	–6.722	12.149	12.168	16.021	15.571	16.292	17.012
Kashgar		5.154	8.064	17.366	17.258	22.973	22.674	21.290	20.924
Kunming		1.398	–2.003	9.133	8.477	13.311	12.088	11.855	11.515
Lanzhou		0.351	2.086	9.911	9.901	12.237	12.639	12.457	12.432
Lhasa		–18.152	–7.855	22.229	17.911	18.108	16.064	28.025	22.961
Mohe		3.857	0.545	13.355	12.485	23.368	21.043	15.959	15.323
Sanya		1.840	–1.887	11.359	10.700	20.029	17.944	14.247	13.530
Shanghai		2.543	1.367	7.671	7.269	15.863	14.885	9.821	9.129
Shenyang		–0.560	–4.246	14.871	14.330	21.271	19.592	19.251	19.291
Urumuqi		–3.449	–1.969	14.216	12.875	17.866	16.649	19.326	17.657
Wenjiang		–3.927	–0.925	7.595	6.844	19.754	19.035	9.127	8.562
Wuhan		8.449	7.134	12.434	11.451	27.807	26.069	15.069	14.104
Yuzhong		–8.907	–7.817	16.649	16.280	17.119	17.388	22.734	20.804
Zhengzhou		–0.046	–1.610	9.437	9.092	15.097	14.193	11.984	11.786
Average		–1.113	–0.808	12.370	11.530	17.878	16.850	15.769	14.874

presents the MBE, MABE, MAPE, and RMSE of the standard and validated R_nl based on national and regional formulas for the 19 radiation stations. The negative MBE, with an average absolute value of approximately 1.0 W/m² for the 19 stations, illustrates that R_nl was slightly underestimated by the two revised formulas. Moreover, the validated R_nl had the lowest average MAPE and RMSE of the 19 stations compared with the other formulas listed in Table 2. In general, the R_nl based on the two revised formulas was relatively more accurate compared with the other calculations over China. Therefore, further modifications must be made using meteorological observations when the R_nl formulas are applied.

As a whole, the average MABE, MAPE, RMSE, and absolute MBE of the 19 stations using the regional formula were smaller than those using the national formula (Table 6). Furthermore, the R_nl based on the regional formula showed less MABE, MAPE, and RMSE than that based on the national formula for most stations. The accuracy of the estimated R_nl, in particular, was significantly improved by the regional formula at the stations located in Eastern China (e.g., Beijing, Chengdu, Guangzhou, Harbin, Kunming, Mohe, Sanya, Shanghai, Shenyang, Wenjiang, Wuhan, and Zhengzhou) and the Tibetan Plateau, while it was slightly improved at the stations located in the northwestern area (e.g., Ejin Banner, Kashgar, Lanzhou, Urumuqi, and Yuzhong) compared with the national formula. The results show that the regional formula was more accurate at estimating R_nl in China than the national formula, and it is essential to separate the eastern and northwestern areas, as well as the Tibetan Plateau, in the development of the method for the determination of R_nl.

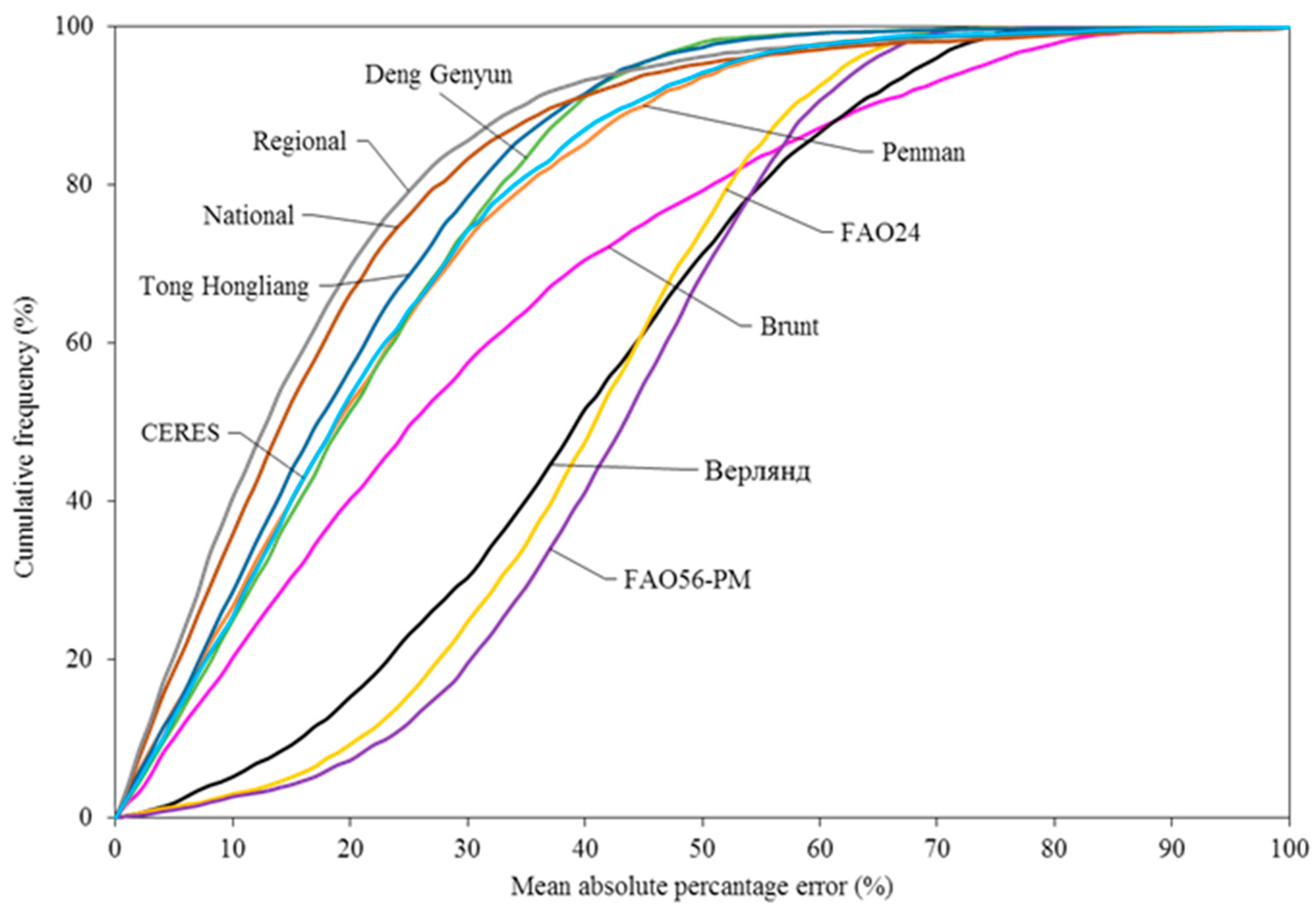
Figure 5 shows the cumulative frequency of MAPE between the standard and estimated monthly net long-wave radiation values based on the seven existing empirical formulas, two refitted formulas, and CERES data. The frequency of MAPE less than 10.0% was 40% and 35% for the revised regional and national formulas, respectively, followed by Tong Hongliang, Deng Genyun, and Penman formulas, as well as CERES data with the frequency ca. 30%, while the frequency did not exceed 5% for Bepлянд, FAO24, and FAO56-PM formulas. The frequency of MAPE less than 15.0% and 20.0% had similar characteristics. When MAPE was over 40.0%, the frequency exceeded 50% for Bepлянд, FAO24 and FAO56-PM formulas. However, the frequency was less than 10% for the revised regional and national formulas. These results illustrated that the calibrated formulas improved the accuracy of estimating R_nl over China compared with the original ones, and were more accurate than the estimations based on the CERES data.

Compared with the other five existing formulas, the Deng Genyun and Tong Hongliang formulas were more accurate at estimating R_nl. Therefore, based on the radiation and observed meteorological data of the 19 radiation stations over China for the full 20 years, we compared the MBE, MABE, MAPE, and RMSE of the standard and estimated R_nl using the revised regional, the Deng Genyun, and the Tong Hongliang formulas to illustrate the effect of the parameter optimization more clearly. Taking the 19 stations as a whole, the correlation between the estimated and standard R_nl using the regional formula was higher than that for the Deng Genyun and Tong Hongliang formulas (

Table 7. Comparison of the standard and estimated monthly net long-wave radiation based on the regional, Deng Genyun, and Tong Hongliang formulas.

Formulas	R	MBE (W/m2)	MABE (W/m2)	MAPE (%)	RMSE (W/m2)
Regional	0.870	–0.590	11.536	16.601	15.432
Deng Genyun	0.860	–14.441	17.871	20.965	24.606
Tong Hongliang	0.827	–10.027	15.107	19.562	20.092

). The MBE of the regional formula was −0.59 W/m² and the absolute value was much smaller than that of the other two formulas. The regional formula also produced a lower MABE, MAPE, and RMSE, indicating that it was more accurate than the Deng Genyun and Tong Hongliang formulas.

For most of the 19 stations, the RMSE of the R_nl based on the regional formula was the smallest among the three formulas (Figure 6). In particular, the regional formula was clearly more accurate than the Deng Genyun formula at the stations located in Northwestern China (e.g., Ejin Banner, Kashgar, Lanzhou, Urumuqi, and Yuzhong) and the Tibetan Plateau. It was also clearly more accurate than the Tong Hongliang formula at the stations located in the eastern area (e.g., Beijing, Chengdu, Guangzhou, Harbin, Kunming, Mohe, Sanya, Shanghai, Shenyang, Wenjiang, Wuhan, and Zhengzhou). Therefore, we recommend this formula as the standard climatology method to calculate the net long-wave radiation over China.

4. Conclusions

The performance of empirical formulas for the estimation of monthly net long-wave radiation (R_nl), with both original parameter values and recalibrated parameters, was tested and compared at 19 radiation stations in China. Meanwhile, the accuracy of the CERES EBAF-Surface Ed 2.8 estimated R_nl also evaluated, along with others from the seven formulas. The monthly R_nl over China was underestimated by all of the existing formulas with original parameters. The Tong Hongliang formula was the best among these methods for estimating R_nl over China, as a whole, followed by the Penman and the Deng Genyun formulas. The estimated R_nl based on the CERES data also showed relatively higher precision in accordance with the three formulas mentioned above. The FAO56-PM formula, with the lowest precision, was not applicable to China. For individual stations, the accuracy of the Deng Genyun formula was the highest on the eastern plain, while the Tong Hongliang formula was suitable for the plateau area because it includes altitude correction in the atmospheric moisture calculation. The revised formulas with recalibrated parameters were more accurate than the seven original formulas and the estimation based on the CERES data. Furthermore, the regional formula produced smaller errors than the formula for the whole of China at most stations, indicating that it is necessary to distinguish different areas in the development of new methods to determine R_nl. The regional formulas were clearly more accurate than the Deng Genyun formula at the stations located in Northwestern China and the Tibetan Plateau, and were clearly more accurate than the Tong Hongliang formula at the stations located in the eastern area. Therefore, the regional formulas developed in this study are recommended as the standard climatology methods to calculate the monthly net long-wave radiation over China.

Compared with other meteorological factors, the low number of stations, short data length, and relatively large observation errors of surface radiation balance components were the main factors limiting the generality of the results drawn from this study over China. Therefore, multi-source data, such as remote sensing and sounding data, must be applied to develop future net long-wave radiation methods. According to this paper, there are discrepancies between observations and estimations from CERES data at the stations over China, which may be mainly caused by cloud. The difference between the meteorological assimilation data from reanalysis and the actual data may be another cause leading to the error in surface R_nl fluxes. However, with the development of technology, the accuracy of satellite-based data will be improved further. Another future study will be carried out to establish separate formulas for the four seasons to improve the precision and accuracy of the net long-wave radiation calculation. In addition, it should be calculated that R_nl under clear-sky and all-sky conditions in China in the future, following the previous study [48].