1. Introduction
The concept of rain clusters are widely used in the research of Chinese rainstorms, so the study on rain clusters in rainstorm is crucial. “Rain cluster” refers to the area surrounded by an isohyetal line of 10 mm/h over a life cycle of more than two hours and on a spatial scale of 10–100 km [
1]. It is a mesoscale convective system (MCS), which is caused by strong local convection, and it is a weather system that directly generates rainstorms [
2]. Rain clusters have a wide prevalence in periods of floods and always occur with disaster weather with strong precipitation, causing serious damage to people’s lives and property, as well as industrial and agricultural production. Therefore, the study on rain clusters has become a hot issue in mesometeorology [
3,
4,
5,
6,
7,
8,
9,
10]. In the literature [
11], Zeng Qingcun pointed out that the improvement of weather forecasting techniques relied on further development of numerical forecast models, technologies, and further knowledge of the regularity of the weather evolution process, which all require the development of corresponding basic theoretical studies [
11]. Therefore, it is important to perform theoretical studies on rain clusters.
The horizontal shape of rain clusters is usually close to circular. Many literatures also treat rain clusters as circular symmetrical shapes to study [
12]. However, the spiral structure is very common in nature. In the atmosphere, the spiral structure occurs as planetary waves, as well as tropical cyclones [
13,
14]. Thus, the existence of the spiral rain clusters becomes one of the most important aspects in the theoretical study on rain clusters. Obviously, the theory of circular symmetry cannot be used in this field. Is it possible to establish a theoretical model of spiral rain clusters? If so, what is the performance of the spiral structure in this model? What are the distribution characteristics of ascending motion and convective precipitation at the spiral arms? These are important questions that must be answered in the theoretical study on rain clusters. In addition, whether or not there are rain clusters with a typical spiral structure, whether or not examples can be given, these must be answered, too. All of the above questions have not been given ready-made answers by our predecessors.
Although there were many studies on rain clusters before this paper [
3,
4,
5,
6,
7,
8,
9,
10], there were no reports and other studies about typical spiral arm rain clusters. However, we found that in the strong lightning and local torrential rain on the morning of 25 August 2008 in Shanghai, the rain detection radar did observe a rain cluster with a typical spiral structure, indicating that the spiral arms could also appear in rain clusters.
At 7:00–8:00 that morning (Beijing time, similarly hereinafter), the seven automatic rainfall stations in Shanghai measured precipitation that exceeded 100 mm, among which the precipitation of Xujiahui station reached 117.5 mm/h, and the station had never met this since it started keeping meteorological records in 1872 [
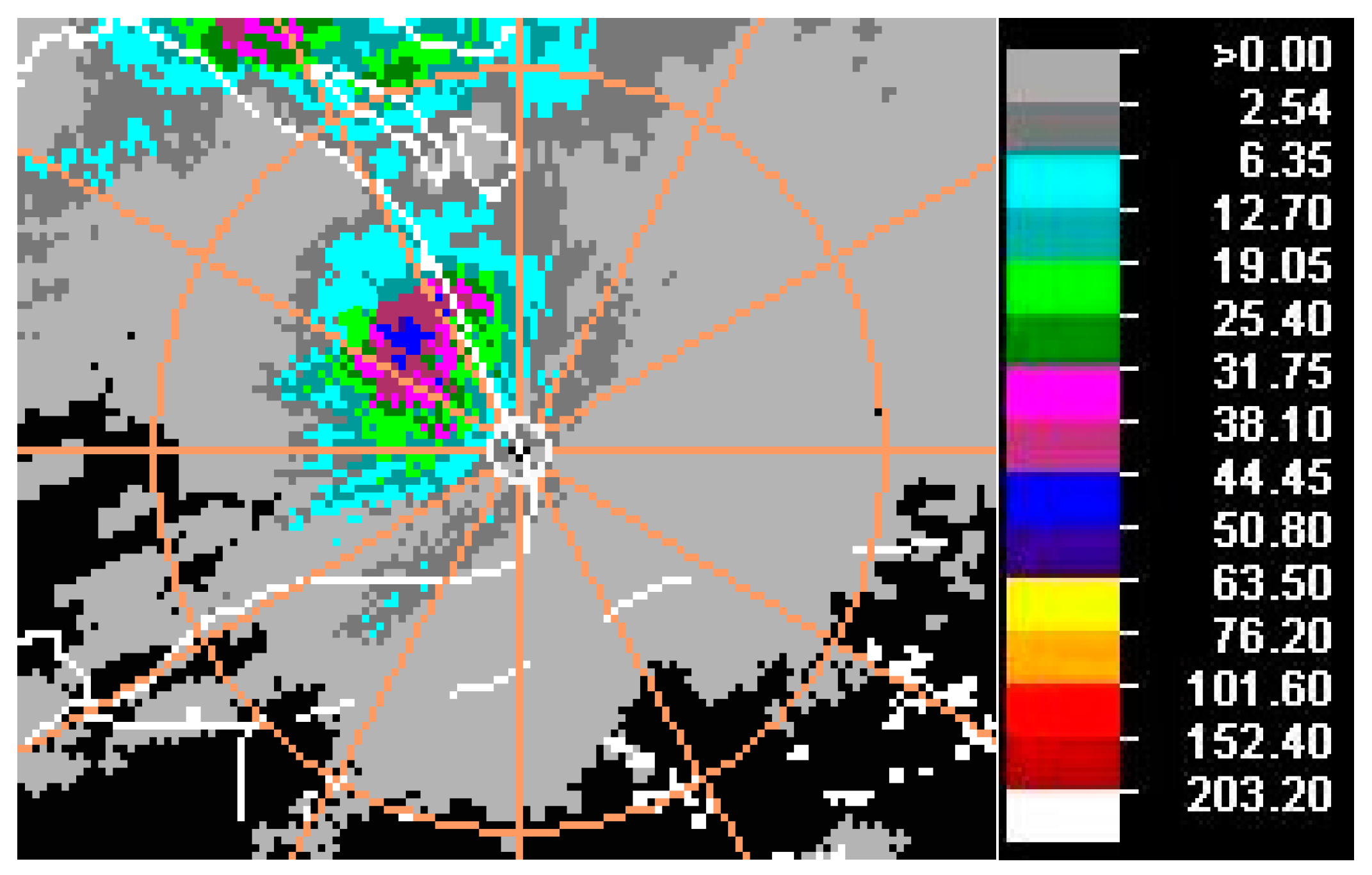
15]. At 9:12, the typical spiral rain clusters were discovered on the Shanghai OHP radar map (see
Figure 1, the white line is the coastline, the white circle is the location of the radar station, the distance from the orange circle to the radar station is about 30 nautical miles (approximately 56 km), the color bar denotes precipitation/h). The figure shows that the rain cluster has two obvious spiral arms, the convective precipitation in the cluster center is at a maximum, decreasing outwardly. The convective precipitation is larger in the spiral arms, and the farther from rain cluster center, the weaker of convective precipitation in the rain cluster and its spiral arms. The horizontal scale of this rain cluster is 30 km.
Since there are no other people’s studies mentioned about typical spiral rain clusters before this paper, it shows that this kind of rain cluster is relatively rare. For this reason, establishing a theoretical model of this kind of rain cluster is more important and necessary. It can not only demonstrate from the dynamics that the existence of the rain clusters is possible and reasonable, but also helps determine the rain clusters’ structure and answers the above questions, further deepening the understanding of this kind of rain cluster, which also has potential application in the prediction, detection, or early warning of rain clusters. In addition, it can also eliminate people’s doubts regarding this isolated case.
We have established a theoretical model of spiral rain clusters and obtained the analytical solution of the horizontal structure equation a few years ago [
16]. However, due to the assumption and approximation during the solutions, there are still two deficiencies in the model of rain clusters. One is that the intensity of the model of the rain cluster is invariable with the changing of
r. The other is that it is not symmetrically round near the center of the model of the rain cluster. In order to correct these deficiencies, this paper introduced a new phase function to the mathematical model and obtained a new horizontal structure equation. The analytical solution of the new equation can, indeed, describe the spiral rain clusters. The results of the model were compared with the actual rain clusters, which answered the above questions.
2. Theoretical Model and Horizontal Structure Equation
In order to facilitate the analysis, the linear Boussinesq equations expressed in cylindrical coordinates under the pseudo-adiabatic assumption was used to describe the system of rain clusters with spiral arms. The equations are as follows:
where
are the two components of the horizontal wind speed, vertical movement, pseudo-equivalent potential temperature, and barometric disturbance, respectively. In addition,
is the typical value of air density;
f is the Coriolis parameter, which can be considered constant for a rain cluster; and
is the wet stratification parameter, which is assumed to be a function of
z, namely,
. Here the pseudo-adiabatic process can simplify the thermal effect of the steam latent heat of condensation. The linear approximation is used because there is no strong gradient wind in rain clusters as tropical cyclones, and can be conveniently used to obtain the horizontal and vertical structure equations. The adoption of Boussinesq approximation is due to our focus on the level of structure of the system; in general, it is feasible to do these approximations on issues of concern in this paper.
The phase function
was then introduced, where
m is the number of spiral arms in the system (m is an integer greater than or equal to zero). It is assumed that
k > 0, and
k/
m is correlated to the included angle between the equiphase line (the spiral line where
is constant, with
m > 0, the curve is the trailing helix, which is also the criterion for the identification of the spiral arms) and the equal-r line (circular line). With
m = 0, the rain cluster has a circularly symmetric structure without spiral arms. Thus, assuming:
where the growth rate
is taken as a positive real number, indicating an unstable situation in the system that is discussed below. Under certain conditions, the unstable system could be considered a developing rain cluster. Since
, and
, we have:
where
W satisfies the vertical boundary condition
The topography is not taken into account, and H is the top attitude of the tropopause or inversion layer.
Θ is the eliminated combining Equations (3.3) and (3.4), deriving:
In the above equation,
, which is the function of
z. The partial derivative of Equations (3.1) and (3.2) are then derived based on
z. Considering Equation (5), it can be obtained that:
from which,
and
may be solved. The partial derivative of Equation (3.5) is then derived on
z, deriving:
The expressions
and
are substituted into Equation (7). Since
, the partial differential equation of
W could be derived as:
in which,
,
, and
.
which is substituted into Equation (8) to conduct variable separation. The variable separation constant is assumed to be
λ > 0, and the vertical and horizontal structure equations of vertical movement could be derived as follows:
which could then reveal the horizontal and vertical structure of developing rain clusters.
The expressions of b and h are substituted in the horizontal structure Equation (9.1), and the expression of a is substituted in the vertical structure Equation (9.2). Then the expression of μ(z) is introduced. Since λ > 0 is constant, and σ is positive constant, λ/σ is further recorded as λ, and λ > 0.
The horizontal structure equation (Equation (9.1)) and vertical structure equation (Equation (9.2)) can then be expressed as:
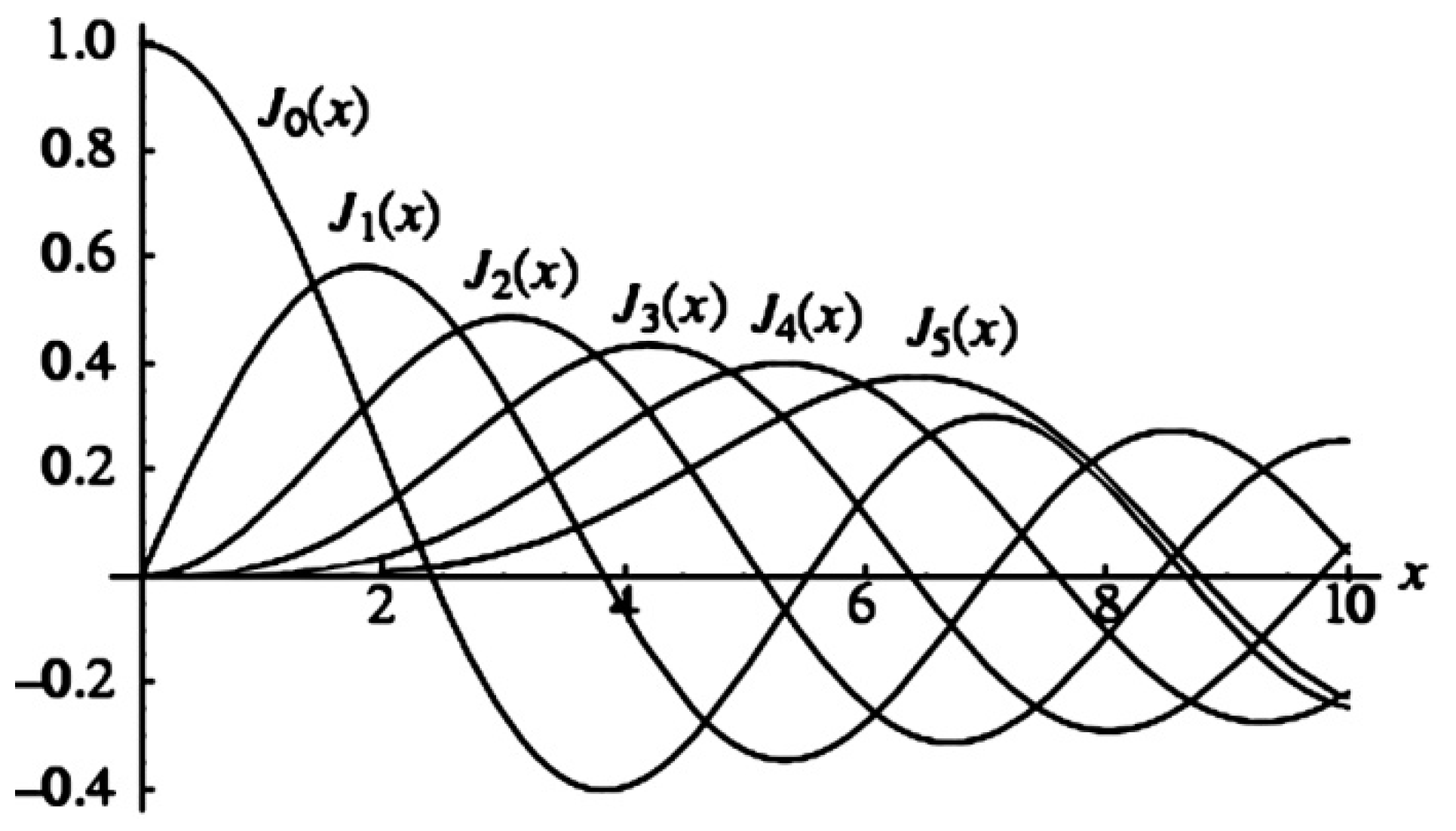
The horizontal structure of rain clusters is discussed in the following section, based on Equation (10.1).
4. Conclusions
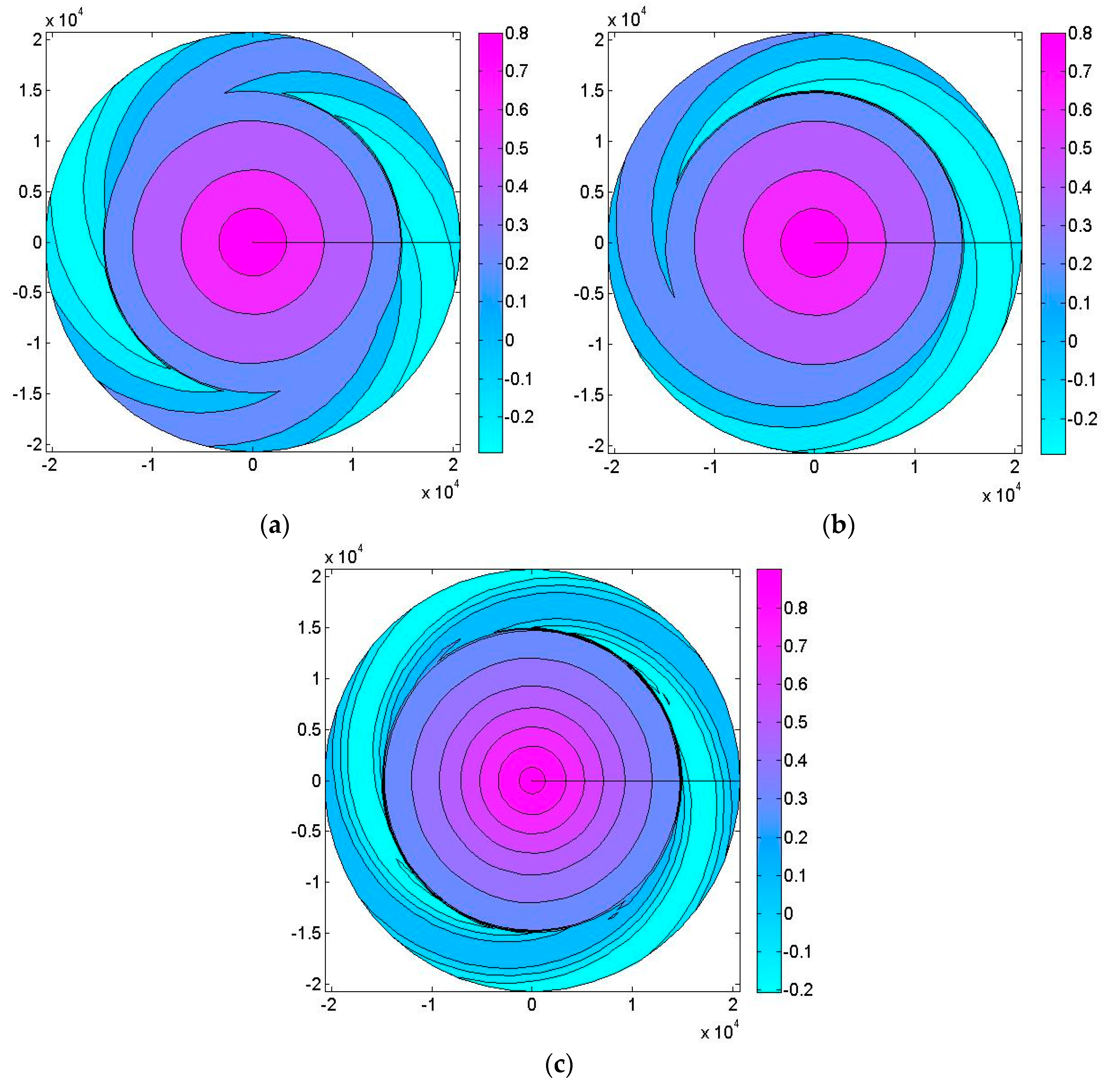
The linear Boussinesq equations in a cylindrical coordinate system were employed in the present study based on the pseudo-adiabatic assumption to study rain clusters. In addition, the horizontal structure equation of rain clusters with spiral arms was also obtained. The main conclusions of this study are: (1) the theoretical rain cluster is circularly symmetric in locations close enough to its center; (2) spiral arms may arise in locations far from the center; (3) the magnitude of ascending movement is strongest in the center, and decreases gradually with increasing distance from the rain cluster center, as do the spiral arms; and (4) the magnitude of ascending movement is also strong on the axis of the spiral arms. The results are consistent not only with the numerical results but also the facts of the observation of the actual rain cluster of the rain detection radar mentioned in this paper.
The theoretical model of spiral rain clusters is successful, the approximation used to establish the model is feasible under certain conditions, and the analysis of the horizontal structure of the model of the rain cluster is reasonable, which is consistent with the actual rain cluster. The theoretical model can answer the questions raised in the introduction and can be used to study the dynamics of spiral rain clusters. The last thing to point out is that due to the limitation of observation and numerical simulation conditions, the theoretical analysis of this paper cannot be quantitatively analyzed and compared with the examples of rain clusters and numerical simulation results, which is the inadequacy of this paper that needs to be improved in the future.