Comparison of Sensible Heat Fluxes Measured by a Large Aperture Scintillometer and Eddy Covariance System over a Heterogeneous Farmland in East China
Abstract
:1. Introduction
2. Observation Site and Micrometeorological Measurement Systems
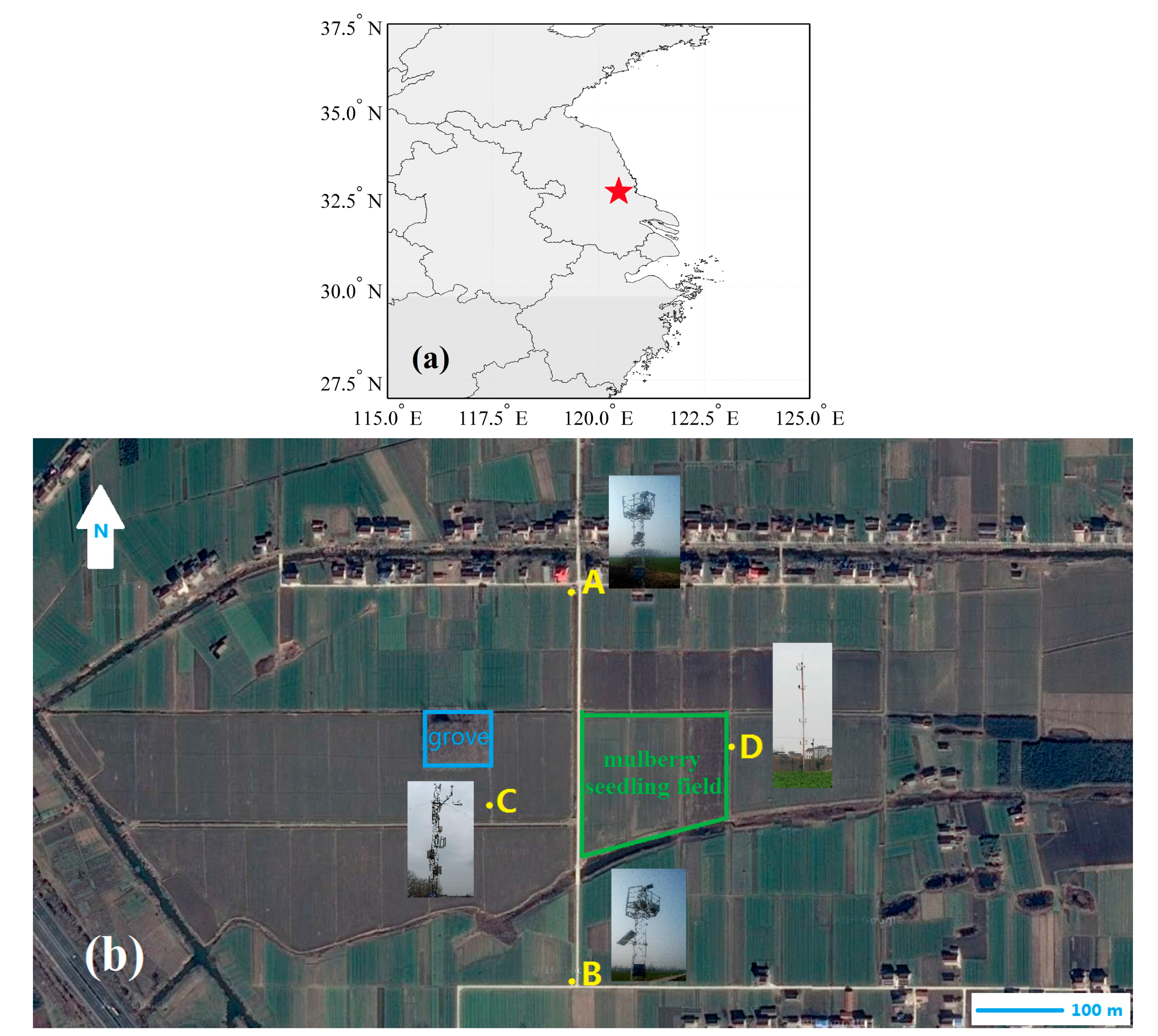
2.1. Observation Site
2.2. Micrometeorological Measurement Systems
2.2.1. Large Aperture Scintillometer
2.2.2. EC System
2.2.3. Automatic Meteorological Station
3. Data Processing Methods
3.1. Parameter Set
3.2. Data Process Scheme of EC
3.3. Scintillometry Method
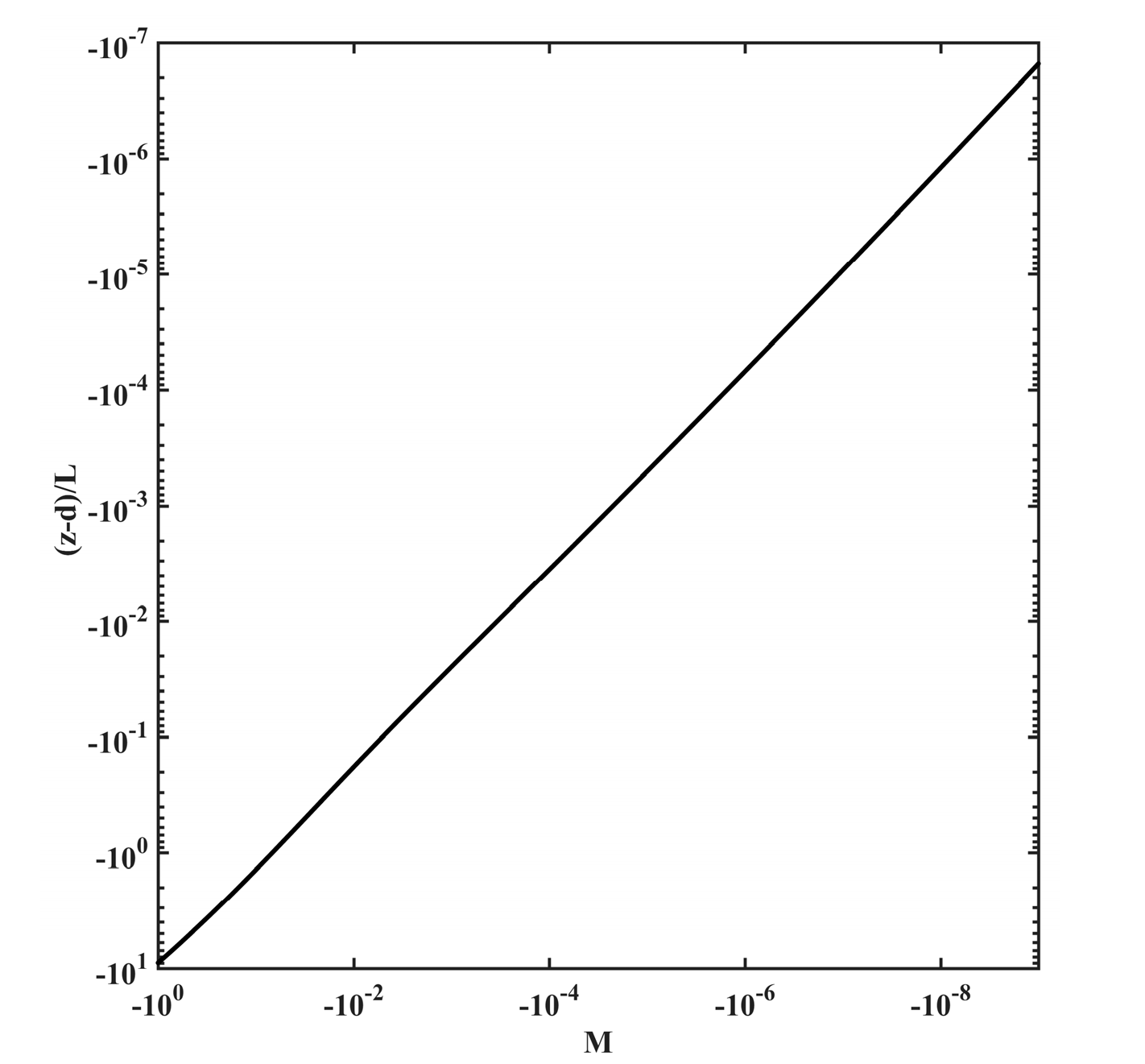
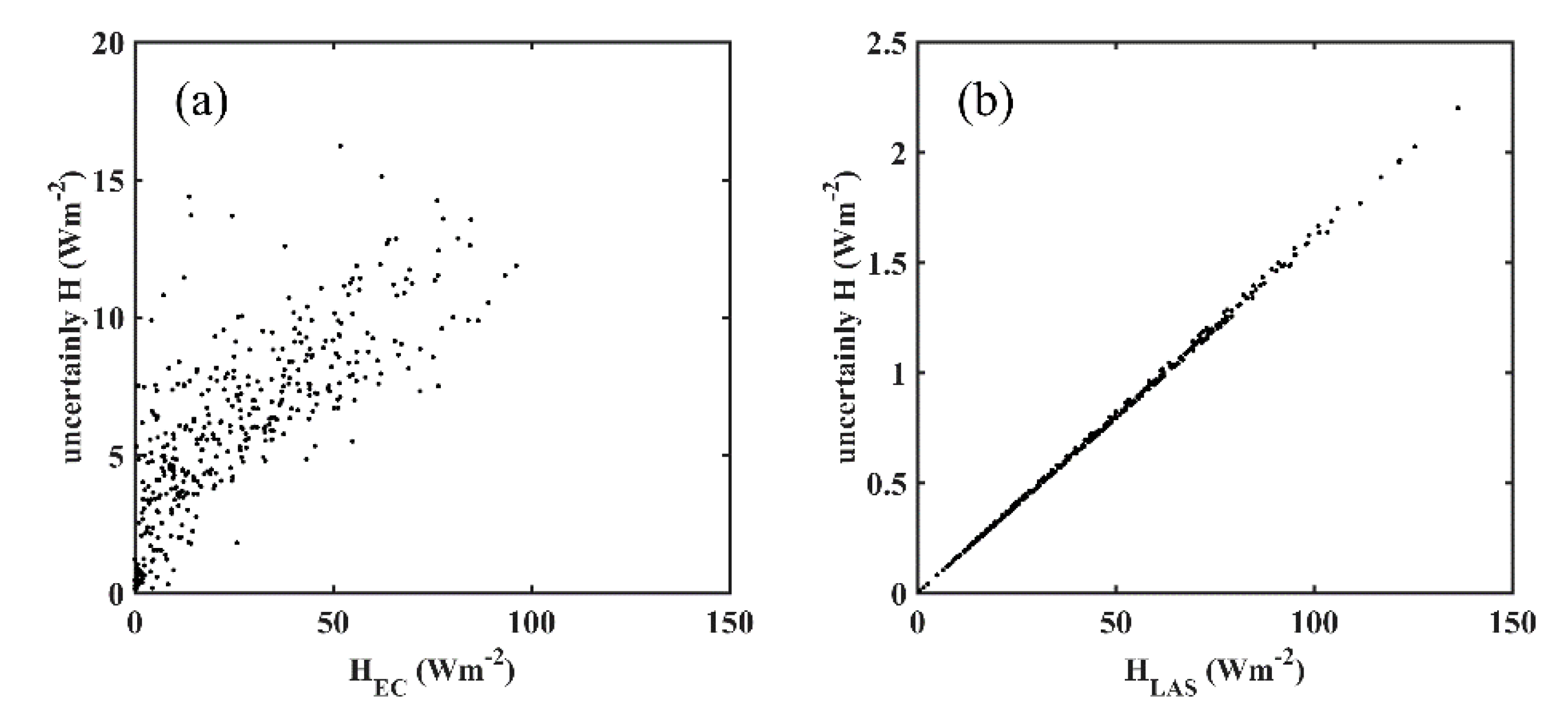
3.4. Calculation Uncertainty
3.5. Footprint Analysis
4. Results
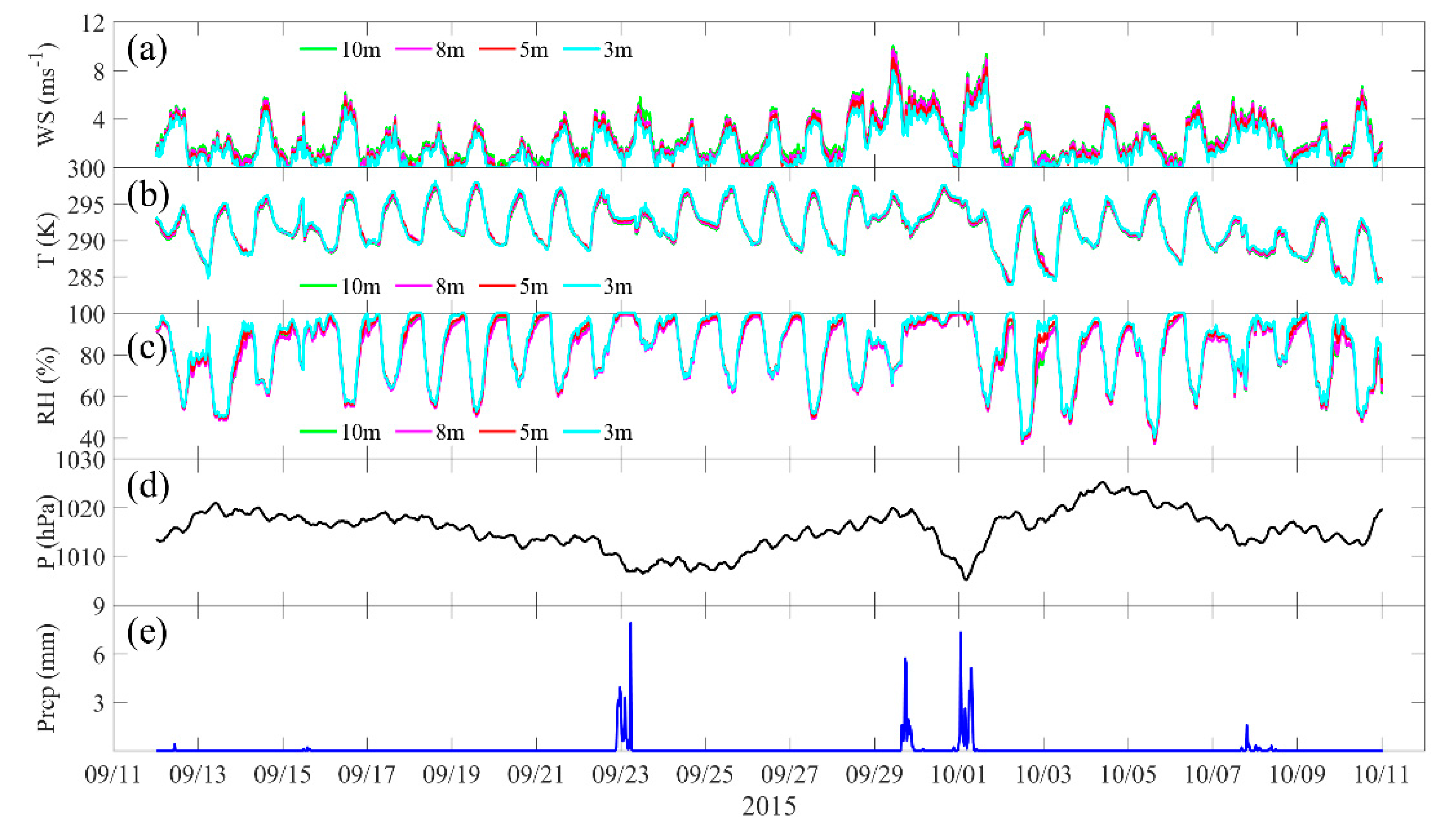
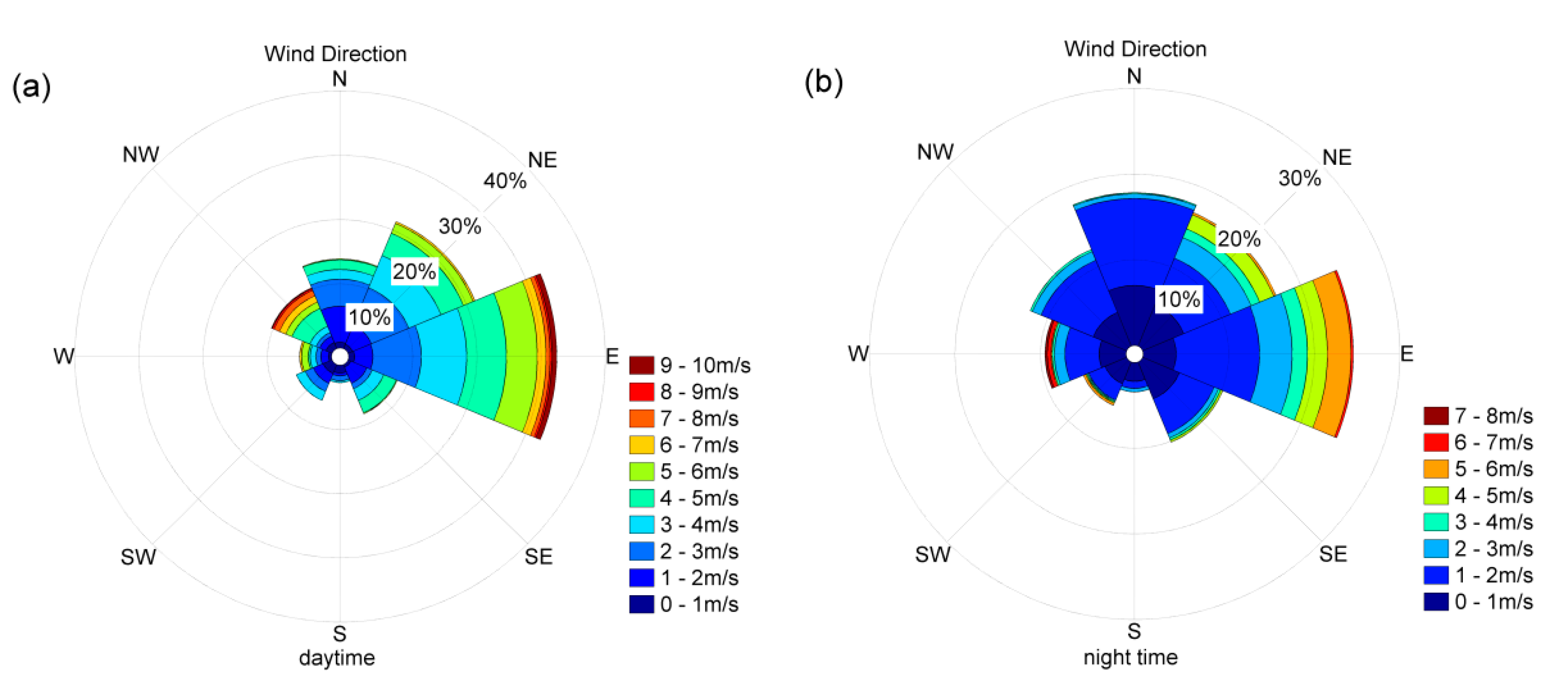
4.1. Meteorological Conditions
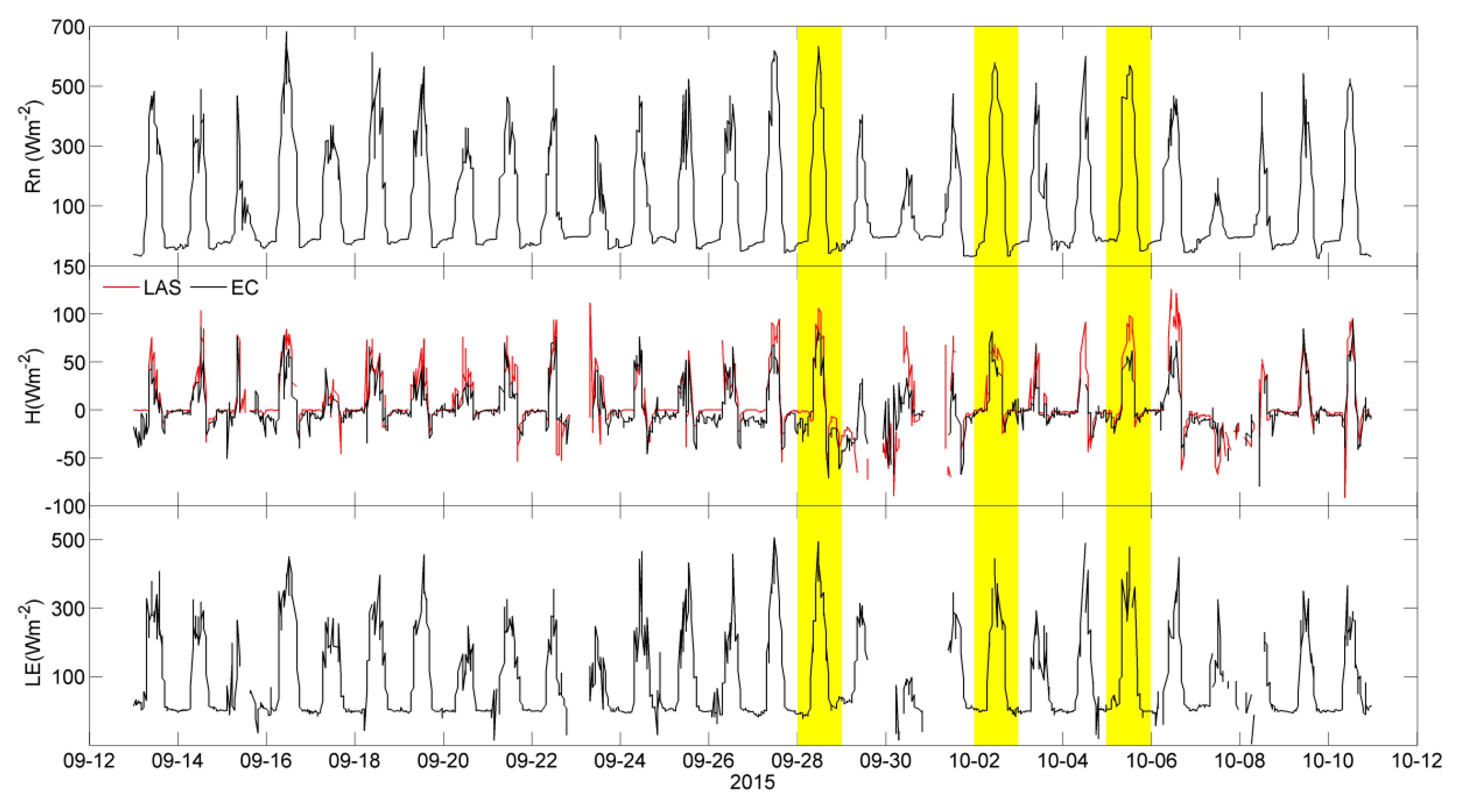
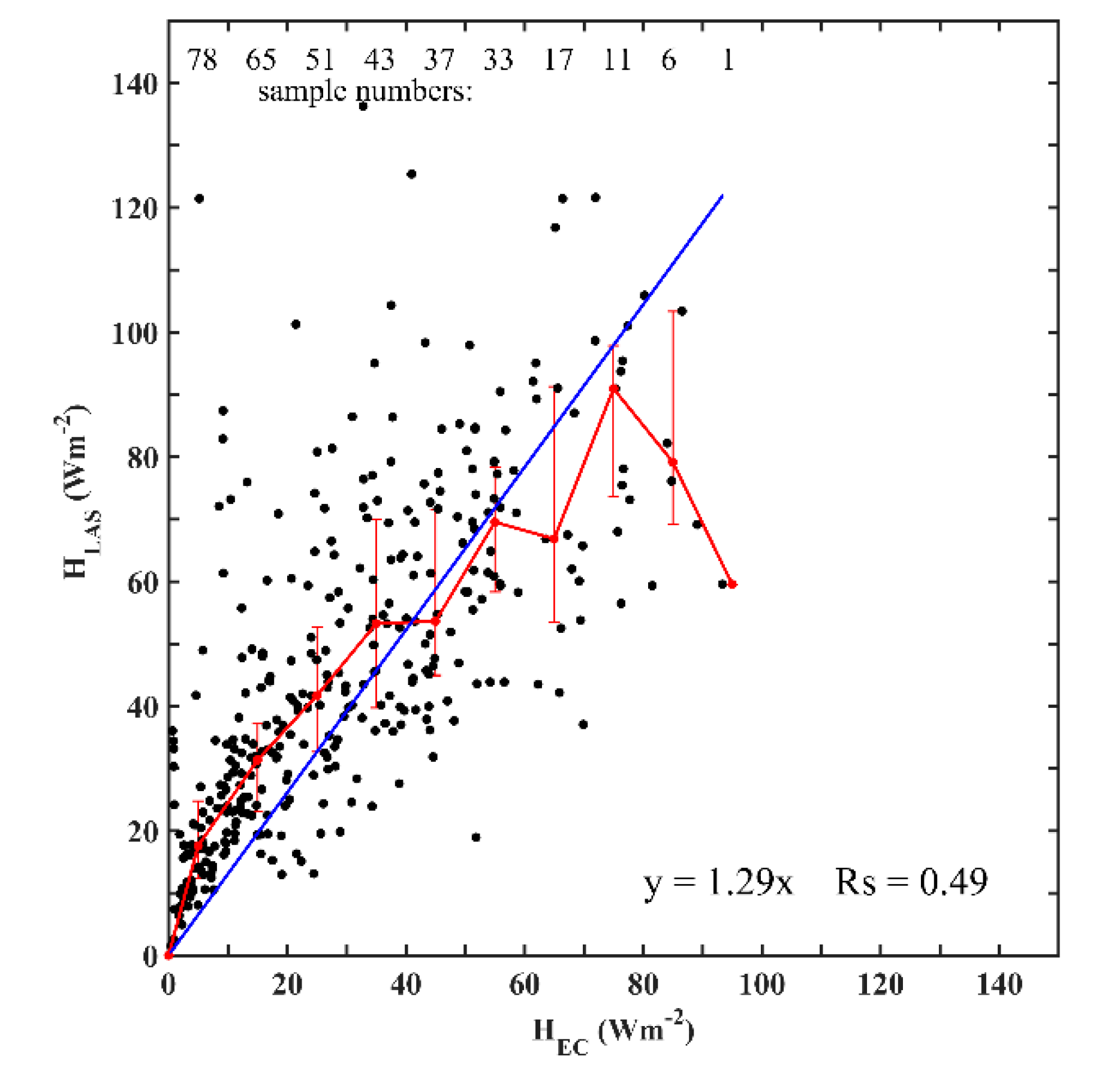
4.2. Turbulent Heat Fluxes
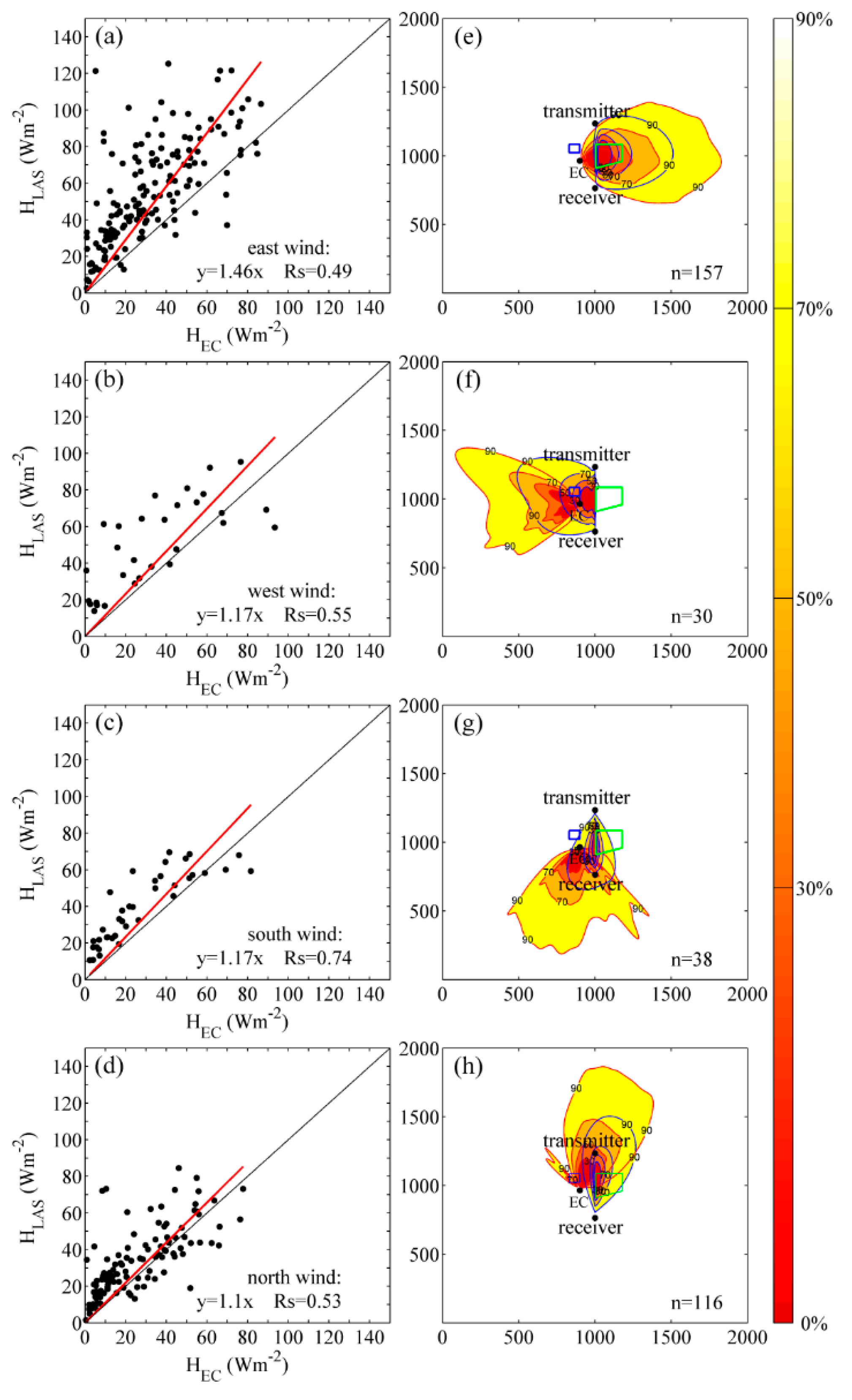
4.3. The Effects of Winds and Associated Footprint on HLAS and HEC
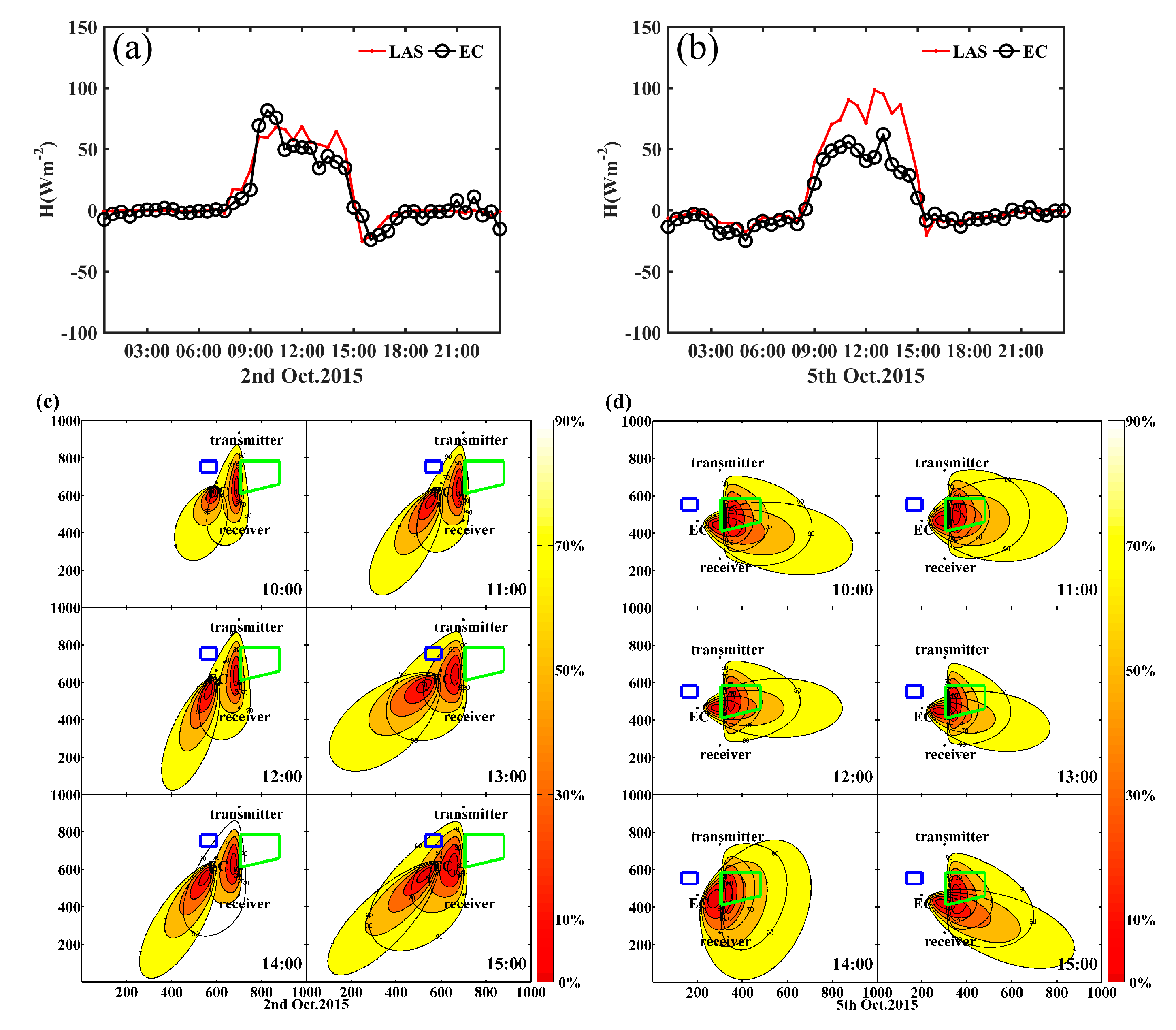
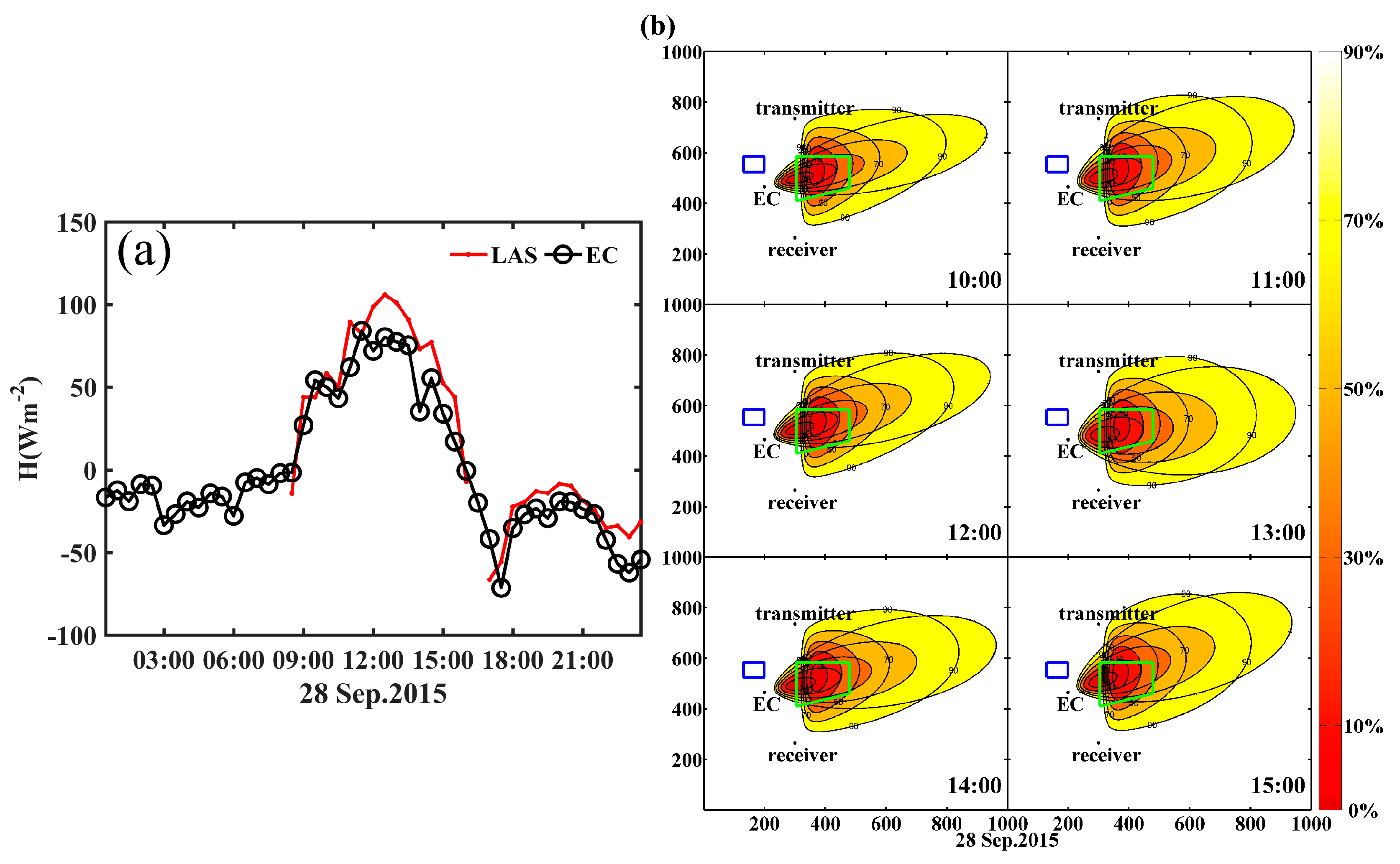
4.4. Case Analysis
4.4.1. Effects of Different Wind Directions
4.4.2. Effects of Different Wind Speed
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liang, L.; Lu, S.; Shang, L. Numerical simulation of effect of loess plateau vegetation change on local climate. Plateau Meteorol. 2008, 27, 293–300. [Google Scholar]
- Pielke, R.A. Influence of the spatial distribution of vegetation and soils on the prediction of cumulus convective rainfall. Rev. Geophys. 2001, 39, 151–177. [Google Scholar] [CrossRef]
- Foley, J.A.; DeFries, R.; Asner, G.P.; Barford, C.; Bonan, G.; Carpenter, S.R.; Chapin, F.S.; Coe, M.T.; Daily, G.C.; Gibbs, H.K. Global consequences of land use. Science 2005, 309, 570–574. [Google Scholar] [CrossRef] [PubMed]
- Findell, K.L.; Shevliakova, E.; Milly, P.; Stouffer, R.J. Modeled impact of anthropogenic land cover change on climate. J. Clim. 2007, 20, 3621–3634. [Google Scholar] [CrossRef]
- Bian, L.; Gao, Z.; Xu, Q.D.; Lu, L.H.; Yanjie, C. Measurement of turbulence transfer in the near-surface layer over the southeastern tibetan plateau. Bound. Layer Meteorol. 2002, 102, 281–300. [Google Scholar] [CrossRef]
- Gao, Z.; Bian, L.; Zhou, X. Measurements of turbulent transfer in the near-surface layer over a rice paddy in China. J. Geophys. Res. Atmos. 2003. [Google Scholar] [CrossRef]
- Gao, Z.; Lenschow, D.H.; Horton, R.; Zhou, M.; Wang, L.; Wen, J. Comparison of two soil temperature algorithms for a bare ground site on the loess plateau in China. J. Geophys. Res. Atmos. 2008. [Google Scholar] [CrossRef]
- Bi, X.; Gao, Z.; Deng, X.; Wu, D.; Liang, J.; Zhang, H.; Sparrow, M.; Du, J.; Li, F.; Tan, H. Seasonal and diurnal variations in moisture, heat, and CO2 fluxes over grassland in the tropical monsoon region of southern China. J. Geophys. Res. Atmos. 2007. [Google Scholar] [CrossRef]
- Bi, X.; Gao, Z.; Liu, Y.; Liu, F.; Song, Q.T.; Huang, J.; Mao, W.K.; Chunxia, L. Observed drag coefficients in high winds in the near offshore of the south china sea. J. Geophys. Res. Atmos. 2015, 120, 6444–6459. [Google Scholar] [CrossRef]
- Kleissl, J.; Hartogensis, O.K.; Gomez, J.D. Test of scintillometer saturation correction methods using field experimental data. Bound. Layer Meteorol. 2010, 137, 493–507. [Google Scholar] [CrossRef]
- Evans, J.G.; McNeil, D.D.; Finch, J.W.; Murray, T.; Harding, R.J.; Ward, H.C.; Verhoef, A. Determination of turbulent heat fluxes using a large aperture scintillometer over undulating mixed agricultural terrain. Agric. For. Meteorol. 2012, 166–167, 221–233. [Google Scholar] [CrossRef]
- McGloin, R.; McGowan, H.; McJannet, D.; Cook, F.; Sogachev, A.; Burn, S. Quantification of surface energy fluxes from a small water body using scintillometry and eddy covariance. Water Resour. Res. 2014, 50, 494–513. [Google Scholar] [CrossRef]
- Lee, S.-H. Determination of turbulent sensible heat flux over a coastal maritime area using a large aperture scintillometer. Bound. Layer Meteorol. 2015, 157, 309–319. [Google Scholar] [CrossRef]
- Bruin, H.A.R.D.; Hurk, B.J.J.M.V.D.; Kohsiek, W. The scintillation method tested over a dry vineyard area. Bound. Layer Meteorol. 1995, 76, 25–40. [Google Scholar] [CrossRef]
- Anandakumar, K. Sensible heat flux over a wheat canopy optical scintillometer measurements and surface renewal analysis estimations. Agric. For. Meteorol. 1999, 96, 145–156. [Google Scholar] [CrossRef]
- Cain, J.D.; Rosier, P.T.W.; Meijninger, W.; Bruin, H.A.R.D. Spatially averaged sensible heat fluxes measured over barley. Agric. For. Meteorol. 2001, 107, 307–322. [Google Scholar] [CrossRef]
- Bouin, M.N.; Legain, D.; Traullé, O.; Belamari, S.; Caniaux, G.; Fiandrino, A.; Lagarde, F.; Barrié, J.; Moulin, E.; Bouhours, G. Using scintillometry to estimate sensible heat fluxes over water: First insights. Bound. Layer Meteorol. 2012, 143, 451–480. [Google Scholar] [CrossRef]
- Ward, H.C.; Evans, J.G.; Grimmond, C.S.B. Infrared and millimetre-wave scintillometry in the suburban environment – part 2: Large-area sensible and latent heat fluxes. Atmos. Meas. Tech. 2015, 8, 1407–1424. [Google Scholar] [CrossRef]
- Bai, J.; Jia, J.; Liu, S.; Xu, Z.; Hu, G.; Zhu, M.; Song, L. Characterizing the footprint of eddy covariance system and large aperture scintillometer measurements to validate satellite-based surface fluxes. IEEE Geosci. Remote Sens. Lett. 2015, 12, 943–947. [Google Scholar]
- Meijninger, W.M.L.; Hartogensis, O.K.; Kousiek, W.; Hoedjes, J.C.B.; Zuurbier, R.M.; Bruin, H.A.R.D. Determination of area-averaged sensible heat fluxes with a large aperture scintillometer over a heterogeneous surface—Flevoland field experiment. Bound. Layer Meteorol. 2002, 105, 37–62. [Google Scholar] [CrossRef]
- Chehbouni, A. Estimation of heat and momentum fluxes over complex terrain using a large aperture scintillometer. Agric. For. Meteorol. 2000, 105, 215–226. [Google Scholar] [CrossRef]
- Beyrich, F.; Bruin, H.A.R.D.; Meijninger, W.L.; Schipper, J.W. Results from one-year continuous operation of a large aperture scintillometer over a heterogeneous land surface. Bound. Layer Meteorol. 2001, 105, 85–97. [Google Scholar] [CrossRef]
- Hemakumara, H.M.; Lalith, C.; Moene, A.F. Evapotranspiration fluxes over mixed vegetations areas measured from large aperture scintillometer. Agric. Water Manag. 2003, 58, 109–112. [Google Scholar] [CrossRef]
- McAneney, K.J.; Green, A.E.; Astill, M.S. Large-aperture scintillometry: The homogeneous case. Agric. For. Meteorol. 1995, 76, 149–162. [Google Scholar] [CrossRef]
- Hoedjes, J.C.B.; Zuurbier, R.M.; Watts, C.J. Large aperture scintillometer used over a homogeneous irrigated area, partly affected by regional advection. Bound. Layer Meteorol. 2002, 105, 99–117. [Google Scholar] [CrossRef]
- Ezzahar, J.; Chehbouni, A.; Er-Raki, S.; Hanich, L. Combining a large aperture scintillometer and estimates of available energy to derive evapotranspiration over several agricultural fields in a semi-arid region. Plant Biosyst. Int. J. Deal. All Asp. Plant Biol. 2009, 143, 209–221. [Google Scholar] [CrossRef]
- Xu, F.; Wang, W.; Wang, J.; Xu, Z.; Qi, Y.; Wu, Y. Area-averaged evapotranspiration over a heterogeneous land surface: Aggregation of multi-point ec flux measurements with high-resolution land-cover map and footprint analysis. Hydrol. Earth Syst. Sci. Discuss. 2016, 1–37. [Google Scholar] [CrossRef]
- Liu, S.M.; Xu, Z.W.; Wang, W.Z.; Jia, Z.Z.; Zhu, M.J.; Bai, J.; Wang, J.M. A comparison of eddy-covariance and large aperture scintillometer measurements with respect to the energy balance closure problem. Hydrol. Earth Syst. Sci. Discuss. 2011, 15, 1291–1306. [Google Scholar] [CrossRef]
- Lu, L.; Cheng, Y.; Bian, L.; Lu, C.; Ding, G. A study of the turbulence fluxes transfer of CO2, sensible heat and latent heat for the surface layer over the typical rice field, yangtdz delta. Chin. J. Geophys. 2003, 46, 1078–1090. [Google Scholar] [CrossRef]
- Timm, A.U.; Roberti, D.R.; Streck, N.A.; Gustavo, G.; de Gonçalves, L.; Acevedo, O.C.; Moraes, O.L.L.; Moreira, V.S.; Degrazia, G.A.; Ferlan, M.; et al. Energy partitioning and evapotranspiration over a rice paddy in southern brazil. J. Hydrometeorol. 2014, 15, 1975–1988. [Google Scholar] [CrossRef]
- Harazono, Y.; Kim, J.; Miyata, A.; Choi, T.; Yun, J.-T.; Kim, J.-W. Measurement of energy budget components during the international rice experiment (irex) in Japan. Hydrol. Process. 1998, 12, 2081–2092. [Google Scholar] [CrossRef]
- Shi, S.; Huang, B.; Liu, S.; Yang, Y.; Huang, Y.; Xu, Z. Development of ameasuring system for surface energy and water vapor fluxes at large scale. Adv. Atmos. Sci. 2010, 25, 1128–1138. [Google Scholar]
- Dyer, A.J. A review of flux-profile relationships. Bound. Layer Meteorol. 1974, 7, 363–372. [Google Scholar] [CrossRef]
- Vickers, D.; Mahrt, L. Quality control and flux sampling problems for tower and aircraft data. J. Atmos. Ocean. Technol. 1997, 14, 512–526. [Google Scholar] [CrossRef]
- Moncrieff, J.; Clement, R.; Finnigan, J.; Meyers, T. Averaging, detrending, and filtering of eddy covariance time series. In Handbook of Micrometeorology; Lee, X.H., Massman, W., Law, B., Eds.; Springer: New York, NY, USA, 2004; pp. 7–31. [Google Scholar]
- Moncrieff, J.B.; Massheder, J.; De Bruin, H.; Elbers, J.; Friborg, T.; Heusinkveld, B.; Kabat, P.; Scott, S.; Soegaard, H.; Verhoef, A. A system to measure surface fluxes of momentum, sensible heat, water vapour and carbon dioxide. J. Hydrol. 1997, 188, 589–611. [Google Scholar] [CrossRef]
- Burba, G.; Schmidt, A.; Scott, R.L.; Nakai, T.; Kathilankal, J.; Fratini, G.; Hanson, C.; Law, B.; McDermitt, D.K.; Eckles, R. Calculating CO2 and H2O eddy covariance fluxes from an enclosed gas analyzer using an instantaneous mixing ratio. Glob. Chang. Biol. 2012, 18, 385–399. [Google Scholar] [CrossRef]
- Wang, T.-I.; Ochs, G.; Clifford, S. A saturation-resistant optical scintillometer to measure Cn2. J. Opt. Soc. Am. 1978, 68, 334–338. [Google Scholar] [CrossRef]
- Hill, R.; Clifford, S.; Lawrence, R. Refractive-index and absorption fluctuations in the infrared caused by temperature, humidity, and pressure fluctuations. J. Opt. Soc. Am. 1980, 70, 1192–1205. [Google Scholar] [CrossRef]
- Wesely, M.L. The combined effect of temperature and humidity fluctuations on refractive index. J. Appl. Meteorol. 1976, 15, 43–49. [Google Scholar] [CrossRef]
- Odhiambo, G.; Savage, M. Sensible heat flux by surface layer scintillometry and eddy covariance over a mixed grassland community as affected by bowen ratio and most formulations for unstable conditions. J. Hydrometeorol. 2009, 10, 479–492. [Google Scholar] [CrossRef]
- Ochs, G.R.; Hill, R.J. Optical-scintillation method of measuring turbulence inner scale. Appl. Opt. 1985, 24, 2430–2432. [Google Scholar] [CrossRef] [PubMed]
- Wyngaard, J.; Izumi, Y.; Collins, S.A. Behavior of the refractive-index-structure parameter near the ground. J. Opt. Soc. Am. 1971, 61, 1646–1650. [Google Scholar] [CrossRef]
- Wyngaard, J.C. On Surface Layer Turbulence; Haugen, D.A., Ed.; Workshop on Micrometeorology; American Meteorological Society: Boston, MA, USA, 1973; pp. 101–149. [Google Scholar]
- Andreas, E.L. Estimating Cn2 over snow and sea ice from meteorological data. J. Opt. Soc. Am. 1988, 5, 481–495. [Google Scholar] [CrossRef]
- Thiermann, V.; Grassl, H. The measurement of turbulent surface-layer fluxes by use of bichromatic scintillation. Bound. Layer Meteorol. 1992, 58, 367–389. [Google Scholar] [CrossRef]
- De Bruin, H.; Kohsiek, W.; Van den Hurk, B. A verification of some methods to determine the fluxes of momentum, sensible heat, and water vapour using standard deviation and structure parameter of scalar meteorological quantities. Bound. Layer Meteorol. 1993, 63, 231–257. [Google Scholar] [CrossRef]
- Kaimal, J.C.; Finnigan, J.J. Atmospheric Boundary Layer Flows: Their Structure and Measurement; Oxford University Press: New York, NY, USA, 1994. [Google Scholar]
- Edson, J.B.; Fairall, C.W. Similarity relationships in the marine atmospheric surface layer for terms in the tke and scalar variance budgets. J. Atmos. Sci. 1998, 55, 2311–2328. [Google Scholar] [CrossRef]
- Gruber, M.; Fochesatto, G.J. A new sensitivity analysis and solution method for scintillometer measurements of area-averaged turbulent fluxes. Bound. Layer Meteorol. 2013, 149, 65–83. [Google Scholar] [CrossRef]
- Finkelstein, P.L.; Sims, P.F. Sampling error in eddy correlation flux measurements. J. Geophys. Res. Atmos. 2001, 106, 3503–3509. [Google Scholar] [CrossRef]
- Gruber, M.A.; Fochesatto, G.J.; Hartogensis, O.K.; Lysy, M. Functional derivatives applied to error propagation of uncertainties in topography to large-aperture scintillometer-derived heat fluxes. Atmos. Meas. Tech. 2014, 7, 2361–2371. [Google Scholar] [CrossRef]
- Hartogensis, O.K.; Watts, C.J.; Rodriguez, J.C.; Bruin, H.A.R.D. Derivation of an effective height for scintillometers la poza experiment in Northwest Mexico. J. Hydrometeorol. 2003, 4, 915–928. [Google Scholar] [CrossRef]
- Peng, G.; Xuhui, C.; Shaomin, L. A flux footprint model for large aperture scintillometer. Acta Sci. Nat. Univ. Pekin 2007, 43, 822–827. [Google Scholar]
- Kormann, R.; Meixner, F.X. An analytical footprint model for non-neutral stratification. Bound. Layer Meteorol. 2001, 99, 207–224. [Google Scholar] [CrossRef]
- Kleissl, J.; Hong, S.-H.; Hendrickx, J.M.H. New mexico scintillometer network: Supporting remote sensing and hydrologic and meteorological models. Bull. Am. Meteorol. Soc. 2009, 90, 207–218. [Google Scholar] [CrossRef]
- Alfieri, J.G.; Blanken, P.D. How representative is a point? The spatial variability of surface energy fluxes across short distances in a sand-sagebrush ecosystem. J. Arid Environ. 2012, 87, 42–49. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, H.; Cai, X.; Song, Y.; Sun, J. Contribution of low-frequency motions to sensible heat fluxes over urban and suburban areas. Bound. Layer Meteorol. 2016, 161, 183–201. [Google Scholar] [CrossRef]
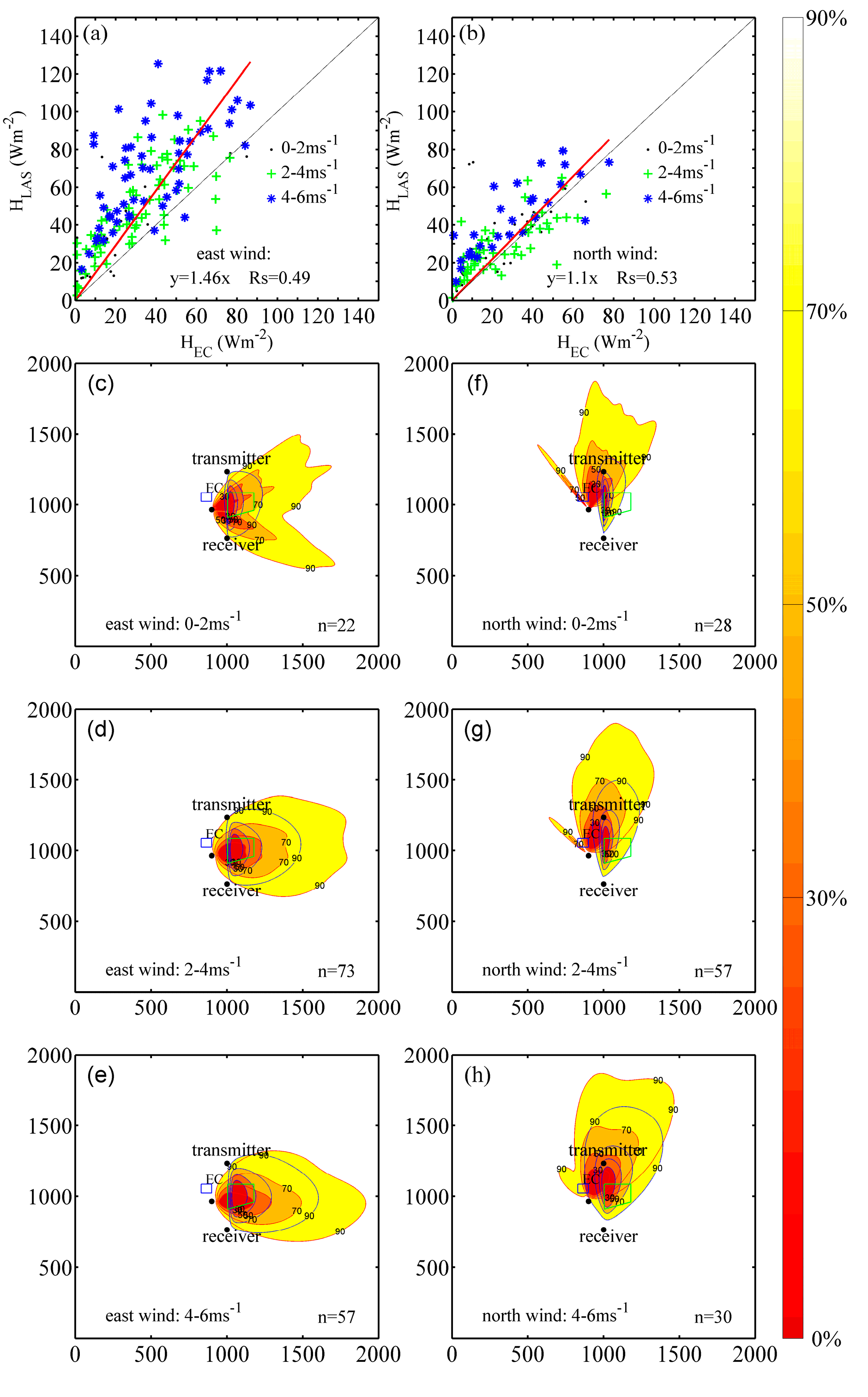
| Wind Direction | Factors | k | Rs | RMSE | LAS Mean | EC Mean |
|---|---|---|---|---|---|---|
| East | (kg m−3) | 1.01 | 0.60 | 9.82 × 10−5 | 1.20 | 1.18 |
| (m s−1) | 0.60 | 0.20 | 0.015 | 0.26 | 0.38 | |
| (K) | 1.97 | 0.11 | 0.025 | −0.21 | −0.079 | |
| North | (kg m−3) | 1.02 | 0.66 | 9.13 × 10−5 | 1.20 | 1.17 |
| (m s−1) | 0.51 | 0.41 | 0.0048 | 0.20 | 0.37 | |
| (K) | 1.6 | 0.25 | 0.013 | −0.16 | −0.067 |
| Date | Rnavg | LEavg | WSavg | WD | HLASavg | HECavg | KLASmavg | KECmavg |
|---|---|---|---|---|---|---|---|---|
| (W m−2) | (W m−2) | (m s−1) | - | (W m−2) | (W m−2) | - | - | |
| 28 September | 499.74 | 360.77 | 5.68 | East | 79.92 | 60.79 | 33.78% | 36.05% |
| 2 October | 497.95 | 350.06 | 3.12 | West | 55.24 | 47.03 | 3.06% | 0% |
| 5 October | 494.84 | 364.84 | 2.91 | East | 76.12 | 41.64 | 45.15% | 21.92% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Gao, Z.; Li, Y.; Tong, B. Comparison of Sensible Heat Fluxes Measured by a Large Aperture Scintillometer and Eddy Covariance System over a Heterogeneous Farmland in East China. Atmosphere 2017, 8, 101. https://doi.org/10.3390/atmos8060101
Li X, Gao Z, Li Y, Tong B. Comparison of Sensible Heat Fluxes Measured by a Large Aperture Scintillometer and Eddy Covariance System over a Heterogeneous Farmland in East China. Atmosphere. 2017; 8(6):101. https://doi.org/10.3390/atmos8060101
Chicago/Turabian StyleLi, Xin, Zhiqiu Gao, Yubin Li, and Bing Tong. 2017. "Comparison of Sensible Heat Fluxes Measured by a Large Aperture Scintillometer and Eddy Covariance System over a Heterogeneous Farmland in East China" Atmosphere 8, no. 6: 101. https://doi.org/10.3390/atmos8060101
APA StyleLi, X., Gao, Z., Li, Y., & Tong, B. (2017). Comparison of Sensible Heat Fluxes Measured by a Large Aperture Scintillometer and Eddy Covariance System over a Heterogeneous Farmland in East China. Atmosphere, 8(6), 101. https://doi.org/10.3390/atmos8060101







