Application of Convective Condensation Level Limiter in Convective Boundary Layer Height Retrieval Based on Lidar Data
Abstract
:1. Introduction
2. Measurement Site, Instruments and Data
3. CBLH Detection Methods
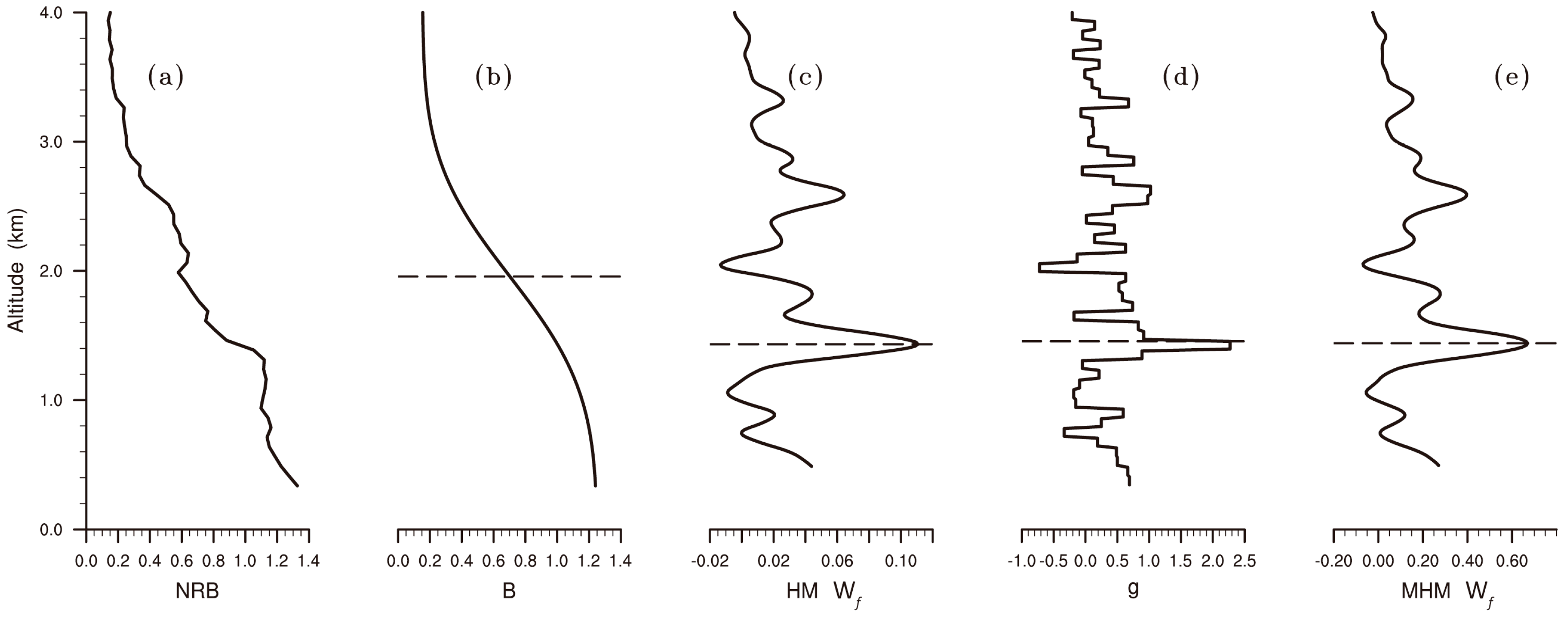
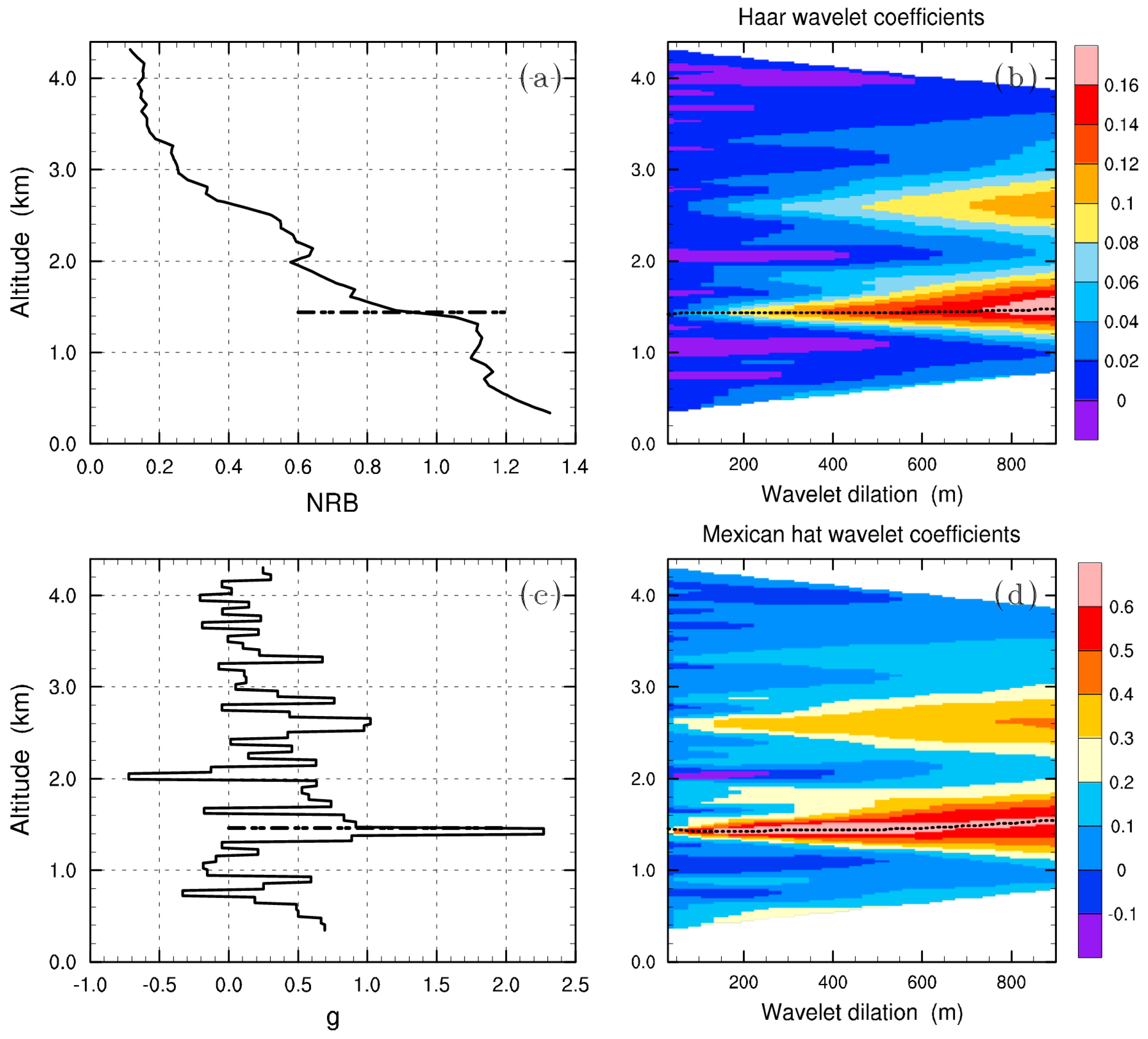
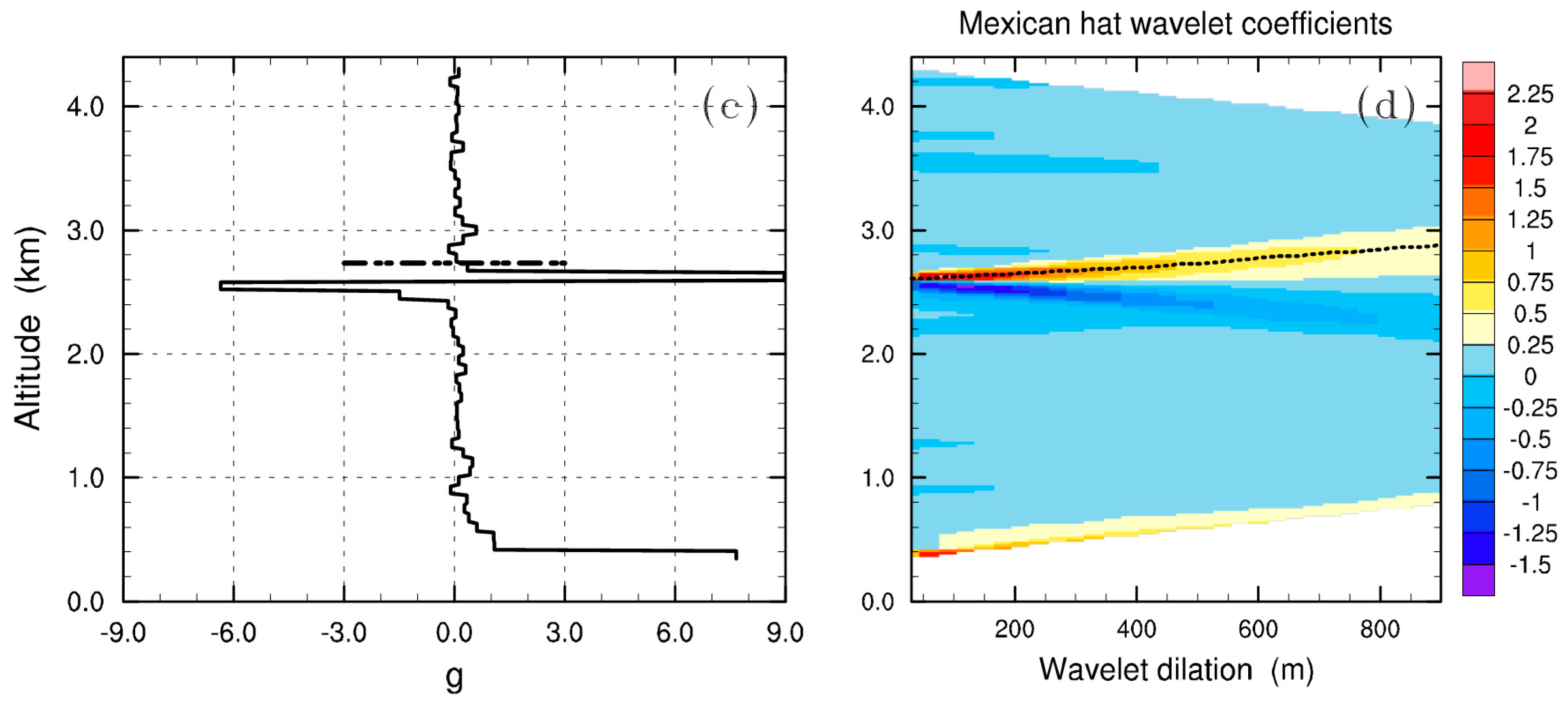
3.1. Methods for Estimating the CBLH from Lidar Backscatter Data
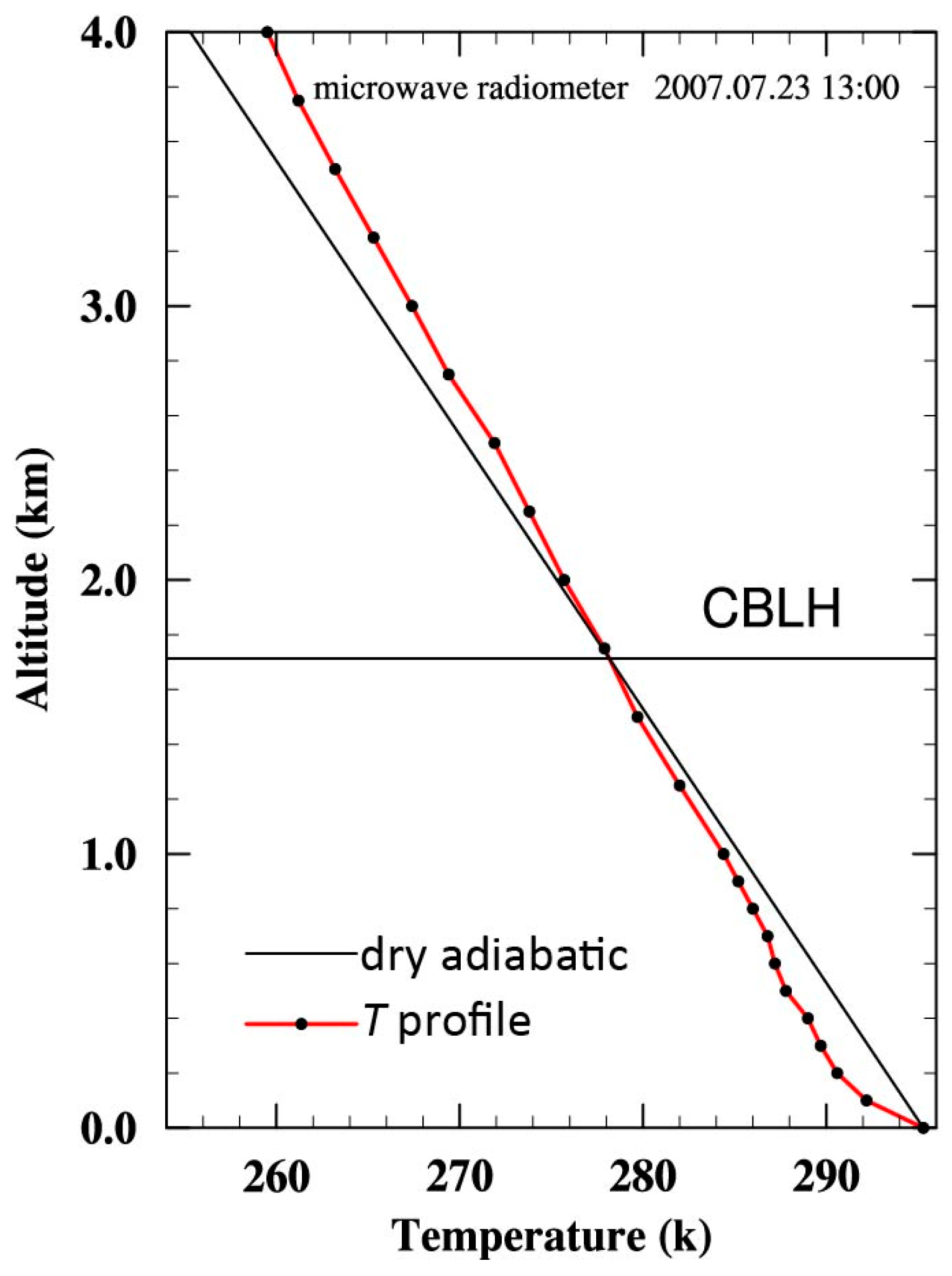
3.2. Methods for Estimating the CBLH from Microwave Radiometer Temperature Data
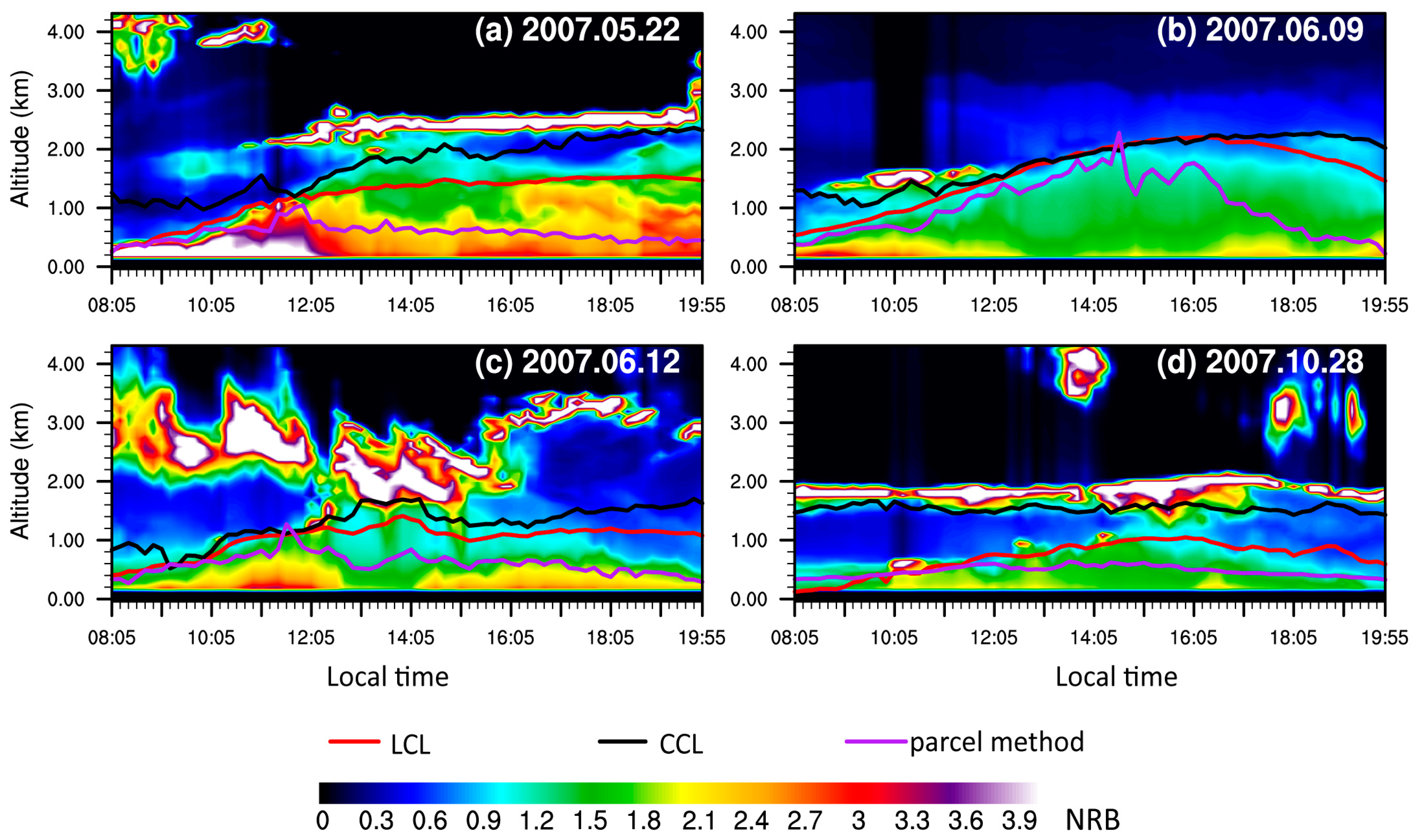
3.3. Convective Condensation Level Limiter
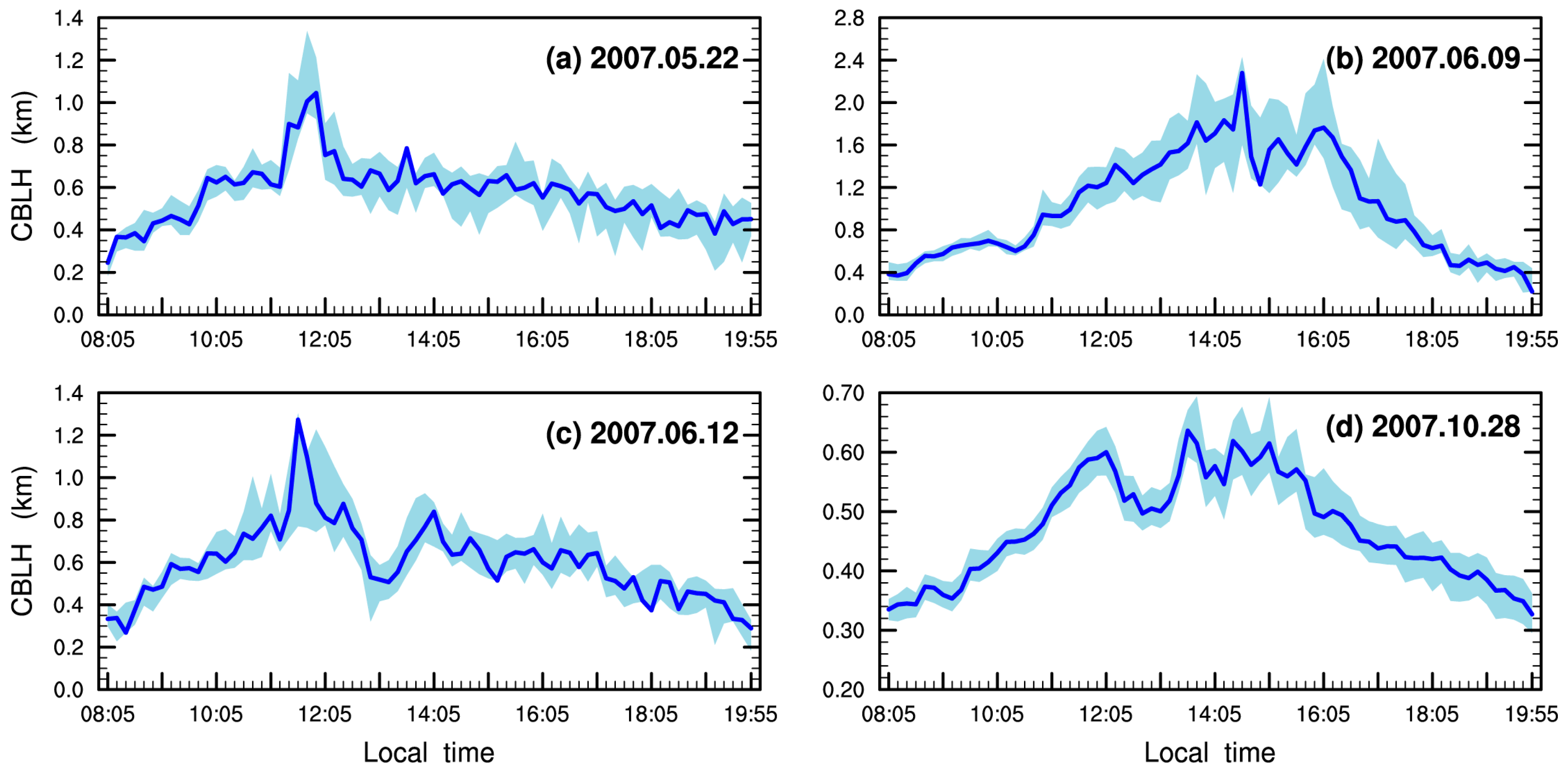
4. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988; pp. 13–16. [Google Scholar]
- Holzworth, C.G. Estimates of mean maximum mixing depths in the contiguous United States. Mon. Weather Rev. 1964, 92, 235–242. [Google Scholar] [CrossRef]
- Menut, L.; Flamant, C.; Pelon, J.; Flamant, P.H. Urban boundary-layer height determination from lidar measurements over the Paris area. Appl. Opt. 1999, 38, 945–954. [Google Scholar] [CrossRef] [PubMed]
- Morille, Y.; Haeffelin, M.; Drobinski, P.; Pelon, J. STRAT: An automated algorithm to retrieve the vertical structure of the atmosphere from single-channel lidar data. J. Atmos. Ocean. Technol. 2007, 24, 761–775. [Google Scholar] [CrossRef]
- Granados-Muñoz, M.J.; Navas-Guzmán, F.; Bravo-Aranda, J.A.; Guerrero-Rascado, J.L.; Lyamani, H.; Fernández-Gálvez, J.; Alados-Arboledas, L. Automatic determination of the planetary boundary layer height using lidar: One-year analysis over southeastern Spain. J. Geophys. Res. 2012, 117, D18208. [Google Scholar] [CrossRef]
- Huang, M.; Gao, Z.; Miao, S.; Chen, F.; Lemone, M.A.; Li, J.; Hu, F.; Wang, L. Estimate of Boundary-Layer Depth over Beijing, China, Using Doppler Lidar Data during SURF-2015. Bound. Layer Meteorol. 2016, 162, 503–522. [Google Scholar] [CrossRef]
- Seibert, P.; Beyrich, F.; Gryning, S.-E.; Joffre, S.; Rasmussen, A.; Tercier, P. Review and intercomparison of operational methods for the determination of the mixing height. Atmos. Environ. 2000, 34, 1001–1027. [Google Scholar] [CrossRef]
- Lammert, A.; Bösenberg, J. Determination of the convective boundary-layer height with laser remote sensing. Bound. Layer Meteorol. 2006, 119, 159–170. [Google Scholar] [CrossRef]
- Sicard, M.; Pérez, C.; Rocadenbosch, F.; Baldasano, J.M.; García-Vizcaino, D. Mixed-layer depth determination in the barcelona coastal area from regular lidar measurements: methods, results and limitations. Bound. Layer Meteorol. 2006, 119, 135–157. [Google Scholar] [CrossRef]
- Emeis, S.; Schäfer, K.; Münkel, C. Surface-based remote sensing of the mixing-layer height—A review. Meteorol. Z. 2008, 17, 621–630. [Google Scholar] [CrossRef] [PubMed]
- Haeffelin, M.; Angelini, F.; Morille, Y.; Martucci, G.; Frey, S.; Gobbi, G.P.; Lolli, S.; O’Dowd, C.D.; Sauvage, L.; Xueref-Rémy, I.; et al. Evaluation of mixing-height retrievals from automatic profiling lidars and ceilometers in view of future integrated networks in Europe. Bound. Layer Meteorol. 2012, 143, 49–75. [Google Scholar] [CrossRef]
- Pappalardo, G.; Amodeo, A.; Apituley, A.; Comeron, A.; Freudenthaler, V.; Linné, H.; Ansmann, A.; Bösenberg, J.; D’Amico, G.; Mattis, I.; et al. EARLINET: Towards an advanced sustainable European aerosol lidar network. Atmos. Meas. Tech. 2014, 7, 2929–2980. [Google Scholar] [CrossRef]
- Atsushi, S.; Nobuo, S.; Ichiro, M.; Kimio, A.; Itsushi, U.; Toshiyuki, M.; Naoki, K.; Kazuma, A.; Akihiro, U.; Akihiro, Y. Continuous observations of Asian dust and other aerosols by polarization lidars in China and Japan during ACE-Asia. J. Geophys. Res. 2004, 109, 1255–1263. [Google Scholar]
- Guerrero-Rascado, J.L.; Landulfo, E.; Antuña, J.C.; Barbosa, H.M.J.; Barja, B.; Bastidas, Á.E.; Bedoya, A.E.; Costa, R.; Estevan, R.; Forno, R.; et al. Latin American Lidar Network (LALINET) for aerosol research: Diagnosis on network instrumentation. J. Atmos. Sol. Terr. Phys. 2016, 138–139, 112–120. [Google Scholar] [CrossRef]
- Welton, E.J.; Campbell, J.R.; Spinhirne, J.D.; Scott, V.S. Global monitoring of clouds and aerosols using a network of micropulse lidar systems. Proc. Int. Soc. Opt. Eng. 2001, 4153, 151–158. [Google Scholar]
- Baars, H.; Ansmann, A.; Engelmann, R.; Althausen, D. Continuous monitoring of the boundary-layer top with lidar. Atmos. Chem. Phys. 2008, 8, 7281–7296. [Google Scholar] [CrossRef]
- Pal, S.; Behrendt, A.; Wulfmeyer, V. Elastic-backscatter-lidar-based characterization of the convective boundary layer and investigation of related statistics. Ann. Geophys. 2010, 28, 825–847. [Google Scholar] [CrossRef]
- Hayden, K.L.; Anlauf, K.J.; Hoff, R.M.; Strapp, J.W.; Bottenheim, J.W.; Wiebe, H.A.; Froude, F.A.; Martin, J.B.; Steyn, D.G.; McKendry, I.G. The vertical chemical and meteorological structure of the boundary layer in the Lower Fraser Valley during Pacific’93. Atmos. Environ. 1997, 31, 2089–2105. [Google Scholar] [CrossRef]
- Flamant, C.; Pelon, J.; Flamant, P.H.; Durand, P. Lidar determination of the entrainment zone thickness at the top of the unstable marine atmospheric boundary layer. Bound. Layer Meteorol. 1997, 83, 247–284. [Google Scholar] [CrossRef]
- Steyn, D.G.; Baldi, M.; Hoff, R.M. The detection of mixed layer depth and entrainment zone thickness from lidar backscatter profiles. J. Atmos. Ocean. Technol. 1999, 16, 953–959. [Google Scholar] [CrossRef]
- Davis, K.J.; Gamage, N.; Hagelberg, C.R.; Kiemle, C.; Lenschow, D.H.; Sullivan, P.P. An objective method for deriving atmospheric structure from airborne lidar observations. J. Atmos. Ocean. Technol. 2000, 17, 1455–1468. [Google Scholar] [CrossRef]
- Cohn, S.A.; Angevine, W.M. Boundary layer height and entrainment zone thickness measured by lidars and wind-profiling radars. J. Appl. Meteorol. 2000, 39, 1233–1247. [Google Scholar] [CrossRef]
- Brooks, I.M. Finding boundary layer top: Application of a wavelet covariance transform to lidar backscatter profiles. J. Atmos. Ocean. Technol. 2003, 20, 1092–1105. [Google Scholar] [CrossRef]
- Pal, S.; Haeffelin, M.; Batchvarova, E. Exploring a geophysical process-based attribution technique for the determination of the atmospheric boundary layer depth using aerosol lidar and near-surface meteorological measurements. J. Geophys. Res. Atmos. 2013, 118, 9277–9295. [Google Scholar] [CrossRef]
- Bravo-Aranda, J.A.; Moreira, G.A.; Navas-Guzmán, F.; Granados-Muñoz, M.J.; Guerrero-Rascado, J.L.; Pozo-Vázquez, D.; Arbizu-Barrena, C.; Reyes, F.J.O.; Mallet, M.; Alados-Arboledas, L. PBL height estimation based on lidar depolarisation measurements (POLARIS). Atmos. Chem. Phys. Discuss. 2016, 1–24. [Google Scholar] [CrossRef]
- Li, H.; Yang, Y.; Hu, X.M.; Huang, Z.W.; Wang, G.Y.; Zhang, B.D.; Zhang, T.J. Evaluation of retrieval methods of daytime convective boundary layer height based on lidar data. J. Geophys. Res. 2017. [Google Scholar] [CrossRef]
- Hennemuth, B.; Lammert, A. Determination of the atmospheric boundary layer height from radiosonde and lidar backscatter. Bound. Layer Meteorol. 2006, 120, 181–200. [Google Scholar] [CrossRef]
- Grimsdell, A.W.; Angevine, W.M. Convective boundary layer height measurement with wind profilers and comparison to cloud base. J. Atmos. Ocean. Technol. 1998, 15, 1331–1338. [Google Scholar] [CrossRef]
- Collaud-Coen, M.; Praz, C.; Haefele, A.; Ruffieux, D.; Kaufmann, P.; Calpini, B. Determination and climatology of the planetary boundary layer height above the swiss plateau by in situ and remote sensing measurements as well as by the COSMO-2 model. Atmos. Chem. Phys. 2014, 14, 13205–13221. [Google Scholar] [CrossRef]
- Angevine, W.M.; White, A.B.; Avery, S.K. Boundary-layer depth and entrainment zone characterization with a boundary-layer profiler. Bound. Layer Meteorol. 1994, 68, 375–385. [Google Scholar] [CrossRef]
- McGrath-Spangler, E.L.; Denning, A.S. Estimates of North American summertime planetary boundary layer depths derived from space-borne lidar. J. Geophys. Res. 2012, 117, D15101. [Google Scholar] [CrossRef]
- Wang, Z.; Sassen, K. Cloud type and macrophysical property retrieval using multiple remote sensors. J. Appl. Meteorol. 2001, 40, 1665–1683. [Google Scholar] [CrossRef]
- Winker, D.M.; Vaughan, M.A. Vertical distribution of clouds over Hampton, Virginia, observed by lidar under the ECLIPS and FIRE ETO programs. Atmos. Res. 1994, 34, 117–133. [Google Scholar] [CrossRef]
- Caicedo, V.; Rappenglueck, B.; Lefer, B.; Morris, G.; Toledo, D.; Delgado, R. Comparison of aerosol lidar retrieval methods for boundary layer height detection using ceilometer backscatter data. Atmos. Meas. Tech. Discuss. 2016, 1–24. [Google Scholar] [CrossRef]
- Huang, Z.; Huang, J.; Bi, J.; Wang, G.; Wang, W.; Fu, Q.; Li, Z.; Tsay, S.-C.; Shi, J. Dust aerosol vertical structure measurements using three MPL lidars during 2008 China-U.S. joint dust field experiment. J. Geophys. Res. 2010, 115, 1307–1314. [Google Scholar] [CrossRef]
- Campbell, J.R.; Hlavka, D.L.; Welton, E.J.; Flynn, C.J.; Turner, D.D.; Spinhirne, J.D.; Scott, V.S.; Wang, I.H. Full-Time, Eye-Safe Cloud and Aerosol Lidar Observation at Atmospheric Radiation Measurement Program Sites: Instruments and Data Processing. J. Atmos. Ocean. Technol. 2002, 19, 431–442. [Google Scholar] [CrossRef]
- Sasano, Y.; Shimizu, H.; Takeuchi, N.; Okuda, M. Geometrical form factor in the laser radar equation: An experimental determination. Appl. Opt. 1979, 18, 3908–3910. [Google Scholar] [CrossRef] [PubMed]
- Dho, S.W.; Park, Y.J.; Kong, H.J. Experimental determination of a geometric form factor in a lidar equation for an inhomogeneous atmosphere. Appl. Opt. 1997, 36, 6009–6010. [Google Scholar] [CrossRef] [PubMed]
- Wandinger, U.; Ansmann, A. Experimental determination of the lidar overlap profile with raman lidar. Appl. Opt. 2002, 41, 511–514. [Google Scholar] [CrossRef] [PubMed]
- Mao, F.; Gong, W.; Li, J. Geometrical form factor calculation using monte carlo integration for lidar. Opt. Laser Technol. 2012, 44, 907–912. [Google Scholar] [CrossRef]
- Chen, R.; Jiang, Y.; Wang, H. Calculation method of the overlap factor and its enhancement for airborne lidar. Opt. Commun. 2014, 331, 181–188. [Google Scholar] [CrossRef]
- Fernald, F.G.; Herman, B.M.; Reagan, J.A. Determination of Aerosol Height Distributions by Lidar. J. Appl. Meteorol. 1972, 11, 482–489. [Google Scholar] [CrossRef]
- Ware, R.; Carpenter, R.; Güldner, J.; Liljegren, J.; Nehrkorn, T.; Solheim, F.; Vandenberghe, F. A multichannel radiometric profiler of temperature, humidity, and cloud liquid. Radio Sci. 2003, 44, 77–88. [Google Scholar] [CrossRef]
- Ruffieux, D.; Nash, J.; Jeannet, P.; Agnew, J.L. The COST 720 temperature, humidity, and cloud profiling campaign: TUC. Meteorol. Z. 2006, 15, 5–10. [Google Scholar] [CrossRef]
- Eresmaa, N.; Karppinen, A.; Joffre, S.M.; Räsänen, J.; Talvitie, H. Mixing height determination by ceilometers. Atmos. Chem. Phys. 2006, 6, 1485–1493. [Google Scholar] [CrossRef]
- Zhang, B.D.; Huang, J.P.; Guo, Y.; Shang, J.; Wu, Q. Retrieval of atmospheric temperature, humidity profile and attenuation estimation using a twele channel ground-based microwave radiometer. J. Lanzhou Univ. (Nat. Sci.) 2015, 2, 193–201. (In Chinese) [Google Scholar]
- Wang, Z.; Cao, X.; Zhang, L.; Notholt, J.; Zhou, B.; Liu, R.; Zhang, B. Lidar measurement of planetary boundary layer height and comparison with microwave profiling radiometer observation. Atmos. Meas. Tech. 2012, 5, 1965–1972. [Google Scholar] [CrossRef]
- Di-Liberto, L.; Angelini, F.; Pietroni, I.; Cairo, F.; Di Donfrancesco, G.; Viola, A.; Argentini, S.; Fierli, F.; Gobbi, G.; Maturilli, M.; et al. Estimate of the arctic convective boundary layer height from lidar observations: a case study. Adv. Meteorol. 2012, 8, 978–988. [Google Scholar] [CrossRef]
- Eresmaa, N.; Härkönen, J.; Joffre, S.M.; Schultz, D.M.; Karppinen, A.; Kukkonen, J. A Three-Step Method for Estimating the Mixing Height Using Ceilometer Data from the Helsinki Testbed. J. Appl. Meteor. Climatol. 2012, 51, 2172–2187. [Google Scholar] [CrossRef]
- Davis, K.J.; Lenschow, D.H.; Oncley, S.P.; Kiemle, C.; Ehret, G.; Giez, A. Role of entrainment in surface-atmosphere interactions over the boreal forest. J. Geophys Res. 1997, 102, 29219–29230. [Google Scholar] [CrossRef]
- Zhou, Z.; Adeli, H. Time-frequency signal analysis of earthquake records using Mexican hat wavelets. Comput. Aided Civ. Inf. 2003, 18, 379–389. [Google Scholar] [CrossRef]
- Rogers, R.; Yau, M. A Short Course in Cloud Physics, 3nd ed.; Pergamon Press: New York, NY, USA, 1989. [Google Scholar]
- Stackpole, J.D. Numerical analysis of atmospheric soundings. J. Appl. Meteorol. 1967, 6, 464–467. [Google Scholar] [CrossRef]
- Stull, R.B. Meteorology Today: For Scientist and Engineers; West Publishing Company: Minneapolis, MN, USA, 1995; p. 385. [Google Scholar]

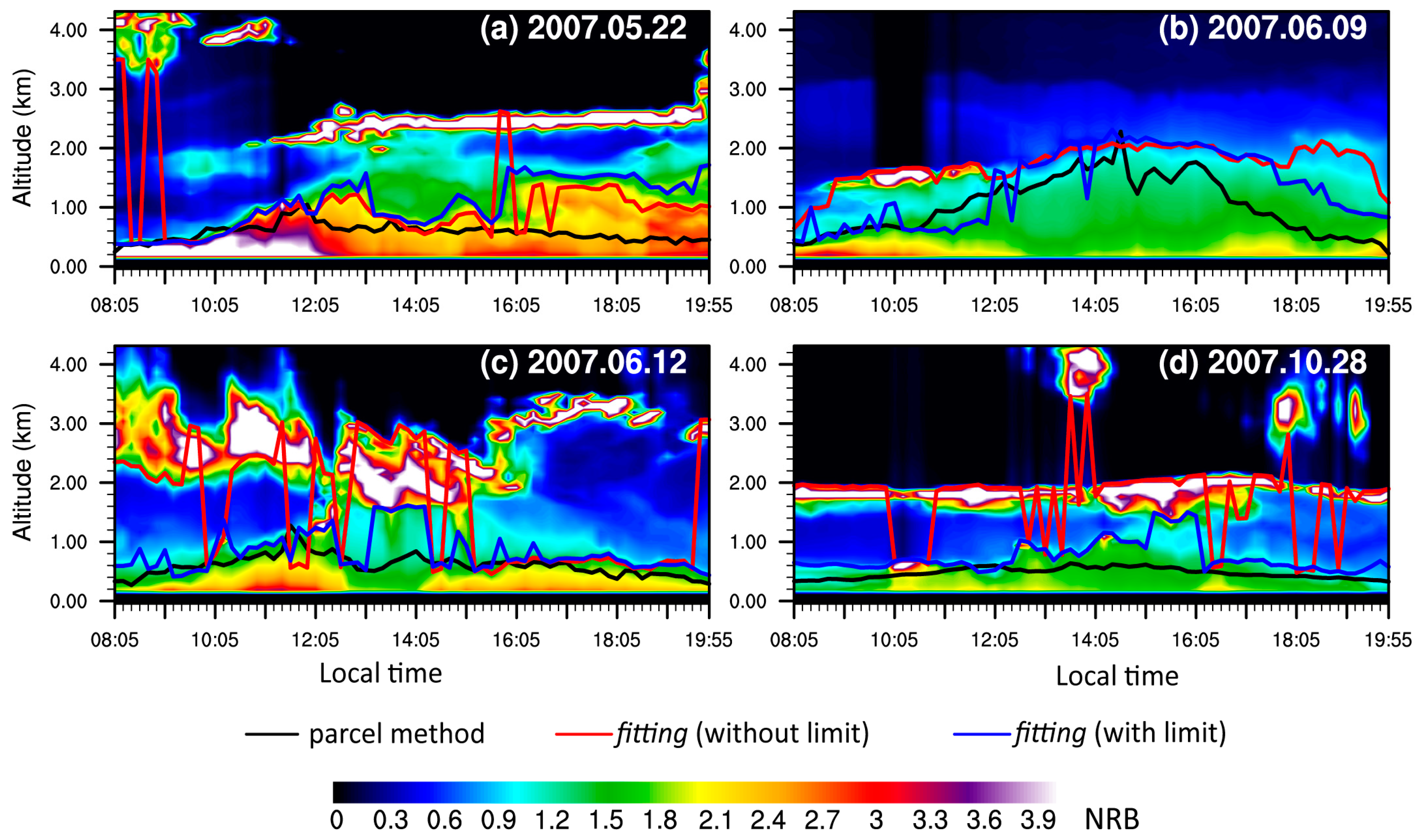
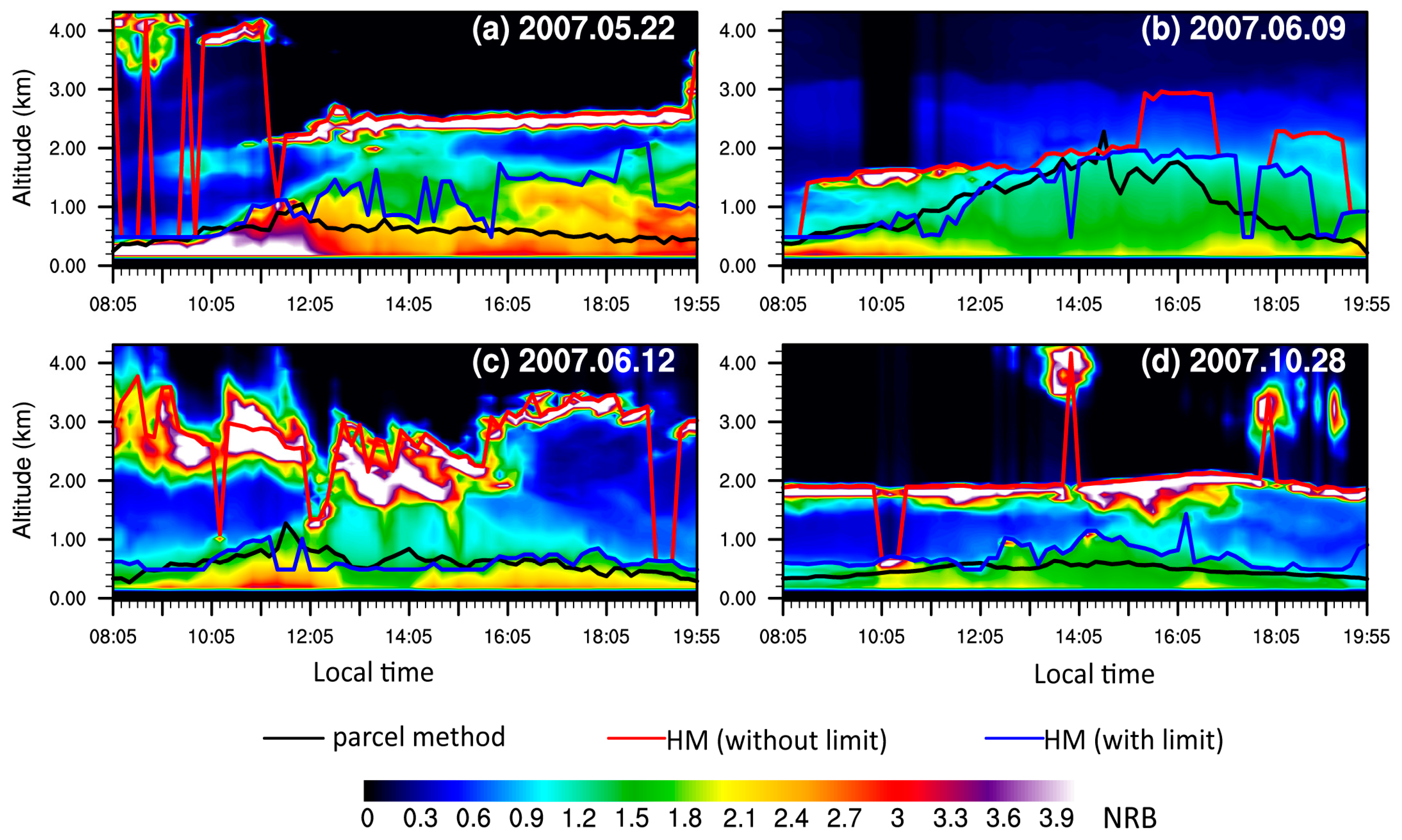
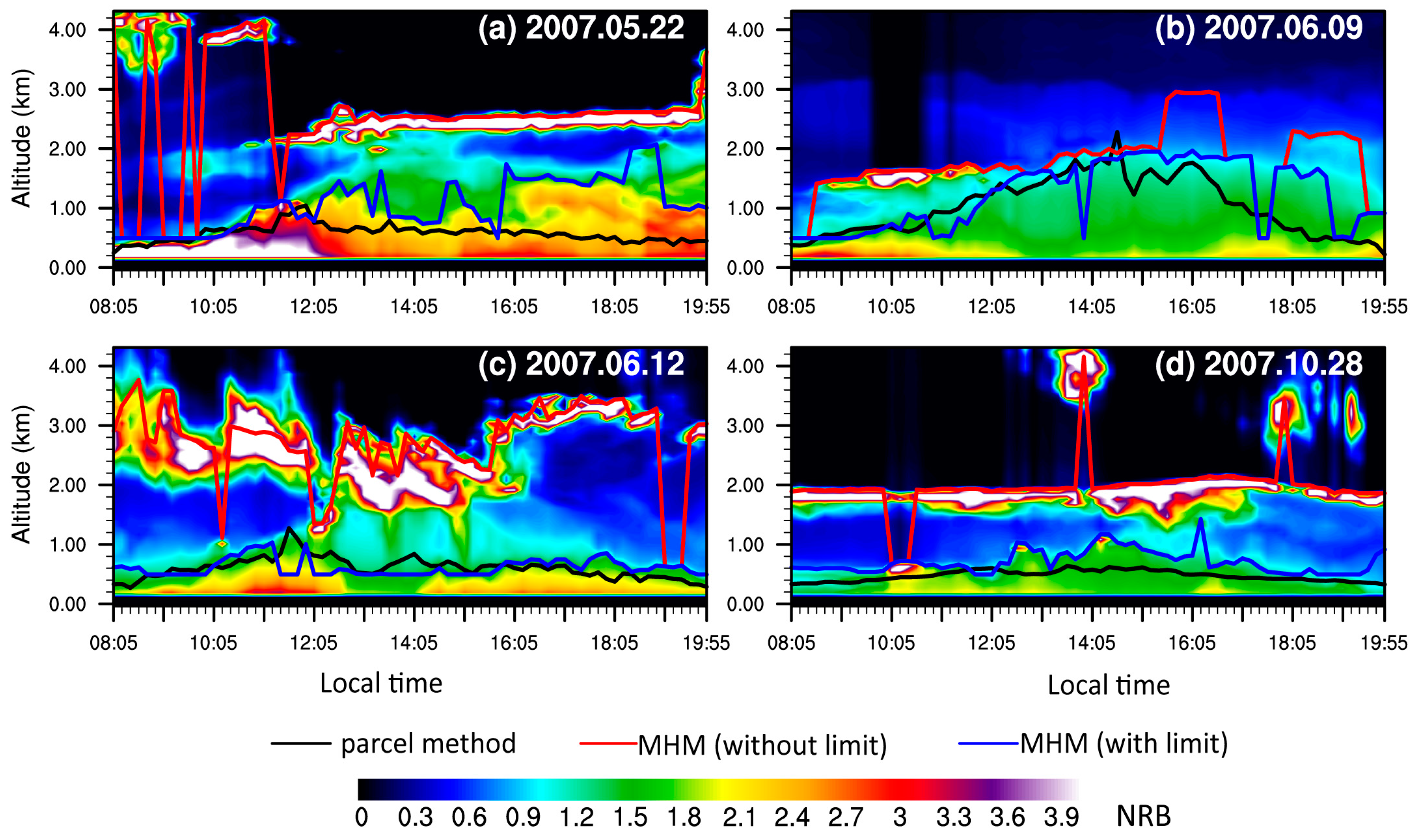
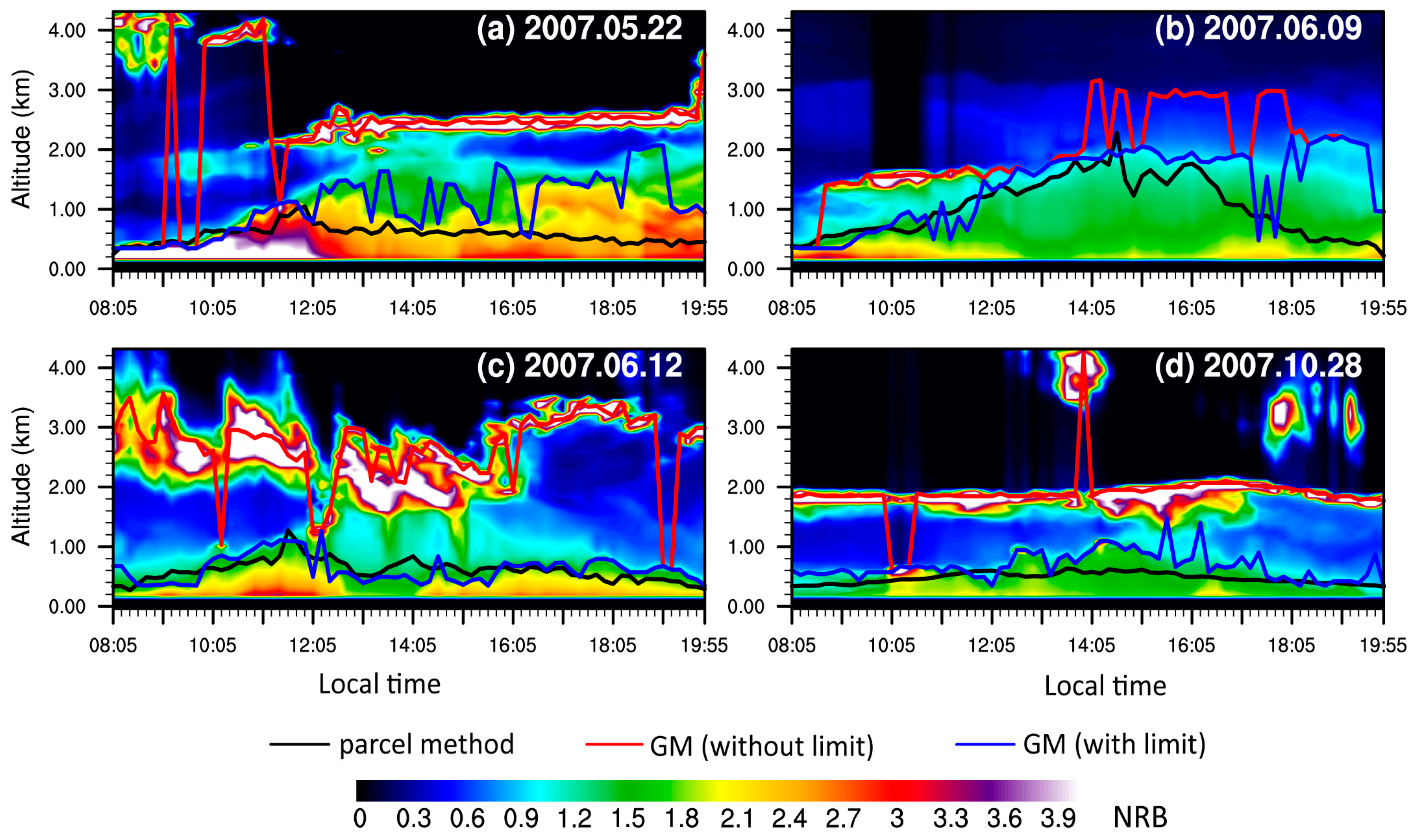
| Date (Year/Month/Day) | GM (Without Limit) | GM (With Limit) | fitting (Without Limit) | fitting (With Limit) | HM (Without Limit) | HM (With Limit) | MHM (Without Limit) | MHM (With Limit) |
|---|---|---|---|---|---|---|---|---|
| 2007.05.22 | 1.796 | 0.532 | 0.530 | 0.507 | 1.949 | 0.522 | 2.001 | 0.513 |
| 2007.06.09 | 0.953 | 0.485 | 0.712 | 0.436 | 0.822 | 0.350 | 0.796 | 0.348 |
| 2007.06.12 | 2.092 | 0.180 | 1.046 | 0.271 | 2.144 | 0.174 | 2.149 | 0.173 |
| 2007.10.28 | 1.412 | 0.222 | 1.263 | 0.279 | 1.480 | 0.243 | 1.494 | 0.244 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Yang, Y.; Hu, X.-M.; Huang, Z.; Wang, G.; Zhang, B. Application of Convective Condensation Level Limiter in Convective Boundary Layer Height Retrieval Based on Lidar Data. Atmosphere 2017, 8, 79. https://doi.org/10.3390/atmos8040079
Li H, Yang Y, Hu X-M, Huang Z, Wang G, Zhang B. Application of Convective Condensation Level Limiter in Convective Boundary Layer Height Retrieval Based on Lidar Data. Atmosphere. 2017; 8(4):79. https://doi.org/10.3390/atmos8040079
Chicago/Turabian StyleLi, Hong, Yi Yang, Xiao-Ming Hu, Zhongwei Huang, Guoyin Wang, and Beidou Zhang. 2017. "Application of Convective Condensation Level Limiter in Convective Boundary Layer Height Retrieval Based on Lidar Data" Atmosphere 8, no. 4: 79. https://doi.org/10.3390/atmos8040079
APA StyleLi, H., Yang, Y., Hu, X.-M., Huang, Z., Wang, G., & Zhang, B. (2017). Application of Convective Condensation Level Limiter in Convective Boundary Layer Height Retrieval Based on Lidar Data. Atmosphere, 8(4), 79. https://doi.org/10.3390/atmos8040079







