Evaluation of Five Grid Datasets against Radiosonde Data over the Eastern and Downstream Regions of the Tibetan Plateau in Summer
Abstract
:1. Introduction
2. Data Sets
2.1. Grid Datasets
2.2. Satellite Data
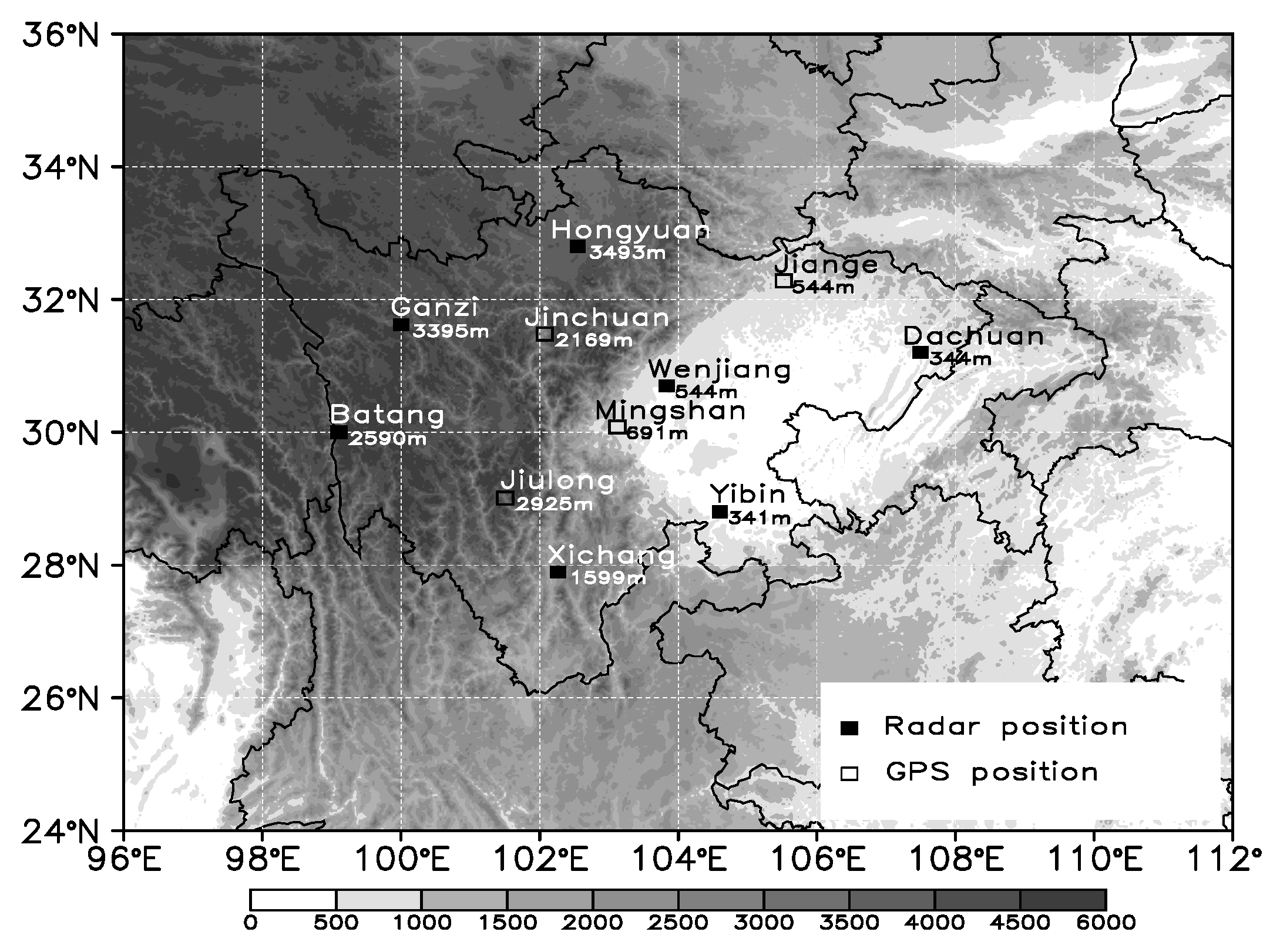
2.3. Radiosonde Data
3. Results
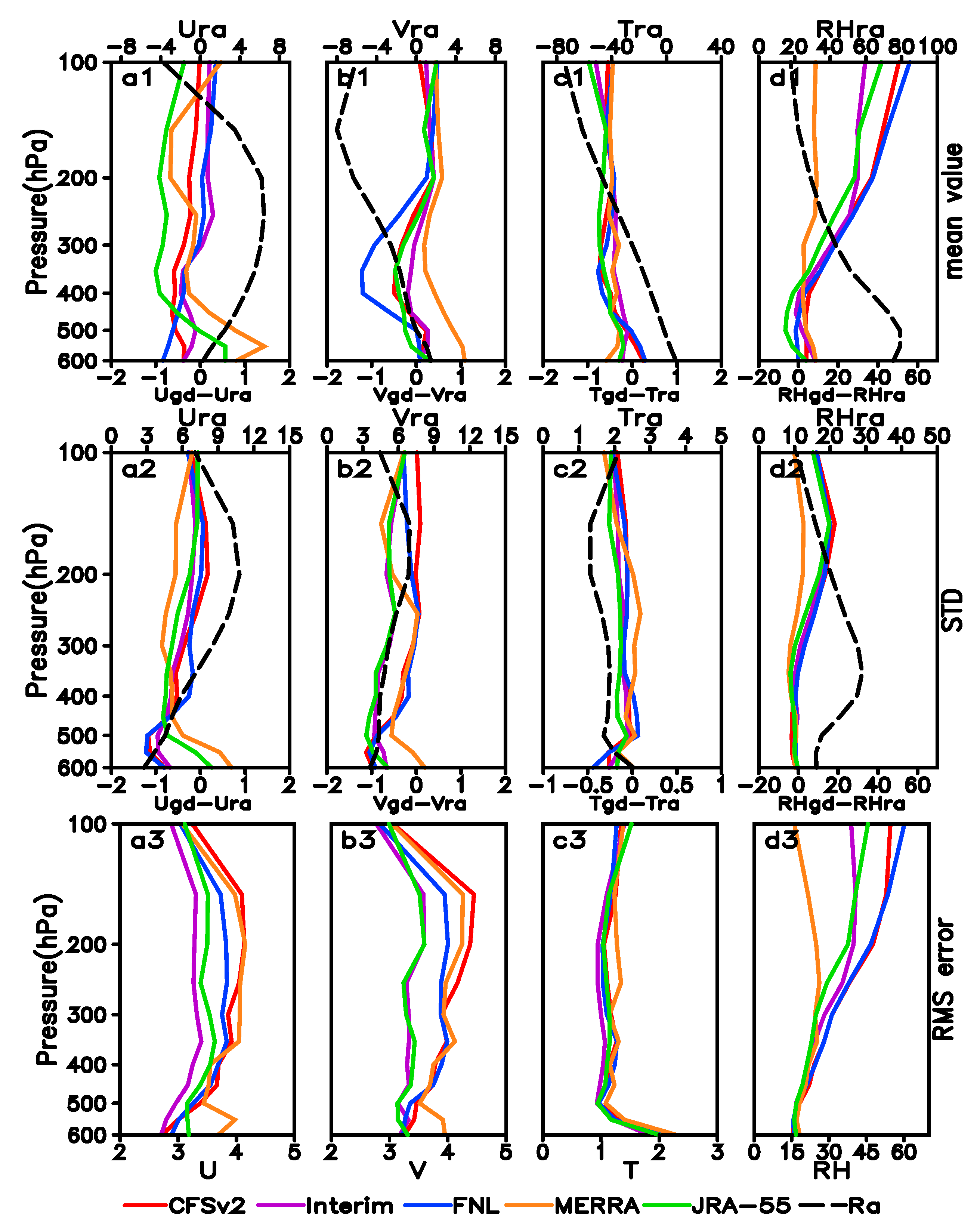
3.1. Overall RMS Error and Mean Bias
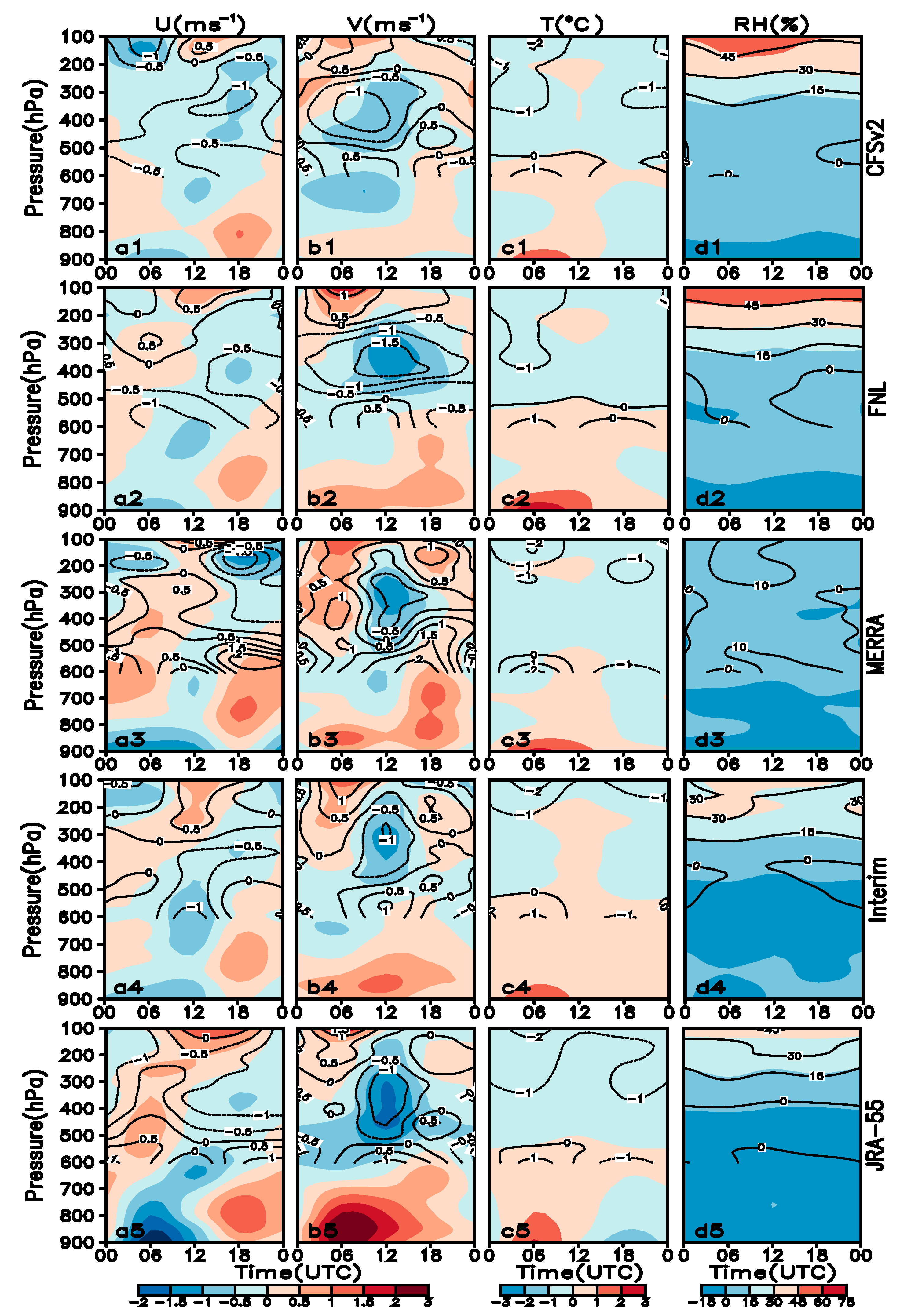
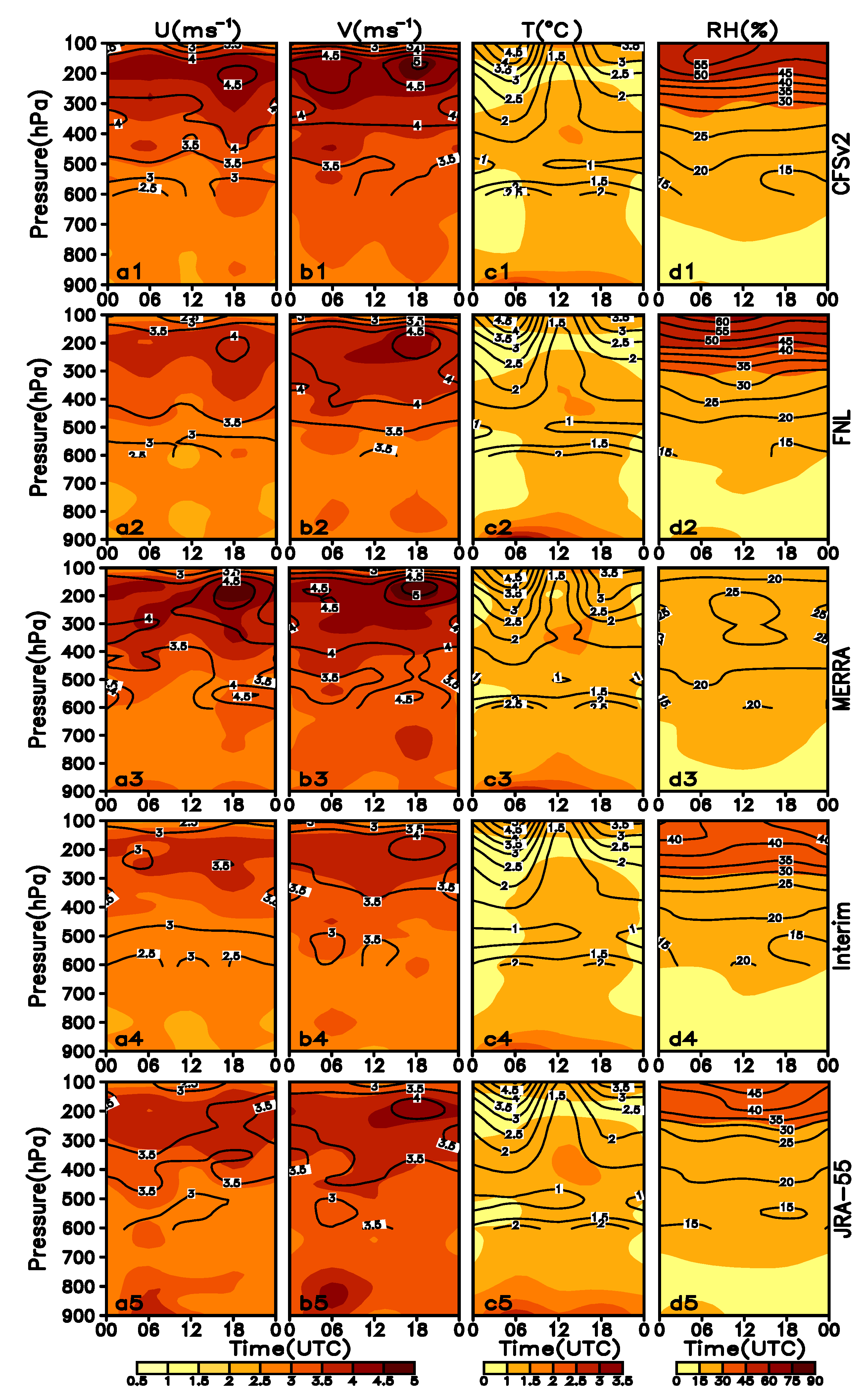
3.2. Diurnal and Interannual Variations of the Mean Bias and RMS Error
3.3. Variations of RMS Error and Bias in Different Weather Conditions
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jiang, X.; Li, Y.; Zhao, X. Characteristics of the Summertime Boundary Layer and Atmospheric Vertical Structure over the Sichuan Basin. J. Meteorol. Soc. Jpn. 2012, 90, 33–54. [Google Scholar] [CrossRef]
- Yeh, T.C.; Lo, S.W.; Chu, P.C. On the heat balance and circulation structure in troposphere over Tibetan Plateau. Acta Meteor. Sin. 1957, 28, 108–121. (In Chinese) [Google Scholar]
- Flohn, H. Large-scale aspects of the ‘summer monsoon’ in South and East Asia. J. Meteorol. Soc. Jpn. 1957, 75, 180–186. [Google Scholar]
- Zhou, X.-P.; Hu, X.-F. A brief analysis and numerical simulation of the Sichuan extraordinarily heavy rainfall event. In Proceedings of the First Sino-American Workshop on Mountain Meteorology, Beijing, China, 18–23 May 1982.
- Kuo, Y.-H.; Cheng, L.; Anthes, R.A. Mesoscale analyses of the Sichuan flood catastrophe. Mon. Rev. 1986, 114, 1984–2003. [Google Scholar] [CrossRef]
- Bao, X.; Zhang, F.; Sun, J. Diurnal variations of warm season precipitation east of the Tibetan Plateau over China. Mon. Weather Rev. 2011, 139, 2790–2810. [Google Scholar] [CrossRef]
- Qian, T.; Zhao, P.; Zhang, F.; Bao, X. Rainy-Season Precipitation over the Sichuan Basin and Adjacent Regions in Southwestern China. Mon. Weather Rev. 2015, 143, 383–394. [Google Scholar] [CrossRef]
- Yanai, M.; Li, C.; Song, Z. Seasonal heating of the Tibetan Plateau and its effects on the evolution of the Asian summer monsoon. J. Meteorol. Soc. Jpn. 1992, 70, 319–351. [Google Scholar]
- Xu, X.; Chen, L.; Zhou, M. The Second Tibetan Plateau Experiment of Atmospheric Sciences: TIPEX-GAME/TIBET; China Meteorological Press: Beijing, China, 2002; p. 236. (In Chinese)
- Zhou, M.; Xu, X.; Bian, L.; Chen, J.; Liu, H.; Zhang, Y.; Li, S.; Zhao, Y. Observations, Diagnostics, and Dynamics of the Atmospheric Boundary Layer over the Tibetan Plateau during TIPEX 1998; China Meteorological Press: Beijing, China, 2000; p. 125. (In Chinese)
- Li, Y.; Gao, W. Atmospheric boundary layer circulation on the eastern edge of the Tibetan Plateau, China, in summer. Arct. Antarct. Alp. Res. 2007, 39, 708–713. [Google Scholar] [CrossRef]
- Betts, A.K.; Köhler, M.; Zhang, Y. Comparison of river basin hydrometeorology in ERA-Interim and ERA-40 reanalysis with observations. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Mao, J.; Shi, X.; Ma, L.; Kaiser, D.P.; Li, Q.; Thornton, P.E. Assessment of reanalysis daily extreme temperatures with China’s homogenized historical dataset during 1979–2001 using probability density functions. J. Clim. 2010, 23, 6605–6623. [Google Scholar] [CrossRef]
- Mooney, P.A.; Mulligan, F.J.; Fealy, R. Comparison of ERA-40, ERA-Interim and NCEP/NCAR reanalysis data with observed surface air temperatures over Ireland. Int. J. Clim. 2010, 31, 545–557. [Google Scholar] [CrossRef]
- Zhao, T.; Fu, C. Comparison of products from ERA-40, NCEP-2, and CRU with station data for summer precipitation over China. Adv. Atmos. Sci. 2006, 23, 593–604. [Google Scholar] [CrossRef]
- Wang, A.; Zeng, X. Evaluation of multireanalysis products with in situ observations over the Tibetan Plateau. J. Geophys. Res. 2012, 117, 214–221. [Google Scholar] [CrossRef]
- Bao, X.; Zhang, F. Evaluation of NCEP-CFSR, NCEP-NCAR, ERA-Interim, and ERA-40 reanalysis datasets against independent sounding observations over the Tibetan Plateau. J. Clim. 2013, 26, 206–214. [Google Scholar] [CrossRef]
- Jiang, X.; Li, Y.; He, G. The Climate Characteristics Analysis of Radiosonde Data over East Part of Tibetan Plateau. Plateau Mt. Meteorol. Res. 2008, 28, 1–9. [Google Scholar]
- Lu, J. Overview of Southwest Vortex; China Meteorology Press: Beijing, China, 1986; pp. 1–270. (In Chinese)
- Tao, S. Rainstorm in China; Science Press: Beijing, China, 1980; pp. 196–199. (In Chinese) [Google Scholar]
- Cheng, L. The vorticity change rate and its heat source for development of Meso-αscale vortex during a persistent heavy rain of 14–22 August 1981. Plateau Meteorol. 1991, 10, 337–350. [Google Scholar]
- Chen, Z.; Min, W.; Cui, C. New Advances in SouthWest China Vortex Research. Plateau Meteotol. 2004, 23, 1–5. [Google Scholar]
- Simmons, A.; Uppala, S.; Dee, D.; Kobayashi, S. ERA-Interim: New ECMWF reanalysis products from 1989 onwards. ECMWF Newsl. 2006, 110, 26–35. [Google Scholar]
- Ebita, A.; Kobayashi, S.; Ota, Y.; Moriya, M.; Kumabe, R.; Onogi, K.; Harada, Y.; Yasui, S.; Miyaoka, K.; Takahashi, K.; et al. The Japanese 55-Year Reanalysis “JRA-55”: An interim report. SOLA 2011, 7, 149–152. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Quart. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Wu, W.-S.; Purser, R.J.; Parrish, D.F. Three-dimensional variational analysis with spatially inhomogeneous covariances. Mon. Weather Rev. 2002, 130, 2905–2916. [Google Scholar] [CrossRef]
- Purser, R.J.; Wu, W.-S.; Parrish, D.F.; Roberts, N.M. Numerical aspects of the application of recursive filters to variational statistical analysis. Part I: Spatially homogeneous and isotropic Gaussian covariances. Mon. Weather Rev. 2003, 131, 1524–1535. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Pan, H.-L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D.; et al. The NCEP Climate Forecast System Reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015–1057. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.-K.; et al. MERRA: NASA’s Modern Era Retrospective Analysis for Research and Applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Shou, S. Synoptic Analysis, 2nd ed.China Meteorological Press: Beijing, China, 2006; p. 322. (In Chinese)
- Li, F. New Developments with Upper-Air Sounding in China; Instruments and Observing Methods Report No. 94; WMO/TD No. 1354; WMO: Geneva, Switzerland, 2006. [Google Scholar]
- NanJing DaQiao Machine Co. Available online: http://www.njdaqiao.com/ (accessed on 15 March 2017).
- Shanghai Changwang Meteotech Co. Available online: http://www.cwqx.com/ (accessed on 15 March 2017).
- He, H.; Zhang, F. Diurnal variations of warm-season precipitation over Northern China. Mon. Weather Rev. 2010, 138, 1017–1025. [Google Scholar] [CrossRef]
- Chen, G.; Iwasaki, T.; Qin, H.; Sha, W. Evaluation of the Warm-Season Diurnal Variability over East Asia in Recent Reanalyses JRA-55, ERA-Interim, NCEP CFSR, and NASA MERRA. Am. Meteorol. Soc. 2014, 27, 5517–5537. [Google Scholar] [CrossRef]

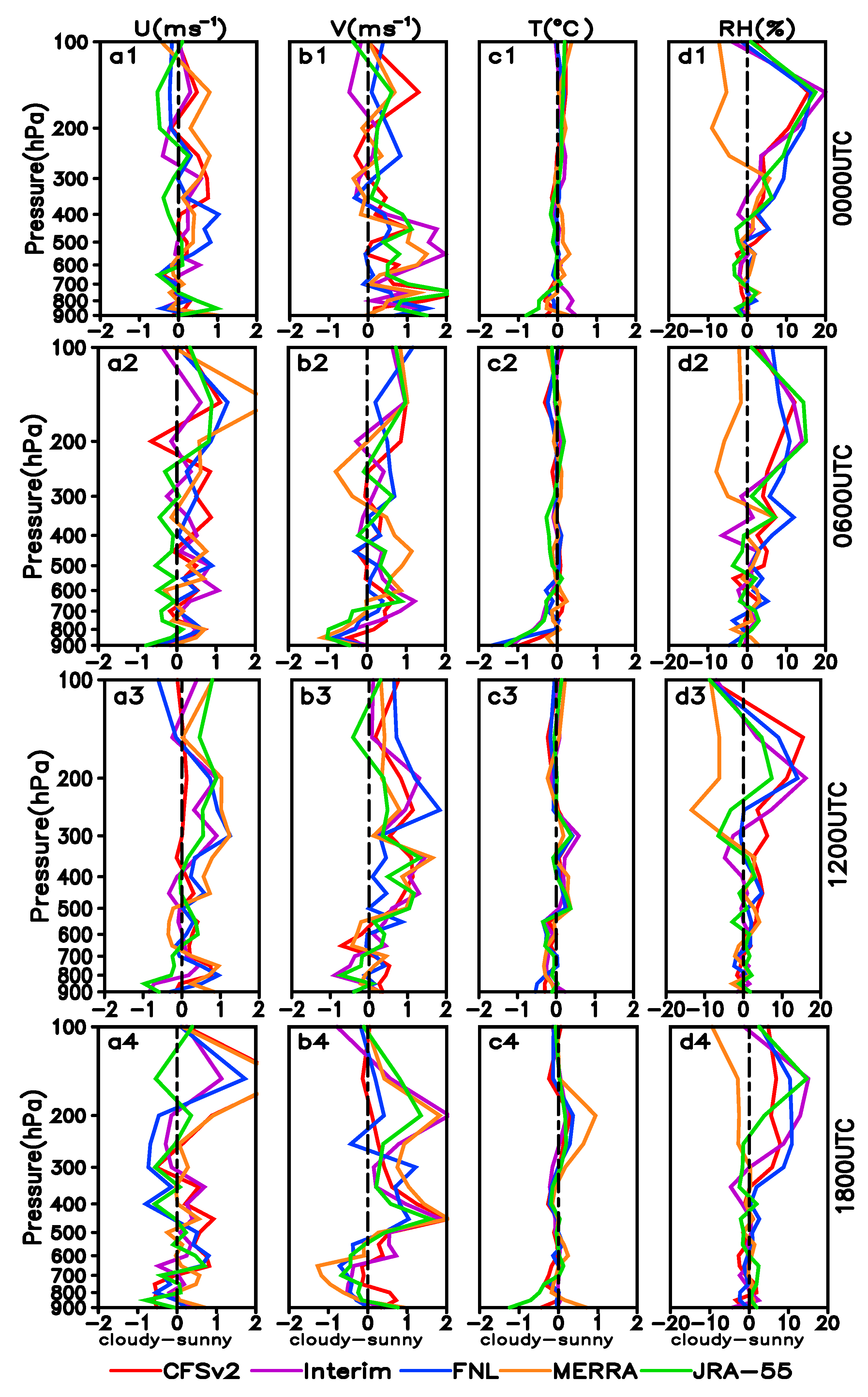

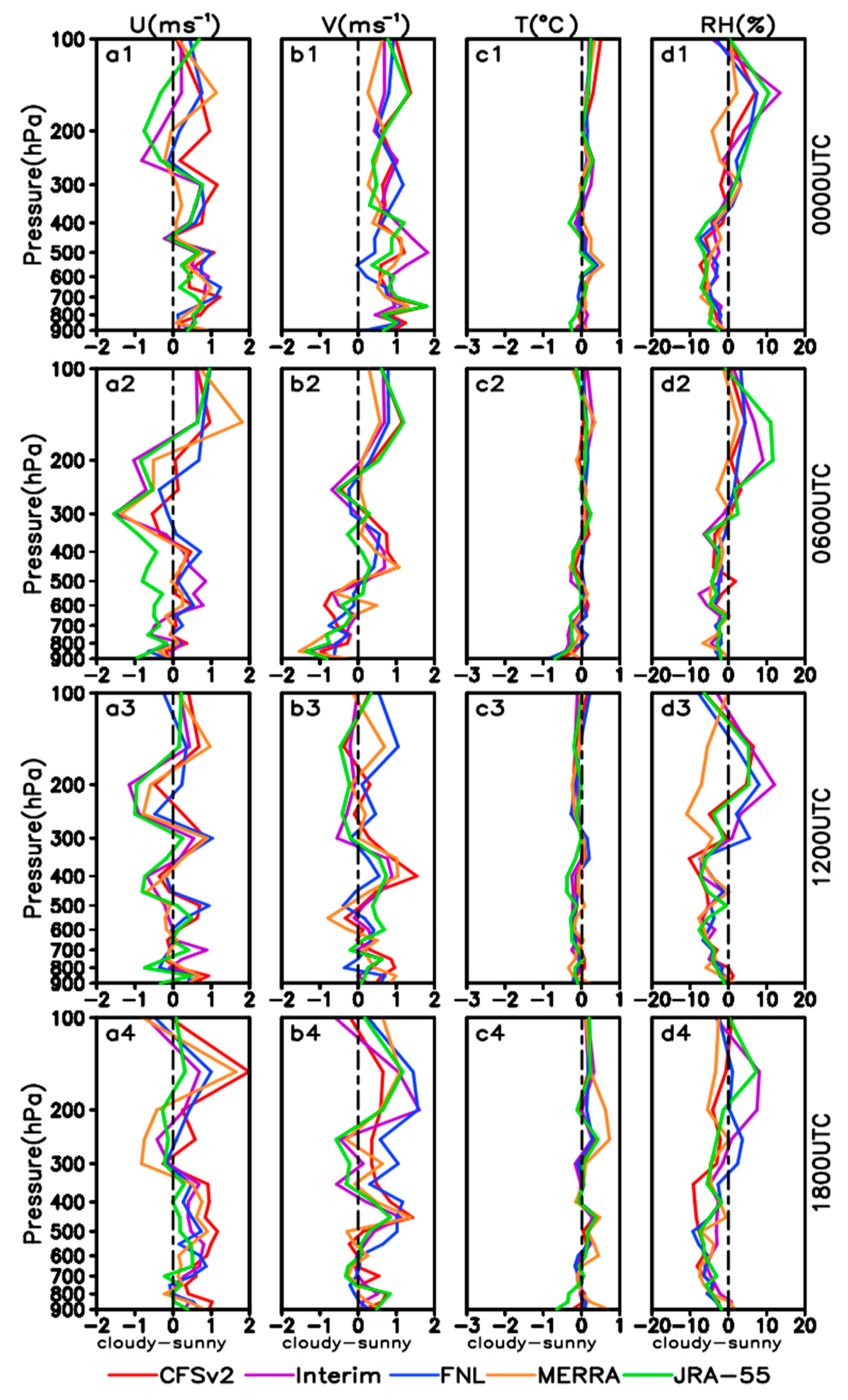
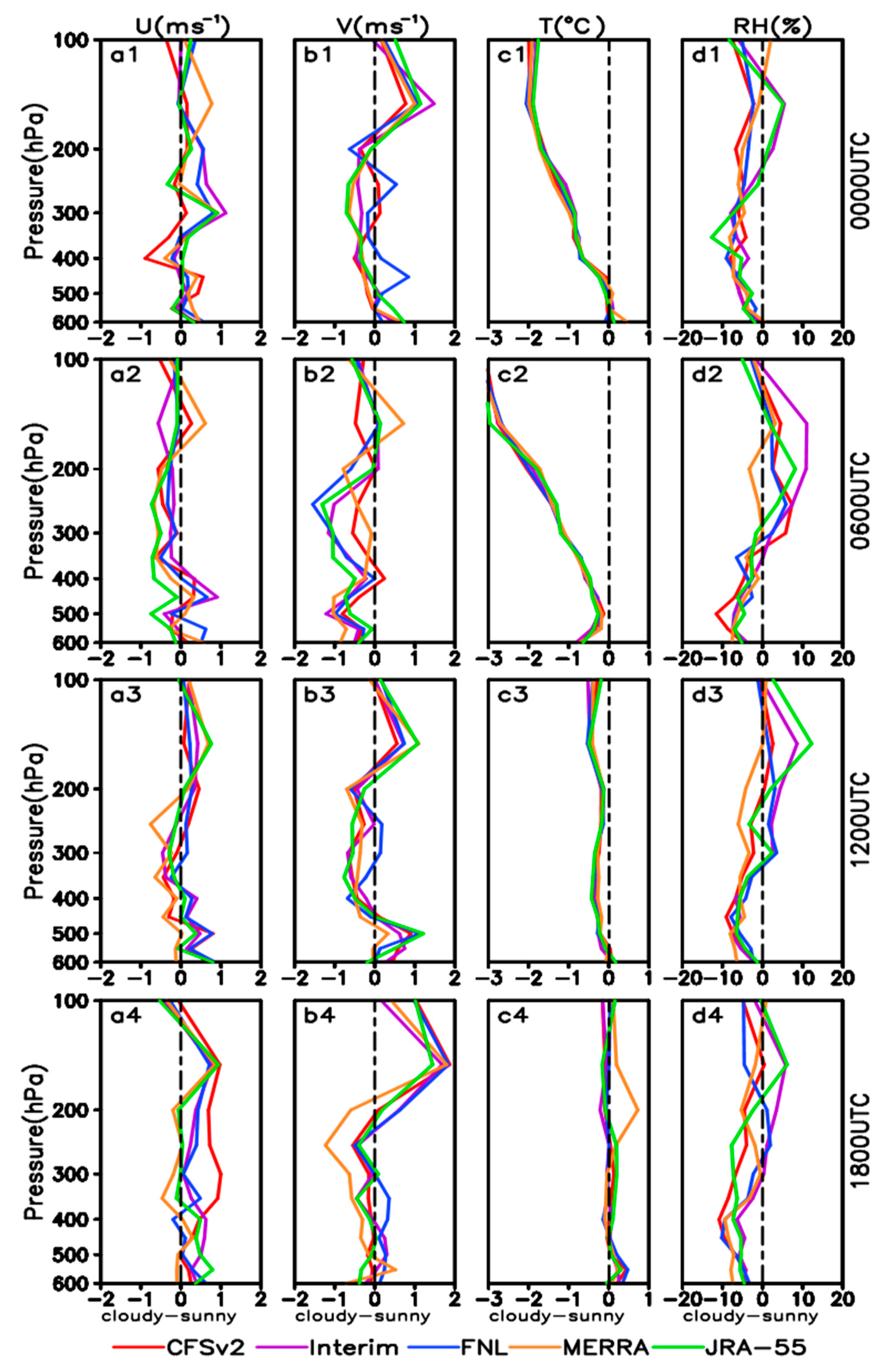
| Mean Bias/ RMS Error | U (m·s−1) | V (m·s−1) | ||||||||
| CFSv2 | FNL | MERRA | Interim | JRA-55 | CFSv2 | FNL | MERRA | Interim | JRA-55 | |
| 200 hPa | 1.1/0.8 | 0.6/0.8 | 0.6/0.5 | 0.9/0.8 | 0.8/1.0 | 0.3/0.7 | 0.3/0.8 | 0.6/0.7 | 0.6/1.8 | 0.9/0.9 |
| 500 hPa | 0.2/0.4 | 0.5/0.3 | 0.5/0.2 | 0.2/0.5 | 0.3/0.3 | 0.3/0.2 | 0.3/0.4 | 0.4/0.2 | 0.6/0.3 | 0.2/0.4 |
| 600 hPa | 0.1/0.4 | 0.2/0.4 | 0.5/0.9 | 0.1/0.5 | 0.2/0.8 | 0.2/1.1 | 0.7/1.2 | 0.4/1.4 | 0.3/1.6 | 0.2/1.1 |
| 700 hPa | 0.3/0.4 | 0.1/0.4 | 0.6/0.7 | 0.2/0.7 | 0.3/0.2 | 0.6/1.0 | 0.7/1.0 | 0.7/0.8 | 0.4/0.8 | 0.4/0.5 |
| 850 hPa | 0.1/0.3 | 0.3/0.4 | 0.4/0.4 | 0.2/0.5 | 0.5/0.4 | 0.8/0.5 | 0.7/1.1 | 0.4/0.3 | 0.8/0.5 | 1.1/1.1 |
| 900 hPa | 0.1/0.2 | 0.7/0.4 | 0.4/0.3 | 0.2/0.7 | 0.7/1.1 | 0.5/0.7 | 0.6/0.5 | 0.4/0.4 | 0.7/0.5 | 1.3/0.6 |
| Mean Bias/ RMS error | T (°C) | RH (%) | ||||||||
| CFSv2 | FNL | MERRA | Interim | JRA-55 | CFSv2 | FNL | MERRA | Interim | JRA-55 | |
| 200 hPa | 0.2/0.1 | 0.3/0.1 | 0.5/0.1 | 0.2/0.1 | 0.2/0.1 | 7/2 | 3/6 | 10/6 | 5/6 | 7/7 |
| 500 hPa | 0.3/0.5 | 0.4/0.7 | 0.4/0.6 | 0.4/0.7 | 0.4/0.6 | 1/4 | 4/4 | 2/3 | 4/3 | 3/6 |
| 600 hPa | 0.2/0.9 | 0.3/0.6 | 0.2/0.5 | 0.3/0.7 | 0.1/0.9 | 4/4 | 8/6 | 4/6 | 2/4 | 2/5 |
| 700 hPa | 0.3/0.2 | 0.3/0.5 | 0.2/0.5 | 0.2/0.6 | 0.4/0.4 | 6/6 | 5/6 | 3/6 | 4/4 | 2/4 |
| 850 hPa | 0.3/0.3 | 0.2/0.3 | 0.4/0.2 | 0.2/0.5 | 0.6/0.2 | 1/2 | 2/1 | 6/3 | 2/1 | 4/2 |
| 900 hPa | 0.5/0.4 | 0.4/0.3 | 0.7/0.5 | 0.4/0.4 | 0.7/0.4 | 2/0 | 4/1 | 8/3 | 1/0 | 4/1 |
| Mean Bias/ RMS Error | U (m·s−1) | V (m·s−1) | ||||||||
| CFSv2 | FNL | MERRA | Interim | JRA-55 | CFSv2 | FNL | MERRA | Interim | JRA-55 | |
| 200 hPa | 0.6/0.5 | 0.3/0.4 | 1.0/1.4 | 0.6/0.9 | 0.5/0.5 | 0.7/0.4 | 0.1/0.7 | 0.8/0.5 | 0.5/0.4 | 0.3/0.4 |
| 500 hPa | 0.4/0.5 | 0.7/0.4 | 0.5/0.2 | 0.8/0.4 | 0.2/0.6 | 0.9/0.4 | 0.5/0.3 | 0.8/0.3 | 0.8/0.3 | 0.3/0.4 |
| 600 hPa | 0.3/0.6 | 0.3/0.5 | 0.7/0.7 | 0.6/0.4 | 0.2/0.6 | 1.0/0.3 | 0.5/1.0 | 1.1/1.2 | 0.5/0.5 | 0.2/0.2 |
| Mean Bias/ RMS error | T (°C) | RH (%) | ||||||||
| CFSv2 | FNL | MERRA | Interim | JRA-55 | CFSv2 | FNL | MERRA | Interim | JRA-55 | |
| 200 hPa | 0.4/0.3 | 0.4/0.3 | 0.5/0.3 | 0.5/0.4 | 0.2/0.3 | 2/4 | 3/7 | 8/6 | 8/8 | 8/8 |
| 500 hPa | 0.1/0.0 | 0.5/0.2 | 0.1/0.1 | 0.1/0.3 | 0.1/0.2 | 4/6 | 7/3 | 2/5 | 2/7 | 2/4 |
| 600 hPa | 0.3/0.3 | 0.1/0.2 | 0.2/0.1 | 0.4/0.3 | 0.4/0.1 | 2/4 | 2/5 | 2/4 | 2/3 | 3/2 |
| Number of Samples | SCB | TP | ||
|---|---|---|---|---|
| Sunny | Cloudy | Sunny | Cloudy | |
| 00:00 UTC | 471 | 98 | 662 | 73 |
| 06:00 UTC | 348 | 85 | 548 | 84 |
| 12:00 UTC | 486 | 62 | 498 | 204 |
| 18:00 UTC | 438 | 68 | 510 | 154 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Y.; Li, G.; Yuan, M.; Xie, X. Evaluation of Five Grid Datasets against Radiosonde Data over the Eastern and Downstream Regions of the Tibetan Plateau in Summer. Atmosphere 2017, 8, 56. https://doi.org/10.3390/atmos8030056
Dong Y, Li G, Yuan M, Xie X. Evaluation of Five Grid Datasets against Radiosonde Data over the Eastern and Downstream Regions of the Tibetan Plateau in Summer. Atmosphere. 2017; 8(3):56. https://doi.org/10.3390/atmos8030056
Chicago/Turabian StyleDong, Yuanchang, Guoping Li, Meng Yuan, and Xiaolin Xie. 2017. "Evaluation of Five Grid Datasets against Radiosonde Data over the Eastern and Downstream Regions of the Tibetan Plateau in Summer" Atmosphere 8, no. 3: 56. https://doi.org/10.3390/atmos8030056
APA StyleDong, Y., Li, G., Yuan, M., & Xie, X. (2017). Evaluation of Five Grid Datasets against Radiosonde Data over the Eastern and Downstream Regions of the Tibetan Plateau in Summer. Atmosphere, 8(3), 56. https://doi.org/10.3390/atmos8030056





