On the Interpretation of Gravity Wave Measurements by Ground-Based Lidars
Abstract
:1. Introduction
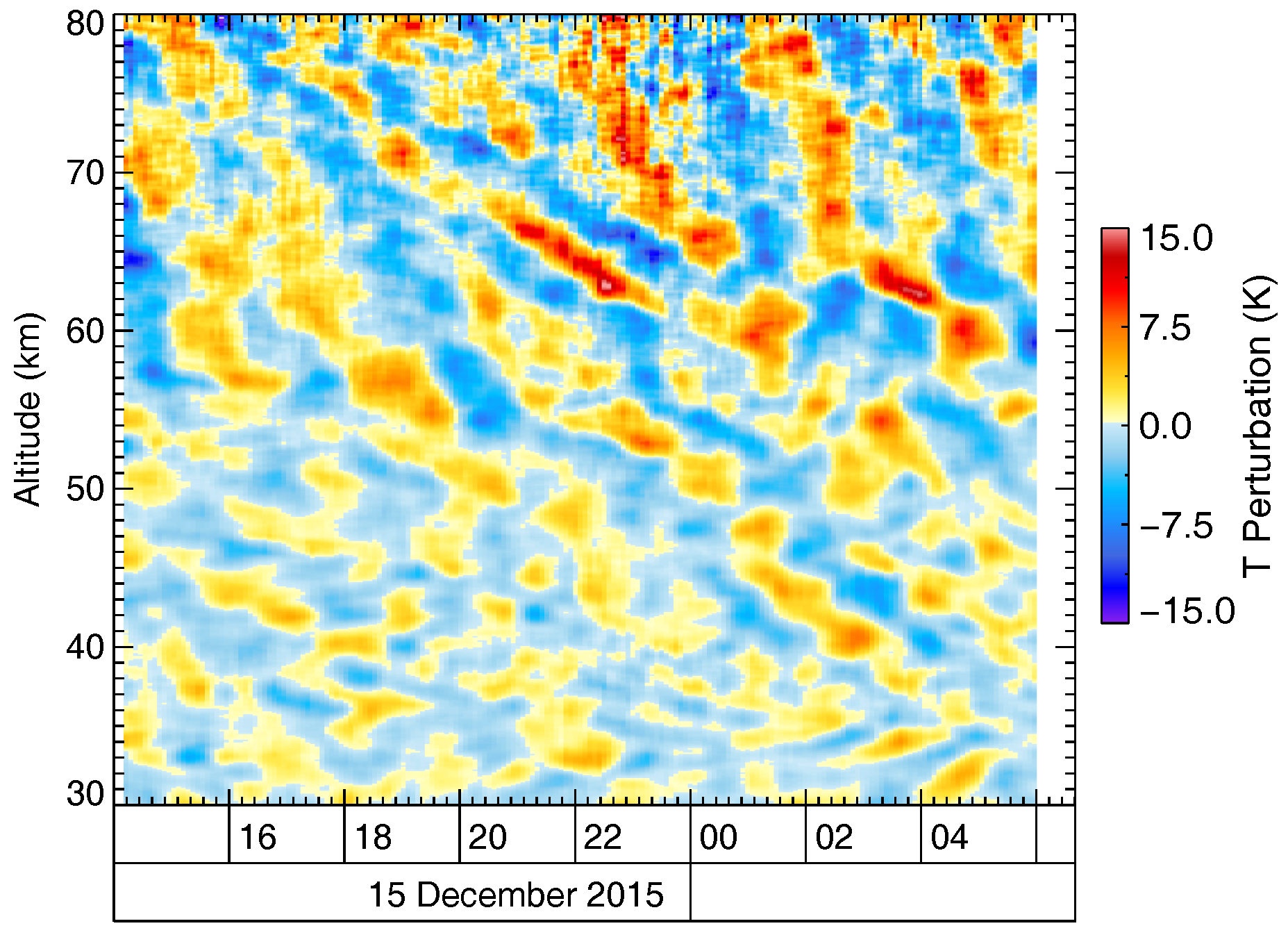
2. Gravity Wave Signatures in Ground-Based Lidar Data
3. Basic Considerations
3.1. Plane Boussinesq Waves
3.2. Wave Packets
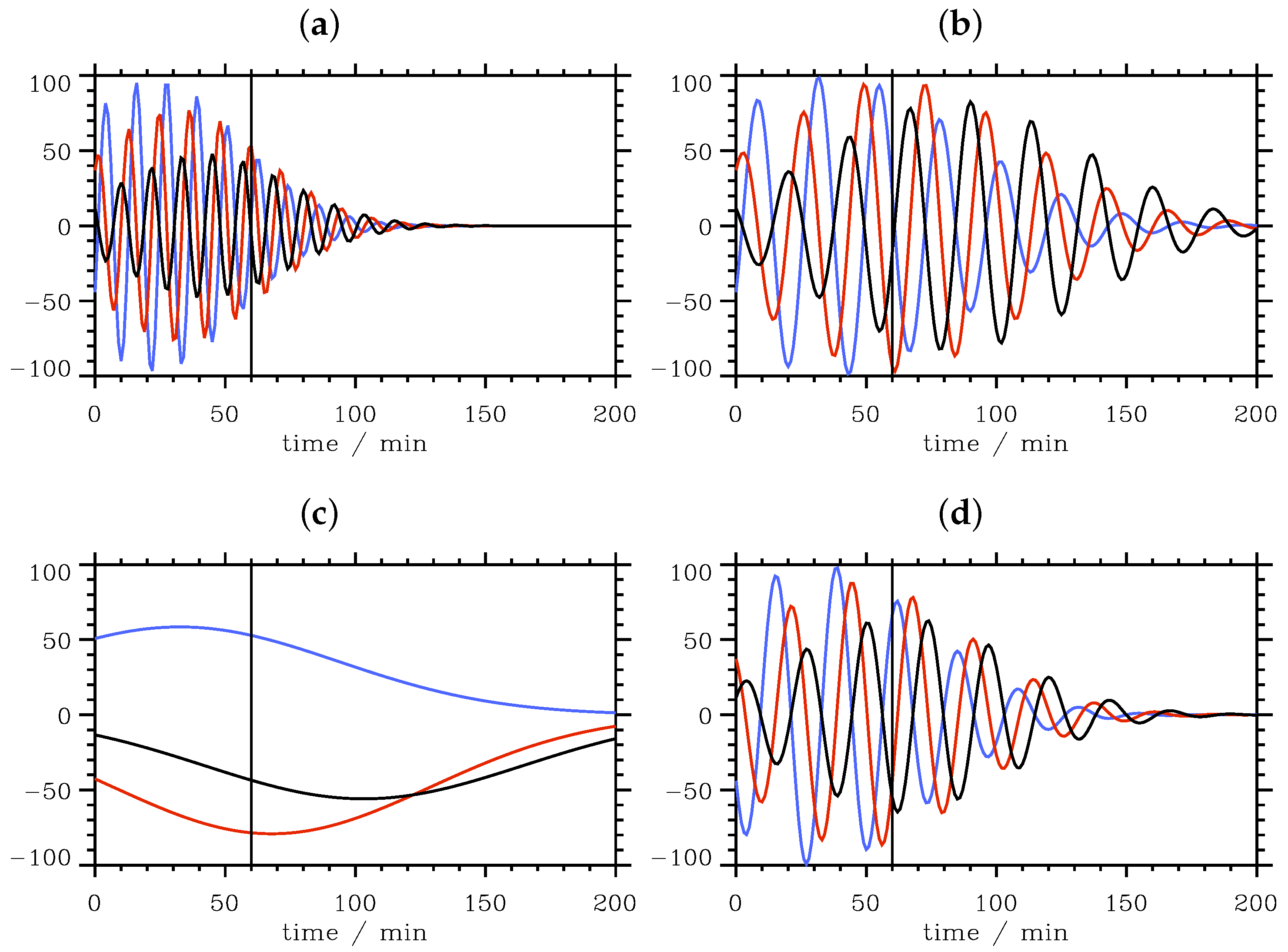
3.3. Doppler Shift
3.4. Illustrations
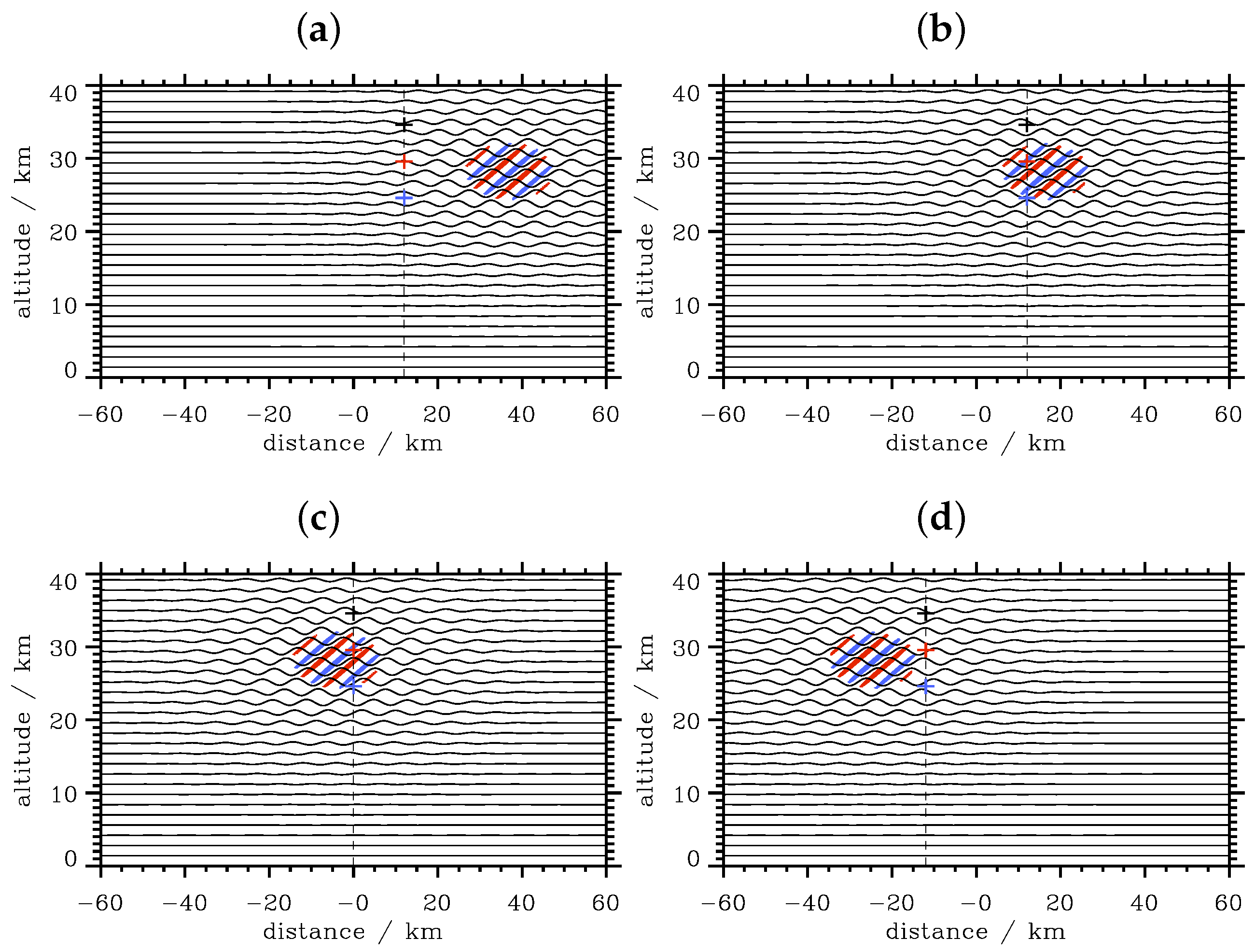
3.4.1. Plane Waves in an Atmosphere with Zero Wind
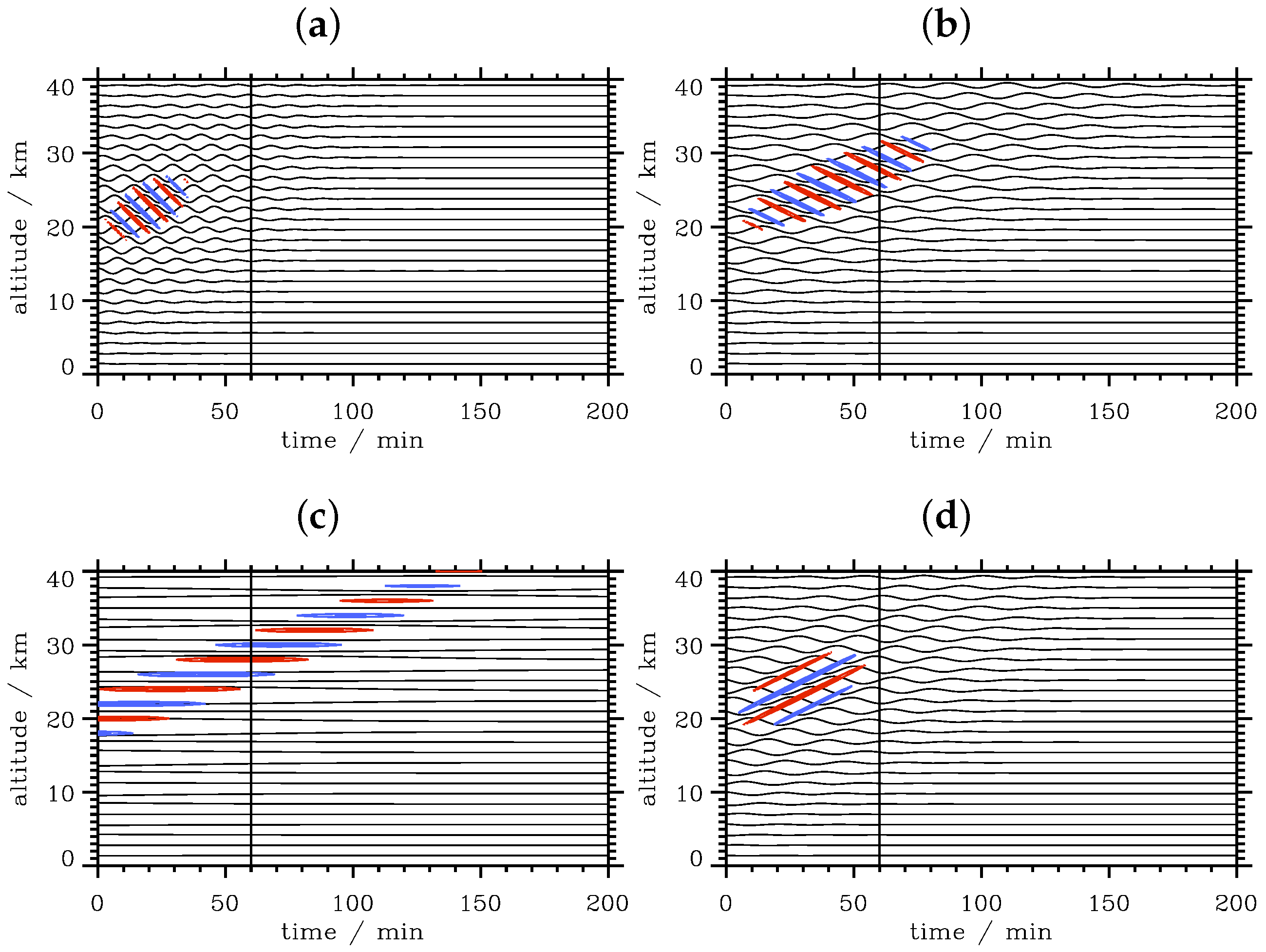
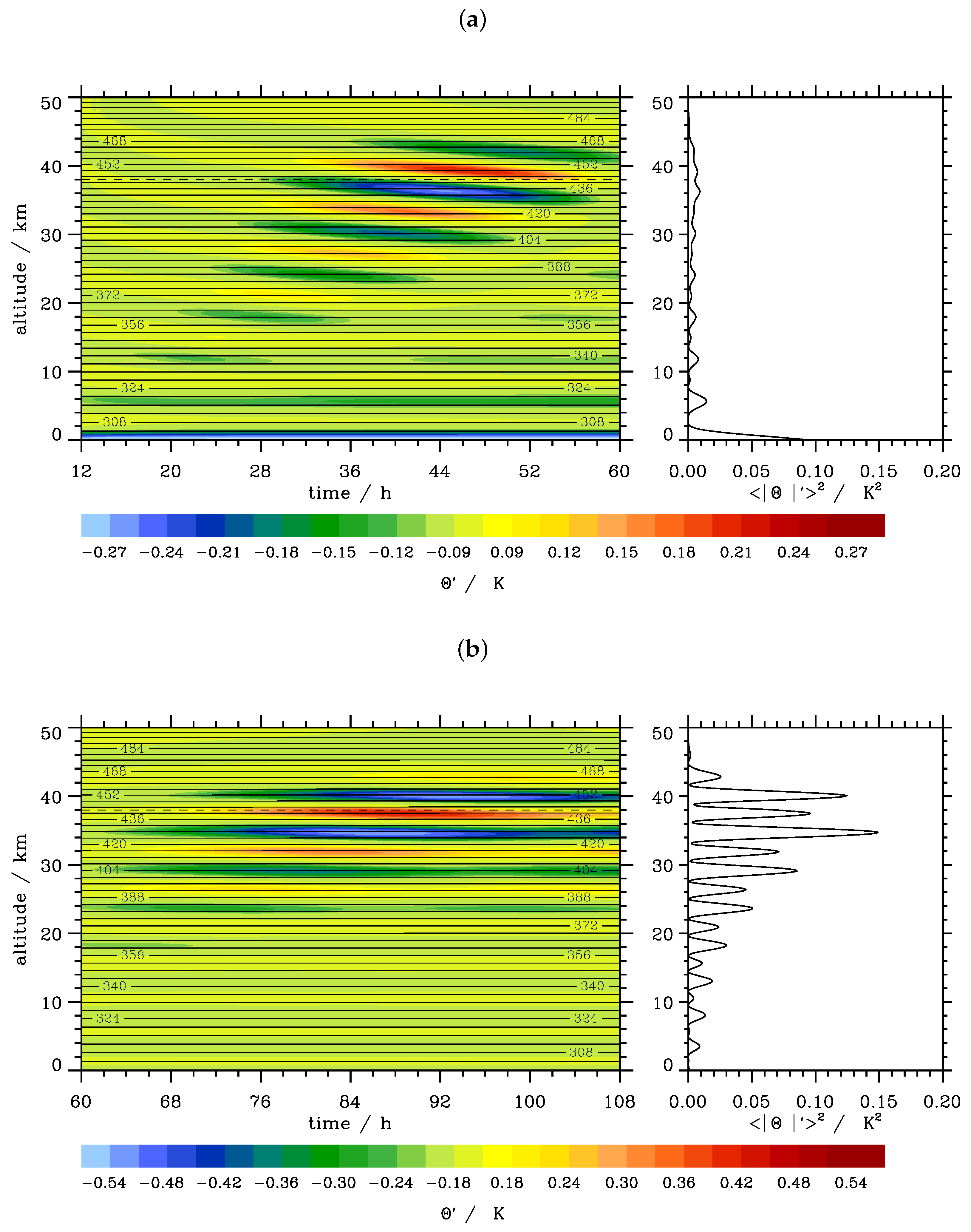
3.4.2. Wave Packets in an Atmosphere with Zero Wind
- (a)
- the observed phase lines belong to a spatially- and temporally-localized wave packet,
- (b)
- the observed phase lines allow the graphical determination of the vertical wavelength and of the ground-based frequency ω,
- (c)
- the observed waves obey a dispersion relation for internal Boussinesq wave like Equation (3),
- (d)
- the background stratification N is nearly constant over an altitude range of at least one vertical wavelength and can be computed from the observation or meteorological data and
- (e)
- there is no mean wind in the atmosphere.
3.4.3. Doppler-Shifted Wave Packets
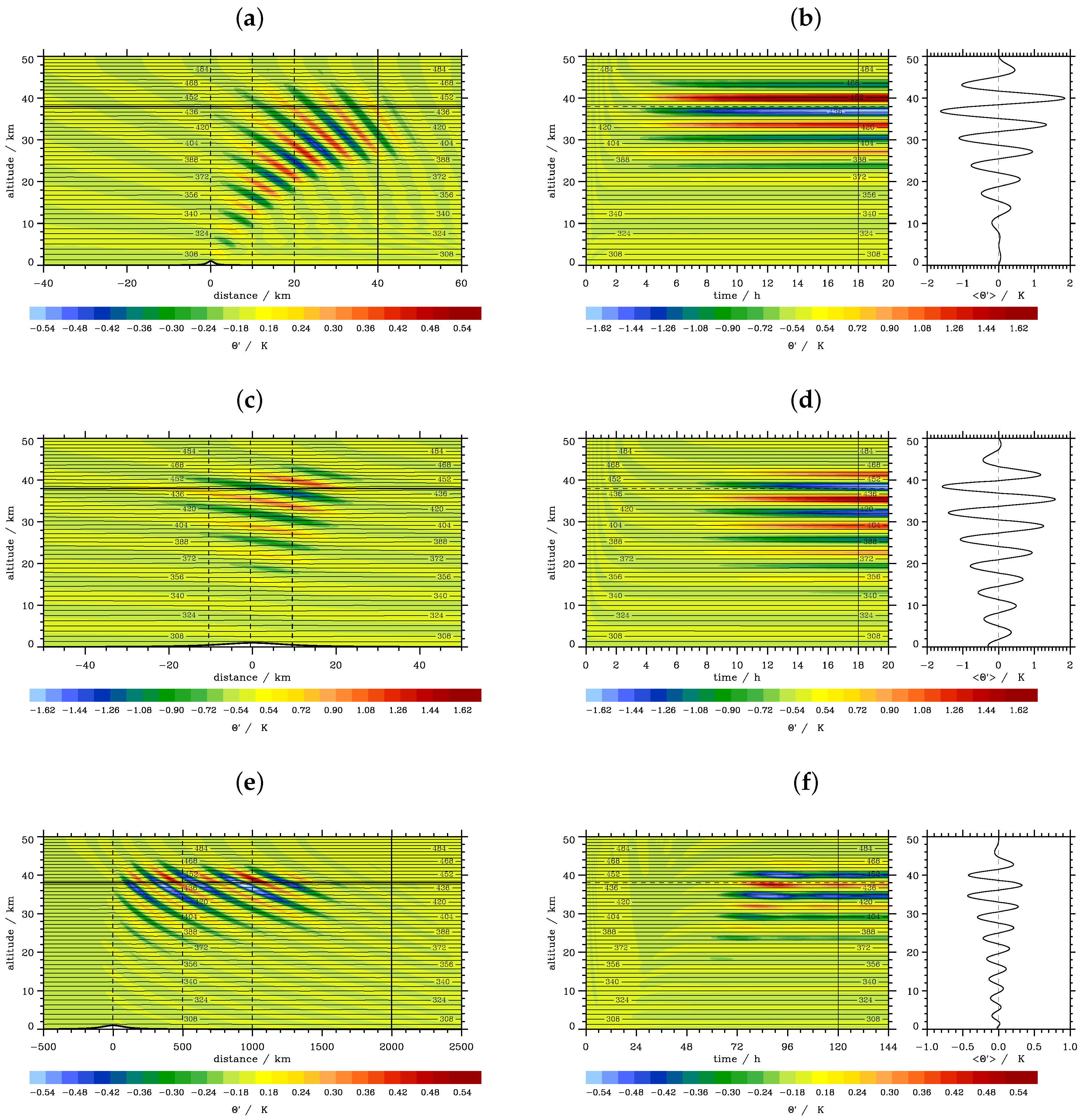
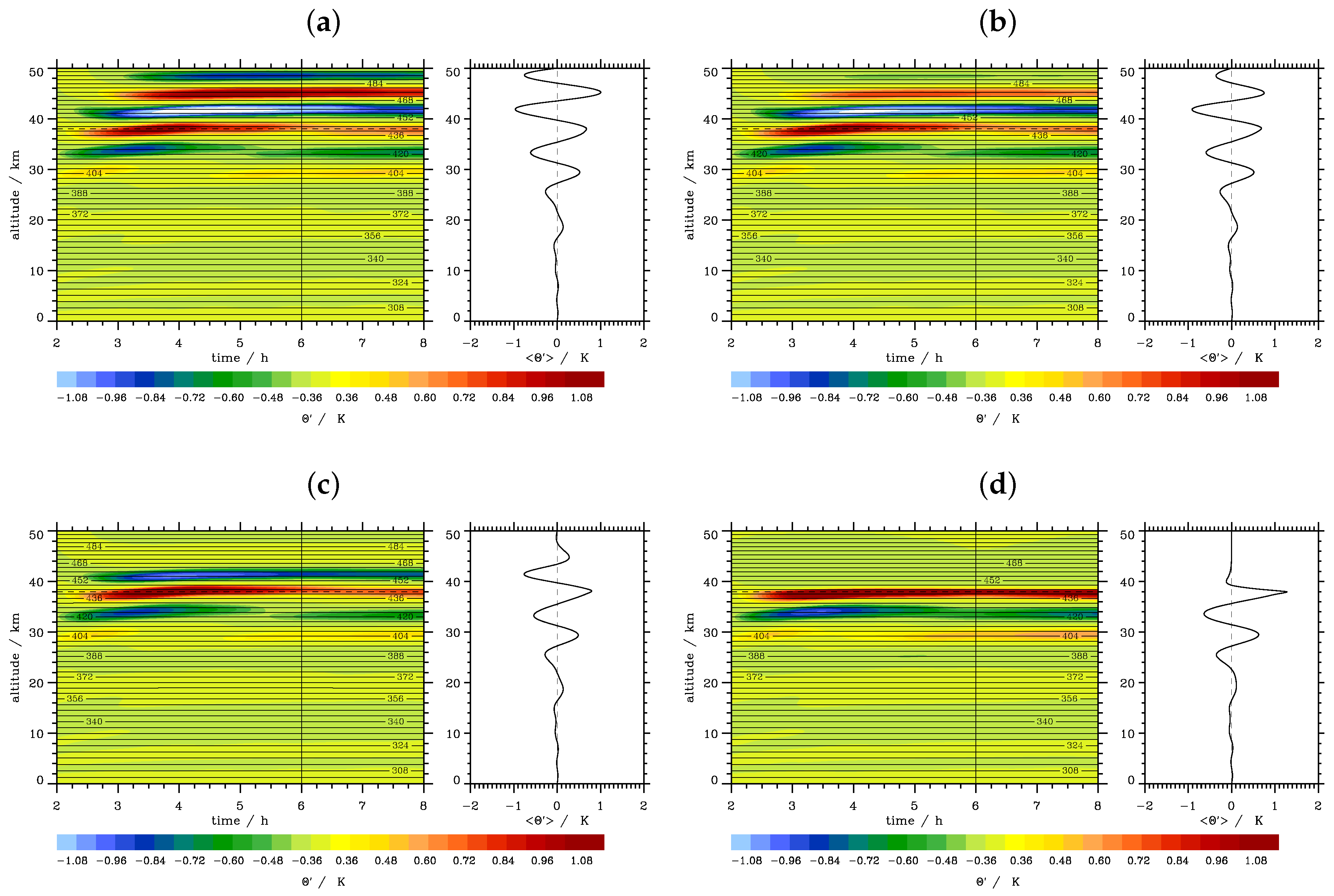
4. Idealized Numerical Simulations
4.1. Archetypal Regimes of Vertically-Propagating Internal Gravity Waves
- (i)
- non-hydrostatic wave regime, the
- (ii)
- hydrostatic “nonrotating” wave regime and the
- (iii)
- hydrostatic “rotating” wave regime.
4.2. Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Setup of the Numerical Simulations
References
- Wilson, R.; Chanin, M.L.; Hauchecorne, A. Gravity waves in the middle atmosphere observed by Rayleigh lidar: 1. Case studies. J. Geophys. Res. Atmos. 1991, 96, 5153–5167. [Google Scholar] [CrossRef]
- Li, T.; She, C.Y.; Liu, H.L.; Leblanc, T.; McDermid, I.S. Sodium lidar observed strong inertia-gravity wave activities in the mesopause region over Fort Collins, Colorado (41° N, 105° W). J. Geophys. Res. Atmos. 2007, 112, D22104. [Google Scholar] [CrossRef]
- Lu, X.; Liu, A.Z.; Swenson, G.R.; Li, T.; Leblanc, T.; McDermid, I.S. Gravity wave propagation and dissipation from the stratosphere to the lower thermosphere. J. Geophys. Res. Atmos. 2009, 114, D11101. [Google Scholar] [CrossRef]
- Chen, C.; Chu, X.; McDonald, A.J.; Vadas, S.L.; Yu, Z.; Fong, W.; Lu, X. Inertia-gravity waves in Antarctica: A case study using simultaneous lidar and radar measurements at McMurdo/Scott Base (77.8° S, 166.7° E). J. Geophys. Res. Atmos. 2013, 118, 2794–2808. [Google Scholar] [CrossRef]
- Suzuki, S.; Lübken, F.-J.; Baumgarten, G.; Kaifler, N.; Eixmann, R.; Williams, B.P.; Nakamura, T. Vertical propagation of a mesoscale gravity wave from the lower to the upper atmosphere. J. Atmos. Sol. Terr. Phys. 2013, 97, 29–36. [Google Scholar] [CrossRef]
- Baumgarten, G.; Fiedler, J.; Hildebrand, J.; Lübken, F.-J. Inertia gravity wave in the stratosphere and mesosphere observed by Doppler wind and temperature lidar. Geophys. Res. Lett. 2015, 42, 10929–10936. [Google Scholar] [CrossRef]
- Ehard, B.; Kaifler, B.; Dörnbrack, A.; Preusse, P.; Eckermann, S.D.; Bramberger, M.; Gisinger, S.; Kaifler, N.; Liley, B.; Wagner, J.; et al. Horizontal propagation of large-amplitude mountain waves into the polar night jet. J. Geophys. Res. Atmos. 2017. [Google Scholar] [CrossRef]
- Chanin, M.L.; Hauchecorne, A. Lidar observation of gravity and tidal waves in the stratosphere and mesosphere. J. Geophys. Res. Oceans 1981, 86, 9715–9721. [Google Scholar] [CrossRef]
- Gardner, C.S.; Miller, M.S.; Liu, C.H. Rayleigh lidar observations of gravity wave activity in the upper stratosphere at Urbana, Illinois. J. Atmos. Sci. 1989, 46, 1838–1854. [Google Scholar] [CrossRef]
- Whiteway, J.A.; Carswell, A.I. Lidar observations of gravity wave activity in the upper stratosphere over Toronto. J. Geophys. Res. Atmos. 1995, 100, 14113–14124. [Google Scholar] [CrossRef]
- Whiteway, J.A.; Duck, T.J.; Donovan, D.P.; Bird, J.C.; Pal, S.R.; Carswell, A.I. Measurements of gravity wave activity within and around the Arctic stratospheric vortex. Geophys. Res. Lett. 1997, 24, 1387–1390. [Google Scholar] [CrossRef]
- Duck, T.J.; Whiteway, J.A.; Carswell, A.I. The gravity wave-arctic stratospheric vortex interaction. J. Atmos. Sci. 2001, 58, 3581–3596. [Google Scholar] [CrossRef]
- Rauthe, M.; Gerding, M.; Höffner, J.; Lübken, F.-J. Lidar temperature measurements of gravity waves over Kühlungsborn (54° N) from 1 to 105 km: A winter-summer comparison. J. Geophys. Res. Atmos. 2006, 111, D24108. [Google Scholar] [CrossRef]
- Yamashita, C.; Chu, X.; Liu, H.L.; Espy, P.J.; Nott, G.J.; Huang, W. Stratospheric gravity wave characteristics and seasonal variations observed by lidar at the South Pole and Rothera, Antarctica. J. Geophys. Res. Atmos. 2009, 114, D12101. [Google Scholar] [CrossRef]
- Alexander, S.P.; Klekociuk, A.R.; Murphy, D.J. Rayleigh lidar observations of gravity wave activity in the winter upper stratosphere and lower mesosphere above Davis, Antarctica (69° S, 78° E). J. Geophys. Res. Atmos. 2011, 116, D13109. [Google Scholar] [CrossRef]
- Ehard, B.; Achtert, P.; Gumbel, J. Long-term lidar observations of wintertime gravity wave activity over northern Sweden. Ann. Geophys. 2014, 32, 1395–1405. [Google Scholar] [CrossRef]
- Khaykin, S.M.; Hauchecorne, A.; Mzé, N.; Keckhut, P. Seasonal variation of gravity wave activity at midlatitudes from 7 years of COSMIC GPS and Rayleigh lidar temperature observations. Geophys. Res. Lett. 2015, 42, 1251–1258. [Google Scholar] [CrossRef]
- Kaifler, B.; Lübken, F.-J.; Höffner, J.; Morris, R.J.; Viehl, T.P. Lidar observations of gravity wave activity in the middle atmosphere over Davis (69° S, 78° E), Antarctica. J. Geophys. Res. Atmos. 2015, 120, 4506–4521. [Google Scholar] [CrossRef]
- Triplett, C.C.; Collins, R.L.; Nielsen, K.; Harvey, V.L.; Mizutani, K. Role of wind filtering and unbalanced flow generation on middle atmosphere gravity wave activity at Chatanika Alaska. Atmosphere 2017, 8, 27. [Google Scholar] [CrossRef]
- Ehard, B.; Kaifler, B.; Kaifler, N.; Rapp, M. Evaluation of methods for gravity wave extraction from middle-atmospheric lidar temperature measurements. Atmos. Meas. Tech. 2015, 8, 4645–4655. [Google Scholar] [CrossRef]
- Le Pichon, A.; Assink, J.D.; Heinrich, P.; Blanc, E.; Charlton-Perez, A.; Lee, C.F.; Keckhut, P.; Hauchecorne, A.; Rüfenacht, R.; Kämpfer, N.; et al. Comparison of co-located independent ground-based middle atmospheric wind and temperature measurements with numerical weather prediction models. J. Geophys. Res. Atmos. 2015, 120, 8318–8331. [Google Scholar] [CrossRef]
- Kaifler, B.; Kaifler, N.; Ehard, B.; Dörnbrack, A.; Rapp, M.; Fritts, D.C. Influences of source conditions on mountain wave penetration into the stratosphere and mesosphere. Geophys. Res. Lett. 2015, 42, 9488–9494. [Google Scholar] [CrossRef]
- Eliassen, A.; Palm, E. On the transfer of energy in stationary mountain waves. Geofys. Publ. 1961, 22, 1–23. [Google Scholar]
- Satomura, T.; Sato, K. Secondary generation of gravity waves associated with the breaking of mountain waves. J. Atmos. Sci. 1999, 56, 3847–3858. [Google Scholar] [CrossRef]
- Sato, K. Sources of gravity waves in the polar middle atmosphere. Adv. Polar Upper Atmos. 2000, 14, 233–240. [Google Scholar]
- Vadas, S.L.; Fritts, D.C.; Alexander, M.J. Mechanism for the generation of secondary waves in wave breaking regions. J. Atmos. Sci. 2003, 60, 194–214. [Google Scholar] [CrossRef]
- Fritts, D.C.; Alexander, M.J. Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 2003, 41. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, S.; Plougonven, R. Uncertainties in using the hodograph method to retrieve gravity wave characteristics from individual soundings. Geophys. Res. Lett. 2004, 31, L11110. [Google Scholar] [CrossRef]
- Sutherland, B.R. Internal Gravity Waves; Cambridge University Press: Cambridge, UK, 2010; p. 394. [Google Scholar]
- Gill, A.E. Atmosphere-Ocean Dynamics; Academic Press: Cambridge, MA, USA, 1982; p. 662. [Google Scholar]
- Whitham, G.B. Linear and Nonlinear Waves; John Wiley and Sons: Chichester, UK, 1974; p. 636. [Google Scholar]
- Nappo, C.J. An Introduction to Atmospheric Gravity Waves, 2nd ed.; Academic Press: Cambridge, MA, USA, 2012; p. 400. [Google Scholar]
- Smolarkiewicz, P.K.; Margolin, L.G. On forward-in-time differencing for fluids: An Eulerian/Semi-Lagrangian Non-Hydrostatic Model for stratified flows. Atmos.-Ocean 1997, 35, 127–152. [Google Scholar] [CrossRef]
- Prusa, J.M.; Smolarkiewicz, P.K.; Wyszogrodzki, A.A. EULAG, a computational model for multiscale flows. Comput. Fluids 2008, 37, 1193–1207. [Google Scholar] [CrossRef]
- Queney, P. The problem of the airflow over mountains: A summary of theoretical studies. Bull. Am. Meteorol. Soc. 1948, 29, 16–26. [Google Scholar]
- Long, R.R. Some aspects of the flow of stratified fluids: I. A theoretical investigation. Tellus 1953, 5, 42–58. [Google Scholar] [CrossRef]
- Dörnbrack, A.; Birner, T.; Fix, A.; Flentje, H.; Meister, A.; Schmid, H.; Browell, E.V.; Mahoney, M.J. Evidence for inertia gravity waves forming polar stratospheric clouds over Scandinavia. J. Geophys. Res. Atmos. 2002, 107, SOL 30-1–SOL 30-18. [Google Scholar] [CrossRef]
- Smolarkiewicz, P.K.; Margolin, L.G. MPDATA: A finite-difference solver for geophysical flows. J. Comput. Phys. 1998, 140, 459–480. [Google Scholar] [CrossRef]
- Smolarkiewicz, P.K. Multidimensional positive definite advection transport algorithm: An overview. Int. J. Numer. Methods Fluids 2006, 50, 1123–1144. [Google Scholar] [CrossRef]
- Smolarkiewicz, P.K.; Margolin, L.O. On forward-in-time differencing for fluids: Extension to a curvilinear framework. Mon. Weather Rev. 1993, 121, 1847–1859. [Google Scholar] [CrossRef]
- Schröttle, J.; Dörnbrack, A. Turbulence structure in a diabatically heated forest canopy composed of fractal Pythagoras trees. Theor. Comput. Fluid Dyn. 2013, 27, 337–359. [Google Scholar] [CrossRef]
- Gisinger, S.; Dörnbrack, A.; Schröttle, J. A modified Darcy’s law. Theor. Comput. Fluid Dyn. 2015, 29, 343–347. [Google Scholar] [CrossRef]
- Kühnlein, C.; Smolarkiewicz, P.K.; Dörnbrack, A. Modelling atmospheric flows with adaptive moving meshes. J. Comput. Phys. 2012, 231, 2741–2763. [Google Scholar] [CrossRef]
- Prusa, J.M.; Smolarkiewicz, P.K.; Garcia, R.R. Propagation and breaking at high altitudes of gravity waves excited by tropospheric forcing. J. Atmos. Sci. 1996, 53, 2186–2216. [Google Scholar] [CrossRef]
- Smolarkiewicz, P.K.; Dörnbrack, A. Conservative integrals of adiabatic Durran’s equations. Int. J. Numer. Methods Fluids 2008, 56, 1513–1519. [Google Scholar] [CrossRef]
- Kühnlein, C.; Dörnbrack, A.; Weissmann, M. High-resolution Doppler lidar observations of transient downslope flows and rotors. Mon. Weather Rev. 2013, 141, 3257–3272. [Google Scholar] [CrossRef]
- Smolarkiewicz, P.K.; Charbonneau, P. EULAG, a computational model for multiscale flows: An MHD extension. J. Comput. Phys. 2013, 236, 608–623. [Google Scholar] [CrossRef]
- Smolarkiewicz, P.K.; Szmelter, J.; Xiao, F. Simulation of all-scale atmospheric dynamics on unstructured meshes. J. Comput. Phys. 2016, 322, 267–287. [Google Scholar] [CrossRef]
- Grinstein, F.F.; Margolin, L.G.; Rider, W. Implicit Large Eddy Simulation: Computing Turbulent Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2007; p. 552. [Google Scholar]
- 1.from B. Dylan: “One of us must know (sooner or later)”; Blonde On Blonde (1966).
- 2.H. Grogger, Simulation of Deep Gravity Wave Propagation Using EULAG, Master Thesis, University of Innsbruck, 2017.
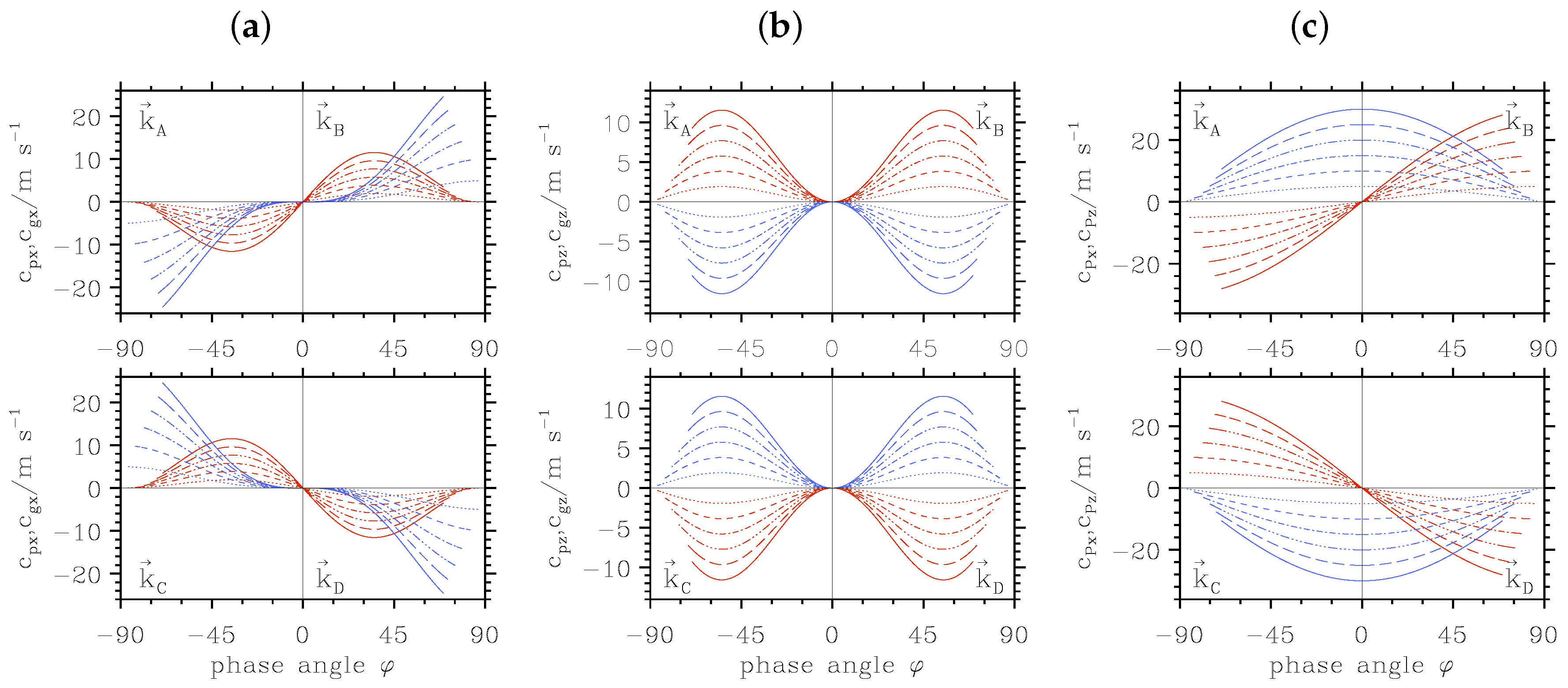
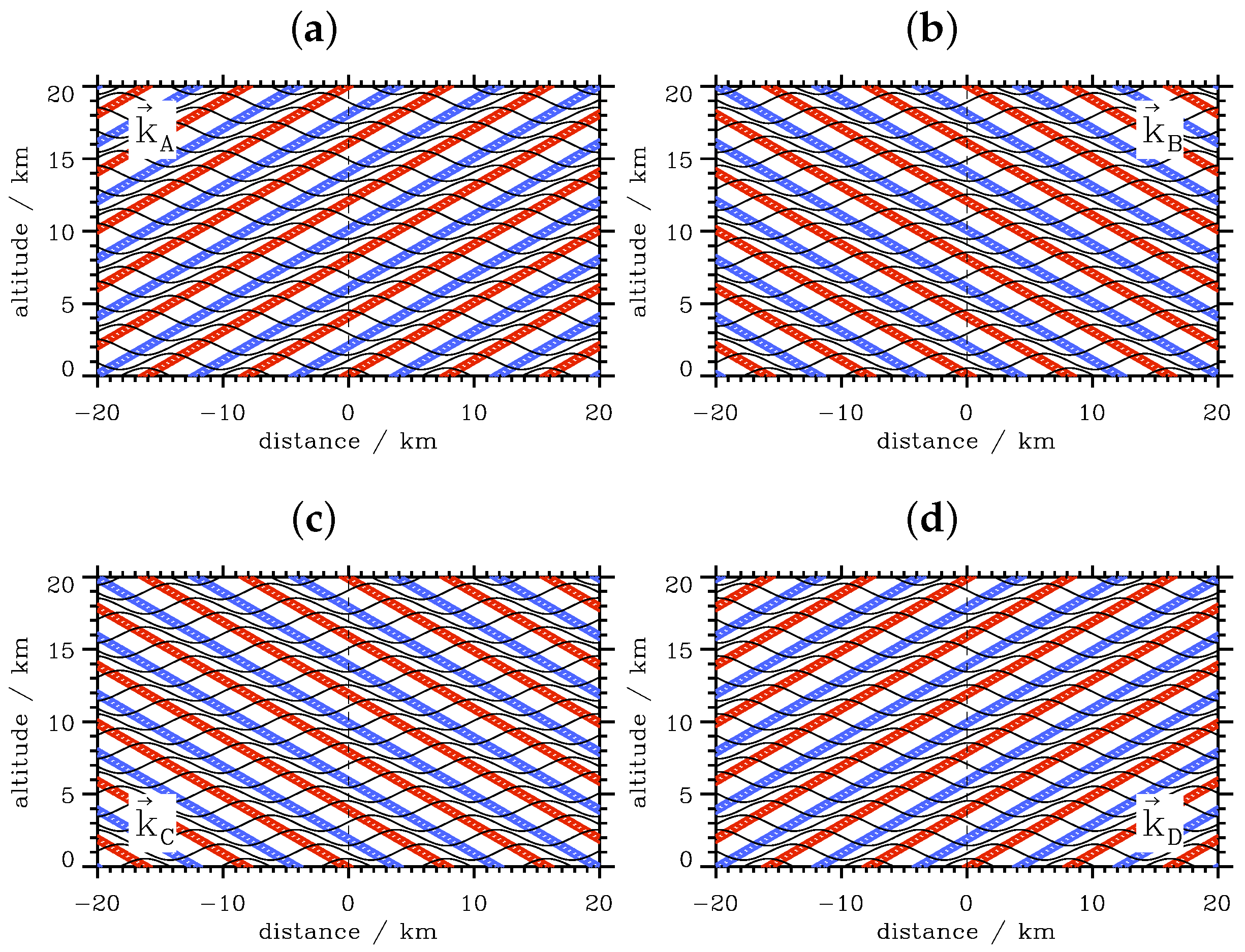

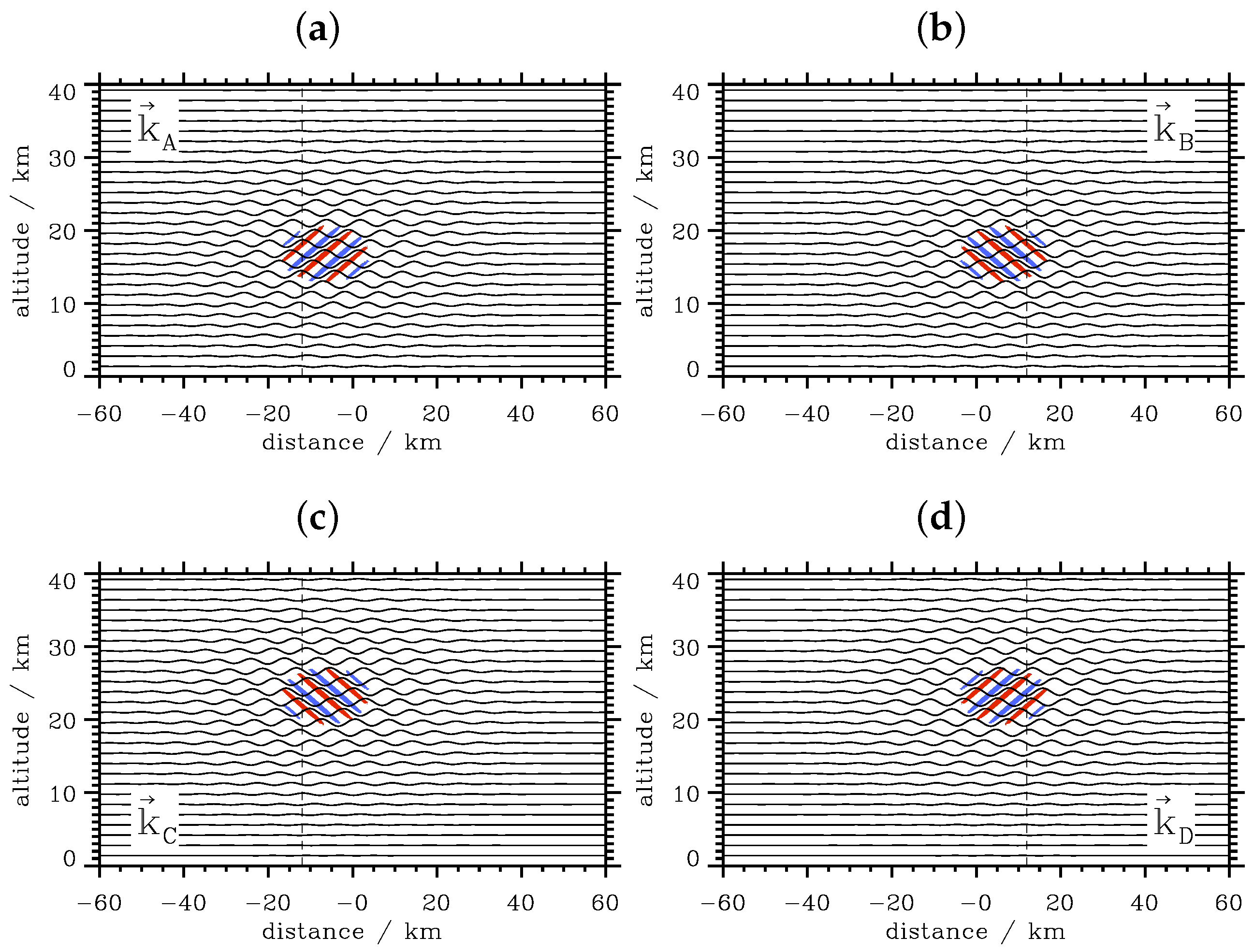

| Case | k | m | φ | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | − | + | −63.4 | 0.0045 | −5.69 | +2.84 | −1.14 | +2.28 | −4.56 | −2.28 |
| B | + | + | +63.4 | 0.0045 | +5.69 | +2.84 | +1.14 | +2.28 | +4.56 | −2.28 |
| C | − | − | +63.4 | 0.0045 | −5.69 | −2.84 | −1.14 | −2.28 | −4.56 | +2.28 |
| D | + | − | −63.4 | 0.0045 | +5.69 | −2.84 | +1.14 | −2.28 | +4.56 | +2.28 |
| Run | L/km | /m | /m | /s | /km | /s | /km | /s |
|---|---|---|---|---|---|---|---|---|
| (i) | 1 | 100 | 100 | 5 | 24 | 1800 | 38 | 900 |
| (ii) | 10 | 1000 | 100 | 5 | 240 | 300 | 38 | 900 |
| (iii) | 100 | 5000 | 100 | 60 | 1200 | 300 | 38 | 3600 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dörnbrack, A.; Gisinger, S.; Kaifler, B. On the Interpretation of Gravity Wave Measurements by Ground-Based Lidars. Atmosphere 2017, 8, 49. https://doi.org/10.3390/atmos8030049
Dörnbrack A, Gisinger S, Kaifler B. On the Interpretation of Gravity Wave Measurements by Ground-Based Lidars. Atmosphere. 2017; 8(3):49. https://doi.org/10.3390/atmos8030049
Chicago/Turabian StyleDörnbrack, Andreas, Sonja Gisinger, and Bernd Kaifler. 2017. "On the Interpretation of Gravity Wave Measurements by Ground-Based Lidars" Atmosphere 8, no. 3: 49. https://doi.org/10.3390/atmos8030049
APA StyleDörnbrack, A., Gisinger, S., & Kaifler, B. (2017). On the Interpretation of Gravity Wave Measurements by Ground-Based Lidars. Atmosphere, 8(3), 49. https://doi.org/10.3390/atmos8030049






