1. Introduction
In recent years, there has been increasing attention paid to developing new applications and planning missions to monitor and deliver quantitative information of near surface rain precipitation. The Global Precipitation Measurement (GPM) mission [
1] is a recent valuable example of measuring precipitation using spaceborne active and passive sensors.
From the ground, measuring systems of rainfall are essential for providing a reference measure for the validation of the satellite rain products over land [
2] as well as to prevent flood hazards (e.g., by using nowcasting algorithms [
3] or assimilation into forecast models [
4]), thus aiding civil protection actions. Ground-based measurements of rainfall can rely on rain gauges [
5], disdrometers [
6], weather radars [
7], and profilers such as the micro rain radars [
8] as well as the use of their combinations, merged with external information like lightning [
9]. Typically, over land, weather radar and rain gauges are used most often as they are a conventional choice in the operational context at national weather service levels.
However, quantitative measurements of rain precipitation at the Earth’s surface using ground-based systems are typically affected by a number of limiting factors due to errors introduced both by the observation instruments used as well as the variability of rainfall in time and space compared to the sampling interval of the acquired measurements. In particular, weather radars can be affected by several error sources, including radar miscalibration [
10], clutter contamination (originated by antenna side lobe contributions, surrounding orography, human-made obstacles, or anomalous propagation effects) [
11], wet radome attenuation [
12], rain-induced attenuation [
13], non-uniform beam filling [
14], radiofrequency interferences [
15], and uncertainties related to the vertical variability of the particle size distribution (PSD) [
16,
17]. In addition, sampling differences in both time and space between radar measurements and reference observations at the surface add to the uncertainties of radar quantitative precipitation estimation [
18] when multi-observation comparisons are carried out. In particular, the vertical variability of PSD directly impacts the variability of the measured radar quantities; for example, the reflectivity factor (
Zhh), the differential reflectivity (
Zdr), and the specific differential phase shift (
Kdp) as well as the estimates of near-surface rain rate (
R), which is usually obtained from the radar quantities measured aloft. In particular, in complex orography environments, when the radar antenna tilts have to be set higher than usual to limit beam blocking (say above 3 or 4 deg with respect to the horizon) or the radar is positioned at a high altitude (e.g., above 1500 m), the differences in the sampled radar quantities aloft with respect to those that would be observed close to the surface can be significant. Some past studies have focused on rain precipitation estimation in complex orography [
19,
20] while others have extensively addressed the issue of the vertical extrapolation of the reflectivity factor,
Zhh, down to the surface level to estimate the rain rate,
R, taking into account, in particular, the distinct signatures of the vertical profile of reflectivity in stratiform and convective rain regimes [
21,
22,
23]. However, as far as the authors have been able to ascertain, none of the works referenced above have addressed the issue of vertical extrapolation when dealing with weather radar dual polarization rain estimation formulas, although there is growing interest in the characterization of the signature of the vertical profile of
Kdp and
Zdr [
24].
The goal of this study is twofold: (i) test the variability of various radar quantitative precipitation estimation (QPE) algorithms in a complex orography environment, including those based on the
R(
Zhh),
R(
Kdp),
R(
Zhh,
Zdr) relationships, as well as those based on one of their combinations; (ii) show the impact of the use of quasi-vertical profiles of rain and
Kdp filtering settings on QPE algorithms. In this work, the acronym VPR, often ambiguously referred to vertical profile of reflectivity, indicates the vertical profile of rain. The use of quasi-VPR, when dealing with dual polarization radar variables, is a key aspect of this study. The term “quasi-VPR” actually refers to the fact that we are not looking at vertical radar observations but instead we derive vertical information by exploiting slanted paths [
25]. In this study, quasi-VPRs are used to overcome the complication that would result if we attempted to perform QPEs using dual polarization estimators (i.e., using
Zhh,
Zdr, and
Kdp or a subset of them at the same time). Indeed, various QPE estimators exist based on several combinations of
Zhh,
Zdr, and
Kdp, with estimation coefficients adapted as a function of rain regimens observed by radar (e.g., [
26,
27]). Those QPE estimators might benefit from the use of quasi-VPR as defined in this study because it allows near surface extrapolations after rain rate retrievals instead of performing them before the retrieval step.
To test the concept of quasi-VPR for QPE, three case studies from the area surrounding Rome, Italy, are considered. These studies include two particularly intense convective events on 15 October 2012 and 14 October 2015 and a stratiform event on 12 October 2012. The C-band Doppler dual polarization research radar Polar55C (hereafter P55C) operated by the National Research Council of Italy (CNR) at the Institute of Atmospheric Sciences and Climate (ISAC) in Tor Vergata, Rome, was used. An objective definition of complex orography is also given in this manuscript, introducing a radar orography index to better mark the boundary for those QPE applications performed in such adverse environments.
The work is organized in six sections.
Section 2 describes the methodological aspects for QPE,
Section 3 gives details on the experimental case studies as well as the radar and rain gauges specifications,
Section 4 summarizes the results, while
Section 5 discusses the results in the light of recent literature. Finally,
Section 6 discusses the conclusions.
3. Experimental Setup and Case Studies
3.1. Description of the Case Studies
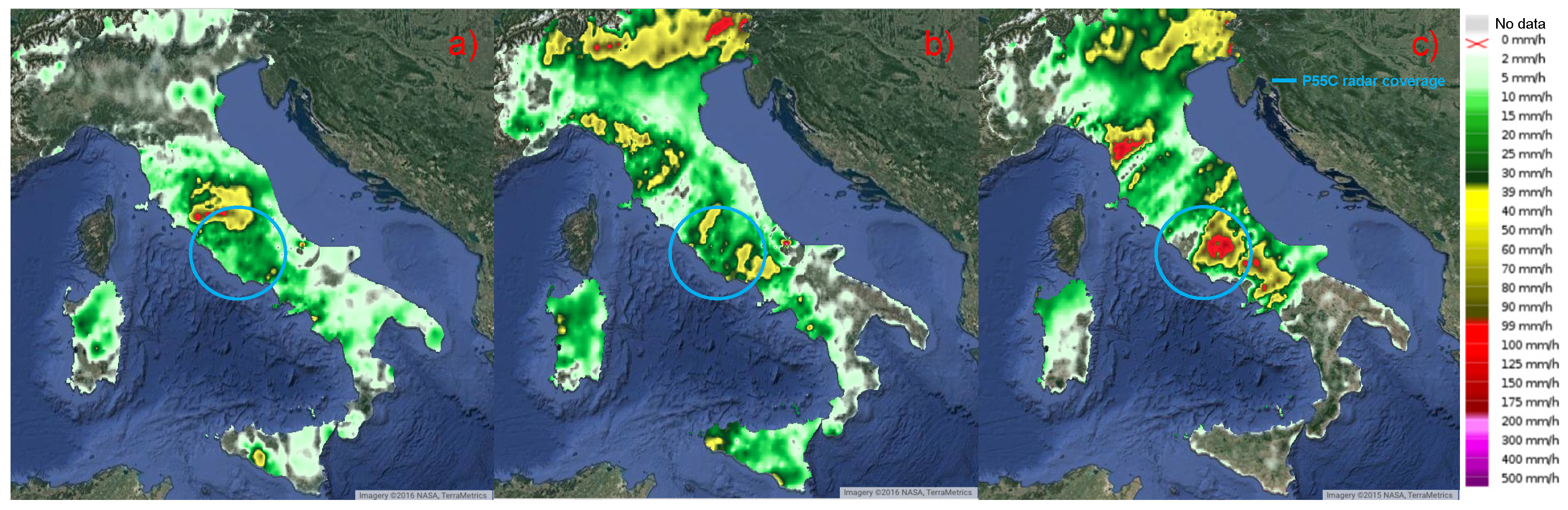
The three cases studied occurred in Italy on 12 and 15 October 2012 and 14 October 2015 in the area surrounding Rome were analyzed. Some of these cases, and in particular those that occurred in 2012, were used in [
9] to investigate the relation between the occurrences of lightning and the radar retrievals of integrated water content. For the sake of clarity,
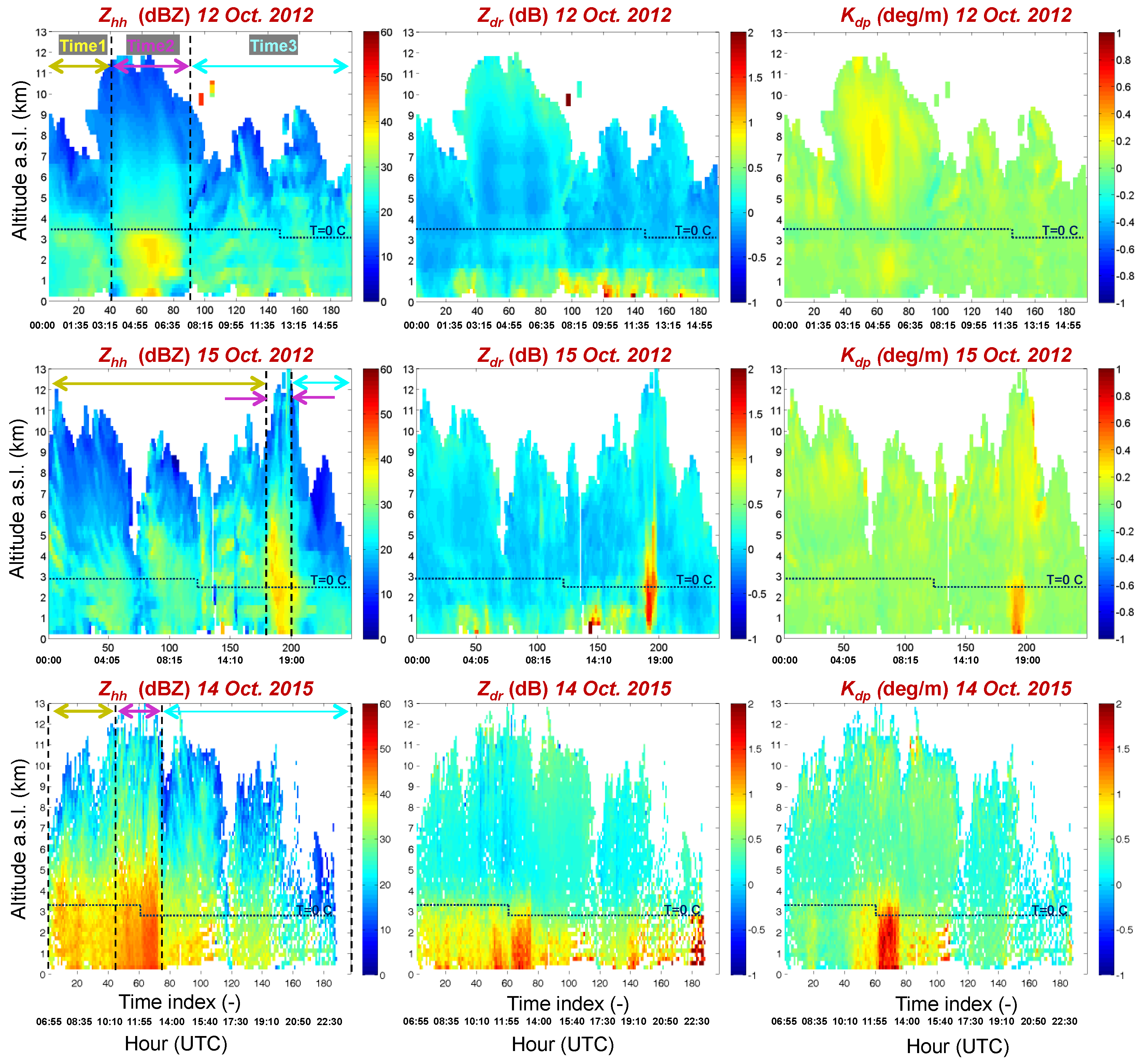
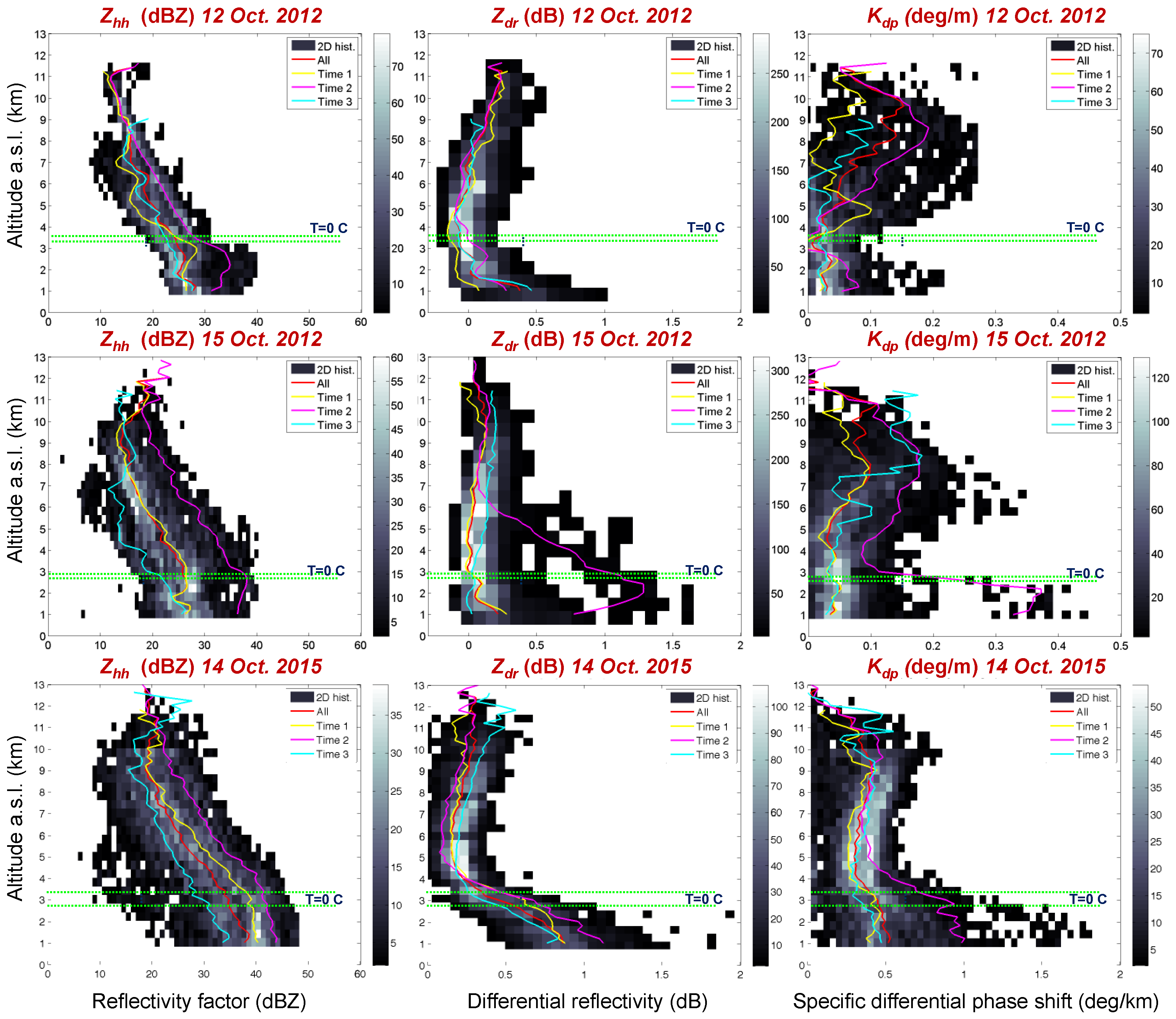
Figure 1 shows the interpolation of the rain accumulations registered on the Italian peninsula over a time interval of 24 h by local rain gauges for those three case studies. The P55C coverage is also shown to better highlight the studied area. In addition,
Figure 2 and
Figure 3 give a compact view of the rainy events seen by the P55C radar in terms of time series of quasi-vertical profiles of
Zhh,
Zdr, and
Kdp and their temporal average, calculated using Equation (5), respectively. It follows a synthetic summary of the three events considered.
12 October 2012. This event, associated with a secondary trough over the central Mediterranean Sea, carried heavy precipitation mainly over the Lazio and Umbria regions on 11–12 October 2012. The storm started over the Tyrrhenian Sea, where several mesoscale convective systems developed during the night of 11 October. Convective systems reached central Italy in the early morning of 12 October, with heavy precipitation over the northern part of the Lazio and Umbria regions. The rain was not persistent, but the maximum cumulative rainfall registered exceeded 150 mm in 6 h (
Figure 1a). The P55C radar was able to observe only part of the convective systems, mainly beyond 80 km from the radar site. In the last part of the event, the system moved to the south and farther away from the radar (100 km). The main activity developed between 03:15 UTC and 08:35 UTC, as shown in
Figure 2, top left, where the time series of the quasi-vertical profile of
Zhh is shown. In terms of temporal averages of quasi-vertical profiles,
Figure 3, top panels, shows the mixed nature of this event, with a stratiform rain regime at the beginning (labeled Time 1 in
Figure 2 and
Figure 3) with the typical pronounced peak of
Zhh just below the freezing level, lower values of
Zdr near zero close to the ground, and accompanied by low values of
Kdp. Within the main phase (Time 2), the quasi-vertical profile of
Zhh moved to higher values with nearly constant behavior below the freezing level.
15 October 2012. This event took place on 14 and 15 October 2012 across a vast area in the western Mediterranean. The regional weather service issued a severe weather warning for central Italy and particularly for the city of Rome. The precipitation event was associated with a trough that deepened significantly over the northern Tyrrhenian Sea, pushed a frontal system eastward, and advected moist air from the Tyrrhenian Sea inland to fuel deep convection on the coast west of Rome. The synoptic scale system moved rapidly to the east and triggered a line of convection that crossed the western half of central Italy from north to south in a few hours. Most of the precipitation produced by this system occurred in the late afternoon of 15 October across the western part of central Italy and on the western slopes of the Apennines chain (
Figure 1b). The main core of the event developed around 17:30 UTC, when a line of convective cells evolved quickly, then started to weaken after 19:00 UTC (
Figure 2, middle left panel). The total rainfall amount recorded in Rome was less than had been predicted. The highest daily amount recorded within the historic area of Rome was modest and equal to 35 mm by operational rain gauge. This event is quite characteristic because it clearly shows a
Zdr tower during the core phase (
Figure 3, middle center panel, “Time 2” curve). The time average profiles in
Figure 3, middle panels, show the convective origin of this event and confirm the values of
Zdr larger than zero well above the freezing level.
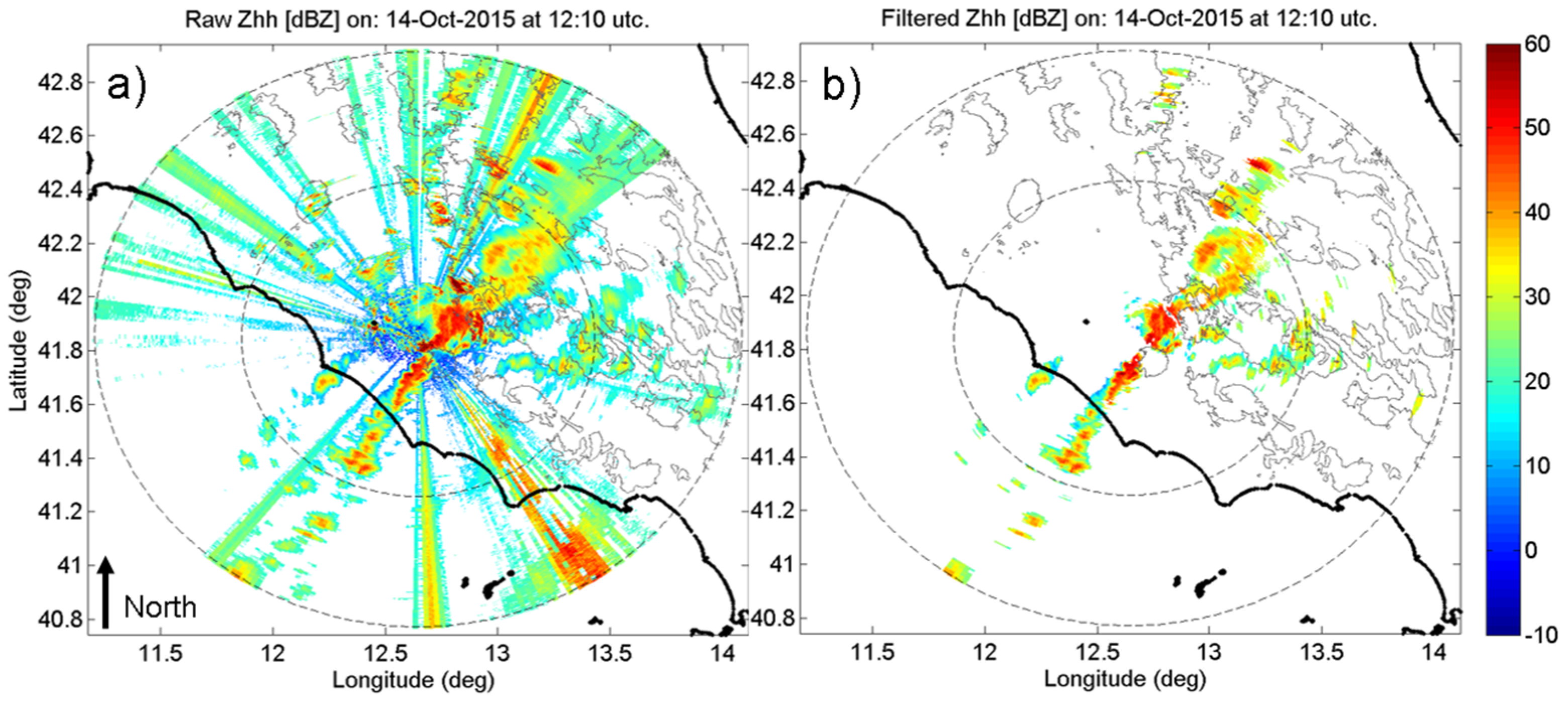
14 October 2015. During October 14 and 15, 2015, strong thunderstorms accompanied by strong winds and heavy rain swept up several regions along central and southern Italy as well as the western and northwestern Balkans, causing floods and landslides across the affected areas. In central Italy, in the Lazio and Abruzzo regions, within the P55C radar coverage, authorities reported landslides and casualties caused by river overflow. In those regions, the extreme weather left three people dead and residents were evacuated for safety on 14 October 2015. A woman died in the town of Paliano near Frosinone after the car she was in fell into a crater that opened up due to flooding after torrential rainfall in the area. Closer to Rome, the Aniene River overflowed its banks at Tivoli, flooding homes and basements and driving some residents onto their roofs for safety. Official sources said 100 people were evacuated from the town of Canistro in the province of L’Aquila in the hills surrounding Rome after the Rio Spalto overflowed. The city of Rome was spared most of the bad weather, while surrounding towns and cities were mostly impacted. The single railway line connecting Rome and Cassino was taken out of action by a landslide. Local rain gauges registered peaks larger than 170 mm within 24 h (
Figure 1c). This event was characterized by a severe convection phase with
Zhh maximum values up to 60 dBZ and vertical maximum extension up to 10–12 km,
Zdr values reaching 2 dB close to the surface and, at some times, extending with positive values over the zero temperature level and
Kdp values around 2 deg/km (
Figure 2 and
Figure 3, bottom panels).
It is worth noting, as with all the case studies discussed here, that the shapes of the average vertical profiles were pretty similar to those found in [
24] for convective and stratiform rain regimes. A particularly distinctive signature of such average profiles is noted for
Zdr and
Kdp, which start sharply increasing just above the freezing level and below it, with different strengths probably depending on the degree of convection of the specific event. This characteristic shape can modify in the presence of
Zdr towers or ice crystal aggregation processes.
3.2. Radar System Specifications
The Polar 55C (P55C) is a research-grade C-band (working at 5.6-GHz carrier frequency, 5.35 cm wavelength) Doppler dual polarized coherent weather radar managed by the Italian CNR-ISAC. Differently from most commercial weather radar systems working with the transmission of simultaneous polarization, the P55C system was designed to operate with a polarization agility and single receiver scheme. This means that the total power is alternately transported by the horizontal and vertical polarized signals thanks to a fast switch that allows the transmitted polarization state to be changed on a pulse-pulse-basis. The reception of the horizontal and vertical polarized components alternate as well. This has a direct implication for the dual polarization variables (especially Zdr), whose quality is expected to be higher than in the systems making use of simultaneous transmissions as the power transmitted is fully transferred to the two orthogonal polarization states.
Due to bus data transfer limitations in the signal processor compared with the number of bits used for encoding the radar variables and their required precision, the output quantities of P55C are only Zhh, Zdr, differential phase shift (φdp), and the Doppler velocity (V).
The P55C is located 15 km southeast of Rome (lat.: 41.8425 N deg, long.:12.6464 E deg, 102 m above sea level) on the roof of the ISAC-CNR. The receiver/transmitter apparatus is a fully coherent one. The transmitter is based on a klystron amplifier which allows for very high pulse-to-pulse and phase stability and uses a nominal peak power of 250 kW. For the data collected, considering PRF and antenna rotation speed, the radar measurements were obtained by averaging about 100 pulses transmitted with a 1250-Hz pulse repetition frequency in range bins spaced 75 m apart. The maximum unambiguous radar range was 120 km. The antenna geometry is a single offset type. This allows obtaining an increased radiation efficiency, avoiding beam blocking by stalls, which could both increase the cross-polarization level and cause differences in radiation patterns in the horizontal and vertical polarizations.
Nominal half-power beam widths are 0.92 and 1.02 deg in azimuth and elevation, respectively. The antenna is not protected by a radome and a direct implication is that we do not have limitations due to radome-induced effects (e.g., wet radome attenuation, azimuthal inhomogeneity, cross-polarization couplings). On the other hand, strong winds can make the antenna operations difficult and the pointing might not be accurate in windy situations. However, for the present study the core of the events analyzed was far enough from the radar most of the time, and the wind on the radar site did not cause particular issues. It is worth highlighting that P55C is a weather radar for research, which gives it a larger flexibility with respect to operating systems. For example, during the rain events, the schedules and the scanning strategies can be changed to optimize the observation capabilities.
3.3. Available Measurements and Settings for the Analyzed Case of Study
For the analyzed events the radar antenna elevation sweeps with respect to the horizontal were set to 0.6, 1.59, 2.61, 4.40, 6.20, 8.28, and 11.00 deg. They built up a radar polar volume that was delivered every 5 min. For the case studies, observations covered time windows from 06:55 UTC to 23:55 UTC, from 00:00 UTC to 16:00 UTC, and from 00:00 to 23:55 for a total of 193, 249, and 197 polar volumes for each acquired radar variable on 12 October 2012, 15 October 2012, and 14 October 2015, respectively.
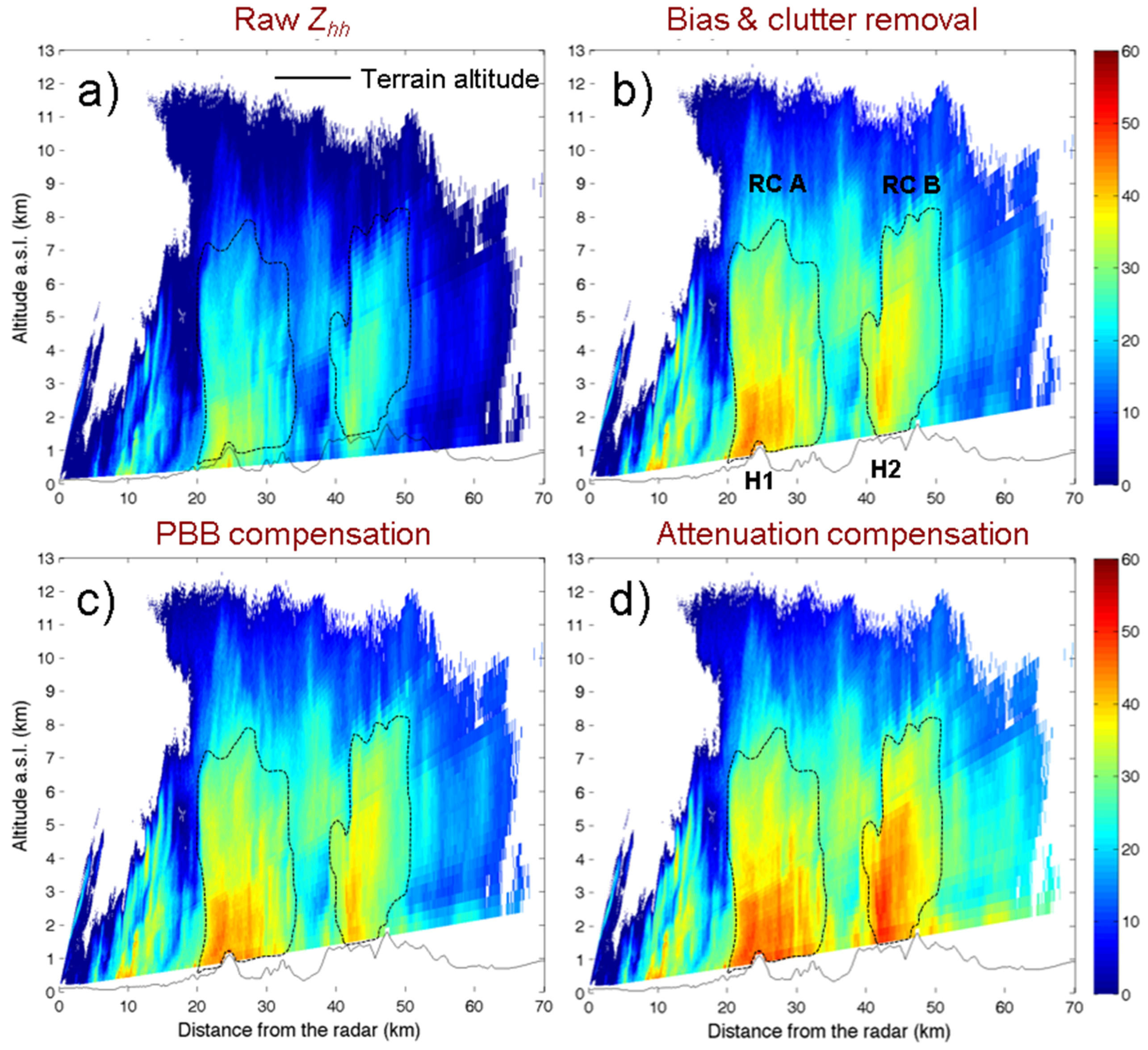
Some range height indicators (RHI) and vertical pointing scans were also scheduled during 14 October 2015 to allow insights into vertical structures of precipitating systems and to deal with Zdr calibration issues. Three sequences of RHI were performed. Sequence 1 includes RHIs at 13:11, 13:17, and 13:21 UTC for the 66 deg azimuth; Sequence 2 includes RHIs at 13:30 and 13:31 UTC for the 190 deg azimuth, and sequence 3 includes RHIs at 13:34 and 13:36 UTC for the 90 deg azimuth. Useful vertical scans were available from 08:10 to 08:14 UTC, for a total of 2160 vertical profiles.
Reference rain gauges were used for comparison with radar QPE. We used rain gauges delivered from the DEWETRA platform, a real-time integrated system for hydro-meteorological and wildfire risk forecasting, monitoring, and prevention. DEWETRA is developed by the CIMA research foundation and is fully operational at the Italian National Department for Civil Protection [
34].
Among other information, DEWETRA collects and stores, on an hourly basis, most of the rain gauges of the local weather services in Italy. A total of 293 rain gauges fall in the P55C radar domain after discarding those stations that show anomalous isolated spikes in terms of hourly rain accumulation greater than 300 mm.
3.4. Definition of Complex Orography
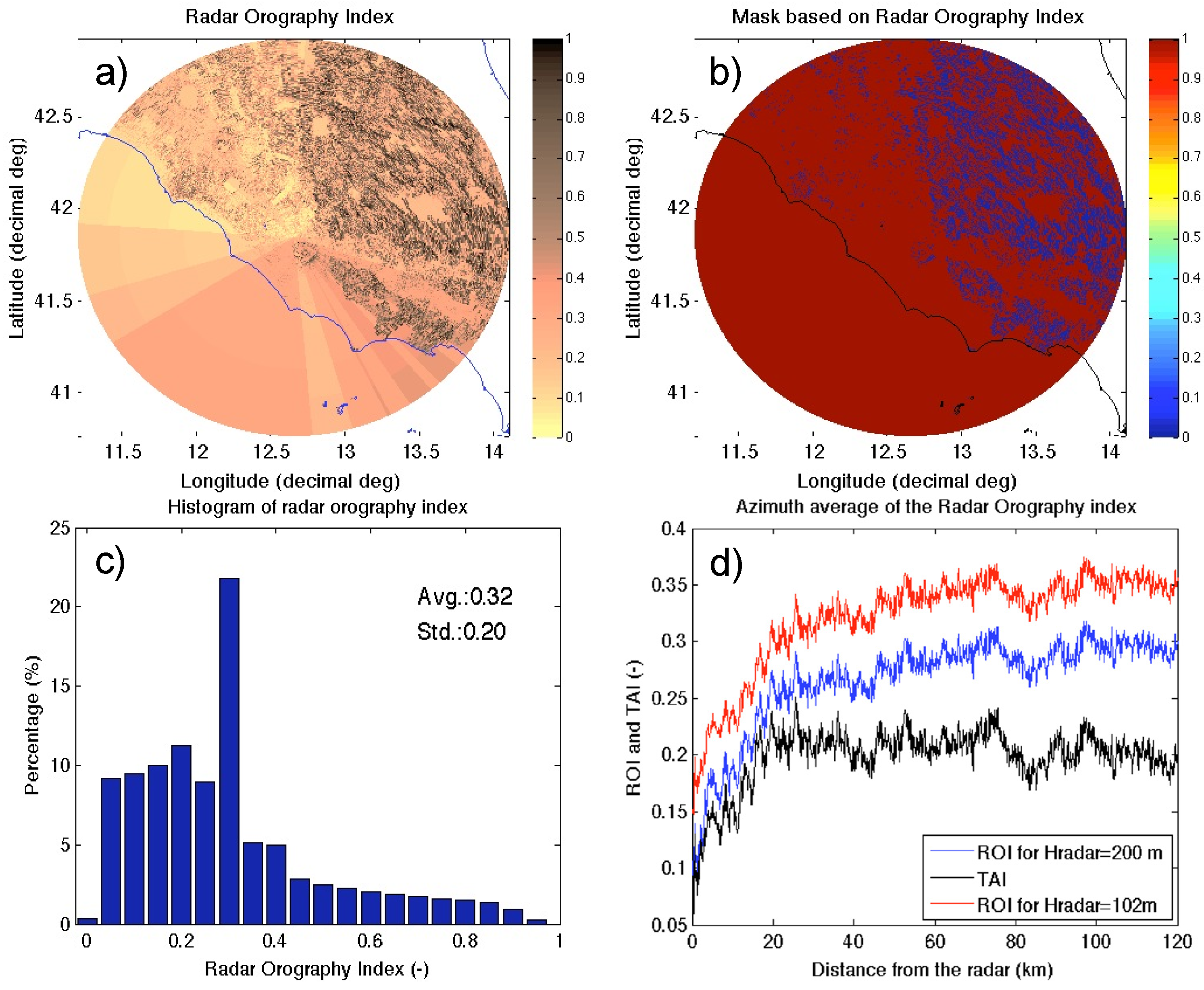
The area covered by the P55C, as shown in
Figure 1, is situated in a diversified environment in terms of variation of terrain altitude. This is a situation often referred to as complex orography. As far as the authors were able to ascertain, there is not a unique and objective definition of complex orography, especially in weather radar studies. Indeed, this is a concept that is often more driven by common sense than by rigorous definition. In this section, we want to make a contribution regarding the definition of a complex orography environment for weather radar studies. The first goal in the analysis of the complex orography environment is to define a new parameter that takes into account both the features of the terrain altitudes and the radar geometry of view. For this reason, we define a radar orography index (ROI). ROI can be useful, for example, for comparing different works dealing with QPE in complex orography, fostering a quantitative categorization of previous and future studies by the degree of complex orography seen by the radar.
The complexity of the orography can be described by the gradient of the terrain altitude (
GTA). However,
GTA alone does not take into account the radar perspective. For example, a radar system positioned on the top of a mountain or in a valley nearby will likely have different QPE performance although the surrounding environment does not change (i.e.,
GTA is the same within the radar coverage domain). For this reason, we consider an additional term, which is the gradient of the radar beam altitude (
GBA). In this way we can define the gradient of the radar orography
GRO as follows:
where at each position
p the operator ∆
rhX is the difference of the altitudes
hX along with the radial direction, and where
δr is the radar radial resolution. The symbol “
X” stands for “TA” or “BA”, indicating the terrain altitudes and sampled radar beams altitudes with respect to sea level. Note that in flat terrain and when considering PPI (plan position indicator) acquisitions,
GBA coincides with the local tangent of the antenna elevation angle. In that special case, sampling at higher elevations produces higher
GRO. In general, the term
GBA increases
GRO as a function of the radar position and the sampling strategy adopted, (e.g., PPI or LBM: lowest elevation beam or VMI: vertical maximum intensity, etc.). A practical example that will be discussed later on will help to clarify this aspect. So far, Equation (8) is not general enough for practical use in different contexts. In order to constrain the dynamic of
GRO to the interval [0, 1] we use an exponential compression formula that allows defining the ROI as follows:
In Equation (9) the coefficient b is chosen so that when GRO reaches its maximum value, ROI = 1 (b = 1/max(GRO)). However, to avoid having the few peaks of GRO corrupt the ROI, we considered the 90th percentile (prc90) of GRO instead of its maximum (b = 1/prc90(GRO)).
For the P55C we calculated ROI assuming an ideal LBM product. The outcome of this calculation is shown in
Figure 4a.
Figure 4b shows a mask buildup by applying a threshold to ROI; that is, assigning 0 to positions having ROI >0.6 and 1 otherwise. This mask can be of some practical use for selecting portions of the radar coverage having a reduced impact of complex orography.
Figure 4c shows the distribution of the ROI values, whereas in
Figure 4d we have drawn average ROIs in two cases: an ideal case where the P55C is positioned at a virtual altitude of 200 m in its actual longitude and latitude position and the actual case, where it is at the altitude of 102 m. In addition, we added the curve of the terrain altitude index (TAI), which is calculated using Equation (9) when
GTA is considered instead of
GRO. These three curves highlight the sensitivity of ROI to the altitude of the radar position with respect to the surrounding terrain orography. In addition, the separation between ROI curves and TAI highlights the contribution of
GRO with respect to
GTA. In the result sections below, the mask in
Figure 4b is used to evaluate the performance of QPEs in different portions of the P55C coverage domain.
4. Results
Results are shown in the form of comparisons of radar rain estimates vs. rain gauge accumulations for the three events studied here. The rain intensities derived from P55C radar, available on average every 5 min, are accumulated on hourly time scales and then are further summed on larger time window to produce multi-hour accumulations. To make the radar-derived rain accumulations temporarily consistent, we considered only those hours where all the 5-min volume acquisitions were available. In doing so, all radar hourly accumulations were made up by considering 12 radar volumes.
Equations (1)–(4) were used to perform estimations of rain rate intensities,
Rq, using single and dual polarization measurements sampled at the lowest elevation beam (LBM), i.e., at positions
p =
pLBM. In addition, Equation (7) was coupled with the four rain estimations in Equations (1)–(4) to carry out the adjustments related to the vertical variability of the rain precipitation and produce estimations at the positions of the ground levels,
p =
pGRD. Equation (7) was used in combination with Equation (6) where
hm = 0 and the coefficients
p1 and
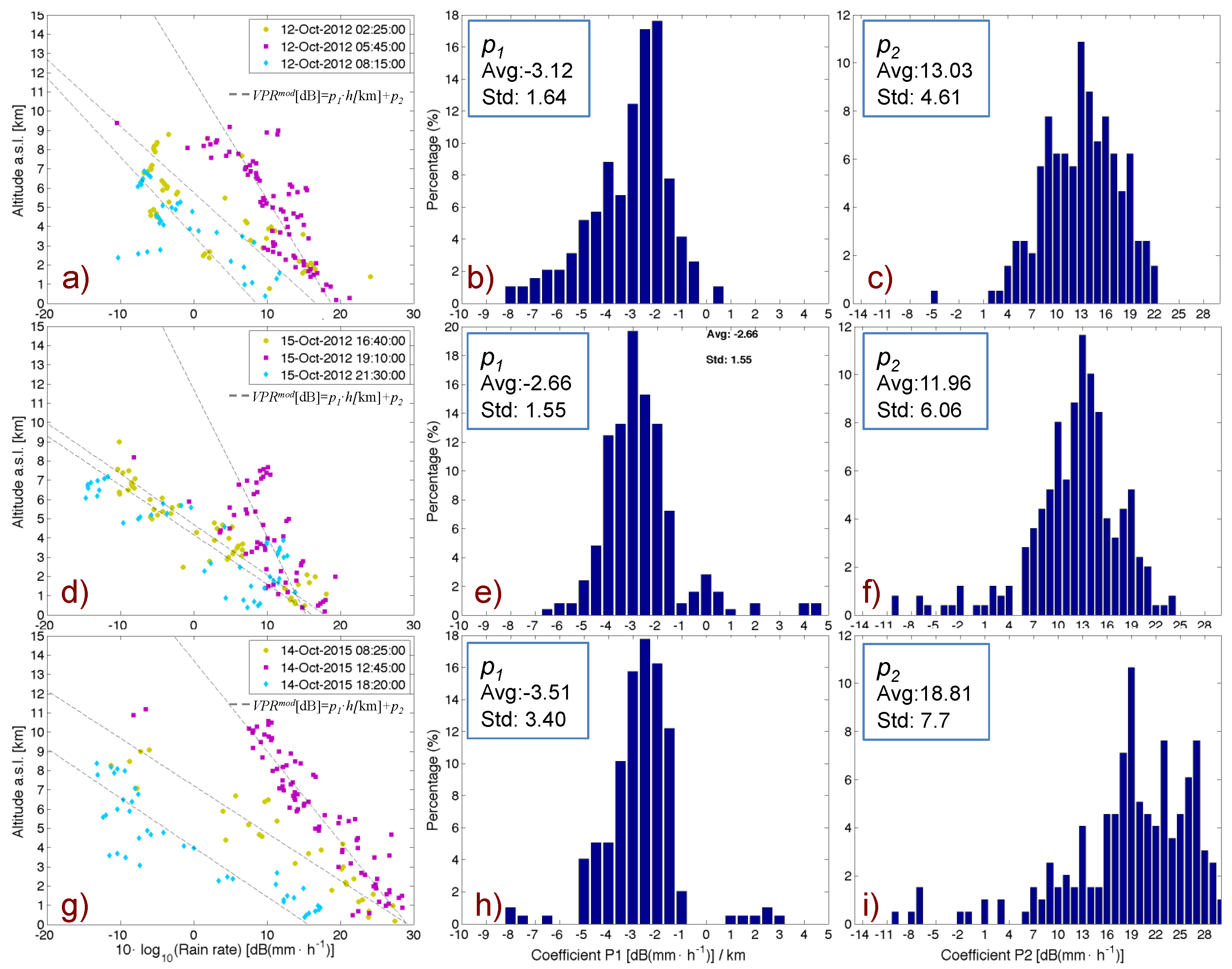
p2 are dynamically calculated at each time step. In this respect,
Figure 5a,d,g, show an example of quasi-vertical profiles of rain estimates and its regression model
VPRmod as formulated in Equations (5) and (6), respectively.
Figure 5b,c,e,f,h,i, show the statistical distribution of the coefficients
p1 and
p2, respectively, for the entire event. It is worth noting that despite the variability of the events, the coefficients
p1 and
p2 are quite stable in terms of average and standard deviation. As a first approximation, the average values of
p1 and
p2 can be used as constant parameters in Equation (6) to adjust the rain estimates aloft and produce estimates closer to those registered at the surface.
To pair the radar estimates and gauge observations, we considered the median of the values of radar hourly accumulations within a circular domain around each rain gauge position. Such choice should smooth the effects due to the time delay needed for the water to fall to the ground as well as the area to point mismatches between the two measurements. The ray of the circular domain is set to 5 km, consistent with typical values of drop fall velocity and horizontal movements of storms. Note that the P55C did not cover the 24 h with a constant time sampling. We limited the rain accumulations only to the hours where the radar variables were available every 5 min, as previously specified.
For an immediate comparison of the performances of the various rain estimators considered for all the events simultaneously,
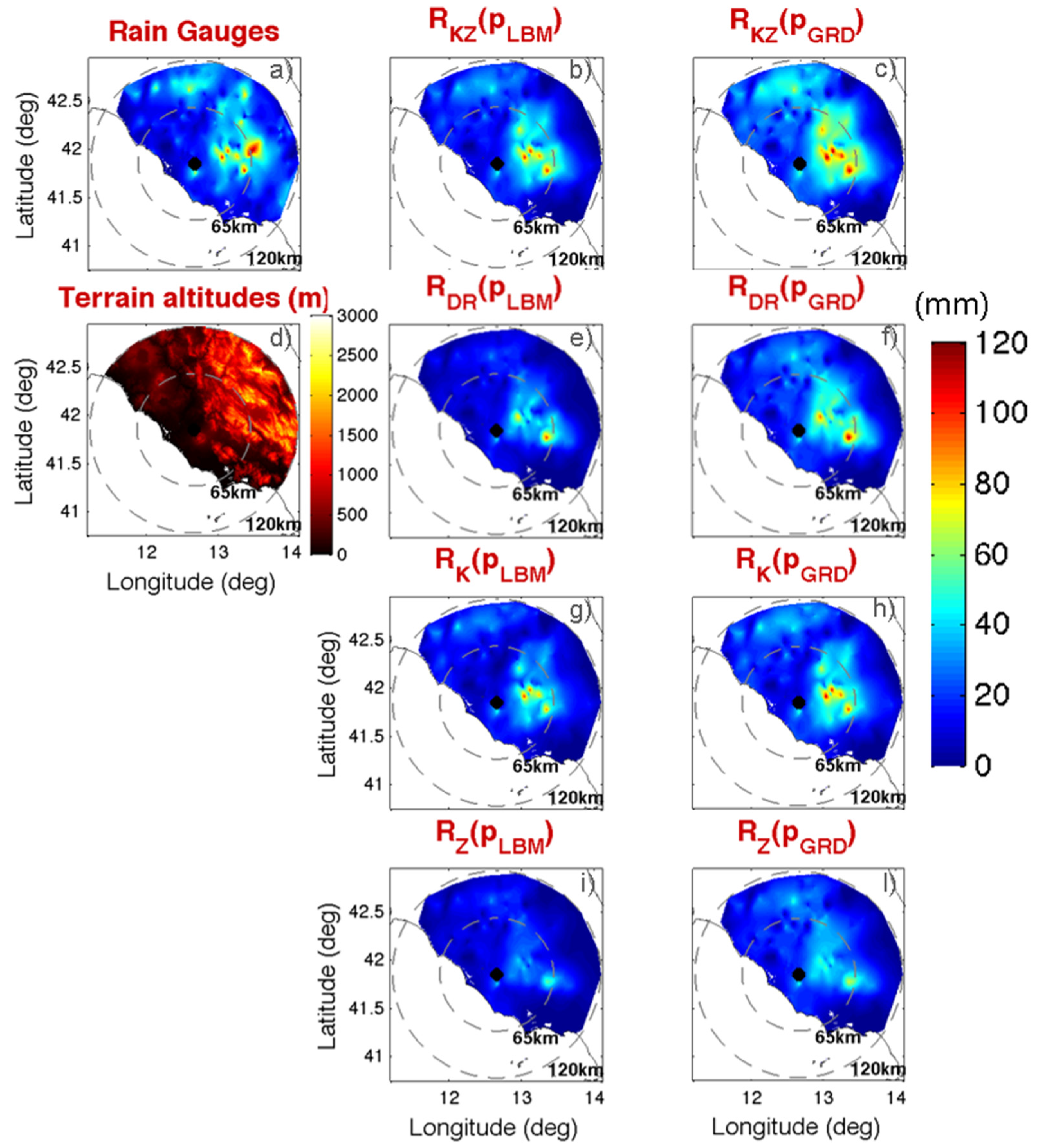
Figure 6 shows the total rain accumulation of the events on 12, 14 October 2012 and 15 October 2015. Actually, to make the comparison more homogeneous and highlight the differences among the various QPE algorithms, we considered the values of the total rain accumulations from the radar at the positions of the rain gauges and then we interpolated them on the radar domain. The same was done for the total accumulations from rain gauges. As can been seen from the rain gauge accumulations (
Figure 6a) the heaviest precipitation was accumulated mainly inland in the eastern area with respect to the radar position, where terrain altitude variations are more pronounced (
Figure 6d). Over all, from this figure a qualitative ranking of the rain estimation algorithm can be done. Looking at the middle column of panels, where the total accumulations of
Rq(
pLBM) are shown, we can see
RZ(
pLBM) behaves most poorly, with large underestimations (
Figure 6i). A large improvement occurs when using
RK(
pLBM), which seems to correctly represent the area of heavy precipitation (
Figure 6g). When introducing
Zdr; i.e., when using
RDR(
pLBM), (
Figure 6e), we have a small improvement with respect to
RZ(
pLBM) but we still register an appreciable underestimation compared to
RK(
pLBM). Finally, when combining all
RK and
RDR into a single rain estimator,
RKZ(
pLBM), (
Figure 6b), we have something that is more consistent with the rain gauges with respect to using
RK(
pLBM) alone. On the other hand, when applying the quasi-vertical profile adjustment (panels in the right columns of
Figure 6) we have an increase of rain precipitation values for all the implemented estimates and a more qualitative agreement with rain gauges, especially in the tendency to represent the maxima of accumulated precipitation (compare, for example,
Figure 6g,h with the reference
Figure 6a). A confirmation of this is given in the example shown in
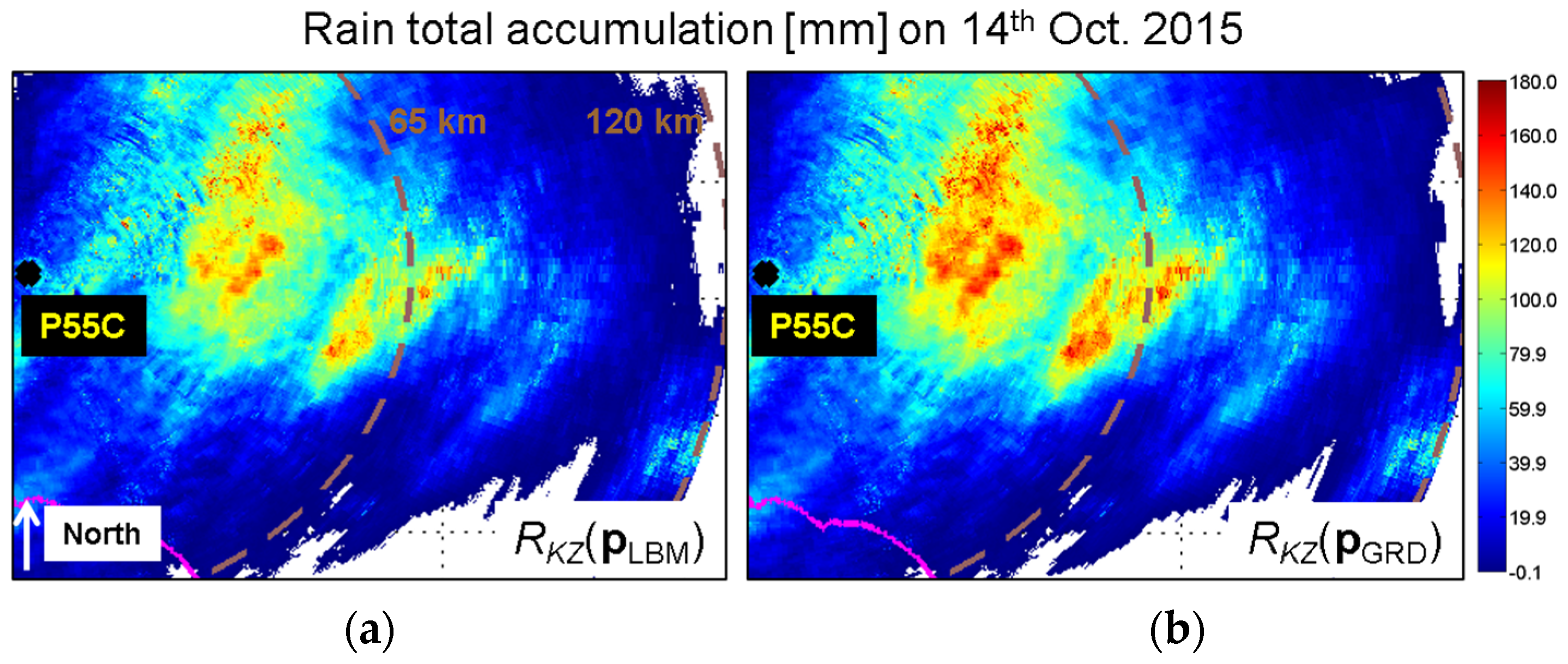
Figure 7, where a zoomed version of
RKZ(
pLBM) and
RKZ(
pGRD) is displayed for the case of 14 October 2015. This figure can be particularly informative in the light of combined radar and rain gauge products. Indeed, in these merging approaches and in particular for those that make use of the Kriging methodology, the spatial structure of the rain field from radar, usually described in terms of spatial covariance or variogram, is used to train the interpolation algorithms [
35]. As is evident in
Figure 7, the spatial structure of rain precipitation fields changes depending on the effect of the spatial adjustment performed (quasi-vertical profile adjustment in our case), and this effect can cause variations in the final results of the combined radar vs. rain gauge products.
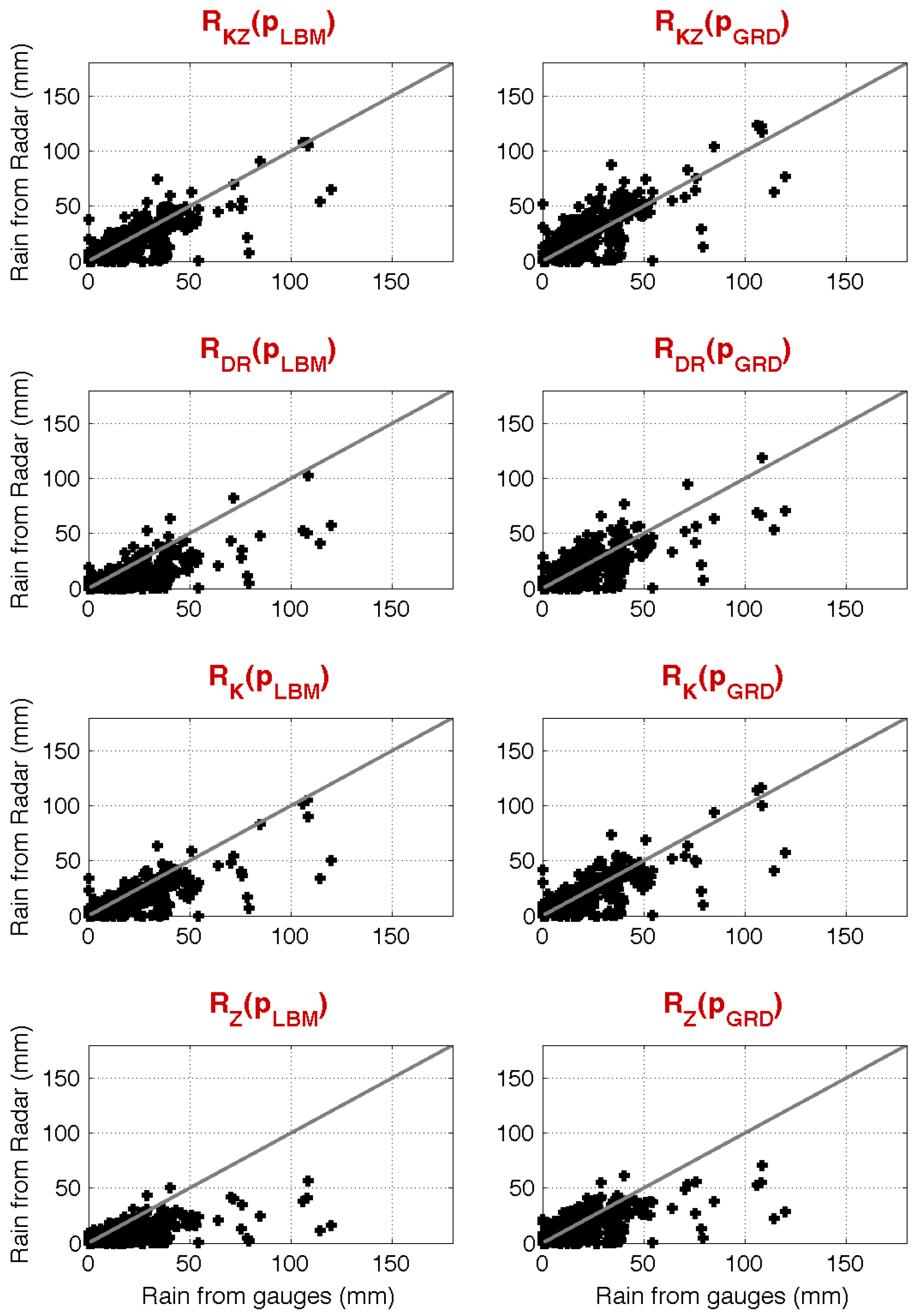
To complete the examination of the results,
Figure 8 shows rain estimator comparisons in terms of total accumulations of radar vs. gauge scatter plots for all the events. Although we note the presence of a significant number of mis-detections (i.e., rain gauge registers rain whereas the radar does not register it), it seems that the use of
Kdp is a key factor when estimating rain in complex orography environments, whereas the use of quasi-vertical profile adjustment is able to partially compensate for the overall bias, although the differences in this case can be subtle. For example, note the distribution of sample pairs around the reference 1:1 line and the error scores discussed below. On the other hand, the estimated precision (the variability of the estimates around the 1:1 line) seems to not get a strong benefit from the application of quasi-vertical profile adjustments.
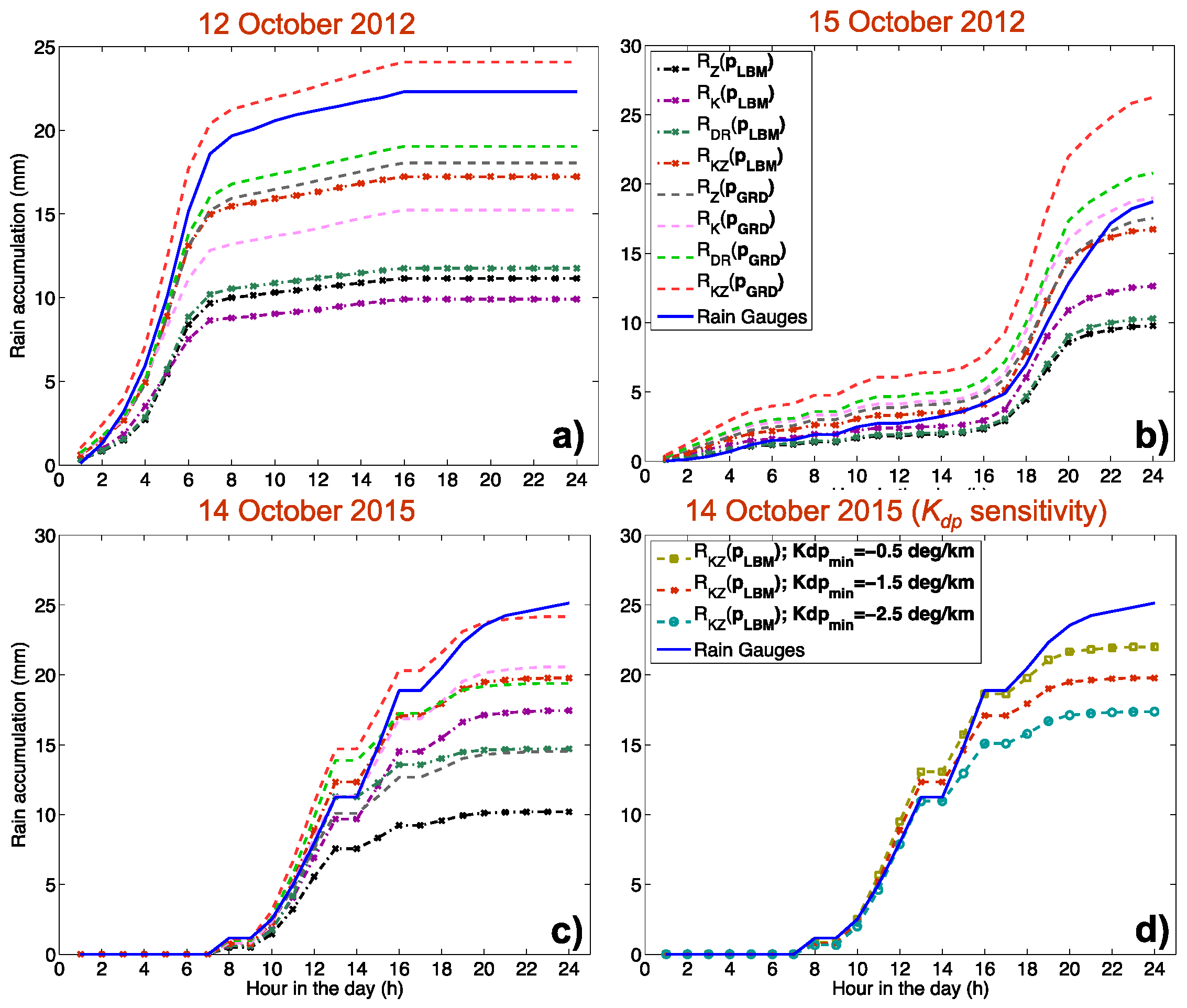
In terms of spatial averages of rain accumulations over time, a clear performance evaluation is shown in
Figure 9 for each case study.
Figure 9a,c confirms the best performance of
RKZ(
pGRD) (red dashed line, which shows the results closest to the blue curve of the rain gauge total accumulation). On the contrary, for the case on 15 October 2012 (
Figure 9b) we have a different outcome, with quite a large overestimation of
RDR(
pGRD) and
RKZ(
pGRD) and the best performance obtained when considering
RZ(
pGRD) or
RK(
pGRD). Finally, it is worth noting that the performance of the
Kdp-based rain estimator depends to some extent on how it is retrieved. In particular,
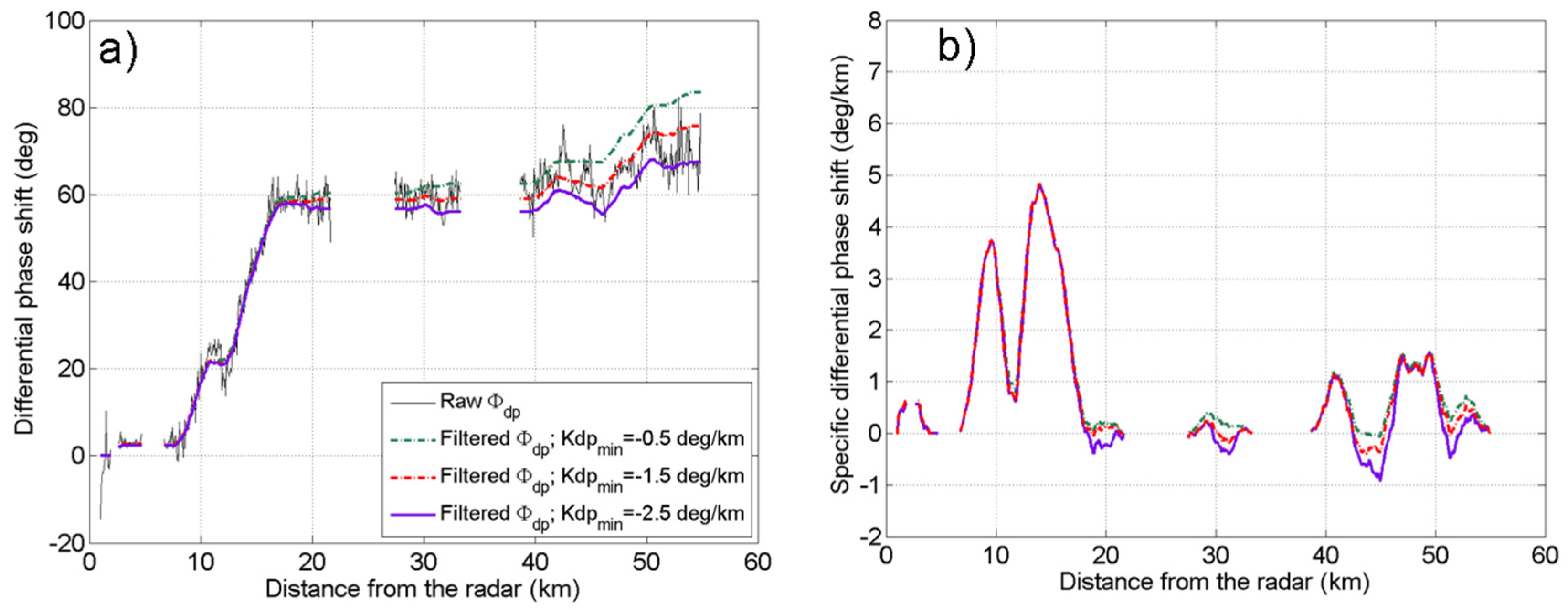
Figure 9d, shows the performance of
RKZ(
pLBM) as a function of four thresholds used (
Kdp_min) for the retrieval of
Kdp as specified in the figure legend for the case study on 14 October 2015. See
Appendix A and
Figure A3 for more details on the filtering of the differential phase shift (
φdp) and
Kdp estimation. For the analyzed cases we used
Kdp_min = −1.5 deg/km, which seems to be a reasonable choice in terms of
φdp filtering.
Looking at more quantitative results,
Table 2,
Table 3 and
Table 4 list the root mean square error, the normalized standard error, the normalized bias, and the correlation coefficient, labeled as RMSE, NSE, NB, and CC, respectively, and defined in
Appendix B, for the various rain estimators implemented for the three case studies. In these tables we also included the error scores obtained when applying a gauge-bias adjustment factor (AF) to
Rq(
pLBM) since many operational QPE algorithms use a gauge-bias correction procedure to fold all of the error sources that compromise the QPEs. Basically, AF is an average ratio of rain gauge accumulations with respect to those from radar estimates as a function of the distance from the radar. We described AF using an exponential law and derived its regression parameters for each of the
Rq(
pLBM) algorithms in Equations (1)–(4) by considering the three case studies together. In addition, the right column in each table lists the average relative improvement between
Rq(
pLBM) and
Rq(
pGRD) when they are evaluated for two distinct parts of the radar domain: the domain where ROI ≤ 0.6 (lower degree of complex orography) and ROI > 0.6 (higher degree of complex orography).
From the tables, we note that there is a maximum improvement of approximately 20% in terms of root mean square error (RMSE) when applying a quasi-vertical profile adjustment on an
RZ estimator (i.e., when moving from
RZ(
pLBM) to
RZ(
pGRD)), although the increment was as low as 4% in the case on 15 October 2012 (
Table 3). The biggest improvement, as noted previously, is made when using
RK. In this case, the improvement from
RZ(
pGRD) to
RK(
pGRD) is between 18% and 30%, with the exception of 15 October 2012, where the improvement reaches only 7%. The combined rain estimator,
RKZ, gives a further small improvement between 6% and 10% with respect to
RK(
pGRD) and between 30% and 38% compared to
RZ(
pGRD). Even in this case, the only exception is given by the performance obtained on 15 October 2012 that register a deterioration of
RKZ(
pGRD) with respect to the other estimators when quasi-vertical profiles are used. Actually, the strongest improvement brought by the use of quasi-vertical profile adjustment seems to be in terms of normalized bias, with results significantly reduced by a factor larger than 25% when moving from
RZ(
pLBM) to
RZ(
pGRD) and from
RKZ(
pLBM) to
RKZ(
pGRD) on 12 and 15 October 2012.
In terms of the adjustment factor (AF), its impact is to increase the correlation coefficient a little bit and in some cases to reduce the bias, but at the same time to produce larger RMSEs. On the other hand, when partitioning the radar scene in the regions most affected by the complex orography (ROI > 0.6) by those with lower complexity (ROI ≤ 0.6), we find that the impact of quasi-vertical profile adjustment is, in most of cases, larger (i.e., more negative) than that in the areas with lower complex orography, as expected. Note that ROI is correlated with QPE; that is, larger ROI corresponds, in most of cases, to larger RMSE. However, to maintain a reasonable size for
Table 2,
Table 3 and
Table 4 we did not list all the error scores as a function of ROI. To have an idea of the correlation of ROI with the RMSE when all the QPE algorithms with no correction are considered, we list the average, standard deviation, and maximum RMSE for ROI ≤ 0.6 and ROI > 0.6, (18.37, 3.80, 27.41) and (25.92, 14.41, 53.67), respectively.
6. Conclusions
This work analyzed three case studies of heavy rain precipitation in Italy that affected the Roman area and caused damage and three casualties, as reported by local news. The C-band dual polarization radar Polar 55 C (P55C), managed by the Institute of Atmospheric Sciences and Climate (ISAC) at the National Research Council of Italy (CNR), tracked the events. The work focused on two aspects scarcely considered by past studies on radar rain estimation: (i) a proposal to objectively define the complexity of an orography scenario with respect to the radar standpoint; and (ii) an evaluation of the benefit brought by the vertical profile extrapolation when using dual polarization QPE algorithms. P55C coverage is well suited to pursue these goals because it includes quite flat regions as well as a part of the Apennine chain with terrain peak altitudes higher than 1500 m and a difference in the P55C radar lowest available bin altitudes and gauge stations of 1240 m on average, with maximum values up to 6 km.
The comparison of radar QPE with rain gauge accumulations indicates that the combined algorithm, which merges together, through a weight factor, the differential phase shift Kdp, the single polarization reflectivity factor Zhh, and the differential reflectivity Zdr, once accurately post-processed, performs better in most of the cases tested than those that make use of Zhh alone, Kdp alone, and Zhh and Zdr. An improvement larger than 25% is found in terms of normalized bias when applying VPR extrapolations to Zhh-based QPE and to the combined QPE algorithm. Many limited improvements are registered in terms of root mean square errors because the error standard deviation probably accounts for most of the discrepancies registered between radar QPE and reference rain gauge.
An additional aspect that emerges from the analysis is that the quality of the Kdp estimates, through its filtering, has an impact on the performance of the QPE algorithms, although this impact is less significant when the combined algorithm is considered. In addition, in one case analyzed, where we observed Zdr columns we found that the VPR adjustment produced quite large overestimations, leading us to conclude that methods based on Zdr can worsen the final results if we do not apply any special care in the preprocessing step as well as in the QPE algorithms.
Although further and more robust analysis in terms of statistical significance will be needed to corroborate our findings and validate our methodology, the results of this work point to a possible operational way to improve the radar QPE algorithms based on dual polarization variables in complex terrain. Future work could be focused on the systematic collection of a considerable number of case studies with different precipitation types from other radar systems in Italy to validate the VPR approach.