Abstract
Several studies have shown that a significant amount of daily air pollution exposure is inhaled during trips. In this study, car drivers assessed their own black carbon exposure under real-life conditions (223 h of data from 2013). The spatiotemporal exposure of the car drivers is modeled using a data science approach, referred to as “microscopic land-use regression” (µLUR). In-vehicle exposure is highly dynamical and is strongly related to the local traffic dynamics. An extensive set of potential covariates was used to model the in-vehicle black carbon exposure in a temporal resolution of 10 s. Traffic was retrieved directly from traffic databases and indirectly by attributing the trips through a noise map as an alternative traffic source. Modeling by generalized additive models (GAM) shows non-linear effects for meteorology and diurnal traffic patterns. A fitted diurnal pattern explains indirectly the complex diurnal variability of the exposure due to the non-linear interaction between traffic density and distance to the preceding vehicles. Comparing the strength of direct traffic attribution and indirect noise map-based traffic attribution reveals the potential of noise maps as a proxy for traffic-related air pollution exposure. An external validation, based on a dataset gathered in 2010–2011, quantifies the exposure reduction inside the vehicles at 33% (mean) and 50% (median). The EU PM Euro 5 PM emission standard (in force since 2009) explains the largest part of the discrepancy between the measurement campaign in 2013 and the validation dataset. The µLUR methodology provides a high resolution, route-sensitive, seasonal and meteorology-sensitive personal exposure estimate for epidemiologists and policy makers.
1. Introduction
Exposure to particulate matter is in Europe regulated by PM-derived standards (Directive 2008/50/EC). This regulation only distinguishes between the size of the particles in large categories (PM10, PM2.5, etc.) and is not source specific. The soot fraction, black carbon (BC), is the part of the PM directly related to combustion processes. Recent evidence, summarized by the World Health Organization, documents the relevance of BC for evaluating traffic-related health effects [1]. Large personal exposure measurement campaigns prove the relevance of the in-traffic exposure contribution [2,3]. Further research into health effects is hampered by the difficulty to measure or model the actual personal exposure to BC. An important reason for this is the strong spatial variability of BC compared to PM10 [4]. Most of the experiments focus on quantifying the differences between different commuting modes [5,6,7,8,9,10,11]. General statistics by road type are provided by Dons and colleagues, showing relevant differences by road class, period of the day and period of the week [12]. Outdoor concentrations are reported to be very dynamic along the individual routes. An extensive study on black carbon exposure for bicyclists showed local changes of a factor 15–20 only due to changing local traffic dynamics and instantaneous meteorology [13]. Especially in the immediate vicinity of traffic lights and complex traffic situations, high exposure levels were found. Other authors reported similar effects based on road classification for different air pollutants [12,14].
When moving from outdoor to in-vehicle concentrations, the variability of the in-vehicle concentrations increases significantly. The influence of the ventilation settings and influence of the speed of the vehicle on the ventilation was addressed by several authors [15,16,17,18,19]. Two important conclusions summarize these studies. Firstly, in “outdoor air ventilation” settings, the outdoor concentration changes are registered very fast inside the vehicle. Lags between 30 and 60 s are detected [15,17]. Secondly, the strongest component of the personal exposure inside the vehicle is the outside concentration due to the tail-pipe emissions of the preceding vehicles [16]. This feature illustrates the complexity of modeling and predicting the real-life personal exposure to traffic-related pollutants inside the vehicles. Several attempts are available in literature. The first instantaneous in-vehicle personal exposure models have been published [20,21]. The exposure models are based on traffic counts, road types, the number of lanes, speed of the traffic and a set of meteorological parameters. The largest study is based on about 300 km of data on a predefined route during a period of six weeks [20]. The authors focus on the comparison of linear models and generalized additive models (GAM) models in the attempts to model the in-vehicle exposure and conclude that the GAM models capture more of the non-linear features in the highly diverse set of exposure descriptors. The authors also mention the lack of instantaneous traffic data and tested the use of more general traffic parameters, such as the annual average daily traffic (AAWT, weekdays only). Predicting instantaneous particulate matter exposure in-vehicle is not very successful at this point due to the interactions between meteorological conditions, local traffic dynamics, ventilation settings, vehicle properties, etc. Other authors build further on these results by excluding the variability due to the ventilation settings [22]. By excluding the variability of the ventilation, these results do not include the correlation between driver-defined ventilation settings and the meteorological conditions. This important and relevant component of the meteorological and seasonal variability is not included due to this design restriction. This approach cannot disentangle the effects of fleet composition, traffic dynamics and meteorological interactions between emission, dispersion and changes in the ventilation settings. Several attempts were made to use data science methods to improve the modeling of in-vehicle exposure. One of the main scientific limitations of these methods is the ‘black box’ nature of data science techniques [23]. Paas and colleagues (2017) present an artificial neural network (ANN) approach for urban near-road PM10, but had to remove the high wind condition to reach a valid artificial neural network model [23].
Lioy and Smith summarized the major challenges for the future of exposure science [24]. Their main conclusion is that restrictions in the experimental designs reduce the applicability of the resulting models in health effects research. In our previous work, a new methodology was proposed to explicitly include all variability in the personal exposure models and, by doing so, provide actual real-life route-sensitive and micro-environment-specific exposure assessments [25]. The in-vehicle exposure model for black carbon was used in [25] as an example case of the methodology. In this publication, we focus on the details of the model selection and model features. In that process, noise maps are used as a low effort, but highly available alternative land use regression traffic attribute. Section 2 addresses the measurement campaign, the methodology and the definition of the covariates. Section 3 presents the data exploration and the models. In Section 4, an external validation is described, and the discrepancies are investigated in detail. The results are discussed in Section 5.
2. Methodology
2.1. Experimental Design and Measurement Processing
The experiment follows the design rules of the µLUR methodology: the dataset should include all relevant variability in the general real-life exposure [25]. To model real-life exposure conditions, an ‘uncontrolled’ citizen science campaign was performed with little knowledge of the vehicle types and personal preferences of the drivers towards the ventilation settings. The nine participants performed their commutes within their daily behavior (weekdays only). The volunteers traveled across the whole region of Flanders and Brussels, the northern region of Belgium (a total area of 13,700 km2; see Figure S1 in the Supplementary Data). The sampling campaign started in December 2012 and ended in November 2013 to cover all seasons. Two participants were sales representative and travelled long distances, partially outside the rush hour. The random trips resulted in an uncontrolled combination of multiple variables: meteorological conditions, background concentration, number of measurements during the different episodes during the day, route choice, actual ventilation settings, participants’ vehicle fleet, and so on. The only design restriction is found in the driver selection. Smokers were excluded (even when they promised not to smoke in the vehicle and/or log their smoking behavior).
The participants carried a GPS and µ-aethalometer (microAeth Model AE-51, AethLabs, San Francisco, CA 94110, USA) The GPS receiver (Haicom III-USB, Taipei City, Taiwan) was positioned under the front wind screen, and the µ-aethalometer was placed on the passenger seat. A total of 340 individual car trips were performed during weekdays, resulting in a total measurement time of 223 h. The quality of the GPS data was manually evaluated, and when the quality was too low, the trip segments were snapped to valid GPS positions (mostly at the beginning of the trips). In the post-processing, the GPS tracks were map-matched to the closest road to avoid misclassifications in the traffic attribution. The black carbon data series was post-processed with the Hagler method to remove the short-term peak values. A very low threshold was used to avoid downgrading the local variability of the BC data series [26]. The resulting one-second smoothed time series was averaged to 10-s periods. The models were evaluated in a temporal resolution of 10 s.
2.2. Model Covariates
The citizen science database was attributed with a set of potential relevant attributes for analysis. In this section, a summary of the covariates is provided (see Table 1). Traffic dynamics-related parameters were deduced from the GPS positions: the speed of the vehicle and the acceleration. The wind speed and temperature were retrieved from the closest location of five meteorological stations throughout Flanders (Figure S2). The meteorological data were made available by the royal meteorological institute of Belgium. The 30-min average BC background concentrations were retrieved from a measurement location provided by the Flemish Environmental Agency (Antwerpen Linkeroever; Figure S3a,b). Traffic and speed limit are available as an hourly average by day of the week and include the diurnal pattern of the traffic for links including down to the level of connections between the smallest villages. In this dataset, the AADT (annual average daily traffic) is available, which results in a single weighted value for the traffic on weekdays on each segment. The alternative traffic attribution is based on a regional LDEN noise map [27], based on the same traffic data (data for the year 2012, see Figure S4a). The LDEN map with the noise emission correction for the day (07:00–19:00), evening (19:00–23:00) and night exposure (23:00–07:00) was adjusted with respectively 0, 5 and 10 dB as defined by the Environmental Noise Directive (European Commission 2002/49/EC). The yearly changes in traffic are typically below 1 percent per year and are representative of the measurement period. In the attribution, LDEN is a single value for the entire day (similar to AADT). To provide a noise map attribute including the diurnal traffic pattern, the daytime noise map Lday was adjusted to an hourly value by applying a standard diurnal pattern. Next to the strong potential local contribution of the traffic to the in-vehicle exposure, more macroscopic dynamics can be expected. Large cities with many roads and higher traffic densities also coincide with increased activities with mid-range impacts on the background levels. To accommodate this mid-range spatial variability, a standard PM10 air pollution map was used for the Flemish region. Furthermore, the street canyon effect was included, using the street canyon index as defined in previous work [13], Supplementary Data. In Figure S5 in the Supplementary Data, the boxplots and frequency statistics of the BC measurements are presented for a few relevant dimensions (hour, weekday, road type, wind speed and temperature).

Table 1.
Overview of the model covariates.
2.3. GAM Modeling and Auto-Correlation in Time Series Analysis
Generalized additive models (GAMs) are regression models where smoothing splines are used instead of linear coefficients for the covariates. This approach has been found to be particularly effective for handling the complex non-linearity associated with air pollution research [20,21]. GAM modeling is presented as a strong complementary tool to the more popular data science methods (neural networks, decision trees, etc.). The additive model in the context of spatial exposure modeling can be written in the form where the outcome variable (the logarithm of the in-vehicle black carbon exposure) is used to improve the potential of the model to predict the highest values:
where vz is the z-th covariate evaluated for trip j at time stamp t; sz(vz,j(t)) is the smooth function of the z-th covariate, n is the total number of covariates and εx,j(t) is the corresponding residual with var(εx,j(t)) = σ2, which is assumed normally distributed. Smooth functions are developed through a combination of model selection and automatic smoothing parameter selection using penalized regression splines, which optimize the fit and try to minimize the number of dimensions in the model. The analysis is based on the GAM modeling function in the R environment for statistical computing [28] with the package “mgcv” [29].
The raw data are time series, and modelling time series can be affected by auto-correlation [30]. A Durbin–Watson test on a generalized linear model of the data confirmed the presence of auto-correlation. The ventilation of the vehicle resulted in a lag between outdoor and in-vehicle concentrations. The ventilation system evacuates and smooths the in-vehicle concentrations. Auto-correlation is therefore a fundamental physical reality. Investigating the lag between the outdoor traffic-related covariates and the in-vehicle concentration implied additional smoothing of the data to match the spatial covariates to the physical properties of the modeled micro-environment. The settings of the ventilation system are unknown, which restricts the options to adjust for the ventilation-related variability in the dataset. Auto-correlation also occurs on longer time scales due to seasonal effects of meteorology, background concentrations and changing traffic conditions as a function of the time of day. The first possibility to address autocorrelation is adjusting the smoothing function [30]. This conflicts with the physical reality of the investigated micro-environment. The alternative is to apply the best possible technique to incorporate the autocorrelation into the modelling process. Many air pollution studies include lags between exposure and outcome, and the methods to address lags have been investigated extensively. In a statistical simulation of different modeling techniques, it was shown that penalized splines were capable of addressing the autocorrelation in such datasets [31]. In a more recent publication, the best practices to evaluate time series in environmental studies include two important pieces of advice: apply flexible spline functions and the model on pooled data over multiple locations [32]. In this specific context, each trip is a random sample of the long-term variability in meteorological conditions and background concentrations, and each trip acts in that perspective as ‘a different location’. Within each trip, the local variability in traffic along the individual’s commuting trajectory is assessed including theshort-term lag due to the ventilation system. In the first step of the modeling process, the lag due to the ventilation system will be quantified. The pooled dataset (including all trips) and the extended set of potential spatial and temporal covariates of different spatial and temporal resolutions fit the best practices for environmental studies in time series analysis mentioned in [32]. The GAM modeling approach has the potential to incorporate the non-linear spatiotemporal aspects of the complex behavior of the in-vehicle exposure including the autocorrelation due to the ventilation system.
3. Data Exploration and Models
3.1. Summary Statistics and Lag Investigation
The physical features of the ventilation of the vehicle result in a lag between outdoor and in-vehicle concentrations. In a first step of the data exploration, this lag has to be explored and quantified. To achieve this, the data were modelled with a set of potential relevant lags. The model based an accumulated lag of 60 s showed the highest deviance explained (Table 2). The accumulated lag of 60 s was calculated as the average of six 10-s values at and after the spatially-evaluated timestamp (referred to as LAG60). The LAG0 model is the weakest model expressing the fact that the local features do not influence the in-vehicle concentrations immediately. LAG120 is less strong compared with LAG60 and expresses a reduced correlation with prior traffic conditions. The black carbon concentrations at a specific moment in time in front of the vehicle affected the in-vehicle exposure within the next min. This matches the available information in the literature [15,17].

Table 2.
Results of the generalized additive models (GAM) to investigate the lag and the weighting of the in-vehicle exposure in relation to the local traffic dynamics, meteorology and traffic attribution. The F-values of the acceleration marked with * express a p-value higher than 2.0 × 10−16. LAG0, lag of 0 s.
The average in-vehicle exposure is 5644 ng/m3. The data were clipped to a minimum value of 100 ng/m3 (the lower measurement threshold of the µ-aethalometer) and at 100,000 ng/m3 as a maximum value. These minimum and maximum values also accommodate the use of the logarithm of the BC exposure in the GAM models. The 10–90% percentiles in 10% steps are: 912, 1668, 2441, 3258, 4146 (median), 5359, 6786, 8746 and 12,187 ng/m3. These values will not be compared to other datasets since this measurement campaign did not aim to achieve an unbiased dataset. The data are, explicitly, only used to investigate and model the short-term variability of the in-vehicle black carbon exposure.
The exposure distribution is strongly skewed (skewness = 3.6), which reduces the capability of the GAM model to predict the less frequent high exposure episodes. The physical properties of the black carbon measurements result in small residuals for low BC values. By applying a weighting function (WBC) for both low and high BC values, the model becomes more sensitive to the low and high exposure values. The resulting variant of the model BC_LAG60_WBC shows a stronger deviance explained compared to the BC_LAG60 model (last row in Table 2). The model fit strength was tested by evaluating the total and average trip exposure prediction versus the measured BC trip exposure, aggregated by trip (Figure 1).
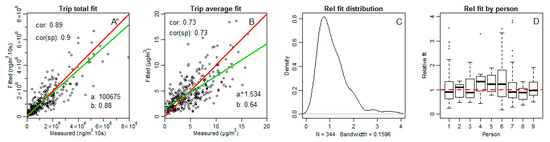
Figure 1.
Trip fitting evaluation of the model BC_LAG60_WBC: (A) total trip fit versus measurement; (B) average trip fit versus measurement; (C) relative trip fit distribution; and (D) relative trip fit distribution by person. The red line indicates y = x. The green line is the linear fit y = a + bx; a and b are presented in the plots.
The total trip exposure prediction is strong (r2 = 0.89, slope = 0.88); on the average trip exposure, the fit is somewhat lower (r2 = 0.73 and slope = 0.63). The automatic use of criteria as AIC for selecting models has been reported previously to be potentially misleading [30]. The reduction of AIC for BC_LAG60_WBC is compensated in the model fit evaluation by improving the slope for the average trip exposure from 0.50–0.63 and deviance explained from 39.1–46.9%. All models in the next sections will be based on the LAG60 exposure dataset with weight WBC.
3.2. Non-Linear In-Vehicle Exposure Characteristics
In this section, we present the non-linear aspects of all covariates. The aim is to illustrate the variability in the measurements and map the specific non-linear characteristics of all the covariates to the potential origin of the in-vehicle exposure variation (see Figure 2). The hourly traffic counts and noise attribution are presented within a single model to illustrate the relative behavior and strength. Other interactions between other sets of covariates exist, as well, but they are only described in a qualitative manner. The diurnal pattern of log (BC) is fitted by using the hour of the day as a covariate, referred to as HourOfDay. The GAM summary statistics are available in Supplementary Data Table S1.

Figure 2.
Splines of the BC_LAG60_WBC GAM model, expressing the non-linear properties of the covariates. The local traffic dynamics are shown in the top left panes (A–C), the meteorological covariates in (D–F), the traffic related covariates in (G–I), the temporal background concentrations for BC and PM10 in (J,K) and the spatial building related attribute in the bottom right pane (L).
The relative speed (actual speed divided by the local speed limit) shows a maximum below 0.5. The peak can be related to dynamic traffic with starts and stops and/or congested traffic. Short distances between vehicles in such traffic conditions result in higher in-vehicle concentrations. The drop-off at low relative speed indicates actual stops or congestion with idling vehicles. This idling effect was also visible for bicyclists in Bangalore, India [33]. The acceleration is the weakest covariate and is numerically highly sensitive to the quality of the GPS readings, but behaves as expected; increased levels when accelerating and decreased levels with moderated deceleration. Strong deceleration, related to actual stops in traffic, shows high variability, which can be due to the short distance to the source when waiting and idling in a queue at a traffic light. The bulk of the data show little to no acceleration and this is reflected in the very low strength of the covariate. The actual speed shows higher values at low speeds and lower values at low speed. The increased levels at low speed can find their origin in congested traffic, as well. The reduction of in-vehicle exposure at high speeds could be linked to the higher efficiency of the ventilation systems at higher speeds as mentioned by Xu [15,34]. Higher speeds also occur in free flow traffic with higher distances between the vehicles. Other interactions with other covariates are evident; the actual speed does for example also relate to the type of road travelled. The absolute speed is lower in strength compared to relative speed, expressing the complex interactions between vehicle speed and traffic dynamics.
The in-vehicle exposure decreases with high wind speeds as expected [20,21,34]. Wind speed is by far the strongest covariate. The temperature shows a distinctive and complex pattern. Very low temperatures and moderate temperatures result in high exposure, and low and very high temperatures result in lower exposure. The high exposure at very low temperatures could relate to the cold periods with high background levels, stable atmosphere and/or due to cold start increased vehicle emission. The high exposure for moderate temperatures and the lower exposure for the highest temperatures can be linked to the changing ventilation settings. At moderate temperatures, fresh outdoor air is enough for cooling and refreshing the vehicle interior; at higher temperatures, air conditioning is turned on, changing the air flow drastically, while the filter removes particles [18,34]. Relative humidity shows increased levels at high values. This potentially links to the light scattering properties of water-saturated BC particles, which can trigger an increased response in the aethalometer [35]. The in-vehicle exposure increases with background concentrations, but for high background concentrations, saturation is occurring.
The large-scale spatial covariate introduced in the model through the PM10 map has an interesting feature. For low values, the covariate is not significant, but at high levels, typically near the major cities, it adds value to the model, expressing higher in-vehicle concentrations in larger cities. This links to the higher density of roads and traffic in and around the cities and can be expressed through several mechanisms (higher urban background, increased traffic congestion, etc.). The street canyon index correlates with the PM10 map, but adds additional spatial detail.
The two traffic-related data sources LDEN and weighted traffic Trafwgt are similar in strength despite the fact that LDEN is only a spatial covariate and Trafwgt is a spatiotemporal covariate. The HourOfDay covariate shows higher concentrations in the morning rush hour compared to the rush hour in the evening, matching the well-known diurnal pattern. This pattern captures the increased emission related to the modified traffic dynamics during rush hours. The HourOfDay covariate is discontinuous because no trips were performed during the night. In the evening, the traffic volumes and exposures are low. In the early morning, traffic is already significant. The data therefore include long-distance commutes along highways before rush hour. This pattern can also express the effect of the stable atmosphere on ambient concentrations. The traffic-related covariates are investigated in detail in Section 3.3.
3.3. Comparing Traffic-Related Data Sources
This section evaluates the strength of the traffic-related data sources and investigates how they relate to the diurnal pattern of the in-vehicle BC exposure. The main focus is on the contrast between traffic covariates including a diurnal pattern and traffic covariates with total daily traffic only. Adding a HourOfDay covariate will enable the models to adjust the traffic data to the in-vehicle exposure pattern and will account for the non-linear aspects between traffic and exposure. The meteorological aspects (wind speed and temperature), background concentration and the street canyon index are, as the strongest components in the BC_LAG60_WBC model, kept as fixed covariates in these model variants. The relative changes in the models with or without the HourOfDay covariate reveal the non-linear behavior between the diurnal patterns of traffic data, hour of the day and the in-vehicle BC exposure. The exercise is performed for the direct traffic attribution (in weighted number of vehicles) and the alternative approach through the noise covariates (LDEN and Lday,hour). In Table 3, the different variants of the GAM models are defined and the matching F-values are shown. Higher F-values express an increased relative strength of the covariate compared to the other covariates within a single model. The models are sorted by deviance explained and AIC. The models and covariates including a diurnal pattern are indicated with †. The simulations were performed for two sets of models. The first set includes the GPS-based relative speed and the acceleration (prefix BC), and the second set does not include the GPS information (prefix BCR).

Table 3.
Results of the GAM models to investigate the strength of the traffic-related data sources of the in-vehicle exposure for different traffic sources, the influence of the HourOfDay and the traffic dynamics. The traffic covariates with † include a diurnal pattern. Traffic covariates without a diurnal pattern outperform the traffic covariates including a diurnal pattern (expressed by higher deviance explained and/or lower F-values for the HourOfDay covariate). The F-values of the acceleration marked with * express a p-value higher than 2.0 × 10−16, but are still significant. BC, black carbon.
The models including the GPS information are the strongest, and within those models, the noise-based models are the strongest. The BC_LDAYWH model has a similar evaluation as BC_LDENWH, but the relative importance of the HourOfDay covariate does not behave as expected. The F-values of the BC_LDAYWH model are higher compared to BC_LDENWH. Since Lday,hour includes a diurnal pattern, less influence of the HourOfDay is expected (lower F-value). This indicates that a higher adjustment of the HourOfDay spline is required to achieve the same model quality. For the models excluding the GPS information, a similar pattern emerges, confirming the mismatch between the hourly traffic covariates and the in-vehicle BC exposure. Improving the temporal resolution of the traffic data does not automatically result in stronger models. The in-vehicle exposure is a complex non-linear function of the traffic. The spline of the HourOfDay covariate fits that complex relation.
As the final model, the LDEN noise map-based model BCR_LDENWH is selected. With a low number of covariates, not requiring the GPS information, it is the most general applicable model in Table 3. The splines of the BCR_LDENWH model are shown in Figure 3.

Figure 3.
Splines of the BCR_LDENWH GAM model: LDEN noise map (A), Wind speed (B), HourOfDay (C), Temperature (D), Black Carbon Background concentration (E) and Street Canyon Index (F).
The trip fit evaluation of the BCR_LDENWH is shown in Figure 4. The correlations and slopes are slightly reduced compared to BC_LAG60_WBC. The six covariates in BCR_LDENWH predict the trip exposure properly. The Pearson and Spearman correlations for the trip total fit are 0.89 and 0.89 and 0.7 and 0.69 for the trip average.

Figure 4.
Trip fitting evaluation of the model BCR_LDENH: (A) total trip fit versus measurement; (B) average trip fit versus measurement; (C) relative trip fit distribution; and (D) relative trip fit distribution by person. The red line indicates y = x. The green line is the linear fit y = a + bx, a and b are presented in the plots.
4. External Validation
4.1. Properties of the External Citizen Science Campaign
A large citizen science campaign for BC exposure was performed in the region of Flanders by Dons and colleagues [2,3,12,36]. The in-vehicle dataset, referred to as external data (EXD) of Dons et al. was used as an independent data source to validate the µLUR model. The main differences between the two measurement datasets are:
- Temporal resolution: 10 s for the µLUR model versus 5-min resolution for EXD
- Year of sampling: 2013 for µLUR, 2010–2011 for EXD
- Season: all year seasonally-balanced campaign for µLUR and an unbalanced combination of summer (six household) and a winter campaign (19 households) for EXD.
The most important similarity between the two campaigns is the availability of GPS data at a similar resolution. The map-matching post-processing was also applied to the GPS data of the external citizen science campaign. The Q1, median, mean and Q3 of the validation data (EXD) are 3805, 6147, 7187 and 9508 ng/m3 and 2040, 4146, 5644 and 7637 ng/m3 for the µLUR. The summary statistics of the two BC campaigns differ significantly (p < 2.2 × 10−16). The difference in the lowest values was expected due to the different resolution measurement campaigns.
4.2. Validation Data Workflow
The µLUR methodology extracts spatiotemporal features from participatory campaigns and applies the micro-environment-specific model to any external mobile population [25]. In this case, the in-vehicle trips of the external data are the micro-environment-specific activities, and they contain the recorded GPS positions and black carbon measurements. The GPS data were pre-processed to match the processing of the µLUR dataset (map matching to the road network). The temporal resolution of the black carbon data series of the external data was five minutes, which prohibits the comparison of the µLUR prediction on the 10-s resolution of the µLUR model. For this reason, the validation was performed at the level of the individual trips. Trips with duration of less than 15 min were excluded from the validation data. The validation is sensitive to all meteorological influences, but the short-term variation within the trip cannot be evaluated.
4.3. External Validation
In Figure 5, the external validation is illustrated. The correlations are strong for the total trip prediction (Pearson 0.82 and Spearman 0.79) and reasonable for the average trip prediction (Pearson 0.50 and Spearman 0.48). The Q1, median, mean and Q3 of the relative trip fit are 32%, 49%, 67% and 74%, expressing a strong underestimation of the exposure measured in the EXD. The median is underestimated by 51%, the mean value by 33%.

Figure 5.
External validation based on BCR_LDENWH: (A) total trip fit versus measurement; (B) average trip fit versus measurement; (C) relative trip fit distribution; and (D) relative trip fit box plot. The green line indicates y = x. The red line is the linear fit y = bx, b is presented in the plots.
4.4. Investigating the Discrepancy
The correlation of the external validation is strong, but the µLUR fails to predict the absolute levels. This implies that the model captures the temporal variability very well, including the meteorological influences and the spatiotemporal variation of the local traffic influences. The first candidate is a potential difference in the use of the ventilation system in both groups of participants. There were restrictions on ventilation use in both citizen science campaigns. Ventilation could bias the datasets due to the lower number of participants in the µLUR campaign, but no objective arguments can be formulated to relate this discrepancy to the ventilation use of the population sample. Ventilation is most likely not the origin of the discrepancy.
The second potential candidate is an actual decline of the emissions of black carbon. The two participatory campaigns are separated by three to four years. In 2009, more stringent EU legislation (Euro 5) reduced particulate matter emission limits for diesel vehicles from 0.025 g/km down to 0.005 g/km. The new legislation could hardly have influenced the fleet composition at the time of the external campaign in 2010 and 2011. To quantify the potential change in the vehicle fleet emission, two options are available.
The first option is to estimate the potential effect of the vehicle fleet composition on the emission of PM by 2013 based on the emission standard. The potential decay is simulated based on the changing composition of the vehicle fleet. Belgium has a relative fast renewal of the fleet, and vehicles are typically replaced after four to five years. In 2013, 30% of the vehicle fleet was already compliant with the Euro 5, resulting in a reduction of the fleet emission by 33%. This matches the mean discrepancy in the external validation.
The second option is to investigate the evolution of black carbon concentrations measured by the official air pollution monitors. Black carbon monitoring started in Flanders in 2010 in five locations near the city of Antwerpen with the main focus on industrial sources. In Antwerpen-Linkeroever, a background location was chosen (also used in the models). One measurement location was chosen close to a major road inside the city (Borgerhout background) at approximately 30 m from the roadside. In these measurement points, the average black carbon concentration dropped by respectively 19% and 17% between 2010 and 2013. This mean reduction does not fully explain the discrepancy in the external validation, but traffic is not the only source of black carbon concentrations. It is interesting to attempt to assess the in-traffic reduction in a higher spatial and temporal resolution. In 2012, an additional monitor was positioned by the Flemish Environmental Agency at 10 m from the main road near the Borgerhout street-side location. This illustrates that the Flemish Environmental Agency was already aware of the potential strong distance to source effects of the black carbon concentrations. These three monitors were used to investigate the long-term evolution of the traffic-related black carbon exposure. In Figure 6, these data series are presented in diurnal patterns by year, with a boxplot for each half hour of the day (the temporal resolution of the monitoring network).

Figure 6.
Diurnal patterns at three long-term black carbon measurement locations in ng/m3 (Flemish Environmental Agency): background location (top), in-city major road at a 30-m distance (mid) and 10-m distance to the same in-city road (bottom). Each half hour element is a boxplot showing Q1, Median, Q3 and whiskers for fifth percentile and ninety-fifth percentile. The colored slopes visualize the annual trend for the third quartile during morning rush hour (red) and the first quartile during night-time (green).
On each chart, two trend lines are shown. The red line is matched to the Q3 levels of the morning rush hour (Q3rush); the green curve is mapped to the lowest Q1 levels during the last hours of the night (Q1ngt). The slopes visualize the decrease of the black carbon concentrations for different indicators within the diurnal pattern of the black carbon. The results are summarized in Table S2 in the Supplementary Data. The yearly average reduction during the night-time hours is higher compared to the all-day levels and the relative difference between Q1ngt and Q1day increases when the measurement location is closer to the closest road (from 20–68% when the distance to the road drops from 30 down to 10 m). The evaluation on Q3rush shows a similar pattern, but the difference between the background location and the in-city background location is much smaller (a relative drop of 12%). The relative reduction at the location closest to the road during rush hour is more than 90%. This illustrates the huge spatial variability of the BC concentrations and very strong distance to source effects. It can be expected that this effect increases even further when closing in on the traffic lanes. The consequences on the in-vehicle exposure are considerable. The overall reduction during a trip inside the vehicle is the result of a complex sample of this spatiotemporal variability, sensitive to the instantaneous meteorology, background concentrations and local traffic and traffic dynamics. The yearly lowest reduction for background locations was quantified through the Q1ngt indicator (−8%) and reaches values of −10% during morning rush hour. A similar evaluation on Q3 provides a typical range for the expected reduction along the trips. The yearly reduction of Q3 for dense traffic locations was quantified through the Q3rush indicator (−10.6%). Over a three-and-a-half year period, this resulted in reductions of up to 32% in the in-city street-side location. This last value is most likely an underestimation of the actual concentration reduction near the vehicle intake when travelling in dense traffic during rush hour.
The participants traveled mainly during rush hour, and the discrepancy of the external validation fits between the values Q1ngt and Q3rush (median minus 51% and mean minus 33%). The reduction of 50% in the median is plausible near the air-intake of the vehicles. The discrepancy in the external validation can be explained by the changes visible in the diurnal patterns of the official measurement stations of the Flemish Government. These two independent sets of information support the conclusion that the discrepancy on the median and mean can be explained by the changes of the PM emission of the vehicle fleet.
5. Discussion
5.1. Translating the Complexity of In-Vehicle Exposure to Applications for Epidemiologists
In Section 3, the complexity of the in-vehicle exposure is illustrated. The technique to evaluate the in-vehicle exposure at an extremely detailed temporal resolution, combined with equally detailed traffic attribution, results in important information. The spatiotemporal aspects of an in-vehicle black carbon exposure campaign were successfully modeled using detailed spatiotemporal attribution. A similar instantaneous model was built for cyclists [13]. In that model, only four parameters were statistically relevant after applying a background correction. The background correction was also investigated for the in-vehicle exposure. This approach failed due to the fact that the background exposure is not a dominant covariate for the in-vehicle exposure. This matches the physics for this specific micro-environment. The strongest component is the distance of the vehicle to the exhaust of the preceding vehicles. The distance to the preceding vehicle is a highly non-linear function of the local traffic density and time of day. Since the distance to the preceding vehicles is unknown, the µLUR model has to provide an indirect solution. This happens by fitting the actual diurnal pattern of the in-vehicle exposure on the traffic data in a data scientific approach.
The physical complexity of the in-vehicle exposure limits the potential to reduce the number of covariates. Disentangling the meteorological effects from the indirectly fitted strongest component (distance to preceding vehicles) was unsuccessful since the changes in the ventilation settings also depend on the meteorological conditions. The µLUR approach can extract the relevant relationships from the gathered data without an analytical solution for the underlying parameter interactions. For epidemiological applications, a full physical model is not necessary, and if a physical model were available, it would not be applicable to the large cohorts due to the lack of input data. The presented µLUR methodology can fulfill the requirements listed in the challenges for the future for exposure science [24,37,38].
A potential objection against the µLUR approach might be the requirement to build and use an instantaneous model. This objection is actually a benefit. Variants of the models can be built that aggregate the model over the yearly average meteorological conditions. This only requires a procedure as illustrated in [39]. This µLUR variant provides the yearly averaged exposure and still incorporates the specific features of the commuting pattern of each individual in the study.
5.2. Noise Maps as a Ubiquitous Traffic Data Source
When evaluating the different options to feed the µLUR with traffic data, the most important conclusion is that the used traffic covariate is not the most crucial feature to build a successful µLUR. Most of the models result in a similar quality. The most important feature of the µLUR is that the models only use a single traffic covariate and not multiple partially correlating traffic covariates. In standard LUR practice, a large set of possible combinations of short and long distance variants of the traffic data are included, which results in a high risk of overfitting the sparse data points [40,41,42]. The high temporal resolution of the µLUR in combination with the non-linear modeling counteracts this by design. When the sampling includes all meteorological conditions and seasonal aspects, the models become robust, as proven by the high correlations found in the external validation. The µLUR methodology itself is partially robust towards the quality of the underlying covariates, as well. The same data layer is used to extract the knowledge from the data and to apply the model to external input data. This translation of spatial and/or temporal features to the exposure under investigation is the fundamental feature of any land use regression solution. The use of a noise map as the underlying traffic layer is not at all required.
Some features of the noise map approach are however very appealing. Noise maps accumulate the noise exposure from different roads when they are in each other’s vicinity. This results in higher values at crossings and complex traffic situations, matching the areas with high traffic dynamics. In this way, the additive nature of the noise maps mimics the traffic emission behavior. The biggest advantage of the noise mapping approach is the availability of such noise maps. The EU member states have to provide these maps for all cities larger than 50,000 inhabitants and update them every five years [43]. In this specific case, the noise map is not built to fulfil the Environmental Noise Directive requirements (END). The used map includes the entire regions of Flanders and Brussels, while END maps outside the agglomerations are restricted to a minimal vehicle count. The END maps are spatially not compatible with citizen science campaigns without spatial restrictions. For larger agglomerations, the spatial extent of the END maps will be adequate for city-wide citizen science campaigns. The noise map used in this work has one important restriction. It lacks the screening of buildings. Especially in the urban areas, this may have resulted in an overestimation of the traffic parameter. In open areas, we expect no impact on the lack of screening due to buildings.
Another relevant feature of the noise map is the inherent logarithmic scale. This has several advantages. Small changes in traffic will not be reflected in strong changes in the noise maps. Typical yearly changes in traffic data of a few percent will not affect the maps and will not add numerical jitter when changing the underlying noise map over time. Traffic data are numerically more sensitive compared to the noise map variant. In the instantaneous model for cyclists, a linear relation was found between the logarithm of BC and the engine-related noise [13]. Performing this exercise on a noise map variant including only the low frequency noise component of the noise emission is a theoretical option, but since that type of noise map is not available as a standard, it is not pursued. The main advantage of this specific noise map is the spatial quality of the road traffic sources (see Figure S3b). The traffic data are provided by the Flemish Government on an idealized network. This network is geographically accurate for major roads, but for local roads, the spatial error can be important. Prior to the calculation of the noise map, the idealized network is routed on the physical routable network (Open Street Map). Due to this procedure, the noise map is very sensitive to the actual physical position. These combined features illustrate that noise maps are a valid traffic attribute for traffic-related air pollution land use regression modelling.
5.3. Spatial Transferability of the Model
The focus in this paper is on the changing emission of the fleet, but to address future applications, an assessment of the spatial transferability is also relevant. The model data and validation data are spatially not intertwined: different individuals with independent commuting patterns. However, they are spatially restricted to Flanders and Brussels. The potential spatial transferability will therefore be mainly related to the fleet composition. Unfortunately, the Belgian passenger car fleet is very specific in both the European and global context due to the high fraction of diesel-powered vehicles. In 2013, 62% of the fleet was diesel-powered, while the EU-15 average was 35%. Recent changes in legislation are reducing the fraction of diesel in the Belgian fleet (59% in 2016). The differences in the fleet compositions throughout Europe and the high number of diesel cars in Belgium are extensively discussed by Cames and Helmers [44]. Due to the specific fleet, this black carbon model will not be transferable as such to other European countries without calibration. The µLUR methodology itself is based on local participatory sensing data [25]. When transferring a model to another geographical context, all covariates and their local features and quality will affect the model. The µLUR model is by design not a stand-alone transferable function, but is highly intertwined with the local features of the external data and the derived covariates. Calibration is an implicit part of the methodology. This might be perceived as a drawback, but most countries have measurement datasets or citizen science projects that can be used to build similar µLUR models. The strongest covariates in this analysis will be valuable input to model other datasets.
5.4. Changes in Particulate Emissions of the Vehicle Fleet
One of the most challenging issues of the health effect research is the long-term evolution of the exposures. The external validation underestimates exposure by 33% (mean) and 50% (median) while the correlations are very good. Recent publications mentioned the improved quality and active development of in-vehicle particle matter filters, specifically tested for exposure to ultrafine particles (UFP). A reduction of 80–90% is achieved with certain specific filters [18]. It is unknown to what extent these types of filters or less performant filters are present in the current vehicle fleet. No specific technical information on the vehicles of the participants is available, but this is identified as a potential origin of unexplained variability. The change in the EU particle matter emission standard for diesel vehicles (Euro 5) largely explains the discrepancy. Since the emission dynamics is complex, the function to adjust the extracted features from the raw data will be complex. This complexity reveals itself in the reduction of the average trip exposure prediction (a drop from 0.70 down to 0.50 from the µLUR evaluation to the external validation). An extended investigation to quantify the spatiotemporal reductions in terms of local traffic, time of day, local traffic dynamics and meteorological conditions is necessary, but the validation dataset has only a temporal resolution of five min. This prohibits further analysis of the detailed spatiotemporal discrepancies between µLUR and the validation data.
The presented technique has strong potential because changes in the emission of the fleet do not only occur in time, but also in space. Low emission zones are the best example. Performing a citizen science campaign across restricted and non-restricted areas might result in µLUR including a spatial covariate for the impact area of a restricted access area. The resulting models will simultaneously address the combined effects of the differences in traffic dynamics and local vehicle fleet composition inside and outside the low emission zone. The µLUR GAM modelling approach has an additional benefit. Most data scientific approaches like neural networks will result in ‘black box’ and ‘now-cast’ models [23]. The generalized models have a feature that makes them much more powerful than the neural network models. The splines of the GAM can be extracted and modified by expert decisions. This is possible because the underlying covariates express actual physical relations. When taking advantage of these features, adjusted models can be built. Past exposure estimation will accommodate the epidemiological questions, and future exposure estimation can address policy support questions.
6. Conclusions
The spatiotemporal aspects of an in-vehicle black carbon exposure participatory campaign were successfully modeled using detailed spatiotemporal attribution. The measurements were attributed with meteorological data and different types of traffic-related data, including noise maps as a proxy for the traffic data. The models including the non-linear aspects of the covariates were modeled with generalized additive models (GAMs). The traffic dynamics and diurnal traffic patterns did not resolve the diurnal patterns of the in-vehicle exposure. The noise maps were not necessary to provide a solution, but have important assets compared to the raw traffic data. The strongest in-vehicle exposure model was based on six parameters with LDEN in combination with a fitted diurnal pattern resolving the diurnal exposure pattern. Noise maps are therefore a valid proxy for air pollution without actual knowledge of the local traffic dynamics. Noise maps are widely available and can increase efficiency and stability in long-term land use regression approaches.
The external validation with a three- to four-year-old external participatory campaign showed a severe underestimation, which could be attributed to the introduction of Euro 5 emission standards. Data science techniques can provide successful prediction models without the need for disentangling the underlying complex interaction of the underlying parameters. The µLUR methodology has the potential to attribute epidemiological databases and provide high quality policy support without requiring full analytical solutions for the in-vehicle air pollution exposure.
Supplementary Materials
The following are available online at www.mdpi.com/2073-4433/8/11/230/s1. Figure S1: Spatial extent of the commutes of the volunteers: raw BC measurements (ng/m3) in a 10 second resolution across the Flemish Region and Brussels (North part of Belgium); Figure S2: Measurement locations for meteorological stations; Figure S3: Black Carbon measurement locations in Belgium of the Flemish Environmental Institute (VMM); Figure S4a: LDEN Noise map for Flanders for 2012; Figure S4b: Detail of the noise map showing the spatial resolution of the low density roads; Figure S5: Overview of spatial and temporal variability in the BC_LAG60 BC data set; Table S1: GAM summary of BCLAG60_WBC model; Table S2: Yearly average reduction at three long-term measurements locations
Acknowledgments
The in-vehicle measurements were performed with the mobile version of the hardware built by Luc Dekoninck and Samuel Dauwe in an extension of the Intelligent Distributed Environment Assessment project (IDEA) (funded by ‘Instituut voor Innovatie door Wetenschap en Technologie Vlaanderen’ Grant IWT-080054). Evi Dons of ‘Vlaams Instituut voor Technologisch Onderzoek’ (VITO) and Hasselt University collected and provided the citizen science validation data. A prior version of this manuscript was developed during the PhD of Luc Dekoninck (2015). We thank Ir. Dick Botteldooren and all members of the PhD evaluation commission for proof-reading early versions of the manuscript. We want to thank the reviewers for their valuable input. The Flemish Environmental Agency (VMM) provided the black carbon measurements of the official monitoring stations. The department of traffic of the Flemish Government provided the traffic data. The noise map for Flanders was calculated in the environmental reporting program by Luc Dekoninck (commissioned by the Flemish Environmental Agency VMM). We also want to thank the volunteers in this citizen science campaign: Marijke, Marc, Pieter, Peter, Iris, Angela, Sara and Veerle. This research did not receive any specific grant from funding agencies in the public or commercial sector.
Author Contributions
The citizen science campaign, modelling and data analysis were performed by Luc Dekoninck as a part of his Luc Int Panis (UHasselt), the driving force in reaching these results by providing the external validation data and adding significant value to the publication.
Conflicts of Interest
The authors declare no conflict of interest.
References
- WHO Europe. Health Effects of Black Carbon; WHO: Geneva, Switzerland, 2012; ISBN 978-92-890-0265-3. [Google Scholar]
- Dons, E.; Int Panis, L.; Van Poppel, M.; Theunis, J.; Willems, H.; Torfs, R.; Wets, G. Impact of time-activity patterns on personal exposure to black carbon. Atmos. Environ. 2011, 45, 3594–3602. [Google Scholar] [CrossRef]
- Dons, E.; Int Panis, L.; Van Poppel, M.; Theunis, J.; Wets, G. Personal exposure to black carbon in transport microenvironments. Atmos. Environ. 2012, 55, 392–398. [Google Scholar] [CrossRef]
- Karner, A.A.; Eisinger, D.S.; Niemeier, D.A. Near-Roadway Air Quality: Synthesizing the Findings from Real-World Data. Environ. Sci. Technol. 2010, 44, 5334–5344. [Google Scholar] [PubMed]
- Both, A.F.; Westerdahl, D.; Fruin, S.; Haryanto, B.; Marshall, J.D. Exposure to carbon monoxide, fine particle mass, and ultrafine particle number in Jakarta, Indonesia: Effect of commute mode. Sci. Total Environ. 2013, 443, 965–972. [Google Scholar] [CrossRef] [PubMed]
- Ioar, R.; Kumar, P.; Hagen-Zanker, A.; de Fatima Andrade, M.; Slovic, A.D.; Pritchard, J.P.; Geurs, K.T. Determinants of black carbon, particle mass and number concentrations in London transport microenvironments. Atmos. Environ. 2017, 161, 247–262. [Google Scholar]
- Williams, R.D.; Knibbs, L.D. Daily personal exposure to black carbon: A pilot study. Atmos. Environ. 2016, 132, 296–299. [Google Scholar] [CrossRef]
- Betancourt, R.M.; Galvis, B.; Balachandran, S.; Ramos-Bonilla, J.P.; Sarmiento, O.L.; Gallo-Murcia, S.M.; Contreras, Y. Exposure to fine particulate, black carbon, and particle number concentration in transportation microenvironments. Atmos. Environ. 2017, 157, 135–145. [Google Scholar] [CrossRef]
- Okokon, E.O.; Yli-Tuomi, T.; Turunen, A.W.; Taimisto, P.; Pennanen, A.; Vouitsis, I.; Samaras, Z.; Voogt, M.; Keuken, M.; Lanki, T. Particulates and noise exposure during bicycle, bus and car commuting: A study in three European cities. Environ. Res. 2017, 154, 181–189. [Google Scholar] [CrossRef] [PubMed]
- Kingham, S.; Longley, I.; Salmond, J.; Pattinson, W.; Shrestha, K. Variations in exposure to traffic pollution while travelling by different modes in a low density, less congested city. Environ. Pollut. 2013, 181, 211–218. [Google Scholar] [CrossRef] [PubMed]
- Qiu, Z.; Song, J.; Xu, X.; Luo, Y.; Zhao, R.; Zhou, W.; Xiang, B.; Hao, Y. Commuter exposure to particulate matter for different transportation modes in Xi’an, China. Atmos. Pollut. Res. 2017, 8, 940–948. [Google Scholar] [CrossRef]
- Dons, E.; Temmerman, P.; Van Poppel, M.; Bellemans, T.; Wets, G.; Int Panis, L. Street characteristics and traffic factors determining road users’ exposure to black carbon. Sci. Total Environ. 2013, 447, 72–79. [Google Scholar] [CrossRef] [PubMed]
- Dekoninck, L.; Botteldooren, D.; Int Panis, L. An instantaneous spatiotemporal model to predict a bicyclist’s black carbon exposure based on mobile noise measurements. Atmos. Environ. 2013, 79, 623–631. [Google Scholar] [CrossRef]
- Hudda, N.; Eckel, S.R.; Knibbs, L.D.; Sioutas, C.; Delfino, R.J.; Fruin, S.A. Linking in-vehicle ultrafine particle exposures to on-road concentrations. Atmos. Environ. 2012, 59, 578–586. [Google Scholar] [CrossRef] [PubMed]
- Knibbs, L.D.; de Dear, R.J.; Morawska, L. Effect of Cabin Ventilation Rate on Ultrafine Particle Exposure inside Automobiles. Environ. Sci. Technol. 2010, 44, 3546–3551. [Google Scholar] [CrossRef] [PubMed]
- Hudda, N.; Kostenidou, E.; Sioutas, C.; Delfino, R.J.; Fruin, S.A. Vehicle and Driving Characteristics That Influence In-Cabin Particle Number Concentrations. Environ. Sci. Technol. 2011, 45, 8691–8697. [Google Scholar] [CrossRef] [PubMed]
- Fruin, S.A.; Hudda, N.; Sioutas, C.; Defino, R.J. Predictive Model for Vehicle Air Exchange Rates Based on a Large, Representative Sample. Environ. Sci. Technol. 2011, 45, 3569–3575. [Google Scholar] [CrossRef] [PubMed]
- Lee, E.S.; Zhu, Y. Application of a High-Efficiency Cabin Air Filter for Simultaneous Mitigation of Ultrafine Particle and Carbon Dioxide Exposures inside Passenger Vehicles. Environ. Sci. Technol. 2014, 48, 2328–2335. [Google Scholar] [CrossRef] [PubMed]
- Ham, W.; Vijayan, A.; Schulte, N.; Herner, J.D. Commuter exposure to PM 2.5, BC, and UFP in six common transport microenvironments in Sacramento, California. Atmos. Environ. 2017, 167, 335–345. [Google Scholar] [CrossRef]
- Li, L.F.; Wu, J.; Hudda, N.; Sioutas, C.; Fruin, S.A.; Delfino, R.J. Modeling the Concentrations of On-Road Air Pollutants in Southern California. Environ. Sci. Technol. 2013, 47, 9291–9299. [Google Scholar] [CrossRef] [PubMed]
- Carslaw, D.C.; Beevers, S.D.; Tate, J.E. Modelling and assessing trends in traffic-related emissions using a generalised additive modelling approach. Atmos. Environ. 2007, 41, 5289–5299. [Google Scholar] [CrossRef]
- Patton, A.P.; Laumbach, R.; Ohman-Strickland, P.; Black, K.; Alimokhtari, S.; Lioy, P.J.; Kipen, H.M. Scripted drives: A robust protocol for generating exposures to traffic-related air pollution. Atmos. Environ. 2016, 143, 290–299. [Google Scholar] [CrossRef] [PubMed]
- Paas, B.; Stienen, J.; Vorländer, M.; Schneider, C. Modelling of Urban Near-Road Atmospheric PM Concentrations Using an Artificial Neural Network Approach with Acoustic Data Input. Environments 2017, 4, 26. [Google Scholar] [CrossRef]
- Lioy, P.J.; Smith, K.R. A discussion of exposure science in the 21st century: A vision and a strategy. Environ. Health Perspect. 2013, 121, 405. [Google Scholar] [CrossRef] [PubMed]
- Dekoninck, L.; Botteldooren, D.; Int Panis, L. Extending Participatory Sensing to Personal Exposure Using Microscopic Land Use Regression Models. Int. J. Environ. Res. Public Health 2017, 14, 586. [Google Scholar] [CrossRef] [PubMed]
- Hagler, G.S.W.; Yelverton, T.L.B.; Vedantham, R.; Hansen, A.D.A.; Turner, J.R. Post-processing method to reduce noise while preserving high time resolution in aethalometer real-time black carbon data. Aerosol Air Qual. Res. 2011, 11, 539–546. [Google Scholar] [CrossRef]
- Update of Noise Indicators (in Dutch) Actualisatie van de Geluidsindicatoren. Available online: http://www.milieurapport.be/Upload/main/0_onderzoeksrapporten/2014/verslag%20Geluidsindicatoren_MIRA_2013_final_TW-red.pdf (accessed on 20 Novemebr 2017).
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2008; ISBN 3-900051-07-0. Available online: http://www.R-project.org (accessed on 20 Novemebr 2017).
- Wood, S.N. On confidence intervals for generalized additive models based on penalized regression splines. Aust. N. Z. J. Stat. 2006, 48, 445–464. [Google Scholar] [CrossRef]
- Kohn, R.; Schimek, M.G.; Smith, M. Spline and kernel regression for dependent data. In Smoothing and Regression: Approaches, Computation, and Application; Wiley: Hoboken, NJ, USA, 2000; pp. 135–158. [Google Scholar]
- Peng, R.D.; Dominici, F.; Louis, T.A. Model choice in time series studies of air pollution and mortality. J. R. Stat. Soc. Ser. A Stat. Soc. 2006, 169, 179–203. [Google Scholar] [CrossRef]
- Bhaskaran, K.; Gasparrini, A.; Hajat, S.; Smeeth, L.; Armstrong, B. Time series regression studies in environmental epidemiology. Int. J. Epidemiol. 2013, 42, 1187–1195. [Google Scholar] [CrossRef] [PubMed]
- Dekoninck, L.; Botteldooren, D.; Panis, L.; Hankey, S.; Jain, G.; Karthik, S.; Marshall, J. Applicability of a noise-based model to estimate in-traffic exposure to black carbon and particle number concentrations in different cultures. Environ. Int. 2015, 74, 89–98. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Liu, S.; Liu, J.; Zhu, Y. Effects of vehicle cabin filter efficiency on ultrafine particle concentration ratios measured in-cabin and on-roadway. Aerosol Sci. Technol. 2011, 45, 234–243. [Google Scholar] [CrossRef]
- Cai, J.; Yan, B.; Kinney, P.L.; Perzanowski, M.S.; Jung, K.; Li, T.; Xiu, G.; Zhang, D.; Olivo, C.; Ross, J.; et al. Optimization approaches to ameliorate humidity and vibration related issues using the MicroAeth black carbon monitor for personal exposure measurement. Aerosol Sci. Technol. 2013, 47, 1196–1204. [Google Scholar] [CrossRef] [PubMed]
- Dons, E.; Van Poppel, M.; Int Panis, L.; De Prins, S.; Berghmans, P.; Koppen, G.; Matheeussen, C. Land use regression models as a tool for short, medium and long term exposure to traffic related air pollution. Sci. Total Environ. 2014, 476, 378–386. [Google Scholar] [CrossRef] [PubMed]
- Khoury, M.J.; Lam, T.K.; Ioannidis, J.P.A.; Hartge, P.; Spitz, M.R.; Buring, J.E.; Chanock, S.J.; Croyle, R.T.; Goddard, K.A.; Ginsburg, G.S.; et al. Transforming epidemiology for 21st century medicine and public health. Cancer Epidemiol. Biomark. Prev. 2013, 22, 508–516. [Google Scholar] [CrossRef] [PubMed]
- Reis, S.; Morris, G.; Fleming, L.E.; Beck, S.; Taylor, T.; White, M.; Depledge, M.H.; Steinle, S.; Sabel, C.E.; Cowie, H.; et al. Integrating health and environmental impact analysis. Public Health 2015, 129, 1383–1389. [Google Scholar] [CrossRef] [PubMed]
- Dekoninck, L.; Botteldooren, D.; Int Panis, L. Using city-wide mobile noise assessments to estimate annual exposure to Black Carbon. Environ. Int. 2015, 83, 192–201. [Google Scholar] [CrossRef] [PubMed]
- Hoek, G.; Beelen, R.; de Hoogh, K.; Vienneau, D.; Gulliver, J.; Fischer, P.; Briggs, D. A review of land-use regression models to assess spatial variation of outdoor air pollution. Atmos. Environ. 2008, 42, 7561–7578. [Google Scholar] [CrossRef]
- Beelen, R.; Hoek, G.; Vienneau, D.; Eeftens, M.; Dimakopoulou, K.; Pedeli, X.; Tsai, M.-Y.; Künzli, N.; Schikowski, T.; Marcon, A.; et al. Development of NO2 and NOx land use regression models for estimating air pollution exposure in 36 study areas in Europe—The ESCAPE project. Atmos. Environ. 2013, 72, 10–23. [Google Scholar] [CrossRef]
- Patton, A.P.; Zamore, W.; Naumova, E.N.; Levy, J.I.; Brugge, D.; Durant, J.L. Transferability and generalizability of regression models of ultrafine particles in urban neighborhoods in the Boston area. Environ. Sci. Technol. 2015, 49, 6051–6060. [Google Scholar] [CrossRef] [PubMed]
- EU Commision. The Environmental Noise Directive (2002/49/EC). Available online: http://ec.europa.eu/environment/noise/directive_en.htm (accessed on 18 Novemebr 2017).
- Cames, M.; Helmers, E. Critical evaluation of the European diesel car boom-global comparison, environmental effects and various national strategies. Environ. Sci. Eur. 2013, 25, 15. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).