A Review of Parametric Descriptions of Tropical Cyclone Wind-Wave Generation
Abstract
:1. Introduction
2. Tropical Cyclone Wind Field
3. Spatial Distribution of Significant Wave Height
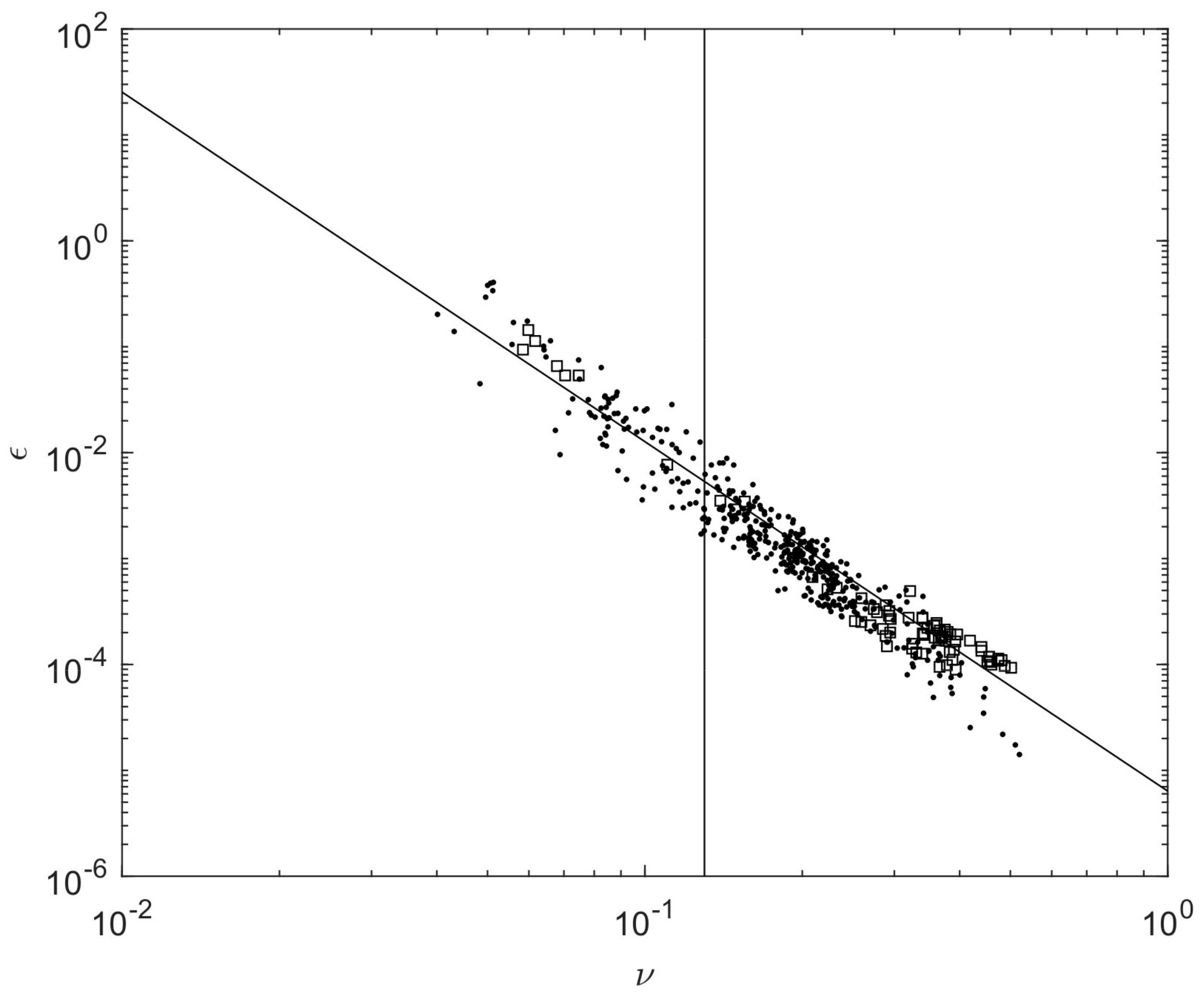
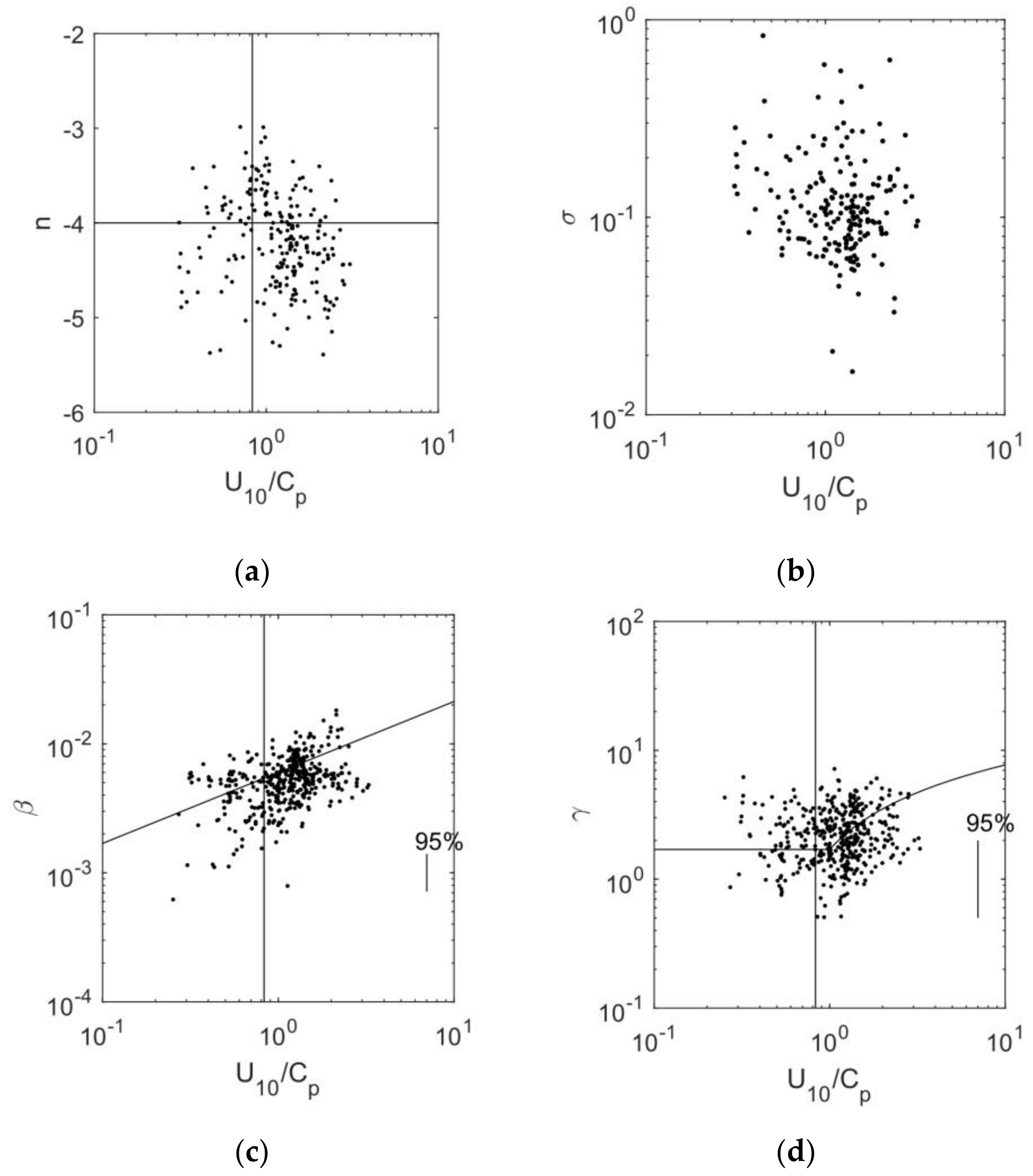
3.1. Energy-Peak Frequency Relationship
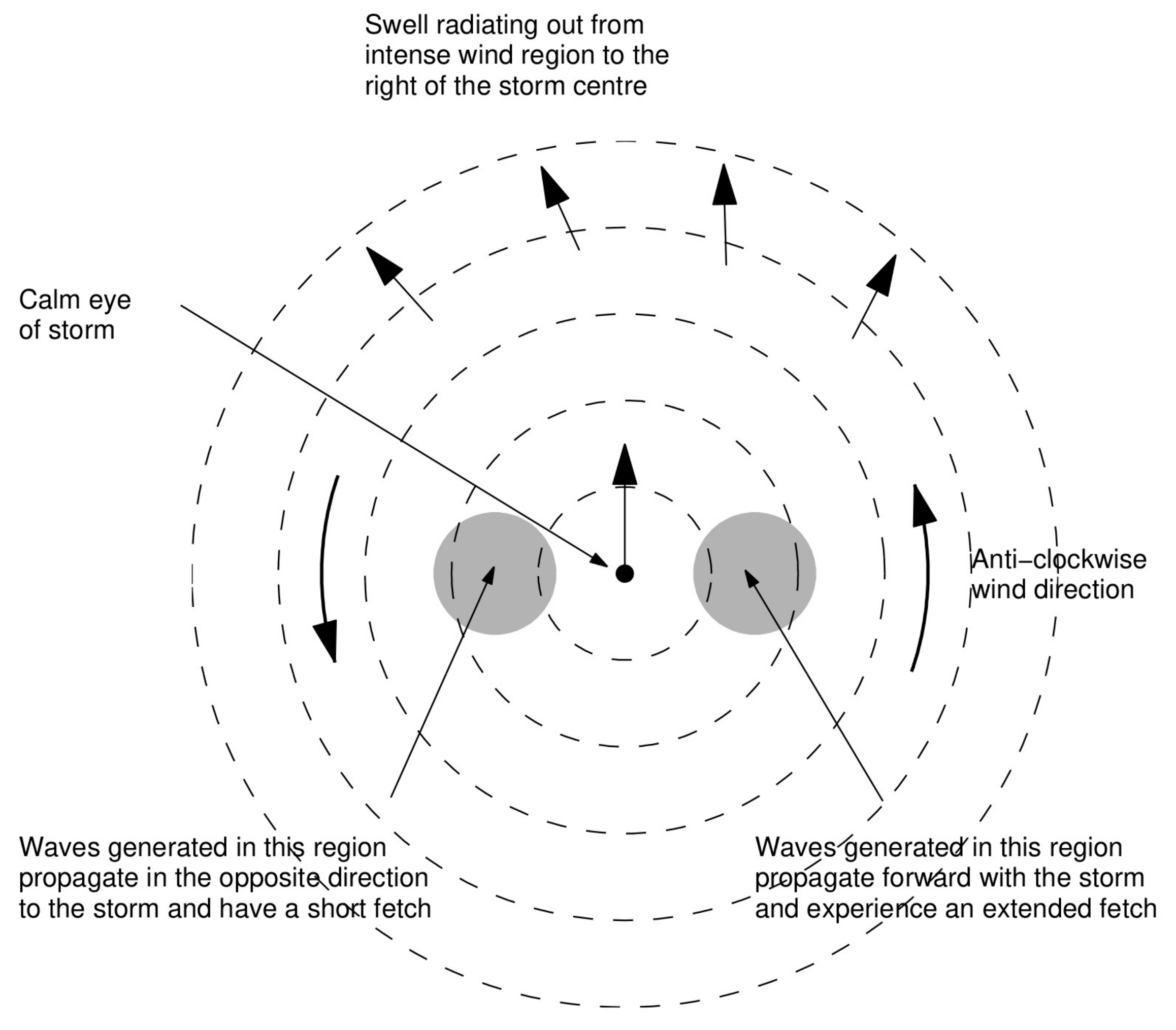
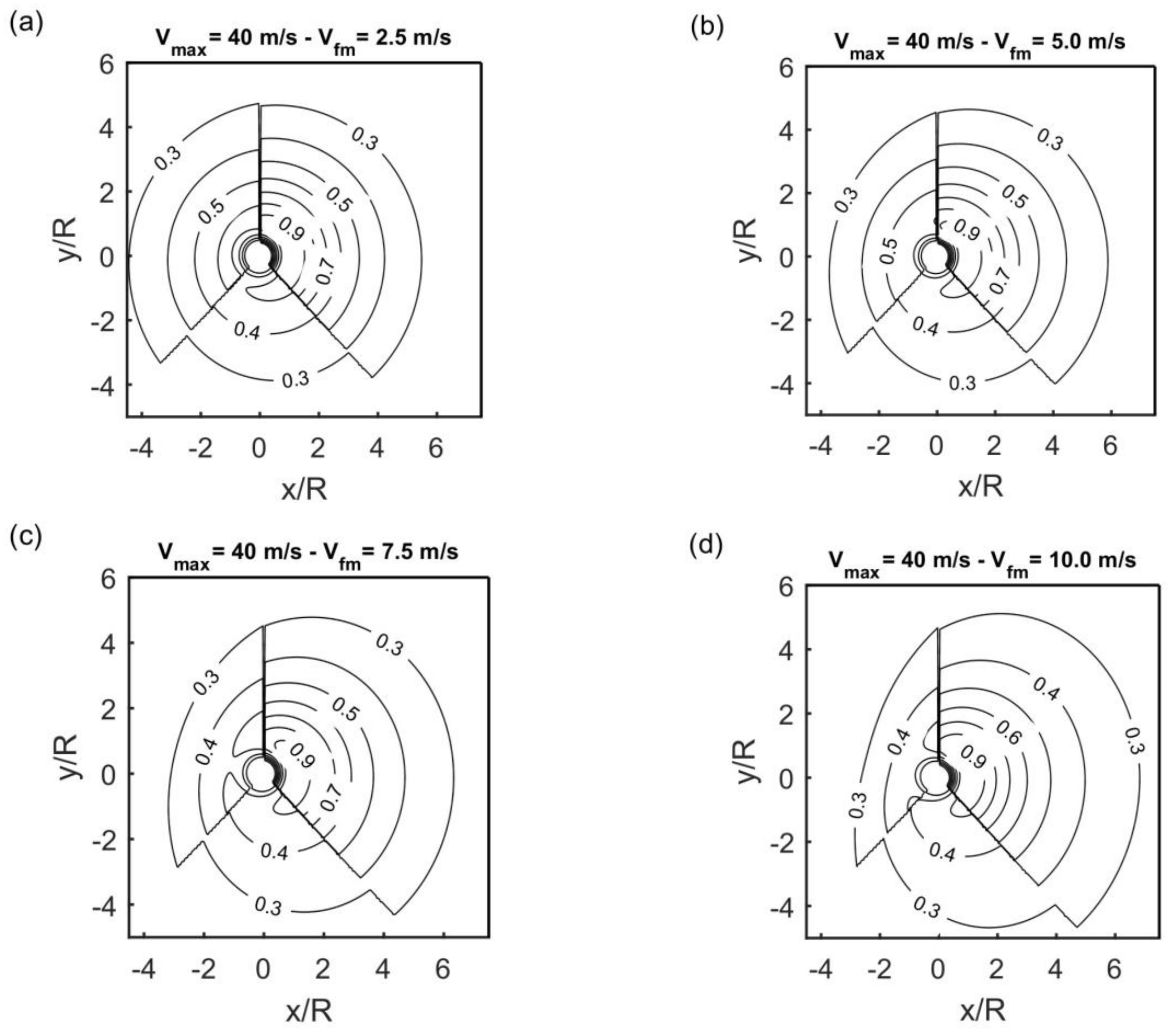
3.2. Defining the Equivalent “Fetch” in a Tropical Cyclone
3.3. Wind Field Curvature
4. One-Dimensional Spectrum
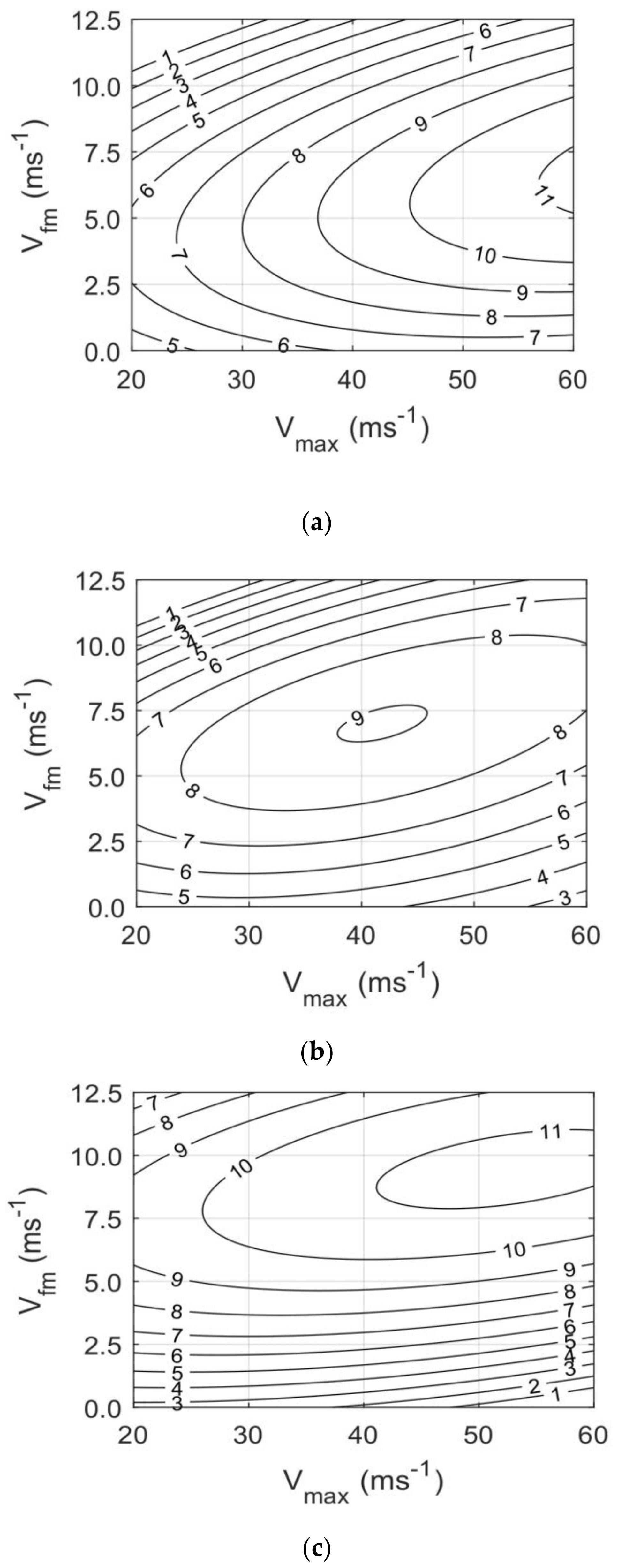
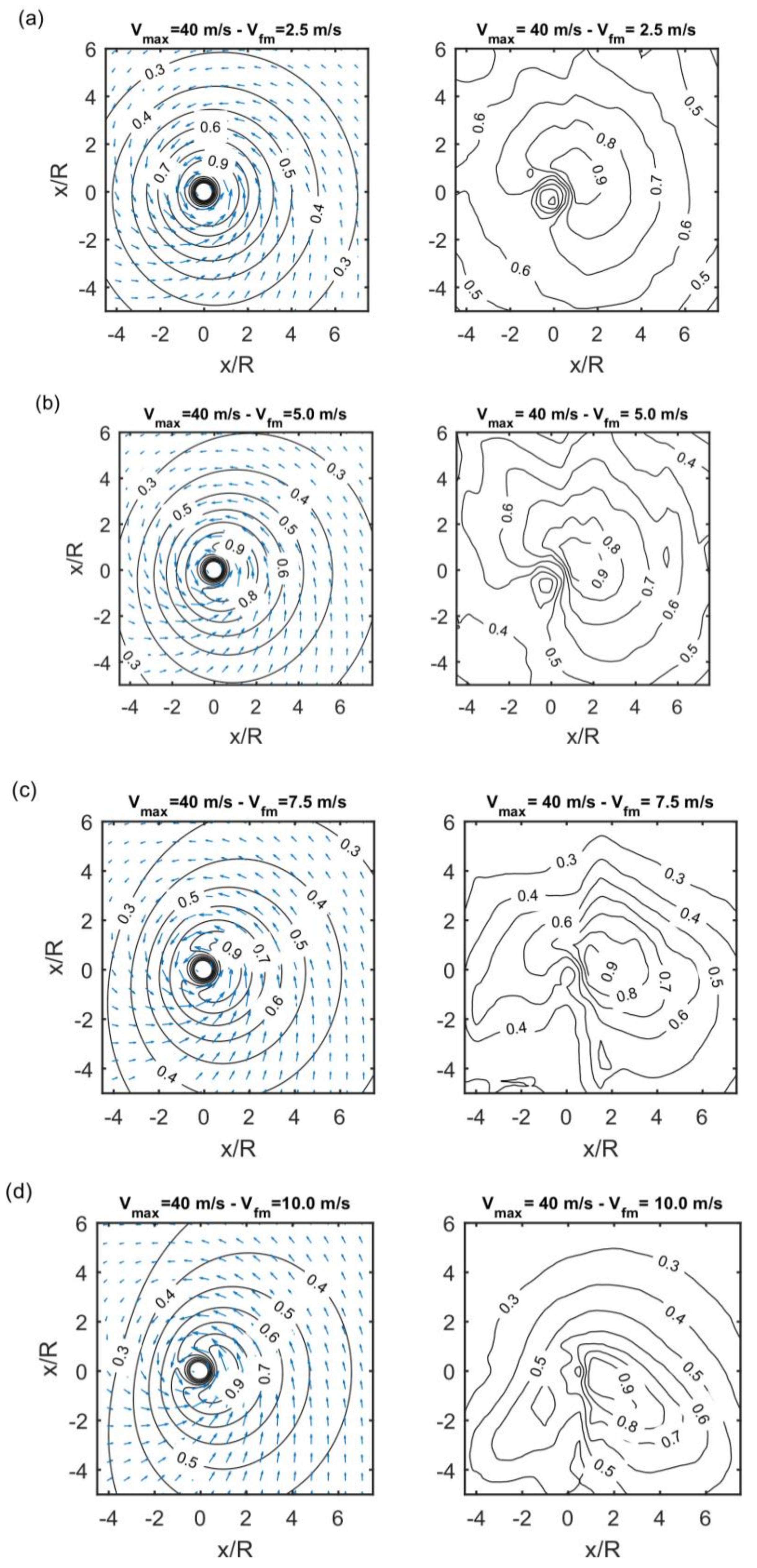
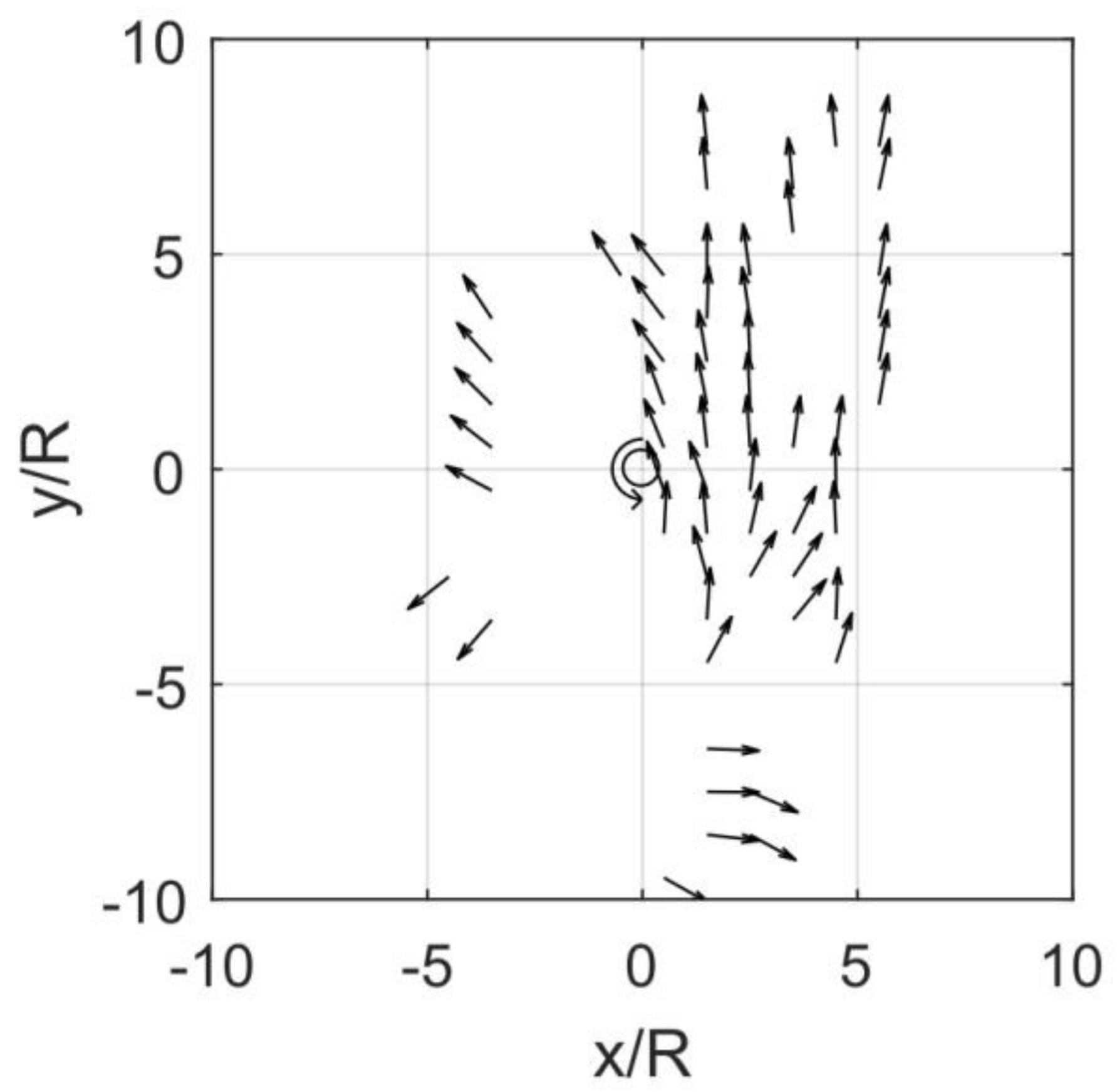
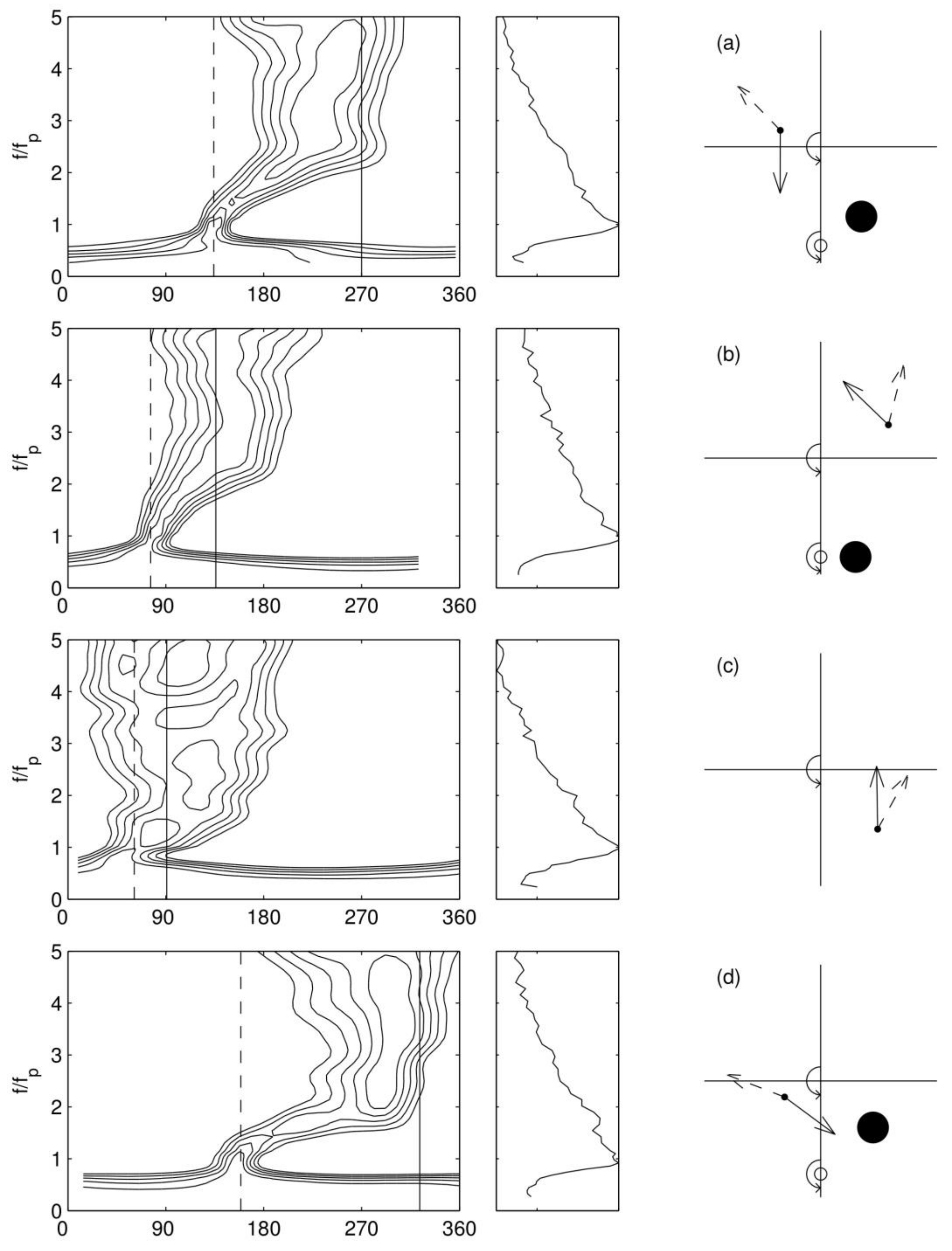
5. Directional Distribution of Waves
6. Physical Processes Active in Tropical Cyclone Wave Generation
7. Discussion and Conclusions
Acknowledgments
Conflicts of Interest
References
- Holland, G.J. An analytical model of the wind and pressure profiles in hurricanes. Mon. Weather Rev. 1980, 108, 1212–1218. [Google Scholar] [CrossRef]
- Schloemer, R.W. Analysis and synthesis of hurricane wind patterns over Lake Okechobee, Florida. In Hydromet Report; Govt Print Office: Washington, DC, USA, 1954; p. 49. [Google Scholar]
- Graham, H.E.; Hudson, G.N. Surface winds near the center of hurricanes (and other cyclones). In NHRP Report; Govt Print Office: Washington, DC, USA, 1960; Volume 39, p. 200. [Google Scholar]
- Smith, R.K. The surface boundary layer of a hurricane. Tellus 1968, 20, 473–484. [Google Scholar] [CrossRef]
- Gray, W.M.; Shea, D.J. The hurricane’s inner core region, II: Thermal stability and dynamic characteristics. J. Atmos. Sci. 1973, 30, 1565–1576. [Google Scholar] [CrossRef]
- Simiu, E.; Patel, V.C.; Nash, J.F. Mean speed profiles of hurricane winds. J. Eng. Mech. Div. Am. Soc. Civ. Eng. 1976, 102, 265–273. [Google Scholar]
- Atkinson, G.D.; Holliday, C.R. Tropical cyclone minimum sea level pressure-maximum sustained wind relationship for western North Pacific. Mon. Weather Rev. 1977, 105, 421–427. [Google Scholar] [CrossRef]
- Wang, G.C. Sea level pressure profile and gusts within a typhoon circulation. Mon. Weather Rev. 1978, 106, 954–960. [Google Scholar] [CrossRef]
- Courtney, J.; Knaff, J.A. Adapting the Knaff and Zehr wind-pressure relationship for operational use in Tropical Cyclone Warning Centres. Aust. Meteorol. Ocean. 2009, 58, 167–179. [Google Scholar] [CrossRef]
- Shea, D.J.; Gray, W.M. The hurricane’s inner core region, I: Symmetric and asymmetric structure. J. Atmos. Sci. 1973, 30, 1544–1564. [Google Scholar] [CrossRef]
- Uhlhorn, E.W.; Klotz, B.W.; Vukicevic, T.; Reasor, P.D.; Rogers, R.F. Observed Hurricane Wind Speed Asymmetries and Relationships to Motion and Environmental Shear. Mon. Weather Rev. 2014. Available online: https://doi.org/10.1175/MWR-D-13-00249.1 (accessed on 18 August 2017).
- Thompson, E.F.; Cardone, V.J. Practical modelling of hurricane surface wind fields. J. Waterw. Port Coast. Ocean Eng. 1996, 122, 195–205. [Google Scholar] [CrossRef]
- McConochie, J.D.; Mason, L.B.; Hardy, T.A. A Coral Sea cyclone wind model intended for wave modelling. In Coasts & Ports 1999: Challenges and Directions for the New Century, Proceedings of the 14th Australasian Coastal and Ocean Engineering Conference and the 7th Australasian Port and Harbour Conference, Perth, Western Australia, 14–16 April, 1999; National Committee on Coastal and Ocean Engineering, Institution of Engineers: Barton, A.C.T., Australia, 1999; pp. 387–392. [Google Scholar]
- Powell, M.D. Evaluations of diagnostic marine boundary layer models applied to hurricanes. Mon. Weather Rev. 1980, 108, 758–766. [Google Scholar] [CrossRef]
- Powell, M.D.; Houston, S.H. Hurricane Andrew’s landfall in South Florida. Part II: Surface wind fields and potential real-time applications. Weather Forecast. 1996, 11, 329–349. [Google Scholar] [CrossRef]
- Powell, M.D.; Murillo, S.; Dodge, P.; Uhlhorn, E.; Gamache, J.; Cardone, V.; Cox, A.; Otero, S.; Carrasco, N.; Annane, B.; et al. Reconstruction of Hurricane Katrina’s wind fields for storm surge and wave hindcasting. Ocean Eng. 2010, 37, 26–36. [Google Scholar] [CrossRef]
- Liu, Q.; Babanin, A.; Fan, Y.; Zieger, S.; Guan, C.; Moon, I.-J. Numerical simulations of ocean surface waves under hurricane conditions: Assessment of existing model performance. Ocean Model. 2017, in press. [Google Scholar] [CrossRef]
- Tolman, H.L.; Alves, J.-H.G. Numerical modeling of wind waves generated by tropical cyclones using moving grids. Ocean Model. 2005, 9, 305–323. [Google Scholar] [CrossRef]
- Ardhuin, F.; Rogers, E.; Babanin, A.; Filipot, J.-F.; Magne, R.; Roland, A.; Van Der Westhuysen, A.; Queffeulou, P.; Lefevre, J.-M.; Aouf, L.; et al. Semi-empirical dissipation source functions for ocean waves: Part I, definition, calibration and validation. J. Phys. Oceanogr. 2010, 40, 1917–1941. [Google Scholar] [CrossRef]
- Harper, B.A. Best practice in tropical cyclone wind hazard modelling: In search of data and emptying the skeleton cupboard. In Proceedings of the 16th Australasian Wind Engineering Society Workshop, Brisbane, Qld, Australia, 18–19 July 2013. [Google Scholar]
- Bretschneider, C.L. Hurricane design—Wave practices. Trans. ASCE 1959, 124, 39–62. [Google Scholar]
- Bretschneider, C.L. A non-dimensional stationary hurricane wave model. In Proceedings of the Fourth Offshore Technology Conference, Houston, TX, USA, 1–3 May 1972. [Google Scholar]
- U.S. Army Corp of Engineers. Shore Protection Manual: Volume I,II,III—Three Volumes; U.S. Army Coastal Engineering Research Center: Vicksburg, MS, USA, 1977. [Google Scholar]
- Ross, D.B. A simplified model for forecasting hurricane generated waves (Abstract). Bull. Am. Meteorol. Soc. 1976, 113–115. [Google Scholar]
- Patterson, M.M. Oceanographic data from Hurricane Camille. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–8 May 1974. OTC-2109-MS. [Google Scholar]
- Whalen, J.E.; Ochi, M.K. Variability of wave spectral shapes associated with hurricanes. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 8–11 May 1978. OTC3228. [Google Scholar]
- Black, J.L. Hurricane Eloise directional wave energy spectra. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 30 April–3 May 1979. OTC 3594. [Google Scholar]
- Ochi, M.K.; Chiu, M.H. Nearshore wave spectra measured during Hurricane David. In Proceedings of the 18th International Confession on Coastal Engineering, Cape Town, South Africa, 14–19 November 1982; ASCE: Hamburg, Germany; pp. 77–86. [Google Scholar]
- Ochi, M.K. On hurricane-generated seas. In Proceedings of the 2nd International Symposium on Ocean Wave Measurement and Analysis, New Orleans, LA, USA, 25–28 July 1993; ASCE: New Orleans, LA, USA, 1993; pp. 374–387. [Google Scholar]
- Young, I.R. Observations of the spectra of hurricane generated waves. Ocean Eng. 1998, 25, 261–276. [Google Scholar] [CrossRef]
- Young, I.R. Directional spectra of hurricane wind-waves. J. Geophys. Res. 2006, 111, C08020. [Google Scholar] [CrossRef]
- Elachi, C.; Thompson, T.W.; King, D.B. Observations of the ocean wave pattern under Hurricane Gloria with synthetic aperture radar. Science 1977, 198, 609–610. [Google Scholar] [CrossRef] [PubMed]
- King, D.B.; Shemdin, O.H. Radar observations of hurricane wave directions. In 16th International Confession on Coastal Engineering; Hamburg, Germany, 1978, ASCE: Hamburg, Germany, 1987; pp. 209–226. [Google Scholar]
- Gonzalez, F.I.; Thompson, T.E.; Brown, W.E.; Weissman, D.E. Seasat wind and wave observations of Northeast Pacific Hurricane Iva, 13 August 1978. J. Geophys. Res. 1982, 87, 3431–3438. [Google Scholar] [CrossRef]
- McLeish, W.; Ross, D.B. Imaging radar observations of directional properties of ocean waves. J. Geophys. Res. 1983, 88, 4407–4419. [Google Scholar] [CrossRef]
- Holt, B.; Gonzalez, F.I. SIR-B observations of dominant ocean waves near hurricane Josephine. J. Geophys. Res. 1986, 91, 8595–8598. [Google Scholar] [CrossRef]
- Beal, R.C.; Gerling, T.W.; Irvine, D.E.; Monaldo, F.M.; Tilley, D.G. Spatial variations of ocean wave directional spectra from the Seasat synthetic aperture radar. J. Geophys. Res. 1986, 91, 2433–2449. [Google Scholar] [CrossRef]
- Young, I.R.; Burchell, G.P. Hurricane generated waves as observed by satellite. Ocean Eng. 1986, 23, 761–776. [Google Scholar] [CrossRef]
- Wright, C.W.; Walsh, E.J.; Vandemark, D.; Krabill, W.B.; Garcia, A.W.; Houston, S.H.; Powell, M.D.; Black, P.G.; Marks, F.D. Hurricane directional wave spectrum spatial variation in the open ocean. J. Phys. Oceanogr. 2001, 31, 2472–2488. [Google Scholar] [CrossRef]
- Black, P.G.; D’Asaro, E.A.; Drennan, W.M.; French, J.R.; Niiler, P.P.; Sanford, T.B.; Terrill, E.J.; Walsh, E.J.; Zhang, J.A. Air-sea exchange in hurricanes: Synthesis of observations from the coupled boundary layer air-sea transfer experiment. Bull. Am. Meteorol. Soc. 2007, 88, 357–374. [Google Scholar] [CrossRef]
- SWAMP Group. Ocean Wave Modelling; Plenum Press: New York, NY, USA, 1985; p. 256. [Google Scholar]
- Young, I.R. A shallow water spectral wave model. J. Geophys. Res. 1988, 93, 5113–5129. [Google Scholar] [CrossRef]
- Young, I.R. A parametric hurricane wave prediction model. J. Waterw. Port Coast. Ocean Eng. 1988, 114, 637–652. [Google Scholar] [CrossRef]
- The WAMDI Group. The WAM model—A third generation ocean wave prediction model. J. Phys. Oceanogr. 1988, 18, 1775–1810. [Google Scholar]
- Bowyer, P.J.; MacAfee, A.W. The theory of trapped-fetch waves within tropical cyclones—An operational perspective. Weather Forecast. 2005, 20, 229–244. [Google Scholar] [CrossRef]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, H.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of wind-wave growth and swell decay during the Joint North SeaWave Project (JONSWAP). In Hydraulic Engineering Reports; Deutches Hydrographisches Institute: Hamburg, Germany, 1973; p. 95. [Google Scholar]
- Donelan, M.A.; Hamilton, J.; Hui, W.H. Directional spectra of wind-generated waves. Philos. Trans. R. Soc. B Ser. A 1985, 315, 509–562. [Google Scholar] [CrossRef]
- Hwang, P.A. Fetch- and duration-limited nature of surface wave growth inside tropical cyclones: With applications to air-sea exchange and remote sensing. J. Phys. Oceanogr. 2016, 46, 41–56. [Google Scholar] [CrossRef]
- Hwang, P.A.; Walsh, E.J. Azimuthal and radial variation of wind-generated surface waves inside tropical cyclones. J. Phys. Oceanogr. 2016, 46, 2605–2621. [Google Scholar] [CrossRef]
- Hwang, P.A.; Fan, Y. Effective fetch and duration of tropical cyclone wind fields estimated from simultaneous wind and wave measurements: Surface wave and air-sea exchange computation. J. Phys. Oceanogr. 2017, 47, 447–470. [Google Scholar] [CrossRef]
- Hwang, P.A.; Fan, Y.; Ocampo-Torres, F.J.; García-Nava, H. Ocean Surface 1 Wave Spectra inside Tropical Cyclones. J. Phys. Oceanogr 2017, in press. [Google Scholar] [CrossRef]
- Walsh, E.J.; Wright, C.W.; Vandemark, D.; Krabill, W.B.; Garcia, A.W.; Houston, S.H.; Murillo, S.T.; Powell, M.D.; Black, P.G.; Marks, F.D. Hurricane directional wave spectrum spatial variation at landfall. J. Phys. Oceanogr. 2002, 32, 1667–1684. [Google Scholar] [CrossRef]
- Fan, Y.; Ginis, I.; Hara, T. The effect of wind-wave-current interaction on air-sea momentum fluxes and ocean response in tropical cyclones. J. Phys. Oceanogr. 2009, 39, 2097–2116. [Google Scholar] [CrossRef]
- Moon, I.-J.; Ginis, I.; Hara, T.; Tolman, H.L.; Wright, C.W.; Walsh, E.J. Numerical simulation of sea surface directional wave spectra under hurricane wind forcing. J. Phys. Oceanogr. 2003, 33, 1680–1706. [Google Scholar] [CrossRef]
- Hu, K.; Chen, Q. Directional spectra of hurricane-generated waves in the Gulf of Mexico. Geophys. Rev. Lett. 2011, 38, L19608. [Google Scholar] [CrossRef]
- Young, I.R.; Vinoth, J. An ‘extended fetch’ model for the spatial distribution of tropical cyclone wind-waves as observed by altimeter. Ocean Eng. 2013, 70, 14–24. [Google Scholar] [CrossRef]
- Zieger, S.; Vinoth, J.; Young, I.R. Joint calibration of multi-platform altimeter measurements of wind speed and wave height over the past 20 years. J. Atmos. Ocean. Technol. 2009, 12, 2549–2564. [Google Scholar] [CrossRef]
- Alves, J.H.G.M.; Tolman, H.L.; Chao, Y.Y. Hurricane-Generated Wind-Wave Research at NOAA/NCEP. NCEP Marine Modeling and Analysis Branch. 2004; Report No: 242, 13. Available online: http://polar.ncep.noaa.gov/mmab/notes.shtml (accessed on 18 August 2017).
- Tolman, H.L. A Third-Generation Model for Wind Waves on Slowly Varying, Unsteady, and Inhomogeneous Depths and Currents. J. Phys. Oceanogr. 1991, 21, 782–797. [Google Scholar] [CrossRef]
- Hwang, P.A.; Wang, D.W. Field measurements of duration limited growth of wind-generated ocean surface waves at young stage of development. J. Phys. Oceanogr. 2004, 34, 2316–2326. [Google Scholar] [CrossRef]
- Ochi, M.K. A Series of JONSWAP Wave Spectra for Offshore Structural Design. Available online: https://www.tib.eu/en/search/id/tema-archive%3ATEMAM84091112475/A-series-of-JONSWAP-wave-spectra-for-offshore-structure/?tx_tibsearch_search[searchspace]=tn (accessed on 18 August 2017).
- Ross, D. Observing and predicting hurricane wind and wave conditions. In Proceedings of the Joint IOC/WMO Seminar on Oceanographic Products and the IGOSS Data Processing and Services System, Moscow, Russia, 2–6 April 1979; pp. 309–321. [Google Scholar]
- Antani, J.K. Mathematical Representation of Hurricane Associated Wave Spectra; UFL/COEL-87-007; University of Florida: Gainesville, FL, USA, 1981. [Google Scholar]
- Foster, E.R. JONSWAP Spectral Formulation Applied to Hurricane Generated Seas; UFL/COEL-82/004; University of Florida: Gainesville, FL, USA, 1982. [Google Scholar]
- Knabb, R.D.; Rhome, J.R.; Brown, D.P. Tropical Cyclone Report: Hurricane Katrina: 23–30 August 2005. Available online: http://www.nhc.noaa.gov/pdf/TCRAL122005Katrina.pdf (accessed on 18 August 2017).
- Liu, P.C.; Chen, H.S.; Doong, D.-J.; Kao, C.C.; Hsu, Y.-J.G. Monstrous ocean waves during Typhoon Krosa. Ann. Geophys. 2008, 26, 1327–1329. [Google Scholar] [CrossRef]
- Wang, D.W.; Mitchell, D.A.; Teague, W.J.; Jarosz, E.; Hulbert, M.S. Extreme waves under Hurricane Ivan. Science 2005, 309, 896. [Google Scholar] [CrossRef] [PubMed]
- Toba, Y. Local balance in the air-sea boundary process. J. Oceanogr. Soc. Jpn. 1973, 29, 209–220. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S.; Cartwright, D.E.; Smith, N.D. Observations of the directional spectrum of sea waves using the motions of a floating buoy. In Ocean Wave Spectra; Prentice Hall: Upper Saddle River, NJ, USA, 1963; pp. 111–136. [Google Scholar]
- Young, I.R. On the measurement of directional wave spectra. Appl. Ocean Res. 1994, 16, 283–294. [Google Scholar] [CrossRef]
- Babanin, A.V.; Soloviev, Y.P. Variability of directional spectra of wind-generated waves, studied by means of wave staff arrays. J. Mar. Freshw. Res. 1998, 49, 89–101. [Google Scholar] [CrossRef]
- Young, I.R.; van Vledder, G.P. The central role of nonlinear interactions in wind-wave evolution. Philos. Trans. R. Soc. B 1993, 342, 505–524. [Google Scholar] [CrossRef]
- Zakharov, V.E. Theoretical interpretations of fetch-limited wind-driven sea observations. Nonlinear Process. Geophys. 2005, 12, 1011–1020. [Google Scholar] [CrossRef]

© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Young, I.R. A Review of Parametric Descriptions of Tropical Cyclone Wind-Wave Generation. Atmosphere 2017, 8, 194. https://doi.org/10.3390/atmos8100194
Young IR. A Review of Parametric Descriptions of Tropical Cyclone Wind-Wave Generation. Atmosphere. 2017; 8(10):194. https://doi.org/10.3390/atmos8100194
Chicago/Turabian StyleYoung, Ian R. 2017. "A Review of Parametric Descriptions of Tropical Cyclone Wind-Wave Generation" Atmosphere 8, no. 10: 194. https://doi.org/10.3390/atmos8100194
APA StyleYoung, I. R. (2017). A Review of Parametric Descriptions of Tropical Cyclone Wind-Wave Generation. Atmosphere, 8(10), 194. https://doi.org/10.3390/atmos8100194




