Water Tank Experiments on Stratified Flow over Double Mountain-Shaped Obstacles at High-Reynolds Number
Abstract
:1. Introduction
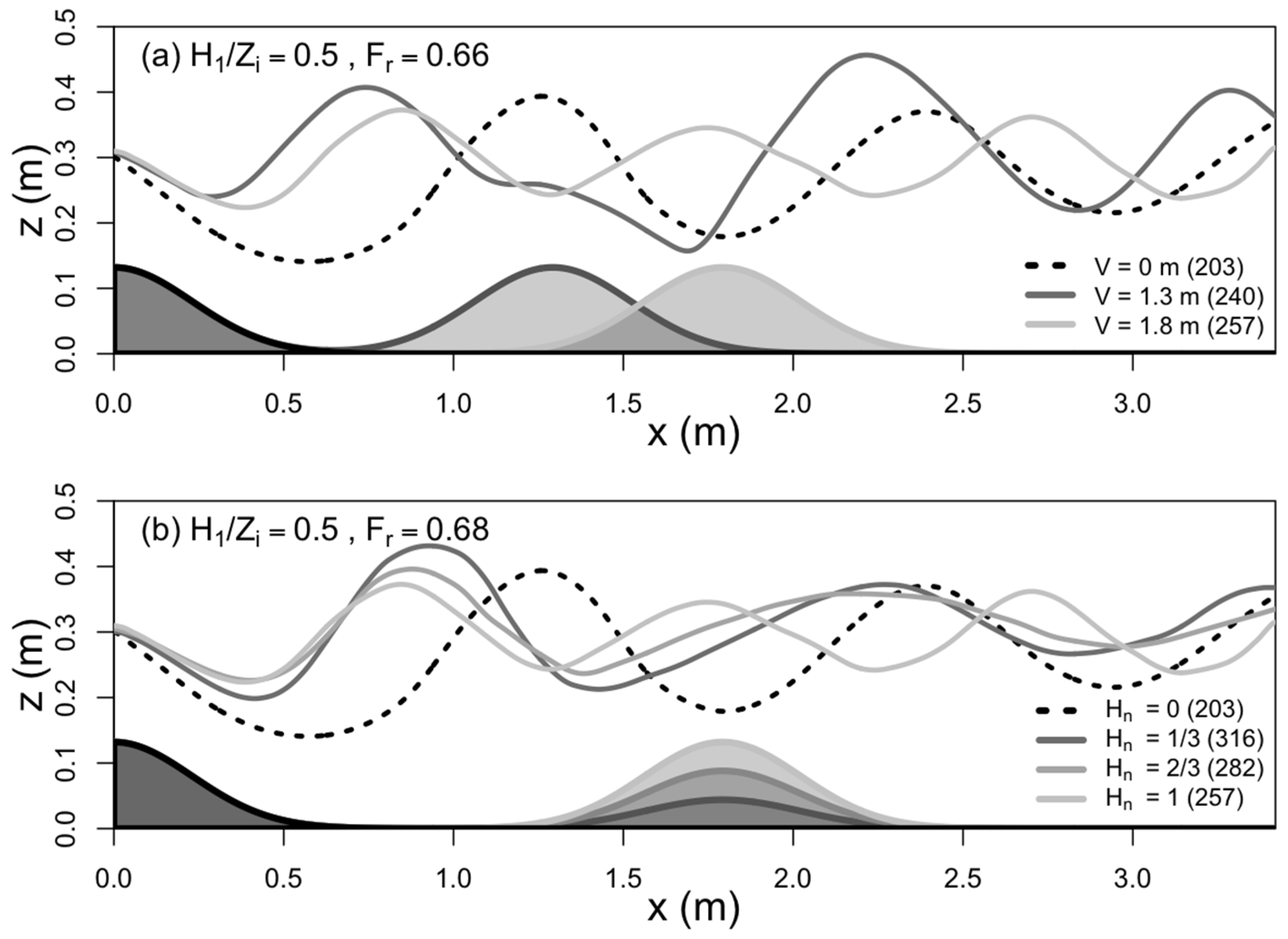
- Test the applicability of wave interference theory to waves trapped on the inversion in dependence on the ratio of ridge separation distance (V) to horizontal lee-wave wavelength (λ);
- Examine the influence of the secondary obstacle height and reproduce conditions under which waves in the lee of the obstacle are totally cancelled;
- Examine the influence of lee-wave interference on rotors;
- Reproduce hydraulic jump rotors and examine the influence of secondary obstacles on them;
- Examine the inner structure of rotor turbulence.
2. Methods
2.1. Experimental Design
2.2. Data Processing
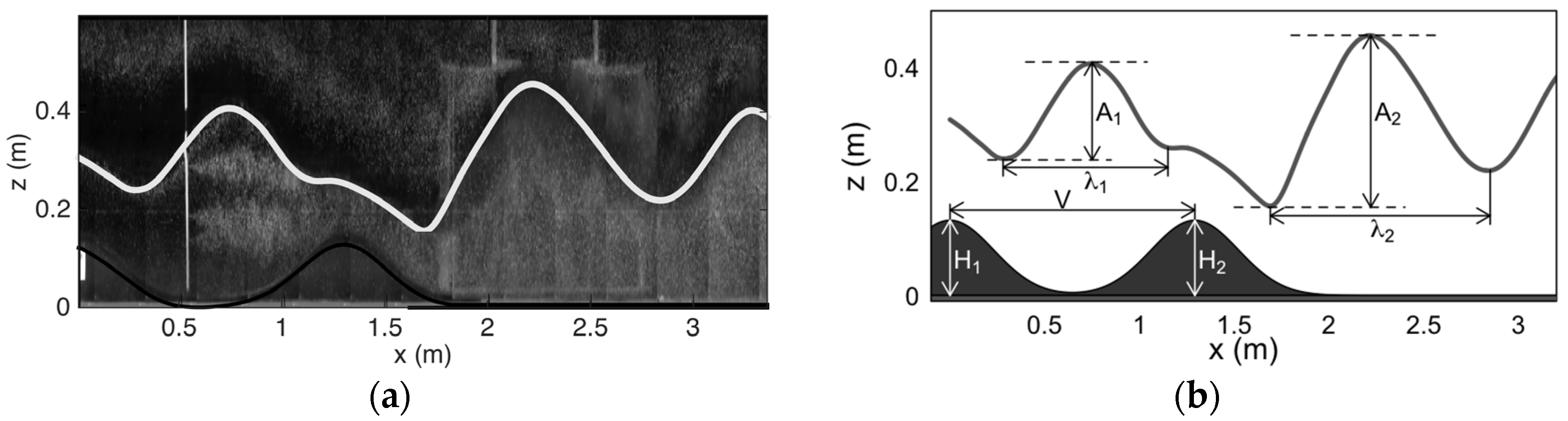
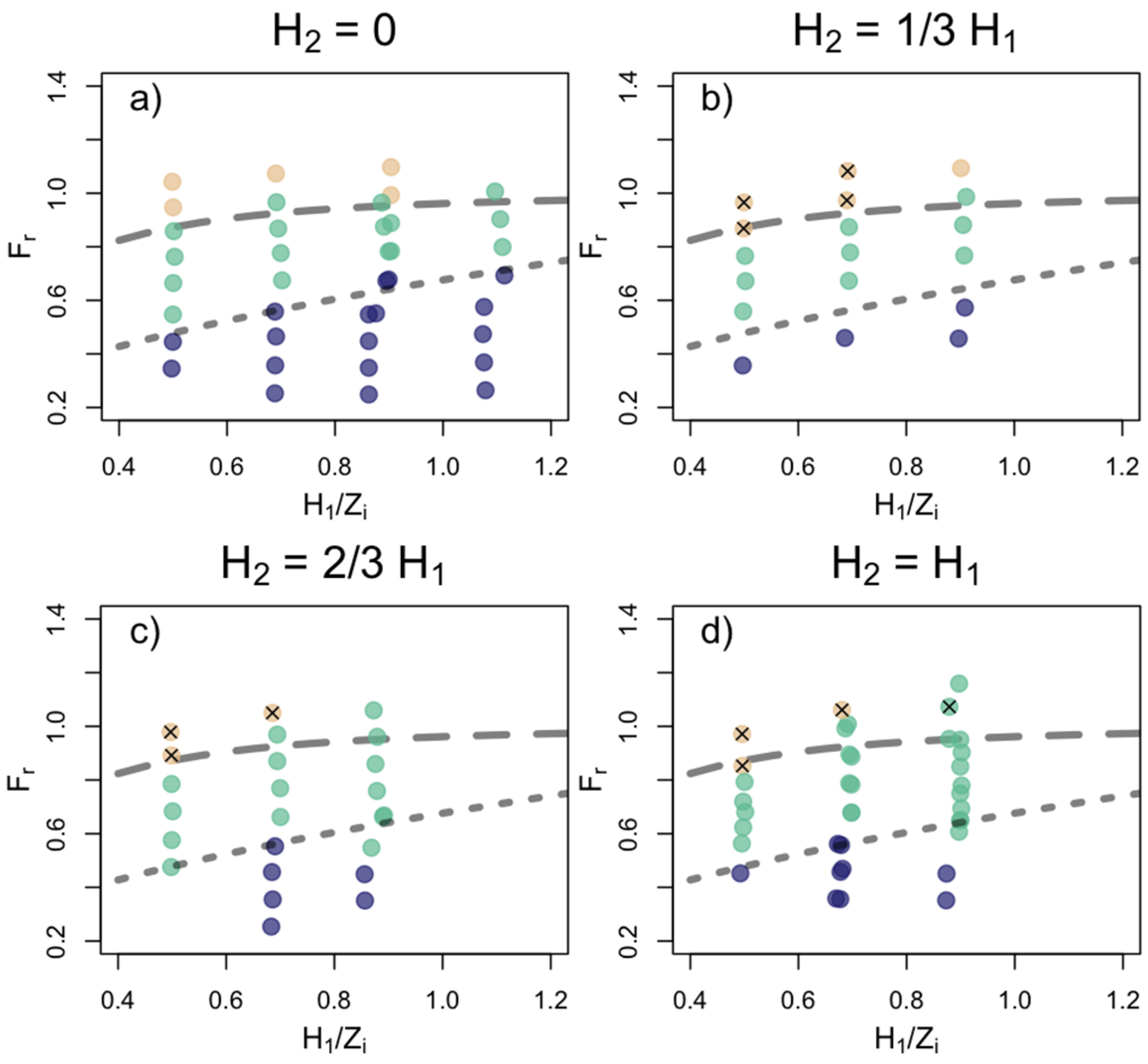
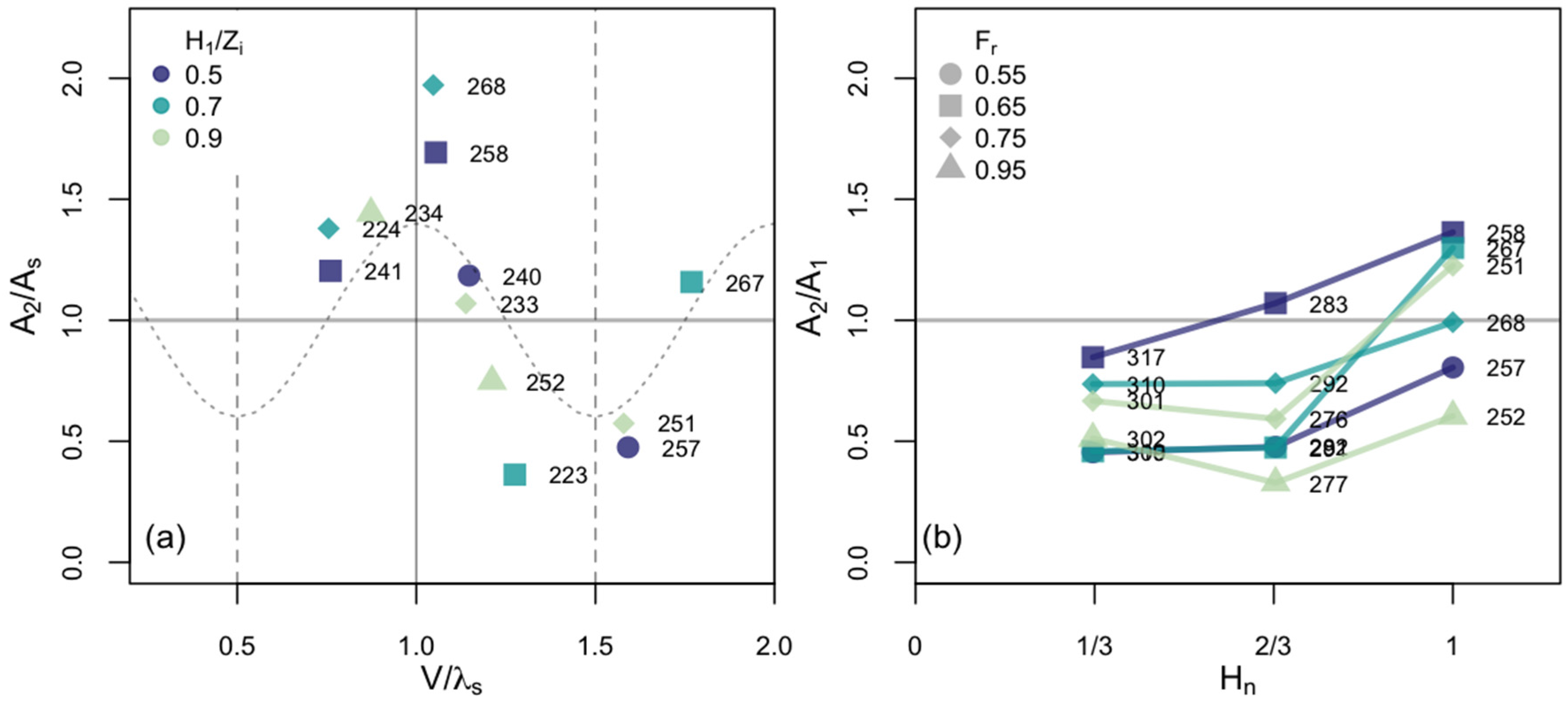
- Amplitude ratios A2/A1 or A2/As, where the numbers denote the obstacle downstream of which the amplitude was calculated (1, 2 and s for first, second and single, respectively).
- Mountain height ratio Hn, defined as the ratio of second to first obstacle height H2/H1.
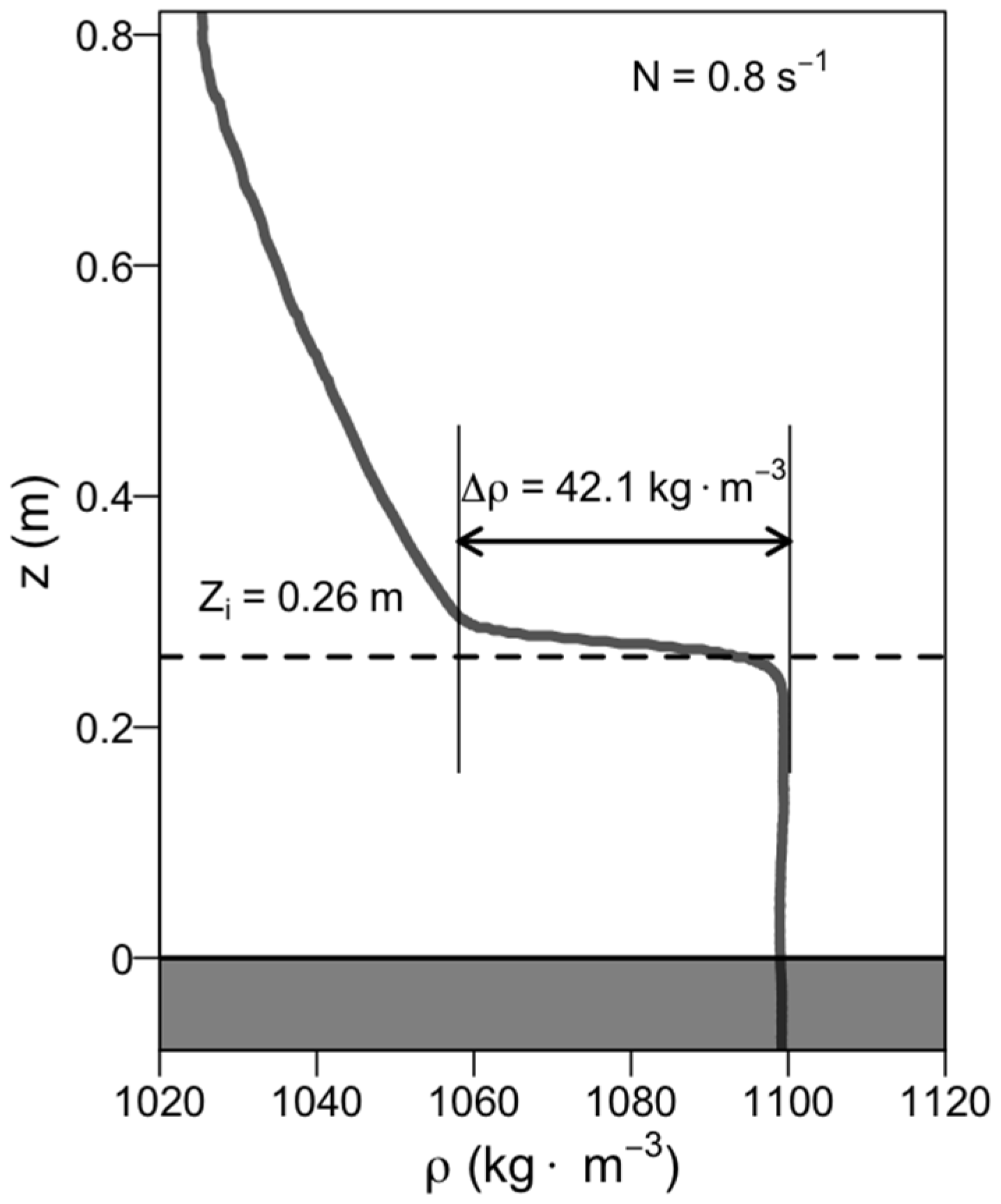
- Dimensionless inversion height H1/Zi, defined as the ratio between first obstacle height and the inversion height.
- Dimensionless wavelength (V/λ), defined as ratio between valley width V, taken as the distance between the ridges of the obstacles, and the lee-wave wavelength.
2.3. Flow Classification
3. Results
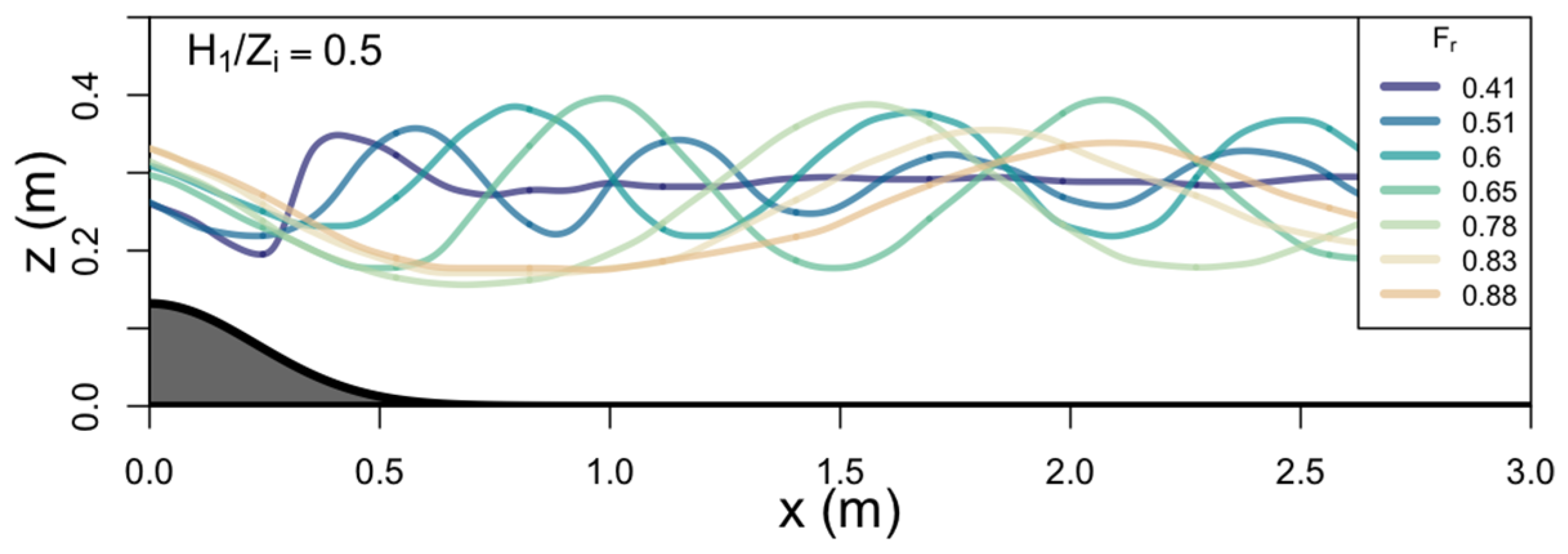
3.1. Flow over an Isolated Obstacle
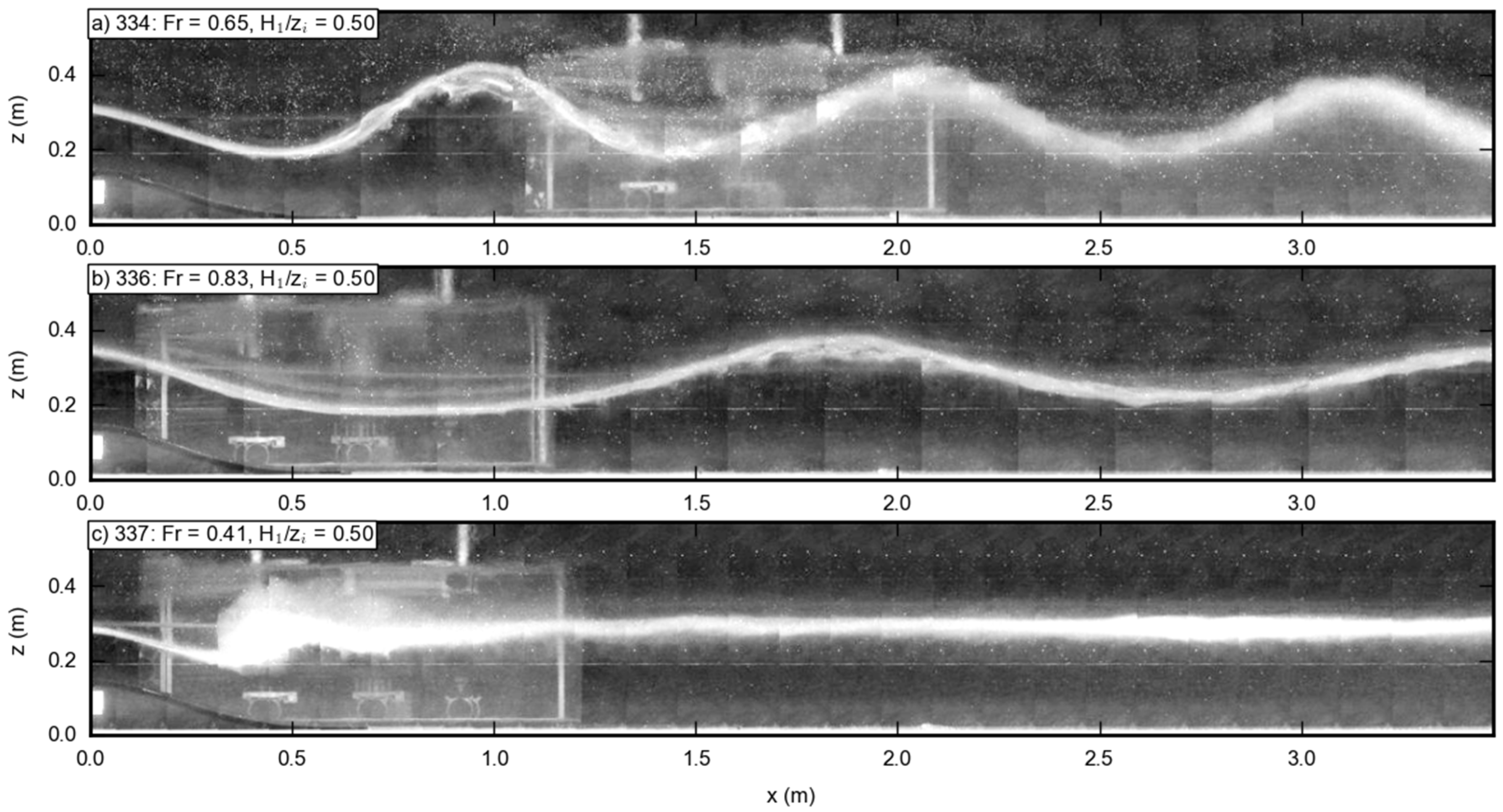
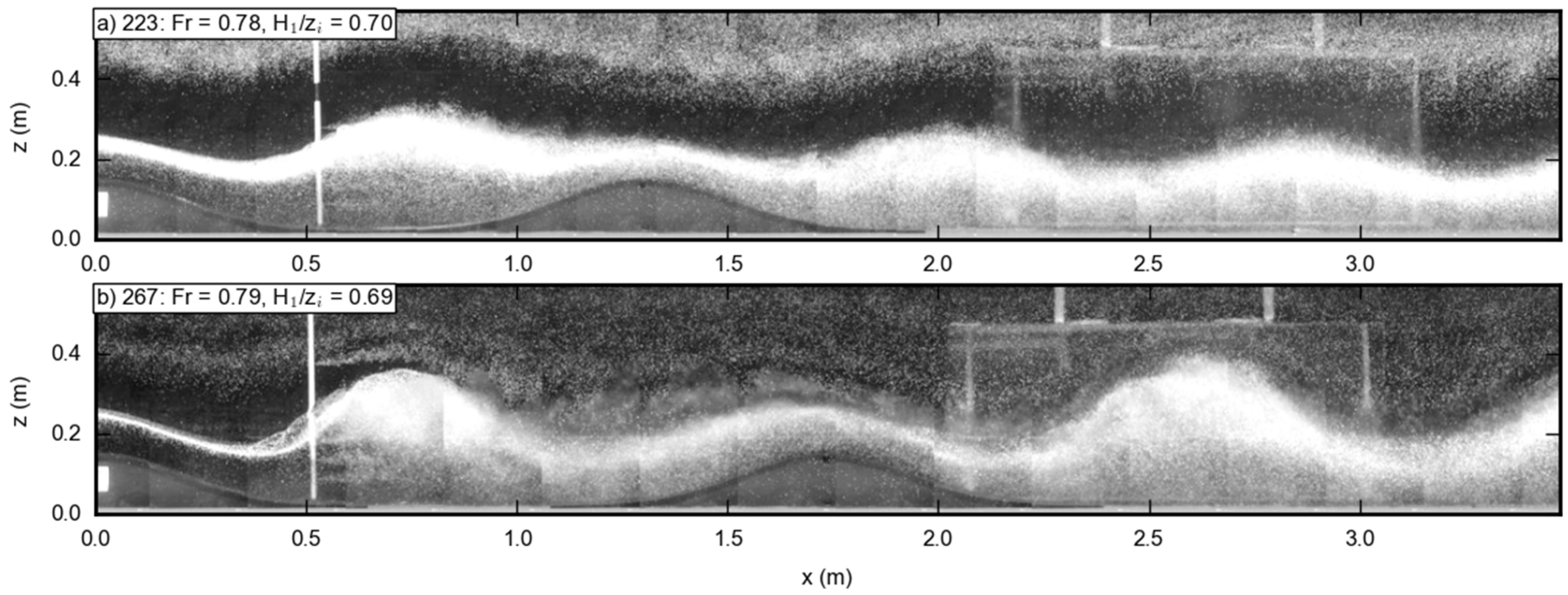
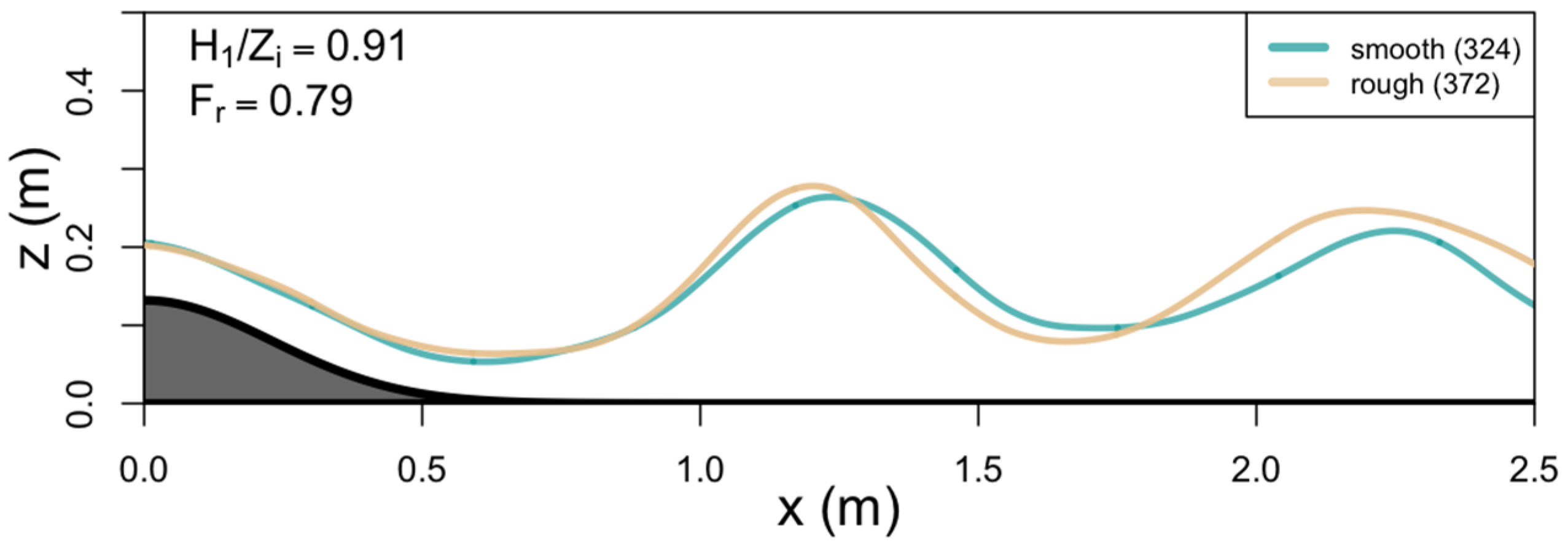
3.2. Flow over Double Obstacles
4. Discussion
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| 2D | two-dimensional |
| 3D | three-dimensional |
| As | Amplitude downstream of a single obstacle |
| A1 | Amplitude downstream of the first obstacle |
| A2 | Amplitude downstream of the second obstacle |
| CNRM | Centre National de Recherches Météorologiques |
| CNRS | Centre National de Recherches Scientifique |
| H1 | Height of the first obstacle |
| H2 | Height of the second obstacle |
| HyIV-CNRS-SecORo | Hydralab IV–CNRS–Secondary Orography and Rotors Experiments |
| λs | Lee-wave wavelength downstream of a single obstacle |
| λ1 | Lee-wave wavelength downstream of the first obstacle |
| λ2 | Lee-wave wavelength downstream of the second obstacle |
| LES | Large Eddy Simulation |
| PIV | Particle Image Velocimetry |
| T-REX | Terrain-Induced Rotor Experiment |
| V | ridge separation distance |
| Zi | height of the density jump (i.e., inversion) |
References
- Reuder, J.; Ablinger, M.; Ágústsson, H.; Brisset, P.; Brynjólfsson, S.; Garhammer, M.; Jóhannesson, T.; Jonassen, M.O.; Kühnel, R.; Lämmlein, S.; et al. FLOHOF 2007: An overview of the mesoscale meteorological field campaign at Hofsjökull, Central Iceland. Meteorol. Atmos. Phys. 2011, 116, 1–13. [Google Scholar] [CrossRef]
- Grubišić, V.; Sachsperger, J.; Caldeira, R.M.A. Atmospheric wake of Madeira: First aerial observations and numerical simulations. J. Atmos. Sci. 2015, 72, 4755–4776. [Google Scholar] [CrossRef]
- Grubišić, V.; Serafin, S.; Strauss, L.; Haimov, S.J.; French, J.R.; Oolman, L.D. Wave-induced boundary layer separation in the lee of the Medicine Bow Mountains. Part II: Numerical modeling. J. Atmos. Sci. 2015, 72, 4865–4884. [Google Scholar] [CrossRef]
- French, J.R.; Haimov, S.J.; Oolman, L.D.; Grubišić, V.; Serafin, S.; Strauss, L. Wave-induced boundary layer separation in the lee of the Medicine Bow Mountains. Part I: Observations. J. Atmos. Sci. 2015, 72, 4845–4863. [Google Scholar] [CrossRef]
- Scorer, R.S. Theory of waves in the lee of mountains. Q. J. R. Meteorol. Soc. 1949, 75, 41–56. [Google Scholar] [CrossRef]
- Long, R.R. Some aspects of the flow of stratified fluids: I. A theoretical investigation. Tellus 1953, 5, 42–58. [Google Scholar] [CrossRef]
- Durran, D.R. Mountain waves. In Mesoscale Meteorology and Forecasting; American Meteorological Society: Boston, MA, USA, 1986; pp. 472–492. [Google Scholar]
- Grubišić, V.; Smith, R.B.; Schär, C. The Effect of bottom friction on shallow-water flow past an isolated obstacle. J. Atmos. Sci. 1995, 52, 1985–2005. [Google Scholar] [CrossRef]
- Smith, R.B.; Jiang, Q.; Doyle, J.D. A theory of gravity wave absorption by a boundary layer. J. Atmos. Sci. 2006, 63, 774–781. [Google Scholar] [CrossRef]
- Jiang, Q.; Doyle, J.D.; Wang, S.; Smith, R.B. On Boundary layer separation in the lee of mesoscale topography. J. Atmos. Sci. 2007, 64, 401–420. [Google Scholar] [CrossRef]
- Smith, C.M.; Skyllingstad, E.D. Investigation of upstream boundary layer influence on mountain wave breaking and lee wave rotors using a large-eddy simulation. J. Atmos. Sci. 2009, 66, 3147–3164. [Google Scholar] [CrossRef]
- Guarino, M.-V.; Teixeira, M.A.C.; Ambaum, M.H.P. Turbulence generation by mountain wave breaking in flows with directional wind shear. Q. J. R. Meteorol. Soc. 2016. [Google Scholar] [CrossRef]
- Bérenger, M.; Gerbier, N. Experimental studies of lee waves in the French Alps. Q.J.R. Meteorol. Soc. 1961, 87, 13–23. [Google Scholar] [CrossRef]
- Queney, P.; Corby, G.; Gerbier, N.; Koschmieder, H.; Zierp, J. The Airflow Over Mountains; WMO Technical Note; WMO: Geneva, Switzerland, 1960. [Google Scholar]
- Scorer, R.S. Dynamics of Meteorology and Climate; Wiley: Chichester, UK, 1997. [Google Scholar]
- Tampieri, F.; Hunt, J.C.R. Two-dimensional stratified fluid flow over valleys: Linear theory and a laboratory investigation. Bound. Layer Meteorol. 1984, 32, 257–279. [Google Scholar] [CrossRef]
- Kimura, F.; Manins, P. Blocking in periodic valleys. Bound. Layer Meteorol. 1988, 44, 137–169. [Google Scholar] [CrossRef]
- Lee, J.T.; Lawson, R.E.; Marsh, G.L. Flow visualization experiments on stably stratified flow over ridges and valleys. Meteorol. Atmos. Phys. 1987, 37, 183–194. [Google Scholar] [CrossRef]
- Gyüre, B.; Jánosi, I.M. Stratified flow over asymmetric and double bell-shaped obstacles. Dyn. Atmos. Oceans 2003, 37, 155–170. [Google Scholar] [CrossRef]
- Grisogono, B.; Pryor, S.C.; Keislar, R.E. Mountain wave drag over double bell-shaped orography. Q. J. R. Meteorol. Soc. 1993, 119, 199–206. [Google Scholar] [CrossRef]
- Vosper, S. Gravity-wave drag on two mountains. Q. J. R. Meteorol. Soc. 1996, 122, 993–999. [Google Scholar] [CrossRef]
- Mayr, G.J.; Gohm, A. 2D Airflow over a double bell-shaped mountain. Meteorol. Atmos. Phys. 2000, 72, 13–27. [Google Scholar] [CrossRef]
- Grubišić, V.; Doyle, J.D.; Kuettner, J.; Dirks, R.; Cohn, S.A.; Pan, L.L.; Mobbs, S.; Smith, R.B.; Whiteman, C.D.; Czyzyk, S.; et al. The terrain-induced rotor experiment. Bull. Am. Meteorol. Soc. 2008, 89, 1513–1533. [Google Scholar] [CrossRef]
- Grubišić, V.; Billings, B.J. The intense lee-wave rotor event of sierra rotors IOP 8. J. Atmos. Sci. 2007, 64, 4178–4201. [Google Scholar] [CrossRef]
- Cohn, S.A.; Grubišić, V.; Brown, W.O.J. Wind profiler observations of mountain waves and rotors during T-REX. J. Appl. Meteorol. Climatol. 2010, 50, 826–843. [Google Scholar] [CrossRef]
- Sheridan, P.; Vosper, S. High-resolution simulations of lee waves and downslope winds over the Sierra Nevada during T-REX IOP 6. J. Appl. Meteorol. Climatol. 2012, 51, 1333–1352. [Google Scholar] [CrossRef]
- Strauss, L.; Serafin, S.; Grubišić, V. Atmospheric rotors and severe turbulence in a long deep valley. J. Atmos. Sci. 2015, 73, 1481–1506. [Google Scholar] [CrossRef]
- Grubišić, V.; Stiperski, I. Lee-wave resonances over double bell-shaped obstacles. J. Atmos. Sci. 2009, 66, 1205–1228. [Google Scholar] [CrossRef]
- Stiperski, I.; Grubišić, V. Trapped lee wave interference in the presence of surface friction. J. Atmos. Sci. 2011, 68, 918–936. [Google Scholar] [CrossRef]
- Doyle, J.D.; Durran, D.R. The Dynamics of Mountain-Wave-Induced Rotors. J. Atmos. Sci. 2002, 59, 186–201. [Google Scholar] [CrossRef]
- Hertenstein, R.F.; Kuettner, J.P. Rotor types associated with steep lee topography: Influence of the wind profile. Tellus A 2005, 57, 117–135. [Google Scholar] [CrossRef]
- Knigge, C.; Etling, D.; Paci, A.; Eiff, O. Laboratory experiments on mountain-induced rotors. Q. J. R. Meteorol. Soc. 2010, 136, 442–450. [Google Scholar] [CrossRef]
- Ágústsson, H.; Ólafsson, H. Simulations of observed lee waves and rotor turbulence. Mon. Weather Rev. 2014, 142, 832–849. [Google Scholar] [CrossRef]
- Stiperski, I.; Ivančan-Picek, B.; Grubišić, V.; Bajić, A. Complex bora flow in the lee of Southern Velebit. Q. J. R. Meteorol. Soc. 2012, 138, 1490–1506. [Google Scholar] [CrossRef]
- Vosper, S.B. Inversion effects on mountain lee waves. Q. J. R. Meteorol. Soc. 2004, 130, 1723–1748. [Google Scholar] [CrossRef]
- Teixeira, M.A.C.; Argaín, J.L.; Miranda, P.M.A. Orographic drag associated with lee waves trapped at an inversion. J. Atmos. Sci. 2013, 70, 2930–2947. [Google Scholar] [CrossRef]
- Sachsperger, J.; Serafin, S.; Grubišić, V. Lee waves on the boundary-layer inversion and their dependence on free-atmospheric stability. Front. Earth Sci. 2015, 70. [Google Scholar] [CrossRef]
- Eiff, O.S.; Bonneton, P. Lee-wave breaking over obstacles in stratified flow. Phys. Fluids 2000, 12, 1073–1086. [Google Scholar] [CrossRef]
- Lacaze, L.; Paci, A.; Cid, E.; Cazin, S.; Eiff, O.; Esler, J.G.; Johnson, E.R. Wave patterns generated by an axisymmetric obstacle in a two-layer flow. Exp. Fluids 2013, 54, 1618. [Google Scholar] [CrossRef] [Green Version]
- Dossmann, Y.; Paci, A.; Auclair, F.; Lepilliez, M.; Cid, E. Topographically induced internal solitary waves in a pycnocline: Ultrasonic probes and stereo-correlation measurements. Phys. Fluids 2014, 26, 056601. [Google Scholar] [CrossRef]
- Sachsperger, J.; Serafin, S.; Grubišić, V.; Stiperski, I.; Paci, A. The amplitude of lee waves on the boundary-layer inversion. Q. J. R. Meteorol. Soc. 2016. [Google Scholar] [CrossRef]
- Muñoz-Esparza, D.; Sauer, J.A.; Linn, R.R.; Kosović, B. Limitations of one-dimensional mesoscale PBL parameterizations in reproducing mountain-wave flows. J. Atmos. Sci. 2015, 73, 2603–2614. [Google Scholar] [CrossRef]
- Wyngaard, J.C. Turbulence in the Atmosphere; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Oertel, H. Prandtl’s Essentials of Fluid Mechanics; Springer: New York, NY, USA, 2004. [Google Scholar]
- Knigge, C. Untersuchungen von Atmosphärichen Gebirgsrotoren mit Hilfe von Laborexperimenten und Grobstruktursimulationen. Ph.D. Thesis, Leibniz Universität Hannover, Hanover, Germany, 25 January 2012. [Google Scholar]
- Baines, P.G. Topographic Effects in Stratified Flows; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
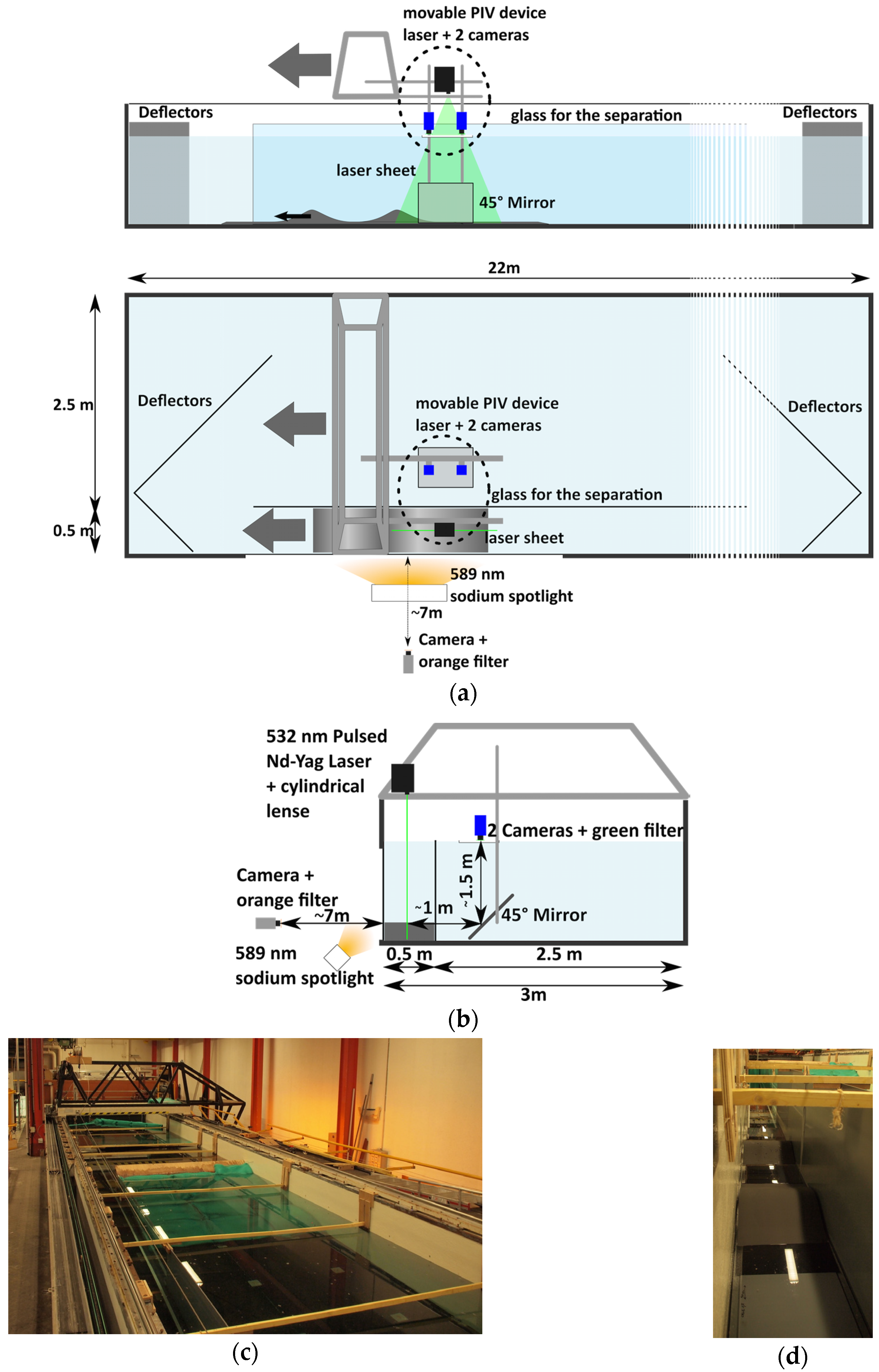

| Hi (m) | 2L2 (cm2) | L0i (cm) | |
|---|---|---|---|
| Primary or Single (H1) | 13.2 | 1060 | 66.3 |
| Secondary (H2) | 13.2 | 1060 | 66.3 |
| Secondary (H2) | 8.8 | 1060 | 62.9 |
| Secondary (H2) | 4.4 | 1060 | 56.8 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stiperski, I.; Serafin, S.; Paci, A.; Ágústsson, H.; Belleudy, A.; Calmer, R.; Horvath, K.; Knigge, C.; Sachsperger, J.; Strauss, L.; et al. Water Tank Experiments on Stratified Flow over Double Mountain-Shaped Obstacles at High-Reynolds Number. Atmosphere 2017, 8, 13. https://doi.org/10.3390/atmos8010013
Stiperski I, Serafin S, Paci A, Ágústsson H, Belleudy A, Calmer R, Horvath K, Knigge C, Sachsperger J, Strauss L, et al. Water Tank Experiments on Stratified Flow over Double Mountain-Shaped Obstacles at High-Reynolds Number. Atmosphere. 2017; 8(1):13. https://doi.org/10.3390/atmos8010013
Chicago/Turabian StyleStiperski, Ivana, Stefano Serafin, Alexandre Paci, Hálfdán Ágústsson, Anne Belleudy, Radiance Calmer, Kristian Horvath, Christoph Knigge, Johannes Sachsperger, Lukas Strauss, and et al. 2017. "Water Tank Experiments on Stratified Flow over Double Mountain-Shaped Obstacles at High-Reynolds Number" Atmosphere 8, no. 1: 13. https://doi.org/10.3390/atmos8010013
APA StyleStiperski, I., Serafin, S., Paci, A., Ágústsson, H., Belleudy, A., Calmer, R., Horvath, K., Knigge, C., Sachsperger, J., Strauss, L., & Grubišić, V. (2017). Water Tank Experiments on Stratified Flow over Double Mountain-Shaped Obstacles at High-Reynolds Number. Atmosphere, 8(1), 13. https://doi.org/10.3390/atmos8010013






