Evaluation of Temperature and Humidity Profiles of Unified Model and ECMWF Analyses Using GRUAN Radiosonde Observations
Abstract
:1. Introduction
2. Data Used and Processing
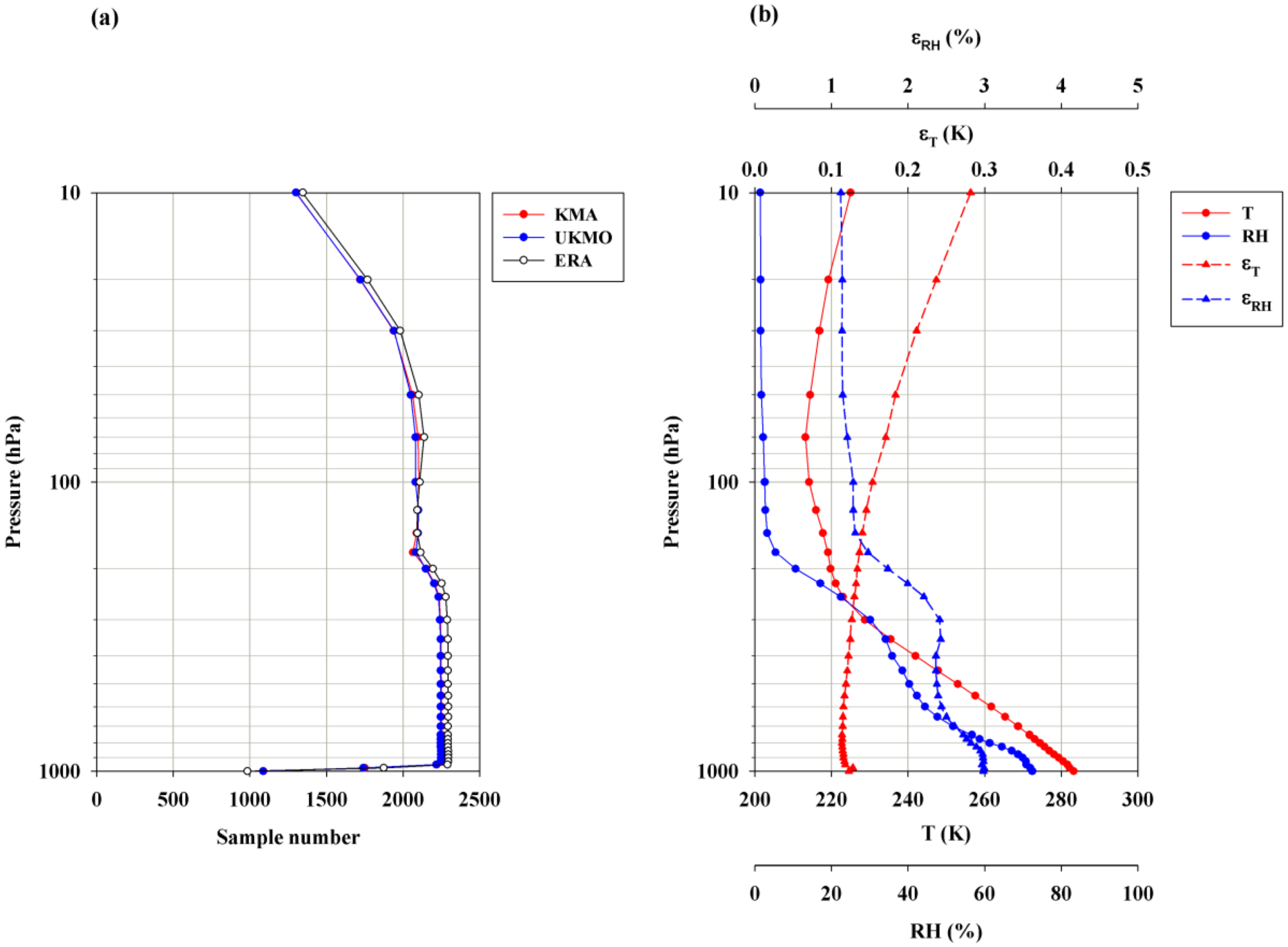
2.1. Construction of Collocated Data
2.2. Conversion of the Relative Humidity
3. Results
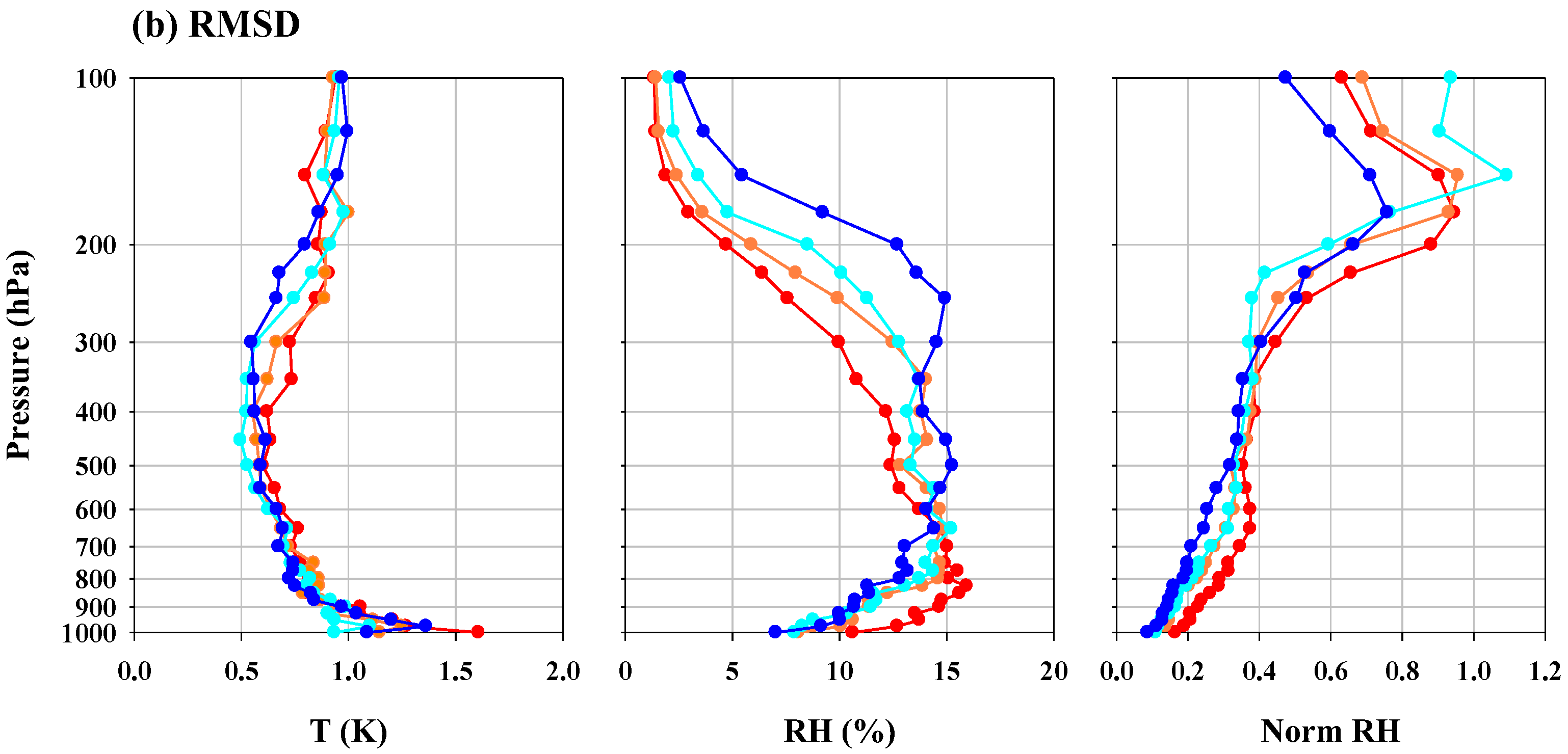
3.1. Mean Statistics
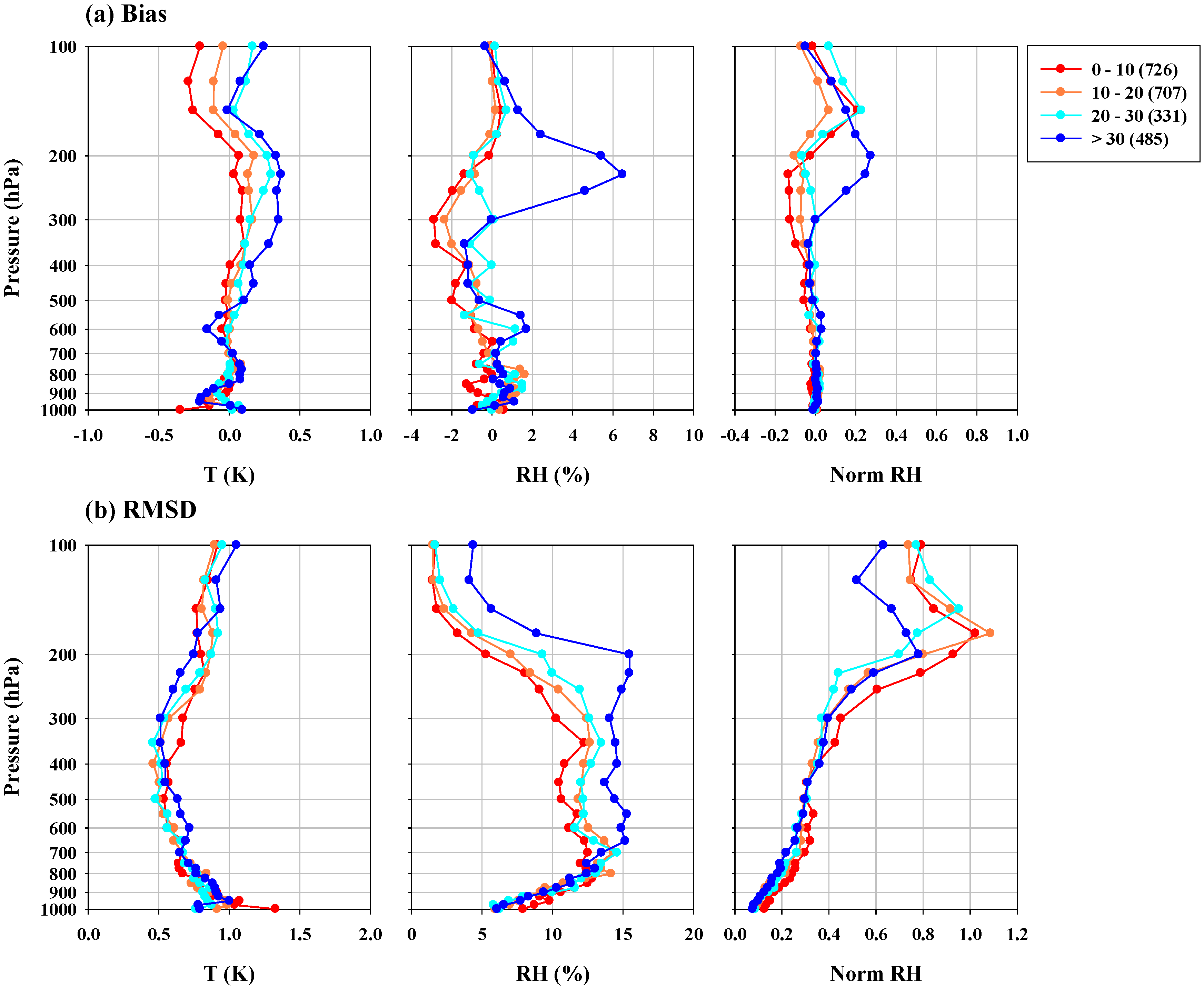
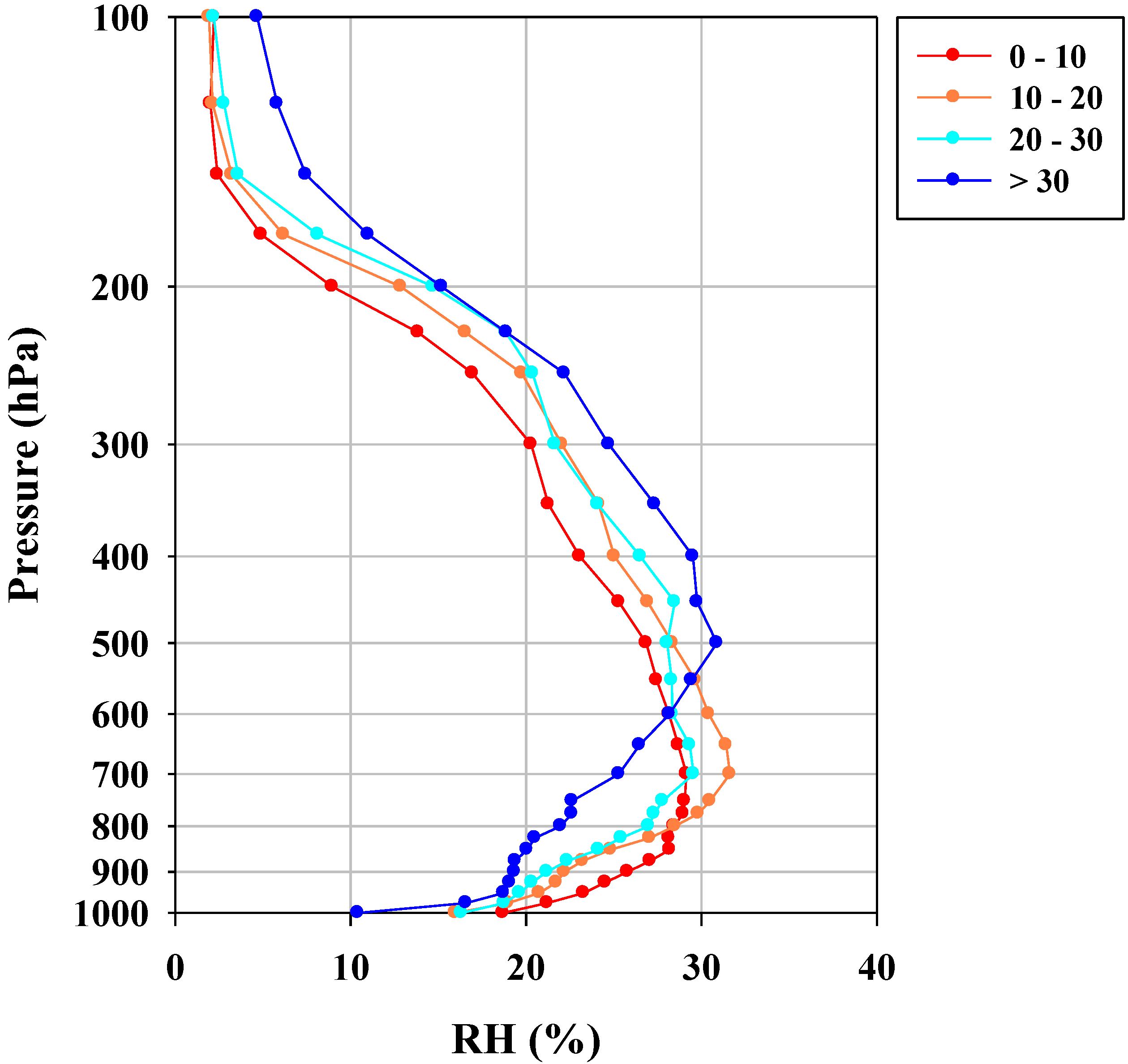
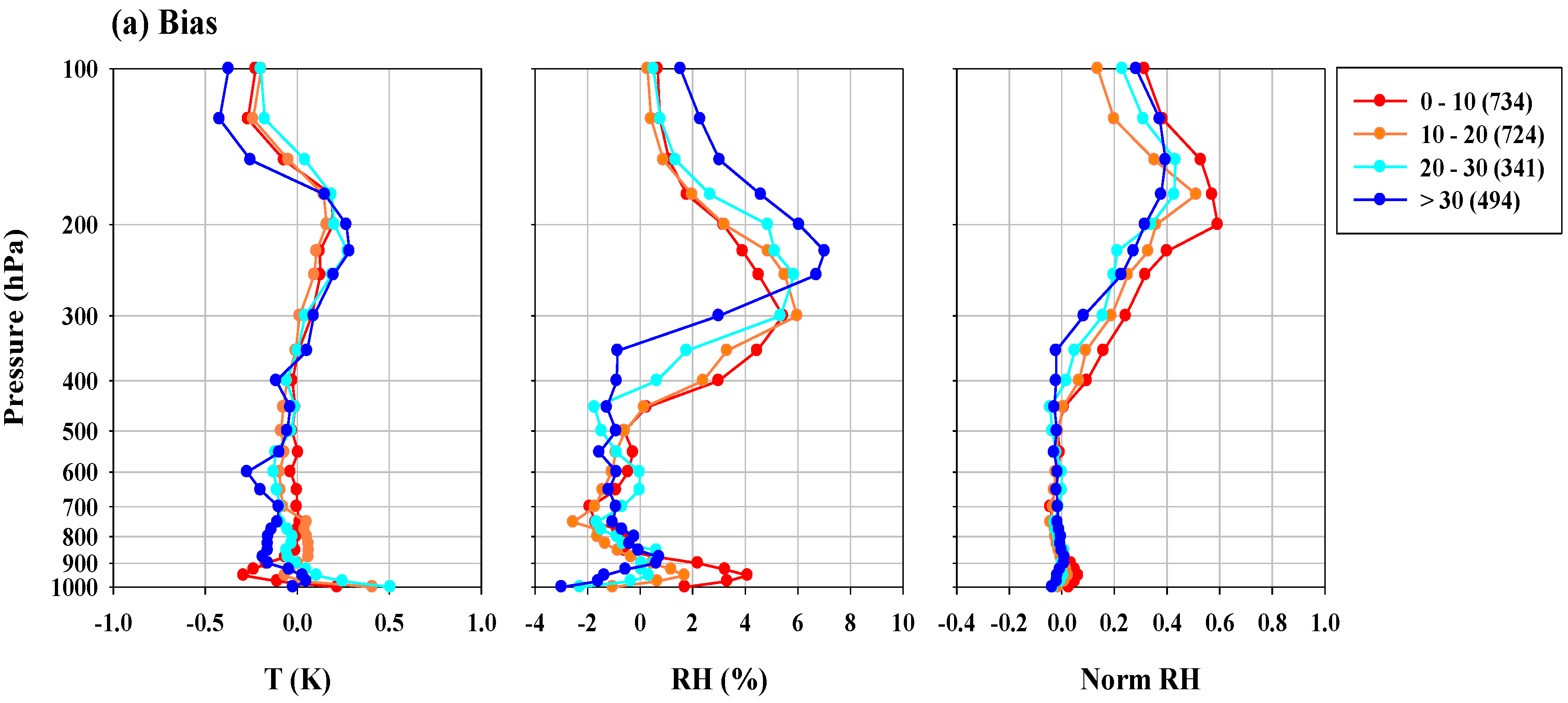
3.2. Moistness-Depending Statistics
4. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Warner, T.T. Numerical Weather and Climate Prediction; Cambridge University Press: New York, NY, USA, 2011. [Google Scholar]
- Lorenc, A.C. Analysis methods for numerical weather prediction. Q. J. R. Meteorol. Soc. 1986, 112, 1177–1194. [Google Scholar] [CrossRef]
- Kalnay, E. Atmospheric Modeling, Data Assimilation, and Predictability; Cambridge University Press: New York, NY, USA, 2003. [Google Scholar]
- Brown, A.; Milton, S.; Cullen, M.; Golding, B.; Mitchell, J.; Shelly, A. Unified modeling and prediction of weather and climate: A 25-year journey. Bull. Am. Meteorol. Soc. 2012, 93, 1865–1877. [Google Scholar] [CrossRef]
- Lorenc, A.C.; Ballard, S.P.; Bell, R.S.; Ingleby, N.B.; Andrews, P.L.F.; Barker, D.M.; Bray, J.R.; Clayton, A.M.; Dalby, T.; Li, D.; et al. The Met. Office global three-dimensional variational data assimilation scheme. Q. J. R. Meteorol. Soc. 2000, 126, 2991–3012. [Google Scholar] [CrossRef]
- Andersson, E.; Hólm, E.; Bauer, P.; Beljaars, A.; Kelly, G.A.; McNally, A.P.; Simmons, A.J.; Thépaut, J.-N.; Tompkins, A.M. Analysis and forecast impact of the main humidity observing systems. Q. J. R. Meteorol. Soc. 2007, 133, 1473–1485. [Google Scholar] [CrossRef]
- Rawlins, F.; Ballard, S.P.; Bovis, K.J.; Clayton, A.M.; Li, D.; Inverarity, G.W.; Lorenc, A.C.; Payne, T.J. The Met Office global four-dimensional variational data assimilation scheme. Q. J. R. Meteorol. Soc. 2007, 133, 347–362. [Google Scholar] [CrossRef]
- Clayton, A.M.; Lorenc, A.C.; Barker, D.M. Operational implementation of a hybrid ensemble/4D-Var global data assimilation system at the Met Office. Q. J. R. Meteorol. Soc. 2013, 139. [Google Scholar] [CrossRef]
- Ingleby, N.B.; Lorenc, A.C.; Ngan, F.; Rawlins, F.; Jackson, D.R. Improved variational analyses using a nonlinear humidity control variable. Q. J. R. Meteorol. Soc. 2013, 139. [Google Scholar] [CrossRef]
- Nash, J.; Oakley, T.; Vömel, H.; Li, W. WMO Intercomparisons of High Quality Radiosonde Systems. Available online: https://www.wmo.int/pages/prog/www/IMOP/publications/IOM-107_Yangjiang.pdf (accessed on 15 July 2016).
- Moradi, I.; Soden, B.; Ferraro, R.; Arkin, P.; Vömel, H. Assessing the quality of humidity measurements from global operational radiosonde sensors. J. Geophys. Res. Atmos. 2013, 118, 8040–8053. [Google Scholar] [CrossRef]
- Dirksen, R.J.; Sommer, M.; Immler, F.J.; Hurst, D.F.; Kivi, R.; Vömel, H. Reference quality upper-air measurements: GRUAN data processing for the Vaisala RS92 radiosonde. Atmos. Meas. Tech. 2014, 7, 4463–4490. [Google Scholar] [CrossRef]
- Lee, J.-W.; Han, S.-O.; Chung, K.-Y. The Improvement of forecast accuracy of the unified model at KMA by using an optimized set of physical options (in Korean with English abstract). J. Korean Meteorol. Soc. 2012, 22, 345–356. [Google Scholar]
- Korea Meteorological Administration Joint WMO Technical Progress Report on the Global Data Processing and Forecasting System and Numerical Weather Prediction Research Activities for 2012. Available online: https://www.wmo.int/pages/prog/www/DPFS/ProgressReports/2012/GDPFS-NWP-2012.html (accessed on 15 July 2016).
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137. [Google Scholar] [CrossRef]
- Sommer, M.; Dirksen, R.; Rohden, C. Brief Description of the RS92 GRUAN Data Product (RS92-GDP); Technical Document 4; GRUAN Lead Centre: Geneva, Switzerland, 2006. [Google Scholar]
- Wang, J.; Zhang, L.; Dai, A.; Immler, F.; Sommer, M.; Vömel, H. Radiation dry bias correction of Vaisala RS92 humidity data and its impact on historical radiosonde data. J. Atmos. Ocean. Technol. 2013, 30, 197–214. [Google Scholar] [CrossRef]
- Sun, B.; Reale, A.; Seidel, D.J.; Hunt, D.C. Comparing radiosonde and COSMIC atmospheric profile data to quantify differences among radiosonde types and the effects of imperfect collocation on comparison statistics. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Miloshevich, L.M.; Vömel, H.; Whiteman, D.; Lesht, B.; Schmidlin, F.J.; Russo, F. Absolute accuracy of water vapor measurements from six operational radiosonde types launched during AWEX-G and implications for AIRS validation. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Anderson, P.S. Mechanism for the behavior of hydroactive materials used in humidity sensors. J. Atmos. Ocean. Technol. 1995, 12, 662–667. [Google Scholar] [CrossRef]
- Hyland, R.W.; Wexler, A. Formulations for the thermodynamic properties of the saturated phases of H2O from 173.15 K to 473.15 K. ASHRAE Trans. 1983, 89, 500–519. [Google Scholar]
- Met Office Joint WMO Technical Progress Report on the Global Data Processing and Forecasting System and Numerical Weather Prediction Research Activities for 2011. Available online: http://www.wmo.int/pages/prog/www/Documents/PublicWeb/www/gdpfs/GDPFS-NWP_Annualreports11/2011_UK.pdf (accessed on 15 July 2016).
- Kwon, E.-H.; Li, J.; Li, J.; Sohn, B.J.; Weisz, E. Use of total precipitable water classification of a priori error and quality control in atmospheric temperature and water vapor sounding retrieval. Adv. Atmos. Sci. 2012, 29, 263–273. [Google Scholar] [CrossRef]
- Kwon, E.-H.; Sohn, B.J.; Smith, W.L.; Li, J. Validating IASI temperature and moisture sounding retrievals over East Asia using radiosonde observations. J. Atmos. Ocean. Technol. 2012, 29, 1250–1262. [Google Scholar] [CrossRef]
- Hilton, F.I.; Newman, S.M.; Collard, A.D. Identification of NWP humidity biases using high-peaking water vapour channels from IASI. Atmos. Sci. Let. 2012, 13, 73–78. [Google Scholar] [CrossRef]




| Code | Name | Country | Location | International Name | ||
|---|---|---|---|---|---|---|
| Latitude | Longitude | Altitude | ||||
| CAB | Cabauw (06260) | Netherlands | 51.97° | 4.92° | 1 m | Cabauw (De Bilt) Experimental Site for Atmospheric Research (CESAR) |
| LIN | Lindenberg (10393) | Germany | 52.21° | 14.12° | 110 m | Lindenberg Meteorological Observatory |
| MAN | Manus | Papua New Guinea | −2.06° | 147.42° | 6 m | Tropical Western Pacific (TWP) Manus Site |
| NAU | Nauru (91532) | Nauru | −0.52° | 166.92° | 7 m | Tropical Western Pacific (TWP) Nauru Site |
| NYA | Ny-Ålesund (01004) | Norway | 78.92° | 11.92° | 5 m | AWIPEV Research Base |
| PAY | Payerne (06610) | Switzerland | 46.81° | 6.95° | 491 m | MeteoSwiss Aerological station Payerne |
| SGP | Lamont (74646) | USA | 36.6° | −97.49° | 320 m | Southern Great Plains (SGP) Central Facility |
| SOD | Sodankyla (20386) | Finland | 67.37° | 26.63° | 179 m | Finnish Meteorological Institute Arctic Research Centre |
| TAT | Tateno (47646) | Japan | 36.06° | 140.13° | 31 m | Tateno Aerological Observatory |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noh, Y.-C.; Sohn, B.-J.; Kim, Y.; Joo, S.; Bell, W. Evaluation of Temperature and Humidity Profiles of Unified Model and ECMWF Analyses Using GRUAN Radiosonde Observations. Atmosphere 2016, 7, 94. https://doi.org/10.3390/atmos7070094
Noh Y-C, Sohn B-J, Kim Y, Joo S, Bell W. Evaluation of Temperature and Humidity Profiles of Unified Model and ECMWF Analyses Using GRUAN Radiosonde Observations. Atmosphere. 2016; 7(7):94. https://doi.org/10.3390/atmos7070094
Chicago/Turabian StyleNoh, Young-Chan, Byung-Ju Sohn, Yoonjae Kim, Sangwon Joo, and William Bell. 2016. "Evaluation of Temperature and Humidity Profiles of Unified Model and ECMWF Analyses Using GRUAN Radiosonde Observations" Atmosphere 7, no. 7: 94. https://doi.org/10.3390/atmos7070094
APA StyleNoh, Y.-C., Sohn, B.-J., Kim, Y., Joo, S., & Bell, W. (2016). Evaluation of Temperature and Humidity Profiles of Unified Model and ECMWF Analyses Using GRUAN Radiosonde Observations. Atmosphere, 7(7), 94. https://doi.org/10.3390/atmos7070094






