Bias Correction for Retrieval of Atmospheric Parameters from the Microwave Humidity and Temperature Sounder Onboard the Fengyun-3C Satellite
Abstract
:1. Introduction
2. Description of MWHTS Instruments’ Characteristics
3. Forward Model and Bias Correction
3.1. Forward Model Simulations
3.2. Bias Correction
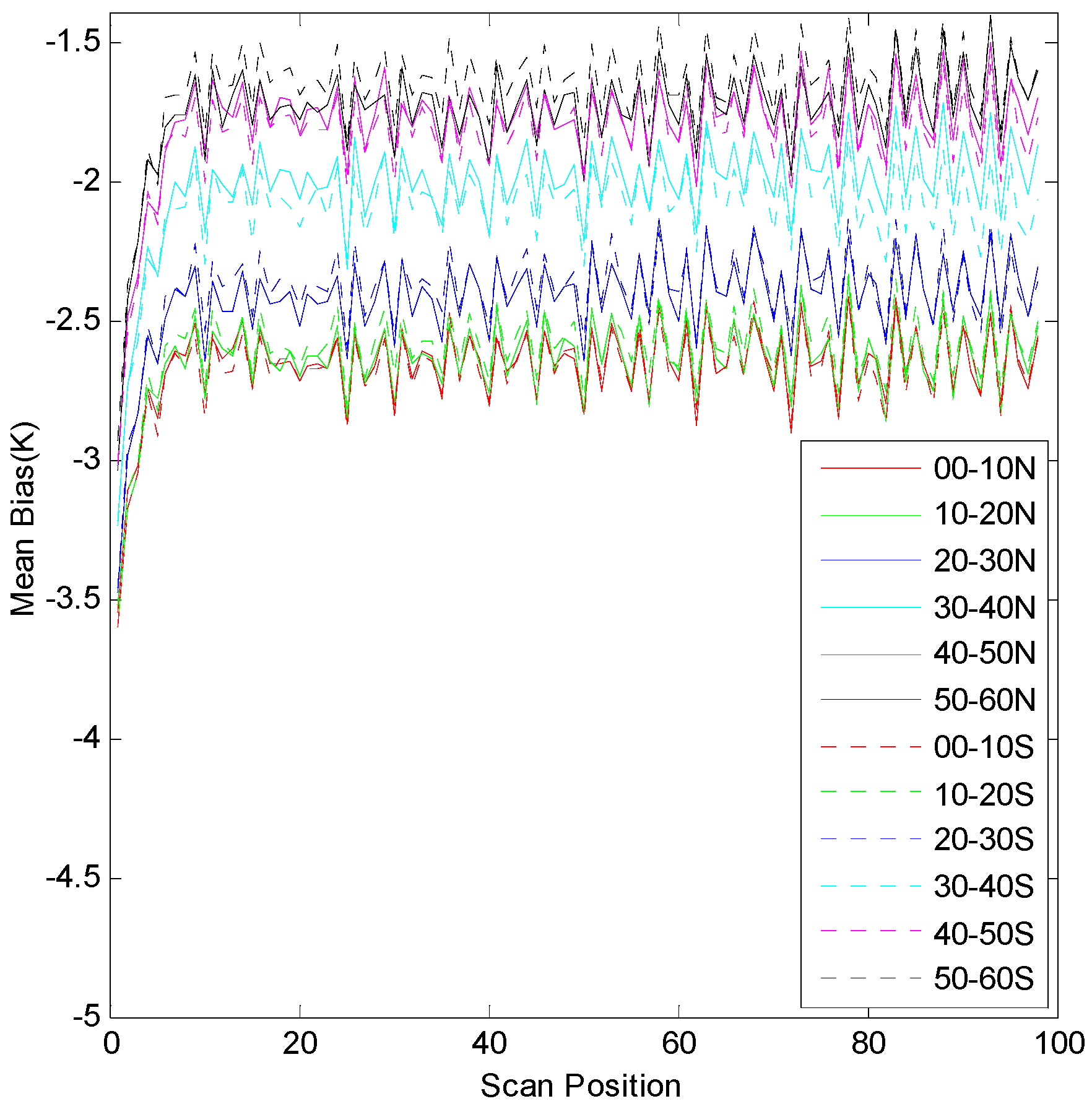
3.2.1. Scan Correction
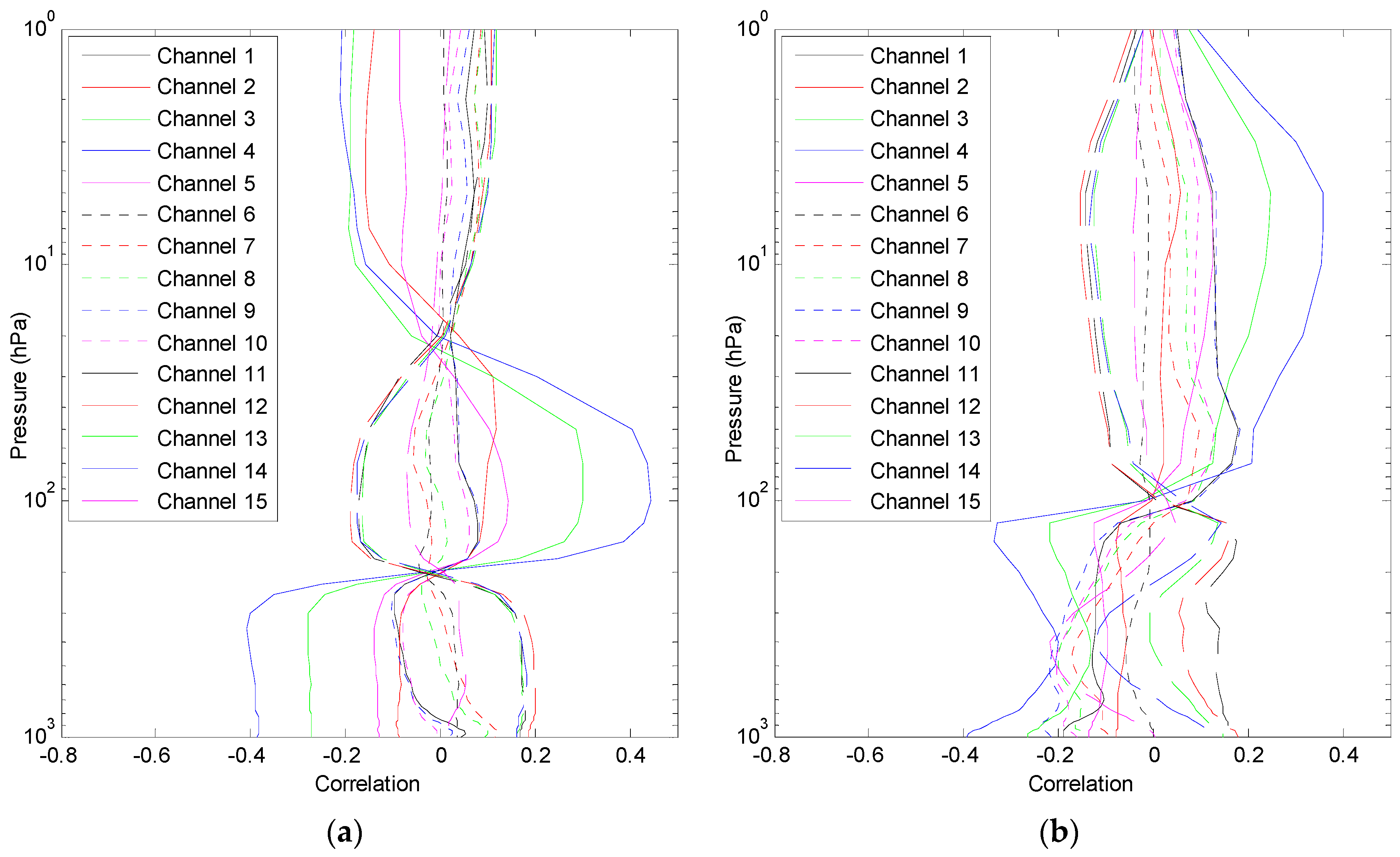
3.2.2. Air-Mass Correction
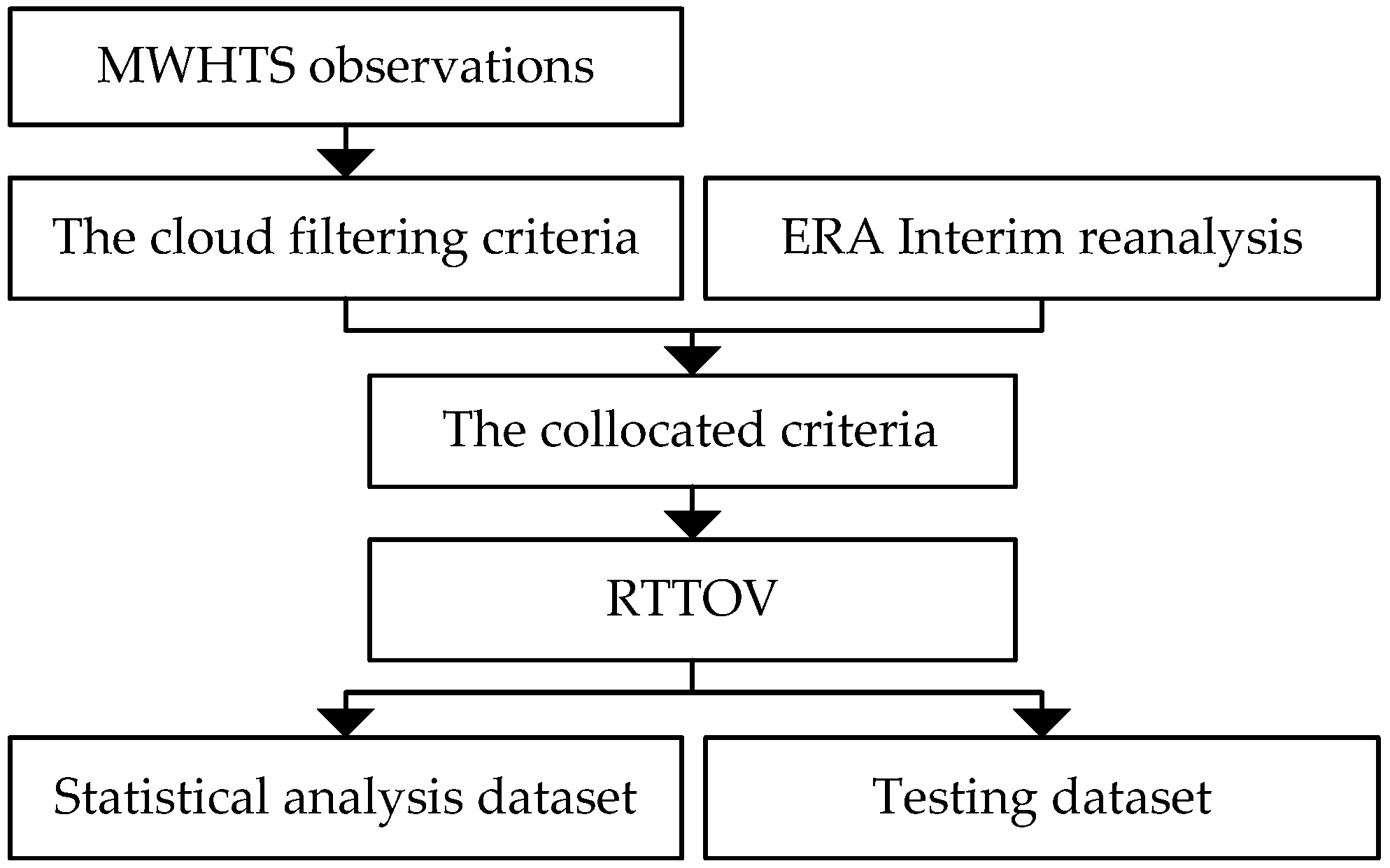
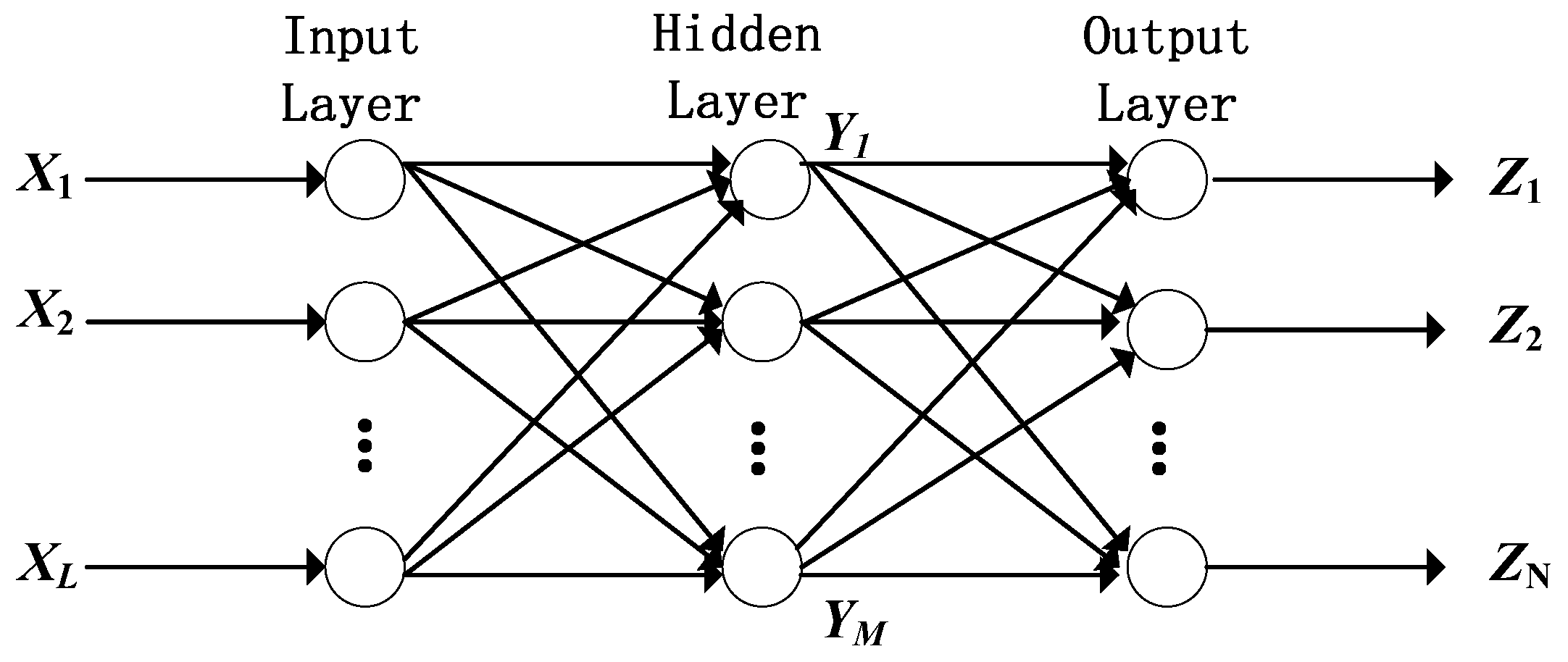
4. Retrieval System for MWHTS
5. Results
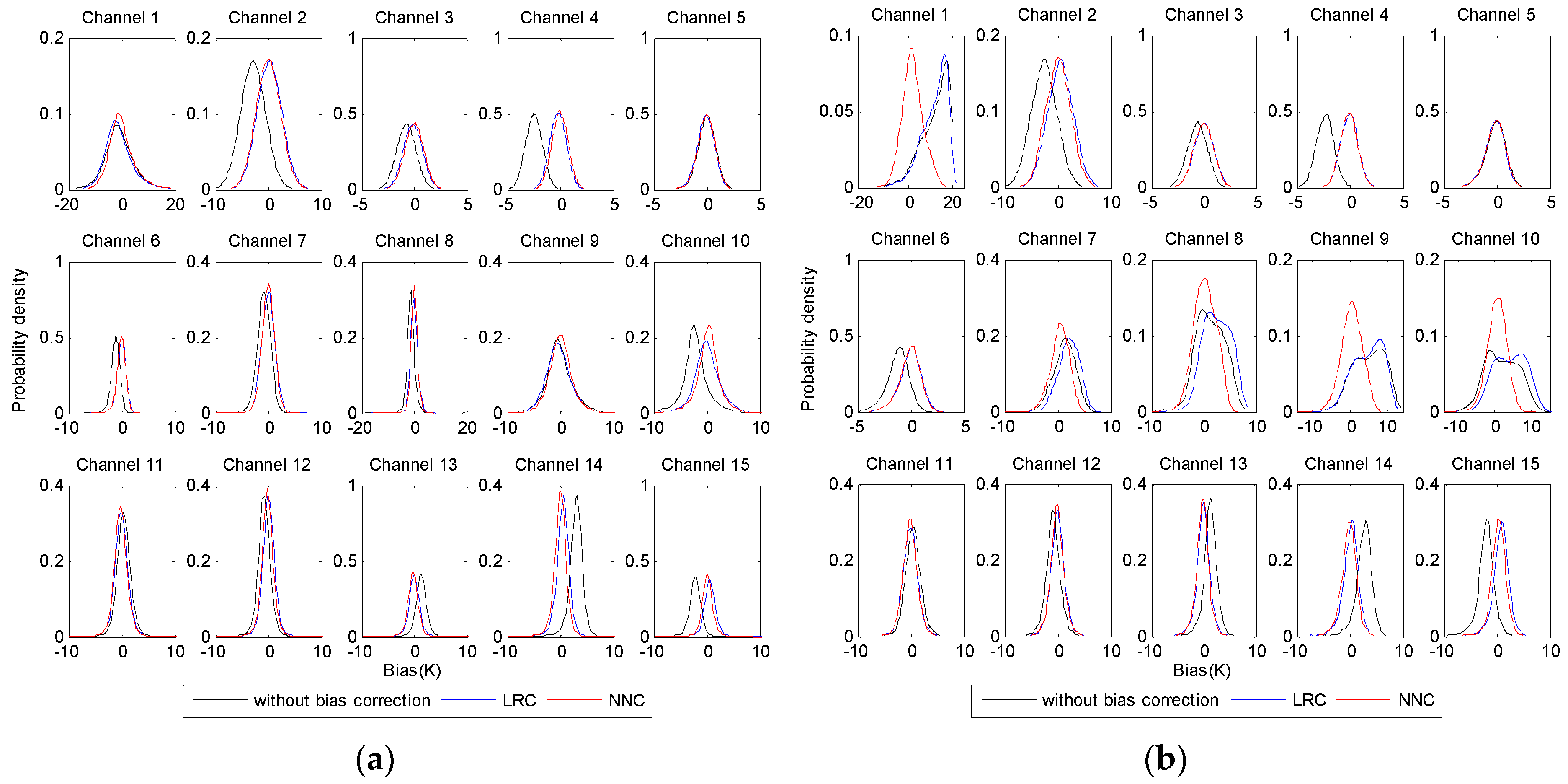
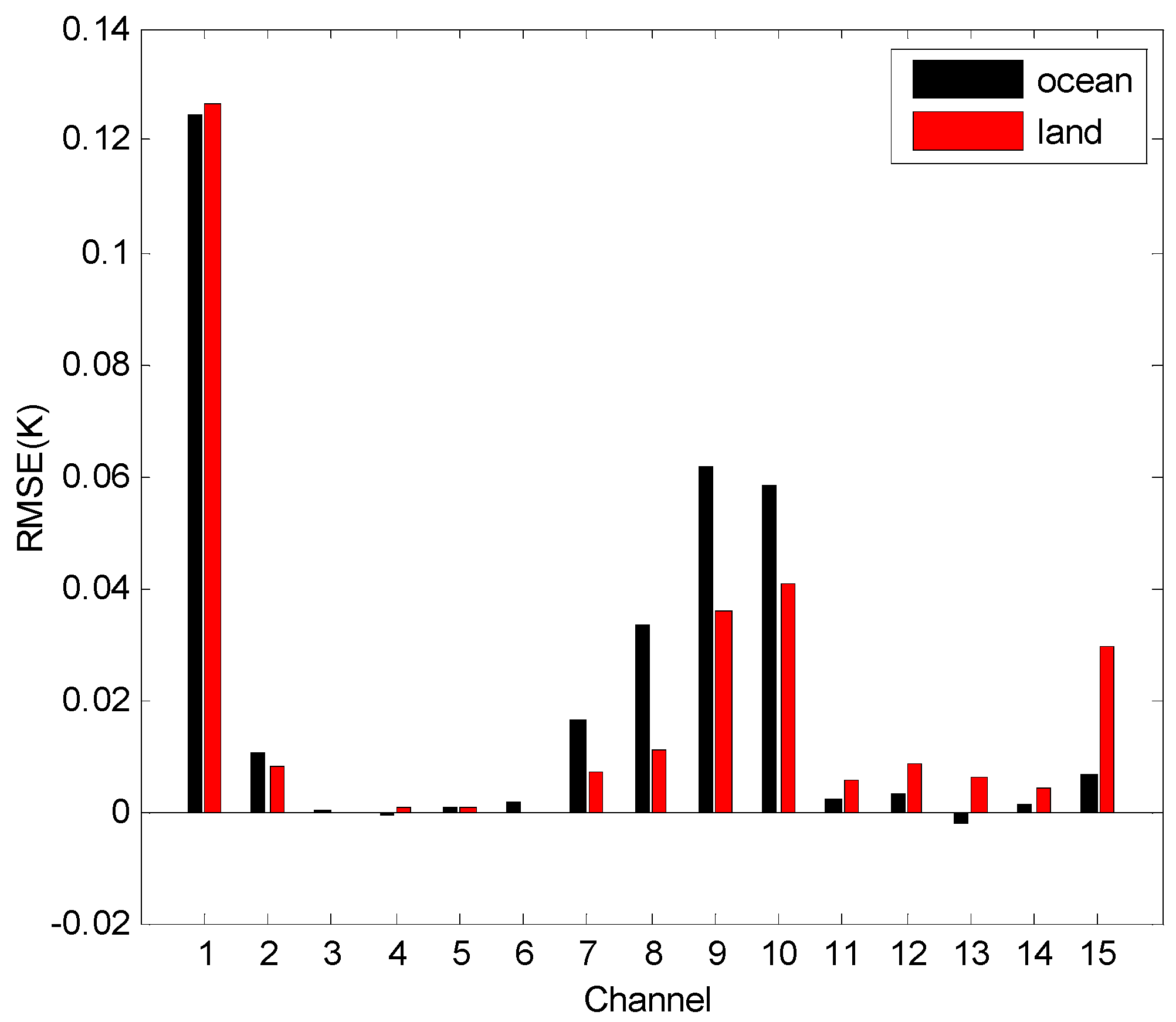
5.1. Bias Correction Results
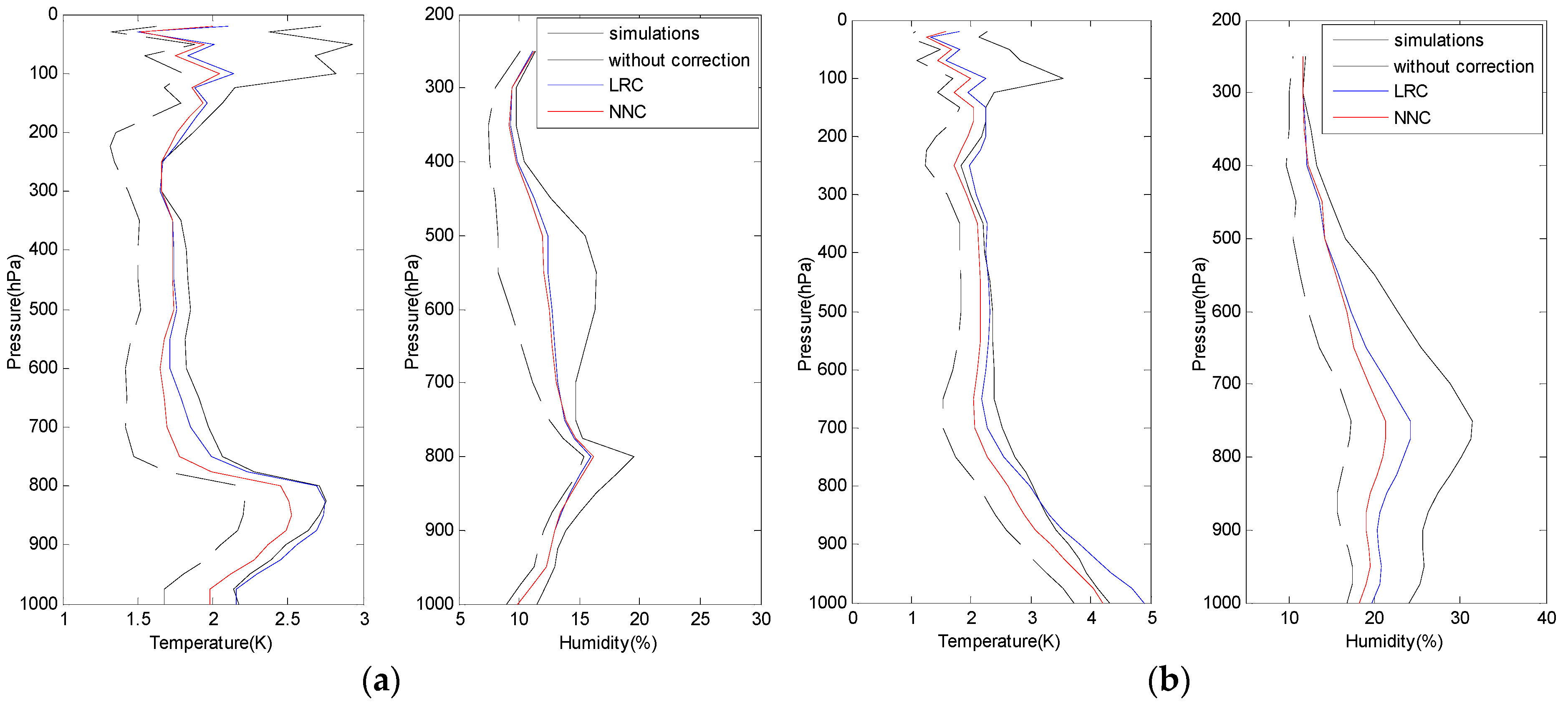
5.2. Results for MWHTS Retrievals
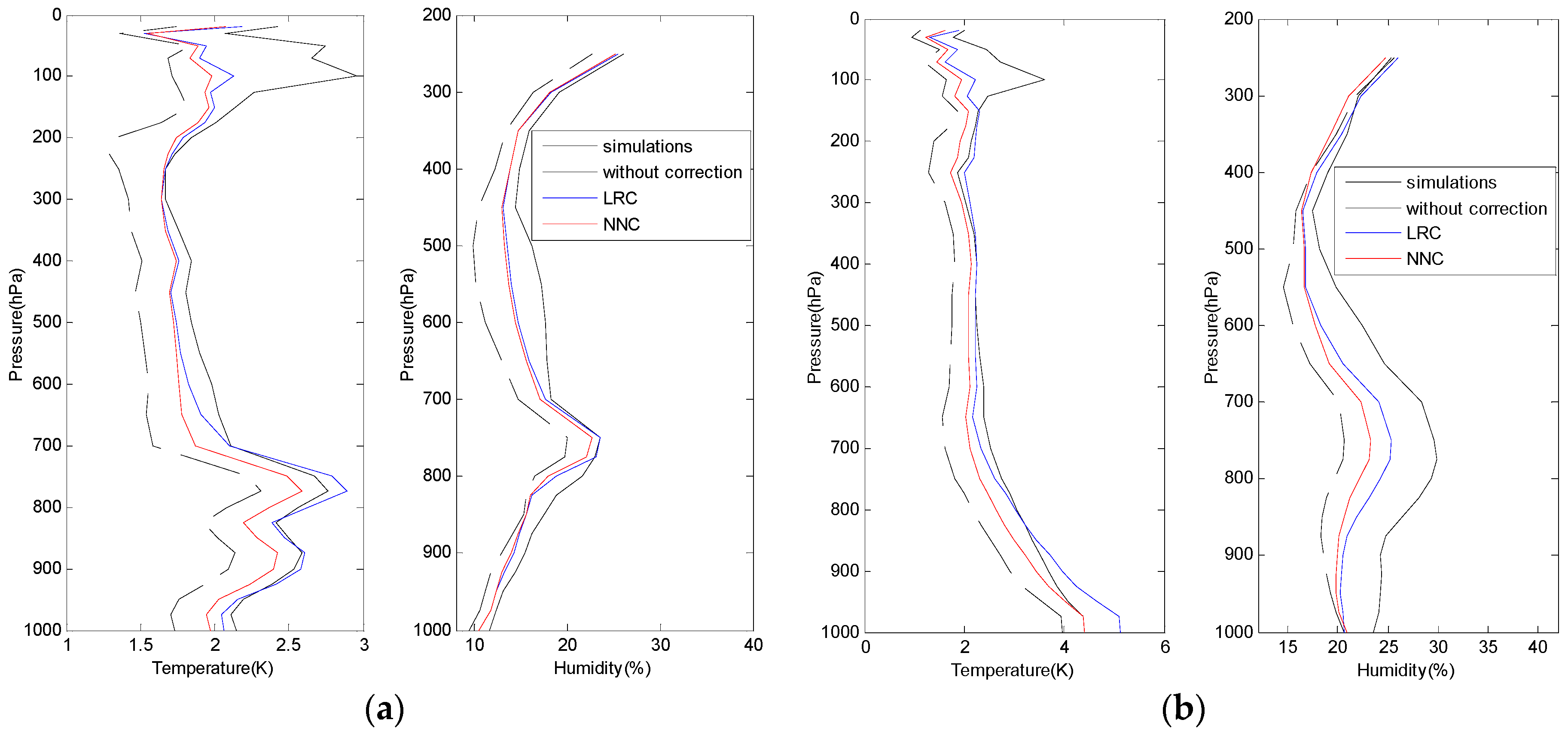
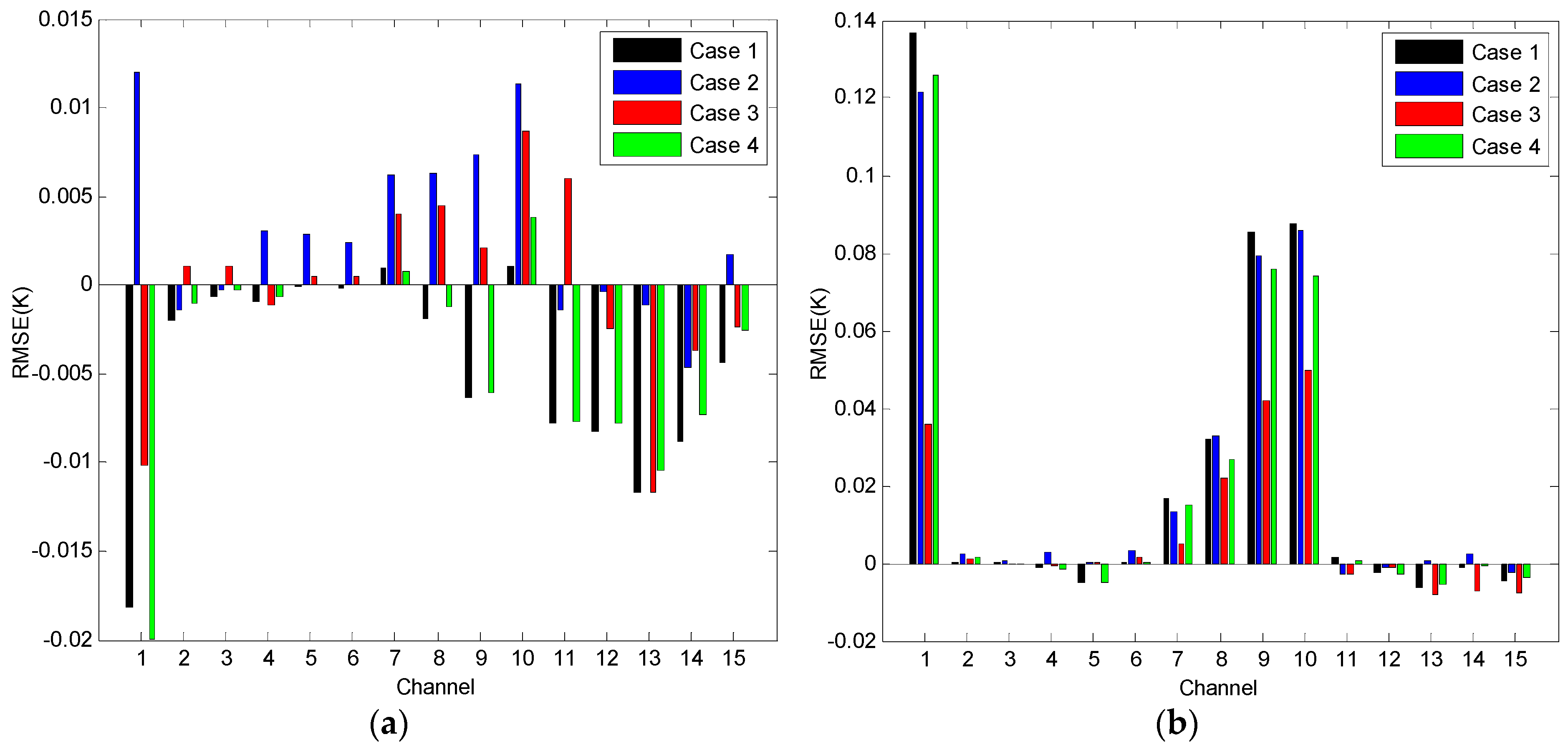
5.3. Evaluation of Algorithm Robustness
5.4. Evaluation of Algorithm Stability
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ebell, K.; Orlandi, E.; Hünerbein, A.; Löhnert, U.; Crewell, S. Combining ground-based with satellite-based measurements in the atmospheric state retrieval: Assessment of the information content. J. Geophys. Res. 2013, 118, 6940–6956. [Google Scholar] [CrossRef]
- Ahn, M.H.; Kim, M.J.; Chung, C.Y.; Suh, A.S. Operational implementation of the ATOVS processing procedure in KMA and its validation. Adv. Atmos. Sci. 2003, 20, 398–414. [Google Scholar] [CrossRef]
- Miao, J.; Kunzi, K.; Heygster, G.; Lachlan-Cope, T.A.; Turner, J. Atmospheric water vapor over Antarctica derived from Special Sensor Microwave/Temperature 2 data. J. Geophys. Res. 2001, 106, 10187–10203. [Google Scholar] [CrossRef]
- Duck, T.J. A microwave satellite water vapor column retrieval for polar winter conditions. Atmos. Meas. Tech. 2016, 9, 2241–2252. [Google Scholar]
- Guo, Y.; Lu, N.M.; Qi, C.L.; Gu, S.Y.; Xu, J.M. Calibration and validation of microwave humidity and temperature sounder onboard FY-3C satellite. Chin. J. Geophys. Chin. 2015, 58, 20–31. [Google Scholar]
- Polyakov, A.; Timofeyev, Y.M.; Virolainen, Y. Comparison of different techniques in atmospheric temperature-humidity sensing from space. Int. J. Remote Sens. 2014, 35, 5899–5912. [Google Scholar]
- Gohil, B.S.; Gairola, R.M.; Mathur, A.K.; Varma, A.K.; Mahesh, C.; Gangwar, R.K.; Pal, P.K. Algorithms for retrieving geophysical parameters from the MADRAS and SAPHIR sensors of the Megha-Tropiques satellite: Indian scenario. Q. J. R. Meteorol. Soc. 2013, 139, 954–963. [Google Scholar] [CrossRef]
- Rao, T.N.; Sunilkumar, K.; Jayaraman, A. Validation of humidity profiles obtained from SAPHIR, on-board Megha-Tropiques. Curr. Sci. India 2013, 104, 1635–1642. [Google Scholar]
- Shi, L. Retrieval of atmospheric temperature profiles from AMSU-A measurements using a neural network approach. J. Atmos. Ocean Technol. 2001, 18, 340–347. [Google Scholar] [CrossRef]
- Chen, H.; Jin, Y.Q. Data validation of Chinese microwave FY-3A for retrieval of atmospheric temperature and humidity profiles during Phoenix typhoon. Int. J. Remote Sens. 2011, 32, 8541–8554. [Google Scholar] [CrossRef]
- Blackwell, W.J.; Chen, F.W. Neural Networks in Atmospheric Remote Sensing; Artech House: Norwood, MA, USA, 2009. [Google Scholar]
- Liu, D.; Lv, C.; Liu, K.; Xie, Y.; Miao, J. Retrieval analysis of atmospheric water vapor for K-band ground-based hyperspectral microwave radiometer. IEEE Trans. Geosci. Remote Sens. 2014, 11, 1835–1839. [Google Scholar]
- Stähli, O.; Murk, A.; Kämpfer, N.; Mätzler, C.; Eriksson, P. Microwave radiometer to retrieve temperature profiles from the surface to the stratopause. Atmos. Meas. Tech. 2013, 6, 2477–2494. [Google Scholar] [CrossRef]
- Bleisch, R.; Kämpfer, N.; Haefele, A. Retrieval of troposphere water vapor by using spectra of a 22 GHz radiometer. Atmos. Meas. Tech. 2011, 4, 1891–1903. [Google Scholar] [CrossRef]
- Weng, F.; Zou, X.; Wang, X.; Yang, S.; Goldberg, M.D. Introduction to Suomi national polar-orbiting partnership advanced technology microwave sounder for numerical weather prediction and tropical cyclone applications. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Dee, D.P. Bias and data assimilation. Q. J. R. Meteorol. Soc. 2005, 131, 3323–3343. [Google Scholar] [CrossRef]
- Auligné, T.; McNally, A.P.; Dee, D.P. Adaptive bias correction for satellite data in a numerical weather prediction system. Q. J. R. Meteorol. Soc. 2007, 133, 631–642. [Google Scholar] [CrossRef]
- Susskind, J.; Rosenfield, J.; Reuter, D. An accurate radiative transfer model for use in the direct physical inversion of HIRS2 and MSU temperature sounding data. J. Geophys. Res. 1983, 88, 8550–8568. [Google Scholar] [CrossRef]
- Smith, W.L.; Woolf, H.M.; Hayden, C.M.; Schreiner, A.J. The physical retrieval TOVS Export Package. In Proceedings of the Technical Proceedings of the First TOVS Study Conference, Igls, Austria, 29 August–2 September 1983.
- Weng, F.; Zhao, L.; Ferraro, R.R.; Poe, G.; Li, X.; Grody, N.C. Advanced microwave sounding unit cloud and precipitation algorithms. Radio Sci. 2003, 38. [Google Scholar] [CrossRef]
- Li, J.; Wolf, W.W.; Menzel, W.P.; Zhang, W.; Huang, H.L.; Achtor, T.H. Global soundings of the atmosphere from ATOVS measurements: The algorithm and validation. J. Appl. Meteorol. 2000, 39, 1248–1268. [Google Scholar] [CrossRef]
- Kelly, G.A.; Flobert, J.F. Radiance tuning. In Proceedings of the Technical Proceedings of the Fourth TOVS Study Conference, Igls, Austria, 16–22 March 1988.
- McMillin, L.M.; Crone, L.J.; Crosby, D.S. Adjusting satellite radiances by regression with an orthogonal transformation to a prior estimate. J. Appl. Meteorol. 1989, 28, 969–975. [Google Scholar] [CrossRef]
- Uddstrom, M. Forward model errors. In Proceedings of the Technical Proceedings of the Sixth TOVS Study Conference, Airlie, VA, USA, 1–6 May 1991.
- Harris, B.A.; Kelly, G. A satellite radiance-bias correction scheme for data assimilation. Q. J. R. Meteorol. Soc. 2001, 127, 1453–1468. [Google Scholar] [CrossRef]
- Dee, D.P. Variational bias correction of radiance data in the ECMWF system. In Proceedings of the Workshop on Assimilation of High Spectral Resolution Sounders in NWP, Reading, UK, 28 June–1 July 2004.
- Dee, D.P.; Uppala, S. Variational bias correction of satellite radiance data in the ERA-Interim reanalysis. Q. J. R. Meteorol. Soc. 2009, 135, 1830–1841. [Google Scholar] [CrossRef]
- Wu, C.Q.; Ma, G.; Qi, C.L.; Guo, Y.; You, R. Retrieval of Atmospheric and Surface Parameters from VASS/FY-3C Data under Non-Precipitation Condition; SPIE Asia Pacific Remote Sensing; International Society for Optics and Photonics: Beijing, China, 2014. [Google Scholar]
- Liebe, H.J.; Hufford, G.A.; Cotton, M.G. Propagation modeling of moist air and suspended water/ice particles at frequencies below 1000 GHz. In Proceedings of the AGARD 52nd Specialists Meeting of Electromagnetic Wave Propagation Panel, Palma De Mallorca, Spain, 17–21 May 1993.
- Karbou, F.; Aires, F.; Prigent, C.; Eymard, L. Potential of Advanced Microwave Sounding Unit-A (AMSU-A) and AMSU-B measurements for atmospheric temperature and humidity profiling over land. J. Geophys. Res. 2005, 110, D07109. [Google Scholar] [CrossRef]
- Lawrence, H.; Bormann, N.; Lu, Q.; Geer, A.; English, S. An Evaluation of FY-3C MWHTS-2 at ECMWF; EUMETSAT/ECMWF Fellowship Programme Research Report, 37; ECMWF: Reading, UK, 2015. [Google Scholar]
- Zou, X.; Wang, X.; Weng, F.; Li, G. Assessments of Chinese Fengyun Microwave Temperature Sounder (MWTS) measurements for weather and climate applications. J. Atmos. Ocean. Technol. 2011, 28, 1206–1227. [Google Scholar] [CrossRef]
- Sivira, R.; Brogniez, H.; Mallet, C.; Oussar, Y. A layer-averaged relative humidity profile retrieval for microwave observations: Design and results for the Megha-Tropiques payload. Atmos. Meas. Tech. 2015, 8, 1055–1071. [Google Scholar] [CrossRef]
- Saunders, R.; Hocking, J.; Rundle, D.; Rayer, P.; Matricardi, M.; Geer, A.; Lupu, C.; Brunel, P.; Vidot, J. RTTOV-11 Science and Validation Report; NWP-SAF Report; Met Office: Exeter, UK, 2013; pp. 1–62.
- Aires, F.; Prigent, C.; Bernardo, F.; Jiménez, C.; Saunders, R.; Brunel, P. A Tool to Estimate Land-Surface Emissivities at Microwave frequencies (TELSEM) for use in numerical weather prediction. Q. J. R. Meteorol. Soc. 2011, 137, 690–699. [Google Scholar] [CrossRef]
- Berrisford, P.; Dee, D.; Poli, P.; Brugge, R.; Fielding, K.; Fuentes, M.; Kallberg, P.; Kobayashi, S.; Uppala, S.; Simmons, A. The ERA-Interim Archive Version 2.0; ERA Report Series 1; European Centre for Medium-Range Weather Forecasts (ECMWF): Reading, UK, 2011. [Google Scholar]
- Buehler, S.A.; Kuvatov, M.; Sreerekha, T.R.; John, V.O.; Rydberg, B.; Eriksson, P.; Notholt, J. A cloud filtering method for microwave upper tropospheric humidity measurements. Atmos. Chem. Phys. 2007, 7, 5531–5542. [Google Scholar] [CrossRef]
- Burns, B.A.; Wu, X.; Diak, G.R. Effects of precipitation and cloud ice on brightness temperatures in AMSU moisture channels. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1429–1437. [Google Scholar] [CrossRef]
- Greenwald, T.J.; Christopher, S.A. Effects of clod clouds on satellite measurements near 183 GHz. J. Geophys. Res. 2002, 107, 4170. [Google Scholar] [CrossRef]
- Hong, G.; Heygster, G.; Miao, J.; Kunzi, K. Detection of tropical deep convective clouds from AMSU-B water vapor channels measurements. J. Geophys. Res. 2005, 110, D05205. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Internal Representations by Error Propagation; Technical Report, DTIC Doument; MIT Press: Cambridge, MA, USA, 1985. [Google Scholar]
- Yao, Z.G.; Chen, H.B.; Lin, L.F. Retrieving atmospheric temperature profiles from AMSU-A data with neural networks. Adv. Atmos. Sci. 2005, 22, 606–616. [Google Scholar]
- Liu, Q.; Weng, F. One-dimensional variational retrieval algorithm of temperature, water vapor, and cloud water profiles from advanced microwave sounding unit (AMSU). IEEE Trans. Geosci. Remote Sens. 2005, 43, 1087–1095. [Google Scholar]
- Boukabara, S.A.; Garrett, K.; Chen, W.; Iturbide-Sanchez, F.; Grassotti, C.; Kongoli, C.; Chen, R.; Liu, Q.; Yan, B.; Weng, F.; et al. MiRS: An all-weather 1DVAR satellite data assimilation and retrieval system. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3249–3272. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.T.; Chuang, H.Y.; Iredell, M.; et al. The NCEP climate forecast system version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- English, S.J. Estimation of temperature and humidity profile information from microwave radiances over different surface types. J. Appl. Meteorol. 1999, 38, 1526–1541. [Google Scholar] [CrossRef]
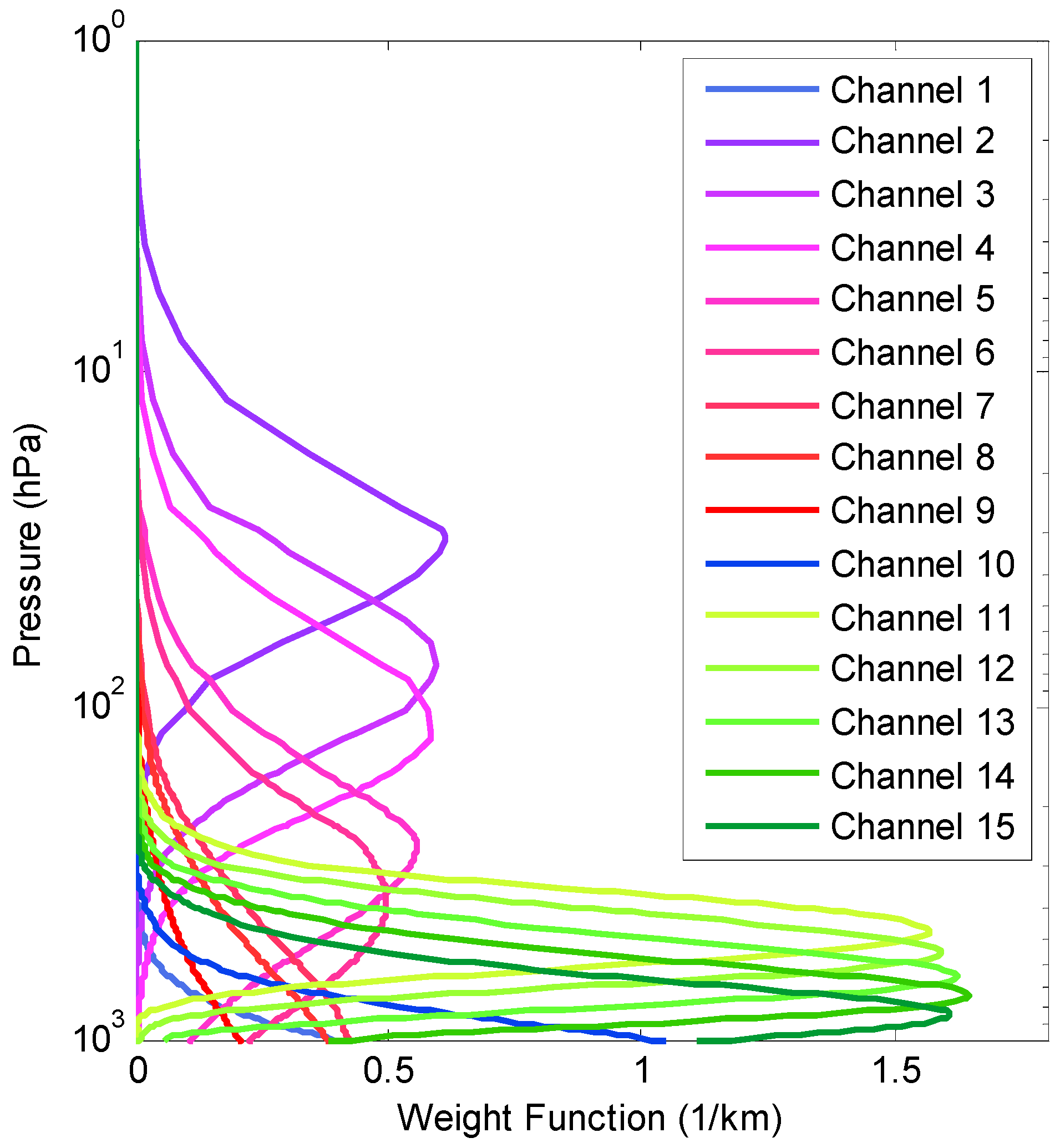


| Channel | Frequency (GHz) | Polarization Angle | Bandwidth (MHz) | Peak WF (hPa) | In-Flight Sensitivity (K) |
|---|---|---|---|---|---|
| 1 | 89 | 1500 | Window | 0.23 | |
| 2 | 118.75 ± 0.08 | 20 | 30 | 1.62 | |
| 3 | 118.75 ± 0.2 | 100 | 50 | 0.75 | |
| 4 | 118.75 ± 0.3 | 165 | 100 | 0.59 | |
| 5 | 118.75 ± 0.8 | 200 | 250 | 0.65 | |
| 6 | 118.75 ± 1.1 | 200 | 350 | 0.52 | |
| 7 | 118.75 ± 2.5 | 200 | Surface | 0.49 | |
| 8 | 118.75 ± 3.0 | 1000 | Surface | 0.27 | |
| 9 | 118.75 ± 5.0 | 2000 | Surface | 0.27 | |
| 10 | 150 | 1500 | Window | 0.34 | |
| 11 | 183.31 ± 1 | 500 | 300 | 0.47 | |
| 12 | 183.31 ± 1.8 | 700 | 400 | 0.34 | |
| 13 | 183.31 ± 3 | 1000 | 500 | 0.3 | |
| 14 | 183.31 ± 4.5 | 2000 | 700 | 0.22 | |
| 15 | 183.31 ± 7 | 2000 | 800 | 0.27 |
| Channel | Site Calibration Test | Cross Comparison | O-B | ||
|---|---|---|---|---|---|
| Mean Error (K) | Mean Deviation (K) | Standard Deviation (K) | Mean Deviation (K) | Standard Deviation (K) | |
| 1 | −1.18 | 2.08 | 1.26 | −2.97 | 4.03 |
| 2 | −0.6 | - | - | −0.93 | 0.43 |
| 3 | −0.71 | - | - | −0.02 | 0.23 |
| 4 | −1.21 | - | - | −1.98 | 0.29 |
| 5 | −1.19 | - | - | 0.28 | 0.27 |
| 6 | −1.25 | - | - | −0.34 | 0.48 |
| 7 | 0.01 | - | - | 0.78 | 1.8 |
| 8 | 0.01 | - | - | 0.8 | 2.26 |
| 9 | 0.89 | - | - | 3.94 | 3.6 |
| 10 | −0.45 | 8.14 | 4.31 | −4.32 | 3.06 |
| 11 | −0.89 | 0.27 | 0.95 | 3.97 | 1.36 |
| 12 | −1.15 | 0.85 | 0.82 | 1.74 | 1.47 |
| 13 | 0.78 | −2.2 | 0.86 | 3.03 | 1.7 |
| 14 | 3.23 | −3.94 | 0.95 | 3.18 | 2.08 |
| 15 | −1.7 | 0.71 | 0.94 | −1.21 | 2.39 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Q.; Wang, Z.; He, J. Bias Correction for Retrieval of Atmospheric Parameters from the Microwave Humidity and Temperature Sounder Onboard the Fengyun-3C Satellite. Atmosphere 2016, 7, 156. https://doi.org/10.3390/atmos7120156
He Q, Wang Z, He J. Bias Correction for Retrieval of Atmospheric Parameters from the Microwave Humidity and Temperature Sounder Onboard the Fengyun-3C Satellite. Atmosphere. 2016; 7(12):156. https://doi.org/10.3390/atmos7120156
Chicago/Turabian StyleHe, Qiurui, Zhenzhan Wang, and Jieying He. 2016. "Bias Correction for Retrieval of Atmospheric Parameters from the Microwave Humidity and Temperature Sounder Onboard the Fengyun-3C Satellite" Atmosphere 7, no. 12: 156. https://doi.org/10.3390/atmos7120156
APA StyleHe, Q., Wang, Z., & He, J. (2016). Bias Correction for Retrieval of Atmospheric Parameters from the Microwave Humidity and Temperature Sounder Onboard the Fengyun-3C Satellite. Atmosphere, 7(12), 156. https://doi.org/10.3390/atmos7120156






