Inverse Modeling of Nitrogen Oxides Emissions from the 2010 Russian Wildfires by Using Satellite Measurements of Nitrogen Dioxide
Abstract
:1. Introduction
2. Data and Method
2.1. Input Data
2.1.1. Satellite Data
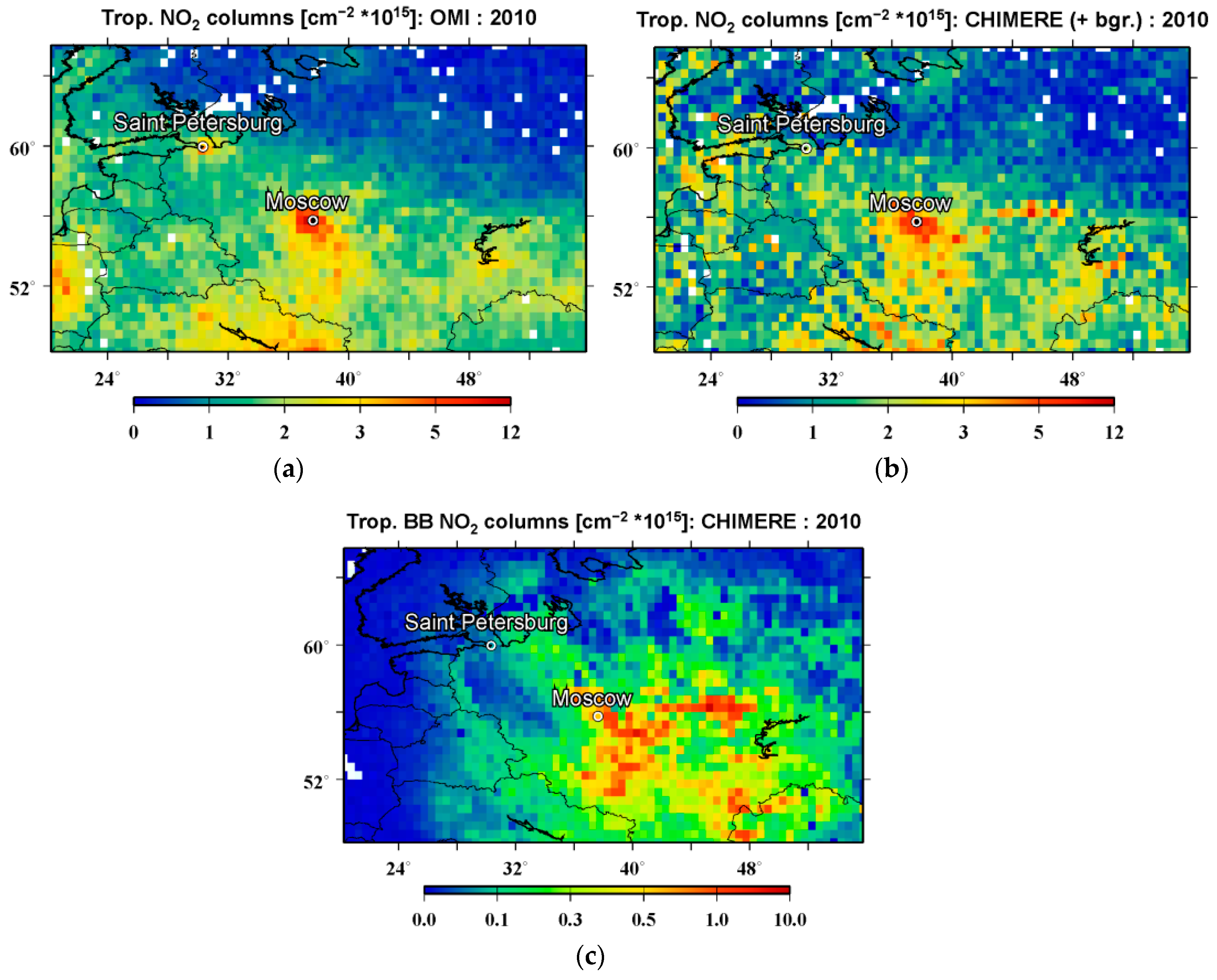
2.1.2. Simulation Data
2.2. Method
3. Results
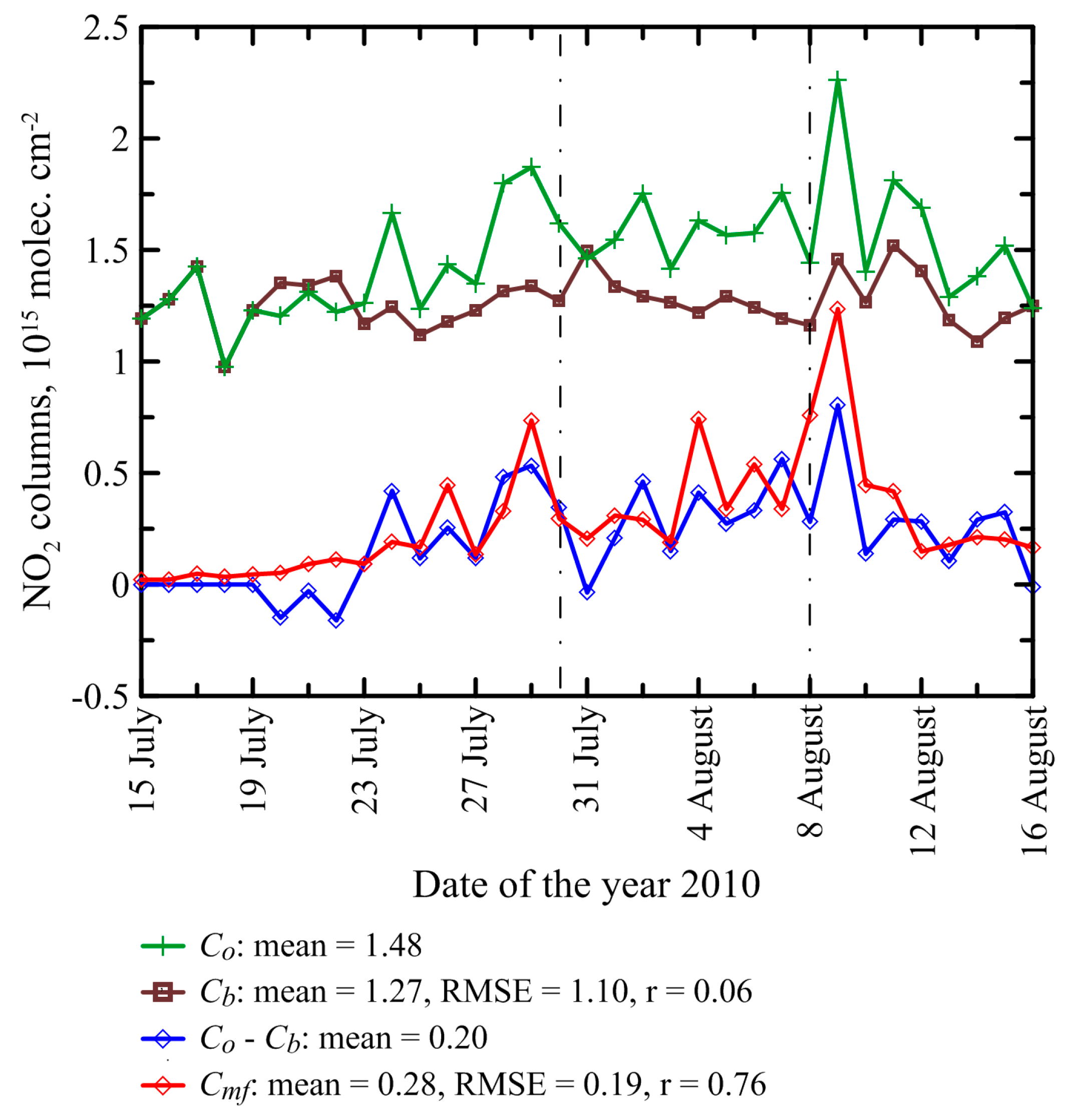
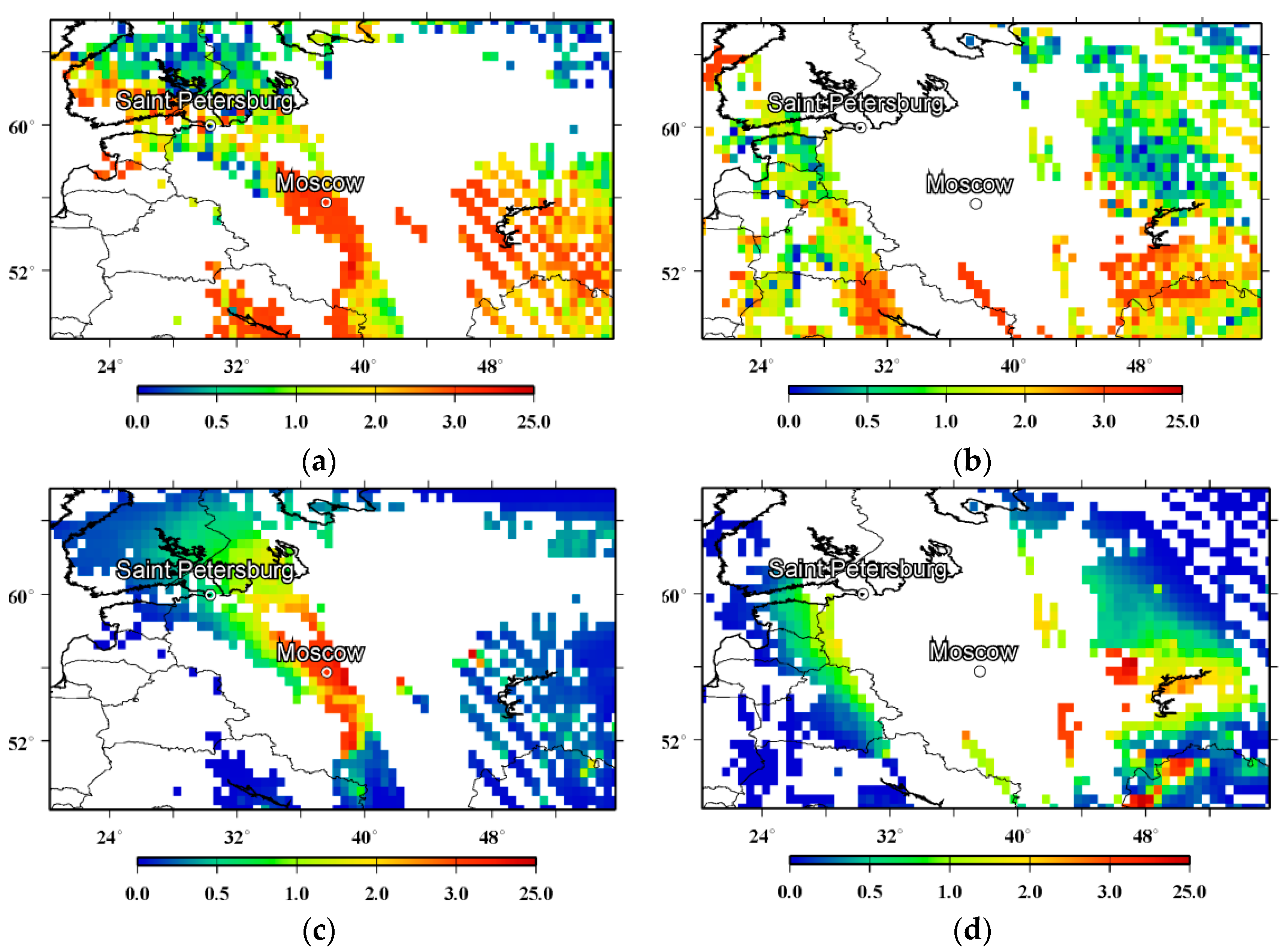
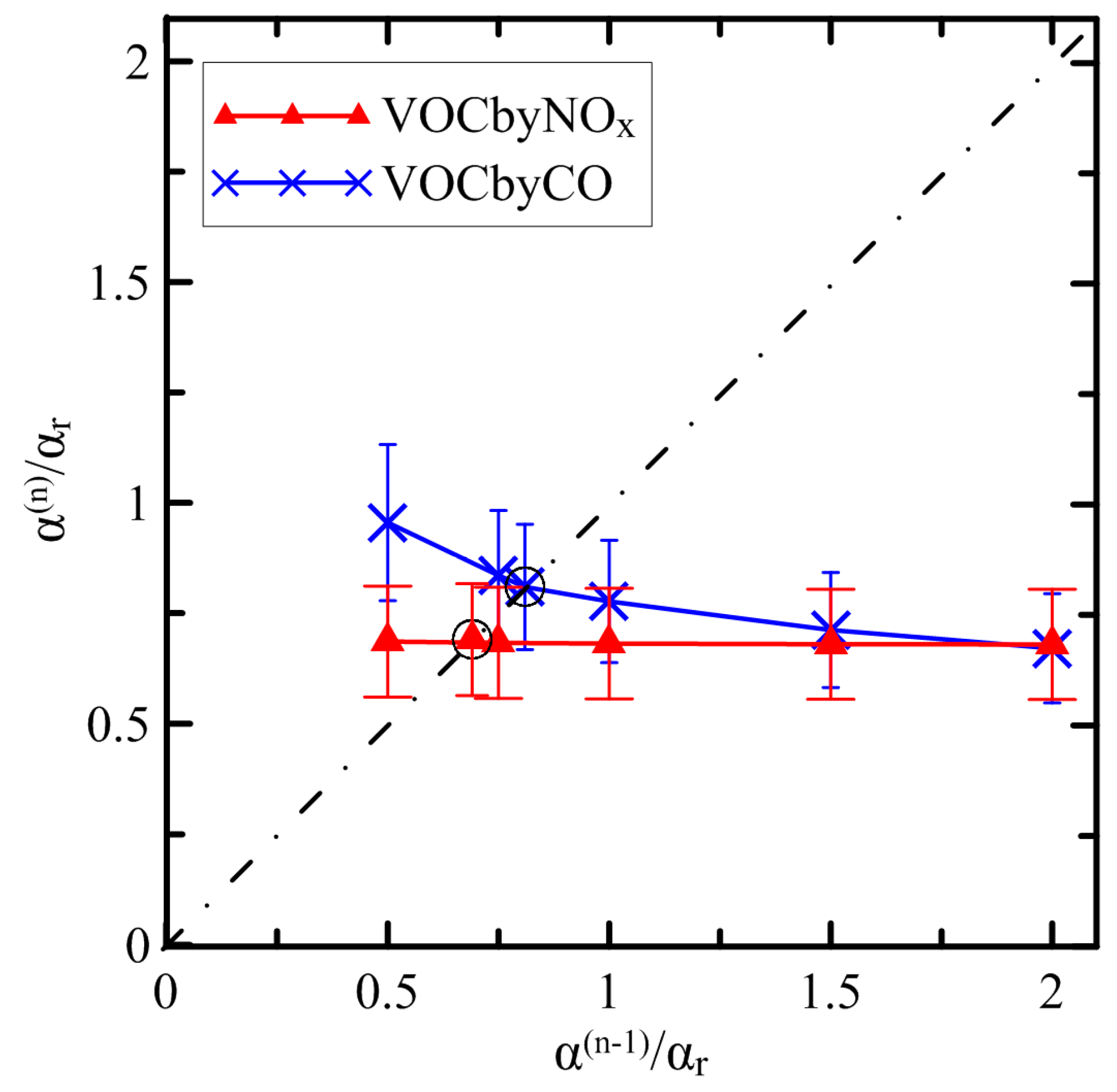
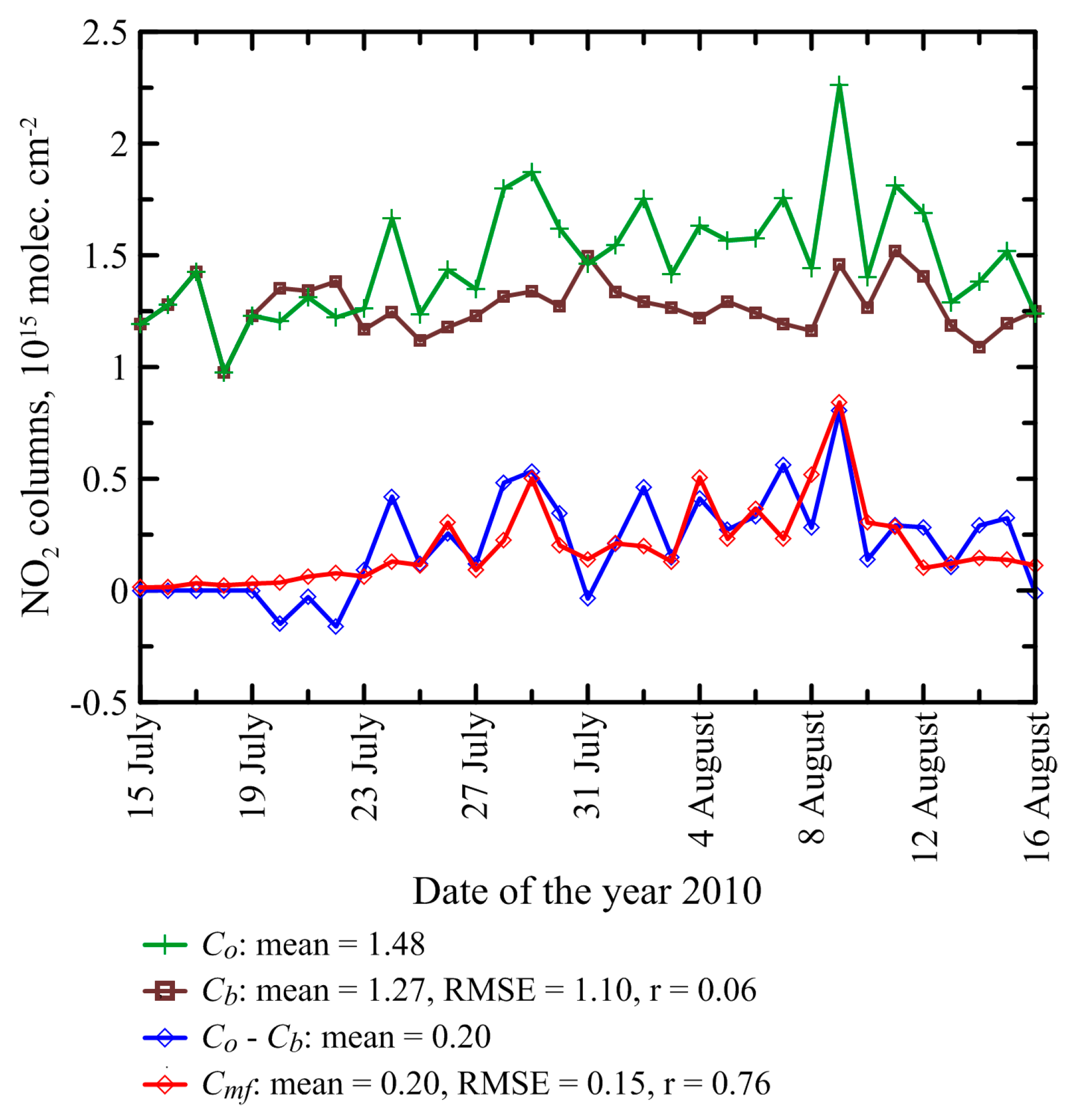
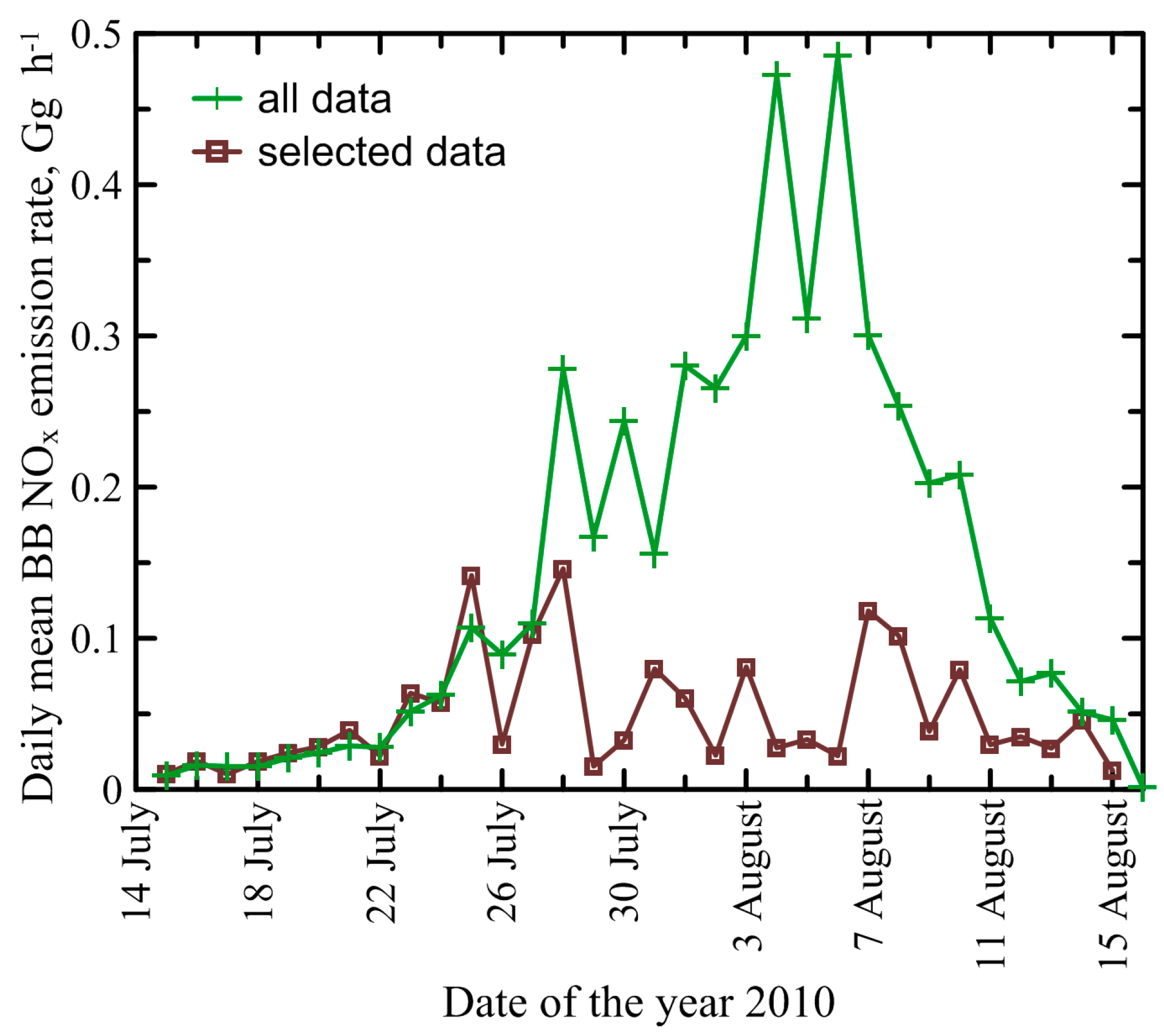
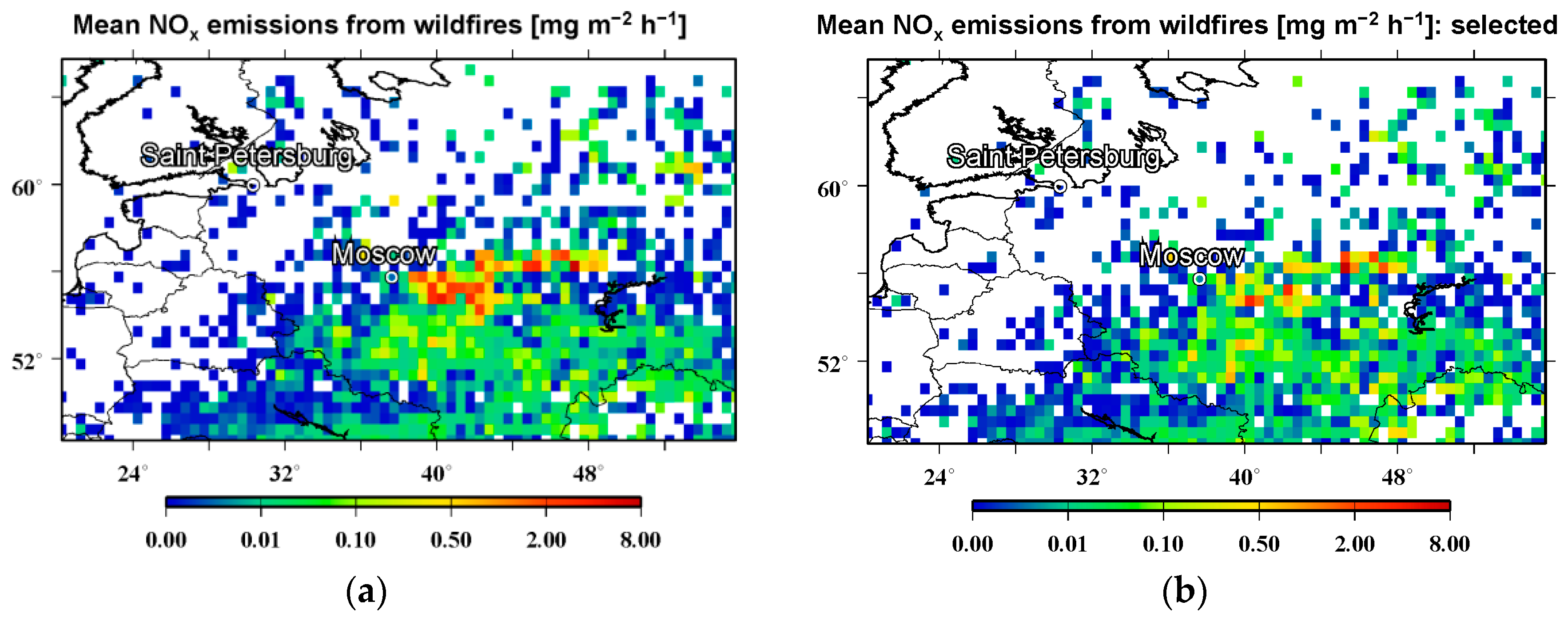
3.1. Estimation of the FRP-to-BBR Conversion Factor
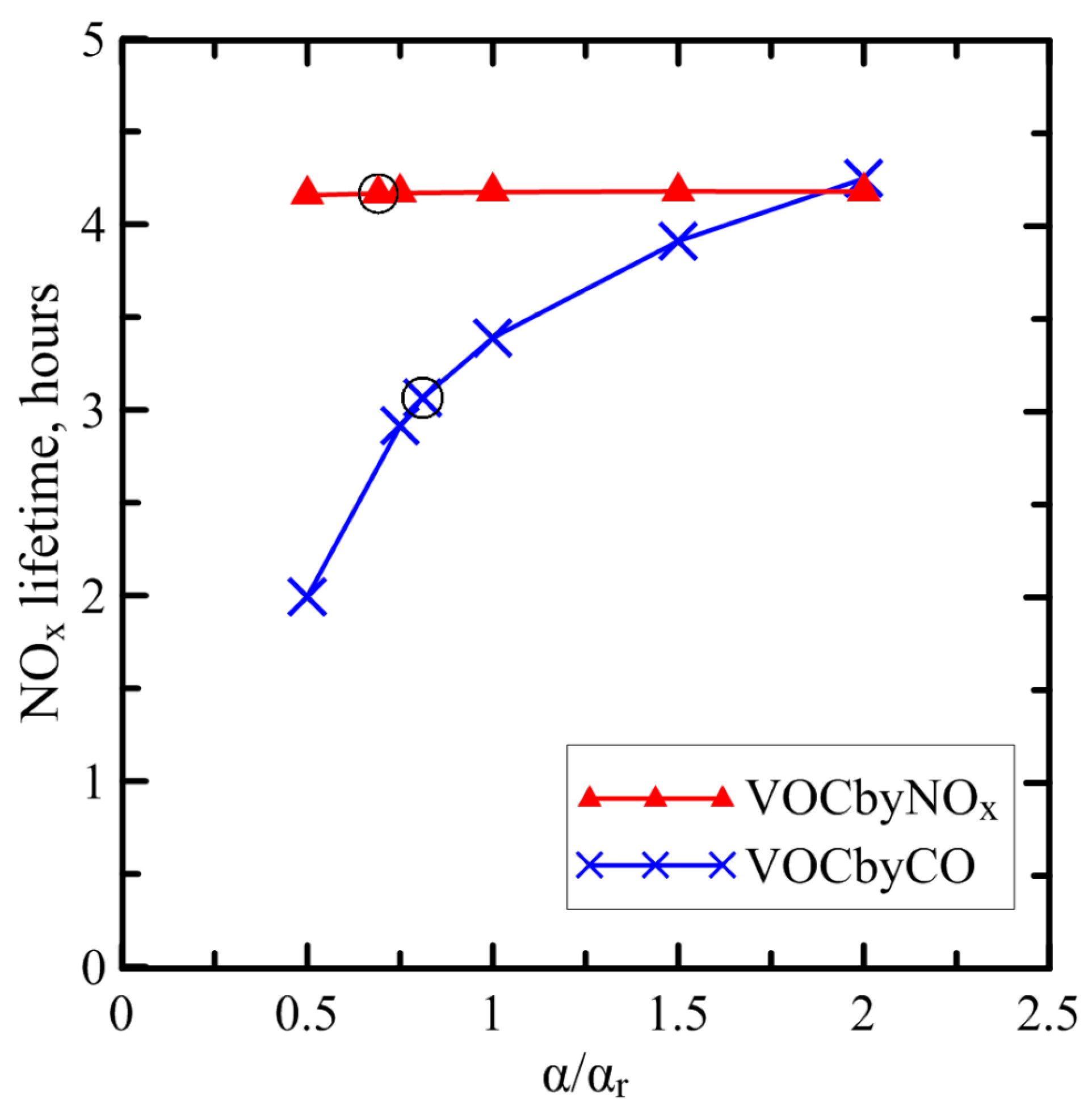
3.2. NOx Lifetime Estimates
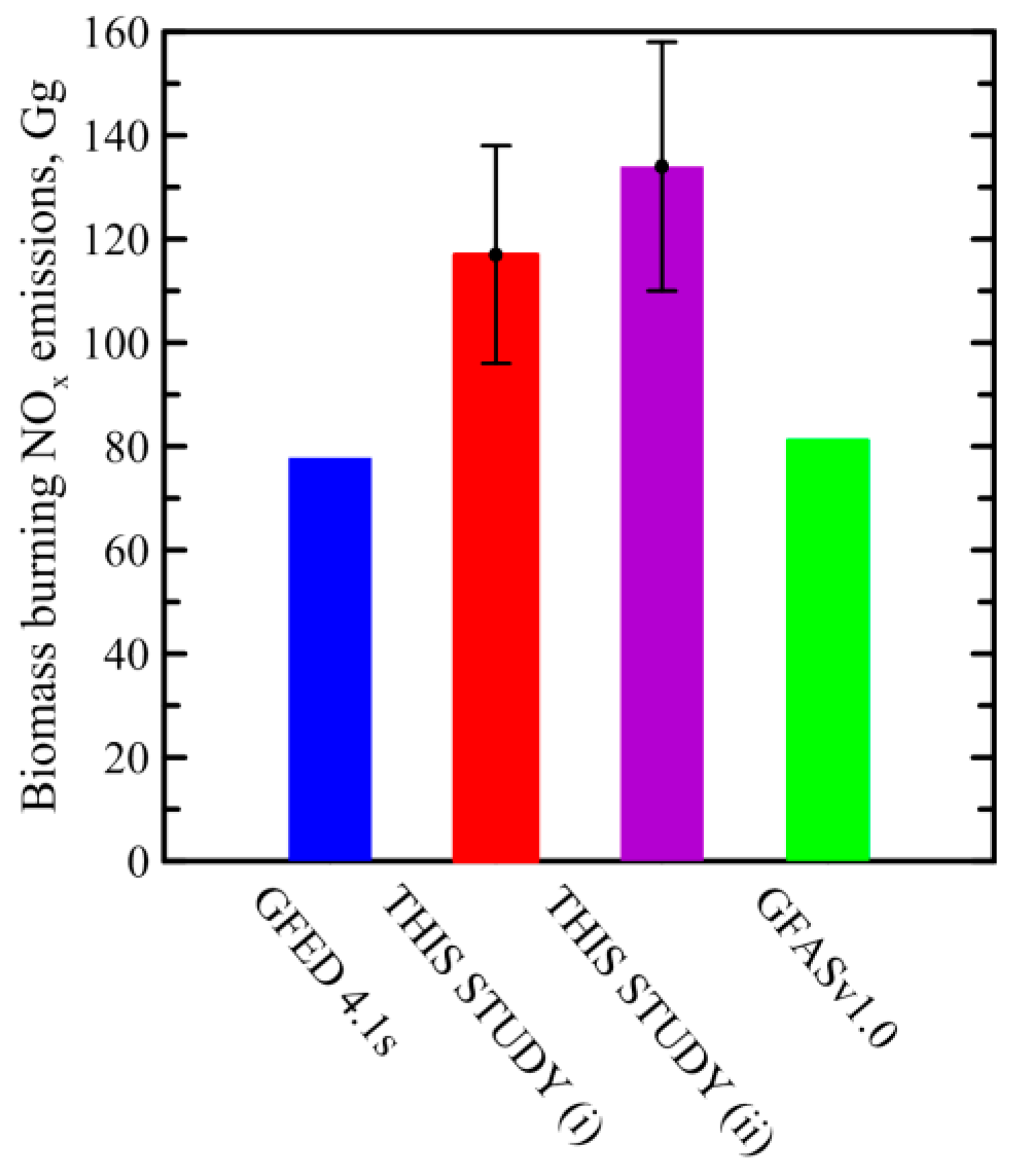
3.3. NOx Emission Estimates
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Seinfeld, J.H.; Pandis, S.N. Chemistry of the troposphere. In Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2006; pp. 204–230. [Google Scholar]
- Monks, P.S. Gas-phase radical chemistry in the troposphere. Chem. Soc. Rev. 2005, 34, 376–395. [Google Scholar] [CrossRef] [PubMed]
- Konovalov, I.B. Nonlinear relationships between atmospheric aerosol and its gaseous precursors: Analysis of long-term air quality monitoring data by means of neural networks. Atmos. Chem. Phys. 2003, 3, 607–621. [Google Scholar] [CrossRef]
- Ng, N.L.; Chhabra, P.S.; Chan, A.W.H.; Surratt, J.D.; Kroll, J.H.; Kwan, A.J.; McCabe, D.C.; Wennberg, P.O.; Sorooshian, A.; Murphy, S.M.; et al. Effect of NOx level on secondary organic aerosol (SOA) formation from the photooxidation of terpenes. Atmos. Chem. Phys. 2007, 7, 5159–5174. [Google Scholar] [CrossRef]
- Jaeglé, L.; Steinberger, L.; Martin, R.V.; Chance, K. Global partitioning of NOx sources using satellite observations: Relative roles of fossil fuel combustion, biomass burning and soil emissions. Faraday Discuss. 2005, 130, 407–423. [Google Scholar] [CrossRef] [PubMed]
- Jaffe, D.A.; Wigder, N.L. Ozone production from wildfires: A critical review. Atmos. Environ. 2012, 51, 1–10. [Google Scholar] [CrossRef]
- Mebust, A.K.; Russell, A.R.; Hudman, R.C.; Valin, L.C.; Cohen, R.C. Characterization of wildfire NOx emissions using MODIS fire radiative power and OMI tropospheric NO2 columns. Atmos. Chem. Phys. 2012, 11, 5839–5851. [Google Scholar] [CrossRef]
- Randerson, J.T.; van der Werf, G.R.; Giglio, L.; Collatz, G.J.; Kasibhatla, P.S. Global Fire Emissions Database; Version 4, (GFEDv4); ORNL DAAC: Oak Ridge, TN, USA, 2015. [Google Scholar]
- Kaiser, J.W.; Heil, A.; Andreae, M.O.; Benedetti, A.; Chubarova, N.; Jones, L.; Morcrette, J.-J.; Razinger, M.; Schultz, M.G.; Suttie, M.; et al. Biomass burning emissions estimated with a global fire assimilation system based on observed fire radiative power. Biogeosciences 2012, 9, 527–554. [Google Scholar] [CrossRef]
- Akagi, S.K.; Yokelson, R.J.; Wiedinmyer, C.; Alvarado, M.J.; Reid, J.S.; Karl, T.; Crounse, J.D.; Wennberg, P.O. Emission factors for open and domestic biomass burning for use in atmospheric models. Atmos. Chem. Phys. 2011, 11, 4039–4072. [Google Scholar] [CrossRef]
- Mebust, A.K.; Cohen, R.C. Space-based observations of fire NOx emission coefficients: A global biome-scale comparison. Atmos. Chem. Phys. 2014, 14, 2509–2524. [Google Scholar] [CrossRef]
- Schreier, S.F.; Richter, A.; Kaiser, J.W.; Burrows, J.P. The empirical relationship between satellite-derived tropospheric NO2 and fire radiative power and possible implications for fire emission rates of NOx. Atmos. Chem. Phys. 2014, 14, 2447–2466. [Google Scholar] [CrossRef]
- Tanimoto, H.K.; Ikeda, K.F.; Boersma, R.J.; van der Garivait, A.S. Interannual variability of nitrogen oxides emissions from boreal fires in Siberia and Alaska during 1996–2011 as observed from space. Environ. Res. Lett. 2015, 10, 065004. [Google Scholar] [CrossRef]
- Schreier, S.F.; Richter, A.; Schepaschenko, D.; Shvidenko, A.; Hilboll, A.; Burrows, J.P. Differences in satellite-derived NOx emission factors between Eurasian and North American boreal forest fires. Atmos. Environ. 2015, 121, 55–65. [Google Scholar] [CrossRef]
- Konovalov, I.B.; Beekmann, M.; Richter, A.; Burrows, J.P. Inverse modelling of the spatial distribution of NOx emissions on a continental scale using satellite data. Atmos. Chem. Phys. 2006, 6, 1747–1770. [Google Scholar] [CrossRef]
- Miyazaki, K.; Eskes, H.J.; Sudo, K. Global NOx emission estimates derived from an assimilation of OMI tropospheric NO2 columns. Atmos. Chem. Phys. 2012, 12, 2263–2288. [Google Scholar] [CrossRef]
- Mijling, B.; van der A, R.J. Using daily satellite observations to estimate emissions of short-lived air pollutants on a mesoscopic scale. J. Geophys. Res. Atmos. 2012, 117, D17302. [Google Scholar] [CrossRef]
- Berezin, E.V.; Konovalov, I.B.; Ciais, P.; Richter, A.; Tao, S.; Janssens-Maenhout, G.; Beekmann, M.; Schulze, E.-D. Multiannual changes of CO2 emissions in China: Indirect estimates derived from satellite measurements of tropospheric NO2 columns. Atmos. Chem. Phys. 2013, 13, 9415–9438. [Google Scholar] [CrossRef]
- Konovalov, I.B.; Beekmann, M.; Kuznetsova, I.N.; Yurova, A.; Zvyagintsev, A.M. Atmospheric impacts of the 2010 Russian wildfires: Integrating modelling and measurements of an extreme air pollution episode in the Moscow region. Atmos. Chem. Phys. 2011, 11, 10031–10056. [Google Scholar] [CrossRef]
- Krol, M.; Peters, W.; Hooghiemstra, P.; George, M.; Clerbaux, C.; Hurtmans, D.; McInerney, D.; Sedano, F.; Bergamaschi, P.; El Hajj, M.; et al. How much CO was emitted by the 2010 fires around Moscow? Atmos. Chem. Phys. 2013, 13, 4737–4747. [Google Scholar] [CrossRef]
- Konovalov, I.B.; Beekmann, M.; Berezin, E.V.; Petetin, H.; Mielonen, T.; Kuznetsova, I.N.; Andreae, M.O. The role of semi-volatile organic compounds in the mesoscale evolution of biomass burning aerosol: A modeling case study of the 2010 mega-fire event in Russia. Atmos. Chem. Phys. 2015, 15, 13269–13297. [Google Scholar] [CrossRef]
- Levelt, P.F.; Hilsenrath, E.; Leppelmeier, G.W.; van den Oord, G.H.J.; Bhartia, P.K.; Tamminen, J.; de Haan, J.F.; Veefkind, J.P. Science objectives of the ozone monitoring instrument. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1199–1208. [Google Scholar] [CrossRef]
- Boersma, K.F.; Eskes, H.J.; Dirksen, R.J.; van der A, R.J.; Veefkind, J.P.; Stammes, P.; Huijnen, V.; Kleipool, Q.L.; Sneep, M.; Claas, J.; et al. An improved tropospheric NO2 column retrieval algorithm for the Ozone Monitoring Instrument. Atmos. Meas. Tech. 2011, 4, 1905–1928. [Google Scholar] [CrossRef]
- TEMIS Portal. Available online: http://www.temis.nl/ (accessed on 17 March 2016).
- Irie, H.; Boersma, K.F.; Kanaya, Y.; Takashima, H.; Pan, X.; Wang, Z.F. Quantitative bias estimates for tropospheric NO2 columns retrieved from SCIAMACHY, OMI, and GOME-2 using a common standard for East Asia. Atmos. Meas. Tech. 2012, 5, 2403–2411. [Google Scholar] [CrossRef]
- Boersma, K.F.; Eskes, H.J.; Brinksma, E.J. Error analysis for tropospheric NO2 retrieval from space. J. Geophys. Res. Atmos. 2004, 109, D04311. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Justice, C.O.; Flynn, L.P.; Kendall, J.D.; Prins, E.M.; Giglio, L.; Ward, D.E.; Menzel, W.P.; Setzer, A.W. Potential global fire monitoring from EOS-MODIS. J. Geophys. Res. 1998, 103, 32215–32238. [Google Scholar] [CrossRef]
- Justice, C.O.; Giglio, L.; Korontzi, S.; Owens, J.; Morisette, J.T.; Roy, D.; Descloitres, J.; Alleaume, S.; Petitcolin, F.; Kaufman, Y. The MODIS fire products. Remote Sens. Environ. 2002, 83, 244–262. [Google Scholar] [CrossRef]
- The NASA Land Processes Distributed Active Archive Center. Available online: https://lpdaac.usgs.gov (accessed on 14 June 2015).
- Remer, L.A.; Kaufman, Y.J.; Tanre, D.; Mattoo, S.; Chu, D.A.; Martins, J.V.; Li, R.-R.; Ichoku, C.; Levy, R.C.; Kleidman, R.G.; et al. The MODIS aerosol algorithm, products, and validation. J. Atmos. Sci. 2005, 62, 947–973. [Google Scholar] [CrossRef]
- The NASA Giovanni-Interactive Visualization and Analysis System. Available online: http://daac.gsfc.nasa.gov/giovanni/ (accessed on 23 June 2014).
- Menut, L.; Bessagnet, B.; Khvorostyanov, D.; Beekmann, M.; Blond, N.; Colette, A.; Coll, I.; Curci, G.; Foret, G.; Hodzic, A.; et al. CHIMERE 2013: A model for regional atmospheric composition modeling. Geosci. Model Dev. 2013, 6, 981–1028. [Google Scholar] [CrossRef]
- The CHIMERE Chemistry-Transport Model. Available online: http://www.lmd.polytechnique.fr/chimere/ (accessed on 30 June 2016).
- Hodzic, A.; Madronich, S.; Bohn, B.; Massie, S.; Menut, L.; Wiedinmyer, C. Wildfire particulate matter in Europe during summer 2003: Meso-scale modeling of smoke emissions, transport and radiative effects. Atmos. Chem. Phys. 2007, 7, 4043–4064. [Google Scholar] [CrossRef]
- Konovalov, I.B.; Beekmann, M.; D’Anna, B.; George, C. Significant light induced ozone loss on biomass burning aerosol: Evidence from chemistry-transport modeling based on new laboratory studies. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Konovalov, I.B.; Berezin, E.V.; Ciais, P.; Broquet, G.; Beekmann, M.; Hadji-Lazaro, J.; Clerbaux, C.; Andreae, M.O.; Kaiser, J.W.; Schulze, E.-D. Constraining CO2 emissions from open biomass burning by satellite observations of co-emitted species: A method and its application to wildfires in Siberia. Atmos. Chem. Phys. 2014, 14, 10383–10410. [Google Scholar] [CrossRef]
- Wooster, M.J.; Roberts, G.; Perry, G.L.W.; Kaufman, Y.J. Retrieval of biomass combustion rates and totals from fire radiative power observations: FRP derivation and calibration relationships between biomass consumption and fire radiative energy release. J. Geophys. Res. 2005, 110, D24311. [Google Scholar] [CrossRef]
- Sofiev, M.; Ermakova, T.; Vankevich, R. Evaluation of the smoke-injection height from wild-land fires using remote-sensing data. Atmos. Chem. Phys. 2012, 12, 1995–2006. [Google Scholar] [CrossRef]
- Madronich, S.; McKenzie, R.E.; Bjorn, L.O.; Caldwell, M.M. Changes in biologically active ultraviolet radiation reaching the earth’s surface. J. Photochem. Photobiol. B Biol. 1998, 46, 5–19. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.-Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF; Version 3; NCAR Tech. Notes-475CSTR; National Center for Atmospheric Research: Boulder, CO, USA, 2008; p. 113. [Google Scholar]
- Eskes, H.J.; Boersma, K.F. Averaging kernels for DOAS total column satellite retrievals. Atmos. Chem. Phys. 2003, 3, 1285–1291. [Google Scholar] [CrossRef]
- Konovalov, I.B.; Beekmann, M.; Vautard, R.; Burrows, J.P.; Richter, A.; Elansky, N.; Nüß, H. Comparison and evaluation of modelled and GOME measurement derived tropospheric NO2 columns over Western and Eastern Europe. Atmos. Chem. Phys. 2005, 5, 169–190. [Google Scholar] [CrossRef]
- Konovalov, I.B.; Elansky, N.F.; Zvyagintsev, A.M.; Belikov, I.B.; Beekmann, M. Validation of chemistry transport model of the lower atmosphere in the central European region of Russia using ground-based and satellite measurement data. Russ. Meteorol. Hydrol. 2009, 34, 236–242. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman & Hall: New York, NY, USA, 1993. [Google Scholar]
- Boersma, K.F.; Eskes, H.J.; Veefkind, J.P.; Brinksma, E.J.; van der A, R.J.; Sneep, M.; van den Oord, G.H.J.; Levelt, P.F.; Stammes, P.; Gleason, J.F.; et al. Near-real time retrieval of tropospheric NO2 from OMI. Atmos. Chem. Phys. 2007, 7, 2103–2118. [Google Scholar] [CrossRef]
- Seinfeld, J.H.; Pandis, S.N. Atmospheric Trace Constituents. In Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2006; pp. 22–24. [Google Scholar]
- Matsueda, M. Predictability of Euro-Russian blocking in summer of 2010. Geophys. Res. Lett. 2011, 38, L06801. [Google Scholar] [CrossRef]
- Andreae, M.O.; Merlet, P. Emission of trace gases and aerosols from biomass burning. Glob. Biogeochem. Cycles 2001, 15, 955–966. [Google Scholar] [CrossRef]
- Huijnen, V.; Flemming, J.; Kaiser, J.W.; Inness, A.; Leitão, J.; Heil, A.; Eskes, H.J.; Schultz, M.G.; Benedetti, A.; Hadji-Lazaro, J.; et al. Hindcast experiments of tropospheric composition during the summer 2010 fires over western Russia. Atmos. Chem. Phys. 2012, 12, 4341–4364. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berezin, E.V.; Konovalov, I.B.; Romanova, Y.Y. Inverse Modeling of Nitrogen Oxides Emissions from the 2010 Russian Wildfires by Using Satellite Measurements of Nitrogen Dioxide. Atmosphere 2016, 7, 132. https://doi.org/10.3390/atmos7100132
Berezin EV, Konovalov IB, Romanova YY. Inverse Modeling of Nitrogen Oxides Emissions from the 2010 Russian Wildfires by Using Satellite Measurements of Nitrogen Dioxide. Atmosphere. 2016; 7(10):132. https://doi.org/10.3390/atmos7100132
Chicago/Turabian StyleBerezin, Evgeny V., Igor B. Konovalov, and Yulia Y. Romanova. 2016. "Inverse Modeling of Nitrogen Oxides Emissions from the 2010 Russian Wildfires by Using Satellite Measurements of Nitrogen Dioxide" Atmosphere 7, no. 10: 132. https://doi.org/10.3390/atmos7100132
APA StyleBerezin, E. V., Konovalov, I. B., & Romanova, Y. Y. (2016). Inverse Modeling of Nitrogen Oxides Emissions from the 2010 Russian Wildfires by Using Satellite Measurements of Nitrogen Dioxide. Atmosphere, 7(10), 132. https://doi.org/10.3390/atmos7100132





