Sensitivity of the Reaction Mechanism of the Ozone Depletion Events during the Arctic Spring on the Initial Atmospheric Composition of the Troposphere
Abstract
:1. Introduction
2. Mathematical Models and Methods
3. Results and Discussion
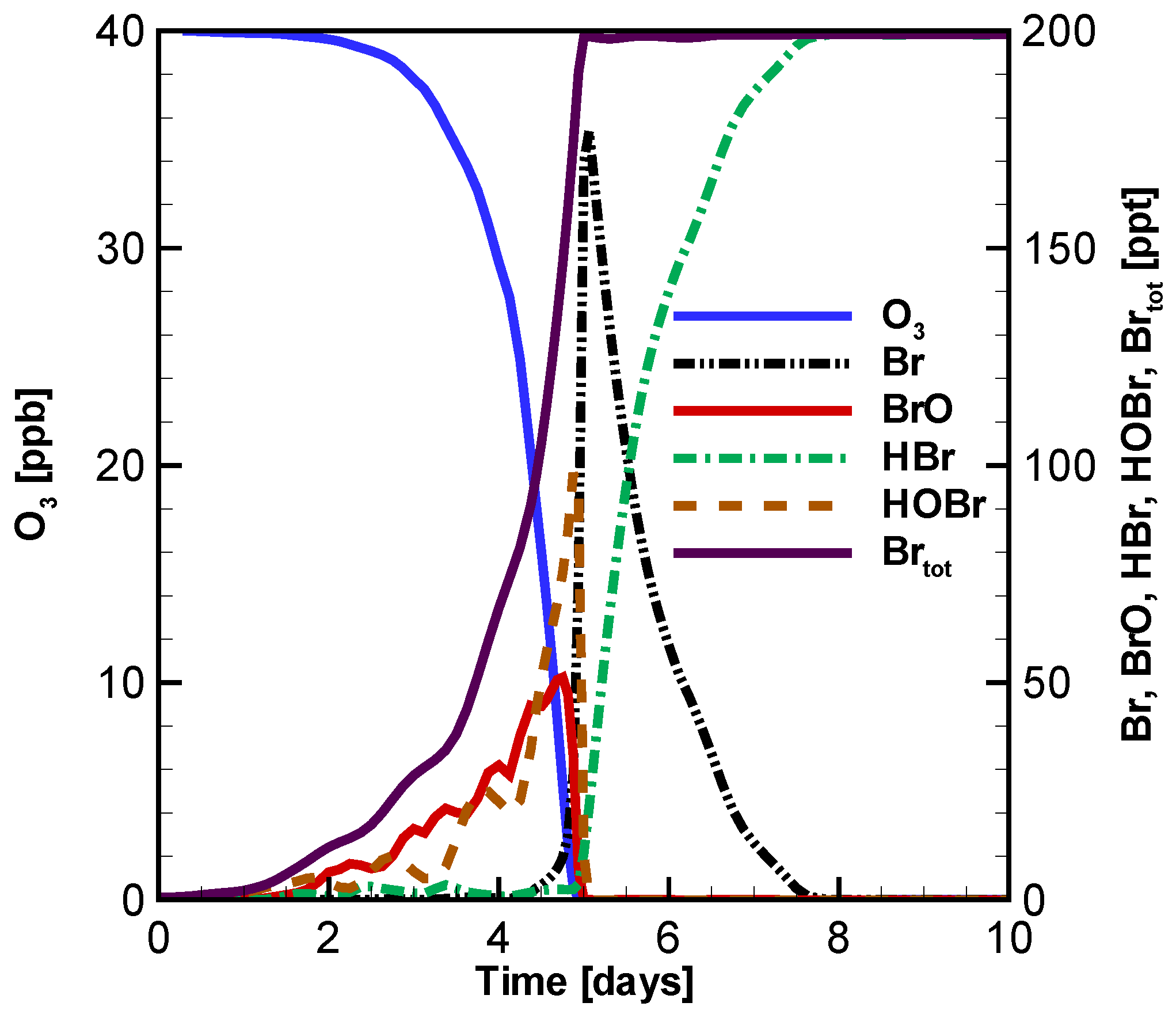
3.1. Temporal Evolution of Ozone and Principal Bromine Species
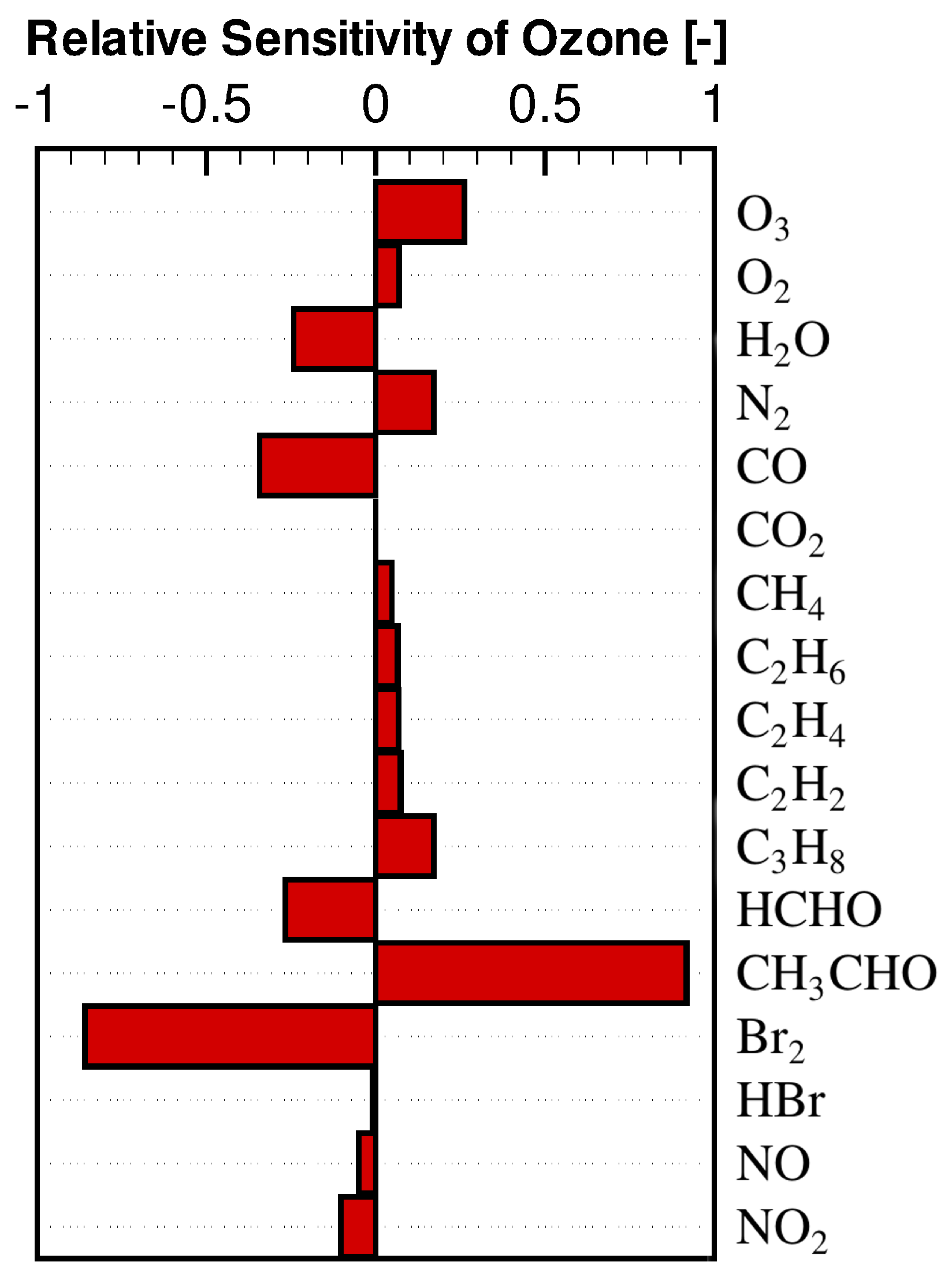
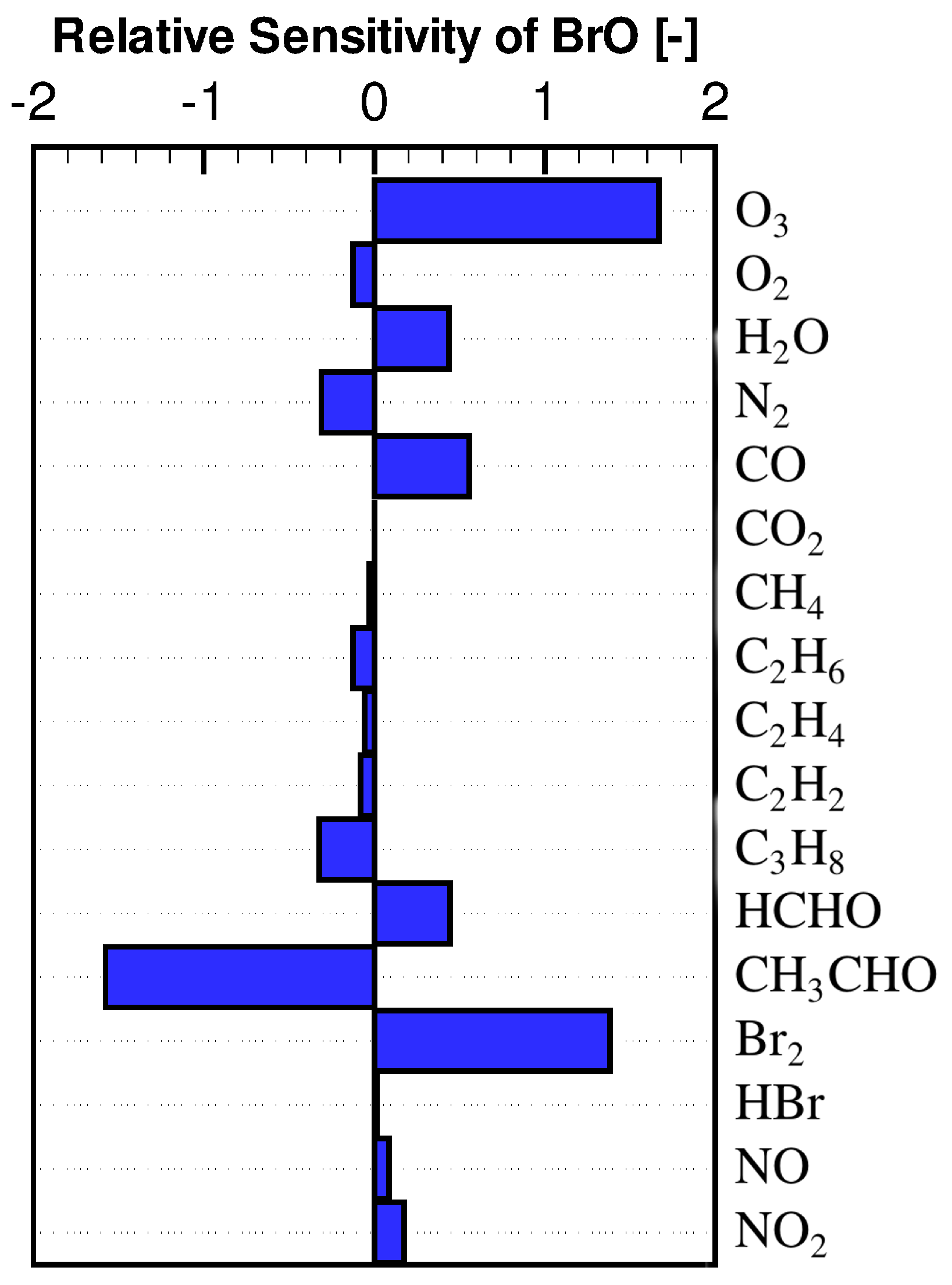
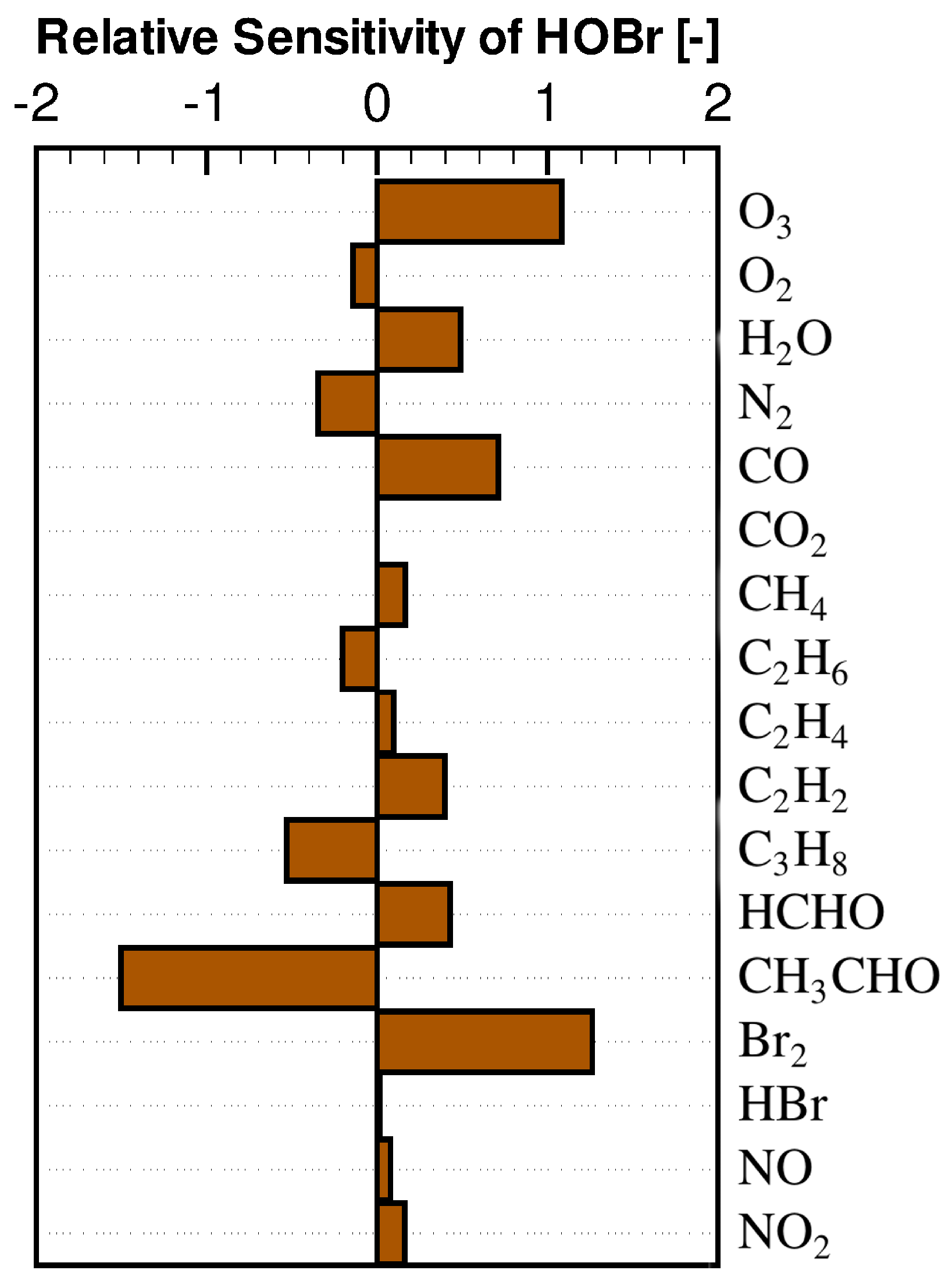
3.2. Concentration Sensitivity Analysis of the Mixing Ratios of Ozone and Bromine Containing Compounds during the ODE
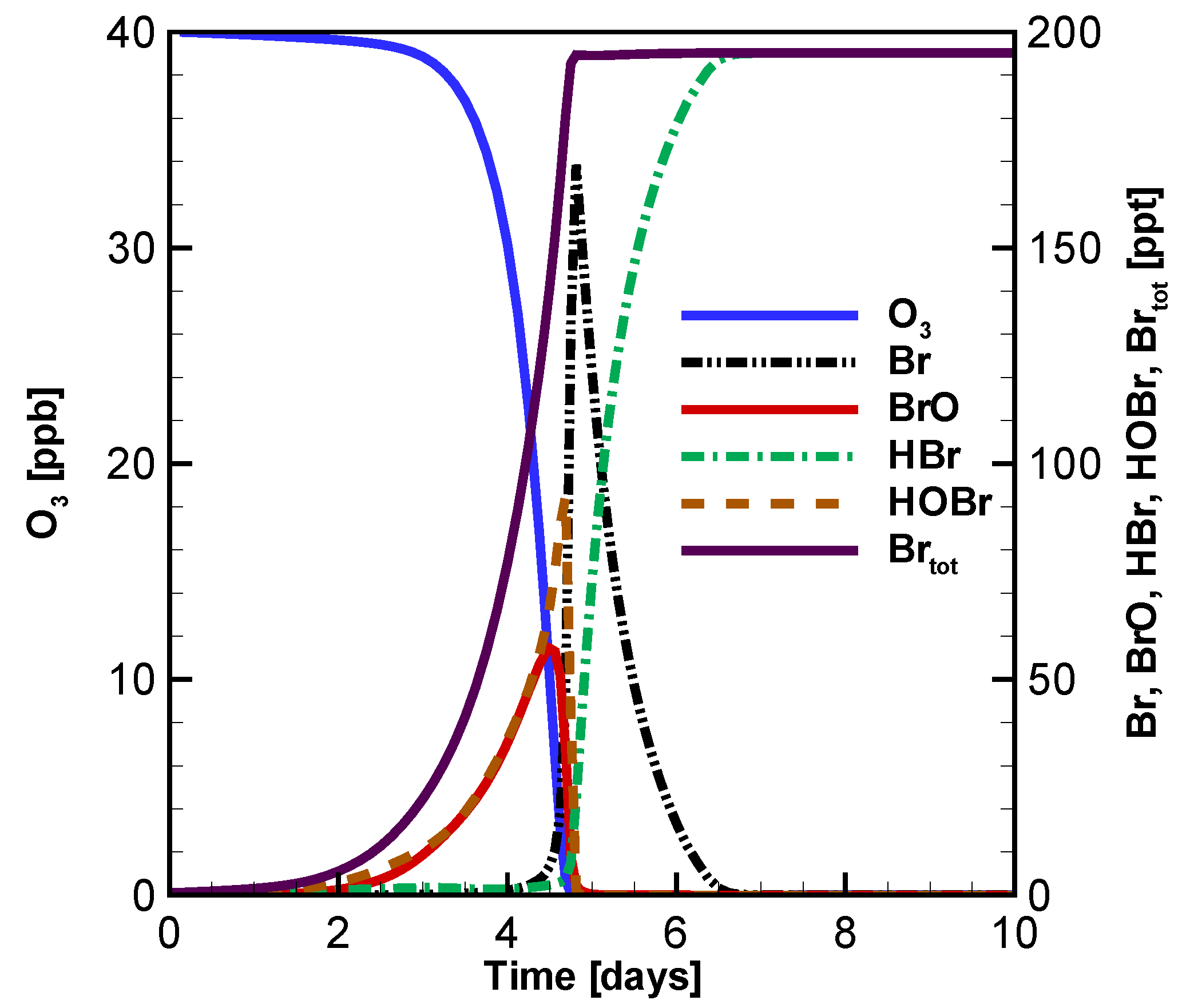
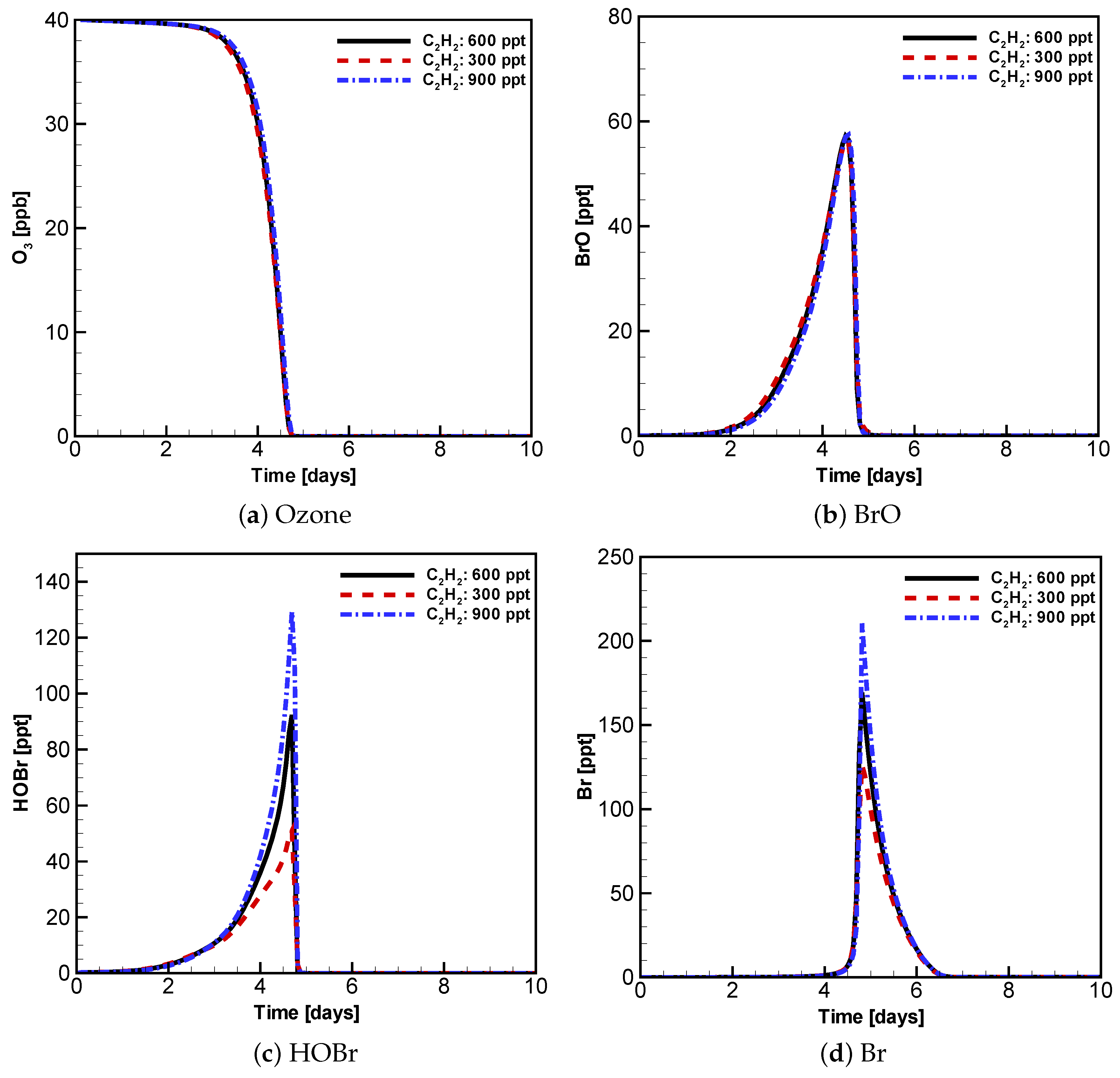
3.3. Evolution of Ozone, BrO, HOBr and Br with Different Initial Atmospheric Composition
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
| Reaction Number | Reaction | k ((molec. cm−3)1 − n·s−1) | Order (n) | Reference |
|---|---|---|---|---|
| (1) | 1 | Lehrer et al. [13] | ||
| (2) | 2 | Atkinson et al. [24] | ||
| (3) | 2 | Atkinson et al. [24] | ||
| (4) | 2 | Atkinson et al. [24] | ||
| (5) | 2 | Atkinson et al. [24] | ||
| (6) | 0.021 | 1 | Lehrer et al. [13] | |
| (7) | 0.014 | 1 | Lehrer et al. [13] | |
| (8) | 2 | Atkinson et al. [24] | ||
| (9) | 2 | Atkinson et al. [24] | ||
| (10) | 2 | Atkinson et al. [24] | ||
| (11) | 1 | Lehrer et al. [13] | ||
| (12) | 2 | Atkinson et al. [24] | ||
| (13) | 2 | Atkinson et al. [24] | ||
| (14) | Cao et al. [17] | |||
| (15) | Cao et al. [17] | |||
| (16) | 2 | Atkinson et al. [24] | ||
| (17) | 2 | Atkinson et al. [24] | ||
| (18) | 2 | Atkinson et al. [24] | ||
| (19) | 2 | Atkinson et al. [24] | ||
| (20) | 2 | Borken [48] | ||
| (21) | 2 | Borken [48] | ||
| (22) | 2 | Barnes et al. [49] | ||
| (23) | 2 | Barnes et al. [49] | ||
| (24) | 2 | Atkinson et al. [24] | ||
| (25) | 2 | Aranda et al. [50] | ||
| (26) | 2 | Aranda et al. [50] | ||
| (27) | 2 | Atkinson et al. [24] | ||
| (28) | 2 | Atkinson et al. [24] | ||
| (29) | 2 | Atkinson et al. [24] | ||
| (30) | 2 | Atkinson et al. [24] | ||
| (31) | 2 | Atkinson et al. [24] | ||
| (32) | 2 | Atkinson et al. [24] | ||
| (33) | 2 | Atkinson et al. [24] | ||
| (34) | 2 | Atkinson et al. [24] | ||
| (35) | 2 | Atkinson et al. [24] | ||
| (36) | 2 | Atkinson et al. [24] | ||
| (37) | 2 | Sander et al. [51] | ||
| (38) | 2 | Atkinson et al. [24] | ||
| (39) | 2 | Atkinson et al. [24] | ||
| (40) | 2 | Atkinson et al. [24] | ||
| (41) | 2 | Atkinson et al. [24] | ||
| (42) | 2 | Atkinson et al. [24] | ||
| (43) | 2 | Atkinson et al. [24] | ||
| (44) | 2 | Atkinson et al. [24] | ||
| (45) | 2 | Atkinson et al. [24] | ||
| (46) | 2 | Mallard et al. [52] | ||
| (47) | 2 | Atkinson et al. [24] | ||
| (48) | 2 | Atkinson et al. [24] | ||
| (49) | 2 | Atkinson et al. [24] | ||
| (50) | 2 | Atkinson et al. [24] | ||
| (51) | 2 | Sander et al. [51] | ||
| (52) | 2 | Sander et al. [51] | ||
| (53) | 2 | Atkinson et al. [24] | ||
| (54) | 2 | Sander et al. [51] | ||
| (55) | 2 | Sander et al. [51] | ||
| (56) | 2 | Atkinson et al. [24] | ||
| (57) | 1 | Lehrer et al. [13] | ||
| (58) | 1 | Lehrer et al. [13] | ||
| (59) | 1 | Lehrer et al. [13] | ||
| (60) | 1 | Lehrer et al. [13] | ||
| (61) | 1 | Lehrer et al. [13] | ||
| (62) | 1 | Lehrer et al. [13] | ||
| (63) | 2 | Atkinson et al. [24] | ||
| (64) | 2 | Atkinson et al. [24] | ||
| (65) | 2 | Atkinson et al. [24] | ||
| (66) | 2 | Atkinson et al. [24] | ||
| (67) | 2 | Atkinson et al. [24] | ||
| (68) | 2 | Atkinson et al. [24] | ||
| (69) | 2 | Atkinson et al. [24] | ||
| (70) | 1 | Atkinson et al. [24] | ||
| (71) | 2 | Atkinson et al. [24] | ||
| (72) | 2 | Atkinson et al. [24] | ||
| (73) | 2 | Atkinson et al. [24] | ||
| (74) | 1 | Lehrer et al. [13] | ||
| (75) | 1 | Lehrer et al. [13] | ||
| (76) | 1 | Lehrer et al. [13] | ||
| (77) | 1 | Lehrer et al. [13] | ||
| (78) | 2 | Atkinson et al. [24] | ||
| (79) | 2 | Atkinson et al. [24] | ||
| (80) | 2 | Atkinson et al. [24] | ||
| (81) | 2 | Atkinson et al. [24] | ||
| (82) | 2 | Atkinson et al. [24] | ||
| (83) | 2 | Atkinson et al. [24] | ||
| (84) | 2 | Atkinson et al. [24] | ||
| (85) | 2 | Atkinson et al. [24] | ||
| (86) | 2 | Atkinson et al. [24] | ||
| (87) | 2 | Atkinson et al. [24] | ||
| (88) | 1 | Lehrer et al. [13] | ||
| (89) | 1 | Lehrer et al. [13] | ||
| (90) | Cao et al. [17] | |||
| (91) | 1 | Fishman and Carney [53] | ||
| (92) | Cao et al. [17] |
| Species | J0 (s−1) | b | c |
|---|---|---|---|
| O3 | 6.85 × 10−5 | 3.510 | 0.820 |
| Br2 | 1.07 × 10−1 | 0.734 | 0.900 |
| BrO | 1.27 × 10−1 | 1.290 | 0.857 |
| HOBr | 2.62 × 10−3 | 1.216 | 0.861 |
| H2O2 | 2.75 × 10−5 | 1.595 | 0.848 |
| HCHO→HO2 | 1.03 × 10−4 | 1.785 | 0.848 |
| HCHO→H2 | 1.08 × 10−4 | 1.431 | 0.853 |
| C2H4O | 1.95 × 10−5 | 4.050 | 0.710 |
| CH3O2H | 1.60 × 10−5 | 1.553 | 0.849 |
| C2H5O2H | 1.60 × 10−5 | 1.553 | 0.849 |
| HNO3 | 1.39 × 10−6 | 2.094 | 0.848 |
| NO2 | 2.62 × 10−2 | 1.068 | 0.871 |
| NO3→NO2 | 6.20 × 10−1 | 0.608 | 0.915 |
| NO3→NO | 7.03 × 10−2 | 0.583 | 0.917 |
| BrONO2 | 3.11 × 10−3 | 1.270 | 0.859 |
| BrNO2 | 1.11 × 10−3 | 1.479 | 0.851 |
References
- Schoenbein, C. Recherches Sur La Nature de L’odeur Qui se Manifeste Dans Certaines Actions Chimiques. C.R. Acad. Sci. Paris 1840, 10, 706–710. [Google Scholar]
- Seinfeld, J.H.; Pandis, S.N. Atmospheric Chemistry and Physics: From Air Pollution to Climate Change; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Lippmann, M. Health effects of tropospheric ozone. Environ. Sci. Technol. 1991, 25, 1954–1962. [Google Scholar] [CrossRef]
- Tropospheric Ozone, the Polluter. Available online: http://www.ucar.edu/learn/1_7_1.htm/ (accessed on 1 July 2016).
- Vingarzan, R. A review of surface ozone background levels and trends. Atmos. Environ. 2004, 38, 3431–3442. [Google Scholar] [CrossRef]
- Oltmans, S.J. Surface ozone measurements in clean air. J. Geophys. Res. Oceans 1981, 86, 1174–1180. [Google Scholar] [CrossRef]
- Bottenheim, J.; Gallant, A.; Brice, K. Measurements of NOY species and O3 at 82°N latitude. Geophys. Res. Lett. 1986, 13, 113–116. [Google Scholar] [CrossRef]
- Barrie, L.A.; Bottenheim, J.W.; Schnell, R.C.; Crutzen, P.J.; Rasmussen, R.A. Ozone destruction and photochemical reactions at polar sunrise in the lower Arctic atmosphere. Nature 1988, 334, 138–141. [Google Scholar] [CrossRef]
- Hönninger, G.; Platt, U. Observations of BrO and its vertical distribution during surface ozone depletion at Alert. Atmos. Environ. 2002, 36, 2481–2489. [Google Scholar] [CrossRef]
- Platt, U.; Hönninger, G. The role of halogen species in the troposphere. Chemosphere 2003, 52, 325–338. [Google Scholar] [CrossRef]
- Simpson, W.R.; von Glasow, R.; Riedel, K.; Anderson, P.; Ariya, P.; Bottenheim, J.; Burrows, J.; Carpenter, L.J.; Frieß, U.; Goodsite, M.E.; et al. Halogens and their role in polar boundary-layer ozone depletion. Atmos. Chem. Phys. 2007, 7, 4375–4418. [Google Scholar] [CrossRef]
- Abbatt, J.P.D.; Thomas, J.L.; Abrahamsson, K.; Boxe, C.; Granfors, A.; Jones, A.E.; King, M.D.; Saiz-Lopez, A.; Shepson, P.B.; Sodeau, J.; et al. Halogen activation via interactions with environmental ice and snow in the polar lower troposphere and other regions. Atmos. Chem. Phys. 2012, 12, 6237–6271. [Google Scholar] [CrossRef]
- Lehrer, E.; Hönninger, G.; Platt, U. A one dimensional model study of the mechanism of halogen liberation and vertical transport in the polar troposphere. Atmos. Chem. Phys. 2004, 4, 2427–2440. [Google Scholar] [CrossRef]
- Strong, C.; Fuentes, J.D.; Davis, R.E.; Bottenheim, J.W. Thermodynamic attributes of Arctic boundary layer ozone depletion. Atmos. Environ. 2002, 36, 2641–2652. [Google Scholar] [CrossRef]
- Morin, S.; Hönninger, G.; Staebler, R.M.; Bottenheim, J.W. A high time resolution study of boundary layer ozone chemistry and dynamics over the Arctic Ocean near Alert, Nunavut. Geophys. Res. Lett. 2005, 32, 165–176. [Google Scholar] [CrossRef]
- Jones, A.E.; Anderson, P.S.; Wolff, E.W.; Turner, J.; Rankin, A.M.; Colwell, S.R. A role for newly forming sea ice in springtime polar tropospheric ozone loss? Observational evidence from Halley station, Antarctica. J. Geophys. Res. Atmos. 2006, 111, 375–390. [Google Scholar] [CrossRef]
- Cao, L.; Sihler, H.; Platt, U.; Gutheil, E. Numerical analysis of the chemical kinetic mechanisms of ozone depletion and halogen release in the polar troposphere. Atmos. Chem. Phys. 2014, 14, 3771–3787. [Google Scholar] [CrossRef]
- Evans, M.J.; Jacob, D.J.; Atlas, E.; Cantrell, C.A.; Eisele, F.; Flocke, F.; Fried, A.; Mauldin, R.L.; Ridley, B.A.; Wert, B.; et al. Coupled evolution of BrOx-ClOx-HOx-NOx chemistry during bromine-catalyzed ozone depletion events in the Arctic boundary layer. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Piot, M.; Von Glasow, R. The potential importance of frost flowers, recycling on snow, and open leads for ozone depletion events. Atmos. Chem. Phys. 2008, 8, 2437–2467. [Google Scholar] [CrossRef]
- Piot, M.; Glasow, R. Modelling the multiphase near-surface chemistry related to ozone depletions in polar spring. J. Atmos. Chem. 2009, 64, 77–105. [Google Scholar] [CrossRef]
- Turanyi, T. KINAL—A program package for kinetic analysis of reaction mechanisms. Comput. Chem. 1990, 14, 253–254. [Google Scholar] [CrossRef]
- Cao, L.; Platt, U.; Gutheil, E. Role of the boundary layer in the occurrence and termination of the tropospheric ozone depletion events in polar spring. Atmos. Environ. 2016, 132, 98–110. [Google Scholar] [CrossRef]
- Atkins, P.; De Paula, J. Elements of Physical Chemistry; Oxford University Press: New York, NY, USA, 2013. [Google Scholar]
- Atkinson, R.; Baulch, D.L.; Cox, R.A.; Crowley, J.N.; Hampson, R.F.; Hynes, R.G.; Jenkin, M.E.; Kerr, J.A.; Rossi, M.; Troe, J. Summary of Evaluated Kinetic and Photochemical Data for Atmospheric Chemistry (Web Version). Available online: http://www.iupac-kinetic.ch.cam.ac.uk/ (accessed on 1 July 2016).
- Staebler, R.; Toom-Sauntry, D.; Barrie, L.; Langendörfer, U.; Lehrer, E.; Li, S.M.; Dryfhout-Clark, H. Physical and chemical characteristics of aerosols at Spitsbergen in the spring of 1996. J. Geophys. Res. Atmos. 1999, 104, 5515–5529. [Google Scholar] [CrossRef]
- Hanson, D.R.; Ravishankara, A.R.; Solomon, S. Heterogeneous reactions in sulfuric acid aerosols: A framework for model calculations. J. Geophys. Res. Atmos. 1994, 99, 3615–3629. [Google Scholar] [CrossRef]
- Sander, R.; Crutzen, P.J. Model study indicating halogen activation and ozone destruction in polluted air masses transported to the sea. J. Geophys. Res. Atmos. 1996, 101, 9121–9138. [Google Scholar] [CrossRef]
- Beare, R.; Macvean, M.; Holtslag, A.; Cuxart, J.; Esau, I.; Golaz, J.C.; Jimenez, M.; Khairoutdinov, M.; Kosovic, B.; Lewellen, D.; et al. An intercomparison of large-eddy simulations of the stable boundary layer. Bound.-Layer Meteorol. 2006, 118, 247–272. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Huff, A.K.; Abbatt, J.P.D. Gas-phase Br2 production in heterogeneous reactions of Cl2, HOCl, and BrCl with halide–ice surfaces. J. Phys. Chem. A 2000, 104, 7284–7293. [Google Scholar] [CrossRef]
- Huff, A.K.; Abbatt, J.P.D. Kinetics and product yields in the heterogeneous reactions of HOBr with ice surfaces containing NaBr and NaCl. J. Phys. Chem. A 2002, 106, 5279–5287. [Google Scholar] [CrossRef]
- Röth, E.P. A fast algorithm to calculate the photonflux in optically dense media for use in photochemical models. Ber. Bunsenges. Phys. Chem. 1992, 96, 417–420. [Google Scholar] [CrossRef]
- Röth, E.P. Description of the Anisotropic Radiation Transfer Model ART To Dermine Photodissociation Coefficients; Berichte des Forschungszentrums Jülich; Forschungszentrum, Zentralbibliothek: Jülich, Germany, 2002; Volume 3960. [Google Scholar]
- Jones, A.E.; Weller, R.; Wolff, E.W.; Jacobi, H.W. Speciation and rate of photochemical NO and NO2 production in Antarctic snow. Geophys. Res. Lett. 2000, 27, 345–348. [Google Scholar] [CrossRef]
- Jones, A.E.; Weller, R.; Anderson, P.S.; Jacobi, H.W.; Wolff, E.W.; Schrems, O.; Miller, H. Measurements of NOx emissions from the Antarctic snowpack. Geophys. Res. Lett. 2001, 28, 1499–1502. [Google Scholar] [CrossRef]
- Grannas, A.M.; Jones, A.E.; Dibb, J.; Ammann, M.; Anastasio, C.; Beine, H.J.; Bergin, M.; Bottenheim, J.; Boxe, C.S.; Carver, G.; et al. An overview of snow photochemistry: Evidence, mechanisms and impacts. Atmos. Chem. Phys. 2007, 7, 4329–4373. [Google Scholar] [CrossRef]
- Jacobi, H.W.; Frey, M.M.; Hutterli, M.A.; Bales, R.C.; Schrems, O.; Cullen, N.J.; Steffen, K.; Koehler, C. Measurements of hydrogen peroxide and formaldehyde exchange between the atmosphere and surface snow at Summit, Greenland. Atmos. Environ. 2002, 36, 2619–2628. [Google Scholar] [CrossRef]
- Gottwald, B.A.; Wanner, G. A reliable rosenbrock integrator for stiff differential equations. Computing 1981, 26, 355–360. [Google Scholar] [CrossRef]
- Valko, P.; Vajda, S. An extended ode solver for sensitivity calculations. Comput. Chem. 1984, 8, 255–271. [Google Scholar] [CrossRef]
- Turányi, T. Sensitivity analysis of complex kinetic systems. Tools and applications. J. Math. Chem. 1990, 5, 203–248. [Google Scholar] [CrossRef]
- Langendörfer, U.; Lehrer, E.; Wagenbach, D.; Platt, U. Observation of filterable bromine variabilities during arctic tropospheric ozone depletion events in high (1 hour) time resolution. J. Atmos. Chem. 1999, 34, 39–54. [Google Scholar] [CrossRef]
- Shepson, P.B.; Sirju, A.P.; Hopper, J.R.; Barrie, L.A.; Young, V.; Niki, H.; Dryfhout, H. Sources and sinks of carbonyl compounds in the Arctic Ocean boundary layer: Polar ice floe experiment. J. Geophys. Res. Atmos. 1996, 101, 21081–21089. [Google Scholar] [CrossRef]
- Custard, K.D.; Thompson, C.R.; Pratt, K.A.; Shepson, P.B.; Liao, J.; Huey, L.G.; Orlando, J.J.; Weinheimer, A.J.; Apel, E.; Hall, S.R. The NOX dependence of bromine chemistry in the Arctic atmospheric boundary layer. Atmos. Chem. Phys. 2015, 15, 8329–8360. [Google Scholar] [CrossRef]
- Hausmann, M.; Platt, U. Spectroscopic measurement of bromine oxide and ozone in the high Arctic during Polar Sunrise Experiment 1992. J. Geophys. Res. Atmos. 1994, 99, 25399–25413. [Google Scholar] [CrossRef]
- Bottenheim, J.W.; Netcheva, S.; Morin, S.; Nghiem, S.V. Ozone in the boundary layer air over the Arctic Ocean: Measurements during the TARA transpolar drift 2006–2008. Atmos. Chem. Phys. 2009, 9, 4545–4557. [Google Scholar] [CrossRef]
- Jacobi, H.W.; Morin, S.; Bottenheim, J.W. Observation of widespread depletion of ozone in the springtime boundary layer of the central Arctic linked to mesoscale synoptic conditions. J. Geophys. Res. Atmos. 2010, 115, 1383–1392. [Google Scholar] [CrossRef]
- Koo, J.H.; Wang, Y.; Kurosu, T.P.; Chance, K.; Rozanov, A.; Richter, A.; Oltmans, S.J.; Thompson, A.M.; Hair, J.W.; Fenn, M.A.; et al. Characteristics of tropospheric ozone depletion events in the Arctic spring: Analysis of the ARCTAS, ARCPAC, and ARCIONS measurements and satellite BrO observations. Atmos. Chem. Phys. 2012, 12, 9909–9922. [Google Scholar] [CrossRef]
- Borken, J. Ozonabbau Durch Halogene in der Arktischen Grenzschicht. Ph.D. Thesis, Heidelberg University, Heidelberg, Germany, 1996. [Google Scholar]
- Barnes, I.; Becker, K.; Overath, R. Oxidation of organic sulfur compounds. In The Tropospheric Chemistry of Ozone in the Polar Regions; Niki, H., Becker, K., Eds.; Springer: Berlin/Heidelberg, Germany, 1993; Volume 7, pp. 371–383. [Google Scholar]
- Aranda, A.; Le Bras, G.; La Verdet, G.; Poulet, G. The BrO + Ch3O2 reaction: Kinetics and role in the atmospheric ozone budget. Geophys. Res. Lett. 1997, 24, 2745–2748. [Google Scholar] [CrossRef]
- Sander, R.; Vogt, R.; Harris, G.W.; Crutzen, P.J. Modelling the chemistry of ozone, halogen compounds, and hydrocarbons in the arctic troposphere during spring. Tellus B 1997, 49, 522–532. [Google Scholar] [CrossRef]
- Mallard, W.G.; Westley, F.; Herron, J.T.; Hampson, R.F.; Frizzel, D.H. NIST Chemical Kinetics Database: Version 5.0 (Web Version). Available online: http://kinetics.nist.gov/ (accessed on 1 May 2014).
- Fishman, J.; Carney, T.A. A one-dimensional photochemical model of the troposphere with planetary boundary-layer parameterization. J. Atmos. Chem. 1984, 1, 351–376. [Google Scholar] [CrossRef]

| Species | Mixing Ratio |
|---|---|
| O3 | 40 ppb |
| Br2 | 0.3 ppt |
| HBr | 0.01 ppt |
| CH4 | 1.9 ppm |
| CO2 | 371 ppm |
| CO | 132 ppb |
| HCHO | 100 ppt |
| CH3CHO | 100 ppt |
| C2H6 | 2.5 ppb |
| C2H4 | 100 ppt |
| C2H2 | 600 ppt |
| C3H8 | 1.2 ppb |
| NO | 5 ppt |
| NO2 | 10 ppt |
| H2O | 800 ppm |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, L.; He, M.; Jiang, H.; Grosshans, H.; Cao, N. Sensitivity of the Reaction Mechanism of the Ozone Depletion Events during the Arctic Spring on the Initial Atmospheric Composition of the Troposphere. Atmosphere 2016, 7, 124. https://doi.org/10.3390/atmos7100124
Cao L, He M, Jiang H, Grosshans H, Cao N. Sensitivity of the Reaction Mechanism of the Ozone Depletion Events during the Arctic Spring on the Initial Atmospheric Composition of the Troposphere. Atmosphere. 2016; 7(10):124. https://doi.org/10.3390/atmos7100124
Chicago/Turabian StyleCao, Le, Min He, Haimei Jiang, Holger Grosshans, and Nianwen Cao. 2016. "Sensitivity of the Reaction Mechanism of the Ozone Depletion Events during the Arctic Spring on the Initial Atmospheric Composition of the Troposphere" Atmosphere 7, no. 10: 124. https://doi.org/10.3390/atmos7100124
APA StyleCao, L., He, M., Jiang, H., Grosshans, H., & Cao, N. (2016). Sensitivity of the Reaction Mechanism of the Ozone Depletion Events during the Arctic Spring on the Initial Atmospheric Composition of the Troposphere. Atmosphere, 7(10), 124. https://doi.org/10.3390/atmos7100124





