Abstract
We present a framework for calculating the total scattering of both non-absorbing and absorbing aerosol at ambient conditions from aircraft data. Our framework is developed emphasizing the explicit use of chemical composition data for estimating the complex refractive index (RI) of particles, and thus obtaining improved ambient size spectra derived from Optical Particle Counter (OPC) measurements. The feasibility of our framework for improved calculations of total scattering is demonstrated using three types of data collected by the U.S. Department of Energy’s (DOE) aircraft during the Two-Column Aerosol Project (TCAP). Namely, these data types are: (1) size distributions measured by a suite of OPC’s; (2) chemical composition data measured by an Aerosol Mass Spectrometer and a Single Particle Soot Photometer; and (3) the dry total scattering coefficient measured by a integrating nephelometer and scattering enhancement factor measured with a humidification system. We demonstrate that good agreement (~10%) between the observed and calculated scattering can be obtained under ambient conditions (RH < 80%) by applying chemical composition data for the RI-based correction of the OPC-derived size spectra. We also demonstrate that ignoring the RI-based correction or using non-representative RI values can cause a substantial underestimation (~40%) or overestimation (~35%) of the calculated scattering, respectively.
Keywords:
aircraft measurements of aerosol microphysical, chemical, and optical components and ambient relative humidity; Ultra-High Sensitivity Aerosol Spectrometer (UHSAS); Passive Cavity Aerosol Spectrometer (PCASP); Cloud and Aerosol Spectrometer (CAS); Aerosol Mass Spectrometer (AMS); Single Particle Soot Photometer (SP2); integrating nephelometer; humidification system; Two-Column Aerosol Project (TCAP) 1. Introduction
Although the importance of atmospheric aerosol in modifying the Earth’s radiation budget has been recognized by many studies [1,2], the extent to which aerosol shapes the regional and global climate is still ambiguous [3,4]. The magnitude and sign of the aerosol-induced changes of the radiation budget at the regional and global scales are highly uncertain, since these changes are influenced substantially by strong temporal and spatial variations of aerosol loading, chemical composition and mixing state [5,6,7]. Since the advent of observational techniques for monitoring these variations from surface, air and space, the diversity of sensors with improved precision and accuracy has increased and corresponding innovative methods have been developed [8,9,10,11]. Aircraft measurements are becoming increasingly important for model validation studies because they can document aerosol variations in remote regions where access to ground-based observations is difficult or unavailable, and offer observations with higher temporal resolution than can typically be attained with satellites [12,13,14].
Comprehensive and integrated measurements of aerosol properties provide an important observational basis for evaluations of climate model predictions and necessarily involve combining data collected by several instruments with different designs and uncertainties. To determine whether these data are consistent and reasonable, a special kind of quantitative comparison experiment is commonly performed. Such an experiment, traditionally referred to as a closure study, compares the measured values of a selected aerosol property with those calculated from independent measurements [15,16,17,18]. For example, an optical closure experiment compares the measured values of an aerosol optical property, such as total scattering coefficient, with those calculated from independently measured size distributions and chemical composition under a variety of conditions [19,20,21]. Good agreement between the measured and calculated aerosol properties (within error bars) indicates consistency of the observational dataset, and bolsters its relevance for further use in global and regional climate model evaluations.
Optical closure studies have become an essential part of testing integrated datasets where simultaneous measurements of the optical, microphysical and chemical properties of aerosol at dry and ambient conditions are available [21,22,23]. Compared to the ground-based instrumentation suites, instrumentation on board aircraft platforms requires particular attention to its design and operation [24] mainly due to payload restrictions (requiring instruments with smaller dimensions and less weight; [25,26]) and abrupt changes in atmospheric and aerosol characteristics during the aircraft’s rapid (about 100 m/s) motion (requiring instruments with faster response time and data acquisition speeds; [27]), which directly impact spatial resolution. While airborne instrumentation and associated data synergy are continuing to evolve on many fronts, rigorous scrutiny of airborne integrated measurements has not always been achieved. Moreover, demands to assess the consistency and reasonableness of integrated airborne data sets have been growing, given the increasingly heavy reliance of process-oriented model evaluations on aircraft measurements [6].
Optical Particle Counters (OPCs) are a common type of airborne instrument for deriving size spectra [24,28,29]. The fundamental quantity measured by OPCs is the amount of light scattered by individual particles over a large solid angle. The amount of scattered light depends on aerosol characteristics, such as size, shape and complex refractive index (RI), which is a function of the particle’s chemical composition. The measured scattered light is converted into particle size using an appropriate scattering theory (e.g., Mie theory for spherical particles) and an assumed or estimated refractive index. For example, several parameterizations have been developed for correcting OPC-derived size distributions for weakly absorbing aerosol using Mie calculations and assuming that the RI-based correction depends on the real part of the complex RI only [30,31]. It is important to note that the assumptions employed for the refractive index may or may not be representative of the observed ambient conditions.
Although Mie theory does allow for the RI-based corrections associated with both the real and imaginary parts of the complex RI [32,33,34], airborne measurements of aerosol chemical composition and absorbing components that are required for the RI estimation are demanding and not always available. The mass loading of black carbon (BC) is an example of one of these absorbing components with relatively sparse relevant measurements [4,35]. As a result, iterative schemes that use assumed values of complex RI in combination with other assumptions are commonly applied to minimize differences between the measured and calculated aerosol properties of interest, such as PM10 [34]. For humid conditions, the particle size distributions exhibit a sensitivity to water uptake by particles [36], and therefore the hygroscopic growth factor (HGF) and its dependence on particle chemical composition must be considered in closure-related studies.
While closure studies using the microphysical, optical, chemical components, and ambient relative humidity (RH) are a well-known framework that has been used intensively for decades [37,38,39], its successful applications are mainly limited to the ground-based observations [21,40,41]. Given the complexity of conducting airborne measurements and the growing demand to use these measurements for process-oriented model validation and climate model assessments, there is a strong need to extend this framework to comprehensive airborne datasets [22,42,43]. The primary purpose of our work is to attempt to formally extend the framework for ground-based optical closure studies to airborne data sets by answering the following three main questions:
- (1)
- What level of agreement can be achieved between the in-flight measured and calculated values of total scattering coefficient at ambient RH?
- (2)
- What is the effect of ignoring the influence of chemical composition data on this agreement?
- (3)
- How sensitive is this agreement to the assumed RI value, particularly if the assumed RI is non-representative of the ambient aerosol?
The first question is associated with the consistency of the airborne measurements of the particle size distributions and optical properties when aerosol chemical composition data are available (a preferred “complete” dataset). The second and third questions can be considered as “practical-oriented” because they are focused mostly on practical situations when information on the chemical composition is not available (an “incomplete” dataset) and assumptions about aerosol composition are required. Given that the dimension/weight of several instruments commonly deployed to measure the aerosol chemical composition, such as the miniaturized version of the aircraft-compatible single particle mass spectrometer (miniSPLAT; [44]) and the Aerodyne Aerosol Mass Spectrometer (AMS), is substantial, they are deployed less frequently on mid-to-large size aerial platforms. Moreover, they cannot be deployed on small aerial platforms, such as small or unmanned aircraft. To assess the extended framework and evaluate the relevant assumptions through answering these three important questions, we use integrated airborne data collected during the recent Two-Column Aerosol Project (TCAP; http://campaign.arm.gov/tcap/) over the North Atlantic Ocean and US coastal region (Cape Cod, MA, USA).
We outline in the next section our approach for extending the ground-based framework for conducting optical closure experiments to airborne data. In Section 3 we briefly describe the TCAP data, which represent mainly non-absorbing aerosol and include measured size spectra, chemical composition and total scattering [45]. The complementary model components of our approach and the corresponding assumptions are discussed in Section 4. These assumptions, such as the homogeneous internal mixture, are reasonable and permit us to calculate the HGF and complex RI at ambient RH when additional information is missing. In Section 5, the calculated and measured total scattering coefficients are compared for the wide range of atmospheric conditions observed during TCAP flights conducted in July of 2012, including conditions with low and high ambient RH. The sensitivity of the calculated scattering to the RI and related issues are further discussed in Section 6. In particular, this section emphasizes that the ability to make complementary measurements of chemical composition holds promise for properly specifying the RI, and thus for improving the accuracy of total scattering calculations. The last section presents a summary of key findings.
2. Approach
Figure 1 outlines the major components and main steps in conducting our optical closure experiment by obtaining total scattering coefficients at ambient RH from airborne measurements and Mie calculations. Although our approach relies heavily on several important components and assumptions, such as homogeneous internal mixture and spherical geometry of particles, introduced earlier by previous studies [21,36,46], well-known challenges experienced in collection and interpretation of airborne data make evaluation of this unified approach mandatory. Our approach, as displayed in Figure 1, involves three major components: (1) integrated measurements of aerosol properties (Figure 1; top panel); (2) calculations of the ambient scattering coefficient using Mie theory and estimated hygroscopic growth factor (HGF) (Figure 1; middle panel), and (3) comparison of the scattering coefficients observed and calculated at ambient conditions (Figure 1; bottom panel). Note in Figure 1 how chemical composition information becomes encoded into the improved size spectra, making calculations of scattering more accurate. The left-hand part of diagram (Figure 1; top and bottom panels) illustrates the process of obtaining the observed total scattering at ambient conditions. For the TCAP data set used in this work, this step involves analyzing the total scattering measured by an airborne nephelometer at low RH and the light scattering hygroscopic growth f(RH) measured using a humidification system. The central part of diagram (Figure 1; top and middle panels) illustrates how the complex RI at dry conditions, derived from the chemical composition data, is used to adjust the particle size distributions. Note that the chemical composition data are also used to estimate the RH-dependent HGF. The latter is required for converting the dry complex RI and dry size spectra into their ambient counterparts. The right-hand part of diagram (Figure 1; top and middle panels) demonstrates how the ambient size spectra are obtained from the original (without RI-based correction) and adjusted (with RI-based correction) OPC-derived size distributions. The ambient complex RI and size distributions (both original and adjusted) are used as input for the Mie calculations. The output is the corresponding model total scattering coefficients calculated at ambient conditions. As we shall see, differences between model coefficients calculated using the original and the adjusted size distributions illustrate the importance of the RI-based correction for the total scattering calculation.
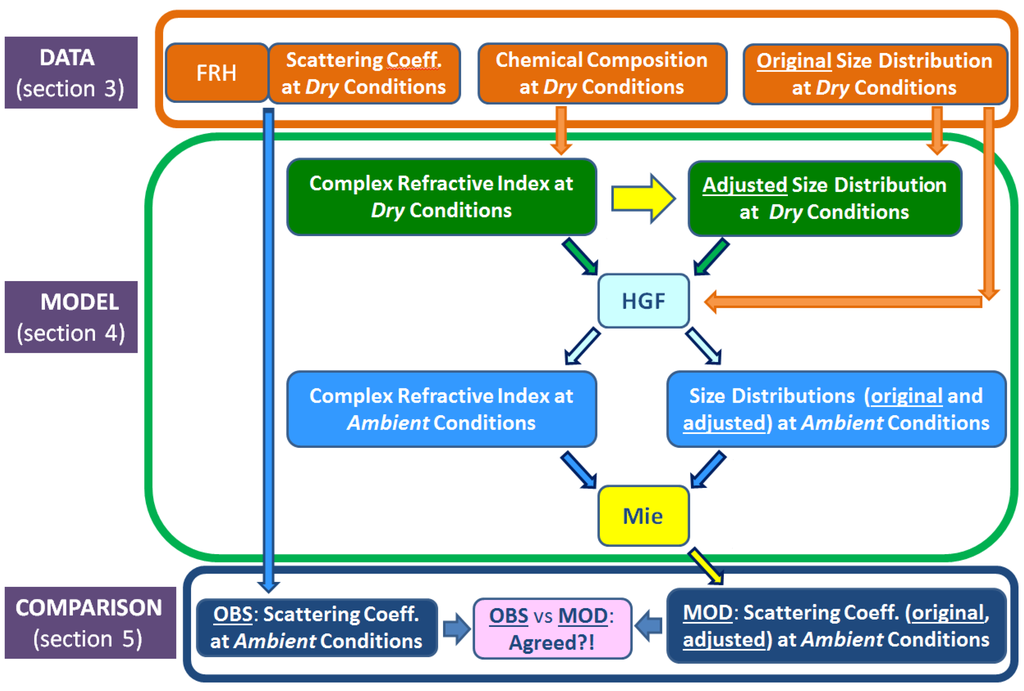
Figure 1.
Schematic diagram summarizing the framework for an optical closure experiment using airborne data. The figure illustrates the link between the measured dry and ambient scattering coefficients (left part of diagram; top and bottom panels) and the connection between the measured dry chemical composition/size spectra and the calculated ambient scattering coefficient (center and right parts of diagram). Ambient size spectra (light blue, right) are obtained from the dry size distributions without (orange) and with (green) the RI-based correction, respectively. The estimated ambient size spectra (light blue, right) together with the ambient RI (light blue, left) are required as input for Mie calculations (yellow) of the corresponding total scattering coefficients (navy blue, right). See indicated text section for details of each component (Data, Model, Comparison).
3. Data
This section is meant to survey the observational components of our framework (Figure 1; top panel) by reviewing the TCAP airborne data used in this investigation. The TCAP field campaign was designed to provide a comprehensive data set that can be used to investigate important climate science questions, including those related to aerosols. Conducted from June 2012 through June 2013, TCAP involved summer and winter periods of intensive aircraft observations that included the U.S. Department of Energy (DOE) Gulfstream-159 (G-1) aircraft. The G-1 typically sampled at multiple altitudes within two atmospheric columns, one located over Cape Cod, MA and a second over the Atlantic Ocean several hundred kilometers from the coast. Details of TCAP are given in Berg et al. [45]. To illustrate performance of our unified approach (Figure 1), we focus on the TCAP summertime data.
An in situ instrumentation suite on board the DOE G-1 aircraft [24] together with airborne remote sensing sensors, such as the Spectrometer for Sky-Scanning, Sun-Tracking Atmospheric Research (4STAR; [26]) and the High Spectral Resolution Lidar (HSRL-2; [8]), were deployed during TCAP. Note that the HSRL-2 was operated aboard a NASA B-200 aircraft. Here, we focus on the instruments relevant to our study to improve calculations of the total scattering coefficient at ambient conditions. These calculations are based on Mie theory and require the ambient aerosol size distribution and complex RI. Aerosol size spectra, chemical composition and total scattering data were collected with high temporal resolution (<1 min) during the TCAP flights. We use these data to compute the corresponding averaged characteristics for each flight leg (FL), which is defined as a straight level run at different altitudes with variable duration of approximately 5–15 min. We employ these FL-averaged aerosol characteristics in our investigation, consistent with earlier studies [28,29,46].
Particle size distributions were measured simultaneously by three airborne OPC instruments: an Ultra-High Sensitivity Aerosol Spectrometer (UHSAS, size range 0.06–1 µm), a Passive Cavity Aerosol Spectrometer (PCASP; size range 0.13–3 µm) and a Cloud and Aerosol Spectrometer (CAS; size range 0.6–>10 µm). These three instruments were mounted within PMS canisters on the same pylon underneath the right wing of the G-1 aircraft. The UHSAS and PCASP were operated with anti-ice heaters enabled and therefore the measured aerosol distributions are assumed to be dry. However, the CAS measured particle size distributions at ambient conditions. All three instruments were calibrated using polystyrene latex sphere (PSL) beads. The measured size distributions from the aforementioned probes are recovered from the raw counts (taking into account collection efficiencies and sampling volumes), merged, and smoothed (Appendix A) using a kernel based on Twomey’s algorithm [42,47,48]. Figure 2 shows the resulting size distributions averaged over each FL on 21 July 2012. The altitude of each FL is shown in Figure 3.
Particle size spectra measured by these three OPC instruments (UHSAS, PCASP, and CAS) cover different particle size ranges. However, these instruments employ a similar underlying operating principle for determining particle size, namely light scattering by individual particles. The conversion of the scattered light into particle size requires the RI, which depends on the chemical composition of particles, thus demanding an accurate RI estimation. During TCAP, information on the organic and inorganic species mass loading and black carbon (BC) mass in individual aerosol particles came from complementary Aerodyne AMS and Droplet Measurement Technology Single Particle Soot Photometer (SP2; 0.06–0.6 µm range of mass-equivalent diameter; [49,50]) measurements, respectively (Figure 3). The AMS has a near unity transmission efficiency for particles with vacuum aerodynamic diameters between 0.06 and 0.6 µm, which falls to 50% at 1 µm, and is negligible above 1.5 µm and below 0.06 µm. The RH inside the SP2 does not exceed 10% and the AMS can differentiate particle-phase water from other species; therefore, the acquired chemical composition data represent dry conditions. Figure 3 illustrates that the aerosol chemical composition on 21 July 2012 was dominated by organic matter (OM); dominance of OM (generally greater than 70%) was observed for all TCAP flights [45].
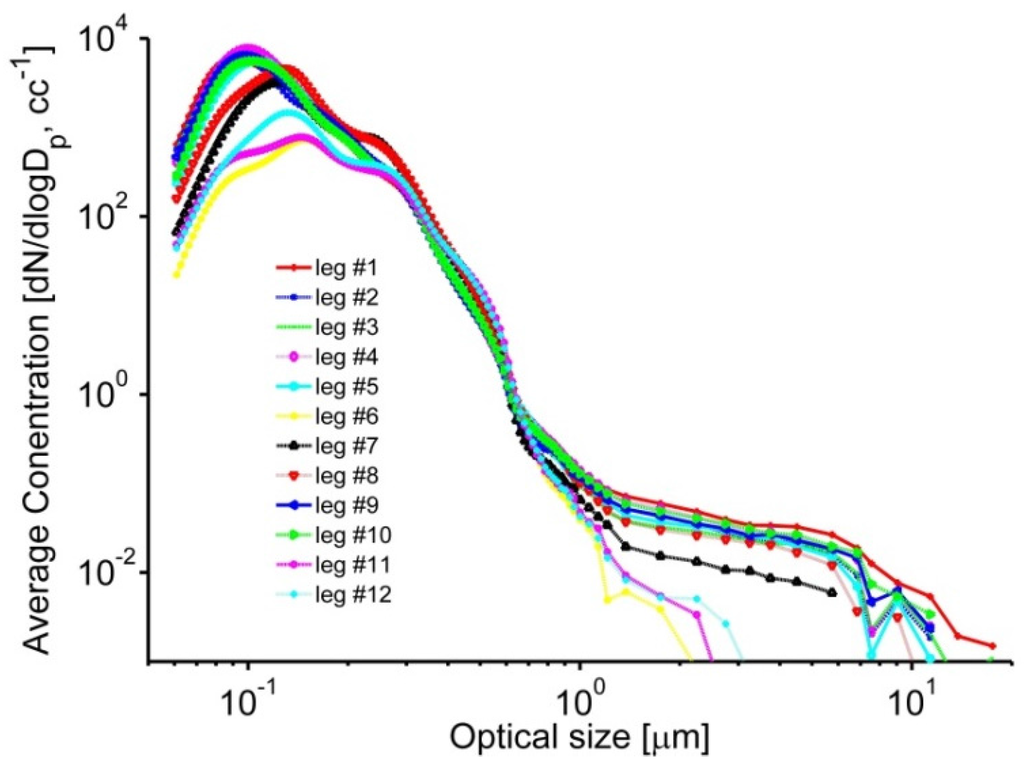
Figure 2.
Example of combined size distributions generated for each FL during a given day (21 July 2012). Here and in the following plots, aerosol characteristics represent FL-averaged values. Elevation and time of each FL are shown in Figure 3.
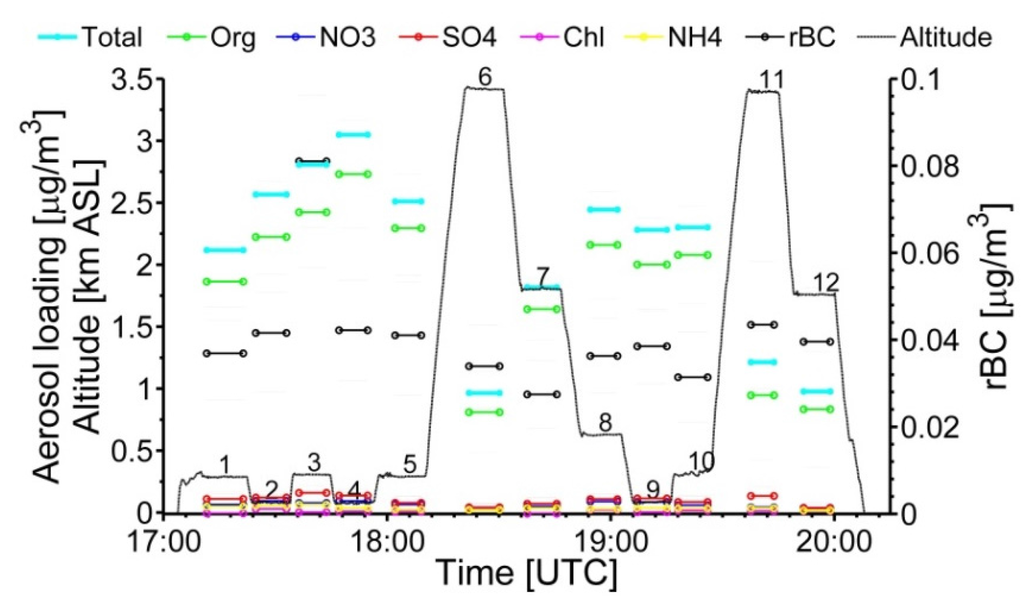
Figure 3.
Example of FL-dependent chemical compositions (colored lines) and BC (thick black lines) mass measured by the AMS and SP2, respectively (21 July 2012). Additionally, altitude (thin black line) as a function of FL is included. FLs are labeled with numbers 1 through 12 on top of the thin black altitude line.
The total scattering coefficient at three wavelengths (0.45, 0.55, 0.7 µm) was measured at dry (RH < 20%) conditions using a TSI integrating nephelometer (Figure 4), while the light scattering hygroscopic growth, known as f(RH), was measured using a humidification system at three defined RHs (near 45%, 65% and 90%) at a single wavelength (0.525 µm) [51]. Similar to Shinozuka et al. [52], we adjust the f(RH) obtained at the 0.525 µm wavelength to the nephelometer wavelengths (0.45, 0.55, 0.7 µm) by multiplying the obtained f(RH) by 0.98, 1.01 and 1.04, respectively. The conventional truncation error correction [53] has been applied to the total scattering measured by the integrating nephelometer. We obtain the total scattering at ambient conditions (σobs) at three wavelengths (0.45, 0.55, 0.7 µm) using both the adjusted f(RH) and spectrally-dependent measured dry total scattering. It is to be noted that measurement uncertainties in the reported total scattering by the integrating nephelometer are quite small (~10%) for sub-µm, but can be considerable for super-µm particles (~50%) [53,54]. For a given FL, we assume that the combined uncertainty of σobs depends on its variability within FL (defined here as the standard deviation) and the measurement uncertainty [46]. In other words, the FL-dependent combined uncertainty in the ambient total scattering coefficient is comparable with the measurement uncertainty (10%) for a homogeneous FL and can exceed it substantially for an inhomogeneous FL where the standard deviation is large.
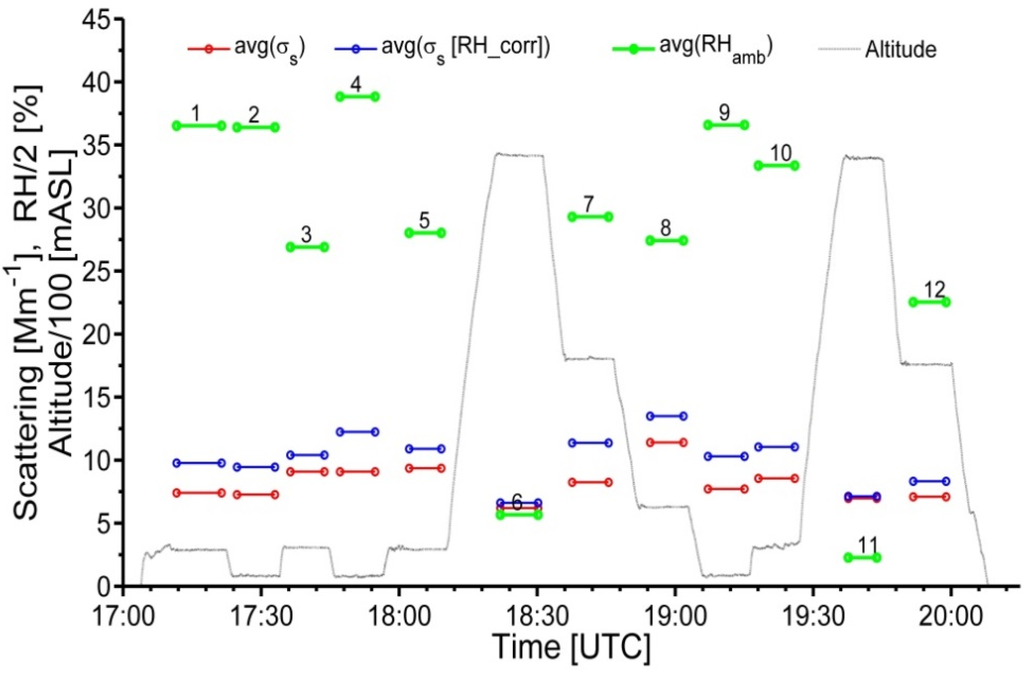
Figure 4.
The same as Figure 3, except for the dry scattering measured by nephelometer (red lines) and ambient scattering obtained with measured f(RH) (blue lines) at 0.55 µm wavelength and ambient RH (green lines). FLs are labeled with numbers 1 through 12 on top of green lines.
TCAP aircraft data were screened prior to use in our study. To ensure that only high quality data are used, two quality assurance screening criteria are applied. First, we check the data streams for consistency between the size spectra, chemical composition and total scattering to prevent invalid data entry. Second, we consider only periods in which all data streams are available. For example, PCASP-measured size distributions were not available for several flights (e.g., 14 and 15 July) and the corresponding combined size distributions were generated from spectra measured by two instruments (UHSAS and CAS) only. These combined distributions obtained without PCASP data are excluded from our analysis. Similar to the size distributions, ambient scattering coefficients were not available for some episodes as well. Given the large uncertainties of the obtained f(RH) at very humid conditions (RH > 80%), the corresponding cases are also excluded from our analysis. Using the quality assurance screening criteria reduces the size of the original dataset by about 30%. A total of 45 TCAP FLs with the good quality data are included in our analysis. Further discussion of TCAP flight data quality can be found in Berg et al. [45].
4. Model and Adjustments
This section outlines the model components of our framework for an airborne optical closure experiment (Figure 1; middle panel) and describes the major assumptions required for estimating the hygroscopic growth factor (Section 4.1), ambient values of complex refractive index (Section 4.2) and correcting the OPC-derived size distributions (Section 4.3). The RI-based corrections of the size spectra together with estimates of HGF and complex RI form the basis for calculating the ambient total scattering (Section 4.4) with improved accuracy.
4.1. Hygroscopic Growth Factor
Water uptake by aerosol particles results in increased particle size and modifies the complex RI [36]. To account for changes associated with water absorption, information on aerosol chemical composition and hygroscopicity is needed. Typically, aerosol particles are a mixture of organic and inorganic substances. We estimate the hygroscopic growth factor of the mixture (HGFmix) from the volume fractions of individual components (ε) and their growth factors as the volume-weighted average [46]:
We convert the mass fractions measured by the AMS and SP2 instruments (Section 2) into the required volume fractions using densities reported in literature and listed in Table 1. We emphasize that the AMS and SP2 data are capturing a limited size range (sub-micron particles; Section 2) only. However, we use the AMS/SP2 data to infer the chemical composition of the entire size range (both sub- and super-micron particles). The application of the AMS/SP2 data for the entire size range should be appropriate for cases where the relative contribution of sub-micron particles to the scattering coefficient is dominant. Given that the aircraft data collected during the TCAP data represent such a favorable case with large contributions of sub-micron particles (Appendix B), application of the AMS/SP2 data for the entire size range is appropriate.

Table 1.
Assumed size-independent density, real and imaginary parts of complex refractive index (RI) at 0.55 µm wavelength, and hygroscopic growth factor (HGF) values used in this study. Values are taken from [46,55,56].
| OM | SO4 | NO3 | Chl | NH4 | BC | Water | |
|---|---|---|---|---|---|---|---|
| Density (g/cm3) | 1.4 | 1.8 | 1.8 | 1.53 | 1.8 | 1.8 | 1.0 |
| RI (real) | 1.45 | 1.52 | 1.5 | 1.64 | 1.5 | 1.85 | 1.33 |
| RI (imag) | 0.0 | 0 | 0 | 0 | 0 | 0.71 | 0 |
| HGF (RH = 80%) | 1.07 | 1.50 | 1.50 | 1.9 | 1.50 | 1.0 | - |
Although the growth factor can be quite sensitive to the particle size [21,57], we assume that particles with different sizes have the same HGFmix. HGFmix from Equation (1) represents the hygroscopic growth factor at a specified relative humidity (RHwet = 80%). To obtain HGFmix for a different humidity, we assume that HGFmix follows the power law form [19,21]:
where RHdry is 30% . The dimensionless exponent γ is calculated as:
Recall that OM is the dominant component of aerosol sampled during the TCAP flights (Figure 2 and [45]). Given that the hygroscopic growth factor of the OM is relatively small compared to other chemical components (Table 1), the calculated RH-dependent HGFmix does not exceed 1.3 and approaches 1 as RH decreases (Figure 5).
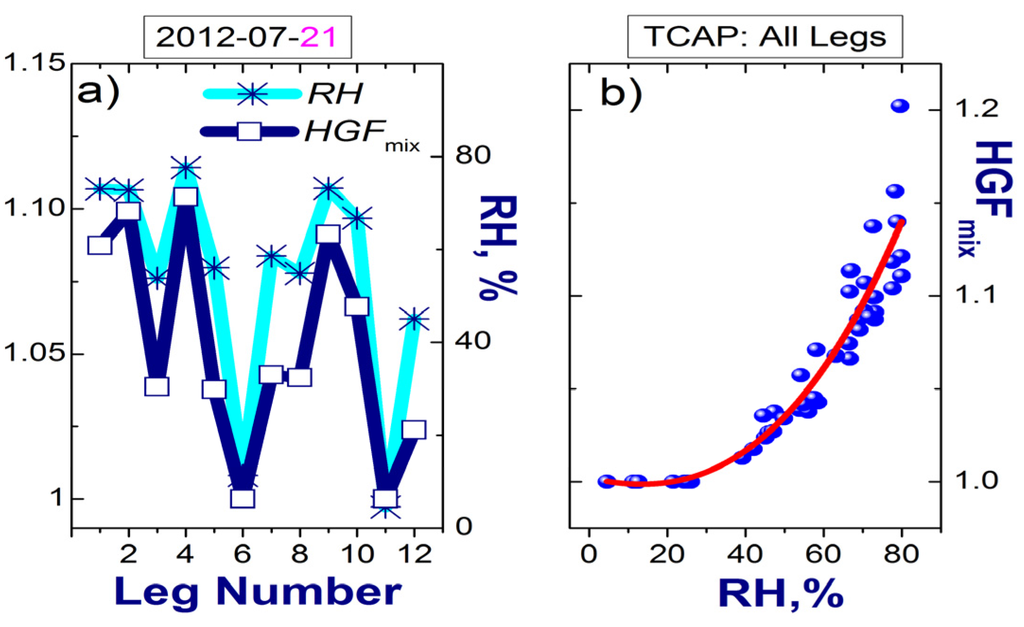
Figure 5.
Example of ambient RH and RH-dependent HGFmix calculated for each FL during a given day (21 July 2012) (a); scatterplot of RH-dependent HGFmix (blue dots) for all TCAP FLs used in this study (Section 3) with polynomial fit (red line) (b).
4.2. Dry and Wet Refractive Indices
We apply a volume weighting approach to calculate the real (ndry) and imaginary (kdry) parts of the complex RI (mdry) of particles at dry conditions:
where mdry,i represents the real (ndry,i) or imaginary (kdry,i) part for each measured chemical component (Table 1). The underlying assumption of this popular approach is that the contribution of each chemical component to the light scattering and absorption is proportional to its volume fraction (εi). It should be emphasized that chemical composition, in general, depends on the particle size [57]. The same is true for the real (ndry) and imaginary (kdry) parts of the complex RI [40]. Here we assume that particles with different sizes have the same chemical composition, and therefore the same RI.
The calculated dry RIs are applied to compute the corresponding ambient values [21,58]:
where HGFmix is the RH-dependent parameter defined in the previous section. As HGFmix increases noticeably (near 1.1; Figure 5a), water becomes an influential component and the ambient RI decreases toward the water RI (Figure 6). In contrast, when HGFmix is quite small (near 1; Figure 5a), the ambient RI increases toward the dry RI (Figure 6). Note that large values of the imaginary part of the RI (e.g., FL numbers 3, 6, 11 and 12) represent conditions where the relative contribution of BC to the total loading is substantial (>3%; Figure 3) and exceeds those for other FLs roughly by a factor of two.
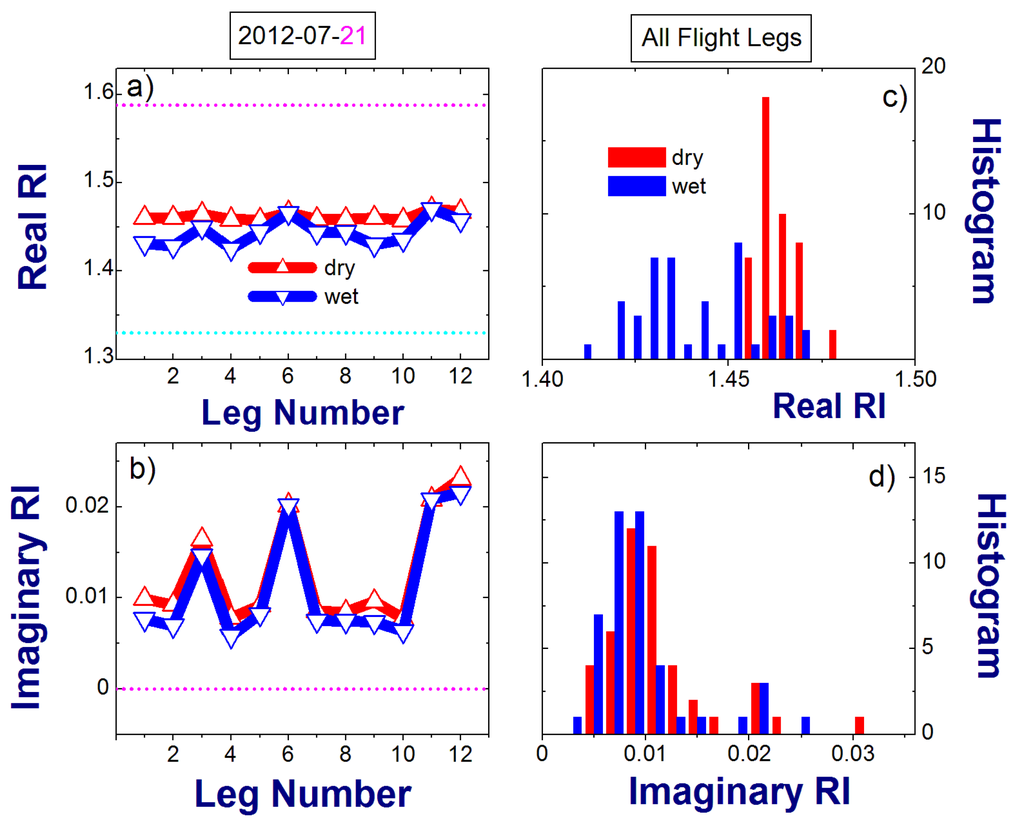
Figure 6.
Example of RH-dependent dry and ambient values of the real and imaginary parts of the complex RI calculated for each FL during a given day (21 July 2012) (a,b); the corresponding histograms obtained for all TCAP FLs (c,d). The real (nOPC = 1.588) and imaginary (kOPC = 0) parts of the complex RI used for OPC calibration are shown in (a) (magenta) and (b) (magenta), respectively. The real RI of water (nwater = 1.33) is also shown (a, cyan). The imaginary RI of water (kwater = 0) is equal to the imaginary RI used for OPC calibration (kOPC = 0).
4.3. Size Distribution
There is a substantial difference between the RI used for OPC calibration (nOPC = 1.588; kOPC = 0) and the FL-dependent dry RI calculated from chemical composition data (Figure 6). To take into account this difference, we apply the RI-based correction to adjust the OPC-derived size distributions (see Appendix C for further discussion). It should be emphasized that the PSL-based OPC calibration applies a RI that very likely overestimates those for the typical sub-micron aerosol. Since a higher RI produces a larger scattering signal, a particle with smaller size and higher RI scatters the same as a particle with larger size and smaller RI. As a result, all of the adjustments of the OPC calibration to the actual RI will increase the size of measured particles, and consequently will increase the total scattering for almost any reasonable size distribution. Moreover, adding an absorbing component further increases the size of the measured particles—after adjustment—due to the reduction of the particle’s scattering and consequent decrease of its optical size. We will illustrate such increases of particle size and scattering in the following two sections.
The size spectra adjustment involves modification of the OPC-measured dry diameter of particles:
where f(Ddry) is the size-dependent scaling factor obtained from theoretical response calculations by extending well-established approaches for correcting the OPC-derived size distributions [30,31,34]. In our work we take advantage of available AMS and SP2 measurements (Section 3) for estimating the complex RI (Section 4.2), and thus our approach can be applied to both non-absorbing and absorbing aerosol.
The original OPC-derived and corrected dry size distributions are related as:
In other words, the size-dependent correction (Equation (6)) modifies the original OPC-derived size spectra in two ways by (1) changing bin boundaries (horizontal shifting; replacement of Ddry with Ddry,adj) and (2) scaling of the normalized number concentration (vertical shifting; term d log Ddry /d log Ddry,adj).
The increase of particle diameter due to the water uptake is expressed as:
where the size-independent HGFmix(RH) is calculated from the chemical composition measurements (Section 4.1).
The corresponding dry and wet size distributions are related by the following equations:
Note that functions in Equation (9) (left-hand versus right-hand side) have different arguments; for example, dN (Dwet) ∕ d log Dwet (Equation (9a); left-hand side) and dN (Ddry) ∕ d log Ddry (Equation (9a); right-hand side). In comparison with the size-dependent scaling factor (Equation (6)), the size-independent adjustment (Equation (8)) associated with water uptake modifies the original OPC-derived size spectra by changing bin boundaries only (horizontal shifting; e.g., replacement of Ddry with Dwet; Equation (9a)); this adjustment does not cause the vertical scaling of the normalized number concentration (Equation (7) versus Equation (9)).
To illustrate the conversion of the measured dry size distribution into the corresponding wet size spectra (Equations (8a) and (9a)), we select two flight legs with high (RH~78%) and low (RH~5%) values of relative humidity (Figure 5a). The RH-related increase of particle size results in the horizontal shifting of the size distribution (wet size spectra versus dry size spectra) and this shifting is seen for the humid conditions (Figure 7a versus c). Since the theoretical response curves are multivalued for a resonance region (particle diameter > 0.5 µm) (Appendix C), the adjusted size distributions obtained at ambient RH with the size-dependent scaling factor (Equations (8b) and (9b)) exhibit a “bumpy” behavior for this region as well (Figure 7b,d).
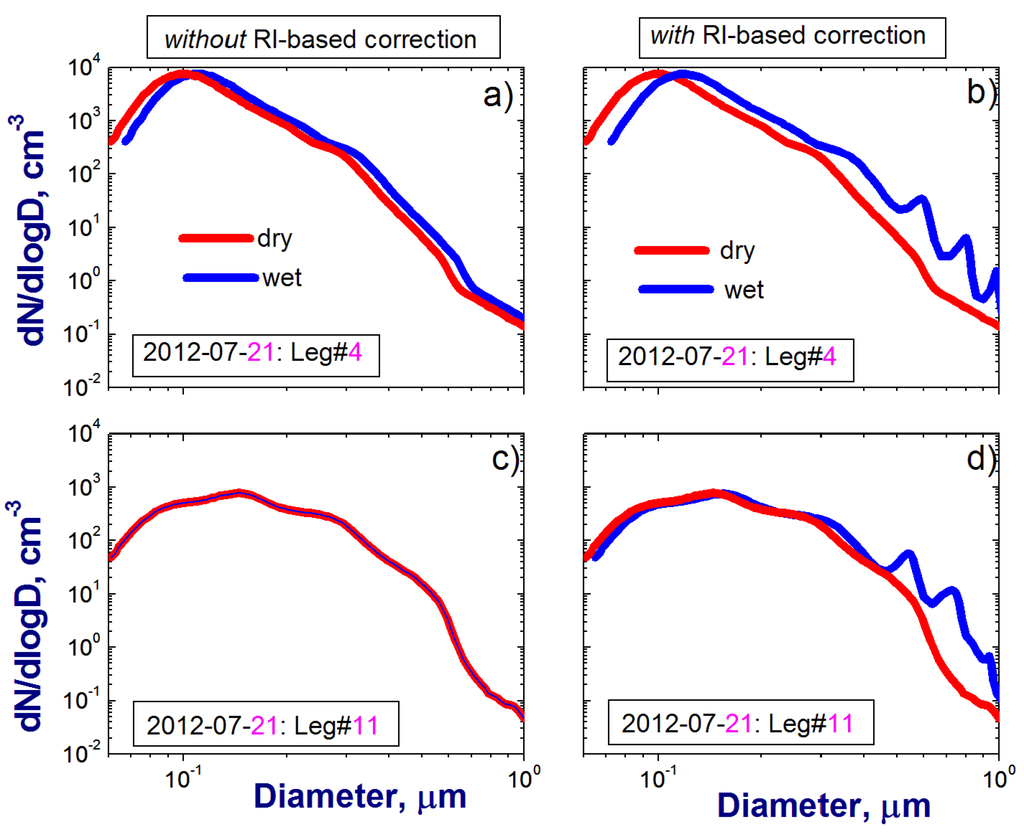
Figure 7.
Example of size distributions obtained for two FLs (21 July 2012) with high (a,b) and low (c,d) values of ambient RH, respectively. Measured dry size distributions (red) are converted into their wet counterparts (blue) without (a,c) and with (b,d) the size-dependent scaling factor.
4.4. Scattering Coefficient Calculations
We calculate the ambient total scattering coefficient using both the ambient complex RI with real (nwet) and imaginary (kwet) parts (e.g., Figure 6a,b) and the ambient size distributions (e.g., Figure 7b,d). The calculations of total scattering coefficients σmod,org and σmod,adj are performed for ambient size distributions obtained without (dN ∕ d log Dwet) and with (dN ∕ d log Dwet,adj) the RI-based correction, respectively. Recall the RI is obtained at a single wavelength (0.55 µm). Results from previous studies [59,60] suggest that the spectral variability of the real part of RI is quite small within the visible spectral range considered here (0.45–0.7 µm). Therefore, the obtained real RI (0.55 µm) is likely representative for this spectral range and it can be applied to calculate the spectrally-resolved total scattering coefficient of weakly-absorbing aerosol. Note that the values of the imaginary part of RI at 0.55 µm wavelength are quite small (Figure 6b) and thus they represent weakly-absorbing aerosol. For such aerosol, the total scattering is only slightly affected by changes of the imaginary part of RI [59,60]; therefore its spectral dependence can be ignored for the dataset considered here. We perform calculations of the total scattering at three wavelengths (0.45, 0.55, 0.7 µm) using the same complex RI obtained at 0.55 µm wavelength.
Our calculations are based on the Mie code developed by Barber and Hill [61] assuming that particles are homogeneous spheres and effective values of the complex RI are size-independent (particles are assumed to be a homogeneous internal mixture; Section 4.2). Note that other computational methods should be applied to calculate optical properties of particles with inhomogeneous internal mixing and aggregate morphology [62] although the influence of the internal mixing and particle geometry on the total scattering is quite small for submicron particles [20,63,64]. We calculate the total scattering coefficients using the original and corrected size distributions with different cut-offs (1- and 2-µm). Large uncertainties (up to 50%) of the measured total scattering associated with coarse mode particles (particle diameter >1 µm) [54], the limited size range of chemical composition data (particle diameter <1.0 µm) (Section 2), and small (<7% on average) relative contribution of coarse mode particles to the scattering coefficient (Appendix B) are the three main factors that led to the selected cut-offs. Note that there is a small difference (~2% on average) between total scattering values calculated for the 1- and 2-µm cut-offs (Appendix B), mainly due to the small fraction of supermicron particles for FLs considered here. Below, we show the ambient scattering coefficients (σmod,org and σmod,adj) calculated with the 2-µm cut-off only.
Uncertainties for the calculated scattering coefficient are associated mainly with ambiguities of the required inputs (ambient size distribution and complex RI) and model assumptions (homogeneous internal mixture). According to previous studies with similar model inputs [65], the uncertainties for the calculated dry total scattering are about 20%. Although assumptions associated with the hygroscopic growth factor estimation (Section 4.1) are likely to introduce additional ambiguities associated with the required inputs, we assume that the uncertainties obtained earlier for the dry scattering (20%) are also representative (at least as a lower limit) for the ambient total scattering considered in our study. The influence of the uncertainties mentioned above on agreement between the observed and calculated values at ambient conditions is considered in the next section.
5. Results
This Section outlines the comparison component of our framework for an airborne optical closure experiment (Figure 1; bottom panel) and includes time series and statistics of the observed and calculated total scattering coefficients at ambient conditions. This Section is designed to address questions 1 (level of agreement for “complete” dataset) and 2 (level of agreement for “incomplete” dataset given that the impact of chemical composition data on improved size spectra is ignored).
Let us start with the time series (Figure 8). The total modeled scattering σmod,org calculated for the original size distribution substantially underestimates the observed scattering σobs for the majority of FLs considered on 21 July 2012. In contrast to σmod,org, the total scattering σmod,adj calculated for the adjusted size distribution matches the observed scattering σobs reasonably well.
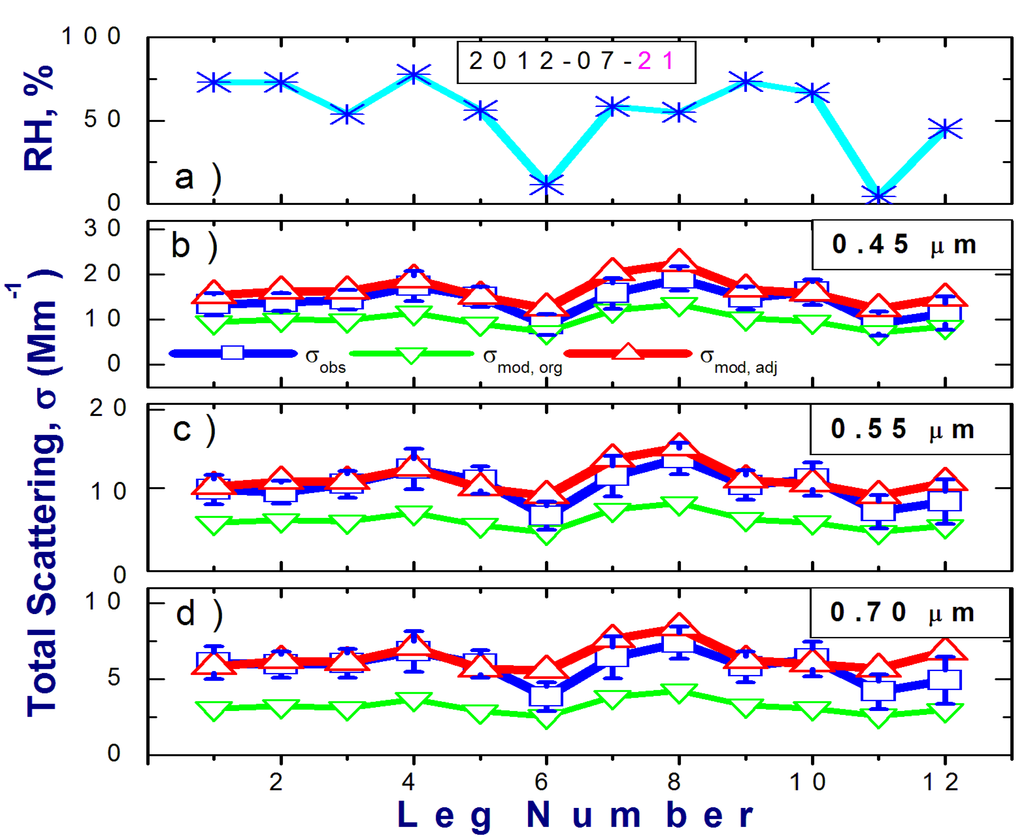
Figure 8.
Ambient RH (a) and spectral values (b–d) of the total scattering coefficient measured (blue) and calculated for the original (green) and RI-based adjusted (red) size distributions for twelve FLs on 21 July 2012 at three wavelengths: (b) 0.45; (c) 0.55 and (d) 0.70 µm. Error bars represent uncertainties of measured scattering coefficient.
The differences in Figure 8 between calculated (σmod,org and σmod,adj) and observed (σobs) scattering illustrate three main points. First, the observed scattering σobs tends to follow the ambient RH variations. For example, the lowest values of σobs occurred for dry conditions (FL numbers 6 and 11, where RH < 10%). Second, inclusion of the hygroscopic growth of particles associated with water uptake alone (Section 4.3) is not sufficient for matching the observed ambient scattering (σmod,org versus σobs). In addition to the hygroscopic growth, application of the RI-based correction to the dry size distributions measured by the OPCs (Section 4.3) is required (σmod,adj versus σobs). Finally, the calculated scattering σmod,adj reproduces reasonably well the observed scattering σobs at all three wavelengths considered here (0.45, 0.55 and 0.70 µm), suggesting that our assumption of a spectrally-independent RI seems reasonable for the weakly-absorbing aerosol sampled during the TCAP flights.
The substantial underestimation of σmod,org versus σobs noticeable in Figure 8 is more obvious in the scatterplot of all considered TCAP FLs shown in Figure 9a. Since both the measured and calculated scattering can exhibit large uncertainties, the bivariate weighted method [66] is used to find the best linear fit. This method owes its popularity [67,68] to its versatility, robustness and ability to use uncertainties of both x and y variables to find the slope and intercept of a best fit straight line to the data [69]; additionally, standard errors of the slope and intercept may be estimated.
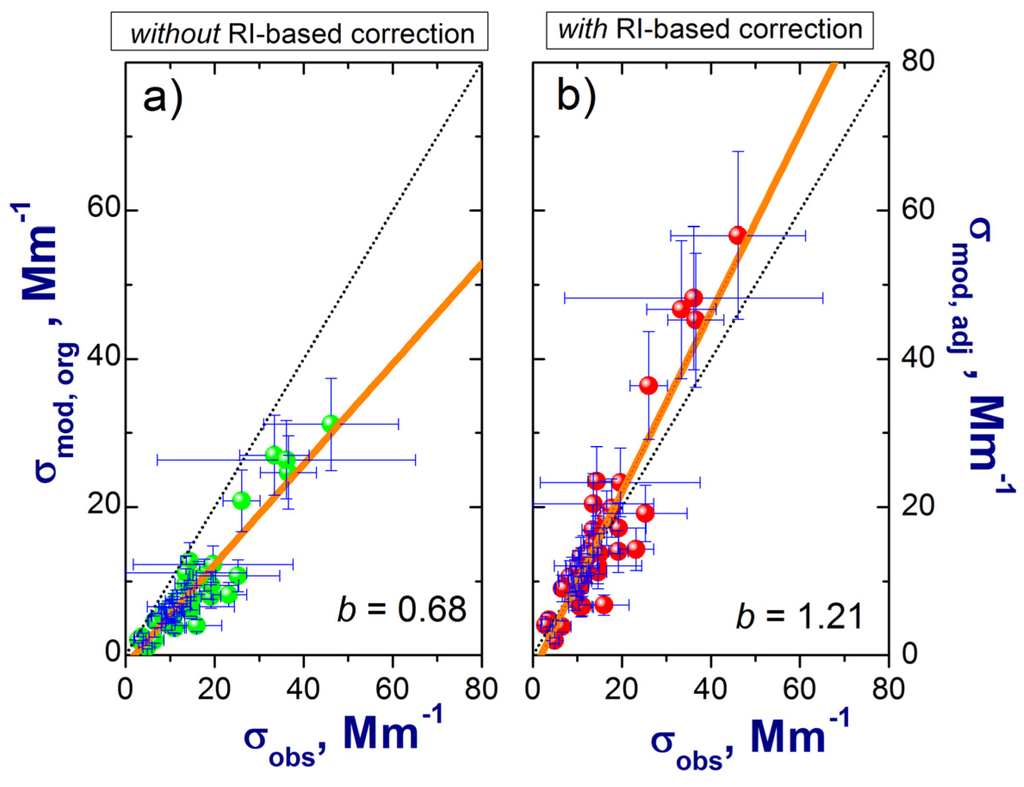
Figure 9.
Comparison of the ambient total scattering observed (σobs) with ambient total scattering calculated (σmod) for the original (a) and adjusted (b) size distributions at 0.55 µm wavelength for all TCAP FLs. Here b is the slope of the linear regression fits to the data (straight orange lines). Error bars represent uncertainties of measured (Section 3) and calculated (Section 4.4) scattering coefficients.
The slope of the corresponding linear regression fit is quite small (0.68; Figure 9a). The slope increases from 0.68 to 1.21 when the RI-based correction is applied to the OPC-derived size distributions (Figure 9a versus b). There are four points with large observed values of scattering coefficient (σobs > 30 Mm−1, Figure 9). Close examination reveals that these points represent either large values of RH (>67%) or highly inhomogeneous FLs (standard deviation of σobs~30 Mm−1). Removal of these points reduces slightly the slope (from 0.68 to 0.65, Figure 9a; and from 1.21 to 1.17, Figure 9b) and increases the intercept (from −1.30 to −1.11, Figure 9a; and from −2.25 to −1.91, Figure 9b). Additionally, such removal reduces the difference between the mean values of σobs and σmod,adj considerably (roughly from 10% to 0.5%), while having little effect on the discrepancy between the mean values of σobs and σmod (about 40%).
Similar changes of parameters (slope and intercept) obtained with the bivariate weighted method can be achieved by increasing the uncertainties of the calculated scattering coefficient but keeping uncertainties of the observed scattering the same (Figure 10). These changes are mostly caused by the influence of four points with large values of the observed/calculated scattering coefficient on the parameters of fitting line. The influence of these points decreases when assumed uncertainties of the calculated scattering are increased. Note that the assumed uncertainties (20%) of the calculated scattering represent dry conditions (Section 4) and thus, they likely are underestimated for FLs with moderate and high RHs (e.g., due to inaccurate treatment of the RH dependence of the HGFmix and its components).
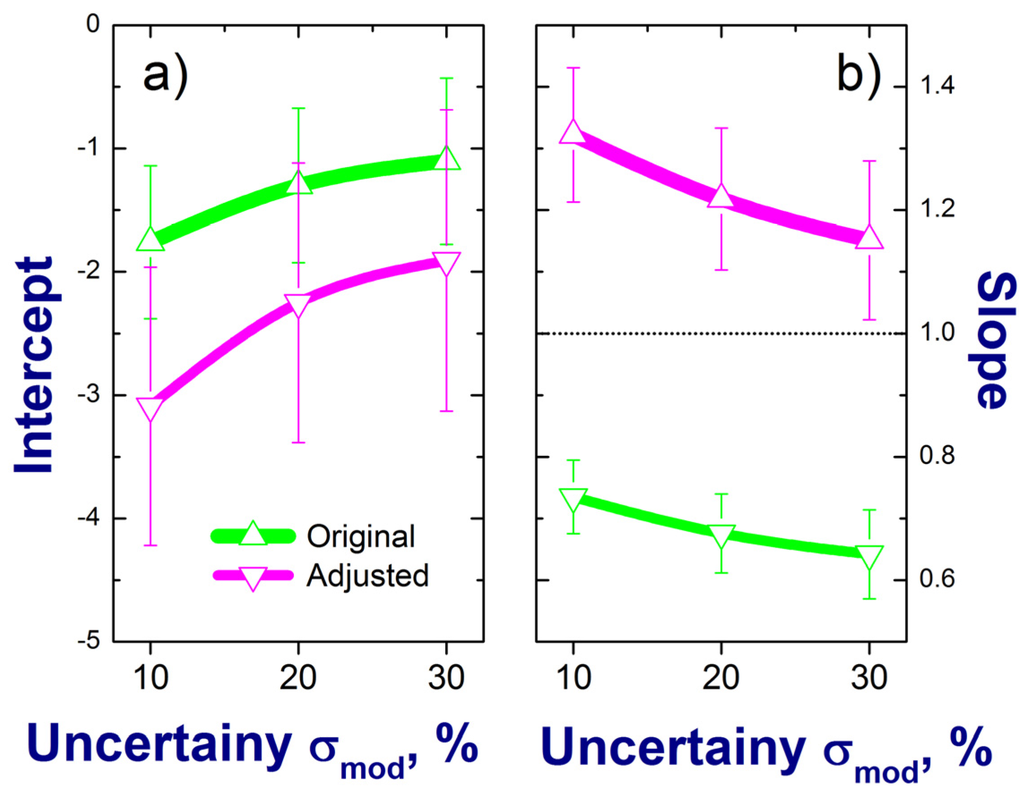
Figure 10.
Intercept (a) and slope (b) of the linear regression fits (e.g., Figure 9) as a function of uncertainty for the ambient total scattering calculated for the original (without RI-based correction) and adjusted (with RI-based correction) size distributions. Error bars represent the standard errors of the displayed parameters (see text for details).
Comparable slopes for linear regression fits (σmod,adj versus σobs) are obtained at the other two wavelengths (0.45 and 0.7 µm) (Table 2). The weak spectral dependence of these slopes suggests that the complex RI obtained at 0.55 µm wavelength could be applied to estimate the spectrally-resolved total scattering within the mid-visible range (0.45–0.70 µm) reasonably well.
On average, the total scattering σmod,org calculated for the original OPC-derived size distribution underestimates the observed scattering σobs substantially (Table 2). For example, underestimation of the mean value exceeds 40% at 0.55 µm wavelength. However, the total scattering σmod,adj calculated for the RI-adjusted size distributions and the observed scattering σobs have comparable mean values (Table 2): the relative difference between them is quite small at three given wavelengths (about 13% at 0.45 µm, 7% at 0.55 µm and 12% at 0.70 µm). In comparison with the mean values, the corresponding standard deviations are in moderate agreement (~40%). In addition to the basic statistics of mean and standard deviation, we calculate the corresponding Root Mean Squared Error (RMSE), which is defined as the root mean squared difference between the observed σobs and the calculated scattering coefficients in question. The corresponding RMSEs are about 7 and 5 Mm−1 for σmod,org and σmod,adj at 0.55 µm wavelength, respectively. In other words, RMSE (σmod,org) overestimates RMSE (σmod,adj) noticeably (~30%).
Overall, the quantitative comparisons (Figure 9 and Table 2) demonstrate clearly that application of the RI-based correction improves the agreement between observed and calculated scattering coefficients, most notably in terms of the mean values and RMSE. Thus, our results are in line with findings from previous studies [30,31], which highlighted the importance of such RI-based corrections and suggested corresponding parameterizations for non-absorbing aerosol. These valuable parameterizations were designed assuming that the RI-based correction was a function of the real part of complex RI only. In our approach, both the real and imaginary parts of the complex RI are used as input and thus it can be applied for both non-absorbing and absorbing aerosol. It should be noted that the single-scattering albedo is moderate (0.93 ± 0.03) for the TCAP dataset considered here, therefore this dataset represents slightly-absorbing aerosol. Further studies are needed to examine the feasibility of our approach for improved calculations of total scattering/absorption for strongly-absorbing aerosol.

Table 2.
Mean and Standard Deviation (StDv) of the observed (σobs) and calculated (σmod,org and σmod,adj) scattering coefficients obtained for all TCAP FLs at three wavelengths: 0.45 µm (top part), 0.55 µm (middle part), and 0.70 µm (bottom part). The corresponding intercept (a), slope (b), their standard errors (in parenthesis) and Root Mean Squared Error (RMSE) also are included. The RMSE is defined as the root mean squared difference between the observed and the calculated scattering coefficients.
| Mean | StDv | RMSE | a | b | |
|---|---|---|---|---|---|
| 0.45 µm | |||||
| σobs | 20.05 | 12.26 | - | - | - |
| σmod,org | 13.70 | 10.42 | 7.49 | −1.58 (0.80) | 0.75 (0.06) |
| σmod,adj | 22.75 | 17.09 | 7.10 | −2.54 (1.33) | 1.24 (0.10) |
| 0.55 µm | |||||
| σobs | 14.85 | 8.98 | - | - | - |
| σmod,org | 8.80 | 6.78 | 6.99 | −1.30 (0.63) | 0.68 (0.06) |
| σmod,adj | 15.89 | 12.17 | 5.01 | −2.25 (1.13) | 1.21 (0.11) |
| 0.70 µm | |||||
| σobs | 8.73 | 5.28 | - | - | - |
| σmod,org | 4.87 | 3.78 | 4.61 | −0.73 (0.45) | 0.64 (0.07) |
| σmod,adj | 9.77 | 7.57 | 3.85 | −1.40 (0.90) | 1.26 (0.15) |
6. Sensitivity Study
This section is designed to supplement the previous one and to address question 3 (level of agreement for “incomplete” dataset given that a non-representative RI is used to correct size spectra). Note that we are able to use aerosol chemical composition data from the TCAP data set to obtain RI-based corrections for each FL. However, as discussed in Section 1, a more common scenario is one where chemical composition information is available only on a limited basis, or not at all. We wish to investigate the sensitivity of the agreement between calculated and observed scattering to the assumed RI value, particularly if the assumed RI is non-representative of the ambient aerosol. Further motivation for this sensitivity test is the reported lack of agreement (outside the 30% measurement uncertainty) between measured and calculated total scattering coefficients obtained recently for the VOCALS-Rex marine atmosphere campaign [46] where a universal refractive index (n* = 1.41 and k* = 0) derived from the entire VOCALS-Rex dataset [29] was used in adjusting observed PCASP size distributions.
Given the strong sensitivity of VOCALS-Rex calculated scattering to size spectra uncertainties [46], it can be hypothesized that the lack of agreement can be associated (at least partially) with the RI specification and its strong impact on the adjusted size distributions. To confirm this hypothesis, we calculate the total scattering from the TCAP data (Section 2) using the procedure previously employed [46] for the VOCALS-Rex dataset. We emphasize that the main difference between their sensitivity-driven procedure and our framework approach (Figure 1) is specification of the RI required for adjusting the OPC-derived size spectra: an assumed universal real RI estimated implicitly from all available aerosol composition measurements (sensitivity-driven procedure) versus a variable complex RI estimated explicitly from the complementary chemical composition data (our framework approach, Section 3, Section 4 and Section 5).
We apply an assumed universal RI (n* = 1.41 and k* = 0), equivalent to that used in VOCALS-Rex analyses, to the entire TCAP dataset and compare the results with those from the variable RI estimated from the TCAP AMS and SP2 data. This assumed RI might reasonably be adopted if TCAP had an “incomplete” data set and we searched the literature for a reasonable universal RI applicable to coastal/marine aerosols sampled aloft. Note that there is a noticeable difference between the assumed RI and the estimated RI (Section 3) for many FLs. Compared with the variable RI, the use of the universal RI in the size spectra adjustment increases the relative contribution of particles with moderate diameter (within 0.4–0.8 µm range) (Figure 11), which scatter light in the visible spectral range most effectively. This relative increase in optically important particles, in turn, is responsible for a substantial rise of the calculated scattering coefficient (Figure 12 and Figure 13a). As a result, the corresponding mean value and RMSE (calculations based on variable RI versus the universal RI) are enhanced by about 25% and 80%, respectively (Table 2 and Table 3). The mean value of the calculated scattering coefficient (based on universal RI) overestimates the mean value of observed scattering by about 35% (Table 3). This substantial overestimation (~35%) of the calculated scattering coefficient: (1) confirms the hypothesis made above regarding the potential strong impact of the RI specification on the calculated scattering and (2) suggests that use of a universal RI specification could be one possible explanation for the lack of agreement noted in the VOCALS-Rex closure study [46].

Figure 11.
Example of size distributions obtained for two FLs (21 July 2012) and different values of RI. Measured dry size distributions are converted into their wet counterparts with the size-dependent scaling factor calculated for universal (cyan, magenta) and variable (blue) RI. Two values of universal RI are assumed: m* = 1.41 (cyan) for a non-absorbing aerosol and m# = 1.41 + 0.01i (magenta) for an absorbing aerosol.
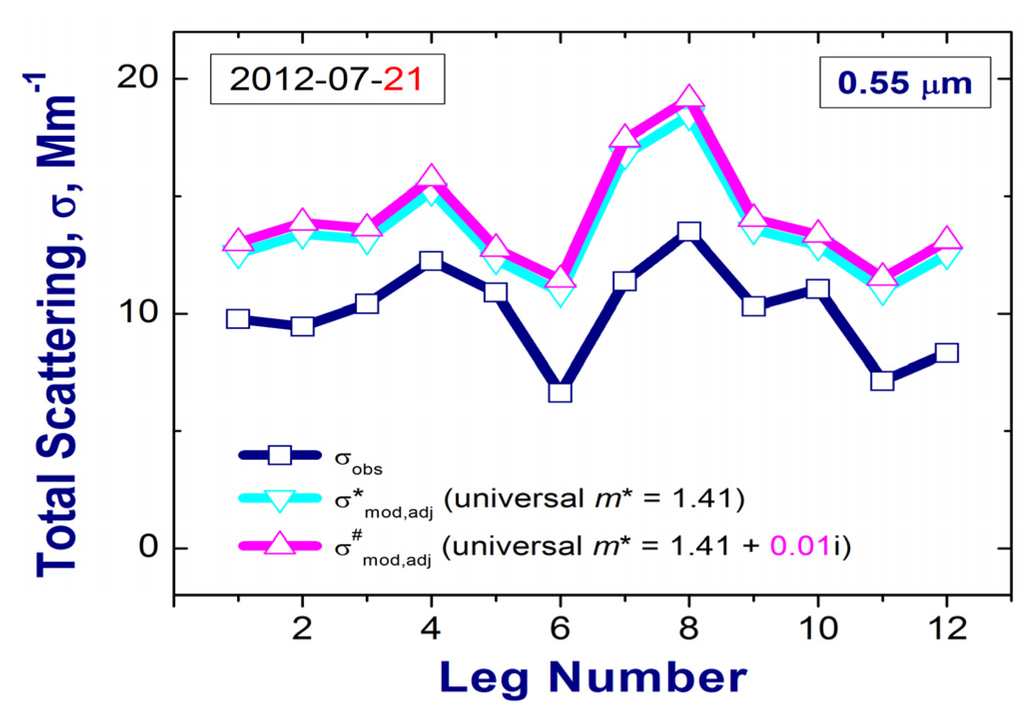
Figure 12.
Total scattering coefficient at 0.55 µm wavelength measured (navy blue) and calculated (cyan, magenta) for size distributions measured on 21 July, 2012 and corrected using two assumed universal RIs: m* = 1.41 (cyan) and m# = 1.41 + 0.01i (magenta).
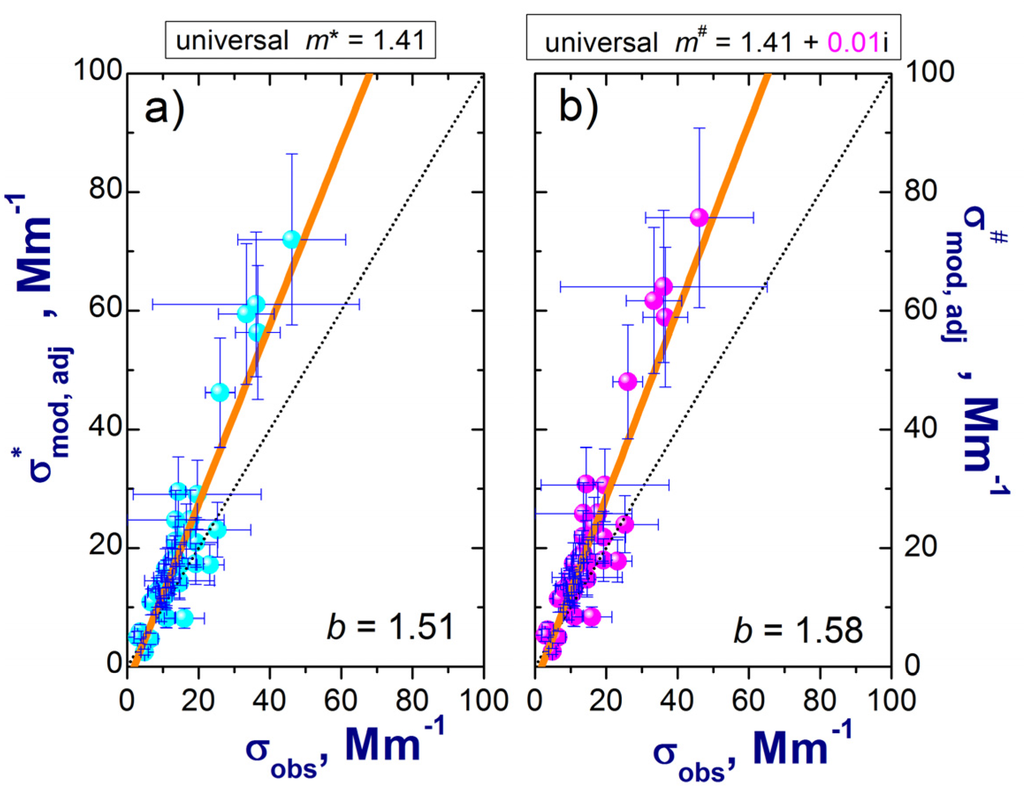
Figure 13.
Comparison of the ambient total scattering observed (σobs) with ambient total scattering calculated (σmod) for the size distributions adjusted with the universal RI. There are two values of assumed universal RI: m* = 1.41 (a) and m# = 1.41 + 0.01i (b). The observed and calculated values of total scattering are obtained at 0.55 µm wavelength for all TCAP FLs. Here, b is the slope of the linear regression fits to the data (straight orange lines). Error bars represent uncertainties of measured (Section 3) and calculated (Section 4.4) scattering coefficients.
To examine the importance of the imaginary part of the complex RI in changing the adjusted size distribution and thereby in modifying the calculated scattering, we focus on the complex RI for an absorbing aerosol (m#). We assume that the corresponding universal complex RI has the real (n# = 1.41) and imaginary (k# = 0.01) parts. This selected value of the imaginary part (k# = 0.01) represents roughly the most frequent value observed under dry conditions during the TCAP campaign (Figure 6). Therefore, the imaginary part is the only difference between the complex RIs assumed for non-absorbing (m* = 1.41) and absorbing (m# = 1.41 + 0.01i) aerosol.
Replacement of the imaginary part of the complex RI (k* = 0 versus k# = 0.01) increases the difference between the corresponding size distributions (Figure 11; cyan curve versus magenta curve). Note that this replacement (k* = 0 versus k# = 0.01) makes the adjusted size distributions “look smoother” within the resonance region (Figure 11; cyan curve versus magenta curve). The difference between the adjusted size distributions (Figure 11) is responsible for the difference between the corresponding total scattering coefficients (Figure 12, Figure 13 and Table 3). In particular, the replacement of the imaginary part of the complex RI (k* = 0 versus k# = 0.01) increases the RMSE by about 10% (Table 3). Therefore, selection of an inappropriate imaginary part of the assumed complex RI can also increase the discrepancy between the calculated total scattering from the observed total scattering.

Table 3.
The same as Table 2 (middle part) except for the scattering coefficients (middle row) and (bottom row) calculated for size distributions adjusted with two universal RIs m* = 1.41 and m# = 1.41 + 0.01i, respectively.
| Mean | StDv | RMSE | a | b | |
|---|---|---|---|---|---|
| σobs | 14.85 | 8.98 | - | - | - |
| 19.82 | 15.46 | 9.17 | −2.85 (1.42) | 1.51 (0.14) | |
| 20.67 | 16.19 | 10.20 | −2.96 (1.48) | 1.58 (0.15) |
The results presented in this Section illustrate that selecting inappropriate values of the real part of RI when adjusting OPC-derived size distributions in an optical closure study can cause substantial overestimation of the calculated scattering coefficient. Moreover, selecting inappropriate values of the imaginary part of RI can increase this overestimation noticeably, even for weakly absorbing aerosol. Therefore, one should not expect closure studies based on such “incomplete” data sets to be as exact as closure studies using “complete” data sets because of all the assumptions that must be made and the high probability that the RI estimates based on these assumptions potentially will be inappropriate. The error in RI estimates likely will be larger for aircraft sampling regimes because of the strong temporal and spatial variability of aerosol sampled by research aircraft. When faced with an “incomplete” data set, another possible approach is to use conventional iterative or optimization schemes, which apply a set of assumed representative RI values for minimizing differences between the measured and calculated aerosol properties of interest [34,40,70]. Such iterative or optimization schemes may possibly improve the RI estimation relative to the approach of assuming a universal RI.
7. Summary
We extend methods for calculating total aerosol scattering at ambient RH, originally developed for ground-based measurements [17,21,41] to the challenging situation of airborne measurements. The importance of such extension is now widely recognized [6,45]. Our extended framework is suitable for conducting optical closure studies using “complete” aircraft data sets, where “complete” means that collocated and concurrent information on particle chemical composition is available. Our approach takes advantage of the existing information on aerosol chemical constituents and explicitly uses it to obtain improved ambient size spectra derived from complementary Optical Particle Counter (OPC) data, and therefore to obtain improved estimates of the total scattering under ambient conditions with low-to-moderate values of relative humidity (RH < 80%).
To illustrate the performance of our approach, we use “complete” aerosol data collected by the DOE G-1 aircraft during the recent Two-Column Aerosol Project (TCAP; http://campaign.arm.gov/tcap/) over the North Atlantic Ocean and US coastal region (Cape Cod, Massachusetts). The integrated data set collected by the G-1 aircraft includes: (1) size distributions measured by three OPCs: an Ultra-High Sensitivity Aerosol Spectrometer (UHSAS; 0.06–1 µm), a Passive Cavity Aerosol Spectrometer (PCASP; 0.1–3 µm) and a Cloud and Aerosol Spectrometer (CAS; 0.6– >10 µm), (2) chemical composition data measured by an Aerosol Mass Spectrometer (AMS; 0.06–0.6 µm) and a Single Particle Soot Photometer (SP2; 0.06–0.6 µm) and (3) the dry total scattering coefficient measured by TSI integrating nephelometer at three wavelengths (0.45, 0.55, 0.7 µm) and f(RH) measured with a humidification system at three RHs (near 45%, 65% and 90%) at a single wavelength (0.525 µm). To illustrate the importance of the chemical composition data in the scattering closure study, we also utilize “incomplete” aerosol data, where “incomplete” means that information on particle chemical composition is not used to obtain the corrected ambient size spectra. The main conclusions are organized along the three main questions we posed at the start of our study:
- Analysis based on using the “complete” data set addresses our first question, namely: What level of agreement between the in-flight measured and calculated values of total scattering coefficient can be achieved at ambient RH? We demonstrate that despite the well-known limitations of airborne measurements and the assumptions required by our approach, we can obtain good agreement between the observed and calculated scattering at three wavelengths (about 13% at 0.45 µm, 7% at 0.55 µm, and 12% at 0.7 µm on average) using the RI-based correction for OPC-derived size spectra and the best available chemical composition data for the RI estimation. We calculate the total scattering coefficient from the combined size spectra (UHSAS, PCASP and CAS data) and aerosol composition (AMS and SP2 data) at ambient conditions with a wide range of relative humidity values (from 5% to 80%). These calculations involve several assumptions, such as the homogeneous internal mixture assumption for estimating the hygroscopic growth factor and complex refractive index (RI) at ambient conditions, and simplified specification of particle geometry (homogeneous spheres) for Mie calculations.
- Analysis based on using an “incomplete” dataset addresses our second question, namely: What is the effect of ignoring the influence of chemical composition data on this agreement? We illustrate that ignoring the RI-based correction in the TCAP data can cause a substantial underestimation (about 40% on average) of the ambient calculated scattering when noticeable discrepancies between the actual RIs and those used for the OPC calibration have occurred. Our findings are in harmony with previous studies, which have highlighted the importance of the RI-based correction and have suggested its parameterization for non-absorbing aerosol assuming that the RI-based correction is a function of real RI only [30,31]. In comparison with these important parameterizations, our approach is more flexible in terms of available inputs (complex RI is estimated explicitly from the complementary chemical composition data), and therefore in terms of the expected applications (both non-absorbing and absorbing aerosol sampled by ground-based and airborne instruments).
- Analysis based on using an “incomplete” dataset also addresses our third question, namely: How sensitive is this agreement to the assumed RI value, particularly if the assumed RI is non-representative of the ambient aerosol? We illustrate in a sensitivity study that using a non-representative universal RI instead of the actual RI can result in a large overestimation (about 35% on average) of the calculated total scattering at ambient RH, and this overestimation is sensitive to specification of the imaginary part of the complex RI, even for weakly-absorbing aerosol. This sensitivity study suggests that the usefulness of assumptions required for universal RI estimation could be marginal, particularly when applied to the strong temporal and spatial variability of aerosol sampled by research aircraft. As a result, calculations of aerosol optical properties based on these assumptions should be used with caution and other possible approaches should be considered to improve the RI estimation. These possibilities include application of conventional iterative or optimization schemes where a set of assumed representative RI values is used to minimize differences between the measured and calculated aerosol properties of interest [34,40,70].
To our knowledge, this work represents the first optical closure study that uses explicitly airborne chemical composition measurements of both non-absorbing and absorbing aerosol components in improving the OPC-derived size spectra. These measurements are employed to extend the capability of well-established methods originally developed for use with comprehensive ground-based measurements. Given the extended flexibility of these methods and the increasing availability of aerosol composition data collected from aircraft platforms, we expect that our approach can be successfully applied for improved understanding of a wide range of sophisticated processes and phenomena related to aerosols, including the time evolution of aerosol properties and dynamical aerosol-cloud interactions [71,72]. We further expect that closer agreement between measured and calculated aerosol properties, indicating the consistency of the observational data set, will improve confidence in, and use of, such observational data sets in global and regional climate model evaluations. For example, appropriate adjustments to optical particle counter data are needed to better understand and evaluate predictions of cloud-aerosol interactions, since cloud condensation nuclei (CCN) calculations are dependent on the aerosol size distribution.
Acknowledgments
The ARM Aerial Facility team is gratefully acknowledged for collecting the aircraft data during TCAP which was supported by the Department of Energy (DOE) Office of Science Atmospheric Radiation Measurement (ARM) and Atmospheric System Research (ASR) Programs. The ARM Aerial Facility is an integral part of the DOE ARM Program. This research was supported by the ARM and ASR Programs. The Pacific Northwest National Laboratory is operated by Battelle Memorial Institute under contract DE-AC06-76RLO 1830. We appreciate valuable discussions with Elaine Chapman (PNNL) and thoughtful comments from two anonymous reviewers that helped improve our paper.
Author Contributions
Abstract (E.K., L.B.), Introduction (E.K., L.B.), Approach (E.K., L.B., M.P., C.F., J.B.), Data (M.P., D.C., J.T., J.S., A.S., B.S.), Model and adjustments (E.K., L.B., M.P., M.O., J.S.), Results (all), Sensitivity study (E.K., L.B., M.P., M.O.), Summary (all). E.K. led the research and manuscript preparation. All authors contributed to data analysis. J.F. supervised research and manuscript writing.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Merging of Size Distributions
This appendix explains how data from overlapping measurements from three instruments (UHSAS, PCASP, and CAS) are merged into the combined size distributions (Figure 2). The best estimate aerosol size distribution can be recovered from the merged raw counts if a Kernel function (R) can first be quantified:
or
The raw counts are measured by the UHSAS, PCASP, and CAS. Furthermore, R can be defined as:
where Q, VTAS, ei,j, A and t are the flow, airspeed, collection efficiency for each probe, CAS laser sample area and the data collection integration time, respectively. From calibrations we know the collection efficiency (ei,j) of each probe within a specified bin size, and the CAS laser sample area (A). The other variables Q (flow) and VTAS (airspeed) are measured by the probes themselves during operation.
To start the recovery process, a rough estimate of has to be provided. The size distribution values dN/d log Dp for UHSAS, CAS, PCASP are first interpolated to the same bin space. The concentration values from the UHSAS, CAS, and or PCASP that overlap in the same bin are averaged together then converted back to dN by multiplying by the d log Dp value for that bin. Using the estimation for , Twomey smoothing is started. The initial number distribution is smoothed until the roughness of the solution has decreased to a set value, normally around 0.96. Roughness of the solution is measured by the average value of the second derivative. This initial trial solution is then ingested into a loop which continues until either the roughness of the solution has decreased below a set limit (typically 0.98), the goodness of the fit decreases, or the maximum number of iterations has been reached. After the loop successfully exits the resulting number distribution is considered the best estimate aerosol size distribution.
Appendix B. Contributions from Particles of Different Sizes to Scattering
To quantify contributions from particles of different sizes to the total scattering, we calculate the ambient scattering coefficient at single wavelength (0.55 µm), where Csca is the scattering cross section, which is a function of particle diameter D and size-independent complex refractive index (m; Equation (5)), dN ∕ d log D is the ambient and corrected number size distribution (Equation (9b)), Dmin~0.07 µm and D* is an assumed cut-off (between 0.1 to 5 µm). Then we calculate normalized scattering coefficient , which represents the relative contribution of particles with D < D* to the total scattering from all particles smaller than 5 µm. Figure B1a shows the mean and standard deviation for ρ (D*) computed for all 45 TCAP flight legs considered in this study (Section 3). Sub-micron particles clearly dominate the total scattering in this case with ρ (D*) reaching about 0.93 and 0.96 for D* = 1 µm and D* = 2 µm, respectively (Figure B1a). The obtained small (~7%, on average) contribution by the super-micron particles to the ambient scattering coefficient confirms the applicability of the simplified approach (Appendix C) to the TCAP airborne data. For events where super-micron particles dominate, for example, aerosol plumes resulting from dust storms [73] or volcanic eruptions [34] application of the strict approach (Appendix C) would be more relevant.
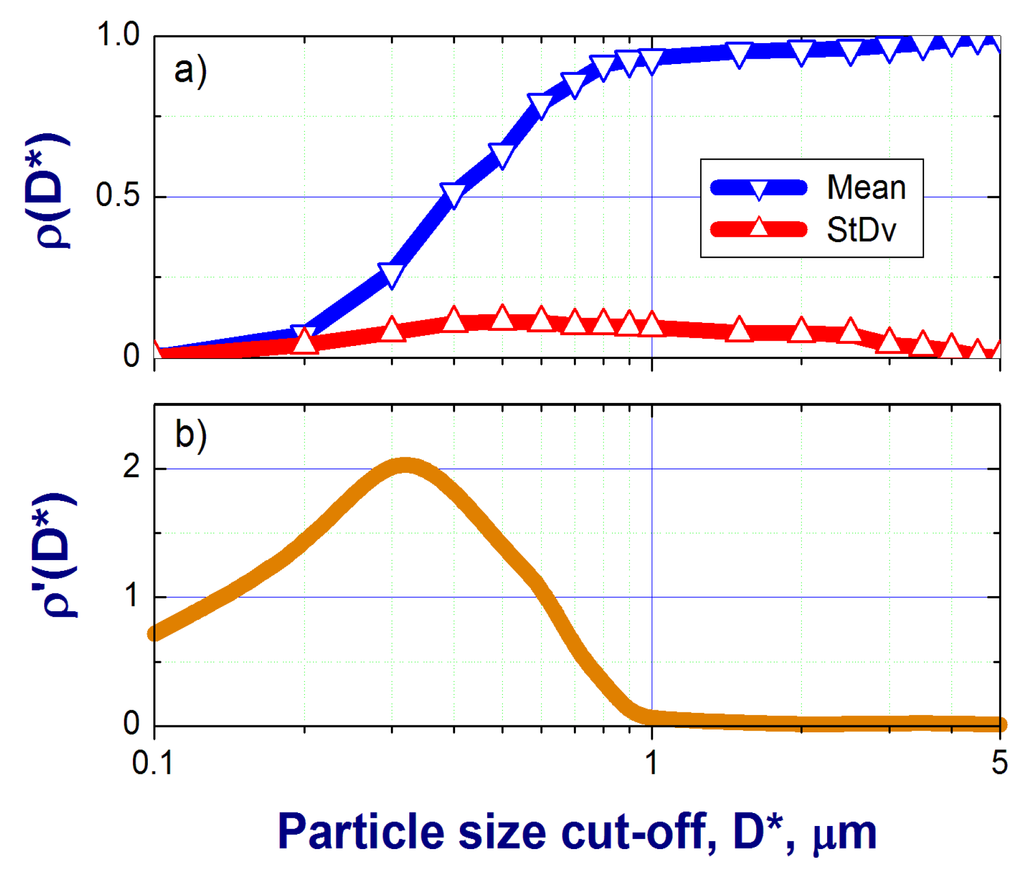
Figure B1.
The normalized scattering coefficient (a) and its derivative (b) as a function of particle size cut-off. The blue line shows the mean for all TCAP flight legs and the red line represents the corresponding standard deviations.
To further illustrate the relative contribution to σmod,adj from different particle size ranges (for a given complex refractive index), we note that the above relation for the ambient scattering coefficient can be rearranged as . Using this rearranged relation, we calculate the derivative of the normalized scattering coefficient as , where . Figure B1b shows that on average particles in the size range between 0.3 and 0.4 µm contribute most strongly to the ambient scattering coefficient, while the corresponding contribution of particles in the “bumpy” region (particle sizes larger than 0.5 µm) is smaller.
Appendix C. Correction of OPC-derived Size Spectra
This appendix includes details related to the calculations of the size-dependent theoretical response curves. The latter are required to obtain an adjusted dry diameter of particles (Equation (6)) and the corresponding dry (Equation (7)) and ambient (Equation (9b)) size distributions using the OPC-derived size spectra. Recall that during the OPC measurements individual particles are illuminated by a laser beam and then the light scattered by the particles is collected over a large solid angle [32,33,34,74]. The wavelength of the illuminating light and solid angle limits are known properties of a given detector [12]. For example, the UHSAS and PCASP collect side-scattered light (~35–135 degrees) at 0.6328 µm and 1.054 µm wavelength, respectively; while the CAS collects forward-scattered (~4–13 degrees) and back-scattered (~5–14 degrees) light at 0.685 µm wavelength. Therefore, strictly speaking, the scaling factors should be calculated for each instrument independently using the specified properties, and then the individual corrected size spectra (UHSAS, PCASP and CAS) should be used to obtain the corresponding merged size distributions. We shall call this the “strict approach.” Another potential approach could include the development of empirical relationships between the scattering measured over the limited range of angles and the total scattering for given compositions and ambient conditions. Such an “empirical approach” would not involve Mie calculations and therefore would relax assumptions and data requirements for the RI-based corrections.
For our study, the individual uncorrected size spectra (UHSAS, PCASP and CAS) are combined to obtain the corresponding merged size distributions (Section 3) and then these merged distributions are corrected. We shall call this the “simplified approach.” The basis of this simplified approach is the assumption that the properties of the PCASP (both the wavelength of the illuminating light and the solid angle limits) are representative of all merged size distributions. Such a simplification is motivated by the fact that the PCASP-derived size distributions represent particles in the 0.13–3 µm size range (Section 2), which scatter light most effectively in the visible spectral range considered here (about 0.2–0.7 µm). It can therefore be expected that the PCASP-derived size distributions contribute most of the total scattering measured by this airborne nephelometer.
We apply the simplified approach to calculate the theoretical response curves (Figure C1) and adjust particle diameters (Figure C2). Let us start with Figure C1. The first curve represents an assumed “experimental” one, which would be obtained from laboratory calibrations for particles with a known RI. Given that uncertainties of the experimental calibration are unknown, the “experimental” curve is the smoothed version of the corresponding theoretical response curve. A polynomial (curvilinear) regression model ([75]; pages 342–347) is applied to generate this smoothed version. Similar smoothed versions have been used previously for different OPCs [34]. The second and third curves represent low and high values of the imaginary part of RI obtained for two FLs (Figure 6b) and illustrate two important points. First, the corresponding curves are comparable and “smooth” for particles with diameter smaller than 0.75 µm; (Figure C1; upper zoom-in panel). In contrast, the curves are quite different and “bumpy” for large particles with diameter between 1.5 µm and 3.0 µm (Figure C1; lower zoom-in panel). Second, the observed “bumpy” behavior is responsible for the well-known multivalued issue, when particles with different diameter can produce the same response (Figure C1; lower zoom-in panel, green curve). In the presented calculations, we assume that the corresponding response is due to a particle with minimal diameter (Figure C1; lower zoom-in panel, red open circle on green curve). The observed differences between the second and third curves (Figure C1) are responsible for the corresponding differences between the adjusted diameters (Figure C2).

Figure C1.
Example of theoretical response curves as a function of dry diameter (Ddry) calculated for spherical particles and different values of complex RI. These values represent polystyrene latex spheres (PSL; navy blue) and those calculated for two FLs (FL = 4, green; FL = 11, magenta; 21 July 2012) from chemical composition measurements under dry conditions. Two complementary zoom-in versions of the calculated response curves are also included to illustrate that these curves may exhibit “smooth” and “bumpy” behavior for different ranges of diameter (see text for details).
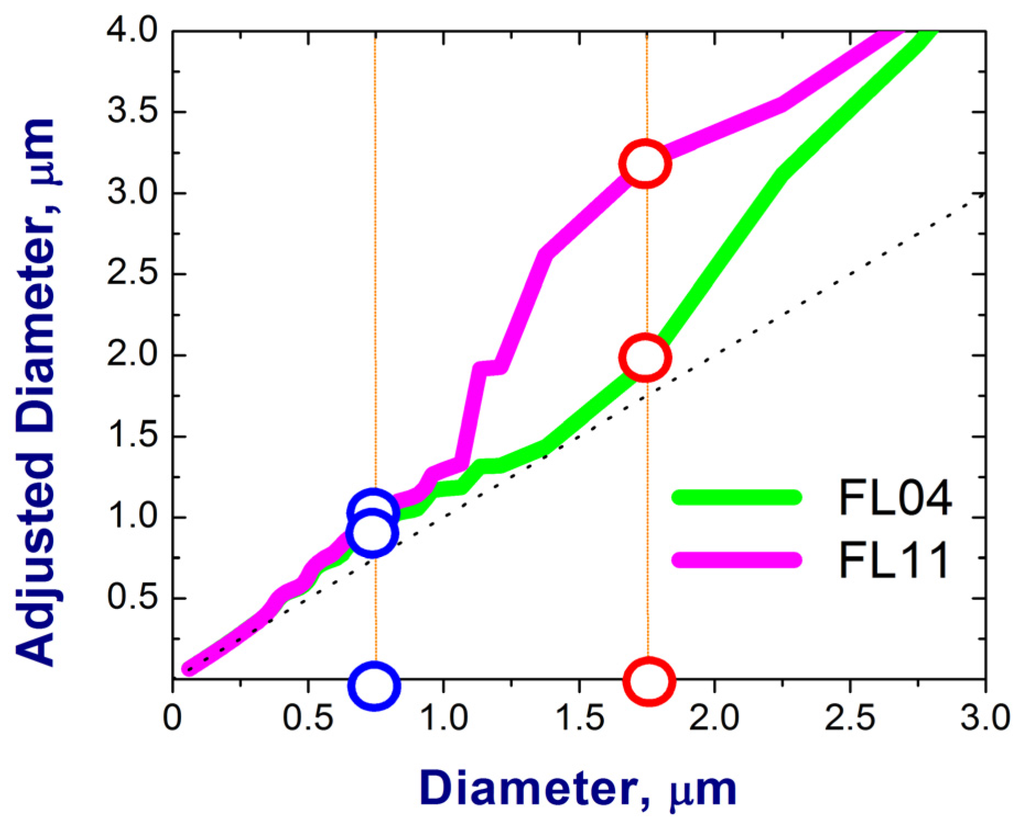
Figure C2.
Adjusted dry diameter (Ddry,adj) as a function of original dry diameter (Ddry) obtained for two FLs (FL = 4, green; FL = 11, magenta; 21 July 2012) from the calculated response curves (Figure C1).
References
- Wang, X.; Heald, C.L.; Ridley, D.A.; Schwarz, J.P.; Spackman, J.R.; Perring, A.E.; Coe, H.; Liu, D.; Clarke, A.D. Exploiting simultaneous observational constraints on mass and absorption to estimate the global direct radiative forcing of black carbon and brown carbon. Atmos. Chem. Phys. 2014, 14, 10989–11010. [Google Scholar] [CrossRef]
- Sundström, A.-M.; Arola, A.; Kolmonen, P.; Xue, Y.; de Leeuw, G.; Kulmala, M. On the use of a satellite remote-sensing-based approach for determining aerosol direct radiative effect over land: A case study over China. Atmos. Chem. Phys. 2015, 15, 505–518. [Google Scholar] [CrossRef]
- Adachi, K.; Chung, S.H.; Buseck, P.R. Shapes of soot aerosol particles and implications for their effects on climate. J. Geophys. Res. 2010, 115, D15206. [Google Scholar] [CrossRef]
- Bond, T.C.; Doherty, S.J.; Fahey, D.W.; Forster, P.M.; Berntsen, T.; DeAngelo, B.J.; Flanner, M.G.; Ghan, S.; Kärcher, B.; Koch, D.; et al. Bounding the role of black carbon in the climate system: A scientific assessment. J. Geophys. Res. Atmos. 2013, 118, 5380–5552. [Google Scholar] [CrossRef]
- China, S.; Mazzoleni, C.; Gorkowski, K.; Aiken, A.C.; Dubey, M.K. Morphology and mixing state of individual freshly emitted wildfire carbonaceous particles. Nat. Comm. 2013, 4, 2122. [Google Scholar] [CrossRef] [PubMed]
- Fast, J.D.; Allan, J.; Bahreini, R.; Craven, J.; Emmons, L.; Ferrare, R.; Hayes, P.L.; Hodzic, A.; Holloway, J.; Hostetler, C.; et al. Modeling regional aerosol and aerosol precursor variability over California and its sensitivity to emissions and long-range transport during the 2010 CalNex and CARES campaigns. Atmos. Chem. Phys. 2014, 14, 10013–10060. [Google Scholar] [CrossRef]
- Washenfelder, R.A.; Attwood, A.R.; Brock, C.A.; Guo, H.; Xu, L.; Weber, R.J.; Ng, N.L.; Allen, H.M.; Ayres, B.R.; Baumann, K.; et al. Biomass burning dominates brown carbon absorption in the rural southeastern United States. Geophys. Res. Lett. 2015, 42, 653–664. [Google Scholar] [CrossRef]
- Müller, D.; Hostetler, C.A.; Ferrare, R.A.; Burton, S.P.; Chemyakin, E.; Kolgotin, A.; Hair, J.W.; Cook, A.L.; Harper, D.B.; Rogers, R.R.; et al. Airborne Multiwavelength High Spectral Resolution Lidar (HSRL-2) observations during TCAP 2012: Vertical profiles of optical and microphysical properties of a smoke/urban haze plume over the northeastern coast of the US. Atmos. Meas. Tech. 2014, 7, 3487–3496. [Google Scholar] [CrossRef]
- Russell, P.B.; Kacenelenbogen, M.; Livingston, J.M.; Hasekamp, O.P.; Burton, S.P.; Schuster, G.L.; Johnson, M.S.; Knobelspiesse, K.D.; Redemann, J.; Ramachandran, S.; Holben, B. A multiparameter aerosol classification method and its application to retrievals from spaceborne polarimetry. J. Geophys. Res. Atmos. 2014, 119, 9838–9863. [Google Scholar] [CrossRef]
- Chaikovskaya, L.; Dubovik, O.; Litvinov, P.; Grudo, J.; Lopatsin, A.; Chaikovsky, A.; Denisov, S. Analytical algorithm for modeling polarized solar radiation transfer through the atmosphere for application in processing complex lidar and radiometer measurements. J. Quant. Spectrosc. Radiat. Trans. 2015, 151, 275–286. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A.; Davis, A.B.; Cairns, B.; Dubovik, O.; Hasekamp, O.P.; Sano, I.; Mukai, S.; Rozanov, V.V.; Litvinov, P.; Lapyonok, T.; et al. Space-based remote sensing of atmospheric aerosols: The multi-angle spectro-polarimetric frontier. Earth-Sci. Rev. 2015. [Google Scholar] [CrossRef]
- Baumgardner, D.; Brenguier, J.L.; Bucholtz, A.; Coe, H.; DeMott, P.; Garrett, T.J.; Gayet, J.F.; Hermann, M.; Heymsfield, A.; Korolev, A.; et al. Airborne instruments to measure atmospheric aerosol particles, clouds and radiation: A cook’s tour of mature and emerging technology. Atmos. Res. 2011, 102, 10–29. [Google Scholar] [CrossRef]
- McFarquhar, G.; Schmid, B.; Korolev, A.; Ogren, J.A.; Russell, P.B.; Tomlinson, J.; Turner, D.D.; Wiscombe, W. Airborne instrumentation needs for climate and atmospheric research. Bull. Amer. Meteor. Soc. 2011, 92, 1193–1196. [Google Scholar] [CrossRef]
- Konwar, M.; Panicker, A.S.; Axisa, D.; Prabha, T.V. Near-cloud aerosols in monsoon environment and its impact on radiative forcing. J. Geophys. Res. Atmos. 2015, 120. [Google Scholar] [CrossRef]
- Russell, P.B.; Kinne, S.A.; Bergstrom, R.W. Aerosol climate effects: Local radiative forcing and column closure experiments. J. Geophys. Res. 1997, 102, 9397–9407. [Google Scholar] [CrossRef]
- Schmid, B.; Livingston, J.M.; Russell, P.B.; Durkee, P.A.; Jonsson, H.H.; Collins, D.R.; Flagan, R.C.; Seinfeld, J.H.; Gassó, S.; Hegg, D.A.; et al. Clear-sky closure studies of lower tropospheric aerosol and water vapor during ACE-2 using airborne sunphotometer, airborne in-situ, space-borne, and ground-based measurements. Tellus B 2000, 52, 568–593. [Google Scholar] [CrossRef]
- Malm, W.C.; Day, D.E.; Carrico, C.; Kreidenweis, S.M.; Collett, J.L., Jr.; McMeeking, G.; Lee, T.; Carrillo, J.; Schichtel, B. Intercomparison and closure calculations using measurements of aerosol species and optical properties during the Yosemite Aerosol Characterization Study. J. Geophys. Res. 2005, 110, D14302. [Google Scholar] [CrossRef]
- Mack, L.A.; Levin, E.J.T.; Kreidenweis, S.M.; Obrist, D.; Moosmüller, H.; Lewis, K.A.; Arnott, W.P.; McMeeking, G.R.; Sullivan, A.P.; Wold, C.E.; et al. Optical closure experiments for biomass smoke aerosols. Atmos. Chem. Phys. 2010, 10, 9017–9026. [Google Scholar] [CrossRef]
- Marshall, J.; Lohmann, U.; Leaitch, W.R.; Lehr, P.; Hayden, K. Aerosol scattering as a function of altitude in a coastal environment. J. Geophys. Res. 2007, 112, D14203. [Google Scholar] [CrossRef]
- Ma, N.; Birmili, W.; Müller, T.; Tuch, T.; Cheng, Y.F.; Xu, W.Y.; Zhao, C.S.; Wiedensohler, A. Tropospheric aerosol scattering and absorption over central Europe: A closure study for the dry particle state. Atmos. Chem. Phys. 2014, 14, 6241–6259. [Google Scholar] [CrossRef]
- Zieger, P.; Fierz-Schmidhauser, R.; Poulain, L.; Müller, T.; Birmili, W.; Spindler, G.; Wiedensohler, A.; Baltensperger, U.; Weingartner, E. Influence of water uptake on the aerosol particle light scattering coefficients of the Central European aerosol. Tellus B 2014, 66, 22716. [Google Scholar] [CrossRef]
- Wang, J.; Flagan, R.C.; Seinfeld, J.H.; Jonsson, H.H.; Collins, D.R.; Russell, P.B.; Schmid, B.; Redemann, J.; Livingston, J.M.; Gao, S.; et al. Clear-column radiative closure during ACE-Asia: Comparison of multiwavelength extinction derived from particle size and composition with results from sunphotometry. J. Geophys. Res. 2002, 107, 4688. [Google Scholar] [CrossRef]
- Parworth, C.; Fast, J.; Mei, F.; Shippert, T.; Sivaraman, C.; Tilp, A.; Watson, T.; Zhang, Q. Long-term measurements of submicrometer aerosol chemistry at the Southern Great Plains (SGP) using an Aerosol Chemical Speciation Monitor (ACSM). Atmos. Environ. 2015, 106, 43–55. [Google Scholar] [CrossRef]
- Schmid, B.; Tomlinson, J.M.; Hubbe, J.M.; Comstock, J.M.; Mei, F.; Chand, D.; Pekour, M.S.; Kluzek, C.D.; Andrews, E.; Biraud, S.C.; et al. The DOE ARM Aerial Facility. Bull. Am. Meteor. Soc. 2014, 95, 723–742. [Google Scholar] [CrossRef]
- Kassianov, E.; Flynn, C.; Redemann, J.; Schmid, B.; Russell, P.B.; Sinyuk, A. Initial assessment of the Spectrometer for Sky-Scanning, Sun-Tracking Atmospheric Research (4STAR)-based aerosol retrieval: Sensitivity study. Atmosphere 2012, 3, 495–521. [Google Scholar] [CrossRef]
- Dunagan, S.; Johnson, R.; Zavaleta, J.; Russell, P.; Schmid, B.; Flynn, C.; Redemann, J.; Shinozuka, Y.; Livingston, J.; Segal-Rosenhaimer, M. Spectrometer for Sky-Scanning Sun-Tracking Atmospheric Research (4STAR): Instrument technology. Remote Sens. 2013, 5, 3872–3895. [Google Scholar] [CrossRef]
- Segal-Rosenheimer, M.; Russell, P.B.; Schmid, B.; Redemann, J.; Livingston, J.M.; Flynn, C.J.; Johnson, R.R.; Dunagan, S.E.; Shinozuka, Y.; Herman, J.; et al. Tracking elevated pollution layers with a newly developed hyperspectral Sun/Sky spectrometer (4STAR): Results from the TCAP 2012 and 2013 campaigns. J. Geophys. Res. Atmos. 2014, 119, 2611–2628. [Google Scholar] [CrossRef]
- Allen, G.; Coe, H.; Clarke, A.; Bretherton, C.; Wood, R.; Abel, S.J.; Barrett, P.; Brown, P.; George, R.; Freitag, S.; et al. South East Pacific atmospheric composition and variability sampled along 20° S during VOCALS-Rex. Atmos. Chem. Phys. 2011, 11, 5237–5262. [Google Scholar] [CrossRef]
- Kleinman, L.I.; Daum, P.H.; Lee, Y.-N.; Lewis, E.R.; Sedlacek, A.J., III; Senum, G.I.; Springston, S.R.; Wang, J.; Hubbe, J.; Jayne, J.; et al. Aerosol concentration and size distribution measured below, in, and above cloud from the DOE G-1 during VOCALS-REx. Atmos. Chem. Phys. 2012, 11, 207–223. [Google Scholar] [CrossRef]
- Liu, Y.; Daum, P.H. The effect of refractive index on size distributions and light scattering coefficients derived from optical particle counters. J. Aerosol. Sci. 2000, 31, 945–957. [Google Scholar] [CrossRef]
- Ames, R.B.; Hand, J.L.; Kreidenweis, S.M.; Day, D.E.; Malm, W.C. Optical measurements of aerosol size distributions in Great Smokey Mountains National Park: Dry aerosol characterization. J. Air Waste Manag. Assoc. 2000, 50, 665–676. [Google Scholar] [CrossRef] [PubMed]
- Garvey, D.M.; Pinnick, R.G. Response characteristics of the particle measuring systems active scattering aerosol spectrometer probe (ASASP-X). Aerosol Sci. Technol. 1983, 2, 477–488. [Google Scholar] [CrossRef]
- Kim, Y.J.; Boatman, J.F. Size calibration corrections for the Forward Scattering Spectrometer Probe (FSSP) for measurement of atmospheric aerosols of different refractive indices. J. Atmos. Oceanic Technol. 1990, 7, 681–688. [Google Scholar] [CrossRef]
- Bukowiecki, N.; Zieger, P.; Weingartner, E.; Juranyi, Z.; Gysel, M.; Neininger, B.; Schneider, B.; Hueglin, C.; Ulrich, A.; Wichser, A.; et al. Ground-based and airborne in-situ measurements of the Eyjafjallajökull volcanic aerosol plume in Switzerland in spring 2010. Atmos. Chem. Phys. 2011, 11, 10011–10030. [Google Scholar] [CrossRef]
- Kondo, Y. Effects of black carbon on climate: Advances in measurement and modeling. Monogr. Environ. Earth Planets 2015, 3, 1–85. [Google Scholar] [CrossRef]
- Kreidenweis, S.M.; Asa-Awuku, A. Aerosol Hygroscopicity: Particle water content and its role in atmospheric processes. Treat. Geochem.: Second Ed. 2013, 5, 331–361. [Google Scholar]
- Jensen, T.L.; Kreidenweis, S.M.; Kim, Y.; Sievering, H.; Pszenny, A. Aerosol distributions measured in the North Atlantic marine boundary layer during ASTEX/MAGE. J. Geophys. Res. 1996, 101, 4455–4467. [Google Scholar]
- Swietlicki, E.; Zhou, J.; Berg, O.H.; Martinsson, B.G.; Frank, G.; Cederfelt, S.-I.; Dusek, U.; Berner, A.; Birmili, W.; Wiedensohler, A.; et al. A closure study of sub-micrometer aerosol particle hygroscopic behavior. Atmos. Res. 1999, 50, 205–240. [Google Scholar] [CrossRef]
- Dusek, U.; Frank, G.P.; Massling, A.; Zeromskiene, K.; Iinuma, Y.; Schmid, O.; Helas, G.; Hennig, T.; Wiedensohler, A.; Andreae, M.O. Water uptake by biomass burning aerosol at sub- and supersaturated conditions: Closure studies and implications for the role of organics. Atmos. Chem. Phys. 2011, 11, 9519–9532. [Google Scholar] [CrossRef]
- Kassianov, E.; Barnard, J.; Pekour, M.; Berg, L.K.; Shilling, J.; Flynn, C.; Mei, F.; Jefferson, A. Simultaneous retrieval of effective refractive index and density from size distribution and light-scattering data: Weakly absorbing aerosol. Atmos. Meas. Tech. 2014, 7, 3247–3261. [Google Scholar] [CrossRef]
- Titos, G.; Jefferson, A.; Sheridan, P.J.; Andrews, E.; Lyamani, H.; Alados-Arboledas, L.; Ogren, J.A. Aerosol light-scattering enhancement due to water uptake during the TCAP campaign. Atmos. Chem. Phys. 2014, 14, 7031–7043. [Google Scholar] [CrossRef]
- Collins, D.R.; Flagan, R.C.; Seinfeld, J.H. Improved inversion of scanning DMA data. Aerosol Sci. Technol. 2002, 36, 1–9. [Google Scholar] [CrossRef]
- Schmid, B.; Ferrare, R.; Flynn, C.; Elleman, R.; Covert, D.; Strawa, A.; Welton, E.; Turner, D.; Jonsson, H.; Redemann, J.; et al. How well do state-of-the-art techniques measuring the vertical profile of tropospheric aerosol extinction compare? J. Geophys. Res. 2006, 111, D05S07. [Google Scholar] [CrossRef]
- Zelenyuk, A.; Imre, D.; Wilson, J.; Zhang, Z.; Wang, J.; Mueller, K. Airborne Single Particle Mass Spectrometers (SPLAT II& miniSPLAT) and new software for data visualization and analysis in a geo-spatial context. J. Am. Soc. Mass Spectrom. 2015, 26, 257–270. [Google Scholar] [CrossRef] [PubMed]
- Berg, L.; Fast, J.D.; Barnard, J.C.; Burton, S.P.; Cairns, B.; Chand, D.; Comstock, J.M.; Dunagan, S.; Ferrare, R.A.; Flynn, C.J.; et al. The Two-Column Aerosol Project: Phase I overview and impact of elevated aerosol layers on aerosol optical depth. J. Geophys. Res. Atmos. 2015. under review. [Google Scholar]
- Esteve, A.R.; Highwood, E.J.; Morgan, W.T.; Allen, G.; Coe, H.; Grainger, R.G.; Brown, P.; Szpek, K. A study on the sensitivities of simulated aerosol optical properties to composition and size distribution using airborne measurements. Atmos. Environ. 2014, 89, 517–524. [Google Scholar] [CrossRef]
- Twomey, S. Comparison of constrained linear inversion and an iterative nonlinear algorithm applied to indirect estimation of particle-size distributions. J. Comput. Phys. 1975, 18, 188–200. [Google Scholar] [CrossRef]
- Markowski, G.R. Improving Twomey’s Algorithm for Inversion of Aerosol Measurement Data. Aerosol Sci. Technol. 1987, 7, 127–141. [Google Scholar] [CrossRef]
- Moteki, N.; Kondo, Y. Effects of mixing state on black carbon measurements by laser-induced incandescence. Aerosol Sci. Technol. 2007, 41, 398–417. [Google Scholar] [CrossRef]
- Sedlacek, A.J., III; Lewis, E.R.; Kleinman, L.; Xu, J.; Zhang, Q. Determination of and evidence for non-core-shell structure of particles containing black carbon using the Single-Particle Soot Photometer (SP2). Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Pekour, M.S.; Schmid, B.; Chand, D.; Hubbe, J.M.; Kluzek, C.D.; Nelson, D.A.; Tomlinson, J.M.; Cziczo, D.J. Development of a new airborne humidigraph system. Aerosol Sci. Technol. 2013, 47, 201–207. [Google Scholar] [CrossRef]
- Shinozuka, Y.; Johnson, R.R.; Flynn, C.J.; Russell, P.B.; Schmid, B.; Redemann, J.; Dunagan, S.E.; Kluzek, C.D.; Hubbe, J.M.; Segal-Rosenheimer, M.; et al. Hyperspectral aerosol optical depths from TCAP flights. J. Geophys. Res. Atmos. 2013, 118, 12180–12194. [Google Scholar] [CrossRef]
- Anderson, T.L.; Ogren, J.A. Determining aerosol radiative properties using the TSI 3563 Integrating Nephelometer. Aerosol Sci. Technol. 1998, 29, 57–69. [Google Scholar] [CrossRef]
- Hallar, A.G.; Strawa, A.W.; Schmid, B.; Andrews, E.; Ogren, J.; Sheridan, P.; Ferrare, R.; Covert, D.; Elleman, R.; Jonsson, H.; et al. Atmospheric Radiation Measurements Aerosol Intensive Operating Period: Comparison of aerosol scattering during coordinated flights. J. Geophys. Res. 2006, 111, D05S09. [Google Scholar] [CrossRef]
- Barnard, J.C.; Fast, J.D.; Paredes-Miranda, G.; Arnott, W.P.; Laskin, A. Technical note: Evaluation of the WRF-Chem “Aerosol chemical to aerosol optical properties” module using data from the MILAGRO campaign. Atmos. Chem. Phys. 2010, 10, 7325–7340. [Google Scholar] [CrossRef]
- Hu, D.; Chen, J.; Ye, X.; Li, L.; Yang, X. Hygroscopicity and evaporation of ammonium chloride and ammonium nitrate: Relative humidity and size effects on the growth factor. Atmos. Environ. 2011, 45, 2349–2355. [Google Scholar] [CrossRef]
- Healy, R.M.; Evans, G.J.; Murphy, M.; Jurányi, Z.; Tritscher, T.; Laborde, M.; Weingartner, E.; Gysel, M.; Poulain, L.; Kamilli, K.A.; et al. Predicting hygroscopic growth using single particle chemical composition estimates. J. Geophys. Res. Atmos. 2014, 119, 9567–9577. [Google Scholar] [CrossRef]
- Pilinis, C.; Charalampidis, P.E.; Mihalopoulos, N.; Pandis, S.N. Contribution of particulate water to the measured aerosol optical properties of aged aerosol. Atmos. Environ. 2014, 82, 144–153. [Google Scholar] [CrossRef]
- Dubovik, O.; Holben, B.; Eck, T.F.; Smirnov, A.; Kaufman, Y.J.; King, M.D.; Tanré, D.; Slutsker, I. Variability of absorption and optical properties of key aerosol types observed in worldwide locations. J. Atmos. Sci. 2002, 59, 590–608. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A. Aerosol Optics: Light Absorption and Scattering by Particles in the Atmosphere; Springer-Berlin: Heidelberg, Germany, 2008; p. 148. [Google Scholar]
- Barber, P.W.; Hill, S.C. Light Scattering by Particles: Computational Methods; World Scientific Publishing: Singapore, 1990. [Google Scholar]
- Scarnato, B.V.; Vahidinia, S.; Richard, D.T.; Kirchstetter, T.W. Effects of internal mixing and aggregate morphology on optical properties of black carbon using a discrete dipole approximation model. Atmos. Chem. Phys. 2013, 13, 5089–5101. [Google Scholar] [CrossRef]
- Lesins, G.; Chylek, P.; Lohmann, U. A study of internal and external mixing scenarios and its effect on aerosol optical properties and direct radiative forcing. J. Geophys. Res. Atmos. 2002, 107, 4094–4106. [Google Scholar] [CrossRef]
- Freney, E.J.; Adachi, K.; Buseck, P.R. Internally mixed atmospheric aerosol particles: Hygroscopic growth and light scattering. J. Geophys. Res. Atmos. 2010, 115, D19210. [Google Scholar] [CrossRef]
- Wex, H.; Neususs, C.; Wendisch, M.; Stratmann, F.; Koziar, C.; Keil, A.; Wiedensohler, A.; Ebert, M. Particle scattering, backscattering, and absorption coefficients: An in situ closure and sensitivity study. J. Geophys. Res. Atmos. 2012, 107, 8122. [Google Scholar] [CrossRef]
- York, D.; Evensen, N.M.; Lopez Martinez, M.; de Basabe Delgado, J. Unified equations for the slope, intercept, and standard errors of the best straight line. Am. J. Phys. 2004, 72, 367–375. [Google Scholar] [CrossRef]
- Petäjä, T.; Mauldin, R.L., III; Kosciuch, E.; McGrath, J.; Nieminen, T.; Paasonen, P.; Boy, M.; Adamov, A.; Kotiaho, T.; Kulmala, M. Sulfuric acid and OH concentrations in a boreal forest site. Atmos. Chem. Phys. 2009, 9, 7435–7448. [Google Scholar] [CrossRef]
- Zieger, P.; Weingartner, E.; Henzing, J.; Moerman, M.; de Leeuw, G.; Mikkilä, J.; Ehn, M.; Petäjä, T.; Clémer, K.; van Roozendael, M.; et al. Comparison of ambient aerosol extinction coefficients obtained from in-situ, MAX-DOAS and LIDAR measurements at Cabauw. Atmos. Chem. Phys. 2011, 11, 2603–2624. [Google Scholar] [CrossRef]
- Cantrell, C.A. Technical Note: Review of methods for linear least-squares fitting of data and application to atmospheric chemistry problems. Atmos. Chem. Phys. 2008, 8, 5477–5487. [Google Scholar] [CrossRef]
- Hand, J.L.; Kreidenweis, S.M. A new method for retrieving particle refractive index and effective density from aerosol size distribution data. Aerosol Sci. Tech. 2002, 36, 1012–1026. [Google Scholar] [CrossRef]
- McComiskey, A.; Feingold, G.; Frisch, A.S.; Turner, D.D.; Miller, M.A.; Chiu, J.C.; Min, Q.; Ogren, J.A. An assessment of aerosol-cloud interactions in marine stratus clouds based on surface remote sensing. J. Geophys. Res. 2009, 114, D09203. [Google Scholar] [CrossRef]
- Modini, R.L.; Frossard, A.A.; Ahlm, L.; Russell, L.M.; Corrigan, C.E.; Roberts, G.C.; Hawkins, L.N.; Schroder, J.C.; Bertram, A.K.; Zhao, R.; et al. Primary marine aerosol-cloud interactions off the coast of California. J. Geophys. Res. Atmos. 2015, 120. [Google Scholar] [CrossRef]
- Yu, H.; Chin, M.; Bian, H.; Yuan, T.; Prospero, J.M.; Omar, A.H.; Remer, L.A.; Winker, D.M.; Yang, Y.; Zhang, Y.; Zhang, Z.; et al. Quantification of trans-Atlantic dust transport from seven-year (2007–2013) record of CALIPSO lidar measurements. Remote Sens. Environ. 2015, 159, 232–249. [Google Scholar] [CrossRef]
- Barnard, J.C.; Harrison, L.C. Monotonic responses from monochromatic optical particle counters. Appl. Opt. 1988, 3, 584–592. [Google Scholar] [CrossRef]
- Kennedy, W.J.; Gentle, J.E. Statistical Computing; Marcel Dekker: New York, NY, USA, 1980. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).