Land-Atmosphere Transfer Parameters in the Brazilian Pantanal during the Dry Season
Abstract
:1. Introduction
2. Site, Experiment and Dataset
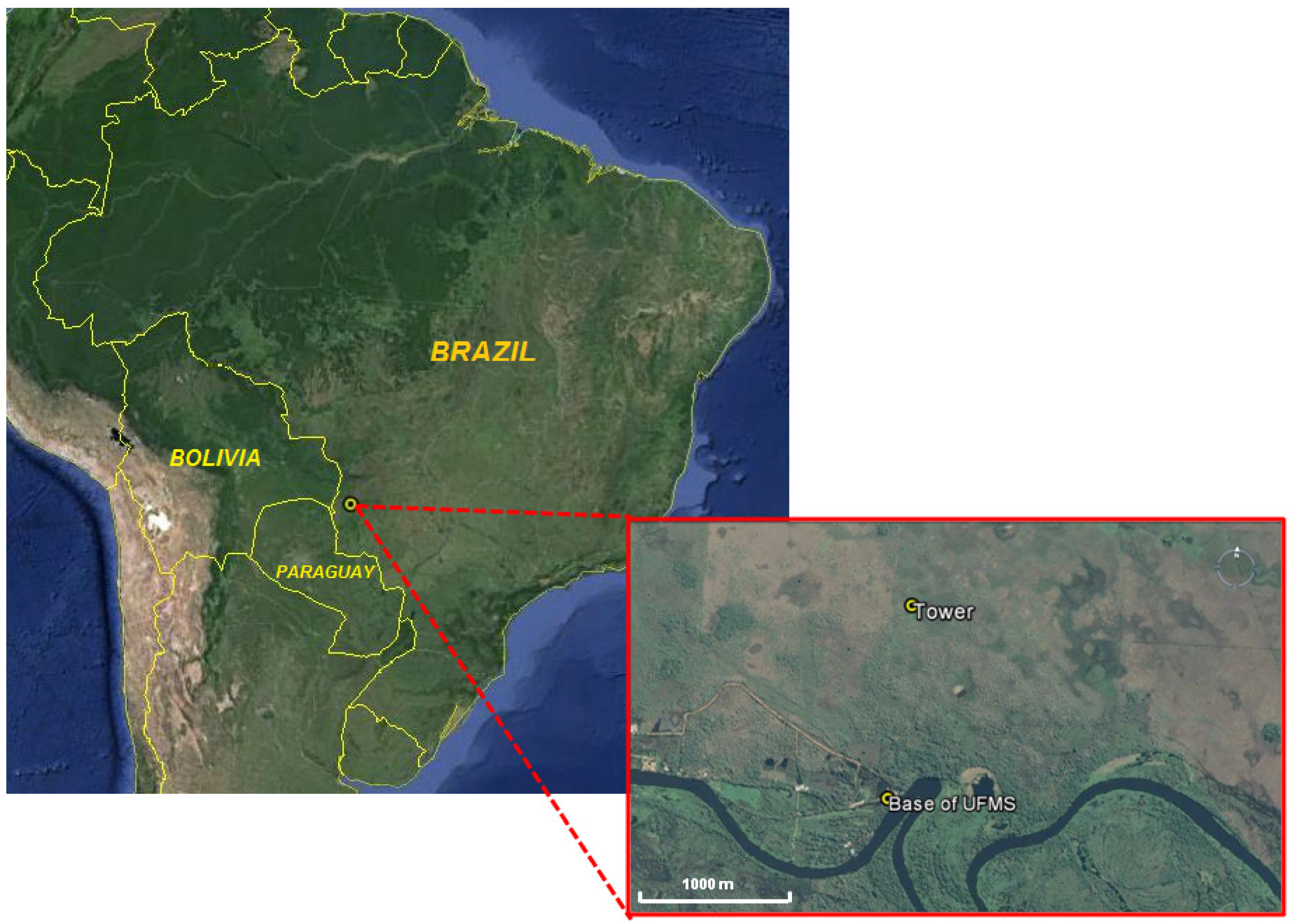

3. Methodology
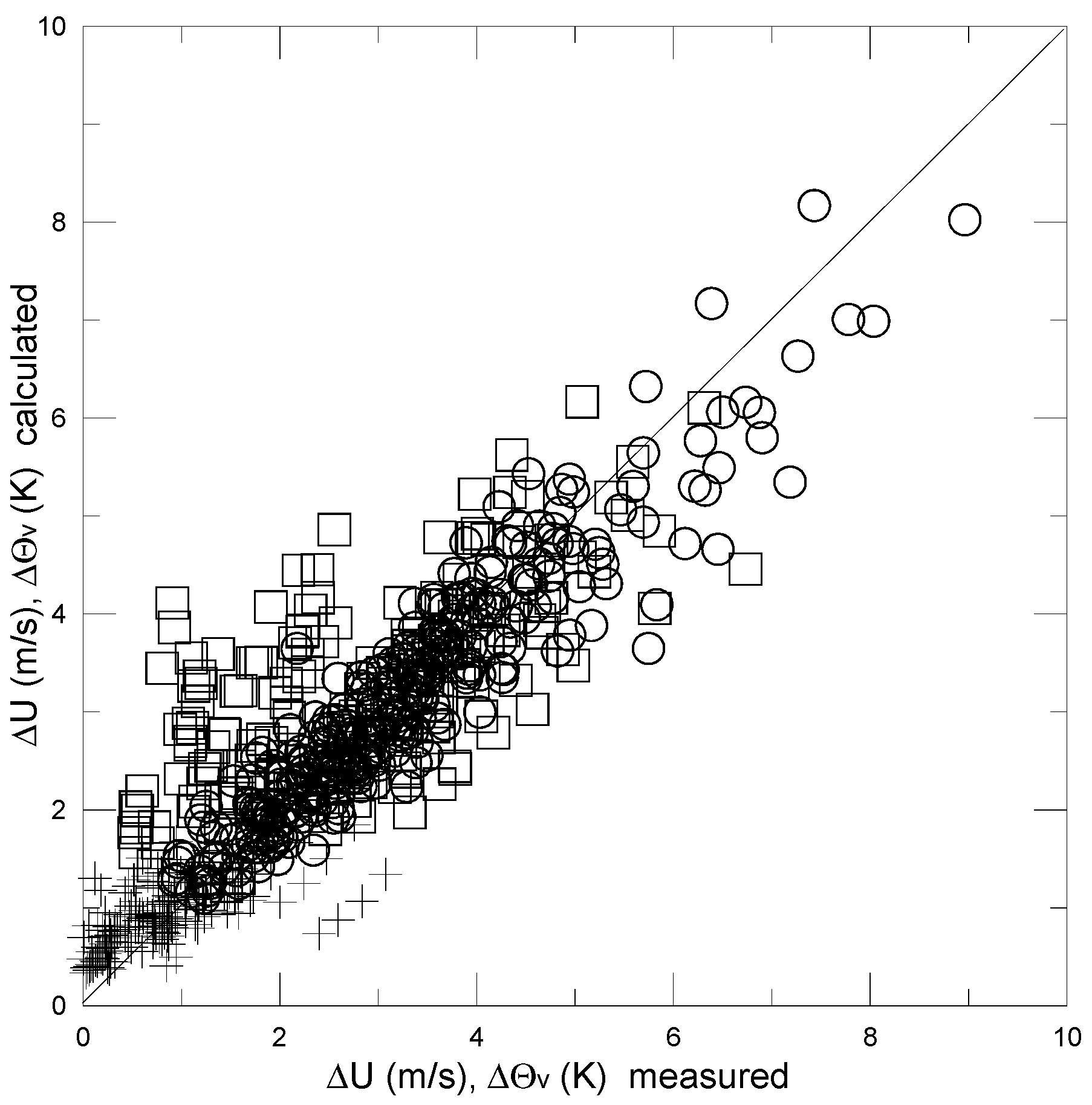
3.1. Wind Speed and Temperature
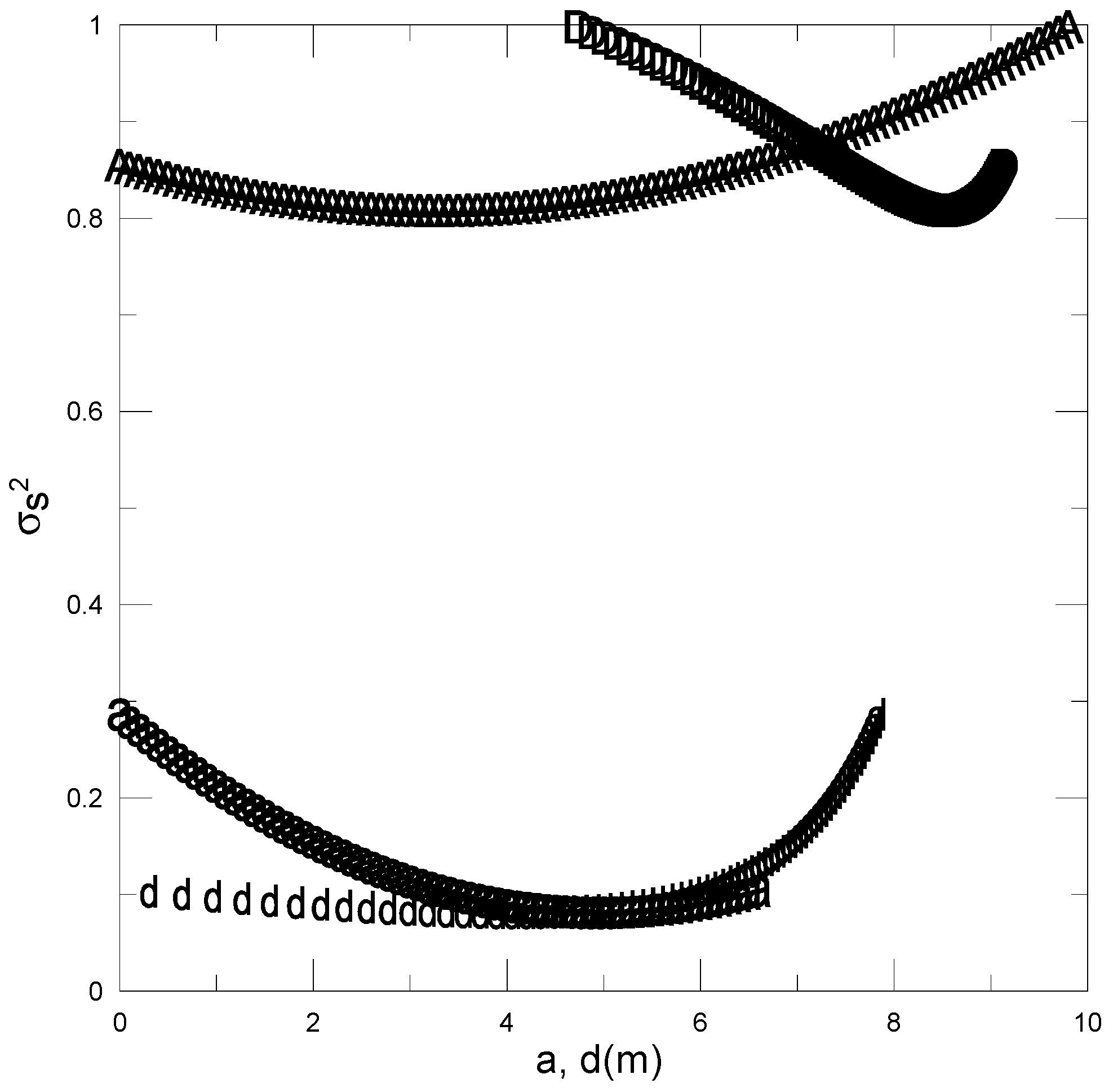
3.2. Water Vapor
4. Parameter Estimation and Discussion
4.1. Temperature and Wind Speed: Estimation of the Surface Length Scales and the Stability Parameter
| U Stable | |||
| Levels | a | d (m) | z0 (m) |
| 1–3 | 4.5 | 1.9 | 0.13 |
| 1–5 | 4.1 | 3.7 | 0.07 |
| 2–3 | 4.9 | 4.2 | 0.09 |
| 2–5 | 4.2 | 5.3 | 0.06 |
| 3–5 | 3.8 | 6.9 | 0.04 |
| Averages | 4.3 ± 0.4 | 4.4 ± 1.8 | 0.08 ± 0.03 |
| U Unstable | |||
| Levels | a | d (m) | z0 (m) |
| 1–3 | 10.2 | 2.7 | 0.05 |
| Θv Stable | |||
| Levels | a | d (m) | z0 (m) |
| 1–2 | 3.0 | 3.6 | 0.17 |
| 1–3 | 1.4 | 6.9 | 0.03 |
| 2–3 | 3.3 | 8.5 | 0.03 |
| Averages | 2.6 ± 1.0 | 6.3 ± 2.5 | 0.08 ± 0.08 |
| U Stable | |||||
| Levels | 1 | 2 | 3 | 5 | Averages |
| z0 (m) | 0.07 | 0.08 | 0.09 | 0.07 | 0.08 ± 0.01 |
| d (m) | 3.8 | 4.1 | 3.5 | 4.4 | 4.0 ± 0.4 |
| U Unstable | |||||
| Levels | 1 | 2 | 3 | 5 | Averages |
| z0 (m) | 0.017 | 0.024 | 0.017 | - | 0.019 ± 0.004 |
| d (m) | 6.8 | 7.7 | 11.0 | - | 8.5 ± 2.2 |
| Θv Stable | |||||
| Levels | 1 | 2 | 3 | 5 | Averages |
| z0 (m) | 0.12 | 0.13 | 0.08 | - | 0.11 ± 0.03 |
| d (m) | 4.8 | 4.8 | 4.9 | - | 4.8 ± 0.1 |
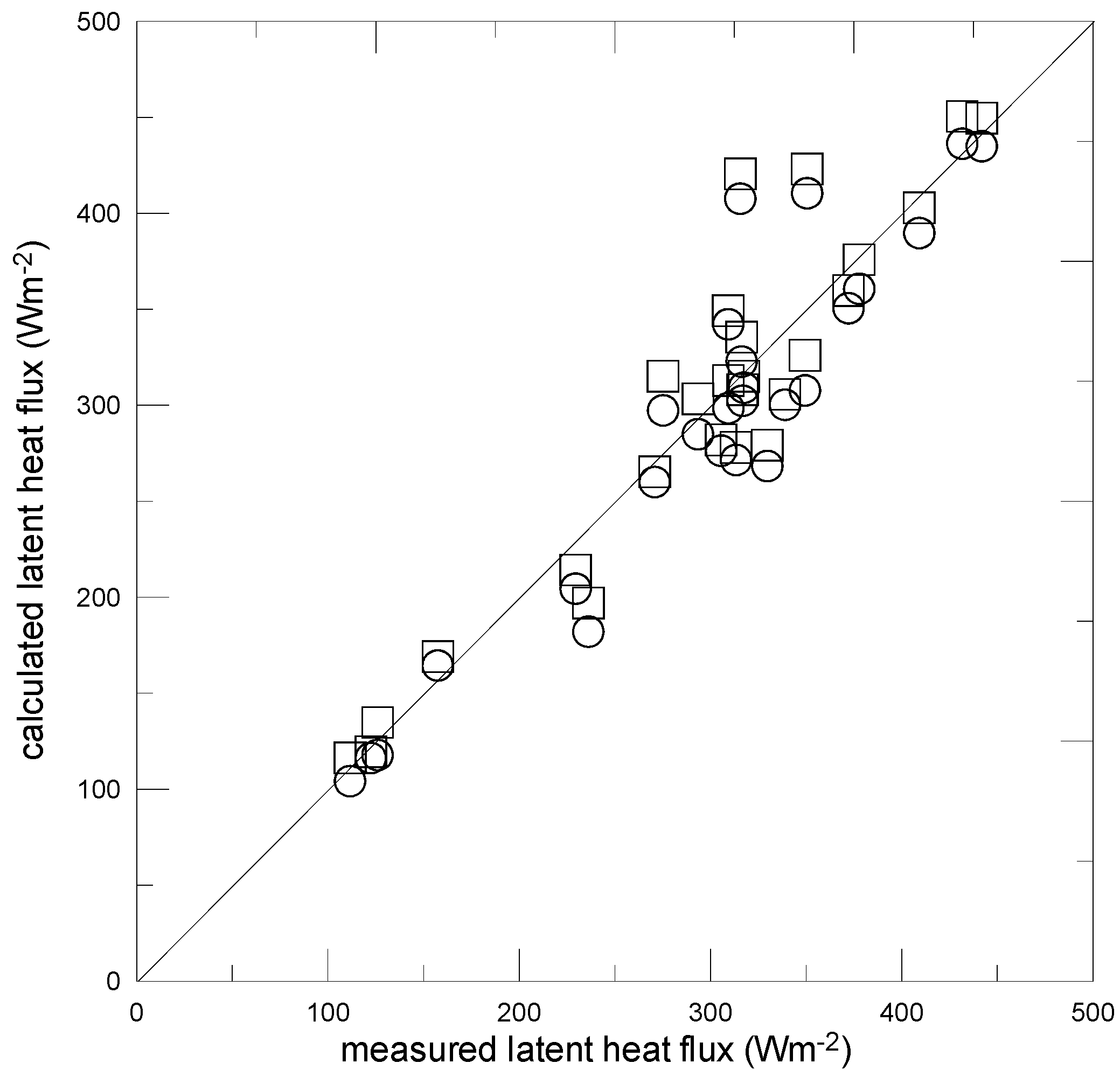
4.2. Water Vapor: Estimation of the Scalar Drag Coefficient
| Level | Ch PM Model (10−3) | Ch Data Average (10−3) | evf |
|---|---|---|---|
| 3 | 7.6 ± 1.5 | 6.8 ± 0.4 | 0.72 ± 0.11 |
| 5 | 6.5 ± 1.2 | 5.4 ± 0.3 | 0.83 ± 0.08 |
4.3. Discussion
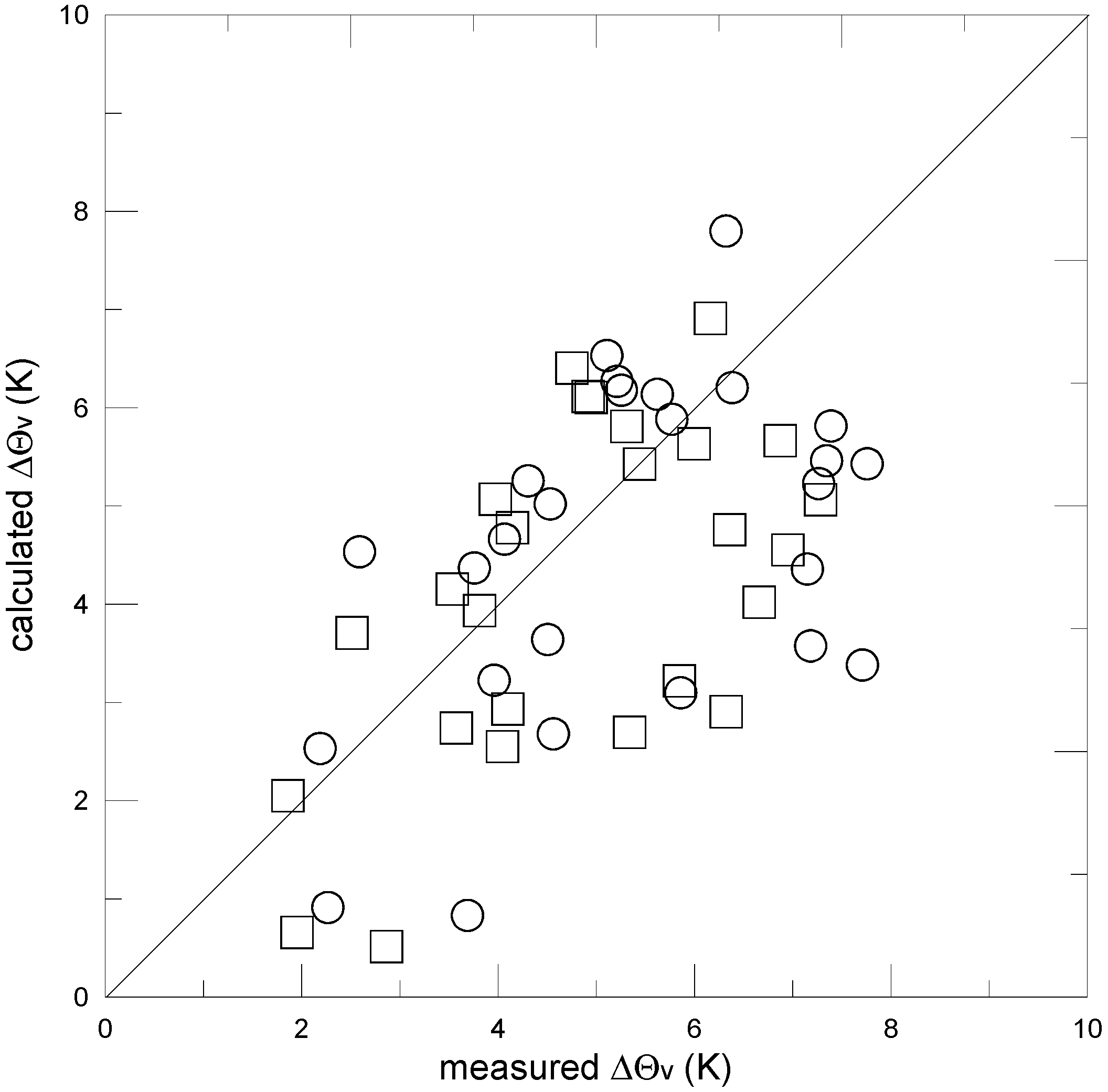
5. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
References
- Garratt, J.R. The Atmospheric Boundary Layer; Cambridge University Press: New York, NY, USA, 1992. [Google Scholar]
- Pielke, R.A. Mesoscale Meteorological Modelling; Academic Press: London, UK, 2002. [Google Scholar]
- Anthes, R.A. Boundary layers in numerical weather predictions. In Proceedings of the Workshop on the Planetary Boundary Layer, Boulder, CO, USA, 14–18 August 1978.
- Arya, S.P.S. Suggested revisions to ceratain Boundary Leyer parameterization schemes used in Atmosppheric Ciculation Models. Mon. Weath. Rev. 1977, 105, 215–227. [Google Scholar] [CrossRef]
- Venkatram, A.; Wyngaard, J.C. Lectures on Air Pollution Modelling; American Meteorological Society: Boston, MA, USA, 1988. [Google Scholar]
- Pasquill, F. Atmospheric Diffusion; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Hagemann, S. An Improved Land Surface Parameter Dataset for Global and Regional Climate Models; Report No. 336; Max Plank Institute for Meteorology: Hamburg, Germany, 2002. [Google Scholar]
- Wieringa, J. Representative roughness parameters for homogeneous terrain. Bound. Layer Meteorol. 1993, 63, 323–363. [Google Scholar] [CrossRef]
- Norman, J.M.; Becker, F. Terminology in thermal infrared remote sensing of natural surfaces. Agric. For. Meteorol. 1995, 77, 153–166. [Google Scholar] [CrossRef]
- De Bruin, H.A.R.; Verhoef, A. A new method to determine the zero plane displacement. Bound. Layer Meteorol. 1997, 116, 385–392. [Google Scholar] [CrossRef]
- Loureiro, J.R.B.; Freire, A.P.S.; Alho, A.T.P.; Ilha, A. The error in origin from first principles. In Proceedings of the International Congress of Mechanical Engineering COBEM, Brasilia, DF, Brazil, 5–9 November 2007.
- Martano, P. Estimation of Surface Roughness Length and Displacement Height from Single-Level Sonic Anemometer Data. J. Appl. Meteorol. 2000, 39, 708–715. [Google Scholar] [CrossRef]
- Businger, J.A.; Wyngaard, J.C.; Izumi, Y.; Bradley, E.F. Flux-Profile relationships in the Atmospheric Surface Layer. J. Atmos. Sci. 1971, 28, 181–189. [Google Scholar] [CrossRef]
- Martano, P. Evapotranspiration estimates over non-homogeneous Mediterranean land cover by a calibrated ‘critical resistance’ approach. Atmosphere 2015, 6, 255–272. [Google Scholar] [CrossRef]
- De Leal Oliveira, M.B.; von Randow, C.; Manzi, A.O.; dos Santos Alvala, R.C.; de Souza, A.; Leitão de Miranda, V.B.R.; Deane de Abreu Sá, L. Fluxos turbulentos de energia sobre o Pantanal Mato-Grossense. Revista Brasileira de Meteorologia 2006, 21, 159–165. (In Portuguese) [Google Scholar]
- Mesquita, F.L.L.; Marques Filho, E.P.; Karam, H.A.; Alvalá, R.C.S. Balanço de radiaçao no Pantanal Mato-Grosense durante a estaçao seca. Revista Brasileira de Meteorologia 2013, 28, 65–74. (In Portuguese) [Google Scholar] [CrossRef]
- Marques Filho, E.P.; Sá, L.D.A.; Karam, H.A.; Alvalá, R.C.S.; Souza, A.; Pereira, M.M.R. Atmospheric surface layer characteristics of turbulence above the Pantanal wetland regarding the similarity theory. Agric. For. Meteorol. 2008, 148, 883–892. [Google Scholar] [CrossRef]
- Zeri, L.M.M.; Abreu Sá, L.D. Scale dependence of coherent structures contribution to the daytime sensible heat flux over Pantanal wetland. Atmos. Sci. Lett. 2011, 12, 200–206. [Google Scholar] [CrossRef]
- Martins, H.S.; Abreu Sá, L.D.; Moraes, O.L.L. Low level jets in the Pantanal wetland nocturnal boundary layer—Case studies. Am. J. Environ. Eng. 2013, 3, 32–47. [Google Scholar] [CrossRef]
- Kondo, J.; Saigusa, N.; Sato, T. A parameterization of evaporation from bare soil surfaces. J. Appl. Meteorol. 1990, 29, 385–389. [Google Scholar] [CrossRef]
- Rana, G.; Katerji, N.; Mastrorilli, M.; el Moujabber, M. A model for predicting actual evapotranspiration under water stress conditions in a Mediterranean region. Theor. Appl. Climatol. 1997, 56, 45–55. [Google Scholar] [CrossRef]
- Brock, F.V.; Richardson, S.J. Meteorological Measurement Systems; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Cava, D.; Contini, D.; Donateo, A.; Martano, P. Analysis of short-term closure of the surface energy balance above short vegetation. Agric. For. Meteorol. 2008, 148, 82–93. [Google Scholar] [CrossRef]
- Martano, P. Inverse parameter estimation of the turbulent surface layer from single-level data and surface temperature. J. Appl. Met. Climatol. 2008, 47, 1027–1037. [Google Scholar] [CrossRef]
- Mesquita, F.L.L.; Marques Filho, E.P.; Souza, R.L.M.; Karam, H.A. Surface Energy Budget over the Pantanal Wetland during the Dry Season. Available online: http://cascavel.ufsm.br/revistas/ojs-2.2.2/index.php/cienciaenatura/article/viewFile/9526/5674 (accessed on 28 May 2015).
- Aster, R.C.; Borchers, B.; Thurber, C.H. Parameter Estimation and Inverse Problems; Academic Press: London, UK, 2005. [Google Scholar]
- Hsieh, C.; Katul, G.; Chi, T. An approximate analytical model for footprint estimation of scalar fluxes in thermally stratified atmospheric flows. Adv. Water Resour. 2000, 23, 765–772. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martano, P.; Filho, E.P.M.; De Abreu Sá, L.D. Land-Atmosphere Transfer Parameters in the Brazilian Pantanal during the Dry Season. Atmosphere 2015, 6, 805-821. https://doi.org/10.3390/atmos6060805
Martano P, Filho EPM, De Abreu Sá LD. Land-Atmosphere Transfer Parameters in the Brazilian Pantanal during the Dry Season. Atmosphere. 2015; 6(6):805-821. https://doi.org/10.3390/atmos6060805
Chicago/Turabian StyleMartano, Paolo, Edson Pereira Marques Filho, and Leonardo Deane De Abreu Sá. 2015. "Land-Atmosphere Transfer Parameters in the Brazilian Pantanal during the Dry Season" Atmosphere 6, no. 6: 805-821. https://doi.org/10.3390/atmos6060805
APA StyleMartano, P., Filho, E. P. M., & De Abreu Sá, L. D. (2015). Land-Atmosphere Transfer Parameters in the Brazilian Pantanal during the Dry Season. Atmosphere, 6(6), 805-821. https://doi.org/10.3390/atmos6060805





