Areal-Averaged Spectral Surface Albedo from Ground-Based Transmission Data Alone: Toward an Operational Retrieval

Abstract

We present here a simple retrieval of the areal-averaged spectral surface albedo using only ground-based measurements of atmospheric transmission under fully overcast conditions. Our retrieval is based on a one-line equation. The feasibility of our retrieval for routine determinations of albedo is demonstrated for different landscapes with various degrees of heterogeneity using three sets of measurements: (1) spectral atmospheric transmission from the Multi-Filter Rotating Shadowband Radiometer (MFRSR) at five wavelengths (415, 500, 615, 673, and 870 nm); (2) tower-based measurements of local surface albedo at the same wavelengths; and (3) areal-averaged surface albedo at four wavelengths (470, 560, 670 and 860 nm) from collocated and coincident Moderate Resolution Imaging Spectroradiometer (MODIS) observations. These integrated datasets cover both temporally long (2008–2013) and short (April–May 2010) periods at the Atmospheric Radiation Measurement (ARM) Southern Great Plains site and the National Oceanic and Atmospheric Administration (NOAA) Table Mountain site, respectively. The calculated root mean square error (RMSE), defined here as the root mean squared difference between the MODIS-derived surface albedo and the retrieved areal-averaged albedo, is quite small (RMSE ≤ 0.015) and comparable with that obtained previously by other investigators for the shortwave broadband albedo. Good agreement between tower-based measurements of daily-averaged surface albedo for completely overcast and non-overcast conditions is also demonstrated.

1. Introduction

Albedo, defined as a ratio of the upwelling irradiance from a surface over the downwelling irradiance reaching that surface, plays an extremely important role in the Earth’s radiation balance [1,2]. To estimate the broadband and/or spectral surface albedo, both tower-based solar radiation measurements [3,4] and remote sensing methods [5,6] have been used. Although the amount and quality of airborne and satellite data with large spatial coverage have improved substantially over the last several decades [7,8], there remain well-known uncertainties associated with surface albedo retrievals from aircraft and space [9,10,11]. These uncertainties mostly originate from the lack of direct measurements of solar radiation incident on the surface. On the other hand, tower-based observations, which measure both incident and reflected components, provide values of the local surface albedo with high temporal resolution. However, these measurements suffer from limited spatial coverage and uneven spatial distribution [12]. Given the importance of obtaining and understanding temporal and spatial changes of surface albedo [13], there is a clear need to improve and extend surface albedo estimates.

In contrast to limited tower-based data, ground-based measurements of downwelling irradiances (in the absence of towers) are abundant and therefore have much larger spatial coverage. These measurements have been used extensively for retrieving optical and microphysical properties of overcast clouds, such as cloud optical depth (τ) and droplet effective radius (r_e). The retrieval of these two important cloud parameters from irradiance measurements alone requires irradiance measurements at two wavelengths, one in the visible and the other in the near-infrared spectral range [14,15]. The conversion of such dual-channel measurements into cloud parameters (τ and r_e) commonly involves radiative transfer (RT) calculations and assumed/measured spectrally resolved values of the surface albedo. Alternatively, the traditional dual-channel methods can be applied for simultaneously estimating τ and surface albedo for an assumed r_e. In particular, Ricchiazzi et al. [16] have introduced such a possibility using spectral solar irradiance measurements and detailed RT calculations.

Here, we revisit this possibility using a simple expression [17], that analytically links the surface albedo (A), asymmetry factor (g) and τ with measured atmospheric transmission under overcast conditions. Note that τ is inversely related to r_e for fixed liquid water path [18,19]. (A lively picture of cloud optical properties and a description of simple analytical and highly sophisticated numerical RT methods are found in [19]). Originally, this semi-empirical expression was used for estimating τ at a single wavelength (415 nm), where the surface albedo is small and depends only weakly on the type of surface (e.g., in the absence of snow and ice; see [20]). In this paper, we apply the Barnard et al. [17] expression to estimate areal-averaged surface albedo using the general framework behind conventional dual-channel methods.

The new retrieval involves spectral measurements of atmospheric transmission from the Multi-Filter Rotating Shadowband Radiometer (MFRSR) at five wavelengths (415, 500, 615, 675, and 870 nm) for finding areal-averaged surface albedo. To evaluate the spectral and seasonal features of the retrieved surface albedo, we compare our albedo retrievals with collocated and coincident satellite- and tower-based albedo measurements. Henceforth, “retrieved” albedo refers to albedos obtained from the MFRSR instrument alone. The MFRSR data were acquired at the well-established Southern Great Plains (SGP) and Table Mountain sites supported by the U.S. Department of Energy’s (DOE’s) Atmospheric Radiation Measurement (ARM) Program (http://www.arm.gov/) and National Oceanic and Atmospheric Administration (NOAA) (http://www.esrl.noaa.gov/), respectively. Previously, tower-based data collected at these sites have been used to evaluate satellite-derived shortwave broadband surface albedo for clear-sky days and selected seasonally dependent conditions with relatively uniform landscapes [21,22].

Our study aims to demonstrate the retrieval feasibility for days with fully overcast and non-overcast (defined as being either clear or partly cloudy) conditions, and landscapes with various degrees of heterogeneity. To this end, our efforts address three main questions: (1) How do the retrieved spectral surface albedo values compare to those obtained from independent satellite- and tower-based measurements? (2) Are albedos derived from overcast skies applicable to clear days? and (3) How sensitive is the difference between the retrieved and measured albedos to surface heterogeneity? The following sections outline our retrieval algorithm (Section 2), review general features of the retrieved and measured albedos (Section 3), describe the integrated datasets relevant to our study (Section 4), and discuss the performance of our retrieval (Section 5).

2. Approach

The concentration and size distribution of cloud droplets control τ and r_e and therefore the relative amount of incoming solar radiation which is reflected, absorbed and transmitted by clouds. Numerical computations of the reflection, absorption and transmission for an overcast cloud layer are almost always based on a one-dimensional (1D) RT approximation [19,23] where the multiple scattering effects associated with surface albedo can be easily incorporated. Corresponding analytical solutions can be obtained for specific cases, including optically thick cloud layers. These solutions provide a general understanding of the impact of cloud/surface properties on atmospheric radiances; moreover, the solutions form the basis for estimating cloud properties operationally through measured irradiances. These solutions have several terms with coefficients related to cloud optical and microphysical properties. Obtaining these coefficients typically involves Mie-based parameterizations (the so-called semi-analytical solutions; [24]), or inferences based on data (the so-called semi-empirical solutions; [17,25]).

Let us consider one of these semi-empirical solutions obtained for optically thick (τ > 5) and non-absorbing clouds [17] in fully overcast conditions. Coefficients of this solution, which represent the conservative scattering case, were found using multi-year measurements of atmospheric transmission at three ARM sites (tropical, continental, and Arctic regions), and complementary transmission-based τ retrievals. For spectral MFRSR data, the solution for τ is expressed by the equation

$${\tau }_{\lambda }=\frac{4}{3}\left(\frac{1}{t_{\lambda }}-1\right)/\left[\left(1-A_{\lambda }\right)\left(1-g_{\lambda }\right)\right]$$

(1)

where t_λ, A_λ and g_λ are normalized atmospheric transmission, surface albedo and asymmetry factor for a given wavelength, respectively; the subscript “λ” indicates the spectral dependence of these parameters. The normalized atmospheric transmission is defined as t_λ = T_λ/μ^1.5, where T_λ and μ are the measured atmospheric transmission and the cosine of solar zenith angle, respectively. Note that Kokhanovsky et al. [24] obtained a similar semi-analytical solution for the simplest case when an optically thick and non-absorbing overcast cloud layer is located above a “black” surface (A_λ = 0) and illustrated that this solution has the potential for retrieving τ and r_e in the framework of conventional dual-channel methods.

Similar to Ricchiazzi et al. [16], we apply this framework for the simultaneous retrievals of τ_λ and A_λ. However, in contrast to Ricchiazzi et al. [16] who used detailed radiative transfer calculations, we apply the simple approach expressed by Equation (1). The latter can be re-written for the surface albedo estimation as

$$A_{\lambda }=1-\frac{4}{3}\left(\frac{1}{t_{\lambda }}-1\right)/\left[{\tau }_{\lambda }\left(1-g_{\lambda }\right)\right]$$

(2).

We emphasize that the replacement of the time-consuming RT calculations by the simple Equations (1) and (2) provides the opportunity for quick and routine retrievals of τ_λ and A_λ from multi-spectral measurements of atmospheric transmission.

The two main steps of our approach are:

(1)

Estimate cloud optical depth at 415 nm using Equation (1). This equation includes the measured normalized transmission (t₄₁₅) and two input parameters (A₄₁₅ and g₄₁₅). These two parameters can either be assumed or obtained from independent measurements. We assume that A₄₁₅ is small (0.03) and does not depend on surface type and solar zenith angle, and that g₄₁₅ is equal to its typical value (0.87) for liquid water clouds [26]. The assumption that A₄₁₅ is small (0.03) is generally a very good assumption for all surfaces except snow, ice, sand, and concrete [20].

(2)

Estimate spectral surface albedo at other wavelengths using Equation (2). This equation includes the measured normalized transmission (t_λ) and two cloud parameters (τ_λ and g_λ) for a given wavelength. Here we assume that cloud optical depth depends only slightly on wavelength within the spectral range considered here (415–870 nm): τ_λ = τ₄₁₅c_λ. Values of the spectrally variable coefficient c_λ are obtained from conventional tables [26]. This coefficient does not vary much from the value of one. We also assume that the asymmetry factor is spectrally independent (g_λ = g₄₁₅) for all wavelengths. Note that the almost spectrally neutral behavior of the two major cloud parameters (τ_λ and g_λ) in the considered spectral range (415 nm to 870 nm) has been confirmed time and time again by many observational and theoretical studies [18,19,26]. The retrieved albedo does not depend on the assumed asymmetry factor (g₄₁₅) and is not very sensitive to the assumed surface albedo (A₄₁₅); see Appendix A.

The retrieval simplifications are motivated, to some extent, by the limited knowledge of cloud and atmospheric properties required for detailed RT calculations. Assumptions made for steps 1 and 2 implicitly assume that the spectral changes of observed atmospheric transmission are determined mostly by the spectral variations of the surface albedo. Whether this simplified approach works can be evaluated by comparing retrieved and measured surface albedos and considering important issues associated with surface inhomogeneity. Let us outline the general features of the measured and retrieved surface albedo and some expected challenges of the retrieval evaluation.

3. Areal-Averaged and Point Surface Albedo

Tower-based instruments mounted at several meters above the ground “see” only a relatively small area. For example, if a downward-looking instrument is mounted about 10 m above the surface, more than 90% of the upwelling radiation comes from an area only 60 meters in diameter below the instrument (Appendix B). Because of this very limited field of view the tower-based measurements represent “local” or “point” values of surface albedo. On the other hand, our retrieval estimates the surface albedo from the measured atmospheric transmission, which includes sunlight reflected by the ground and then “bounced” back to the surface by the cloud deck. The amount of “bounced” sunlight is proportional to the upwelling radiation at cloud base (Appendix B). Since overcast and optically thick clouds are frequently located above 0.5 km above the ground [27,28], irradiances reflected by the cloud back to the surface come from a wide surface area—much larger than the limited area seen by a tower-mounted sensor. Thus, our transmission-based retrievals represent “areal-averaged” values of surface albedo.

Theoretically, the measured local and retrieved values of surface albedo would be identical if both the measurements and retrievals of surface albedo were performed over an absolutely homogeneous surface. However, there is growing empirical evidence that for the majority of landscapes the surface albedo exhibits large variability over a wide range of spatial scales [12]. Therefore, a meaningful comparison of the local and areal-averaged values of surface albedo is typically obscured by challenges associated with surface inhomogeneity and spatial representativeness of point measurements for determining the areal-averages [21,29]. Weighted averages of point albedo data are commonly applied for approximating the areal-averaged surface albedo for landscapes with various degrees of heterogeneity [30].

Our simple retrieval relies on the application of 1D RT theory and, therefore it does not account for several important RT drivers, including changes of cloud optical properties at small spatial and temporal scales. To reduce the potential impact of these small-scale changes on our retrievals, daily-averaged values of the retrieved and measured surface albedo are considered because averaging suppresses random noise. Moreover, recognizing that the diurnal variability of surface albedo associated with solar zenith angle changes is more pronounced when the sun is low in the sky (μ < 0.4) [4,31], we calculate the daily-averaged values of surface albedo only for larger solar zenith angles (μ > 0.4). Finally, our retrieval does not explicitly account for the atmospheric aerosol located beneath a cloud layer, which can modify the transmission of a cloudy atmosphere and, thus, can change the difference between the local and areal-averaged values of surface albedo. Recently, Jäkel et al. [32] demonstrated that the anticipated aerosol impact on this difference is much smaller than the impact of surface heterogeneity for moderate aerosol loading (aerosol optical depth < 0.4) and the spectral range (415–870 nm) considered here.

4. Data Description

We use data collected at two continental sites in United States: the ARM SGP Central Facility located in Oklahoma (https://www.arm.gov/sites/sgp/C) and the NOAA Table Mountain site located in Colorado (http://www.esrl.noaa.gov/gmd/grad/surfrad/tablemt.html). Hereafter, the terms “ARM site” and “NOAA site” will refer to these two well-established sites with suites of many instruments. Included in this collection of instruments are collocated ground-based MFRSRs and tower-based, downward-looking Multi-Filter Radiometers (MFRs; the MFR is the sensing head of an MFRSR) for measuring spectral atmospheric transmission and surface albedo, respectively. In addition to the spectral radiation measurements, the instrumentation includes broadband shortwave pyranometers. We use these measurements along with a standard approach [33] for identifying completely overcast conditions (although data from the broadband, silicon MFRSR channel can be used for the same purpose obviating the need for pyranometer measurements).

Recall that our method is designed to retrieve the areal-averaged surface albedo for cases when the sky is completely overcast (Section 2). We again emphasize that tower-based measurements of surface albedo are performed for both the overcast and non-overcast skies and thus represent diffuse and total albedos, respectively [22]. The diffuse (total) albedo is defined as the ratio between the total upward and diffuse (total) downward irradiances. In contrast to the diffuse albedo, the total albedo with the diffuse and direct-beam components depends substantially on the solar zenith angle (SZA) and this dependence is governed mainly by the direct-beam albedo [22]. The latter can be obtained from the diffuse and total albedos measured during “nearby” overcast and clear-sky conditions [4]. Here, we use tower-based measurements of the diffuse and total albedo for assessing the representativeness of the overcast values of surface albedo for non-overcast conditions, as explained below.

The ARM and NOAA sites have distinct visual appearances from the air and ground (Figure 1 and Figure 2) mainly due to different surface types. The ARM site represents three major landscape classes: vegetated, partly vegetated and non-vegetated land cover with strong seasonal variability [34]. To sample this variability, the ARM site includes two downward-pointing MFRs mounted at 25 m and at 10 m above the ground on the 60- and 10-m towers (Figure 1), respectively. Two upward-looking MFRSRs are deployed at the surface. The 60-m tower [35] is located within a managed field where a variety of crops are planted and harvested irregularly year to year according to a given farming plan. For example, wheat is planted occasionally in winter near the 60-m tower [34]. In contrast, the 10-m tower is located in an unmanaged pasture where seasonal changes of surface albedo are quite consistent on annual time scales.

Compared to the ARM site (Figure 1), the NOAA site (Figure 2) has poorly vegetated “brown” sub-area surrounded by partly vegetated regions with “green” patches (Figure 2; bottom part). These patches define different types of vegetation, such as grass, bushes and trees. The 10-m tower with downward-looking MFR mounted at 8 m is located within the “brown” sub-area (Figure 2).

Figure 1. Aerial image of the Southern Great Plains (SGP) site (left, taken from Google maps on 7 May 2014) and ground-based image of 60-m tower (right, from [35]). The aerial image (about 1 × 1 km²) indicates the locations of the ground-based Multi-Filter Rotating Shadowband Radiometer (MFRSR) and the two towers (60-m and 10-m) with downward- and upward-looking Multi-Filter Radiometers (MFRs). Also, the image illustrates that these towers are located within sub-areas with different surface types.

Figure 1. Aerial image of the Southern Great Plains (SGP) site (left, taken from Google maps on 7 May 2014) and ground-based image of 60-m tower (right, from [35]). The aerial image (about 1 × 1 km²) indicates the locations of the ground-based Multi-Filter Rotating Shadowband Radiometer (MFRSR) and the two towers (60-m and 10-m) with downward- and upward-looking Multi-Filter Radiometers (MFRs). Also, the image illustrates that these towers are located within sub-areas with different surface types.

Figure 2. Aerial image of the National Oceanic and Atmospheric Administration (NOAA) site (left, taken from Google maps on 7 May 2014) and ground-based image of the 10-m tower (right, from http://www.esrl.noaa.gov/gmd/grad/surfrad/tablemt.html). The image (about 1 × 1 km²) illustrates that this tower is surrounded by several sub-areas with different surface types, including “brown” soil and “green” vegetation.

Figure 2. Aerial image of the National Oceanic and Atmospheric Administration (NOAA) site (left, taken from Google maps on 7 May 2014) and ground-based image of the 10-m tower (right, from http://www.esrl.noaa.gov/gmd/grad/surfrad/tablemt.html). The image (about 1 × 1 km²) illustrates that this tower is surrounded by several sub-areas with different surface types, including “brown” soil and “green” vegetation.

For our analysis, we consider the MFRSR and MFR data collected at five wavelengths (415, 500, 615, 675 and 870 nm) during a fairly short interval at the NOAA site (April–May 2010) and a much longer period at the ARM site (2008–2013). The selection of these locations and periods is driven mainly by the wide diversity of surface types and the availability and quality of relevant data. Our analysis involves: (1) retrieving the areal-averaged surface albedo from the measured atmospheric transmission; and (2) comparing the retrieved and measured values of surface albedo. At the ARM site, we use the measured tower-based values for calculating the weighted average albedo ($A_{\lambda }^a$)

$$A_{\lambda }^a=\left(1-f\right)A_{\lambda }^{10}+f{A}_{\lambda }^{25}$$

(3)

where $A_{\lambda }^{10}$ and $A_{\lambda }^{25}$ are the “local” 10-m and 25-m values of tower-based surface albedo, and the fraction f determines the relative contribution of these local values to the weighted average surface albedo. As a first approximation, we assume that f = 0.5 and that it does not depend on time and wavelength; that is, we simply average the two values. Only samples with good quality local data ($A_{\lambda }^{10}$ and $A_{\lambda }^{25}$) are used for calculating the average. Since the NOAA site has only one tower, a weighted average cannot be estimated from the tower data. Therefore, the tower-based NOAA albedos represent point values.

The ground-based measurements are accompanied by collocated satellite observations. In particular, we use the Moderate Resolution Imaging Spectroradiometer (MODIS) white-sky surface albedo data at four wavelengths (470, 560, 670 and 860 nm). These data, with product designation MCD43B3 (https://lpdaac.usgs.gov/products/modis_products_table/mcd43b3; 1-km resolution), were downloaded from the MODIS Reprojection Tool Web Interface (MRTWeb) site (https://mrtweb.cr.usgs.gov/). White-sky albedos are obtained for nominal wavelengths of 470, 560, 670, and 860 nm. We used these albedos for calculating the areal-averaged surface albedo in a 5 × 5 km² area surrounding the ARM and NOAA sites approximately centered over the site in question. These albedo values ($A_{\lambda }^m$) are considered as a reference (not necessarily ground “truth”) in our evaluation.

Only MODIS albedo values of the highest quality are used for this study. The quality information for each pixel is given in the MODIS product, MCD43B2, also downloaded from the MRTWeb site. The quality flags are discussed in https://lpdaac.usgs.gov/products/modis_products_table/mcd43b2, under the heading of “layers”, with variable name “BRDF_Albedo_Band_Quality”. We only used so-called “best quality” data (quality flag equal to zero). Using the best quality data reduced the size of the original data sets, depending on MODIS band and location. For the NOAA site, only 10 points of band 3 (470 nm) data, out of a total of 175, were not of highest quality. Excluding these data made no significant difference in the analysis. For the SGP site, the number of excluded points depended on the season. For the winter season, defined as December, January, and February, about 35% of the pixels were excluded (including points that were deleted by our own quality assurance scheme). For the other seasons the number of rejected points was much less. For spring (March, April, May), summer (June, July August), and fall (September, October, November) the reduction of points was 7%, 27%, and 13%, respectively. Exclusion of these points made a difference of at most 0.01 in derived MODIS albedos, with the largest changes occurring in winter; the changes during the other seasons were insignificant.

Given good quality data, we start with visual inspection of the temporal and spectral changes of the retrieved and measured/derived albedos (Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8). Such inspection is aimed to illustrate qualitative similarities and differences between albedos obtained from different platforms (e.g., similar seasonal trends and relative position of maximum values). We also include the corresponding quantitative comparisons (Table 1 and Table 2) using calculated root mean square error (RMSE) values. Similar to an earlier study [21], we assume that a good agreement is achieved if the RMSE does not exceed 0.015.

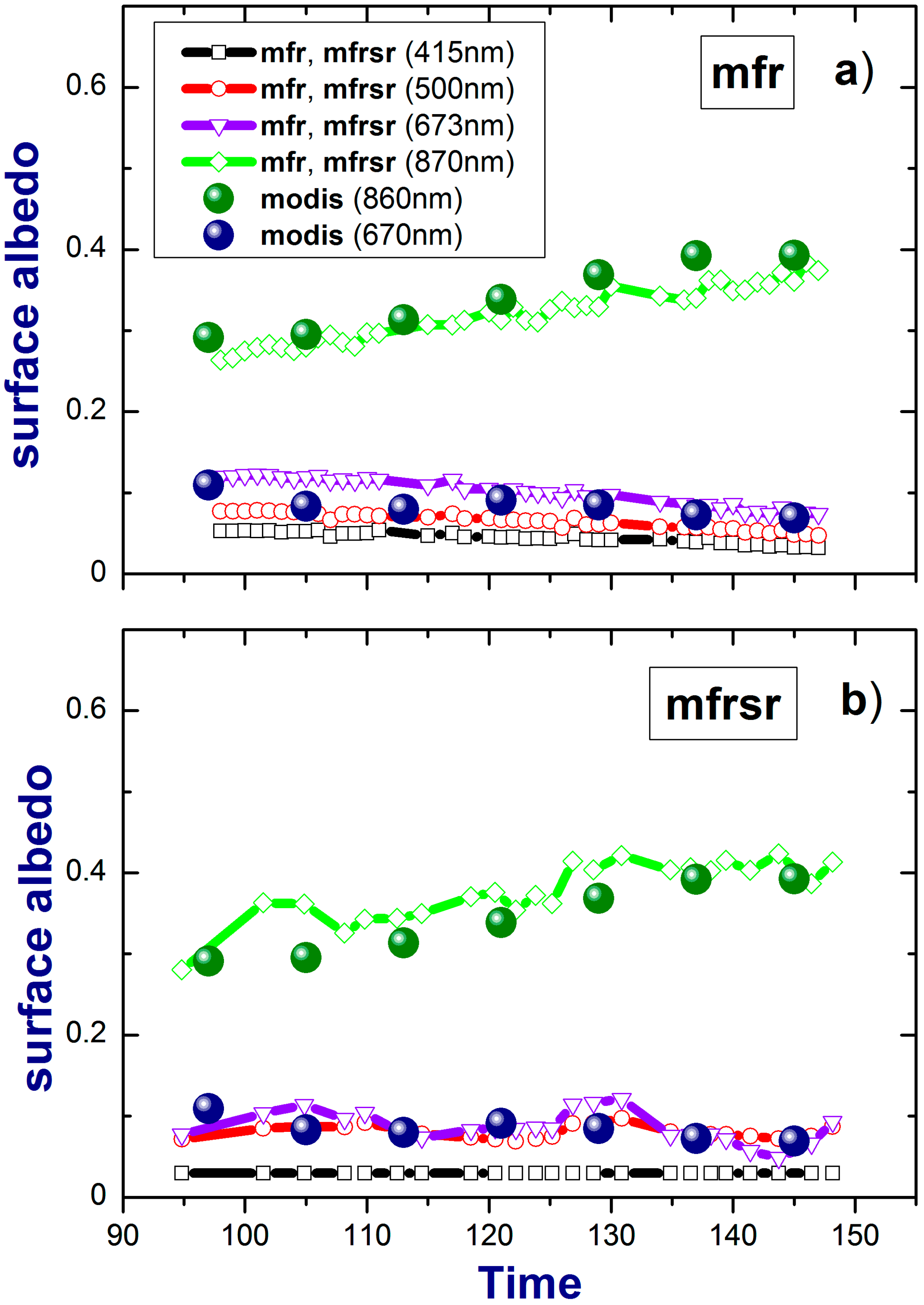
Figure 3. Time series of the (a) tower-measured local and (b) MFRSR-retrieved areal-averaged surface albedo at the NOAA site during the two-month period (April–May 2010). Here time is day of year. Black, red, purple and green colors define the surface albedo values at four wavelengths (415, 500, 673 and 870 nm). Also, the MODIS-derived surface albedo values at two wavelengths (670 and 860 nm) are included (blue, green dots).

Figure 3. Time series of the (a) tower-measured local and (b) MFRSR-retrieved areal-averaged surface albedo at the NOAA site during the two-month period (April–May 2010). Here time is day of year. Black, red, purple and green colors define the surface albedo values at four wavelengths (415, 500, 673 and 870 nm). Also, the MODIS-derived surface albedo values at two wavelengths (670 and 860 nm) are included (blue, green dots).

In line with this study [21], we calculate the RMSE values for comparing our retrieved areal-averaged surface albedo and albedos derived from satellites. The RMSE is defined as the root mean squared difference between the MODIS surface albedo and the technique in question. More explicitly, we find the difference between the MODIS albedo at these wavelengths (500, 615, 673, and 870 nm) and the albedo of the instrument of interest. These differences are squared, averaged, and the square root is taken to find the RMSE. To calculate the RMSE, the MODIS surface albedo values have been interpolated/extrapolated to four of the five MFRSR/MFR wavelengths (500, 615, 673, 870 nm) using linear interpolation/extrapolation. We do not extrapolate the MODIS data to 415 nm because the extrapolation “reach” from 470 nm (a 55 nm interval) is considered to be too extreme. On the other hand, we consider the extrapolation of MODIS data from 860 nm to 870 nm (a 10 nm interval) to be acceptable. Also, we calculate the corresponding RMSEs (MODIS surface albedo versus tower-based surface albedos) for estimating how well the measured “local” tower-based albedos represent albedos for the large (5 × 5 km²) area encompassing the ARM and NOAA sites.

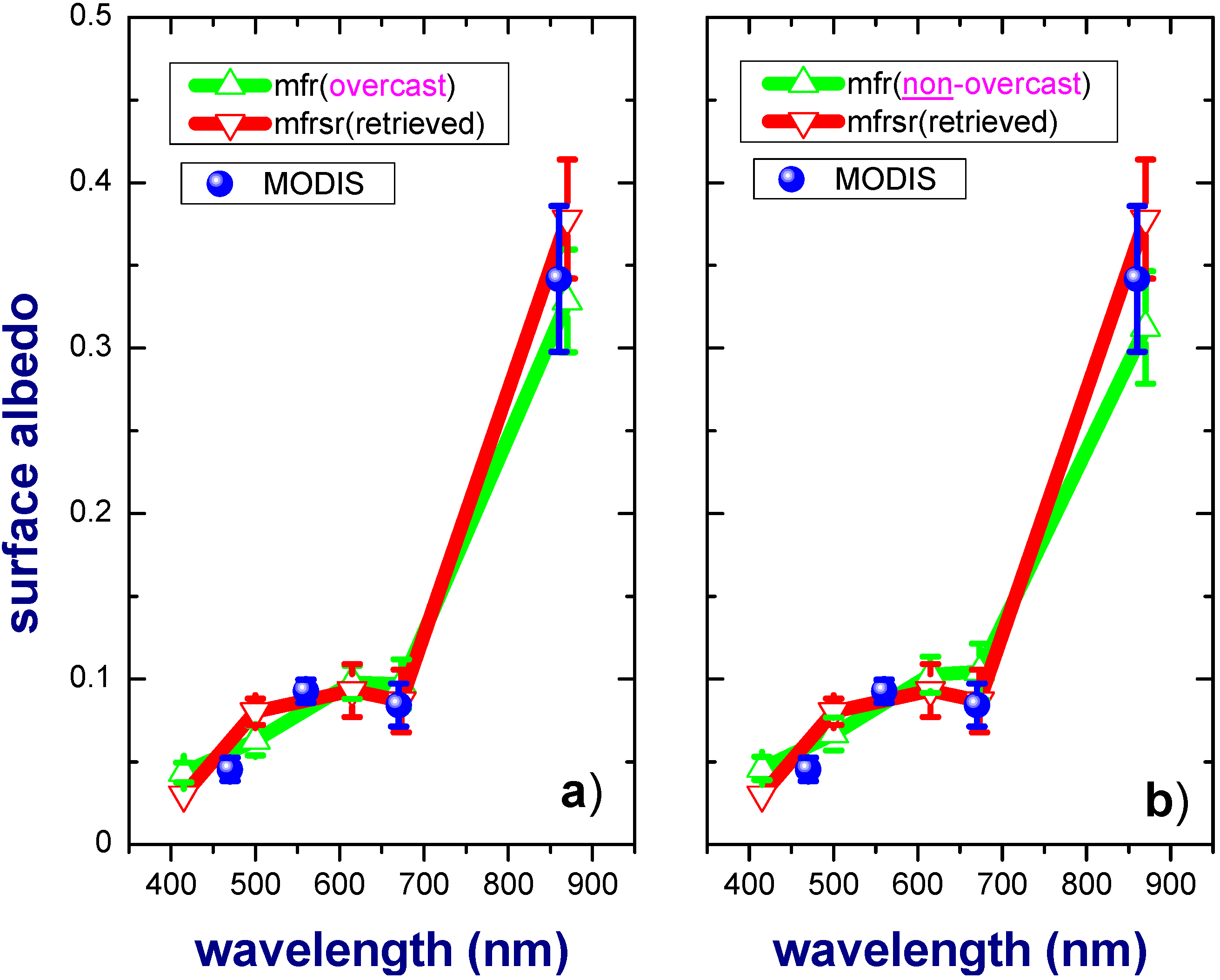
Figure 4. Mean values (±standard deviations) of the tower-measured local (green), MFRSR-retrieved areal-averaged (red) and MODIS-derived (blue) white-sky surface albedos as a function of wavelength. The mean local values represent overcast (a) and non-overcast (b) conditions that occurred during the two-month period of interest (Figure 3). The MODIS-derived albedos are plotted at the MODIS nominal wavelengths of 470, 560, 670, and 860 nm. For both figures, the MODIS-derived and MFRSR-retrieved albedos are the same.

Figure 4. Mean values (±standard deviations) of the tower-measured local (green), MFRSR-retrieved areal-averaged (red) and MODIS-derived (blue) white-sky surface albedos as a function of wavelength. The mean local values represent overcast (a) and non-overcast (b) conditions that occurred during the two-month period of interest (Figure 3). The MODIS-derived albedos are plotted at the MODIS nominal wavelengths of 470, 560, 670, and 860 nm. For both figures, the MODIS-derived and MFRSR-retrieved albedos are the same.

Three comparison-related comments should be made. First, the white-sky albedo represents the effects of diffuse radiation in the surface albedo derivation from MODIS data [22]. Thus, the white-sky albedo is directly comparable with the diffuse surface albedo measured/retrieved under overcast conditions. For non-overcast conditions, the MODIS-derived blue-sky albedo with the white-sky (for diffuse radiation) and black-sky (for direct beam) components is commonly assumed to be equivalent to the measured total surface albedo [22]. Second, the white-sky albedo is frequently assumed to be time-invariant during a day. In contrast to the white-sky albedo, the black-sky albedo has a well-known “U” shape with the smallest value occurring at local solar noon. As a result, the white-sky albedo overestimates (underestimates) the blue-sky albedo at local noon (near sunrise/sunset) (e.g., [22]; Figure 1). The magnitude of these overestimation/underestimations depends on relative contribution of the diffuse radiation to the total downward irradiance, and therefore on the atmospheric properties (e.g., aerosol loading). Third, the expected biases associated with these blue-sky albedo overestimation/underestimations will be partially canceled out during time integration over that part of the day when the solar zenith angle is relatively small. As a result, the difference between the daily-averaged white-sky and blue-sky albedos could be smaller than differences in the instantaneous values of white-sky and blue-sky albedos during a day (e.g., near local noon and/or near sunset/sunrise). Accordingly, we expect that the daily-averaged white-sky albedo could approximate quite well the daily-averaged total albedo measured under non-overcast conditions.

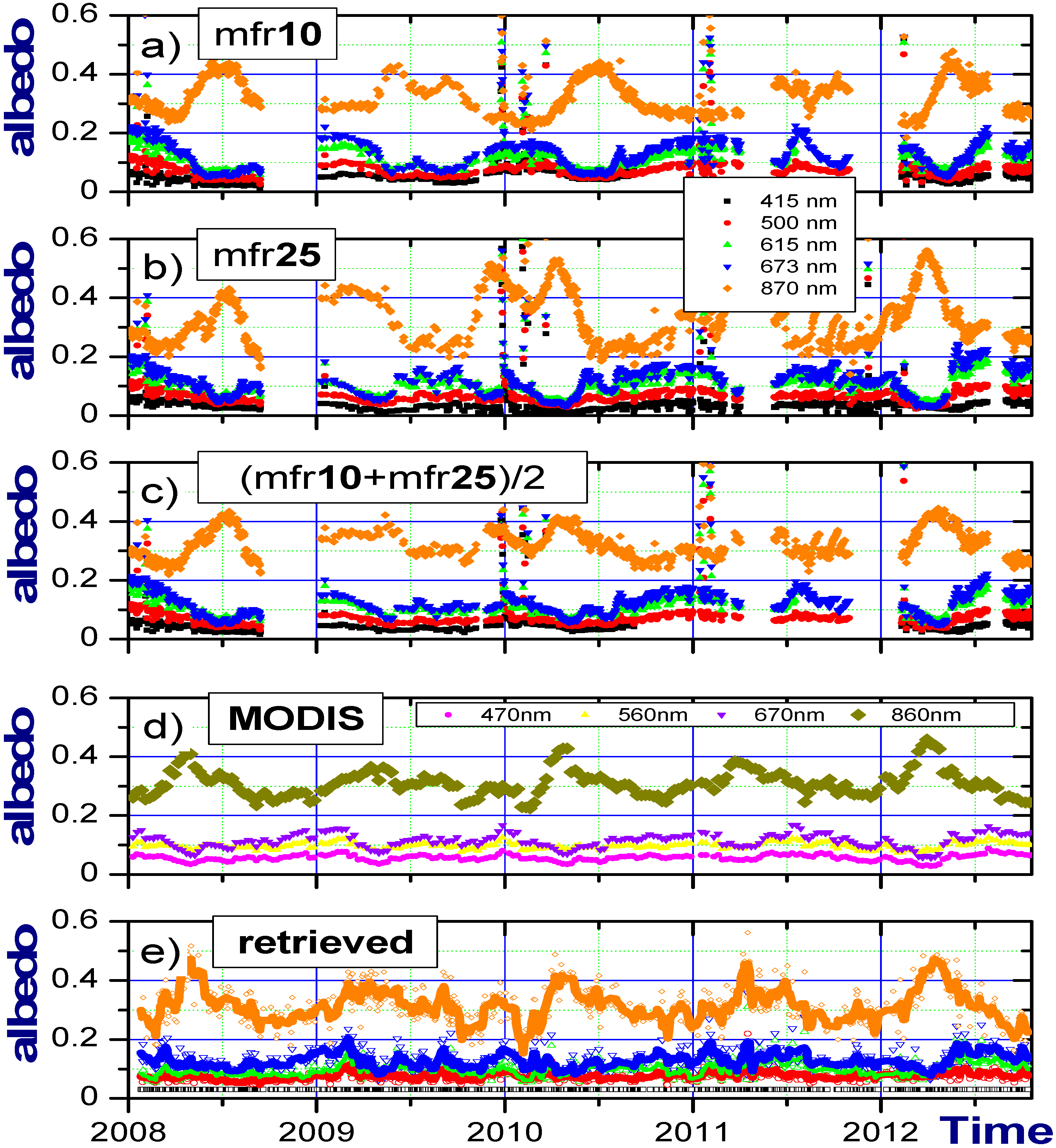
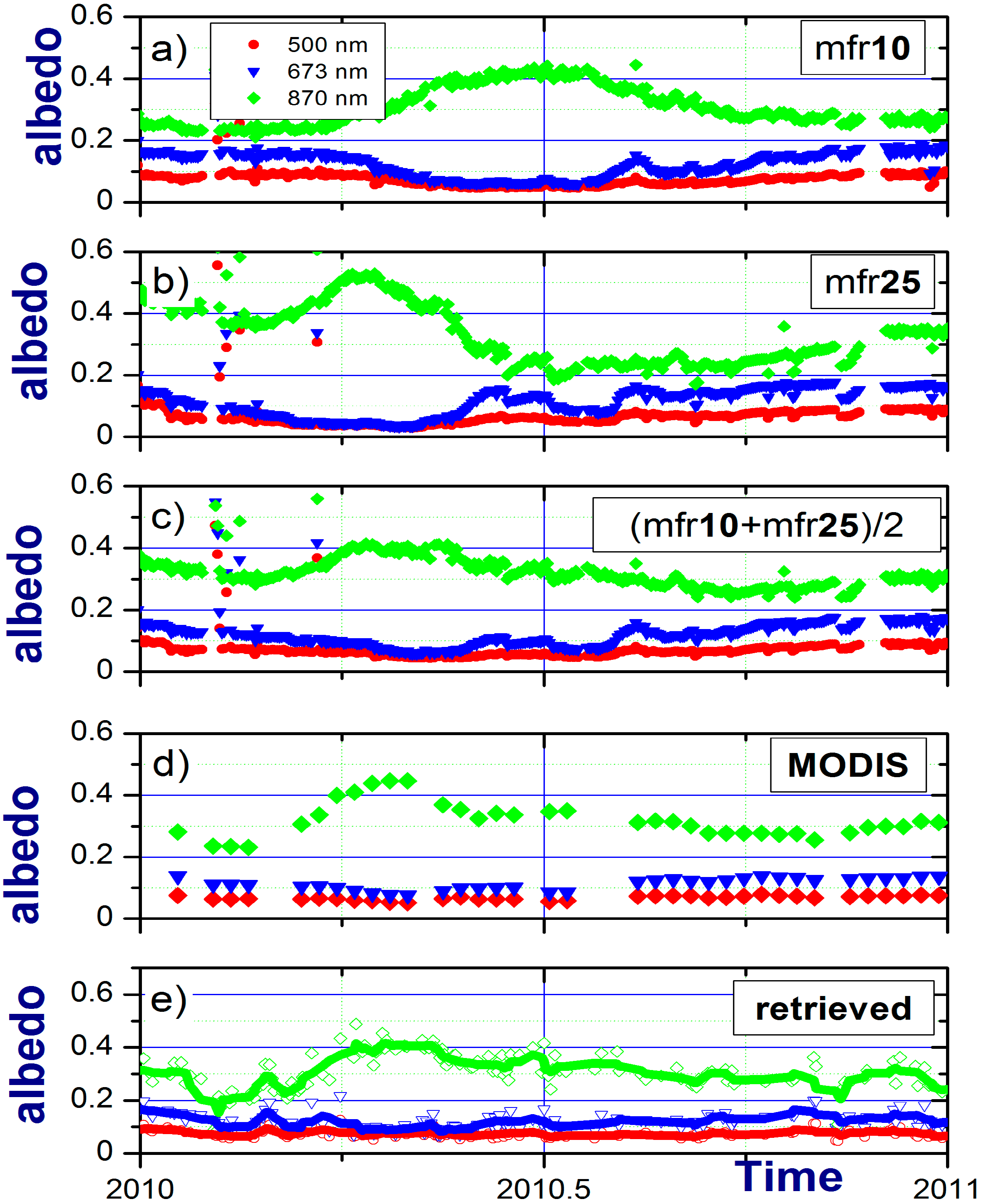
Figure 5. Time series of the tower-measured 10-m (a) and 25-m (b) surface albedo at the ARM site, their weighted average (c), MODIS-derived (d) and MFRSR-retrieved areal-averaged surface albedo (e) for one-year period (2010). Red, blue and green colors define the surface albedo values (a–c,e) at three MFR/MFRSR wavelengths (500, 673 and 870 nm). The MODIS data have been interpolated to these MFRSR wavelengths; (e) Solid lines (red, green, and blue) represent the smoothed versions of MFRSR-retrieved surface albedos at these wavelengths (500, 673 and 870 nm) (boxcar averaging; 5 points). Appendix C includes related version of Figure 5 for other years and wavelengths.

Figure 5. Time series of the tower-measured 10-m (a) and 25-m (b) surface albedo at the ARM site, their weighted average (c), MODIS-derived (d) and MFRSR-retrieved areal-averaged surface albedo (e) for one-year period (2010). Red, blue and green colors define the surface albedo values (a–c,e) at three MFR/MFRSR wavelengths (500, 673 and 870 nm). The MODIS data have been interpolated to these MFRSR wavelengths; (e) Solid lines (red, green, and blue) represent the smoothed versions of MFRSR-retrieved surface albedos at these wavelengths (500, 673 and 870 nm) (boxcar averaging; 5 points). Appendix C includes related version of Figure 5 for other years and wavelengths.

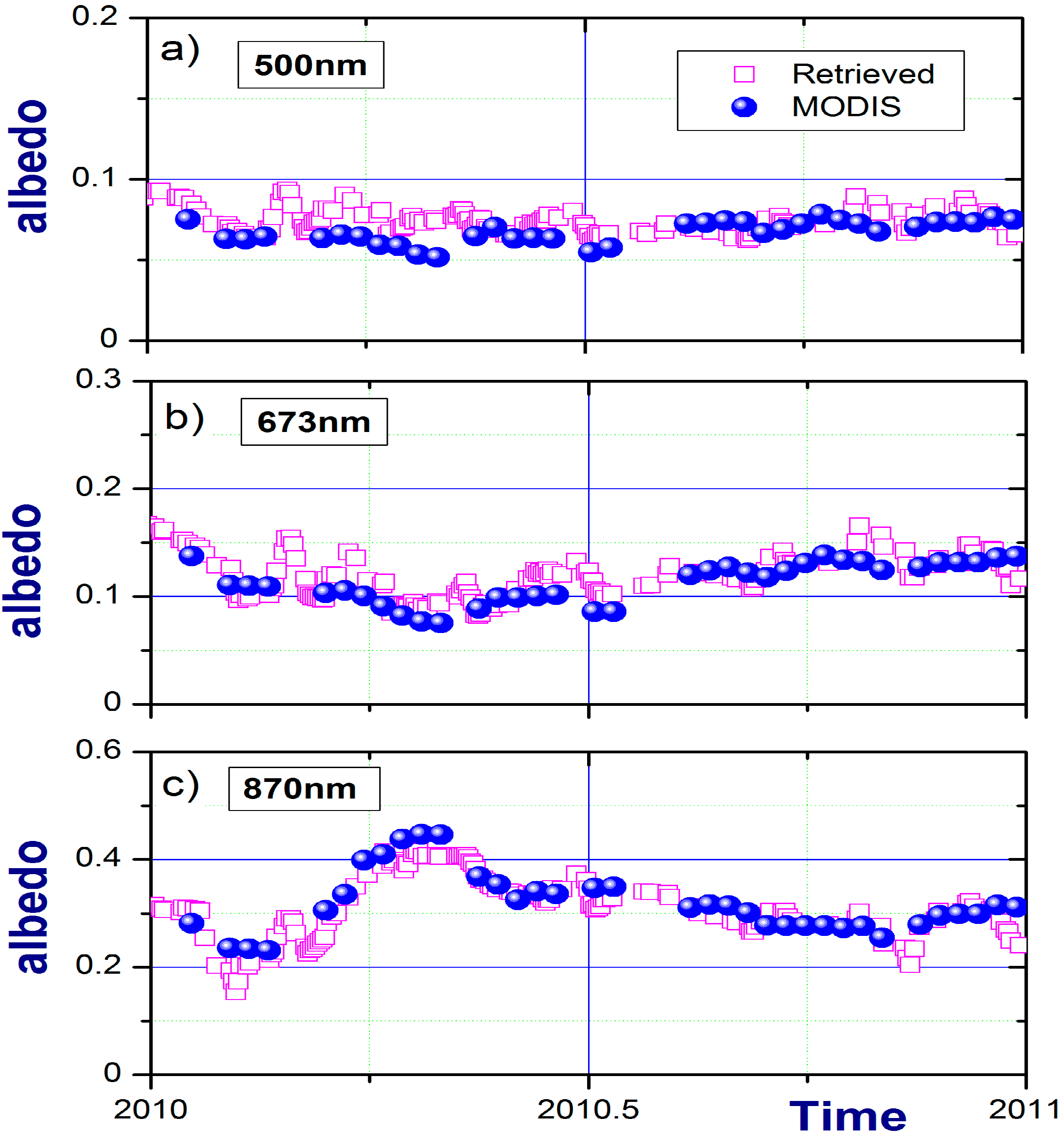
Figure 6. Time series of the MFRSR-retrieved areal-averaged surface albedo (magenta) and MODIS-derived albedo (blue) at three MFR/MFRSR wavelengths: 500 nm (a); 673 nm (b); and 870 nm (c) for one-year period (2010). In contrast to Figure 5, these time series are segregated by wavelength and focus on the comparison of the retrieved and MODIS-derived albedos.

Figure 6. Time series of the MFRSR-retrieved areal-averaged surface albedo (magenta) and MODIS-derived albedo (blue) at three MFR/MFRSR wavelengths: 500 nm (a); 673 nm (b); and 870 nm (c) for one-year period (2010). In contrast to Figure 5, these time series are segregated by wavelength and focus on the comparison of the retrieved and MODIS-derived albedos.

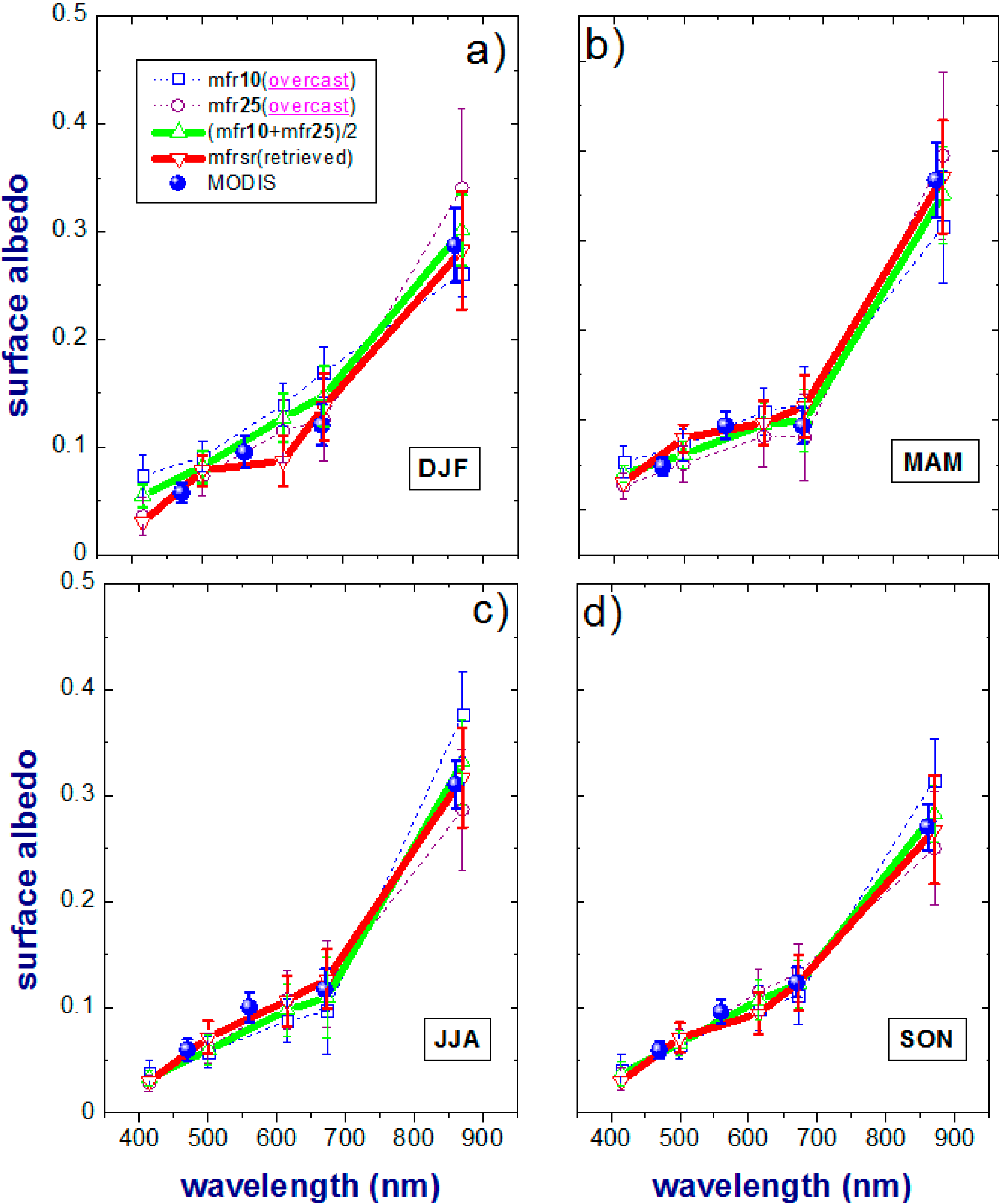
Figure 7. Spectral surface albedo values for overcast conditions during five-year period (2008–2013). Mean values (±standard deviations) of the tower-measured 10-m (blue-dotted) and 25-m (magenta-dotted) albedo, their weighted average (solid-green), MODIS-derived (blue) and areal-averaged albedo (solid-red) as a function of wavelength for four seasons: winter (a); spring (b); summer (c) and fall (d).

Figure 7. Spectral surface albedo values for overcast conditions during five-year period (2008–2013). Mean values (±standard deviations) of the tower-measured 10-m (blue-dotted) and 25-m (magenta-dotted) albedo, their weighted average (solid-green), MODIS-derived (blue) and areal-averaged albedo (solid-red) as a function of wavelength for four seasons: winter (a); spring (b); summer (c) and fall (d).

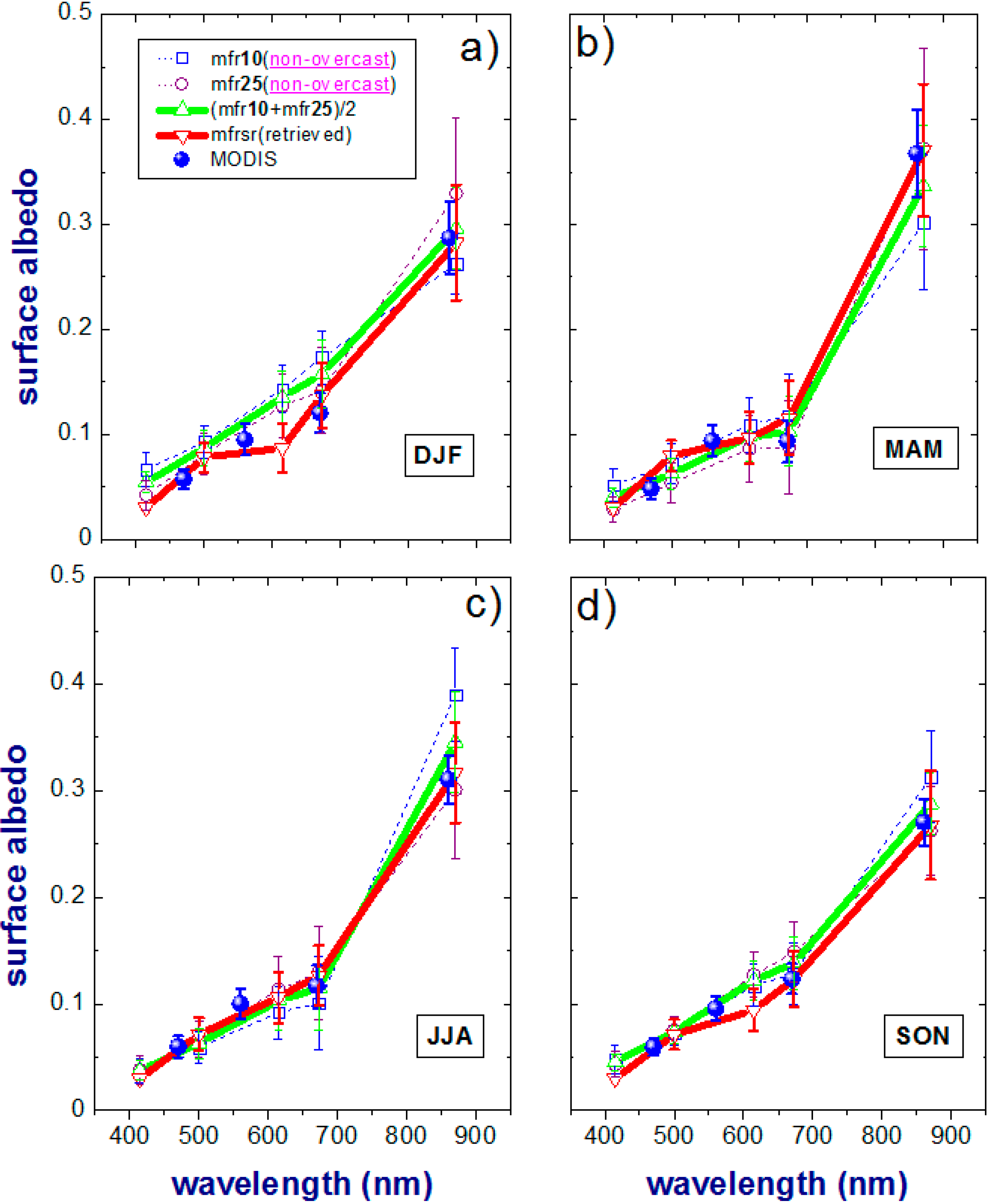
Figure 8. Spectral surface albedo values for non-overcast conditions during five-year period (2008–2013). Mean values (±standard deviations) of the tower-measured 10-m (blue-dotted) and 25-m (magenta-dotted) albedo, their weighted average (solid-green), MODIS-derived (blue) and areal-averaged albedo (solid-red) as a function of wavelength for four seasons: winter (a); spring (b); summer (c) and fall (d).

Figure 8. Spectral surface albedo values for non-overcast conditions during five-year period (2008–2013). Mean values (±standard deviations) of the tower-measured 10-m (blue-dotted) and 25-m (magenta-dotted) albedo, their weighted average (solid-green), MODIS-derived (blue) and areal-averaged albedo (solid-red) as a function of wavelength for four seasons: winter (a); spring (b); summer (c) and fall (d).

Table 1. Time-averaged albedos and the corresponding standard deviations (in parenthesis) derived from the indicated platforms for the NOAA site. For the tower data, both fully overcast and non-overcast conditions are shown. The MODIS data have been interpolated/extrapolated to the nominal MFRSR wavelengths. The root mean square error (RMSE) is also shown (bottom row) using the MODIS albedos as the reference. The two lowest RMSEs are indicated in bold.

Wavelength (nm)	MFRSR (Overcast)	MODIS (White Sky)	Tower (Overcast)	Tower (Non-Overcast)
415	0.030 (0.0)	-	0.044 (0.006)	0.046 (0.007)
500	0.080 (0.008)	0.061 (0.006)	0.063 (0.009)	0.066 (0.010)
615	0.093 (0.016)	0.088 (0.008)	0.098 (0.010)	0.103 (0.011)
673	0.087 (0.019)	0.088 (0.012)	0.098 (0.015)	0.104 (0.017)
870	0.378 (0.036)	0.355 (0.043)	0.329 (0.031)	0.312 (0.034)
RMSE	0.015	-	0.015	0.024

Table 1. Time-averaged albedos and the corresponding standard deviations (in parenthesis) derived from the indicated platforms for the NOAA site. For the tower data, both fully overcast and non-overcast conditions are shown. The MODIS data have been interpolated/extrapolated to the nominal MFRSR wavelengths. The root mean square error (RMSE) is also shown (bottom row) using the MODIS albedos as the reference. The two lowest RMSEs are indicated in bold.

Wavelength (nm)	MFRSR (Overcast)	MODIS (White Sky)	Tower (Overcast)	Tower (Non-Overcast)
415	0.030 (0.0)	-	0.044 (0.006)	0.046 (0.007)
500	0.080 (0.008)	0.061 (0.006)	0.063 (0.009)	0.066 (0.010)
615	0.093 (0.016)	0.088 (0.008)	0.098 (0.010)	0.103 (0.011)
673	0.087 (0.019)	0.088 (0.012)	0.098 (0.015)	0.104 (0.017)
870	0.378 (0.036)	0.355 (0.043)	0.329 (0.031)	0.312 (0.034)
RMSE	0.015	-	0.015	0.024

Table 2. Time-averaged albedos and the corresponding standard deviations (in parenthesis) derived from the indicated platforms for the ARM site, segregated by season: winter (a), spring (b), summer (c), fall (d). For the tower data, both fully overcast and non-overcast conditions are shown. The MODIS data have been interpolated/extrapolated to the nominal MFRSR wavelengths. The root mean square error (RMSE) is also shown (bottom row) using the MODIS albedos as the reference. The two lowest RMSE are indicated in bold.

(a).

(a).

Wave Length (nm)	MFRSR (Retrieved)	MODIS (Derived)	Tower (Weighted-Average)		Tower (10-m)		Tower (25-m)
	Overcast	White-Sky	Overcast	Non-Overcast	Overcast	Non-Overcast	Overcast	Non-Overcast
415	0.030 (0.0)	-	0.054 (0.011)	0.054 (0.010)	0.073 (0.020)	0.066 (0.016)	0.035 (0.018)	0.042 (0.014)
500	0.078 (0.014)	0.070 (0.009)	0.082 (0.015)	0.087 (0.017)	0.095 (0.014)	0.093 (0.016)	0.073 (0.019)	0.081 (0.020)
615	0.087 (0.023)	0.108 (0.015)	0.127 (0.023)	0.135 (0.025)	0.139 (0.020)	0.143 (0.022)	0.115 (0.029)	0.127 (0.030)
673	0.137 (0.031)	0.113 (0.019)	0.147 (0.028)	0.157 (0.032)	0.169 (0.023)	0.173 (0.026)	0.125 (0.039)	0.141 (0.041)
870	0.283 (0.055)	0.296 (0.034)	0.301 (0.033)	0.296 (0.039)	0.261 (0.023)	0.263 (0.029)	0.340 (0.074)	0.329 (0.072)
RMSE	0.009	-	0.010	0.014	0.019	0.020	0.012	0.012

(b).

(b).

Wave Length (nm)	MFRSR (Retrieved)	MODIS (Derived)	Tower (Weighted-Average)		Tower (10-m)		Tower (25-m)
	Overcast	White-Sky	Overcast	Non-Overcast	Overcast	Non-Overcast	Overcast	Non-Overcast
415	0.030 (0.0)	-	0.040 (0.009)	0.040 (0.009)	0.053 (0.018)	0.052 (0.016)	0.026 (0.014)	0.028 (0.012)
500	0.079 (0.015)	0.063 (0.010)	0.061 (0.015)	0.062 (0.015)	0.072 (0.018)	0.071 (0.019)	0.051 (0.020)	0.053 (0.019)
615	0.097 (0.025)	0.093 (0.015)	0.095 (0.023)	0.098 (0.023)	0.109 (0.026)	0.109 (0.026)	0.081 (0.034)	0.086 (0.032)
673	0.115 (0.035)	0.098 (0.020)	0.099 (0.035)	0.103 (0.033)	0.118 (0.041)	0.118 (0.040)	0.080 (0.048)	0.088 (0.044)
870	0.371 (0.063)	0.381 (0.042)	0.351 (0.054)	0.337 (0.058)	0.315 (0.063)	0.302 (0.064)	0.394 (0.093)	0.372 (0.096)
RMSE	0.006		0.008	0.011	0.018	0.021	0.007	0.005

(c).

(c).

Wave Length (nm)	MFRSR (Retrieved)	MODIS (Derived)	Tower (Weighted-Average)		Tower (10-m)		Tower (25-m)
	Overcast	White-Sky	Overcast	Non-Overcast	Overcast	Non-Overcast	Overcast	Non-Overcast
415	0.030 (0.0)	-	0.033 (0.007)	0.037 (0.009)	0.037 (0.012)	0.037 (0.011)	0.028 (0.008)	0.038 (0.014)
500	0.072 (0.015)	0.073 (0.010)	0.059 (0.014)	0.063 (0.014)	0.057 (0.015)	0.059 (0.015)	0.062 (0.014)	0.067 (0.017)
615	0.106 (0.024)	0.109 (0.014)	0.097 (0.024)	0.103 (0.027)	0.087 (0.021)	0.092 (0.025)	0.107 (0.028)	0.114 (0.031)
673	0.127 (0.028)	0.120 (0.019)	0.109 (0.038)	0.115 (0.040)	0.096 (0.041)	0.101 (0.044)	0.122 (0.041)	0.129 (0.044)
870	0.317 (0.047)	0.321 (0.023)	0.331 (0.040)	0.345 (0.047)	0.376 (0.040)	0.390 (0.044)	0.287 (0.057)	0.301 (0.064)
RMSE	0.004		0.012	0.014	0.033	0.038	0.018	0.012

(d).

(d).

Wave Length (nm)	MFRSR (Retrieved)	MODIS (Derived)	Tower (Weighted-Average)		Tower (10-m)		Tower (25-m)
	Overcast	White-Sky	Overcast	Non-Overcast	Overcast	Non-Overcast	Overcast	Non-Overcast
415	0.030 (0.0)	-	0.037 (0.011)	0.045 (0.008)	0.041 (0.015)	0.048 (0.013)	0.032 (0.011)	0.043 (0.012)
500	0.071 (0.014)	0.072 (0.008)	0.066 (0.012)	0.074 (0.011)	0.064 (0.013)	0.073 (0.012)	0.068 (0.012)	0.075 (0.013)
615	0.094 (0.020)	0.109 (0.011)	0.107 (0.019)	0.122 (0.018)	0.099 (0.021)	0.117 (0.020)	0.115 (0.022)	0.127 (0.021)
673	0.123 (0.026)	0.126 (0.014)	0.122 (0.023)	0.138 (0.025)	0.111 (0.027)	0.128 (0.029)	0.133 (0.027)	0.149 (0.028)
870	0.268 (0.051)	0.278 (0.022)	0.282 (0.027)	0.287 (0.029)	0.315 (0.039)	0.313 (0.043)	0.250 (0.053)	0.262 (0.041)
RMSE	0.009		0.004	0.010	0.021	0.018	0.016	0.017

In an earlier study, Jin et al. [21] used 30-m spatial resolution Landsat Enhanced Thematic Mapper Plus (ETM+) images to show that the degree of surface heterogeneity (at a 1 km² spatial scale) over the ARM and NOAA sites is generally smaller during the growing seasons (e.g., spring and summer) compared to the non-growing seasons (e.g., winter). Thus, we expect that agreement between the surface albedo values calculated from 1-km MODIS data and those retrieved by our simple approaches—tower-based and MFRSR-based—would be better for the growing seasons as well. Moreover, it is increasingly apparent that the spectral and spatial features for many regions are almost temporally invariant within a relatively short (1–4 weeks) period, and this weak temporal variability forms the basis for improved and simultaneous retrievals of aerosol and surface properties [36]. Therefore, we expect that our retrievals of “overcast” surface albedo would be representative for non-overcast days, as long as these days are not separated too far in time from the overcast days. We further discuss these two expectations related to seasonally varying surface heterogeneity and the representativeness of overcast retrievals in the next section.

5. Results

We start with the time series of the daily-averaged surface albedo measured at the NOAA site (Figure 3) during spring (April–May 2010). The “local” albedo values from the three wavelengths (415, 500, and 673 nm) of the tower MFR measurements are largest in the beginning of this period and then decrease slightly (Figure 3a). In contrast, the 870-nm surface albedo increases substantially (Figure 3a) during this period.

It is well-known that bare soil tends to have a larger albedo than green surfaces for wavelengths less than 700 nm, but above 700 nm, green surfaces have a larger albedo [3,20,34]. Therefore, the opposite trends for the surface albedo measured at the visible (673 nm) and near-infrared (870 nm) wavelengths (Figure 3a) can be explained by seasonal evolution of nearby vegetation seen by the 8-m downward-looking MFR. That is, as increasing amounts of greening and growing vegetation cover bare ground surfaces (more green and less brown exposed to the downwelling irradiance), the albedo for wavelengths less than 700 nm decreases, while the albedo above 700 nm increases. The corresponding MODIS surface albedos at two wavelengths (670 and 860 nm) also exhibit similar trends. Our retrieved areal-averaged surface albedo from the MFRSR data shows a weak day-to-day variability at 673 nm wavelength and an increasing trend at 870 nm wavelength (Figure 3b) in the same fashion as the MODIS surface albedo.

On average, the retrieved surface albedo captures the spectral changes of MODIS surface albedo reasonably well (Figure 3b; Table 1). The identical (0.015) RMSE values obtained for the retrieved areal-averaged MFRSR-based and measured point (tower) surface albedo under overcast conditions suggest that the degree of surface heterogeneity is quite small for the NOAA site during the period considered here (April–May 2010). This finding is in harmony with the previous results obtained for the growing seasons [21]. Even the RMSE values of 0.015 obtained for the spectral surface albedo for April–May 2010 are comparable with the value of 0.018 obtained earlier by other investigators for the 1 × 1 km² shortwave broadband surface albedo at this NOAA site during the April–September 2001 growing season [21].

Although the time series of the measured daily-averaged local (tower) surface albedo represents both overcast and non-overcast days (Figure 3a), distinct ups and downs in the time series–perhaps correlated with overcast versus non-overcast days–are not evident. This smoothness suggests that over several days or even weeks, overcast and non-overcast days have quite similar daily-averaged values, provided the overcast and non-overcast days are not separated by long periods of time. In other words, the daily-averaged overcast values are fairly representative for temporally “nearby” non-overcast days for both local and areal-averaged values.

This is clearly seen by comparing Figure 4a–b; each Figure shows the spectral variation of albedos at the NOAA site (where the albedos have been averaged over the two month period). Figure 4a shows results based on fully overcast days for both tower MFR-based measurements and MFRSR-based retrievals. Figure 4b is based on the MFRSR-based retrievals for overcast days while the tower MFR-based averages are from non-overcast days. There is scarcely any difference between these two graphs. This finding is consistent with the generally accepted assumption about almost temporally invariant surface properties within a relatively short period [36], and suggests that albedos derived from our retrieval can be successfully extended to days that are not fully overcast by interpolating between days when retrievals are possible.

Let us examine the longer time series of the surface albedo measured at the ARM site (Figure 5 and Figure 6). The seasonal changes of surface albedo are well-defined and attributed mostly to the corresponding seasonal variations of vegetation described thoroughly by McFarlane et al. [34]. As expected, the contribution of snow-covered areas to the measured surface albedo is occasionally large during the winter, and this contribution is responsible for infrequent outliers characterized by large values of the measured surface albedo (Figure 5a,b). Since the 10- and 25-m downward-looking MFRs see different sub-areas, a noticeable difference between $A_{\lambda }^{10}$ and $A_{\lambda }^{25}$ occurs quite often. For example, $A_{870}^{10}$ exceeds $A_{870}^{25}$ by about a factor of two for the summer of 2010 (Figure 5a,b; time = 2010.5).

The average surface albedo ($A_{870}^a$) derived from the tower measurements exhibits well-defined seasonal changes (Figure 5c) similar to its local components (Figure 5a,b). However, the range of $A_{870}^a$ variations is much smaller compared to the corresponding ranges of local values for a given period of interest (Figure 5c versus Figure 5a,b). For example, we consider the year 2010 again: the range (maximum minus minimum values) is about 0.3 and 0.2 for the local $A_{870}^{25}$ (Figure 5b) and the weighted average $A_{870}^a$ (Figure 5c) albedo, respectively. In addition to the substantial range reduction, the averaging of the two tower albedos can alter noticeably the pattern of seasonal and sub-seasonal changes, such as shifting peak positions of the surface albedo within a given period of interest (Figure 5c versus Figure 5a,b): peaks are observed during summer (around time = 2010.5) and spring (near time = 2010.3) for $A_{870}^{10}$ (Figure 5a) and weighted average $A_{870}^a$ (Figure 5c) albedo, respectively.

There are visual similarities between time series of the weighted average $A_{\lambda }^a$ (Figure 5c), MODIS-derived $A_{\lambda }^m$ (Figure 5d), and the retrieved areal-averaged $A_{\lambda }^r$ (Figure 5e) values. These similarities include comparable ranges and similar seasonal patterns during several periods of interest. To illustrate, we compare their seasonal patterns for year 2010: $A_{870}^a$ , $A_{870}^m$ and $A_{870}^r$ reach the maximum values during spring (near time = 2010.3), and then all exhibit comparable decreasing trends until the summer (around time = 2010.7). Although a visual inspection of the temporal changes demonstrates a reasonable resemblance of the retrieved $A_{\lambda }^r$ and MODIS-derived $A_{\lambda }^m$ spectral values (Figure 6), we follow with a more quantitative comparison. For this comparison we must remove snow-contaminated points from the tower time series. These points are associated with large values of measured surface albedo (Figure 5a,b). We remove all points where the measured surface albedo at 415 nm wavelength exceeds 0.1. These points occur only in winter and are likely associated with snow-related events, such as an either fully or partly snow covered surface seen by the tower-based instruments.

Our quantitative analysis is embodied in Figure 4, Figure 7 and Figure 8, which show the spectral behavior of the surface albedos, where the albedos at each wavelength have been averaged over time. First, considering the NOAA site (Figure 4), there is quite good qualitative agreement between our derived albedos, the albedos from the tower, and the albedos obtained from satellite data (Note that in Figure 4, the MODIS albedos are plotted at their nominal wavelengths). For the ARM site, the albedos are seasonally segregated with seasons defined as: winter (December-January-February; DJF), spring (March-April-May; MAM), summer (June-July-August; JJA) and fall (September-October-November; SON). Reasonable qualitative agreement between all techniques is also apparent. The only instance where the agreement is compromised occurs in the winter season for a wavelength of 615 nm (Figure 7a). Here, the significant difference between $A_{\lambda }^a$ and $A_{\lambda }^r$ at 615 nm wavelength could be attributed to nearby sub-areas with “brown” dead vegetation [34] unseen by the tower-based instruments.

In contrast to this singular point, the retrieved $A_{\lambda }^r$ , weighted average $A_{\lambda }^a$ and MODIS-derived $A_{\lambda }^m$ surface albedo exhibit very consistent spectral variation (Figure 7a). As a result, the corresponding RMSEs (0.009 and 0.010) are comparable as well (Table 2a). For the spring (MAM), summer (JJA), and fall (SON) with lower degrees of surface heterogeneity, the retrieved surface albedo $A_{\lambda }^r$ is a good approximation for the corresponding weighted average $A_{\lambda }^a$ (Figure 7b–d; Table 2b–d). Moreover, the retrieved albedo $A_{\lambda }^r$ matches the observational MODIS reference albedos $A_{\lambda }^m$ very well at four wavelengths (500, 615, 675 and 870 nm) (Figure 7b–d): the resultant RMSE does not exceed 0.009 for all four seasons (Table 2a–d). We emphasize that the corresponding RMSE calculated for the 10-m surface albedo $A_{\lambda }^{10}$ can be considerably larger (up to 0.033) than that calculated for the retrieved areal-averaged albedo $A_{\lambda }^r$ (Table 2b–d), suggesting that the 10-m local surface albedo is not representative of an areal-averaged albedo. With only a few exceptions, the good agreement between the mean values of $A_{\lambda }^a$ and $A_{\lambda }^r$ is even evinced for non-overcast (Figure 8) conditions. The observed resemblance (overcast versus non-overcast results), obtained at the NOAA (Figure 4; Table 1) and ARM (Figure 7 and Figure 8; Table 2) sites, confirms our expectation that the daily-averaged overcast retrievals of the areal-averaged surface albedo can be representative of non-overcast days.

6. Summary

We introduce a simple approach for retrieving the areal-averaged surface albedo from atmospheric transmission alone, measured at the surface under completely overcast conditions. The development of our approach with operational possibilities is motivated by earlier successful attempts [16] that used the conventional concept of dual-channel measurements and detailed radiative transfer (RT) calculations. In contrast to the previous studies that relied on time-consuming numerical RT simulations, our approach uses the semi-empirical equation [17], which analytically links the optical properties of an overcast cloud layer and the surface albedo with atmospheric transmission. Such a simple approach provides an opportunity for operational retrievals of areal-averaged surface albedo and cloud properties when multi-spectral measurements of the atmospheric transmission are available.

We retrieve the areal-averaged surface albedo using the atmospheric transmission measured at five wavelengths (415, 500, 615, 673 and 870 nm) by ground-based Multi-Filter Rotating Shadowband Radiometers (MFRSR) deployed at two continental sites in the United States, the ARM Southern Great Plains (SGP) site and the NOAA Table Mountain site. These sites, supported by ARM (http://www.arm.gov/) and NOAA (http://www.esrl.noaa.gov/), include towers for measuring surface albedo at five MFRSR wavelengths. The ground- and tower-based measurements of surface albedo are compared with corresponding Moderate Resolution Imaging Spectroradiometer (MODIS) satellite measurements. For our evaluation, we use 5 × 5 km² MODIS-derived white-sky surface albedo values at four nominal wavelengths (470, 560, 670 and 860 nm). These MODIS values are interpolated/extrapolated to the four MFRSR wavelengths (500, 615, 673, 870 nm) and are considered as reference values. We calculate the root mean square error (RMSE), which is defined as the root mean squared difference between the MODIS surface albedo and the retrieved/measured surface albedo. The NOAA and ARM integrated datasets with the ground-based and MODIS components cover short (April–May 2010) and long (2008–2013) periods, respectively.

At the NOAA site with its single tower (10-m), both the MFRSR-based retrieved areal-averaged albedo and the tower-based measured albedo resemble, on average, the temporal trends and the spectral behavior of the MODIS-derived surface albedo reasonably well. The corresponding RMSEs between the MODIS albedos and the retrieved and measured albedos are identical (0.015), and comparable with that obtained previously for the 1 × 1 km² shortwave broadband surface albedo during the growing seasons [21]. At the ARM site with its two towers (60-m and 10-m), similarly good agreement is obtained for the MFRSR-based retrieved areal-averaged surface albedo values (RMSE ≤ 0.009) and tower-based weighted averages (RMSE ≤ 0.012). The fact that the retrieved albedos compare favorably with both the satellite and tower-averaged albedos suggests that the retrieved albedos are indeed representative of area-wide albedos. For surface albedos measured at the 10-m tower, the corresponding seasonally-dependent RMSE can be very large (up to 0.033), suggesting that albedos measured under the 10-m tower may not be representative of albedos of a larger area.

At the NOAA and ARM sites, we demonstrate that the tower-based daily averages of surface albedo are comparable for completely overcast and non-overcast conditions. This is consistent with the generally accepted assumption about surface properties being almost temporally invariant within a relatively short period [36]. Note that there is a solar-zenith angle dependence on clear days that agrees with the cloudy-sky albedo when averaged over the day. Therefore, our retrieval originally developed for overcast conditions likely can be adapted for non-overcast conditions, when retrievals are not possible, by interpolating between retrievals on overcast days.

We demonstrate the feasibility of our simple approach for different landscapes with various degrees of heterogeneity. Despite its simplicity, our approach shows promise in routinely obtaining the areal-averaged surface albedo from surface measurements of multi-spectral atmospheric transmission. Since conventional measurements of atmospheric transmission are available at many well-established [37] and temporal (e.g., ARM Mobile Facilities; http://www.arm.gov/sites/amf) sites worldwide, this critical information on spectral surface albedo should be highly beneficial for validating and improving large-scale models [38]. Additionally, our retrieval technique can easily be extended to hyperspectral ground-based instruments with fine spectral resolution, such as the SAS-He [39]. In this case, it may be possible to extend spectral surface albedo measurements out to 1700 nm over selected spectral regions.