1. Introduction
Nuclear safety aims to protect and prevent accidents in facilities that handle radioactive materials as well as, through computational systems and human resources, to mitigate risks and consequences in cases of radioactive release into the atmosphere [
1]. This is the most important concept following the licensing criteria and regulations and the design guidelines, ensuring the proper construction and operation of nuclear power plants (NPPs), and it must be strictly adhered to maintain the effectiveness of protection measures for the population and the environment [
2].
To license the construction of a nuclear power plant, it is a prerequisite to carry out a radiological environmental impact assessment, among others, which includes the study of the effects of radioactive emissions and their potential risks to the population and the environment [
3]. These emissions can follow various pathways, originating from different release points and exhibiting different behaviors depending on the external factors that influence the transport, dispersion and deposition of the material present in the radioactive cloud [
4,
5].
To assess potential emissions, considering that nuclear facilities may release radionuclides into the atmosphere under routine operational conditions and through unintentional events, radiological modeling can be applied. This method also allows an estimation of the concentration of radioactive material in air, water and soil as well as the potential health risks to exposed individuals. This concentration of radioactive material is identified in the form of clouds, or radioactive plumes, that can be transported throughout the environment [
6].
The magnitude of exposure to atmospheric releases of radionuclides depends on the atmospheric transport, diffusion and deposition process. Therefore, it is necessary to assess the transport and fate of pollutants and contaminants, such as radionuclides, when they reach the exposure point or the receptor and the pollutant concentration present in the air, water and soil at the exposure location. Ideally, assessments of the concentration are carried out based on measurements of pollutants in air, soil and water or radioactivity resulting from these releases.
However, in situ measurements are not always feasible for many reasons but mainly due to the high cost involved and the time required to sample wide areas and conduct the respective laboratory analysis. Instead, mathematical models capable of estimating the environmental impact of radionuclide emissions must be used [
7,
8]. Over the years, several mathematical and computational atmospheric dispersion models have been developed for this purpose, such as CAP88-PC [
9], which uses a regulatory compliance tool under the National Emissions Standard for Hazardous Air Pollutants; HotSpot [
10] and Rascal (Radiological Assessment System for Consequence Analysis) [
10], which use a simple Gaussian dispersion model; CALPUFF (California Puff Model), which uses a non-steady-state PUFF-type dispersion model [
11]; HPAC (Hazar Prediction and Assessment Capability), which uses the Lagrangian SCIPUFF Puff Model [
12]; HYSPLIT (Hybrid Single Particle Lagrangian Integrated Trajectory Model), which uses a Lagrangian model [
13]; ADMS (Atmospheric Dispersion Modelling System), which uses an advanced Gaussian model [
14]; MATCH (Multi-scale Atmospheric Transport and Chemistry Model), which uses a large-scale Eulerian model [
15]; and AERMOD (Atmospheric Dispersion Model), which uses a more advanced bi-Gaussian model [
16], suitable for the needs of each modeled scenario [
8].
Thus, these mathematical and computational models are adapted to the needs of each scenario, allowing for the assessment of the impact caused by potentially released radionuclides on the public and the environment, as they consider calculations of all contaminant material released by a specific source, such as that discharged by an NPP after a nuclear accident. Their approaches may include three fundamental aspects: the dispersion of the radioactive plume, the rate at which the cloud is diluted as it is transported and the mechanism by which the material is removed from the atmosphere, soil and water [
8].
This article addresses a case study that evaluated the atmospheric dispersion of a radioactive plume released after a hypothetical accident (Large Break Loss of Coolant Accident, LBLOCA), simulated for the Pressurized Water Reactor (PWR) NPP called Angra 2, located at the Almirante Alvaro Alberto Nuclear Complex. Modeling was carried out using AERMOD and RESRAD-BIOTA codes and aims to collect data for the analysis of Cs-137 dose rates when deposited in soil and water, as well as its risks to human health, to support decision-making in radiological release scenarios affecting the environment.
AERMOD is an integrated code for mesoscale atmospheric pollutant dispersion modeling up to 50 km, developed in partnership by the American Meteorological Society (AMS) and the U.S. Environmental Protection Agency (EPA). It is composed of a dispersion model, which simulates the dispersion of a radioactive plume under steady-state conditions; AERMET, the meteorological preprocessor, which converts surface and upper air data into parameters accepted by the AERMOD interface format; and AERMAP, the terrain preprocessor, which incorporates elevation and topographic characteristics, allowing for the consideration of complex terrain [
17]. Studies such as those of Mosfata Kalhor et al. [
16], Abubakar Sadiq Aliyu [
18] and S. Gaehmi Far [
19] indicate that AERMOD is a reliable and widely accepted reference model for calculating concentrations of radioactive pollutants in the environment.
The RESRAD-BIOTA code was developed through a partnership between the U.S. Department of Energy, the U.S. Environmental Protection Agency and the U. S. Nuclear Regulatory Commission. RESRAD-BIOTA provides a full spectrum of analysis capabilities, including conservative and cost-effective screening methods (using concentration guides) [
20]. Several studies [
21,
22,
23,
24] demonstrate that the application of this code is flexible and effective for assessing the environmental impact of radiation and the risks to potentially exposed individuals.
AERMOD presents an advantage over other codes, as it allows for detailed atmospheric dispersion modeling based on real meteorological data and terrain characteristics, accurately representing the movement, concentration and deposition of these radionuclides while complying with international regulations [
16]. RESRAD-BIOTA, which meets international environmental protection guidelines (IAEA, DOE, EPA, ICRP), when associated with AERMOD, enables a more precise and less conservative assessment of radiological impact in aquatic environments and soil based on concentrations calculated through the atmospheric dispersion of radionuclides modeled in AERMOD.
This article is organized as follows:
Section 1 presents the topic addressed in the article;
Section 2 presents the modeling methodology used, including the specificities of radionuclide dispersion modeling in air and on surface water as well as simulations using AERMOD, RESRAD-BIOTA 1.8 and Python 3.11 calculations;
Section 3 presents and discusses the results; and
Section 4 presents the conclusions of the study.
2. Materials and Methods
2.1. The Regulatory Model: AERMOD
AERMOD VIEW represents a local-scale Gaussian computational mathematical model used for both simple and complex topographies [
8]. It incorporates building downwash algorithms, advanced deposition parameters, local terrain effects and advanced meteorological turbulence calculations. The parameters, including year, month, day, hour, cloud cover, dry bulb temperature, relative humidity, pressure, wind direction and speed, cloud height and precipitation, represent the minimum surface meteorological data required to execute AERMOD [
16].
The significance of AERMOD lies in its being a computational modeling code for atmospheric dispersion that fully incorporates the regulatory model of the United States Environmental Protection Agency (EPA). Quality control of analyses is carried out through intercomparison programs maintained by the International Atomic Energy Agency (IAEA), the EPA, and the Institute for Radiation Protection and Dosimetry (IRD) of the Brazilian National Nuclear Energy Commission (CNEN).
2.2. Mathematical Model of Air Concentration—AERMOD
For stable boundary layer (SBL) conditions, the AERMOD VIEW concentration expression has a Gaussian form and is similar to that used in many other steady-state plume models. The concentration is calculated using Equation (1) [
17], with
Cs being the total concentration (SBL) in g/m
−3,
Q being the source emission rate in g/s,
being the wind speed in m/s,
σzs being the total dispersion in the SBL,
Fy being the horizontal function distribution,
zieff being the effective mixed-layer height and
hes being the plume height.
The convective boundary layer (CBL) is considered one of the main innovations of the model compared to previous regulatory models. It is assumed that portions of the plume are released into updrafts and downdrafts moving with the mean wind. The vertical and lateral velocities of each segment are treated as random variables, described by their respective probability density functions (PDFs). The mean concentration is determined from the PDFs of the position of particles emitted from the source, obtained based on the PDFs of vertical and lateral velocities [
17].
For unstable conditions, the CBL concentration (Cc) is found by summing the concentration from the sources:
- (a)
Direct;
- (b)
Indirect;
- (c)
Penetrated.
- (a)
Direct source—the portion of the plume mass that first reaches the ground and all subsequent
ψ reflections of the mass at
z = zi and
z = 0 (where
zi is the height of the mixed layer). The concentration was calculated using Equation (2) [
17]:
with
Cd being the total concentration in g/m
3,
Q being the source emission rate in g/s,
Fy being the horizontal distribution function,
Fp being the fraction of plume mass contained in the CBL,
λj being the weighting coefficient for the updraft,
being the wind speed in m/s,
σzs being the total vertical dispersion in the SBL,
σzj being the total vertical dispersion for updrafts and downdrafts,
Zieff being the effective mixed-layer height,
hes being the plume height and
Ψdj being the total height of the direct-origin plume, given by Equation (3):
- (b)
Indirect source—the portion of the plume mass that first reaches
zj and all subsequent reflections of the specific mass at
z = 0 and
z = zi. For the indirect source, a plume rise (Δ
hi) is added to delay the downward dispersion of material from the top of the CBL. The concentration was calculated using Equation (4) [
17]:
where
Ψrj = Ψdj − Δ
hi and
z is
zr (for horizontal plume state) or
zp (for terrain-following state) and with Ψrj being the total height of the indirect-source plume in m.
- (c)
Penetrated source (above the top of the CBL)—included to account for material that has initially penetrated the elevated inversion but is subsequently entrained and dispersed into the growing CBL. The concentration was calculated using Equation (5) [
17]:
where
σzp is the total dispersion for the penetrated source in (
m) and
hep is the plume height of the penetrated source above the stack base in (
m). For the horizontal plume state, the total
Cc concentration was calculated using Equation (6) [
17]:
where:
Cd,
Cr and
Cp are the contributions from the direct, indirect and penetrated sources, respectively.
2.3. RESRAD-BIOTA
In this study, the REDRAD-BIOTA 1.8 code was used to calculate the dose rate on the surface of water and soil potentially contaminated by radioactive elements. The modeling of water is based on the principles of mass transfer, radioactive decay, bioaccumulation and radionuclide transport. Soil modeling results from the radiation emitted by radionuclides present in the soil. The radioactive elements present on these surfaces may contaminate the air and various food sources. Based on this, the dose rate is calculated as a function of the activity concentration in the soil and the attenuation factors of the medium [
25].
It is important to emphasize that RESRAD-BIOTA was used as a tool to apply the concentration values calculated in AERMOD, identified in water and soil, after the release of radioactive material into the environment at a rate of 35.3 m3/day, equivalent to 0.5 g/s, in order to convert this concentration into dose rates.
2.4. Mathematical Model of Concentrations in Water—RESRAD-BIOTA 1.8
The RESRAD-BIOTA 1.8 code was employed to apply the maximum concentrations found in water, derived from AERMOD modeling, enabling the identification of dose rates in this environment. The calculation model used by RESRAD-BIOTA 1.8 to determine aquatic surface dose rates is represented in Equation (7) [
25]:
where
BGGwater,human,i in [Bq/m
3] is the concentration of radionuclide
i, based on the screening level assumption, which numerically corresponds to the dose rate
DLh for potentially exposed individuals;
DLh is the dose limit for exposed individuals, adjustable by the user when necessary; 0.001 is the dose conversion factor in [L/m
3];
Biv,h in [L/kg] is the mass concentration factor for exposed individuals for a given radionuclide;
DCFint,i in [(Gy/y)/(Bq/kg)] is the internal dose conversion factor used to estimate the dose rate; and
DCFext,water,i in [(Gy/y)/(Bq/m
3)] is the external dose coefficient used to estimate dose rates for individuals immersed in contaminated water.
2.5. Mathematical Model of Concentrations on the Soil Surface—RESRAD-BIOTA 1.8
The RESRAD-BIOTA 1.8 code was used to apply the maximum concentrations found on the soil surface based on modeling performed with AERMOD, enabling the identification of dose rates in this environment. The calculation model employed by RESRAD-BIOTA 1.8 for estimating soil surface dose rates is shown in Equation (8) [
23]:
where
BGGsoil,human,i in [Bq/m
3] is the concentration of radionuclide
i, based on the screening level assumption, which numerically corresponds to the dose rate
DLh for potentially exposed individuals;
DLh is the dose limit for exposed individuals, adjustable by the user when necessary; 0.001 is the dose conversion factor in [L/m
3];
Biv,h in [L/kg] is the mass concentration factor for exposed individuals for a given radionuclide;
DCFint,i in [(Gy/y)/(Bq/kg)] is the internal dose conversion factor used to estimate the dose rate; and
DCFext,soil,i in [(Gy/y)/(Bq/m
3)] is the external dose coefficient used to estimate dose rates for individuals immersed in contaminated soil.
AERMOD and RESRAD-BIOTA are widely validated models, recognized by international regulatory agencies and suitable for the scope of the present study, presenting a methodological application. Accordingly, the use of these consolidated, robust and recognized tools ensures both the reliability of the results and the relevance of the research.
2.6. Study Area—Central Nuclear Amirante Álvaro Alberto, BR
This study used a radionuclide dispersion scenario following a hypothetical LOCA (Loss of Coolant Accident) simulated for the PWR Angra 2 plant, located at the Almirante Álvaro Alberto Nuclear Power Plant. Angra 2 is located at Itaorna Beach, in the municipality of Angra dos Reis, along the Rio-Santos highway in Rio de Janeiro, Brazil, occupying an area of 1.6 km
2 [
26]. The highlighted terrain surrounding the facility, features a mountainous and coastal environment, with rugged relief near the sea.
This region is encompassed by Emergency Planning Zones (ZPEs), which were created to coordinate and plan emergency responses in radiological events, with the primary purpose of ensuring the safety of the surrounding population and environment. For this nuclear plant, the ZPEs are divided into 3 km, 5 km, 10 km and 15 km zones. The response actions of the External Emergency Plan of the State of Rio de Janeiro (PEE/RJ), led by the State Civil Defense in cooperation with Eletronuclear and the National Nuclear Energy Commission (CNEN), cover the ZPE areas [
27].
The potential release of radioactive material from a nuclear power plant is governed by the containment leakage rate, filtering efficiency, internal containment pressure and the performance of engineered safety features (ESFs) [
28]. For the analysis, meteorological data was obtained from the National Institute of Meteorology [
29], including cloud cover (
CC), dry temperature (
DP), relative humidity (
RH), pressure (
P), wind direction (
WD), wind speed (
WS), ceiling height (
CH), precipitation (
PR) and global radiation (
GR). Modeling was performed for January (
M) 2024 (
Y), with Pollutant concentrations analyzed hourly over 24 h (
HR) across 21 days (
D), as presented in
Appendix A.
It is important to highlight that the selection of January 2024 as the analysis period, as well as the choice of Cs-137, aimed to provide a representative example for the application of the methodology without conceptual compromise to the study. Nevertheless, the analysis of different seasons, atmospheric conditions and radionuclides may be incorporated into future studies, thereby expanding the scope of the results.
The INMET data was processed using AERMET, a meteorological preprocessor that converts station-collected data for use in the AERMOD interface [
17]. Atmospheric sounding data was used to determine the temperature profile and boundary layer height. Soundings were conducted twice daily, early morning and noon, to characterize the stable and convective boundary layers. For other hours, AERMET interpolated boundary layer height values. Hourly meteorological data was applied to estimate turbulence, friction velocity, Monin–Obukhov length (used to characterize thermal stability of the near-surface boundary layer), convective velocity scale, mechanical and convective mixing heights and sensible heat flux. Surface characteristic variations were analyzed based on seasonal changes, the roughness coefficient and albedo [
8].
To support full plume behavior analysis, in conjunction with atmospheric sounding data, the leakage rate of radioactive materials to the environment was calculated and entered into AERMOD. For this study, a pollutant leakage rate of 4.75 × 10
−4 per day was considered, based on the containment free volume of Angra 2 (74,275 m
3), resulting in a pollutant release of 35.3 m
3/day, equivalent to 0.5 g/s, meaning that half the source term was released to the environment. Equation (9) presents the leakage rate calculation, adapted from permissible leakage rate criteria for PWR containment according to the guidelines from the NRC and [
4]:
where
Ld is the daily leakage rate,
X is the pollutant emission fraction into the atmosphere and
Vt is the containment free volume.
For atmospheric release modeling, Cs-137 was defined as a point source, representing emissions through a stack. Its location was established in Cartesian coordinates (X,Y), consistent with the project’s reference system, and the terrain elevation at the emission point was considered. The physical parameters of the stack were defined as follows: a base elevation of 150 m, a release height of 100 m, emission rates of 0.5 g/s, an existing temperature of 56 °C, a stack diameter of 2.14 m, an exit velocity of 12 m/s and an exit flow rate of 43.16 m3/s.
The emission was assumed to be continuous. Since the model, AERMOD, is linear in relation to the emission rate, the results obtained can be proportionally rescaled for other activity levels. If the emission is not continuous but time-dependent, the model allows the use of an external file containing the temporal profile of the released activity. In this study, however, a fixed emission rate was considered without hourly variation.
As Cs-137 is predominantly released in the form of particles/aerosols, representative physical properties were assigned for deposition calculations. The mean aerodynamic diameter of the particles was set to 0.5 μm, with a density of 2000 kg/m3. These parameters enable AERMOD to estimate the dry deposition velocity (Vd) as a function of meteorological conditions. For wet deposition, a scavenging coefficient of approximately 2.0 × 10−5 s−1 was adopted, a typical value for fine particles subject to precipitation.
Receptor points were distributed in a regular Cartesian grid covering the region of interest, in addition to discrete receptors at specific locations. These receptors allow the evaluation of Cs-137 dispersion and deposition across space. Model outputs were configured to provide average Cs-137 concentrations in Bq/m3 for periods of up to one (1) month, enabling the generation of a risk map.
Using the calculated emission rate entered into AERMOD, modeling was performed with a steady-state plume model. AERMOD automatically identifies whether the atmospheric regime for each simulation hour is stable (SBL) or convective (CBL), based on meteorological data provided by AERMET. Both atmospheric conditions were observed in the region and considered in separate periods of the simulation.
In the stable boundary layer (SBL), the concentration is assumed to be Gaussian in both vertical and horizontal dimensions, using Brigg’s equation (1984), with wind and temperature gradients evaluated at the stack top and mid-plume rise. In the convective boundary layer (CBL), horizontal distribution is also Gaussian, but vertical distribution follows a bi-Gaussian probability density function.
For both CBL and SBL sources, AERMOD accounts for enhanced lateral dispersion due to plume meander, influenced by wind direction fluctuations, variable wind speeds, atmospheric turbulence and stability [
17].
2.7. Dose Rate Conversion Factor in Python
After concentration modeling and dose calculations in AERMOD and RESRAD-BIOTA 1.8, Python was used to standardize the dose rate units, enabling analysis of radioactive plume behavior in the air, water and soil. From the concentrations provided in μg/m
3, the activity concentration of Cs-137 in Bq/m
3 was first calculated using Equation (10) [
30]:
where
M is the molar mass of Cs-137,
Na is Avogadro’s number and
T is the half-life. Subsequently, the concentration in μg/m
3 was converted to a dose rate in μSv/h using Equation (11) [
30]:
It should be noted that all the equations presented in the Methods section were effectively employed in the internal calculations performed by the AERMOD and RESRAD-BIOTA codes. The inclusion of these mathematical expressions was not merely illustrative but aimed to explicitly present the theoretical foundations of the model, thereby enabling the researcher to fully understand how the results are derived from the provided inputs.
3. Results
To evaluate the results, the planetary boundary layer (PBL) [
17] was used as a substitute for Pasquill–Gifford stability classes. The stability of the PBL was defined based on its height (H), considered convective for
H > 0 (CBL) and stable for
H < 0 (SBL). This atmospheric regime parameter is automatically defined by AERMOD for each simulation hour based on meteorological data provided by AERMET [
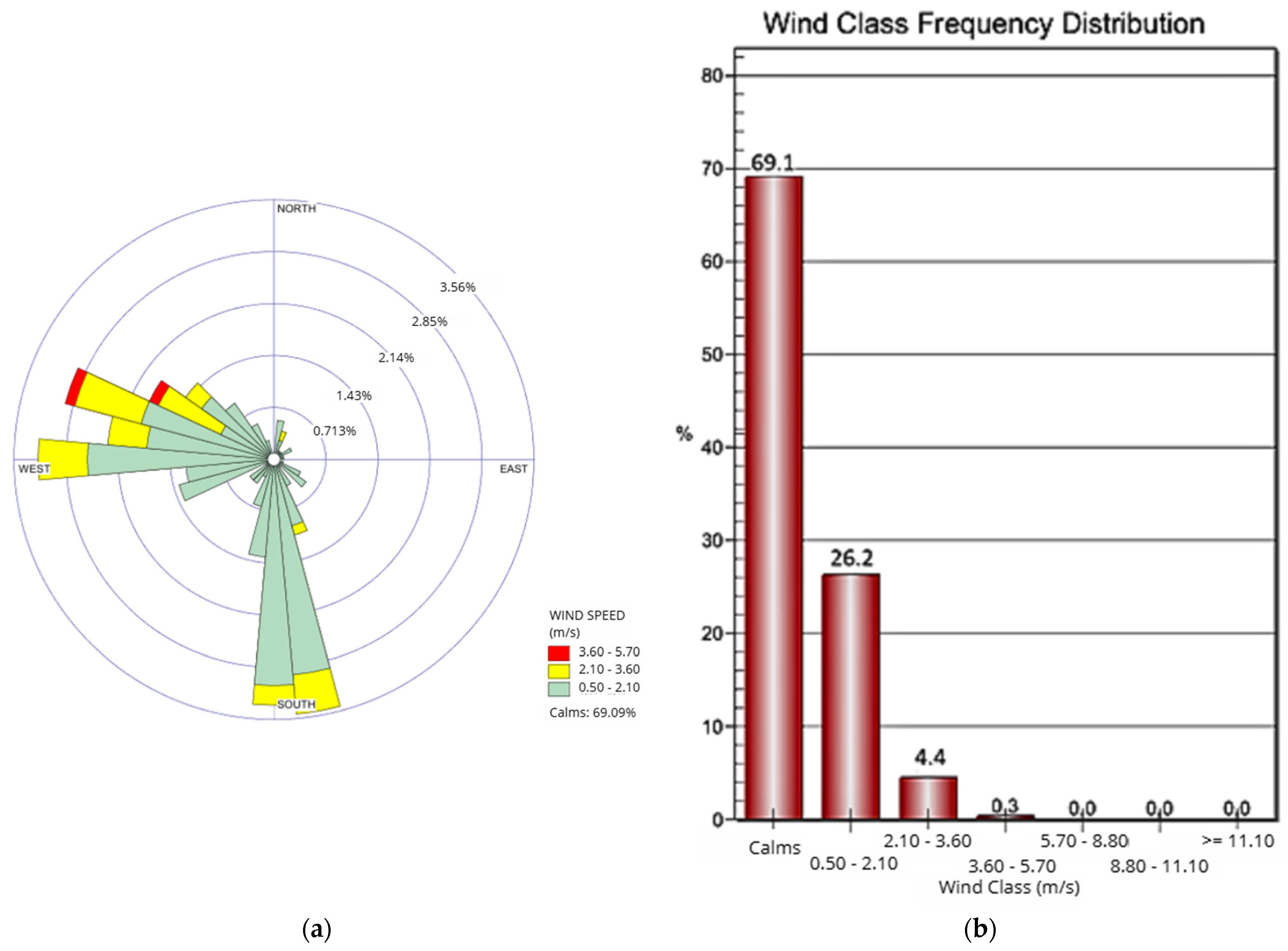
17]. Based on the meteorological data processed by AERMOD, stable atmospheric conditions were observed 95.3% of the time, with light winds ranging from 0.50 m/s to 3.60 m/s and low atmospheric turbulence, which may favor the accumulation of pollutants near the emission source. This behavior can be seen in
Figure 2a,b.
Although stability class F is typically associated with clear and calm nights, its occurrence in 95.3% of the analyzed period can be justified without indicating errors in the input parameters. In particular, certain high-pressure episodes may suppress sea breezes and promote persistent radioactive inversions in the surface layers, leading to extended periods of strong stability. On the other hand, the representativeness of the meteorological station (sheltered location, anemometer height or calm conditions recorded at the surface, while winds are present at higher levels) may result in the overestimation of atmospheric stability class F. Considering these factors, the code automatically identifies and classifies stability.
At certain points, stronger winds were observed, ranging from 3.60 m/s to 5.70 m/s, for 4.7% of the time. This indicates the presence of atmospheric stability class C [
17], considered slightly unstable. In such cases, the plume may disperse more moderately in the atmosphere, transporting radioactive material to farther regions from the source. This behavior is also illustrated in
Figure 2a,b.
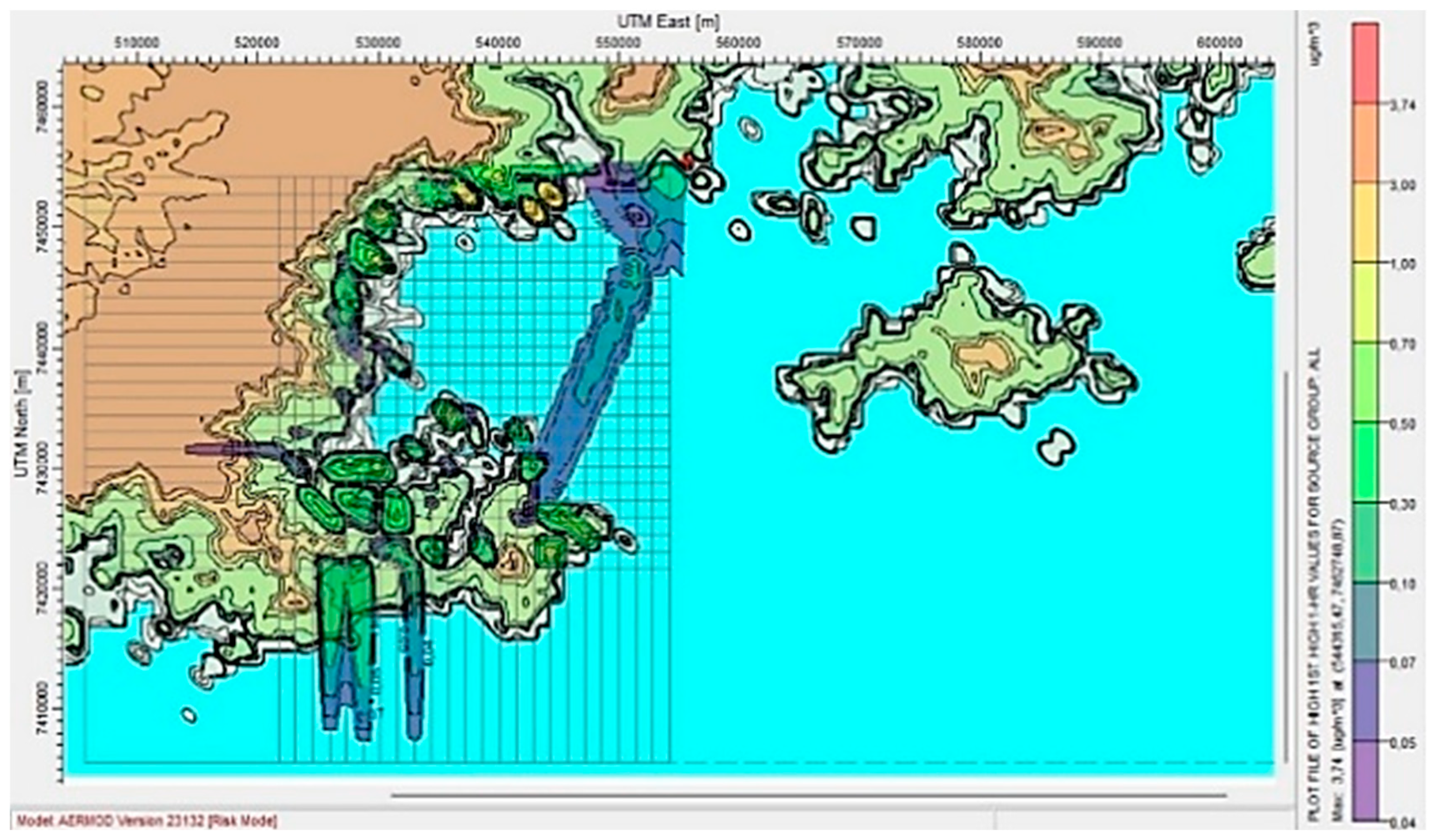
The terrain surrounding the power plant, based on topographic data processed by AERMOD, is characterized by steep hills and mountainous relief. The region is part of the Serra do Mar mountain range, which follows the southeastern coast of Brazil. The terrain is rugged, with elevations covered by Atlantic Forest vegetation. The coastline around the plant is marked by coves, islands and small beaches, resulting in highly irregular topography. The plant itself is situated between the mountains and the sea, on a narrow coastal strip [
31]. These features can be observed in
Figure 3 and
Figure 4, which represent the region around the potential radioactive release source.
The risk map generated by AERMOD, as shown in
Figure 3, illustrates the spatial distribution of simulated values through a color gradient. Cool colors (blue/green) correspond to low concentrations or risk values, whereas warm colors (yellow/red) indicate the regions with higher predicted values. The observed pattern reflects plume dispersion along the prevailing wind direction, with the areas of greatest impact generally located downstream of the source, where the plume reaches the ground. It is important to emphasize that the colors should be interpreted relatively and always in conjunction with the scale legend, which defines the correspondence between color, magnitude and physical unit.
Studies using tracers show that topographic features affect runoff and infiltration and, consequently, the concentration of Cs-137 in soils. Areas with rugged terrain promote radionuclide mobility via erosion and drainage, whereas flat regions may retain more radionuclides in the surface soil [
32]. Once Cs-137 is deposited in the soil, it becomes adsorbed by clay minerals. Water also serves as an environmental pathway for the transport of Cs-137, which has high solubility and can bind to sediments in surface waters. This behavior, combined with atmospheric conditions, explains the dispersion of the radioactive plume across the region outlined in
Figure 3 and
Figure 4 as well as the potential environmental impact [
32].
Based on mesoscale calculations after long-term emissions using meteorological data from a single station during the month of January, it was observed that the most significant concentrations occurred during the first 24 h. The maximum concentration of Cs-137 was 3.74 μg/m3 in the air at 4 km from the source, 3.00 μg/m3 in the soil at 42 km and 0.30 μg/m3 in the water at 6 km. These estimates correspond to dose rates of 3.24 μSv/h, 2.6 μSv/h and 0.26 μSv/h, respectively.
Atmospheric stability class F, present for 95.3% of the analyzed period, is associated with high atmospheric stability, typically occurring on clear, windless nights. These conditions can result in low atmospheric turbulence, reduced vertical mixing of the plume, predominantly horizontal dispersion and high concentrations of contaminants near the source, potentially accompanied by thermal inversions that hinder vertical dispersion. Since the release was modeled from the stack height under weak wind conditions, the plume moved slowly, increasing the residence time of Cs-137 in the atmosphere and elevating contamination levels along its path. The low turbulence limited the spread of the plume, keeping the radioactive material concentrated in a narrow corridor and reducing dispersion to upper atmospheric layers, thus increasing exposure risks near the source. These characteristics justify the dose rates in the air, as shown in
Table 1.
The maximum concentration in the soil at a considerable distance from the source can be explained by external factors that dispersed the plume to more remote areas. The presence of atmospheric stability class C, which introduces moderate atmospheric instability, even if only 4.7% of the time, along with terrain-induced turbulence and local deposition patterns, may lead to a non-homogeneous contaminant distribution, with possible accumulation zones in valleys and on slopes due to wind flow and atmospheric deposition. These factors may account for the soil dose rates presented in
Table 1.
Cs-137, being highly soluble in water, can gradually disperse in marine environments. Part of the radioactive material may adhere to clay particles and organic matter, accumulating at the bottom of lakes or rivers, or settle as particles or aerosols directly on water surfaces. Under stability class F, this deposition may be greater due to the lack of turbulence and efficient atmospheric mixing. Precipitation is another factor that justifies Cs-137 concentrations in water, as rain can capture airborne particles and carry them into the sea. These aspects may explain the dose rates observed in the water, as shown in
Table 1.
The assessment of exposure to potential receptors and the environment over the initial 24 h period, which showed the greatest impact and Cs-37 concentrations in air, water and soil, allowed for the estimation of radiation dose rates at the hypothetical accident site and surrounding areas. It also enabled modeling of the radioactive cloud and its movement, facilitating the identification of areas requiring evacuation.
High levels of external exposure to Cs-137 can result in severe burns, acute radiation sickness and, potentially, death. Such exposure may occur through mishandling of a powerful industrial Cs-137 source, a nuclear explosion or a major nuclear accident. Symptoms observed in victims of accidents involving high-dose radiation release into the atmosphere are referred to as acute radiation syndrome [
33]. The median lethal dose is between 4 and 4.5 Sv, meaning that out of every 100 individuals exposed to this dose, approximately half are expected to die. In
Table 2, Luiz Tauhata et al. [
33] used a reference for estimating the risk of acute radiation syndrome based on a hypothetical LBLOCA release scenario.
Given that Cs-137 has a half-life of approximately 30 years, it can remain in the environment for decades. Although the quantity of Cs-137 decreases over time, its presence may persist environmentally. However, due to its behavior, such as dilution and sediment adsorption, Cs-137 concentrations in this study remained below safety thresholds, ensuring that public health and the environment are not at risk within the considered scenarios [
34].
When compared with the radiation exposure limits indicated in
Table 2, the doses associated with the concentrations are below the levels that cause adverse health effects. For example, acute syndromes such as mild hematopoietic effects (2–4 Sv), gastrointestinal effects (6–7 Sv) or central nervous system damage (>10 Sv) occur at doses far higher than those resulting from the modeled Cs-137 dispersion in this study. Even subclinical effects (<1 Sv), which correspond to the lowest range in the table, are not reached under the simulated conditions.
Thus, although Cs-137 is a radionuclide with a long half-life and potential environmental concern, the results obtained with AERMOD indicate that, for the release scenarios considered, public health and the environment remain within safe exposure margins, in accordance with international regulatory guidelines such as those of the ICRP and the IAEA.
4. Discussion
This study highlights the fundamental role of modeling using the regulatory AERMOD code, which enhances the accuracy and reliability of radiological assessments during potential accidents involving the release of radioactive material into the environment (air, water and soil). The integration of AERMOD with RESRAD-BIOTA 1.8 has proven to be highly effective, as it also enables analysis of contamination in water and soil, representing an innovative and efficient option for practical applications in radiological emergency scenarios. This integration offers an unprecedented level of detail and efficiency in risk assessments.
In the considered scenario, the levels of radioactivity in water, soil and air were found to be negligible. Due to the low concentrations, the dose rates of Cs-137 remained below the safety thresholds established in radiological protection standards, ruling out any risk of acute radiation syndrome in the population. Similarly, the environment was shown to be free of threats, considering the analyzed period, terrain and external influencing factors. The methodology based on the calculation of the emission rate [g/s] enables an estimation of radiation concentrations and dose rates received by potentially exposed populations at varying distances from the source while also taking exposure time into account. Moreover, it allows for the modeling of exclusion zones and the definitions of more effective evacuation strategies, providing a more realistic, quantitative and integrated approach. This enables a more precise assessment of contaminant dispersion, radiological impacts and the necessary mitigation actions.
Potential accidents involving radioactive releases into the environment may exhibit more dynamic and time-variable release patterns due to the influence of external factors. However, the radioactive release represented by a continuous point source of 0.5 g/s can be justified by the fact that AERMOD is linear in relation to the emission rate such that results obtained with the fixed rate can be rescaled for any alternative release scenario. Continuous emissions constitute a standard methodological approach in dispersion studies, allowing for simplification of the modeling and ensuring comparability between scenarios.
The results suggest that the effects of topographic parameters must be considered in both current and future environmental risk assessments, as mountains, valleys and other rugged terrain features can channel air flow, concentrating or dispersing the radioactive plume unevenly. Likewise, analysis of radioactive material behavior in the marine environment is essential to assess long-term ecological risks, given the potential for transport by ocean currents, which can expand the affected area.
This methodology supports emergency planning by enabling continuous monitoring and the timely update of radiological data, as the scenario was modeled using real and continuously updated input data. Therefore, this dynamic approach is essential for developing strategies to mitigate the effects of potential radiological accidents, facilitating both visualization and communication with stakeholders.
It is noteworthy that the results obtained in this study demonstrate full credibility, as they were generated using AERMOD, which is officially recommended and validated by the U.S. Environmental Protection Agency (EPA) and widely applied in regulatory assessments worldwide. AERMOD was developed based on extensive experimental campaigns and has been compared with multiple observational datasets, having demonstrated consistent performance across different dispersion scenarios. The reliability of this research can also be considered robust given that the input parameters were carefully selected from official INMET databases. Therefore, the conclusions presented remain consistent with both national and international standards for atmospheric dispersion modeling.
The mathematical model applied in the methodology has undergone extensive validation and benchmarking processes across different sites and meteorological conditions such that its inherent uncertainties and performance are already widely documented in the EPA’s technical literature. Sensitivity analyses may be conducted in future studies to explore variability associated with meteorological conditions, emission rates and terrain characteristics, should further refinement of risk assessments be required in specific contexts.