1. Introduction
With the development of urbanization, high-rise and high-density buildings have become the mainstream typology in modern cities [
1,
2]. Such compact urban forms suppress the circulation of fresh air [
3,
4], which has accelerated the spread of infectious diseases such as the COVID-19 pandemic [
5,
6]. Meanwhile, dense building configurations hinder the formation of horizontal ventilation corridors, especially in highly built-up cities like Hong Kong. While building height variations can restrict horizontal airflow, studies show they enhance vertical ventilation [
7,
8]. For high-density urban areas, introducing height variability into building morphology is a potential strategy to improve vertical ventilation performance.
In recent years, with the rapid advancement of computing power and simulation techniques, numerical simulation methods have been widely applied. In studies investigating the impacts of height-asymmetric building clusters on ventilation and pollutant dispersion, researchers have adopted several types of height heterogeneity models. These include normal distributions, height-staggered configurations, single dominant tall buildings, and realistic urban clusters or their simplified forms.
For building groups with normally distributed heights, Wang et al. [
9] found that when the plan area index is low, height non-uniformity leads to a decrease in pedestrian-level wind speed ratio. In contrast, when the plan area index is high, the pedestrian-level wind speed ratio increases. Ishida et al. [
10] used numerical simulations while keeping the plan area index constant. Their results showed that height non-uniformity enhances energy dissipation within the urban canopy. This accelerates the generation and dissipation of turbulence above the canopy. Moreover, the total energy dissipation was found to be negatively correlated with the overall urban ventilation rate.
For staggered-height building groups, Hang and Li [
7] found that height non-uniformity could weaken or even disrupt the recirculating vortices in the wake region, thereby increasing the air exchange rate. Hang et al. [
11] further reported that the volume of pedestrian-level ventilation increases with the standard deviation of building height. They also found that momentum transport, driven by turbulent diffusion between the canopy and the overlying air, grows with increasing height variability. Goulart et al. [
12] observed strong vertical airflow along the windward and leeward sides of taller buildings and enhanced turbulence intensity above shorter buildings. Tominaga [
8] concluded that nonuniform height distributions strengthen overall urban ventilation performance. In addition, Zeng et al. [
13] analyzed three types of street canyons with different height differences. They observed distinct airflow patterns on the windward and leeward sides of upwind and downwind streets.
For single tall buildings, Oke [
14] established fundamental fluid flow principles through systematic investigations of idealized single buildings; Meena RK et al. [
15] studied four high-rise buildings with distinct cross-sectional geometries, demonstrating that building cross-section critically impacts wind load distribution.
Several scholars have selected real urban building clusters as research subjects. For example, Yoshida et al. [
16] studied the actual building clusters in Kyoto, Japan, and found a reduction in the vertical momentum flux transfer efficiency within the urban canopy layer; Antoniou et al. [
17] calculated the air delay index of real urban building clusters using numerical methods, revealing that height-asymmetric configurations lead to a decrease in the air delay index; Takemi et al. [
18] investigated turbulent airflow and strong wind hazards in commercial areas of Kyoto (including historical buildings) through numerical simulations, demonstrating that the complexity of real building arrangements and height heterogeneity enhance airflow instability and gustiness of surface winds in the urban canopy layer; Duan et al. [
19] provided optimization design recommendations for high-rise residential buildings based on studies of real building clusters in Xuzhou City.
Although previous studies have explored building height non-uniformity through various modeling strategies, most rely on idealized assumptions that limit their applicability to complex real-world settings. Systematic investigations using actual urban morphologies remain relatively scarce, particularly in revealing how height variability affects both intra-block and downstream ventilation performance.
To address this gap, this study conducts a detailed survey of urban morphology in Hefei, China, and selects 20 real building blocks with diverse height, density, and standard deviation characteristics. Using CFD simulations, we investigate the impact of realistic height non-uniformity on ventilation efficiency and pollutant dispersion. Compared with previous works that typically focus on abstracted forms or isolated flow effects, this study highlights the importance of morphological synergy—i.e., the combined role of density control and height variability—in shaping vertical airflow dynamics. The results aim to provide technical support for optimizing vertical ventilation corridors in high-density pedestrian zones.
The structure of this paper is as follows:
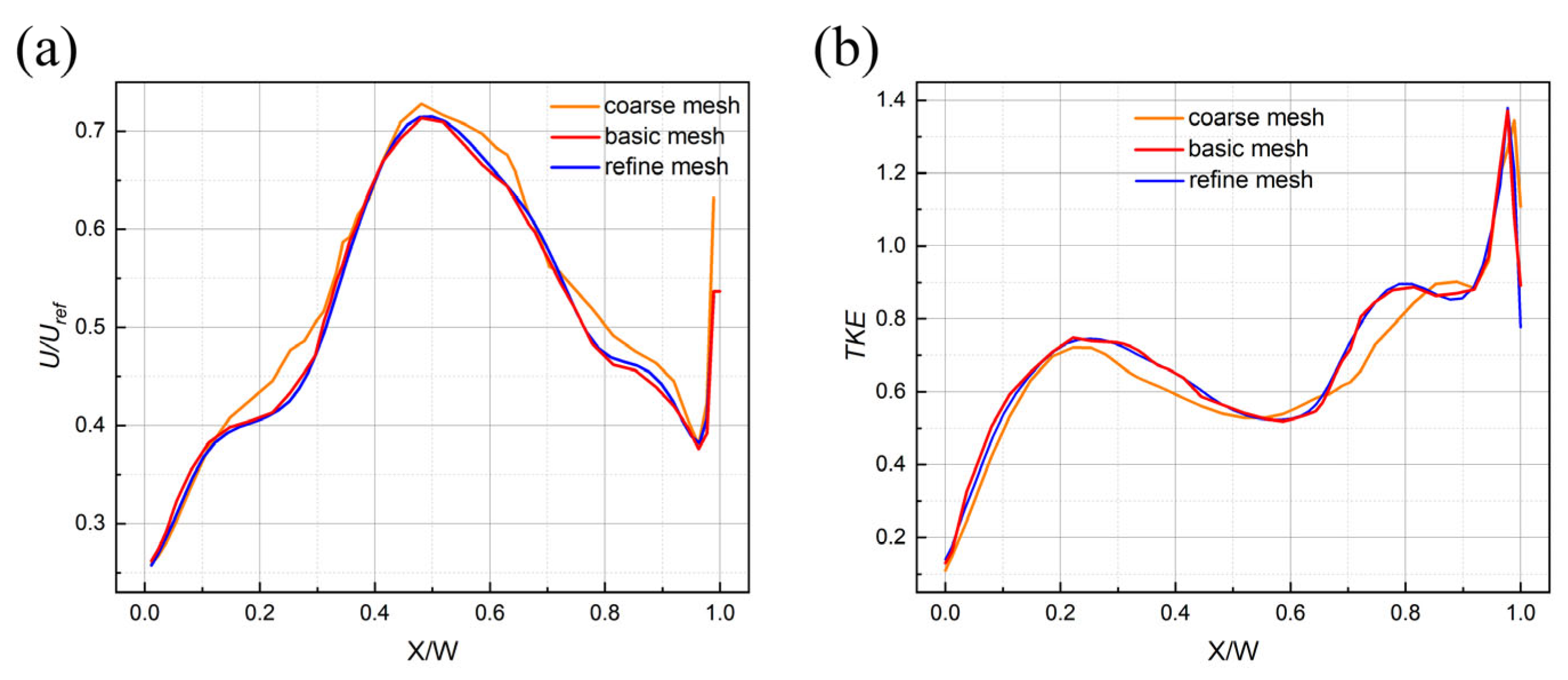
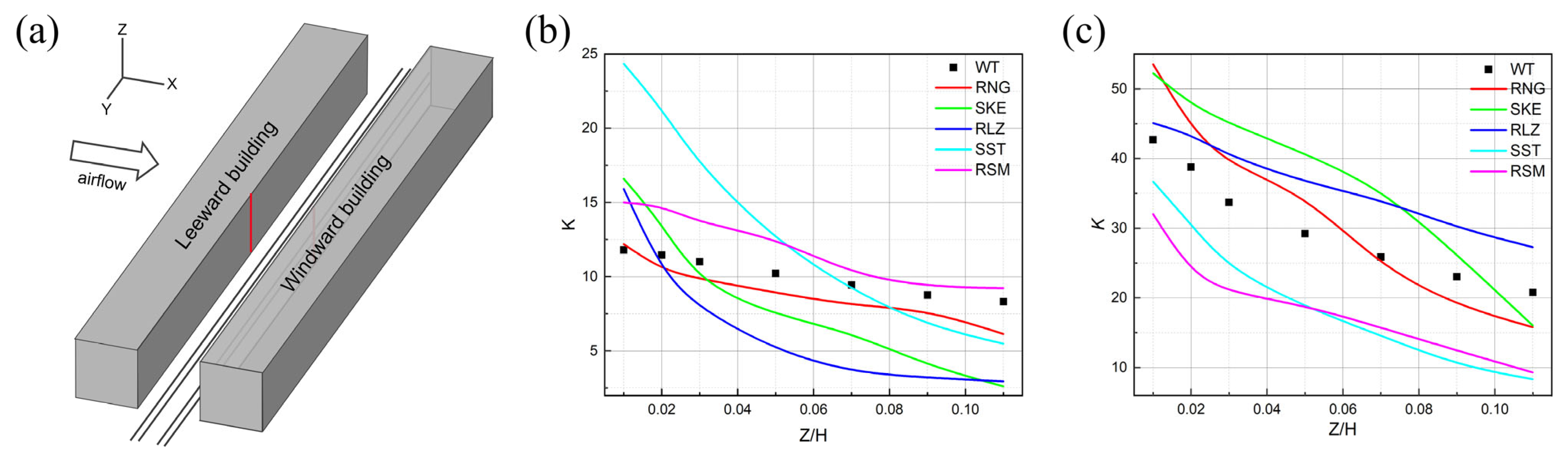
Section 2 presents the details of the physical model, computational domain, boundary conditions, and model validation, including (i) a grid sensitivity study and (ii) a comparison with wind tunnel experiments. In
Section 3, ventilation performance and pollutant concentration distributions within the target site and its downstream region are introduced and discussed, based on wind velocity, pollutant transport, air exchange rate (
ACH), air residence time (
τc), and net escape velocity (
NEV*).
Section 4 discusses the broader implications of the findings, including the limitations of this study, future research directions, and practical strategies for urban ventilation optimization.
Section 5 provides the final conclusions. The specific flow chart is shown in
Figure 1.
3. Results
This section builds upon the model established in
Section 2.1. This study analyzes the target site and its impact on downstream building clusters from several aspects. These include wind speed, pollutant dispersion characteristics, and the relationships between urban morphology parameters (
H,
ρ, and
σ) and ventilation metrics such as
ACH,
τc, and
NEV*. Optimization strategies for vertical ventilation corridors are proposed based on numerical simulation results.
The concept of ACH is used in many street canyon ventilation problems. It represents the air exchange volume between the inside and outside of the street canyon per unit time [
29]. The
ACH of a 3D independent street canyon comprises the following three components [
30]:
where
ACHTOP+ is the
ACH in the positive
z-axis direction through the top of the street canyon.
ACHSide1+ is the
ACH in the positive
x-axis direction.
ACHSide2+ is the
ACH in the negative
x-axis direction.
The ventilation performance of the entire street canyon will be evaluated by the canyon
τc [
31]. The calculation formula is as follows:
where
c is the local concentration of passive tracer gas (kg/m
3),
Q is the pollutant emission rate (Kg/s), and
V is the street canyon volume. The average pollutant concentration
Ɵ signifies the overall air quality of the street canyon, whereas
τc represents the time scale for a parcel of pollutant being removed from the street canyon.
The ventilation volume in the pedestrian breathing zone is calculated using
NEV* as the evaluation factor. The purging flow rate (
PFR) (m
3/s) calculation formula is as follows [
32]:
where
PFR indicates how much fresh air is provided to the area,
m is the spatially averaged concentration (kg/m
3) of the street canyon,
Q is the pollutant release rate (Kg/m
3·s), and
V is the volume of the considered area.
The calculation formula for
NEV* is as follows [
33,
34]:
where
Aped is the whole area of boundaries of the entire pedestrian respiration volume.
3.1. Wind Speed Distribution
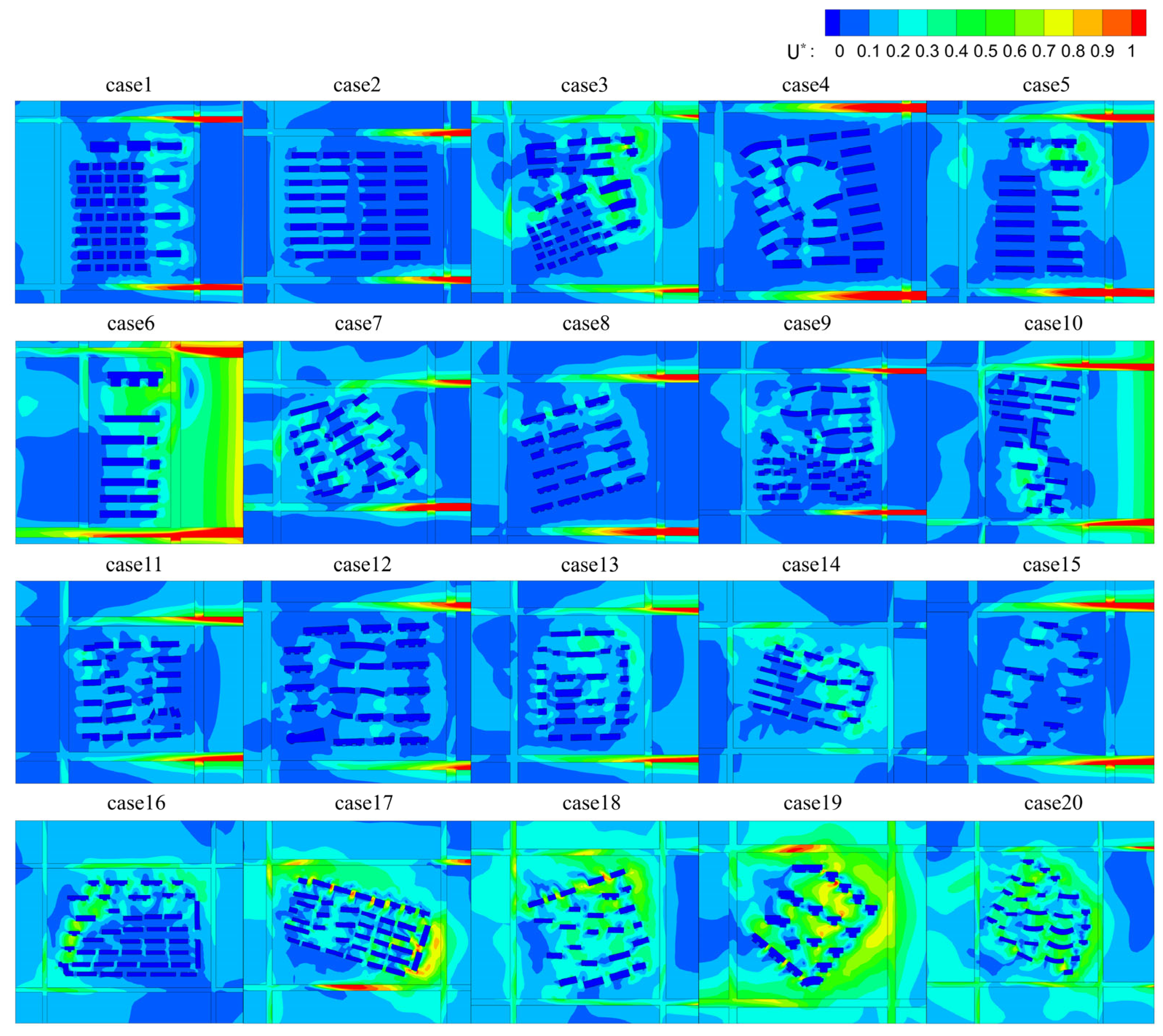
For comparative analysis purposes, the wind speed distribution of height-asymmetric building clusters was analyzed using non-dimensional wind velocity. An analysis was conducted based on the wind speed contour plots at pedestrian height (
Z = 1.5 m), as shown in
Figure 7. From the wind speed distributions of the 20 selected cases, a clear correlation between wind speed patterns and building height is observed. The overall distribution exhibits a typical gradient characteristic—higher wind speeds at the edges and lower within the interior. This phenomenon results from the blocking and frictional effects of buildings, which gradually dissipate the kinetic energy of the incoming flow, leading to reduced wind speeds as airflow penetrates deeper into the urban block. For example, in case 1,
H is relatively low. Both peripheral and interior wind speeds are relatively uniform. High-speed zones are widely distributed along the site edges, allowing smoother wind penetration into the interior. In contrast, case 20 has a much higher
H. High-speed zones are limited near the periphery, while elevated wind speeds are observed only within narrow building gaps, indicating that incoming airflow is strongly obstructed, resulting in restricted circulation throughout the block.
Overall, in the low-rise cases (case 1–case 5), the relatively low building heights allow for stable and uniform airflow within the blocks. In the mid-rise cases (case 6–case 15), increasing building heights cause greater fluctuations in wind speed. The obstruction effect becomes more prominent, and the number of low-speed zones within the block increases. Irregular layouts in this group are also more likely to generate stagnant air pockets. In the high-rise cases (case 16–case 20), the wind speed distribution becomes more complex, dominated by strong turbulence and vortex formation. These cases exhibit the most pronounced airflow obstruction. For instance, in case 18 and case 19, the wind speed contour plots reveal high-speed regions above and along the sides of buildings, while significant low-speed and turbulent zones emerge in the wake regions behind them.
3.2. Pollutant Distribution
For the convenience of analysis, a dimensionless concentration is introduced for analysis [
32], and the definition of the dimensionless pollutant concentration is as follows:
where
C is the pollutant concentration (Kg/m
3),
U0 is the flow mean velocity (m/s),
H is the building height (m),
L is the length of the line source (m), and
Q is the total emission (Kg/s).
To analyze pollutant distribution patterns at the pedestrian level, this section continues to utilize pollutant concentration contours at
Z = 1.5 m (
Figure 8). Key findings are as follows: pollutant concentration distributions vary significantly across the 20 sites. This spatial heterogeneity strongly correlates with the layout and morphology of the building clusters. A characteristic edge-elevated, internally heterogeneous distribution pattern dominates the urban fabric.
In low-rise cases (case 1–case 5), smooth airflow and well-formed ventilation pathways contribute to uniformly low pollutant concentrations. For instance, in case 1, buildings are regularly arranged with relatively even spacing, resulting in multiple effective air channels and enhanced pollutant dispersion. Although case 2 also features an orderly layout, elevated concentrations are observed in certain edge areas, likely due to local wind direction or surrounding environmental interference. In mid-rise cases (case 6–case 15), increasing building height leads to more pronounced fluctuations in pollutant concentrations. Airflow obstruction intensifies, especially in dense clusters such as case 9, where pollutant accumulation is evident. Conversely, in more dispersed configurations like case 12, pollutant removal is more efficient due to improved flow continuity. High-rise cases (cases 16–20) show a polarized pattern in pollutant distribution. High concentrations appear around tall building perimeters, while low concentrations are found in interior spaces. This behavior reflects the interplay of several key factors, including the blockage effect of ρ, the capacity for ventilation corridor formation, and proximity to pollutant sources. Edge zones are particularly prone to pollutant buildup due to the combined influence of external inflow and internal recirculation.
3.2.1. Influence of Average Building Height on the Target Block
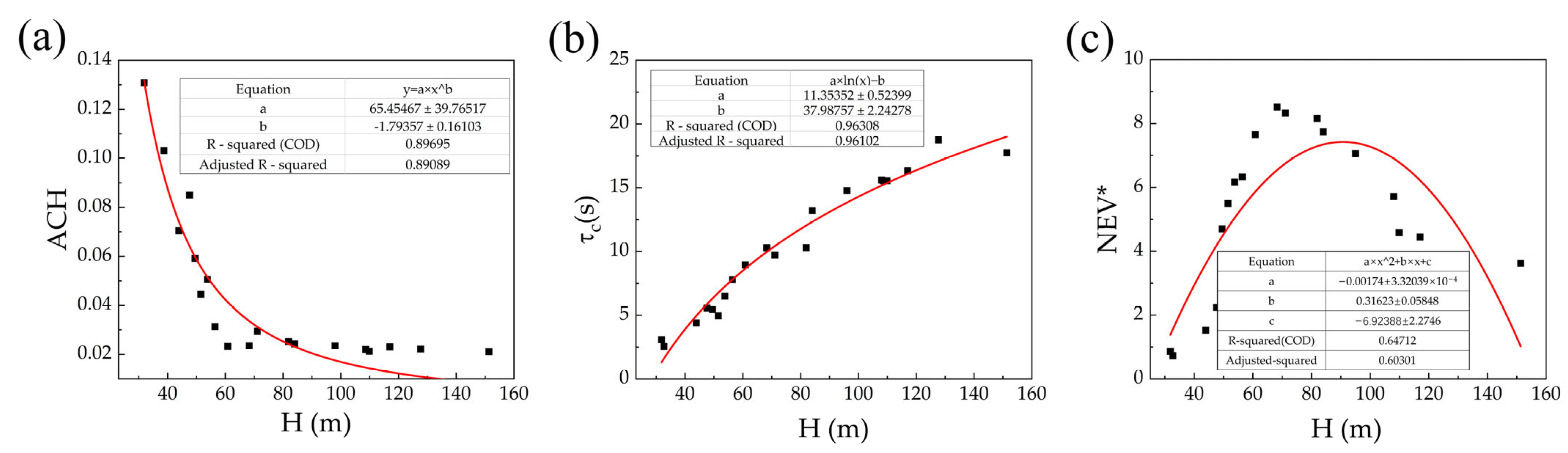
As shown in
Figure 9, the relationships between the mean building height of the target site and three ventilation-related parameters—
ACH,
τc, and
NEV*—exhibit clear stage-dependent characteristics. In the low-rise stage (0–60 m),
ACH remains relatively high (0.13–0.03 m/s),
τc is short (0–10 s), and
NEV* gradually increases (1–8). These trends indicate that short buildings offer the least resistance to airflow, enabling horizontal winds to effectively penetrate the site and maintain relatively good ventilation performance. As the H increases to the mid-rise range (60–100 m), all three parameters show marked changes. The ACH drops below 0.025 m/s and tends to stabilize;
τc rapidly increases to around 14 s; and
NEV* decreases below 7. This suggests the following: Once buildings reach the average urban canopy height, the “street canyon effect” starts to take over. Horizontal ventilation becomes increasingly restricted, while vertical mixing remains insufficient. As a result, there is a significant drop in overall ventilation efficiency.
When building heights exceed 100 m, entering the high-rise stage, the trends diverge. The inlet exchange rate stays low, indicating persistent stagnation near the ground. The growth in τc slows (15–17 s), suggesting a sustained near-ground influence from super-tall buildings. Meanwhile, NEV* shows a modest rebound, increasing from 3 to 5. This reflects the emergence of a “rooftop ventilation effect”. Strong shear flows near the tops of buildings enhance vertical mixing, partially compensating for weak ventilation at ground level. This parameter divergence reveals the formation of a more complex airflow structure in high-rise environments, where near-ground and upper-layer ventilation behave distinctly.
Overall, the results indicate that the 60–100 m height range is a critical threshold for wind environment transition. Below 60 m, the influence of building morphology on airflow is primarily horizontal. Above 100 m, vertical mixing becomes more pronounced. This trend provides important insight into ventilation behavior across different height regimes. Mid-rise clusters are most prone to poor ventilation, while super-tall groups may improve local airflow through enhanced vertical exchange.
3.2.2. Influence of Average Building Height on Downstream Building Group of the Target Block
As shown in
Figure 10, the relationships between ACH,
τc, and
NEV* of the downstream building group and the mean building height of the target site are presented. The results reveal that, when analyzed as a single factor, the ventilation performance of the downstream area differs significantly from that of the target site and is more sensitive to changes in upstream building height. The realistic building model does not fully capture the decay of turbulence intensity with distance, which adds complexity to airflow behavior in downstream zones.
For
ACH, the downstream group exhibits a much narrower range (0–0.06 m/s) compared to the target site (0–0.15 m/s), with the maximum value reduced by approximately 60%. As the mean height of the target site increases, the downstream
ACH rapidly declines. This suggests that although the target site may retain acceptable ventilation, its shielding and disturbance effects substantially weaken the interaction between the downstream group and the ambient wind field.
τc in the downstream area also shows a distinct pattern. From
Figure 10b, it is evident that under the same average building height, the
τc in the downstream building group is generally 25–30% higher than that in the target block. For example, at a height of 40 m,
τc in the downstream group exceeds that of the target site by approximately 20%; near 100 m, the downstream area continues to exhibit longer
τc. This difference can be attributed mainly to the fact that the downstream group lies within the leeward zone of the target block, where airflow momentum has been substantially dissipated by the upstream buildings, resulting in reduced wind speed. In addition, the shielding effect of the target block promotes the development of recirculation zones downstream, further inhibiting air exchange efficiency. Compared with the target block, the downstream group experiences insufficient rooftop shear flow and vertical ventilation development, making it more prone to pollutant and stagnant air accumulation in the leeward area. Regarding
NEV*, the downstream region reaches its maximum (~4.2) when the mean height of the target site is around 40 m, while the peak value at the target site is significantly higher (~8.7). This means the pollutant removal capacity in the downstream area is only about 48% of that in the target site. As the upstream height increases,
NEV* in the downstream group declines further, suggesting that pollutants become increasingly difficult to disperse in these zones, thereby obstructing effective urban ventilation pathways.
3.3. Influence of Building Density on the Target Block and Its Downstream Building Group
As shown in
Figure 11, the relationships between
ρ of the target site and three key ventilation indicators—
τc,
NEV*, and
τc in the downstream building group—are analyzed. The results indicate that
τc in the target site exhibits a significant exponential correlation with
ρ (R
2 = 0.9157). As the density increases from 0.10 to 0.30,
τc rises sharply from 5.5 s to over 16 s, an increase of more than 190%. This confirms that high-density building configurations severely obstruct airflow, intensifying pollutant retention and reducing ventilation efficiency. In the low-density range (
ρ < 0.15), the target site’s
τc is 20–35% lower than that of the downstream area, indicating better airflow and weaker blockage effects. Furthermore, the density–
τc relationship in the downstream group appears linear, while that of the target site follows a distinct exponential trend. This contrast suggests a lagged ventilation response in the downstream region, where wind field regulation is less sensitive compared to the target site.
In contrast, the relationship between NEV* and ρ shows obvious segmented changes. In the low-density stage (ρ < 0.13), NEV* gradually increases and reaches a peak (around 11) within a specific density range. Beyond this critical point (ρ > 0.15), NEV* drops sharply and stabilizes between 1 and 2; the lowest value falls below 1.0, which is only about 9% of the peak. This trend implies that within a certain density range, structural airflow channels may be triggered, enhancing pollutant dispersion. However, once the density exceeds this threshold, such ventilation pathways collapse, leading to a drastic drop in escape efficiency.
Cross-analysis between ρ and H further reveals that when H > 90 m and ρ > 0.20, the downstream group’s τc exceeds that of the target site by approximately 25–40%. This indicates that the combined effect of height and density significantly impedes local air renewal. Two primary reasons may explain this: (i) taller buildings intensify shielding and recirculation effects on the leeward side; (ii) high-density layouts hinder ventilation corridor formation and reduce both horizontal and vertical wind continuity. As the downstream group is situated on the leeward side of the prevailing wind, pollutant accumulation and air stagnation are more likely. By contrast, the target site, being more exposed to wind pressure and lateral flow, experiences slower increases in τc. Under the combined condition of H ≈ 90 m and ρ ≈ 0.2, the downstream area’s τc is 32% higher than that of the target site, further confirming the amplified shielding effect and wind stagnation accumulation in leeward zones.
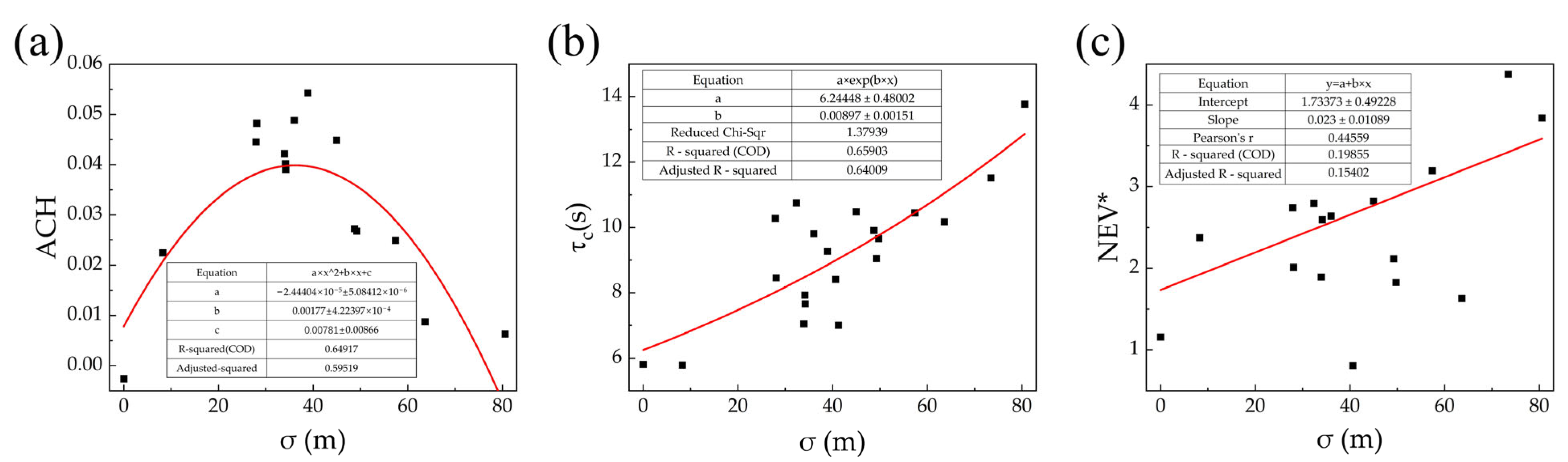
3.4. Influence of Building Height Standard Deviation on the Target Block and Its Downstream Building Group
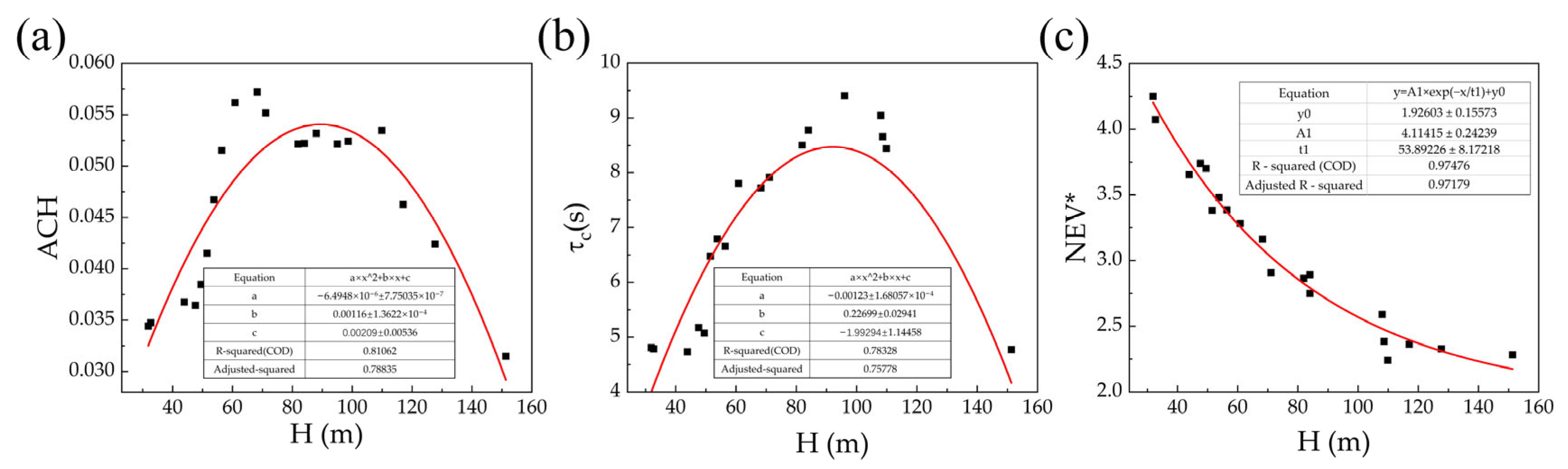
3.4.1. Influence of Building Height Standard Deviation on the Target Block
Figure 12 illustrates the relationships between σ and three key ventilation parameters at the target site:
ACH,
τc, and
NEV*.
As shown in
Figure 12a,
ACH exhibits a distinct parabolic relationship with
σ (R
2 = 0.69). This indicates that height variability significantly influences wind-driven ventilation at the site entrance. As the
σ increases, the
ACH first rises and then declines, reaching its peak around
σ ≈ 30–40 (m). This suggests the presence of an “optimal range” of height variation for enhancing airflow penetration and promoting vertical disturbance at the site boundary.
Figure 12b shows that
τc increases exponentially with
σ (m). When
σ > 50 (m),
τc rises sharply, suggesting that larger height differences cause stronger disturbances in the upper wind profile. In such cases, some taller buildings may induce a “cap effect”, impeding the smooth dispersion of air in upper layers. Thus, excessive height variability is detrimental to upper-level ventilation.
Figure 12c demonstrates an exponential decay between
NEV* and
σ. As
σ (m) increases,
NEV* rapidly declines, a trend consistent with the increase in
τc observed in
Figure 12b. This further confirms that although significant height variation can enhance local turbulence at the lower level, it restricts the overall pollutant removal path, making it more difficult for air to escape into the atmospheric boundary layer.
The coupling between ρ and height variability reveals a clear threshold effect in ventilation regulation. When
ρ < 0.15,
σ = 30~50 (m) can effectively enhance
ACH (
Figure 11a), elevate
NEV* to a local peak (
Figure 11b), and significantly reduce
τc (
Figure 11a). These results indicate that under low-density conditions, height variability can effectively induce turbulent disturbances, thereby improving ventilation performance within the building cluster. However, as ρ continues to increase—especially beyond 0.20—even when σ remains in its optimal range,
ACH declines sharply (
Figure 12a),
τc continues to rise (
Figure 12b), and
NEV* drops significantly (
Figure 12c). This demonstrates that ρ is the key factor limiting the ventilation regulation effect of σ. In high-density environments, the ventilation benefits induced by height variations are offset by the overall enclosure characteristics of the building cluster morphology. In conclusion, urban form optimization should consider the coupled mechanism of “vertical perturbation–lateral resistance”. Coordinated control of ρ and height heterogeneity can jointly enhance vertical ventilation performance.
3.4.2. Influence of Building Height Standard Deviation on the Downstream Building Group of the Target Block
Figure 13 illustrates the relationships between σ of the downstream building group and three ventilation parameters:
ACH,
τc, and
NEV*. The plots reveal functional dependencies between
σ (m) and these parameters in the downstream building group, though with weaker statistical significance and regularity compared to the target site. Specifically,
ACH follows a parabolic trend with
σ (m) (
Figure 12a), peaking at
σ ≈ 35–40 (m) (≈0.04 m/s). This peak value is 20% lower than that observed in the target site, indicating that while an “optimal
σ (m)” exists for vertical perturbation in the downstream building group, its effectiveness is significantly constrained by the upstream target site. This optimal range of
σ ≈ 35–40 likely reflects a balance between promoting vertical turbulence and maintaining pathway continuity for airflow. Moderate height variability breaks up horizontal stagnation zones and enhances upward mixing, while avoiding the excessive obstruction caused by highly irregular building forms.
τc exhibits an exponential increase with
σ, accelerating when
σ > 50 (m). This suggests excessive height variations create pronounced reverse pressure zones and recirculation bands between buildings, obstructing upper-level air escape pathways and prolonging ventilation cycles.
NEV* shows a weakly correlated positive trend with
σ (m) (R
2 = 0.15402), implying substantial interference from external factors. Nevertheless, the general trend confirms that moderate height variations enhance vertical gas escape, though this effect saturates or even diminishes beyond a critical
σ (m) threshold. In conclusion,
σ (m) holds potential for regulating local vertical ventilation, but its efficacy is closely tied to
ρ. In high-density clusters, increasing height variations alone fail to mitigate overall ventilation deficits and may instead amplify recirculation due to intensified local perturbations.
4. Discussion
Although this study systematically analyzes the effects of average building height, density, and height variability on ventilation and pollutant dispersion based on realistic urban blocks, several limitations remain. First, the limited number of samples may not fully represent the diversity of urban forms. Second, the simulations did not account for wind direction variability, internal heat sources, or the influence of vegetation, all of which may interact with airflow. Moreover, the potential interdependence between building density and height variation warrants further decoupled analysis. Future research should expand the study scope to include multiple cities and climate conditions, incorporate multi-directional wind scenarios across the year, and integrate factors such as energy consumption and pollutant source intensity to build a more comprehensive urban microclimate framework. Practically, urban design should limit excessive building density while introducing moderate height variation (with a recommended standard deviation of 35–40), maintain uninterrupted ventilation corridors along prevailing winds, and avoid overly enclosed configurations. In poorly ventilated areas, staggered and well-spaced building arrangements are recommended to improve airflow exchange and enhance urban wind environments in high-density zones.