Impact of Large Eddies on Flux-Gradient Relations in the Unstable Surface Layer Based on Measurements over the Tibetan Plateau
Abstract
1. Introduction
2. Theory and Experimental Data
2.1. Monin-Obukhov Similarity Theory and Classical Flux-Gradient Relations
2.2. Improved Flux-Gradient Relations Accounting for Large Eddy Effects
2.3. TIPEX-III Dataset and Data Processing
3. Results
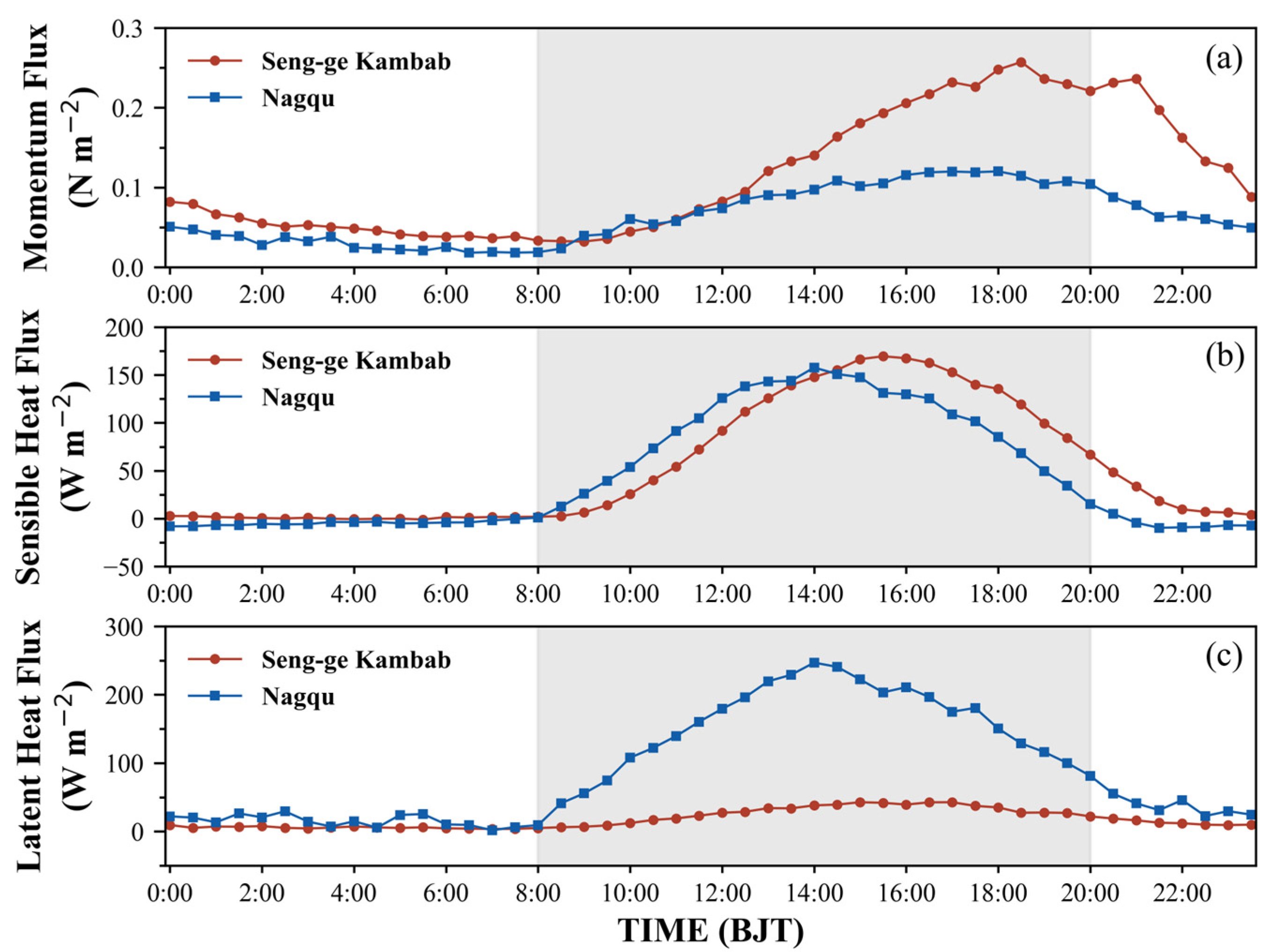
3.1. Turbulence Characteristics in the Unstable Surface Layer over the Tibetan Plateau
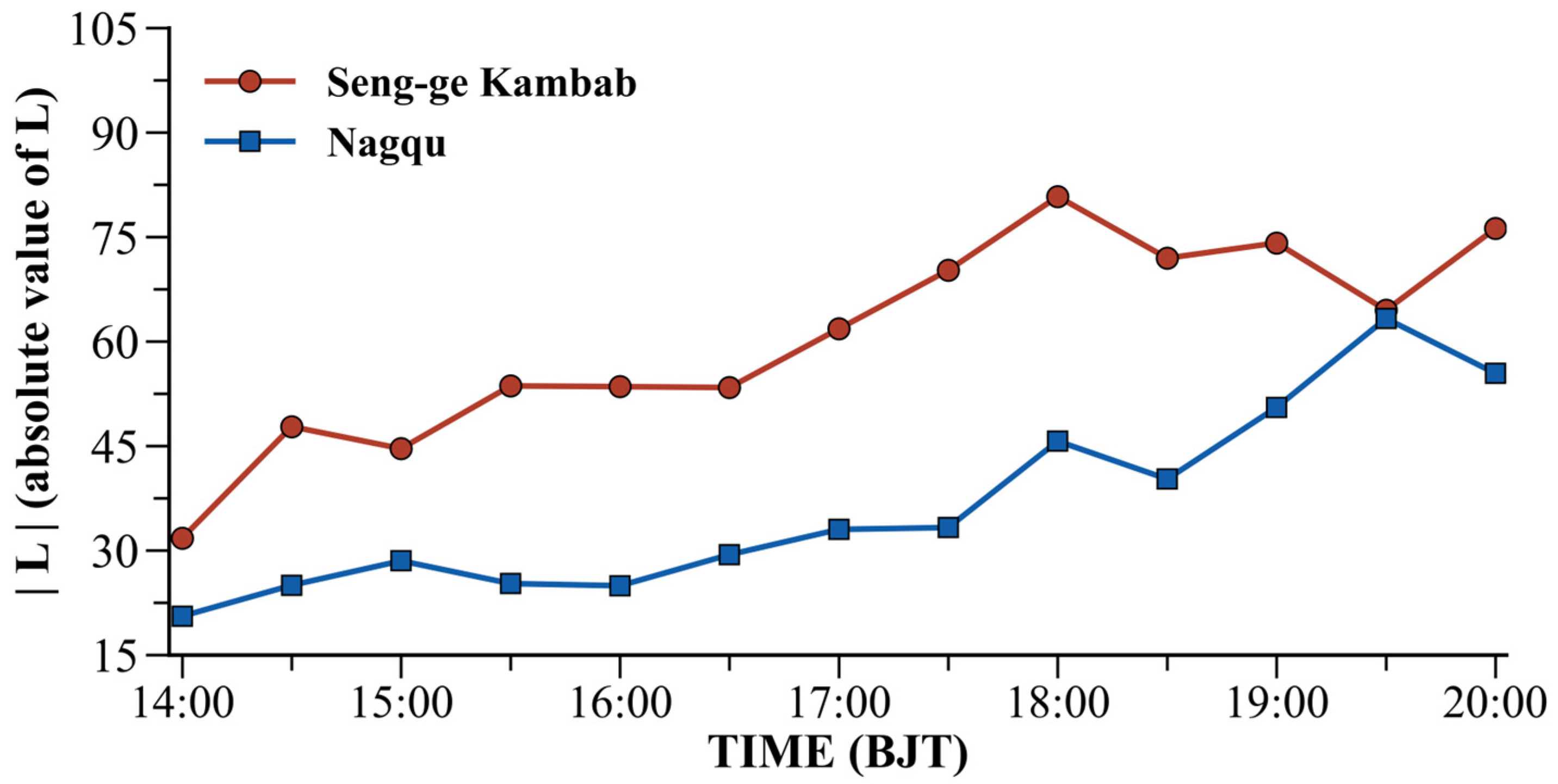
3.2. Characteristics of the Planetary Boundary Layer Height (PBLH) over the Tibetan Plateau
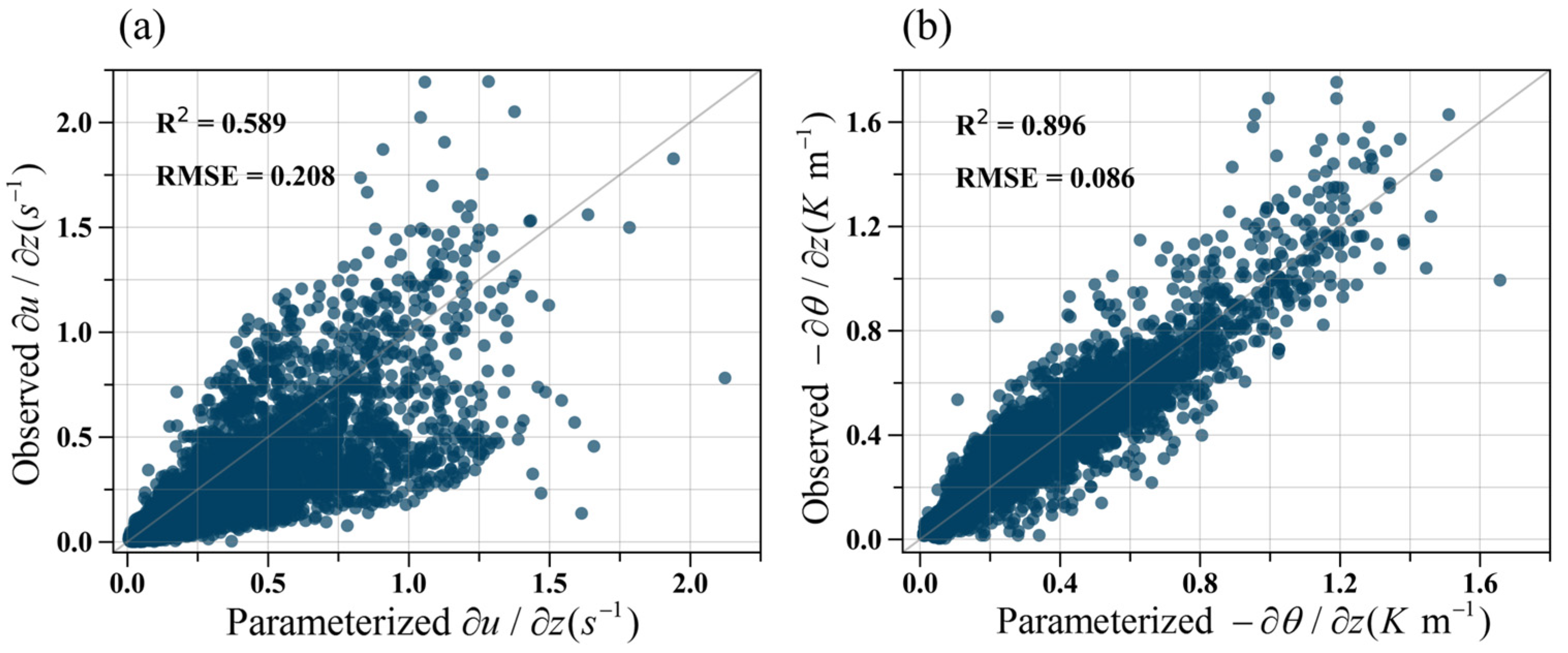
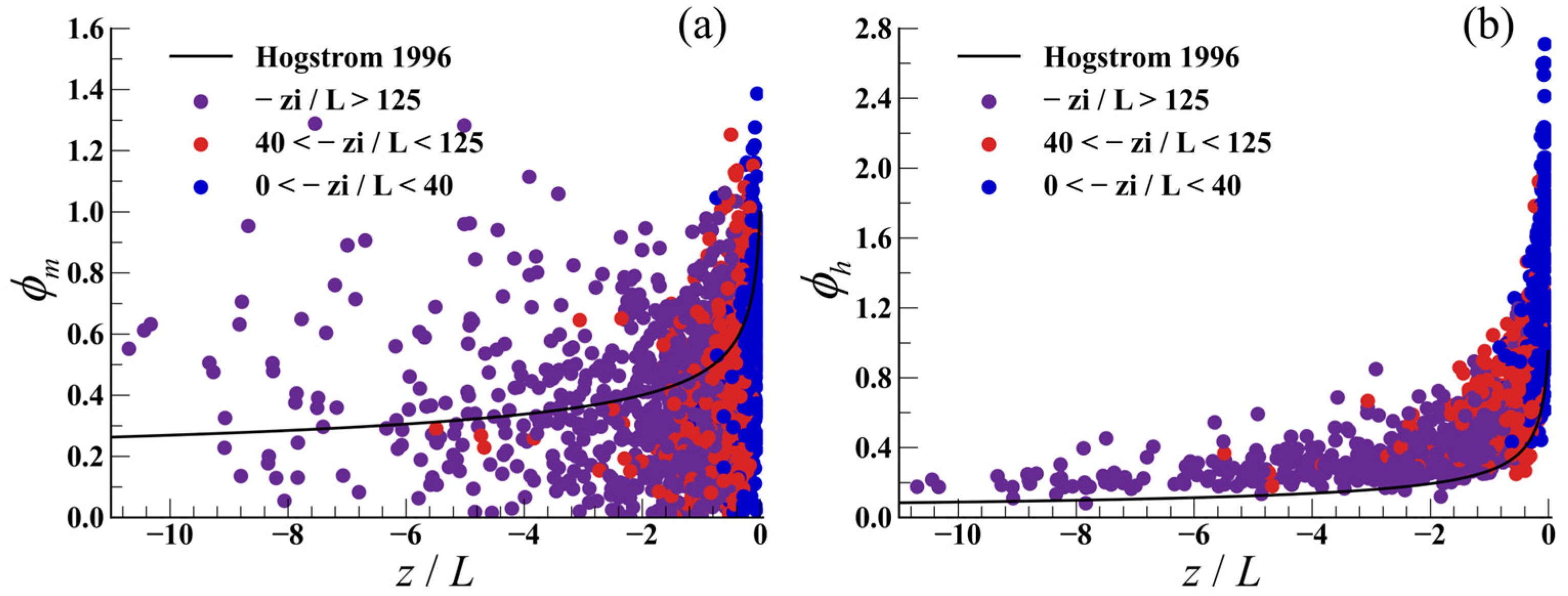
3.3. Nondimensional Flux-Gradient Relations in the Unstable Surface Layer over the Tibetan Plateau
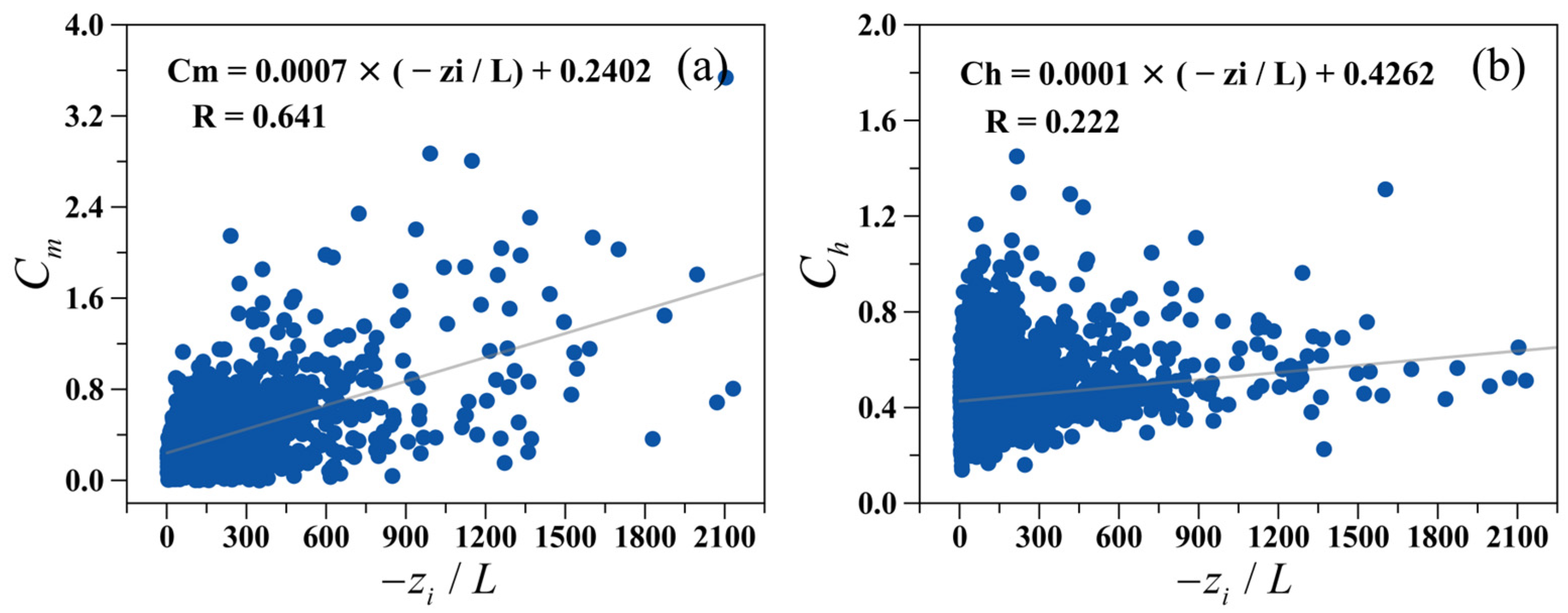
3.4. Factors Influencing Classical Flux-Gradient Relations
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Monin, A.S.; Obukhov, A.M. Basic Laws of Turbulent Mixing in the Atmospheric Surface Layer. Contrib. Geophys. Inst. Slovak Acad. Sci. 1954, 24, 163–187. [Google Scholar]
- Businger, J.A.; Wyngaard, J.C.; Izumi, Y.; Bradley, E.F. Flux-profile relationships in the atmospheric surface layer. J. Atmos. Sci. 1971, 28, 181–189. [Google Scholar] [CrossRef]
- Dyer, A.J. A Review of Flux-Profile Relationships. Bound.-Layer Meteorol. 1974, 7, 363–372. [Google Scholar] [CrossRef]
- Panofsky, H.A.; Dutton, J.A. Atmospheric Turbulence; John Wiley & Sons: New York, NY, USA; Chichester, UK; Toronto, ON, Canada; Singapore, 1984. [Google Scholar]
- Hogstrom, U. Non-dimensional Wind and Temperature Profiles in the Atmospheric Surface Layer: A Re-Evaluation. Bound.-Layer Meteorol. 1988, 42, 55–78. [Google Scholar] [CrossRef]
- Hogstrom, U. Review of Some Basic Characteristics of the Atmospheric Surface Layer. Bound.-Layer Meteorol. 1996, 78, 215–246. [Google Scholar] [CrossRef]
- Panofsky, H.A.; Tennekes, H.; Lenschow, D.H.; Wyngaard, J.C. The Characteristics of Turbulent Velocity Components in the Surface Layer under Convective Conditions. Bound.-Layer Meteorol. 1977, 11, 355–361. [Google Scholar] [CrossRef]
- Khanna, S.; Brasseur, J.G. Analysis of Monin–Obukhov similarity from large-eddy simulation. J. Fluid Mech. 1997, 345, 251–286. Available online: https://ui.adsabs.harvard.edu/abs/1997JFM...345..251K/abstract (accessed on 10 November 2024).
- Katul, G.G.; Konings, A.G.; Porporato, A. Mean Velocity Profile in a Sheared and Thermally Stratified Atmospheric Boundary Layer. Phys. Rev. Lett. 2011, 107, 268502. [Google Scholar] [CrossRef]
- Banerjee, T.; Li, D.; Juang, J.; Katul, G. A spectral budget model for the longitudinal turbulent velocity in the stable atmospheric surface layer. J. Atmos. Sci. 2016, 73, 145–166. [Google Scholar] [CrossRef]
- Li, Q.; Gentine, P.; Mellado, J.P.; McColl, K.A. Implications of Nonlocal Transport and Conditionally Averaged Statistics on Monin–Obukhov Similarity Theory and Townsend’s Attached Eddy Hypothesis. J. Atmos. Sci. 2018, 75, 3403–3431. [Google Scholar] [CrossRef]
- Salesky, S.T.; Chamecki, M. Random Errors in Turbulence Measurements in the Atmospheric Surface Layer: Implications for Monin–Obukhov Similarity Theory. J. Atmos. Sci. 2012, 69, 3700–3714. [Google Scholar] [CrossRef]
- Sorbjan, Z. On similarity in the atmospheric boundary layer. Bound.-Layer Meteorol. 1986, 34, 377–397. [Google Scholar] [CrossRef]
- Deardorff, J.W. Numerical Investigation of Neutral and Unstable Planetary Boundary Layers. J. Atmos. Sci. 1972, 29, 91–115. [Google Scholar] [CrossRef]
- Kaimal, J.C.; Wyngaard, J.C.; Izumi, Y.; Coté, O.R. Spectral Characteristics of Surface-Layer Turbulence. Q. J. R. Meteorol. Soc. 1972, 98, 563–589. [Google Scholar] [CrossRef]
- Steeneveld, G.J.; Holtslag, A.A.M.; Debruin, H.A.R. Fluxes and Gradients in the Convective Surface Layer and the Possible Role of Boundary-Layer Depth and Entrainment Flux. Bound.-Layer Meteorol. 2005, 116, 237–252. [Google Scholar] [CrossRef]
- McNaughton, K.G. On the Kinetic Energy Budget of the Unstable Atmospheric Surface Layer. Bound.-Layer Meteorol. 2006, 118, 83–107. [Google Scholar] [CrossRef]
- Gioia, G.; Guttenberg, N.; Goldenfeld, N.; Chakraborty, P. Spectral Theory of the Turbulent Mean-Velocity Profile. Phys. Rev. Lett. 2010, 105, 184501. [Google Scholar] [CrossRef]
- Katul, G.G.; Li, D.; Chamecki, M.; Bou-Zeid, E. Mean Scalar Concentration Profile in a Sheared and Thermally Stratified Atmospheric Surface Layer. Phys. Rev. 2013, 87, 023004. [Google Scholar] [CrossRef]
- Gao, Z.; Liu, H.; Russell, E.S.; Huang, J.; Foken, T.; Oncley, S.P. Large Eddies Modulating Flux Convergence and Divergence in a Disturbed Unstable Atmospheric Surface Layer. J. Geophys. Res. Atmos. 2016, 121, 1475–1492. [Google Scholar] [CrossRef]
- McColl, K.A.; Katul, G.G.; Gentine, P.; Entekhabi, D. Mean-Velocity Profile of Smooth Channel Flow Explained by a Cospectral Budget Model with Wall-Blockage. Phys. Fluids. 2016, 28, 035107. [Google Scholar] [CrossRef]
- Mellado, J.P.; Van Heerwaarden, C.C.; Garcia, J.R. Near-Surface Effects of Free Atmosphere Stratification in Free Convection. Bound.-Layer Meteorol. 2016, 159, 69–95. [Google Scholar] [CrossRef]
- Cheng, Y.; Li, Q.; Li, D.; Gentine, P. Logarithmic Profile of Temperature in Sheared and Unstably Stratified Atmospheric Boundary Layers. Phys. Rev. Fluids. 2021, 6, 034606. [Google Scholar] [CrossRef]
- Johansson, C.; Smedman, A.-S.; Högström, U.; Brasseur, J.G.; Khanna, S. Critical test of the validity of Monin–Obukhov similarity during convective conditions. J. Atmos. Sci. 2001, 58, 1549–1566. [Google Scholar] [CrossRef]
- Liu, S.; Zeng, X.; Dai, Y.; Shao, Y. Further improvement of surface flux estimation in the unstable surface layer based on large-eddy simulation data. J. Geophys. Res. Atmos. 2019, 124, 9839–9854. [Google Scholar] [CrossRef]
- Zhao, P.; Xu, X.; Chen, F.; Guo, X.; Zheng, X.; Liu, L.; Hong, Y.; Li, Y.; La, Z.; Peng, H. The Third Atmospheric Scientific Experiment for Understanding the Earth–Atmosphere Coupled System over the Tibetan Plateau and Its Effects. Bull. Am. Meteorol. Soc. 2018, 99, 757–776. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, X.; Liu, H.; Li, Y.; Li, Y.; Hu, Z.; Gao, X.; Ma, Y.; Sun, J.; Lenschow, D.H.; et al. Analysis of land surface parameters and turbulence characteristics over the Tibetan Plateau and surrounding region. J. Geophys. Res. Atmos. 2016, 121, 9540–9560. [Google Scholar] [CrossRef]
- Che, J.; Zhao, P. Characteristics of the summer atmospheric boundary layer height over the Tibetan Plateau and influential factors. Atmos. Chem. Phys. 2021, 21, 5253–5268. [Google Scholar] [CrossRef]
- Liu, S.Y.; Liang, X.Z. Observed diurnal cycle climatology of planetary boundary layer height. J. Clim. 2010, 23, 5790–5809. [Google Scholar] [CrossRef]
- Katul, G.G.; Porporato, A.; Shah, S.; Bou-Zeid, E. Two phenomenological constants explain similarity laws in stably stratified turbulence. Phys. Rev. E 2014, 89, 023007. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Garratt, J.R. The Atmospheric Boundary Layer; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Pirozzoli, S.; Bernardini, M.; Verzicco, R.; Orlandi, P. Mixed convection in turbulent channels with unstable stratification. J. Fluid Mech. 2017, 821, 482–516. [Google Scholar] [CrossRef]
- Liu, S.; Zeng, X.; Dai, Y.; Yuan, H.; Wei, N.; Wei, Z.; Lu, X.; Zhang, S. A Surface Flux Estimation Scheme Accounting for Large-Eddy Effects for Land Surface Modeling. Geophys. Res. Lett. 2022, 49, e2022GL101754. [Google Scholar] [CrossRef]
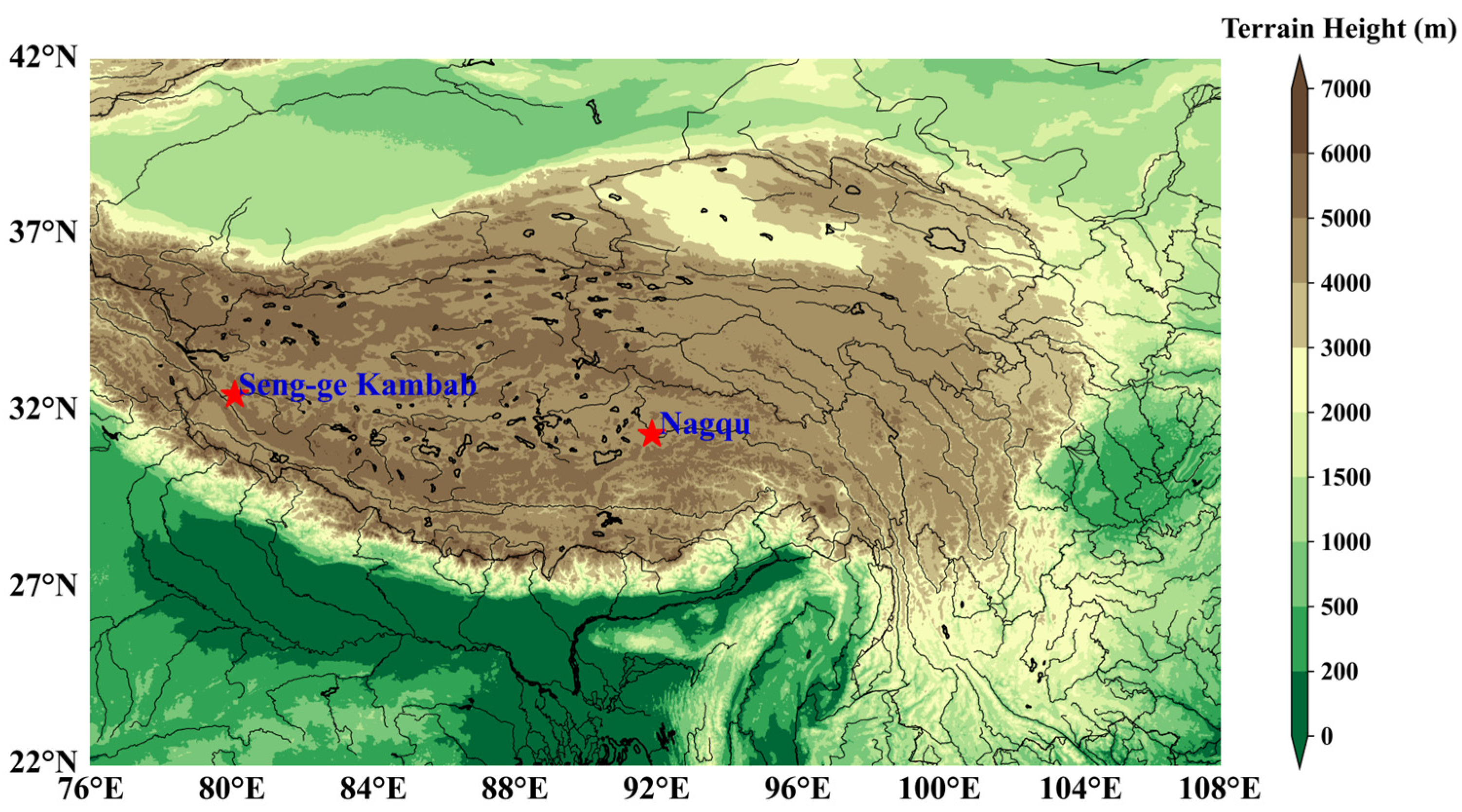





| Site Location | Longitude and Latitude | Elevation (m) | Land Cover Type | Observation Heights (m) | Sonic Anemometer Height (m) |
|---|---|---|---|---|---|
| Seng-ge Kambab | 80.1° E, 32.5° N | 4278 | Bare soil with few obstacles | 1, 2, 4, 8, 18 | 5 |
| Nagqu | 91.9° E, 31.4° N | 4509 | Alpine steppe | 0.75, 1.5, 3, 6, 12 | 3.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Li, L.; Shi, Q.; Liu, S. Impact of Large Eddies on Flux-Gradient Relations in the Unstable Surface Layer Based on Measurements over the Tibetan Plateau. Atmosphere 2025, 16, 391. https://doi.org/10.3390/atmos16040391
Huang H, Li L, Shi Q, Liu S. Impact of Large Eddies on Flux-Gradient Relations in the Unstable Surface Layer Based on Measurements over the Tibetan Plateau. Atmosphere. 2025; 16(4):391. https://doi.org/10.3390/atmos16040391
Chicago/Turabian StyleHuang, Huishan, Lingke Li, Qingche Shi, and Shaofeng Liu. 2025. "Impact of Large Eddies on Flux-Gradient Relations in the Unstable Surface Layer Based on Measurements over the Tibetan Plateau" Atmosphere 16, no. 4: 391. https://doi.org/10.3390/atmos16040391
APA StyleHuang, H., Li, L., Shi, Q., & Liu, S. (2025). Impact of Large Eddies on Flux-Gradient Relations in the Unstable Surface Layer Based on Measurements over the Tibetan Plateau. Atmosphere, 16(4), 391. https://doi.org/10.3390/atmos16040391





