Abstract
In modern communication, the electromagnetic spectrum serves as the carrier for information transmission, and the only medium enabling information exchange anywhere, anytime. To adapt to the changing dynamics of a complex electromagnetic environment, electromagnetic spectrum allocation algorithms must not only meet the demands for efficiency and intelligence but also possess anti-jamming capabilities to achieve the best communication effect. Focusing on intelligent wireless communication, this paper proposes a multi-agent hybrid game spectrum allocation method under incomplete information and based on the Monte Carlo counter-factual regret minimization algorithm. Specifically, the method first utilizes frequency usage and interference information from both sides to train agents through extensive simulations using the Monte Carlo Method, allowing the trial values to approach the expected values. Based on the results of each trial, the counterfactual regret minimization algorithm is employed to update the frequency selection strategies for both the user and the interferer. Subsequently, the trained agents from both sides engage in countermeasure communication. Finally, the probabilities of successful communication and successful interference for both sides are statistically analyzed. The results show that under the multi-agent hybrid game spectrum allocation method based on the Monte Carlo counter-factual regret minimization algorithm, the probability of successful interference against the user is 32.5%, while the probability of successful interference by the jammer is 37.3%. The average simulation time per round is 3.06 s. This simulation validates the feasibility and effectiveness of the multi-agent hybrid game spectrum allocation module based on the Monte Carlo counter-factual regret minimization algorithm.
1. Introduction
The propagation of electromagnetic waves is closely related to the atmospheric environment. It is mainly influenced by factors such as atmospheric refraction, temperature, humidity, air pressure, and ionospheric effects [1]. Atmospheric refraction causes the propagation path of radio waves to bend, especially when there are significant changes in temperature and air pressure. Increased humidity leads to signal attenuation, which is particularly pronounced in higher frequency bands (such as microwaves and millimeter waves). The ionosphere in the atmosphere has refractive or reflective effects on shortwave frequencies, and solar activity and changes in the Earth’s magnetic field further impact their propagation characteristics. Weather phenomena like precipitation and thunderstorms can also cause signal attenuation or multipath propagation, affecting signal quality. Furthermore, different frequency bands exhibit different propagation behaviors in the atmosphere: low-frequency waves mainly rely on ionospheric reflection, while high-frequency waves are more affected by atmospheric humidity, temperature variations, and precipitation [2]. Therefore, the atmospheric environment has a significant impact on electromagnetic spectrum allocation.
With the rapid evolution of various radio communication systems and the increasing density of radio signals, the utilization of radio frequencies has become increasingly saturated [3]. Communication protocols and signal types are diversifying, while advanced modulation technologies have made communication signals more flexible and varied. The development and application of various radio devices have led to a proliferation of numerous, dynamically overlapping radio signals in the electromagnetic space, resulting in frequent signal overlap and a progressively complex electromagnetic environment [4]. Furthermore, the advancement of software-defined radio technology has provided many devices with greater opportunities for interference and the utilization of radio spectrum resources, which can disrupt normal communication [5]. In this non-cooperative supervisory control scenario, effectively protecting one’s electronic devices and systems from adversarial interference, is crucial for ensuring spectrum resource advantages [6] and supporting B5G and 6G communication [7] and in a complex electromagnetic environment [8].
In recent years, research into multi-agent technology has regained significant attention. The study of multi-agent games has gradually expanded from simple games involving just two agents, such as Go and Tic-Tac-Toe [9], to more complex domains. This includes large-scale network games like StarCraft [10], multi-robot cooperation in physical scenarios, and simulation-based combat scenarios in modern warfare contexts. In a multi-agent environment, each agent improves its strategy by interacting with the environment and receiving rewards, thereby seeking the optimal strategy for that environment. This process is known as multi-agent reinforcement learning [11]. Multi-agent reinforcement learning is a key artificial intelligence technology for solving multi-agent games. It achieves the optimal strategies for multiple agents by solving Nash equilibrium strategies in stochastic games [12]. In multi-agent reinforcement learning, the large state and joint action spaces of multiple agents lead to challenges with the explosion of search space dimensions, which restricts the effectiveness of learning strategies. In recent years, deep learning has enabled high-dimensional feature representation through the use of deep networks for function approximation and convolutional networks for feature extraction [13]. Deep reinforcement learning is a fusion of deep learning and reinforcement learning [14]. It employs deep networks for the expression and iterative updating of policies, effectively addressing the challenges of feature extraction and representation in high-dimensional spaces. When applied to the multi-agent domain, this leads to multi-agent deep reinforcement learning, which is currently one of the most promising directions [15]. The introduction of game theory provides a theoretical foundation for handling competitive and cooperative relationships among multiple agents, while also defining optimal strategies through Nash equilibrium in stochastic games [16]. The MaxMinQ-learning algorithm addresses the zero-sum game problem for two players [17]. The Nash-Q-learning algorithm uses quadratic programming to solve Nash equilibrium points, tackling general multi-agent games [18]. The WoLF-PH algorithm, by employing the PHC algorithm to learn and improve strategies, replaces the quadratic programming approach and reduces the algorithmic complexity, significantly enhancing convergence speed [18]. Claus and colleagues introduced evolutionary algorithms into multi-agent systems, enabling agents to exhibit collaborative evolution. However, this approach applies only to agents operating under cooperative relationships [19,20,21]. The introduction of deep learning has provided novel approaches for multi-agent reinforcement learning. The Multi-Agent Deep Deterministic Policy Gradient (MADDPG) algorithm improves upon traditional Actor-Critic (AC) methods by employing a centralized training and decentralized execution approach. It enhances the experience replay mechanism and trains a Critic requiring global information and an Actor requiring local information for each agent. Additionally, each agent can have its own reward function. These improvements enable MADDPG [22] to handle both competitive and cooperative scenarios, as well as mixed game problems. However, due to the complex interrelations between agents in mixed games, this algorithm also faces challenges, such as the lack of a systematic basis for manually designing reward functions and difficulties in training multiple agents from scratch to converge. Therefore, research into reinforcement learning-based multi-agent cooperative adversarial methods holds significant value.
Meng et al. proposed an orthogonal genetic algorithm based on the idea of mixed niches. At the same time, we use a standard genetic algorithm and a micro genetic algorithm to optimize the model. The model has the advantages of fast convergence, strong stability and good optimization effect [23]. This method is only applicable to fixed scenario allocation and is not suitable for rapidly changing adversarial scenarios. Chen et al. discuss some featured game models to investigate spectrum allocation for task-driven UAV communication networks [24]. However, the article did not apply it to practical scenarios and only discussed the application of game theory to spectrum allocation. In summary, multi-agent decision-making algorithms under mixed games have many areas that require improvement. Addressing the rules for the changing dynamics of a complex electromagnetic environment, this paper proposes a multi-agent hybrid game spectrum allocation method based on the Monte Carlo counter-factual regret minimization (MCCFR) algorithm. The goal is to enhance the rationality, effectiveness, and intelligence of spectrum allocation in complex electromagnetic environment and to validate the feasibility and effectiveness of the MCCFR-based multi-agent hybrid game spectrum allocation module. The main contributions of this article are as follows: (1) It proposes a multi-agent hybrid game spectrum allocation method based on the MCCFR algorithm. This method addresses the dynamic changes in spectrum allocation within complex electromagnetic environments. Introducing a multi-agent hybrid game model based on the MCCFR algorithm enhances spectrum allocation’s rationality, effectiveness, and intelligence. (2) It constructs a spectrum allocation model based on incomplete information games: Through the framework of incomplete information games, this paper proposes a novel spectrum allocation model that adapts to complex electromagnetic environments and changing game dynamics, providing theoretical support for multi-agent collaborative decision-making. (3) It verifies the feasibility and effectiveness of the MCCFR-based multi-agent hybrid game spectrum allocation module; simulation results show that the probability of interference for the frequency being affected is 32.5%. The probability of successful interference from the interfering party is 37.3%. This verifies the feasibility and effectiveness of the multi-agent hybrid game spectrum allocation module based on the Monte Carlo Counterfactual Regret Minimization (MCCFR) algorithm. The organization of this paper is as follows: Section 2 provides an overview of the primary methods used in this study and constructs a spectrum allocation model based on incomplete information games. Section 3 employs the proposed spectrum allocation model in game-theoretic adversarial scenarios to verify and analyze the feasibility and effectiveness of the multi-agent hybrid game spectrum allocation module based on the MCCFR algorithm. Section 4 presents the conclusion of the paper.
2. Methods and Model
2.1. Methods
2.1.1. Monte Carlo Method (MCM)
The MCM is a computational technique based on probability and statistics. It primarily uses random numbers to solve mathematical problems. The core principle involves obtaining a solution to a given problem by performing a large number of random samples.
The MCM involves drawing simple subsamples from a population to conduct sampling experiments. The variables represent N independent random variables that share the same distribution, with the same expected value and variance , where . According to the law of large numbers, for any ε > 0, the following holds:
According to Bernoulli’s Law, if the probability of event A occurring is P(A) and in N independent and repeated trials, the event A occurs n times, then the frequency of event A is n/N. Therefore, for any ε > 0, the following holds:
From the above analysis, it can be concluded that when N is sufficiently large, the sample mean converges to E(xi) in probability. Similarly, the frequency n/N approaches the probability P(A). This demonstrates the convergence property of the MCM, where the estimates derived from random sampling converge to the true values as the number of samples increases.
2.1.2. Counterfactual Regret Minimization
Nash equilibrium is the hallmark solution in games with incomplete information, signifying that no participant can gain higher payoffs by unilaterally deviating from the Nash equilibrium strategy. To address the problem of solving Nash equilibrium in such games, Zinkevich and colleagues pioneered the counterfactual regret minimization (CFR) algorithm. This algorithm decomposes the overall regret minimization problem into individual information sets, computing local regret values independently. The algorithm aims to minimize the average global regret by minimizing the regret for each information set. During iterative updates, the regret-matching algorithm is employed to ensure that, as the number of iterations increases, the average strategy gradually converges to the Nash equilibrium strategy. The CFR algorithm is currently one of the mainstream methods for generating efficient strategies in games with incomplete information.
2.2. Model
2.2.1. Modeling Approach
Firstly, it is important to clarify the specific problem and application scenario for spectrum allocation. The multi-agent, mixed-game decision-making for spectrum allocation is based on game theory methods, using MCM algorithm as the strategy for spectrum allocation, and employing the CRF algorithm as evaluation metrics for agent rewards and punishments to adjust frequency selection strategies. To accelerate the computational speed of the algorithm, perturbation methods are used to enhance the Monte Carlo acceleration algorithm. The multi-agent spectrum allocation approach based on MCCFR is illustrated in Figure 1.
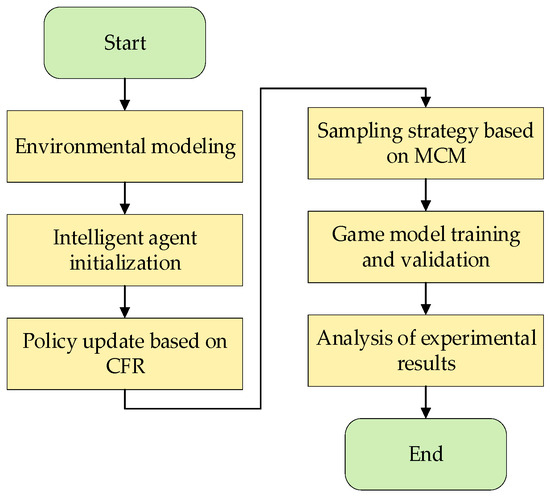
Figure 1.
Multi-agent, mixed-game decision-making for spectrum allocation approach.
(1) Environment Modeling
Game Environment: construct a game environment capable of simulating tasks such as electromagnetic spectrum management, including parameters such as spectrum characteristics, equipment deployment locations, action trajectories, timing of actions, and frequency usage priorities.
State Representation: define the state for each agent, including its position, spectrum usage, and opponent behaviors.
Reward Mechanism: design a reasonable reward mechanism to incentivize agents to take actions that align with the task objectives in a multi-agent game.
(2) Agent Initialization
Agent Types: define the different types of agents participating in the game, such as frequency management agents.
Strategy Representation: represent each agent’s strategy using an MCCFR network, which takes the current state as input and outputs the probability distribution of possible actions.
(3) Strategy Update Based on CRF
Counterfactual Regret Value Update: Before each game simulation, calculate the counterfactual regret values at each decision point and adjust strategies based on these regret values. For initial iterations, set the counterfactual regret values and frequency strategies at each decision point to 0.5, indicating equal probability for all frequency bands with no bias.
(4) Sampling Strategy Based on MCM Algorithm
Use Monte Carlo sampling methods to simulate multiple game processes, calculate regret values for each simulation, and obtain the average counterfactual regret values. Update strategies based on these values.
(5) Game Model Training and Validation
Conduct extensive simulations in the modeled environment to gradually update agent strategies. Determine the optimal strategies through rewards, punishments, and regret minimization.
Establish reasonable validation metrics such as strategy payoffs, spectrum utilization, and action efficiency. Validate the model’s performance in different task scenarios and analyze its feasibility and effectiveness in real-world applications.
(6) Experimentation and Results Analysis
Set up various game task scenarios to simulate realistic electromagnetic spectrum management tasks. Evaluate the model’s performance using experimental data and analyze its performance across different scenarios.
Validate the effectiveness of each agent’s strategy under different adversarial conditions, assess the performance and stability of various strategies, and ensure the achievement of intended goals in complex game environments. Based on experimental results, propose directions and methods for further optimizing the model.
The red–blue confrontation is widely applied in various fields such as military, cybersecurity, and artificial intelligence training, serving as the foundation for multi-team confrontation research. In-depth study of two-party game problems not only lays a solid foundation for more complex multi-team confrontations but also provides an extensible decision-making framework. Therefore, this paper, based on the red–blue confrontation game scenario, utilizes the MCCFRA algorithm to achieve intelligent selection and decision-making, thereby enhancing the optimization capabilities of confrontation strategies. Next, we will briefly describe the process of building intelligent agents for both the red and blue parties
2.2.2. Modeling of Red Team Defensive Agents
In a multi-agent mixed game decision-making system based on the MCCFR algorithm, the primary task of the Red Team defensive agents is to adjust their frequency allocation strategy based on the interference caused by Blue Team attacking agents on the current communication frequency bands. This adjustment is made using a CFR algorithm and is optimized under incomplete information using an MCM algorithm. The frequency allocation process for Red Team defensive agents is illustrated in Table 1, with the input and output parameters detailed in Table 2. In addition, the space and time complexity of all approaches are also evaluated [25]. The time complexity of the MC algorithm is O (Na + N), where Na and N is the maximum number of iterations. We can see that the MCCFR algorithm has low complexity and is suitable as a frequency selection algorithm.

Table 1.
The frequency allocation process for Red Team defensive agents.

Table 2.
Parameters for the Red Team Defensive Agents.
The spectrum allocation process is as follows:
- (1)
- Environment modeling
The game environment for the Red Team defensive agents is set as a cluster communication environment with 8 agents. The agents are divided into two groups of 4: the first 4 agents form the ground communication cluster, and the remaining 4 agents form the aerial communication cluster. Each agent’s main task is to manage frequency based on MCCFR strategies, considering spectrum parameters, equipment deployment locations, action trajectories, timing of actions, and frequency priorities. Each agent has five candidate frequency points, ranging from 30 MHz to 3000 MHz.
- (2)
- Frequency selection for communication links based on MCM
Using the MCM algorithm, select frequencies based on the communication frequency points of each agent. If the regret values and frequency selection strategy values are empty (initial training rounds), assign equal regret values and selection probabilities to all candidate frequency bands, i.e., 50% each. If the regret values and selection strategy values are not empty, choose the communication frequency band based on these values.
- (3)
- Communication link calculation
Calculate the path loss (L), received power, signal-to-noise ratio (SNR), and bit error rate (BER) of the communication link based on spectrum parameters, transceiver parameters, antenna parameters, equipment deployment locations, action trajectories, timing of actions, and environmental parameters. In the calculation of L, we considered the effects of atmospheric gases and rainfall on propagation. We have plotted the relationship between specific attenuation and rain rate, dry air, and water vapor based on the methods described in ITU-R P.676-11 [26] and 838-3 [27], as shown in Figure 2. Figure 2A,B illustrate the relationship between frequency and specific attenuation under different polarization modes and rainfall rates. From the figures, we can observe that as the frequency increases, the specific attenuation gradually increases, and the higher the rainfall rate, the more sensitive the specific attenuation is to frequency changes. Additionally, the specific attenuation under horizontal polarization is slightly higher than that under vertical polarization. In the figure, at a rainfall rate of 50 mm/h and a frequency of 3 GHz under horizontal polarization, the specific attenuation reaches its maximum value, which is only 0.0171 dB/km, and its impact on path loss can be considered negligible for the small-scale scenario described in this paper.
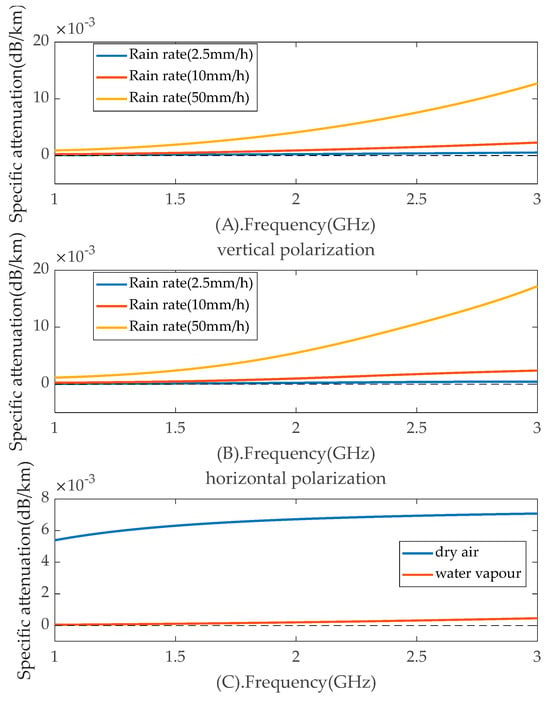
Figure 2.
Relationship of the rain rate, air and specific attenuation. (A) Relationship of the rain rate and specific attenuation in vertical polarization. (B) Relationship of the rain rate and specific attenuation in horizontal polarization. (C) Relationship of the air and specific attenuation.
Figure 2C shows the relationship between specific attenuation and dry and water vapor at different frequencies. Dry air has a greater impact on specific attenuation than water vapor, and specific attenuation increases with frequency. At 3 GHz, the specific attenuation due to dry air reaches its maximum value of only 0.0071 dB/km. By combining Figure 2, we can observe that the impact of atmospheric gases and rainfall on propagation attenuation is minimal in the frequency range of 30 MHz to 3000 MHz. Since we are primarily focused on UAV communication with relatively short transmission distances, in order to reduce algorithm complexity, we adopt the method suggested in ITU-R P.525 Recommendation [28] to calculate L. Among them, the calculation of L in ITU-R P.525 is shown in the following formula.
where, f is the frequency (in MHz); d is the distance (in km).
- (1)
- Determination of communication link interference
Compare the interference received power calculated by the interference source (as returned by the game program) with the received power of the communication link to determine whether the link is interfered.
- (2)
- Punish the agent
If the communication link is determined to be interfered, penalize the Red Team defensive agent.
- (3)
- Reward the agent
If the communication link is determined to be free of interference, reward the Red Team defensive agent.
- (4)
- Calculate Regret Values and Update Regret and Strategy Values Based on CFR
Update the regret values and frequency selection strategy for the candidate frequency points based on the current interference situation of the selected frequency band, using the CFR algorithm. This will serve as a reference for future frequency selection.
2.2.3. Modeling of Blue Team Attacking Agents
The modeling of blue team agents is fundamentally similar to that of the red team, so redundant details are omitted here. The difference lies in the fact that the blue team attacking agents operate in a clustered jamming environment, consisting of 8 agents that interfere with the red team defensive agents. The primary task of the blue team attacking agents is to manage frequency allocation through a game-based strategy using MCCFR, considering factors such as spectrum parameters, equipment deployment positions, action trajectories, timing, and frequency priority. The jamming agents have three candidate jamming frequency bands: 30 MHz to 300 MHz, 300 MHz to 1000 MHz, and 1000 MHz to 3000 MHz, which are used to interfere with the red team’s defensive agents.
In a multi-agent mixed game decision-making scenario based on the MCCFR algorithm, the primary task of the blue team attacking agents is to adjust their jamming frequency strategy using a CFR algorithm. This adjustment is based on the interference observed in the red team’s communications and the current jamming frequency band chosen by the blue team’s attacking agents. The selection of jamming frequencies under incomplete information is achieved using an MCM algorithm.
The spectrum allocation flowchart for the blue team’s attacking agents is shown in Table 3, with the input and output parameters detailed in Table 4.

Table 3.
The spectrum allocation for the blue team’s attacking agents.

Table 4.
Red team defensive agent parameters description.
3. Verification and Analysis
3.1. Interference Determination
In electromagnetic countermeasures, common types of jamming include targeted jamming, blocking jamming, tracking jamming, comb jamming, and scanning jamming. In this study, the blue team attacking agents use blocking jamming to conduct interference attacks against the red team defensive agents.
Under blocking jamming, whether the blue team’s agents interfere with the red team’s agents is determined by the signal-to-interference-plus-noise ratio (SINR). If SINR > 10 dB, it is considered that the blue team’s agents have successfully interfered with the red team’s agents. The level of interference is calculated based on the ratio of the bandwidth of the jamming signal to the bandwidth of the communication signal, the following holds:
where Bj is the bandwidth of the jamming signal (MHz), and Bs is the bandwidth of the communication signal (MHz).
The classification standards for blocking jamming levels are shown in Table 5. Rbw is the ratio of jamming signal bandwidth to communication signal bandwidth.

Table 5.
The classification standards for blocking jamming levels are as follows.
3.2. Typical Scenario Analysis
In a 50 km × 50 km area, there are two groups of communication devices. Each group consists of four defensive intelligent agents. The communication devices within each group communicate randomly with each other. Within a 40-km radius of the communication devices, there are eight attacking intelligent agents. The attacking devices interfere with all defensive devices within the interference frequency band. When SINR exceeds 10 dB, interference is considered present, and the interference level is calculated according to the corresponding formula.
The red team defensive agents and the blue team jamming intelligent agents move in real-time, and the relative positional relationship between the communication devices and the jamming devices is illustrated in Figure 3.
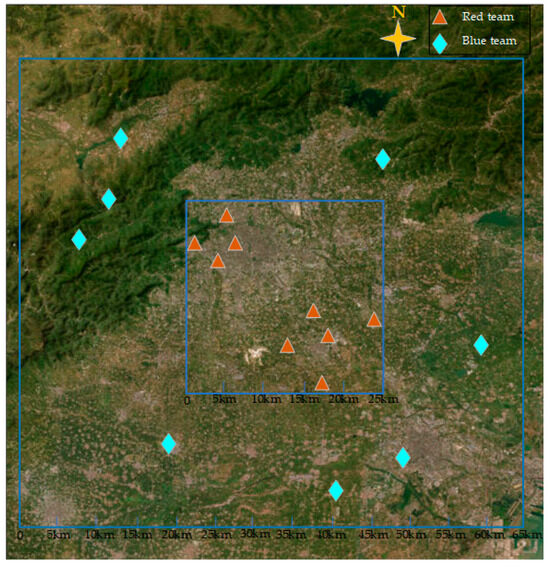
Figure 3.
Position distribution diagram of the red and blue teams.
The parameter settings for the red team defensive and blue team attacking agents are shown in Table 6. In this simulation, the red team defensive agents have five selectable communication frequencies within the 30 MHz to 3000 MHz range: 40 MHz, 500 MHz, 900 MHz, 2200 MHz, and 2700 MHz. The transmission power (Pt), transmission antenna gain, and reception antenna gain (Gr) are set as specified in Table 6. The location information for the communication devices is updated in real-time. This simulation is configured with 8 reference locations, as shown in Table 6. The modulation scheme is set to 6, and the coding scheme is set to ’MPSK’. The blue team jamming agents have 3 selectable interference frequency bands within the 30 MHz to 3000 MHz range: 30 MHz to 300 MHz, 300 MHz to 1000 MHz, and 1000 MHz to 3000 MHz. The transmission power (Pt), transmission antenna gain, and reception antenna gain (Gr) are specified in Table 6. The location information for the jamming devices is also updated in real-time, with 8 reference locations set for this simulation, as indicated in Table 6.

Table 6.
Parameters for simulating and running the intelligent agents.
The software in this paper is primarily developed using Qt Creator 5.12.12, while the MCCFR algorithm is implemented on the Python platform and generates a “.pyd” file, which is then called by Qt. Creator. This simulation wargaming software uses the frequency usage parameters of both the red and blue sides, as shown in Table 6, as input. During the simulation process, the red-side agents intelligently select frequencies for communication using the MCCFR algorithm based on predefined trajectory and frequency usage information to avoid interference. Meanwhile, the blue side employs the MCCFR algorithm to select frequencies for interference intelligently. Figure 4 illustrates the simulation scenario constructed using the developed software. During the simulation, the red and blue opposing teams move along predefined trajectories and make frequency allocation decisions based on the MCCFR algorithm. In the figure, the black sectors represent the blue team’s jamming areas and directions, the red lines indicate disrupted communications between red team agents due to jamming, and the green lines signify successful link establishment and normal communication for the red team.
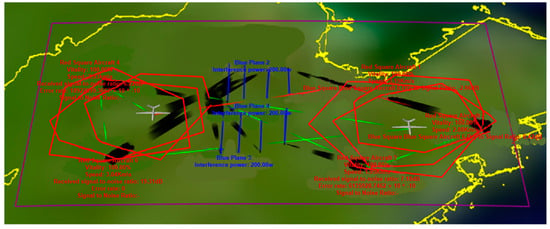
Figure 4.
Simulation and deduction interface.
In the simulation interface, partial information is displayed below the red and blue agents, including the blue team’s jamming power and the red team’s signal-to-noise ratio (SNR), jamming-to-signal ratio (JSR), and bit error rate (BER). Additionally, detailed information about both teams’ agents is shown in the expanded panel on the left side of the interface, as illustrated in Figure 5.
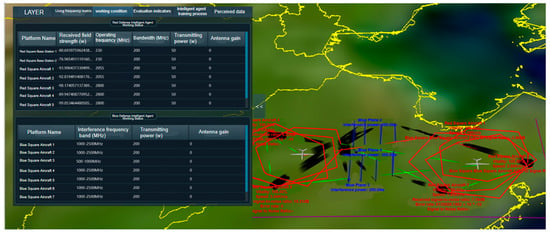
Figure 5.
Detailed working status of game adversarial agents.
To avoid the stochastic noise introduced by Monte Carlo simulations, we conducted 100 simulation rounds. We verified by calculating the total interference and the sum of interferences for agents of the red team and blue team over the 100 rounds. Figure 6 shows the comparison of interference counts for red team defensive agents based on the MCCFR and MC strategies. From the figure, it can be observed that in 100 rounds of simulation, the interference counts for agents based on the MCCFR algorithm are consistently lower than those based on the MC algorithm. Among the eight agents employing the two algorithms, the MCCFR-based agents experienced an average reduction of 11 interference instances compared to the MC-based agents. Notably, Agent 6 exhibited the greatest reduction in interference counts, with a decrease of 20 instances.
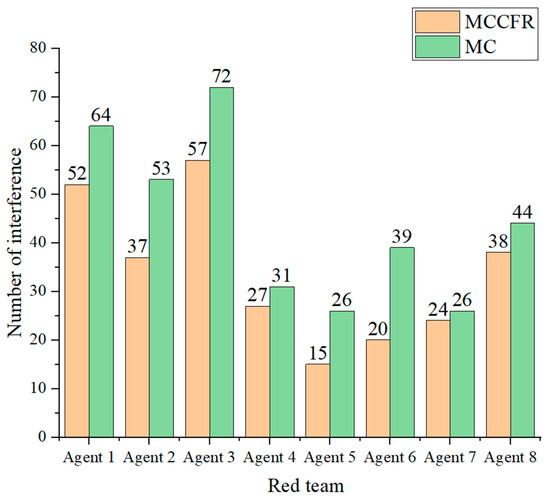
Figure 6.
Comparison of interference counts for red team defensive agents based on the MCCFR and MC strategy.
Figure 7 compares jamming failures for blue team attacking agents based on the MCCFR and MC strategies. The figure shows that in 100 rounds of simulation, the number of successful jamming attempts by agents based on the MCCFR algorithm is consistently higher than that of agents based on the MC algorithm. Among the eight agents employing the two algorithms, the MCCFR-based agents achieved an average increase of 14 successful jamming attempts compared to the MC-based agents. Notably, Agent 5 exhibited the most significant improvement in jamming success, increasing 27 instances.
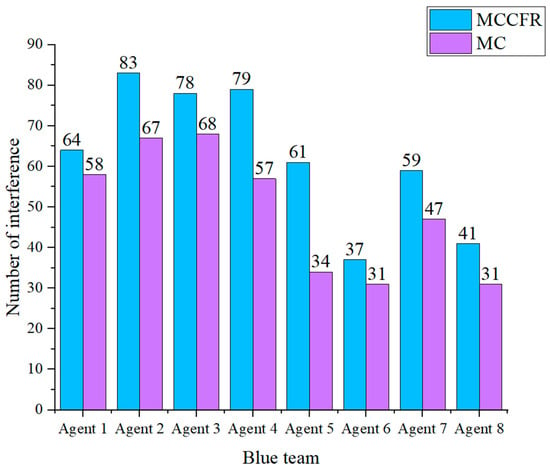
Figure 7.
Comparison of jamming failures for blue team attacking agents based on the MCCFR and MC strategy.
Figure 8 illustrates the frequency selection counts and the interference counts for the chosen frequency bands by the red team agent. It is evident from the figure that the red team agent selected 40 MHz as the central frequency for communication the most frequently, with a total of 228 selections, accounting for 28.50% of all frequency selections. This frequency band experiences interference only 64 times, resulting in an interference percentage of just 28.07%. The red team agent selects 80 MHz as the central frequency for communication the least frequently, with only 80 selections, representing 10.00% of all frequency selections. This frequency band experiences interference 42 times, resulting in an interference percentage of 52.50%. In contrast, the selection of 2700 MHz as the central frequency by the red team is the second most frequent after 40 MHz, with a total of 220 selections, accounting for 27.5% of the total frequency choices. This frequency was interfered with only 50 times by the blue team agent, yielding an interference probability of 22.73%. From the above statistical analysis, it is evident that the red team agent, using the MCCFR algorithm in 100 simulation runs, can avoid interference from the frequency bands selected by the blue team attacking agents, thereby reducing the probability of interference.
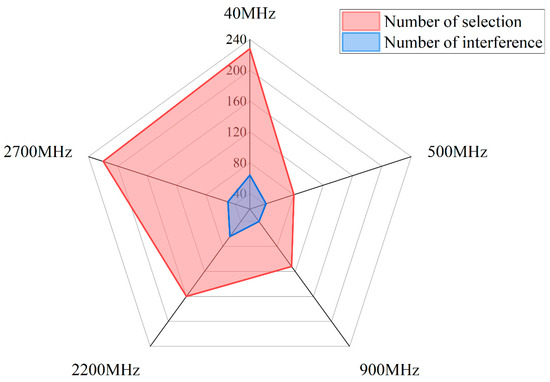
Figure 8.
Histogram of frequency selection counts and interference counts for red team agents based on the MCCFR strategy.
Figure 9 illustrates the number of times the blue team agent selecting specific frequency bands for interference and the number of successful interference events for those bands. It can be observed that the blue team agent most frequently selects the 300 MHz to 1000 MHz band for interference, with a total of 346 selections, accounting for 43.25% of all frequency band choices. Successful interference occurs 135 times in this band, resulting in an interference percentage of 39.02%. The next most frequently selected band is 1000 MHz to 3000 MHz, chosen 264 times, representing 33.00% of all selections. Successful interference in this band occurs 99 times, yielding an interference percentage of 37.5%. The blue team intelligent agent selects the 30 MHz to 300 MHz band for interference the least frequently, with only 190 selections, which accounts for 23.75% of all frequency band choices. Successful interference in this band occurs 64 times, resulting in an interference percentage of 33.69%. The statistical results indicate that there is a direct proportionality between the number of times the blue team intelligent agent selecting a frequency band for interference and the interference percentage, demonstrating that the MCCFR algorithm effectively optimized the choice of interference bands.
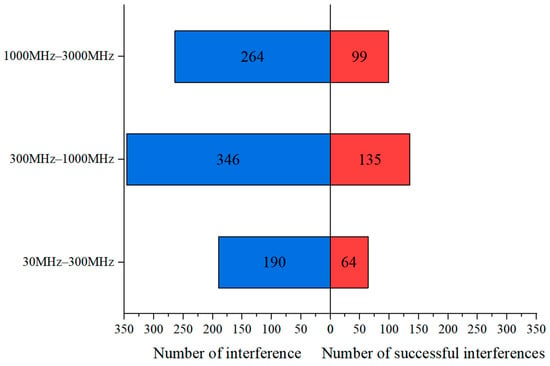
Figure 9.
The statistics of frequency selection counts and successful interference counts for the blue team agent based on the MCCFR strategy.
Figure 10 displays the statistics of interference and interference probability for both the red team defense and the blue team attack in a multi-player incomplete information game. It can be observed that the probability of interference experienced by the red team defensive agent is 32.5%, which is lower than the interference probability of the attacking agents at 37.3%. This discrepancy is primarily due to the overlap in frequency band selections among the eight attacking agents on the blue team, leading to two or more attacking agents interfering with the same defensive agent.
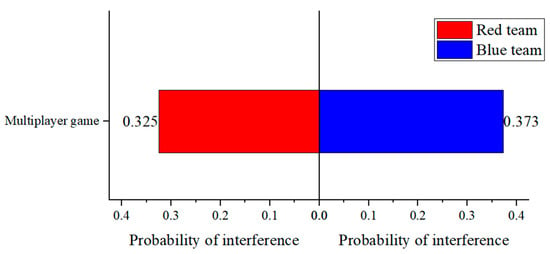
Figure 10.
Statistics of interference and interference probabilities for both red and blue teams in a multi-player game.
Table 7 presents a comparison of convergence times. It can be observed that the simulation time for a multi-player incomplete information game, the single simulation time is 6.28 s, and the average time for 100 iterations of the algorithm is 3.06 s. This indicates that the MCCFR-based mixed strategy game algorithm exhibits the advantage of faster convergence. The reason why the time for a single simulation is longer than running 100 simulations is mainly because the program needs to be initialized and third-party libraries need to be loaded before the simulation starts, which consumes a lot of time. In multiple simulations, the program and third-party libraries only need to be initialized and loaded during the first simulation, so the average time for multiple simulations is less than that for a single simulation.

Table 7.
Comparison of convergence times.
4. Conclusions
This paper aimed to implement spectrum allocation decision-making in multi-agent mixed games based on the MCCFR algorithm. To achieve this objective, we first analyzed the current research landscape, including the background of electronic countermeasures, multi-player incomplete information games, and multi-agent reinforcement learning algorithms, as well as the strategies of the CFR algorithm. We also validated the main functional performance indicators through simulation. The results indicated that, under the multi-agent mixed game spectrum allocation method based on the MCCFR algorithm, the probability of interference for the frequency band being targeted was 32.5%, while the probability of successful interference by the attacking agents was 37.3%. The average time for a single simulation round was 3.06 s. The simulation validation confirms the feasibility and effectiveness of the multi-agent mixed game spectrum allocation module based on the MCCFR algorithm. In the future, we plan to incorporate an adaptive learning rate adjustment mechanism. This will be combined with the MCCFR algorithm to dynamically adjust the rate of strategy updates for the agents during the game, thereby avoiding convergence to local optima. In future work, we will thoroughly investigate the impact of propagation and internal effects, particularly the potential influence of factors such as multipath fading, diffraction, noise fluctuations, and transient external interference on system performance. Shannon’s capacity theorem and the quantum-inspired spectrum allocation method is also the focus of our future work.
Author Contributions
Conceptualization, G.K., M.T. and X.Z.; methodology, X.Z., X.X. and H.D.; software, X.X., L.H. and H.D.; validation, X.X., L.H. and H.D.; formal analysis, M.T., X.Z. and H.D.; investigation, G.K. and M.T.; resources, X.Z., X.X. and H.D.; data curation, X.Z. and H.D.; writing—original draft preparation, G.K., M.T., X.Z. and X.X.; writing—review and editing, G.K., M.T. and X.Z.; visualization, M.T., X.X. and L.H.; supervision, G.K. and M.T.; project administration, G.K. and M.T.; funding acquisition, G.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, J.; Hao, Y.; Yang, C. The Current Progress and Future Prospects of Path Loss Model for Terrestrial Radio Propagation. Electronics 2023, 12, 4959. [Google Scholar] [CrossRef]
- Xu, M.; Olaimat, M.; Tang, T.; Ramahi, O.M.; Aldhaeebi, M.; Jin, Z.; Zhu, M. Numerical Modeling of the Radio Wave over-the-Horizon Propagation in the Troposphere. Atmosphere 2022, 13, 1184. [Google Scholar] [CrossRef]
- Serkov, A.; Kasilov, O.; Lazurenko, B.; Pevnev, V.; Trubchaninova, K. Strategy of Building a Wireless Mobile Communication System in the Conditions of Electronic Counteraction. Electronics 2023, 12, 160–170. [Google Scholar] [CrossRef]
- Zhang, C. The Construction and Characteristics of Foreign Army’s Electronic Countermeasure Equipment. SHS Web Conf. 2021, 96, 01012. [Google Scholar] [CrossRef]
- Lv, Q.; Zhang, W.; Feng, W.; Xing, M. Deep Neural Network-Based Interrupted Sampling Deceptive Jamming Countermeasure Method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 9073–9085. [Google Scholar] [CrossRef]
- Wang, J.; Yang, C.; An, W. Regional Refined Long-term Predictions Method of Usable Frequency for HF Communication Based on Machine Learning over Asia. IEEE Trans. Antennas Prop. 2022, 70, 4040–4055. [Google Scholar] [CrossRef]
- Wang, J.; Yang, C.; Yan, N. Study on digital twin channel for the B5G and 6G communication. Chin. J. Radio Sci. 2021, 36, 340–348. [Google Scholar]
- Wang, J.; Shi, D. Cyber-Attacks Related to Intelligent Electronic Devices and Their Countermeasures: A Review. In Proceedings of the 2018 53rd International Universities Power Engineering Conference (UPEC), Glasgow, UK, 4–7 September 2018; pp. 1–6. [Google Scholar]
- Tu, Z. Design and Implementation of an Artificial Intelligence Gomoku System. Master’s Thesis, Hunan University, Changsha, China, 2016. [Google Scholar]
- Zhang, H.; Li, D.; He, Y. Artificial Intelligence and “StarCraft”: New Progress in Multi-Agent Game Research. Unmanned Syst. Technol. 2019, 2, 5–16. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Introduction to Reinforcement Learning; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Bichler, M.; Fichtl, M.; Oberlechner, M. Computing Bayes–Nash Equilibrium Strategies in Auction Games via Simultaneous Online Dual Averaging. Oper. Res. 2023; ahead of print. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Henderson, P.; Islam, R.; Bachman, P.; Pineau, J.; Precup, D.; Meger, D. Deep Reinforcement Learning That Matters. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Du, W.; Ding, S. A survey on multi-agent deep reinforcement learning: From the perspective of challenges and applications. Artif. Intell. Rev. 2021, 54, 3215–3238. [Google Scholar] [CrossRef]
- Hu, J.; Wellman, M.P. Nash Q-Learning for General-Sum Stochastic Games. J. Mach. Learn. Res. 2003, 4, 1039–1069. [Google Scholar]
- Lee, D.; Defourny, B.; Powell, W.B. Bias-Corrected Q-Learning to Control Max-Operator Bias in Q-Learning. In Proceedings of the IEEE Symposium on Adaptive Dynamic Programming and Reinforcement Learning, Singapore, 16–18 April 2013; pp. 93–99. [Google Scholar]
- Bowling, M.; Veloso, M. Multiagent Learning Using a Variable Learning Rate. Artif. Intell. 2002, 136, 215–250. [Google Scholar] [CrossRef]
- Claus, C.; Boutilier, C. The Dynamics of Reinforcement Learning in Cooperative Multiagent Systems. In Proceedings of the Fifteenth National Conference on Artificial Intelligence (AAAI), Madison, WI, USA, 26–30 July 1998. [Google Scholar]
- Lauer, M.; Riedmiller, M. An Algorithm for Distributed Reinforcement Learning in Cooperative Multi-Agent Systems. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Takamatsu, Japan, 30 October–5 November 2000; pp. 120–126. [Google Scholar]
- Kok, J.R.; Vlassis, N. Sparse Cooperative Q-Learning. In Proceedings of the Twenty-First International Conference on Machine Learning (ICML), Banff, AB, Canada, 4–8 July 2004; pp. 481–488. [Google Scholar]
- Lowe, R.; Wu, Y.; Tamar, A.; Harb, J.; Pieter Abbeel, O.; Mordatch, I. Multi-Agent Actor-Critic for Mixed Cooperative-Competitive Environments. arXiv 2017, arXiv:1706.02275. [Google Scholar]
- Meng, Y.; Qi, P.; Lei, Q.; Zhang, Z.; Ren, J.; Zhou, X. Electromagnetic Spectrum Allocation Method for Multi-Service Irregular Frequency-Using Devices in the Space–Air–Ground Integrated Network. Sensors 2022, 22, 9227. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Wu, Q.; Xu, Y.; Qi, N.; Fang, T.; Liu, D. Spectrum Allocation for Task-Driven UAV Communication Networks Exploiting Game Theory. IEEE Wirel. Commun. 2021, 28, 174–181. [Google Scholar] [CrossRef]
- Thakur, P.; Kumar, A.; Pandit, S.; Singh, G.; Satashia, S.N. Performance Analysis of Cognitive Radio Networks Using Channel-Prediction-Probabilities and Improved Frame Structure. Digit. Commun. Netw. 2018, 4, 287–295. [Google Scholar] [CrossRef]
- ITU-R. P.676-11; Attenuation by Atmospheric Gases and Related Effects. International Telecommunication Union: Geneva, Switzerland, 2022.
- ITU-R. P.838-3; Specific Attenuation Model for Rain for Use in Prediction Methods. International Telecommunication Union: Geneva, Switzerland, 2005.
- ITU-R. P.525-5; Calculation of Free-Space Attenuation. International Telecommunication Union: Geneva, Switzerland, 2024.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).