Characteristics of Aerosol Number Concentration Power Spectra and Their Influence on Flux Measurements
Abstract
1. Introduction
2. Experiment and Data Processing Methods
2.1. Experiment
2.2. Data Quality Control
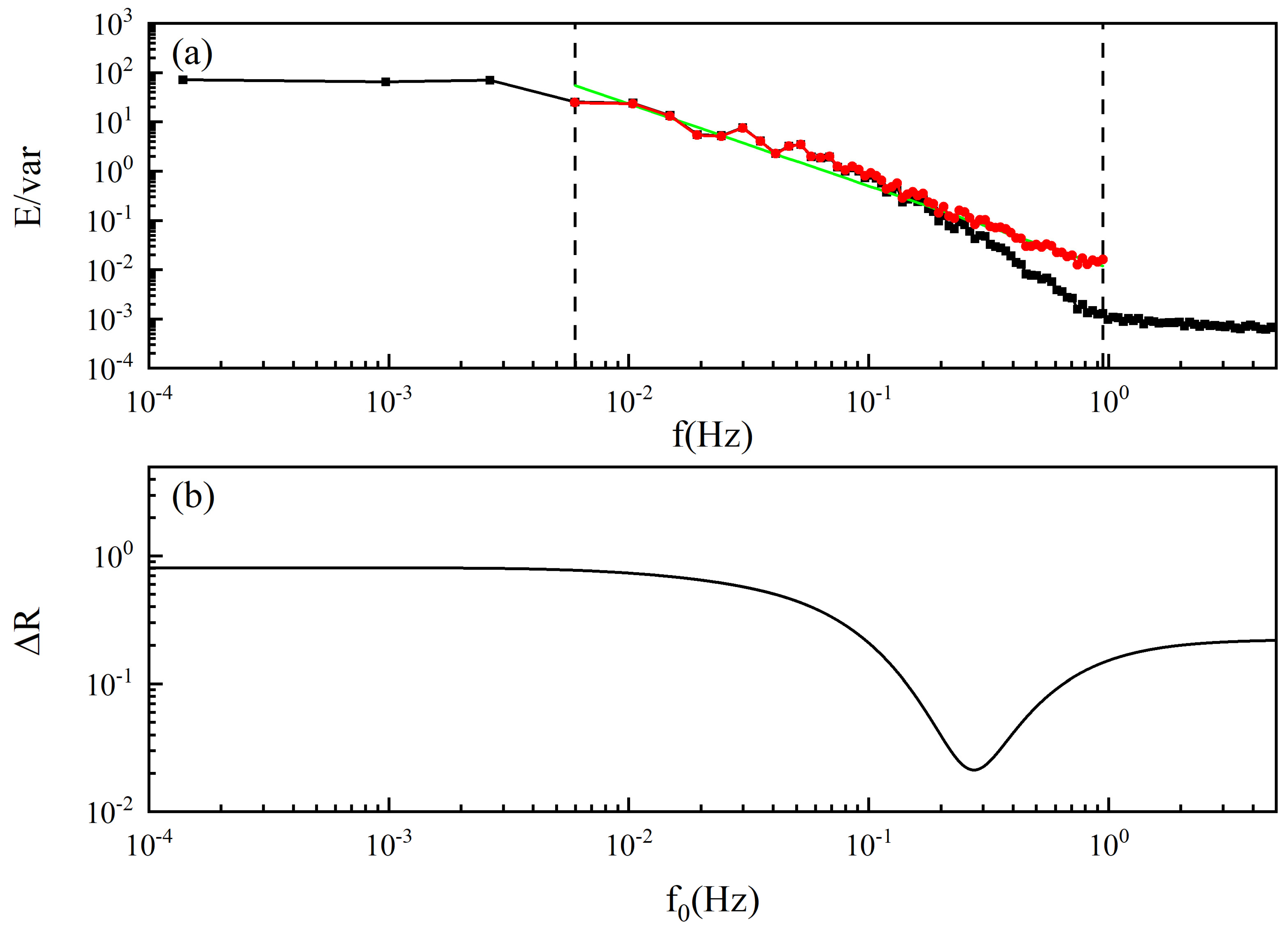
2.3. A Description Method of the High-Frequency Attenuation Characteristics of the Aerosol Concentration Fluctuation Power Spectrum
2.4. Correction Methods for High-Frequency Power Spectra of Aerosol Concentration Fluctuation
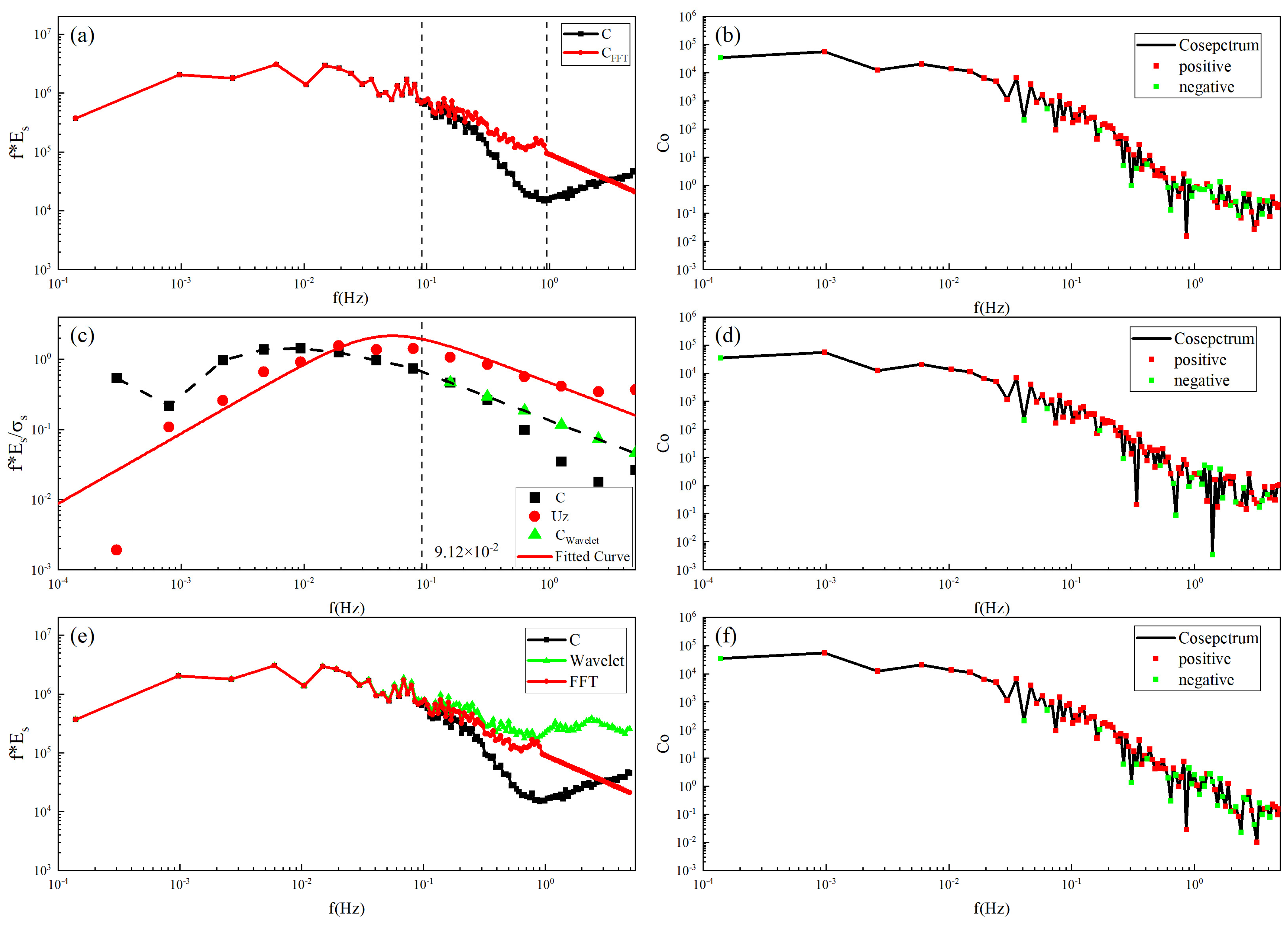
2.4.1. Correction Based on the FFT Method
2.4.2. Correction Based on the Wavelet-Based Method
3. Results
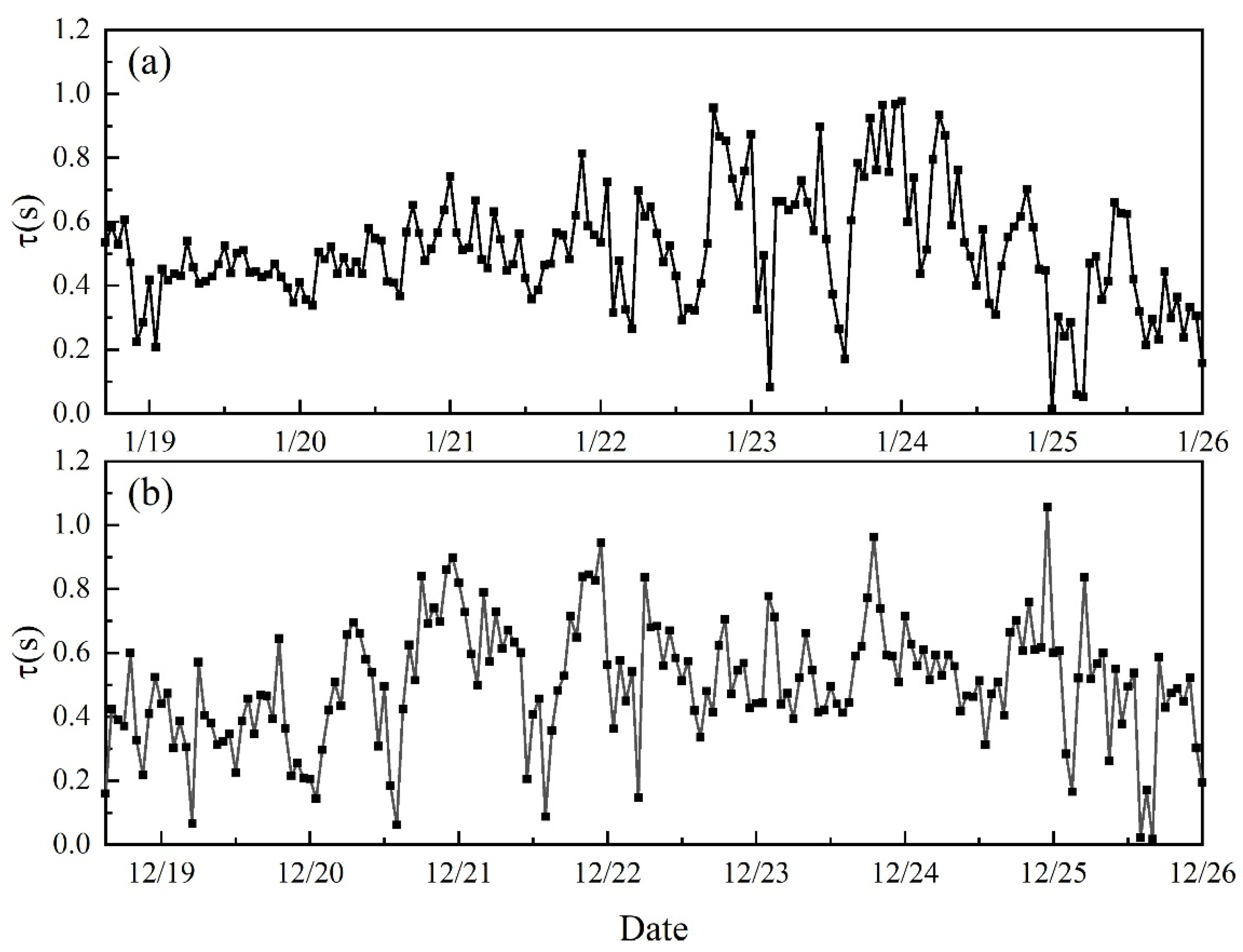
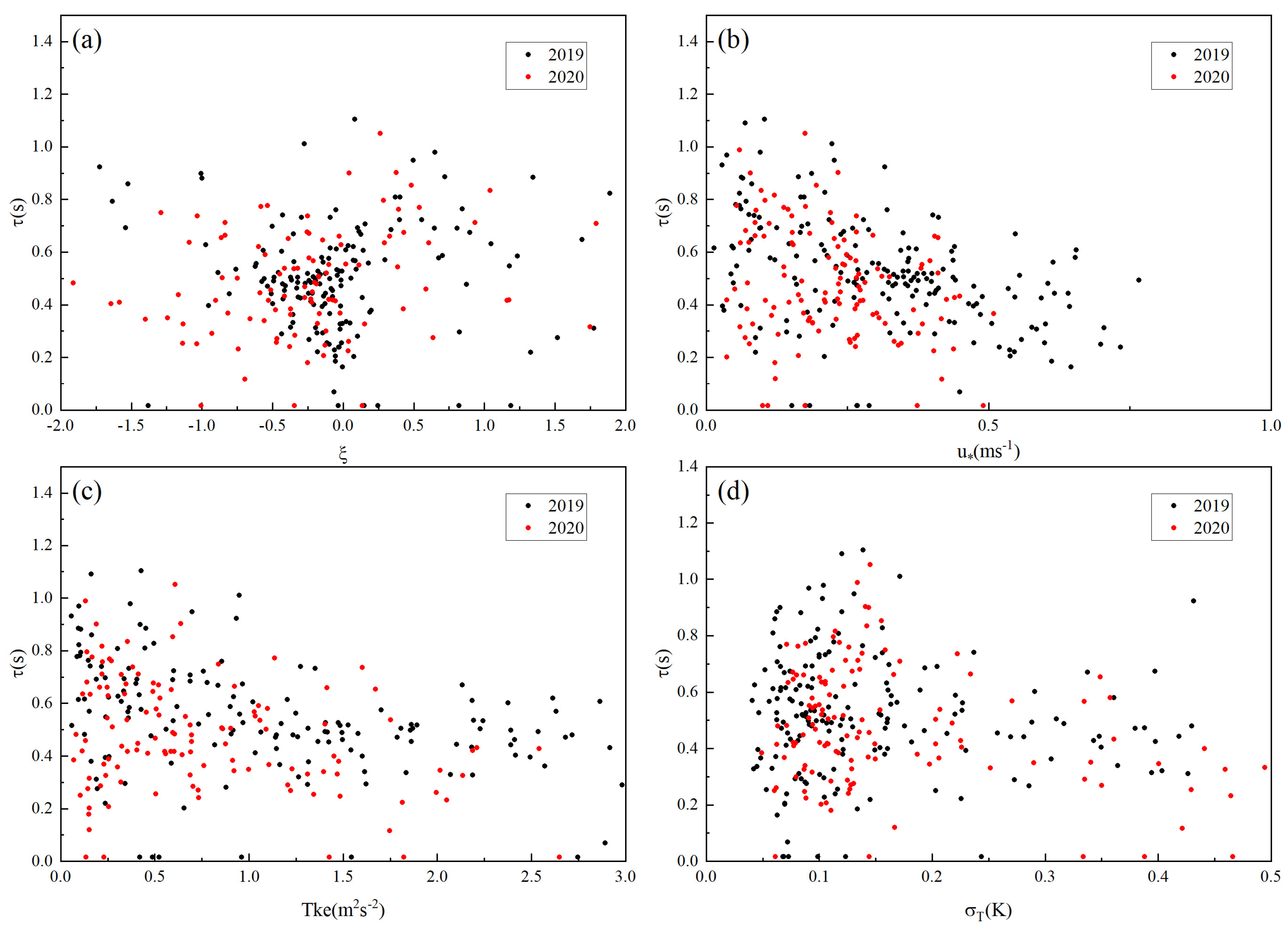
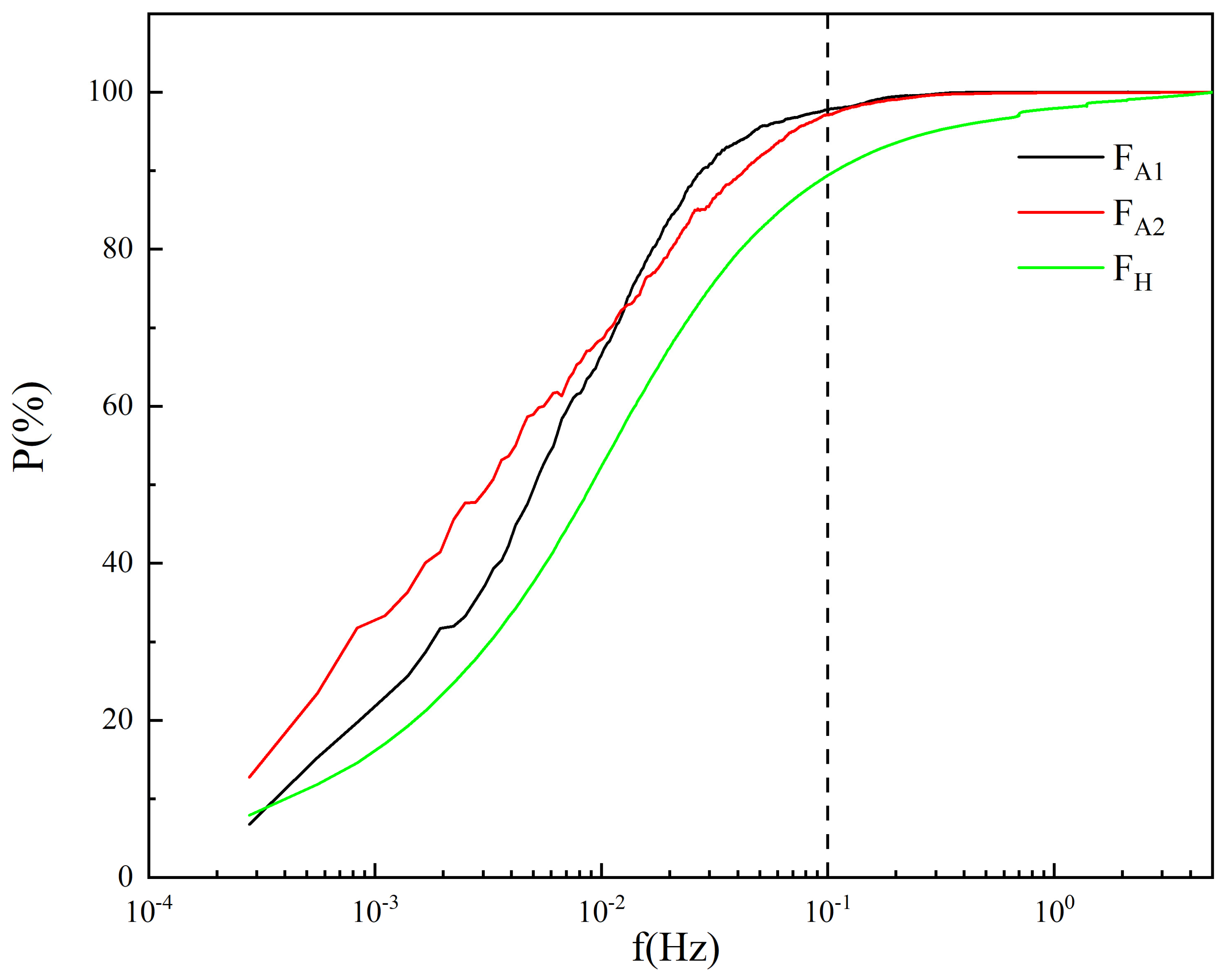
3.1. Characteristics of Aerosol Number Concentration Spectrum
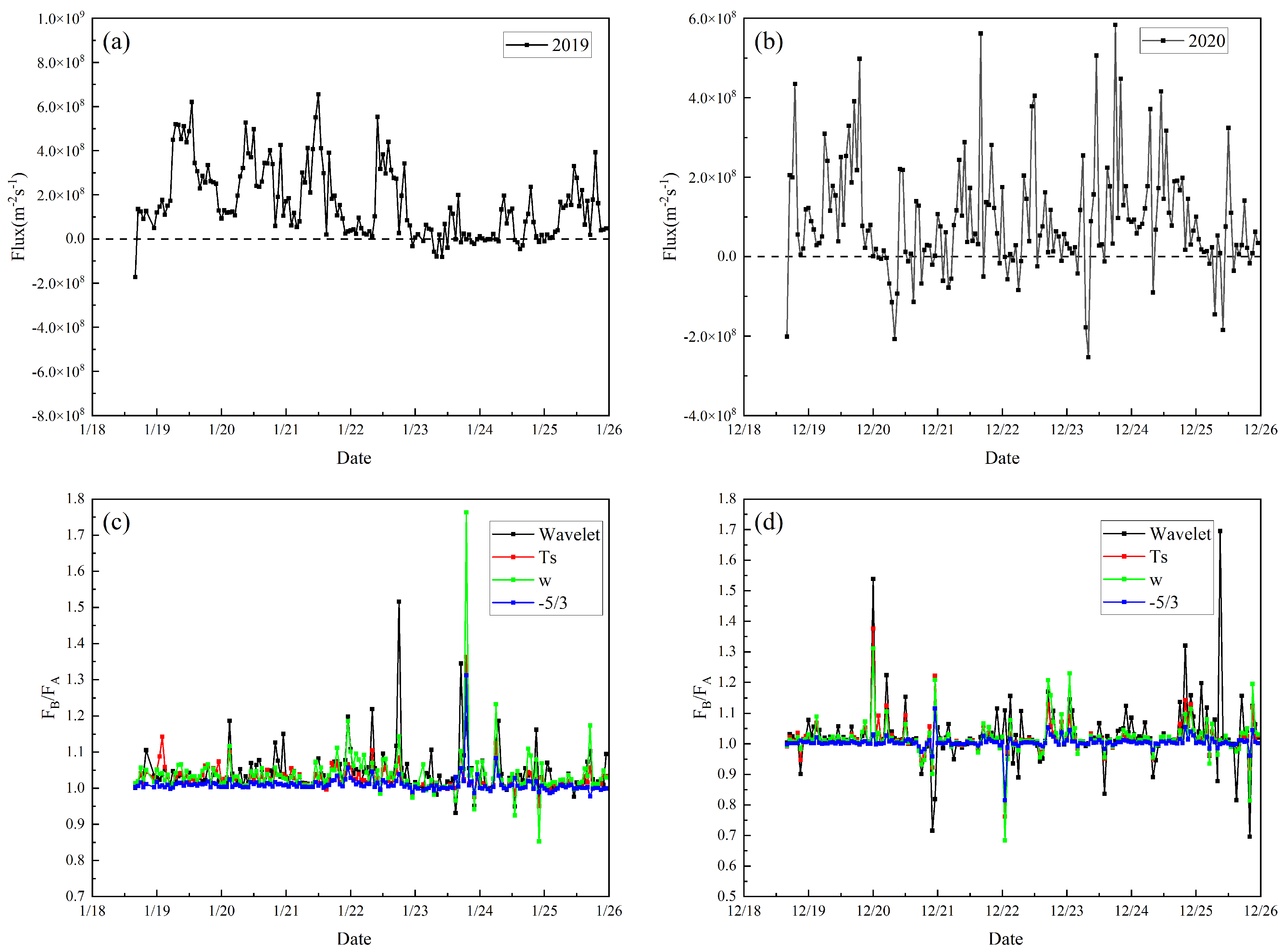
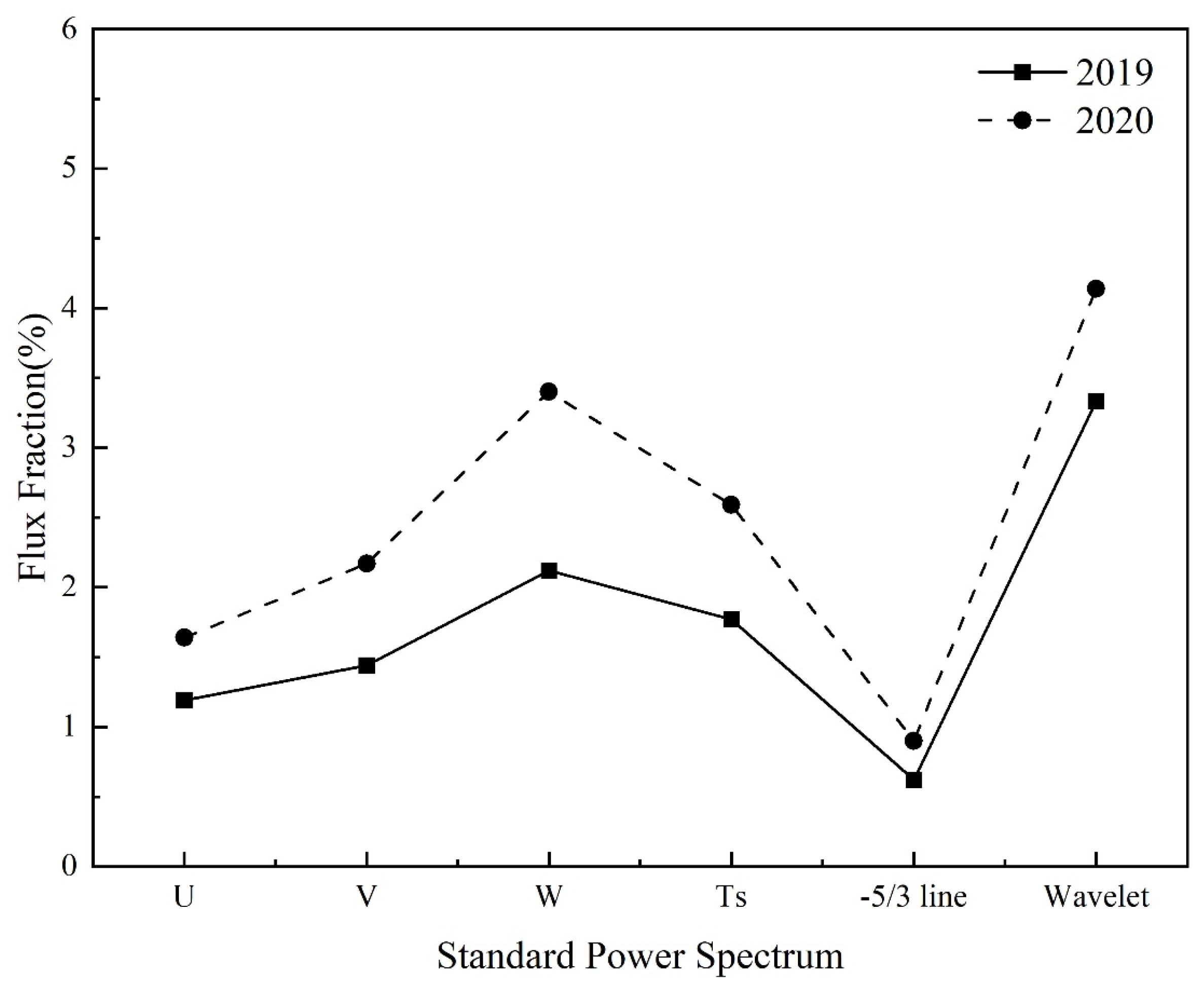
3.2. The Results of Two Correction Methods for High-Frequency Attenuation Correction and the Influence on Flux Measurement
4. Conclusions and Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, R.-J.; Zhang, Y.; Bozzetti, C.; Ho, K.-F.; Cao, J.-J.; Han, Y.; Daellenbach, K.R.; Slowik, J.G.; Platt, S.M.; Canonaco, F.; et al. High secondary aerosol contribution to particulate pollution during haze events in China. Nature 2014, 514, 218–222. [Google Scholar] [CrossRef] [PubMed]
- Mahowald, N.; Ward, D.S.; Kloster, S.; Flanner, M.G.; Heald, C.L.; Heavens, N.G.; Hess, P.G.; Lamarque, J.F.; Chuang, P.Y. Aerosol Impacts on Climate and Biogeochemistry. Annu. Rev. Environ. Resour. 2011, 36, 45–74. [Google Scholar] [CrossRef]
- Kobayashi, H.; Hayashi, M.; Shiraishi, K.; Nakura, Y.; Enomoto, T.; Miura, K.; Takahashi, H.; Igarashi, Y.; Naoe, H.; Kaneyasu, N.; et al. Development of a polarization optical particle counter capable of aerosol type classification. Atmos. Environ. 2014, 97, 486–492. [Google Scholar] [CrossRef]
- Qin, J.; Tang, W.; Yang, K.; Lu, N.; Niu, X.; Liang, S. An efficient physically based parameterization to derive surface solar irradiance based on satellite atmospheric products. J. Geophys. Res. Atmos. 2015, 120, 4975–4988. [Google Scholar] [CrossRef]
- Li, Y.; Cai, X.; Li, M.; Jiang, Z.; Tang, F.; Zhang, S.; Shui, T.; Zhu, S. Review of the Urban Carbon Flux and Energy Balance Based on the Eddy Covariance Technique. Aerosol Air Qual. Res. 2024, 24, 230245. [Google Scholar] [CrossRef]
- Yuan, R.; Luo, T.; Sun, J.; Liu, H.; Fu, Y.; Wang, Z. A new method for estimating aerosol mass flux in the urban surface layer using LAS technology. Atmos. Meas. Tech. 2016, 9, 1925–1937. [Google Scholar] [CrossRef]
- Yuan, R.; Luo, T.; Sun, J.; Zeng, Z.; Ge, C.; Fu, Y. A new method for measuring the imaginary part of the atmospheric refractive index structure parameter in the urban surface layer. Atmos. Meas. Tech. Phys. 2015, 15, 2521–2531. [Google Scholar] [CrossRef]
- Hill, R.J. Spectra of fluctuations in refractivity, temperature, humidity, and the temperature-humidity cospectrum in the inertial and dissipation ranges. Radio Sci. 1978, 13, 953–961. [Google Scholar] [CrossRef]
- Batchelor, G.K. Kolmogoroff’s theory of locally isotropic turbulence. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1947; Volume 43, pp. 533–559. [Google Scholar]
- Tiwari, S.; Srivastava, A.; Bisht, D.; Parmita, P.; Srivastava, M.K.; Attri, S. Diurnal and seasonal variations of black carbon and PM2.5 over New Delhi, India: Influence of meteorology. Atmos. Res. 2013, 125–126, 50–62. [Google Scholar] [CrossRef]
- Jokinen, T.; Kontkanen, J.; Lehtipalo, K.; Manninen, H.E.; Aalto, J.; Porcar-Castell, A.; Garmash, O.; Nieminen, T.; Ehn, M.; Kangasluoma, J.; et al. Solar eclipse demonstrating the importance of photochemistry in new particle formation. Sci. Rep. 2017, 7, srep45707. [Google Scholar] [CrossRef]
- Ahlm, L.; Krejci, R.; Nilsson, E.D.; Mårtensson, E.M.; Vogt, M.; Artaxo, P. Emission and dry deposition of accumulation mode particles in the Amazon Basin. Atmos. Meas. Tech. 2010, 10, 10237–10253. [Google Scholar] [CrossRef]
- Vogt, M.; Nilsson, E.D.; Ahlm, L.; MÕrtensson, E.M.; Johansson, C. Seasonal and diurnal cycles of 0.25–2.5 mu m aerosol fluxes over urban Stockholm, Sweden. Tellus Ser. B Chem. Phys. Meteorol. 2011, 63, 935–951. [Google Scholar] [CrossRef]
- Aslan, T.; Peltola, O.; Ibrom, A.; Nemitz, E.; Rannik, Ü.; Mammarella, I. The high-frequency response correction of eddy covariance fluxes—Part 2: An experimental approach for analysing noisy measurements of small fluxes. Atmos. Meas. Tech. 2021, 14, 5089–5106. [Google Scholar] [CrossRef]
- Massman, W. A simple method for estimating frequency response corrections for eddy covariance systems. Agric. For. Meteorol. 2000, 104, 185–198. [Google Scholar] [CrossRef]
- Ripamonti, G.; Järvi, L.; Mølgaard, B.; Hussein, T.; Nordbo, A.; Hämeri, K. The effect of local sources on aerosol particle number size distribution, concentrations and fluxes in Helsinki, Finland. Tellus B Chem. Phys. Meteorol. 2013, 65, 19786. [Google Scholar] [CrossRef]
- Horst, T.W. A simple formula for attenuation of eddy fluxes measured with first-order-response scalar sensors. Bound. Layer Meteorol. 1997, 82, 219–233. [Google Scholar] [CrossRef]
- De Ligne, A.; Heinesch, B.; Aubinet, M. New Transfer Functions for Correcting Turbulent Water Vapour Fluxes. Bound. Layer Meteorol. 2010, 137, 205–221. [Google Scholar] [CrossRef]
- Ibrom, A.; Dellwik, E.; Flyvbjerg, H.; Jensen, N.O.; Pilegaard, K. Strong low-pass filtering effects on water vapour flux measurements with closed-path eddy correlation systems. Agric. For. Meteorol. 2007, 147, 140–156. [Google Scholar] [CrossRef]
- Nordbo, A.; Katul, G. A Wavelet-Based Correction Method for Eddy-Covariance High-Frequency Losses in Scalar Concentration Measurements. Bound. Layer Meteorol. 2012, 146, 81–102. [Google Scholar] [CrossRef]
- Enroth, J.; Kangasluoma, J.; Korhonen, F.; Hering, S.; Picard, D.; Lewis, G.; Attoui, M.; Petäjä, T. On the time response determination of condensation particle counters. Aerosol Sci. Technol. 2018, 52, 778–787. [Google Scholar] [CrossRef]
- Oosterwijk, A.; Henzing, B.; Järvi, L. On the application of spectral corrections to particle flux measurements. Environ. Sci. Nano 2018, 5, 2315–2324. [Google Scholar] [CrossRef]
- Cheng, Y.; Li, Q.; Grachev, A.; Argentini, S.; Fernando, H.J.S.; Gentine, P. Power-Law Scaling of Turbulence Cospectra for the Stably Stratified Atmospheric Boundary Layer. Bound. Layer Meteorol. 2020, 177, 1–18. [Google Scholar] [CrossRef]


| Experiment No. | Time | Site | Intake Pipe | The Time Spent by the Air Sample to Go Through the Sampling Line | Reynolds Number | Flow Rate |
|---|---|---|---|---|---|---|
| 1 | 18 January 2019–27 February 2019 | On the tower, 18 m from the bottom of the tower | 2 m stainless-steel intake pipe and 1 m hose, inner diameter of 4 mm | 1.51 s | 540 | 1.5 L/min |
| 2 | 11 March 2019–1 April 2019 | 1 m from the bottom of the tower | None | 1.5 L/min | ||
| 3 | 18 December 2020–26 December 2020 | On the tower, 15 m from the bottom of the tower | 2 m stainless-steel intake pipe and 1 m hose, inner diameter of 4 mm | 1.51 s | 540 | 1.5 L/min |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Yuan, R.; Zhu, B.; Zhao, Q.; Zhu, X.; Liu, Y.; Li, Y. Characteristics of Aerosol Number Concentration Power Spectra and Their Influence on Flux Measurements. Atmosphere 2025, 16, 332. https://doi.org/10.3390/atmos16030332
Liu H, Yuan R, Zhu B, Zhao Q, Zhu X, Liu Y, Li Y. Characteristics of Aerosol Number Concentration Power Spectra and Their Influence on Flux Measurements. Atmosphere. 2025; 16(3):332. https://doi.org/10.3390/atmos16030332
Chicago/Turabian StyleLiu, Hao, Renmin Yuan, Bozheng Zhu, Qiang Zhao, Xingyu Zhu, Yuan Liu, and Yongchang Li. 2025. "Characteristics of Aerosol Number Concentration Power Spectra and Their Influence on Flux Measurements" Atmosphere 16, no. 3: 332. https://doi.org/10.3390/atmos16030332
APA StyleLiu, H., Yuan, R., Zhu, B., Zhao, Q., Zhu, X., Liu, Y., & Li, Y. (2025). Characteristics of Aerosol Number Concentration Power Spectra and Their Influence on Flux Measurements. Atmosphere, 16(3), 332. https://doi.org/10.3390/atmos16030332





