Influence of Climate and Solar Variability on Growth Rings of Araucaria angustifolia in Três Barras National Forest (Brazil)
Abstract
1. Introduction
2. Materials and Methods
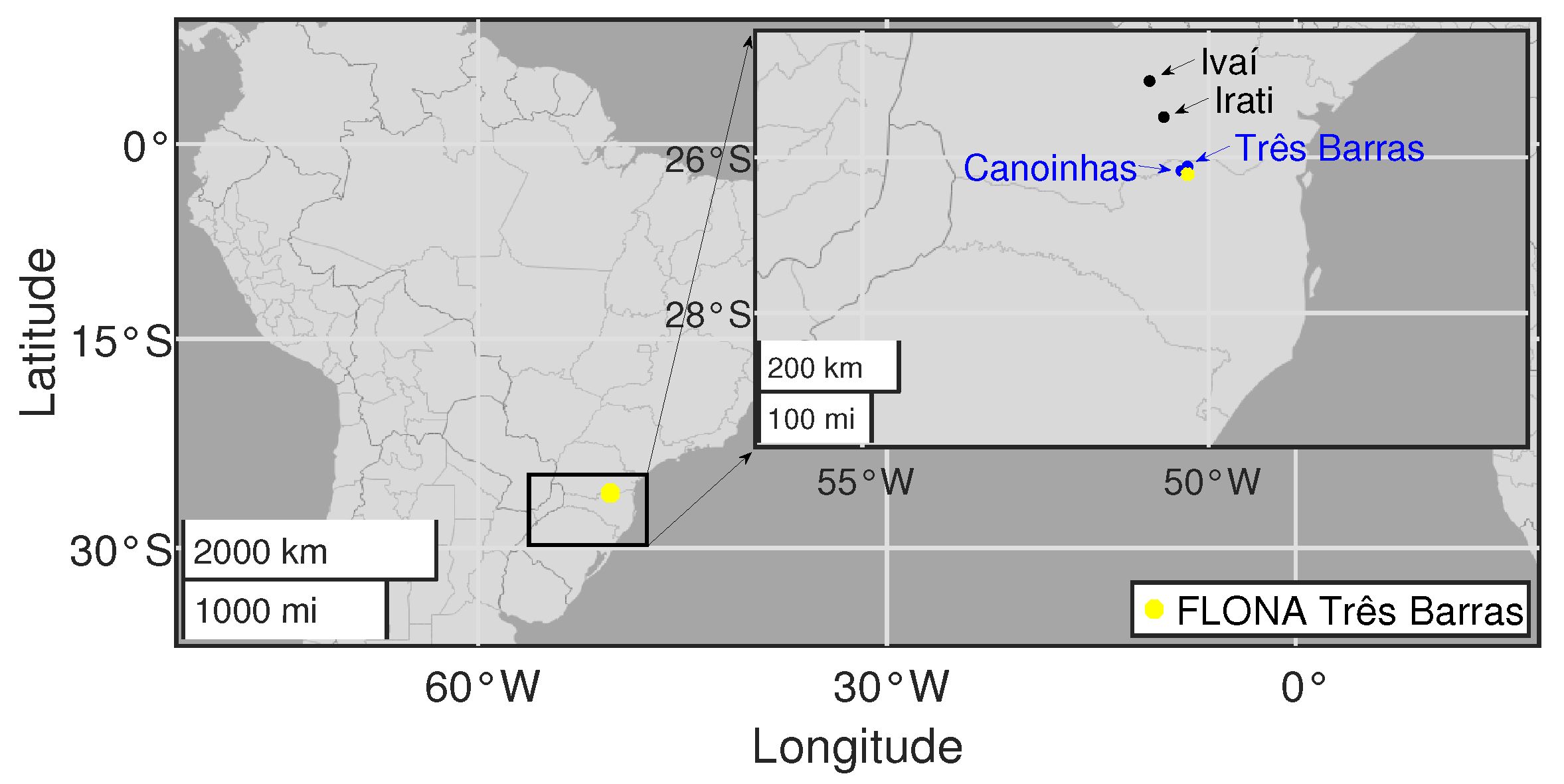
2.1. Regional Climate
2.2. Data Acquisition
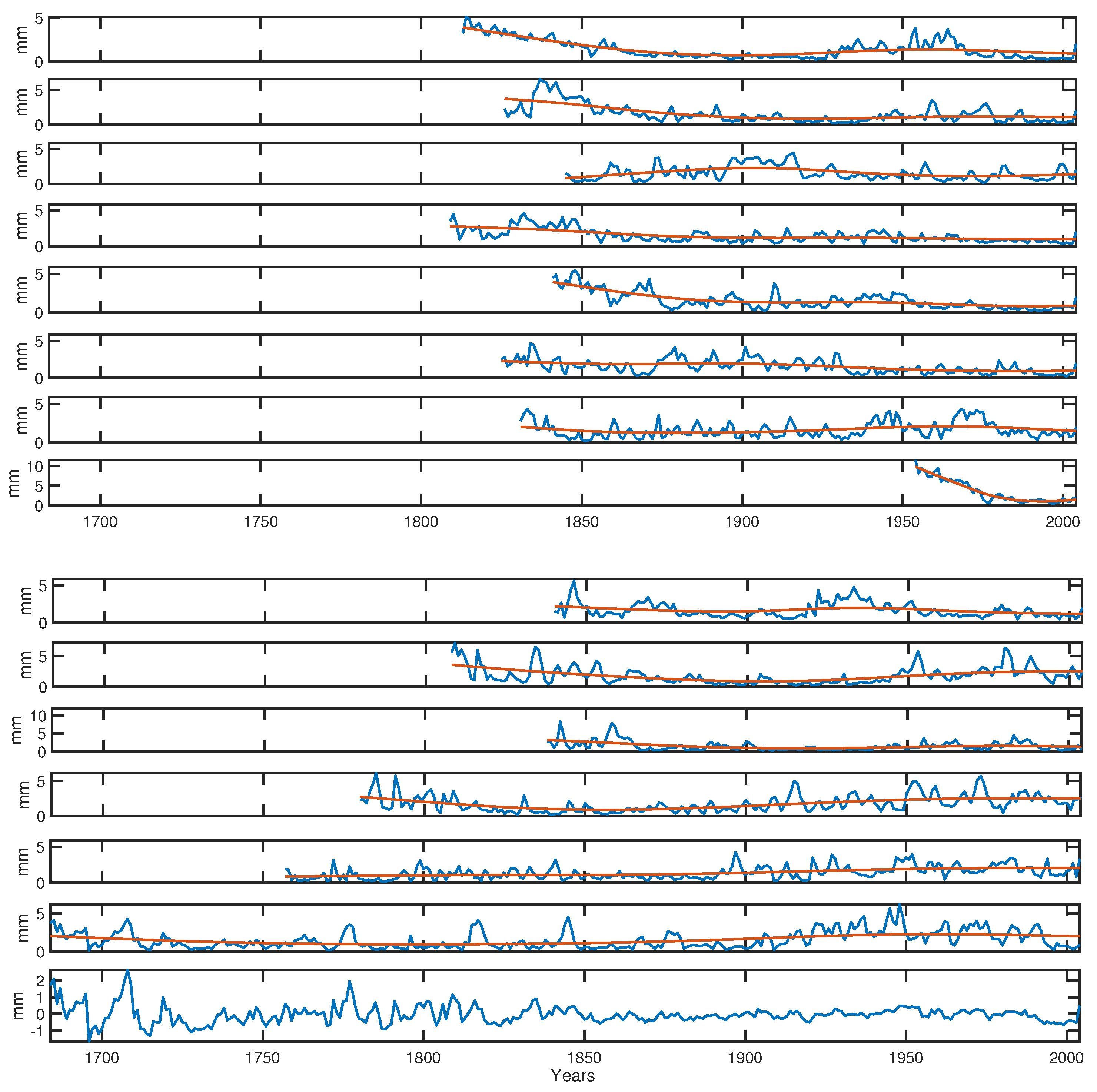
2.3. Detrending
2.4. Climatic and Geophysical Data
2.5. Continuous Wavelet Transform
3. Development of the Tree-Ring Index
4. Wavelet Analysis of Climate and Tree-Ring Relationships
5. Seasonal Correlation Analysis of Climate and Tree Growth
6. Final Remarks
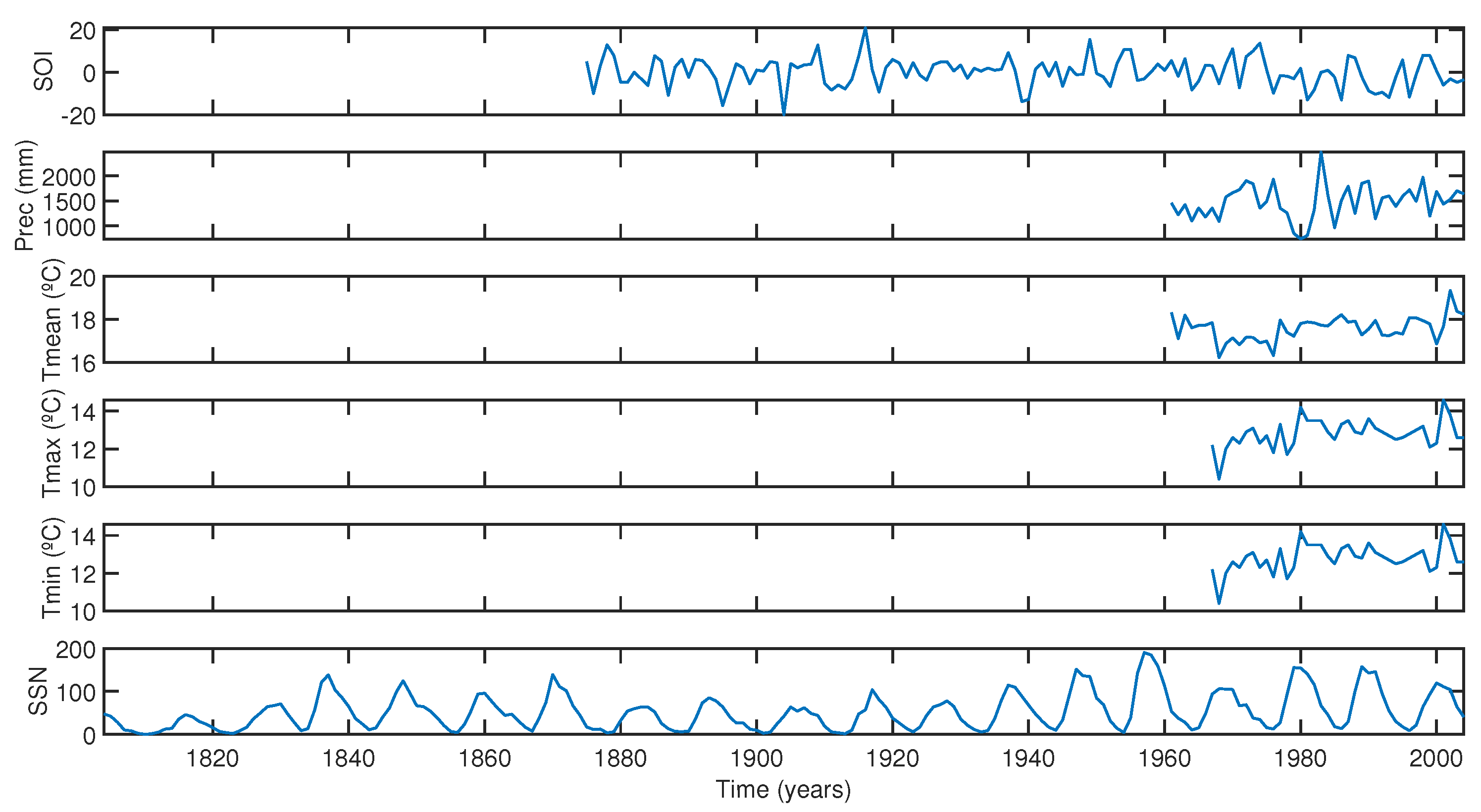
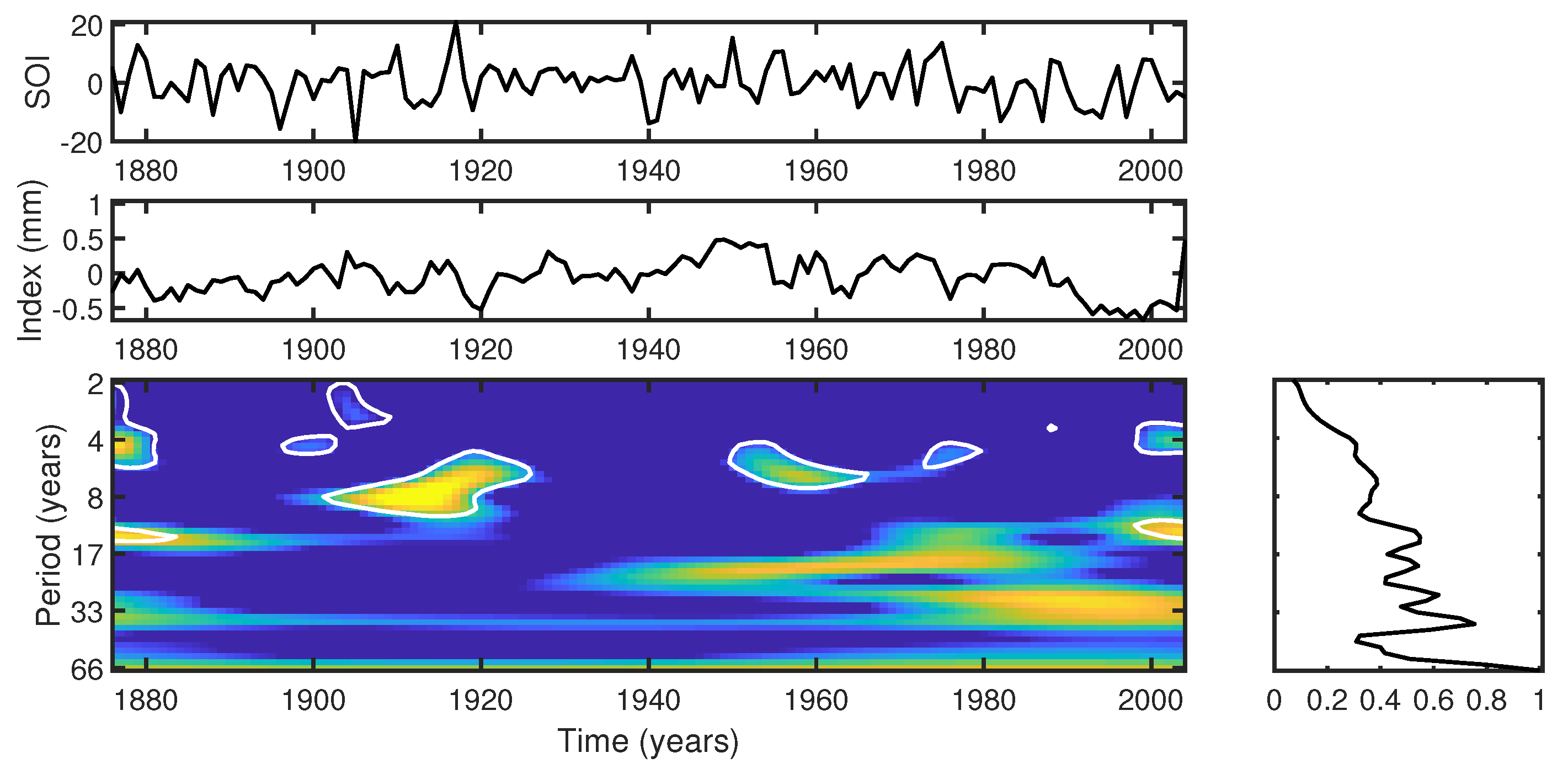
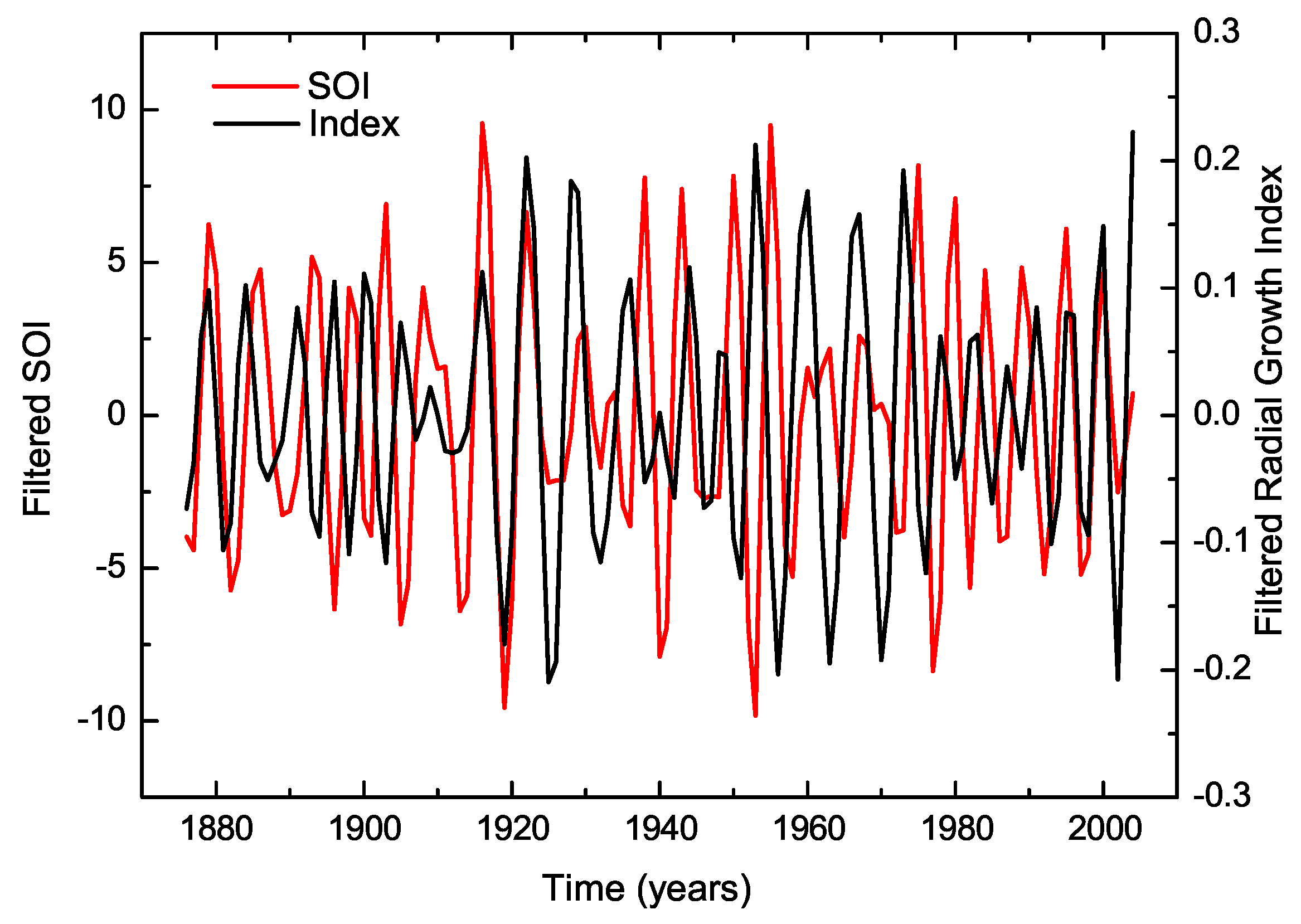
- The ENSO events exhibit a complex influence on the tree-ring index. Cross-wavelet analysis indicates significant power in the 2–8-year band during specific intervals, suggesting interdependence between the tree-ring index and the SOI. Intense El Niño events, such as those in 1982–1983 and 1997–1998, might disrupted the correlation between the index and SOI, highlighting the non-stationary response of trees to climatic fluctuations.
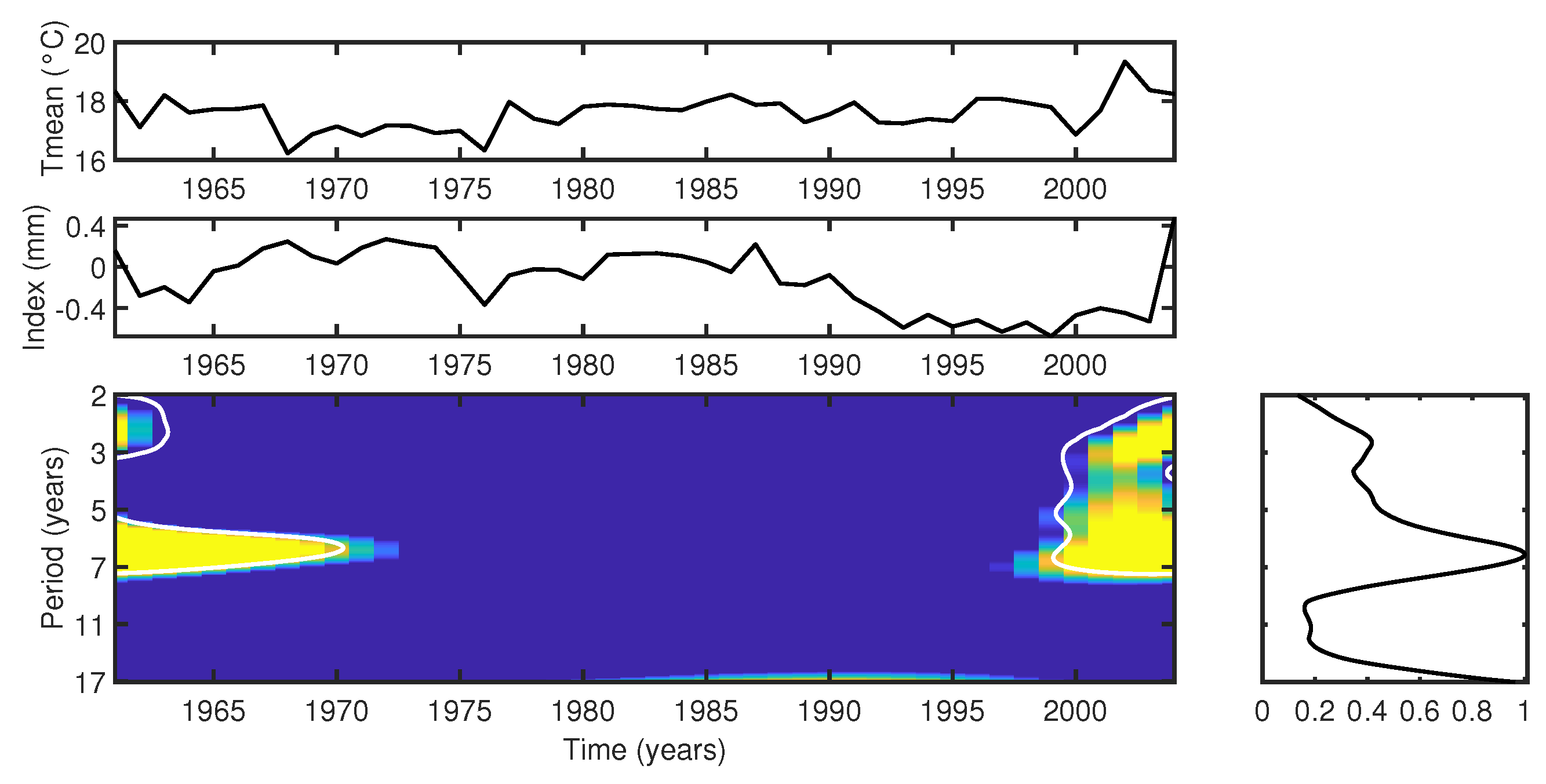
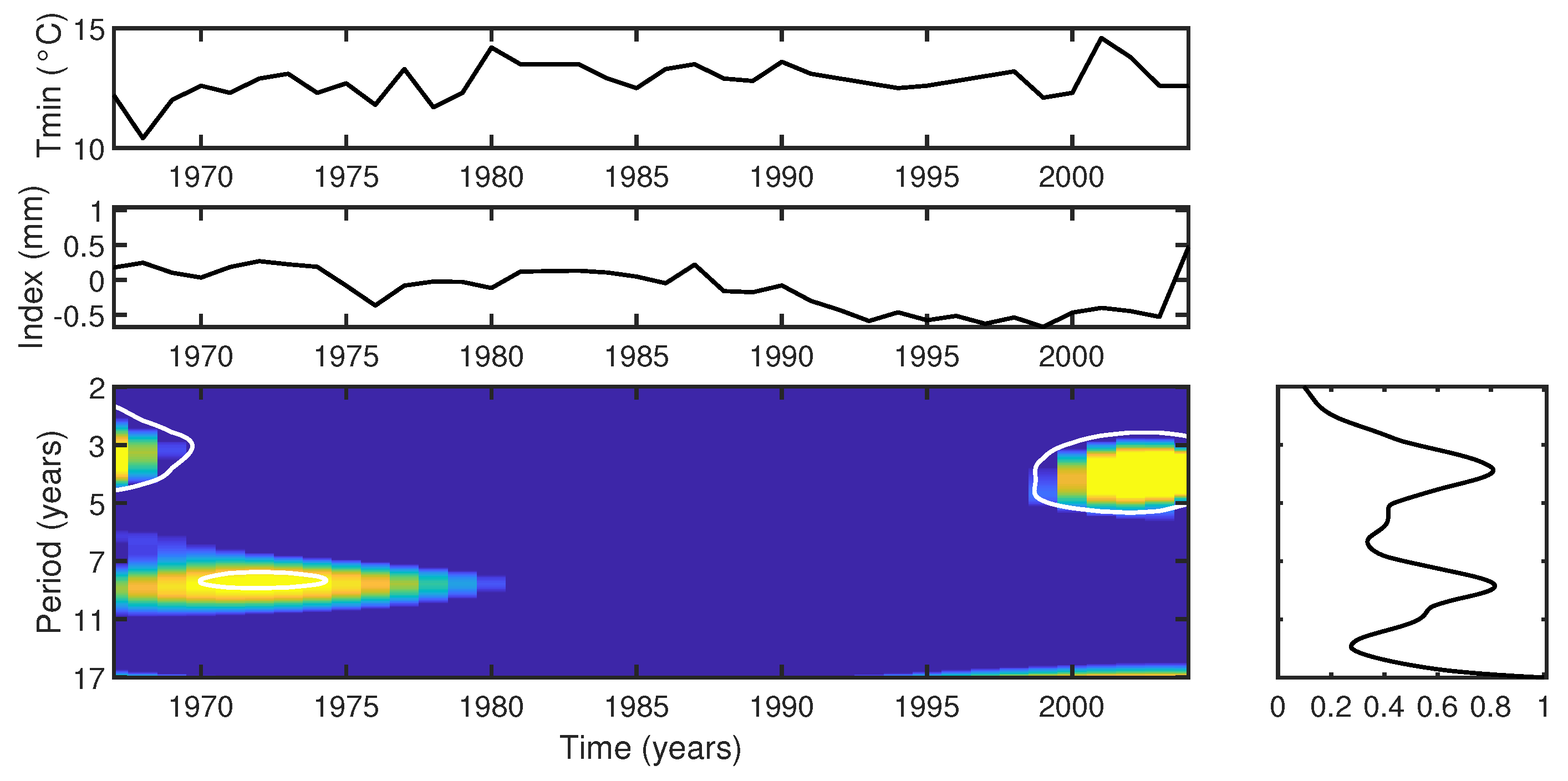
- Cross-wavelet analysis shows that the Araucaria angustifolia tree-ring index from FLONA Três Barras is highly responsive to temperature fluctuations, particularly during periods of cooler temperatures (mean of 17 °C, years 1961–1970) and warmer conditions (mean of 19 °C, post-2002). The trees demonstrated a notable sensitivity to temperature variability, with pronounced growth responses during hot summers and mild winters. However, the period of reduced growth observed between 1991 and 1999 shows no correlation with temperature changes, suggesting that other factors, such as local microclimatic variations (e.g., humidity, soil moisture, or local temperature anomalies), may have played a role in influencing tree growth during this interval.
- The analysis underscores the significant impact of precipitation on Araucaria angustifolia, particularly during drought periods (5–7-year and 3–5-year bands in 1970–1978 and 1986–1990, respectively). The trees demonstrate greater responsiveness to precipitation variability during these dry periods, emphasizing the intricate relationship between tree growth and rainfall patterns.
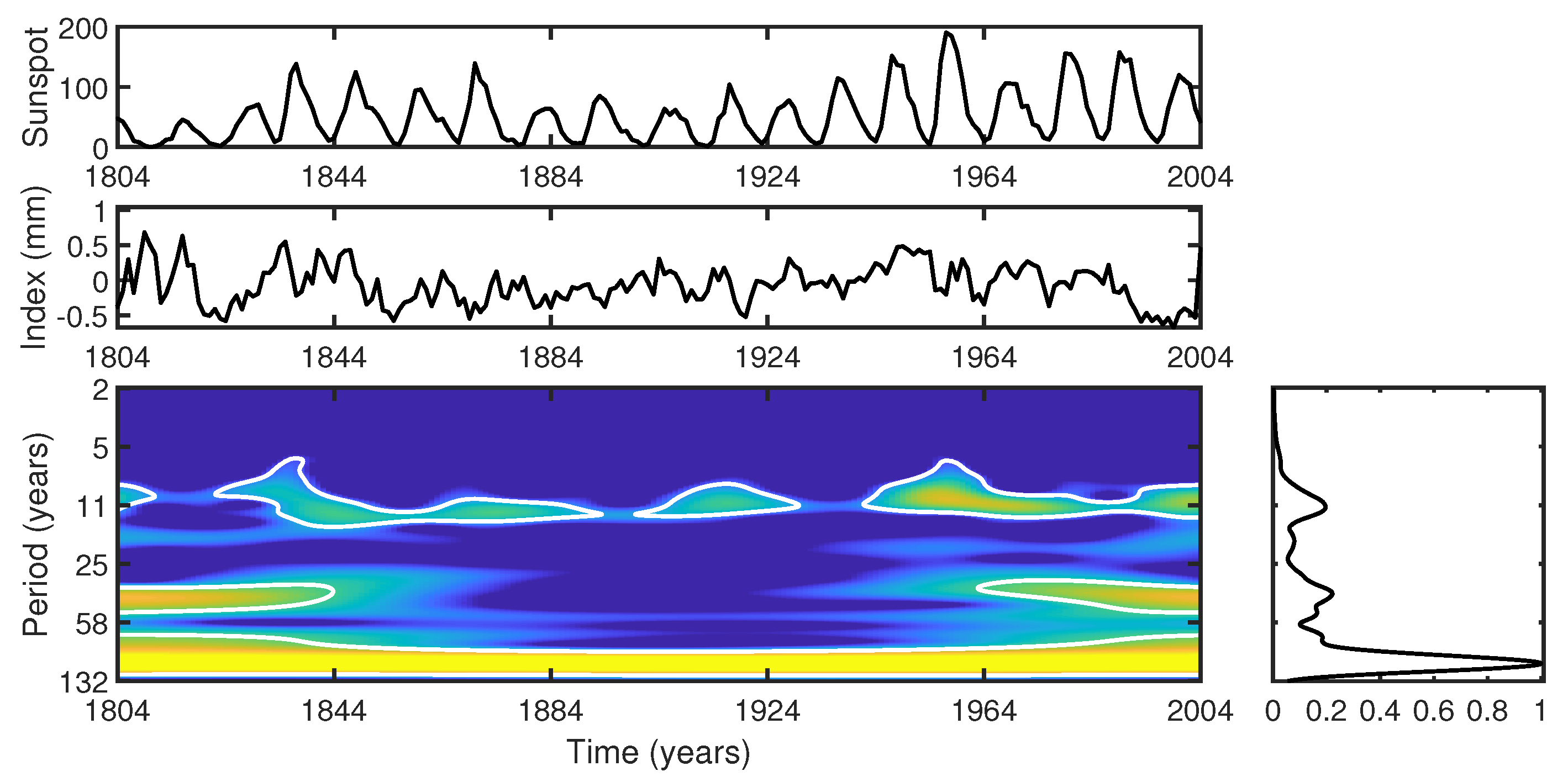
- Cross-wavelet analysis reveals a dominant periodicity of around 11 years, corresponding to the Schwabe solar cycle. Furthermore, significant cross-wavelet power in the 25–58-year band suggests an association with longer-term solar cycles such as the Hale and Gleissberg cycles, and possibly the fourth harmonic of the Suess cycle, indicating the complex interaction between solar cycles and tree growth.
- ENSO was identified as the primary climatic forcing driving tree-ring growth between 1910–1935 and 1990–2004, based on significant cross-wavelet power in the 4–8-year band. Between 1936 and 1989, other external factors influenced tree response, possibly indicating anthropogenic impacts or localized microclimate effects.
- Seasonal correlation analysis revealed specific seasonal intervals, such as 1-month, 3-month, and 6-month periods, during which temperature and precipitation significantly influenced tree growth. For example, a negative correlation was observed for a 3-month season ending in March of the previous year (, ) and a 6-month season ending in January of the previous year (, ). This seasonal perspective addresses the inherent limitations of our wavelet analysis, which relied on an annual dataset and, due to the Nyquist criterion, can only resolve periodicities greater than two years. Seasonal correlation analysis complements the wavelet approach by filling this gap and capturing sub-annual variations in climate-tree growth interactions. Furthermore, since wavelet phase analysis primarily focuses on the temporal alignment of signals, it does not capture lagged influences shorter than two years, such as the impact of climatic conditions from the previous year. As a result, this aspect was not addressed in the present study.
- Araucaria angustifolia emerges as a valuable species for studying the past climate in southern Brazil, given its highly responsive to climatic variations. Due to its endangered status, protective measures are essential not only for continued scientific inquiry into past environmental conditions but also to safeguard the livelihoods of local communities who rely on its seeds and timber for economic sustenance. Ensuring the conservation of this species is crucial for maintaining both ecological integrity and socio-economic stability in the region.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hoyt, D.V.; Schatten, K.H. The Role of the Sun in Climate Change; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Stute, M.; Clement, A.; Lohmann, G. Global climate models: Past, present, and future. Proc. Natl. Acad. Sci. USA 2001, 98, 10529–10530. [Google Scholar] [CrossRef]
- Thompson, L. Climate change: The evidence and our options. Behav. Anal. 2010, 33, 153–170. [Google Scholar] [CrossRef]
- Roe, G.; Baker, M.; Herla, F. Centennial glacier retreat as categorical evidence of regional climate change. Nat. Geosci. 2017, 10, 95–99. [Google Scholar] [CrossRef]
- Stevens-Rumann, C.S.; Kemp, K.B.; Higuera, P.E.; Harvey, B.J.; Rother, M.T.; Donato, D.C.; Morgan, P.; Veblen, T.T. Evidence for declining forest resilience to wildfires under climate change. Ecol. Lett. 2018, 21, 243–252. [Google Scholar] [CrossRef] [PubMed]
- Neukom, R.; Steiger, N.; Gómez-Navarro, J.J.; Wang, J.; Werner, J.P. No evidence for globally coherent warm and cold periods over the preindustrial Common Era. Nature 2019, 571, 550–554. [Google Scholar] [CrossRef] [PubMed]
- Dubreuil, V.; Fante, K.P.; Planchon, O.; Sant’Anna Neto, J.L. Climate change evidence in Brazil from Köppen’s climate annual types frequency. Int. J. Climatol. 2019, 39, 1446–1456. [Google Scholar] [CrossRef]
- Averchenkova, A.; Fankhauser, S.; Finnegan, J.J. The impact of strategic climate legislation: Evidence from expert interviews on the UK Climate Change Act. Clim. Policy 2021, 21, 251–263. [Google Scholar] [CrossRef]
- Nordemann, D.; Rigozo, N.; Faria, H. Solar activity and El-Niño signals observed in Brazil and Chile tree ring records. Adv. Space Res. 2005, 35, 891–896. [Google Scholar] [CrossRef]
- Rigozo, N.; Nordemann, D.; Echer, E.; Vieira, L.; Pereira de Souza Echer, M.; Prestes, A. Tree-ring width wavelet and spectral analysis of solar variability and climatic effects on a Chilean cypress during the last two and a half millennia. Clim. Past Discuss. 2005, 1, 121–135. [Google Scholar] [CrossRef]
- Rigozo, N.; Nordemann, D.; Echer, E.; Evangelista, H.; Pereira de Souza Echer, M.; Prestes, A. Solar and climate imprint differences in tree ring width from Brazil and Chile. J. Atmos. Sol.-Terr. Phys. 2007, 69, 449–458. [Google Scholar] [CrossRef]
- Rampelotto, P.H.; Rigozo, N.R.; da Rosa, M.B.; Prestes, A.; Frigo, E.; Souza Echer, M.P.; Nordemann, D.J.R. Variability of rainfall and temperature (1912–2008) parameters measured from Santa Maria (29∘41′ S, 53∘48′ W) and their connections with ENSO and solar activity. J. Atmos. Sol.-Terr. Phys. 2012, 77, 152–160. [Google Scholar] [CrossRef]
- Melvin, T.M.; Briffa, K.R. CRUST: Software for the implementation of Regional Chronology Standardisation: Part 2. Further RCS options and recommendations. Dendrochronologia 2014, 32, 343–356. [Google Scholar] [CrossRef]
- Biondi, F.; Waikul, K.K. DENDROCLIM2002: A C++ program for statistical calibration of climate signals in tree-ring chronologies. Comput. Geosci. 2004, 30, 303–311. [Google Scholar] [CrossRef]
- Jevsenak, J.; Levanič, T. dendroTools: R package for studying linear and nonlinear responses between tree-rings and daily environmental data. Dendrochronologia 2018, 48, 32–39. [Google Scholar] [CrossRef]
- Zang, C.S.; Biondi, F. treeclim: An R package for the numerical calibration of proxy-climate relationships. Ecography 2015, 38, 431–436. [Google Scholar] [CrossRef]
- Rigozo, N.R.; Viieira, L.E.A.; Echer, E.; Nordemann, D.J.R. Wavelet analysis of Solar-ENSO imprints in tree ring data from southern brazil in the last century. Clim. Chang. 2003, 60, 329–340. [Google Scholar] [CrossRef]
- Prestes, A.; Klausner, V.; Rojahn da Silva, I.; Ojeda-González, A.; Lorensi, C. Araucaria growth response to solar and climate variability in South Brazil. Ann. Geophys. 2018, 36, 717–729. [Google Scholar] [CrossRef]
- Muraja, D.; Klausner, V.; Prestes, A.; Rojahn da Silva, I. Ocean–atmosphere interaction identified in tree-ring time series from southern Brazil using cross-wavelet analysis. Theor. Appl. Climatol. 2023, 153, 1177–1189. [Google Scholar] [CrossRef]
- Kogan, F. Satellite-Observed Sensitivity of World Land Ecosystems to El Niño/La Niña. Remote Sens. Environ. 2000, 74, 445–462. [Google Scholar] [CrossRef]
- Grimm, A.M.; Ferraz, S.E.T.; Gomes, J. Precipitation anomalies in Southern Brazil associated with El Niño and La Niña events. J. Clim. 1998, 11, 2863–2880. [Google Scholar] [CrossRef]
- Stuiver, M.; Quay, P.D. Changes in Atmospheric Carbon-14 Attributed to a Variable Sun. Science 1980, 207, 11–19. [Google Scholar] [CrossRef] [PubMed]
- Rigozo, N.; Nordemann, D.; Echer, E.; Zanandrea, A.; Gonzalez, W. Solar Variability Effects Studied by Tree-Ring Data Wavelet Analysis. Adv. Space Res. 2002, 29. [Google Scholar] [CrossRef]
- Nordemann, D.J.R.; Rigozo, N.R.; Echer, E.; Vieira, L.E.A. Solar activity and El Ninõ effects on Southern Brazil Araucaria ring widths (1955–1997). In Proceedings of the International Conference on Dendrochronology, Quebec, QC, Canada, 22–27 August 2002. [Google Scholar]
- Nordemann, D.J.R.; Rigozo, N.R. Árvores Contam uma História do Sol. Sci. Am. 2003, 2, 30–37. [Google Scholar]
- Rigozo, N.; Evangelista, H.; Nordemann, D.; Echer, E.; Pereira de Souza Echer, M.; Prestes, A. The Medieval and Modern Maximum solar activity imprints in tree ring data from Chile and stable isotope records from Antarctica and Peru. J. Atmos. Sol.-Terr. Phys. 2008, 70, 1012–1024. [Google Scholar] [CrossRef]
- Prestes, A. Relação Sol-Terra Estudada Através de Anéis de Crescimento de Coníferas do Holoceno Recente e Triássico. 2009. Ph.D. Thesis, Instituto Nacional de Pesquisas Espaciais, São José dos Campos, Brazil, 2009. [Google Scholar]
- Prestes, A.; Rigozo, N.R.; Nordemann, D.J.R.; Wrasse, C.M.; Souza Echer, M.P.; Echer, E.; da Rosa, M.B.; Rampelotto, P.H. Sun-earth relationship inferred by tree growth rings in conifers from Severiano de Almeida, Southern Brazil. J. Atmos. Sol.-Terr. Phys. 2011, 73, 1587–1593. [Google Scholar] [CrossRef]
- Rigozo, N.; Lisi, C.; Filho, M.; Prestes, A.; Nordemann, D.; Pereira de Souza Echer, M.; Echer, E.; Evangelista, H.; Rigozo, V. Solar-Terrestrial Signal Record in Tree Ring Width Time Series from Brazil. Pure Appl. Geophys. 2012, 169, 2181–2191. [Google Scholar] [CrossRef]
- Li, Q.; Liu, Y.; Deng, R.; Liu, R.; Song, H.; Wang, Y.; Li, G. Combination of Tree Rings and Other Paleoclimate Proxies to Explore the East Asian Summer Monsoon and Solar Irradiance Signals: A Case Study on the North China Plain. Atmosphere 2020, 11, 1180. [Google Scholar] [CrossRef]
- Opała-Owczarek, M.; Galstyan, H.; Owczarek, P.; Sayadyan, H.; Vardanyan, T. Dendrochronological Potential of Drought-Sensitive Tree Stands in Armenia for the Hydroclimate Reconstruction of the Lesser Caucasus. Atmosphere 2021, 12, 153. [Google Scholar] [CrossRef]
- Charbonneau, P. Dynamo models of the solar cycle. Living Reviews in Solar Physics. Living Rev. Sol. Phys. 2010, 7, 3. [Google Scholar] [CrossRef]
- Hathaway, D.H. The solar cycle. Living Rev. Sol. Phys. 2015, 12, 4. [Google Scholar] [CrossRef] [PubMed]
- Solanki, S.K.; Fligge, M. Solar irradiance since 1874 revisited. Geophys. Res. Lett. 1998, 25, 341–344. [Google Scholar] [CrossRef]
- Fontana, C.; Reis-Avila, G.; Nabais, C.; Botosso, P.; Oliveira, J.M. Dendrochronology and climate in the Brazilian Atlantic Forest: Which species, where and how. Neotrop. Biol. Conserv. 2018, 13, 321–333. [Google Scholar] [CrossRef]
- Silva, D.O.; Prestes, A.; Klausner, V.; de Souza, T.G.G. Climate Influence in Dendrochronological Series of Araucaria angustifolia from Campos do Jordão, Brazil. Atmosphere 2021, 12, 957. [Google Scholar] [CrossRef]
- Oliveira, J.; Adenesky, E.F.; Quadros, K. Avaliação do crescimento do lenho de Araucaria angustifolia No Planalto Norte De Santa Catarina. Floresta 2017, 47, 155–164. [Google Scholar] [CrossRef]
- Albiero-Júnior, A.; Venegas-González, A.; Rodríguez-Catón, M.; Oliveira, J.M.; Longhi-Santos, T.; Galvão, F.; Temponi, L.G.; Botosso, P.C. Edge Effects Modify the Growth Dynamics and Climate Sensitivity of Araucaria angustifolia Trees. Tree-Ring Res. 2020, 76, 11–26. [Google Scholar] [CrossRef]
- Scipioni, M.C.; Fontana, C.; Oliveira, J.M.; Santini Junior, L.; Roig, F.A.; Tomazello-Filho, M. Effects of cold conditions on the growth rates of a subtropical conifer. Dendrochronologia 2021, 68, 125858. [Google Scholar] [CrossRef]
- das Neves Brandes, A.F.; Albuquerque, R.P.; Lisi, C.S.; de Lemos, D.N.; Nicola, L.R.M.; Melo, A.L.F.; Barros, C.F. The growth responses of Araucaria angustifolia to climate are adjusted both spatially and temporally at its northern distribution limit. For. Ecol. Manag. 2021, 487, 119024. [Google Scholar] [CrossRef]
- Scipioni, M.C.; Dobner, M., Jr.; Longhi, S.J.; Vibrans, A.C.; Schneider, P.R. The last giant Araucaria trees in southern Brazil. Sci. Agric. 2019, 76, 220–226. [Google Scholar] [CrossRef]
- Magnanini, A.; Magnanini, C. Árvores gigantescas da Terra e as Maiores Assinaladas no Brasil; CNRBMA: São Paulo, Brazil, 2002; 20p. [Google Scholar]
- Maack, R. Geografia Física do Estado do Paraná; José Olympio: Curitiba, Brazil, 1968. [Google Scholar]
- Lindmann, C.A. A Vegetação no Rio Grande do Sul; EDUSP: Belo Horizonte, Brazil, 1974. [Google Scholar]
- Castro, M.; Barbosa, A.; Pompeu, P.; Eisenlohr, P.V.; Pereira, G.d.A.; Apgaua, D.M.G.; Pires-Oliveira, J.C.; Barbosa, J.P.R.A.D.; Fontes, M.A.L.; dos Santos, R.M.; et al. Will the emblematic southern conifer Araucaria angustifolia survive to climate change in Brazil? Biodivers. Conserv. 2020, 29, 291–607. [Google Scholar] [CrossRef]
- Mundo, I.; Juñent, F.R.R.; Villalba, R.; Kitzberger, T.; Barrera, M. Araucaria araucana tree-ring chronologies in Argentina: Spatial growth variations and climate influences. Trees 2011, 26, 443–458. [Google Scholar] [CrossRef]
- Silva, D.O.; Klausner, V.; Prestes, A.; Macedo, H.G.; Aakala, T.; Silva, I.R. Principal Components Analysis: An Alternative Way for Removing Natural Growth Trends. Pure Appl. Geophys. 2021, 178, 3131–3149. [Google Scholar] [CrossRef]
- Avila, B.P.; Henzel, A.; Foesch, M.D.S.; Almeida, E.W.D.; Molina, A.; Guarino, E. Importance of Pinhao in the Conservation of Araucaria Forests and the Social Role of the Consumer Market. Floresta 2023, 53, 413–422. [Google Scholar] [CrossRef]
- Marchioro, C.A.; Santos, K.L.; Siminski, A. Present and future of the critically endangered Araucaria angustifolia due to climate change and habitat loss. Forestry 2020, 93, 401–410. [Google Scholar] [CrossRef]
- Wilson, O.J.; Mayle, F.E. A conservation assessment of Brazil’s iconic and threatened Araucaria Forest-Campos mosaic. Biol. Conserv. 2024, 296, 110650. [Google Scholar] [CrossRef]
- Behling, H.; Verissimo, N.; Bauermann, S.G.; Bordignon, S.A.; Evaldt, A.C.P. Late Holocene Vegetation History and Early Evidence of Araucaria angustifolia in Caçapava do Sul in the Lowland Region of Rio Grande do Sul State, Southern Brazil. Braz. Arch. Biol. Technol. 2016, 59, e16150264. [Google Scholar] [CrossRef]
- Rigozo, N.R.; Nordemann, D.J.R.; Echer, E.; Vieira, L.E.A. Search for Solar Periodicities in Tree-ring Widths from Concórdia (S.C., Brazil). Pure Appl. Geophys. 2004, 161, 221–233. [Google Scholar] [CrossRef]
- Gurgel, J.; Gurgel Filho, O. Evidências de raças geográficas no pinheiro-brasileiro, Araucaria angustifolia (Bert.) O. Ktze. Ciência E Cult. 1965, 17, 33–39. [Google Scholar]
- de Oliveira, J.R.; Filho, E.A.; de Quadros, K.E. Avaliação do crescimento do lenho de Araucaria angustifolia no planalto norte de Santa Catarina. Floresta 2017, 47, 155–164. [Google Scholar] [CrossRef]
- Dutra, T.L.; Stranz, A. História das Araucariaceae: A contribuição dos fósseis para o entendimento das adaptações modernas da família, com vistas a seu manejo e conservação. In Tecnologia, Diagnóstico e Planejamento Ambiental; Ronchi, L., Wöhl, O., Eds.; Unissinos: São Leopoldo, Brazil, 2003; pp. 293–351. [Google Scholar]
- Santarosa, E.; de Oliveira, J.M.; Roig, F.A.; Pillar, V.D. Crescimento Sazonal em Araucaria angustifolia: Evidências anatômicas. Rev. Bras. De Biociências 2007, 5, 618–620. [Google Scholar]
- Oliveira, J.M.; Roig, F.A.; Pillar, V.D. Climatic signals in tree-rings of Araucaria angustifolia in the southern Brazilian highlands. Austral Ecol. 2010, 35, 134–147. [Google Scholar] [CrossRef]
- Brasil, M.d.M.A. Portaria MMA n∘ 443, de 17 de dezembro de 2014, dispõem sobre as espécies da flora brasileira ameaçadas de extinção. 2014. Available online: http://cncflora.jbrj.gov.br/portal/static/pdf/portaria_mma_443_2014.pdf (accessed on 6 December 2021).
- MMA/ICMBIO. Plano de Manejo da Floresta Nacional de trêS Barras—Volume I—Diagnóstico; Technical Report; Instituto Chico Mendes de ConservaçãO da Biodiversidade: Brasília, Brazil, 2016.
- Rizzini, C.T. Tratado de fitogeografia do Brasil: Aspectos Ecológicos; Hucitec/Edusp: São Paulo, Brazil, 1979. [Google Scholar]
- da Cunha Marques, A. Planejamento da paisagem da floresta nacional de Três Barras (Três Barras—SC): Subsídios ao plano de manejo. Rev. Geogr. 2007, 1. [Google Scholar] [CrossRef]
- Stefenon, V.M.; Gailing, O.; Finkeldey, R. Genetic structure of Araucaria angustifolia (Araucariaceae) populations in Brazil: Implications for the in situ conservation of genetic resources. Plant Biol. 2007, 94, 516–525. [Google Scholar] [CrossRef]
- de Sousa, V.A.; Reeves, P.; Reilley, A.; de Aguiar, A.V.; Stefenon, V.M.; Richards, C. Genetic diversity and biogeographic determinants of population structure in Araucaria angustifolia (Bert.) O. Ktze. Conserv. Genet. 2020, 21, 217–229. [Google Scholar] [CrossRef]
- Nimer, E. Climatologia do Brasil; IBGE: Rio de Janeiro, Brazil, 1989.
- Webb, E.; Magi, B. The Ensemble Oceanic Niño Index. Int. J. Climatol. 2022, 42, 5321–5341. [Google Scholar] [CrossRef]
- Suhadi, S.; Putri, J.K.; Iskandar, I.; Supari, S.; Irfan, M.; Ariska, M.; Akhsan, H. Morlet’S Wavelet Analysis on El NiñO Southern Oscillation (Enso) and the Indian Ocean Dipole (IOD) For 84 Years: 1940–2023. Indones. Phys. Rev. 2024, 7, 552–561. [Google Scholar] [CrossRef]
- Grissino-Mayer, H. Evaluating Crossdating Accuracy: A Manual and Tutorial for the Computer Program COFECHA. Tree-Ring Res. 2001, 57, 205–221. [Google Scholar]
- Wigley, T.M.L.; Briffa, K.R.; Jones, P.D. On the Average Value of Correlated Time Series, with Applications in Dendroclimatology and Hydrometeorology. J. Appl. Meteorol. Climatol. 1984, 23, 201–213. [Google Scholar] [CrossRef]
- Helama, S.; Lindholm, M.; Timonen, M.; Eronen, M. Detection of climate signal in dendrochronological data analysis: A comparison of tree-ring standardization methods. Theor. Appl. Climatol. 2004, 79, 239–254. [Google Scholar] [CrossRef]
- Fowler, A.M. Variance Stabilization Revisited: A Case For Analysis Based On Data Pooling. Tree-Ring Res. 2009, 65, 129–145. [Google Scholar] [CrossRef]
- Cook, E.; Kairiukstis, L. Methods of Dendrochronology—Applications in the Environmental Sciences; Springer Netherlands: Dordrecht, The Netherlands, 1990. [Google Scholar]
- Fritts, H.C. Tree Rings and Climate; The University of Arizona Press: Tucson, AZ, USA, 1976. [Google Scholar]
- Shiyatov, S.G.; Mazepa, V.S. Some New Approaches in the Consideration of More Reliable Dendroclimatological Series and in the Analysis of Cycle Components; Methods of Dendrochronology; Kairiukstis, L., Cook, E.R., Eds.; International Institute for Applied Systems Analysis: Laxenburg, Austria; Polish Academy of Sciences-System Research Institute: Warsaw, Poland, 1987. [Google Scholar]
- Conover, W. Practical Nonparametric Statistics, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1980; p. 493. [Google Scholar]
- Silva Muraja, D.O.; Klausner, V.; Prestes, A.; Aakala, T.; Macedo, H.G.; Rojahn da Silva, I. Exploring the Centennial-Scale Climate History of Southern Brazil with Ocotea porosa (Nees & Mart.) Barroso Tree-Rings. Atmosphere 2023, 14, 1463. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Percival, D.B.; Walden, A.T. Wavelet Methods for Time Series Analysis; Cambridge Series in Statistical and Probabilistic Mathematics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
- Schweingruber, F.H. Tree Rings: Basics and Applications of Dendrochronology; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Wilmking, M.; Maaten-Theunissen, M.; Maaten, E.; Scharnweber, T.; Buras, A.; Biermann, C.; Gurskaya, M.; Hallinger, M.; Lange, J.; Shetti, R.; et al. Global assessment of relationships between climate and tree growth. Glob. Chang. Biol. 2020, 26, 3212–3220. [Google Scholar] [CrossRef] [PubMed]
- Meko, D.M.; Touchan, R.; Anchukaitis, K.J. Seascorr: A MATLAB program for identifying the seasonal climate signal in an annual tree-ring time series. Comput. Geosci. 2011, 37, 1234–1241. [Google Scholar] [CrossRef]
- Pereira de Souza Echer, M.; Echer, E.; Nordemann, D.; Rigozo, N.; Prestes, A. Wavelet analysis of a centennial (1895–1994) southern Brazil rainfall series (Pelotas, 31∘46′19′′ S 52∘20′33′′ W). Clim. Chang. 2008, 87, 489–497. [Google Scholar] [CrossRef]
- Miyahara, H.; Yokoyama, Y.; Yamaguchi, Y.T. Influence of the Schwabe/Hale solar cycles on climate change during the Maunder Minimum. Proc. Int. Astron. Union 2010, 264, 427–433. [Google Scholar] [CrossRef]
- Raspopov, O.M.; Shumilov, O.; Kasatkina, E.A.; Turunen, E.; Lindholm, M. 35-year Climatic Bruckner Cycle - Solar Control of Climate Variability? In Proceedings of the The Solar Cycle and Terrestrial Climate, Solar and Space Weather, Tenerife, Spain, 25–29 September 2000; Wilson, A., Ed.; ESA Special Publication: Paris, France, 2000; Volume 463, p. 517. [Google Scholar]
- Raspopov, O.; Dergachev, V.; Shumilov, O.; Kolstrom, T.; Lindholm, M.; Merilainen, J.; Eggertsson, O.; Vasiliev, S.S.; Kuzmin, A.; Yu Kirtsidely, I.; et al. Dendrochonological evidence of long-term variations in solar activity and climate. In International Conference Tree Rrings and People–Abstracts; Kaennel, D.M., Bräker, O.U., Eds.; Swiss Federal Research Institute WSL: Davos Dorf, Switzerland, 2001; pp. 22–26. [Google Scholar]
- Dai, A.; Wigley, T.M.L. Global Patterns of ENSO-induced Precipitation. Geophys. Res. Lett. 2000, 27, 1283–1286. [Google Scholar] [CrossRef]
- Kurths, J.; Spiering, C.; Muller-Stoll, W.; Striegler, U. Search for solar periodicities in Miocene tree ring widths. Terra Nova 1993, 5, 359–363. [Google Scholar] [CrossRef]
- Damon, P.E.; Eastoe, C.J.; Hughes, M.K.; Kalin, R.M.; Long, A.; Peristykh, A.N. Secular Variation of Δ14C During the Medieval Solar Maximum: A Progress Report. Radiocarbon 1997, 40, 343–350. [Google Scholar] [CrossRef]




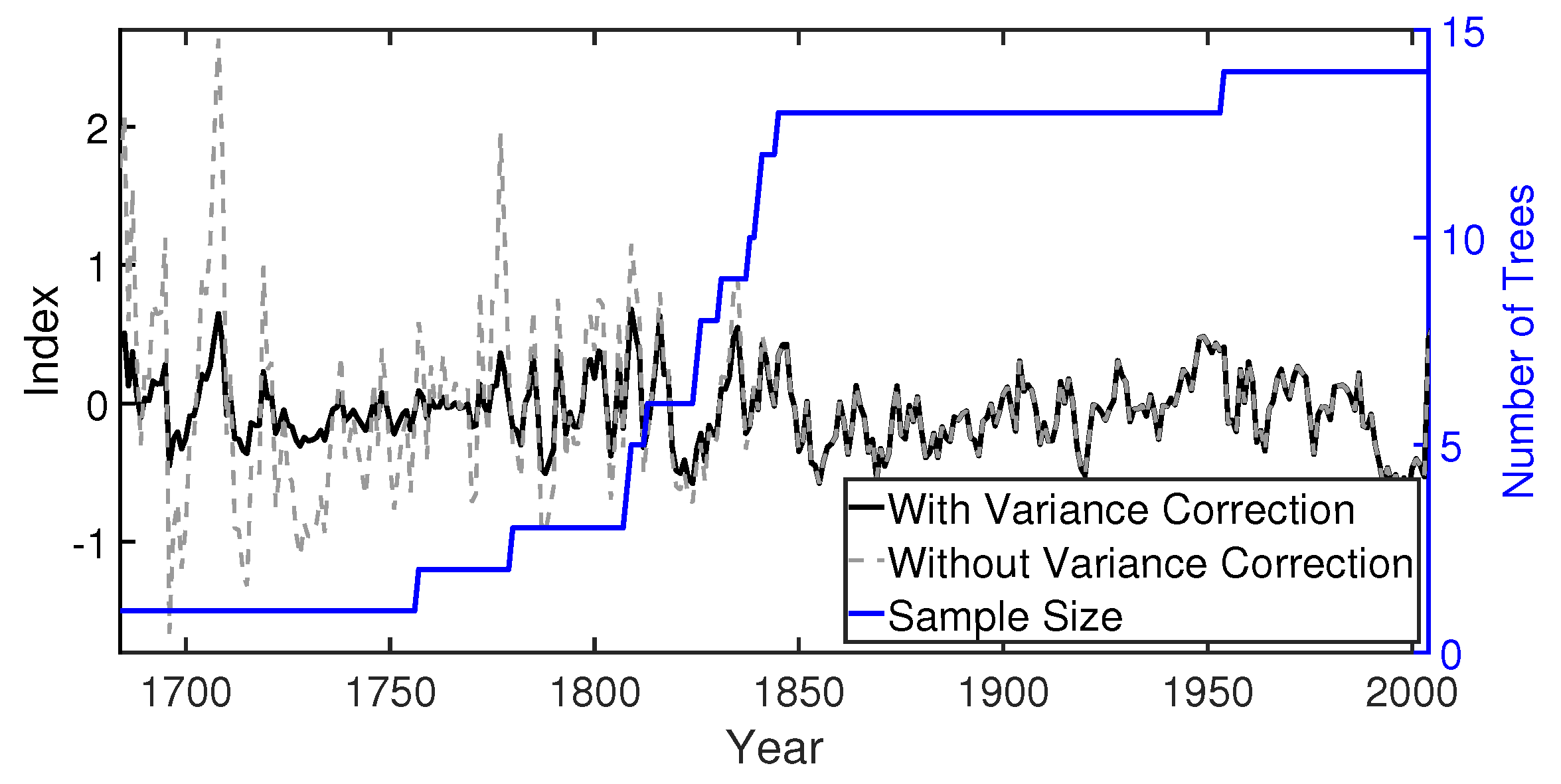
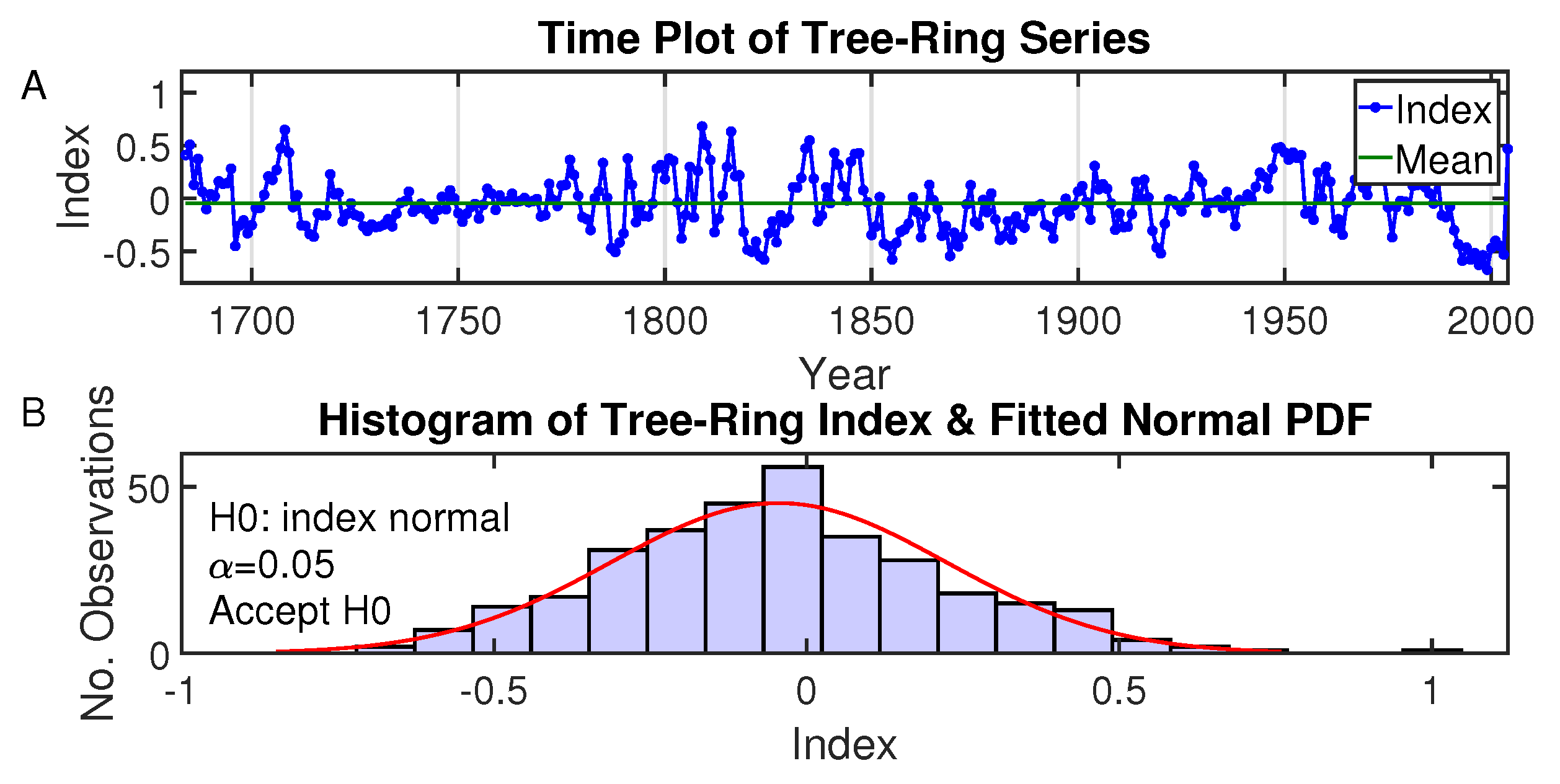




| First Year of Expressed Population Signal (EPS) > 0.85 | Number of Individual Trees (t) Needed for EPS > 0.85 | Series Intercorrelation | Subsample Signal Strength (SSS) | Average Mean Sensitivity |
|---|---|---|---|---|
| 1804 | 5 | 0.55 | 0.64–0.70 | 0.70 |
| Parameter | Period | r | p-Value | |
|---|---|---|---|---|
| SOI | 1875–2004 | 0.09 | 0.008 | 0.2733 |
| Precipitation | 1961–2004 | −0.018 | 0.000 | 0.9194 |
| Mean Temperature | 1961–2004 | −0.146 | 0.021 | 0.6185 |
| Maximum Temperature | 1967–2004 | −0.040 | 0.002 | 0.8732 |
| Minimum Temperature | 1967–2004 | −0.043 | 0.002 | 0.8322 |
| Sunspots | 1804–2004 | 0.002 | 0.000 | 0.9817 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muraja, D.O.S.; Klausner, V.; Prestes, A.; da Silva, A.C.; Lemes, C.L. Influence of Climate and Solar Variability on Growth Rings of Araucaria angustifolia in Três Barras National Forest (Brazil). Atmosphere 2025, 16, 287. https://doi.org/10.3390/atmos16030287
Muraja DOS, Klausner V, Prestes A, da Silva AC, Lemes CL. Influence of Climate and Solar Variability on Growth Rings of Araucaria angustifolia in Três Barras National Forest (Brazil). Atmosphere. 2025; 16(3):287. https://doi.org/10.3390/atmos16030287
Chicago/Turabian StyleMuraja, Daniela Oliveira Silva, Virginia Klausner, Alan Prestes, Aline Conceição da Silva, and Cecília Leite Lemes. 2025. "Influence of Climate and Solar Variability on Growth Rings of Araucaria angustifolia in Três Barras National Forest (Brazil)" Atmosphere 16, no. 3: 287. https://doi.org/10.3390/atmos16030287
APA StyleMuraja, D. O. S., Klausner, V., Prestes, A., da Silva, A. C., & Lemes, C. L. (2025). Influence of Climate and Solar Variability on Growth Rings of Araucaria angustifolia in Três Barras National Forest (Brazil). Atmosphere, 16(3), 287. https://doi.org/10.3390/atmos16030287









