The Fluid Ionosphere

Abstract

In this review paper, the equations of motion describing the fluid dynamics of the ionosphere are constructed step by step, so that any master or post-graduate student may get familiar with the general theory of the “traditional” approach to Ionospheric Physics, in which chemicals forming the Earth’s upper atmosphere are represented as fluids in mutual interaction. The hypotheses on which the smooth-field fluid representation is based are discussed in terms of microscopic dynamics of the gas particles; this discussion is oriented to prepare the reader for the post-fluid approaches to the physics of turbulence. The fluid-dynamical picture of the ionosphere is the most classical and conceptually simple one, and this makes it extremely widespread in terms of theoretical models and applications. The advantages and achievements of this theory are highlighted, its limits are discussed, and perspectives to go beyond it sketched.

1. Introduction

The aim of this review is to present the general differential equations describing the Earth’s ionosphere system as composed of a certain number of classical fluids interacting one with the others in a mechanical, thermodynamical and chemical way. Each of these fluids represents a component of the ionosphere (ions, free electrons and neutrals). Mechanical interactions lead to energy and momentum exchanges. Thermodynamical interactions yield thermal exchanges of energy. Finally, the presence of chemical reactions allows for transformation of one fluid into another one via production and loss processes. Last but not least, elecromagnetic fields are generated by and influence the dynamics of all those chemical species, many of which are electrically charged. The name we give to this system is generically ionospheric local medium (LIM), because its properties may depend on the position $\overrightarrow{r}$ and on time t. Here, the equations of evolution of the LIM are constructed step by step in great detail, taking into account all the aforementioned aspects (mechanical, thermodynamical, electrodynamic and chemical) within a classical fluid approximation; through the concept of fluid parcel, the dynamics is introduced, keeping a macroscopic classical point of view that does need suitable hypotheses of Statistical Mechanics, but does not stem from a particular microscopic dynamics and calculations on it. Great attention is paid to carefully explaining what all these approximations mean and what their implications are.

The great advantage of using fluid dynamics to describe the LIM is that it allows us to use all the well-known analytical and numeric machinery already constructed and widely used for neutral fluids, e.g., in hydrodynamics, oceanography and atmospheric circulation modeling. That machinery is the use of partial differential equations (PDEs) on well-defined space-time domains, with suitable initial and boundary conditions needed for the different regions of the Earth’s ionosphere. Using the fluid approach, a wide literature of physics-based ionospheric models was created; see, for example, [1,2,3,4].

The popularity of the fluid-dynamical picture of the LIM is also due to its very intuitive approach; even if the microscopic interactions among the particles forming a medium are critical to let it be treatable as a fluid, the rationale of writing its fluid PDEs does not invoke directly any knowledge of that microscopic physics, making the fluid approach the most understandable and straightforward to introduce.

The review is organized as follows.

Section 2 is devoted to the rigorous definition of the system at hand and to the explanation of the approximations used.

In Section 3, the equations of motion are written down fully, including mass, momentum and internal energy balance for each constituent, plus Maxwell Equations for electromagnetic fields. Also, constitutive hypotheses are presented, to make the system closed mathematically. The dynamical system is formed by coupled PDEs plus constitutive hypotheses as constraints.

Section 4 uses the results obtained in Section 3 to develop some examples and applications to concrete ionospheric phenomenology. In particular, one treats the LIM as a gaseous conductor, and writes down its electrological relationships.

Finally, Section 5 underlines the limits of the fluid description of the LIM, already sketched when the hypotheses are needed to consider it as a fluid in Section 2. Then, some further developments are traced, most of all in terms of what happens when the conditions for fluid approximation are removed, then introducing ideas for post-fluid formalism [5,6,7,8].

2. The System

The system of interest here is the Earth’s upper atmosphere, considered above the minimum height at which the ionization due to solar radiation or cosmic rays is so important for affecting the propagation of electromagnetic waves [9]; this might appear a technology-centered definition, but actually, this “threshold height” coincides with the height at which the atmospheric medium is active from an electromagnetic point of view, which is a rather intrinsic physical concept. All in all, our reasoning holds from approximately 60 km height up to the magnetopause of the Earth, in many different declinations [10]. Actually, some authors use “ionosphere” only to refer to the electrically charged chemicals, i.e., ions and free electrons. Yet, as the equations of motion of these charged species do involve neutrals, and as the equations of neutrals can be expressed formally as those of the charged species, suitably putting their electric charge to zero, we are considering them as part of our system.

The reference frame used here is mainly the one co-rotating with the solid Earth, referred to as Solid Earth Reference Frame (SERF). Sometimes, it will be of use to introduce another auxiliary reference frame, namely the Neutral Wind Reference Frame (NeWReF); see below. Last but not least, the unit system used will always be the MKSA system.

The system of interest is neither a closed nor an isolated one [11]; it interacts mechanically and radiatively with what lies below it (lower atmosphere, lithosphere and hydrosphere) and with the space environment surrounding the Earth (i.e., the solar wind, the solar radiation and cosmic rays). The system also exchanges matter with what is below it and above it.

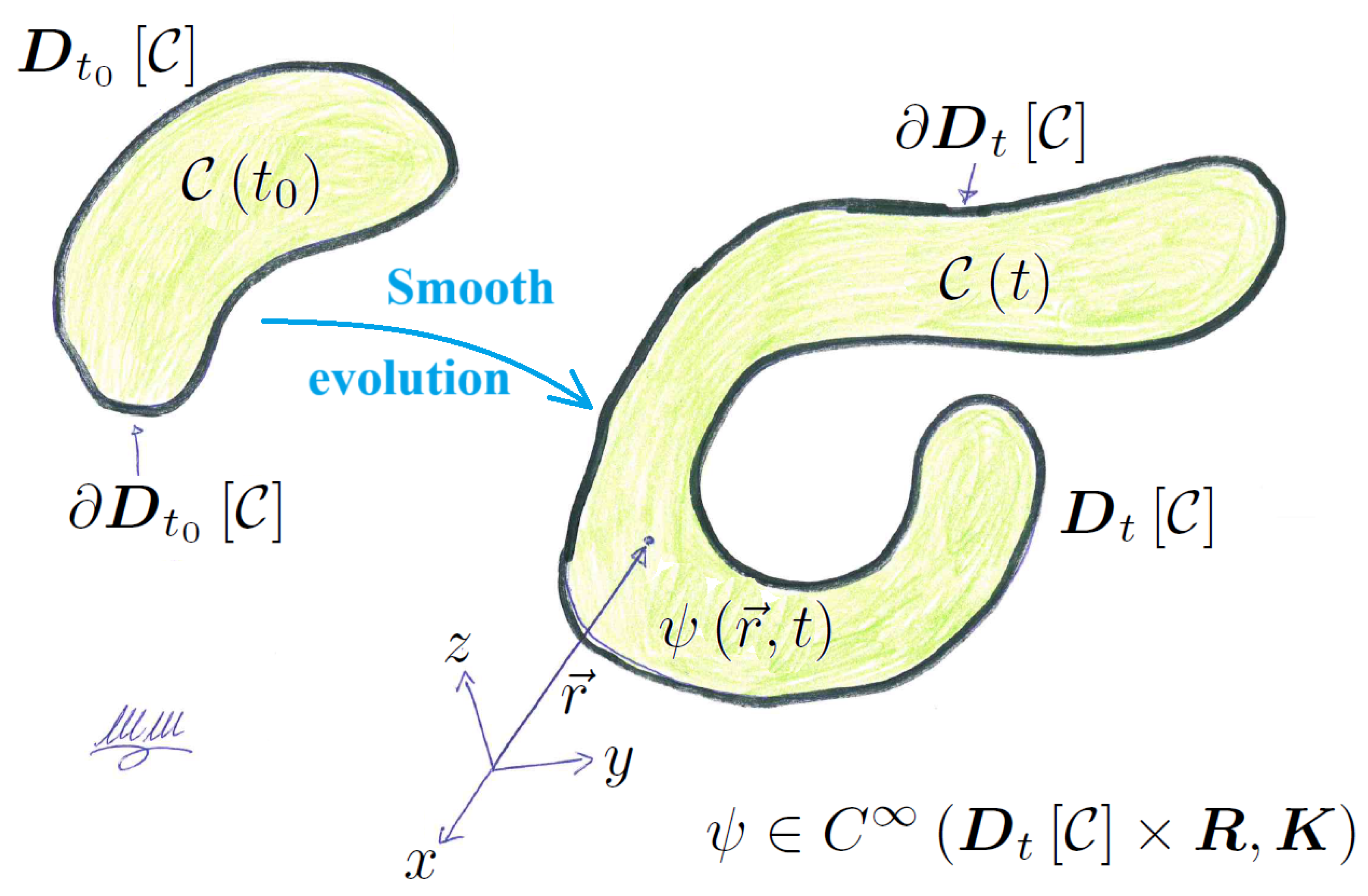
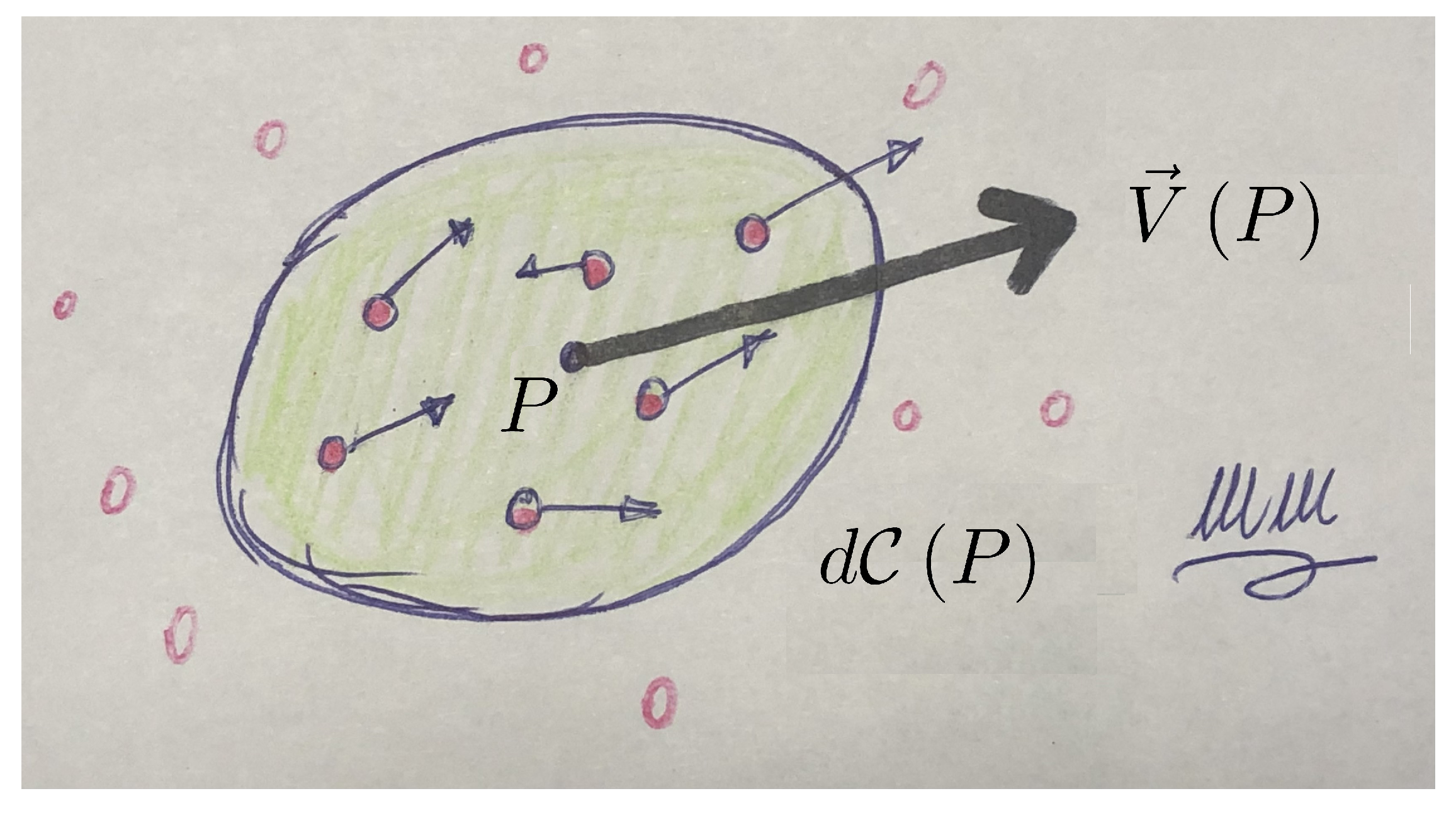
2.1. Smooth and Deterministic: The Continua

After decades of experiments in different fields, and a deep and sometimes dividing debate, between the beginning of the XIX century and the beginning of the XX century, scientists largely agreed on the fact that the world is made of very tiny systems, such as molecules, atoms, electrons, and all elementary particles, which render matter granular. However, for a couple of centuries at that time, they had already developed a picture of macroscopic material systems as continua, i.e., extended distributions of matter occupying finite portions of the physical space and experiencing and applying forces all over their volume and surface. Since the early discoveries of Fluid Mechanics and their application to both liquids and gases, by the end of the XVIII century [12], the Earth’s atmosphere could be well considered a continuum; the discovery of the ionosphere by itself took place in 1901 thanks to Marconi’s trans-oceanic electromagnetic transmission (even if a conducting layer in the upper atmosphere had been postulated by Gauss in 1839) [13], so one may state that the continuum conception of the LIM was a natural consequence of the discovery of this “upper region” of the Earth’s atmosphere [14].

From the invention of calculus, physicists had given a precise mathematical meaning to the Latin proverb Natura non facit saltus, taken by Leibniz as a manifesto for modelling physical systems; any physical quantity should have a smooth dependence on the variables it is a function of, namely, this should be a $C^{\infty }$-dependence. Not only should physical quantities be continuous functions of each other, but also differentiable, possibly an infinite number of times, which is the definition of “mathematical smoothness”. This “philosophy of non-roughness” applies to the description of continua, stating that if a macroscopic continuum $\mathcal{C}$ occupies a volume ${\mathit{D}}_t\left[\mathcal{C}\right]$ at a certain time t, any positional quantity $\psi \left(\overrightarrow{r},t\right)$ describing its state (e.g., mass density, velocity, pressure…) must be a smooth field allover ${\mathit{D}}_t\left[\mathcal{C}\right]$:

$$\psi \in C^{\infty }\left({\mathit{D}}_t\left[\mathcal{C}\right]\times \mathit{R},\mathit{K}\right),$$

(1)

where the factor “$\times \mathit{R}$” encodes the time dependence of $\psi$ and $\mathit{K}$ the mathematical set of values of $\psi \left(\overrightarrow{r},t\right)$ (numbers, vectors, tensors…). In Figure 1, the assessment (1) is illustrated. A greenish continuum $\mathcal{C}$ evolves from an initial configuration $\mathcal{C}\left(t_0\right)$ to a later one $\mathcal{C}\left(t\right)$ through a supposed smooth evolution; this means that any local quantity $\psi$ describing it undergoes precisely the condition (1). Actually, considering the border of the sets $\mathit{D}\left[\mathcal{C}\right]$, the region where the local proxies of the continuum stop being defined, or may be understood to go from a finite value to zero “within no distance”, one should replace (1) with something more precise like $\psi \in C^{\infty }\left(\left({\mathit{D}}_t\left[\mathcal{C}\right]\setminus \partial {\mathit{D}}_t\left[\mathcal{C}\right]\right)\times \mathit{R},\mathit{K}\right)$ (i.e., excluding the border of the medium domain; this does not, however, lighten the request (1) in terms of physical hypotheses).

Despite its high requests on the mathematical description of matter reality, this picture has been able to give very satisfactory theories, such as hydrodynamics, magneto-hydrodynamics, elasticity theory and many more [15]. Note that the picture satisfying (1) is also a deterministic picture, as the smooth time-behavior of $\psi$ excludes noise from its time evolution, which is another very strong requirement; the LIM is indeed a system prone to several different descriptions, among which the fluid picture is only one [16].

Even if the continuous picture of macroscopic systems is very beautiful, at a certain point the granular nature of matter was experimentally proved, and in order to reconcile the latter with the smooth picture of macroscopic bodies, some reasoning had to be introduced, namely the so called continuous limit of pointlike particle systems. The fluid dynamics (FD) of the ionosphere is one important product of this “ideology”, which has an elegant and effective rationale, but relies on precise and not-very-universal properties of the microscopic systems at hand.

The central concept of the continuous limit construction is considering “small” portions of the continuum $d\mathcal{C}$, referred to as parcels, and makes use of the following reasoning (the term “small” has to be specified later). In such a $d\mathcal{C}$, there exist $\mathcal{N}\left(d\mathcal{C}\right)$ elementary components of the macroscopic matter system, each of which is moving with a certain velocity. In general, these $\mathcal{N}\left(d\mathcal{C}\right)$ components may or may not have all the same chemical nature, hence the same mass; the local representation of the neighborhood $d\mathcal{C}$ within the continuum is obtained considering the center of mass P of those $\mathcal{N}\left(d\mathcal{C}\right)$ components, to which the velocity of the center of mass of the $\mathcal{N}\left(d\mathcal{C}\right)$ particles is attributed as $\overrightarrow{V}\left(P\right)$. The local representation of the continuum at P is constructed starting by saying that the parcel of continuum $d\mathcal{C}\left(P\right)$ moves with velocity $\overrightarrow{V}\left(P\right)$. Figure 2 represents an illustration of this idea. Recalling the definition of center of mass, we may say that the point P is attributed the mass-average velocity of the $\mathcal{N}\left(d\mathcal{C}\left(P\right)\right)$ particles within $d\mathcal{C}\left(P\right)$, i.e., the total linear momentum of the matter in $d\mathcal{C}\left(P\right)$.

The bridge between the micro-physics of particles and macro-physics of continua was traced by Statistical Mechanics, in which the macroscopic appearance of the world is conceived as the statistical sum of all the microscopic, fluctuating contributions of particles. Boltzmann’s Kinetic Theory paved the way for a quantitative study of those cumulative effects of what the micro-components are doing; this makes it possible to recover the local variables $\psi$ in (1) as suitable momenta of the statistical distributions of the $\mathcal{N}\left(d\mathcal{C}\left(P\right)\right)$ particles in $d\mathcal{C}\left(P\right)$ [17]. This is how mass density, bulk velocity, pressure, tension… are defined in FD. This sounds quite intuitive, as we humans simply accept that our senses, and our classical instruments, simply sense the world of elementary particles “defocussing” their tiny details, and saving only a coarse-grained, average picture of it. In this reasoning, when one looks at the $\mathcal{N}\left(d\mathcal{C}\left(P\right)\right)$ particles within the parcel $d\mathcal{C}\left(P\right)$ of center of mass P, the position $\overrightarrow{r}$ mentioned in the FD fields $\psi \left(\overrightarrow{r},t\right)$ is the position vector of P. In what follows, $\overrightarrow{r}$ and P are used with the same meaning.

All in all, the macroscopic picture $\psi$ would be obtained via a “statistical” method:

$$\psi \left(P,t\right)={〈{\psi }_{\mathrm{micro}}〉}_{d\mathcal{C}\left(P\right),t},$$

(2)

where ${\psi }_{\mathrm{micro}}$ is some physical quantity depending on the single particle variables, and ${〈\dots 〉}_{d\mathcal{C}\left(P\right),t}$ a sign of suitable statistical averaging (whatever this may mean at this early point) performed within $d\mathcal{C}\left(P\right)$ at time t. In order to rely on a statistical procedure as (2), one first needs an important ingredient to the very existence of the $\psi$s; the number $\mathcal{N}\left(d\mathcal{C}\left(P\right)\right)$ has to be so huge as to point towards the thermodynamic limit:

$$\mathcal{N}\left(d\mathcal{C}\left(P\right)\right)=O\left(N_A\right).$$

(3)

This is the first tough requirement to go from particle physics to FD, which had become a necessity once molecules, atoms and all their tinier fellows were discovered. In any statistical theory, due to the Central Limit Theorem [18], there must be enough particles forming the system to be able to neglect stochastic fluctuations, which is precisely what one needs to do in order for $\psi$ to be a deterministic (hence, time-smooth) process. Note: The condition (3), which may sound definitely sensible considering a small glass of water to contain $N_A$s of ${\mathrm{H}}_2\mathrm{O}$ molecules, is not at all obvious when one would like to represent the physics of galaxies (made of “few” solar systems) or even a finite portion of very dilute space plasmas (made of “few” p and $e^{-}$) with FD, in which the constituents are all but $N_A$s of bodies. In those cases, the theory of small thermodynamic systems, large fluctuations and extreme events have to be invoked [19].

Once we have defined the continuum quantities $\psi$ as non-fluctuating fields on ${\mathit{D}}_t\left[\mathcal{C}\right]$, one has to have them smooth, as prescribed by (1). This means that, if one has two “nearby” points P and $P^{\prime }$ within ${\mathit{D}}_t\left[\mathcal{C}\right]$ separated by some “small” displacement $\delta \overrightarrow{r}$, as in Figure 3, one has to be able to calculate the non-fluctuating value $\psi \left(P,t\right)$ as $\psi \left(P,t\right)={〈{\psi }_{\mathrm{micro}}〉}_{d\mathcal{C}\left(P\right),t}$, the non-fluctuating value $\psi \left(P^{\prime },t\right)={〈{\psi }_{\mathrm{micro}}〉}_{d\mathcal{C}\left(P^{\prime }\right),t}$, and then find the incremental limit between them with respect to the $P-P^{\prime }=\delta \overrightarrow{r}$ distance to exist:

$${\displaystyle \underset{\left|\delta \overrightarrow{r}\right|\to 0}{lim}}{\displaystyle \frac{∥\psi \left(P,t\right)-\psi \left(P^{\prime },t\right)∥}{\left|\delta \overrightarrow{r}\right|}}<+\infty \forall \delta \overrightarrow{r}.$$

(4)

Equally, there must also exist the limit

$${\displaystyle \underset{\delta t\to 0}{lim}}{\displaystyle \frac{∥\psi \left(P,t+\delta t\right)-\psi \left(P,t\right)∥}{\delta t}}<+\infty$$

(5)

defining the instantaneous rate of change with time of $\psi \left(P,t\right)={〈{\psi }_{\mathrm{micro}}〉}_{d\mathcal{C}\left(P\right),t}$. Actually, the two requirements (4) and (5) demand for differentiability of $\psi$ in space and time, while the requirement (1) is much stronger because it means $\psi$ has infinite space and time derivatives; clearly, (1) implies both (4) and (5). More cleanly, one could replace the two requirements (4) and (5), obtaining the entire (1) by assessing

$$\exists m,n\in \mathit{N}/\left\{\begin{array}{cc}\hfill & ∥\psi \left(P,t\right)-\psi \left(P^{\prime },t\right)∥=O\left({\left|\delta \overrightarrow{r}\right|}^m\right),\hfill \\ \\ \hfill & ∥\psi \left(P,t+\delta t\right)-\psi \left(P,t\right)∥=O\left(\delta t^n\right):\hfill \end{array}\right.$$

(6)

The differences between $\psi$ at two (macroscopically) nearby points or at two nearby times must scale to zero as a positive integer powers of the distance or of the time lapse considered. Clearly, this (6) rules out any turbulent regime of classical fluids [20]. In (4), (5) and (6), the symbol $∥\dots ∥$ refers to a length in the set of the values of $\psi \left(P,t\right)$, for instance, the absolute value for real numbers, or Pitagora Theorem norm for three-dimensional vectors.

The construction of the continuum representation of a macroscopic system of matter is all based on the definitions (2) satisfying the conditions (6), starting with the definition of a velocity field $\overrightarrow{V}\left(P,t\right)$ as described before and sketched in Figure 2, and a mass density field $\rho \left(P,t\right)$, defined for the matter in $d\mathcal{C}\left(P\right)$ as the ratio ${\displaystyle \frac{M\left(d\mathcal{C}\left(P\right)\right)}{d\mathcal{V}}}$, where $M\left(d\mathcal{C}\left(P\right)\right)$ is the total mass of particles forming $d\mathcal{C}\left(P\right)$, and $d\mathcal{V}$ the parcel volume. Defining these $\rho \left(P,t\right)$ and $\overrightarrow{V}\left(P,t\right)$ helps us explain how “small” the “parcel” must be taken around P; reference is made to the idea of macroscopic infinitesimal portion [21], for which one starts to ideally shrink the volume in $\mathcal{C}$ around P and applies the definitions to smaller and smaller volumes $d\mathcal{V}$. At a certain size of $d\mathcal{V}$, one stops seeing $\rho \left(P,t\right)$ and $\overrightarrow{V}\left(P,t\right)$ fluctuating, while if one shrinks too much, fluctuations re-appear. At the beginning of this “plateau” of the $\psi$ values with decreasing $d\mathcal{V}$, one stops including in the parcel regions of the continuum in different local conditions; when fluctuations re-appear at too small values of $d\mathcal{V}$, the number $\mathcal{N}\left(d\mathcal{C}\left(P\right)\right)$ does not satisfy the condition (3) anymore, and the granularity of matter is not appreciated in terms of fluctuations.

Concluding this rapid introduction to continua, which is the necessary foreword to FD, we refer again to Figure 2; the set of particles in $d\mathcal{C}\left(P\right)$ have their $3\mathcal{N}\left(d\mathcal{C}\left(P\right)\right)$ degrees of freedom, three of which have been taken into account considering the position of P and the velocity $\overrightarrow{V}\left(P\right)$. These are the center of mass variables [22]. What about the other $3\left(\mathcal{N}\left(d\mathcal{C}\left(P\right)\right)-1\right)$ degrees of freedom, namely the variables relative to P, e.g., the difference between the position of each of the $\mathcal{N}\left(d\mathcal{C}\left(P\right)\right)$ particles of $d\mathcal{C}\left(P\right)$ and that of P, and their canonically conjugated momenta? Treating such a huge number of relative variables is necessary to completely describe the phase space of the $\mathcal{N}\left(d\mathcal{C}\left(P\right)\right)$ particles in the parcel, but although it is sensible to use the per se deterministic variables $\left(\overrightarrow{r}\left(P\right),\overrightarrow{p}\left(P\right)\right)$ for the center of mass P of the parcel, where $\overrightarrow{p}\left(P\right)=M\left(d\mathcal{C}\left(P\right)\right)\overrightarrow{V}\left(P\right)$ represents the total momentum of $d\mathcal{C}\left(P\right)$, the $3\left(\mathcal{N}\left(d\mathcal{C}\left(P\right)\right)-1\right)=O\left(N_A\right)$ relative variables of the parcel will be treated in a statistical way. That is, while $\overrightarrow{V}\left(P\right)$ is already a field $\psi \left(\overrightarrow{r},t\right)$, like those involved in Equations (1) and (2), the positions ${\overrightarrow{q}}_i^{\mathrm{rel}}\stackrel{\mathrm{def}}{=}{\overrightarrow{r}}_i-\overrightarrow{r}\left(P\right)$ of the $i=1,\dots$, $\mathcal{N}\left(d\mathcal{C}\left(P\right)\right)$ particles in the parcel relative to P and their conjugate momenta become the subject of the $d\mathcal{C}\left(P\right)$-local statistical mechanics. As the dynamics in this relative phase space

$${\Gamma }_{\mathrm{rel}}=\left\{\left({\overrightarrow{q}}_1^{\mathrm{rel}},{\overrightarrow{p}}_1^{\mathrm{rel}}\right),\dots ,\left({\overrightarrow{q}}_{\mathcal{N}\left(d\mathcal{C}\left(P\right)\right)-1}^{\mathrm{rel}},{\overrightarrow{p}}_{\mathcal{N}\left(d\mathcal{C}\left(P\right)\right)-1}^{\mathrm{rel}}\right)\right\}$$

is treated statistically, because $dim{\Gamma }_{\mathrm{rel}}=O\left(N_A\right)$, the statistical distributions on ${\Gamma }_{\mathrm{rel}}$ become the completion of the description of the exactly $\mathcal{N}\left(d\mathcal{C}\left(P\right)\right)$ particles in $d\mathcal{C}\left(P\right)$.

On theoretical grounds, describing statistically the relative variables within the parcel may consist of the dynamics of the Gibbs distribution in ${\Gamma }_{\mathrm{rel}}$; see [17,23]. In practice, one always assumes the particles in $d\mathcal{C}\left(P\right)$ to be represented by some kinetic theory that will cut the BBGKY hierarchy in ${\Gamma }_{\mathrm{rel}}$ to one-particle distributions. Moreover, as the only well-established statistical mechanics is equilibrium thermodynamics, the $d\mathcal{C}\left(P\right)$-local kinetic theory will converge to the definition of local thermodynamic variables attributed to the point $P\in {\mathit{D}}_t\left[\mathcal{C}\right]$ of position vector $\overrightarrow{r}$, as new smooth fields $\psi \left(\overrightarrow{r},t\right)$. All in all, the $3\mathcal{N}\left(d\mathcal{C}\left(P\right)\right)$ microscopic degrees of freedom of the particles in the parcel will turn into the three of the center of mass plus an equilibrium thermodynamics for the $3\left(\mathcal{N}\left(d\mathcal{C}\left(P\right)\right)-1\right)$ relative coordinates, representing the inner structure of $d\mathcal{C}\left(P\right)$, converging, however, to some other local smooth continuum system variables $\psi \left(\overrightarrow{r},t\right)$ (e.g., the pressure, or density, and temperature; see Section 3.4 and Section 3.5).

With this, the FD philosophy of the LIM is established; before moving on to the system composition, let us review:

• the system is formed by parcels with thermodynamic numbers of particles (3);
• the statistical mechanics of these particles converges to space- and time-differentiable emerging variables (6);
• the system is locally in thermal equilibrium, hence described via a kinetic theory converging to a local equilibrium thermodynamics.

The requirement 1 makes it possible to have well-defined non-fluctuating statistics tout court; the requirement 2 leads to the feasibility of deterministic smooth FD at all. Last but not least, the requirement 3 is the path leading to FD as we know it today. The thorny debate about physical regimes when those requirements do not appear to be met cannot be treated in this self-contained review, the reader is referred to more theoretical manuscripts for more information about it, for instance, [18,19,20].

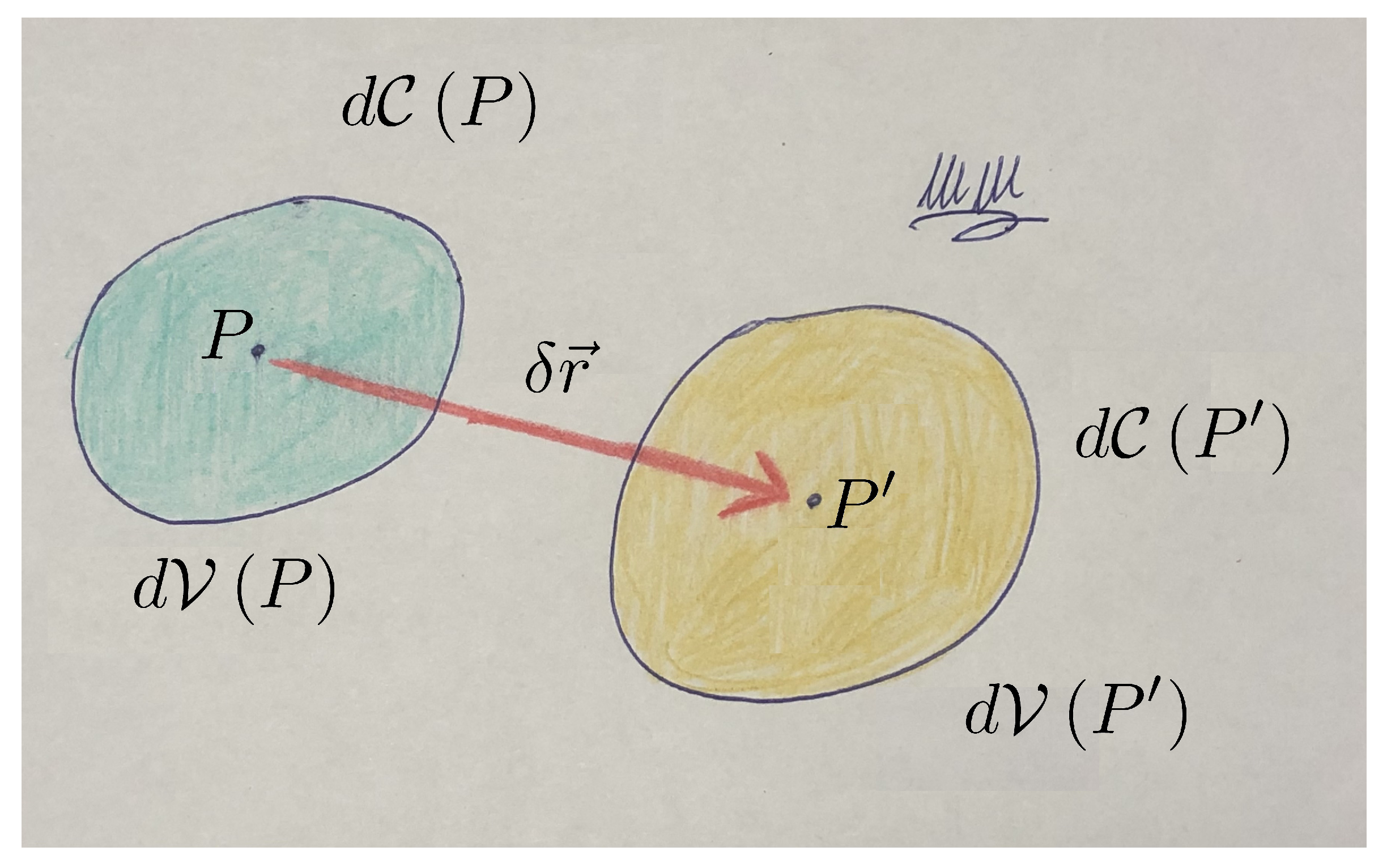
2.2. The System: Matter and Interactions

Let us now introduce how all this theoretical background is applied to the Earth’s ionosphere.

The system is considered to be formed by S chemical species, indicated as $X_I$, with $I=1,2,\dots ,S$. For example, molecular species such as O₂, N₂, CO₂, NH₄, but also atomic species such as O and N, are in this list. If the neutral species considered are

$$\begin{array}{cccccc}{\mathrm{O}}_2,& {\mathrm{N}}_2,& {\mathrm{CO}}_2,& {\mathrm{NH}}_4,& \mathrm{O},& \mathrm{N}\end{array}$$

and the ion species are

$$\begin{array}{cc}{\mathrm{NO}}^{+},& {\mathrm{O}}_2^{-},\end{array}$$

then the example composition reads:

$$\begin{array}{c}\begin{array}{cccccc}{X}_1={\mathrm{O}}_2,& X_2={\mathrm{N}}_2,& X_3={\mathrm{CO}}_2,& X_4={\mathrm{NH}}_4,& X_5=\mathrm{O},& X_6=\mathrm{N},\end{array}\hfill \\ \\ \begin{array}{ccc}{X}_7={\mathrm{NO}}^{+},& X_8={\mathrm{O}}_2^{-},& X_9=e^{-}.\end{array}\hfill \end{array}$$

(7)

In the ionosphere, these S chemicals are in the state of gases. Each of the different gases is an extended system of matter represented as a continuum ${\mathcal{C}}_I$ in the way discussed before, i.e., with parcel dynamics; at each point P of the space, a parcel $d{\mathcal{C}}_I\left(P\right)$ is considered for the I-th chemical, with a center of mass velocity ${\overrightarrow{V}}_I\left(P\right)$ and the I-th relative phase space ${\Gamma }_{\mathrm{rel}}^{\left(I\right)}\left(P\right)$ described via statistical mechanics, in general, more practically via P-local equilibrium thermodynamics.

This is only the matter part; there is a field part too, made of those fundamental force fields acting on the atmospheric gases: gravity and electromagnetic fields. Due to the average speeds of the subsystems in the SERF, and the energy of the processes treated, here we represent everything in terms of classical physics, involving only small sips of Special Relativity, here and there, when the electromagnetic fields are to be transformed from a first observer to another one. Gravity will not be a dynamical variable of the system!

Every component ${\mathcal{C}}_I$ experiences the action of the gravitational field defined around the Earth, which includes the field of properly massive origin, the inertial positional forces and the time varying field due to the tidal action of other celestial bodies. From a general relativistic point of view, one should also include the Coriolis force in the gravitational field, while here the Coriolis force will be kept separate from the whole “effective” gravity. In general, one can write:

$$\overrightarrow{g}={\overrightarrow{g}}_0+{\overrightarrow{g}}_{\Omega }+{\overrightarrow{g}}_{\mathrm{tide}}.$$

(8)

Coriolis forces are thus due to Coriolis acceleration field

$${\overrightarrow{g}}_{CI}=-2\overrightarrow{\Omega }\times {\overrightarrow{V}}_I,$$

where $\overrightarrow{\Omega }$ is the rotation vector of the Earth as seen in a frame in which this Coriolis force is not experienced, and ${\overrightarrow{V}}_I$ the fluid velocity of the I-th species, constructed as explained before.

Electromagnetic fields are experienced only by charged continua (in the example (7), the ions ${\mathcal{C}}_7$ and ${\mathcal{C}}_8$ and the electrons ${\mathcal{C}}_9$), and for these particles, their strength is much more important than that of gravity. In general, there is the geomagnetic field ${\overrightarrow{B}}_0$, which is considered as a rigid external field, and some non-geomagnetic, perturbing magnetic field ${\overrightarrow{B}}_{\mathrm{temp}}$, due to temporary phenomena (e.g., the geomagnetic storms), so that one has

$$\overrightarrow{B}={\overrightarrow{B}}_0+{\overrightarrow{B}}_{\mathrm{temp}}.$$

(9)

Many electric fields of different origin are also present, and this will be clarified later.

Quite the opposite to what happens to gravity, the electromagnetic fields acting on the ${\mathcal{C}}_I$s undergo important back reactions due to charge displacements, net currents and dynamoes produced by the motion of these fluids. The “complete” dynamical system we will deal with will then include all these fluids ${\mathcal{C}}_I$ plus the fields $\overrightarrow{E}$ and $\overrightarrow{B}$ influenced by the atmospheric motions (it should be stated that the mechanics of the ${\mathcal{C}}_I$s are only a part of the source of the atmospheric $\overrightarrow{E}$ and $\overrightarrow{B}$, since $\overrightarrow{B}$ is generated, in its component ${\overrightarrow{B}}_0$ in Equation (9), by some conducting lavic movement inside the solid Earth [24]).

2.3. Fluid Matter Variables

Every single chemical component ${\mathcal{C}}_I$ is described as made of particles of mass $m_I$ and electrical charge $q_I$; we will use ${\rho }_I$ to indicate mass density, $N_I$ for numerical density and ${\delta }_I$ for charge density. These quantities are related as:

$$\begin{array}{cc}{\rho }_I=m_I{N}_I,& {\delta }_I=q_I{N}_I.\end{array}$$

(10)

Of course, ${\rho }_I\left(\overrightarrow{r},t\right)$, $N_I\left(\overrightarrow{r},t\right)$ and ${\delta }_I\left(\overrightarrow{r},t\right)$ are proper fluid fields like the ${\psi }_I\left(\overrightarrow{r},t\right)$ discussed in Section 2.1.

The components involved can be neutral species

$$q_I=0$$

(11)

or charged ones

$$q_I\ne 0.$$

(12)

In ionospheric studies, the use of $N_I$ is often preferred instead of ${\rho }_I$, because the numerical densities of particles enter the typical expressions of cross-sections, determining the production and loss rates of the ${\mathcal{C}}_I$s in chemical processes, and also because the expressions of many measurable quantities are entered by the numerical density $N_e$ of free electrons. For what concerns ${\delta }_I$, one must say that the functional relationship (10) renders it practically equivalent to $N_I$ or ${\rho }_I$ for the charged species, while when $q_I=0$, it simply vanishes.

About these ${\delta }_I$s, in general, a constraint of neutrality of the LIM

$${\displaystyle \sum _I}{\delta }_I=0$$

(13)

may exist, besides the global one:

$${\int }_{{\mathrm{R}}^3}{\displaystyle \sum _I}{\delta }_I\left(\overrightarrow{r},t\right)d^{3}x=0.$$

(14)

The constraint (13) is a standard in many applications of ionospheric physics, even if particular regions, such as the dawn and dusk terminator, may violate it.

Local thermal equilibrium is assumed for each ${\mathcal{C}}_I$; then, temperature fields $T_I\left(\overrightarrow{r},t\right)$ will come into the play. It is useful to remember that the different chemicals have different temperatures, and they are not in thermal equilibrium with the others; for example, electron temperature has been measured at about 900$°$ K, while positive ions were found around 2500$°$ K in the polar E layer at about 150 km height, when intense electric fields are present, as reported in [25]. This should not be surprising, despite the different ${\mathcal{C}}_I$s being in thermal contact with each other. As they are moving, floating and interacting, these gases are in a very different condition from that of fluids in a calorimeter. This also keeps the system far from a global thermodynamic equilibrium.

The continuous approach, which is largely valid for studying plasma and neutrals of the “standard” ionosphere, cannot be used to describe the rain of high-energy particles entering the Earth’s atmosphere from space, because of the hypothesis of local thermal equilibrium, which is lacking for them.

2.4. Dynamical Variables for Matter

A fluid occupying a certain volume in the space is fully described when, point by point and time by time, its velocity field, mass density and tensions are given [26]; this means that for each constituent ${\mathcal{C}}_I$, one should use the $SO\left(3\right)$-vector

$${\overrightarrow{V}}_I=\left(V_I^x\left(\overrightarrow{r},t\right),V_I^y\left(\overrightarrow{r},t\right),V_I^z\left(\overrightarrow{r},t\right)\right)$$

(15)

(bulk velocity given by the center of mass velocity of the parcel with the center of mass in $\overrightarrow{r}$), the $SO\left(3\right)$-scalar

$${\rho }_I={\rho }_I\left(\overrightarrow{r},t\right)$$

(16)

(bulk mass density) and the distinct elements of the stress tensor

$$T_I^{ij}=T_I^{ij}\left(\overrightarrow{r},t\right)$$

(17)

with $i,j=x,y,z$, a two rank $SO\left(3\right)$-tensor. Usual fluids, such as those at hand, have symmetric stress tensor, so that one has six independent components $T_I^{ij}\left(\overrightarrow{r},t\right)$. This ${\rho }_I$, ${\overrightarrow{V}}_I$, and $T_I^{ij}$ give all the fields to describe each continuum ${\mathcal{C}}_I$ composing the atmosphere in the Eulerian picture. However, tensions are not further variables to be added to ${\overrightarrow{V}}_I$ and ${\rho }_I$; the $T_I^{ij}$s are in general functionally dependent on the velocity field ${\overrightarrow{V}}_I$, and “fluids” are classified into different species according to the mathematical form of the dependence

$$T_I^{ij}=T_I^{ij}\left({\overrightarrow{V}}_I,\dots \right).$$

(18)

The tension dependence on velocities is restricted in general to a particular subdivision of $T_I^{ij}$, which can be written as the sum of a pure positional addendum and on another term depending on the ${\overrightarrow{V}}_I$s too:

$$T_I^{ij}=p_I\left(\overrightarrow{r}\right){\delta }^{ij}+{\tau }_I^{ij}\left({\overrightarrow{V}}_I,\overrightarrow{r},\dots \right).$$

(19)

The continuum ${\mathcal{C}}_I$ is defined as fluid if

$${\overrightarrow{V}}_I=0\Rightarrow {\tau }_I^{ij}=0$$

(20)

holds. In the very particular case in which

$$\begin{array}{ccc}{\tau }_I^{ij}\left({\overrightarrow{V}}_I\right)=0& \forall & {\overrightarrow{V}}_I\end{array}$$

(21)

one speaks about ideal fluids. The definition (20) means that the system is not able to exert any off-diagonal stress when it is at rest. The statement (21) indicates as ideal fluids those fluids unable to exert off-diagonal stresses also when they are moving.

The $SO\left(3\right)$-scalar $p_I\left(\overrightarrow{r}\right)$ in (19) is the hydrostatic pressure. The case of perfect fluids well represents the ${\mathcal{C}}_I$s in very dilute regions [27]. Note that since $p_I$ is a scalar under the rotation group, it must be related to the trace of $T_I^{ij}$, so that ${\tau }_I^{ij}$ is traceless.

In order to describe energy exchanges, the thermodynamical nature of the system must be taken into account; then another quantity is introduced, the local temperature $T_I\left(\overrightarrow{r},t\right)$, which is also an $SO\left(3\right)$-scalar. The full set of dynamical variables we have introduced to describe each ${\mathcal{C}}_I$ is then given by the density ${\rho }_I$, the velocity ${\overrightarrow{V}}_I$, the pressure $p_I$, the ${\tau }_I^{ij}$ tensor and the temperature $T_I$, giving a set of 12 unknowns in the equations of motion. In Section 3.4, the roles of $T_I$ and $p_I$ will be clarified from a fully mechanical point of view, as coarse-grained proxies of the microscopic degrees of freedom of the matter of the fluid at hand, contained in the volume $dV\left(P\right)$, in terms of variables relative to the center of mass of the “parcel”.

The various fluids ${\mathcal{C}}_I$ are generally classified and studied as follows [28]:

• Neutral particles. Various molecules or atoms (e.g., O, N, O₂, N₂, CO₂, NH₄ and so on) with zero electric charge: These ones are the major part, both numerically as well as massively, of all the high atmosphere, up to the level of about 1000 km height, the starting point of a region where practically all the matter is ionized. From that point on, one speaks about plasmasphere.
  If each neutral species is indicated with the index $h=1,2,\dots$, the speed of their center of mass is point by point some field $\overrightarrow{U}$, defined as follows in terms of partial matter densities ${\rho }_h$ and velocities ${\overrightarrow{U}}_h$:

  $$\begin{array}{cc}\overrightarrow{U}={\displaystyle \frac{1}{\rho }}{\displaystyle \sum _h}{\rho }_h{\overrightarrow{U}}_h,& \rho ={\displaystyle \sum _h}{\rho }_h.\end{array}$$

  (22)
  This velocity undergoes a proper dynamics that may be attributed to the neutral matter as a unique fluid ${\mathcal{C}}_0$.
• Negative ions. These are the species which have captured one or more electrons. These particles are very rare and their presence is practically negligible in general. Nevertheless, one should consider them when dealing with the lower part of the ionosphere, as the region D and the lower E [10]. Negative ion abundance is reasonably non-negligible only under 95 km, even if, in particular conditions, this can be false. Sometimes, a coefficient ${\lambda }_Y$ is defined for each negative ion $Y^{-}$ as

  $${\lambda }_Y={\displaystyle \frac{N_{Y^{-}}}{N_e}},$$

  (23)

  giving the measure of the contribution of the species $Y^{-}$ to the ionospheric negative charge, relative to the electron one.
• Positive ions. These are the neutrals that have lost one or more electrons. Actually, the 2- or 3-valent positive ions are very rare, so we can restrict ourselves to the study of 1-valent positive ions. When the constraint (13) holds and no negative ions exist, positive ions have a numerical density equal to that of free electrons.
• Electrons. Electrons are the most important element for ionospheric phenomenology as far as electromagnetic disturbances are concerned, because of their very small mass, which gives them a great mobility [9], making them very effective in producing local and travelling electromagnetic fields.

In general, one could represent in a Lagrangian way the fluid motion as the evolution of a manifold, a domain continuously filled in with matter, and describe its motion as the transformations undergone by this manifold. The manifold can stretch, roll, it can be deformed by tensions, its center of mass moves under the action of external forces. Basically, one physical portion of it can be identified as the evolution of a fixed portion of the initial continuum [26]. This way of representing the evolution of a continuous system has led to a Hamiltonian description of fluids alternative to the local approach (for reference, see [29,30,31,32]).

In the absence of chemical reactions, the mass of the parcel $d{\mathcal{C}}_I$ remains constant:

$$\mathrm{NO}\mathrm{CHEMISTRY}\Rightarrow {\displaystyle \frac{d}{dt}}m\left(d{\mathcal{C}}_I\right)=0,$$

(24)

where ${\displaystyle \frac{d}{dt}}$ is the operator making the time derivative along the motion [33]. What happens if chemical reactions take place? When chemical reactions enter the fluid dynamics, it is convenient to treat the systems as non-constant mass systems, writing:

$$\mathrm{CHEMISTRY}\Rightarrow {\displaystyle \frac{d}{dt}}m\left(d{\mathcal{C}}_I\right)=G_I\left(d{\mathcal{C}}_I\right).$$

(25)

This $G_I\left(d{\mathcal{C}}_I\right)$ is the variation rate of the mass of the parcel as following the parcel motion, and it can be either positive or negative, according to production or loss processes.

The description of the fluid $d{\mathcal{C}}_I$ is referred to as Lagrangian or substantial, because the quantities used refer to the degrees of freedom of a material portion of the system ${\mathcal{C}}_I$; on the contrary, fluids are often described in the Eulerian or local way, in which one describes the situation via quantities thought of as properties of the spatial point at hand [26]. When some quantity $\mathcal{G}$ is attributed to a fluid, the relationship between the Lagrangian version ${\mathcal{G}}_L$ and the Eulerian version ${\mathcal{G}}_E$ of it is given in terms of time derivatives, and reads

$${\displaystyle \frac{d{\mathcal{G}}_L}{dt}}={\displaystyle \frac{\partial {\mathcal{G}}_E}{\partial t}}+\overrightarrow{V}·\overrightarrow{\partial }{\mathcal{G}}_E,$$

(26)

where $\overrightarrow{V}$ is the local speed of the fluid to which $\mathcal{G}$ is attributed (for ionospheric continua, the $\mathcal{G}$s and $\overrightarrow{V}$ in (26) have a chemical species index I).

It has already been stated that the extended system $d{\mathcal{C}}_I\left(\overrightarrow{r}\right)$ has center of mass (CoM) variables and relative-to-CoM (R2CoM) variables as explained in [22] and references therein. The evolution of the CoM variables will be governed by Newton’s principle as explained in Section 3.3 below. For what concerns the R2CoM variables, a statistical approach is used for them in ordinary fluid dynamics; for more, the reader is referred to Section 3.4.

2.5. Electromagnetic Dynamical Variables

The mathematical tools describing the system are completed when the variables used for the electromagnetic fields are given. At each point $\overrightarrow{r}$ in the space around the Earth, an electric vector $\overrightarrow{E}$ and a magnetic vector $\overrightarrow{B}$ can be given, both time- as well as position-dependent:

$$\begin{array}{cc}\overrightarrow{E}=\overrightarrow{E}\left(\overrightarrow{r},t\right),& \overrightarrow{B}=\overrightarrow{B}\left(\overrightarrow{r},t\right).\end{array}$$

(27)

These electric and magnetic fields are obviously governed by Maxwell equations. While there exists a Lagrangian description of fluids with a straightforward interpretation, electromagnetic fields do have only an immediate Eulerian dynamics; this is why all the $d{\mathcal{C}}_I$-dynamics are reformulated in local terms, through the translation (26).

In general, the electromagnetic field in a point of interest will be the superposition of many fields of different origin.

The magnetic field $\overrightarrow{B}$ is given by the superposition of a “permanent” geomagnetic component ${\overrightarrow{B}}_0$, which is generated by sources in the interior of the solid Earth, and other “temporary” terms, indicated collectively as ${\overrightarrow{B}}_{\mathrm{temp}}$ in (9). ${\overrightarrow{B}}_0$ is not constant in the long term, because it has been proved to vary; roughly speaking, it is some dipole magnetic field that slowly rotates and changes its shape. At Italian latitudes and longitudes, for instance, it is representable as a rigid dipole migrating about one prime per year. Actually, this dipole ${\overrightarrow{B}}_0$ is not rigid, and its motion should be studied in a complex theoretical way (see [24] and references therein). However, the variability of this ${\overrightarrow{B}}_0$ takes place on timescales which are too long compared to the processes usually discussed in LIM modelling.

The inclusion of a field in the system at hand as a dynamical variable depends, by the way, on the inclusion of its sources; since we decided not to include the currents inside the solid Earth in our system, we will regard the geomagnetic field generated by them as an external constant field ${\overrightarrow{B}}_0$. On the contrary, the part ${\overrightarrow{B}}_{\mathrm{temp}}$ can be affected by ionospheric or magnetospheric sources.

The electric field $\overrightarrow{E}$ is generally produced by charge separations related to the motions of the ionospheric plasma. In many cases, this $\overrightarrow{E}$ can be considered as slowly varyingwith time, and treated as electrostatic, and so a potential $\varphi$ giving $\overrightarrow{E}=-\overrightarrow{\partial }\varphi$ is introduced.

3. Equations of Motion

The equations ruling the motion of the atmospheric system are essentially those of classical Newtonian physics, plus thermodynamics, plus classical electrodynamics.

For the electromagnetic fields, the four Maxwell equations will be used directly, while for what concerns the matter part, conservation principles applied to the parcel $d{\mathcal{C}}_I\left(\overrightarrow{r},t\right)$ dynamics will drive the reasoning.

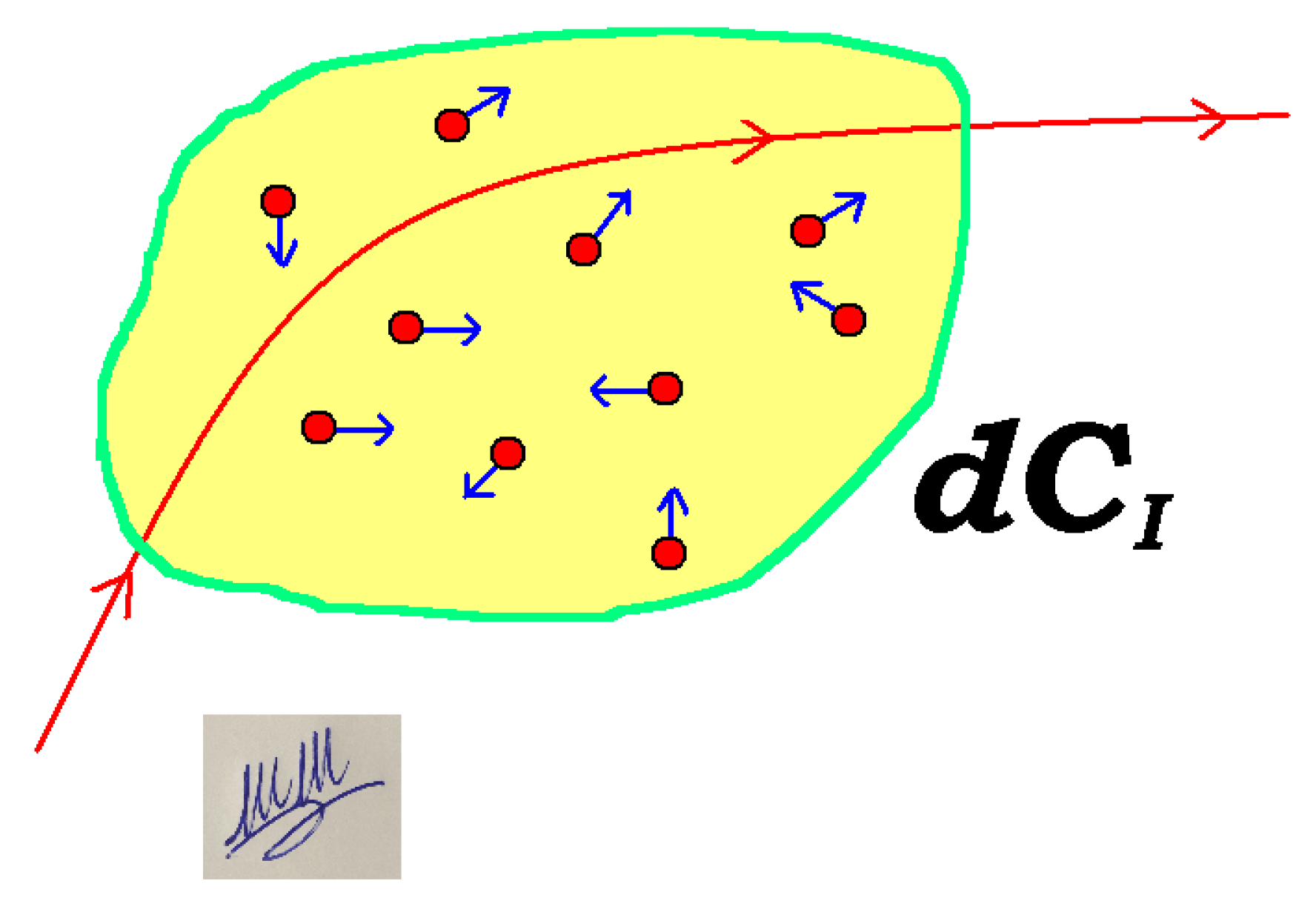
3.1. Mass Balance

The mass balance is written for the I-th species by considering that each of the many species present in the atmosphere undergoes creation and destruction due to chemical and photochemical processes. Neutrals are “destroyed” in ionization and “reconstructed” due to recombination of electrons and positive ions, or detachment of electrons away from the negative ions. In the same way, free electrons are created in ionization together with positive ions, in the detachment processes of negative ions, and destroyed in general in attachments and recombinations. Finally, positive ions are created together with electrons in ionization processes, and destroyed in recombinations.

In general, the mass balance can be obtained by elaborating Equation (25); if the parcel of the I-th element is some $d{\mathcal{C}}_I$ which occupies a volume $d\mathcal{V}$, and the mass density is ${\rho }_I$, one can write:

$$\begin{array}{ccc}m\left(d{\mathcal{C}}_I\right)={\rho }_{I}d\mathcal{V}& \Rightarrow & {\displaystyle \frac{d}{dt}}\left({\rho }_{I}d\mathcal{V}\right)=G_I\left(d{\mathcal{C}}_I\right).\end{array}$$

The total derivative is applied as

$${\displaystyle \frac{d{\rho }_I}{dt}}d\mathcal{V}+{\rho }_I{\displaystyle \frac{d}{dt}}\left(d\mathcal{V}\right)=G_I\left(d{\mathcal{C}}_I\right),$$

(28)

and all we have to do is to write ${\displaystyle \frac{d{\rho }_I}{dt}}d\mathcal{V}+{\rho }_I{\displaystyle \frac{d}{dt}}\left(d\mathcal{V}\right)$ as a function of the matter degrees of freedom presented in Section 2.4. The physical quantities we will involve in our discussion are the density ${\rho }_I$ and the velocity ${\overrightarrow{V}}_I$ of the parcel.

The density is already involved explicitly in (28); one has to evaluate ${\displaystyle \frac{d}{dt}}\left(d\mathcal{V}\right)$ in terms of the parcel velocity. The variation of the measure $d\mathcal{V}$ can be calculated considering that the measure of $d\mathcal{V}$ changes due to the motion of the points on its surface $\partial \left(d\mathcal{V}\right)$, so that this time derivative is the outgoing flux of this speed:

$${\displaystyle \frac{d}{dt}}\left(d\mathcal{V}\right)={\displaystyle \underset{\partial \left(d\mathcal{V}\right)}{\int }}\left({\overrightarrow{V}}_I·\widehat{n}\right)d^{2}S.$$

(29)

When Stokes theorem is applied to this integral, one has

$${\displaystyle \frac{d}{dt}}\left(d\mathcal{V}\right)={\displaystyle \underset{d\mathcal{V}}{\int }}\left(\overrightarrow{\partial }·{\overrightarrow{V}}_I\right)d^{3}x.$$

Considering the smallness of $d\mathcal{V}$, it is possible to write:

$${\displaystyle \frac{d}{dt}}\left(d\mathcal{V}\right)=\left(\overrightarrow{\partial }·{\overrightarrow{V}}_I\right)d\mathcal{V}.$$

(30)

Placing (30) into Equation (28), we can write:

$${\displaystyle \frac{d{\rho }_I}{dt}}d\mathcal{V}+{\rho }_I\left(\overrightarrow{\partial }·{\overrightarrow{V}}_I\right)d\mathcal{V}=G_I\left(d{\mathcal{C}}_I\right)$$

(31)

The mass source term $G_I\left(d{\mathcal{C}}_I\right)$ can be imagined as proportional to the total mass of the parcel as $G_I\left(d{\mathcal{C}}_I\right)\propto m\left(d{\mathcal{C}}_I\right)={\rho }_{I}d\mathcal{V}=m_I{N}_{I}d\mathcal{V}$, because each particle in the parcel may undergo the same chemical reactions with the same probability distributions, so that $G_I\left(d{\mathcal{C}}_I\right)\propto m_{I}d\mathcal{V}$ may be written as:

$$G_I\left(d{\mathcal{C}}_I\right)=m_I{\Gamma }_{I}d\mathcal{V},$$

(32)

where $m_I$ is the mass of the single particle of the I-th species and the source field ${\Gamma }_I$, suitably defined in (32). This expresses Equation (31) involving the Lagrangian derivative of ${\rho }_I$:

$${\displaystyle \frac{d{\rho }_I}{dt}}+{\rho }_I\left(\overrightarrow{\partial }·{\overrightarrow{V}}_I\right)=m_I{\Gamma }_I,$$

(33)

and going from the Lagrangian to the local expression of ${\displaystyle \frac{d{\rho }_I}{dt}}$, one has:

$$\begin{array}{c}{\displaystyle \frac{d{\rho }_I}{dt}}={\partial }_t{\rho }_I+{\overrightarrow{V}}_I·\overrightarrow{\partial }{\rho }_I\\ \Downarrow \\ {\partial }_t{\rho }_I+{\overrightarrow{V}}_I·\overrightarrow{\partial }{\rho }_I+{\rho }_I\left(\overrightarrow{\partial }·{\overrightarrow{V}}_I\right)=m_I{\Gamma }_I.\end{array}$$

The total space derivative

$${\overrightarrow{V}}_I·\overrightarrow{\partial }{\rho }_I+{\rho }_I\left(\overrightarrow{\partial }·{\overrightarrow{V}}_I\right)=\overrightarrow{\partial }·\left({\rho }_I{\overrightarrow{V}}_I\right)$$

is recognized, then Equation (33) turns out to read:

$${\partial }_t{\rho }_I+\overrightarrow{\partial }·\left({\rho }_I{\overrightarrow{V}}_I\right)=m_I{\Gamma }_I.$$

(34)

It is useful to write the source term ${\Gamma }_I$ as the difference

$${\Gamma }_I=P_I-L_I$$

(35)

between the local rate of production $P_I$ of the I-th species, and the corresponding rate of loss $L_I$. Equation (34) is then re-written as:

$${\partial }_t{\rho }_I+\overrightarrow{\partial }·\left({\rho }_I{\overrightarrow{V}}_I\right)=m_I\left(P_I-L_I\right),$$

(36)

Each species has its own loss and production term in (36), but these are not all independent; their forms encode the chemical processes taking place in the ionosphere, which have the elementary constituents of the continua ${\mathcal{C}}_I$ as reagents or products. These reactions undergo some conservation relations, and the source terms in (36) must satisfy those conservation laws. The matter of the total system

$$\mathcal{C}={\displaystyle \bigcup _I}{\mathcal{C}}_I$$

(37)

must have constant mass (under the hypothesis that no nuclear reaction takes place, and considering not to discuss the loss or gain of chemicals due to some matter exchange with the near-Earth space). This means that there must exist a total mass balance equation with zero source,

$${\partial }_t\rho +\overrightarrow{\partial }·\left(\rho \overrightarrow{V}\right)=0,$$

(38)

where $\rho$ is the total mass density of the multi-fluid system and $\overrightarrow{V}$ is “the right vector” to take part in Equation (38) (where the “right vector” $\overrightarrow{V}$ is defined a few lines below). The way of deducing the total Equation (38) from Equation (36) is straightforward; it suffices to sum them all and define $\overrightarrow{V}$ accordingly, which will turn out to be rather intuitive. Summing all of Equation (36) over the chemical species, one obtains

$${\displaystyle \sum _I}\left[{\partial }_t{\rho }_I+\overrightarrow{\partial }·\left({\rho }_I{\overrightarrow{V}}_I\right)\right]={\displaystyle \sum _I}{m}_I\left(P_I-L_I\right).$$

Total quantities are recognized straigthforwardly. First of all, the total density

$${\displaystyle \sum _I}{\rho }_I=\rho ,$$

(39)

while transport terms give the right addendum in (38) when $\overrightarrow{V}$ is defined so as to satisfy:

$${\displaystyle \sum _I}{\rho }_I{\overrightarrow{V}}_I=\rho \overrightarrow{V}.$$

(40)

This is a well-known quantity in mass kinematics: $\overrightarrow{V}$ is like the “speed of the center of mass” for all the fluids. Due to these definitions, we have

$${\partial }_t\rho +\overrightarrow{\partial }·\left(\rho \overrightarrow{V}\right)={\displaystyle \sum _I}{m}_I\left(P_I-L_I\right).$$

(41)

If Equation (41) has to coincide with Equation (38), enforcing the mass conservation, we must have

$${\displaystyle \sum _I}{m}_I\left(P_I-L_I\right)=0,$$

(42)

which is the mass conservation condition on the production and loss terms $P_I$ and $L_I.$ Equation (42) is a basic condition for aeronomical chemistry, claiming that chemicals are not created or destroyed “out of the blue” or “into nothing”, but simply turned from one into another. The only external contribution to this apparently closed system balance is the supply of energy from solar photons, which are destroyed when photochemical processes take place. Yet, these photons will not be recognized as a further species of chemicals, essentially as long as chemical, and not nuclear, reactions take place, so the energy of these massless photons will not be translated into mass.

The constraint (42) is not the only condition one has to fulfill when writing the production and loss terms. Conservation of the electrical charge must be taken into account as well. In order to obtain the charge conservation condition, let us go back to (36) and divide it by $m_I$, which is clearly a constant parameter. What one obtains is

$${\partial }_t\left({\displaystyle \frac{{\rho }_I}{m_I}}\right)+\overrightarrow{\partial }·\left({\displaystyle \frac{{\rho }_I}{m_I}}{\overrightarrow{V}}_I\right)=P_I-L_I.$$

Conventions (10) give

$${\partial }_t{N}_I+\overrightarrow{\partial }·\left(N_I{\overrightarrow{V}}_I\right)=P_I-L_I,$$

(43)

which is the balance equation for number densities. This Equation (43) is the key continuity equation for any additive quantity held by the single fluid species; an example of such quantities is indeed the electric charge. Equation (43) is multiplied by the I-th electric charge

$${\partial }_t\left(q_I{N}_I\right)+\overrightarrow{\partial }·\left(q_I{N}_I{\overrightarrow{V}}_I\right)=q_I\left(P_I-L_I\right)$$

and definitions (10) are turned to again, so that:

$${\partial }_t{\delta }_I+\overrightarrow{\partial }·\left({\delta }_I{\overrightarrow{V}}_I\right)=q_I\left(P_I-L_I\right).$$

(44)

If $\delta$ is the total electric charge density of the whole system of fluids, then one would like to obtain

$${\partial }_t\delta +\overrightarrow{\partial }·{\overrightarrow{J}}_q=0,$$

(45)

and this is obtained by summing all of Equation (44) as ${\displaystyle \sum _I}\left[{\partial }_t{\delta }_I+\overrightarrow{\partial }·\left({\delta }_I{\overrightarrow{V}}_I\right)\right]={\displaystyle \sum _I}{q}_I\left(P_I-L_I\right)$ and recognizing

$$\begin{array}{cc}{\displaystyle \sum _I}{\delta }_I=\delta ,& {\displaystyle \sum _I}{\delta }_I{\overrightarrow{V}}_I={\overrightarrow{J}}_q.\end{array}$$

(46)

This gives

$${\partial }_t\delta +\overrightarrow{\partial }·{\overrightarrow{J}}_q={\displaystyle \sum _I}{q}_I\left(P_I-L_I\right),$$

(47)

so that if Equation (47) has to be equivalent to electric charge conservation, the following condition on the $P_I$s and $L_I$s

$${\displaystyle \sum _I}{q}_I\left(P_I-L_I\right)=0$$

(48)

must be realized.

In general, if an extensive quantity H exists and has density ${\eta }_I$ for the I-th continuous species, and total density

$${\displaystyle \sum _I}{\eta }_I=\eta ,$$

(49)

one can define its total current as

$${\overrightarrow{J}}_{\mathrm{H}}={\displaystyle \sum _I}{\eta }_I{\overrightarrow{V}}_I.$$

(50)

The single species balance equation for H reads

$${\partial }_t{\eta }_I+\overrightarrow{\partial }·\left({\eta }_I{\overrightarrow{V}}_I\right)=h_I\left(P_I-L_I\right),$$

(51)

where $h_I$ is the amount of H carried by the single particle of the I-th species. This yields

$${\partial }_t\eta +\overrightarrow{\partial }·{\overrightarrow{J}}_{\mathrm{H}}={\displaystyle \sum _I}{h}_I\left(P_I-L_I\right),$$

(52)

giving finally

$$\begin{array}{ccc}{\partial }_t\eta +\overrightarrow{\partial }·{\overrightarrow{J}}_{\mathrm{H}}=0& \iff & {\displaystyle \sum _I}{h}_I\left(P_I-L_I\right)=0\end{array}$$

(53)

as a “total H conservation condition”.

3.2. Chemical Space Formalism

A particularly suitable symbolism for fluid with dynamics, loss and production processes, is referred to as vector chemical space formalism.

There is one Equation (36) for each chemical species. Let S be the total number of chemical species. Let us rearrange the mass conservation to involve the numerical concentration instead:

$$\begin{array}{ccc}{\partial }_t{N}_I+{\partial }_i{J}_I^i=P_I-L_I,& I=1,\dots ,S,& {\overrightarrow{J}}_I=N_I{\overrightarrow{V}}_I,\end{array}$$

(54)

Then, let us consider that these S equations are the components of the following system:

$${\partial }_t{\displaystyle \underline{N}}+{\partial }_i{{\displaystyle \underline{J}}}^i={\displaystyle \underline{P}}-{\displaystyle \underline{L}}$$

(55)

(where ${\displaystyle \underline{N}}$, ${{\displaystyle \underline{J}}}^i$, ${\displaystyle \underline{P}}$ and ${\displaystyle \underline{L}}$ are S-component real vector in the “space of chemicals”; in Equations (54) and (55), the summation over $i=x,y,z$ is intended in the terms ${\partial }_i{J}_I^i$ and ${\partial }_i{{\displaystyle \underline{J}}}^i$. Summations take place over repeated indices in contravariant positions). The local conservation constraint (53) for any conserved quantity H is read as an orthogonality relationship in ${\mathit{R}}^S$ between the collection of the values ${\displaystyle \underline{h}}$ and the collection of the source terms:

$$\begin{array}{cc}{\displaystyle \underline{h}}·{\displaystyle \underline{\Gamma }}=0,& {\displaystyle \underline{\Gamma }}={\displaystyle \underline{P}}-{\displaystyle \underline{L}}.\end{array}$$

(56)

Equation (55) is referred to as species–vector continuity, and its components are coupled via the source term ${\displaystyle \underline{\Gamma }}$ that satisfies (56). In fact, this source term depends on the densities

$${\displaystyle \underline{\Gamma }}={\displaystyle \underline{P}}\left({\displaystyle \underline{N}};\overrightarrow{r},t\right)-{\displaystyle \underline{L}}\left({\displaystyle \underline{N}};\overrightarrow{r},t\right),$$

and maybe on the time and position explicitly, so that Equation (55) overall reads:

$${\partial }_t{\displaystyle \underline{N}}+{\partial }_i{{\displaystyle \underline{J}}}^i={\displaystyle \underline{\Gamma }}\left({\displaystyle \underline{N}};\overrightarrow{r},t\right).$$

(57)

In order to understand Equation (57) in a general way, we must classify explicitly the properties of the function ${\displaystyle \underline{\Gamma }}\left({\displaystyle \underline{N}},\dots \right)$, its possible symmetries and the simplifications. Turning back to the components ${\partial }_t{N}_I+{\partial }_i{J}_I^i={\Gamma }_I$, we can appreciate the various levels of coupling between different species by expanding ${\displaystyle \underline{\Gamma }}$ in the densities, via a simple Taylor series approach, e.g., up to the third order:

$$\begin{array}{c}{\Gamma }_I\left({\displaystyle \underline{N}}\right)={\Gamma }_I\left(0\right)+{\displaystyle \frac{\partial {\Gamma }_I}{\partial N_J}}\left(0\right)N_J+{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\partial }^2{\Gamma }_I}{\partial N_J\partial N_H}}\left(0\right)N_J{N}_H+\hfill \\ \\ +{\displaystyle \frac{1}{6}}{\displaystyle \frac{{\partial }^3{\Gamma }_I}{\partial N_J\partial N_H\partial N_K}}\left(0\right)N_J{N}_H{N}_K+O\left(N^4\right)\hfill \end{array}$$

(58)

(the following reasoning makes exact sense as long as ${\displaystyle \underline{\Gamma }}\left({\displaystyle \underline{N}}\right)$ has a convergent Taylor series; otherwise, it is just an approximation). When such expressions are put into (54)

$$\begin{array}{c}{\partial }_t{N}_I+{\partial }_i{J}_I^i={\Gamma }_I\left(0\right)+{\displaystyle \frac{\partial {\Gamma }_I}{\partial N_J}}\left(0\right)N_J+\hfill \\ \\ +{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\partial }^2{\Gamma }_I}{\partial N_J\partial N_H}}\left(0\right)N_J{N}_H+{\displaystyle \frac{1}{6}}{\displaystyle \frac{{\partial }^3{\Gamma }_I}{\partial N_J\partial N_H\partial N_K}}\left(0\right)N_J{N}_H{N}_K+O\left(N^4\right)\hfill \end{array}$$

(59)

one discovers that the various terms involve zero, one, two, three, … species of particles, and thus correspond to chemical processes with zero, one, two, three, … chemicals involved. It is not said that in the n-th-order term, n different species are involved; in fact, there are terms in ${\displaystyle \underline{\Gamma }}$ in which a given $N_I$ can appear with a degree higher than one. These different momenta of ${\Gamma }_I$ in the space of species must form a function which satisfies the constraint (56). Putting (58) into it, one has

$$\begin{array}{c}{\displaystyle \sum _I}{q}_I\left[{\Gamma }_I\left(0\right)+{\displaystyle \frac{\partial {\Gamma }_I}{\partial N_J}}\left(0\right)N_J+{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\partial }^2{\Gamma }_I}{\partial N_J\partial N_H}}\left(0\right)N_J{N}_H+\right.\hfill \\ \\ \left.+{\displaystyle \frac{1}{6}}{\displaystyle \frac{{\partial }^3{\Gamma }_I}{\partial N_J\partial N_H\partial N_K}}\left(0\right)N_J{N}_H{N}_K+\dots \right]=0.\hfill \end{array}$$

(60)

The various terms must each be zero, because we are setting to zero a polynomial in the components of ${\displaystyle \underline{N}}$. For the zeroth order, one has

$${\displaystyle \sum _I}{q}_I{\Gamma }_I\left(0\right)=0,$$

(61)

which essentially means the impossibility of creating charge in the empty space, with ${\displaystyle \underline{N}}=0$. One can see in Chapman ionization theory in [9,27] an explicit application of this. For example, if our model atmosphere is represented by the three species X, $X^{+}$ and $e^{-}$, Equation (61) reads

$$0·{\Gamma }_X\left(0\right)+e{\Gamma }_{X^{+}}\left(0\right)-e{\Gamma }_{e^{-}}\left(0\right)=0,$$

that is,

$${\Gamma }_{X^{+}}\left(0\right)={\Gamma }_{e^{-}}\left(0\right).$$

(62)

3.3. Momentum Balance (Newton’s $\overrightarrow{F}=m\overrightarrow{a}$)

The fluids ${\mathcal{C}}_I$ composing the system described at the beginning of this section are made out of point particles that essentially obey Newton’s principles. In the approximation described in Section 2.3, the initial condition Cauchy problem

$$\left\{\begin{array}{c}\overrightarrow{F}=m\overrightarrow{a},\hfill \\ \\ \begin{array}{cc}\overrightarrow{r}\left(0\right)={\overrightarrow{r}}_0,& \overrightarrow{v}\left(0\right)={\overrightarrow{v}}_0\end{array}\hfill \end{array}\right.$$

for a particle of mass m can be transported to the continuous system of the I-th constituent as the Navier–Stokes equation [17], which is exactly Newton’s Second Principle, or equally the linear momentum balance, written for the parcel.

The linear momentum of the parcel is some $\overrightarrow{p}\left(d{\mathcal{C}}_I\right)$, so we have

$${\displaystyle \frac{d}{dt}}\overrightarrow{p}\left(d{\mathcal{C}}_I\right)=d{\overrightarrow{F}}_I.$$

(63)

If its mass is referred to as $m_I\left(d\mathcal{V}\right)$ and we use the symbol $d{\overrightarrow{F}}_I$ to indicate the force experienced by this $d{\mathcal{C}}_I$, we can write:

$${\displaystyle \frac{d}{dt}}\left(m_I\left(d\mathcal{V}\right){\overrightarrow{V}}_I\right)=d{\overrightarrow{F}}_I,$$

(64)

stressing again that ${\overrightarrow{V}}_I$ is the velocity of the center of mass of the parcel $d{\mathcal{C}}_I$ at hand. From Equation (25), this can be written as:

$$G_I\left(d{\mathcal{C}}_I\right){\overrightarrow{V}}_I+m_I\left(d\mathcal{V}\right){\displaystyle \frac{d{\overrightarrow{V}}_I}{dt}}=d{\overrightarrow{F}}_I.$$

(65)

The mass of the parcel reads

$$m_I\left(d\mathcal{V}\right)={\rho }_{I}d\mathcal{V},$$

(66)

and considering also the definition (32), Equation (65) can be written as:

$$\left(m_I{\Gamma }_I{\overrightarrow{V}}_I+{\rho }_I{\displaystyle \frac{d{\overrightarrow{V}}_I}{dt}}\right)d\mathcal{V}=d{\overrightarrow{F}}_I.$$

(67)

The volume element ${\rho }_{I}d\mathcal{V}$ can be factorized on both sides of (67) by defining

$$d{\overrightarrow{F}}_I={\overrightarrow{f}}_{I}d\mathcal{V},$$

(68)

so that all in all, one has

$$m_I{\Gamma }_I{\overrightarrow{V}}_I+{\rho }_I{\displaystyle \frac{d{\overrightarrow{V}}_I}{dt}}={\overrightarrow{f}}_I.$$

(69)

This (69) will be written in local terms by applying (26) to the fluid velocity itself, so as to obtain

$${\rho }_I{\partial }_t{\overrightarrow{V}}_I+{\rho }_I\left({\overrightarrow{V}}_I·\overrightarrow{\partial }\right){\overrightarrow{V}}_I={\overrightarrow{f}}_I-m_I{\Gamma }_I{\overrightarrow{V}}_I.$$

(70)

In order to enumerate the forces composing $d{\overrightarrow{F}}_I$, we have to list those systems acting on the portion of fluid. The parcel $d{\mathcal{C}}_I$ interacts with the following systems:

• the electromagnetic fields $\overrightarrow{E}$ and $\overrightarrow{B}$ defined at its position;
• the gravitational field $\overrightarrow{g}$ defined at its position;
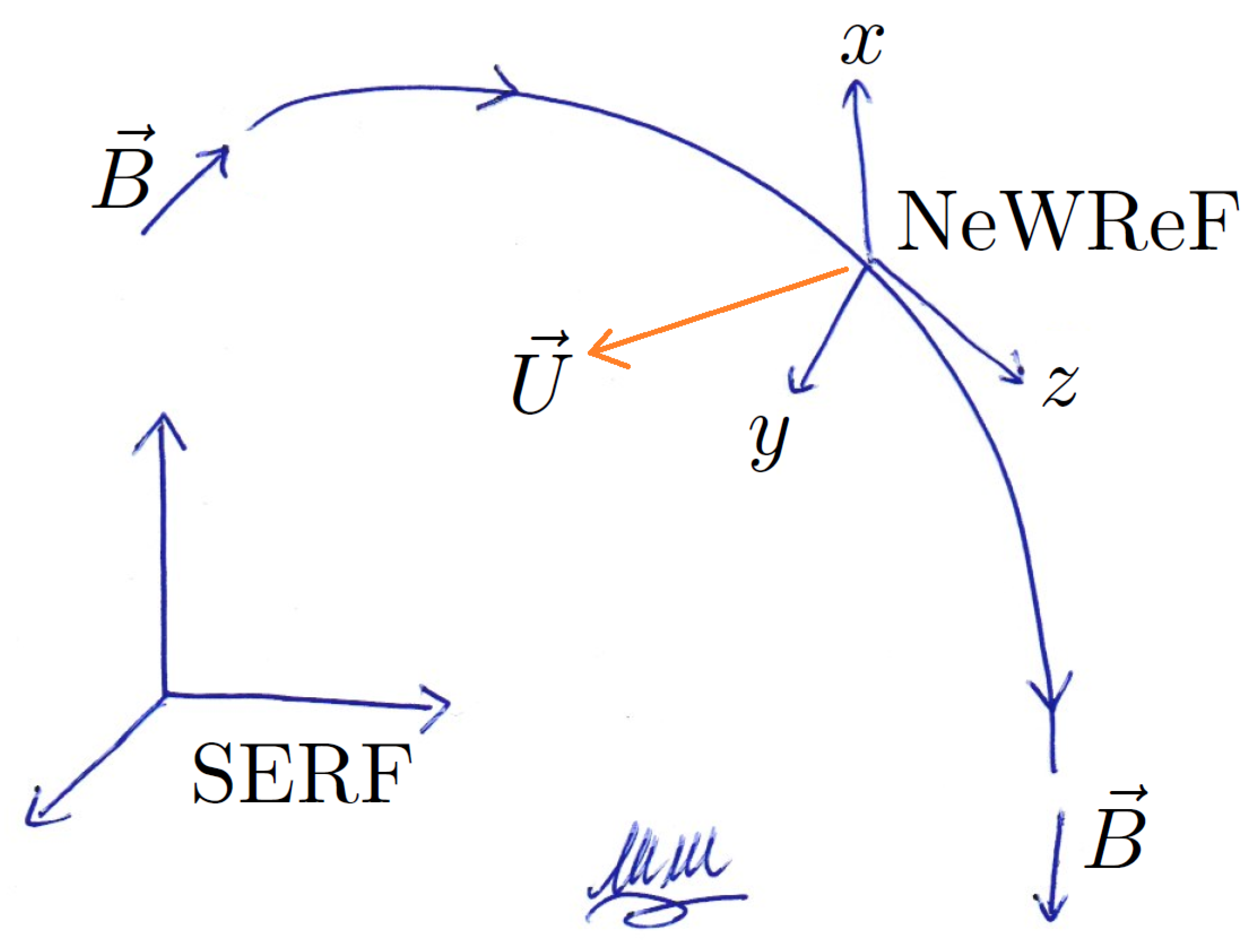
• the inertial forces measured in the reference frame co-rotating with the Earth (the SERF);
• the remaining part of the system ${\mathcal{C}}_I$ which interacts with $d{\mathcal{C}}_I$ at the border $\partial \left(d\mathcal{V}\right)$ through the nearby parcels;
• the other systems ${\mathcal{C}}_J$ with $J\ne I$;
• the mechanical waves passing by the position of $d{\mathcal{C}}_I$.

Let us come to the complete expression of the force $d{\overrightarrow{F}}_I={\overrightarrow{f}}_{I}d\mathcal{V}$; as announced before, let us assume that ${\mathcal{C}}_I$ is a generic charged fluid and let us attribute to $d{\mathcal{C}}_I$ a total electric charge

$$d{q}_I={\delta }_{I}d\mathcal{V}.$$

(71)

This charge $d{q}_I$ makes $d{\mathcal{C}}_I$ experience a force $d{\overrightarrow{F}}_{Iem}$ due to the presence of the electromagnetic field, which is written in Newtonian terms as

$$d{\overrightarrow{F}}_{Iem}=d{q}_I\left(\overrightarrow{E}+{\overrightarrow{V}}_I\times \overrightarrow{B}\right),$$

(72)

where the fields are those defined in Section 2.5.

The second force acting on $d{\mathcal{C}}_I$ is the gravitational force, represented as

$$d{\overrightarrow{F}}_{Igrav}=m_I\left(d\mathcal{V}\right){\overrightarrow{g}}_{eff}:$$

(73)

The field ${\overrightarrow{g}}_{eff}$ is obtained in the SERF. It is basically composed by the Kepler-like gravitational potential ${\overrightarrow{g}}_0$ given by the rest mass of the Earth, plus the positional part of the inertial forces due to the Earth’s motion. If the angular velocity $\overrightarrow{\Omega }$ of the Earth is supposed to be constant within the timescales treated here, we can say that ${\overrightarrow{g}}_{eff}$ includes ${\overrightarrow{g}}_0$ and the centrifugal force:

$$\begin{array}{cc}{\overrightarrow{g}}_{eff}={\overrightarrow{g}}_0+{\overrightarrow{g}}_{\Omega },& {\overrightarrow{g}}_{\Omega }=-\overrightarrow{\Omega }\times \left(\overrightarrow{\Omega }\times \overrightarrow{r}\right).\end{array}$$

(74)

The Coriolis force is calculated for the parcel of mass $m_I\left(d\mathcal{V}\right)$ and velocity ${\overrightarrow{V}}_I$ as:

$$d{\overrightarrow{F}}_{IC}=-2m_I\left(d\mathcal{V}\right)\overrightarrow{\Omega }\times {\overrightarrow{V}}_I=-2{\rho }_I\overrightarrow{\Omega }\times {\overrightarrow{V}}_{I}d\mathcal{V}.$$

(75)

The force applied by the rest of ${\mathcal{C}}_I$ on the $d{\mathcal{C}}_I$ under exam through the border $\partial \left(d\mathcal{V}\right)$ of the small volume can be expressed as an integral over the surface $\partial \left(d\mathcal{V}\right)$ of the outward flux of an $SO\left(3\right)$-tensor of rank 2, referred to as the tension tensor; this has been indicated in Section 2.4 as $T_I^{ij}$, and one can write:

$$d{F}_{I\partial }^i=-{\displaystyle \underset{\partial \left(d\mathcal{V}\right)}{\int }}{T}_I^{ij}{n}_j{d}^{2}S,$$

(76)

where $d^{2}S$ is the infinitesimal element of the area of $\partial \left(d\mathcal{V}\right)$ and $n_j$ the outward pointing versor locally perpendicular to $\partial \left(d\mathcal{V}\right)$. From Stokes theorem, one can write

$${\displaystyle \underset{\partial \left(d\mathcal{V}\right)}{\int }}{T}_I^{ij}{n}_j{d}^{2}S={\displaystyle \underset{d\mathcal{V}}{\int }}{\partial }_j{T}_I^{ij}{d}^{3}x,$$

which can be approximated as

$${\displaystyle \underset{d\mathcal{V}}{\int }}{\partial }_j{T}_I^{ij}{d}^{3}x\simeq {\partial }_j{T}_I^{ij}d\mathcal{V}$$

as $d\mathcal{V}$ tends to zero. When the symbol ${\mathbf{T}}_I$ is used for the tensor variable whose components are the $T_I^{ij}$, the force $d{\overrightarrow{F}}_{I\partial }$ may be written as

$$d{\overrightarrow{F}}_{I\partial }=-\overrightarrow{\partial }·{\mathbf{T}}_{I}d\mathcal{V}.$$

(77)

In general, Equation (19) holds, and divides ${\mathbf{T}}_I$ into a pressure part and a viscous part. When this is put into Equation (76), one has

$$d{\overrightarrow{F}}_{I\partial }=-\overrightarrow{\partial }·\left(p_I\mathbf{1}+{\tau }_I\right)d\mathcal{V}=\left(-\overrightarrow{\partial }{p}_I-\overrightarrow{\partial }·{\tau }_I\right)d\mathcal{V}.$$

(78)

The forces due to the other systems ${\mathcal{C}}_{J\ne I}$ are viscosity forces that can be seen as the friction due to the motion of the parcel $d{\mathcal{C}}_I$ through the viscous medium ${\mathcal{C}}_{J\ne I}$. Let the velocity of ${\mathcal{C}}_J$ be ${\overrightarrow{V}}_J$ at the position of the parcel $d{\mathcal{C}}_I$; if the time frequency of collision between an I and a J particle at $\overrightarrow{r}$ per unit mass is some ${\nu }_{IJ}$, the friction force $d{\overrightarrow{F}}_{JI}$ is

$$d{\overrightarrow{F}}_{JI\nu }=-{\nu }_{IJ}{m}_I\left(d\mathcal{V}\right)\left({\overrightarrow{V}}_I-{\overrightarrow{V}}_J\right);$$

then the total friction force due to the systems ${\mathcal{C}}_{J\ne I}$ reads

$$d{\overrightarrow{F}}_{I\nu }=-{\rho }_{I}d\mathcal{V}{\displaystyle \sum _{J\ne I}}{\nu }_{IJ}\left({\overrightarrow{V}}_I-{\overrightarrow{V}}_J\right).$$

(79)

The last system interacting with $d{\mathcal{C}}_I$ can be any mechanical wave field traveling through the atmosphere. When such a wave goes across the space, it carries momentum and energy, and can exchange these quantities with whatever it meets. In particular, this may be conveniently as the divergence of a tensor $-\overrightarrow{\partial }·{\tau }_{Iw}$, so the volume force applied by a mechanical wave reads:

$$d{\overrightarrow{F}}_{Iw}=-\overrightarrow{\partial }·{\tau }_{Iw}d\mathcal{V}.$$

(80)

We are finally in the position of writing the force ${\overrightarrow{f}}_I$ completely, getting rid of the infinitesimal volume $d\mathcal{V}$, as:

$$\begin{array}{c}{\rho }_I{\partial }_t{\overrightarrow{V}}_I+{\rho }_I\left({\overrightarrow{V}}_I·\overrightarrow{\partial }\right){\overrightarrow{V}}_I+m_I{\Gamma }_I{\overrightarrow{V}}_I={\delta }_I\left(\overrightarrow{E}+{\overrightarrow{V}}_I\times \overrightarrow{B}\right)+{\rho }_I{\overrightarrow{g}}_{eff}+\hfill \\ \\ -2{\rho }_I\overrightarrow{\Omega }\times {\overrightarrow{V}}_I-\overrightarrow{\partial }{p}_I-\overrightarrow{\partial }·{\tau }_I-{\rho }_I{\displaystyle \sum _{J\ne I}}{\nu }_{IJ}\left({\overrightarrow{V}}_I-{\overrightarrow{V}}_J\right)-\overrightarrow{\partial }·{\tau }_{Iw}.\hfill \end{array}$$

(81)

Equation (81) is the Navier–Stokes equation for theI-th fluid involved in the system, and it is clearly coupled with all the other fluids ${\mathcal{C}}_{J\ne I}$, and with the electromagnetic fields. One may work with the number densities of the chemical species, putting (10) into (81):

$$\begin{array}{c}{N}_I{\partial }_t{\overrightarrow{V}}_I+N_I\left({\overrightarrow{V}}_I·\overrightarrow{\partial }\right){\overrightarrow{V}}_I+{\Gamma }_I{\overrightarrow{V}}_I={\displaystyle \frac{q_I}{m_I}}{N}_I\left(\overrightarrow{E}+{\overrightarrow{V}}_I\times \overrightarrow{B}\right)+N_I{\overrightarrow{g}}_{eff}+\hfill \\ \\ -2N_I\overrightarrow{\Omega }\times {\overrightarrow{V}}_I-{\displaystyle \frac{1}{m_I}}\overrightarrow{\partial }{p}_I-{\displaystyle \frac{1}{m_I}}\left(\overrightarrow{\partial }·{\tau }_I+\overrightarrow{\partial }·{\tau }_{Iw}\right)-N_I{\displaystyle \sum _{J\ne I}}{\nu }_{IJ}\left({\overrightarrow{V}}_I-{\overrightarrow{V}}_J\right).\hfill \end{array}$$

(82)

Wherever the I-th element is present and $N_I\ne 0$, this can be further written as

$$\begin{array}{c}{\partial }_t{\overrightarrow{V}}_I+\left({\overrightarrow{V}}_I·\overrightarrow{\partial }\right){\overrightarrow{V}}_I+{\displaystyle \frac{{\Gamma }_I}{N_I}}{\overrightarrow{V}}_I={\displaystyle \frac{q_I}{m_I}}\left(\overrightarrow{E}+{\overrightarrow{V}}_I\times \overrightarrow{B}\right)+{\overrightarrow{g}}_{eff}-2\overrightarrow{\Omega }\times {\overrightarrow{V}}_I+\hfill \\ \\ -{\displaystyle \frac{1}{N_I{m}_I}}\overrightarrow{\partial }{p}_I-{\displaystyle \frac{1}{N_I{m}_I}}\left(\overrightarrow{\partial }·{\tau }_I+\overrightarrow{\partial }·{\tau }_{Iw}\right)-{\displaystyle \sum _{J\ne I}}{\nu }_{IJ}\left({\overrightarrow{V}}_I-{\overrightarrow{V}}_J\right).\hfill \end{array}$$

(83)

The sum of the two tensor terms $\overrightarrow{\partial }·{\tau }_I+\overrightarrow{\partial }·{\tau }_{Iw}$ is often referred to as a unique term ${\vartheta }_I={\tau }_I+{\tau }_{Iw}$, so that

$$\begin{array}{c}{\partial }_t{\overrightarrow{V}}_I+\left({\overrightarrow{V}}_I·\overrightarrow{\partial }\right){\overrightarrow{V}}_I+{\displaystyle \frac{{\Gamma }_I}{N_I}}{\overrightarrow{V}}_I={\displaystyle \frac{q_I}{m_I}}\left(\overrightarrow{E}+{\overrightarrow{V}}_I\times \overrightarrow{B}\right)+{\overrightarrow{g}}_{eff}-2\overrightarrow{\Omega }\times {\overrightarrow{V}}_I+\hfill \\ \\ -{\displaystyle \frac{1}{N_I{m}_I}}\overrightarrow{\partial }{p}_I-{\displaystyle \frac{1}{N_I{m}_I}}\overrightarrow{\partial }·{\vartheta }_I-{\displaystyle \sum _{J\ne I}}{\nu }_{IJ}\left({\overrightarrow{V}}_I-{\overrightarrow{V}}_J\right).\hfill \end{array}$$

(84)

As ${\tau }_{Iw}$ is mainly a friction term, the ${\vartheta }_I$ in (84) is generally referred to as general viscosity tensor.

3.4. Internal Energy Balance

The quantities $p_I$, $N_I$ or ${\tau }_I$ refer to the “inner structure” of $d{\mathcal{C}}_I$, which is composed of particles. As the parcel $d{\mathcal{C}}_I$ does contain a number of particles of the I-th chemical on the order of Avogadro’s number, it is considered a thermodynamical system, and its physical variables undergo thermodynamical relations; then, $p_I$, $N_I$ and ${\tau }_I$ will be involved in an internal energy balance

$$dU=/dQ+/dL.$$

(85)

where U is the internal energy, $/dQ$ is a portion of energy thermically exchanged and $/dL$ is a portion of work. The signs in (85) are chosen so that $/dQ$ is the heat acquired by the system, and $/dL$ is the quantity of mechanical work exerted on the parcel [34]. It is very important to underline that the energy balance we are speaking about is a thermal balance; we are not discussing the energy that $d{\mathcal{C}}_I$ releases or incorporates due to its center of mass motion throughout the space; here, we deal with energy exchanges that concern the internal degrees of freedom of the mechanical system $d{\mathcal{C}}_I$ treated in terms of equilibrium thermodynamics of the $O\left(N_A\right)$ particles of the parcel (this is why Equation (85) does not contain any potential energy term due to mechanical work done by external conservative forces on the center of mass degrees of freedom, i.e., no gravitational or electrostatic energy term). The inner structure of $d{\mathcal{C}}_I$ is mimicked again in Figure 4.

Let us consider the three elements $dU$, $/dQ$ and $/dL$ and write them in terms of the degrees of freedom of ${\mathcal{C}}_I$. These quantities $dU$, $/dQ$ and $/dL$ are variations/increments happening while the parcel CoM moves along the trajectory during some time $dt$ of a displacement $d{\overrightarrow{r}}_I={\overrightarrow{V}}_{I}dt$. This means that $dU\left(d{\mathcal{C}}_I\right)$ is, for example, the Lagrangian variation of the internal energy of the parcel $d{\mathcal{C}}_I$, so that:

$$dU\left(d{\mathcal{C}}_I\right)=dt{\displaystyle \frac{d}{dt}}U\left(d{\mathcal{C}}_I\right).$$

(86)

In order to write $U\left(d{\mathcal{C}}_I\right)$ correctly, we must first of all consider that it is a function of volume and temperature of the gas to which it refers:

$$U\left(d{\mathcal{C}}_I\right)=U\left(d\mathcal{V},T_I\right).$$

One can write its value working on the volume–temperature plane starting at some point $\mathrm{O}=\left(d\mathcal{V},T_0\right)$ with the same volume of the parcel, and integrate along an iso-volumic trajectory

$$U\left(d{\mathcal{C}}_I\right)=\underset{T_0}{\overset{T_I}{\int }}{C}_{VI}\left(T\right)dT+U_{\mathrm{O}}\left(d{\mathcal{C}}_I\right),$$

(87)

where $U_{\mathrm{O}}\left(d{\mathcal{C}}_I\right)$ is the energy at the point $\mathrm{O}$, and $T_0$ its temperature. Due to this expression, the variation $dU\left(d{\mathcal{C}}_I\right)$ on the left-hand side of (86) must be carefully calculated as

$$dU\left(d{\mathcal{C}}_I\right)=dt{\displaystyle \frac{dU\left(d{\mathcal{C}}_I\right)}{dt}}=dt{\displaystyle \frac{d}{dt}}\left[\underset{T_0}{\overset{T_I}{\int }}{C}_{VI}\left(T\right)dT+U_{\mathrm{O}}\left(d{\mathcal{C}}_I\right)\right].$$

(88)

It is possible to make this derivative when all the time dependencies are carefully considered; this is carried out in Appendix A. All in all, the result turns out to read:

$$dU\left(d{\mathcal{C}}_I\right)=\left[m_I{\Gamma }_I\underset{T_0}{\overset{T_I}{\int }}{c}_{VI}\left(T\right)dT+{\rho }_I{c}_{VI}\left(T_I\right)\left({\partial }_t{T}_I+{\overrightarrow{V}}_I·\overrightarrow{\partial }{T}_I\right)\right]dtd\mathcal{V}.$$

(89)

A little argument requires a comparison between this (89) and the expression (86). In Equation (86), $U\left(d{\mathcal{C}}_I\right)$ is not a scalar field in the physical space, but a function of the parcel degrees of freedom relative to its center of mass. When the expression (87) is introduced, one considers this as evidence, making $U\left(d{\mathcal{C}}_I\right)$ depend on $\overrightarrow{r}$ and t through the temperature $T_I$, so that the mathematical framework to arrive at the local representation is gained. What one must keep in mind is that the thermodynamics of $d{\mathcal{C}}_I\left(\overrightarrow{r}\right)$ just depends on the local position due to belonging to the parcel of CoM, equal to $\overrightarrow{r}$ at time t.

Let us turn to the term $/d{Q}_I$ of thermal exchange of energy between the parcel and the environment. Three mechanisms of heat exchange must be considered: thermal conduction $/d{Q}_{I,T}$, due to temperature differences between the $d{\mathcal{C}}_I$ and the nearby parcels; mechanical dissipation $/d{Q}_{I,w}$ due to interaction with the environmental part of ${\mathcal{C}}_I$ (and related to the tensor ${\tau }_I$); heat internal production and dispersion $/d{Q}_{I,int}$ due to other processes, more explicitly discussed below:

$$/d{Q}_I=/d{Q}_{I,T}+/d{Q}_{I,w}+/d{Q}_{I,int}.$$

(90)

Let us examine these addenda one by one.

The quantity of heat exchanged by the parcel due to thermal gradients can be expressed as the integral of the heat current all around the surface $\partial \left(d\mathcal{V}\right)$; considering that the heat spontaneously flows from warmer to cooler regions, one can write

$$/d{Q}_{I,T}=dt{\displaystyle \underset{\partial \left(d\mathcal{V}\right)}{\int }}{\kappa }_I\overrightarrow{\partial }{T}_I·\widehat{n}{d}^{2}S,$$

(91)

where $-{\kappa }_I\overrightarrow{\partial }{T}_I$ is the thermal current, and ${\kappa }_I$ the I-th thermal conductivity. The integral in (91) is positive when $\overrightarrow{\partial }{T}_I$ points from inside to outside the surface $\partial \left(d\mathcal{V}\right)$, so that the environment being hotter than the parcel will give a positive $/d{Q}_{I,T}$ to $d{\mathcal{C}}_I$. Mathematical symbols in (91) are the same as in (76). Transforming the surface integral in (91) via Stokes theorem

$$/d{Q}_{I,T}=dt{\displaystyle \underset{d\mathcal{V}}{\int }}\overrightarrow{\partial }·\left({\kappa }_I\overrightarrow{\partial }{T}_I\right)d^{3}x$$

and considering the smallness of the material parcel, one has:

$$/d{Q}_{I,T}=\overrightarrow{\partial }·\left({\kappa }_I\overrightarrow{\partial }{T}_I\right)d\mathcal{V}dt.$$

(92)

The quantity $/d{Q}_{I,w}$ is indicated in general as

$$/d{Q}_{I,w}={\Phi }_{I}d\mathcal{V}dt.$$

(93)

In a similar manner, we introduce a quantity $Q_I$ so that

$$/d{Q}_{I,int}={\rho }_I{Q}_{I}d\mathcal{V}dt.$$

(94)

The total heat contribution is included in the Equation (85) of internal energy as:

$$\begin{array}{c}\left[m_I{\Gamma }_I{\displaystyle {\int }_{T_0}^{T_I}}{c}_{VI}\left(T\right)dT+{\rho }_I{c}_{VI}\left(T_I\right)\left({\partial }_t{T}_I+{\overrightarrow{V}}_I·\overrightarrow{\partial }{T}_I\right)\right]dtd\mathcal{V}=\hfill \\ \\ =\overrightarrow{\partial }·\left({\kappa }_I\overrightarrow{\partial }{T}_I\right)d\mathcal{V}dt+{\Phi }_{I}d\mathcal{V}dt+{\rho }_I{Q}_{I}d\mathcal{V}dt+/dL.\hfill \end{array}$$

(95)

Let us now examine the work term. Consider that this infinitesimal work $/dL\left(d{\mathcal{C}}_I\right)$ is the portion of work done by the environment on the thermodynamical degrees of freedom of the parcel in the time $dt$. In particular, $/dL$ is the expansion work made by varying the value of $d\mathcal{V}$:

$$/dL=-p_{I}d\left(d\mathcal{V}\right)=-p_{I}dt{\displaystyle \frac{d}{dt}}\left(d\mathcal{V}\right)$$

(this expansion–compression work is different from the acceleration of the center of mass of $d{\mathcal{C}}_I$; the latter would be calculated through the power of the external forces applied to the $d{\mathcal{C}}_I$ in the momentum balance). Equation (30) leads to:

$$/dL=-p_I\left(\overrightarrow{\partial }·{\overrightarrow{V}}_I\right)d\mathcal{V}dt,$$

(96)

and the internal energy equation is finally added to (81) as a proper equation of motion

$$\begin{array}{c}{m}_I{\Gamma }_I{\displaystyle {\int }_{T_o}^{T_I}}{c}_{VI}\left(T\right)dT+{\rho }_I{c}_{VI}\left(T_I\right)\left({\partial }_t{T}_I+{\overrightarrow{V}}_I·\overrightarrow{\partial }{T}_I\right)=\hfill \\ \\ =\overrightarrow{\partial }·\left({\kappa }_I\overrightarrow{\partial }{T}_I\right)+\Phi +{\rho }_I{Q}_I-p_I\left(\overrightarrow{\partial }·{\overrightarrow{V}}_I\right).\hfill \end{array}$$

(97)

The whole set of “fundamental” equations involving the matter degrees of freedom can be displayed as

$$\left\{\begin{array}{c}{\partial }_t{\rho }_I+\overrightarrow{\partial }·\left({\rho }_I{\overrightarrow{V}}_I\right)=m_I{\Gamma }_I,\hfill \\ \\ {\rho }_I{\partial }_t{\overrightarrow{V}}_I+{\rho }_I\left({\overrightarrow{V}}_I·\overrightarrow{\partial }\right){\overrightarrow{V}}_I+m_I{\Gamma }_I{\overrightarrow{V}}_I={\delta }_I\left(\overrightarrow{E}+{\overrightarrow{V}}_I\times \overrightarrow{B}\right)+{\rho }_I{\overrightarrow{g}}_{eff}+\hfill \\ \\ -2{\rho }_I\overrightarrow{\Omega }\times {\overrightarrow{V}}_I-\overrightarrow{\partial }{p}_I-\overrightarrow{\partial }·{\tau }_I-{\rho }_I{\displaystyle \sum _{J\ne I}}{\nu }_{IJ}\left({\overrightarrow{V}}_I-{\overrightarrow{V}}_J\right)-\overrightarrow{\partial }·{\tau }_{Iw},\hfill \\ \\ m_I{\Gamma }_I{\displaystyle {\int }_{T_o}^{T_I}}{c}_{VI}\left(T\right)dT+{\rho }_I{c}_{VI}\left(T_I\right)\left({\partial }_t{T}_I+{\overrightarrow{V}}_I·\overrightarrow{\partial }{T}_I\right)=\hfill \\ \\ =\overrightarrow{\partial }·\left({\kappa }_I\overrightarrow{\partial }{T}_I\right)+\Phi +{\rho }_I{Q}_I-p_I\left(\overrightarrow{\partial }·{\overrightarrow{V}}_I\right),\hfill \end{array}\right.$$

(98)

which give us $1+3+1=5$ PDEs. The unknowns involved in them total more than five, so let us remember that they are

$$\begin{array}{ccccc}{\rho }_I,& V_I^i,& p_I,& {\tau }_I^{ij},& T_I\end{array}$$

for each fluid, giving $1+3+1+6+1=12$ quantities for each ${\mathcal{C}}_I$. Some more relationships must be added, in order to have a well-posed problem.

3.5. Some More Relationships

The next relationship that is useful to obtain as many equations as the dynamical variables is the angular momentum balance for the parcel $d{\mathcal{C}}_I$, which actually gives some useful aid. Indeed, the fact that there must be angular momentum conservation in fluid dynamics leads instead to some constraints on the stress tensors, which should be symmetric for the matter systems [26]. Actually, this reduces the components of ${\tau }_I^{ij}$ from 6 to 3. We are then left with $\left({\rho }_I,{\overrightarrow{V}}_I,p_I,{\tau }_I^{ij},T_I\right)$, with nine unknowns, while the system (98) contains just $1+3+1=5$ equations.

The fundamental equations for fluids are all in (98); writing them, we are finished with exploiting the general laws concerning every kind of fluid. This means that in order to obtain a number of equations equal to the number of matter unknowns, one has to start with particular hypotheses defining the special kind of fluid one is dealing with.

First of all, since we are treating the parcel $d{\mathcal{C}}_I$ of the fluid just like a thermodynamical system, we can turn to thermodynamics to find other useful equations. When the hypotheses described in Section 2.3 for the classical continuous description hold, we can say that the system is locally near its thermodynamical equilibrium, it has a well-defined state (represented by $p_I$ and $T_I$), and evolves by undergoing quasi-static transformations. As long as local thermodynamical equilibrium is supposed, some equation of state will hold and the tension $p_I$, the density ${\rho }_I$ and the temperature $T_I$ will be constrained to fulfill some relationship of the form:

$$f_I\left(p_I,{\rho }_I,T_I\right)=0$$

(99)

(as discussed in [5], this may not be always the case; in general, the local equilibrium hypothesis is consistent with smooth dynamics). In general, the ionospheric fluids and the thermosphere are assumed to be ideal gases [27]. For a volume V of $n_I$ moles of ideal gas ${\mathcal{C}}_I$, one has

$$p_{I}V=n_{I}R{T}_I;$$

when the system is the parcel $d{\mathcal{C}}_I$ one has $V=d\mathcal{V}$ and $n_I$ is the ratio between the mass of $d{\mathcal{C}}_I$ and the molar mass of the I-th gas ${\mu }_I$:

$$\begin{array}{ccc}{p}_{I}d\mathcal{V}={\displaystyle \frac{m\left(d{\mathcal{C}}_I\right)}{{\mu }_I}}R{T}_I,& p_{I}d\mathcal{V}={\displaystyle \frac{{\rho }_{I}d\mathcal{V}}{{\mu }_I}}R{T}_I,& p_I={\displaystyle \frac{{\rho }_I}{{\mu }_I}}R{T}_I.\end{array}$$

When the Avogadro number $N_A$ is involved, the equation of state turns into the following form:

$$p_I={\displaystyle \frac{{\rho }_I}{m_I}}{k}_B{T}_I,$$

where $k_B=1.3811\times {10}^{-23}\mathrm{Joule}/\mathrm{mol}·\mathrm{K}°$ is the Boltzmann factor. Then, (99) reads

$$m_I{p}_I={\rho }_I{k}_B{T}_I.$$

(100)

Equation (99) adds one relationship to the five equations in (98); then, we have six conditions, five PDEs and one constraint, the nine variables $\left({\rho }_I,{\overrightarrow{V}}_I,p_I,{\tau }_I^{ij},T_I\right)$, and three more equations are still needed.

Other important relationships increasing the number of useful equations up to nine, and thus eliminating the underdetermination question of the boundary problem given by (98) and (99), are provided by the dependence (18) giving the tensor ${\mathbf{T}}_I$ in terms of the velocity ${\overrightarrow{V}}_I$, in particular of the non-ideal part ${\tau }_I$. These relationships will be of the form

$${\tau }_I^{ij}={\tau }_I^{ij}\left({\overrightarrow{V}}_I,\dots \right)$$

(101)

and will total as many as the components of ${\tau }_I$, i.e., three more conditions, as these off-diagonal terms are symmetric, as ${\tau }_I^{ij}={\tau }_I^{ji}$, due to the angular momentum conservation.

As explained in [15], the components ${\tau }_I^{ij}$ are expected to be composed of linear functions of the space-gradients of ${\overrightarrow{V}}_I$; fluid viscosity tries to keep the nearby strata of the fluid in solidal motion, so the strength of its force must be (at least) linear in these infinitesimal differences; moreover, the viscous forces must be zero when the fluids move with rigid rotation

$$\begin{array}{cccc}{V}_I^i={{ϵ}^i}_{jk}{\Omega }_I^j{x}^k,& {\partial }_i{\Omega }_I^j=0& \Rightarrow & {\tau }_I^{ij}\left({\overrightarrow{V}}_I,\dots \right)=0,\end{array}$$

(102)

because in this case, no relative velocity exists between two points of the system. Thanks to this reasoning, the form suggested in [15] reads

$${\tau }_{Iij}\left({\overrightarrow{V}}_I,{\eta }_I,{\zeta }_I\right)={\eta }_I\left({\partial }_j{V}_{Ii}+{\partial }_i{V}_{Ij}-{\displaystyle \frac{2}{3}}{\delta }_{ij}{\partial }_k{V}_I^k\right)+{\zeta }_I{\delta }_{ij}{\partial }_k{V}_I^k.$$

(103)

${\eta }_I$ and ${\zeta }_I$ are two constant scalar coefficients characterizing the nature of the fluid ${\mathcal{C}}_I$. This form of ${\tau }_I$ is referred to as Newtonian viscosity, and it turns out to be the best-fitting solution for the atmospheric fluids.

When the divergence of this ${\tau }_I$ is evaluated, one obtains

$$\overrightarrow{\partial }·{\tau }_I={\eta }_I{\partial }^2{\overrightarrow{V}}_I+\left({\displaystyle \frac{{\eta }_I}{3}}+{\zeta }_I\right)\overrightarrow{\partial }\left(\overrightarrow{\partial }·{\overrightarrow{V}}_I\right),$$

and introducing

$${\eta }_I^{\prime }={\displaystyle \frac{{\eta }_I}{3}}+{\zeta }_I$$

(104)

one immediately writes

$$\overrightarrow{\partial }·{\tau }_I={\eta }_I{\partial }^2{\overrightarrow{V}}_I+{\eta }_I^{\prime }\overrightarrow{\partial }\left(\overrightarrow{\partial }·{\overrightarrow{V}}_I\right).$$

(105)

As the three assumptions (101) are made and the ${\tau }_I^{ij}$ are not independent anymore but rather expressed as functions of ${\overrightarrow{V}}_I$, the equations of motion form the following partial differential equation and constraint system:

$$\left\{\begin{array}{c}{\partial }_t{\rho }_I+\overrightarrow{\partial }·\left({\rho }_I{\overrightarrow{V}}_I\right)=m_I{\Gamma }_I,\hfill \\ \\ {\rho }_I{\partial }_t{\overrightarrow{V}}_I+{\rho }_I\left({\overrightarrow{V}}_I·\overrightarrow{\partial }\right){\overrightarrow{V}}_I+m_I{\Gamma }_I{\overrightarrow{V}}_I={\delta }_I\left(\overrightarrow{E}+{\overrightarrow{V}}_I\times \overrightarrow{B}\right)+{\rho }_I{\overrightarrow{g}}_{eff}+\hfill \\ \\ -2{\rho }_I\overrightarrow{\Omega }\times {\overrightarrow{V}}_I-\overrightarrow{\partial }{p}_I-\overrightarrow{\partial }·{\tau }_I\left({\overrightarrow{V}}_I,\dots \right)-{\rho }_I{\displaystyle \sum _{J\ne I}}{\nu }_{IJ}\left({\overrightarrow{V}}_I-{\overrightarrow{V}}_J\right)-\overrightarrow{\partial }·{\tau }_{Iw},\hfill \\ \\ m_I{\Gamma }_I\underset{T_o}{\overset{T_I}{\int }}{c}_{VI}\left(T\right)dT+{\rho }_I{c}_{VI}{\partial }_t{T}_I+{\rho }_I{c}_{VI}{\overrightarrow{V}}_I·\overrightarrow{\partial }{T}_I=\hfill \\ \\ =\overrightarrow{\partial }·\left({\kappa }_I\overrightarrow{\partial }{T}_I\right)+{\Phi }_I+{\rho }_I{Q}_I-p_I\left(\overrightarrow{\partial }·{\overrightarrow{V}}_I\right),\hfill \\ \\ f_I\left(p_I,{\rho }_I,T_I\right)=0.\hfill \end{array}\right.$$

(106)

Through the assumption (105), one finally obtains:

$$\left\{\begin{array}{c}{\partial }_t{\rho }_I+\overrightarrow{\partial }·\left({\rho }_I{\overrightarrow{V}}_I\right)=m_I{\Gamma }_I,\hfill \\ \\ {\rho }_I{\partial }_t{\overrightarrow{V}}_I+{\rho }_I\left({\overrightarrow{V}}_I·\overrightarrow{\partial }\right){\overrightarrow{V}}_I+m_I{\Gamma }_I{\overrightarrow{V}}_I={\delta }_I\left(\overrightarrow{E}+{\overrightarrow{V}}_I\times \overrightarrow{B}\right)+{\rho }_I{\overrightarrow{g}}_{eff}+\hfill \\ \\ -2{\rho }_I\overrightarrow{\Omega }\times {\overrightarrow{V}}_I-\overrightarrow{\partial }{p}_I-\eta {\partial }^2{\overrightarrow{V}}_I-{\eta }^{\prime }\overrightarrow{\partial }\left(\overrightarrow{\partial }·{\overrightarrow{V}}_I\right)-{\rho }_I{\displaystyle \sum _{J\ne I}}{\nu }_{IJ}\left({\overrightarrow{V}}_I-{\overrightarrow{V}}_J\right)-\overrightarrow{\partial }·{\tau }_{Iw},\hfill \\ \\ m_I{\Gamma }_I\underset{T_o}{\overset{T_I}{\int }}{c}_{VI}\left(T\right)dT+{\rho }_I{c}_{VI}{\partial }_t{T}_I+{\rho }_I{c}_{VI}{\overrightarrow{V}}_I·\overrightarrow{\partial }{T}_I=\hfill \\ \\ =\overrightarrow{\partial }·\left({\kappa }_I\overrightarrow{\partial }{T}_I\right)+{\Phi }_I+{\rho }_I{Q}_I-p_I\left(\overrightarrow{\partial }·{\overrightarrow{V}}_I\right),\hfill \\ \\ f_I\left(p_I,{\rho }_I,T_I\right)=0.\hfill \end{array}\right.$$

(107)

Possible solutions, i.e., motions for the fluid, are found when one writes explicitly the quantities ${\Gamma }_I$, ${\Phi }_I$ and $Q_I$ in terms of the other variables, making hypotheses like (99) and (105). These assumptions will be referred to as constitutive hypotheses. The system of PDEs and the equation of state (107) are namely all we need to describe the ionospheric gases as “smooth” fluids.

The term $\overrightarrow{\partial }·{\tau }_{Iw}$ in the Navier–Stokes equation can be calculated when a field of mechanical waves is assigned: otherwise, one should add another dynamical variable representing the field of elastic oscillation throughout the medium, say $\overrightarrow{u}$, and its own equation of motion, then evaluate the force $-\overrightarrow{\partial }·{\tau }_{Iw}$ as a function of $\overrightarrow{u}$. The elastic oscillations are usually thought of as a dissipative perturbation of the continuum that propagates throughout the system, superimposed on the motions described by the field ${\overrightarrow{V}}_I$; we can say that the medium with velocity ${\overrightarrow{V}}_I$ can be regarded as some background along which the perturbation $\overrightarrow{u}$ travels.

Note that the study of large structures of the Earth’s atmosphere as a collection of shells of matter is generally dealt with by assuming the velocity to be divergenceless, i.e., assuming the fluid to be incompressible.

$$\overrightarrow{\partial }·{\overrightarrow{V}}_I=0:$$

(108)

This (108) means there is no source and no sink in the flow of the ${\mathcal{C}}_I$ fluid, as Equation (30) says. When this incompressibility hypothesis is made, Equation (107) can be re-written as

$$\left\{\begin{array}{c}{\partial }_t{\rho }_I+{\overrightarrow{V}}_I·\overrightarrow{\partial }{\rho }_I=m_I{\Gamma }_I,\hfill \\ \\ {\rho }_I{\partial }_t{\overrightarrow{V}}_I+{\rho }_I\left({\overrightarrow{V}}_I·\overrightarrow{\partial }\right){\overrightarrow{V}}_I+m_I{\Gamma }_I{\overrightarrow{V}}_I={\delta }_I\left(\overrightarrow{E}+{\overrightarrow{V}}_I\times \overrightarrow{B}\right)+{\rho }_I{\overrightarrow{g}}_{eff}+\hfill \\ \\ -2{\rho }_I\overrightarrow{\Omega }\times {\overrightarrow{V}}_I-\overrightarrow{\partial }{p}_I-\eta {\partial }^2{\overrightarrow{V}}_I-{\rho }_I{\displaystyle \sum _{J\ne I}}{\nu }_{IJ}\left({\overrightarrow{V}}_I-{\overrightarrow{V}}_J\right)-\overrightarrow{\partial }·{\tau }_{Iw},\hfill \\ \\ m_I{\Gamma }_I\underset{T_o}{\overset{T_I}{\int }}{c}_{VI}\left(T\right)dT+{\rho }_I{c}_{VI}{\partial }_t{T}_I+{\rho }_I{c}_{VI}{\overrightarrow{V}}_I·\overrightarrow{\partial }{T}_I=\hfill \\ \\ =\overrightarrow{\partial }·\left({\kappa }_I\overrightarrow{\partial }{T}_I\right)+{\Phi }_I+{\rho }_I{Q}_I,\hfill \\ \\ f_I\left(p_I,{\rho }_I,T_I\right)=0.\hfill \end{array}\right.$$

(109)

It is important to underline that (108) and (109) are essentially approximations; in general, ionospheric continua are compressible fluids. Nevertheless, this $\overrightarrow{\partial }·{\overrightarrow{V}}_I=0$ works fine for neutrals; the charged part of the upper atmosphere shows compressibility along the magnetic field $\overrightarrow{B}$ and incompressibility perpendicular to it.

3.6. Maxwell Equations

The system (107), or its incompressible equivalent (109), contains six more variables that may either be assigned as “external” rigid fields, or integrated consistently as dynamical variables: the electromagnetic fields $\overrightarrow{E}$ and $\overrightarrow{B}$, subject to Maxwell Equations that couple them to charged matter.

The equations of motion for $\overrightarrow{E}$ and $\overrightarrow{B}$ are the well-known Maxwell equations [28], which can be written in $SO\left(3\right)$-vector formalism as

$$\left\{\begin{array}{c}\begin{array}{cc}\overrightarrow{\partial }·\overrightarrow{E}={\displaystyle \frac{\delta }{{\epsilon }_0}},& \overrightarrow{\partial }·\overrightarrow{B}=0,\end{array}\hfill \\ \\ \begin{array}{cc}\overrightarrow{\partial }\times \overrightarrow{E}=-{\partial }_t\overrightarrow{B},& \overrightarrow{\partial }\times \overrightarrow{B}={\mu }_0\left({\overrightarrow{J}}_q+{\epsilon }_0{\partial }_t\overrightarrow{E}\right).\end{array}\hfill \end{array}\right.$$

(110)

The sources of $\overrightarrow{E}$ and $\overrightarrow{B}$ are related to ${\mathcal{C}}_I$ local respective quantities. In particular, the distribution $\delta$ reads:

$$\delta ={\displaystyle \sum _I}{\delta }_I,$$

(111)

or equivalently:

$$\delta ={\displaystyle \sum _I}{q}_I{N}_I,\delta ={\displaystyle \sum _I}{\displaystyle \frac{q_I}{m_I}}{\rho }_I.$$

(112)

The vector ${\overrightarrow{J}}_q$ is calculated as follows:

$${\overrightarrow{J}}_q={\displaystyle \sum _I}{q}_I{N}_I{\overrightarrow{V}}_I\stackrel{\mathrm{def}}{=}{\displaystyle \sum _I}{q}_I{\overrightarrow{J}}_I.$$

(113)

These two source fields couple the (charged) ionospheric matter with the electromagnetic fields. The densities $\delta$ and ${\overrightarrow{J}}_q$ are related to each other by a charge conservation balance that reads:

$${\partial }_t\delta +\overrightarrow{\partial }·{\overrightarrow{J}}_q=0.$$

(114)

There is no source term anyway, and this is a very severe conservation; the whole gauge nature of the electromagnetic field does depend on ${\partial }_t\delta +\overrightarrow{\partial }·{\overrightarrow{J}}_q$ being zero [35].

Equation (110) may be expressed as follows:

$$\left\{\begin{array}{c}\begin{array}{cc}\overrightarrow{\partial }·\overrightarrow{E}={\displaystyle \sum _I}{\displaystyle \frac{q_I}{{\epsilon }_0}}{N}_I,& \overrightarrow{\partial }·\overrightarrow{B}=0,\end{array}\hfill \\ \\ \begin{array}{cc}\overrightarrow{\partial }\times \overrightarrow{E}=-{\partial }_t\overrightarrow{B},& \overrightarrow{\partial }\times \overrightarrow{B}={\mu }_0\left({\displaystyle \sum _I}{q}_I{N}_I{\overrightarrow{V}}_I+{\epsilon }_0{\partial }_t\overrightarrow{E}\right).\end{array}\hfill \end{array}\right.$$

(115)

Maxwell Equation (115) are conveniently specialized to describe the LIM excluding extremely fast phenomena, making the following approximations:

• the displacement current is considered much smaller than the matter currents

  $$\left|{\epsilon }_0{\partial }_t\overrightarrow{E}\right|\ll \left|{\overrightarrow{J}}_q\right|,$$

  and is usually neglected:

  $${\epsilon }_0{\partial }_t\overrightarrow{E}\simeq 0;$$

  (116)
• the magnetic field produced by ionospheric currents is much smaller than the geomagnetic one

  $$\left|\delta \overrightarrow{B}\right|\ll {\overrightarrow{B}}_0,$$

  and it is assumed as zero too; this leads to the electrostatic nature of $\overrightarrow{E}$, considering that ${\partial }_t{\overrightarrow{B}}_0=0$ and that the approximation $\delta \overrightarrow{B}\simeq 0$ ends up yielding ${\partial }_t\overrightarrow{B}=0$, so that:

  $$\overrightarrow{\partial }\times \overrightarrow{E}\simeq 0;$$

  (117)
• electric charge densities producing important electric fields are very small, and so are their time derivatives

  $${\partial }_t\delta \simeq 0,$$

  so that the corresponding currents must be thought of as divergenceless:

  $$\overrightarrow{\partial }·{\overrightarrow{J}}_q\simeq 0,$$

  (118)

  and this is practically true almost everywhere in the ionosphere.

When the assumptions (116), (117) and (118) are considered, Equation (110) become:

$$\left\{\begin{array}{c}\begin{array}{ccc}\overrightarrow{\partial }·\overrightarrow{E}={\displaystyle \frac{\delta }{{\epsilon }_0}},& \overrightarrow{\partial }·\overrightarrow{B}=0,& \overrightarrow{\partial }·{\overrightarrow{J}}_q=0,\end{array}\hfill \\ \\ \begin{array}{cc}\overrightarrow{\partial }\times \overrightarrow{E}=0,& \overrightarrow{\partial }\times \overrightarrow{B}={\mu }_0{\overrightarrow{J}}_q,\end{array}\hfill \end{array}\right.$$

(119)

or

$$\left\{\begin{array}{c}\begin{array}{ccc}\overrightarrow{\partial }·\overrightarrow{E}={\displaystyle \sum _I}{\displaystyle \frac{q_I}{{\epsilon }_0}}{N}_I,& \overrightarrow{\partial }·\overrightarrow{B}=0,& \overrightarrow{\partial }·\left({\displaystyle \sum _I}{q}_I{N}_I{\overrightarrow{V}}_I\right)=0,\end{array}\hfill \\ \\ \begin{array}{cc}\overrightarrow{\partial }\times \overrightarrow{E}=0,& \overrightarrow{\partial }\times \overrightarrow{B}={\mu }_0{\displaystyle \sum _I}{q}_I{N}_I{\overrightarrow{V}}_I.\end{array}\hfill \end{array}\right.$$

(120)

As the electric neutrality is assumed, one has a divergenceless electric field too

$$\overrightarrow{\partial }·\overrightarrow{E}=0.$$

However, there are very important exceptions to this case, as in the case of terminators and the consequent “fountain effect”; see [28,36].

3.7. Neutral Components

In this subsection, we will consider the application of Equation (106) to the case of neutral constituents, those ${\mathcal{C}}_I$ for which one has:

$$q_I=0.$$

(121)

Putting (121) into (106), one finds

$$\left\{\begin{array}{c}{\partial }_t{\rho }_h+\overrightarrow{\partial }·\left({\rho }_h{\overrightarrow{V}}_h\right)=m_h{\Gamma }_h,\hfill \\ \\ {\rho }_h{\partial }_t{\overrightarrow{V}}_h+{\rho }_h\left({\overrightarrow{V}}_h·\overrightarrow{\partial }\right){\overrightarrow{V}}_h+m_h{\Gamma }_h{\overrightarrow{V}}_h={\rho }_h{\overrightarrow{g}}_{eff}-2{\rho }_h\overrightarrow{\Omega }\times {\overrightarrow{V}}_h+\hfill \\ \\ -\overrightarrow{\partial }{p}_h-\overrightarrow{\partial }·{\tau }_h\left({\overrightarrow{V}}_h,\dots \right)-{\rho }_h{\displaystyle \sum _{J\ne h}}{\nu }_{hJ}\left({\overrightarrow{V}}_h-{\overrightarrow{V}}_J\right)-\overrightarrow{\partial }·{\tau }_{hw},\hfill \\ \\ m_h{\Gamma }_h\underset{T_O}{\overset{T_h}{\int }}{c}_{Vh}\left(T\right)dT+{\rho }_h{c}_{Vh}{\partial }_t{T}_h+{\rho }_h{c}_{Vh}{\overrightarrow{V}}_h·\overrightarrow{\partial }{T}_h=\hfill \\ \\ =\overrightarrow{\partial }·\left({\kappa }_h\overrightarrow{\partial }{T}_h\right)+{\Phi }_h+{\rho }_h{Q}_h-p_h\left(\overrightarrow{\partial }·{\overrightarrow{V}}_h\right),\hfill \\ \\ f_h\left(p_h,{\rho }_h,T_h\right)=0:\hfill \end{array}\right.$$

(122)

of course, one can eliminate the electromagnetic part of the forces.

Equation (122) are usable in their own right as field equations describing the single neutral species interacting with all the other parts of the physical system. However, as one is often interested in treating the ionosphere as the charged part of the atmosphere embedded in the system of neutrals as a whole, it is useful to define the two quantities $\rho$ and $\overrightarrow{U}$ as in (22) to describe the neutrals all together, and consider obtaining equations for these collective variables starting from (122). The equations are summed over the neutral species as

$$\left\{\begin{array}{c}{\partial }_t{\displaystyle \sum _h}{\rho }_h+\overrightarrow{\partial }·\left({\displaystyle \sum _h}{\rho }_h{\overrightarrow{V}}_h\right)={\displaystyle \sum _h}{m}_h{\Gamma }_h,\hfill \\ \\ {\displaystyle \sum _h}{\rho }_h{\partial }_t{\overrightarrow{V}}_h+{\displaystyle \sum _h}{\rho }_h\left({\overrightarrow{V}}_h·\overrightarrow{\partial }\right){\overrightarrow{V}}_h+{\displaystyle \sum _h}{m}_h{\Gamma }_h{\overrightarrow{V}}_h={\displaystyle \sum _h}{\rho }_h{\overrightarrow{g}}_{eff}-2{\displaystyle \sum _h}{\rho }_h\overrightarrow{\Omega }\times {\overrightarrow{V}}_h+\hfill \\ \\ -\overrightarrow{\partial }{\displaystyle \sum _h}{p}_h-\overrightarrow{\partial }·{\displaystyle \sum _h}{\tau }_h\left({\overrightarrow{V}}_h,\dots \right)-{\displaystyle \sum _h}{\rho }_h{\displaystyle \sum _{J\ne h}}{\nu }_{hJ}\left({\overrightarrow{V}}_h-{\overrightarrow{V}}_J\right)-{\displaystyle \sum _h}\overrightarrow{\partial }·{\tau }_{hw},\hfill \\ \\ {\displaystyle \sum _h}{m}_h{\Gamma }_h\underset{T_O}{\overset{T_h}{\int }}{c}_{Vh}\left(T\right)dT+{\displaystyle \sum _h}{\rho }_h{c}_{Vh}{\partial }_t{T}_h+{\displaystyle \sum _h}{\rho }_h{c}_{Vh}{\overrightarrow{V}}_h·\overrightarrow{\partial }{T}_h=\hfill \\ \\ =\overrightarrow{\partial }·\left({\displaystyle \sum _h}{\kappa }_h\overrightarrow{\partial }{T}_h\right)+{\displaystyle \sum _h}{\Phi }_h+{\displaystyle \sum _h}{\rho }_h{Q}_h-{\displaystyle \sum _h}{p}_h\left(\overrightarrow{\partial }·{\overrightarrow{V}}_h\right).\hfill \end{array}\right.$$

(123)

Summing over h, the equation of state would not make any sense. Instead, one can add an equation of state for the whole neutral matter if suitable assumptions can be made.

Consider the mass balance equations summed. The left-hand side of the first PDE in (123) can be transformed by using the definitions (22); moreover, giving the following definition:

$$G_0={\displaystyle \sum _h}{m}_h{\Gamma }_h,$$

(124)

one ends up with

$${\partial }_t\rho +\overrightarrow{\partial }·\left(\rho \overrightarrow{U}\right)=G_0.$$

(125)

There are regions of the atmosphere in which the rate $G_0$ can be neglected with respect to the other rate of production loss, essentially those where the presence of neutrals prevails over that of charged species. There is also a region in which the ionization is so small that it can be neglected completely; in this case, one should set

$$G_0\simeq 0$$

(126)

and then (125) becomes the total mass conservation paradigm tout court, as neutrals are basically the only form of matter:

$${\partial }_t\rho +\overrightarrow{\partial }·\left(\rho \overrightarrow{U}\right)=0.$$

(127)

When (127) holds, the equations of motion of the whole system reduce to (122), and one has no need to refer to the equations of charged species, or to what comes out from (123) when neutrals are treated as a unique fluid component.

On the other hand, there are regions in which neutrals almost do not exist, such as the plasmasphere, where the atmospheric matter is fully ionized. In these cases, one can neglect the density $\rho$ compared to the ${\rho }_I$s of charged species. Then, Equation (125) becomes unimportant; the dynamical effect of neutrals becomes simply some perturbative drag affecting the motion of plasma. In such situations, the perturbative drag is simply considered as an assigned external term.

As usual, the most difficult case is that in which $G_0$ must be considered different from zero. If one defines some mass of the “average neutral species”

$$m_0={\displaystyle \frac{{\displaystyle \sum _h}{m}_h{N}_h}{{\displaystyle \sum _h}{N}_h}}$$

(128)

and also

$${\Gamma }_0={\displaystyle \frac{1}{m_0}}{\displaystyle \sum _h}{m}_h{\Gamma }_h,$$

(129)

the mass balance equation for neutrals turns out to be:

$${\partial }_t\rho +\overrightarrow{\partial }·\left(\rho \overrightarrow{U}\right)=m_0{\Gamma }_0.$$

(130)

Equation (130) is then put in (123) replacing the first one:

$$\left\{\begin{array}{c}{\partial }_t\rho +\overrightarrow{\partial }·\left(\rho \overrightarrow{U}\right)=m_0{\Gamma }_0,\hfill \\ \\ {\displaystyle \sum _h}{\rho }_h{\partial }_t{\overrightarrow{V}}_h+{\displaystyle \sum _h}{\rho }_h\left({\overrightarrow{V}}_h·\overrightarrow{\partial }\right){\overrightarrow{V}}_h+{\displaystyle \sum _h}{m}_h{\Gamma }_h{\overrightarrow{V}}_h={\displaystyle \sum _h}{\rho }_h{\overrightarrow{g}}_{eff}-2{\displaystyle \sum _h}{\rho }_h\overrightarrow{\Omega }\times {\overrightarrow{V}}_h+\hfill \\ \\ -\overrightarrow{\partial }{\displaystyle \sum _h}{p}_h-\overrightarrow{\partial }·{\displaystyle \sum _h}{\tau }_h\left({\overrightarrow{V}}_h,\dots \right)-{\displaystyle \sum _h}{\rho }_h{\displaystyle \sum _{J\ne h}}{\nu }_{hJ}\left({\overrightarrow{V}}_h-{\overrightarrow{V}}_J\right)-{\displaystyle \sum _h}\overrightarrow{\partial }·{\tau }_{hw},\hfill \\ \\ {\displaystyle \sum _h}{m}_h{\Gamma }_h\underset{T_O}{\overset{T_h}{\int }}{c}_{Vh}\left(T\right)dT+{\displaystyle \sum _h}{\rho }_h{c}_{Vh}{\partial }_t{T}_h+{\displaystyle \sum _h}{\rho }_h{c}_{Vh}{\overrightarrow{V}}_h·\overrightarrow{\partial }{T}_h=\hfill \\ \\ =\overrightarrow{\partial }·\left({\displaystyle \sum _h}{\kappa }_h\overrightarrow{\partial }{T}_h\right)+{\displaystyle \sum _h}{\Phi }_h+{\displaystyle \sum _h}{\rho }_h{Q}_h-{\displaystyle \sum _h}{p}_h\left(\overrightarrow{\partial }·{\overrightarrow{V}}_h\right).\hfill \end{array}\right.$$

(131)

Let us now consider the second equation in (131); one would like to obtain a Navier–Stokes equation for all the neutrals as a whole, and some manipulations are necessary in order to accomplish this, precisely those revealed in Appendix B. One finally obtains an equation involving $\rho$ and $\overrightarrow{U}$ only:

$${\displaystyle \frac{d}{dt}}\left(\rho \overrightarrow{U}\right)=\rho {\overrightarrow{g}}_{eff}-2\overrightarrow{\Omega }\times \rho \overrightarrow{U}-\overrightarrow{\partial }p-\overrightarrow{\partial }·{\tau }_0-\overrightarrow{\partial }·{\tau }_{0w}-{\displaystyle \sum _Y}{\nu }_{0Y}\rho \left(\overrightarrow{U}-{\overrightarrow{V}}_Y\right).$$

(132)

For applied studies, the divergence $-\overrightarrow{\partial }·{\tau }_0$ must be written more explicitly $\overrightarrow{\partial }·{\tau }_0={\eta }_0{\partial }^2\overrightarrow{U}$, as the neutral component of the LIM is considered a Newtonian fluid (all the neutrals are), so that:

$$\begin{array}{c}{\displaystyle \frac{d}{dt}}\left(\rho \overrightarrow{U}\right)=\rho {\overrightarrow{g}}_{eff}-2\rho \overrightarrow{\Omega }\times \overrightarrow{U}-\overrightarrow{\partial }p-{\eta }_0{\partial }^2\overrightarrow{U}+\hfill \\ \\ -{\eta }_0^{\prime }\overrightarrow{\partial }\left(\overrightarrow{\partial }·\overrightarrow{U}\right)-\overrightarrow{\partial }·{\tau }_{0w}-{\displaystyle \sum _Y}{\nu }_{0Y}\rho \left(\overrightarrow{U}-{\overrightarrow{V}}_Y\right).\hfill \end{array}$$

(133)

In order to study the large-scale phenomena, we usually assume

$$\overrightarrow{\partial }·\overrightarrow{U}=0,$$

(134)

so that the equation reads:

$${\displaystyle \frac{d}{dt}}\left(\rho \overrightarrow{U}\right)=\rho {\overrightarrow{g}}_{eff}-2\rho \overrightarrow{\Omega }\times \overrightarrow{U}-\overrightarrow{\partial }p-{\eta }_0{\partial }^2\overrightarrow{U}-\overrightarrow{\partial }·{\tau }_{0w}-{\displaystyle \sum _Y}{\nu }_{0Y}\rho \left(\overrightarrow{U}-{\overrightarrow{V}}_Y\right).$$

(135)

In general, the incompressibility (134) is an approximation that works fine in “quiet” conditions, i.e., when small-scale mixing and turbulent phenomena are neglected. It is better said that under the turbopause, for describing the neutral matter evolution at macroscopic scales, one thinks of a gas of extended structures, the eddies, to which the velocity $\overrightarrow{U}$ is attributed. The viscosity ${\eta }_0$ is then the coefficient evaluated in the eddy interaction theory. At the same large scales, the fluid over the turbopause is treated as a perfect gas of molecules, and the factor $\eta$ is the viscosity due to particle collisions.

As neutral atmosphere incompressiblity is postulated, one can re-write (131) as:

$$\left\{\begin{array}{c}{\partial }_t\rho +\overrightarrow{\partial }·\left(\rho \overrightarrow{U}\right)=m_0{\Gamma }_0,\hfill \\ \\ {\displaystyle \frac{d}{dt}}\left(\rho \overrightarrow{U}\right)=\rho {\overrightarrow{g}}_{eff}-2\rho \overrightarrow{\Omega }\times \overrightarrow{U}-\overrightarrow{\partial }p-\overrightarrow{\partial }·{\tau }_0-\overrightarrow{\partial }·{\tau }_{0w}-{\displaystyle \sum _Y}{\nu }_{0Y}\rho \left(\overrightarrow{U}-{\overrightarrow{V}}_Y\right),\hfill \\ \\ {\displaystyle \sum _h}{m}_h{\Gamma }_h\underset{T_O}{\overset{T_h}{\int }}{c}_{Vh}\left(T\right)dT+{\displaystyle \sum _h}{\rho }_h{c}_{Vh}{\partial }_t{T}_h+{\displaystyle \sum _h}{\rho }_h{c}_{Vh}{\overrightarrow{V}}_h·\overrightarrow{\partial }{T}_h=\hfill \\ \\ =\overrightarrow{\partial }·\left({\displaystyle \sum _h}{\kappa }_h\overrightarrow{\partial }{T}_h\right)+{\displaystyle \sum _h}{\Phi }_h+{\displaystyle \sum _h}{\rho }_h{Q}_h-{\displaystyle \sum _h}{p}_h\left(\overrightarrow{\partial }·{\overrightarrow{V}}_h\right).\hfill \end{array}\right.$$

(136)

Let us deal with the last of Equation (136), namely thermodynamics. First of all, one has to assume that all the neutral species have the same temperature:

$$T_h=T.$$

(137)

Then

$$\begin{array}{c}{\displaystyle \sum _h}{m}_h{\Gamma }_h\underset{T_O}{\overset{T}{\int }}{c}_{Vh}\left(T^{\prime }\right)d{T}^{\prime }+{\partial }_{t}T{\displaystyle \sum _h}{\rho }_h{c}_{Vh}+\overrightarrow{\partial }T·{\displaystyle \sum _h}{\rho }_h{c}_{Vh}{\overrightarrow{V}}_h=\hfill \\ \\ =\overrightarrow{\partial }·\left(\overrightarrow{\partial }T{\displaystyle \sum _h}{\kappa }_h\right)+{\displaystyle \sum _h}{\Phi }_h+{\displaystyle \sum _h}{\rho }_h{Q}_h-{\displaystyle \sum _h}{p}_h\left(\overrightarrow{\partial }·{\overrightarrow{V}}_h\right).\hfill \end{array}$$

The extensive quantities for the neutral fluid as a whole can be obtained simply by summing the partial ones; then one has

$$\begin{array}{ccc}{\displaystyle \sum _h}{\kappa }_h={\kappa }_0,& {\displaystyle \sum _h}{\Phi }_h={\Phi }_0,& {\displaystyle \sum _h}{\rho }_h{Q}_h=\rho Q_0,\end{array}$$

(138)

and is able to write the equation of internal energy balance as:

$$\begin{array}{c}{\displaystyle \sum _h}{m}_h{\Gamma }_h\underset{T_O}{\overset{T}{\int }}{c}_{Vh}\left(T^{\prime }\right)d{T}^{\prime }+{\partial }_{t}T{\displaystyle \sum _h}{\rho }_h{c}_{Vh}+\overrightarrow{\partial }T·{\displaystyle \sum _h}{\rho }_h{c}_{Vh}{\overrightarrow{V}}_h=\hfill \\ \\ =\overrightarrow{\partial }·\left({\kappa }_0\overrightarrow{\partial }T\right)+{\Phi }_0+\rho Q_0-{\displaystyle \sum _h}{p}_h\left(\overrightarrow{\partial }·{\overrightarrow{V}}_h\right).\hfill \end{array}$$

The last term on the right-hand side is the sum over all the contributions of mechanical work passed to thermodynamical degrees of freedom for the neutral components, so it is the total work applied to the neutrals as a whole. One has:

$$-{\displaystyle \sum _h}{p}_h\left(\overrightarrow{\partial }·{\overrightarrow{V}}_h\right)d\mathcal{V}dt=/d{L}_0$$

and since the neutrals as a whole are considered a unique fluid, one still has

$$/d{L}_0=-p_0\left(\overrightarrow{\partial }·\overrightarrow{U}\right)d\mathcal{V}dt,$$

and then

$$\begin{array}{c}{\displaystyle \sum _h}{m}_h{\Gamma }_h\underset{T_O}{\overset{T}{\int }}{c}_{Vh}\left(T^{\prime }\right)d{T}^{\prime }+{\partial }_{t}T{\displaystyle \sum _h}{\rho }_h{c}_{Vh}+\overrightarrow{\partial }T·{\displaystyle \sum _h}{\rho }_h{c}_{Vh}{\overrightarrow{V}}_h=\hfill \\ \\ =\overrightarrow{\partial }·\left({\kappa }_0\overrightarrow{\partial }T\right)+{\Phi }_0+\rho Q_0-p_0\left(\overrightarrow{\partial }·\overrightarrow{U}\right).\hfill \end{array}$$

With similar reasoning, one can also write

$$\begin{array}{c}{\displaystyle \sum _h}{m}_h{\Gamma }_h\underset{T_O}{\overset{T}{\int }}{c}_{Vh}\left(T^{\prime }\right)d{T}^{\prime }=m_0{\Gamma }_0\underset{T_O}{\overset{T}{\int }}{c}_{V0}\left(T^{\prime }\right)d{T}^{\prime },\hfill \\ \\ {\displaystyle \sum _h}{c}_{Vh}{\rho }_h{\partial }_{t}T=\rho c_{V0}{\partial }_{t}T,\hfill \\ \\ {\displaystyle \sum _h}{\rho }_h{c}_{Vh}{\overrightarrow{V}}_h·\overrightarrow{\partial }T=\rho c_{V0}\overrightarrow{U}·\overrightarrow{\partial }T.\hfill \end{array}$$

With all these positions, one concludes:

$$\begin{array}{c}{m}_0{\Gamma }_0\underset{T_O}{\overset{T}{\int }}{c}_{V0}\left(T^{\prime }\right)d{T}^{\prime }+\rho c_{V0}{\partial }_{t}T+\rho c_{V0}\overrightarrow{U}·\overrightarrow{\partial }T=\hfill \\ \\ =\overrightarrow{\partial }·\left({\kappa }_0\overrightarrow{\partial }T\right)+{\Phi }_0+\rho Q_0-p_0\left(\overrightarrow{\partial }·\overrightarrow{U}\right),\hfill \end{array}$$

(139)

so that the full system of equations for the neutrals as a whole can be read as

$$\left\{\begin{array}{c}{\partial }_t\rho +\overrightarrow{\partial }·\left(\rho \overrightarrow{U}\right)=m_0{\Gamma }_0,\hfill \\ \\ {\displaystyle \frac{d}{dt}}\left(\rho \overrightarrow{U}\right)=\rho {\overrightarrow{g}}_{eff}-2\rho \overrightarrow{\Omega }\times \overrightarrow{U}-\overrightarrow{\partial }p-\overrightarrow{\partial }·{\tau }_0-\overrightarrow{\partial }·{\tau }_{0w}-{\displaystyle \sum _Y}{\nu }_{0Y}\rho \left(\overrightarrow{U}-{\overrightarrow{V}}_Y\right),\hfill \\ \\ m_0{\Gamma }_0\underset{T_O}{\overset{T}{\int }}{c}_{V0}\left(T^{\prime }\right)d{T}^{\prime }+\rho c_{V0}{\partial }_{t}T+\rho c_{V0}\overrightarrow{U}·\overrightarrow{\partial }T=\overrightarrow{\partial }·\left({\kappa }_0\overrightarrow{\partial }{T}_0\right)+{\Phi }_0+\rho Q_0-p_0\left(\overrightarrow{\partial }·\overrightarrow{U}\right),\hfill \\ \\ f_0\left(\rho ,p_0,T\right)=0:\hfill \end{array}\right.$$

(140)

Clearly, in (140), an equation of state $f_0\left(\rho ,p_0,T\right)=0$ is assumed to exist for the neutral part of the atmosphere as a whole, and after assuming that all the $T_h$s are equal, this sounds rather reasonable; this is just a strong mixing statement.

A final remark is worth making here, before going on. The construction of a “total neutral” equivalent fluid makes it possible to define the neutral wind reference frame (NeWReF), which will be very useful later, namely the one with speed $\overrightarrow{U}$ point by point (see Section 4.1).

3.8. Charged Components

Let us finally specialize Equation (107) for charged chemicals. When no approximation is made, the equations for charged fluids look like exactly the same way as (107), but realistic specializations are very useful to study the ionosphere.

The mass balance equation is exactly written as

$${\partial }_t{\rho }_I+\overrightarrow{\partial }·\left({\rho }_I{\overrightarrow{V}}_I\right)=m_I{\Gamma }_I,$$

(141)

as discussed in Section 3.1.

The linear momentum conservation for charged species reads:

$$\begin{array}{c}{m}_I{N}_I{\partial }_t{\overrightarrow{V}}_I+m_I{N}_I\left({\overrightarrow{V}}_I·\overrightarrow{\partial }\right){\overrightarrow{V}}_I+m_I{\Gamma }_I{\overrightarrow{V}}_I=q_I{N}_I\overrightarrow{E}+{\overrightarrow{V}}_I\times \left(q_I{N}_I\overrightarrow{B}+2m_I{N}_I\overrightarrow{\Omega }\right)+\hfill \\ \\ +m_I{N}_I{\overrightarrow{g}}_{eff}-\overrightarrow{\partial }{p}_I-m_I{N}_I{\displaystyle \sum _{J\ne I}}{\nu }_{IJ}\left({\overrightarrow{V}}_I-{\overrightarrow{V}}_J\right)-\overrightarrow{\partial }·{\tau }_I-\overrightarrow{\partial }·{\tau }_{Iw}.\hfill \end{array}$$

(142)

In order to treat (142) for the ionospheric plasma, some approximations are assumed.

First of all, since the charged species are very dilute in all the parts of the atmosphere, we can neglect both the self-viscosity term of ${\mathcal{C}}_I$ and the transmission of the momentum from the mechanical waves to ${\mathcal{C}}_I$:

$$\begin{array}{cccc}{q}_I\ne 0& \Rightarrow & \overrightarrow{\partial }·{\tau }_I\simeq 0,& \overrightarrow{\partial }·{\tau }_{Iw}\simeq 0.\end{array}$$

(143)

This approximation is justified in different ways in the different regions of the upper atmosphere. In its lower region, where one can speak about the ionosphere properly, the charged matter is extremely less abundant than the neutral one; for $q_I\ne 0$, the fluids ${\mathcal{C}}_I$ are very dilute gases merged in the much denser medium ${\mathcal{C}}_0$. This renders the forces “applied by the charged matter on itself” much weaker than those applied by ${\mathcal{C}}_0$, and completely negligible. When the ionospheric–plasmaspheric limit is passed, neutrals are not present anymore in practice, then the force density $\overrightarrow{\partial }·{\tau }_I+\overrightarrow{\partial }·{\tau }_{Iw}$ for the plasma cannot be negligible with respect to those other terms, but it becomes negligible by itself due to the low density of the very plasma at those heights. One can say that (143) holds everywhere, and Equation (142) becomes:

$$\begin{array}{c}{m}_I{N}_I{\partial }_t{\overrightarrow{V}}_I+m_I{N}_I\left({\overrightarrow{V}}_I·\overrightarrow{\partial }\right){\overrightarrow{V}}_I+m_I{\Gamma }_I{\overrightarrow{V}}_I=q_I{N}_I\overrightarrow{E}+{\overrightarrow{V}}_I\times \left(q_I{N}_I\overrightarrow{B}+2m_I{N}_I\overrightarrow{\Omega }\right)+\hfill \\ \\ +m_I{N}_I{\overrightarrow{g}}_{eff}-\overrightarrow{\partial }{p}_I-m_I{N}_I{\displaystyle \sum _{J\ne I}}{\nu }_{IJ}\left({\overrightarrow{V}}_I-{\overrightarrow{V}}_J\right).\hfill \end{array}$$

(144)

There are other negligible terms.

The velocity-skew-linear force

$${\overrightarrow{V}}_I\times \left(q_I{N}_I\overrightarrow{B}+2m_I{N}_I\overrightarrow{\Omega }\right)$$

can be approximated; due to the very small mass of the particles forming the plasma, and to their diluteness, one can write

$$q_I{N}_{I}B\gg 2m_I{N}_I\Omega ,$$

(145)

and when this is used, the velocity force can be approximated as

$${\overrightarrow{V}}_I\times \left(q_I{N}_I\overrightarrow{B}+2m_I{N}_I\overrightarrow{\Omega }\right)\simeq {\overrightarrow{V}}_I\times q_I{N}_I\overrightarrow{B},$$

so that Coriolis forces disappear from (144); after a little bit of algebra, one has:

$${\partial }_t{\overrightarrow{V}}_I+\left({\overrightarrow{V}}_I·\overrightarrow{\partial }\right){\overrightarrow{V}}_I+{\displaystyle \frac{{\Gamma }_I}{N_I}}{\overrightarrow{V}}_I={\overrightarrow{g}}_{eff}+{\displaystyle \frac{q_I}{m_I}}\overrightarrow{E}+{\displaystyle \frac{q_I}{m_I}}{\overrightarrow{V}}_I\times \overrightarrow{B}-{\displaystyle \frac{1}{m_I{N}_I}}\overrightarrow{\partial }{p}_I-{\displaystyle \sum _{J\ne I}}{\nu }_{IJ}\left({\overrightarrow{V}}_I-{\overrightarrow{V}}_J\right).$$

(146)

Equation (146) can be specialized for each charged species. If the chemical reactions are neglected in the Navier–Stokes PDE:

$${\displaystyle \frac{{\Gamma }_I}{N_I}}{\overrightarrow{V}}_I\simeq \overrightarrow{o}$$

(147)

Equation (146) reduces to

$${\displaystyle \frac{d{\overrightarrow{V}}_I}{dt}}={\overrightarrow{g}}_{eff}+{\displaystyle \frac{q_I}{m_I}}\overrightarrow{E}+{\displaystyle \frac{q_I}{m_I}}{\overrightarrow{V}}_I\times \overrightarrow{B}-{\displaystyle \frac{1}{m_I{N}_I}}\overrightarrow{\partial }{p}_I-{\displaystyle \sum _{J\ne I}}{\nu }_{IJ}\left({\overrightarrow{V}}_I-{\overrightarrow{V}}_J\right).$$

(148)

Otherwise, one must re-start from Equation (146) and write

$${\displaystyle \frac{d}{dt}}\left(N_I{\overrightarrow{V}}_I\right)={\displaystyle \frac{q_I}{m_I}}{N}_I\overrightarrow{E}+{\displaystyle \frac{q_I}{m_I}}{N}_I{\overrightarrow{V}}_I\times \overrightarrow{B}+N_I{\overrightarrow{g}}_{eff}-{\displaystyle \frac{1}{m_I}}\overrightarrow{\partial }{p}_I-N_I{\displaystyle \sum _{J\ne I}}{\nu }_{IJ}\left({\overrightarrow{V}}_I-{\overrightarrow{V}}_J\right)$$

(149)

(the production loss term is, if any, contained in the Lagrangian derivative ${\displaystyle \frac{d}{dt}}\left(N_I{\overrightarrow{V}}_I\right)$, involving ${\displaystyle \frac{d{N}_I}{dt}}$). An example of how (147) holds true is given in Appendix C.

Equations (148) or (149) can be adapted to any charged species; however, in this section, we will use a particularly simplified atmospheric picture, in which only two charged species are present; positive 1-valent ions, with charge $+e$ and mass M, and electrons, with charge $-e$ and mass m. In this picture, negative ions and multi-valent ions are completely neglected. Moreover, the approximation (147) will be considered as true, so we will start from Equation (148). This model of population $\left\{{\mathcal{C}}_I\right\}=\left(X,X^{+},e^{-}\right)$ can be applied, e.g., to the topside of the ionosphere and to the plasmasphere (where $X^{+}$ represents different chemicals for the different regions). For negative ions, one should refer to what is reported, for example, in [10]. Note also that physical models of the free electron density $N_e$ are influenced seriously by the presence of negative ions, as shown in [37].

3.8.1. Ion Motions

The specialization of (148) to the $\left(e,M\right)$ positive ions reads:

$${\displaystyle \frac{d{\overrightarrow{V}}_i}{dt}}={\overrightarrow{g}}_{eff}+{\displaystyle \frac{e}{M}}\overrightarrow{E}+{\displaystyle \frac{e}{M}}{\overrightarrow{V}}_i\times \overrightarrow{B}-{\displaystyle \frac{1}{M{N}_i}}\overrightarrow{\partial }{p}_i-{\nu }_{ie}\left({\overrightarrow{V}}_i-{\overrightarrow{V}}_e\right)-{\nu }_{in}\left({\overrightarrow{V}}_i-\overrightarrow{U}\right),$$

(150)

where $\overrightarrow{U}$ is the bulk velocity of neutral matter, and ${\overrightarrow{V}}_e$ that of electrons. These positive ions are considered as a perfect gas in local thermodynamical equilibrium:

$$p_i=N_i{k}_B{T}_i.$$

(151)

Last but not least, ions undergo mass balance:

$${\partial }_t{N}_i+\overrightarrow{\partial }·\left(N_i{\overrightarrow{V}}_i\right)={\Gamma }_i.$$

(152)

The equations of motion for the positive ionic species then read:

$$\left\{\begin{array}{c}\begin{array}{cc}{\partial }_t{N}_i+\overrightarrow{\partial }·\left(N_i{\overrightarrow{V}}_i\right)={\Gamma }_i,& p_i=N_i{k}_B{T}_i,\end{array}\hfill \\ \\ {\displaystyle \frac{d{\overrightarrow{V}}_i}{dt}}={\overrightarrow{g}}_{eff}+{\displaystyle \frac{e}{M}}\overrightarrow{E}+{\displaystyle \frac{e}{M}}{\overrightarrow{V}}_i\times \overrightarrow{B}-{\displaystyle \frac{1}{M{N}_i}}\overrightarrow{\partial }{p}_i-{\nu }_{ie}\left({\overrightarrow{V}}_i-{\overrightarrow{V}}_e\right)-{\nu }_{in}\left({\overrightarrow{V}}_i-\overrightarrow{U}\right).\hfill \end{array}\right.$$

(153)

In many cases, the electron–ion collision frequency ${\nu }_{ie}$ is negligible with respect to neutral–ion collision frequency ${\nu }_{in}$, and so Equation (153) read

$$\left\{\begin{array}{c}\begin{array}{cc}{\partial }_t{N}_i+\overrightarrow{\partial }·\left(N_i{\overrightarrow{V}}_i\right)={\Gamma }_i,& p_i=N_i{k}_B{T}_i,\end{array}\hfill \\ \\ {\displaystyle \frac{d{\overrightarrow{V}}_i}{dt}}={\overrightarrow{g}}_{eff}+{\displaystyle \frac{e}{M}}\overrightarrow{E}+{\displaystyle \frac{e}{M}}{\overrightarrow{V}}_i\times \overrightarrow{B}-{\displaystyle \frac{1}{M{N}_i}}\overrightarrow{\partial }{p}_i-{\nu }_{in}\left({\overrightarrow{V}}_i-\overrightarrow{U}\right):\hfill \end{array}\right.$$

(154)

This is the case of the low ionosphere, where the probability of meeting neutrals is much higher than that of meeting electrons.

On the opposite side, in the high ionosphere, neutrals are almost absent, so that one has ${\nu }_{in}=0$ and (153) must be re-written as:

$$\left\{\begin{array}{c}\begin{array}{cc}{\partial }_t{N}_i+\overrightarrow{\partial }·\left(N_i{\overrightarrow{V}}_i\right)={\Gamma }_i,& p_i=N_i{k}_B{T}_i,\end{array}\hfill \\ \\ {\displaystyle \frac{d{\overrightarrow{V}}_i}{dt}}={\overrightarrow{g}}_{eff}+{\displaystyle \frac{e}{M}}\overrightarrow{E}+{\displaystyle \frac{e}{M}}{\overrightarrow{V}}_i\times \overrightarrow{B}-{\displaystyle \frac{1}{M{N}_i}}\overrightarrow{\partial }{p}_i-{\nu }_{ie}\left({\overrightarrow{V}}_i-{\overrightarrow{V}}_e\right).\hfill \end{array}\right.$$

(155)

3.8.2. Electron Motions

Let us specialize Equation (148) to electrons, identified by $\left(-e,m\right)$, so the version of Equation (148) for them reads

$${\displaystyle \frac{d{\overrightarrow{V}}_e}{dt}}={\overrightarrow{g}}_{eff}-{\displaystyle \frac{e}{m}}\overrightarrow{E}-{\displaystyle \frac{e}{m}}{\overrightarrow{V}}_e\times \overrightarrow{B}-{\displaystyle \frac{1}{m{N}_e}}\overrightarrow{\partial }{p}_e-{\nu }_{en}\left({\overrightarrow{V}}_e-\overrightarrow{U}\right)-{\nu }_{ei}\left({\overrightarrow{V}}_e-\overrightarrow{U}\right).$$

(156)

If the electrons are considered as a perfect gas without quantum effects, the law

$$p_e=N_e{k}_B{T}_e$$

(157)

is added; for what concerns the mass balance, one can write

$${\partial }_t{N}_e+\overrightarrow{\partial }·\left(N_e{\overrightarrow{V}}_e\right)={\Gamma }_e.$$

(158)

Free electrons due to ionization are then described by the set of equations

$$\left\{\begin{array}{c}\begin{array}{cc}{\partial }_t{N}_e+\overrightarrow{\partial }·\left(N_e{\overrightarrow{V}}_e\right)={\Gamma }_e,& p_e=N_e{k}_B{T}_e,\end{array}\hfill \\ \\ {\displaystyle \frac{d{\overrightarrow{V}}_e}{dt}}={\overrightarrow{g}}_{eff}-{\displaystyle \frac{e}{m}}\overrightarrow{E}-{\displaystyle \frac{e}{m}}{\overrightarrow{V}}_e\times \overrightarrow{B}-{\displaystyle \frac{1}{m{N}_e}}\overrightarrow{\partial }{p}_e-{\nu }_{en}\left({\overrightarrow{V}}_e-\overrightarrow{U}\right)-{\nu }_{ei}\left({\overrightarrow{V}}_e-\overrightarrow{U}\right).\hfill \end{array}\right.$$

(159)

When the ion–electron collisions are neglected with respect to neutral–electron ones:

$${\nu }_{ei}\ll {\nu }_{en}$$

(160)

it is possible to write:

$$\left\{\begin{array}{c}\begin{array}{cc}{\partial }_t{N}_e+\overrightarrow{\partial }·\left(N_e{\overrightarrow{V}}_e\right)={\Gamma }_e,& p_e=N_e{k}_B{T}_e,\end{array}\hfill \\ \\ {\displaystyle \frac{d{\overrightarrow{V}}_e}{dt}}={\overrightarrow{g}}_{eff}-{\displaystyle \frac{e}{m}}\overrightarrow{E}-{\displaystyle \frac{e}{m}}{\overrightarrow{V}}_e\times \overrightarrow{B}-{\displaystyle \frac{1}{m{N}_e}}\overrightarrow{\partial }{p}_e-{\nu }_{en}\left({\overrightarrow{V}}_e-\overrightarrow{U}\right).\hfill \end{array}\right.$$

(161)

Approximation (160) holds in the low–middle ionosphere, while in the highest layers, one has ${\nu }_{en}=0$, as no neutrals can be found there:

$$\left\{\begin{array}{c}\begin{array}{cc}{\partial }_t{N}_e+\overrightarrow{\partial }·\left(N_e{\overrightarrow{V}}_e\right)={\Gamma }_e,& p_e=N_e{k}_B{T}_e,\end{array}\hfill \\ \\ {\displaystyle \frac{d{\overrightarrow{V}}_e}{dt}}={\overrightarrow{g}}_{eff}-{\displaystyle \frac{e}{m}}\overrightarrow{E}-{\displaystyle \frac{e}{m}}{\overrightarrow{V}}_e\times \overrightarrow{B}-{\displaystyle \frac{1}{m{N}_e}}\overrightarrow{\partial }{p}_e-{\nu }_{en}\left({\overrightarrow{V}}_e-\overrightarrow{U}\right)-{\nu }_{ei}\left({\overrightarrow{V}}_e-\overrightarrow{U}\right).\hfill \end{array}\right.$$

(162)

The two rates ${\Gamma }_i$ and ${\Gamma }_e$ appearing in (153) and (159), respectively, are not independent, as stated in Section 3.1, and Equation (48) holds:

$$e{\Gamma }_i-e{\Gamma }_e=0,$$

(163)

so that as the statement ${\Gamma }_i={\Gamma }_e\equiv \Gamma$ is made, one has:

$${\partial }_t{N}_i+\overrightarrow{\partial }·\left(N_i{\overrightarrow{V}}_i\right)=\Gamma ,{\partial }_t{N}_e+\overrightarrow{\partial }·\left(N_e{\overrightarrow{V}}_e\right)=\Gamma .$$

(164)

The rate $\Gamma$ represents the rate of the events $X\mapsto X^{+}+e^{-}$, each of which will “create” a positive ion and a free electron, so it is no surprise that \Gamma represents both the $e^{-}$ as well as the $X^{+}$ production loss rate.

4. The Quiet Ionosphere

The presence of plasma in the upper atmosphere renders the matter in this region a gaseous conductor, because free charges can make macroscopic motions under the action of electromagnetic fields. Obtaining a description of the system as a conductor at equilibrium, with the geomagnetic field impressed, requires the medium to be in local mechanical equilibrium, namely no bulk acceleration for the continua ${\mathcal{C}}_I$:

$${\displaystyle \frac{d{\overrightarrow{V}}_I}{dt}}=0.$$

(165)

What one wants to find is a relationship between the charged species motions and the electromagnetic fields present under the static condition (165); in this condition, one speaks about the quiet ionosphere.

When the conditions (165) are put into (84), the momentum balance turns into a relationship between the ${\overrightarrow{V}}_I$s and the electromagnetic fields:

$${\overrightarrow{g}}_{eff}+{\displaystyle \frac{q_I}{m_I}}\overrightarrow{E}+{\displaystyle \frac{q_I}{m_I}}{\overrightarrow{V}}_I\times \overrightarrow{B}-{\displaystyle \frac{1}{m_I{N}_I}}\overrightarrow{\partial }{p}_I-{\displaystyle \sum _{J\ne I}}{\nu }_{JI}\left({\overrightarrow{V}}_I-{\overrightarrow{V}}_J\right)-{\nu }_{nI}\left({\overrightarrow{V}}_I-\overrightarrow{U}\right)=0$$

(166)

(note that, to obtain (166) from (84) and (165), some approximations were considered, namely those discussed in Section 3). The two assumptions ${\partial }_t{\overrightarrow{V}}_I\simeq 0$ and $\left({\overrightarrow{V}}_I·\overrightarrow{\partial }\right){\overrightarrow{V}}_I\simeq 0$, implying ${\displaystyle \frac{d{\overrightarrow{V}}_I}{dt}}\simeq 0$, are both supported, in practice, by the experimental reality of the ionosphere in “geomagnetically quiet conditions”. For this, let us denote as $\tau$ the response time of the medium to the applied forces, and as L the characteristic length of the velocity field space variability. Then, one can say

$$\begin{array}{cc}{\partial }_t{\overrightarrow{V}}_I=O\left({\displaystyle \frac{V}{\tau }}\right),& \left({\overrightarrow{V}}_I·\overrightarrow{\partial }\right){\overrightarrow{V}}_I=O\left({\displaystyle \frac{V^2}{L}}\right).\end{array}$$

The other terms of the acceleration in (84) involving the velocity satisfy:

$$\begin{array}{cc}{\displaystyle \sum _{J\ne I}}{\nu }_{JI}\left({\overrightarrow{V}}_I-{\overrightarrow{V}}_J\right)=O\left({\displaystyle \frac{V}{\Delta t}}\right),& {\displaystyle \frac{q_I}{m_I}}{\overrightarrow{V}}_I\times \overrightarrow{B}=O\left({\displaystyle \frac{V}{{\tau }_I\left(B\right)}}\right),\end{array}$$

where $\Delta t$ is the inverse of the collisional frequency and ${\tau }_I\left(B\right)$ is the gyration period of the I-th species around the magnetic field line. In the experimental reality, one always has $\tau \gg \Delta t,{\tau }_I\left(B\right)$ so that one may set ${\partial }_t{\overrightarrow{V}}_I\simeq 0$. Moreover, in the quiet atmosphere, the length L is usually much larger than gyration radii and free mean paths (length scales associated to Lorentz force and collisional friction, respectively), so that the approximation $\left({\overrightarrow{V}}_I·\overrightarrow{\partial }\right){\overrightarrow{V}}_I\simeq 0$ also holds. From the above-supported (166), one has:

$$m_I{N}_I{\overrightarrow{g}}_{eff}+q_I{N}_I\left(\overrightarrow{E}+{\overrightarrow{V}}_I\times \overrightarrow{B}\right)-\overrightarrow{\partial }{p}_I-m_I{N}_I{\displaystyle \sum _{J\ne I}}{\nu }_{JI}\left({\overrightarrow{V}}_I-{\overrightarrow{V}}_J\right)-m_I{N}_I{\nu }_{nI}\left({\overrightarrow{V}}_I-\overrightarrow{U}\right)=0,$$

(167)

and here, the equation of state (99) can be used to write $p_I$ in terms of $N_I$ and the temperature $T_I$

$$\begin{array}{c}{m}_I{N}_I{\overrightarrow{g}}_{eff}+q_I{N}_I\left(\overrightarrow{E}+{\overrightarrow{V}}_I\times \overrightarrow{B}\right)-\overrightarrow{\partial }\left(N_I{k}_B{T}_I\right)+\hfill \\ \\ -m_I{N}_I{\displaystyle \sum _{J\ne I}}{\nu }_{JI}\left({\overrightarrow{V}}_I-{\overrightarrow{V}}_J\right)-m_I{N}_I{\nu }_{nI}\left({\overrightarrow{V}}_I-\overrightarrow{U}\right)=0.\hfill \end{array}$$

(168)

In general, the medium is treated as electrically neural point by point, so that the densities satisfy the constraint

$${\displaystyle \sum _I}{q}_I{N}_I=0.$$

(169)

It is not pleonastic to remember that (169) is held true only around those places where

$${\displaystyle \sum _I}{q}_I\overrightarrow{\partial }·{\overrightarrow{V}}_I\simeq 0$$

(170)

due to the continuity equation. This excludes places like the neighborhood of the terminators, as already noticed. Due to (169), and because we have assumed the ionosphere to be made out of X, $X^{+}$ and $e^{-}$ only, one may safely write:

$$N_i=N_e\stackrel{\mathrm{def}}{=}N.$$

(171)

Equation (168) can be used to determine the velocities ${\overrightarrow{V}}_I$ as functions of the other quantities. This will depict the stream portrait of the continuum ${\mathcal{C}}_I$ when it is under mechanical equilibrium (165) point by point.

The Navier–Stokes equation for the system of the two charged species “i” and “e” at mechanical equilibrium reads:

$$\begin{array}{c}{\overrightarrow{g}}_{eff}+{\displaystyle \frac{e}{M}}\overrightarrow{E}+{\displaystyle \frac{e}{M}}{\overrightarrow{V}}_i\times \overrightarrow{B}-{\displaystyle \frac{1}{MN}}\overrightarrow{\partial }{p}_i+\hfill \\ \\ -{\nu }_{ei}\left({\overrightarrow{V}}_i-{\overrightarrow{V}}_e\right)-{\nu }_{ni}\left({\overrightarrow{V}}_i-\overrightarrow{U}\right)=0,\hfill \\ \\ {\overrightarrow{g}}_{eff}-{\displaystyle \frac{e}{m}}\overrightarrow{E}-{\displaystyle \frac{e}{m}}{\overrightarrow{V}}_e\times \overrightarrow{B}-{\displaystyle \frac{1}{mN}}\overrightarrow{\partial }{p}_e+\hfill \\ \\ -{\nu }_{ei}\left({\overrightarrow{V}}_e-{\overrightarrow{V}}_i\right)-{\nu }_{ne}\left({\overrightarrow{V}}_e-\overrightarrow{U}\right)=0.\hfill \end{array}$$

(172)

where one can assume that ion–electron collisions are rare.

$${\nu }_{ie}\simeq 0,$$

(173)

The equilibrium momentum balance equations read:

$$\left\{\begin{array}{c}mN{\overrightarrow{g}}_{eff}-eN\left(\overrightarrow{E}+{\overrightarrow{V}}_e\times \overrightarrow{B}\right)-k_B\overrightarrow{\partial }\left(N{T}_e\right)-mN{\nu }_{en}\left({\overrightarrow{V}}_e-\overrightarrow{U}\right)=0,\hfill \\ \\ MN{\overrightarrow{g}}_{eff}+eN\left(\overrightarrow{E}+{\overrightarrow{V}}_i\times \overrightarrow{B}\right)-k_B\overrightarrow{\partial }\left(N{T}_i\right)-MN{\nu }_{in}\left({\overrightarrow{V}}_i-\overrightarrow{U}\right)=0.\hfill \end{array}\right.$$

(174)

On the contrary, if the ion collision frequency is the only relevant ${\nu }_{IJ}$

$${\nu }_{ne}\simeq 0,$$

(175)

Equation (172) will read:

$$\left\{\begin{array}{c}mN{\overrightarrow{g}}_{eff}-eN\left(\overrightarrow{E}+{\overrightarrow{V}}_e\times \overrightarrow{B}\right)-k_B\overrightarrow{\partial }\left(N{T}_e\right)-mN{\nu }_{ei}\left({\overrightarrow{V}}_e-{\overrightarrow{V}}_i\right)=0,\hfill \\ \\ MN{\overrightarrow{g}}_{eff}+eN\left(\overrightarrow{E}+{\overrightarrow{V}}_i\times \overrightarrow{B}\right)-k_B\overrightarrow{\partial }\left(N{T}_i\right)-MN{\nu }_{ei}\left({\overrightarrow{V}}_i-{\overrightarrow{V}}_e\right)=0.\hfill \end{array}\right.$$

(176)

4.1. Thermal Homogeneity and the NeWReF

These systems (174) and (176) can be restricted to the case of thermally homogeneous regions

$$\overrightarrow{\partial }{T}_I=0.$$

(177)

This (177) should not be misunderstood; the ionosphere never has null temperature gradients, and here one simply means that we are going to treat small enough regions so that the same temperature $T_I$ exists all over it. When this assumption holds, it is possible to go on as follows for (174):

$$\left\{\begin{array}{c}mN{\overrightarrow{g}}_{eff}-eN\left(\overrightarrow{E}+{\overrightarrow{V}}_e\times \overrightarrow{B}\right)-k_B{T}_e\overrightarrow{\partial }N-mN{\nu }_{en}\left({\overrightarrow{V}}_e-\overrightarrow{U}\right)=0,\hfill \\ \\ MN{\overrightarrow{g}}_{eff}+eN\left(\overrightarrow{E}+{\overrightarrow{V}}_i\times \overrightarrow{B}\right)-k_B{T}_i\overrightarrow{\partial }N-MN{\nu }_{in}\left({\overrightarrow{V}}_i-\overrightarrow{U}\right)=0,\hfill \end{array}\right.$$

(178)

While for (176), one has:

$$\left\{\begin{array}{c}mN{\overrightarrow{g}}_{eff}-eN\left(\overrightarrow{E}+{\overrightarrow{V}}_e\times \overrightarrow{B}\right)-k_B{T}_e\overrightarrow{\partial }\left(N\right)-mN{\nu }_{ei}\left({\overrightarrow{V}}_e-{\overrightarrow{V}}_i\right)=0,\hfill \\ \\ MN{\overrightarrow{g}}_{eff}+eN\left(\overrightarrow{E}+{\overrightarrow{V}}_i\times \overrightarrow{B}\right)-k_B{T}_i\overrightarrow{\partial }\left(N\right)-MN{\nu }_{ei}\left({\overrightarrow{V}}_i-{\overrightarrow{V}}_e\right)=0.\hfill \end{array}\right.$$

(179)

The electrology of the quiet ionosphere as a conductor is essentially that of a conducting object dragged through the geomagentic field by the motions of neutral matter. In order to simplify our reasoning, it is convenient to work in the NeWReF, because this simplifies the dynamics observed. This NeWReF sees the ionosphere as more similar to some conductor studied in its reference frame, in which traditional electrological quantities, such as resistivity, are easily defined and applied. Equations (178) and (179) are written as the SERF observer sees them, with ${\overrightarrow{g}}_{eff}$ containing the inertial position forces, negligible Coriolis acceleration and neutral wind velocity equal to $\overrightarrow{U}$. One can also describe the same system as seen by a reference frame that has, point by point and time by time, the speed $\overrightarrow{U}$ of the neutral wind with respect to the SERF. The fields $\overrightarrow{E}$ and $\overrightarrow{B}$ are relativistic quantities, and will be measured as

$$\begin{array}{cc}{\overrightarrow{E}}^{\prime }={\displaystyle \frac{1}{\sqrt{1-{\displaystyle \frac{U^2}{c^2}}}}}\left(\overrightarrow{E}+\overrightarrow{U}\times \overrightarrow{B}\right),& {\overrightarrow{B}}^{\prime }={\displaystyle \frac{1}{\sqrt{1-{\displaystyle \frac{U^2}{c^2}}}}}\left(\overrightarrow{B}-{\displaystyle \frac{1}{c^2}}\overrightarrow{U}\times \overrightarrow{E}\right)\end{array}$$

(180)

in the NeWReF. In the non-relativistic wind limit

$$U{c}^{-1}\ll 1,$$

(181)

which is definitely met, one can neglect the ${\displaystyle \frac{U^2}{c^2}}$ effects, putting

$$\sqrt{1-{\displaystyle \frac{U^2}{c^2}}}\simeq 1$$

and write:

$$\begin{array}{cc}{\overrightarrow{E}}^{\prime }\simeq \overrightarrow{E}+\overrightarrow{U}\times \overrightarrow{B},& {\overrightarrow{B}}^{\prime }\simeq \overrightarrow{B}-{\displaystyle \frac{1}{c^2}}\overrightarrow{U}\times \overrightarrow{E}.\end{array}$$

The Earth’s ionosphere is a specific situation in which

$$\left|\overrightarrow{B}\right|\gg {\displaystyle \frac{1}{c^2}}\left|\overrightarrow{U}\times \overrightarrow{E}\right|$$

(182)

so that the transformations giving the electromagnetic fields $\left({\overrightarrow{E}}^{\prime },{\overrightarrow{B}}^{\prime }\right)$ measured in the neutral wind frame in terms of those $\left(\overrightarrow{E},\overrightarrow{B}\right)$ measured by the Earth-solidal observer, rather read:

$$\begin{array}{cc}{\overrightarrow{E}}^{\prime }=\overrightarrow{E}+\overrightarrow{U}\times \overrightarrow{B},& {\overrightarrow{B}}^{\prime }=\overrightarrow{B}.\end{array}$$

(183)

Note that only the electric fields are changed. Note also that (182) simply means that the Lorentz currents due to the neutral drag produce magnetic inductions much smaller than the magnetic field measured in the SERF.

As observed in [28], the relations (183) seem to indicate that the sources of the electric fields change significantly when a “low-relativistic” transformation is applied, while those of the magnetic field do not. This is true; it can be seen rigorously in the case of a well-conducting medium, as explained in the following. Suppose that to make a Lorentz transformation from some system S and a second system translating rigidly with respect to it, with speed

$$\overrightarrow{U}=U\widehat{z}:$$

(184)

the relativistic theory says that the collection of four quantities $\left(c\delta ,\overrightarrow{J}\right)$ transforms as a 4-vector, i.e.,

$$\left\{\begin{array}{c}\begin{array}{cc}{J}_x^{\prime }=J_x,& J_y^{\prime }=J_y,\end{array}\hfill \\ \\ \begin{array}{cc}{J}_z^{\prime }={\displaystyle \frac{1}{\sqrt{1-{\beta }^2}}}\left(J_z-\beta c\delta \right),& {\delta }^{\prime }={\displaystyle \frac{1}{\sqrt{1-{\beta }^2}}}\left(\delta -{\displaystyle \frac{\beta }{c}}{J}_z\right),\end{array}\hfill \end{array}\right.$$

(185)

where $\beta ={\displaystyle \frac{U}{c}}$. If we make a Taylor expansion up to $O\left(\beta \right)$, we obtain

$$\left\{\begin{array}{c}\begin{array}{cc}{J}_x^{\prime }=J_x,& J_y^{\prime }=J_y,\end{array}\hfill \\ \\ \begin{array}{cc}{J}_z^{\prime }=J_z-c\beta \delta +\dots ,& {\delta }^{\prime }=\delta -{\displaystyle \frac{1}{c}}\beta J_z+\dots \end{array}\hfill \end{array}\right.$$

so that, if $\Delta f$ is the difference between the values in $S^{\prime }$ and in S of a quantity f, one has

$$\begin{array}{cc}\Delta J_z=-c\beta \delta ,& \Delta \delta =-{\displaystyle \frac{1}{c}}\beta J_z.\end{array}$$

The relative variations are

$$\begin{array}{cc}{\displaystyle \frac{\Delta J_z}{J_z}}=-{\displaystyle \frac{c\beta \delta }{J_z}},& {\displaystyle \frac{\Delta \delta }{\delta }}=-{\displaystyle \frac{\beta J_z}{c\delta }},\end{array}$$

and if we evaluate their ratio, we obtain:

$${\displaystyle \frac{\Delta \delta }{\delta }}{\left({\displaystyle \frac{\Delta J_z}{J_z}}\right)}^{-1}={\displaystyle \frac{J_z^2}{c^2{\delta }^2}}.$$

(186)

From (186), we obtain that if a very little charge density produces an intense current $J_z$, via intense electric fields in an importantly conducting medium, the ionosphere, one has

$${\displaystyle \frac{\Delta \delta }{\delta }}{\left({\displaystyle \frac{\Delta J_z}{J_z}}\right)}^{-1}\gg 1,$$

which means a dependence of the electric density on the reference frame much higher than the current dependence.

Passing from the SERF to the NeWReF, the matter velocities are transformed as

$${\overrightarrow{v}}^{\prime }=\overrightarrow{v}-\overrightarrow{U}$$

(187)

in the non-relativistic limit, so that one has to put the expressions

$$\left\{\begin{array}{c}\begin{array}{cc}{\overrightarrow{V}}_e={\overrightarrow{V}}_e^{\prime }+\overrightarrow{U},& {\overrightarrow{V}}_i={\overrightarrow{V}}_i^{\prime }+\overrightarrow{U},\end{array}\hfill \\ \\ \begin{array}{cc}\overrightarrow{E}={\overrightarrow{E}}^{\prime }-\overrightarrow{U}\times {\overrightarrow{B}}^{\prime },& \overrightarrow{B}={\overrightarrow{B}}^{\prime }\end{array}\hfill \end{array}\right.$$

(188)

in Equation (178), obtaining:

$$\left\{\begin{array}{c}mN{\overrightarrow{g}}_{eff}-eN\left({\overrightarrow{E}}^{\prime }+{\overrightarrow{V}}_e^{\prime }\times {\overrightarrow{B}}^{\prime }\right)-k_B{T}_e\overrightarrow{\partial }N-mN{\nu }_{en}{\overrightarrow{V}}_e^{\prime }=0,\hfill \\ \\ MN{\overrightarrow{g}}_{eff}+eN\left({\overrightarrow{E}}^{\prime }+{\overrightarrow{V}}_i^{\prime }\times {\overrightarrow{B}}^{\prime }\right)-k_B{T}_i\overrightarrow{\partial }N-MN{\nu }_{in}{\overrightarrow{V}}_i^{\prime }=0,\hfill \end{array}\right.$$

(189)

or in Equation (179), obtaining:

$$\left\{\begin{array}{c}mN{\overrightarrow{g}}_{eff}-eN\left({\overrightarrow{E}}^{\prime }+{\overrightarrow{V}}_e^{\prime }\times {\overrightarrow{B}}^{\prime }\right)-k_B{T}_e\overrightarrow{\partial }N-mN{\nu }_{ei}{\overrightarrow{V}}_e^{\prime }=0,\hfill \\ \\ MN{\overrightarrow{g}}_{eff}+eN\left({\overrightarrow{E}}^{\prime }+{\overrightarrow{V}}_i^{\prime }\times {\overrightarrow{B}}^{\prime }\right)-k_B{T}_i\overrightarrow{\partial }N-MN{\nu }_{ei}{\overrightarrow{V}}_i^{\prime }=0.\hfill \end{array}\right.$$

(190)

Dividing by $N{m}_I{\nu }_I$ and collecting the terms involving the velocity in (189) and in (190), one has

$$\left\{\begin{array}{c}{\overrightarrow{V}}_e^{\prime }+{\displaystyle \frac{e}{m{\nu }_{en}}}{\overrightarrow{V}}_e^{\prime }\times {\overrightarrow{B}}^{\prime }={\displaystyle \frac{1}{{\nu }_{en}}}{\overrightarrow{g}}_{eff}-{\displaystyle \frac{e}{m{\nu }_{en}}}{\overrightarrow{E}}^{\prime }-{\displaystyle \frac{k_B{T}_e}{m{\nu }_{en}}}\overrightarrow{\partial }\left(lnN\right),\hfill \\ \\ {\overrightarrow{V}}_i^{\prime }-{\displaystyle \frac{e}{M{\nu }_{in}}}{\overrightarrow{V}}_i^{\prime }\times {\overrightarrow{B}}^{\prime }={\displaystyle \frac{1}{{\nu }_{in}}}{\overrightarrow{g}}_{eff}+{\displaystyle \frac{e}{M{\nu }_{in}}}{\overrightarrow{E}}^{\prime }-{\displaystyle \frac{k_B{T}_i}{M{\nu }_{in}}}\overrightarrow{\partial }\left(lnN\right)\hfill \end{array}\right.$$

(191)

and

$$\left\{\begin{array}{c}{\overrightarrow{V}}_e^{\prime }+{\displaystyle \frac{e}{m{\nu }_{ei}}}{\overrightarrow{V}}_e^{\prime }\times {\overrightarrow{B}}^{\prime }={\displaystyle \frac{1}{{\nu }_{ei}}}{\overrightarrow{g}}_{eff}-{\displaystyle \frac{e}{m{\nu }_{ei}}}{\overrightarrow{E}}^{\prime }-{\displaystyle \frac{k_B{T}_e}{m{\nu }_{ei}}}\overrightarrow{\partial }\left(lnN\right),\hfill \\ \\ {\overrightarrow{V}}_i^{\prime }-{\displaystyle \frac{e}{M{\nu }_{ei}}}{\overrightarrow{V}}_i^{\prime }\times {\overrightarrow{B}}^{\prime }={\displaystyle \frac{1}{{\nu }_{ei}}}{\overrightarrow{g}}_{eff}+{\displaystyle \frac{e}{M{\nu }_{ei}}}{\overrightarrow{E}}^{\prime }-{\displaystyle \frac{k_B{T}_i}{M{\nu }_{ei}}}\overrightarrow{\partial }\left(lnN\right)\hfill \end{array}\right.$$

(192)

respectively. It is important to make an argument about the fact that no new forces appear in the NeWReF with respect to those in the SERF, and this is in principle wrong. Yet, we are considering the condition in which all the species ${\mathcal{C}}_I$ have null acceleration, so that one has ${\displaystyle \frac{d\overrightarrow{U}}{dt}}\simeq 0$ too, implying no new linear acceleration forces in NeWReF with respect to what is seen in SERF. Moreover, we will consider the $\left(x^{\prime },y^{\prime },z^{\prime }\right)$ axes of the NeWReF time by time and point by point, parallel to the axes in the SERF, so that no new rotational forces may appear.

At this point, it is useful to define the following coefficients:

$$\begin{array}{cccc}{K}_I={\displaystyle \frac{q_{I}B}{m_I{\nu }_I}},& D_I={\displaystyle \frac{k_B{T}_I}{m_I{\nu }_I}},& b_I={\displaystyle \frac{q_I}{m_I{\nu }_I}},& H_I={\displaystyle \frac{k_B{T}_I}{m_I{g}_{eff}}},\end{array}$$

(193)

because, through them, Equations (191) and (192) are unified as:

$$\left\{\begin{array}{c}{\overrightarrow{V}}_e^{\prime }-K_e{\overrightarrow{V}}_e^{\prime }\times \widehat{b}={\displaystyle \frac{D_e}{H_e}}{\widehat{g}}_{eff}+b_e{\overrightarrow{E}}^{\prime }-D_e\overrightarrow{\partial }\left(lnN\right),\hfill \\ \\ {\overrightarrow{V}}_i^{\prime }-K_i{\overrightarrow{V}}_i^{\prime }\times \widehat{b}={\displaystyle \frac{D_i}{H_i}}{\widehat{g}}_{eff}+b_i{\overrightarrow{E}}^{\prime }-D_i\overrightarrow{\partial }\left(lnN\right),\hfill \\ \\ \widehat{b}=\mathrm{vers}{\overrightarrow{B}}^{\prime }=\mathrm{vers}\overrightarrow{B},{\widehat{g}}_{eff}=\mathrm{vers}{\overrightarrow{g}}_{eff}.\hfill \end{array}\right.$$

(194)

The ultimate use of defining the $K_I$s is to use them as conductivity parameters; indeed, this $K_I$ reads

$$K_I={\displaystyle \frac{{\Omega }_I}{{\nu }_I}},$$

(195)

where ${\Omega }_I={\displaystyle \frac{q_{I}B}{m_I}}$ represents the gyration frequency of the ${\mathcal{C}}_I$ particles within the field $\overrightarrow{B}$, and ${\nu }_I$ is the most relevant collisional frequency affecting their motion. All in all, Equation (195) states that the $K_I$ measures the relevance of magnetic forces relative to the dissipation ones in the charged particle dynamics, being de facto a conductivity measurement. Then, the $K_I\to 0$ limit represents the isolating limit, while the hyperconductive limit is $K_I\to +\infty$.

4.2. An Anisotropic Conductor: Role of $\overrightarrow{B}$

We have already stated that electric charges do move much more easily along the magnetic field $\overrightarrow{B}$ than perpendicular to it. It is then expected that the conductance features of the LIM will be different along $\overrightarrow{B}$ and across it. What is usually done is to subdivide the local 3D-space of the ionospheric medium into some $\mathit{R}$ along $\overrightarrow{B}$ and some ${\mathit{R}}^2$ perpendicular to it. In Cartesian coordinates of local $SO\left(3\right)$-vectors, one defines the $\overrightarrow{B}$-parallel and $\overrightarrow{B}$-perpendicular projectors

$$\begin{array}{cc}{P}_{ij}^{//}\left(B\right)={\displaystyle \frac{B_i{B}_j}{B^2}},& P_{ij}^{\perp }\left(B\right)={\delta }_{ij}-{\displaystyle \frac{B_i{B}_j}{B^2}}\end{array}$$

(196)

(these projectors are the same when written in the NeWReF and in the SERF, as ${\overrightarrow{B}}^{\prime }=\overrightarrow{B}$).

The analysis starts using some “generalized velocities”

$$\begin{array}{ccc}{\overrightarrow{W}}_e^{\prime }={\overrightarrow{V}}_e^{\prime }-K_e{\overrightarrow{V}}_e^{\prime }\times \widehat{b},& {\overrightarrow{W}}_i^{\prime }={\overrightarrow{V}}_i^{\prime }-K_i{\overrightarrow{V}}_i^{\prime }\times \widehat{b},& \widehat{b}={\displaystyle \frac{\overrightarrow{B}}{\left|\overrightarrow{B}\right|}},\end{array}$$

(197)

that coincide with the real velocities when the magnetic field is suppressed. These ${\overrightarrow{W}}^{\prime }$ read:

$$\left\{\begin{array}{c}{\overrightarrow{W}}_e^{\prime }={\displaystyle \frac{D_e}{H_e}}{\widehat{g}}_{eff}+b_e{\overrightarrow{E}}^{\prime }-D_e\overrightarrow{\partial }\left(lnN\right),\hfill \\ \\ {\overrightarrow{W}}_i^{\prime }={\displaystyle \frac{D_i}{H_i}}{\widehat{g}}_{eff}+b_i{\overrightarrow{E}}^{\prime }-D_i\overrightarrow{\partial }\left(lnN\right).\hfill \end{array}\right.$$

(198)

We will treat the two of (198) as one equation, omitting the species index and putting ${\overrightarrow{V}}_I^{\prime }=\overrightarrow{v}$ and $K_I=K$ for simplicity. One has

$$\overrightarrow{v}-K\overrightarrow{v}\times \overrightarrow{B}={\displaystyle \frac{1}{\nu }}{\overrightarrow{g}}_{eff}+b{\overrightarrow{E}}^{\prime }-{\displaystyle \frac{k_{B}T}{nM\nu }}\overrightarrow{\partial }n\equiv {\overrightarrow{W}}^{\prime }\left(F\right)$$

(where the vector ${\overrightarrow{W}}^{\prime }\left(F\right)$ is ${\overrightarrow{W}}^{\prime }$ written as a function of the forced applied). Working with the local Cartesian components, one has

$$v_j-K{\epsilon }_{jhk}{v}^h{B}^k=W_j^{\prime }\left(F\right).$$

(199)

In order to work with the transverse and longitudinal components, we can apply to (199) the two projectors defined in (196); doing so, one performs all the calculations reported in Appendix D, and finally obtains:

$${\overrightarrow{v}}_{\perp }={\mathcal{A}}^{-1}\left(K\right)·{\overrightarrow{W}}_{\perp }^{\prime }\left(F\right),$$

(200)

where the matrix ${\mathcal{A}}^{-1}\left(K\right)$ is the one reported in (A20). Note the two limits, easily interpreted via Equation (195):

$$\begin{array}{cc}{\displaystyle \underset{K\to 0}{lim}}{\mathcal{A}}^{-1}\left(K\right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right),& {\displaystyle \underset{K\to +\infty }{lim}}{\mathcal{A}}^{-1}\left(K\right)=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 1\end{array}\right).\end{array}$$

(201)

Since ${\overrightarrow{W}}_{\perp }^{\prime }\left(F\right)$ lies on the plane $x^{\prime }O{y}^{\prime }$, orthogonal to $\overrightarrow{B}=B{\widehat{k}}^{\prime }$ in Appendix D, one obtains:

$${\overrightarrow{W}}_{\perp }^{\prime }\left(F\right)=\left(\begin{array}{c}{w}_x\\ w_y\\ 0\end{array}\right)$$

(see also Figure 5), and applies the matrix ${\mathcal{A}}^{-1}\left(K\right)$ in (A20) to this vector, in order to obtain

$${\mathcal{A}}^{-1}\left(K\right)·{\overrightarrow{W}}_{\perp }^{\prime }\left(F\right)=\left(\begin{array}{c}{\displaystyle \frac{1}{1+K^2}}{w}_x+{\displaystyle \frac{K}{1+K^2}}{w}_y\\ -{\displaystyle \frac{K}{1+K^2}}{w}_x+{\displaystyle \frac{1}{1+K^2}}{w}_y\\ 0\end{array}\right).$$

Let us turn again to (201). In the $K\to +\infty$ limit, the tensor ${\mathcal{A}}^{-1}\left(K\right)$ projects directly along the magnetic axis; when the conductivity becomes very large, the component ${\overrightarrow{v}}_{\perp }$ tends to become the component of ${\overrightarrow{W}}_{\perp }^{\prime }$ along $\overrightarrow{B}$, which is clearly zero. So, this model does not allow for motions orthogonal to $\overrightarrow{B}$ for K exactly infinite. When the ionosphere is “tremendously conducting”, it allows only for motion along $\overrightarrow{B}$ of the charged species.

The vector ${\mathcal{A}}^{-1}\left(K\right)·{\overrightarrow{W}}_{\perp }^{\prime }\left(F\right)$ is still orthogonal to $\overrightarrow{B}$, and can be decomposed into the two directions ${\overrightarrow{W}}_{\perp }^{\prime }\left(F\right)$ and ${\overrightarrow{W}}_{\perp }^{\prime }\left(F\right)\times \widehat{B}$ spanning the cross-$\overrightarrow{B}$ plane. The direction ${\overrightarrow{W}}_{\perp }^{\prime }\left(F\right)\times \widehat{B}$ is

$${\overrightarrow{W}}_{\perp }^{\prime }\left(F\right)\times \widehat{B}=\left(\begin{array}{c}{w}_y\\ -w_x\\ 0\end{array}\right),$$

(202)

so the decomposition reads:

$${\left({\overrightarrow{V}}_I^{\prime }\right)}_{\perp }={\displaystyle \frac{1}{1+K_I^2}}{\left({\overrightarrow{W}}_I^{\prime }\right)}_{\perp }+{\displaystyle \frac{K_I}{1+K_I^2}}{\left({\overrightarrow{W}}_I^{\prime }\right)}_{\perp }\times \widehat{b}.$$

(203)

The full solution giving the velocity of the I-th species in the stationary case reads:

$${\overrightarrow{V}}_I^{\prime }={\left({\overrightarrow{W}}_I^{\prime }\right)}_{//}+{\displaystyle \frac{1}{1+K_I^2}}{\left({\overrightarrow{W}}_I^{\prime }\right)}_{\perp }+{\displaystyle \frac{K_I}{1+K_I^2}}{\left({\overrightarrow{W}}_I^{\prime }\right)}_{\perp }\times \widehat{b}.$$

(204)

This is expanded as:

$$\begin{array}{c}{\overrightarrow{V}}_I^{\prime }={\displaystyle \frac{D_I}{H_I}}{\left({\widehat{g}}_{eff}\right)}_{//}+b_I{\overrightarrow{E}}_{//}^{\prime }-{\displaystyle \frac{D_I}{N}}{\left(\overrightarrow{\partial }N\right)}_{//}+\hfill \\ \\ +{\displaystyle \frac{{\left({\overrightarrow{g}}_{eff}\right)}_{\perp }}{{\nu }_I\left(1+K_I^2\right)}}+{\displaystyle \frac{b_I}{1+K_I^2}}{\overrightarrow{E}}_{\perp }^{\prime }-{\displaystyle \frac{D_I}{1+K_I^2}}{\displaystyle \frac{{\overrightarrow{\partial }}_{\perp }N}{N}}+\hfill \\ \\ +{\displaystyle \frac{K_I}{1+K_I^2}}{\displaystyle \frac{1}{{\nu }_{I}B}}\left({\overrightarrow{g}}_{eff}\times \overrightarrow{B}\right)-{\displaystyle \frac{K_I}{1+K_I^2}}{\displaystyle \frac{D_I}{B}}{\displaystyle \frac{\overrightarrow{\partial }N}{N}}\times \overrightarrow{B}+{\displaystyle \frac{K_I}{1+K_I^2}}{\displaystyle \frac{b_I}{B}}{\overrightarrow{E}}^{\prime }\times \overrightarrow{B}.\hfill \end{array}$$

(205)

In order to understand the limit $K_I\gg 1$ in which the gyration prevails over the inter-particle collisions, it is convenient to expand a la Taylor the coefficients

$$\begin{array}{cc}{\displaystyle \frac{1}{1+K_I^2}},& {\displaystyle \frac{K_I}{1+K_I^2}}\end{array}$$

with respect to $K_I^{-1}$, obtaining

$$\begin{array}{cc}{\displaystyle \frac{1}{1+K_I^2}}=K_I^{-2}-K_I^{-4}+O\left(K_I^{-6}\right)& {\displaystyle \frac{K_I}{1+K_I^2}}=K_I^{-1}-K_I^{-3}+O\left(K_I^{-5}\right):\end{array}$$

(206)

If one has $K_I\gg 1$, it is possible to truncate those expressions as

$$\begin{array}{cc}{\displaystyle \frac{1}{1+K_I^2}}=K_I^{-2}+\dots ,& {\displaystyle \frac{K_I}{1+K_I^2}}=K_I^{-1}+\dots \end{array}$$

(207)

When $K_I^{-1}$ tends to zero, the surviving terms are:

$$\begin{array}{c}{\displaystyle \underset{K_I\gg 1}{lim}}{\overrightarrow{V}}_I^{\prime }={\displaystyle \frac{D_I}{H_I}}{\left({\widehat{g}}_{eff}\right)}_{//}+b_I{\overrightarrow{E}}_{//}^{\prime }-{\displaystyle \frac{D_I}{N}}{\left(\overrightarrow{\partial }N\right)}_{//}+\hfill \\ \\ +{\displaystyle \frac{1}{{\nu }_I{K}_{I}B}}\left({\overrightarrow{g}}_{eff}\times \overrightarrow{B}\right)-{\displaystyle \frac{D_I}{B{K}_I}}{\displaystyle \frac{\overrightarrow{\partial }N}{N}}\times \overrightarrow{B}+{\displaystyle \frac{b_I}{B{K}_I}}{\overrightarrow{E}}^{\prime }\times \overrightarrow{B}.\hfill \end{array}$$

(208)

Considering the definitions (193), one has:

$$\begin{array}{c}{\displaystyle \underset{K_I\gg 1}{lim}}{\overrightarrow{V}}_I^{\prime }={\displaystyle \frac{1}{B^2}}{\overrightarrow{E}}^{\prime }\times \overrightarrow{B}-{\displaystyle \frac{k_B{T}_I}{q_I{B}^2}}{\displaystyle \frac{\overrightarrow{\partial }N}{N}}\times \overrightarrow{B}+{\displaystyle \frac{m_I}{q_I{B}^2}}\left({\overrightarrow{g}}_{eff}\times \overrightarrow{B}\right)+\hfill \\ \\ +{\displaystyle \frac{q_I}{m_I{\nu }_I}}{\overrightarrow{E}}_{//}^{\prime }+{\displaystyle \frac{1}{{\nu }_I}}{\left({\overrightarrow{g}}_{eff}\right)}_{//}-{\displaystyle \frac{k_B{T}_I}{N{m}_I{\nu }_I}}{\left(\overrightarrow{\partial }N\right)}_{//}.\hfill \end{array}$$

(209)

In the limit $K_I\gg 1$, the terms depending on the species at hand are

$$\begin{array}{c}{\displaystyle \frac{q_I}{m_I{\nu }_I}}{\overrightarrow{E}}_{//}^{\prime }+{\displaystyle \frac{1}{{\nu }_I}}{\left({\overrightarrow{g}}_{eff}\right)}_{//}+{\displaystyle \frac{m_I}{q_I{B}^2}}\left({\overrightarrow{g}}_{eff}\times \overrightarrow{B}\right)+\hfill \\ \\ -{\displaystyle \frac{k_B{T}_I}{N{m}_I{\nu }_I}}{\left(\overrightarrow{\partial }N\right)}_{//}-{\displaystyle \frac{k_B{T}_I}{q_I{B}^2}}{\displaystyle \frac{\overrightarrow{\partial }N}{N}}\times \overrightarrow{B},\hfill \end{array}$$

while the term

$${\overrightarrow{V}}_{EB}^{\prime }={\displaystyle \frac{1}{B^2}}{\overrightarrow{E}}^{\prime }\times \overrightarrow{B}$$

(210)

is the same for every charged species, and is referred to as E-cross-B drift. When gravitational and concentration gradient effects are negligible, the part of ${\overrightarrow{V}}_I^{\prime }$ orthogonal to $\overrightarrow{B}$ is reduced to the E-cross-B drift only for all the charged species. Due to this condition, it is impossible to have any net current perpendicular to the magnetic field.

In the non-conducting limit $K_I\to 0$, the inter-particle collisions prevail on the gyration

$${\displaystyle \underset{K_I\to 0}{lim}}{\overrightarrow{V}}_I^{\prime }={\left({\overrightarrow{W}}_I^{\prime }\right)}_{//}+{\left({\overrightarrow{W}}_I^{\prime }\right)}_{\perp }={\overrightarrow{W}}_I^{\prime }\left(F\right):$$

(211)

In this case, one experiences a viscous motion for the charged species, with the velocity directed as the forces ${\overrightarrow{W}}_i^{\prime }\left(F\right)$. In this regime, negative and positive particles have different motions because they undergo different electromagnetic forces.

We are finally in the position to treat the ionospheric medium as an anisotropic conductor.

4.3. Ohm’s Law for the Ionosphere

All the work performed up to here has been useful to describe the local ionospheric equilibrium as a conductor, and give its Ohm’s law.

If the local electric field is $\overrightarrow{E}$, we will look for the expression

$${\overrightarrow{J}}_q={\overrightarrow{J}}_q\left(\overrightarrow{E}\right)$$

(212)

relating the electric current to the given field. In general, the relation (212) is a smooth dependence of any kind

$$J_k\left(\overrightarrow{E}\right)=J_k\left(0\right)+\sum _{n=1}^{+\infty }{\displaystyle \frac{{\partial }^n{J}_k}{\partial E_{i_1}\dots \partial E_{i_n}}}\left(0\right)E_{i_1}\dots E_{i_n}$$

(213)

(the subscript “q” has been omitted for simplicity in the local Cartesian components $J_h$ of ${\overrightarrow{J}}_q$; the $SO\left(3\right)$-tensor summation convention on indices is again in use) and in our case, we will make a linear medium assumption:

$$J_k\left(\overrightarrow{E}\right)=J_k\left(0\right)+{\displaystyle \frac{\partial J_k}{\partial E_i}}\left(0\right)E_i.$$

(214)

Equation (214) may be re-written defining the conducibility tensor

$${\sigma }^{ki}={\displaystyle \frac{\partial J_k}{\partial E^i}}\left(0\right),$$

(215)

so that one has

$${\overrightarrow{J}}_q\left(\overrightarrow{E}\right)={\overrightarrow{J}}_q\left(0\right)+\sigma ·\overrightarrow{E};$$

(216)

using fussy primes in the NeWReF:

$${\overrightarrow{J}}_q^{\prime }\left({\overrightarrow{E}}^{\prime }\right)={\overrightarrow{J}}_q^{\prime }\left(0\right)+{\sigma }^{\prime }·{\overrightarrow{E}}^{\prime }.$$

(217)

${\sigma }^{\prime }$ will be constructed in the NeWReF directly, then it will be transformed to the SERF.

If the medium is “the simplest dirty plasma possible”:

$$\left\{{\mathcal{C}}_I\right\}=\left\{X^{+},e^{-},X\right\},$$

then the electric current reads:

$${\overrightarrow{J}}_q^{\prime }=Ne\left({\overrightarrow{V}}_i^{\prime }-{\overrightarrow{V}}_e^{\prime }\right).$$

This vector is calculated explicitly in all its three components $\left(J_x^{\prime },J_y^{\prime },J_z^{\prime }\right)$ in the NeWReF through the calculations in Appendix E. Only some part of the electric currents is determined by the electric field ${\overrightarrow{E}}^{\prime }$, since the concentration gradient and gravity force contribute as well. Searching for the form (217) for the part of ${\overrightarrow{J}}^{\prime }$ determined by the electric field, one has

$$\left\{\begin{array}{c}{J}_x^{\prime }\left(E^{\prime }\right)=\left({\displaystyle \frac{Ne{b}_i}{1+K_i^2}}-{\displaystyle \frac{Ne{b}_e}{1+K_e^2}}\right)E_x^{\prime }+\left({\displaystyle \frac{Ne{K}_i{b}_i}{1+K_i^2}}-{\displaystyle \frac{Ne{K}_e{b}_e}{1+K_e^2}}\right)E_y^{\prime },\hfill \\ \\ J_y^{\prime }\left(E^{\prime }\right)=\left({\displaystyle \frac{Ne{b}_i}{1+K_i^2}}-{\displaystyle \frac{Ne{b}_e}{1+K_e^2}}\right)E_y^{\prime }-\left({\displaystyle \frac{Ne{K}_i{b}_i}{1+K_i^2}}-{\displaystyle \frac{Ne{K}_e{b}_e}{1+K_e^2}}\right)E_x^{\prime },\hfill \\ \\ J_z^{\prime }\left(E^{\prime }\right)=Ne\left(b_i-b_e\right)E_z^{\prime }\hfill \end{array}\right.$$

(218)

(consider the definitions (193)). Then, the non-vanishing components of ${\sigma }^{\prime }$ read:

$$\left\{\begin{array}{c}{\sigma }_{xx}^{\prime }={\sigma }_{yy}^{\prime }={\displaystyle \frac{Ne{b}_i}{1+K_i^2}}-{\displaystyle \frac{Ne{b}_e}{1+K_e^2}}\equiv {\sigma }_P,\hfill \\ \\ {\sigma }_{xy}^{\prime }=-{\sigma }_{yx}^{\prime }={\displaystyle \frac{Ne{K}_i{b}_i}{1+K_i^2}}-{\displaystyle \frac{Ne{K}_e{b}_e}{1+K_e^2}}\equiv -{\sigma }_H,\hfill \\ \\ {\sigma }_{zz}^{\prime }=Ne\left(b_i-b_e\right)\equiv {\sigma }_0.\hfill \end{array}\right.$$

(219)

${\sigma }^{\prime }$ can be written as a matrix:

$${\sigma }^{\prime }=\left(\begin{array}{ccc}{\displaystyle \frac{Ne{b}_i}{1+K_i^2}}-{\displaystyle \frac{Ne{b}_e}{1+K_e^2}}& {\displaystyle \frac{Ne{K}_i{b}_i}{1+K_i^2}}-{\displaystyle \frac{Ne{K}_e{b}_e}{1+K_e^2}}& 0\\ {\displaystyle \frac{Ne{K}_e{b}_e}{1+K_e^2}}-{\displaystyle \frac{Ne{K}_i{b}_i}{1+K_i^2}}& {\displaystyle \frac{Ne{b}_i}{1+K_i^2}}-{\displaystyle \frac{Ne{b}_e}{1+K_e^2}}& 0\\ 0& 0& Ne\left(b_i-b_e\right)\end{array}\right).$$

(220)

The part ${\overrightarrow{J}}_q^{\prime }\left(0\right)$ of the electric current, which is determined by non-electric factors, can be written by introducing two more tensors ${\alpha }^{\prime }$ and ${\beta }^{\prime }$. If the tensor

$${\alpha }^{\prime }=\left(\begin{array}{ccc}{\displaystyle \frac{Ne}{1+K_i^2}}{\displaystyle \frac{1}{{\nu }_i}}-{\displaystyle \frac{Ne}{1+K_e^2}}{\displaystyle \frac{1}{{\nu }_e}}& {\displaystyle \frac{Ne{K}_i}{1+K_i^2}}{\displaystyle \frac{1}{{\nu }_i}}-{\displaystyle \frac{Ne{K}_e}{1+K_e^2}}{\displaystyle \frac{1}{{\nu }_e}}& 0\\ {\displaystyle \frac{Ne{K}_e}{1+K_e^2}}{\displaystyle \frac{1}{{\nu }_e}}-{\displaystyle \frac{Ne{K}_i}{1+K_i^2}}{\displaystyle \frac{1}{{\nu }_i}}& {\displaystyle \frac{Ne}{1+K_i^2}}{\displaystyle \frac{1}{{\nu }_i}}-{\displaystyle \frac{Ne}{1+K_e^2}}{\displaystyle \frac{1}{{\nu }_e}}& 0\\ 0& 0& {\displaystyle \frac{Ne}{{\nu }_i}}-{\displaystyle \frac{Ne}{{\nu }_e}}\end{array}\right)$$

(221)

and also

$${\beta }^{\prime }=\left(\begin{array}{ccc}{\displaystyle \frac{e{D}_e}{1+K_e^2}}-{\displaystyle \frac{e{D}_i}{1+K_i^2}}& {\displaystyle \frac{e{K}_e{D}_e}{1+K_e^2}}-{\displaystyle \frac{e{K}_i{D}_i}{1+K_i^2}}& 0\\ {\displaystyle \frac{e{K}_i{D}_i}{1+K_i^2}}-{\displaystyle \frac{e{K}_e{D}_e}{1+K_e^2}}& {\displaystyle \frac{e{D}_e}{1+K_e^2}}-{\displaystyle \frac{e{D}_i}{1+K_i^2}}& 0\\ 0& 0& -e\left(D_i-D_e\right)\end{array}\right)$$

(222)

are defined, the linear relation between ${\overrightarrow{J}}_q^{\prime }$ and its causes takes the form:

$${\overrightarrow{J}}_q^{\prime }={\sigma }^{\prime }·{\overrightarrow{E}}^{\prime }+{\alpha }^{\prime }·{\overrightarrow{g}}_{eff}+{\beta }^{\prime }·\overrightarrow{\partial }N.$$

(223)

The electric addendum

$${\overrightarrow{J}}_{qE}^{\prime }\stackrel{\mathrm{def}}{=}{\overrightarrow{J}}_q^{\prime }-{\overrightarrow{J}}_q^{\prime }\left(0\right)={\sigma }^{\prime }·{\overrightarrow{E}}^{\prime }$$

can be put into the form

$$\begin{array}{cc}{\overrightarrow{J}}_{qE}^{\prime }={\sigma }_P{\overrightarrow{E}}_{\perp }^{\prime }-{\sigma }_H\left({\overrightarrow{E}}_{\perp }^{\prime }\times \widehat{B}\right)+{\sigma }_0{\overrightarrow{E}}_{//}^{\prime },& \left\{\begin{array}{c}{\overrightarrow{B}}^{\prime }=B{\widehat{k}}^{\prime },\hfill \\ \\ {\overrightarrow{E}}_{//}^{\prime }=E_z^{\prime }{\widehat{k}}^{\prime },\hfill \\ \\ {\overrightarrow{E}}_{\perp }^{\prime }=E_x^{\prime }{\widehat{i}}^{\prime }+E_y^{\prime }{\widehat{j}}^{\prime }.\hfill \end{array}\right.\end{array}$$

(224)

Let us give an order of magnitude for the various contributions to ${\overrightarrow{J}}_q^{\prime }$. Fixing the height as:

$$\begin{array}{ccc}h=300\mathrm{km}& \Rightarrow & N_e=20\times {10}^{11}{\mathrm{m}}^{-3}\end{array}$$

for a realistic equatorial daytime condition, we have:

$$\begin{array}{cc}{\sigma }_P,{\sigma }_H\ll {\sigma }_0,& {\sigma }_0\simeq 39.8\mathrm{O}\mathrm{h}\mathrm{m}/\mathrm{m}.\end{array}$$

With an electric field $\overrightarrow{E}$ of

$$E\simeq 50\mathrm{m}\mathrm{V}/\mathrm{m}$$

one obtains:

$${\sigma }_{0}E\simeq 1.99\times {10}^{-3}\mathrm{A}/{\mathrm{m}}^2.$$

According to the values of the involved quantities as given in [28,37], the elements of the matrix ${\alpha }^{\prime }$ are:

$$\begin{array}{ccc}{\alpha }_{xx}^{\prime }={\alpha }_{yy}^{\prime }\simeq 4\times {10}^{-11}{\mathrm{As}}^2/{\mathrm{m}}^3,& {\alpha }_{xy}^{\prime }\simeq 4\times {10}^{-9}{\mathrm{As}}^2/{\mathrm{m}}^3,& {\alpha }_{zz}^{\prime }\simeq 4\times {10}^{-7}{\mathrm{As}}^2/{\mathrm{m}}^3,\end{array}$$

so that

$$\begin{array}{ccc}{\alpha }_{xx}^{\prime }{g}_{eff}\simeq 3.9\times {10}^{-10}\mathrm{A}/{\mathrm{m}}^2,& {\alpha }_{xy}^{\prime }{g}_{eff}\simeq 4\times {10}^{-8}\mathrm{A}/{\mathrm{m}}^2,& {\alpha }_{zz}^{\prime }{g}_{eff}\simeq 4\times {10}^{-6}\mathrm{A}/{\mathrm{m}}^2.\end{array}$$

The matrix ${\beta }^{\prime }$ has the following values instead:

$$\begin{array}{ccc}{\beta }_{xx}^{\prime }={\beta }_{yy}^{\prime }\simeq 1.9\times {10}^{-16}{\mathrm{Am}}^2,& {\beta }_{xy}^{\prime }\simeq 1.6\times {10}^{-18}{\mathrm{Am}}^2,& {\beta }_{zz}^{\prime }\simeq 0\end{array}$$

and since we assume

$$\begin{array}{ccc}\Delta \ell =20\mathrm{km}& \Rightarrow & \Delta N_e=5\times {10}^{11} {\mathrm{m}}^{-3}\end{array}$$

we can say:

$$\begin{array}{ccc}{\beta }_{xx}^{\prime }\partial N_e\simeq 4.75\times {10}^{-9}\mathrm{A}/{\mathrm{m}}^2,& {\beta }_{xy}^{\prime }\partial N_e\simeq 4\times {10}^{-11}\mathrm{A}/{\mathrm{m}}^2,& {\beta }_{zz}^{\prime }\partial N_e\simeq 0.\end{array}$$

These values, even if roughly calculated, show that the non-electric contributions to ${\overrightarrow{J}}_q$ are negligible with respect to the electric ones.

Equation (223) can be transformed to the SERF, where it becomes

$${\overrightarrow{J}}_q=\sigma ·\left(\overrightarrow{E}+\overrightarrow{U}\times \overrightarrow{B}\right)+\alpha ·{\overrightarrow{g}}_{eff}+\beta ·\overrightarrow{\partial }N,$$

(225)

since ${\overrightarrow{J}}_q^{\prime }=\overrightarrow{J}$, ${\overrightarrow{E}}^{\prime }=\overrightarrow{E}+\overrightarrow{U}\times \overrightarrow{B}$ and the $SO\left(3\right)$-tensors stay unchanged, because they do not rotate, and the field on which they depend is the magnetic field $\overrightarrow{B}$, which remains unchanged due to Equation (183).

Let us turn to (224); in the SERF, we can write

$${\overrightarrow{J}}_q={\sigma }_P{\overrightarrow{E}}_{\perp }-{\sigma }_H\left({\overrightarrow{E}}_{\perp }\times \widehat{B}\right)+{\sigma }_0{\overrightarrow{E}}_{//}+\sigma ·\left(\overrightarrow{U}\times \overrightarrow{B}\right)+\alpha ·{\overrightarrow{g}}_{eff}+\beta ·\overrightarrow{\partial }N,$$

so that the part of ${\overrightarrow{J}}_q$ of electric origin reads

$${\overrightarrow{J}}_{qE}={\sigma }_P{\overrightarrow{E}}_{\perp }-{\sigma }_H\left({\overrightarrow{E}}_{\perp }\times \widehat{B}\right)+{\sigma }_0{\overrightarrow{E}}_{//}.$$

(226)

The term

$$-{\sigma }_H\left({\overrightarrow{E}}_{\perp }\times \widehat{B}\right)=\left({\displaystyle \frac{N{e}^{2}b}{M\nu +\frac{e^2{B}^2}{M\nu }}}-{\displaystyle \frac{N{e}^{2}b}{M\nu +\frac{e^2{B}^2}{M\nu }}}\right)\overrightarrow{E}\times \overrightarrow{B}\equiv {\overrightarrow{J}}_{EB}$$

(227)

is considered as the part of the electric current due to the E-cross-B drift. This ${\overrightarrow{J}}_{EB}$ tends to zero when conducibilities K diverge; in fact, the expression

$${\overrightarrow{J}}_{EB}=\left({\displaystyle \frac{Ne{K}_i{b}_i}{1+K_i^2}}-{\displaystyle \frac{Ne{K}_e{b}_e}{1+K_e^2}}\right)\left({\overrightarrow{E}}_{\perp }\times \widehat{B}\right)$$

(228)

can be Taylor-expanded in $K_I^{-1}$ up to the linear terms. In this way, we obtain

$$\left\{\begin{array}{c}{\displaystyle \frac{Ne{K}_i{b}_i}{1+K_i^2}}={\displaystyle \frac{Ne{b}_i}{K_i}}-{\displaystyle \frac{Ne{b}_i}{K_i^3}}+O\left(K_i^{-5}\right)={\displaystyle \frac{Ne{b}_i}{K_i}}+\dots ={\displaystyle \frac{Ne}{B}}+\dots ,\hfill \\ \\ {\displaystyle \frac{Ne{K}_e{b}_e}{1+K_e^2}}={\displaystyle \frac{Ne{b}_e}{K_e}}-{\displaystyle \frac{Ne{b}_e}{K_e^3}}+O\left(K_e^{-5}\right)={\displaystyle \frac{Ne{b}_e}{K_e}}+\dots ={\displaystyle \frac{Ne}{B}}+\dots ,\hfill \end{array}\right.$$

so that for negligible $K_i^{-1}$ and $K_e^{-1}$, the factor ${\displaystyle \frac{Ne{K}_i{b}_i}{1+K_i^2}}-{\displaystyle \frac{Ne{K}_e{b}_e}{1+K_e^2}}$ is the difference of two equal quantities, i.e., it vanishes. The following limit holds:

$${\displaystyle \underset{o\left(K\right)\to 0}{lim}}{\overrightarrow{J}}_{EB}=0.$$

(229)

This was already highlighted on page 45.

Equation (225) of the upper atmosphere as a conducting medium can be used “directly”, i.e., to calculate the currents observed in the presence of a given electric field; it can also be used “inversely”, obtaining the fields $\overrightarrow{E}$ necessary to produce the given currents. The latter is the most important use of Equations (225) and (223), where the fields necessary for the observed currents are deduced, so that one tries to understand their possible geophysical/space origin.

4.4. Ionospheric Electrostatic Fields

Ionospheric electric fields exist because magnetic, gravity and pressure forces produce (even slightly) different effects on ions and electrons; when ions and electrons move differently and become separated, the local neutrality of the medium can be violated, so some $\delta \ne 0$ arises at some position. The local charge separation does produce an electric field so that

$$\overrightarrow{\partial }·\overrightarrow{E}={\displaystyle \frac{\delta }{{\epsilon }_0}}.$$

(230)

As these $\delta$s may vary with time, they create an increase in a local current too, since $\overrightarrow{\partial }·{\overrightarrow{J}}_q=-{\partial }_t\delta$, while $\delta$ passes from zero to a finite value, or vice versa. In the stationary condition described here, the current ${\overrightarrow{J}}_q$ is a divergenceless vector; in any case, this is a dynamical equilibrium, since the very complicated forces $\overrightarrow{W}\left(F\right)$ yield some ${\overrightarrow{J}}_q$, which is, in general, $\overrightarrow{\partial }·{\overrightarrow{J}}_q\ne 0$. This will, in turn, produce a field $\overrightarrow{E}$ re-assessing charges and currents, up to the moment in which ${\partial }_t\delta =0$ holds again, and then $\overrightarrow{\partial }·{\overrightarrow{J}}_q=0$.

In the case that one has some electric charge [28], for instance,

$$\delta \simeq 9·{10}^{-17}{\mathrm{C}\mathrm{m}}^{-3},$$

the electric field is constant over a distance of $L=1\mathrm{km}$, with a value

$$E\simeq 10{\mathrm{mV}\mathrm{m}}^{-1}:$$

In order to see how long $\overrightarrow{\partial }·{\overrightarrow{J}}_q\ne 0$ will last, one considers this unknown time $\tau$ and writes:

$${\displaystyle \frac{\delta }{\tau }}={\displaystyle \frac{E}{L}}\sigma \Rightarrow \tau ={\displaystyle \frac{L\delta }{\sigma E}},$$

and sees that the solenoidal nature of ${\overrightarrow{J}}_q$ is restored within some microsecond:

$$\tau \simeq {10}^{-6}\mathrm{s}.$$

Processes in which neutral winds (those of speed $\overrightarrow{U}$ in the foregoing pages) produce ionospheric motions that induce electric charge separations, and currents and electric fields, are referred to as dynamo processes. The power spent by the wind dynamo on the system is positive

$$w_{\mathrm{wind}}>0,$$

as the wind actively drags the ionospheric medium. In the steady regime, the atmospheric winds spend some power $w_{\mathrm{wind}}$ on the plasma motion, balancing exactly the power $w_{\mathrm{E}}$

$$w_{\mathrm{E}}=\overrightarrow{E}·{\overrightarrow{J}}_q$$

exerted by $\overrightarrow{E}$ on ${\overrightarrow{J}}_q$:

$$\begin{array}{ccc}{w}_{\mathrm{wind}}+w_{\mathrm{E}}=0& \Rightarrow & w_{\mathrm{wind}}=-\overrightarrow{E}·{\overrightarrow{J}}_q.\end{array}$$

Neutral winds move the ionosphere across the geomagnetic field, so their power is positive, and this leads to the negativity of $w_{\mathrm{E}}$

$$\overrightarrow{E}·{\overrightarrow{J}}_q<0,$$

according to the fact that this $\overrightarrow{E}$ arises in opposition to the motion separating the charges. This dynamo basically works in the same way as the functioning of a battery closed on a conductor; in this way, the electrostatic $\overrightarrow{E}$ due to the wind-induced separation of charges tries to make the charges fall back on their opposite-sign fellows, driving $\delta$ to zero, like the field of a short circuit, nullifying the work of the battery.

In the upper atmosphere, there also exists an opposite mechanism in which some external electric field does some positive work on the electric charges of the plasma, i.e., on the currents. These currents, in turn, spend power on the neutral matter, this time doing negative work on them; this is the mechanism of the auroral currents induced by the electrodynamic field, in turn due to the precipitation of the charged solar wind. In this case, the external field due to the solar wind gives some positive power to the currents

$$w_{\mathrm{E}}={\overrightarrow{E}}_{\mathrm{ext}}·{\overrightarrow{J}}_q>0,$$

while the current transmission through the thermosphere dissipates power via the Joule effect, heating the atmosphere. This mechanism is referred to as ion drag because inside these current regions, the ions are the ones that mainly interact with neutrals, due to inertial reasons (see also the approximation (173) in which the electron drag is neglected).

4.5. Electric Field “Propagation”

Due to the anisotropy of the tensor $\sigma$, the upper atmosphere can be electrically represented as a conducting cage formed by the geomagnetic field lines along which charges move as freely as along a metallic wire, and across which they cannot move, precisely because ${\sigma }_0\gg {\sigma }_H,{\sigma }_P$. For example, at mid and high latitudes, one has

$$\begin{array}{ccc}h\simeq 3000\mathrm{km}& \Rightarrow & {\displaystyle \frac{{\sigma }_P}{{\sigma }_0}}\simeq {10}^{-6}.\end{array}$$

Using the definitions (219) and (193), one recognizes

$${\displaystyle \frac{{\sigma }_P}{{\sigma }_0}}={\displaystyle \frac{Mm{\nu }_i{\nu }_e\left(Mm{\nu }_i{\nu }_e+e^2{B}^2\right)}{\left(m^2{\nu }_e^2+e^2{B}^2\right)\left(M^2{\nu }_i^2+e^2{B}^2\right)}}=O\left({\nu }^2\right)$$

(231)

and

$${\displaystyle \frac{{\sigma }_H}{{\sigma }_0}}={\displaystyle \frac{e^{2}BMm{\nu }_i{\nu }_e\left(M{\nu }_i-m{\nu }_e\right)}{\left(m^2{\nu }_e^2+e^2{B}^2\right)\left(M^2{\nu }_i^2+e^2{B}^2\right)}}=O\left({\nu }^4\right),$$

(232)

and sees clearly that where collision frequencies tend to vanish, those rations do too, obtaining the approximation (233) (see below). This reduces the tensor $\sigma$ simply to the tensor equal to ${\sigma }_0$ along $\overrightarrow{B}$, vanishing in the directions perpendicular to it.

In the roughest approximation, for ${\sigma }_0\to \infty$, we can think of the field lines of $\overrightarrow{B}$ as perfectly conducting lines, which are equipotential, and with $\overrightarrow{E}$, which is orthogonal to them point by point; see Figure 6.

In this subsection, we want to discuss two examples of how the geomagnetic conducting cage affects the configuration of $\overrightarrow{E}\left(\overrightarrow{r},t\right)$. On the one hand, we want to discuss how perturbations $\delta \overrightarrow{E}$ propagate along the $\overrightarrow{B}$-lines; on the other hand, we want to discuss how those perturbations $\delta \overrightarrow{E}$ may be produced by the injection of $\overrightarrow{B}$-aligned currents at high latitudes.

All the calculations are performed in the quiet ionosphere approximation, i.e., considering the $\overrightarrow{B}$-lines as conducting wires in electrostatic equilibrium.

4.5.1. Pole to Equator $\delta \overrightarrow{E}$ “Propagation”

Let us consider the equations describing $\overrightarrow{E}$ in the electrostatic regime. Within the approximation

$${\displaystyle \frac{{\sigma }_{H,P}}{{\sigma }_0}}\simeq 0$$

(233)

one can see that if some electric field is produced in a point of the $\overrightarrow{B}$ line, this is expected to propagate all along the line, perpendicular to it point by point, in the same order of time in which charges displaced on a conductor weakly out of equilibrium re-displace and reach equilibrium again. This is a possible mechanism for the propagation of electric fields from high latitudes at low height to low latitudes at high height, as observed in a electric field correlation study [38], in which some equatorial $\delta \overrightarrow{E}$ takes place almost simultaneously with some polar $\delta \overrightarrow{E}$ with the same time behavior. This is heuristically understandable by looking at the geomagnetic dipole profile, represented in Figure 7; if some field $\overrightarrow{E}$ is produced at the polar oval at some point P of height h (due to the injection of charged particles by the solar wind, for example, which causes $\delta \ne 0$ locally), this will be transported as a vector orthogonal to the geomagnetic line up to equatorial latitudes to a point $P^{\prime }$ of height $h^{\prime }$, which can be much higher than h, due to the shape of the dipolar geomagnetic line. This is grossly how the precipitation of charged matter at low heights in the polar zone can yield a variation $\delta \overrightarrow{E}$ of the ionospheric electric field at low latitudes, at much higher quotes.

All this reasoning has to be put into a quantitative frame.

When the stationary condition $\overrightarrow{\partial }·{\overrightarrow{J}}_q=0$ holds, the PDE for $\overrightarrow{E}$ of the ionosphere is written by using (225)

$$\overrightarrow{\partial }·\left(\sigma ·\overrightarrow{E}\right)=-\overrightarrow{\partial }·\left[\sigma ·\left(\overrightarrow{U}\times \overrightarrow{B}\right)\right]-\overrightarrow{\partial }·\left(\alpha ·{\overrightarrow{g}}_{eff}\right)-\overrightarrow{\partial }·\left(\beta ·\overrightarrow{\partial }N\right);$$

Then, going to the NeWReF, we have:

$$\overrightarrow{\partial }·\left(\sigma ·\overrightarrow{E}\right)=-\overrightarrow{\partial }·\left(\alpha ·{\overrightarrow{g}}_{eff}\right)-\overrightarrow{\partial }·\left(\beta ·\overrightarrow{\partial }N\right)$$

(234)

(we are omitting species indices for simplicity). If “non-electric” contributions to the electric current are negligible $\alpha ·{\overrightarrow{g}}_{eff}+\beta ·\overrightarrow{\partial }N\simeq 0$, the equation for $\overrightarrow{E}$ reads:

$$E_j{\partial }_i{\sigma }^{ij}+{\sigma }^{ij}{\partial }_i{E}_j=0.$$

(235)

Equation (235) state that the source of $\overrightarrow{E}$ can be a discontinuity in the conducibility of the medium, as can be seen by writing it as

$${\sigma }^{ij}{\partial }_i{E}_j=-E_j{\partial }_i{\sigma }^{ij},$$

(236)

as happens, for example, at the terminators. The stationary condition $\overrightarrow{\partial }·{\overrightarrow{J}}_q=0$ is a quasi-equilibrium condition, so $\overrightarrow{E}$ is reasonably “quasi-electrostatic”, and we look for solutions of (235) in the form of gradients of a scalar function $\varphi$ (the electrostatic potential):

$$\exists \varphi /\overrightarrow{E}=-\overrightarrow{\partial }\varphi .$$

(237)

The electrostatic potential is related to ${\overrightarrow{J}}_q$ as

$$\overrightarrow{\partial }·{\overrightarrow{J}}_q=-{\partial }_j\varphi {\partial }_i{\sigma }^{ij}-{\sigma }^{ij}{\partial }_i{\partial }_j\varphi .$$

(238)

The PDE for $\varphi$ reads:

$${\partial }_j\varphi {\partial }_i{\sigma }^{ij}+{\sigma }^{ij}{\partial }_i{\partial }_j\varphi =0.$$

(239)

For quasi-homogeneous media

$$\left|{\partial }_j\varphi {\partial }_i{\sigma }^{ij}\right|\ll \left|{\sigma }^{ij}{\partial }_i{\partial }_j\varphi \right|,$$

(240)

meaning that we are working in regions where $\sigma$ is slowly dependent on space coordinates, the solenoidal current condition reads

$${\sigma }^{ij}{\partial }_i{\partial }_j\varphi =0.$$

(241)

This has some sense, as one sees, for instance, looking at Figure 2.6 of [28], one can redact this table:

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial {\sigma }_P}{\partial h}}\simeq 4\times {10}^{-12}÷6\times {10}^{-11}\mathrm{Ohm}/{\mathrm{m}}^2,\hfill \\ \\ {\displaystyle \frac{\partial {\sigma }_H}{\partial h}}\simeq 9.9\times {10}^{-11}\mathrm{Ohm}/{\mathrm{m}}^2,\hfill \\ \\ {\displaystyle \frac{\partial {\sigma }_0}{\partial h}}\simeq 1.13\times {10}^{-4}÷1.2\times {10}^{-4}\mathrm{Ohm}/{\mathrm{m}}^2.\hfill \end{array}\right.$$

Clearly, conditions (240) exclude $\sigma$-discontinuity regions as the terminators.

The more general PDE (239) is processed with some algebraic manipulation, thoroughly illustrated in Appendix F. Its solution is found in terms of $\varphi \left(x,y,z\right)$, where z is the local magnetic direction and x and y the coordinates perpendicular to it (see Figure 5). An assumption is made about how ${\sigma }_0$ and ${\sigma }_P$ depend on z (see Equation (A43)), and the following solution is given, in terms of a Fourier series:

$$\begin{array}{c}\varphi \left(x,y,z\right)=\hfill \\ \\ =e^{-{\displaystyle \frac{1}{2}}{c}_0\sqrt{{\displaystyle \frac{{\sigma }_P\left(z\right)}{{\sigma }_0\left(z\right)}}}z}{\displaystyle \sum _{{\overrightarrow{k}}_{\perp }}}{f}_0\left({\overrightarrow{k}}_{\perp }\right)e^{i{k}_{x}x+i{k}_{y}y}\left[A_{+}\left(k_{\perp }^2\right)e^{{\displaystyle \frac{1}{2}}\sqrt{c_0^2+4k_{\perp }^2}\sqrt{{\displaystyle \frac{{\sigma }_P\left(z\right)}{{\sigma }_0\left(z\right)}}}z}+\right.\hfill \\ \\ \left.+A_{-}\left(k_{\perp }^2\right)e^{-{\displaystyle \frac{1}{2}}\sqrt{c_0^2+4k_{\perp }^2}\sqrt{{\displaystyle \frac{{\sigma }_P\left(z\right)}{{\sigma }_0\left(z\right)}}}z}\right].\hfill \end{array}$$

(242)

This solution of the anisotropic Poisson Equation (239) gives some indications about the propagation of the electrostatic disturbances along the geomagnetic lines. Of course, the term “propagation” has to be taken with some care, as (239) is an equilibrium, time-independent PDE; it will not describe how electric waves travel, rather how electrostatic fields re-arrange in case of perturbation of an equilibrium, to reach another equilibrium. These solutions are characterized by the value of $k_{\perp }^2$; this ${\overrightarrow{k}}_{\perp }$ is formally the wave vector of the potential along the directions orthogonal to the geomagnetic lines, and the inverse of its strength ${\ell }_{\perp }={\displaystyle \frac{2\pi }{k_{\perp }}}$ gives the characteristic (wave)length of the potential perpendicular to $\overrightarrow{B}$. The ${\overrightarrow{k}}_{\perp }$-th addendum in (242) varies orthogonally to $\overrightarrow{B}$ on scales of this order; the inverse of the strength of ${\overrightarrow{k}}_{\perp }$ gives roughly the transverse extension of the electrostatic potential structures around the geomagnetic line.

We induce the variation

$$\varphi \to \varphi +\delta \varphi$$

in the electrostatic potential all over the $\overrightarrow{B}$-line, passing from a stationary condition to another one, still stationary; in such a case, the field $\delta \varphi$ must solve the electrostatic equation too, because that PDE is linear, and then it must have the form (242)

$$\begin{array}{c}\delta \varphi \left(x,y,z\right)=\hfill \\ \\ =e^{-{\displaystyle \frac{1}{2}}{c}_0\sqrt{{\displaystyle \frac{{\sigma }_P\left(z\right)}{{\sigma }_0\left(z\right)}}}z}{\displaystyle \sum _{{\overrightarrow{k}}_{\perp }}}{F}_0\left({\overrightarrow{k}}_{\perp }\right)e^{i{k}_{x}x+i{k}_{y}y}\left[B_{+}\left(k_{\perp }^2\right)e^{{\displaystyle \frac{1}{2}}\sqrt{c_0^2+4k_{\perp }^2}\sqrt{{\displaystyle \frac{{\sigma }_P\left(z\right)}{{\sigma }_0\left(z\right)}}}z}+\right.\hfill \\ \\ \left.+B_{-}\left(k_{\perp }^2\right)e^{-{\displaystyle \frac{1}{2}}\sqrt{c_0^2+4k_{\perp }^2}\sqrt{{\displaystyle \frac{{\sigma }_P\left(z\right)}{{\sigma }_0\left(z\right)}}}z}\right],\hfill \end{array}$$

(243)

just as $\varphi$ and ${\varphi }^{\prime }=\varphi +\delta \varphi$ do. In particular, one can write:

$$\delta \varphi \left(x,y,0\right)={\displaystyle \sum _{{\overrightarrow{k}}_{\perp }}}{F}_0\left({\overrightarrow{k}}_{\perp }\right)e^{i{k}_{x}x+i{k}_{y}y}\left[B_{+}\left(k_{\perp }^2\right)+B_{-}\left(k_{\perp }^2\right)\right].$$

(244)

This $\delta \varphi \left(x,y,0\right)$ is the potential variation produced at some $z=0$, which we consider to be in the polar region; on the other hand, the difference between $\delta \varphi \left(x,y,z\right)$ and $\delta \varphi \left(x,y,0\right)$

$$\begin{array}{c}\delta \varphi \left(x,y,z\right)-\delta \varphi \left(x,y,0\right)=\hfill \\ \\ ={\displaystyle \sum _{{\overrightarrow{k}}_{\perp }}}{F}_0\left({\overrightarrow{k}}_{\perp }\right)e^{i{k}_{x}x+i{k}_{y}y}\left\{e^{-{\displaystyle \frac{1}{2}}{c}_0\sqrt{{\displaystyle \frac{{\sigma }_P\left(z\right)}{{\sigma }_0\left(z\right)}}}z}\left[B_{+}\left(k_{\perp }^2\right)e^{{\displaystyle \frac{1}{2}}\sqrt{c_0^2+4k_{\perp }^2}\sqrt{{\displaystyle \frac{{\sigma }_P\left(z\right)}{{\sigma }_0\left(z\right)}}}z}+\right.\right.\hfill \\ \\ \left.\left.+B_{-}\left(k_{\perp }^2\right)e^{-{\displaystyle \frac{1}{2}}\sqrt{c_0^2+4k_{\perp }^2}\sqrt{{\displaystyle \frac{{\sigma }_P\left(z\right)}{{\sigma }_0\left(z\right)}}}z}\right]-B_{+}\left(k_{\perp }^2\right)-B_{-}\left(k_{\perp }^2\right)\right\}\hfill \end{array}$$

can be expanded in power series as

$$\begin{array}{c}\delta {\varphi }_{{\overrightarrow{k}}_{\perp }}\left(x,y,z\right)-\delta {\varphi }_{{\overrightarrow{k}}_{\perp }}\left(x,y,0\right)=\hfill \\ \\ =F_0\left({\overrightarrow{k}}_{\perp }\right)e^{i{k}_{x}x+i{k}_{y}y}\left\{{\displaystyle \frac{1}{2}}\sqrt{c_0^2+{\displaystyle \frac{16{\pi }^2}{{\ell }_{\perp }^2}}}\left[B_{+}\left(k_{\perp }^2\right)-B_{-}\left(k_{\perp }^2\right)\right]\sqrt{{\displaystyle \frac{{\sigma }_P\left(z\right)}{{\sigma }_0\left(z\right)}}}z+\right.\hfill \\ \\ \left.-{\displaystyle \frac{1}{2}}{c}_0\left[B_{+}\left(k_{\perp }^2\right)+B_{-}\left(k_{\perp }^2\right)\right]\sqrt{{\displaystyle \frac{{\sigma }_P\left(z\right)}{{\sigma }_0\left(z\right)}}}z+O\left({\displaystyle \frac{{\sigma }_P\left(z\right)}{{\sigma }_0\left(z\right)}}{z}^2\right)\right\}:\hfill \end{array}$$

(245)

Since the term $\sqrt{{\displaystyle \frac{{\sigma }_P}{{\sigma }_0}}}$ is very small in the upper atmosphere, one can say that the huge part of $\delta \varphi \left(x,y,z\right)-\delta \varphi \left(x,y,0\right)$ is already included in (245). Now, it is instructive to note that

$${\displaystyle \underset{{\ell }_{\perp }\to 0}{lim}}\left[\delta \varphi \left(x,y,z\right)-\delta \varphi \left(x,y,0\right)\right]\gg {\displaystyle \underset{{\ell }_{\perp }\to +\infty }{lim}}\left[\delta \varphi \left(x,y,z\right)-\delta \varphi \left(x,y,0\right)\right]:$$

(246)

Those perturbative structures of the electrostatic potential that have smaller transverse scales show larger differences along the geomagnetic line between $z=0$ and some other point on the line. Thus, wide structures are propagated much more invariantly along$\overrightarrow{B}$; structures larger than some kilometers arrive almost unaffected at such low latitudes that they almost reach the plasmasphere (as $h^{\prime }>h$, so “the same structure” is “lifted up”), dominating its dynamics. In Figure 8, a pictorial comparison between huge and small electrostatic structure propagation is shown.

The behavior predicted by (246) is even more important on the transverse gradients of $\varphi$, i.e., on the fields ${\overrightarrow{E}}_{\perp }$; from (242), we can write

$$\begin{array}{c}{\overrightarrow{E}}_{\perp }\left(x,y,z\right)=-e^{-{\displaystyle \frac{1}{2}}{c}_0\sqrt{{\displaystyle \frac{{\sigma }_P\left(z\right)}{{\sigma }_0\left(z\right)}}}z}{\displaystyle \sum _{{\overrightarrow{k}}_{\perp }}}{\overrightarrow{k}}_{\perp }{f}_0\left({\overrightarrow{k}}_{\perp }\right)e^{i{k}_{x}x+i{k}_{y}y}\left[A_{+}\left(k_{\perp }^2\right)e^{{\displaystyle \frac{1}{2}}\sqrt{c_0^2+4k_{\perp }^2}\sqrt{{\displaystyle \frac{{\sigma }_P\left(z\right)}{{\sigma }_0\left(z\right)}}}z}+\right.\hfill \\ \\ \left.+A_{-}\left(k_{\perp }^2\right)e^{-{\displaystyle \frac{1}{2}}\sqrt{c_0^2+4k_{\perp }^2}\sqrt{{\displaystyle \frac{{\sigma }_P\left(z\right)}{{\sigma }_0\left(z\right)}}}z}\right],\hfill \end{array}$$

(247)

while from (245), one may write

$$\begin{array}{c}\delta {\overrightarrow{E}}_{\perp {\overrightarrow{k}}_{\perp }}\left(x,y,z\right)-\delta {\overrightarrow{E}}_{\perp {\overrightarrow{k}}_{\perp }}\left(x,y,0\right)=\hfill \\ \\ =-{\overrightarrow{k}}_{\perp }{F}_0\left({\overrightarrow{k}}_{\perp }\right)e^{i{k}_{x}x+i{k}_{y}y}\left\{{\displaystyle \frac{1}{2}}\sqrt{c_0^2+4k_{\perp }^2}\left[B_{+}\left(k_{\perp }^2\right)-B_{-}\left(k_{\perp }^2\right)\right]\sqrt{{\displaystyle \frac{{\sigma }_P\left(z\right)}{{\sigma }_0\left(z\right)}}}z+\right.\hfill \\ \\ \left.-{\displaystyle \frac{1}{2}}{c}_0\left[B_{+}\left(k_{\perp }^2\right)+B_{-}\left(k_{\perp }^2\right)\right]\sqrt{{\displaystyle \frac{{\sigma }_P\left(z\right)}{{\sigma }_0\left(z\right)}}}z+O\left({\displaystyle \frac{{\sigma }_P\left(z\right)}{{\sigma }_0\left(z\right)}}{z}^2\right)\right\}.\hfill \end{array}$$

(248)

In the upper ionosphere and prodotonosphere, the limit ${\displaystyle \frac{{\sigma }_0}{{\sigma }_{H,P}}}\to \infty$ holds almost perfectly. Then, the geomagnetic lines are perfect conductors, and the electric field is rigorously perpendicular to them

$$E_{//}=0,$$

(249)

for any equilibrium current regime. The condition (249) renders the mathematics of the problem much simpler, but the most interesting phenomena from an ionospheric point of view take place where it does not hold at all. One such case is that discussed in [39], in which an abrupt time change in $\sigma$ induced by an exceptional photochemical event (a Gamma Ray Burst from deep space) causes a non-trivial time evolution of ${\overrightarrow{E}}_{//}$.

4.5.2. Current Injection and Perturbation Fields

In the same spirit of reasoning about equilibrium states, one can face the following problem: What happens when we inject a current ${\overrightarrow{J}}_q$ at $z=0$, as in Figure 9?

Some current ${\overrightarrow{J}}_q$ is injected at some reference position $z=0$ along a geomagnetic line, e.g., by a magnetic storm. This will yield a charge concentration perturbation and cause the presence of an electric field $\overrightarrow{E}$ all along the $\overrightarrow{B}$-line with a delay of the order of lightspeed propagation time. The re-arrangement of the electric charges will lead very soon to a new electrostatic equilibrium, and we want to know the expression of $\overrightarrow{E}\left(\dots ,z\right)$ once ${\overrightarrow{J}}_q\left(\dots ,0\right)$ is fixed. Note that the currents injected in magnetic storms always have a finite $\overrightarrow{B}$-aligned component $J_z$ because the charged cosmic particles travel along the magnetic lines (at least their guiding centers [11]).

Again, the basic assumption is that the geomagnetic line is perfectly conducting, so that the approximation

$$\overrightarrow{E}={\overrightarrow{E}}_{\perp }$$

holds. The useful relationships are then:

$$\begin{array}{cc}{\overrightarrow{\partial }}_{\perp }·{\overrightarrow{J}}_{\perp }+{\partial }_z{J}_z=0,& E_{//}=0⟹E_z=0.\end{array}$$

(250)

From Equation (247), one has, for ${\displaystyle \frac{{\sigma }_P}{{\sigma }_0}}\to 0$,

$${\displaystyle \underset{{\displaystyle \frac{{\sigma }_P}{{\sigma }_0}}\to 0}{lim}}{\overrightarrow{E}}_{\perp }=-{\displaystyle \sum _{{\overrightarrow{k}}_{\perp }}}{\overrightarrow{k}}_{\perp }{f}_0\left({\overrightarrow{k}}_{\perp }\right)e^{i{k}_{x}x+i{k}_{y}y}\left[A_{+}\left(k_{\perp }^2\right)+A_{-}\left(k_{\perp }^2\right)\right]:$$

(251)

It is easily seen from here that in the limit ${\displaystyle \frac{{\sigma }_P}{{\sigma }_0}}\to 0$ the whole dependence on the geomagnetic coordinate disappears, so that the solution of (250) can be looked for with the condition:

$${\partial }_z{\overrightarrow{E}}_{\perp }=0.$$

(252)

The current orthogonal to the magnetic field is

$${\overrightarrow{J}}_{\perp }={\sigma }_{\perp }·{\overrightarrow{E}}_{\perp },$$

so that the continuity equation reads

$${\overrightarrow{\partial }}_{\perp }·\left({\sigma }_{\perp }·{\overrightarrow{E}}_{\perp }\right)=-{\partial }_z{J}_z.$$

(253)

When this is integrated along the geomagnetic line from $z=0$ up to some $z_0$, one has:

$$\underset{0}{\overset{z_0}{\int }}\left[{\overrightarrow{\partial }}_{\perp }·\left({\sigma }_{\perp }·{\overrightarrow{E}}_{\perp }\right)\right]dz=J_z\left(0\right)-J_z\left(z_0\right).$$

(254)

If the indices a and b are used to span the plane perpendicular to $\overrightarrow{B}$, we re-write it like this:

$$\underset{0}{\overset{z_0}{\int }}{\partial }_a\left({\sigma }^{ab}{E}_b\right)dz=J_z\left(0\right)-J_z\left(z_0\right).$$

Under the hypothesis (252), the field $E_b$ can be extracted from the integration, so that one has:

$${\partial }_a\left(E_b\underset{0}{\overset{z_0}{\int }}{\sigma }^{ab}dz\right)=J_z\left(0\right)-J_z\left(z_0\right).$$

With the definition

$${\Sigma }_{ab}\left(x,y,z_0\right)\stackrel{\mathrm{def}}{=}\underset{0}{\overset{z_0}{\int }}{\sigma }_{ab}\left(x,y,z\right)dz$$

(255)

and the assumption to arrest the integration (254) at some value $z_0$ where $J_z$ vanishes

$$J_z\left(z_0\right)=0,$$

(256)

we can write:

$${\partial }_a\left[{\Sigma }^{ab}\left(\dots ,z_0\right)E_b\right]=J_z\left(0\right).$$

(257)

Equation (257) is important because it puts in relation the electric field ${\overrightarrow{E}}_{\perp }$ taken at a point $z_0$ on a geomagnetic line with the value of the longitudinal current in $z=0$; due to the nature of the geomagnetic field, $J_z\left(0\right)$ is the field-aligned current we can find in the polar oval, the flux of charged particles entering the ionosphere along the geomagnetic lines. It is possible to write:

$${\partial }_x\left({\Sigma }_P{E}_x\right)-{\partial }_x\left({\Sigma }_H{E}_y\right)+{\partial }_y\left({\Sigma }_H{E}_x\right)+{\partial }_y\left({\Sigma }_P{E}_y\right)=J_z\left(0\right).$$

(258)

If the ionosphere is assumed to be (locally) homogeneous, this becomes

$${\Sigma }_P\left(\dots ,z_0\right)\left({\partial }_x{E}_x+{\partial }_y{E}_y\right)+{\Sigma }_H\left(\dots ,z_0\right)\left({\partial }_y{E}_x-{\partial }_x{E}_y\right)=J_z\left(0\right)$$

and since $\overrightarrow{E}$ does not depend on z and an orthogonal decomposition of the divergence operator has been carried out, we have:

$${\Sigma }_P\left(\dots ,z_0\right){\overrightarrow{\partial }}_{\perp }·{\overrightarrow{E}}_{\perp }+{\Sigma }_H\left(\dots ,z_0\right)\left({\partial }_y{E}_x-{\partial }_x{E}_y\right)=J_z\left(0\right).$$

(259)

The term ${\Sigma }_H\left({\partial }_y{E}_x-{\partial }_x{E}_y\right)$ is proportional to the component of $\overrightarrow{\partial }\times \overrightarrow{E}$ along z, but since we are dealing here with a potential field, we have:

$$\begin{array}{ccc}\overrightarrow{\partial }\times \overrightarrow{E}=0& \Rightarrow & {\partial }_y{E}_x-{\partial }_x{E}_y=0.\end{array}$$

(260)

This turns (259) into:

$${\overrightarrow{\partial }}_{\perp }·{\overrightarrow{E}}_{\perp }={\displaystyle \frac{J_z\left(0\right)}{{\Sigma }_P}}.$$

From (252), we can say ${\overrightarrow{\partial }}_{\perp }·{\overrightarrow{E}}_{\perp }=\overrightarrow{\partial }·\overrightarrow{E}$ so that:

$$\overrightarrow{\partial }·\overrightarrow{E}={\displaystyle \frac{J_z\left(0\right)}{{\Sigma }_P}}.$$

(261)

Due to Gauss’s electrostatic law

$$\overrightarrow{\partial }·\overrightarrow{E}={\displaystyle \frac{\delta }{{\epsilon }_0}}$$

(262)

we can directly put the electric charge into (259), so we can relate the injected current $J_z$ with the electric charge density in the ionosphere

$$\delta ={\displaystyle \frac{{\epsilon }_0}{{\Sigma }_P}}{J}_z\left(0\right).$$

(263)

The magnetic field $\overrightarrow{B}$ enters toward the Earth in the northern region and comes out of it in the southern one; then a positive $J_z$ in the north means a positive charge flux towards the ground. From Equation (263), this means that $\delta$ has to be positive. In the southern region, some density $\delta >0$ in the ionosphere corresponds to currents flowing upward.

5. Conclusions

The aim of this review paper is to write all the equations concerning the evolution of the ionosphere, with great care given to illustrating their construction, focusing on each mathematical step, and highlighting each physical assumption.

The ionosphere is described as a system of mutually interacting fluids that exchange mechanical energy, momentum and heat; they are also subject to chemical reactions that alter their relative abundance. The possibility of turning one of these fluids into another via reactions is a very important characteristic of the ionospheric dynamics; from the definition of mass change rate $G\left(d{\mathcal{C}}_I\right)$ given in (25), the whole sequence of the appearance of the production-loss terms ${\Gamma }_I$ descends, in the Navier–Stokes equations as well as in the internal energy balance.

The content of this review is a pre-requisite for studying ionospheric modeling from first principles; armed with the full set of fluid-dynamical and thermodynamical equations describing the evolution of the continua ${\mathcal{C}}_I$, one is in the position to use suitable specializations of these differential relations in order to predict different phenomena of the ionospheric system.

In the program developed here, it is important to highlight the depth of assuming that the LIM can be represented as a continuum, as well as to disclose its effects as far as possible. This was carried out in Section 2, where the system is presented.

As the LIM is formed by the continua $\left\{{\mathcal{C}}_I\right\}$, its dynamics is constructed basing on classical mechanics, equilibrium thermodynamics and classical electrodynamics, arriving at rich but compact self-consistent systems of coupled PDEs. These are the system (107) for matter, plus the quasi-stationary Maxwell Equation (120). Usually, some simplifications are made to treat the LIM; a unique neutral continuum is introduced, evolving according to the PDEs in (140); moreover, the charged part of the LIM is represented by a unique positive ion species $X^{+}$, plus free electrons $e^{-}$. These continua are subject to the dynamics (153) and (153), respectively.

As in many problems, it can be of great use to describe the electrology of the LIM as that of a gaseous continuous conductor, the force-free assumption (153) is made and a proper conductance tensor study is carried out in Section 4, making possible our study of the ionospheric electrostatic equilibrium and some implications of it.

Even if a great and important part of the physics of the Earth’s ionosphere can be studied within the fluid approach [28,37], it is important to underline that there are regions of the LIM and phenomena that cannot be described in this way satisfactorily. Whenever one deals with local conditions very highly variable either with space or time, the space- or time-smoothness of the LIM does not hold on suitably small space- or timescales. The ionospheric irregularities generating radio scintillations [40], for instance, need to be treated, breaking determinism via a stochastic form of theory [41,42]. More in general, in all the situations, the conditions (6) cannot be met, and the ionospheric local quantities are better represented as fractal measures instead of smooth fields [43]. Representing the ionospheric local quantities $\Psi \left(\overrightarrow{r},t\right)$ describing the LIM as the sum of a smooth part $\psi \left(\overrightarrow{r},t\right)$, described by the fluid theory, and some other part $\delta \psi \left(\overrightarrow{r},t\right)$ encoding the irregularities

$$\Psi \left(\overrightarrow{r},t\right)=\psi \left(\overrightarrow{r},t\right)+\delta \psi \left(\overrightarrow{r},t\right),$$

we could say that $\psi$ will represent some fluid background, while $\delta \psi$ will be treated by other mathematical tools more suited for the cases in which the requirements 1, 2 an 3 on page 7 in Section 2.1 do not hold.

It is convenient to conclude this review referring the reader to further studies in the still partly unexplored land of post-fluid, or beyond-continuum, descriptions. Beyond the easy “smooth” picture emerging from Section 2, the dirty plasma forming the LIM should be treated via a multi-chemical kinetic theory, of through higher-order truncations of the BBGKY hierarchy. Another approach is allowing extended singular regions to exist in the $\left\{{\mathcal{C}}_I\right\}$ system, either considering the local proxies as fractal measures [44], or closing the dynamics with noise terms, mimicking local irregularities [45], instead of the smooth equilibrium hypotheses discussed in Section 3.5. All these beyond-continuum pictures could probably enrich our description, and maybe comprehension, of “difficult” regimes, as ionospheric turbulence.