Spatio-Temporal Evaluation of MSWEP, CHIRPS and ERA5-Land Reveals Regional-Specific Responses Across Complex Topography in Bolivia
Abstract
1. Introduction
2. Data and Methodology
2.1. Study Area
2.2. Data
2.2.1. Weather Stations
2.2.2. The Multi-Source Weighted-Ensemble Precipitation (MSWEP) Dataset V2.2
2.2.3. The Climate Hazards Center InfraRed Precipitation with Stations (CHIRPS) V2
2.2.4. ERA5-Land Precipitation Data
2.3. Methods
2.3.1. Validation of Predicted Precipitation Data
2.3.2. Combined Accuracy Index (CAI)
2.3.3. Trend Analysis
3. Results
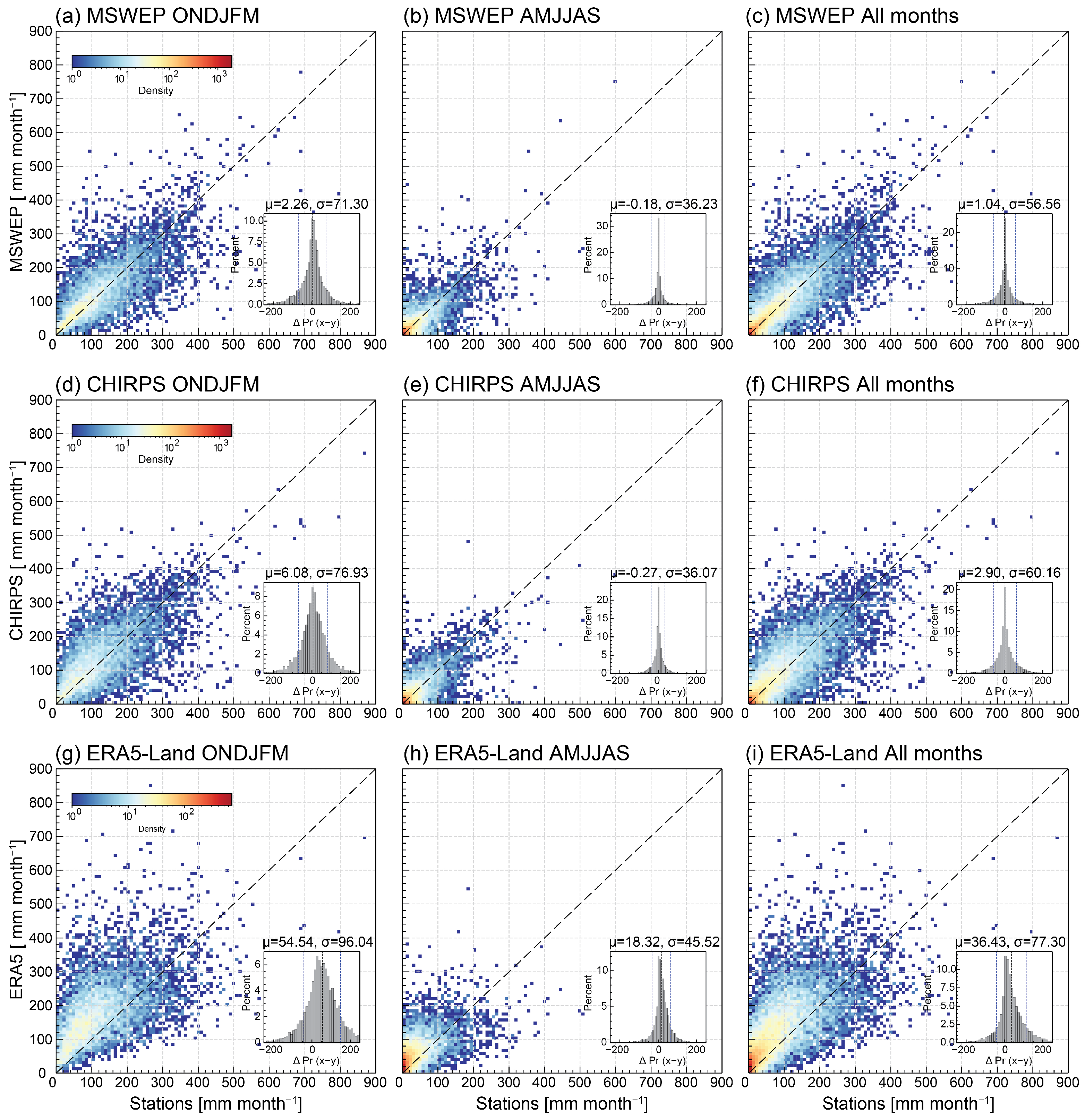
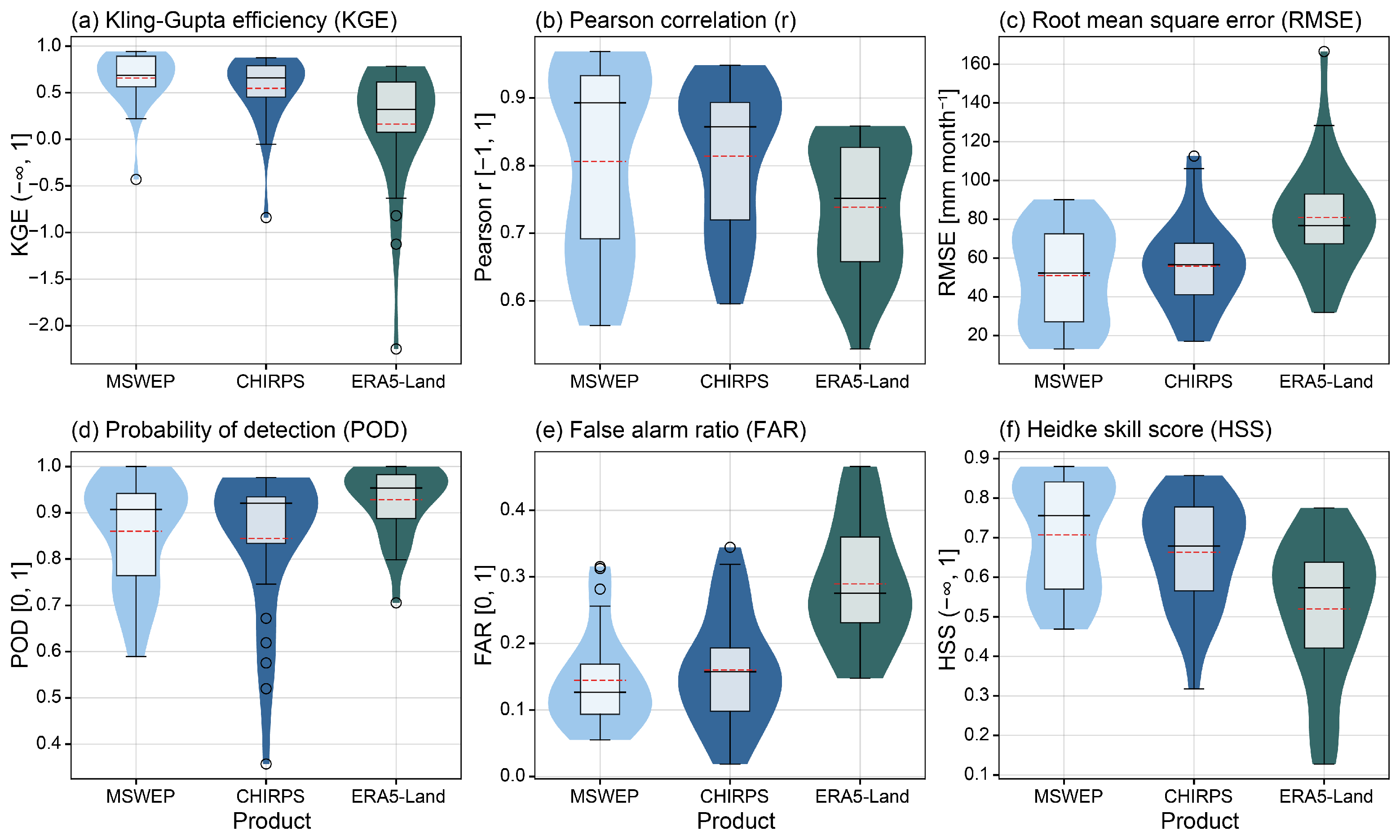
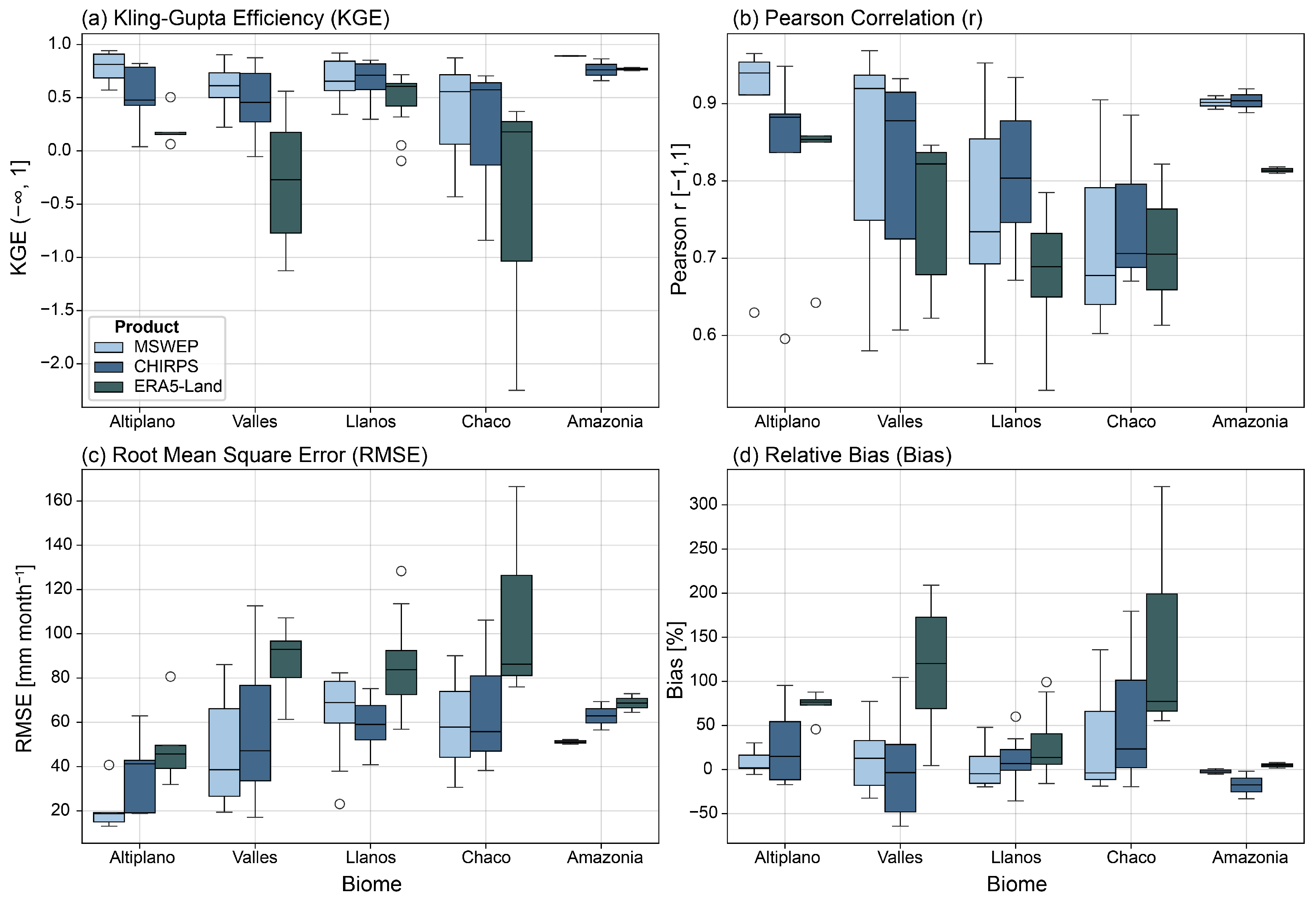
3.1. Overall Performance
3.2. Combined Accuracy Index (CAI)
3.3. Continuous Metrics
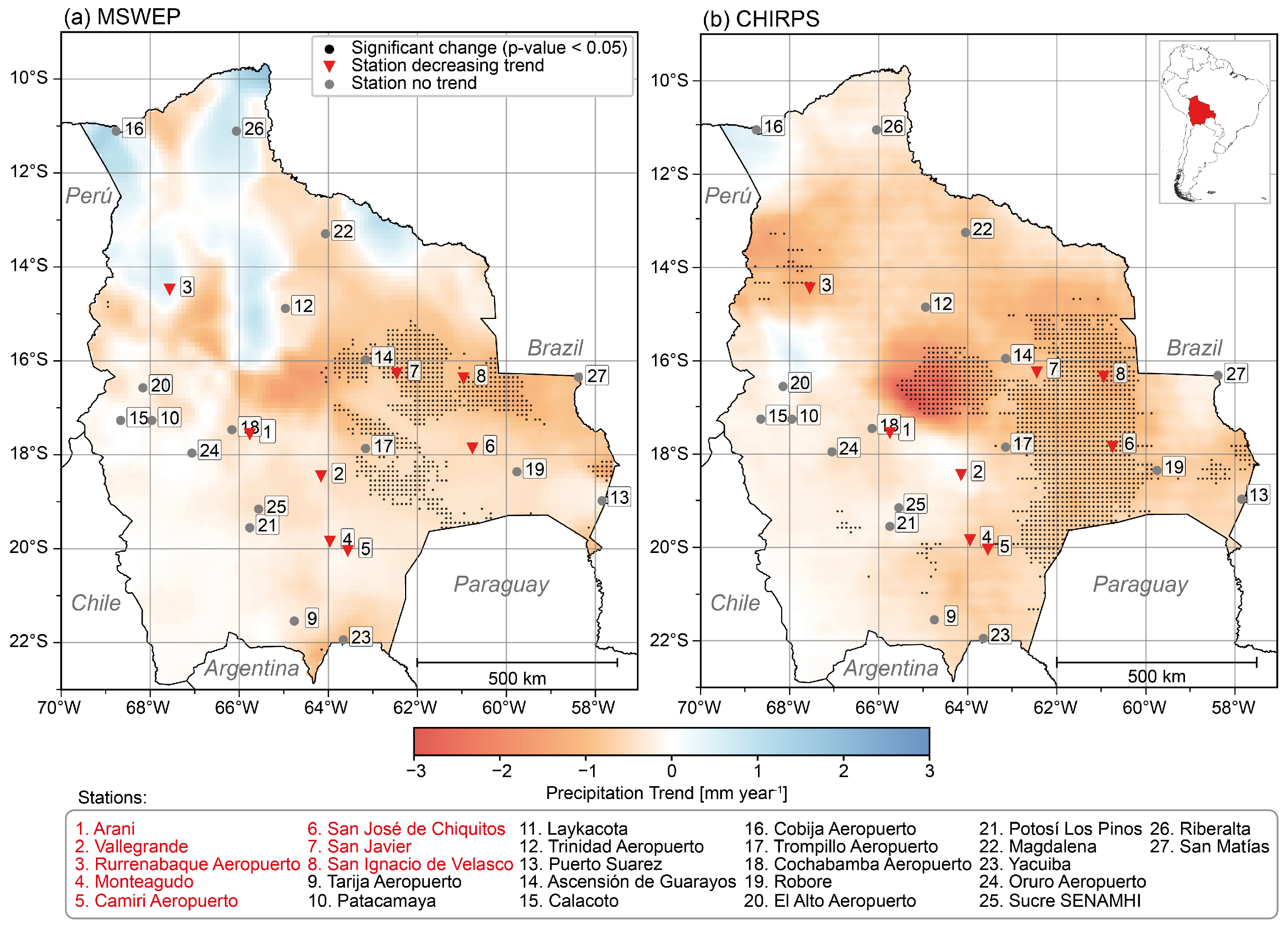
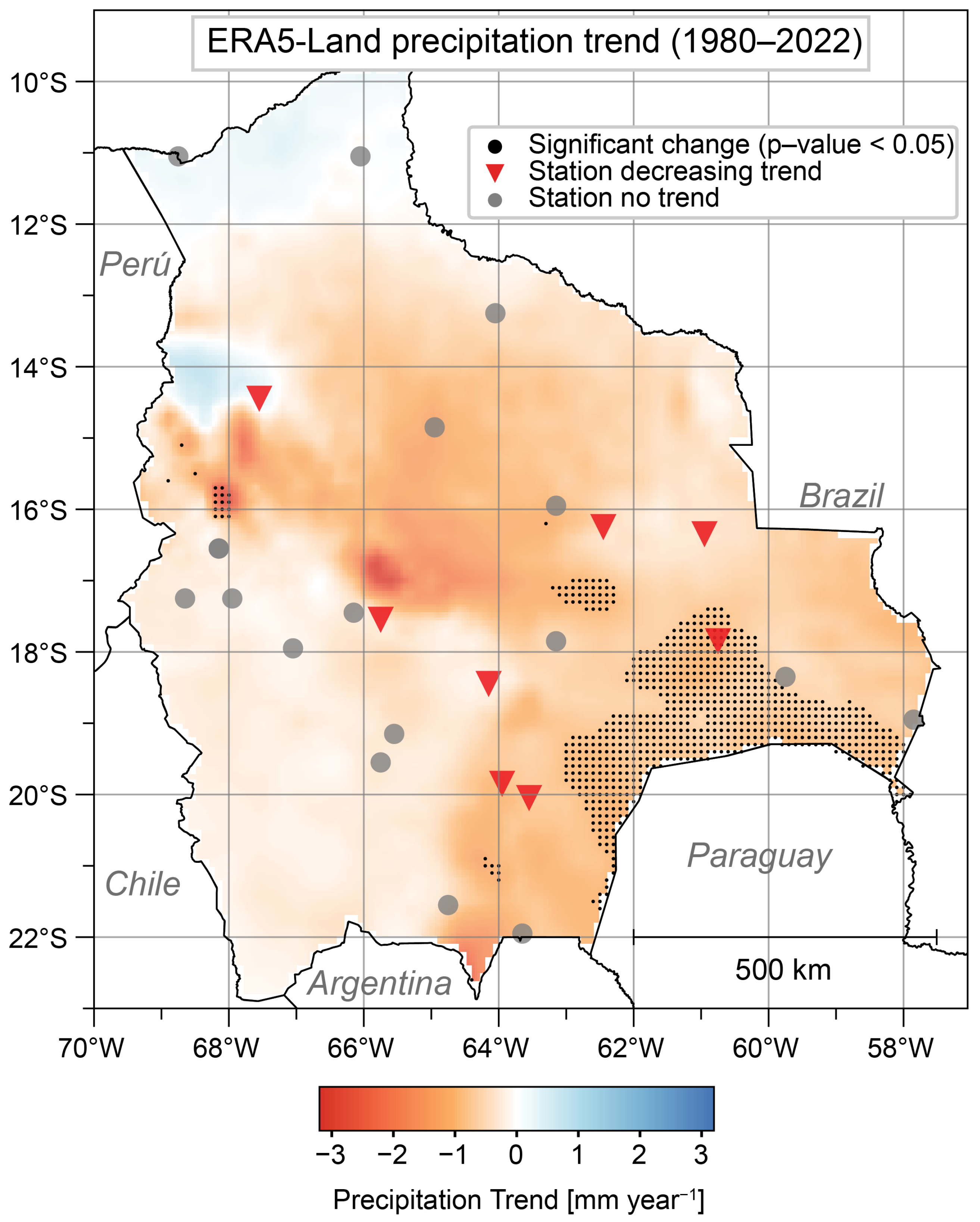
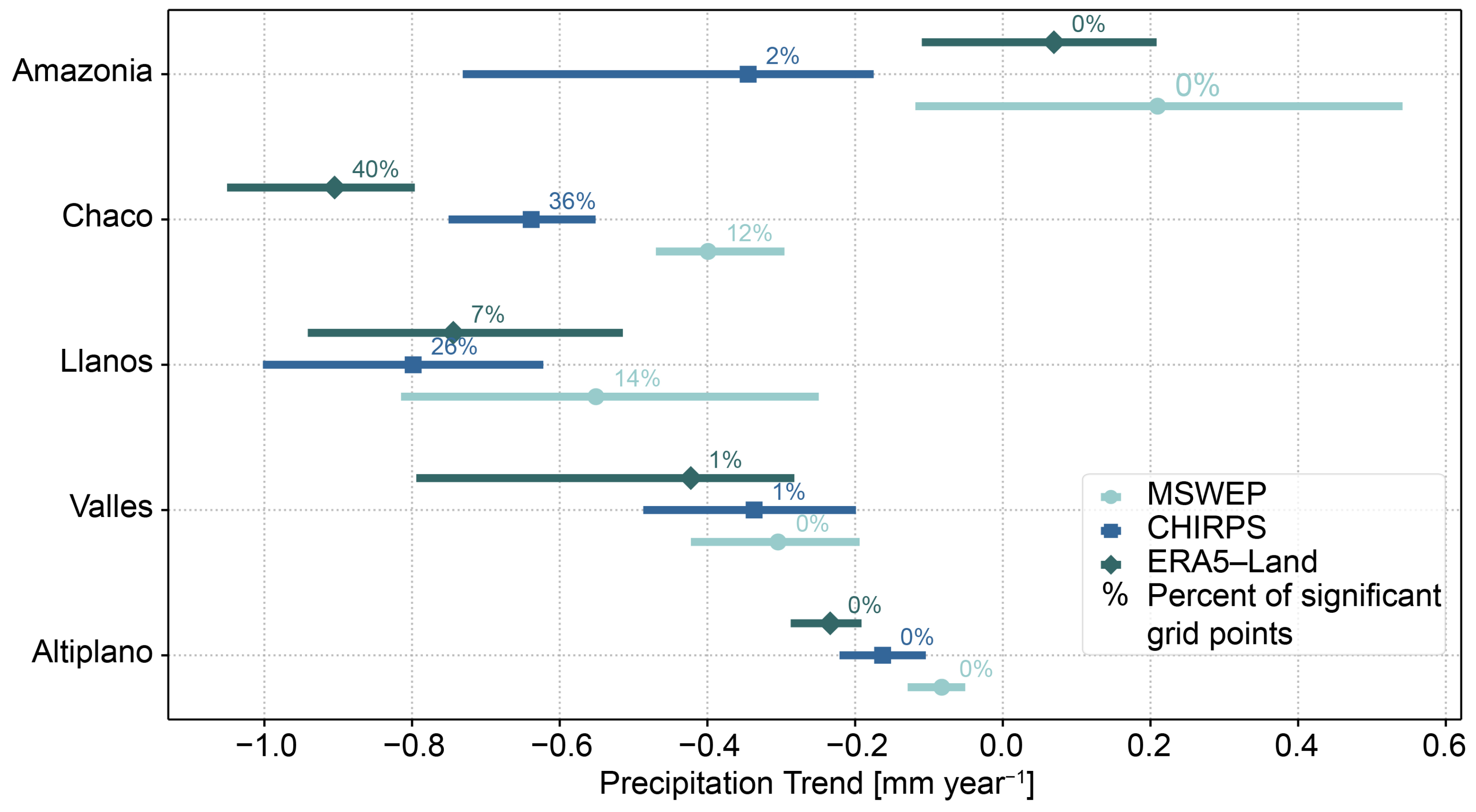
3.4. Trend Analysis
4. Discussion
4.1. Dataset Performance and Regional Differences
4.2. Causes of Systematic Biases
4.3. Contribution of Reanalysis Products
4.4. Methodological Contributions
4.5. Regional Context
4.6. Limitations and Future Directions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AR(1) | First-order Autoregressive |
| CHETSSEL | Carbon-Hydrology Tiled ECMWF Forecasts Scheme for Surface Exchanges over Land |
| CHIRPS | Climate Hazards Group InfraRed Precipitation with Stations |
| CMORPH | Climate Prediction Center Morphing technique |
| ERA5-Land | ECMWF Reanalysis v5 Land |
| FAR | False Alarm Ratio |
| GHCN-D | Global Historical Climatology Network daily |
| GSOD | Global Surface Summary of the Day |
| HSS | Heidke Skill Score |
| IFS | Integrated Forecasting System |
| KGE | Kling–Gupta Efficiency |
| MSWEP | Multi-Source Weighted-Ensemble Precipitation |
| RMSE | Root Mean Square Error |
| OLS | Ordinary Least Squares |
| PERSIANN-CCS | Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks—Cloud Classification System |
| POD | Probability of Detection |
| WAM | ECMWF Wave Model |
References
- Kidd, C.; Becker, A.; Huffman, G.; Muller, C.; Joe, P.; Skofronick-Jackson, G.; Kirschbaum, D. So, how much of the Earth’s surface is covered by rain gauges? Bull. Am. Meteorol. Soc. 2017, 98, 69–78. [Google Scholar] [CrossRef]
- Condom, T.; Martínez, R.; Pabón, J.; Costa, F.; Pineda, L.; Nieto, J.; Villacis, M. Climatological and Hydrological Observations for the South American Andes: In situ Stations, Satellite, and Reanalysis Data Sets. Front. Earth Sci. 2020, 8, 92. [Google Scholar] [CrossRef]
- Seiler, C.; Hutjes, R.; Kabat, P. Climate Variability and Trends in Bolivia. J. Appl. Meteorol. Climatol. 2013, 52, 130–146. [Google Scholar] [CrossRef]
- Navarro, G.; Ferreira, W. Biogeografía de Bolivia. In Libro Rojo de Parientes Silvestres de Cultivos de Bolivia; VMABCC, Ed.; Plural editores: La Paz, Bolivia, 2009; pp. 23–39. [Google Scholar]
- Ibisch, P. Biodiversity Conservation in Bolivia: History, Trends and Challenges. In Environmental Issues in Latin America and the Caribbean; Romero, A., West, S., Eds.; Springer: Dordrecht, The Netherlands, 2005; pp. 55–71. [Google Scholar]
- Liu, J.; Shangguan, D.; Liu, S.; Ding, Y.; Wang, S.; Wang, X. Evaluation and comparison of CHIRPS and MSWEP daily-precipitation products in the Qinghai-Tibet Plateau during the period of 1981–2015. Atmos. Res. 2019, 230, 104634. [Google Scholar] [CrossRef]
- Huffman, G.; Bolvin, D.; Braithwaite, D.; Hsu, K.L.; Joyce, R.; Kidd, C.; Nelkin, E.; Sorooshian, S.; Stocker, E.; Tan, J.; et al. Integrated Multi-satellite Retrievals for the Global Precipitation Measurement (GPM) Mission (IMERG). In Satellite Precipitation Measurement: Volume 1; Levizzani, V., Kidd, C., Kirschbaum, D., Kummerow, C., Nakamura, K., Turk, F., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 343–353. [Google Scholar]
- Xie, P.; Joyce, R.; Wu, S.; Yoo, S.H.; Yarosh, Y.; Sun, F.; Lin, R. Reprocessed, Bias-Corrected CMORPH Global High-Resolution Precipitation Estimates from 1998. J. Hydrometeorol. 2017, 18, 1617–1641. [Google Scholar] [CrossRef]
- Nguyen, P.; Shearer, E.; Tran, H.; Ombadi, M.; Hayatbini, N.; Palacios, T.; Huynh, P.; Braithwaite, D.; Updegraff, G.; Hsu, K.; et al. The CHRS Data Portal, an easily accessible public repository for PERSIANN global satellite precipitation data. Sci. Data 2019, 6, 180296. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Cepeda Arias, E.; Cañon Barriga, J. Performance of high-resolution precipitation datasets CHIRPS and TerraClimate in a Colombian high Andean Basin. Geocarto Int. 2022, 37, 17382–17402. [Google Scholar] [CrossRef]
- López-Bermeo, C.; Montoya, R.; Caro-Lopera, F.; Díaz-García, J. Validation of the accuracy of the CHIRPS precipitation dataset at representing climate variability in a tropical mountainous region of South America. Phys. Chem. Earth Parts A/B/C 2022, 127, 103184. [Google Scholar] [CrossRef]
- Prakash, S. Performance assessment of CHIRPS, MSWEP, SM2RAIN-CCI, and TMPA precipitation products across India. J. Hydrol. 2019, 571, 50–59. [Google Scholar] [CrossRef]
- Li, L.; Wang, Y.; Wang, L.; Hu, Q.; Zhu, Z.; Li, L.; Li, C. Spatio-temporal accuracy evaluation of MSWEP daily precipitation over the Huaihe River Basin, China: A comparison study with representative satellite- and reanalysis-based products. J. Geogr. Sci. 2022, 32, 2271–2290. [Google Scholar] [CrossRef]
- Xu, Z.; Wu, Z.; He, H.; Wu, X.; Zhou, J.; Zhang, Y.; Guo, X. Evaluating the accuracy of MSWEP V2.1 and its performance for drought monitoring over mainland China. Atmos. Res. 2019, 226, 17–31. [Google Scholar] [CrossRef]
- Gomis-Cebolla, J.; Rattayova, V.; Salazar-Galán, S.; Francés, F. Evaluation of ERA5 and ERA5-Land reanalysis precipitation datasets over Spain (1951–2020). Atmos. Res. 2023, 284, 106606. [Google Scholar] [CrossRef]
- Jiao, D.; Xu, N.; Yang, F.; Xu, K. Evaluation of spatial-temporal variation performance of ERA5 precipitation data in China. Sci. Rep. 2021, 11, 17956. [Google Scholar] [CrossRef] [PubMed]
- Romero-Hernández, C.; Avila-Diaz, A.; Quesada, B.; Medeiros, F.; Cerón, W.; Guzman-Escalante, J.; Ocampo-Marulanda, C.; Rodrigues Torres, R.; Zuluaga, C. Bias-corrected high-resolution precipitation datasets assessment over a tropical mountainous region in Colombia: A case of study in Upper Cauca River Basin. J. S. Am. Earth Sci. 2024, 140, 104898. [Google Scholar] [CrossRef]
- Russell, A.; Gnanadesikan, A.; Zaitchik, B. Are the Central Andes Mountains a Warming Hot Spot? J. Clim. 2017, 30, 3589–3608. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, Y.; Yang, Y. Using High-Density Rain Gauges to Validate the Accuracy of Satellite Precipitation Products over Complex Terrains. Atmosphere 2020, 11, 633. [Google Scholar] [CrossRef]
- Garreaud, R.; Vuille, M.; Clement, A. The climate of the Altiplano: Observed current conditions and mechanisms of past changes. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2003, 194, 5–22. [Google Scholar] [CrossRef]
- Garreaud, R.; Vuille, M.; Compagnucci, R.; Marengo, J. Present-day South American climate. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2009, 281, 180–195. [Google Scholar] [CrossRef]
- Arias, B.C.E.; Tito, L.; Aragón, O. Atlas de Riesgo Agropecuario y Cambio Climático para la Soberanía Alimentaria; Ministerio de Desarrollo Rural y Tierras: La Paz, Bolivia, 2014; p. 320. [Google Scholar]
- Abadi, A.; Rowe, C.; Andrade, M. Climate regionalization in Bolivia: A combination of non-hierarchical and consensus clustering analyses based on precipitation and temperature. Int. J. Climatol. 2020, 40, 4408–4421. [Google Scholar] [CrossRef]
- Fernández-Duque, B.; Vicente-Serrano, S.; Maillard, O.; Domínguez-Castro, F.; Peña-Angulo, D.; Noguera, I.; Azorin-Molina, C.; El Kenawy, A. Long-term observed changes of air temperature, relative humidity and vapour pressure deficit in Bolivia, 1950–2019. Int. J. Climatol. 2023, 43, 6484–6504. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.; Maillard, O.; Peña-Angulo, D.; Domínguez-Castro, F.; Noguera, I.; Lorenzo-Lacruz, J.; Azorin-Molina, C.; Juez, C.; Guijarro, J.; Halifa-Marín, A.; et al. Evaluation of long-term changes in precipitation over Bolivia based on observations and Coupled Model Intercomparison Project models. Int. J. Climatol. 2022, 43, 1431–1447. [Google Scholar] [CrossRef]
- Beck, H.; Wood, E.; Pan, M.; Fisher, C.; Miralles, D.; van Dijk, A.; McVicar, T.; Adler, R. MSWEP V2 Global 3-Hourly 0.1° Precipitation: Methodology and Quantitative Assessment. Bull. Am. Meteorol. Soc. 2019, 100, 473–500. [Google Scholar] [CrossRef]
- Beck, H.; Pan, M.; Roy, T.; Weedon, G.; Pappenberger, F.; van Dijk, A.; Huffman, G.; Adler, R.; Wood, E. Daily evaluation of 26 precipitation datasets using Stage-IV gauge-radar data for the CONUS. Hydrol. Earth Syst. Sci. 2019, 23, 207–224. [Google Scholar] [CrossRef]
- Beck, H.; Vergopolan, N.; Pan, M.; Levizzani, V.; van Dijk, A.; Weedon, G.; Brocca, L.; Pappenberger, F.; Huffman, G.; Wood, E. Global-scale evaluation of 22 precipitation datasets using gauge observations and hydrological modeling. Hydrol. Earth Syst. Sci. 2017, 21, 6201–6217. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Liu, R.; Zhang, X.; Wang, W.; Wang, Y.; Liu, H.; Ma, M.; Tang, G. Global-scale ERA5 product precipitation and temperature evaluation. Ecol. Indic. 2024, 166, 112481. [Google Scholar] [CrossRef]
- Xie, W.; Yi, S.; Leng, C.; Xia, D.; Li, M.; Zhong, Z.; Ye, J. The evaluation of IMERG and ERA5-Land daily precipitation over China with considering the influence of gauge data bias. Sci. Rep. 2022, 12, 8085. [Google Scholar] [CrossRef]
- Wasserman, L. All of Nonparametric Statistics, 1st ed.; Springer: New York, NY, USA, 2006; p. 270. [Google Scholar]
- Cohn, T.; Lins, H. Nature’s style: Naturally trendy. Geophys. Res. Lett. 2005, 32, 1–5. [Google Scholar] [CrossRef]
- von Storch, H.; Zwiers, F. Statistical Analysis in Climate Research; Cambridge University Press: Cambridge, UK, 1999; p. 484. [Google Scholar]
- Seabold, S.; Perktold, J. Statsmodels: Econometric and Statistical Modeling with Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010. [Google Scholar]
- Bretherton, C.; Widmann, M.; Dymnikov, V.; Wallace, J.; Bladé, I. The Effective Number of Spatial Degrees of Freedom of a Time-Varying Field. J. Clim. 1999, 12, 1990–2009. [Google Scholar] [CrossRef]
- Huber Magoffin, R.; Hales, R.; Erazo, B.; Nelson, E.; Larco, K.; Miskin, T. Evaluating the Performance of Satellite Derived Temperature and Precipitation Datasets in Ecuador. Remote Sens. 2023, 15, 5713. [Google Scholar] [CrossRef]
- Xavier, A.; Rudke, A.; Serrão, E.; Terassi, P.; Pontes, P. Evaluation of Satellite-Derived Products for the Daily Average and Extreme Rainfall in the Mearim River Drainage Basin (Maranhão, Brazil). Remote Sens. 2021, 13, 4393. [Google Scholar] [CrossRef]
- Ali, S.; Chen, Y.; Azmat, M.; Kayumba, P.; Ahmed, Z.; Mind’je, R.; Ghaffar, A.; Qin, J.; Tariq, A. Long-Term Performance Evaluation of the Latest Multi-Source Weighted-Ensemble Precipitation (MSWEP) over the Highlands of Indo-Pak (1981–2009). Remote Sens. 2022, 14, 4773. [Google Scholar] [CrossRef]
- Alijanian, M.; Rakhshandehroo, G.; Mishra, A.; Dehghani, M. Evaluation of satellite rainfall climatology using CMORPH, PERSIANN-CDR, PERSIANN, TRMM, MSWEP over Iran. Int. J. Climatol. 2017, 37, 4896–4914. [Google Scholar] [CrossRef]
- Blacutt, L.A.; Herdies, D.L.; de Gonçalves, L.G.G.; Vila, D.A.; Andrade, M. Precipitation comparison for the CFSR, MERRA, TRMM3B42 and Combined Scheme datasets in Bolivia. Atmos. Res. 2015, 163, 117–131. [Google Scholar] [CrossRef]
- Hafizi, H.; Sorman, A. Assessment of 13 Gridded Precipitation Datasets for Hydrological Modeling in a Mountainous Basin. Atmosphere 2022, 13, 143. [Google Scholar] [CrossRef]
- Mekonnen, K.; Velpuri, N.; Leh, M.; Akpoti, K.; Owusu, A.; Tinonetsana, P.; Hamouda, T.; Ghansah, B.; Paranamana, T.; Munzimi, Y. Accuracy of satellite and reanalysis rainfall estimates over Africa: A multi-scale assessment of eight products for continental applications. J. Hydrol. Reg. Stud. 2023, 49, 101514. [Google Scholar] [CrossRef]
- Ullah, W.; Wang, G.; Ali, G.; Tawia Hagan, D.; Bhatti, A.; Lou, D. Comparing Multiple Precipitation Products against In-Situ Observations over Different Climate Regions of Pakistan. Remote Sens. 2019, 11, 628. [Google Scholar] [CrossRef]
- Abbas, H.; Song, W.; Wang, Y.; Xiang, K.; Chen, L.; Feng, T.; Linghu, S.; Alam, M. Validation of CRU TS v4.08, ERA5-Land, IMERG v07B, and MSWEP v2.8 Precipitation Estimates Against Observed Values over Pakistan. Remote Sens. 2024, 16, 4803. [Google Scholar] [CrossRef]
- Wu, X.; Zhao, N. Evaluation and Comparison of Six High-Resolution Daily Precipitation Products in Mainland China. Remote Sens. 2022, 15, 223. [Google Scholar] [CrossRef]
- Zambrano-Bigiarini, M.; Nauditt, A.; Birkel, C.; Verbist, K.; Ribbe, L. Temporal and spatial evaluation of satellite-based rainfall estimates across the complex topographical and climatic gradients of Chile. Hydrol. Earth Syst. Sci. 2017, 21, 1295–1320. [Google Scholar] [CrossRef]
- Arregocés, H.; Rojano, R.; Pérez, J. Validation of the CHIRPS dataset in a coastal region with extensive plains and complex topography. Case Stud. Chem. Environ. Eng. 2023, 8, 100452. [Google Scholar] [CrossRef]
- Chao, L.; Deng, Y.; Wang, S.; Ren, J.; Zhang, K.; Wang, G. Development of a two-stage correction framework for satellite, multi-source Merged, and reanalysis precipitation products Across the Huang-Huai-Hai Plain, China, During 2000–2020. Remote Sens. 2025, 17, 2809. [Google Scholar] [CrossRef]
- Kimani, M.; Hoedjes, J.; Su, Z. Bayesian Bias Correction of Satellite Rainfall Estimates for Climate Studies. Remote Sens. 2018, 10, 1074. [Google Scholar] [CrossRef]
- Gu, L.; Yin, J.; Wang, S.; Chen, J.; Qin, H.; Yan, X.; He, S.; Zhao, T. How well do the multi-satellite and atmospheric reanalysis products perform in hydrological modelling. J. Hydrol. 2023, 617, 128920. [Google Scholar] [CrossRef]
- Valencia, S.; Marín Palacio, D.; Gómez, D.; Hoyos, N.; Salazar, J.F.; Villegas, J.C. Spatio-temporal assessment of gridded precipitation products across topographic and climatic gradients in Colombia. Atmos. Res. 2023, 285, 106643. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, J.; Wang, G.; Ruben, G.B.; Bao, Z.; Liu, Y.; Liu, C.; Jin, J. Error Correction of Multi-Source Weighted-Ensemble Precipitation (MSWEP) over the Lancang-Mekong River Basin. Remote Sens. 2021, 13, 312. [Google Scholar] [CrossRef]
- Sapucci, C.R.; Mayta, V.C.; da Silva Dias, P.L. Evaluation of diverse-based precipitation data over the Amazon Region. Theor. Appl. Climatol. 2022, 149, 1167–1193. [Google Scholar] [CrossRef]
- Lavers, D.A.; Simmons, A.; Vamborg, F.; Rodwell, M.J. An evaluation of ERA5 precipitation for climate monitoring. Q. J. R. Meteorol. Soc. 2022, 148, 3152–3165. [Google Scholar] [CrossRef]
- Tarek, M.; Brissette, F.; Arsenault, R. Evaluation of the ERA5 reanalysis as a potential reference dataset for hydrological modelling over North America. Hydrol. Earth Syst. Sci. 2020, 24, 2527–2544. [Google Scholar] [CrossRef]
- Thorne, P.W.; Vose, R.S. Reanalyses Suitable for Characterizing Long-Term Trends. Bull. Am. Meteorol. Soc. 2010, 91, 353–362. [Google Scholar] [CrossRef]
- Garreaud, R. A plausible atmospheric trigger for the 2017 coastal El Niño. Int. J. Climatol. 2018, 38, e1296–e1302. [Google Scholar] [CrossRef]
- André, J.; D’Andrea, F.; Drobinski, P.; Muller, C. Regimes of Precipitation Change Over Europe and the Mediterranean. J. Geophys. Res. Atmos. 2024, 129, e2023JD040413. [Google Scholar] [CrossRef]
- Maillard, O.; Vides-Almonacid, R.; Salazar, Á.; Larrea-Alcazar, D. Effect of Deforestation on Land Surface Temperature in the Chiquitania Region, Bolivia. Land 2022, 12, 2. [Google Scholar] [CrossRef]
- Guo, B.; Xu, T.; Yang, Q.; Zhang, J.; Dai, Z.; Deng, Y.; Zou, J. Multiple Spatial and Temporal Scales Evaluation of Eight Satellite Precipitation Products in a Mountainous Catchment of South China. Remote Sens. 2023, 15, 1373. [Google Scholar] [CrossRef]
- Zhu, S.; Liu, Z. Comprehensive quantitative assessment of the performance of fourteen satellite precipitation products over Chinese mainland. Clim. Dyn. 2024, 62, 6799–6818. [Google Scholar] [CrossRef]
- Kumar, V.; Borgemeister, C.; Tischbein, B.; Kumar, N. Evaluation and inter-comparison of twenty-three gridded rainfall products representing a typical urban monsoon climate in India. Theor. Appl. Climatol. 2024, 155, 9529–9553. [Google Scholar] [CrossRef]
- Samantaray, A.; Mooney, P.; Vivacqua, C. Bergen metrics: Composite error metrics for assessing performance of climate models using EURO-CORDEX simulations. Geosci. Model Dev. 2024, 17, 3321–3339. [Google Scholar] [CrossRef]
- Hamed, K.; Ramachandra Rao, A. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Phinney, B. Canadian streamflow trend detection: Impacts of serial and cross-correlation. Hydrol. Sci. J. 2003, 48, 51–63. [Google Scholar] [CrossRef]
- Zhao, K.; Wulder, M.; Hu, T.; Bright, R.; Wu, Q.; Qin, H.; Li, Y.; Toman, E.; Mallick, B.; Zhang, X.; et al. Detecting change-point, trend, and seasonality in satellite time series data to track abrupt changes and nonlinear dynamics: A Bayesian ensemble algorithm. Remote Sens. Environ. 2019, 232, 111330. [Google Scholar] [CrossRef]
- Bayazit, M.; Önöz, B. To prewhiten or not to prewhiten in trend analysis? Hydrol. Sci. J. 2007, 52, 611–624. [Google Scholar] [CrossRef]
- Bürger, G. Trends? Complicated answers to a simple question. Hydrol. Sci. J. 2023, 68, 1680–1692. [Google Scholar] [CrossRef]
- Feron, S.; Cordero, R.R.; Damiani, A.; MacDonell, S.; Pizarro, J.; Goubanova, K.; Valenzuela, R.; Wang, C.; Rester, L.; Beaulieu, A. South America is becoming warmer, drier, and more flammable. Commun. Earth Environ. 2024, 5, 23. [Google Scholar] [CrossRef]
- Hiraga, Y.; Tahara, R.; Meza, J. A methodology to estimate Probable Maximum Precipitation (PMP) under climate change using a numerical weather model. J. Hydrol. 2025, 652, 132659. [Google Scholar] [CrossRef]
- Lagos-Zúñiga, M.; Balmaceda-Huarte, R.; Regoto, P.; Torrez, L.; Olmo, M.; Lyra, A.; Pareja-Quispe, D.; Bettolli, M.L. Extreme indices of temperature and precipitation in South America: Trends and intercomparison of regional climate models. Clim. Dyn. 2022, 62, 4541–4562. [Google Scholar] [CrossRef]
- Viale, M.; Valenzuela, R.; Garreaud, R.D.; Ralph, F.M. Impacts of Atmospheric Rivers on Precipitation in Southern South America. J. Hydrometeorol. 2018, 19, 1671–1687. [Google Scholar] [CrossRef]
- Montini, T.L.; Jones, C.; Carvalho, L.M.V. The South American Low-Level Jet: A New Climatology, Variability, and Changes. J. Geophys. Res. Atmos. 2019, 124, 1200–1218. [Google Scholar] [CrossRef]
- Salazar, A.; Baldi, G.; Hirota, M.; Syktus, J.; McAlpine, C. Land use and land cover change impacts on the regional climate of non-Amazonian South America: A review. Glob. Planet. Change 2015, 128, 103–119. [Google Scholar] [CrossRef]
- Su, D.; Zhong, J.; Xu, Y.; Lv, L.; Liu, H.; Fan, X.; Han, L.; Wang, F. SAL Method Applied in Grid Forecasting Product Verification with Three-Source Fusion Product. Atmosphere 2024, 15, 1366. [Google Scholar] [CrossRef]
- Hiraga, Y.; Tahara, R. Sensitivity of localized heavy rainfall in Northern Japan to WRF physics parameterization schemes. Atmos. Res. 2025, 314, 107802. [Google Scholar] [CrossRef]
- Huerta, A.; Serrano-Notivoli, R.; Bronnimann, S. SC-PREC4SA: A serially complete daily precipitation dataset for South America. Sci. Data 2025, 12, 1006. [Google Scholar] [CrossRef] [PubMed]
| Metric | Formula | Best Value [Min, Max] |
|---|---|---|
| Continuous performance metrics | ||
| Pearson correlation | 1 [−1, 1] | |
| Relative bias | 0, (, ∞) | |
| Root mean squared error | 0, [0, ∞) | |
| Normalized RMSE | 0, [0, ∞) | |
| Mean bias error | 0, (, ∞) | |
| Kling–Gupta efficiency | 1, (, 1] | |
| Categorical performance metrics | ||
| Probability of detection | 1, [0, 1] | |
| False alarm ratio | 0, [0, 1] | |
| Heidke skill score | 1, (, 1] | |
| Region | Product | Mean | Median | SD | Q25 | Q75 | Min | Max |
|---|---|---|---|---|---|---|---|---|
| MSWEP | −0.11 | −0.08 | 0.10 | −0.13 | −0.05 | −0.74 | 0.04 | |
| Altiplano | CHIRPS | −0.17 | −0.17 | 0.10 | −0.22 | −0.11 | −1.22 | 0.08 |
| ERA5-Land | −0.25 | −0.23 | 0.10 | −0.29 | −0.19 | −0.94 | −0.06 | |
| MSWEP | −0.32 | −0.32 | 0.20 | −0.41 | −0.21 | −1.15 | 0.46 | |
| Valles | CHIRPS | −0.38 | −0.34 | 0.31 | −0.48 | −0.21 | −2.37 | 0.45 |
| ERA5-Land | −0.58 | −0.42 | 0.56 | −0.79 | −0.28 | −3.27 | 0.91 | |
| MSWEP | −0.50 | −0.55 | 0.46 | −0.81 | −0.25 | −1.64 | 1.10 | |
| Llanos | CHIRPS | −0.87 | −0.80 | 0.41 | −1.00 | −0.63 | −3.16 | −0.12 |
| ERA5-Land | −0.76 | −0.74 | 0.34 | −0.94 | −0.51 | −2.84 | 0.40 | |
| MSWEP | −0.41 | −0.40 | 0.16 | −0.46 | −0.31 | −1.26 | −0.09 | |
| Chaco | CHIRPS | −0.65 | −0.64 | 0.12 | −0.74 | −0.56 | −0.98 | −0.32 |
| ERA5-Land | −0.95 | −0.90 | 0.24 | −1.05 | −0.80 | −2.61 | −0.58 | |
| MSWEP | 0.22 | 0.19 | 0.48 | −0.09 | 0.51 | −0.86 | 1.81 | |
| Amazonia | CHIRPS | −0.44 | −0.33 | 0.46 | −0.68 | −0.19 | −1.53 | 0.63 |
| ERA5-Land | 0.44 | 0.83 | 2.87 | −1.32 | 2.50 | −17.96 | 9.02 |
| Region | Product | Count | Mean | Median | SD | Q25 | Q75 |
|---|---|---|---|---|---|---|---|
| Altiplano | CHIRPS | 26 | −0.26 | −0.25 | 0.04 | −0.27 | −0.23 |
| CHIRPS | 81 | −0.77 | −0.68 | 0.23 | −0.74 | −0.64 | |
| Valles | MSWEP | 2 | −0.91 | −0.91 | 0.00 | −0.91 | −0.91 |
| ERA5-Land | 17 | −2.10 | −2.27 | 0.75 | −2.64 | −1.41 | |
| CHIRPS | 4127 | −1.19 | −1.01 | 0.50 | −1.20 | −0.89 | |
| Llanos | MSWEP | 559 | −0.88 | −0.87 | 0.20 | −1.01 | −0.76 |
| ERA5-Land | 276 | −0.90 | −0.89 | 0.14 | −0.99 | −0.79 | |
| CHIRPS | 1573 | −0.75 | −0.76 | 0.11 | −0.83 | −0.67 | |
| Chaco | MSWEP | 134 | −0.47 | −0.46 | 0.08 | −0.48 | −0.44 |
| ERA5-Land | 441 | −0.89 | −0.86 | 0.16 | −0.99 | −0.79 | |
| Amazonia | CHIRPS | 65 | −1.40 | −1.37 | 0.11 | −1.49 | −1.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salazar, Á.; Larrea-Alcázar, D.M.; Bertin, A.; Gouin, N.; Pareja, A.; Morales, L.; Maillard, O.; Ocampo-Melgar, D.; Squeo, F.A. Spatio-Temporal Evaluation of MSWEP, CHIRPS and ERA5-Land Reveals Regional-Specific Responses Across Complex Topography in Bolivia. Atmosphere 2025, 16, 1281. https://doi.org/10.3390/atmos16111281
Salazar Á, Larrea-Alcázar DM, Bertin A, Gouin N, Pareja A, Morales L, Maillard O, Ocampo-Melgar D, Squeo FA. Spatio-Temporal Evaluation of MSWEP, CHIRPS and ERA5-Land Reveals Regional-Specific Responses Across Complex Topography in Bolivia. Atmosphere. 2025; 16(11):1281. https://doi.org/10.3390/atmos16111281
Chicago/Turabian StyleSalazar, Álvaro, Daniel M. Larrea-Alcázar, Angéline Bertin, Nicolas Gouin, Alejandro Pareja, Luis Morales, Oswaldo Maillard, Diego Ocampo-Melgar, and Francisco A. Squeo. 2025. "Spatio-Temporal Evaluation of MSWEP, CHIRPS and ERA5-Land Reveals Regional-Specific Responses Across Complex Topography in Bolivia" Atmosphere 16, no. 11: 1281. https://doi.org/10.3390/atmos16111281
APA StyleSalazar, Á., Larrea-Alcázar, D. M., Bertin, A., Gouin, N., Pareja, A., Morales, L., Maillard, O., Ocampo-Melgar, D., & Squeo, F. A. (2025). Spatio-Temporal Evaluation of MSWEP, CHIRPS and ERA5-Land Reveals Regional-Specific Responses Across Complex Topography in Bolivia. Atmosphere, 16(11), 1281. https://doi.org/10.3390/atmos16111281













