Modeling Tropical Cyclone Boundary Layer Wind Fields over Ocean and Land: A Comparative Assessment
Abstract
1. Introduction
2. Parametric TC Wind Field Models
2.1. Gradient Wind Field Model
2.2. Four Selected TC Boundary Layer Models
2.2.1. The Model of M95
2.2.2. The Model of K01
2.2.3. The Model of Y21a
2.2.4. The Model of Y21b
2.3. Simulation Setups
2.3.1. Grid Systems
2.3.2. Modification for Landfall TC Wind Field Simulations
3. Results
3.1. Idealized TC Case Study
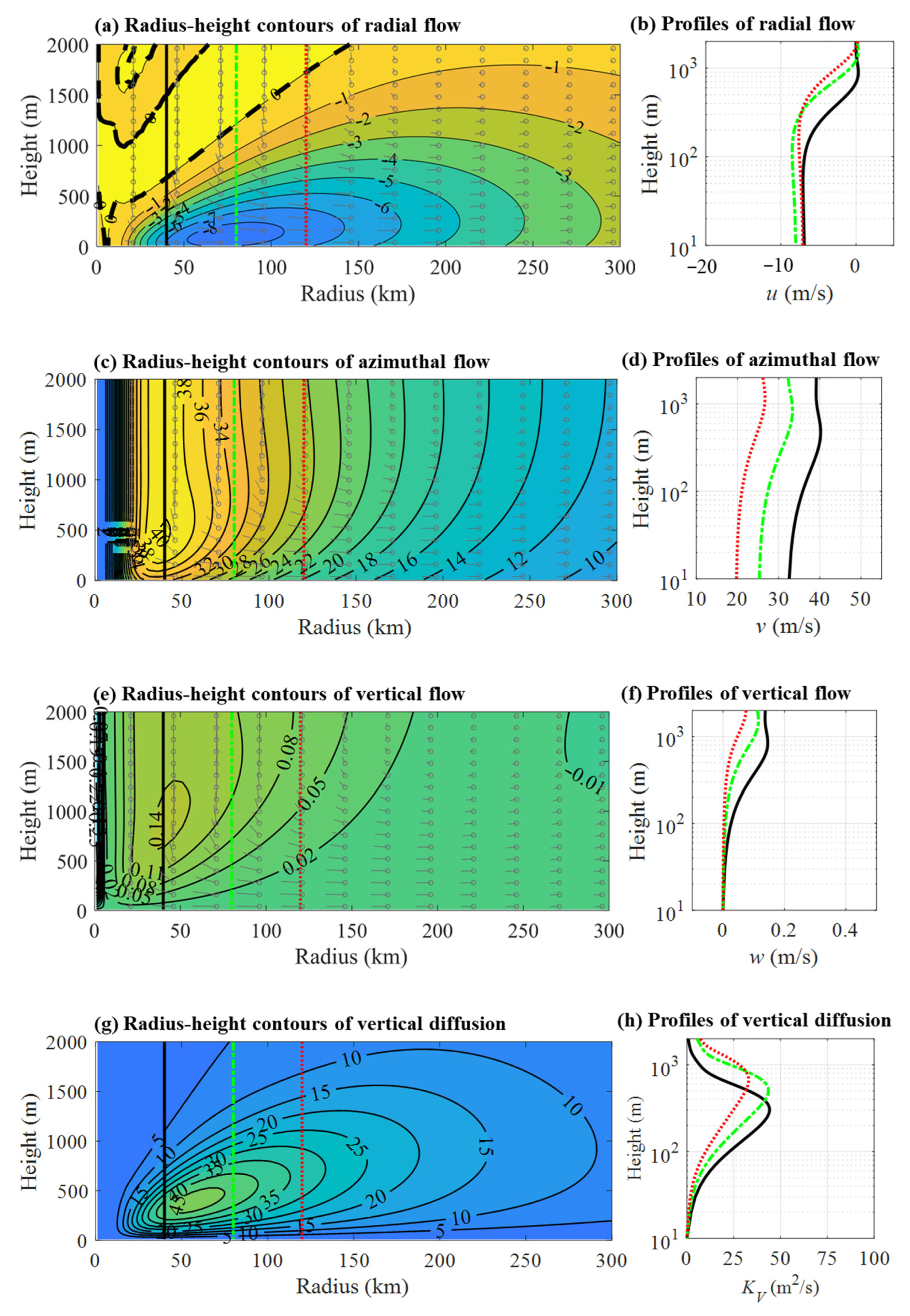
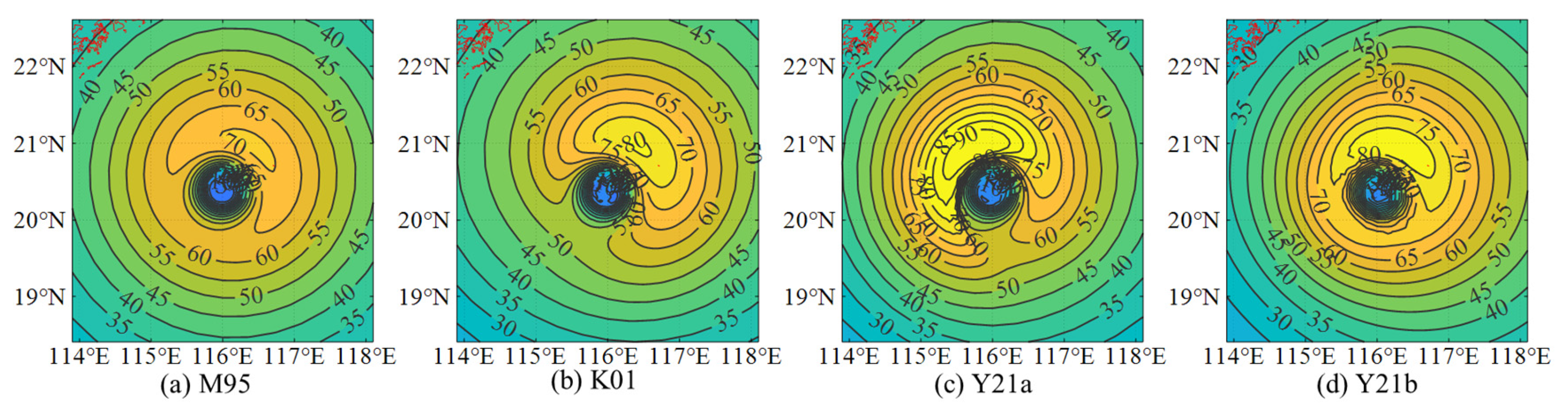
3.1.1. Simulation Results of M95
3.1.2. Simulation Results of K01
3.1.3. Simulation Results of Y21a
3.1.4. Simulation Results of Y21b
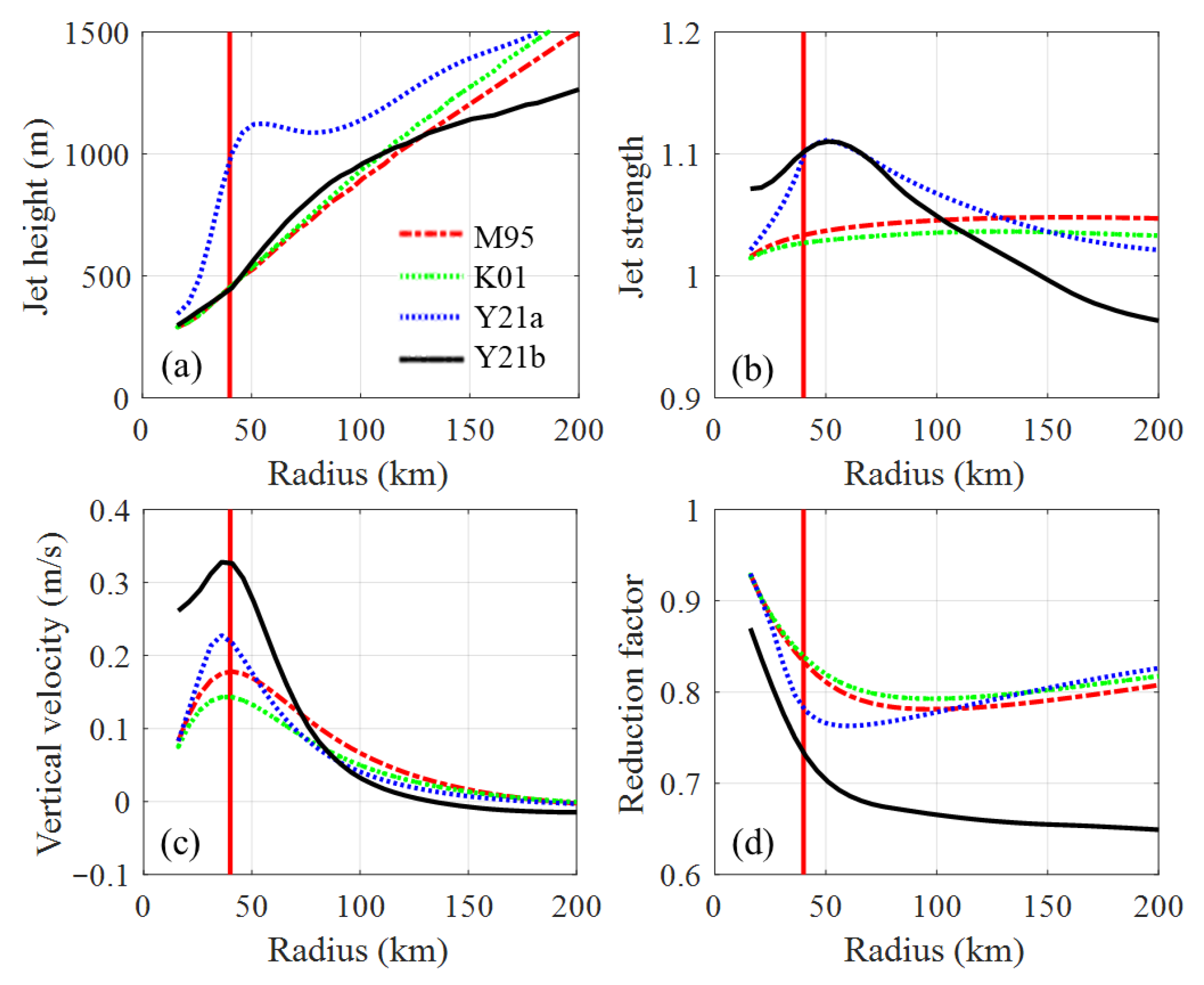
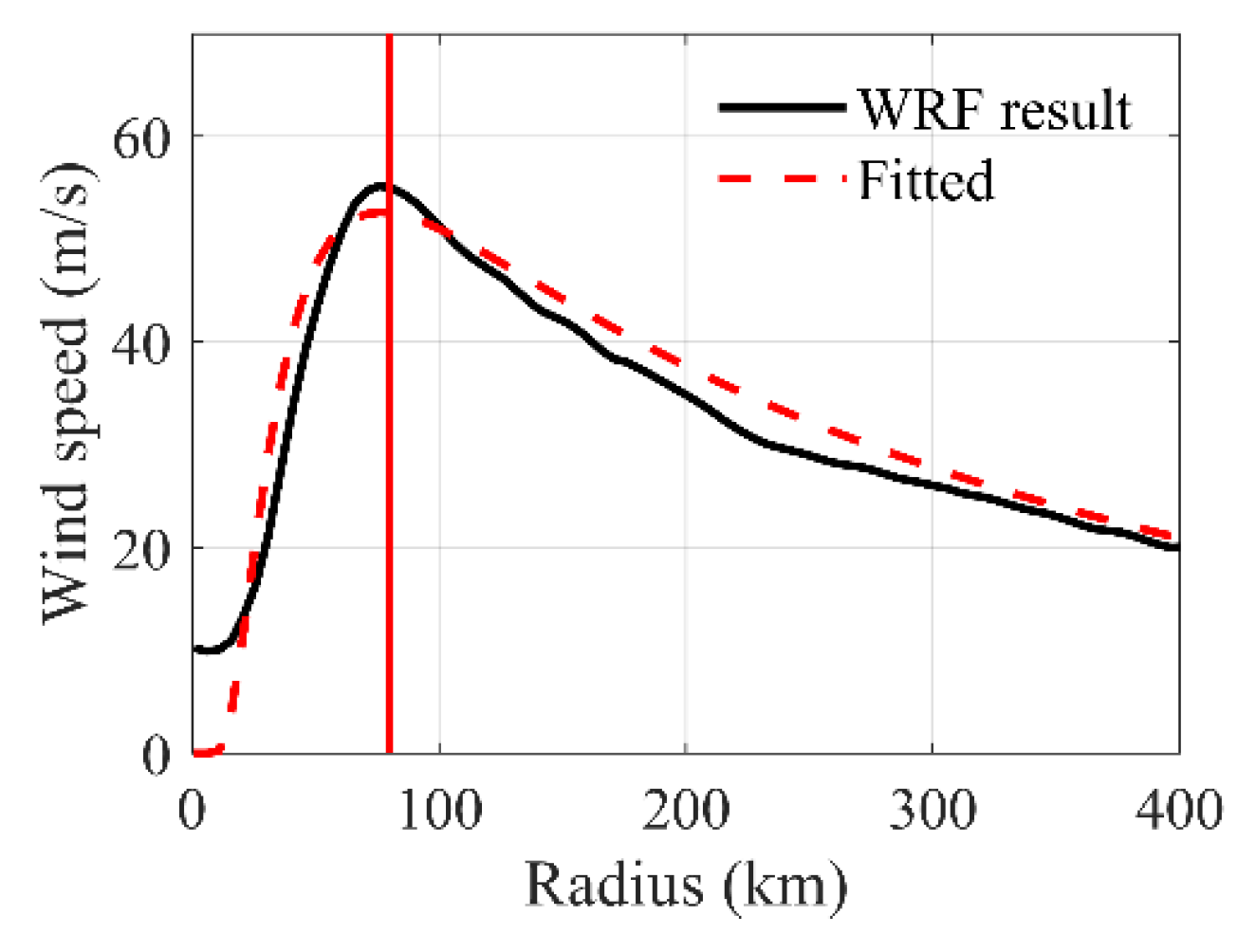
3.1.5. Comparison of Radial Profiles
3.1.6. Comparison of Model Computational Efficiencies
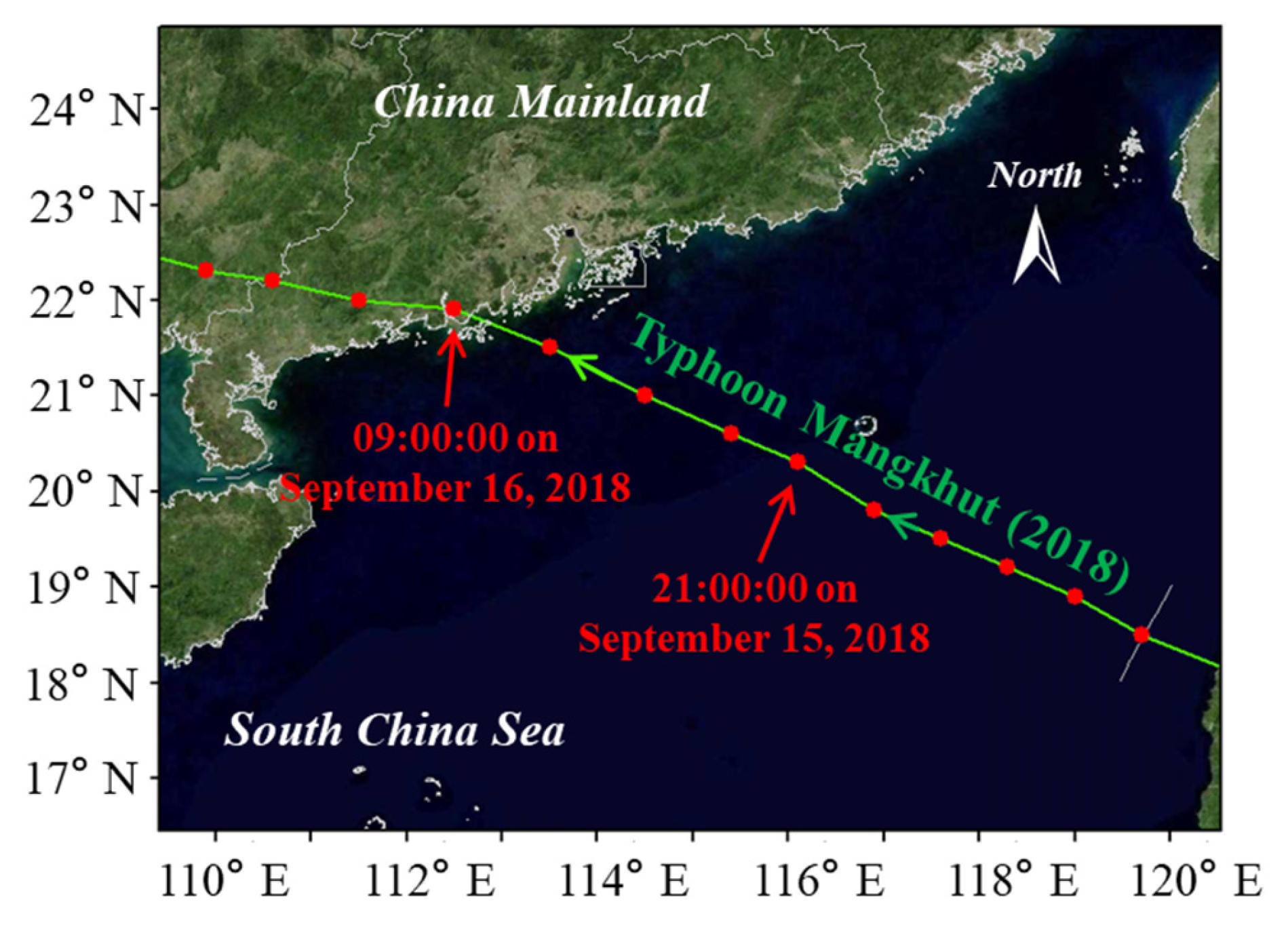
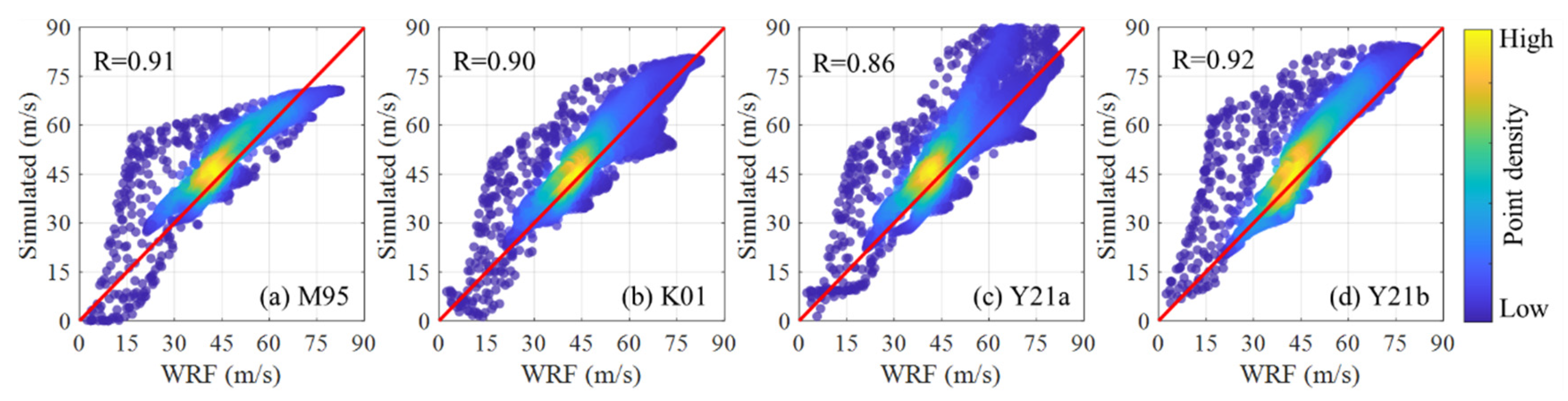
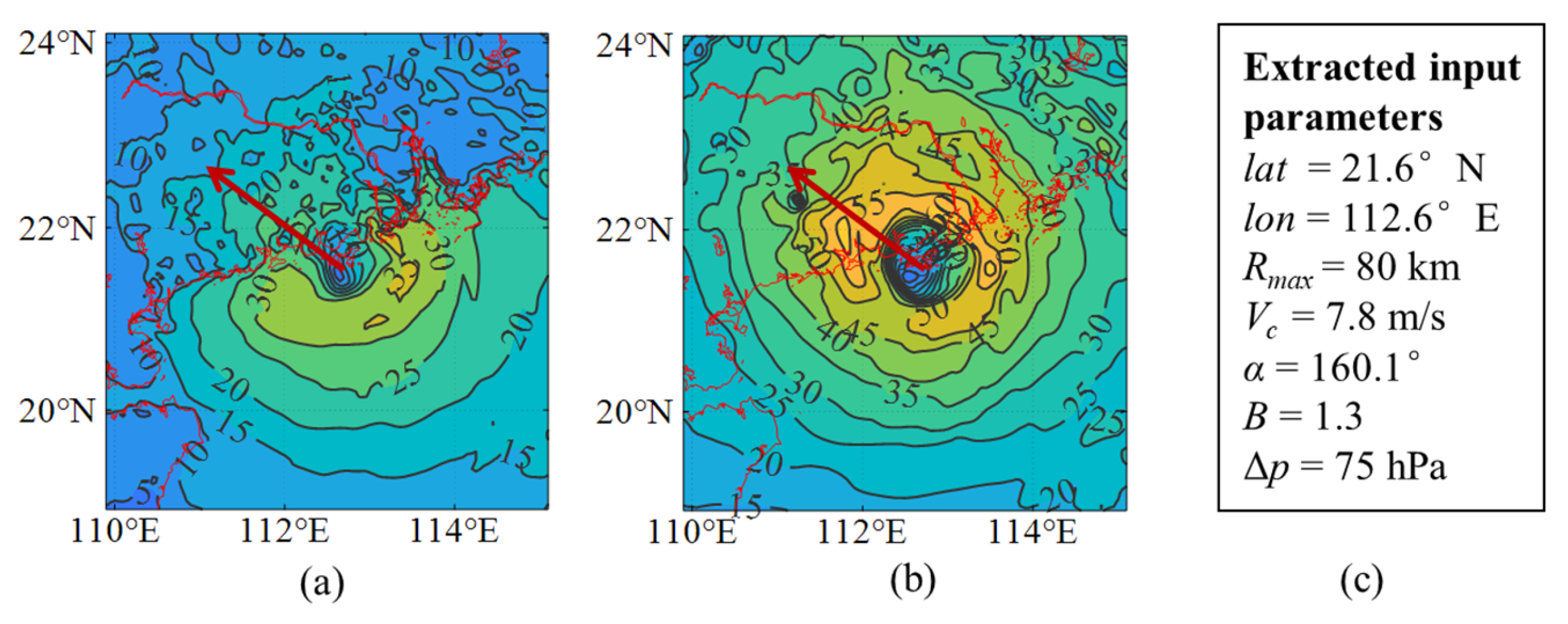
3.2. Comparisons with WRF Results: Typhoon Mangkhut (2018)
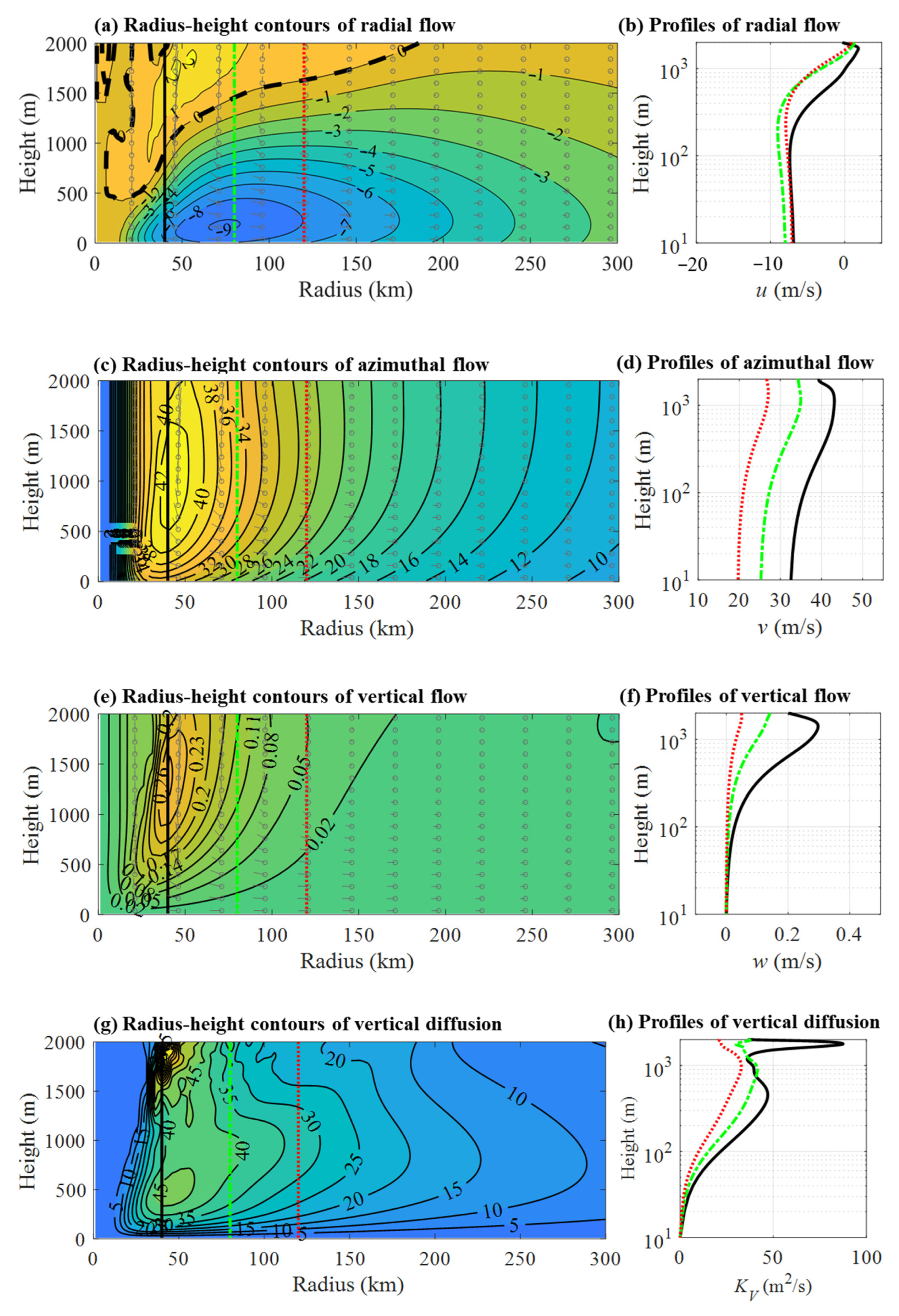
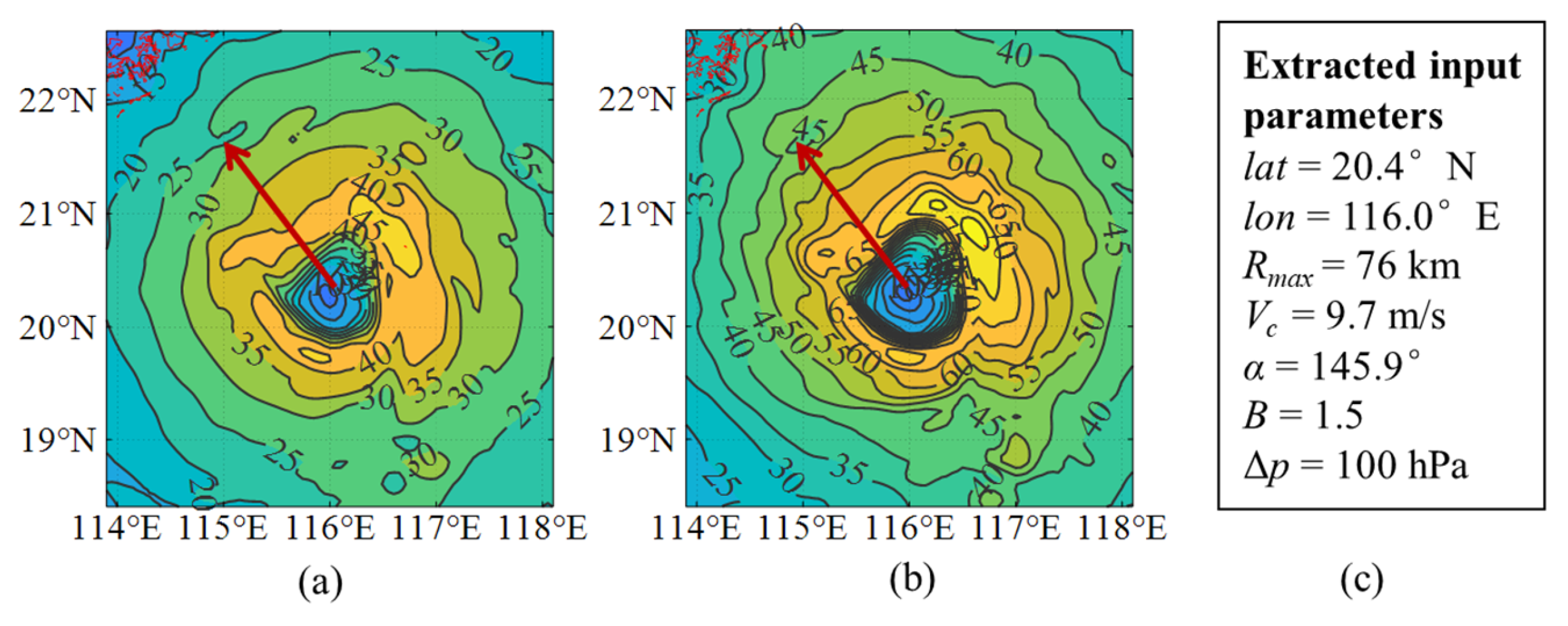
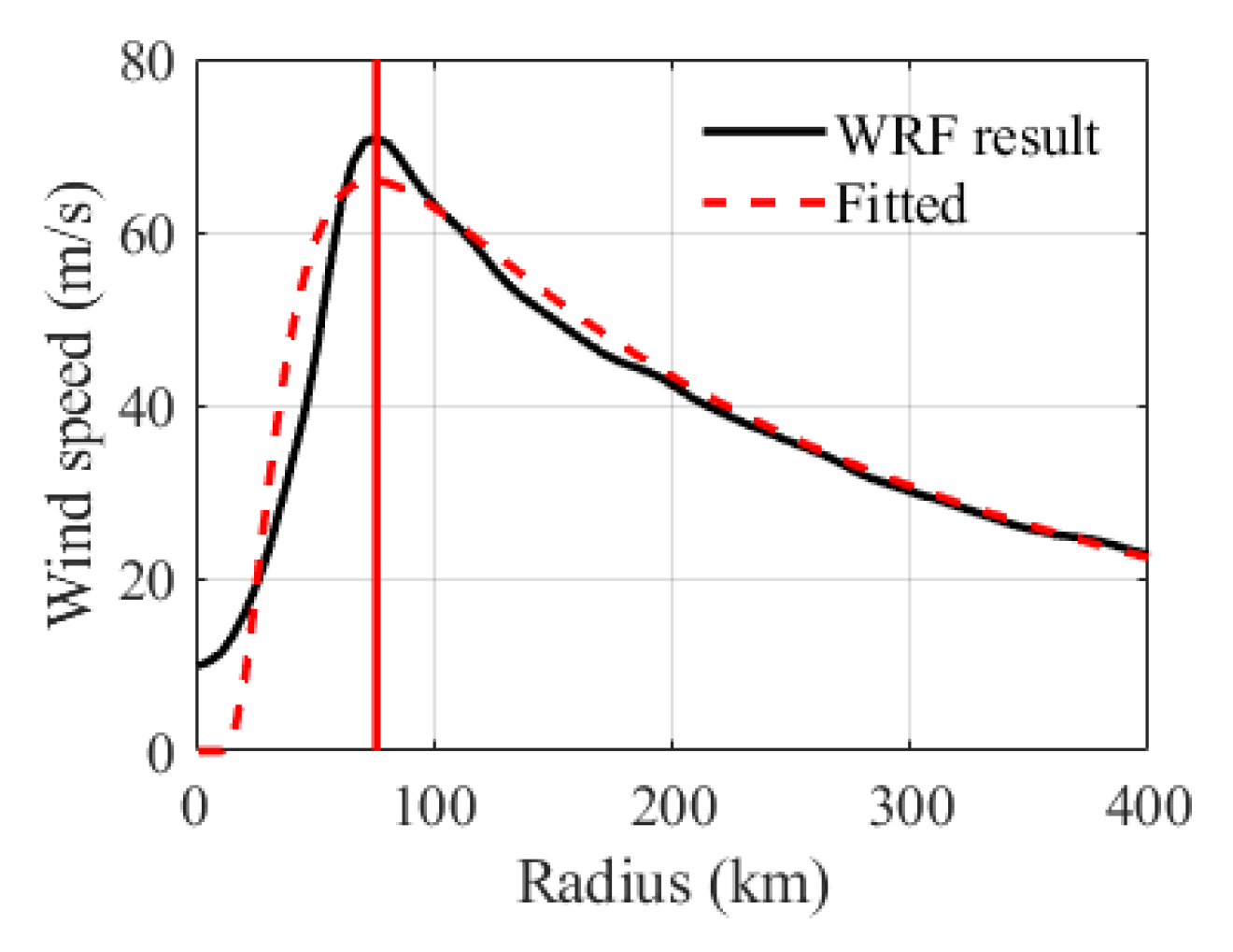
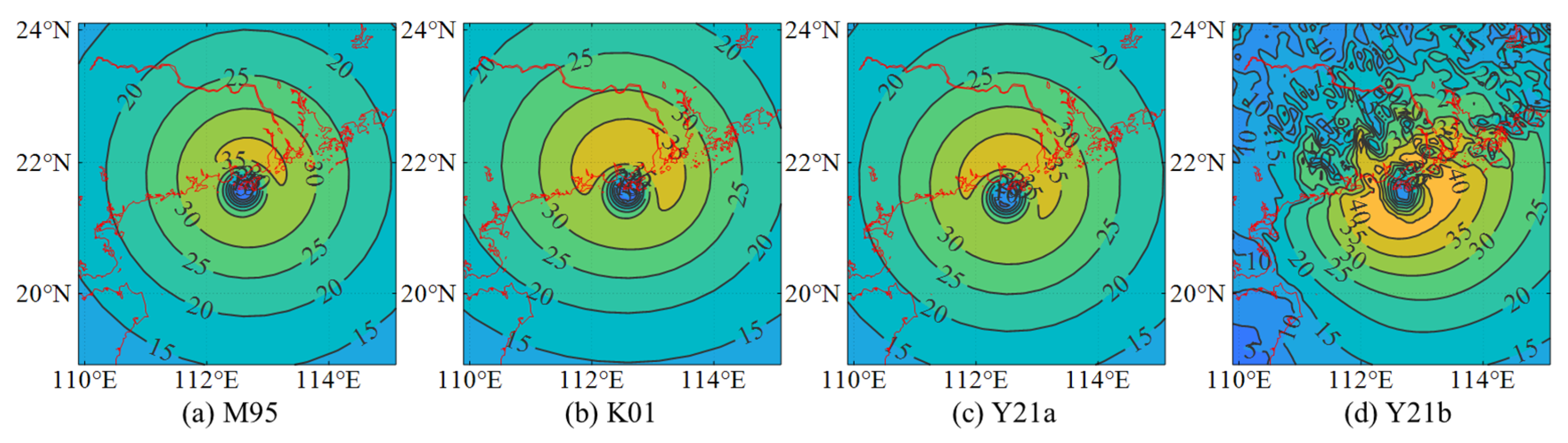
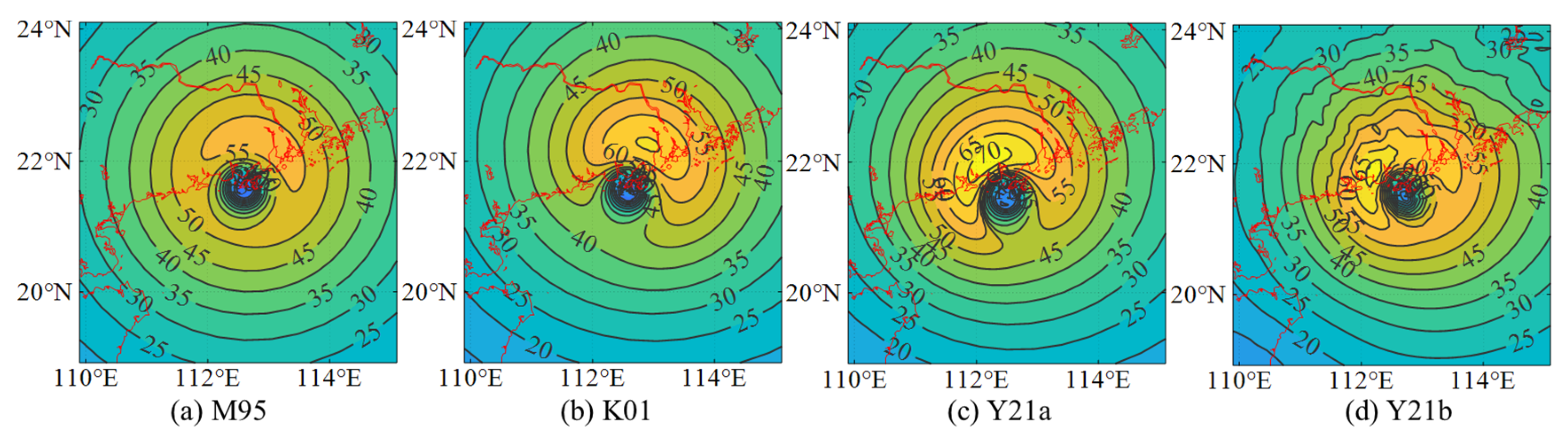
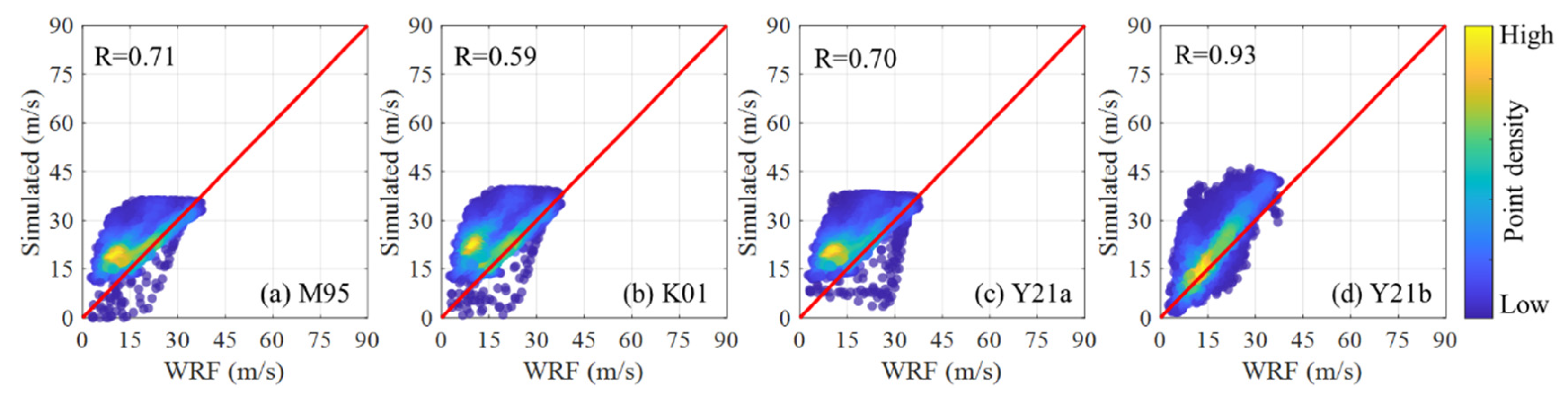
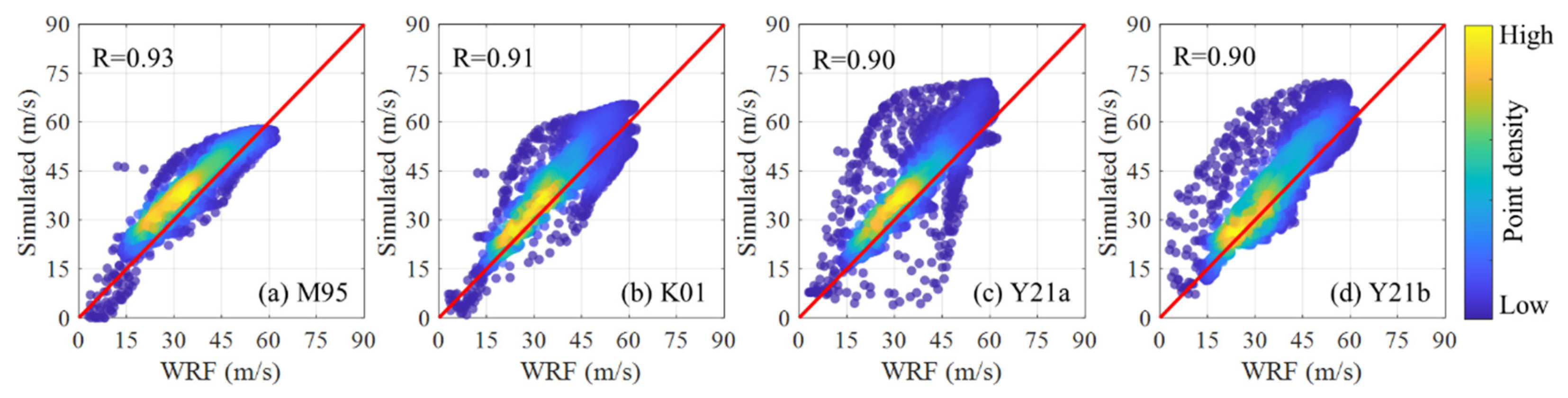
3.2.1. TC Wind Field over the Ocean
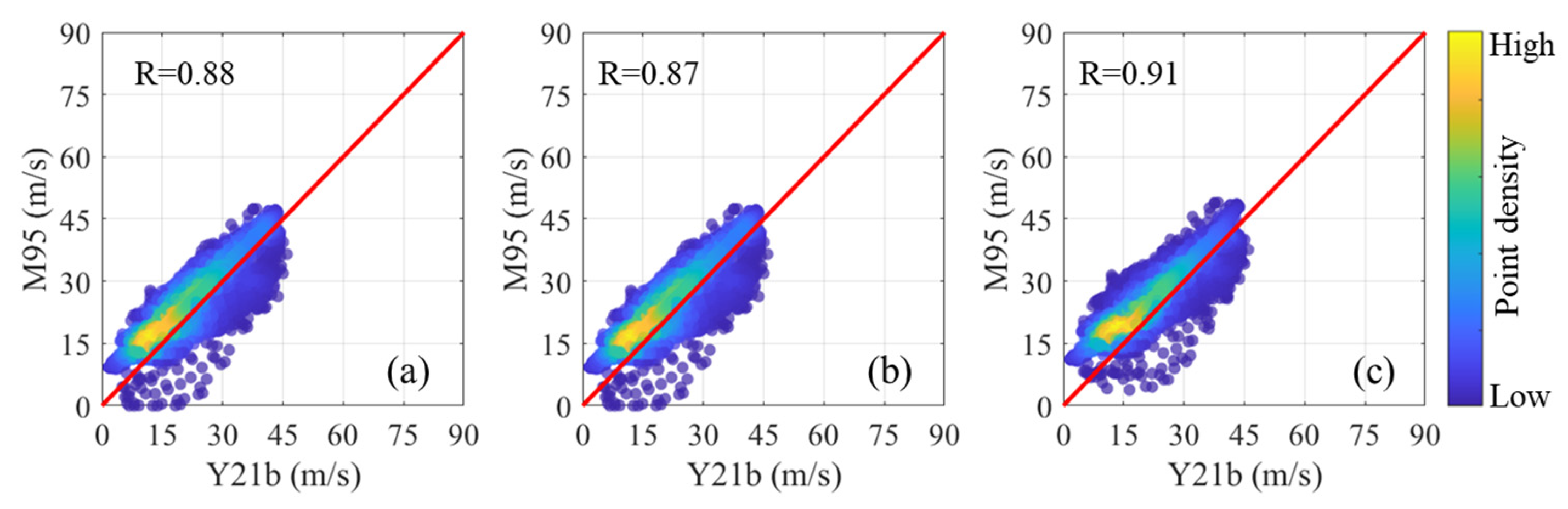
3.2.2. TC Wind Field at Landfall
3.2.3. Evaluation of TC Wind Field Modifications
4. Discussion and Limitation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rappaport, E.N. Fatalities in the United States from Atlantic Tropical Cyclones: New Data and Interpretation. Bull. Am. Meteorol. Soc. 2014, 95, 341–346. [Google Scholar] [CrossRef]
- Chen, J.; Chavas, D.R. The Transient Responses of an Axisymmetric Tropical Cyclone to Instantaneous Surface Roughening and Drying. J. Atmos. Sci. 2020, 77, 2807–2834. [Google Scholar] [CrossRef]
- Tong, B.; Hu, G.; Deng, Y.; Huang, Y.; He, Y. Deep-learning based simulation of tropical cyclone genesis in Northwest Pacific. J. Wind Eng. Ind. Aerodyn. 2025, 257, 106003. [Google Scholar] [CrossRef]
- Kepert, J.D. A Simple Model of the Tropical Cyclone Boundary Layer at Landfall. Mon. Weather Rev. 2025, 153, 589–603. [Google Scholar] [CrossRef]
- Kepert, J.D. Landfall-Induced Changes in Tropical Cyclone Veronica’s Surface Winds. Mon. Weather Rev. 2025, 153, 605–616. [Google Scholar] [CrossRef]
- Wong, M.L.M.; Chan, J.C.L. Modeling the Effects of Land–Sea Roughness Contrast on Tropical Cyclone Winds. J. Atmos. Sci. 2007, 64, 3249–3264. [Google Scholar] [CrossRef]
- Powell, M.D.; Houston, S.H. Hurricane Andrew’s landfall in South Florida. Part II: Surface wind fields and potential real-time applications. Weather Forecast. 1996, 11, 329–349. [Google Scholar] [CrossRef]
- Powell, M.D.; Dodge, P.P.; Black, M.L. The landfall of Hurricane Hugo in the Carolinas: Surface wind distribution. Weather Forecast. 1991, 6, 379–399. [Google Scholar] [CrossRef]
- Dong, M.; Ji, C.; Chen, F.; Wang, Y. Numerical Study of Boundary Layer Structure and Rainfall after Landfall of Typhoon Fitow (2013): Sensitivity to Planetary Boundary Layer Parameterization. Adv. Atmos. Sci. 2019, 36, 431–450. [Google Scholar] [CrossRef]
- Tuleya, R.E.; Kurihara, Y. A numerical simulation of the landfall of tropical cyclones. J. Atmos. Sci. 1978, 35, 242–257. [Google Scholar] [CrossRef]
- Powell, M.D. Changes in the low-level kinematic and thermodynamic structure of Hurricane Alicia (1983) at landfall. Mon. Weather Rev. 1987, 115, 75–99. [Google Scholar] [CrossRef]
- Kepert, J. The Dynamics of Boundary Layer Jets within the Tropical Cyclone Core. Part I: Linear Theory. J. Atmos. Sci. 2001, 58, 2469–2484. [Google Scholar] [CrossRef]
- Montgomery, M.T.; Smith, R.K.; Nguyen, S.V. Sensitivity of tropical-cyclone models to the surface drag coefficient. Q. J. R. Meteorol. Soc. 2010, 136, 1945–1953. [Google Scholar] [CrossRef]
- Holland, G.J. An analytic model of the wind and pressure profiles in hurricanes. Mon. Weather Rev. 1980, 108, 1212–1218. [Google Scholar] [CrossRef]
- Willoughby, H.E.; Rahn, M.E. Parametric Representation of the Primary Hurricane Vortex. Part I: Observations and Evaluation of the Holland (1980) Model. Mon. Weather Rev. 2004, 132, 3033–3048. [Google Scholar] [CrossRef]
- Hong, H.P.; Li, S.H.; Duan, Z.D. Typhoon Wind Hazard Estimation and Mapping for Coastal Region in Mainland China. Nat. Hazards Rev. 2016, 17, 04016001. [Google Scholar] [CrossRef]
- Li, S.H.; Hong, H.P. Typhoon wind hazard estimation for China using an empirical track model. Nat. Hazards 2016, 82, 1009–1029. [Google Scholar] [CrossRef]
- Li, Y.; Cheung, K.K.W.; Chan, J.C.L. Numerical study on the development of asymmetric convection and vertical wind shear during tropical cyclone landfall. Q. J. R. Meteorol. Soc. 2014, 140, 1866–1877. [Google Scholar] [CrossRef]
- Nolan, D.S.; McNoldy, B.D.; Yunge, J. Evaluation of the Surface Wind Field over Land in WRF Simulations of Hurricane Wilma (2005). Part I: Model Initialization and Simulation Validation. Mon. Weather Rev. 2021, 149, 679–695. [Google Scholar] [CrossRef]
- Yang, J.; Chen, Y.; Tang, Y.; Yan, G.; Duan, Z. A high-fidelity parametric model for tropical cyclone boundary layer wind field by considering effects of land cover and terrain. Atmos. Res. 2021, 260, 105701. [Google Scholar] [CrossRef]
- Kepert, J.D. Choosing a Boundary Layer Parameterization for Tropical Cyclone Modeling. Mon. Weather Rev. 2012, 140, 1427–1445. [Google Scholar] [CrossRef]
- Hong, X.; Hong, H.P.; Li, J. Solution and validation of a three dimensional tropical cyclone boundary layer wind field model. J. Wind Eng. Ind. Aerodyn. 2019, 193, 103973. [Google Scholar] [CrossRef]
- Tzvi, G.-C.; Somerville, R.C.J. On the use of a coordinate transformation for the solution of the Navier-Stokes equations. J. Comput. Phys. 1975, 17, 209–228. [Google Scholar] [CrossRef]
- Fei, R.; Wang, Y.Q.; Li, Y.L. Contribution of Vertical Advection to Supergradient Wind in Tropical Cyclone Boundary Layer: A Numerical Study. J. Atmos. Sci. 2021, 78, 1057–1073. [Google Scholar] [CrossRef]
- Snaiki, R.; Wu, T. An analytical model for rapid estimation of hurricane supergradient winds. J. Wind Eng. Ind. Aerodyn. 2020, 201, 104175. [Google Scholar] [CrossRef]
- Liu, J.; Li, B. A deep learning model for predicting mechanical behaviors of dynamic power cable of offshore floating wind turbine. Mar. Struct. 2025, 99, 103705. [Google Scholar] [CrossRef]
- Yang, L.; Li, B.; Dong, Y.; Hu, Z.; Zhang, K.; Li, S. Large-amplitude rotation of floating offshore wind turbines: A comprehensive review of causes, consequences, and solutions. Renew. Sustain. Energy Rev. 2025, 211, 115295. [Google Scholar] [CrossRef]
- Jian, W.; Cao, D.; Lo, E.Y.; Huang, Z.; Chen, X.; Cheng, Z.; Gu, H.; Li, B. Wave runup on a surging vertical cylinder in regular waves. Appl. Ocean Res. 2017, 63, 229–241. [Google Scholar] [CrossRef]
- Wang, X.; Qiao, D.; Jin, L.; Yan, J.; Wang, B.; Li, B.; Ou, J. Numerical investigation of wave run-up and load on heaving cylinder subjected to regular waves. Ocean Eng. 2023, 268, 113415. [Google Scholar] [CrossRef]
- Meng, Y.; Masahiro, M.; Kazuki, H. An analytical model for simulation of the wind field in a typhoon boundary layer. J. Wind Eng. Ind. Aerodyn. 1995, 56, 291–310. [Google Scholar] [CrossRef]
- Yang, J.; Chen, Y.; Zhou, H.; Duan, Z. A height-resolving tropical cyclone boundary layer model with vertical advection process. Nat. Hazards 2021, 107, 723–749. [Google Scholar] [CrossRef]
- Giammanco, I.M.; Schroeder, J.L.; Powell, M.D. GPS Dropwindsonde and WSR-88D Observations of Tropical Cyclone Vertical Wind Profiles and Their Characteristics. Weather Forecast. 2013, 28, 77–99. [Google Scholar] [CrossRef]
- Willoughby, H.E.; Darling, R.W.R.; Rahn, M.E. Parametric Representation of the Primary Hurricane Vortex. Part II: A New Family of Sectionally Continuous Profiles. Mon. Weather Rev. 2006, 134, 1102–1120. [Google Scholar] [CrossRef]
- Georgiou, P.N.; Davenport, A.G.; Vickery, B.J. Design wind speeds in regions dominated by tropical cyclones. J. Wind Eng. Ind. Aerodyn. 1983, 13, 139–152. [Google Scholar] [CrossRef]
- Batts, M.E.; ASCE, A.M.; Russell, L.R.; Simiu, E. Hurricane Wind Speeds in The United States. J. Struct. Div. 1980, 106, 2001–2016. [Google Scholar] [CrossRef]
- Du, H.; Yu, P.; Zhu, L.; Fei, K.; Gao, L. Assessing the performances of parametric wind models in predicting storm surges in the Pearl River Estuary. J. Wind Eng. Ind. Aerodyn. 2023, 232, 105265. [Google Scholar] [CrossRef]
- Chen, Y.; Duan, Z. A statistical dynamics track model of tropical cyclones for assessing typhoon wind hazard in the coast of southeast China. J. Wind Eng. Ind. Aerodyn. 2018, 172, 325–340. [Google Scholar] [CrossRef]
- Georgiou, P.N. Design Wind Speeds in Tropical Cyclone-Prone Regions; University of Western Ontario: London, ON, Canada, 1985. [Google Scholar]
- Vickery, P.J.; Skerlj, P.F.; Steckley, A.C.; Twisdale, L.A. Hurricane Wind Field Model for Use in Hurricane Simulations. J. Struct. Eng. 2000, 126, 1203–1221. [Google Scholar] [CrossRef]
- Vickery, P.J.; Skerlj, P.F.; Twisdale, L.A. Simulation of Hurricane Risk in the U.S. Using Empirical Track Model. J. Struct. Eng. 2000, 126, 1222–1237. [Google Scholar] [CrossRef]
- Sparks, P.R.; Huang, Z. Gust factors and surface-to-gradient wind-speed ratios in tropical cyclones. J. Wind Eng. Ind. Aerodyn. 2001, 89, 1047–1058. [Google Scholar] [CrossRef]
- Powell, M.D.; Vickery, P.J.; Reinhold, T.A. Reduced drag coefficient for high wind speeds in tropical cyclones. Nature 2003, 422, 279–283. [Google Scholar] [CrossRef] [PubMed]
- Powell, M.; Soukup, G.; Cocke, S.; Gulati, S.; Morisseau-Leroy, N.; Hamid, S.; Dorst, N.; Axe, L. State of Florida hurricane loss projection model: Atmospheric science component. J. Wind Eng. Ind. Aerodyn. 2005, 93, 651–674. [Google Scholar] [CrossRef]
- Vickery, P.J.; Wadhera, D.; Powell, M.D.; Chen, Y. A Hurricane Boundary Layer and Wind Field Model for Use in Engineering Applications. J. Appl. Meteorol. Climatol. 2009, 48, 381–405. [Google Scholar] [CrossRef]
- Shapiro, L.J. The Asymmetric Boundary layer Flow Under a Translating Hurricane. J. Atmos. Sci. 1983, 40, 1984–1998. [Google Scholar] [CrossRef]
- Thompson, E.F.; Cardone, V.J. Practical modeling of hurricane surface wind fields. J. Waterw. Port Coast. Ocean Eng. 1996, 122, 195–205. [Google Scholar] [CrossRef]
- Kepert, J.; Wang, Y. The Dynamics of Boundary Layer Jets within the Tropical Cyclone Core. Part II: Nonlinear Enhancement. J. Atmos. Sci. 2001, 58, 2485–2501. [Google Scholar] [CrossRef]
- Snaiki, R.; Wu, T. A linear height-resolving wind field model for tropical cyclone boundary layer. J. Wind Eng. Ind. Aerodyn. 2017, 171, 248–260. [Google Scholar] [CrossRef]
- Fang, G.; Zhao, L.; Cao, S.; Ge, Y.; Pang, W. A novel analytical model for wind field simulation under typhoon boundary layer considering multi-field correlation and height-dependency. J. Wind Eng. Ind. Aerodyn. 2018, 175, 77–89. [Google Scholar] [CrossRef]
- Holton, J.R. An Introduction to Dynamic Meteorology, 4th ed.; Elsevier Academic Press: Boston, MA, USA, 2007. [Google Scholar] [CrossRef]
- Markert, A.; Griffin, R.; Knupp, K.; Molthan, A.; Coleman, T. A Spatial Pattern Analysis of Land Surface Roughness Heterogeneity and its Relationship to the Initiation of Weak Tornadoes. Earth Interact. 2019, 23, 1–28. [Google Scholar] [CrossRef]
- Ek, M.B.; Mitchell, K.E.; Lin, Y.; Rogers, E.; Grunmann, P.; Koren, V.; Gayno, G.; Tarpley, J.D. Implementation of Noah land surface model advances in the National Centers for Environmental Prediction operational mesoscale Eta model. J. Geophys. Res. Atmos. 2003, 108, 1–12. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Liu, Z.; Berner, J.; Wang, W.; Powers, J.G.; Duda, M.G.; Huang, X.Y. A Description of the Advanced Research WRF Model Version 4; NCAR/TN-556+STR; NCAR: Boulder, CO, USA, 2019. [Google Scholar]
- Xue, L.; Li, Y.; Song, L.; Chen, W.; Wang, B. A WRF-based engineering wind field model for tropical cyclones and its applications. Nat. Hazards 2017, 87, 1735–1750. [Google Scholar] [CrossRef]
- Dodla, V.B.; Desamsetti, S.; Yerramilli, A. A comparison of HWRF, ARW and NMM models in Hurricane Katrina (2005) simulation. Int. J. Environ. Res. Public Health 2011, 8, 2447–2469. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Wang, N.; Huang, X.; Wang, Z. Enhancing power grid resilience during tropical cyclones: Deep learning-based real-time wind forecast corrections for dynamic risk prediction. Reliab. Eng. Syst. Saf. 2025, 263, 111284. [Google Scholar] [CrossRef]
- National Centers for Environmental Prediction, N.W.S., NOAA, U.S. Department of Commerce. NCEP FNL Operational Model Global Tropospheric Analyses, Continuing from July 1999. Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory. Boulder, CO. Available online: https://gdex.ucar.edu/datasets/d083002/ (accessed on 8 October 2024).
- Meng, Y.; Masahiro, M.; Kazuki, H. A numerical study of the wind field in a typhoon boundary layer. J. Wind Eng. Ind. Aerodyn. 1997, 67–68, 437–448. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. A Hierarchy of Turbulence Closure Models for Planetary Boundary Layers. J. Atmos. Sci. 1974, 31, 1791–1806. [Google Scholar] [CrossRef]
- Chen, Y.; Yau, M.K. Asymmetric Structures in a Simulated Landfalling Hurricane. J. Atmos. Sci. 2003, 60, 2294–2312. [Google Scholar] [CrossRef][Green Version]
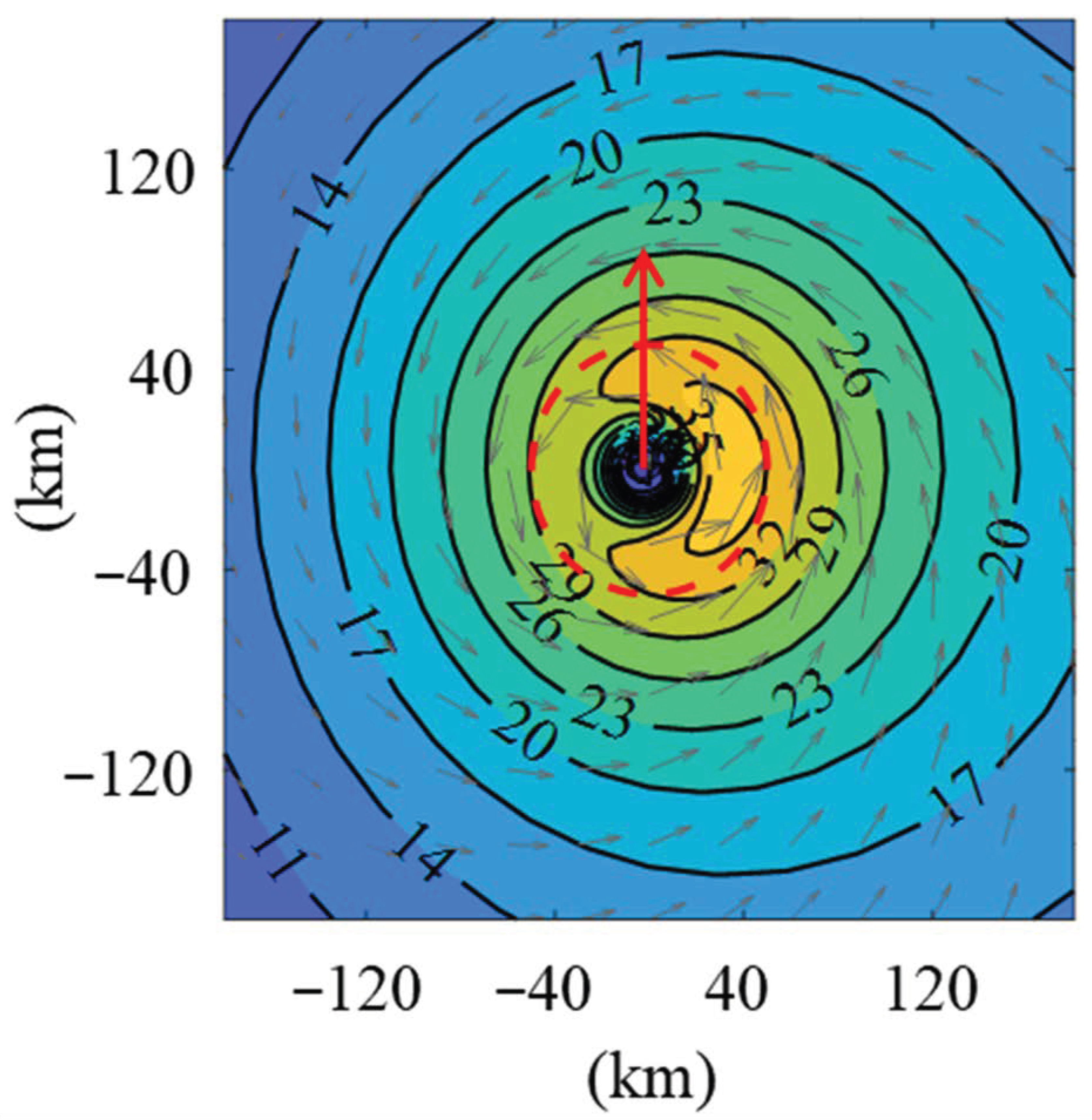
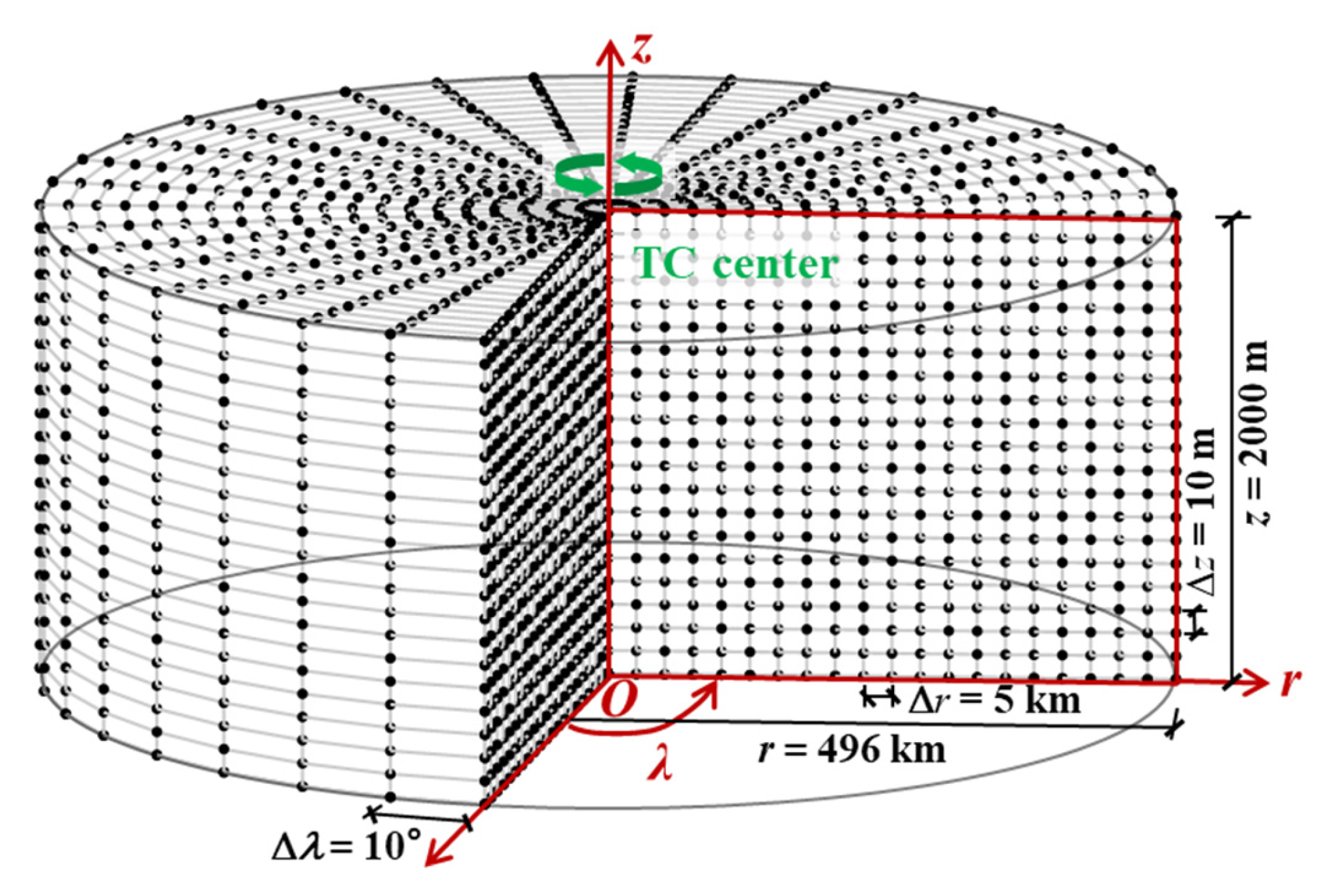
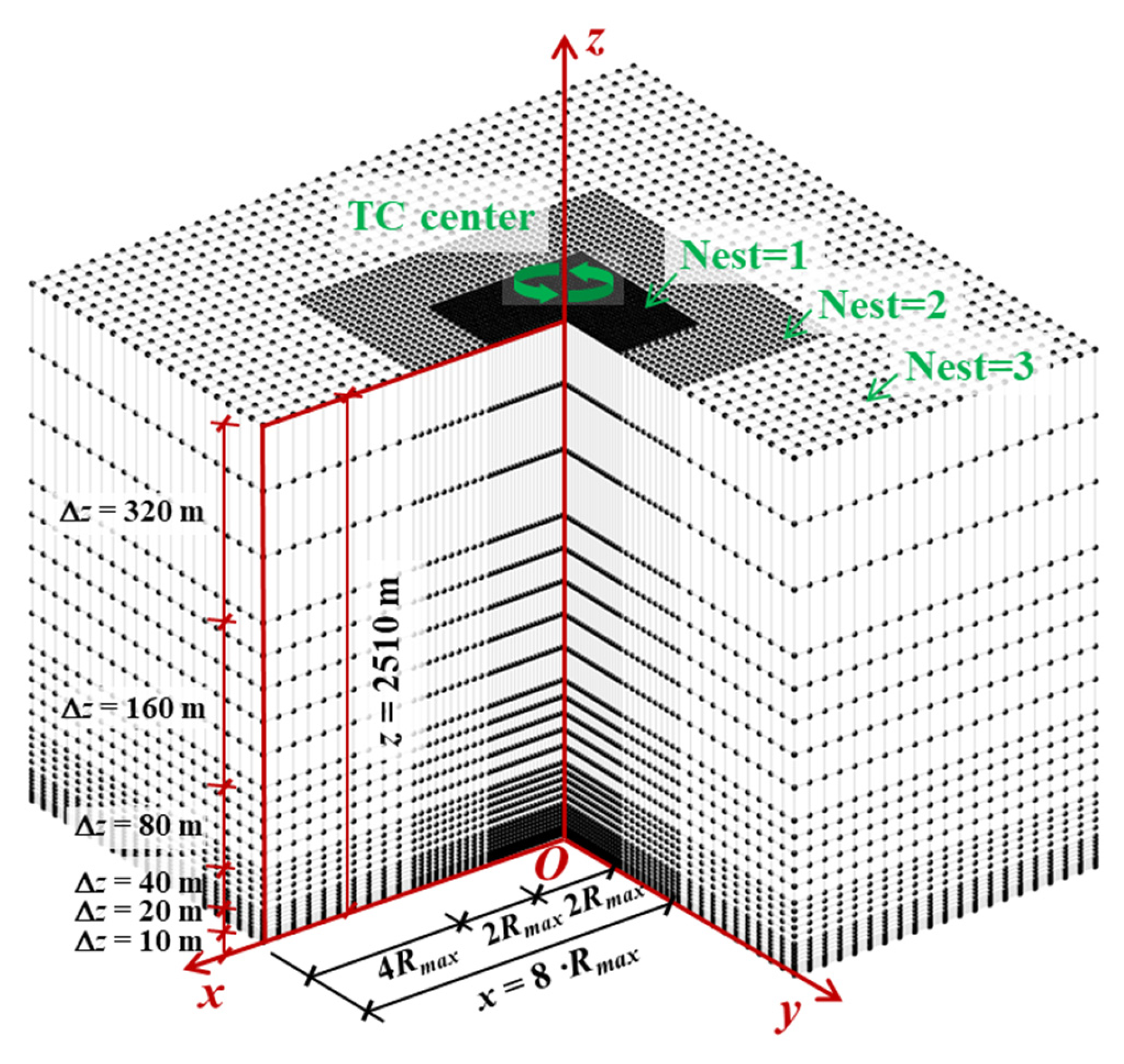
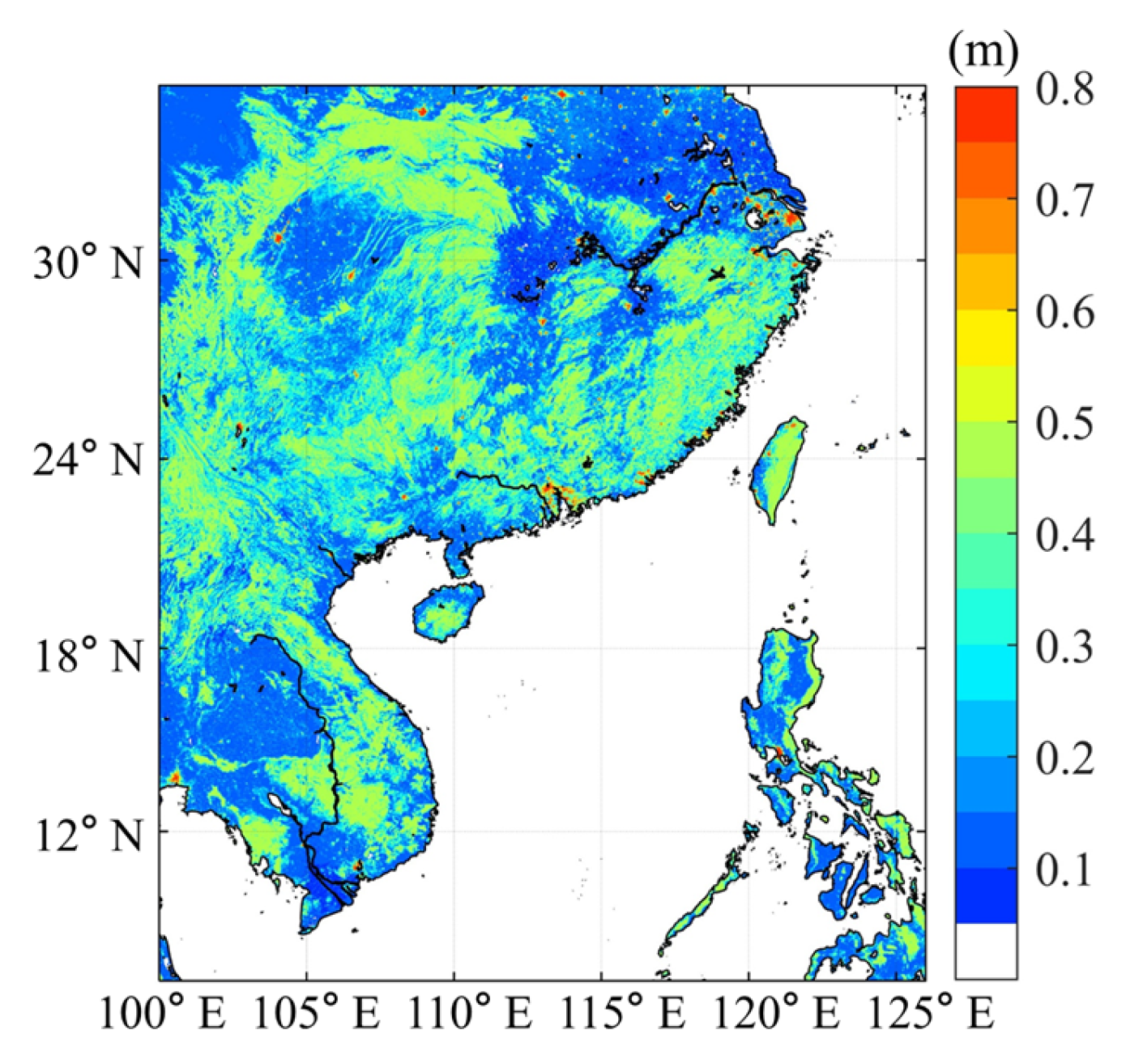



| Batts, et al. [35] | Georgiou [38] | Vickery, et al. [39], Vickery, et al. [40] | Sparks and Huang [41] | Powell, et al. [42] | Powell, et al. [43] | Vickery, et al. [44] | |
|---|---|---|---|---|---|---|---|
| Reduction factor | 0.865 | 0.825 (0.5 Rmax < r < 2 Rmax), 0.75 (r > 5 Rmax) | 0.7–0.72 | 0.65 | 0.71 | 0.73 | 0.67–0.74 |
| Land Cover Types | z0 | Land Cover Types | z0 |
|---|---|---|---|
| Urban and built-up land | 0.80 | Mixed forest | 0.50 |
| Dryland cropland and pasture | 0.15 | Water bodies | 0.0001 |
| Irrigated cropland and pasture | 0.10 | Herbaceous wetland | 0.20 |
| Mixed dryland/irrigated cropland and pasture | 0.15 | Wooded wetland | 0.40 |
| Cropland/grassland mosaic | 0.14 | Baren or sparsely vegetated | 0.01 |
| Cropland/woodland mosaic | 0.20 | Herbaceous tundra | 0.10 |
| Grassland | 0.12 | Wooded tundra | 0.30 |
| Shrubland | 0.05 | Mixed tundra | 0.15 |
| Mixed shrubland/grassland | 0.06 | Bare ground tundra | 0.10 |
| Savanna | 0.15 | Snow or ice | 0.001 |
| Deciduous broadleaf forest | 0.50 | Playa | 0.01 |
| Deciduous needleleaf forest | 0.50 | Lava | 0.15 |
| Evergreen broadleaf forest | 0.50 | White sand | 0.01 |
| Evergreen needleleaf forest | 0.50 |
| M95 | K01 | Y21a | Y21b | |
|---|---|---|---|---|
| Time (s) | 6.9 | 0.8 | 24.22 | 212 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Zhao, J.-W.; Tang, Y.-N.; Duan, Z.-D. Modeling Tropical Cyclone Boundary Layer Wind Fields over Ocean and Land: A Comparative Assessment. Atmosphere 2025, 16, 1280. https://doi.org/10.3390/atmos16111280
Yang J, Zhao J-W, Tang Y-N, Duan Z-D. Modeling Tropical Cyclone Boundary Layer Wind Fields over Ocean and Land: A Comparative Assessment. Atmosphere. 2025; 16(11):1280. https://doi.org/10.3390/atmos16111280
Chicago/Turabian StyleYang, Jian, Jiu-Wei Zhao, Ya-Nan Tang, and Zhong-Dong Duan. 2025. "Modeling Tropical Cyclone Boundary Layer Wind Fields over Ocean and Land: A Comparative Assessment" Atmosphere 16, no. 11: 1280. https://doi.org/10.3390/atmos16111280
APA StyleYang, J., Zhao, J.-W., Tang, Y.-N., & Duan, Z.-D. (2025). Modeling Tropical Cyclone Boundary Layer Wind Fields over Ocean and Land: A Comparative Assessment. Atmosphere, 16(11), 1280. https://doi.org/10.3390/atmos16111280






