A Vine Copula Framework for Non-Stationarity Detection Between Precipitation and Meteorological Factors and Possible Driving Factors
Abstract
1. Introduction
2. Study Area and Data
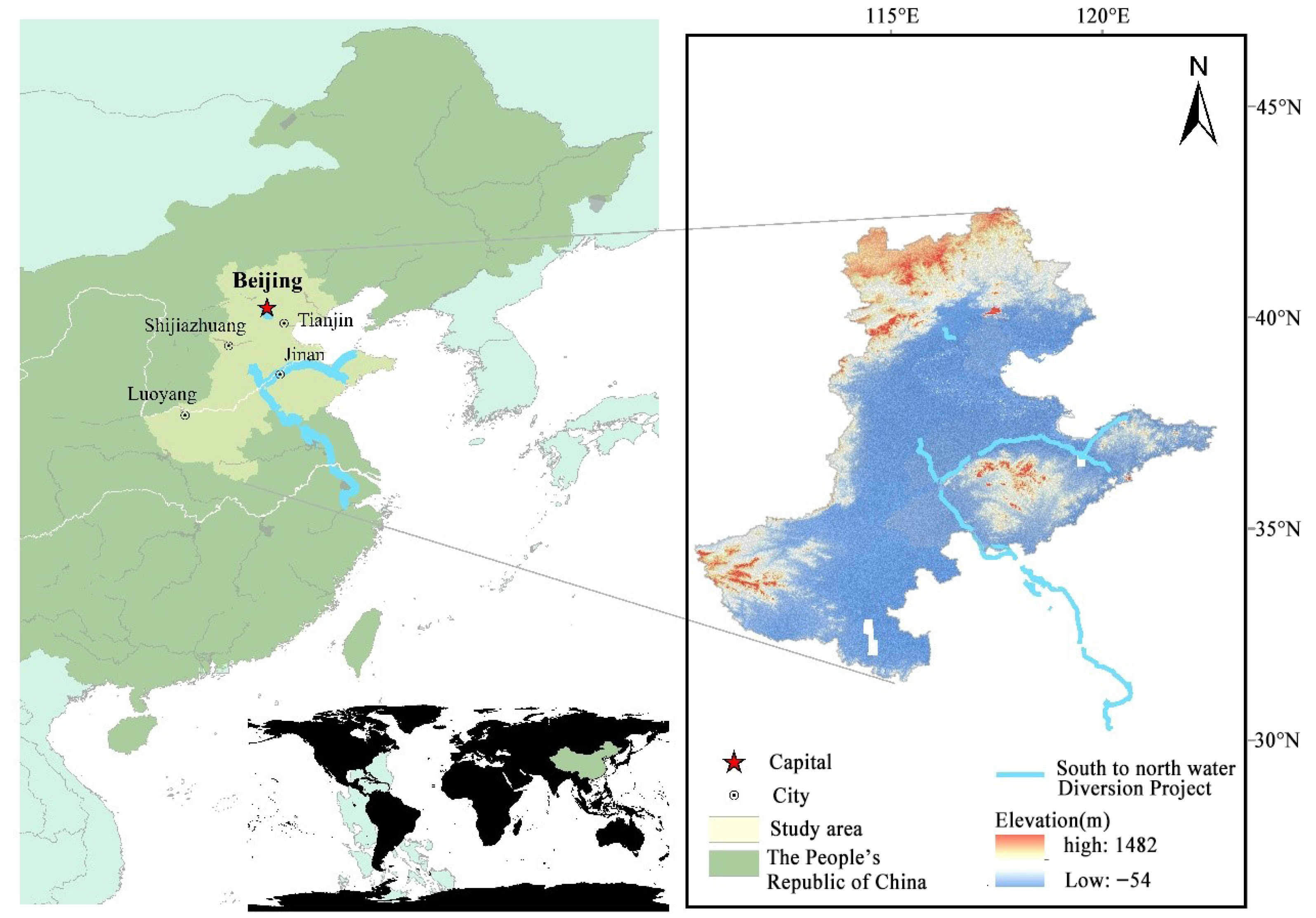
2.1. Overview of the Study Area
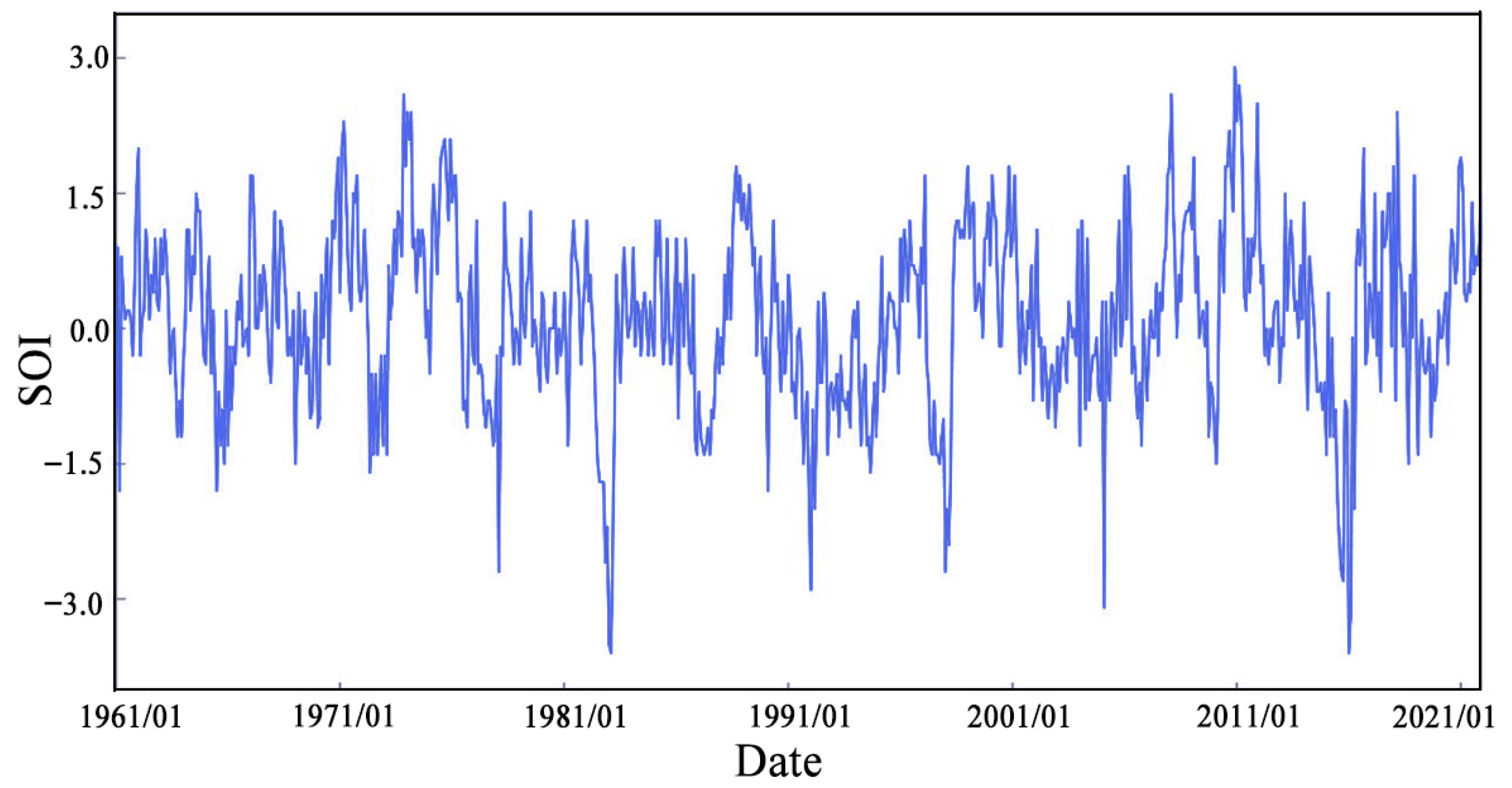
2.2. Data Sources
3. Methods
3.1. Nonparametric Kernel Density Estimation Methods
3.2. Vine Copula
3.3. Multivariate Joint Change Point Test
3.4. Total Probability Formula Based Orthogonal Experiments
4. Results
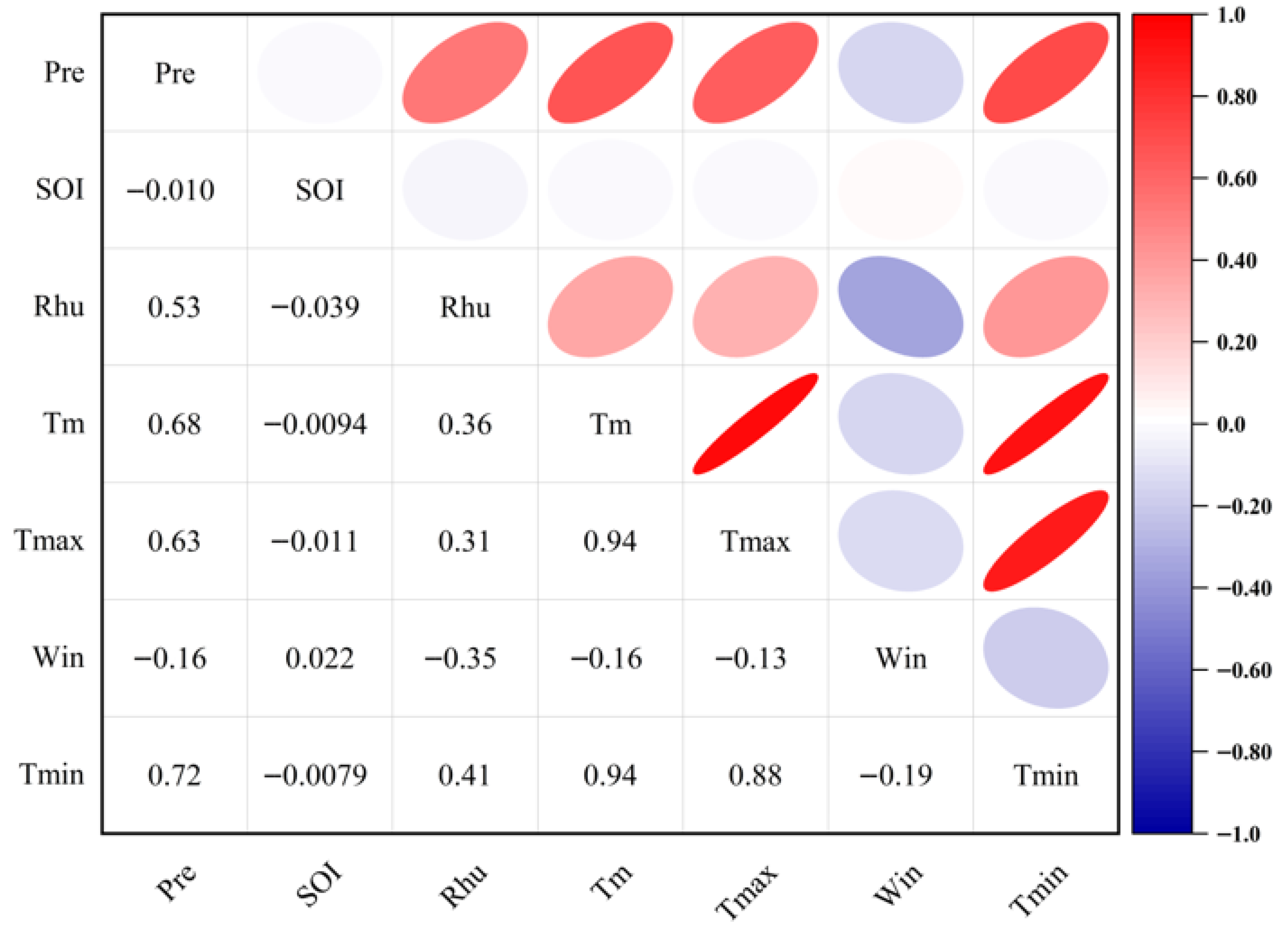
4.1. Multivariate Correlation Analysis and Marginal Distribution Fitting
- For the Gamma distribution, θ θ > 0;
- For the Lognormal distribution, .
4.2. Structure and Parameters of Vine Copula
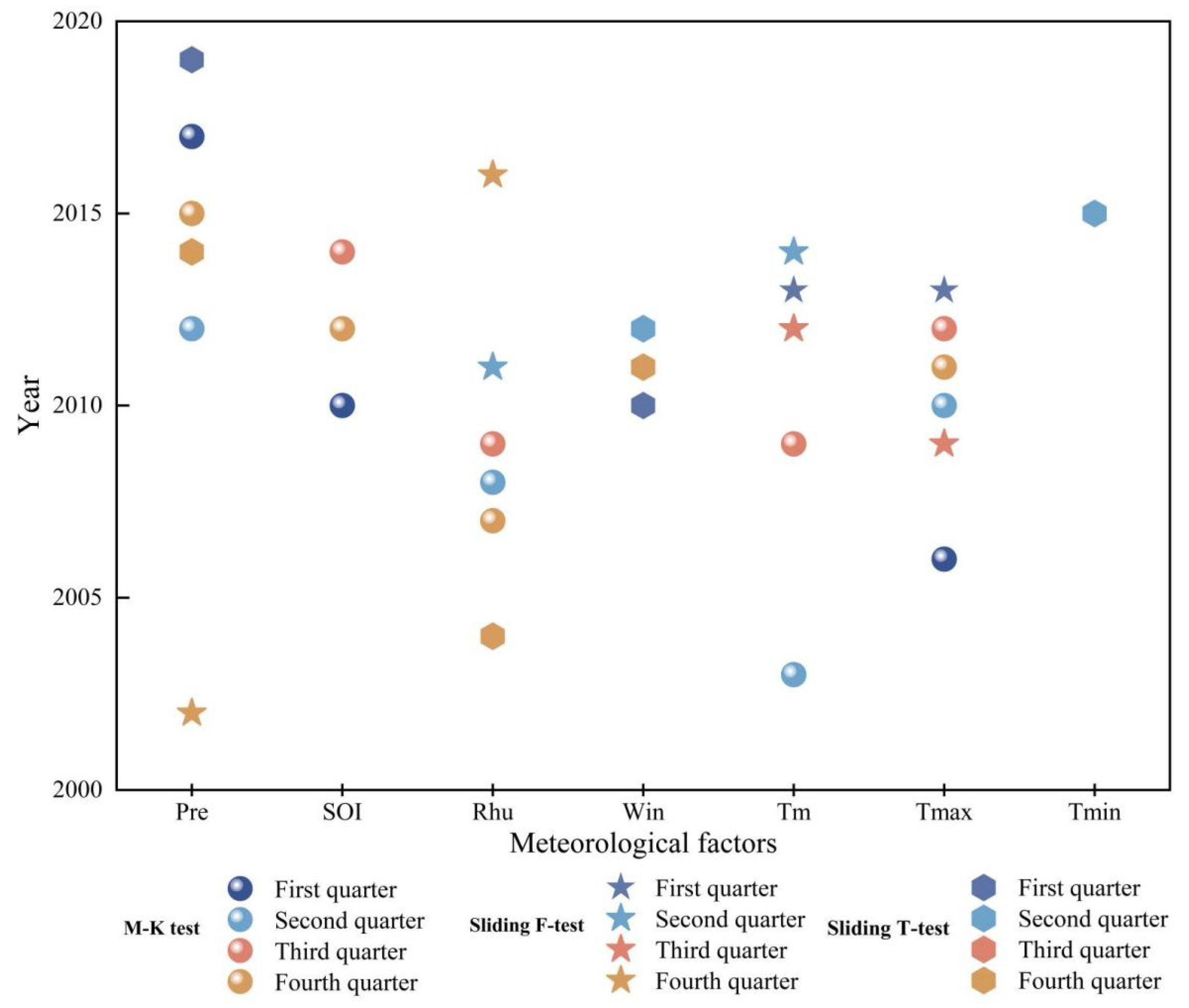
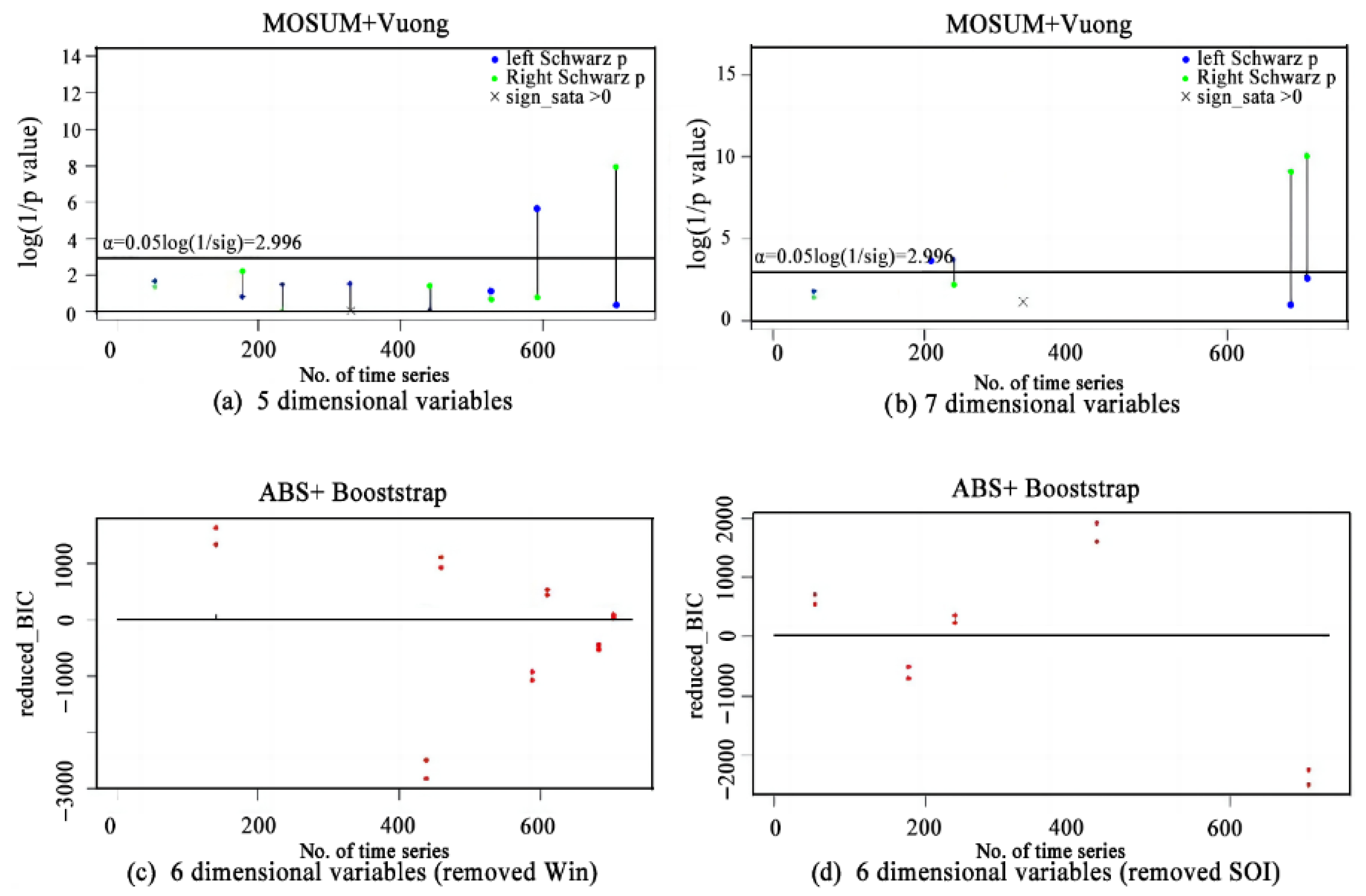
4.3. Detection of Change Point for Testing the Non-Stationarity of Multivariables
5. Discussion
6. Conclusions
- (1)
- Pre follows a gamma distribution, SOI follows a normal distribution, and Tm, Tmax, Rhu, Win, and Tmin follow the KDE distribution. The R-Vine copula provides the best fit for the multivariate joint distribution.
- (2)
- Change points in single factors often preceded change points in the joint distribution, indicating that changes in individual factors can influence alterations in the overall joint distribution.
- (3)
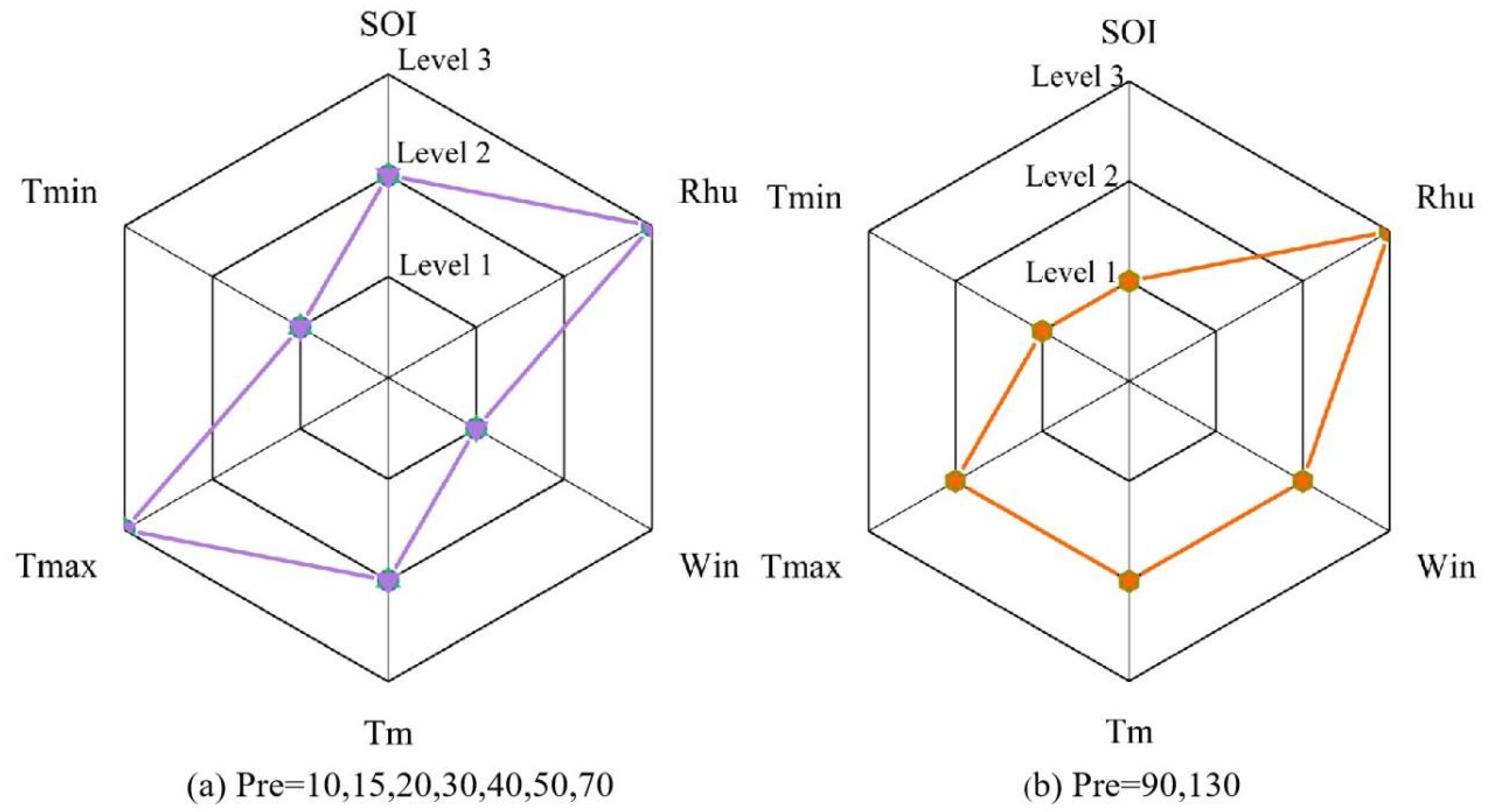
- Tmin, Win, and Tmax exhibit greater sensitivity to variations in precipitation levels in the Huang-Huai-Hai region. As precipitation increases, the influence of Rhu on the multivariate joint distribution intensifies. Higher values of Rhu and Tmax correspond to better CDF values in the multivariate joint distribution. Additionally, higher precipitation values lead to increased SOI values, which in turn result in higher CDF values for the multivariate joint distribution.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Espinosa, L.A.; Portela, M.M.; Matos, J.P. Climate change trends in a European coastal metropolitan area: Rainfall, temperature, and extreme events (1864–2021). Atmosphere 2022, 13, 1995. [Google Scholar] [CrossRef]
- Zhang, W.; Luo, M.; Gao, S. Compound hydrometeorological extremes: Drivers, mechanisms and methods. Front. Earth Sci. 2021, 9, 673495. [Google Scholar] [CrossRef]
- He, S.; Wang, H. Oscillating relationship between the East Asian winter monsoon and ENSO. J. Clim. 2013, 26, 9819–9838. [Google Scholar] [CrossRef]
- Sun, B.; Wang, H. Interannual variation of the spring and summer precipitation over the three river source region in China and the associated regimes. J. Clim. 2018, 31, 7441–7457. [Google Scholar] [CrossRef]
- Park, C.; Son, S.W.; Kim, H. Distinct features of atmospheric rivers in the early versus late East Asian summer monsoon and their impacts on monsoon rainfall. J. Geophys. Res. Atmos. 2021, 126, e2020JD033537. [Google Scholar] [CrossRef]
- Sun, Y.; Li, J. Synergistic effect of El Niño and the North Pacific Oscillation on wintertime precipitation over southeastern China and the East China Sea Kuroshio area. Clim. Dyn. 2022, 58, 1635–1649. [Google Scholar] [CrossRef]
- Zeng, Y.; Yang, L. Triggering mechanism of an extreme rainstorm process near the Tianshan Mountains in Xinjiang, an arid region in China, based on a numerical simulation. Adv. Meteorol. 2020, 2020, 8828060. [Google Scholar] [CrossRef]
- Sun, B.; Wang, H.; Zhou, B.; Li, H.; Zhu, B. A review on the interannual and interdecadal variations of water vapor transport over China during past decades. Water Resour. Prot. 2020, 31, 644–653. [Google Scholar]
- Fan, Z.X.; Thomas, A. Decadal changes of reference crop evapotranspiration attribution: Spatial and temporal variability over China 1960–2011. J. Hydrol. 2018, 560, 461–470. [Google Scholar] [CrossRef]
- Shi, Z.; Zhou, P.; Li, X.; Cheng, H.; Sha, Y.; Xie, X.; Liu, H.; Wu, J.; Liu, X. Distinct Holocene precipitation trends over arid Central Asia and linkages to westerlies and Asian monsoon. Quat. Sci. Rev. 2021, 266, 107055. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, X.; Guo, E.; Cong, L.; Wang, Y. Characteristics of the spatial and temporal distribution of drought in Northeast China, 1961–2020. Water 2024, 16, 234. [Google Scholar] [CrossRef]
- Gleason, J.A.; Kratz, N.R.; Greeley, R.D.; Fagliano, J.A. Under the weather: Legionellosis and meteorological factors. EcoHealth 2016, 13, 293–302. [Google Scholar] [CrossRef]
- Poornima, S.; Pushpalatha, M. Prediction of rainfall using intensified LSTM based recurrent neural network with weighted linear units. Atmosphere 2019, 10, 668. [Google Scholar] [CrossRef]
- Sadeghi, M.; Asanjan, A.A.; Faridzad, M.; Nguyen, P.; Hsu, K.; Sorooshian, S.; Braithwaite, D. PERSIANN-CNN: Precipitation estimation from remotely sensed information using artificial neural networks–convolutional neural networks. J. Hydrometeorol. 2019, 20, 2273–2289. [Google Scholar] [CrossRef]
- Grange, S.K.; Lewis, A.C.; Carslaw, D.C. Source apportionment advances using polar plots of bivariate correlation and regression statistics. Atmos. Environ. 2016, 145, 128–134. [Google Scholar] [CrossRef]
- Lin, W.; Song, S. Calculation method of joint probability for flood based on mixed Copula function. J. Hydraul. Eng. 2021, 40, 40–51. [Google Scholar]
- Achite, M.; Bazrafshan, O.; Wałęga, A.; Azhdari, Z.; Krakauer, N.; Caloiero, T. Meteorological and hydrological drought risk assessment using multi-dimensional copulas in the Wadi Ouahrane Basin in Algeria. Water 2022, 14, 653. [Google Scholar] [CrossRef]
- Yang, X.; Li, Y.; Huang, G.; Li, Y.; Liu, Y.; Zhou, X. Development of a multi-GCMs Bayesian copula method for assessing multivariate drought risk under climate change: A case study of the Aral Sea basin. Catena 2022, 212, 106048. [Google Scholar] [CrossRef]
- Zavareh, M.M.; Mahjouri, N.; Rahimzadegan, M.; Rahimpour, M. A drought index based on groundwater quantity and quality: Application of multivariate copula analysis. J. Clean. Prod. 2023, 417, 137959. [Google Scholar] [CrossRef]
- Razmkhah, H.; Fararouie, A.; Ravari, A.R. Multivariate flood frequency analysis using bivariate copula functions. Water Resour. Manag. 2022, 36, 729–743. [Google Scholar] [CrossRef]
- Yang, R.; Wu, S.Q.; Gao, X.P.; Zhang, C. A vine copula-based study on identification of multivariate water environmental risk under different connectivity of rivers and lakes. J. Hydraul. Eng. 2020, 51, 606–616. [Google Scholar] [CrossRef]
- Song, S.; Wu, Y.H.; Xu, B.S.; Wu, G.; Zhang, J. Pair copula technique of seismic vulnerability assessment of cable-stayed bridge system. Mech. Eng. 2021, 38, 110–123. [Google Scholar]
- Xiong, X.; Cribben, I. Beyond linear dynamic functional connectivity: A vine copula change point model. J. Comput. Graph. Stat. 2022, 32, 853–872. [Google Scholar] [CrossRef]
- Smeenk, M.L.W.J.; Agramunt, J.; Bonger, K.M. Recent developments in bioorthogonal chemistry and the orthogonality within. Curr. Opin. Chem. Biol. 2021, 60, 79–88. [Google Scholar] [CrossRef]
- Wu, J.; Gao, X. A gridded daily observation dataset over China region and comparison with the other datasets. Chin. J. Geophys. 2013, 56, 1102–1111. [Google Scholar] [CrossRef]
- Parzen, E. On estimation of a probability density function and mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
- Czado, C.; Jeske, S.; Hofmann, M. Selection strategies for regular vine copulae. J. Société Française Stat. 2013, 154, 174–191. [Google Scholar]
- Czado, C.; Nagler, T. Vine copula based modeling. Annu. Rev. Stat. Appl. 2022, 9, 453–477. [Google Scholar] [CrossRef]
- Fryzlewicz, P. Wild binary segmentation for multiple change-point detection. Ann. Stat. 2014, 42, 2243–2281. [Google Scholar] [CrossRef]
- Eichinger, B.; Kirch, C. A MOSUM procedure for the estimation of multiple random change points. Bernoulli 2018, 24, 526–564. [Google Scholar] [CrossRef]
- Vuong, Q.H. Likelihood ratio tests for model selection and non-nested hypotheses. Econometrica 1989, 57, 307–333. [Google Scholar] [CrossRef]
- Politis, D.N.; Romano, J.P. The stationary bootstrap. J. Am. Stat. Assoc. 1994, 89, 1303–1313. [Google Scholar] [CrossRef]
- Liu, L.H.; Zhang, Q.W.; Wang, Y.D.; Gu, X. Research progress on heavy metal migration model at watershed scale. China Environ. Sci. 2023, 43, 4229–4238. [Google Scholar]
- Gijbels, I.; Veraverbeke, N.; Omelka, M. Conditional copulas, association measures and their applications. Comput. Stat. Data Anal. 2011, 55, 1919–1932. [Google Scholar] [CrossRef]
- Nazeri Tahroudi, M.; Ramezani, Y.; de Michele, C.; Mirabbasi, R. Multivariate analysis of rainfall and its deficiency signatures using vine copulas. Int. J. Climatol. 2022, 42, 2005–2018. [Google Scholar] [CrossRef]
- Fasano, G.; Franceschini, A. A multidimensional version of the Kolmogorov–Smirnov test. Mon. Not. R. Astron. Soc. 1987, 225, 155–170. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE). Geosci. Model Dev. 2014, 7, 1525–1534. [Google Scholar] [CrossRef]
- Neuhaus, G. Asymptotic power properties of the Cramér–von Mises test under contiguous alternatives. J. Multivar. Anal. 1976, 6, 95–110. [Google Scholar] [CrossRef]
- Chakrabarti, A.; Ghosh, J.K. AIC, BIC and recent advances in model selection. In Philosophy of Statistics; Elsevier: Amsterdam, The Netherlands, 2011; pp. 583–605. [Google Scholar] [CrossRef]
- Hamed, K.H.; Rao, A.R. A modified Mann–Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, J.; Jiang, H.; Shi, X. Intelligent optimized wind resource assessment and wind turbines selection in Huitengxile of Inner Mongolia, China. Appl. Energy 2013, 109, 239–253. [Google Scholar] [CrossRef]
- Ling, M.; Han, H.; Hu, X.; Xia, Q.; Guo, X. Drought characteristics and causes during summer maize growth period on Huang-Huai-Hai Plain based on daily scale SPEI. Agric. Water Manag. 2023, 280, 108198. [Google Scholar] [CrossRef]
- Xie, T.; Huang, W.; Chang, S.; Zheng, F.; Chen, J.; Chen, J.; Chen, F. Moisture sources of extreme precipitation events in arid Central Asia and their relationship with atmospheric circulation. Int. J. Climatol. 2021, 41, E271–E282. [Google Scholar] [CrossRef]
- Wang, L.; Wang, J.; He, F.; Wang, Q.; Zhao, Y.; Lu, P.; Huang, Y.; Cui, H.; Deng, H. Spatial–temporal variation of extreme precipitation in the Yellow–Huai–Hai–Yangtze Basin of China. Sci. Rep. 2023, 13, 9312. [Google Scholar] [CrossRef] [PubMed]

| Factor | Connotation | Unit | Factor | Connotation | Unit |
|---|---|---|---|---|---|
| Pre | Precipitation | mm | Tmin | Minimum daily temperature | °C |
| Tm | Average temperature | °C | Win | Mean wind speed | m/s |
| Tmax | Maximum daily temperature | °C | Rhu | Relative humidity | % |
| Meteorological Factor | Gamma Distribution | Normal Distribution | Log-Normal Distribution | KDE Distribution | K-S Test Boundary Values |
|---|---|---|---|---|---|
| Pre | (0.9117, 59.1133) | (53.8931, 54.6152) | (3.3468, 1.3005) | h = 10.5299 | 0.0515 |
| 0.0457 | 0.1633 | 0.0627 | 0.0860 | ||
| SOI | / | (0.1098, 1.0091) | / | h = 0.254469 | |
| 0.0412, 0.0170 | 0.0391, 0.0182 | ||||
| Rhu | (41.9012, 1.5416) | (64.5934, 9.8813) | (4.1561, 0.1561) | h = 3.22985 | |
| 0.0429, 0.0227 | 0.0452, 0.0249 | 0.0442, 0.5835 | 0.0271, 0.0090 | ||
| Win | (19.9033, 0.1286) | (2.5586, 0.5930) | (0.9141, 0.2228) | h = 0.164217 | |
| 0.0603 | 0.0785 | 0.0505, 0.0256 | 0.0264, 0.0097 | ||
| Tm | (1.6843, 7.3195) | (11.7905, 10.2552) | / | h = 4.09806 | |
| 0.2232 | 0.1243 | 0.0505 | |||
| Tmax | (3.0909, 5.7196) | (17.6689, 10.0729) | (2.4382, 1.8716) | h = 3.88532 | |
| 0.1712 | 0.1323 | 0.3541 | 0.0508 | ||
| Tmin | / | (6.8733, 10.1775) | / | 3.98215 | |
| 0.1156 | 0.0497 |
| Variable Combinations | Vine Copula Types | Cvm | Cvm P | KS | KS P | AIC | BIC |
|---|---|---|---|---|---|---|---|
| 7-dimensional variables | R-Vine | 0.0123 | 0.9938 | 0.7327 | 0.7385 | −11,615.21 | −11,514.11 |
| D-Vine | 0.0306 | 0.9163 | 0.8591 | 0.7385 | −11,478.7 | −11,372.99 | |
| C-Vine | 0.0125 | 1.0000 | 0.7228 | 0.8372 | −11,629.8 | −11,528.69 | |
| 6-1 dimensional variables | R-Vine | 0.0423 | 0.9325 | 0.9103 | 0.9205 | −10,901.18 | −10,832.24 |
| D-Vine | 0.0352 | 0.9125 | 1.2471 | 0.5103 | −10,901.18 | −10,832.24 | |
| C-Vine | 0.0632 | 0.5675 | 1.5673 | 0.416 | −10,560.46 | −10,491.53 | |
| 6-2 dimensional variables | R-Vine | 0.0581 | 0.8438 | 1.0931 | 0.7713 | −11,593.14 | −11,519.6 |
| D-Vine | 0.0543 | 0.5438 | 1.3922 | 0.6038 | −11,609.95 | −11,541.02 | |
| C-Vine | 0.0347 | 0.9913 | 0.8738 | 0.9300 | −11,611.81 | −11,538.28 | |
| 5-dimensional variables | R-Vine | 0.0507 | 0.8875 | 1.7038 | 0.4688 | −10,879.82 | −10,833.86 |
| D-Vine | 0.1534 | 0.7725 | 1.3229 | 0.8295 | −10,879.82 | −10,833.86 | |
| C-Vine | 0.1893 | 0.5038 | 2.0186 | 0.5200 | −10,544.38 | −10,498.42 |
| SOI | Rhu (%) | Win (m/s) | Tm (°C) | Tmax (°C) | Tmin (°C) | Pre (mm) | |||
|---|---|---|---|---|---|---|---|---|---|
| Level 1 | −0.5 | 56.81 | 2.09 | 2.42 | 8.32 | −2.19 | 10 | 30 | 70 |
| CDF Values | 0.268 | 0.2531 | 0.2594 | 0.2498 | 0.2472 | 0.2571 | 0.1893 | 0.4428 | 0.7283 |
| Level 2 | 0.1 | 63.92 | 2.43 | 12.91 | 19.42 | 7.5 | 15 | 40 | 90 |
| CDF Values | 0.4925 | 0.4934 | 0.493 | 0.5025 | 0.5134 | 0.5053 | 0.2635 | 0.5355 | 0.8091 |
| Level 3 | 0.8 | 72.02 | 2.88 | 21.68 | 27.66 | 16.41 | 20 | 50 | 110 |
| CDF Values | 0.7521 | 0.7407 | 0.7441 | 0.7689 | 0.7775 | 0.7608 | 0.3296 | 0.6120 | 0.9052 |
| Pre (mm) | Range | Ranking of Impact | |||||
|---|---|---|---|---|---|---|---|
| SOI | Rhu | Win | Tm | Tmax | Tmin | ||
| 10 | 3258.84 | 3160.43 | 3301.87 | 3333.17 | 3530.88 | 3675.17 | Tmin > Tmax > Tm > Win > SOI > Rhu |
| 15 | 925.32 | 920.72 | 1094.76 | 1020.97 | 1091.47 | 1195.18 | Tmin > Win > Tmax > Tm > SOI > Rhu |
| 20 | 1672.58 | 1658.12 | 1904.06 | 1805.52 | 1882.83 | 2037.00 | Tmin > Win > Tmax > Tm > SOI > Rhu |
| 30 | 3031.47 | 2933.94 | 3375.74 | 3185.02 | 3261.16 | 3529.29 | Tmin > Win > Tmax > Tm > SOI > Rhu |
| 40 | 3766.26 | 3529.62 | 4180.83 | 3863.63 | 3945.85 | 4278.19 | Tmin > Win > Tmax > Tm > SOI > Rhu |
| 50 | 3843.26 | 3544.47 | 4232.92 | 3831.04 | 3935.80 | 4220.70 | Win > Tmin > Tmax > SOI > Tm > Rhu |
| 70 | 2284.45 | 4021.97 | 2725.68 | 2272.93 | 2448.92 | 4409.38 | Tmin > Rhu > Win > Tmax > SOI > Tm |
| 90 | 2327.19 | 2833.38 | 2349.73 | 1105.99 | 2196.39 | 3047.03 | Tmin > Rhu > Win > SOI > Tmax > Tm |
| 130 | 2373.34 | 2279.27 | 2796.66 | 512.88 | 2624.83 | 2406.64 | Win > Tmax > Tmin > SOI > Rhu > Tm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Jiang, D.; Wang, H.; Han, C.; Sang, G. A Vine Copula Framework for Non-Stationarity Detection Between Precipitation and Meteorological Factors and Possible Driving Factors. Atmosphere 2025, 16, 1262. https://doi.org/10.3390/atmos16111262
Liu Y, Jiang D, Wang H, Han C, Sang G. A Vine Copula Framework for Non-Stationarity Detection Between Precipitation and Meteorological Factors and Possible Driving Factors. Atmosphere. 2025; 16(11):1262. https://doi.org/10.3390/atmos16111262
Chicago/Turabian StyleLiu, Yang, Daijing Jiang, Haijun Wang, Cong Han, and Guoqing Sang. 2025. "A Vine Copula Framework for Non-Stationarity Detection Between Precipitation and Meteorological Factors and Possible Driving Factors" Atmosphere 16, no. 11: 1262. https://doi.org/10.3390/atmos16111262
APA StyleLiu, Y., Jiang, D., Wang, H., Han, C., & Sang, G. (2025). A Vine Copula Framework for Non-Stationarity Detection Between Precipitation and Meteorological Factors and Possible Driving Factors. Atmosphere, 16(11), 1262. https://doi.org/10.3390/atmos16111262




