Abstract
Reliable precipitation inputs are essential for hydrological modeling, yet global precipitation products often exhibit substantial discrepancies that introduce significant uncertainties into streamflow simulations and projections. In this study, we assessed the relative contribution of precipitation dataset uncertainty to discharge simulations and projections, in comparison with uncertainties from model structure, model parameters, and climate projections, in the Liujiang catchment, southwest China. Three widely used satellite-based products (CHIRPS, PERSIANN, and IMERG) and one reanalysis dataset (ERA5) were combined with three hydrological models of varying structural complexity to simulate streamflow. Using an ANOVA-based variance decomposition framework, we quantified the contributions of different uncertainty sources under both historical and future climate conditions. Results showed that precipitation input uncertainty dominates discharge simulations during the calibration period, contributing over 60% of total variance particularly at high flows, while interactions among precipitation, model structure, and parameters govern low-flow simulations. Under future climate scenarios, climate projection uncertainty overwhelmingly dominates discharge predictions with 50–80% of uncertainty contribution, yet precipitation products still contribute significantly across time scales. The compensation of precipitation biases by hydrological models can cause parameter values to deviate from their true physical meaning. This deviation may further amplify the differences in discharge projections driven by different precipitation products under future climate conditions and increase the overall uncertainty of streamflow projections. Overall, this study introduced an integrated approach to simultaneously assess precipitation uncertainty across flow regimes and future climate scenarios. These results emphasized the necessity of using ensemble approaches that incorporate multiple precipitation products in hydrological forecasting and impact studies, particularly in data-scarce regions reliant on global datasets.
1. Introduction
Precipitation, as the primary driver of the hydrological cycle, is essential for accurate hydrological modeling, flood forecasting, and water resources management [1,2,3]. However, in data-scarce or ungauged regions, obtaining reliable precipitation observations remains a big challenge. In such cases, the global precipitation datasets, particularly satellite and reanalysis precipitation products, provide an important alternative [4]. These datasets can offer consistent, near-global coverage with relatively high temporal and spatial resolution, enabling hydrological simulations even in remote, mountainous, and rural areas where ground-based observations are limited or unavailable. Nowadays, a number of global precipitation datasets have been released and available for research related to water resources [5,6].
Although global precipitation products were widely used in the streamflow simulation, they still contain substantial inherent uncertainties, and significant differences exist among different products [7,8,9]. These uncertainties mainly arise from sensor measurement errors, the frequency of sampling, retrieval algorithms and the representation of cloud physics [10,11,12]. In recent years, a number of studies have compared satellite and reanalysis-based precipitation products against gauge observations to assess their performance across different regions [13,14]. Overall, these studies demonstrate the performance of different precipitation products varies substantially across climatic and topographic regions, and no single product consistently outperforms others globally [11,15]. Furthermore, when these precipitation products are applied in the hydrological simulation, precipitation errors can be partly compensated through parameter calibration to some extent [16,17,18,19], leading to strong interactions between precipitation inputs and model structures. Such interactions further complicate the relationship between precipitation datasets and simulated streamflow, making it challenging to identify an optimal precipitation product for a specific region. Consequently, the use of global precipitation products for streamflow prediction in data-scarce or ungauged basins inevitably involves considerable uncertainty. A systematic understanding of how the uncertainty from the different global precipitation datasets contributes to streamflow simulation uncertainty is therefore essential for improving hydrological prediction and supporting effective water resources management.
Precipitation uncertainty represents a critical component of overall streamflow simulation and forecasting uncertainty, and its influence on hydrological model performance has been widely investigated. Typically, there are three primary approaches to measure or estimate precipitation: ground-based rain gauges, weather radar, and satellite-based sensors [14,20,21]. Rain gauges remain the most common source of observed precipitation data and are often used as the reference for validation. However, gauges only provide point-scale measurements, which may fail to adequately capture the spatial heterogeneity of rainfall fields, especially in regions with complex topography or sparse observation networks. As a result, numerous studies have examined the effects of gauge density and spatial distribution on streamflow simulations and highlighted their significant impacts [22,23,24], leading to efforts aimed at optimizing gauge network design to reduce representativeness errors. In contrast, radar-derived rainfall estimates are obtained remotely and indirectly, and are therefore subject to uncertainties arising from hardware limitations, signal processing, and retrieval algorithms [25,26]. Previous research has documented that radar rainfall uncertainties, including random errors, systematic biases, and spatiotemporal dependencies, can propagate through hydrological models and exert substantial impacts on simulated streamflow [21,27,28].
For satellite-based precipitation products, given the wide range of precipitation datasets now available, most studies have focused on intercomparison of different products by evaluating their ability to drive hydrological simulations and attempting to identify the most suitable product for specific catchments [10,29,30,31]. Only a limited number of studies have directly investigated the contribution of precipitation product uncertainty to overall streamflow simulation uncertainty and compared it to other sources of uncertainty. Ma et al. (2018) [32] quantified the contributions of input uncertainty from three precipitation products in rainfall–runoff simulations and demonstrated that input uncertainty dominated the total predictive uncertainty in the distributed Coupled Routing and Excess Storage (CREST) model. Whereas for another lumped model, structure uncertainty was the leading source of total uncertainty. Qi et al. (2019) [33] evaluated six high-resolution precipitation products in a small basin in northern China and quantified the contributions of precipitation product and model structure uncertainty to discharge simulations. Their results showed that precipitation input was the dominant source of uncertainty in medium-magnitude flows, whereas for small and large discharges, hydrological models contribute most of the uncertainties. Although these studies provide valuable preliminary insights into the role of precipitation product uncertainty in streamflow simulations, how the precipitation dataset interacts with other uncertainty factors, e.g., model structure and parameter, and contribute to the uncertainty of discharge simulation is still needed further explored. Moreover, these studies mainly focused on discharge simulations under historical conditions. To the best of our knowledge, very few studies have explicitly examined the contribution of global precipitation product uncertainty to discharge prediction under future climate scenarios.
In this paper, the contribution of global precipitation dataset uncertainty to ensemble discharge simulation and projection uncertainty was investigated in the Liujiang catchment, located in southwest China.Three widely used global satellite precipitation products (PERSIANN, IMERG and CHIRPS) and a reanalysis precipitation dataset ERA5 are evaluated in three different hydrological models of different structures for the streamflow simulation and projections. Following the comparison of simulation results driven by different precipitation inputs, an analysis of variance (ANOVA)-based error decomposition framework is applied to quantify the relative contributions of precipitation datasets, model structures, model parameters, climate projections, and their interactions to the total uncertainty during both the historical calibration period and future climate scenarios. This work would enhance our understanding of how precipitation uncertainty propagates through hydrological models to influence ensemble discharge predictions and clarifies the role of global precipitation products as a source of uncertainty in streamflow simulation and projection, particularly in data-scarce or ungauged catchments.
2. Description of Study Site and Datasets
The Liuzhou catchment, located in the middle–upper reaches of the Pearl River Basin, is the second largest tributary of the Xijiang River. It originates from Dushan County, Guizhou Province, with a drainage area of approximately 46,000 km2 (Figure 1). The basin exhibits an overall topographic gradient from high elevations in the northwest to lower elevations in the southeast. The upstream region, except for the river source area, is predominantly characterized by metamorphic rock–dominated gorges with elevations generally exceeding 1000 m. The middle and lower reaches are dominated by karst landforms, with a large proportion of mountainous and hilly terrain, well-developed surface karst features, and extensive underground river networks. The mean elevation ranges from 500 to 1000 m, with cultivated land concentrated in certain areas and a relatively dense population. Overall, karst terrain accounts for approximately 41.14% of the total basin area.
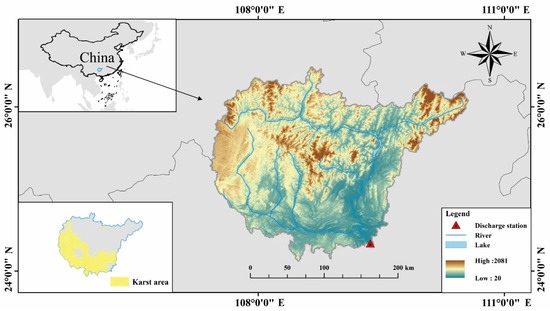
Figure 1.
Location of Liujiang catchment.
The basin is situated in a typical subtropical monsoon climate zone, with a mean annual temperature of 17–20 °C and annual precipitation ranging from 1200 to 1800 mm. Although the basin receives abundant rainfall, its temporal distribution is highly uneven, with approximately 70% of the annual precipitation occurring between April and September. To simulate the streamflow of Liujiang catchment, this study employed three widely used satellite-based precipitation datasets, CHIRPS, PERSIANN, and IMERG, along with a reanalysis dataset ERA5.
CHIRPS (Climate Hazards Group Infrared Precipitation with Stations) [34] is a quasi-global (50° S–50° N), land-only precipitation product with a high spatial resolution of 0.05°. It used a novel interpolation procedure to blend satellite-derived cold cloud duration rainfall estimates with in situ gauge observations using a two-phase smart interpolation approach. CHIRPS provides daily to monthly precipitation data ranging from 1981 to near-present with relatively low latency (~2 days for preliminary products and ~3 weeks for final products), and low bias, making it particularly useful in data-scarce regions.
PERSIANN (Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks) [35] is a long-term, near-global (60° S–60° N), 0.25° daily precipitation dataset generated using an artificial neural network applied to GridSat-B1 infrared satellite observations. A bias-adjustment procedure using GPCP monthly precipitation ensures temporal consistency and accuracy while retaining fine-scale spatial and temporal variability. This dataset maintains stable algorithm parameters throughout its record, allowing for consistent characterization of both convective and stratiform rainfall.
IMERG (Integrated Multi-satellite Retrievals for GPM) [36] is a NASA product estimating global surface precipitation rates at a high resolution of 0.1° every half-hour beginning 2000 under the GPM mission. It was generated from combining passive microwave (PMW) and infrared data of the GPM constellation satellites and calibrated by gauge analysis of the Global Precipitation Climatology Center (GPCC). The fine spatial and temporal resolution of IMERG data allows them to be accumulated to the scale of the application for increased skill, which can be used for global-scale applications as well as over regions with sparse or no reliable surface observations.
ERA5 [37] is the fifth-generation ECMWF atmospheric reanalysis, spanning 1950 to the present with a spatial resolution of 31 km, 137 vertical levels, and hourly output. It is produced using the IFS Cy41r2 forecast model with a 12 h 4D-Var assimilation system, complemented by a 10-member Ensemble of Data Assimilations to quantify uncertainty. Compared with its predecessor ERA-Interim, ERA5 incorporates higher resolution, more variables, enhanced model physics, and an expanded range of reprocessed satellite and in situ observations.
The differences among these four datasets primarily stem from their different data sources, retrieval algorithms, and processing methodologies. CHIRPS relies mainly on infrared satellite observations blended with gauge data, while IMERG combines multi-satellite microwave and infrared estimates with gauge-based bias correction. PERSIANN estimates precipitation from infrared brightness temperatures via a neural network, followed by a bias-adjustment procedure using GPCP dataset. In contrast, ERA5 derives precipitation fields from a physically consistent numerical weather prediction model assimilating multi-source observations. The four precipitation datasets exhibit distinct temporal and spatial resolutions: CHIRPS (0.05°, daily), PERSIANN (0.25°, daily), IMERG (0.1°, half-hourly), and ERA5 (0.25°, hourly). These differences in resolution, along with variations in data sources (e.g., infrared vs. microwave sensors, gauge correction methods, and model assimilation techniques), represent potential sources of uncertainty in rainfall estimates, particularly in capturing the spatial heterogeneity and intensity distribution of precipitation, especially in complex terrain. For all datasets, the daily precipitation data were downloaded and converted to daily areal averages based on the catchment boundary. These processed data then served as the precipitation input for the hydrological models. Figure 2 presents the annual precipitation of the Liujiang catchment from 2001 to 2009 as estimated by four precipitation datasets. All datasets show the similar interannual variability of precipitation, but with notable differences in magnitude. ERA5 consistently produces the highest estimates throughout the period, and the overestimation is significant from 2001 to 2006. In contrast, CHIRPS and IMERG provide very similar annual precipitation. PERSIANN generally provides the lowest annual precipitation in most years compared to other datasets. These differences highlight the systematic biases among precipitation datasets, which may have important impact on streamflow simulations and projections.
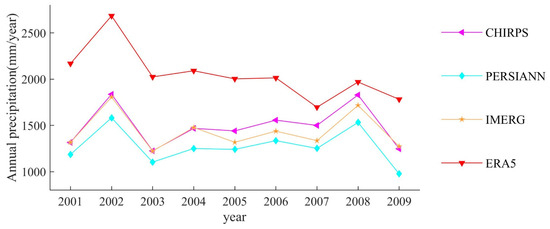
Figure 2.
Annual precipitation comparison of different precipitation products from 2001 to 2009.
3. Methodology
3.1. Three Different Hydrological Models
Currently, a wide range of hydrological models have been developed and applied for simulating catchment discharge. Given the extensive carbonate rock distribution in the study region and the complex hydrological processes characteristic of karst aquifers, two widely used karst-specific models, varKarst and KarstMod, were selected (Figure 3). In addition, the conceptual HBV model, originally developed for non-karst catchments, was also included to account for structural uncertainty in the ensemble analysis.
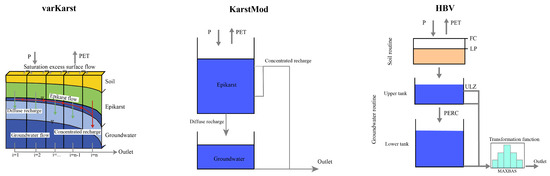
Figure 3.
Structures of three karst hydrological models.
The varKarst model [38] is a semi-distributed karst hydrological model that partitions the aquifer into three compartments: the soil layer, the epikarst, and the saturated groundwater zone. The soil layer controls evapotranspiration, infiltration, and saturation overland flow generation when its maximum storage is exceeded. Infiltration and saturation excess water recharges the epikarst linear reservoir and the epikarst then transfers water to the saturated zone through two pathways: concentrated recharge to a conduit reservoir and diffuse recharge to a fissure reservoir. The total simulated discharge is the sum of flows from both reservoirs. A key feature of varKarst is the use of a Pareto function to represent the spatial heterogeneity of soil and epikarst thickness and hydraulic properties, enabling realistic simulation of aquifer heterogeneity. This model has been widely applied to karst spring and catchment studies.
KarstMod is a flexible karst modeling platform [39], with the structure applied here originally proposed by [40]. The model consists of two reservoirs: one for the soil/epikarst zone and another for the saturated zone. The epikarst reservoir receives precipitation input and accounts for evapotranspiration losses. It has two outlets: a fast-flow outlet and a slow recharge outlet to the lower reservoir. Fast flow is modeled using a nonlinear hysteretic function to capture changing hydrological connectivity under different saturation conditions. The simulated discharge is the sum of fast flow from the epikarst reservoir and flow from the saturated reservoir.
The HBV model comprises soil and groundwater routines. The soil routine estimates actual evapotranspiration (AET) and effective recharge. Groundwater is represented by two interconnected tanks, with the upper tank producing overflow when a threshold is exceeded, generating both fast and slow flow components. The combined outflows are routed through a triangular weighting function to produce catchment discharge.
The three selected hydrological models have fundamentally different structural designs and representations of internal hydrological processes, which allows for a comprehensive assessment of model structural uncertainty. For each model, PET is estimated by a simplified Penman-Monteith equation proposed by Huang and Chen (2014) [41], which only needs daily minimum and maximum temperature. These temperature data during the simulation period are calculated from the meteorological stations within the catchment. For all models, the measured daily discharges from 1998 to 2009 were used for model calibration with the first three years of data as the warm-up period to eliminate the uncertainty from the initial conditions.
3.2. Future Climate Projections
To quantitatively assess the contribution of precipitation data uncertainty to the overall uncertainty in future discharge predictions, four sets of climate projections from the CORDEX–East Asia initiative (GERICS-MPI, GERICS-NCC, ICTP-MPI, and ICTP-NCC) were selected to represent the uncertainty from climate model projections. These datasets are generated by different institutions using distinct driving global climate models, thereby capturing the combined effects of institutional and model-related differences on future precipitation and temperature estimates. In this paper, the daily precipitation and temperature data under the RCP8.5 gas emission scenario from 2030 to 2059 were used to drive hydrological models for future discharge simulation and uncertainty decomposition.
Figure 4 presents the annual and monthly mean precipitation and temperature of the four climate projections during the future period. For annual precipitation, all products exhibit pronounced interannual variability and noticeable differences in magnitude. ICTP-MPI and ICTP-NCC generally project wetter conditions, whereas GERICS-MPI tends to give the lowest annual precipitation in multiple years. All products show a clear seasonal pattern in monthly precipitation, with peaks during the rainy season from May to August. These wet months also correspond to the period with the largest differences in monthly precipitation among different projections. In June, the largest difference between ICTP-NCC and GERICS-MPI is about 140 mm. Annual mean temperature projections indicate a consistent warming trend across all four products, but with differences in both the rate of increase and the baseline temperature values. GERICS-MPI and GERICS-NCC consistently simulate higher annual mean temperatures compared to ICTP-MPI and ICTP-NCC. For monthly mean temperature, their differences are most apparent during the dry season from November to March, with GERICS-MPI and GERICS-NCC projecting noticeably warmer winter conditions than GERICS-MPI and GERICS-NCC.
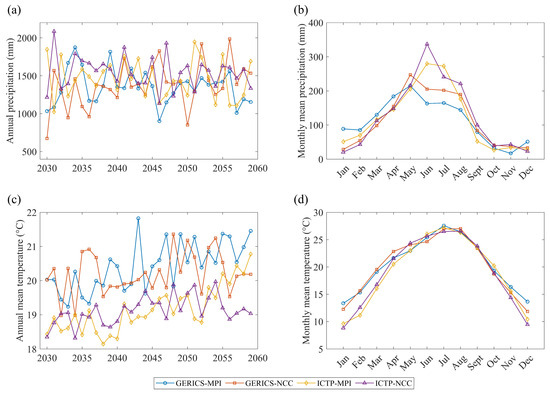
Figure 4.
Variations in annual and average monthly precipitation in the future period (2030–2059), (a) Annual precipitation, (b) Monthly mean precipitation, (c) Annual mean temperature, (d) Monthly mean temperature.
3.3. ANOVA Method
The analysis of variance (ANOVA) was applied to quantify the relative contribution of different sources of uncertainty to discharge simulation and prediction [32,42]. In this study, we separately assessed the role of precipitation uncertainty during the calibration period and in future discharge projections. For the calibration period, three major sources of uncertainty were considered: (1) precipitation input (four datasets: CHIRPS, PERSIANN, IMERG, and ERA5); (2) model structural uncertainty (three models: varKarst, KarstMod, and HBV); (3) parameter uncertainty. For the discharge prediction under future climate conditions, the extra climate prediction uncertainty was further included which contains four climate projections (GERICS-MPI, GERICS-NCC, ICTP-MPI, and ICTP-NCC).
Model performance for each combination of factors was evaluated using the Kling–Gupta Efficiency (KGE) as the objective function, which jointly accounts for correlation, variability, and bias between simulated and observed discharge. Parameter uncertainty was addressed using a Monte Carlo sampling approach, in which 100,000 parameter sets were randomly sampled from the feasible range of each model. For each model, only the top 1000 parameter sets ranked by KGE were retained to represent the parameter uncertainty and to predict the discharge in the future projection.
Based on the ANOVA theory, total error variance can be decomposed into the contributions from each factor’s main effect and their interactions. For illustration, considering three factors in the calibration period, total error variance (SST) of discharge simulations can be described as
where SSA, SSB and SSC are error contribution of precipitation uncertainty, model structure uncertainty and parameter uncertainty, respectively. is the total error contribution of their interactions.
Each term in Equation (1) can be estimated as follows.
where I, J and K represent the number of precipitation datasets, models and parameter sets, respectively. Yo,o,o is the average KGE among all the simulations. The symbol i indicates the average KGE over a particular index. Then, the uncertainty contribution (η) of each factor is calculated by the following equations.
4. Results
4.1. Calibration Results of Different Precipitation Products
The calibration performance, evaluated using the objective KGE, of the three hydrological models driven by four precipitation datasets is presented in Figure 5. For each model, the top 1000 parameter realizations were retained to represent parameter uncertainty. The results show that the choice of precipitation dataset has a significant impact on discharge simulations and the same precipitation input can yield markedly different results across different models. For varKarst, IMERG provides the highest median KGE (about 0.77), while PERSIANN and ERA5 give the relatively bad simulation result with median values of KGE below 0.65. KarstMod achieves relatively high performance with IMERG, CHIRPS, and ERA5, but its efficiency drops substantially when driven by PERSIANN. In contrast, HBV exhibits intermediate performance among three models with a relatively smaller discrepancies among rainfall products. ERA5 slightly outperforms IMERG, whereas PERSIANN yields the lowest KGE values. Overall, IMERG delivers the most consistent and reliable performance across all three models, while PERSIANN consistently shows the worst results. The performance of ERA5 varies across different models highlighting the critical role of interactions between precipitation datasets and model structures. These findings underscore the importance of both precipitation dataset selection and model structural choice in achieving good discharge simulations.
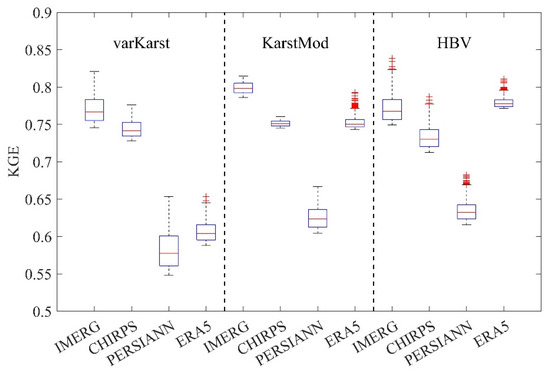
Figure 5.
Calibration results of three hydrological models driven by different precipitation datasets.
Figure 6 compares the average discharge simulations of the three hydrological models driven by four precipitation datasets at both interannual and monthly scales. At the interannual scale, IMERG, CHIRPS, and PERSIANN yield relatively consistent annual streamflow estimates that are close to the observations, whereas ERA5 produces substantially higher discharge during 2001–2006, likely due to its overestimation of annual precipitation compared with the other datasets (Figure 2). At the monthly scale, all products capture the pronounced streamflow seasonality, with peak flows from May to July and low flows during November to February. However, ERA5 systematically overestimates discharge from February to July, while IMERG, CHIRPS, and PERSIANN provide results that are more consistent with the observations. Compared with the calibration results in Figure 5, PERSIANN exhibits relatively low KGE values, indicating that its poor streamflow performance is mainly related to daily scale biases, although its long-term water balance is reasonably reproduced at annual and monthly scales. In contrast, ERA5 achieves relatively high KGE values in KarstMod and HBV (Figure 5), but it consistently overestimates discharge at both interannual and seasonal scales (Figure 6), suggesting that its high KGE is primarily attributable to relatively better reproduction of daily discharge dynamics.
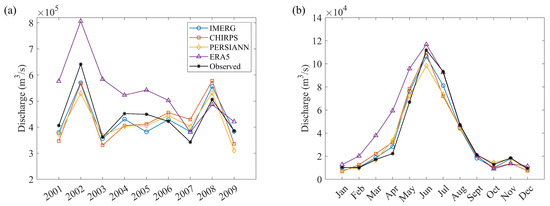
Figure 6.
Average simulation results of three different models driven by each precipitation data: (a) annual discharge; (b) monthly discharge.
4.2. Uncertainty Analysis in the Calibration Period
The AVOVA method was applied to decompose the contributions of three uncertainty sources (precipitation data, model structure and model parameter) and their interaction to the daily discharge simulations during the calibration period. Among all uncertainty factors, precipitation data provide a major contribution to the total uncertainty, particularly in the early wet period when streamflow begins to rise slowly. During this period, the uncertainty contribution from precipitation data often exceeds 60% and can even surpass 80% at certain times. The low impact of precipitation data on the discharge uncertainty mainly happens in the low discharge period. whereas for the uncertainty from the model structure, it has a higher contribution mainly in high-flow periods and its proportion can hardly exceed 50%. In most periods, the uncertainty contribution from model structure is always smaller than that from precipitation data with only exception for some small daily discharge period. In contrast, the model parameter always plays only a minor role in the discharge uncertainty, generally accounting for less than 5% of the total uncertainty, with slightly higher contributions (up to about 10%) during low-flow conditions. Compared to their individual uncertainty contributions, their interactions give a pronounced contribution to the total uncertainty during low-flow period, exceeding 60% in some low discharges. Whereas for other times, the contribution from the interaction remains below 40%. Figure 7b further illustrates how the uncertainty contribution from different factors varies with discharge. As discharge increases, the contribution of precipitation data and model structure to the total uncertainty rises, while the uncertainty contribution of interactions gradually declines. Parameter uncertainty remains consistently small across all flow ranges. At very low flows (below the 25th quantile), interactions dominate the total uncertainty, accounting for more than 50% of the variance. Precipitation data gradually become the dominant uncertainty source with the increase in discharge and its contribution consistently outweighs model structure.
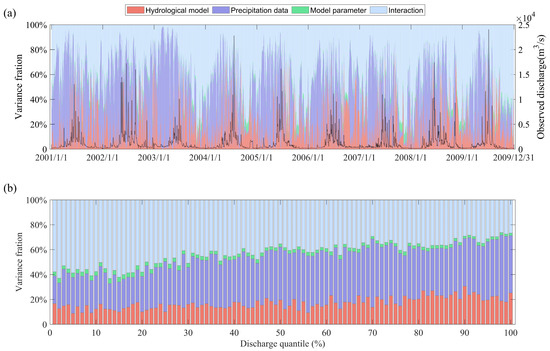
Figure 7.
Contributions of uncertainty sources to (a) daily discharges and (b) discharge quantiles based on daily observations.
Figure 8 summarizes the monthly contributions of different uncertainty sources to discharge simulations during the calibration period. The results are consistent with the previous analysis. Precipitation data contribute most uncertainties of the simulated discharge during the transition from dry to wet months (February–June), with its maximum contribution reaching about 60% in April when runoff begins to rise rapidly. As streamflow decreases toward the dry months, the contribution of precipitation data gradually declines and reaches its minimum in low-flow months. In contrast, the contribution of interactions among uncertainty sources becomes most pronounced in dry months, exceeding 50% in October, whereas their influence is lowest in wet months. The effect of model structure is more evident during high-flow months, yet its uncertainty contribution remains much lower than that of parameter data. The precipitation data and model structure only show similar contributions in October. Model parameter uncertainty remains negligible throughout all months, always below 5%, with slightly higher values during dry months than in wet months. The dominance of precipitation uncertainty during the rising limb and high-flow periods can be attributed to the high sensitivity of runoff generation to rainfall intensity and spatial distribution during these phases. In contrast, during low-flow periods, streamflow is primarily governed by slower groundwater discharge and basin storage release processes, which are more strongly influenced by the complex interactions between model structures and parameters, hence the larger contribution from interaction uncertainty.
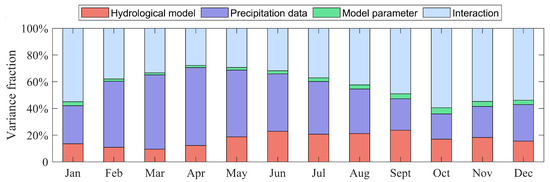
Figure 8.
Contributions of different uncertainty sources to discharge simulations at the monthly scale during the calibration period.
Overall, these results indicate that precipitation data dominate the simulation uncertainty during the discharge rising and wet-flow periods, whereas interactions are the primary source of uncertainty under low-flow conditions. Model structure exerts a secondary but less pronounced influence, while model parameters consistently contribute only marginally to the overall discharge uncertainty.
4.3. Uncertainty Analysis in the Future Period
Figure 9 presents the average prediction results of the three hydrological models calibrated with different precipitation datasets under future scenarios. In contrast to the simulation results during the calibration period (Figure 6), the ERA5-calibrated models predict substantially lower annual and monthly discharges than those calibrated with the other datasets, whereas the PERSIANN-calibrated models produce the highest values. The predictions of CHIRPS- and IMERG-calibrated models are relatively close to each other. These prediction differences from ERA5 and PERSIANN calibration models mainly arise from the compensating effect of parameter calibration with respect to precipitation biases. Specifically, among the four precipitation datasets, ERA5 generally has much higher precipitation estimations (Figure 2). To achieve satisfactory calibration performance, ERA5-driven models require parameter adjustments during the calibration to enhance evapotranspiration, thereby reducing effective infiltration to make the simulation closer to the observed streamflow. As a result, ERA5-calibrated models tend to simulate higher evapotranspiration and consequently much lower discharge under the same meteorological conditions compared to the model calibrated by other precipitation datasets. Conversely, PERSIANN underestimates precipitation relative to other precipitation datasets. To compensate, model calibration reduces evapotranspiration through parameter adjustment, which increases effective infiltration and leads to higher predicted discharge. This indicates that although model calibration can improve performance to some extent, it may also cause model parameters to deviate substantially from their true values. Such parameter deviations can in turn lead to significant biases in streamflow predictions under future climate scenarios.
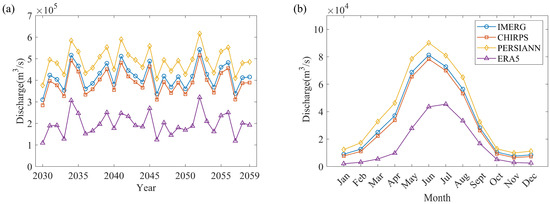
Figure 9.
Average discharge predictions of the three hydrological models calibrated with different precipitation datasets under future scenarios (2023–2059): (a) annual discharge and (b) monthly mean discharge.
Figure 10 quantifies the sources of uncertainty in future discharge projections (2023–2059) using the ANOVA method. Climate prediction uncertainty dominates for most of the period, generally accounting for more than 50% of the variance and occasionally exceeding 80%, highlighting the critical role of climate projection spread in future streamflow predictions. Interactions among different sources provide the second-largest contribution, with higher fractions at low-flow conditions and smaller contributions at high flows. The influence of precipitation datasets is much weaker than that of climate predictions, typically remaining below 20%. The uncertainty attributable to model structure is even smaller, usually less than 10%, while model parameter uncertainty remains negligible, similar to the calibration period. Figure 10 further illustrates the variation in uncertainty contributions with discharge. As discharge increases, the uncertainty contribution from the climate projection rises steadily, exceeding 80% at the highest quantiles, whereas the relative impact of interactions declines. The variance fraction associated with precipitation data initially increases with discharge but decreases once the discharge quantile exceeds 60%. Structural and parameter uncertainties remain limited across all flow conditions, especially at high flows. Overall, climate predictions govern the majority of discharge prediction uncertainty, particularly at medium to high flows, while the interaction dominates under low-flow conditions. Precipitation datasets exert a tertiary influence which is much larger than model structure. The contribution of model parameters to the total uncertainty is consistently negligible compared to other factors.
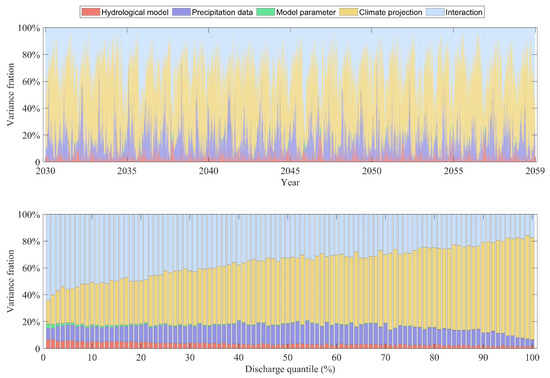
Figure 10.
Source analysis of discharge prediction uncertainty under the future scenarios.
The contributions of different uncertainty sources to the total uncertainty of monthly discharge predictions are shown in Figure 11. The results indicates that climate model uncertainty dominates throughout the year, typically accounting for 40–70% of the total variance, with particularly high contributions in the wet months (May–August). Interactions among uncertainty sources also contribute substantially, particularly in the dry months (October–January), when their maximum fraction reaches 40%. The influence of precipitation data is moderate, contributing around 10–20% throughout the year, with relatively higher values in the early wet season (April–June) which is similar to the calibration period. In contrast, the uncertainties associated with hydrological model structure and model parameters remain very small, typically less than 10% in all months.
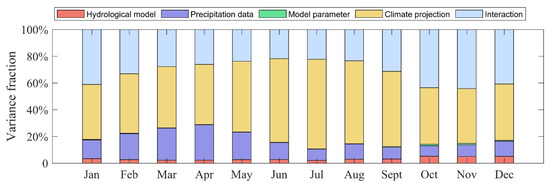
Figure 11.
Contributions of different uncertainty sources to discharge prediction at the monthly scale under the future scenarios.
5. Discussion
Although the selected precipitation datasets have been bias-corrected against ground observations, differences remain due to variations in their input sources or data assimilation techniques. In this study, the four selected precipitation datasets selected also exhibit substantial discrepancies in the Liujiang catchment. When these datasets are applied for hydrological simulations, due to the adaption of parameter calibration for precipitation biases [16,43,44], some datasets have comparable streamflow simulations. However, our results also reveal that model performance differs considerably depending on both the precipitation dataset and the model structure. For example, ERA5-driven simulations perform much better with KarstMod and HBV than with varKarst, indicating that the ability of models to compensate for precipitation biases varies with structural design, which is consistent with the findings of Oudin et al. (2006) [16]. Such differences can be attributed to the representation of hydrological processes; models with more flexible structures may redistribute water fluxes more effectively to mask certain precipitation errors. In contrast, PERSIANN consistently produces poor results across all three models, suggesting that calibration cannot effectively compensate for its errors. Stephens et al. (2022) [18] investigated the types of precipitation errors that hydrological models can address and found that models are less capable of correcting errors in rainfall timing compared to errors in magnitude or variance. Thus, the poor performance of PERSIANN is most likely associated with its inadequate representation of rainfall timing, whereas the discrepancies in ERA5 are primarily attributable to its severe overestimation of rainfall magnitude.
Despite employing hydrological models with markedly different structures and internal process representations (karst-specific and non-karst models), the results indicate that the impact of precipitation dataset to discharge simulation uncertainty still outweighs both model structure and parameter uncertainty. Our finding that precipitation input uncertainty is the dominant source of uncertainty during high-flow periods aligns with Ma et al. (2018) [32] and Qi et al. (2019) [33]. This is mainly due to the substantial differences that remain among available precipitation products. As the primary diver of hydrological models, precipitation errors can directly propagate into runoff simulations, especially the systematic error and its error in rainfall occurrence [45]. Therefore, the large difference among precipitation datasets can inevitably exert a dominant impact on discharge simulation uncertainty. More specifically, the contributions of both precipitation dataset and model structure to discharge uncertainty increase with discharge magnitude, this suggests that high-flow simulations are particularly sensitive to accurate precipitation inputs and appropriate mode structures [15,46,47,48]. In contrast, interaction among different factors dominate the uncertainty of low-flow simulations and the uncertainty contribution from precipitation data is relatively low. This is probably due to the climate characteristic of Liujiang catchment with distinct dry and wet periods. The most low-flow periods generally occur during the dry months when rainfall is scarce and much lower than potential evapotranspiration. Under such conditions, most precipitation is consumed by evapotranspiration before infiltration, leading to limited effective infiltration and rainfall-driven variability in streamflow. Therefore, the streamflow variation is mainly related to catchment storage-release process, which is mainly controlled by the model structure, model parameter and their interaction together, rather than by direct precipitation input. Since model parameters are also closely related to precipitation data, their combined influence further amplifies the role of interactions. As a result, interactions among these factors make the largest contribution to uncertainty in low-flow simulations.
When extending the analysis to future climate scenarios, the results show that climate projection uncertainty overwhelmingly dominates discharge prediction uncertainty except for the low-flow periods. This finding is consistent with previous studies [49,50,51,52] which shows the larger uncertainty source from climate projections in the discharge prediction. The large spread among climate projections can be attributed to differences in climate model structures, internal climate variability, and regional downscaling methods [53]. Nevertheless, the precipitation dataset remains the important source of uncertainty which is much larger than the model structure and parameter. Importantly, the results also indicate that the calibration-induced parameter bias can further exacerbate predictive spread across datasets. For instance, ERA5 tends to overestimate rainfall relative to observations, which forces calibration to increase evapotranspiration-related parameters to match observed streamflow. As a consequence, in future projections, ERA5-driven models simulate much higher evapotranspiration and significantly lower discharge compared to models calibrated with other precipitation datasets. This suggests that while model adaptation to precipitation errors can enhance simulation performance during calibration, the calibrated parameters may deviate substantially from their true values [16,54], potentially amplifying biases in discharge predictions under future climate conditions. These findings underscore the critical need to account for calibration-induced parameter distortions when using reanalysis or satellite rainfall products in climate impact assessments. In addition, the interaction also gives important contributions to the total discharge projection uncertainty particularly in the low-flow period because of the climate characteristic of the study catchment and the complex interplay among precipitation input, model structure, and parameterization.
This study also has several limitations that need to be further consideration. First, in this paper, we only adopted lumped hydrological models to simulate catchment discharge without explicitly accounting for the spatial heterogeneity of precipitation inputs. In reality, different precipitation datasets not only differ in mean catchment rainfall but may also exhibit substantial differences in spatial variability, which may amplify discrepancies in simulated streamflow. Therefore, the contribution of precipitation input uncertainty to discharge simulations may be partly underestimated in this study. Second, besides precipitation, PET as another key model input also carries considerable uncertainties arising from both meteorological data and estimation methods [55,56]. Moreover, previous studies have indicated a compensatory relationship between precipitation and PET in streamflow simulations [19]. Future research could further incorporate PET uncertainty into the analysis to achieve a more accurate assessment of the sources of discharge simulation uncertainty.
6. Conclusions
Global precipitation datasets, such as satellite-based products and reanalysis data, are widely used in hydrological simulations. However, different datasets often exhibit substantial discrepancies, which in turn introduce large uncertainties into discharge simulations. In this study, three widely used satellite precipitation products (CHIRPS, PERSIANN, and IMERG) and one reanalysis dataset (ERA5) were employed to simulate streamflow in the Liujiang catchment. To account for structural uncertainty, three hydrological models with distinct internal structures and process representations were applied. Using the ANOVA method, we quantified the contributions of precipitation input uncertainty to streamflow simulations and projections, and compared them with uncertainties from model structure, model parameters, and climate projections. The results revealed significant differences among the four precipitation datasets and demonstrated that streamflow simulations were strongly influenced by both precipitation input and model selection. In some cases, hydrological models were able to partially compensate for precipitation biases, allowing datasets with large discrepancies to yield similar or even improved discharge simulations. During calibration, precipitation uncertainty contributed over 60% of total variance in rising limb periods, far exceeding model structure (<20%) and parameter (<5%) effects. Under future scenarios, while climate projections dominated (50–80%), precipitation datasets consistently accounted for 15–25% of uncertainty across flow conditions, significantly larger than structural uncertainties (<10%). Overall, this study highlights the critical and persistent role of global precipitation product uncertainty in hydrological simulations and climate change projections. The methodological framework developed here provides a robust approach for quantifying uncertainty contributions across different hydrological regimes and future scenarios. Our findings have direct implications for water resources management and climate adaptation planning. They emphasize the necessity of using ensemble approaches that incorporate multiple precipitation products in hydrological forecasting and impact studies, particularly in data-scarce regions reliant on global datasets. This is crucial for improving the reliability of flood risk assessments and water security projections under climate change. Future work should further integrate uncertainty from potential evapotranspiration (PET) estimates into the overall uncertainty budget. A comprehensive assessment that concurrently considers uncertainties from both precipitation and PET inputs is crucial for a more complete and realistic quantification of total uncertainty in hydrological projections.
Author Contributions
Y.C., Y.Q. and L.L. designed the experiments; Y.Q., Y.C. and N.M. performed the experiments, analyzed the data and wrote the original draft; all authors provided helpful suggestions revised the document and figures. All authors have read and agreed to the published version of the manuscript.
Funding
This study has received funding from National Natural Science Foundation of China (No. 42572302).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
All precipitation datasets used in this study are publicly available from open-access websites. The observed discharge data for the Liujiang catchment can be provided upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest. The HeNan Third Geology and Mineral Survey Institute Co., Ltd. had no role in the design of the study; in the collection, analyses, or interpretation of data; in writing of the manuscript, or in the decision to publish results.
References
- Khatakho, R.; Talchabhadel, R.; Thapa, B.R. Evaluation of Different Precipitation Inputs on Streamflow Simulation in Himalayan River Basin. J. Hydrol. 2021, 599, 126390. [Google Scholar] [CrossRef]
- Strauch, M.; Bernhofer, C.; Koide, S.; Volk, M.; Lorz, C.; Makeschin, F. Using Precipitation Data Ensemble for Uncertainty Analysis in SWAT Streamflow Simulation. J. Hydrol. 2012, 414–415, 413–424. [Google Scholar] [CrossRef]
- Tudaji, M.; Nan, Y.; Tian, F. Assessing the Value of High-Resolution Rainfall and Streamflow Data for Hydrological Modeling: An Analysis Based on 63 Catchments in Southeast China. Hydrol. Earth Syst. Sci. 2025, 29, 1919–1937. [Google Scholar] [CrossRef]
- Kidd, C.; Huffman, G. Global Precipitation Measurement. Meteorol. Appl. 2011, 18, 334–353. [Google Scholar] [CrossRef]
- Liu, S.; Wang, J.; Wang, H. Assessing 10 Satellite Precipitation Products in Capturing the July 2021 Extreme Heavy Rain in Henan, China. J. Meteorol. Res. 2022, 36, 798–808. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.-L. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
- Chang, Y.; Qi, Y.; Wang, Z. Comprehensive Evaluation of IMERG, ERA5-Land and Their Fusion Products in the Hydrological Simulation of Three Karst Catchments in Southwest China. J. Hydrol. Reg. Stud. 2024, 52, 101671. [Google Scholar] [CrossRef]
- Shaowei, N.; Jie, W.; Juliang, J.; Xiaoyan, X.; Yuliang, Z.; Fan, S.; Linlin, Z. Comprehensive Evaluation of Satellite-Derived Precipitation Products Considering Spatial Distribution Difference of Daily Precipitation over Eastern China. J. Hydrol. Reg. Stud. 2022, 44, 101242. [Google Scholar] [CrossRef]
- Taye, M.; Mengistu, D.; Sahlu, D. Performance Evaluation of Multiple Satellite Rainfall Data Sets in Central Highlands of Abbay Basin, Ethiopia. Eur. J. Remote Sens. 2023, 56, 2233686. [Google Scholar] [CrossRef]
- Alazzy, A.A.; Lü, H.; Chen, R.; Ali, A.B.; Zhu, Y.; Su, J. Evaluation of Satellite Precipitation Products and Their Potential Influence on Hydrological Modeling over the Ganzi River Basin of the Tibetan Plateau. Adv. Meteorol. 2017, 2017, 3695285. [Google Scholar] [CrossRef]
- Dembélé, M.; Schaefli, B.; van de Giesen, N.; Mariéthoz, G. Suitability of 17 Gridded Rainfall and Temperature Datasets for Large-Scale Hydrological Modelling in West Africa. Hydrol. Earth Syst. Sci. 2020, 24, 5379–5406. [Google Scholar] [CrossRef]
- Laiti, L.; Mallucci, S.; Piccolroaz, S.; Bellin, A.; Zardi, D.; Fiori, A.; Nikulin, G.; Majone, B. Testing the Hydrological Coherence of High-Resolution Gridded Precipitation and Temperature Data Sets. Water Resour. Res. 2018, 54, 1999–2016. [Google Scholar] [CrossRef]
- Jiang, Q.; Li, W.; Fan, Z.; He, X.; Sun, W.; Chen, S.; Wen, J.; Gao, J.; Wang, J. Evaluation of the ERA5 Reanalysis Precipitation Dataset over Chinese Mainland. J. Hydrol. 2021, 595, 125660. [Google Scholar] [CrossRef]
- Zhang, Y.; Zheng, X.; Li, X.; Lyu, J.; Zhao, L. Evaluation of the GPM-IMERG V06 Final Run Products for Monthly/Annual Precipitation under the Complex Climatic and Topographic Conditions of China. J. Appl. Meteorol. Climatol. 2023, 62, 929–946. [Google Scholar] [CrossRef]
- Gebrechorkos, S.H.; Leyland, J.; Dadson, S.J.; Cohen, S.; Slater, L.; Wortmann, M.; Ashworth, P.J.; Bennett, G.L.; Boothroyd, R.; Cloke, H.; et al. Global-Scale Evaluation of Precipitation Datasets for Hydrological Modelling. Hydrol. Earth Syst. Sci. 2024, 28, 3099–3118. [Google Scholar] [CrossRef]
- Oudin, L.; Perrin, C.; Mathevet, T.; Andréassian, V.; Michel, C. Impact of Biased and Randomly Corrupted Inputs on the Efficiency and the Parameters of Watershed Models. J. Hydrol. 2006, 320, 62–83. [Google Scholar] [CrossRef]
- Oudin, L.; Andréassian, V.; Perrin, C.; Anctil, F. Locating the Sources of Low-Pass Behavior within Rainfall-Runoff Models. Water Resour. Res. 2004, 40, 3291. [Google Scholar] [CrossRef]
- Stephens, C.M.; Pham, H.T.; Marshall, L.A.; Johnson, F.M. Which Rainfall Errors Can Hydrologic Models Handle? Implications for Using Satellite-Derived Products in Sparsely Gauged Catchments. Water Resour. Res. 2022, 58, 29331. [Google Scholar] [CrossRef]
- Wang, J.; Zhuo, L.; Rico-Ramirez, M.A.; Abdelhalim, A.; Han, D. Interacting Effects of Precipitation and Potential Evapotranspiration Biases on Hydrological Modeling. Water Resour. Res. 2023, 59, 33323. [Google Scholar] [CrossRef]
- Emmanuel, I.; Payrastre, O.; Andrieu, H.; Zuber, F. A Method for Assessing the Influence of Rainfall Spatial Variability on Hydrograph Modeling. First Case Study in the Cevennes Region, Southern France. J. Hydrol. 2017, 555, 314–322. [Google Scholar] [CrossRef]
- Velásquez, N.; Krajewski, W.F.; Seo, B.-C. Assessing the Impact of Radar-Rainfall Uncertainty on Streamflow Simulation. J. Hydrometeorol. 2025, 26, 169–184. [Google Scholar] [CrossRef]
- Bárdossy, A.; Das, T. Influence of Rainfall Observation Network on Model Calibration and Application. Hydrol. Earth Syst. Sci. 2008, 12, 77–89. [Google Scholar] [CrossRef]
- Xu, H.; Xu, C.-Y.; Chen, H.; Zhang, Z.; Li, L. Assessing the Influence of Rain Gauge Density and Distribution on Hydrological Model Performance in a Humid Region of China. J. Hydrol. 2013, 505, 1–12. [Google Scholar] [CrossRef]
- Yin, Z.; Liao, W.; Lei, X.; Wang, H.; Wang, R. Comparing the Hydrological Responses of Conceptual and Process-Based Models with Varying Rain Gauge Density and Distribution. Sustainability 2018, 10, 3209. [Google Scholar] [CrossRef]
- He, X.; Refsgaard, J.C.; Sonnenborg, T.O.; Vejen, F.; Jensen, K.H. Statistical Analysis of the Impact of Radar Rainfall Uncertainties on Water Resources Modeling. Water Resour. Res. 2011, 47, W09526. [Google Scholar] [CrossRef]
- Vignal, B.; Galli, G.; Joss, J.; Germann, U. Three Methods to Determine Profiles of Reflectivity from Volumetric Radar Data to Correct Precipitation Estimates. J. Appl. Meteorol. 2000, 39, 1715–1726. [Google Scholar] [CrossRef]
- HABIB, E.; ADUVALA, A.V.; MESELHE, E.A. Analysis of Radar-Rainfall Error Characteristics and Implications for Streamflow Simulation Uncertainty. Hydrol. Sci. J. 2008, 53, 568–587. [Google Scholar] [CrossRef]
- Zhu, D.; Peng, D.Z.; Cluckie, I.D. Statistical Analysis of Error Propagation from Radar Rainfall to Hydrological Models. Hydrol. Earth Syst. Sci. 2013, 17, 1445–1453. [Google Scholar] [CrossRef]
- Fei, K.; Chen, M.; Zhou, Y.; Du, H.; Deng, S.; Gao, L. Streamflow and Surface Soil Moisture Simulation Capacity of High-Resolution Satellite-Derived Precipitation Estimate Datasets: A Case Study in Xijiang River Basin, China. J. Hydrol. Reg. Stud. 2022, 42, 101163. [Google Scholar] [CrossRef]
- Ji, H.; Peng, D.; Gu, Y.; Liang, Y.; Luo, X. Evaluation of Multiple Satellite Precipitation Products and Their Potential Utilities in the Yarlung Zangbo River Basin. Sci. Rep. 2022, 12, 13334. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, G.; Nanding, N.; Chen, W. Hydrological Evaluation of Satellite-Based Precipitation Products in Hunan Province. Remote Sens. 2022, 14, 3127. [Google Scholar] [CrossRef]
- Ma, Q.; Xiong, L.; Liu, D.; Xu, C.-Y.; Guo, S. Evaluating the Temporal Dynamics of Uncertainty Contribution from Satellite Precipitation Input in Rainfall-Runoff Modeling Using the Variance Decomposition Method. Remote Sens. 2018, 10, 1876. [Google Scholar] [CrossRef]
- Qi, W.; Zhang, C.; Fu, G.; Sweetapple, C.; Zhou, H. Evaluation of Global Fine-Resolution Precipitation Products and Their Uncertainty Quantification in Ensemble Discharge Simulations. Hydrol. Earth Syst. Sci. 2016, 20, 903–920. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The Climate Hazards Infrared Precipitation with Stations—A New Environmental Record for Monitoring Extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Ashouri, H.; Hsu, K.-L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily Precipitation Climate Data Record from Multisatellite Observations for Hydrological and Climate Studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.-L.; Joyce, R.J.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Stocker, E.F.; Tan, J. Integrated Multi-Satellite Retrievals for the Global Precipitation Measurement (GPM) Mission (IMERG). In Satellite Precipitation Measurement: Volume 1; Springer: New York, NY, USA, 2020; pp. 343–353. [Google Scholar]
- Soci, C.; Hersbach, H.; Simmons, A.; Poli, P.; Bell, B.; Berrisford, P.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Radu, R.; et al. The ERA5 Global Reanalysis from 1940 to 2022. Q. J. R. Meteorol. Soc. 2024, 150, 4014–4048. [Google Scholar] [CrossRef]
- Hartmann, A.; Barberá, J.A.; Andreo, B. On the Value of Water Quality Data and Informative Flow States in Karst Modelling. Hydrol. Earth Syst. Sci. 2017, 21, 5971–5985. [Google Scholar] [CrossRef]
- Mazzilli, N.; Guinot, V.; Jourde, H.; Lecoq, N.; Labat, D.; Arfib, B.; Baudement, C.; Danquigny, C.; Dal Soglio, L.; Bertin, D. KarstMod: A Modelling Platform for Rainfall—Discharge Analysis and Modelling Dedicated to Karst Systems. Environ. Model. Softw. 2019, 122, 103927. [Google Scholar] [CrossRef]
- Tritz, S.; Guinot, V.; Jourde, H. Modelling the Behaviour of a Karst System Catchment Using Non-Linear Hysteretic Conceptual Model. J. Hydrol. 2011, 397, 250–262. [Google Scholar] [CrossRef]
- Huang, Q.; Chen, Z. Applicability of Evapotranspiration Equations for the Pearl River Basin. Trop. Geogr. 2014, 34, 737–745. (In Chinese) [Google Scholar]
- Bosshard, T.; Carambia, M.; Goergen, K.; Kotlarski, S.; Krahe, P.; Zappa, M.; Schär, C. Quantifying Uncertainty Sources in an Ensemble of Hydrological Climate-Impact Projections. Water Resour. Res. 2013, 49, 1523–1536. [Google Scholar] [CrossRef]
- Wang, J.; Zhuo, L.; Han, D.; Liu, Y.; Rico-Ramirez, M.A. Hydrological Model Adaptability to Rainfall Inputs of Varied Quality. Water Resour. Res. 2023, 59, 32484. [Google Scholar] [CrossRef]
- Zeng, Q.; Chen, H.; Xu, C.-Y.; Jie, M.-X.; Chen, J.; Guo, S.-L.; Liu, J. The Effect of Rain Gauge Density and Distribution on Runoff Simulation Using a Lumped Hydrological Modelling Approach. J. Hydrol. 2018, 563, 106–122. [Google Scholar] [CrossRef]
- Miao, C.; Gou, J.; Hu, J.; Duan, Q. Impacts of Different Satellite-Based Precipitation Signature Errors on Hydrological Modeling Performance Across China. Earth’s Future 2024, 12, e2024EF004954. [Google Scholar] [CrossRef]
- Bárdossy, A.; Anwar, F. Why Do Our Rainfall–Runoff Models Keep Underestimating the Peak Flows? Hydrol. Earth Syst. Sci. 2023, 27, 1987–2000. [Google Scholar] [CrossRef]
- Dayal, D.; Pandey, A.; Gupta, P.K.; Kalura, P. Investigating the Utility of Satellite-Based Precipitation Products for Simulating Extreme Discharge Events: An Exhaustive Model-Driven Approach for a Tropical River Basin in India. Environ. Monit. Assess. 2024, 196, 608. [Google Scholar] [CrossRef] [PubMed]
- van Kempen, G.; van der Wiel, K.; Melsen, L.A. The Impact of Hydrological Model Structure on the Simulation of Extreme Runoff Events. Nat. Hazards Earth Syst. Sci. 2021, 21, 961–976. [Google Scholar] [CrossRef]
- Addor, N.; Rössler, O.; Köplin, N.; Huss, M.; Weingartner, R.; Seibert, J. Robust Changes and Sources of Uncertainty in the Projected Hydrological Regimes of Swiss Catchments. Water Resour. Res. 2014, 50, 7541–7562. [Google Scholar] [CrossRef]
- Her, Y.; Yoo, S.-H.; Cho, J.; Hwang, S.; Jeong, J.; Seong, C. Uncertainty in Hydrological Analysis of Climate Change: Multi-Parameter vs. Multi-GCM Ensemble Predictions. Sci. Rep. 2019, 9, 4974. [Google Scholar] [CrossRef]
- Kingston, D.G.; Thompson, J.R.; Kite, G. Uncertainty in Climate Change Projections of Discharge for the Mekong River Basin. Hydrol. Earth Syst. Sci. 2011, 15, 1459–1471. [Google Scholar] [CrossRef]
- Zhang, L.; Yuan, F.; Wang, B.; Ren, L.; Zhao, C.; Shi, J.; Liu, Y.; Jiang, S.; Yang, X.; Chen, T.; et al. Quantifying Uncertainty Sources in Extreme Flow Projections for Three Watersheds with Different Climate Features in China. Atmospheric Res. 2021, 249, 105331. [Google Scholar] [CrossRef]
- Evin, G.; Hingray, B.; Thirel, G.; Ducharne, A.; Strohmenger, L.; Corre, L.; Tramblay, Y.; Vidal, J.-P.; Bonneau, J.; Colleoni, F.; et al. Uncertainty Sources in a Large Ensemble of Hydrological Projections: Regional Climate Models and Internal Variability Matter. EGUsphere 2025, 2025, 1–43. [Google Scholar] [CrossRef]
- Kabir, T.; Pokhrel, Y.; Felfelani, F. On the Precipitation-Induced Uncertainties in Process-Based Hydrological Modeling in the Mekong River Basin. Water Resour. Res. 2022, 58, e2021WR030828. [Google Scholar] [CrossRef]
- Akhter, M.; Ahanger, M.A. Uncertainty in Evapotranspiration Inputs Impacts Hydrological Modeling. Water Sci. Technol. 2024, 91, 235–251. [Google Scholar] [CrossRef]
- Jayathilake, D.I.; Smith, T. Assessing the Impact of PET Estimation Methods on Hydrologic Model Performance. Hydrol. Res. 2020, 52, 373–388. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).