A Novel Classification Framework for VLF/LF Lightning-Radiation Electric-Field Waveforms
Abstract
1. Introduction
- To extract effective VLF/LF lightning waveform information, an improved Kalman filter (IKF) is proposed to eliminate high-frequency interferences. In IKF, the Kalman gain can be adjusted dynamically based on the maximum entropy criterion, contributing to an optimal cutoff frequency.
- To enhance feature representativeness and recognition capabilities, an attention-based multi-fusion convolutional neural network (AMCNN) is proposed to identify different VLF/LF lightning waveforms. Moreover, an optimized feature fusion structure based on attention module is developed to improve classification accuracy and speed.
- Integrated with the IKF and AMCNN, a novel detection framework called IKF-AMCNN is further presented for VLF/LF lightning waveform classification. Extensive experiments are carried out and the comparative result validates the effectiveness of the IKF-AMCNN.
2. Improved Kalman Filter
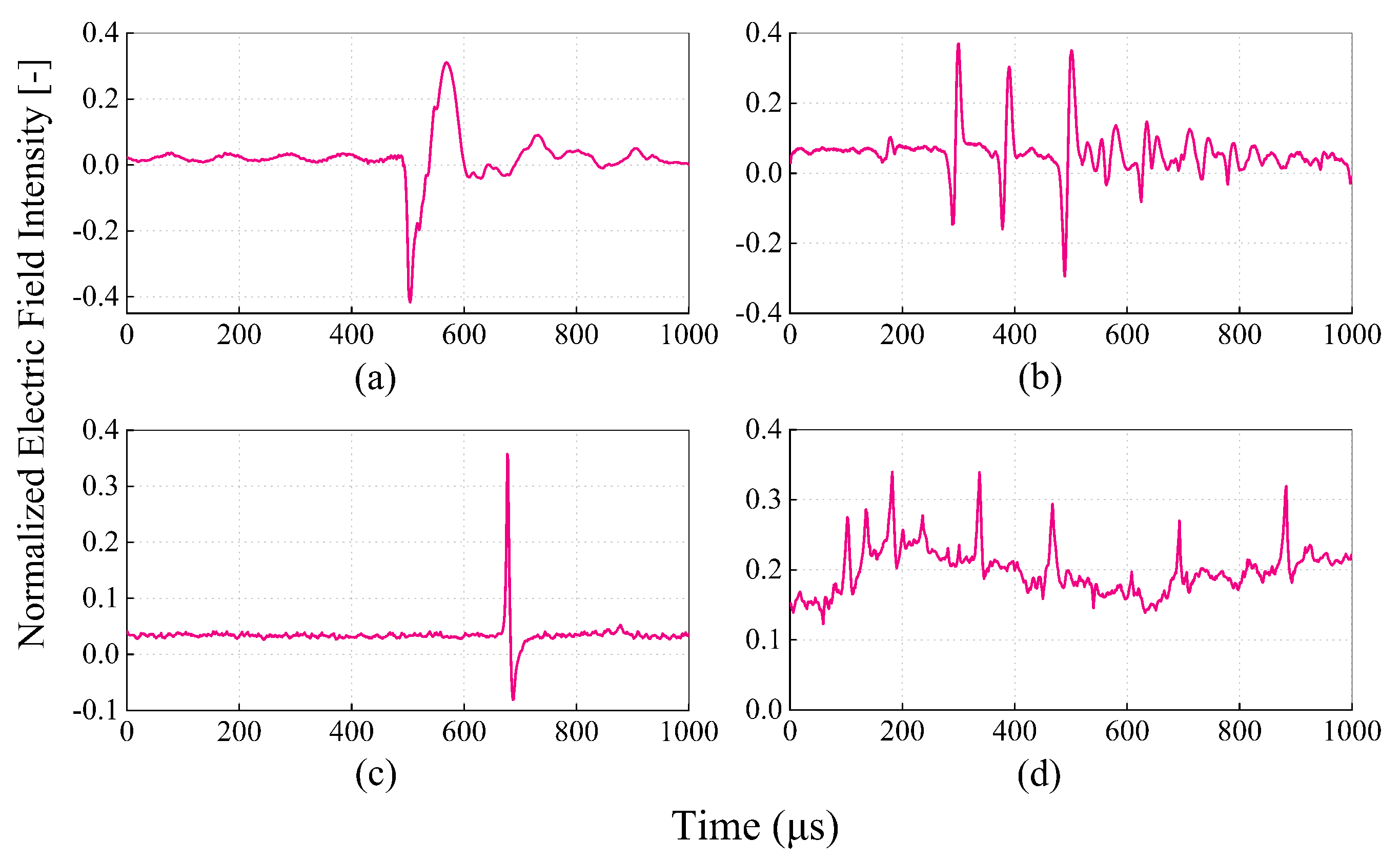
2.1. Lightning Waveform Dataset
2.2. Principle of KF
2.3. Proposed IKF
3. Attention-Based Multi-Fusion Convolutional Neural Network
3.1. Principle of CNN
3.2. Proposed AMCNN
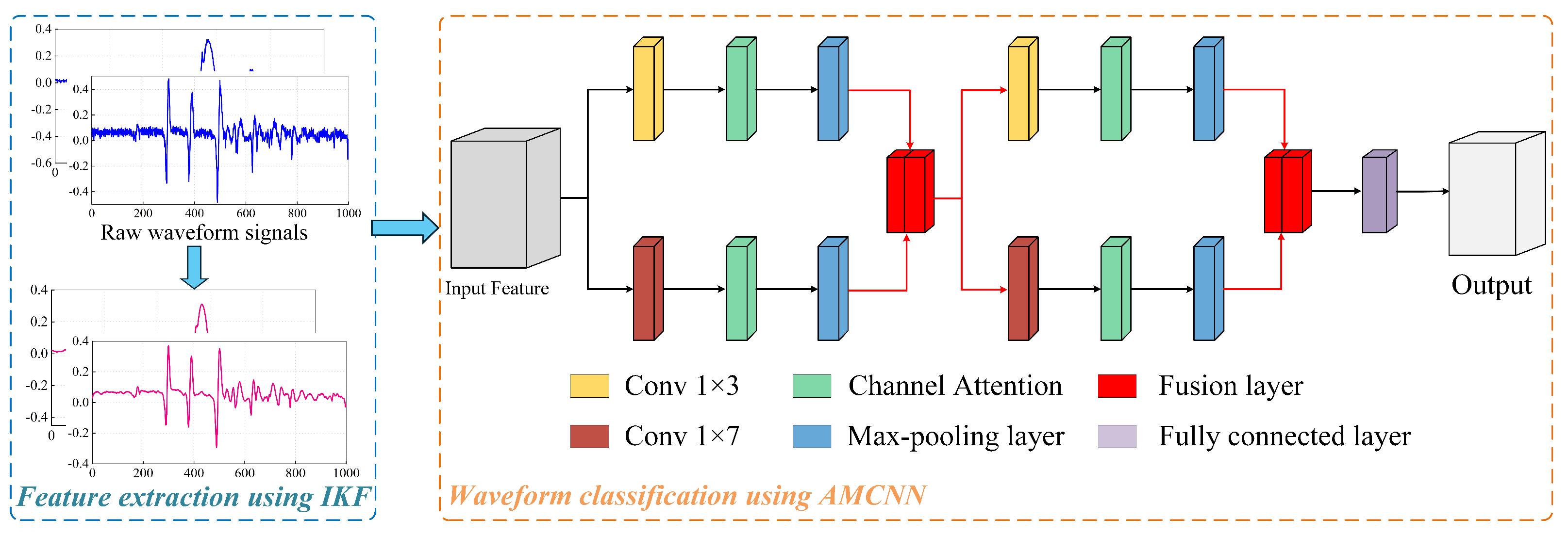
4. Waveform Classification Framework Based on IKF and AMCNN
- Feature extraction using IKF: Eliminate high-frequency interferences by using the IKF method, where the Kalman gain can be adjusted dynamically based on the maximum entropy criterion, enhancing the robustness of feature extraction. Next, effective waveform features are obtained and then inputted into the classifier after normalization processing.
- Waveform classification using AMCNN: Establish an AMCNN classification model where the convolution and convolution are used to extract the fine-grained local details and broad global patterns by integrating the channel attention module, respectively. Then, different distinct information is combined at the fusion layer, enhancing the effectiveness of the waveform information. Following two fusion layers, the AMCNN employs five fully connected layers to produce the final waveform classification output.
5. Experimental Analysis
5.1. Training and Verification
5.2. Classification Performance Under Different Training Set Proportions
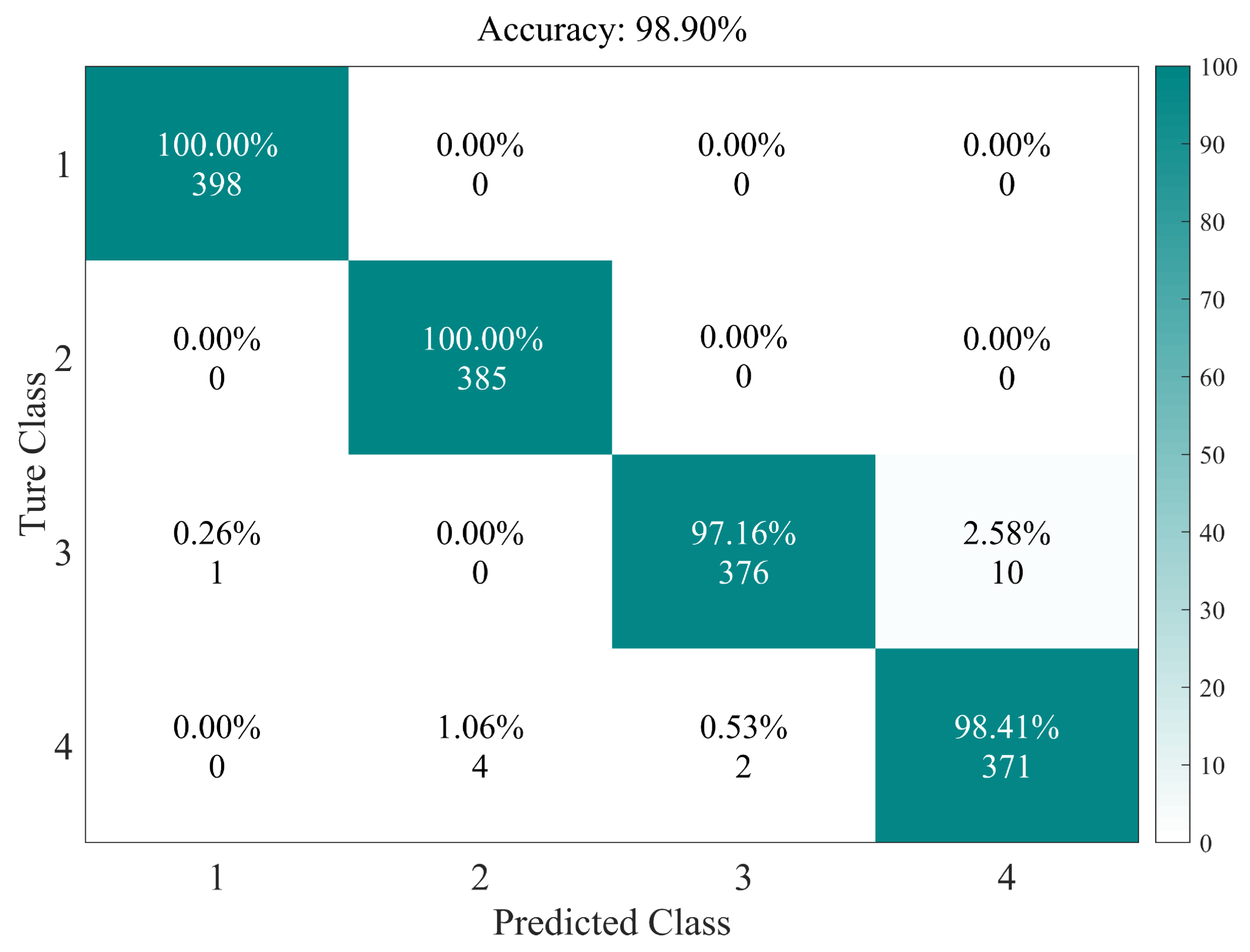
5.3. Verification for IKF-AMCNN
5.4. Comparison with Other Methods
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Karnas, G.; Maslowski, G.; Rakov, V. Frequency spectra features of electric field waveforms produced by close and middle-range compact intracloud discharges and their discrimination from cloud-to-ground lightning. Electr. Power Syst. Res. 2025, 243, 111498. [Google Scholar] [CrossRef]
- Smith, W.R.; Lay, E.H.; Fitch, K.E.; Emmons, D.J. Analyzing LF/VLF lightning waveforms to estimate D-region electron density profiles. Adv. Space Res. 2025, 76, 3850–3866. [Google Scholar] [CrossRef]
- Cao, J.; Du, Y.; Ding, Y.; Qi, R.; Chen, M.; Li, Z.; Zhao, X.; Andreotti, A. Lightning Protection with a Differentiated Configuration of Arresters in a Distribution Network. IEEE Trans. Power Deliv. 2023, 38, 409–419. [Google Scholar] [CrossRef]
- Deng, Y.; Li, M.; Wang, Y.; He, X.; Wen, X.; Lan, L.; Ma, Y.; Pan, H. Relationship Between Lightning Activity and Terrain in High-Altitude Mountainous Areas. IEEE Trans. Power Deliv. 2023, 38, 3561–3570. [Google Scholar] [CrossRef]
- Wang, K.; Zhong, F.; Song, J.; Yu, Z.; Tang, L.; Tang, X.; Yao, Q. Power System Frequency Estimation with Zero Response Time Under Abrupt Transients. IEEE Trans. Circuits Syst. I Regul. Pap. 2025, 72, 467–480. [Google Scholar] [CrossRef]
- Mohammad Sabri, M.H.; Ahmad, M.R.; Mohd Nor Azami, M.A.; Abidin Abd Aziz, M.Z.; Takayanagi, Y.; Morimoto, T.; Shamsul Baharin, S.A. Electromagnetic field radiation between 1 and 10 GHz emitted by lightning flashes from tropical thunderstorms. Measurement 2025, 256, 118418. [Google Scholar] [CrossRef]
- Song, J.; Zhang, J.; Kuang, H.; Wen, H. Dynamic Synchrophasor Estimation Based on Weighted Real-Valued Sinc Interpolation Method. IEEE Sens. J. 2023, 23, 588–598. [Google Scholar] [CrossRef]
- Rakov, V.A.; Uman, M.A. Lightning: Physics and Effects; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Nag, A.; Rakov, V.A. Pulse trains that are characteristic of preliminary breakdown in cloud-to-ground lightning but are not followed by return stroke pulses. J. Geophys. Res. Atmos. 2008, 113, D01102. [Google Scholar] [CrossRef]
- Leal, A.F.; Rakov, V.A.; Rocha, B.R. Compact intracloud discharges: New classification of field waveforms and identification by lightning locating systems. Electr. Power Syst. Res. 2019, 173, 251–262. [Google Scholar] [CrossRef]
- Cajas Ordóñez, S.A.; Samanta, J.; Suárez-Cetrulo, A.L.; Carbajo, R.S. Intelligent Edge Computing and Machine Learning: A Survey of Optimization and Applications. Future Internet 2025, 17, 417. [Google Scholar] [CrossRef]
- Schauer, J.; Goodarzi, P.; Morsch, J.; Schütze, A. A Performance Study of Deep Neural Network Representations of Interpretable ML on Edge Devices with AI Accelerators. Sensors 2025, 25, 5681. [Google Scholar] [CrossRef]
- Zhu, Y.; Bitzer, P.; Rakov, V.; Ding, Z. A Machine-Learning Approach to Classify Cloud-to-Ground and Intracloud Lightning. Geophys. Res. Lett. 2021, 48, e2020GL091148. [Google Scholar] [CrossRef]
- Zhu, Y.; Stock, M.; Lapierre, J.; DiGangi, E. Upgrades of the Earth Networks Total Lightning Network in 2021. Remote Sens. 2022, 14, 2209. [Google Scholar] [CrossRef]
- Ma, J.; Liu, J.; Qiu, W.; Tang, Q.; Wang, Q.; Li, C.; Peretto, L.; Teng, Z. An Intelligent Classification Framework for Complex PQDs Using Optimized KS-Transform and Multiple Fusion CNN. IEEE Trans. Ind. Inform. 2024, 20, 1776–1785. [Google Scholar] [CrossRef]
- Salles, R.S.; de Oliveira, R.A.; Rönnberg, S.K.; Mariscotti, A. Analytics of Waveform Distortion Variations in Railway Pantograph Measurements by Deep Learning. IEEE Trans. Instrum. Meas. 2022, 71, 2516211. [Google Scholar] [CrossRef]
- Peng, C.; Liu, F.; Zhu, B.; Wang, W. A Convolutional Neural Network for Classification of Lightning LF/VLF Waveform. In Proceedings of the 2019 11th Asia-Pacific International Conference on Lightning (APL), Hong Kong, China, 12–14 June 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Xiao, L.; Chen, W.; Wang, Y.; Bian, K.; Fu, Z.; Xiang, N.; He, H.; Cheng, Y. Toward an Interpretable CNN Model for the Classification of Lightning-Produced VLF/LF Signals. J. Geophys. Res. Atmos. 2023, 128, e2023JD039517. [Google Scholar] [CrossRef]
- Wang, J.; Huang, Q.; Ma, Q.; Chang, S.; He, J.; Wang, H.; Zhou, X.; Xiao, F.; Gao, C. Classification of VLF/LF Lightning Signals Using Sensors and Deep Learning Methods. Sensors 2020, 20, 1030. [Google Scholar] [CrossRef] [PubMed]
- Gao, C.; Wang, J.; Zhou, X.; Xiao, F.; Ma, Q. Classification of Lightning Electric Field Waveform Based on Deep Residual One-Dimensional Convolutional Network. In Proceedings of the Advances in Natural Computation, Fuzzy Systems and Knowledge Discovery; Meng, H., Lei, T., Li, M., Li, K., Xiong, N., Wang, L., Eds.; Springer: Cham, Switzerland, 2021; pp. 1648–1659. [Google Scholar]
- Fan, X.; Kong, J.; Wang, H.; Huang, K.; Zhao, T.; Li, L. Multi-Scale Electromechanical Impedance-Based Bolt Loosening Identification Using Attention-Enhanced Parallel CNN. Appl. Sci. 2025, 15, 9715. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the European Conference on Computer Vision (ECCV); Springer: Cham, Switzerland, 2018; Volume 11211, pp. 3–19. [Google Scholar] [CrossRef]
- Hou, Y.; Li, T.; Wang, J.; Ma, J.; Chen, Z. A lightweight transformer based on feature fusion and global–local parallel stacked self-activation unit for bearing fault diagnosis. Measurement 2024, 236, 115068. [Google Scholar] [CrossRef]
- Leal, A.F.R.; Rakov, V.A. Characterization of Lightning Electric Field Waveforms Using a Large Database: 1. Methodology. IEEE Trans. Electromagn. Compat. 2021, 63, 1155–1162. [Google Scholar] [CrossRef]
- Zhang, J.; Song, J.; Li, C.; Xu, X.; Wen, H. Novel Frequency Estimator for Distorted Power System Signals Using Two-Point Iterative Windowed DFT. IEEE Trans. Ind. Electron. 2024, 71, 13372–13383. [Google Scholar] [CrossRef]
- Wang, K.; Wang, J.; Song, J.; Tang, L.; Shan, X.; Wen, H. Accurate DFT Method for Power System Frequency Estimation Considering Multi-Component Interference. IEEE Trans. Instrum. Meas. 2023, 72, 6505611. [Google Scholar] [CrossRef]
- Riaz, W.; Ullah, A.; Ji, J.C. Multi-Scale Attention Networks with Feature Refinement for Medical Item Classification in Intelligent Healthcare Systems. Sensors 2025, 25, 5305. [Google Scholar] [CrossRef]
- Wang, Y.; Gu, S.; Fang, Y.; Xu, Y.; Chen, Y.; Li, P. Compact electric field change meter and its application in lightning detection and fault analysis for power grids. In Proceedings of the 2020 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Beijing, China, 6–10 September 2020; pp. 1–4. [Google Scholar] [CrossRef]




| Layer Type | Branch | Kernel Size | Output Channels | Stride | Activation |
|---|---|---|---|---|---|
| Input Feature | / | / | 64 | / | / |
| Conv 1 × 3 | Branch 1 | 1 × 3 | 64 | 1 | PReLU |
| Channel Attention | Branch 1 | / | 64 | / | Sigmoid |
| Max-Pooling | Branch 1 | 1 × 2 | 32 | 2 | / |
| Conv 1 × 7 | Branch 2 | 1 × 7 | 64 | 1 | PReLU |
| Channel Attention | Branch 2 | / | 64 | / | Sigmoid |
| Max-Pooling | Branch 2 | 1 × 2 | 32 | 2 | / |
| Fusion 1 | / | / | 64 | / | / |
| Conv 1 × 3 Second Block | Branch 1 | 1 × 3 | 64 | 1 | PReLU |
| Channel Attention | Branch 1 | / | 64 | / | Sigmoid |
| Max-Pooling | Branch 1 | 1 × 2 | 32 | 2 | / |
| Conv 1 × 7 Second Block | Branch 2 | 1 × 7 | 64 | 1 | PReLU |
| Channel Attention | Branch 2 | / | 64 | / | Sigmoid |
| Max-Pooling | Branch 2 | 1 × 2 | 32 | 2 | / |
| Fusion 2 | / | / | 64 | / | / |
| Type | Accuracy (%) | Average (%) |
|---|---|---|
| RS | 100 | 98.9 |
| PB | 100 | |
| NBE | 97.2 | |
| IC | 98.4 |
| Method | Accuracy | |||
|---|---|---|---|---|
| RS | PB | NBE | IC | |
| CNN | 93.6% ± 0.8% | 93.0% ± 0.6% | 91.7% ± 0.8% | 93.5% ± 0.8% |
| KF-CNN | 94.2% ± 0.6% | 93.5% ± 0.5% | 92.5% ± 0.8% | 93.9% ± 0.7% |
| IKF-CNN | 95.4% ± 0.4% | 95.1% ± 0.6% | 94.3% ± 0.5% | 94.7% ± 0.4% |
| KF-AMCNN | 98.5% ± 0.3% | 97.1% ± 0.4% | 96.1% ± 0.5% | 96.3% ± 0.3% |
| IKF-AMCNN | 100% ± 0.0% | 100% ± 0.0% | 97.2% ± 0.2% | 98.4% ± 0.3% |
| Method | Accuracy | |||
|---|---|---|---|---|
| RS | PB | NBE | IC | |
| SVM | 90.2% ± 0.9% | 89.6% ± 1.1% | 91.2% ± 1.2% | 87.5% ± 1.4% |
| RF | 88.2% ± 1.3% | 85.7% ± 1.5% | 89.7% ± 1.1% | 86.5% ± 1.5% |
| 1D ResNet | 97.0% ± 0.5% | 96.1% ± 0.6% | 94.6% ± 0.8% | 95.8% ± 0.5% |
| IKF-AMCNN | 100% ± 0.0% | 100% ± 0.0% | 97.2% ± 0.2% | 98.4% ± 0.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Jiang, T.; Li, D.; Zhang, Y.; Li, X.; Wang, Y.; Gao, J. A Novel Classification Framework for VLF/LF Lightning-Radiation Electric-Field Waveforms. Atmosphere 2025, 16, 1130. https://doi.org/10.3390/atmos16101130
Sun W, Jiang T, Li D, Zhang Y, Li X, Wang Y, Gao J. A Novel Classification Framework for VLF/LF Lightning-Radiation Electric-Field Waveforms. Atmosphere. 2025; 16(10):1130. https://doi.org/10.3390/atmos16101130
Chicago/Turabian StyleSun, Wenxing, Tingxiu Jiang, Duanjiao Li, Yun Zhang, Xinru Li, Yunlong Wang, and Jiachen Gao. 2025. "A Novel Classification Framework for VLF/LF Lightning-Radiation Electric-Field Waveforms" Atmosphere 16, no. 10: 1130. https://doi.org/10.3390/atmos16101130
APA StyleSun, W., Jiang, T., Li, D., Zhang, Y., Li, X., Wang, Y., & Gao, J. (2025). A Novel Classification Framework for VLF/LF Lightning-Radiation Electric-Field Waveforms. Atmosphere, 16(10), 1130. https://doi.org/10.3390/atmos16101130





