Numerical Simulation of Tornado-like Vortices Induced by Small-Scale Cyclostrophic Wind Perturbations
Abstract
1. Introduction
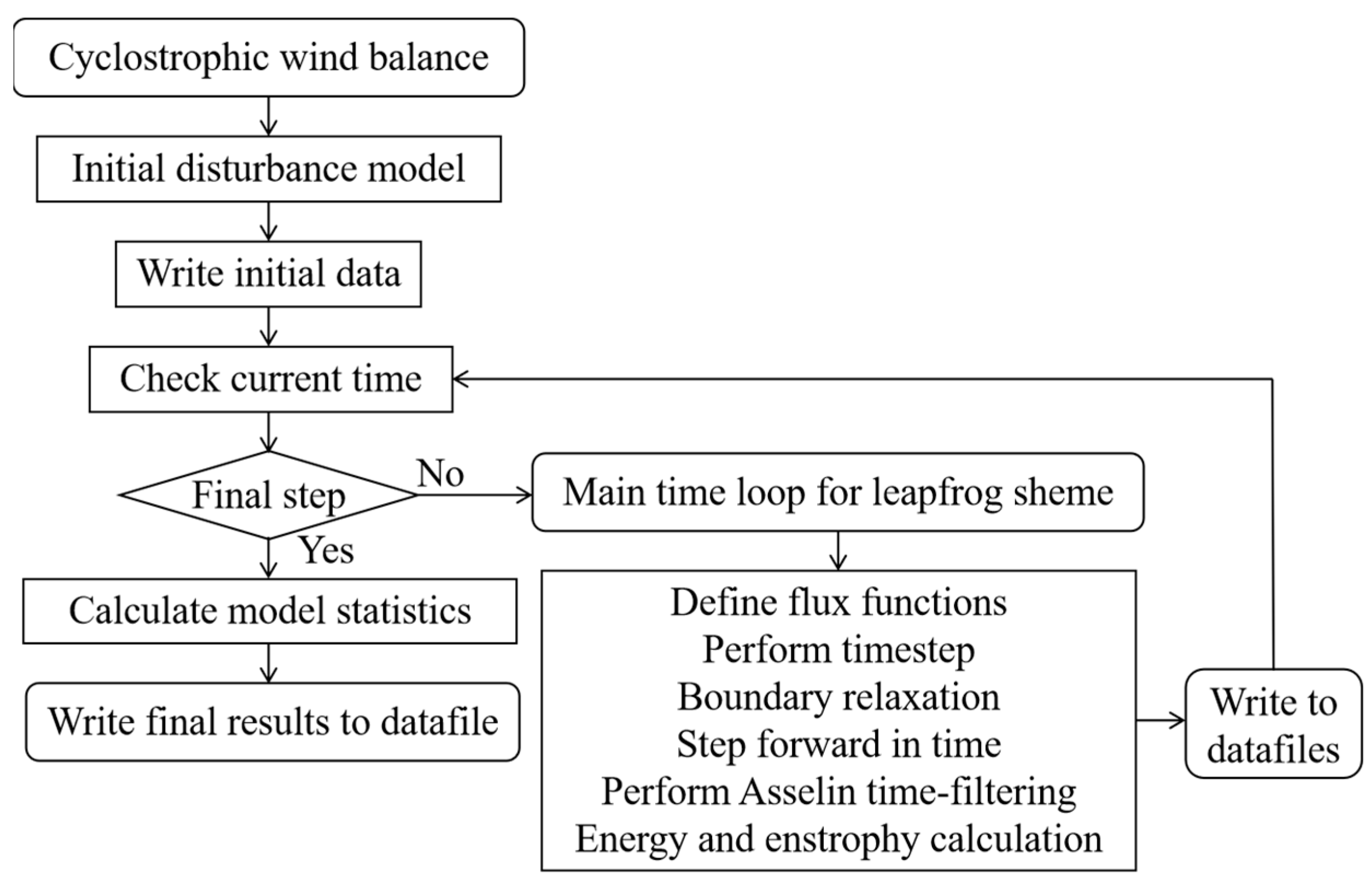
2. Model and Methods
2.1. Introduction of the Shallow-Water Equation Model
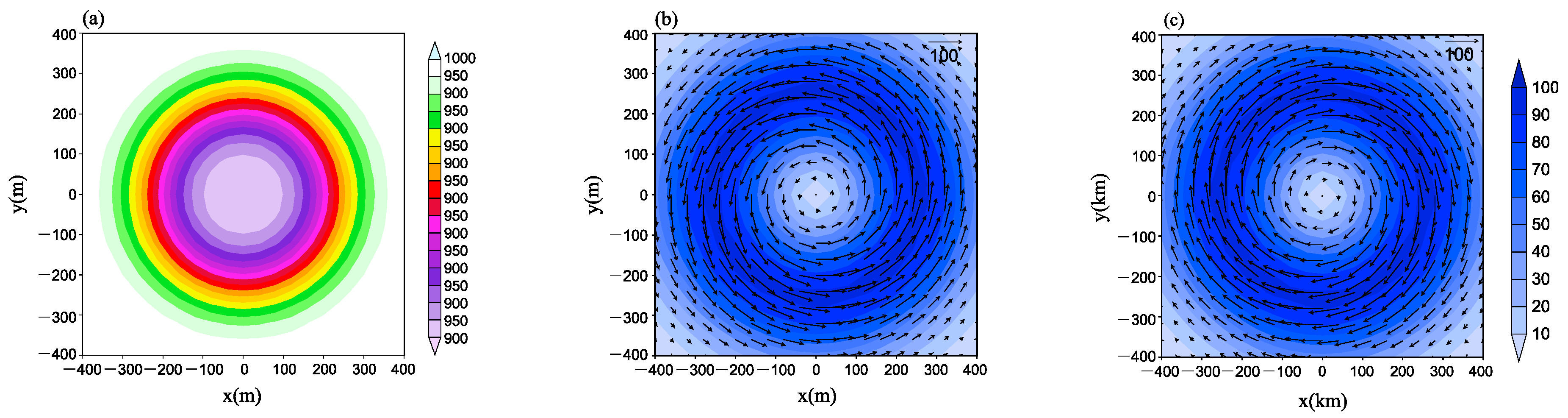
2.2. Initial Field of Tornado
2.3. Experiment Protocol
3. Numerical Simulation
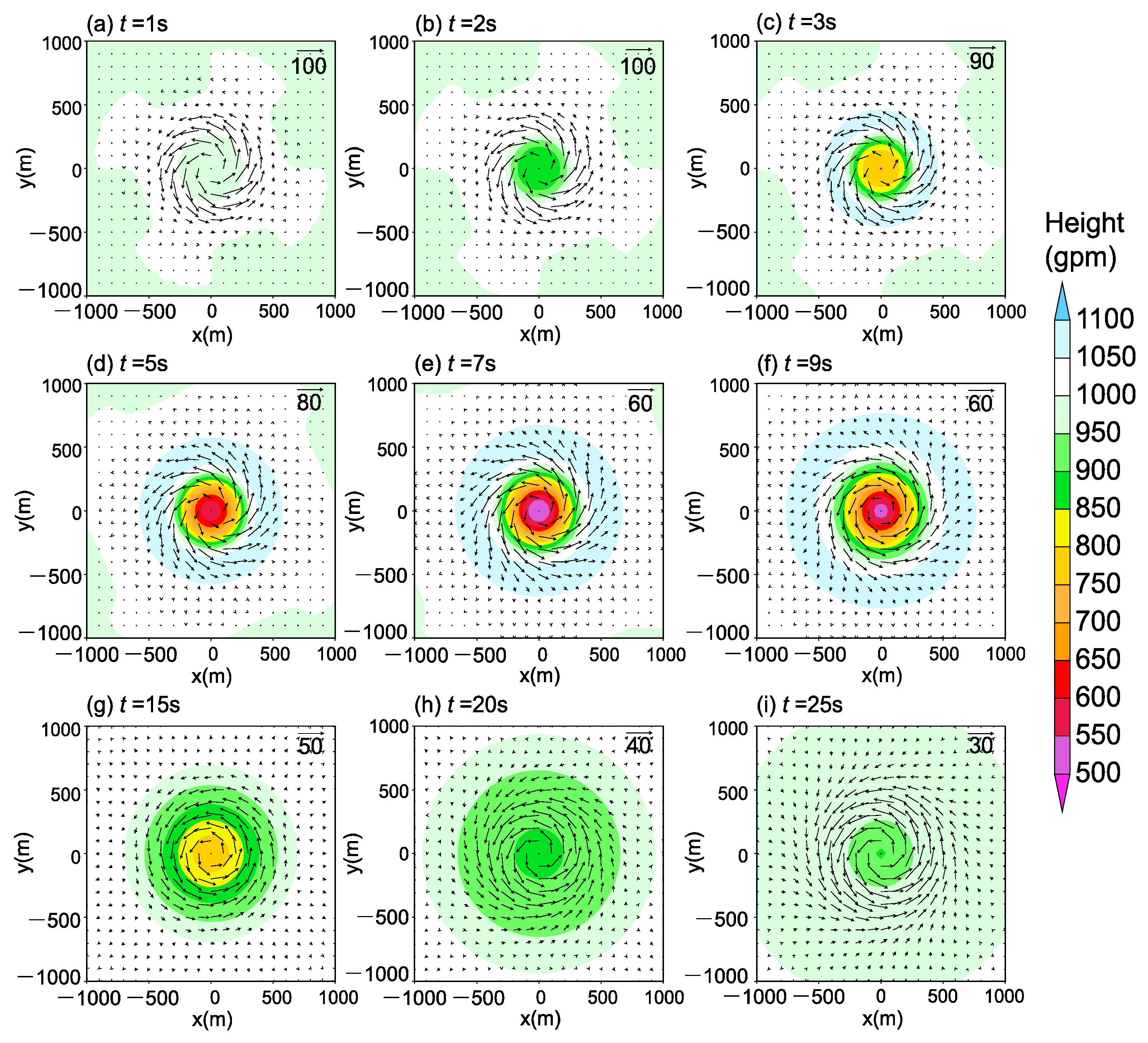
3.1. EXP1
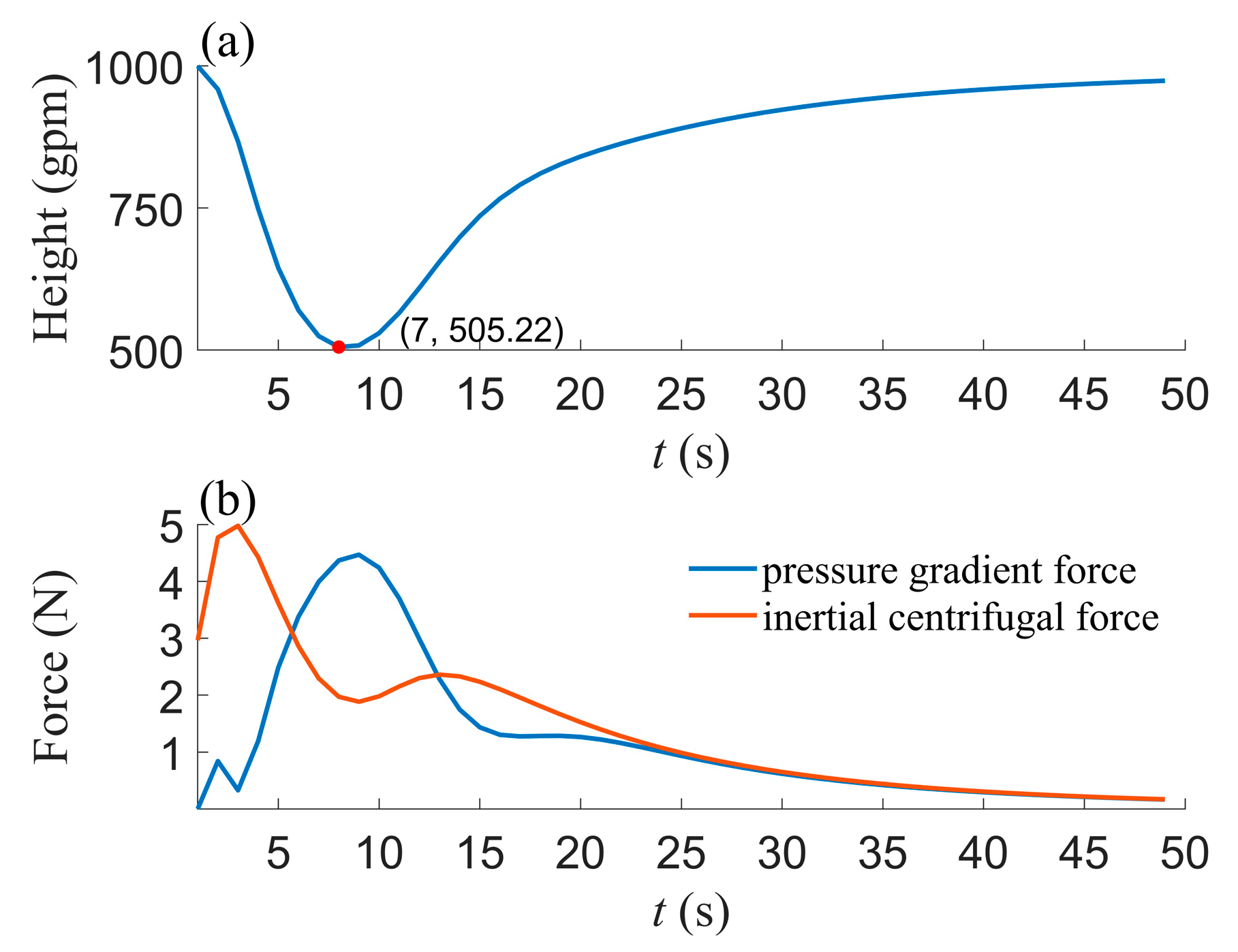
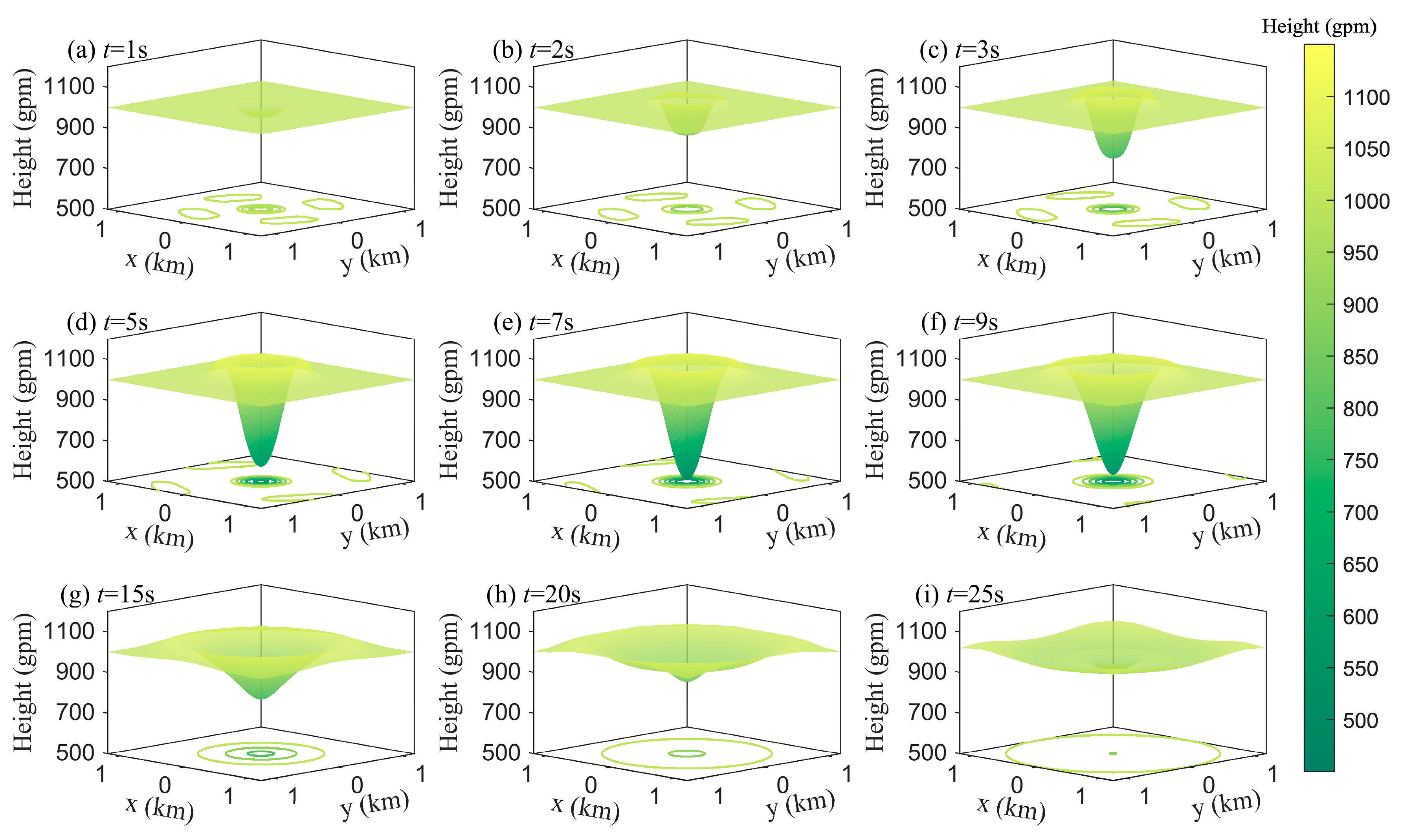
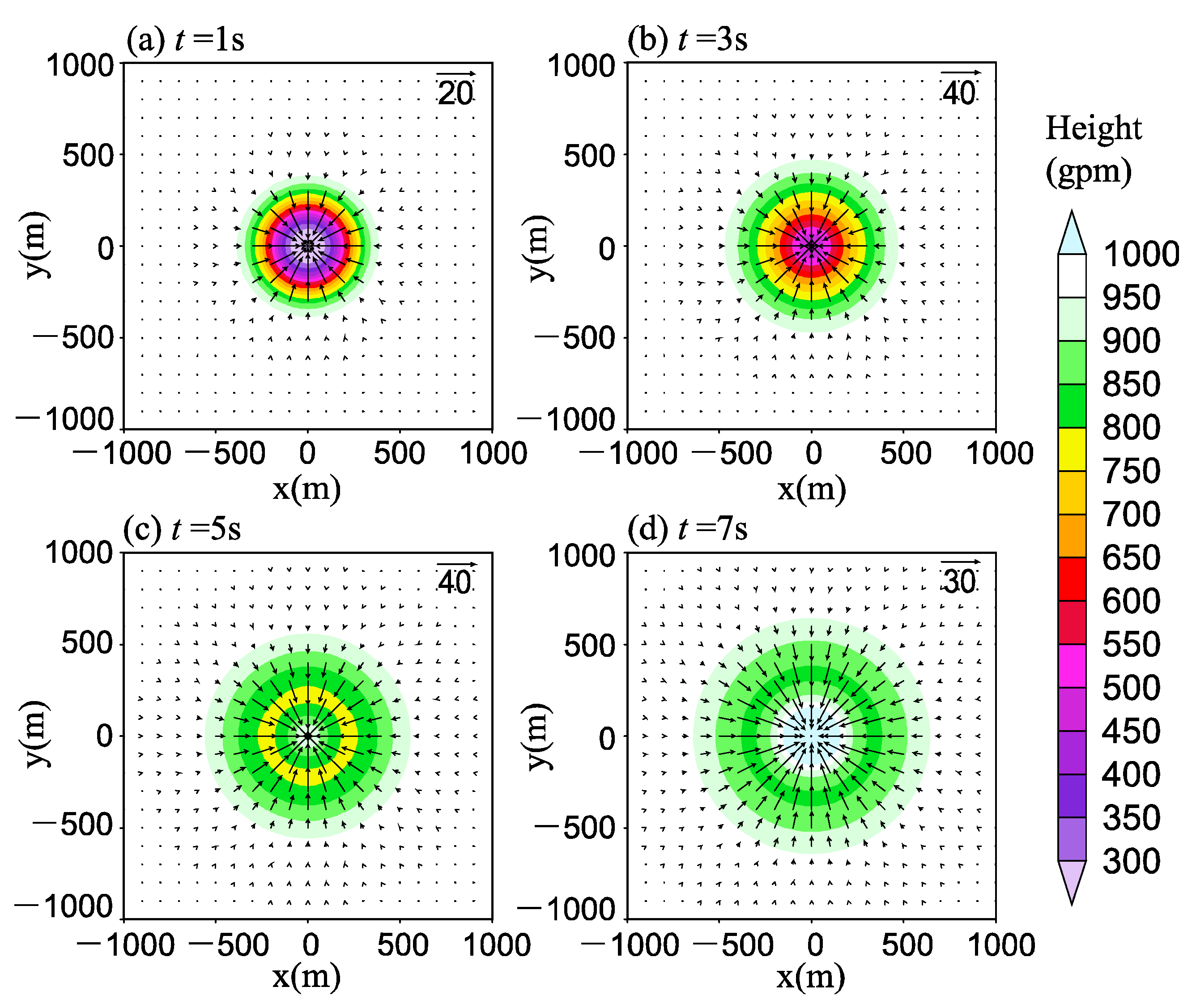
3.1.1. Geopotential Height
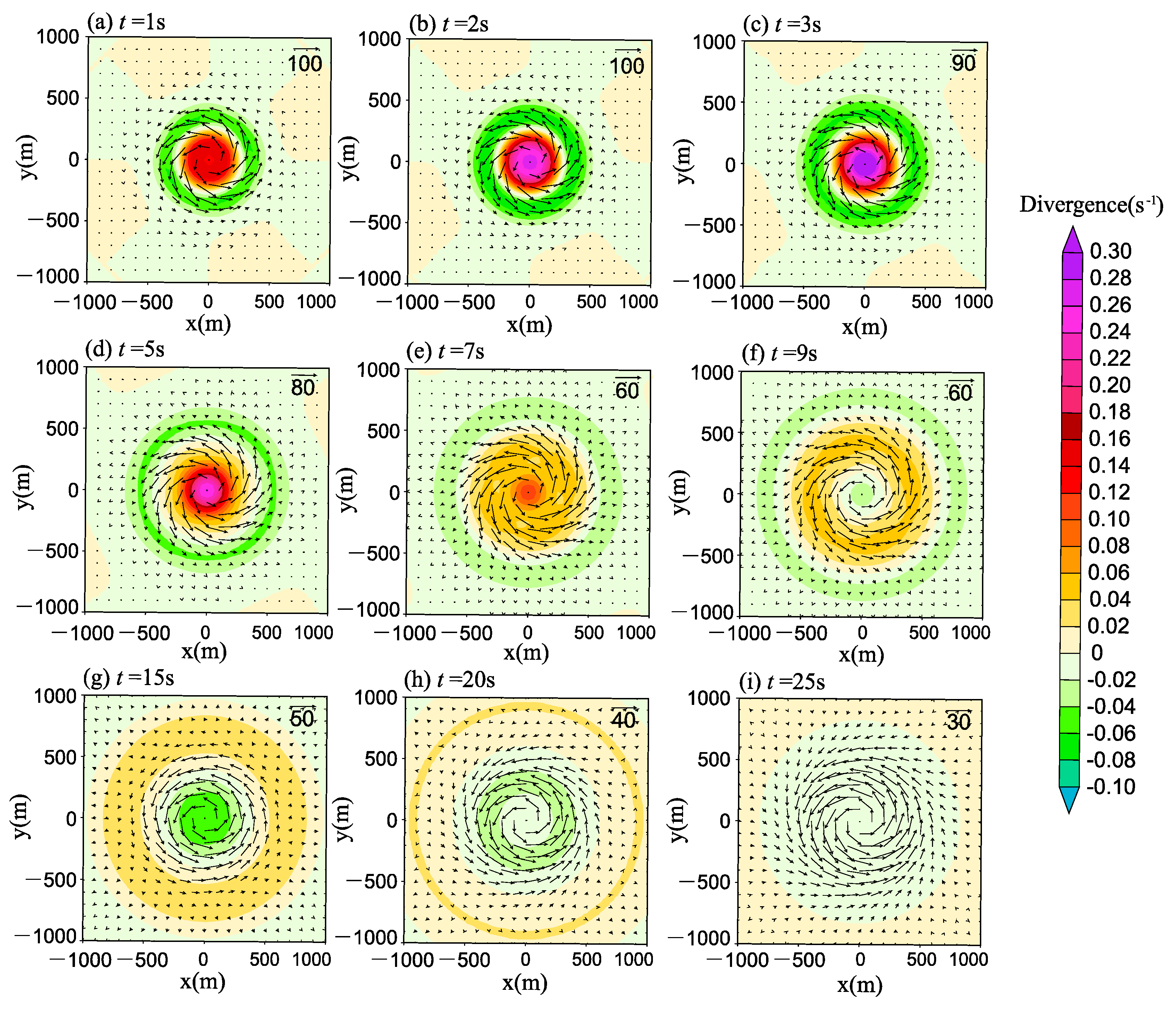
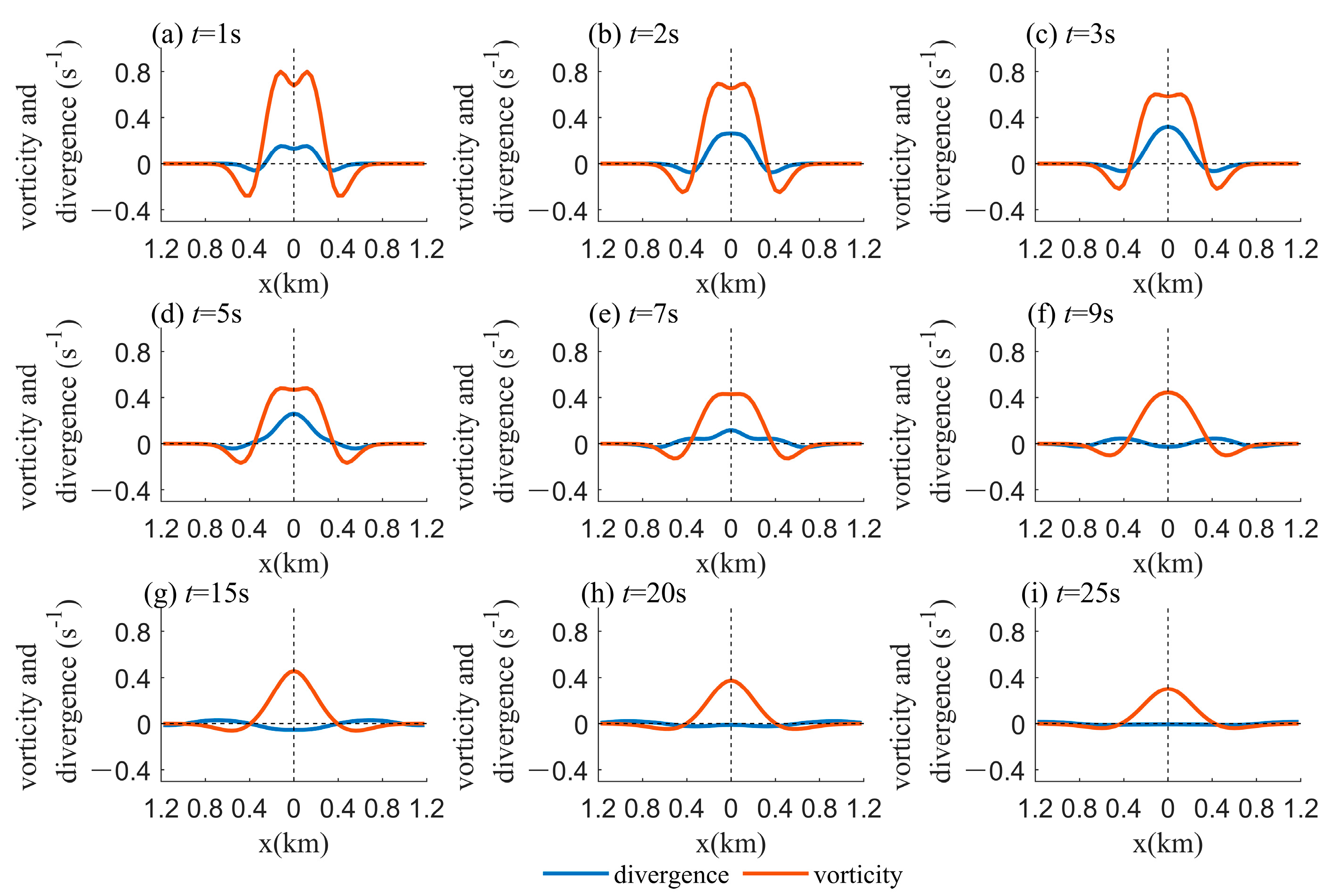
3.1.2. Divergence and Vorticity
3.2. EXP2
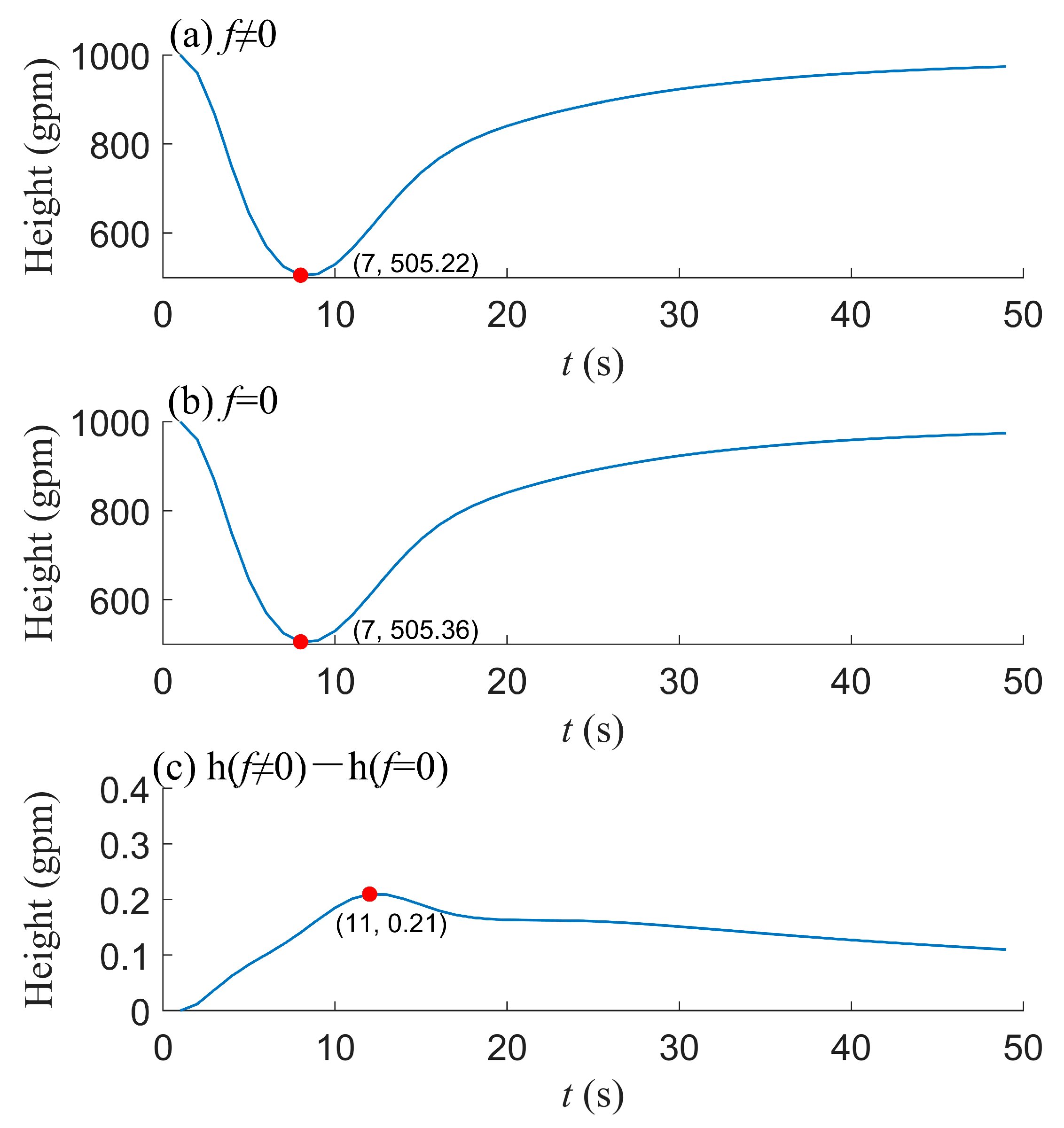
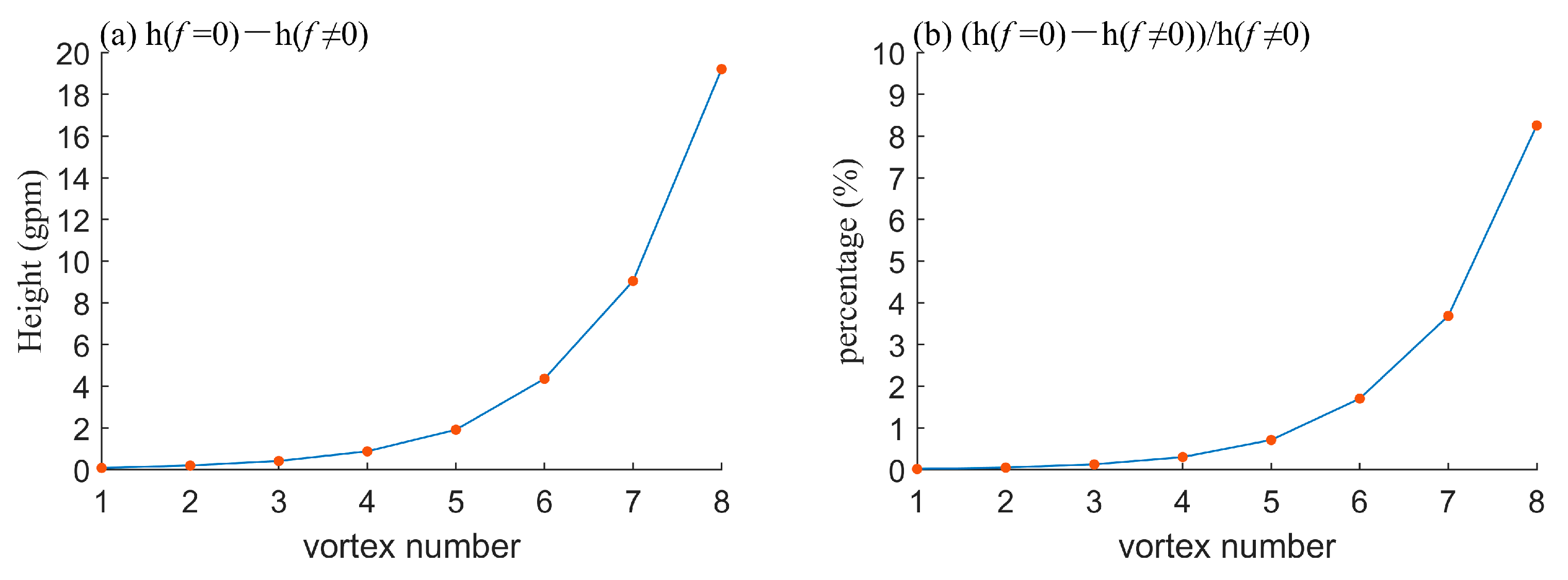
3.3. EXP3
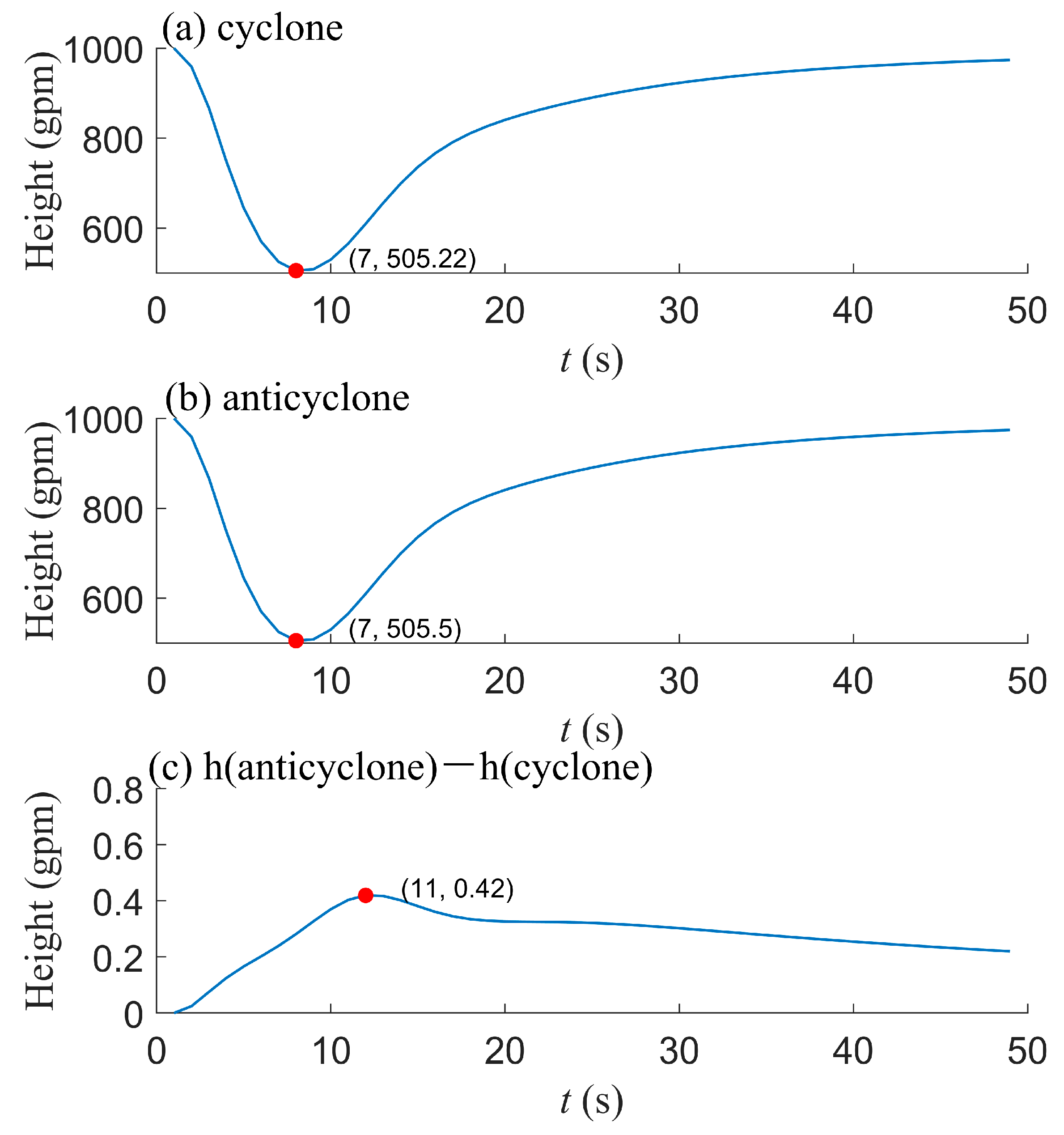
3.4. EXP4
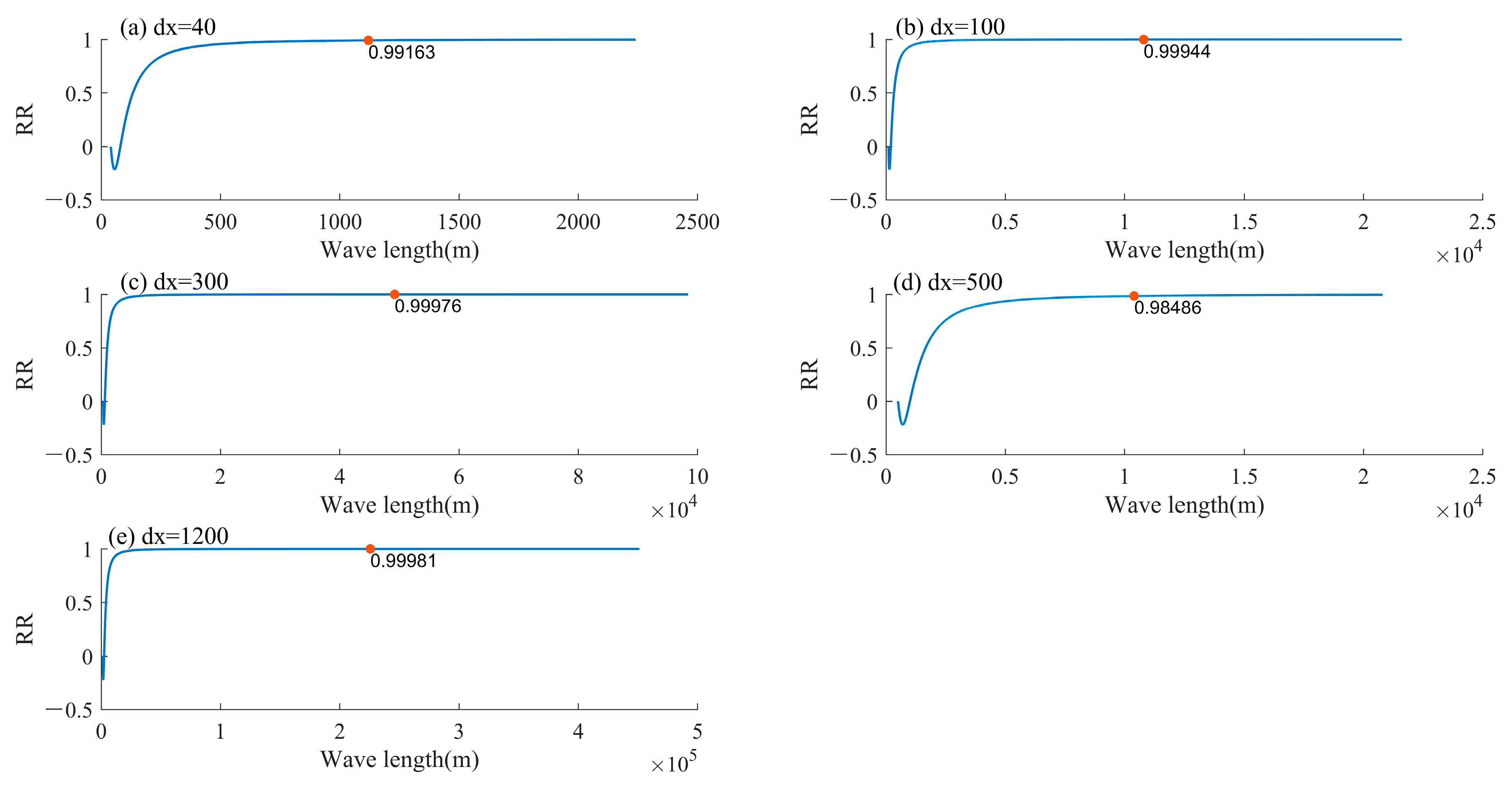
3.5. Error Analysis of Difference Scheme
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wurman, J.; Kosiba, K. Finescale Radar Observations of Tornado and Mesocyclone Structures. Weather Forecast. 2013, 28, 1157–1174. [Google Scholar] [CrossRef]
- Spiridonov, V.; Baez, J.; Telenta, B.; Jakimovski, B. Prediction of extreme convective rainfall intensities using a free-running 3-D sub-km-scale cloud model initialized from WRF km-scale NWP forecasts. J. Atmos. Solar-Terr. Phys. 2020, 209, 105401. [Google Scholar] [CrossRef]
- Davies-Jones, R.; Brooks, H.E. Mesocyclone from a theoretical perspective. In The Tornado: Its Structure, Dynamics, Prediction, and Hazards; American Geophysical Union: Washington, DC, USA, 1993; Volume 79, pp. 105–114. [Google Scholar]
- Dahl, J.M.L.; Parker, M.D.; Wicker, L.J. Imported and stormgenerated near-ground vertical vorticity in a simulated supercell. J. Atmos. Sci. 2014, 71, 3027–3051. [Google Scholar] [CrossRef]
- Parker, M.D.; Dahl, J.M.L. Production of near-surface vertical vorticity by idealized downdrafts. Mon. Weather Rev. 2015, 143, 2795–2816. [Google Scholar] [CrossRef]
- Fischer, J.; Dahl, J.M.L. Transition of Near-Ground Vorticity Dynamics during Tornadogenesis. J. Atmos. Sci. 2022, 79, 467–483. [Google Scholar] [CrossRef]
- Dahl, J.M.L.; Fischer, J. On the Origins of Vorticity in a Simulated Tornado-Like Vortex. J. Atmos. Sci. 2023, 80, 1361–1380. [Google Scholar] [CrossRef]
- Rasmussen, E.N.; Blanchard, D.O. A baseline climatology of sounding-derived supercell and tornado forecast parameters. Weather Forecast. 1998, 13, 1148–1164. [Google Scholar] [CrossRef]
- Markowski, P.M.; Richardson, Y.P. The influence of environmental low-level shear and cold pools on tornadogenesis: Insights from idealized simulations. J. Atmos. Sci. 2014, 71, 243–275. [Google Scholar] [CrossRef]
- Coffer, B.E.; Parker, M.D. Simulated supercells in nontornadic and tornadic VORTEX2 environments. Mon. Weather Rev. 2017, 145, 149–180. [Google Scholar] [CrossRef]
- Trapp, R.J.; Weisman, M.L. Low-level mesovortices within squall lines and bow echoes. Part II: Their genesis and implications. Mon. Weather Rev. 2003, 131, 2804–2823. [Google Scholar] [CrossRef]
- Schenkman, A.D.; Xue, M.; Hu, M. Tornadogenesis in a high-resolution simulation of the 8 May 2003 Oklahoma City supercell. J. Atmos. Sci. 2014, 71, 130–154. [Google Scholar] [CrossRef]
- Fischer, J.; Dahl, J.M.L. The relative importance of updraft and cold pool characteristics in supercell tornadogenesis using highly idealized simulations. J. Atmos. Sci. 2020, 77, 4089–4107. [Google Scholar] [CrossRef]
- Flournoy, M.D.; Coniglio, M.C. Origins of vorticity in a simulated tornadic mesovortex observed during PECAN on 6 July 2015. Mon. Weather Rev. 2019, 147, 107–134. [Google Scholar] [CrossRef]
- Tao, T.; Tamura, T. Numerical study of the 6 May 2012 Tsukuba supercell tornado: Vorticity sources responsible for tornadogenesis. Mon. Weather Rev. 2020, 148, 1205–1228. [Google Scholar] [CrossRef]
- Boyer, C.H.; Dahl, J.M. The mechanisms responsible for large near-surface vertical vorticity within simulated supercells and quasi-linear storms. Mon. Weather Rev. 2020, 148, 4281–4297. [Google Scholar] [CrossRef]
- Ye, D.Z.; Li, M.T. The adaptation between the pressure and the wind field in the Meso- and Small-Scale motion. Acta Meteorol. Sin. 1964, 4, 409–423. (In Chinese) [Google Scholar]
- Zavolgenskiy, M.V.; Rutkevich, P.B. Tornado funnel-shaped cloud as convection in a cloudy layer. Adv. Sci. Res. 2009, 3, 17–21. [Google Scholar] [CrossRef][Green Version]
- Pashitskii, É.A. Nonlinear vortex dynamics in open nonequilibrium systems with bulk mass loss and a generation mechanism for tornadoes and typhoons. J. Exp. Theor. Phys. 2010, 110, 1026–1041. [Google Scholar] [CrossRef]
- Carbajal, N.; León-Cruz, J.F.; Pineda-Martínez, L.F.; Tuxpan-Vargas, J.; Gaviño-Rodríguez, J.H. Occurrence of Anticyclonic Tornadoes in a Topographically Complex Region of Mexico. Adv. Meteorol. 2019, 2019, 2763153. [Google Scholar] [CrossRef]
- Fabrizio, M. Turbulence phenomena for viscous fluids: Vortices and instability. Appl. Math. Comput. 2020, 376, 125094. [Google Scholar] [CrossRef]
- Oliveira, M.I.; Xue, M.; Roberts, B. Trailing Horizontal Vortices in Observed and Numerically Simulated Tornadoes. Bull. Amer. Meteorol. Soc. 2022, 103, E2768–E2790. [Google Scholar] [CrossRef]
- Davies-Jones, R. Invented Forces in Supercell Models. J. Atmos. Sci. 2021, 78, 2927–2939. [Google Scholar] [CrossRef]
- Peters, J.M.; Coffer, B.E.; Parker, M.D.; Nowotarski, C.J.; Mulholland, J.P.; Nixon, C.J.; Allen, J.T. Disentangling the Influences of Storm-Relative Flow and Horizontal Streamwise Vorticity on Low-Level Mesocyclones in Supercells. J. Atmos. Sci. 2023, 80, 129–149. [Google Scholar] [CrossRef]
- Roberts, B.; Xue, M.; Dawson, D.T., II. The Effect of Surface Drag Strength on Mesocyclone Intensification and Tornadogenesis in Idealized Supercell Simulations. J. Atmos. Sci. 2020, 77, 1699–1721. [Google Scholar] [CrossRef]
- Snider, C.R. An Anticyclonic Tornado. Mon. Weather Rev. 1976, 104, 1186–1187. [Google Scholar] [CrossRef]
- Fujita, T.T. Anticyclonic tornadoes. Weatherwise 1977, 30, 51–64. [Google Scholar] [CrossRef]
- Niino, H.; Fujitani, T.; Watanabe, N. A Statistical Study of Tornadoes and Waterspouts in Japan from 1961 to 1993. J. Clim. 1997, 10, 1730–1752. [Google Scholar] [CrossRef]
- Chernokulsky, A.V.; Kurgansky, M.V.; Mokhov, I.I.; Shikhov, A.; Azhigov, I.; Selezneva, E.; Zakharchenko, D.; Antonescu, B.; Kühne, T. Tornadoes in Northern Eurasia: From the Middle Age to the Information Era. Mon. Weather Rev. 2020, 148, 3081–3110. [Google Scholar] [CrossRef]
- Bluestein, H.B.; French, M.M.; Snyder, J.C.; Houser, J.B. Doppler Radar Observations of Anticyclonic Tornadoes in Cyclonically Rotating, Right-Moving Supercells. Mon. Weather Rev. 2016, 144, 1591–1616. [Google Scholar] [CrossRef]
- Nielsen-Gammon, J.W.; Read, W.L. Detection and interpretation of left-moving severe thunderstorms using the WSR-88D: A case study. Weather Forecast. 1995, 10, 127–140. [Google Scholar] [CrossRef]
- Knupp, K.R.; Cotton, W.R. An intense, quasi-steady thunderstorm over mountainous terrain. Part II: Doppler radar observations of the storm morphological structure. J. Atmos. Sci. 1982, 39, 343–358. [Google Scholar] [CrossRef]
- Monteverdi, J.P.; Blier, W.; Stumpf, G.J.; Pi, W.; Anderson, K. First WSR-88D Documentation of an Anticyclonic Supercell with Anticyclonic Tornadoes: The SunnyvaleCLos Altos, California, Tornadoes of 4 May 1998. Mon. Weather Rev. 2001, 129, 2805–2814. [Google Scholar] [CrossRef]
- Bunkers, M.J.; Stoppkotte, J.W. Documentation of a rare tornadic left-moving supercell. J. Sev. Storms Meteorol. 2007, 2, 1559–5404. [Google Scholar] [CrossRef]
- Brown, J.M.; Knupp, K.R. The Iowa cyclonic-anticyclonic tornado pair and its parent thunderstorm. Mon. Weather Rev. 1980, 108, 1626–1646. [Google Scholar] [CrossRef]
- Fujita, T.T. Tornadoes and downbursts in the context of generalized planetary scales. J. Atmos. Sci. 1981, 38, 1511–1534. [Google Scholar] [CrossRef]
- Wurman, J.; Kosiba, K.; Robinson, P.; Marshall, T. The role of multiple-vortex tornado structure in causing storm researcher fatalities. Bull. Am. Meteorol. Soc. 2014, 95, 31–45. [Google Scholar] [CrossRef]
- Bluestein, H.B.; Snyder, J.C.; Houser, J.B. A multiscale overview of the El Reno, Oklahoma, tornadic supercell of 31 May 2013. Weather Forecast. 2015, 30, 525–552. [Google Scholar] [CrossRef]
- Snyder, J.C.; Bluestein, H.B.; Wienhoff, Z.B.; Kuster, C.M.; Reif, D.W. An Analysis of an Ostensible Anticyclonic Tornado from 9 May 2016 Using High-Resolution, Rapid-Scan Radar Data. Weather Forecast. 2020, 35, 1685–1712. [Google Scholar] [CrossRef]
- Erbes, G. A semi-Lagrangian method of characteristic for the shallow-water equations. Mon. Weather Rev. 1993, 121, 3443–3452. [Google Scholar] [CrossRef]
- Ying, S.J.; Chang, C.C. Exploratory model study of tornado-like vortex dynamics. J. Atmos. Sci. 1970, 27, 3–14. [Google Scholar] [CrossRef]
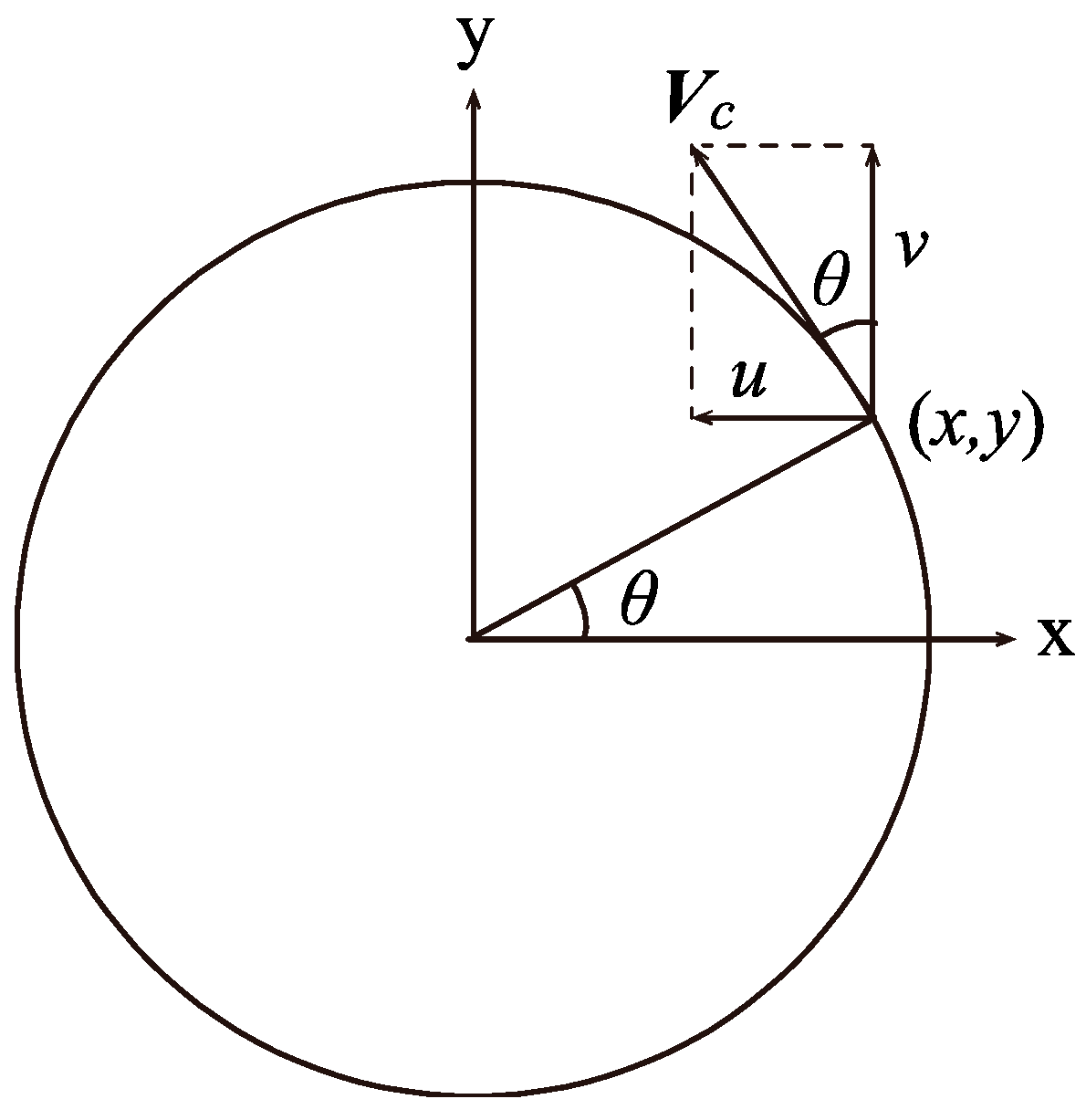


| Test Name | Initial Field Perturbation Type | Coriolis Parameter f (s−1) | Purpose |
|---|---|---|---|
| EXP1 | Cyclonic wind field | 7.292 × 10−5 | Simulate the evolution process of a single given cyclonic wind field. |
| EXP2 | Geopotential height perturbation | 7.292 × 10−5 | Simulate the evolution process of a single given pressure field. |
| EXP3 | Cyclonic wind field | 7.292 × 10−5 or 0 | Simulate the evolution process of a single given cyclonic wind field considering or without considering the Coriolis force. Sixteen tests were designed to analyze the influence of the Coriolis force in vortices with different scales, as seen in Table 2. |
| EXP4 | Anticyclonic wind field | 7.292 × 10−5 | Simulate the evolution process of the perturbation of a single given anticyclonic wind field. |
| Test Name | Diameter of Vortex (km) | f (s−1) | Test Name | Diameter of Vortex (km) | f (s−1) |
|---|---|---|---|---|---|
| EXP3.1 | 0.56 | 0 | EXP3.9 | 0.56 | 7.292 × 10−5 |
| EXP3.2 | 1.2 | 0 | EXP3.10 | 1.2 | 7.292 × 10−5 |
| EXP3.3 | 2.48 | 0 | EXP3.11 | 2.48 | 7.292 × 10−5 |
| EXP3.4 | 5.4 | 0 | EXP3.12 | 5.4 | 7.292 × 10−5 |
| EXP3.5 | 11.2 | 0 | EXP3.13 | 11.2 | 7.292 × 10−5 |
| EXP3.6 | 24.6 | 0 | EXP3.14 | 24.6 | 7.292 × 10−5 |
| EXP3.7 | 52 | 0 | EXP3.15 | 52 | 7.292 × 10−5 |
| EXP3.8 | 112.8 | 0 | EXP3.16 | 112.8 | 7.292 × 10−5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Jiang, Y.; Chen, C.; Zhang, Y.; He, H.; Chen, X.; Zhong, R. Numerical Simulation of Tornado-like Vortices Induced by Small-Scale Cyclostrophic Wind Perturbations. Atmosphere 2025, 16, 108. https://doi.org/10.3390/atmos16010108
Liu Y, Jiang Y, Chen C, Zhang Y, He H, Chen X, Zhong R. Numerical Simulation of Tornado-like Vortices Induced by Small-Scale Cyclostrophic Wind Perturbations. Atmosphere. 2025; 16(1):108. https://doi.org/10.3390/atmos16010108
Chicago/Turabian StyleLiu, Yuhan, Yongqiang Jiang, Chaohui Chen, Yun Zhang, Hongrang He, Xiong Chen, and Ruilin Zhong. 2025. "Numerical Simulation of Tornado-like Vortices Induced by Small-Scale Cyclostrophic Wind Perturbations" Atmosphere 16, no. 1: 108. https://doi.org/10.3390/atmos16010108
APA StyleLiu, Y., Jiang, Y., Chen, C., Zhang, Y., He, H., Chen, X., & Zhong, R. (2025). Numerical Simulation of Tornado-like Vortices Induced by Small-Scale Cyclostrophic Wind Perturbations. Atmosphere, 16(1), 108. https://doi.org/10.3390/atmos16010108





