Study on Downscaling Correction of Near-Surface Wind Speed Grid Forecasts in Complex Terrain
Abstract
1. Introduction
2. Data and Methods
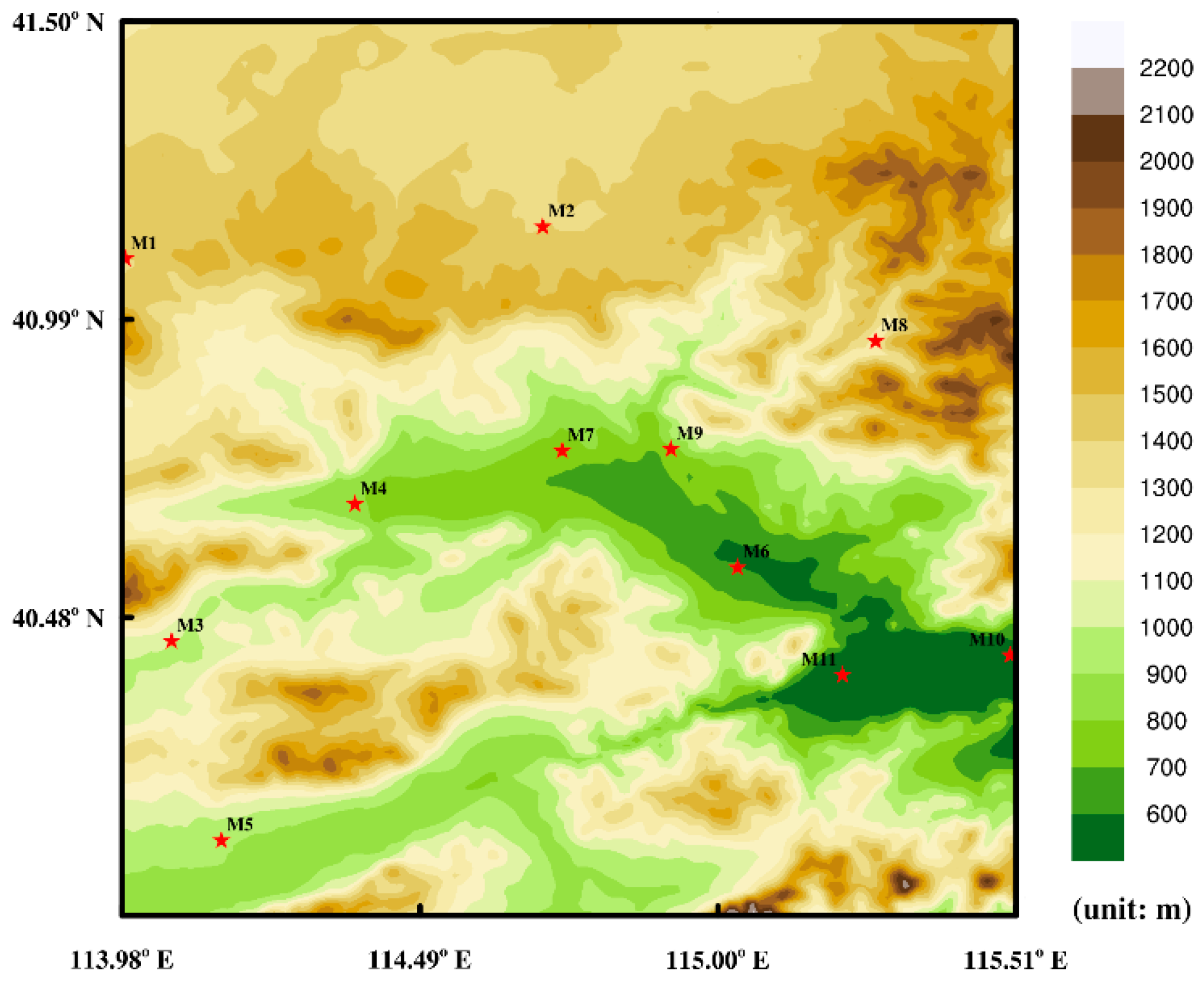
2.1. Study Area and Period
2.2. Data
2.3. Methods
2.3.1. Machine Learning Algorithm
- (1)
- High accuracy: Random forest improves prediction accuracy by integrating multiple decision trees. The prediction results of each tree are determined by voting or averaging, thereby reducing the bias and variance of a single model.
- (2)
- Handling high-dimensional data: Random forest can handle a large number of features (high-dimensional data) and has an inherent feature importance evaluation mechanism during feature selection, making it perform well on complex datasets.
- (3)
- Resistance to overfitting: Since random forest uses an ensemble of multiple trees and each tree is trained on a subset of the data and features, this “bagging” and “random feature selection” method effectively reduces the risk of overfitting.
- (4)
- Robustness: Random forest is robust to missing values and noisy data. It can provide stable prediction results even when there are some outliers or missing values in the data.
- (5)
- Parallelization: The training process of random forest can be parallelized because the training of each tree is independent. This makes it highly efficient in processing large-scale datasets.
- (6)
- Ease of use: The random forest algorithm is relatively simple and easy to use, often requiring minimal parameter tuning. A random forest model with default parameter settings usually provides good performance.
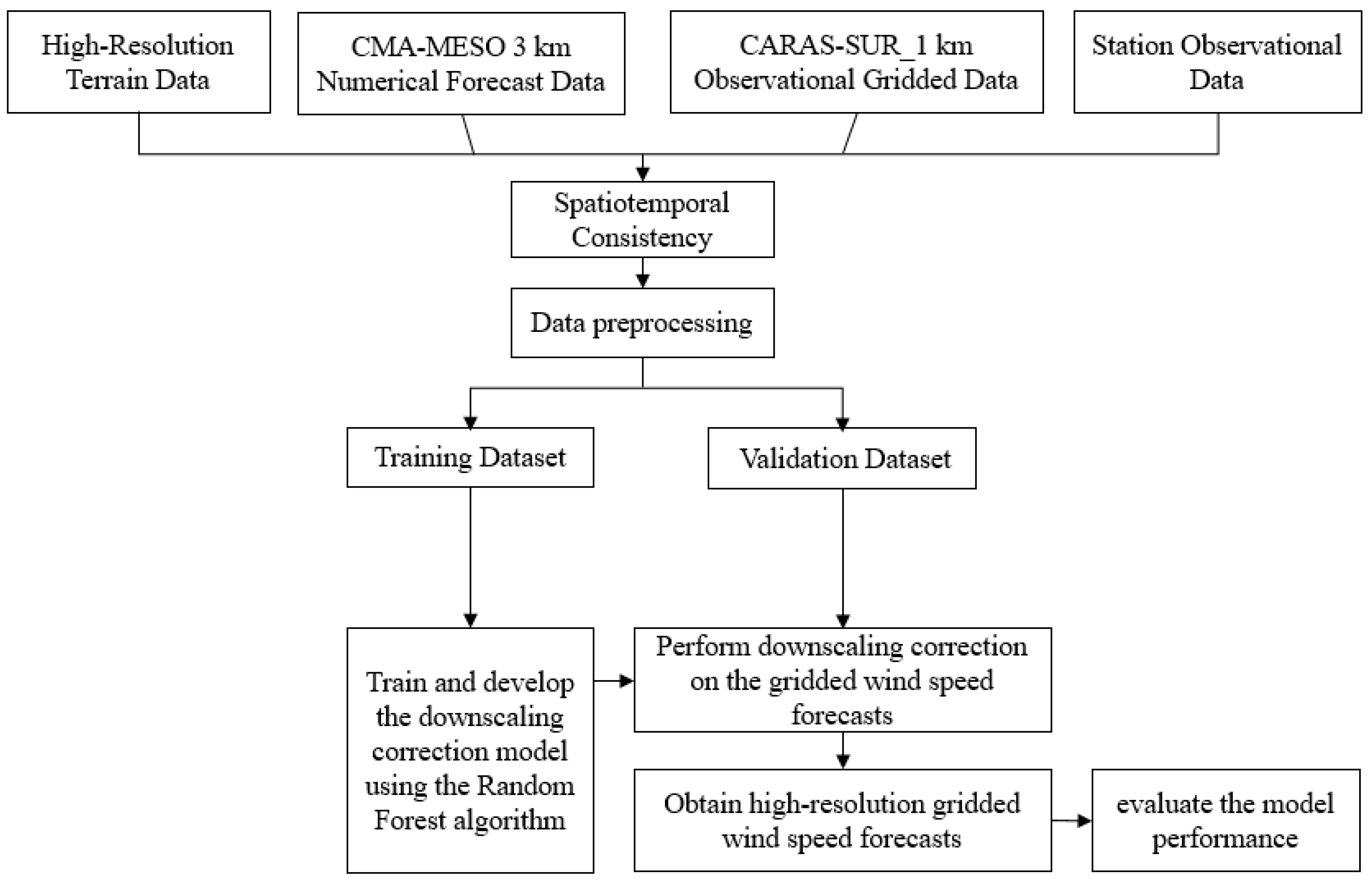
2.3.2. Model Construction and Evaluation
- (1)
- Spatiotemporal Consistency: Using the CARAS-SUR_1 km ground truth grid data as the spatiotemporal target, the CMA-MESO 3 km numerical forecast data are filled according to the principle of identical values for 1 km × 1 km grids inside each 3 km × 3 km grid, resulting in a dataset with a spatial resolution of 1 km and hourly intervals. The detailed terrain data are processed into a 1 km spatial resolution dataset by arithmetic averaging within each grid. Station observation data are matched to the 1 km grids in the study area based on the nearest distance principle and are temporally matched on an hourly basis.
- (2)
- Data Preprocessing: The 21 variables from the CMA-MESO 3 km data, along with the 10 m wind speed and the grid latitude and longitude from the CARAS-SUR_1 km ground truth grid data, are extracted. Data for all variables are standardized to avoid the issue of smaller numerical values contributing less during training and to improve computational speed [30]. Due to the good completeness of the dataset, there are no missing values during the study period. The study area has a spatial resolution of 1 km × 1 km, comprising a total of 154 × 154 grids. Therefore, the training dataset consist of 80 × 24 × 154 × 154 samples, and the validation dataset consist of 43 × 24 × 154 × 154 samples, with each sample having 24 feature variables and 1 target variable.
- (3)
- Model Training: The feature vector is constructed from 24 variables (see Table 1) selected from the CMA-MESO 3 km output, including 10 m wind speed, 2 m temperature, 2 m relative humidity, surface pressure, and the geopotential height, wind speed, temperature, and humidity at 500 hPa, 700 hPa, 850 hPa, and 925 hPa, forecast lead time, and static geographic information (grid point longitude, latitude, and terrain elevation). The target variable is the 10 m wind speed from the CARAS-SUR_1 km ground truth grid data. The random forest downscaling correction model is established to achieve the downscaled output of near-surface wind speed grid forecast. The grid search method is used to tune three key parameters of the random forest model (n_estimators, max_depth, min_samples_split), and the final selected parameter values are the default settings of the model.
- (4)
- Validation and Evaluation: The CARAS-SUR_1 km ground truth grid data are used as the observational ground truth for model construction and validation. The wind speed forecasts before and after downscaling correction are evaluated. To further assess the model’s effectiveness, this study selects wind speed observation data from national meteorological stations during the validation period to evaluate the model’s performance in terms of spatial, temporal, and various wind speed categories. Additionally, specific analyses of the model performance during strong wind events are selected to comprehensively evaluate the performance of the wind speed forecast downscaling correction model.
2.3.3. Validation Methods
3. Results and Discussion
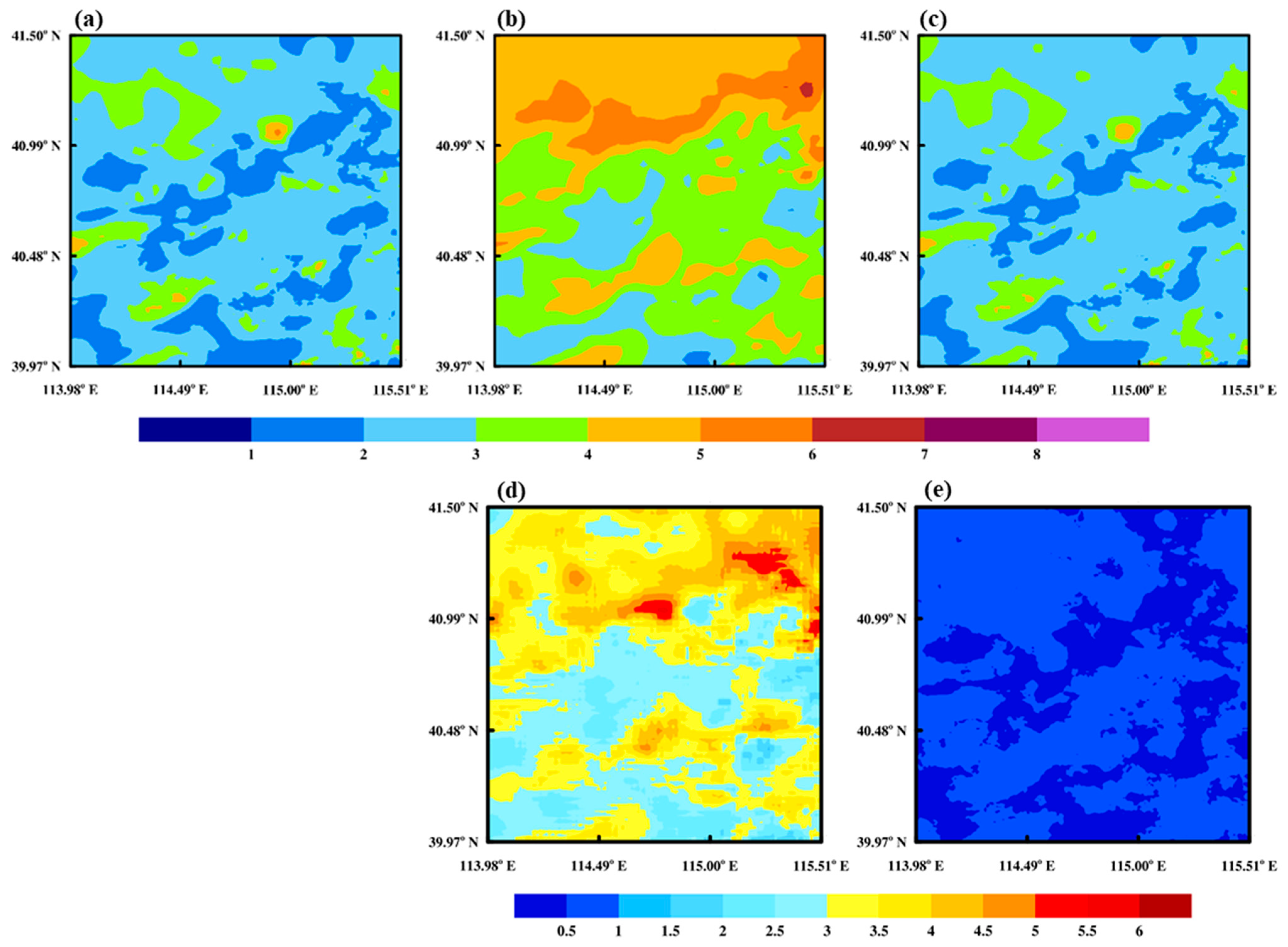
3.1. Spatial Distribution Characteristics of Correction Effects
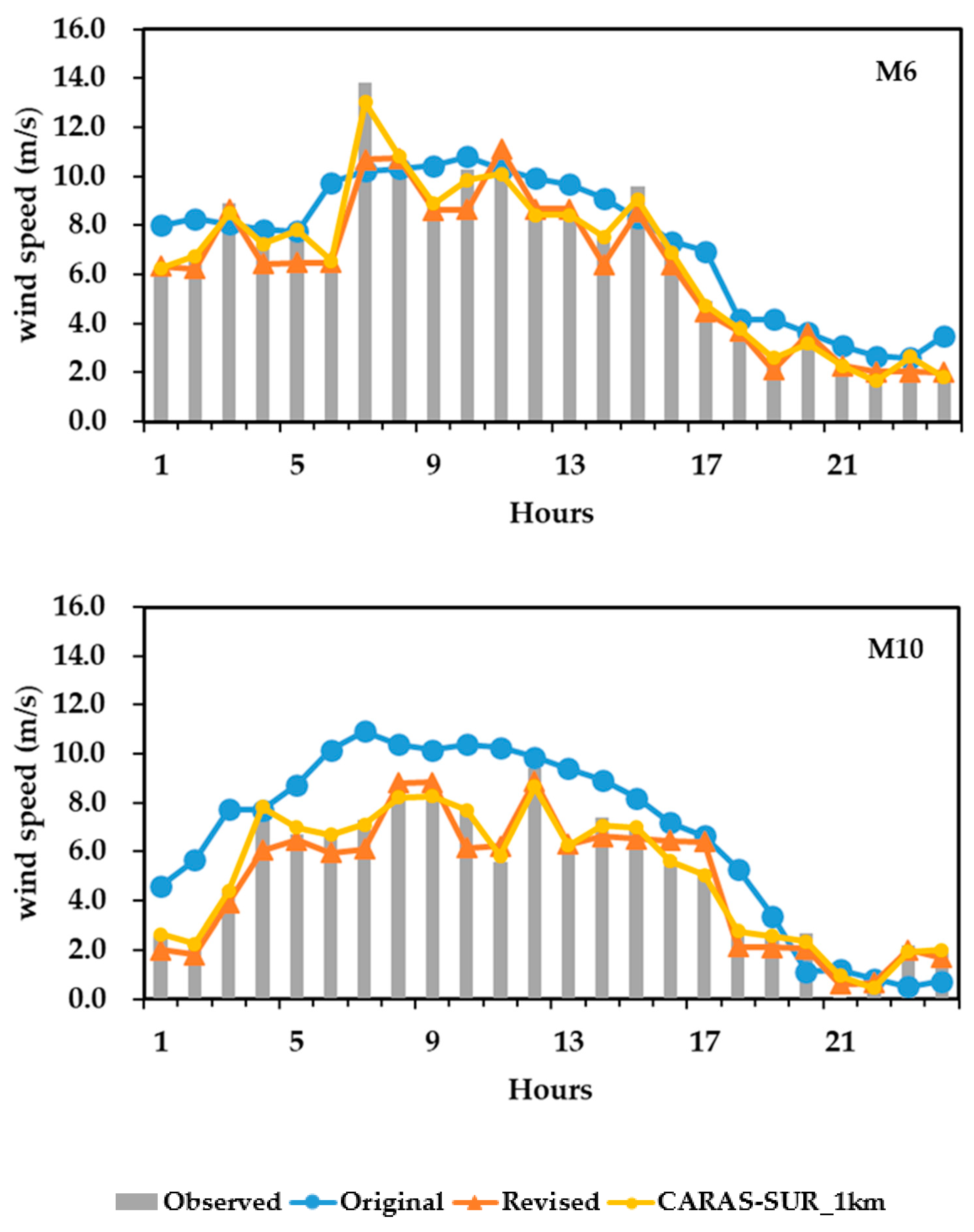
3.1.1. Grid Validation
3.1.2. Station Validation
3.2. Temporal Variation Characteristics of Correction Effect
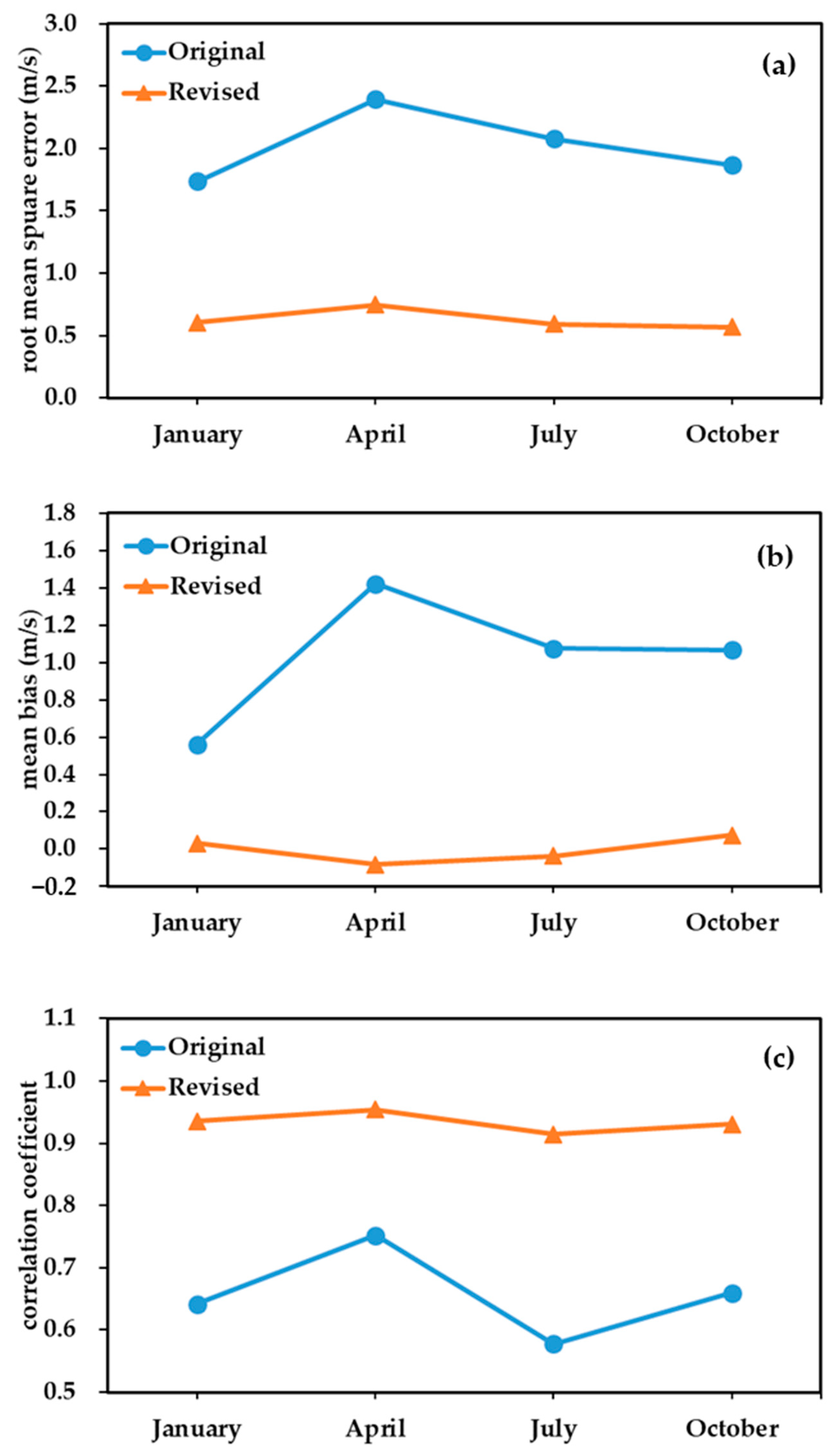
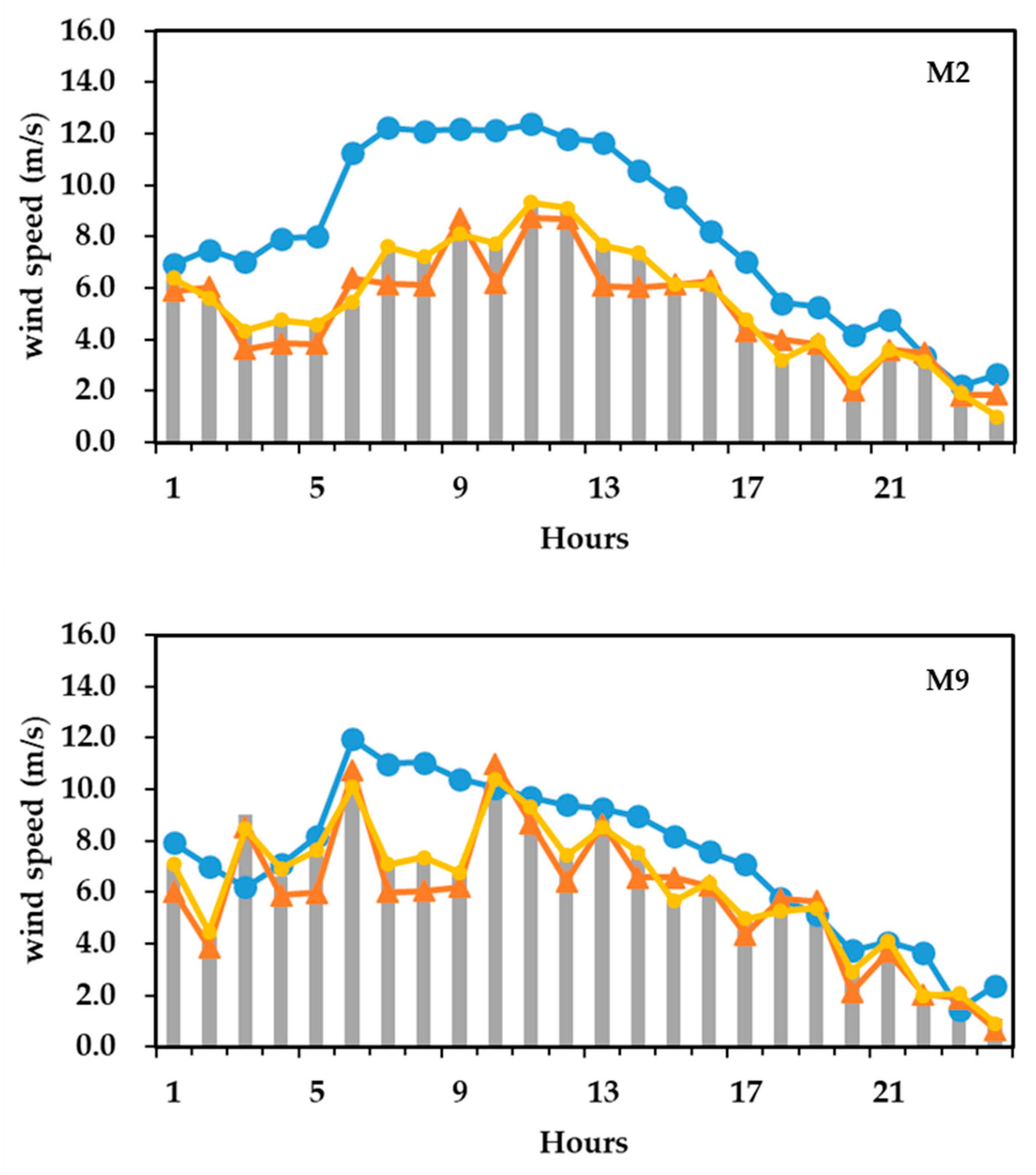
3.2.1. Wind Speed Correction Effects for Representative Months of Each Season
3.2.2. Wind Speed Correction Effects for Different Forecast Lead Times
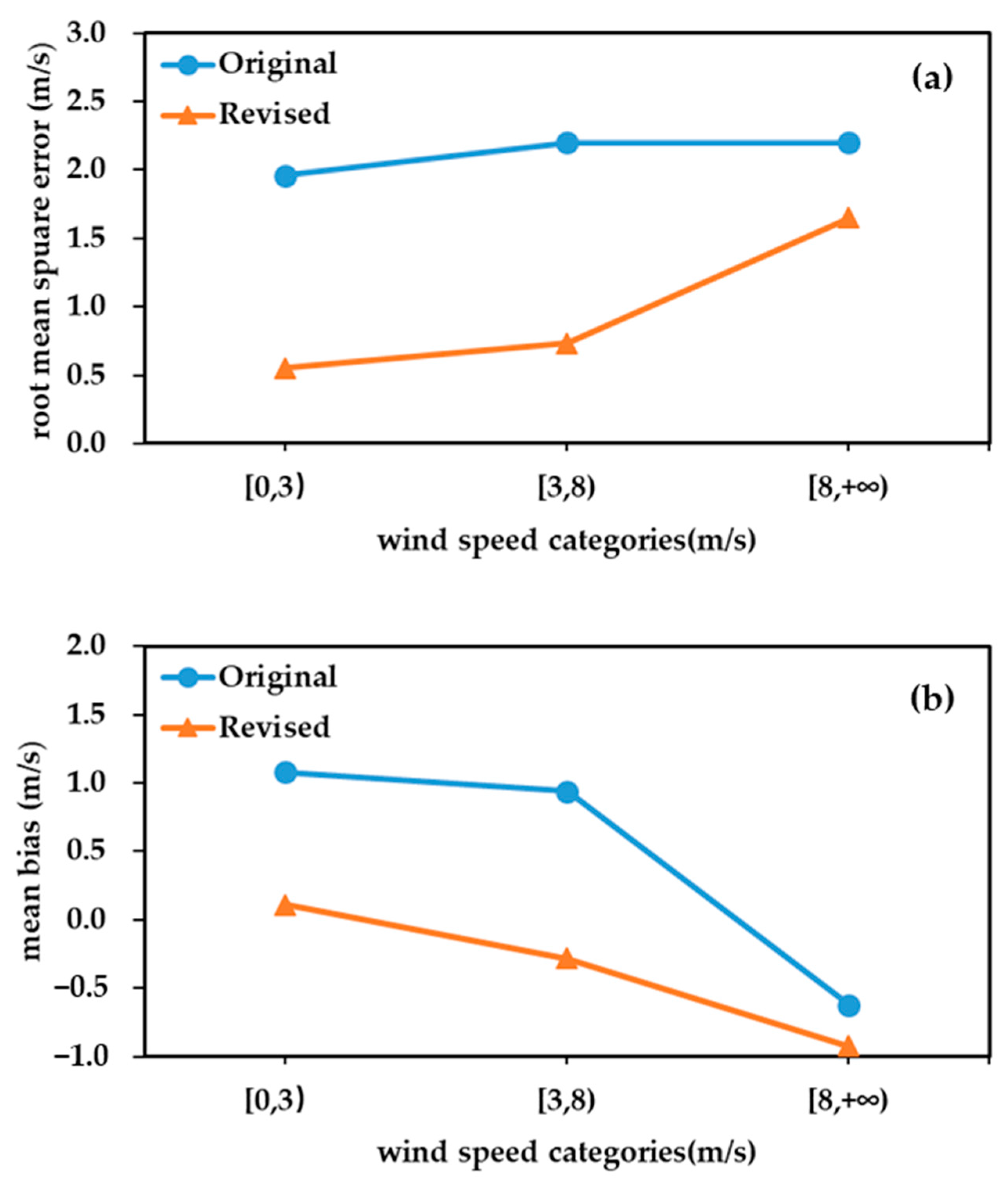
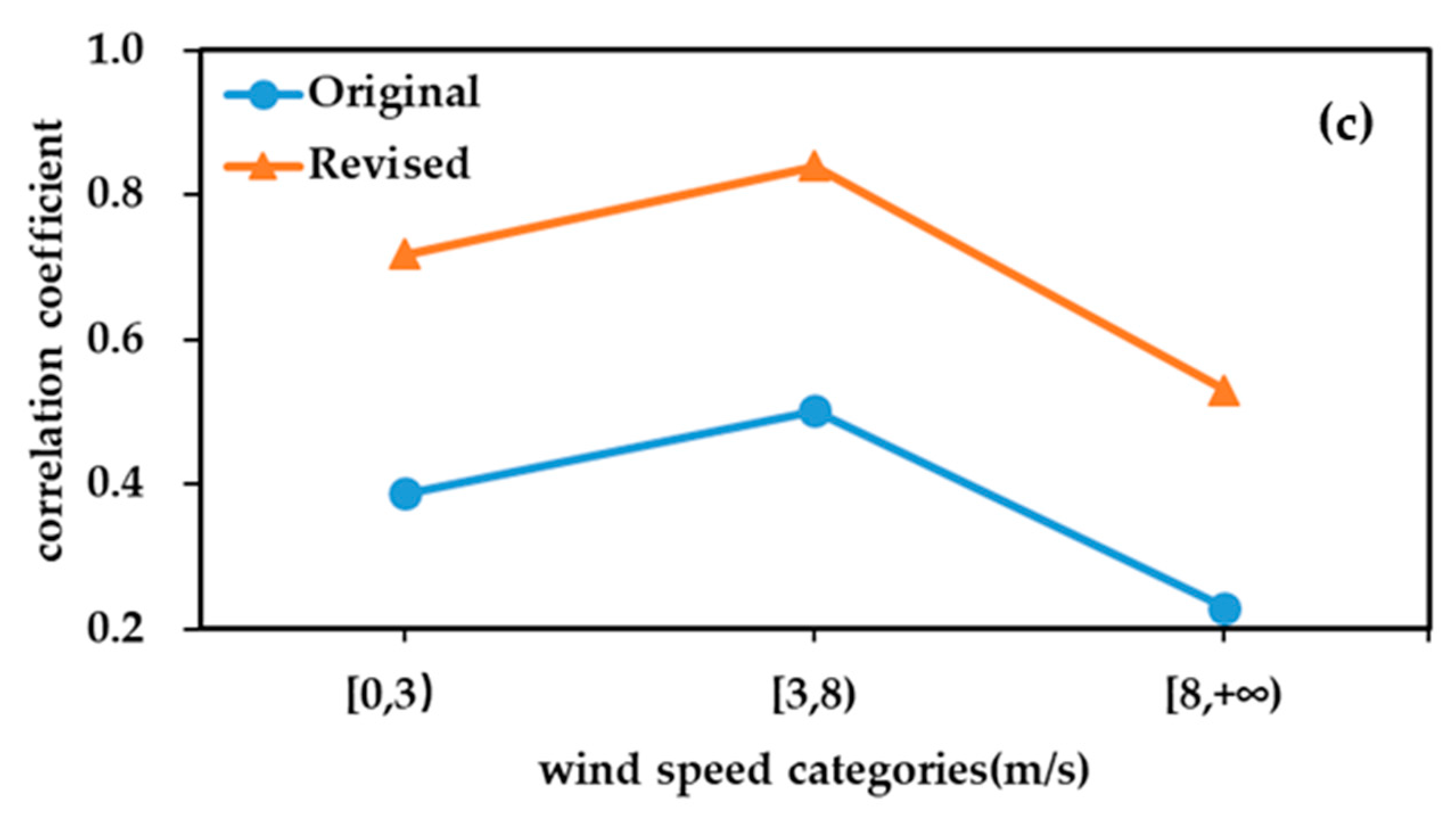
3.3. Correction Effects of Different Wind Speed Levels
3.4. Analysis of Correction Effects for Strong Wind Cases
4. Conclusions
- The evaluation with ground truth grid data indicates that, after downscaling correction, the spatial distribution of grid forecast wind speeds in the entire complex terrain study area becomes more refined, with the spatial resolution improving from 3 km to 1 km, reflecting the fine-scale terrain effects. The corrected wind speed significantly reduces the forecast errors compared to the model forecasts, with the forecast accuracy markedly improved. The mean bias (BIAS) decreases from 2.25 m/s to 0.02 m/s, basically eliminating the model’s systematic errors. The root mean square error (RMSE) decreases from 3.26 m/s to 0.52 m/s, reducing the model’s random errors, with an RMSE improvement rate of approximately 83.97%. The correlation coefficient (R) improves from 0.68 to 0.96.
- In terms of spatiotemporal variation characteristics, the wind speed grid forecast downscaling correction method shows more significant improvements in high-altitude complex terrain areas, forecasts beyond 12 h, and spring wind speed forecasts. The corrected wind speed forecast errors are more stable in both time and space, with forecast errors caused by terrain, forecast lead time, and seasonal factors significantly reduced. For wind speed levels below 8 m/s, the RMSE decreases from 2.02 m/s to 0.59 m/s, with an RMSE improvement rate of 70.55%, indicating a significant correction improvement. For wind speed levels above 8 m/s, the RMSE decreases from 2.20 m/s to 1.65 m/s, with an RMSE improvement rate of 24.98%, showing good correction effects for wind speeds above 5 on the Beaufort scale.
- The specific performance of the forecast wind speeds before and after downscaling correction is analyzed by selecting the strong wind event in Zhangjiakou on 26 April 2022. During this weather event, the forecast wind speeds in the study area are generally overestimated. After downscaling correction, the spatial distribution of the forecast wind speeds becomes more refined and closely matches the ground truth grid and station observations, with consistent spatial distribution. The RMSE in the strong wind-affected area decreases from 2.17 m/s to 0.83 m/s, with an RMSE improvement rate of 61.71%, indicating significant downscaling correction effects, especially in the Bashang Plateau and valley regions. The downscaling corrected results have significant reference value.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.C.; Xiao, Y.; Deng, H. Research on short-term wind speed correction technology of wind farm based on ELM. Meteor Mon. 2016, 42, 466–471. [Google Scholar]
- Ye, X.L.; Gu, R.; Deng, H.; Chen, H.; Yang, X. Modification technology research of short-term wind speed in wind farm based on WRF model and PSO-LSSVM method. Power Syst. Prot. Control 2017, 45, 48–54. [Google Scholar]
- Wang, H.; Li, Y.; Wu, Z.H.; Guo, P. Advances in researches on mechanisms and forecast techniques of high winds in China. Meteorol. Sci. Technol. 2019, 47, 600–607. [Google Scholar]
- Zhu, H.F.; Wang, D.Y.; Guan, Z.Y.; Liu, Y.; Fu, Y.F. Effects of different initial fields on grapes numerical prediction. Acta Meteorol. Sin. 2007, 65, 493–502. [Google Scholar]
- Zhang, G.J.; Wang, M.H.; Lu, C.S.; Bao, Q.; Wang, Y. Development of parameterizations of atmospheric physical processes for high resolution global climate models and their applications. China Basic Sci. 2017, 19, 40–44. [Google Scholar]
- Carvalho, D.; Rocha, A.; Gomez-Gesteira, M.; Santos, C. A sensitivity study of the WRF model in wind simulation for an area of high wind energy. Environ. Model. Softw. 2012, 33, 23–34. [Google Scholar] [CrossRef]
- Xiao, Q.Y.; Hu, F.; Fan, S.J. Model output statistics and wind power numerical prediction. Resour. Sci. 2017, 39, 116–124. [Google Scholar]
- Sun, J.B.; Qian, Y.Z.; Chen, P.Y.; Zheng, Z.; Le, Y.L. The Artificial neural network method on the station wind in landfall typhoon. Meteor Mon. 2010, 36, 81–86. [Google Scholar]
- Zjavka, L. Wind speed forecast correction models using polynomial neural networks. Renew. Energy 2015, 83, 998–1006. [Google Scholar] [CrossRef]
- Deng, H.; Zhang, Y.C.; Gu, R.; Huang, F.; Zhi, X.L. Correction method of short-term wind speed in wind farm research based on PCA and RBF neural network. Meteorol. Sci. Technol. 2018, 46, 10–15. [Google Scholar]
- QI, S.B.; WANG, W.Q.; ZHANG, X.Y. Wind speed and wind power prediction based on SVM. East China Electr. Power 2009, 37, 1600–1603. [Google Scholar]
- Kong, L.B.; Zhao, Y.R.; Wang, J.J.; Tong, J.L.; Dang, Z.L.; Zhang, W.Y. Modification of wind speed based on SVM. J. Southwest Univ. (Nat. Sci. Ed.) 2014, 36, 194–200. [Google Scholar]
- Lin, Y.J.; Kruger, U.; Zhang, J.P.; Wang, Q.; Lamont, L.; El Chaar, L. Seasonal analysis and prediction of wind energy using random forests and ARX model structures. IEEE Trans. Control Syst. Technol. 2015, 23, 1994–2002. [Google Scholar] [CrossRef]
- Sun, Q.D.; Jiao, R.L.; Xia, J.J.; Yan, Z.W.; Li, H.C.; Sun, J.H.; Wang, L.Z.; Liang, Z.M. Adjusting wind speed prediction of numerical weather forecast model based on machine learning methods. Meteorol. Mon. 2019, 45, 426–436. [Google Scholar]
- Xu, L.N.; Shen, Y.B.; Feng, Z.; Ye, H. Applicability research and integrated application of various correction methods for wind speed forecast in a wind farm. Arid Land Geogr. 2022, 45, 1114–1124. [Google Scholar]
- Zhang, T.J.; Yan, P.C.; Zhang, Z.Y.; Duan, H.X.; Wang, Y.S.; Li, Y.H. Application of various technologies in modification of wind speed forecast in wind farms. J. Arid Meteorol. 2018, 36, 835–844. [Google Scholar]
- Shi, L.; Xu, L.N.; Hao, Y.Z. The correction of forecast wind speed in a wind farm based on partitioning of the high correlation of wind speed. J. Appl. Meteorol. Sci. 2016, 27, 506–512. [Google Scholar]
- Su, X.; Li, C. Jiangsu offshore wind speed calibration based on optimal threat score and frequency matching. Mar. Sci. Bull. 2020, 39, 548–557. [Google Scholar]
- Wu, D.; Tian, H.Q.; Liu, H.; Wang, J.J.; Zuo, C.L.; Xu, J.J. Bias correction of wind speed forecasts for the WRF model in Anhui province based on the analog Kalman filter method. J. Meteorol. Environ. 2023, 39, 31–37. [Google Scholar]
- Yang, C.; Jiang, Y.J.; Yu, Z.S.; Jiang, W.D.; Kang, L.L.; Wang, L.J. Correction technology of regional wind speed forecasting based on partial least squares regression. Meteorol. Mon. 2019, 45, 676–684. [Google Scholar]
- Zeng, X.Q.; Xue, F.; Yao, L.; Zhao, S.R. Comparative study of different error correction methods on model output wind field. J. Appl. Meteorol. Sci. 2019, 30, 49–60. [Google Scholar]
- Mao, B.; Yang, H.; Zhou, S.J.; Yang, K.Q.; Chen, M. Deep learning method for wind speed grid point forecasting data correction based on CMA-REPS. J. Chengdu Univ. Inf. Technol. 2023, 38, 264–270. [Google Scholar]
- Han, L.; Chen, M.X.; Chen, K.K.; Chen, H.N.; Zhang, Y.B.; Lu, B.; Song, L.Y.; Qin, R. A Deep Learning Method for Bias Correction of ECMWF 24–240 h Forecasts. Adv. Atmos. Sci. 2021, 38, 1444–1459. [Google Scholar] [CrossRef]
- Yang, X.; Dai, K.; Zhu, Y.J. Calibration of Gridded Wind Speed Forecasts Based on Deep Learning. J. Meteor. Res. 2023, 37, 757–774. [Google Scholar] [CrossRef]
- Gerges, F.; Boufadel, M.C.; Bou-Zeid, E.; Nassif, H.; Wang, J.T.L. Downscaling Daily Wind Speed with Bayesian Deep Learning for Climate Monitoring. Int. J. Data Sci. Anal. 2024, 17, 411–424. [Google Scholar] [CrossRef]
- Ferrarin, L.; Stucchi, L.; Bocchiola, D. Statistical Downscaling of GCMs Wind Speed Data for Trend Analysis of Future Scenarios: A Case Study in the Lombardy Region. Theor. Appl. Climatol. 2024, 155, 4875–4890. [Google Scholar] [CrossRef]
- Wang, H.; Yin, S.; Yue, T.; Chen, X.; Chen, D. Developing a Dynamic-Statistical Downscaling Framework for Wind Speed Prediction for the Beijing 2022 Winter Olympics. Clim. Dyn. 2024. [Google Scholar] [CrossRef]
- Shin, J.Y.; Min, B.; Kim, K.R. High-Resolution Wind Speed Forecast System Coupling Numerical Weather Prediction and Machine Learning for Agricultural Studies—A Case Study from South Korea. Int. J. Biometeorol. 2022, 66, 1429–1443. [Google Scholar] [CrossRef]
- Hao, L.; Li, W. Relationship between Circulation Patterns in North China and Climate in Hebei. Trans. Atmos. Sci. 2009, 32, 618–626. [Google Scholar]
- Yuan, S.; Qi, J.; Wang, W.; Huang, N. Short-term Wind Speed Prediction Using Regularized Extreme Learning Machine. Power Syst. Clean Energy 2016, 32, 62–68. [Google Scholar]


| Number | Name | Number | Name |
|---|---|---|---|
| 1 | Elevation | 13 | Horizontal wind speed at 700 hPa |
| 2 | Lat | 14 | Geopotential height at 700 hPa |
| 3 | Lon | 15 | Relative humidity at 700 hPa |
| 4 | Forecast duration | 16 | Temperature at 700 hPa |
| 5 | Wind speed at 10 m | 17 | Horizontal wind speed at 850 hPa |
| 6 | Surface pressure | 18 | Geopotential height at 850 hPa |
| 7 | Relative humidity at 2 m | 19 | Relative humidity at 850 hPa |
| 8 | Air temperature at 2 m | 20 | Temperature at 850 hPa |
| 9 | Horizontal wind speed at 500 hPa | 21 | Horizontal wind speed at 925 hPa |
| 10 | Geopotential height at 500 hPa | 22 | Geopotential height at 925 hPa |
| 11 | Relative humidity at 500 hPa | 23 | Relative humidity at 925 hPa |
| 12 | Temperature at 500 hPa | 24 | Temperature at 925 hPa |
| Sites | Observed Mean (m/s) | Revision Status | RMSE (m/s) | BIAS (m/s) | R | C (%) |
|---|---|---|---|---|---|---|
| M1 | 2.75 | original | 2.50 | 1.80 | 0.74 | 65.82 |
| revised | 0.86 | −0.08 | 0.95 | |||
| M2 | 2.89 | original | 2.61 | 1.93 | 0.70 | 76.35 |
| revised | 0.62 | −0.03 | 0.96 | |||
| M3 | 2.37 | original | 1.77 | 0.46 | 0.64 | 65.96 |
| revised | 0.60 | −0.01 | 0.93 | |||
| M4 | 1.85 | original | 1.83 | 0.87 | 0.67 | 68.80 |
| revised | 0.57 | 0.01 | 0.91 | |||
| M5 | 1.74 | original | 2.09 | 1.18 | 0.62 | 74.68 |
| revised | 0.53 | 0.08 | 0.92 | |||
| M6 | 2.81 | original | 1.78 | 0.50 | 0.73 | 65.25 |
| revised | 0.62 | −0.12 | 0.96 | |||
| M7 | 2.07 | original | 1.86 | 0.81 | 0.69 | 69.53 |
| revised | 0.57 | −0.03 | 0.95 | |||
| M8 | 1.69 | original | 1.88 | 0.90 | 0.67 | 60.72 |
| revised | 0.74 | 0.15 | 0.88 | |||
| M9 | 2.58 | original | 2.12 | 1.11 | 0.69 | 69.22 |
| revised | 0.65 | −0.12 | 0.94 | |||
| M10 | 2.11 | original | 2.18 | 1.38 | 0.74 | 74.29 |
| revised | 0.56 | 0.03 | 0.95 | |||
| M11 | 1.54 | original | 1.33 | 0.28 | 0.65 | 59.70 |
| revised | 0.54 | 0.08 | 0.91 |
| Sites | Observed Mean (m/s) | Revision Status | RMSE (m/s) | BIAS (m/s) | R | C (%) |
|---|---|---|---|---|---|---|
| M2 | 5.52 | original | 3.05 | 2.66 | 0.93 | 71.97 |
| revised | 0.85 | −0.36 | 0.94 | |||
| M9 | 6.28 | original | 1.89 | 1.11 | 0.84 | 58.96 |
| revised | 0.78 | −0.46 | 0.97 | |||
| M6 | 6.80 | original | 1.45 | 0.57 | 0.91 | 35.87 |
| revised | 0.93 | −0.50 | 0.97 | |||
| M10 | 5.09 | original | 2.28 | 1.58 | 0.90 | 66.50 |
| revised | 0.76 | −0.31 | 0.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Li, Z.; Shen, Y. Study on Downscaling Correction of Near-Surface Wind Speed Grid Forecasts in Complex Terrain. Atmosphere 2024, 15, 1090. https://doi.org/10.3390/atmos15091090
Liu X, Li Z, Shen Y. Study on Downscaling Correction of Near-Surface Wind Speed Grid Forecasts in Complex Terrain. Atmosphere. 2024; 15(9):1090. https://doi.org/10.3390/atmos15091090
Chicago/Turabian StyleLiu, Xin, Zhimin Li, and Yanbo Shen. 2024. "Study on Downscaling Correction of Near-Surface Wind Speed Grid Forecasts in Complex Terrain" Atmosphere 15, no. 9: 1090. https://doi.org/10.3390/atmos15091090
APA StyleLiu, X., Li, Z., & Shen, Y. (2024). Study on Downscaling Correction of Near-Surface Wind Speed Grid Forecasts in Complex Terrain. Atmosphere, 15(9), 1090. https://doi.org/10.3390/atmos15091090







