Statistical Analysis of Atmospheric Ducts in the Yellow and Bohai Seas of China and Study of Their Electromagnetic Wave Propagation Characteristics
Abstract
1. Introduction
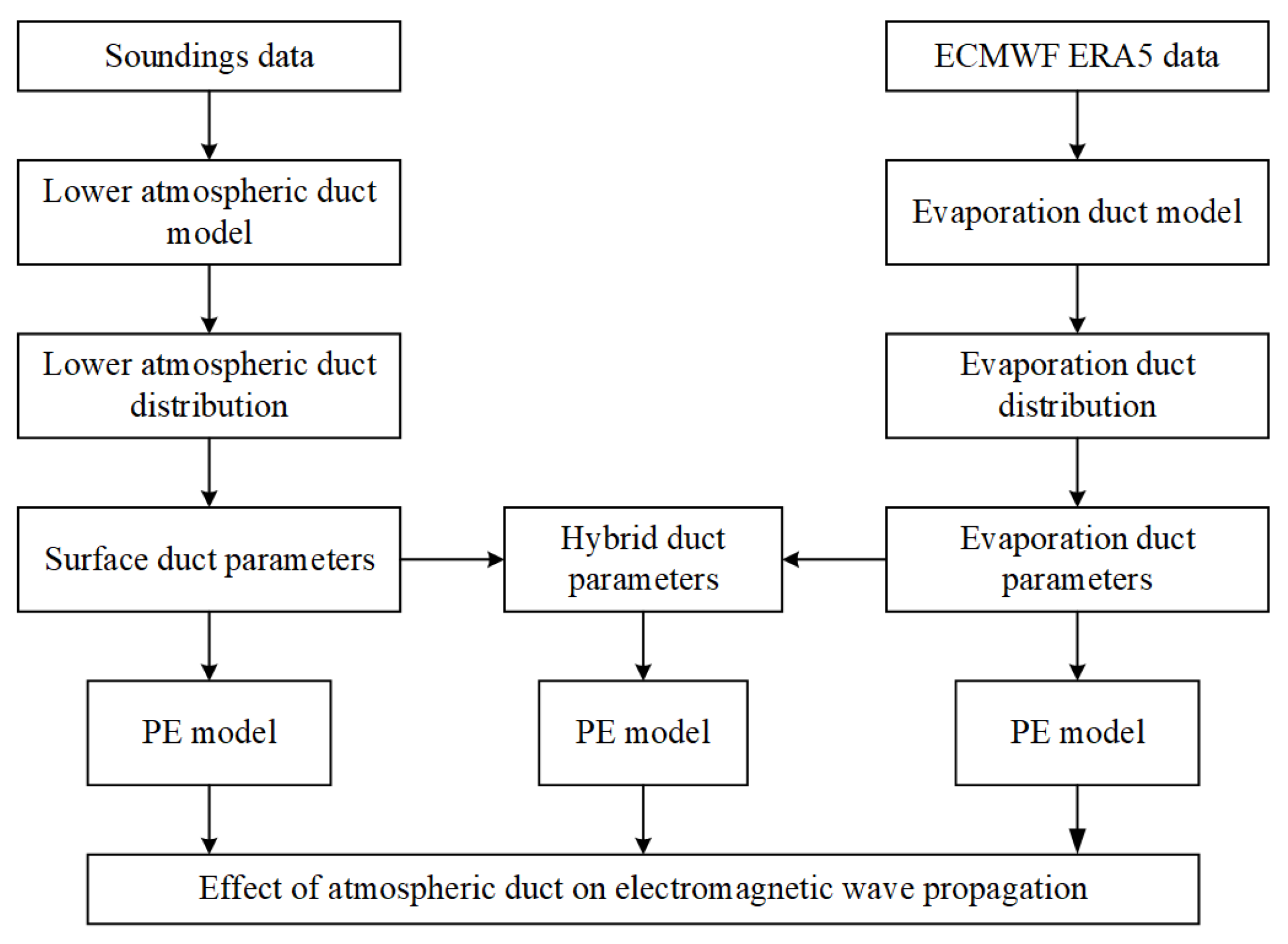
2. Materials and Methods
2.1. Data
2.1.1. Sounding Data
2.1.2. Reanalysis Data
2.2. Atmospheric Duct Model
2.2.1. Lower Atmospheric Ducts
2.2.2. Evaporation Duct Model
2.3. Evaporation Duct Diagnostic Model
2.4. Parabolic Equation Model
3. Results and Discussion
3.1. Analysis of Atmospheric Duct Distribution Characteristics in the Bohai Sea and Yellow Sea
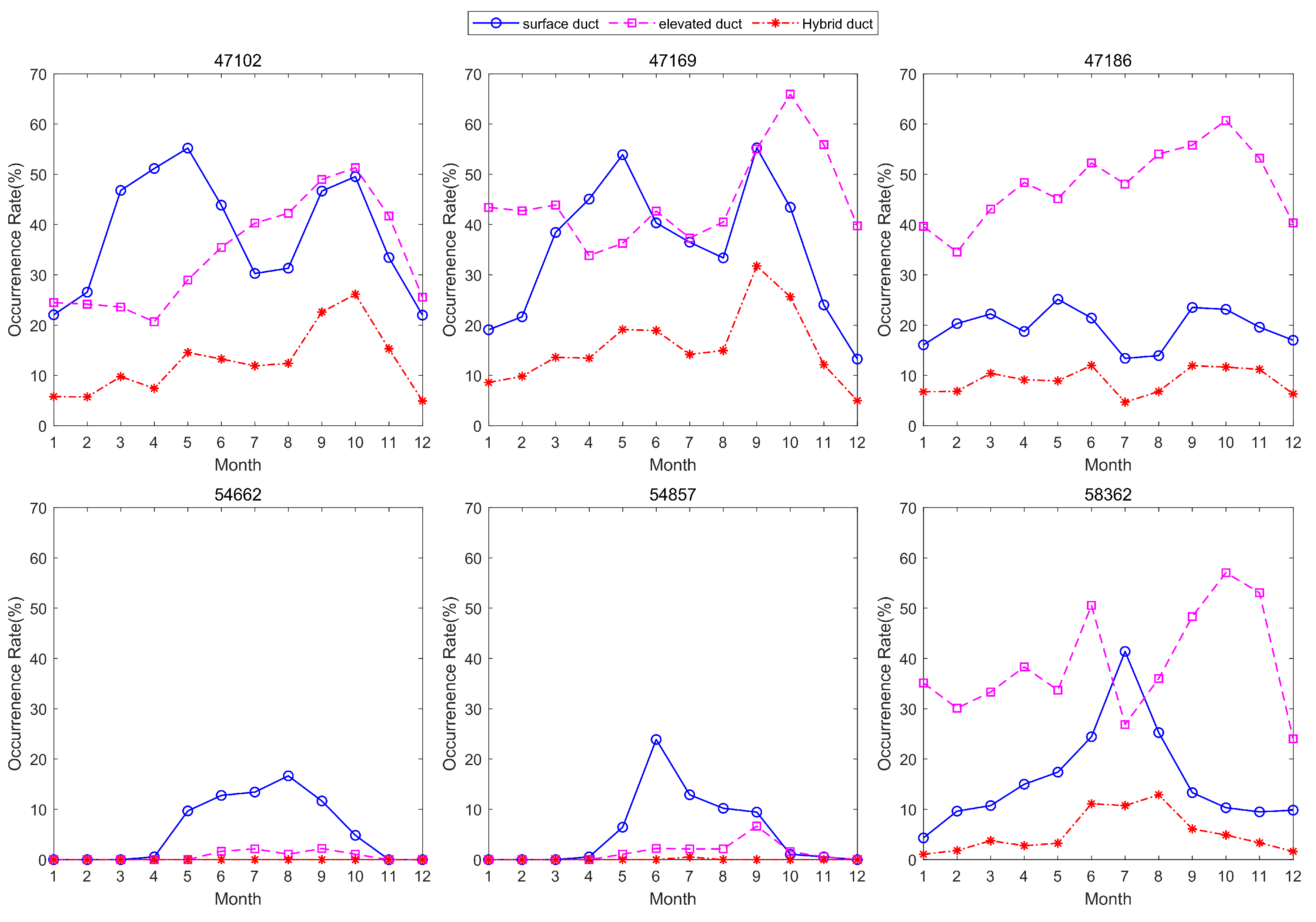
3.1.1. Distribution Characteristics of Lower Atmospheric Ducts
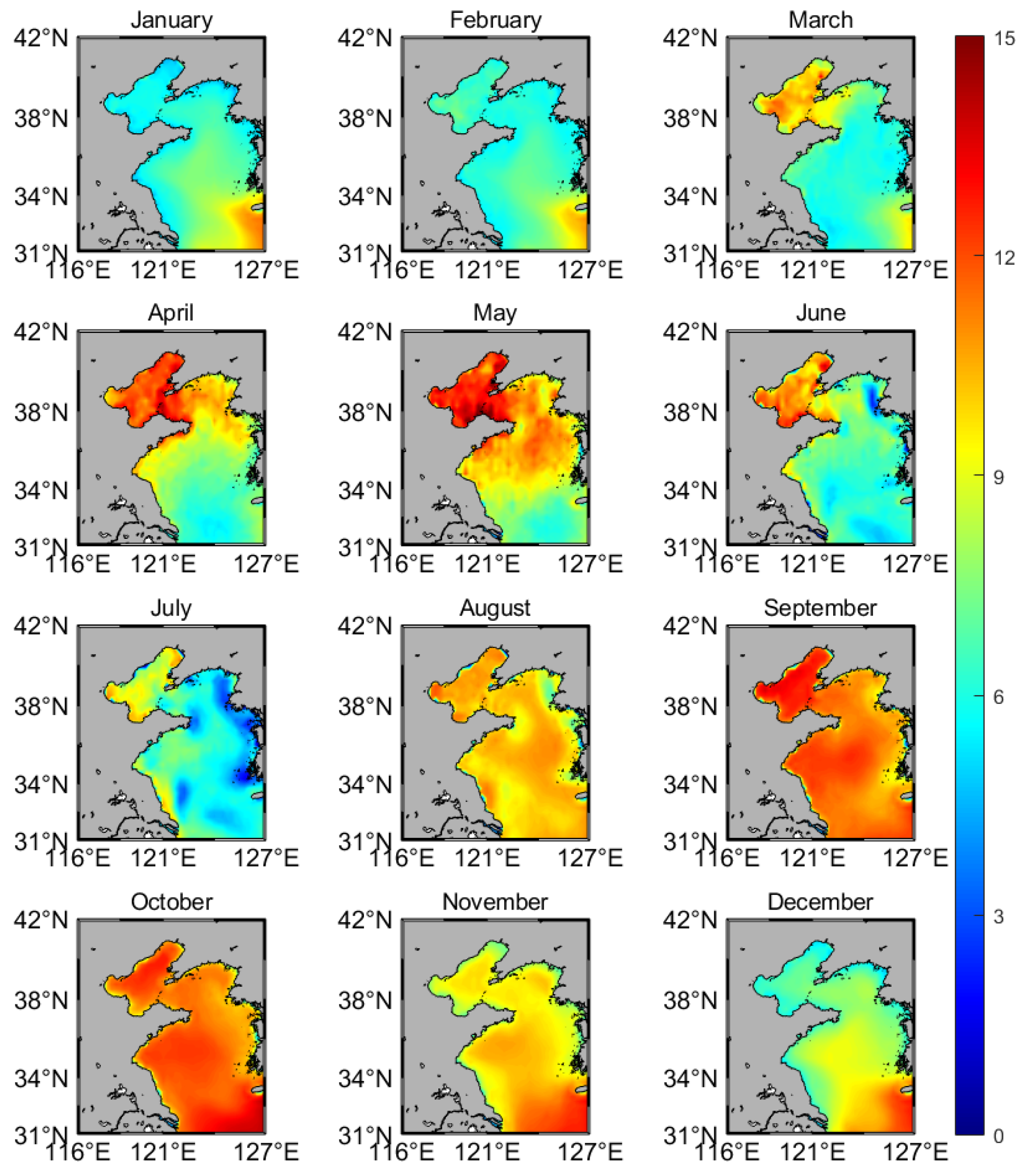
3.1.2. Distribution Characteristics of Evaporation Ducts
3.2. Electromagnetic Wave Propagation Characteristics in Atmospheric Ducting Environments
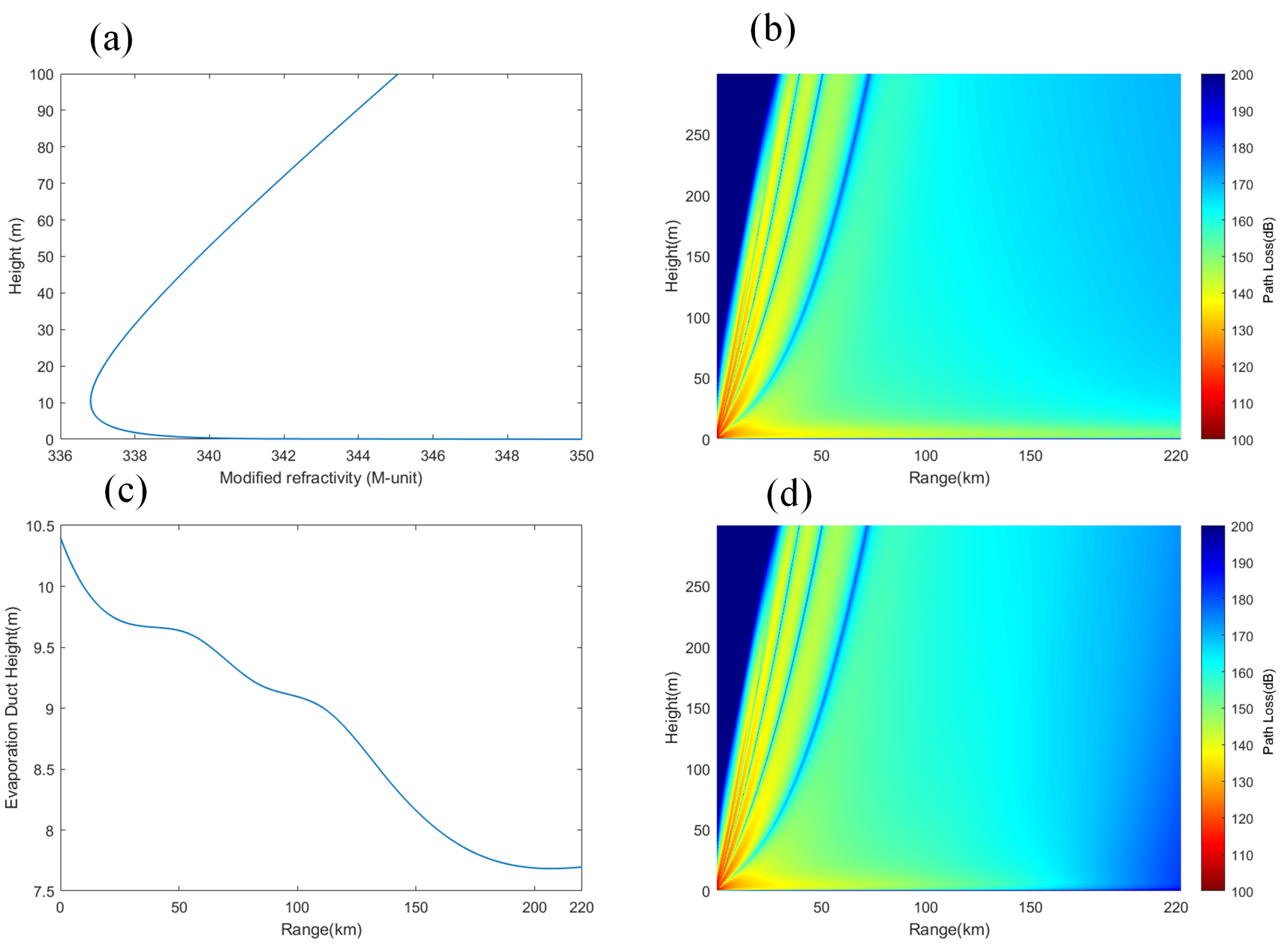
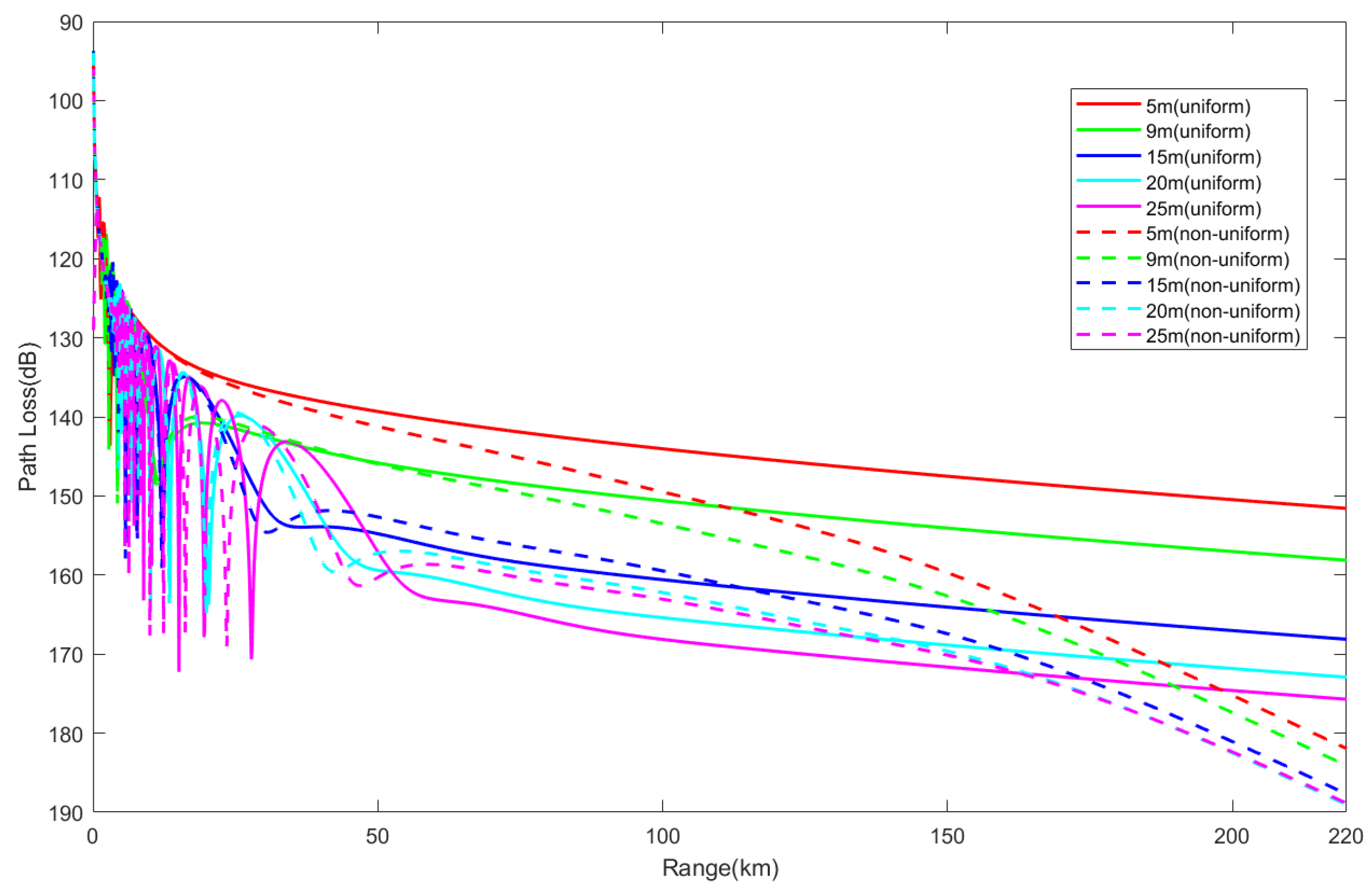
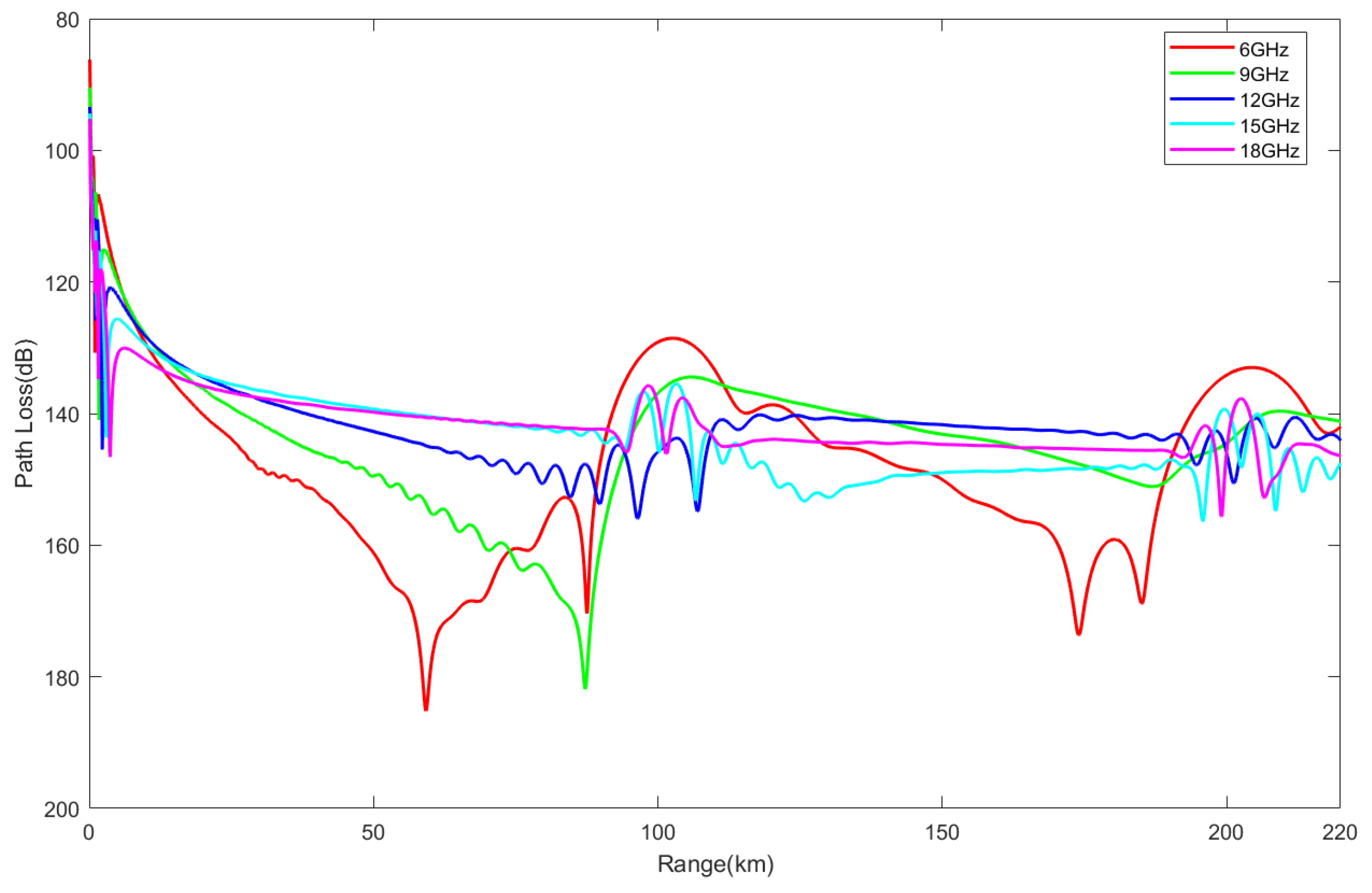
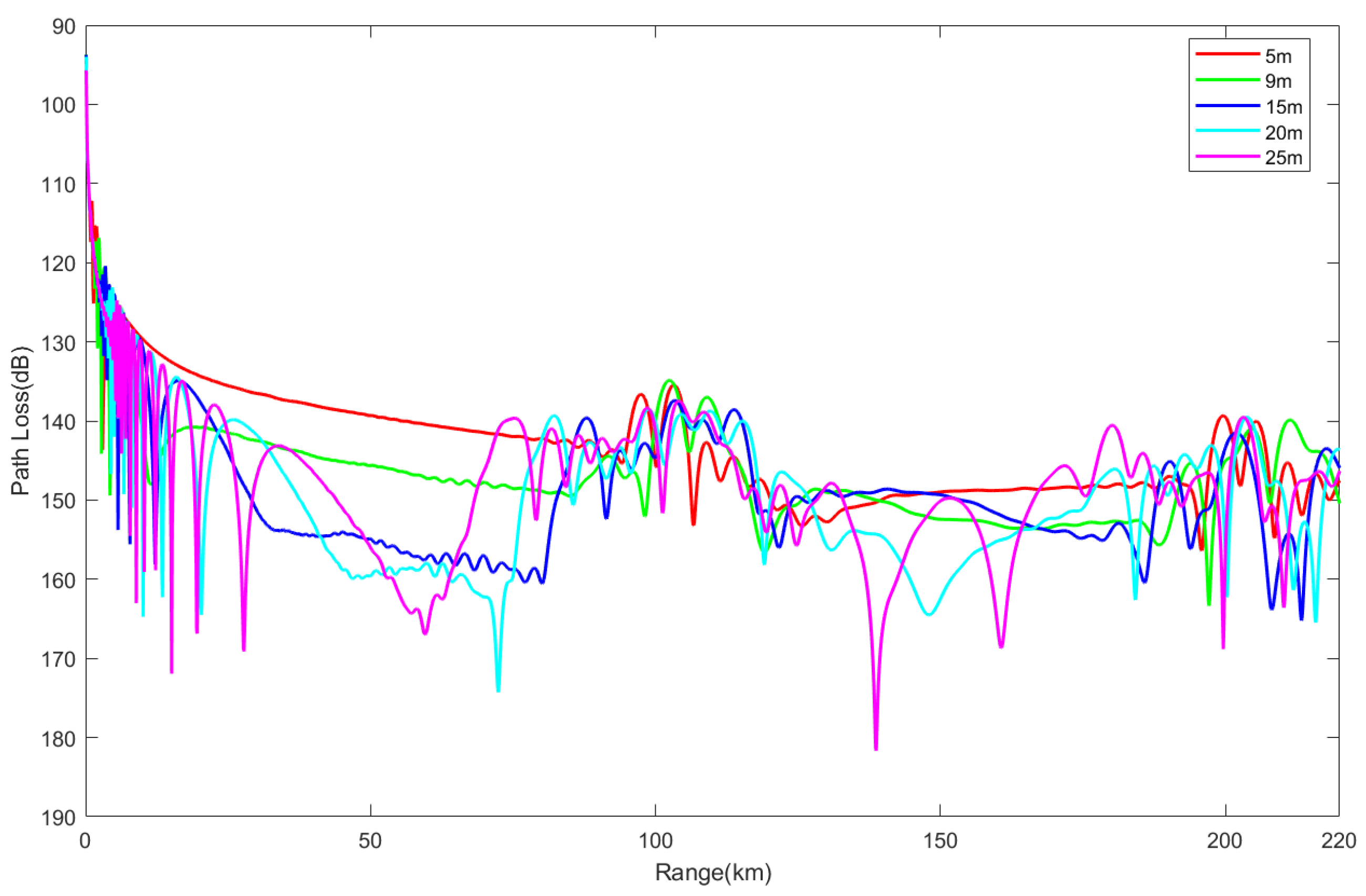
3.2.1. Electromagnetic Wave Propagation Characteristics in Evaporation Duct Environments
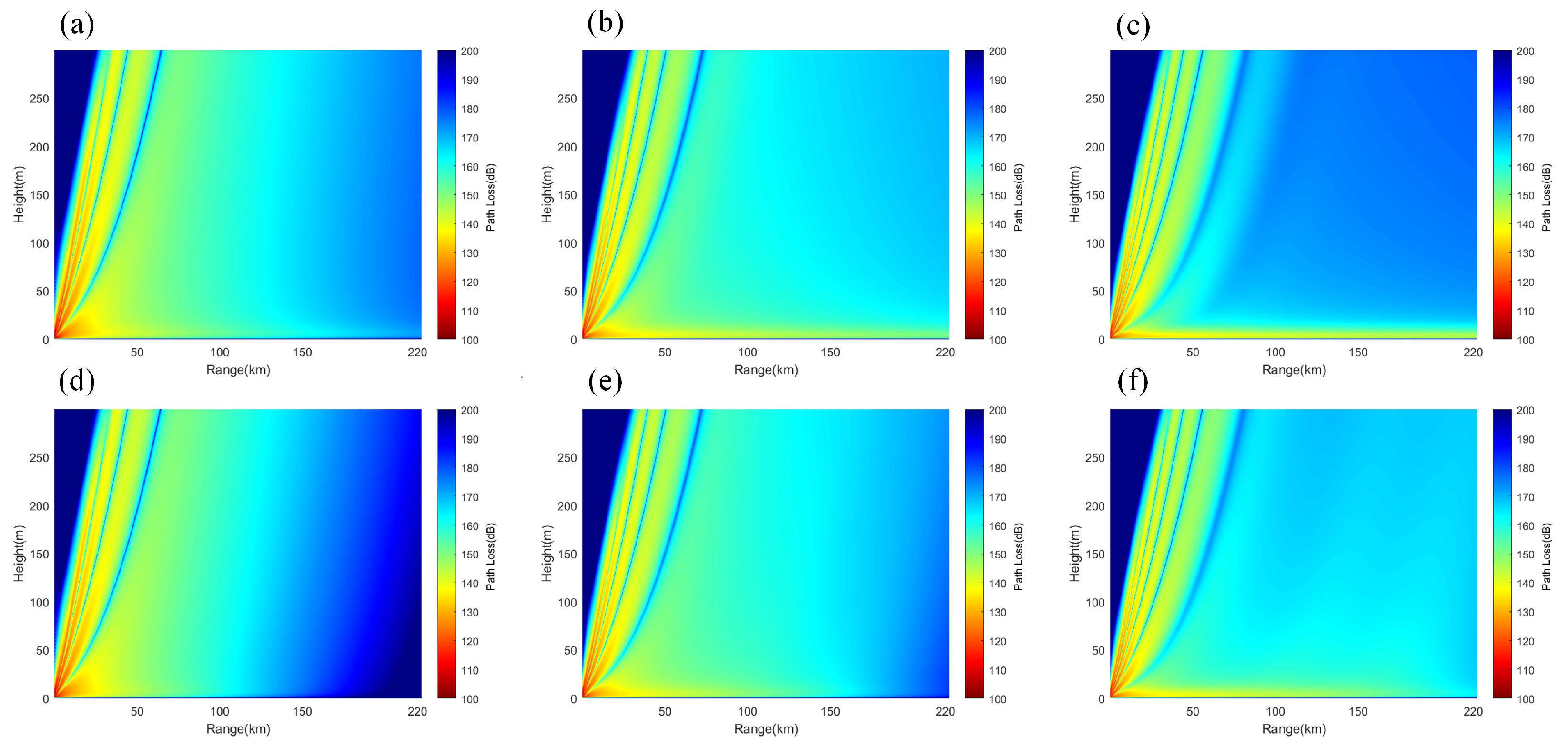
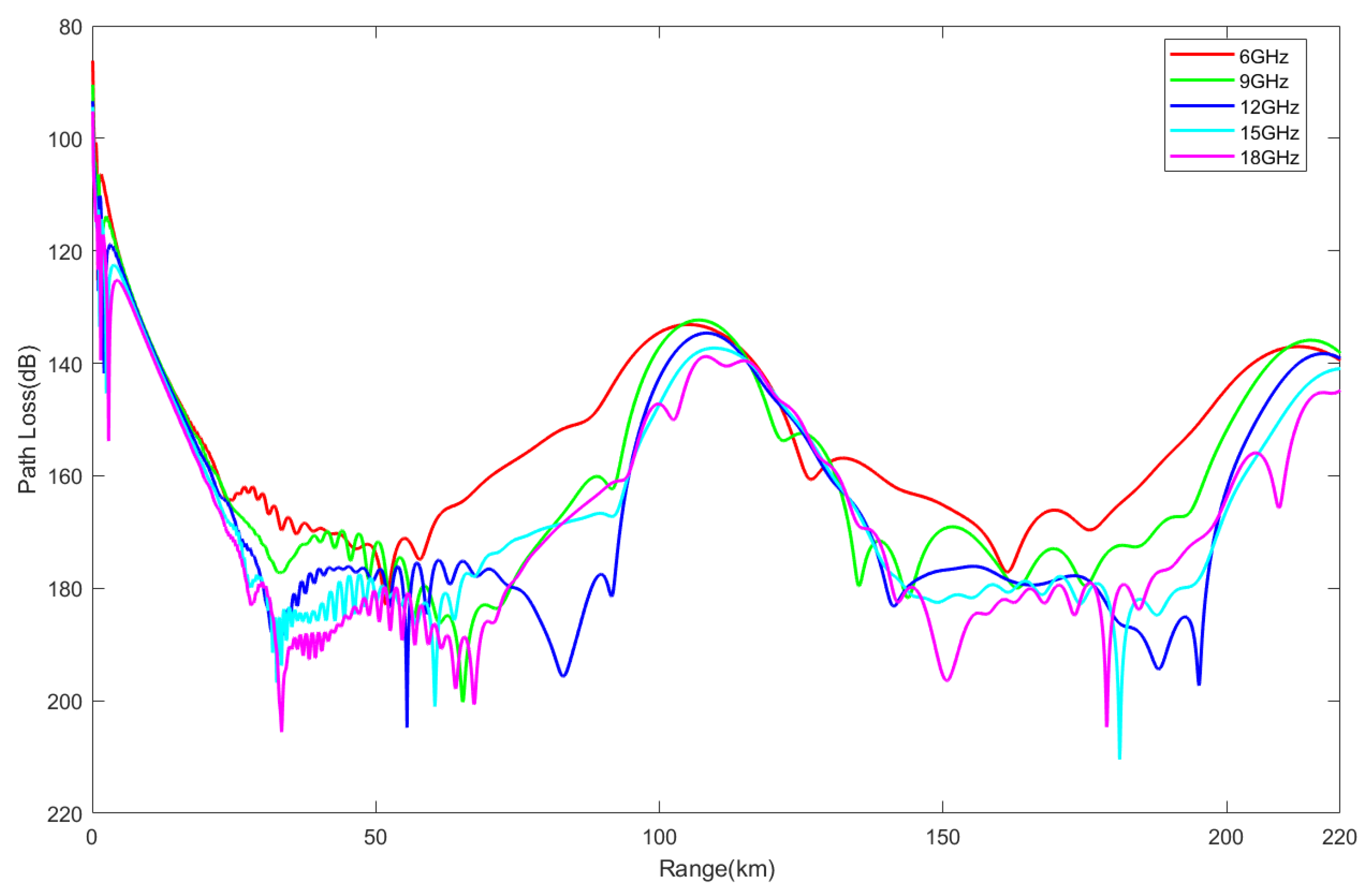
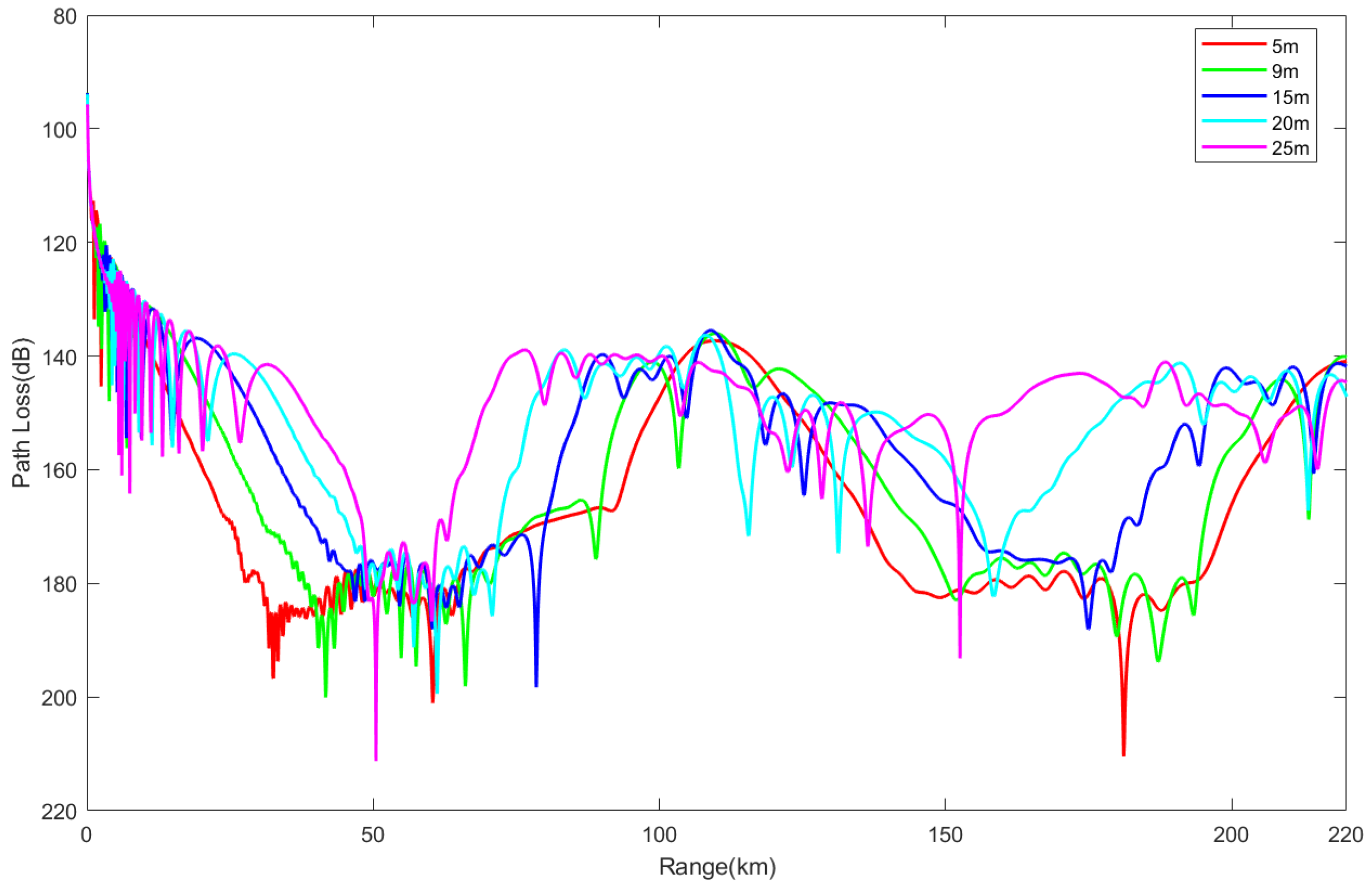
3.2.2. Electromagnetic Wave Propagation Characteristics in Surface Duct Environments
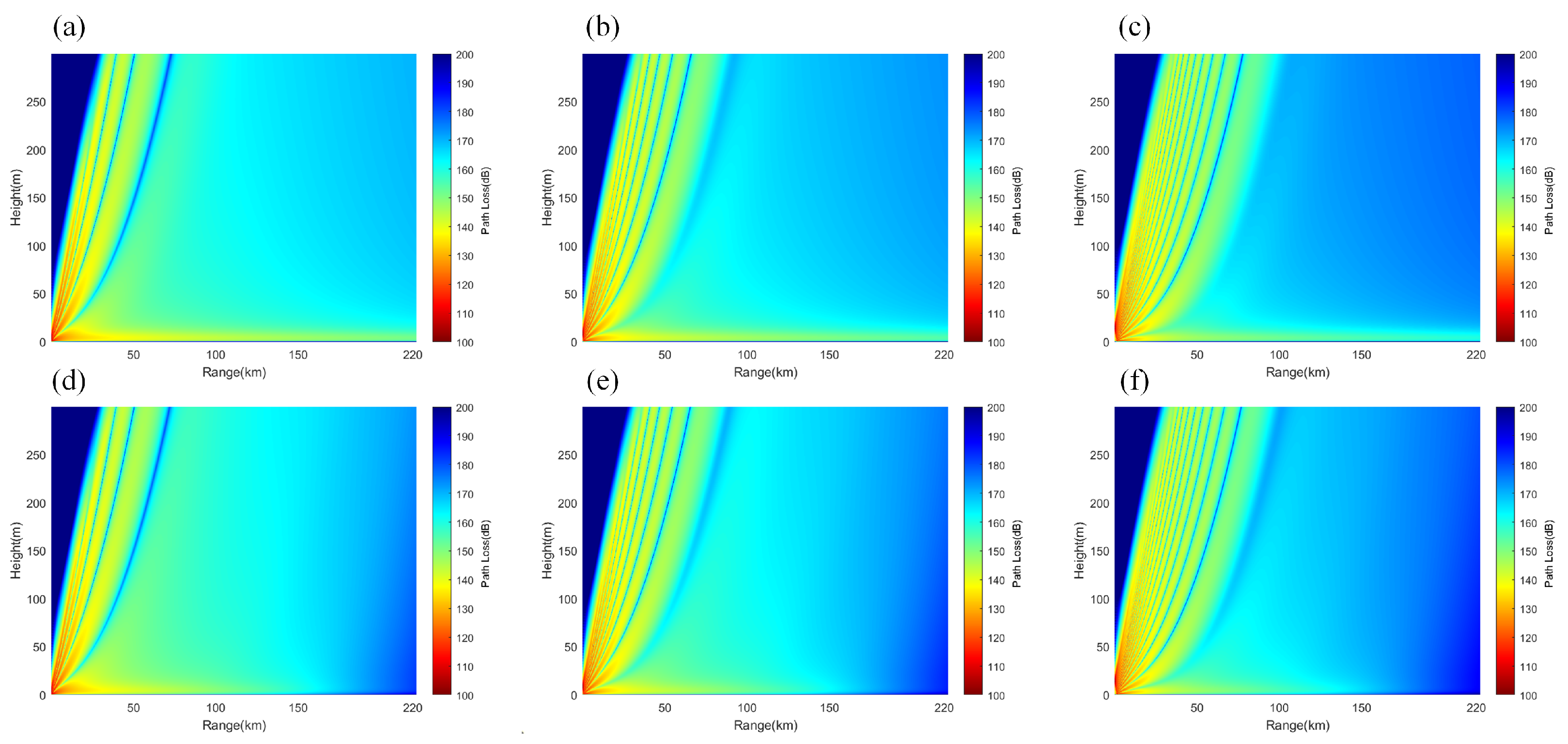
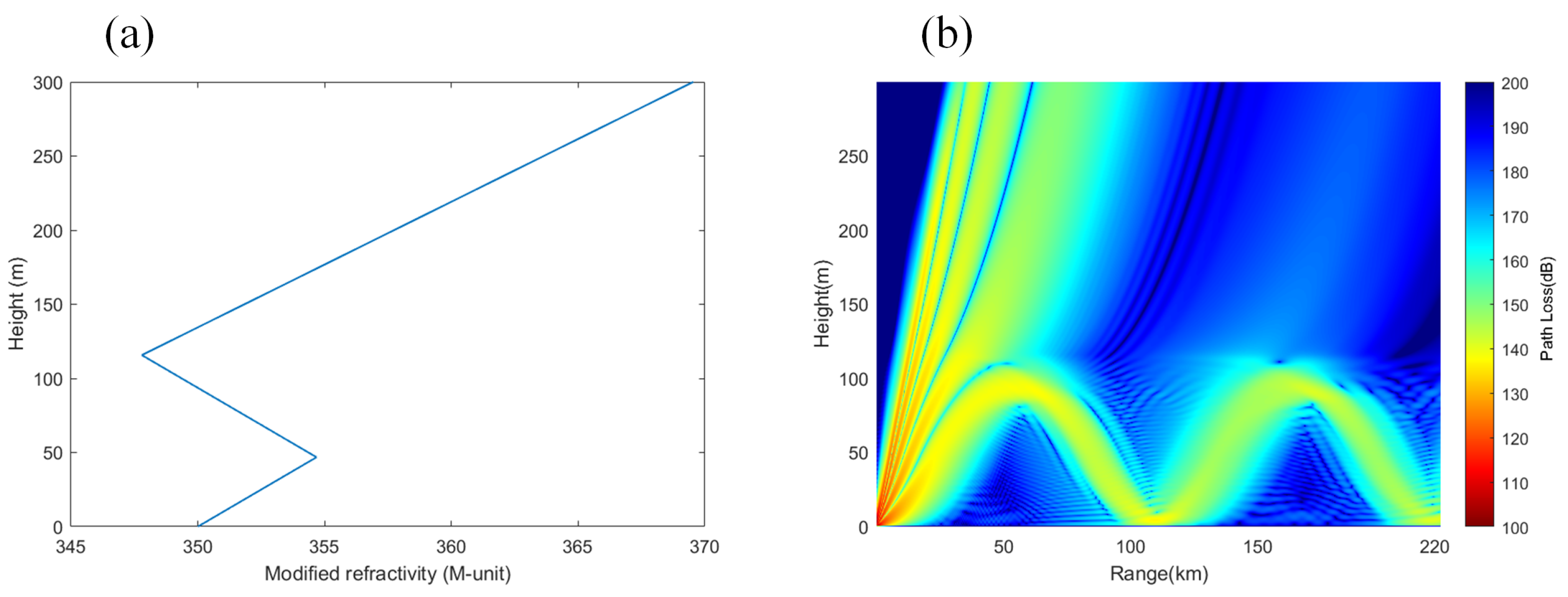
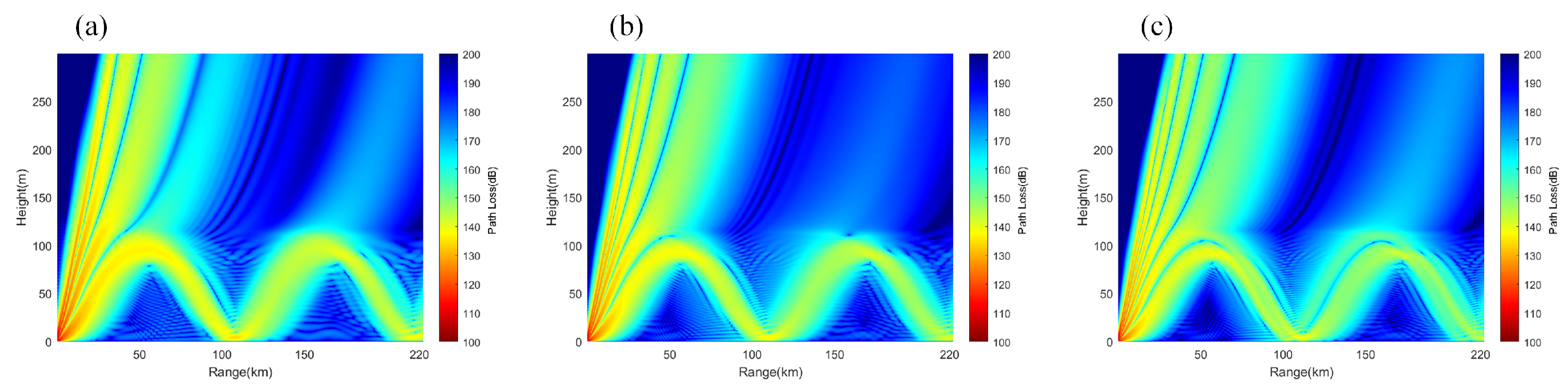
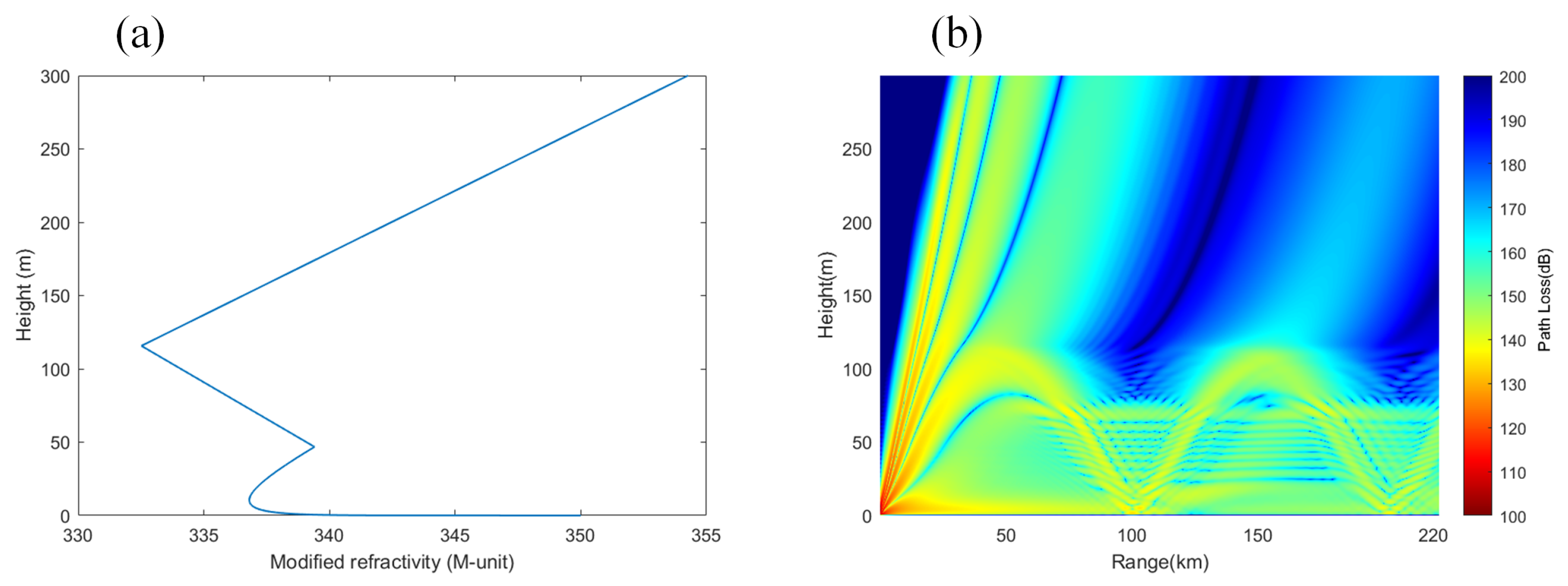
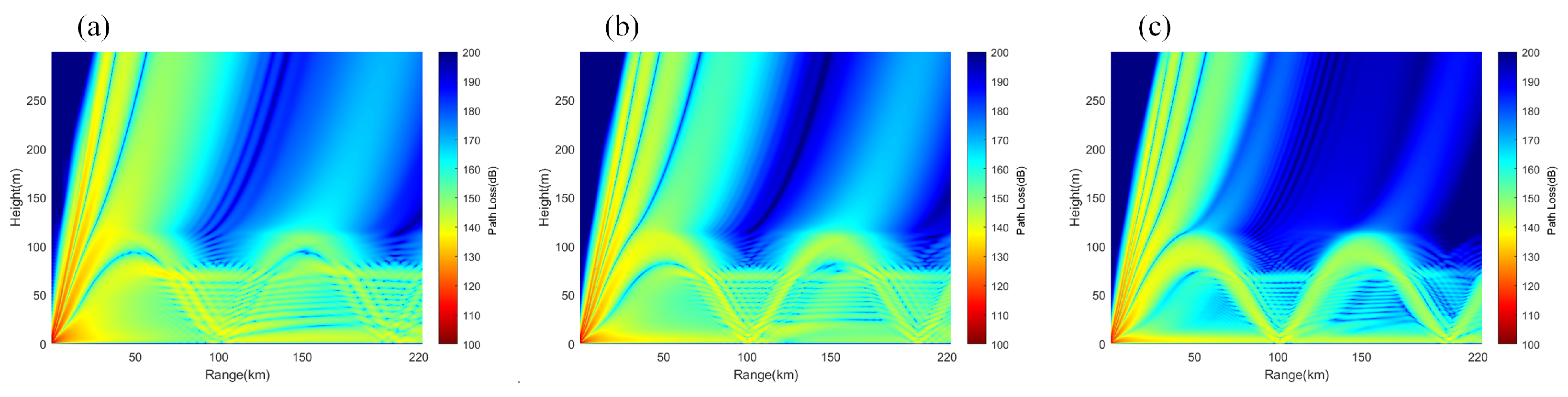
3.2.3. Electromagnetic Wave Propagation Characteristics in Hybrid Duct Environments
4. Conclusions
- Evaporation duct distribution characteristics: In the Bohai Sea region, the height of evaporation ducts is highest in spring and autumn (13 m) and lowest in winter (7 m); in the Yellow Sea region, it is highest in autumn (12 m) and lowest in summer (6 m). The height distribution of ducts in the Yellow Sea is uneven, as it is higher in the southeast and lower in the northwest from November to March, while it is higher in the north and lower in the south in April and May.
- Low-altitude atmospheric duct distribution characteristics: Surface ducts have a higher occurrence rate from May to September and a lower rate from October to April of the following year; elevated ducts have the highest occurrence rate in October (60%).
- Electromagnetic wave propagation characteristics: In an evaporation duct environment, propagation loss increases slowly with distance, and the loss in a non-uniform environment is greater than in a uniform environment; in a surface duct environment, the propagation loss exhibits periodic fluctuations with distance, with fluctuation amplitudes exceeding 47 dB. The propagation loss in a mixed duct environment is between that of evaporation ducts and surface ducts, filling the shadow area from 10 m to 70 m.
- Impacts of frequency and antenna height: In an evaporation duct environment, the higher the frequency and the lower the antenna height, the smaller the propagation loss; in a surface duct environment, the frequency has a smaller impact, but increasing the antenna height widens the low-propagation-loss region. In a mixed duct environment, at low frequencies and antenna heights greater than the evaporation duct height, the propagation characteristics are similar to those of surface ducts; at high frequencies and antenna heights lower than the evaporation duct height, the characteristics are similar to those of evaporation ducts.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, L.; Zhao, X.; Liu, Y. The Statistical Characteristics of Atmospheric Ducts Observed Over Stations in Different Regions of American Mainland Based on High-Resolution GPS Radiosonde Soundings. Front. Environ. Sci. 2022, 10, 946226. [Google Scholar] [CrossRef]
- Pastore, D.M.; Greenway, D.P.; Stanek, M.J.; Wessinger, S.E.; Haack, T.; Wang, Q.; Hackett, E.E. Comparison of atmospheric refractivity estimation methods and their influence on radar propagation predictions. Radio Sci. 2021, 56, 1–17. [Google Scholar]
- Huang, L.F.; Liu, C.G.; Wang, H.G.; Zhu, Q.L.; Zhang, L.J.; Han, J.; Zhang, Y.S.; Wang, Q.N. Experimental analysis of atmospheric ducts and navigation radar over-the-horizon detection. Remote Sens. 2022, 14, 2588. [Google Scholar] [CrossRef]
- Wang, S.; Yang, K.; Shi, Y.; Zhang, H.; Yang, F.; Hu, D.; Dong, G.; Shu, Y. Long-term over-the-horizon microwave channel measurements and statistical analysis in evaporation ducts over the Yellow Sea. Front. Mar. Sci. 2023, 10, 1077470. [Google Scholar] [CrossRef]
- Yang, C.; Wang, J.; Ma, J. Exploration of X-band communication for maritime applications in the South China Sea. IEEE Antennas Wirel. Propag. Lett. 2021, 21, 481–485. [Google Scholar] [CrossRef]
- Yang, C.; Wang, J. The investigation of cooperation diversity for communication exploiting evaporation ducts in the South China Sea. IEEE Trans. Antennas Propag. 2022, 70, 8337–8347. [Google Scholar] [CrossRef]
- Robinson, L.; Newe, T.; Burke, J.; Toal, D. A simulated and experimental analysis of evaporation duct effects on microwave communications in the Irish Sea. IEEE Trans. Antennas Propag. 2022, 70, 4728–4737. [Google Scholar] [CrossRef]
- Ma, J.; Wang, J.; Yang, C. Long-range microwave links guided by evaporation ducts. IEEE Commun. Mag. 2022, 60, 68–72. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, S.; Shi, Y.; Yang, K. Measurements and analysis of maritime wireless channel at 8 GHz in the South China Sea region. IEEE Trans. Antennas Propag. 2022, 71, 2674–2681. [Google Scholar] [CrossRef]
- Qiu, Z.; Zhang, C.; Wang, B.; Hu, T.; Zou, J.; Li, Z.; Chen, S.; Wu, S. Analysis of the accuracy of using ERA5 reanalysis data for diagnosis of evaporation ducts in the East China Sea. Front. Mar. Sci. 2023, 9, 1108600. [Google Scholar] [CrossRef]
- Shi, Y.; Yang, K.; Yang, Y.; Ma, Y. A new evaporation duct climatology over the South China Sea. J. Meteorol. Res. 2015, 29, 764–778. [Google Scholar] [CrossRef]
- Shi, Y.; Yang, K.; Yang, Y.; Ma, Y. Spatio-temporal distribution of evaporation duct for the South China Sea. In Proceedings of the OCEANS 2014-TAIPEI, Taipei, Taiwan, 7–10 April 2014; pp. 1–6. [Google Scholar]
- Shi, Y.; Wang, S.; Yang, F.; Yang, K. Statistical analysis of hybrid atmospheric ducts over the Northern South China sea and their influence on over-the-horizon electromagnetic wave propagation. J. Mar. Sci. Eng. 2023, 11, 669. [Google Scholar] [CrossRef]
- Huang, L.; Zhao, X.; Liu, Y.; Yang, P.; Ding, J.; Zhou, Z. The diurnal variation of the evaporation duct height and its relationship with environmental variables in the south China Sea. IEEE Trans. Antennas Propag. 2022, 70, 10865–10875. [Google Scholar] [CrossRef]
- Yang, C.; Shi, Y.; Wang, J.; Feng, F. Regional spatiotemporal statistical database of evaporation ducts over the South China Sea for future long-range radio application. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 6432–6444. [Google Scholar] [CrossRef]
- Yang, C.; Shi, Y.; Wang, J. The Preliminary Investigation of Communication Characteristics Using Evaporation Duct across the Taiwan Strait. J. Mar. Sci. Eng. 2022, 10, 1493. [Google Scholar] [CrossRef]
- Yang, K.D.; Ma, Y.L.; Shi, Y. Spatio-temporal distributions of evaporation duct for the West Pacific Ocean. Acta Phys. Sin. 2009, 58, 7339–7350. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, K.; Shi, Y. Spatial and temporal variability of the evaporation duct in the Gulf of Aden. Tellus A Dyn. Meteorol. Oceanogr. 2016, 68, 29792. [Google Scholar] [CrossRef]
- Yang, N.; Su, D.; Wang, T. Atmospheric ducts and their electromagnetic propagation characteristics in the Northwestern South China Sea. Remote Sens. 2023, 15, 3317. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, Y.; Qiao, J.; Li, J.; Zhou, C. Statistical Analysis of the Spatiotemporal Distribution of Lower Atmospheric Ducts over the Seas Adjacent to China, Based on the ECMWF Reanalysis Dataset. Remote Sens. 2022, 14, 4864. [Google Scholar] [CrossRef]
- Li, X.; Sheng, L.; Wang, W. Elevated Ducts and Low Clouds over the Central Western Pacific Ocean in Winter Based on GPS Soundings and Satellite Observation. J. Ocean. Univ. China 2021, 20, 244–256. [Google Scholar] [CrossRef]
- Cheng, Y.; Zha, M.; You, Z.; Zhang, Y. Duct climatology over the south China sea based on European center for medium range weather forecast reanalysis data. J. Atmos. Sol.-Terr. Phys. 2021, 222, 105720. [Google Scholar] [CrossRef]
- Zhu, J.; Zou, H.; Kong, L.; Zhou, L.; Li, P.; Cheng, W.; Bian, S. Surface atmospheric duct over Svalbard, Arctic, related to atmospheric and ocean conditions in winter. Arct. Antarct. Alp. Res. 2022, 54, 264–273. [Google Scholar] [CrossRef]
- Feng, G.; Huang, J.; Su, H. A new ray tracing method based on piecewise conformal transformations. IEEE Trans. Microw. Theory Tech. 2022, 70, 2040–2052. [Google Scholar] [CrossRef]
- Ozgun, O.; Sahin, V.; Erguden, M.E.; Apaydin, G.; Yilmaz, A.E.; Kuzuoglu, M.; Sevgi, L. PETOOL v2.0: Parabolic Equation Toolbox with evaporation duct models and real environment data. Comput. Phys. Commun. 2020, 256, 107454. [Google Scholar] [CrossRef]
- Barrios, A.; Patterson, W.; Sprague, R. Advanced propagation model (APM) version 2.1. 04 computer software configuration item (CSCI) documents. Spawar Syst. Cent. San Diego Tech. Dig. 2007, 3214, 10–21236. [Google Scholar]
- Wang, Q.; Burkholder, R.J.; Yardim, C.; Xu, L.; Pozderac, J.; Christman, A.; Fernando, H.J.; Alappattu, D.P.; Wang, Q. Range and height measurement of X-band EM propagation in the marine atmospheric boundary layer. IEEE Trans. Antennas Propag. 2019, 67, 2063–2073. [Google Scholar] [CrossRef]
- Wang, Q.; Alappattu, D.P.; Billingsley, S.; Blomquist, B.; Burkholder, R.J.; Christman, A.J.; Creegan, E.D.; De Paolo, T.; Eleuterio, D.P.; Fernando, H.J.S.; et al. CASPER: Coupled air–sea processes and electromagnetic ducting research. Bull. Am. Meteorol. Soc. 2018, 99, 1449–1471. [Google Scholar] [CrossRef]
- Yang, F.; Yang, K.; Shi, Y.; Wang, S.; Zhang, H.; Zhao, Y. The effects of rainfall on over-the-Horizon propagation in the evaporation duct over the south China Sea. Remote Sens. 2022, 14, 4787. [Google Scholar] [CrossRef]
- Shi, Y.; Yang, K.D.; Yang, Y.X.; Ma, Y.L. Experimental verification of effect of horizontal inhomogeneity of evaporation duct on electromagnetic wave propagation. Chin. Phys. B 2015, 24, 044102. [Google Scholar] [CrossRef]
- Lin, J.; Qing-hong, L.; Yong-gang, Z. Diagnosis of the Inhomogeneous Evaporation Duct and Its Effects on the Electromagnetic Wave Propagation of the Radar. In Proceedings of the 2019 Cross Strait Quad-Regional Radio Science and Wireless Technology Conference (CSQRWC), Taiyuan, China, 18–21 July 2019; pp. 1–3. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Mahafza, B.R. Introduction to Radar Analysis; Chapman and Hall/CRC: London, UK, 2017. [Google Scholar]
- Dutton, E. A Meteorological Model for Use in the Study of Rainfall Effects on Atmospheric Radio Telecommunications; US Department of Commerce: Washington, DC, USA, 1971; Volume 1. [Google Scholar]
- Debye, P.J.W. Polar Molecules; The Chmical Catalog Co.: New York, NY, USA, 1929. [Google Scholar]
- Zhang, J. Methods of Retrieving Tropospheric Ducts above Ocean Surface Using Radar Sea Clutter and GPS Signals. Ph.D. Thesis, Xidian University, Xi’an, China, 2012. [Google Scholar]
- Gerstoft, P.; Rogers, L.T.; Krolik, J.L.; Hodgkiss, W.S. Inversion for refractivity parameters from radar sea clutter. Radio Sci. 2003, 38, 18/6–18/7. [Google Scholar] [CrossRef]
- Paulus, R.A. Specification for Environmental Measurements to Assess Radar Sensors. NOSC TD 1989. Available online: https://apps.dtic.mil/sti/citations/ADA219127 (accessed on 17 August 2024).
- Paulus, R. Practical application of an evaporation duct model. Radio Sci. 1985, 20, 887–896. [Google Scholar] [CrossRef]
- Musson-Genon, L.; Gauthier, S.; Bruth, E. A simple method to determine evaporation duct height in the sea surface boundary layer. Radio Sci. 1992, 27, 635–644. [Google Scholar] [CrossRef]
- Babin, S.M.; Young, G.S.; Carton, J.A. A new model of the oceanic evaporation duct. J. Appl. Meteorol. Climatol. 1997, 36, 193–204. [Google Scholar] [CrossRef]
- Babin, S.M.; Dockery, G.D. LKB-based evaporation duct model comparison with buoy data. J. Appl. Meteorol. Climatol. 2002, 41, 434–446. [Google Scholar] [CrossRef]
- Xiangming, G.; Leke, L.; Dongliang, Z.; Yongsheng, L.; Lijun, Z.; Shifeng, K. Comparison of evaporation duct models and microwave transhorizon propagation experiment. Chin. J. Radio Sci. 2021, 36, 150–155. [Google Scholar]
- Tetens, O. Uber einige meteorologische Begriffe. Z. Geophys. 1930, 6, 297–309. [Google Scholar]
- Levy, M. Parabolic Equation Methods for Electromagnetic Wave Propagation; Number 45; IET: London, UK, 2000. [Google Scholar]
- Ozgun, O.; Apaydin, G.; Kuzuoglu, M.; Sevgi, L. PETOOL: MATLAB-based one-way and two-way split-step parabolic equation tool for radiowave propagation over variable terrain. Comput. Phys. Commun. 2011, 182, 2638–2654. [Google Scholar] [CrossRef]
- Guo, X.; Kang, S.; Han, J.; Zhang, Y.; Wang, H.; Zhang, S. Evaporation duct database and statistical analysis for the Chinese sea areas. Chin. J. Radio Sci. 2013, 28, 1147–1152. [Google Scholar]
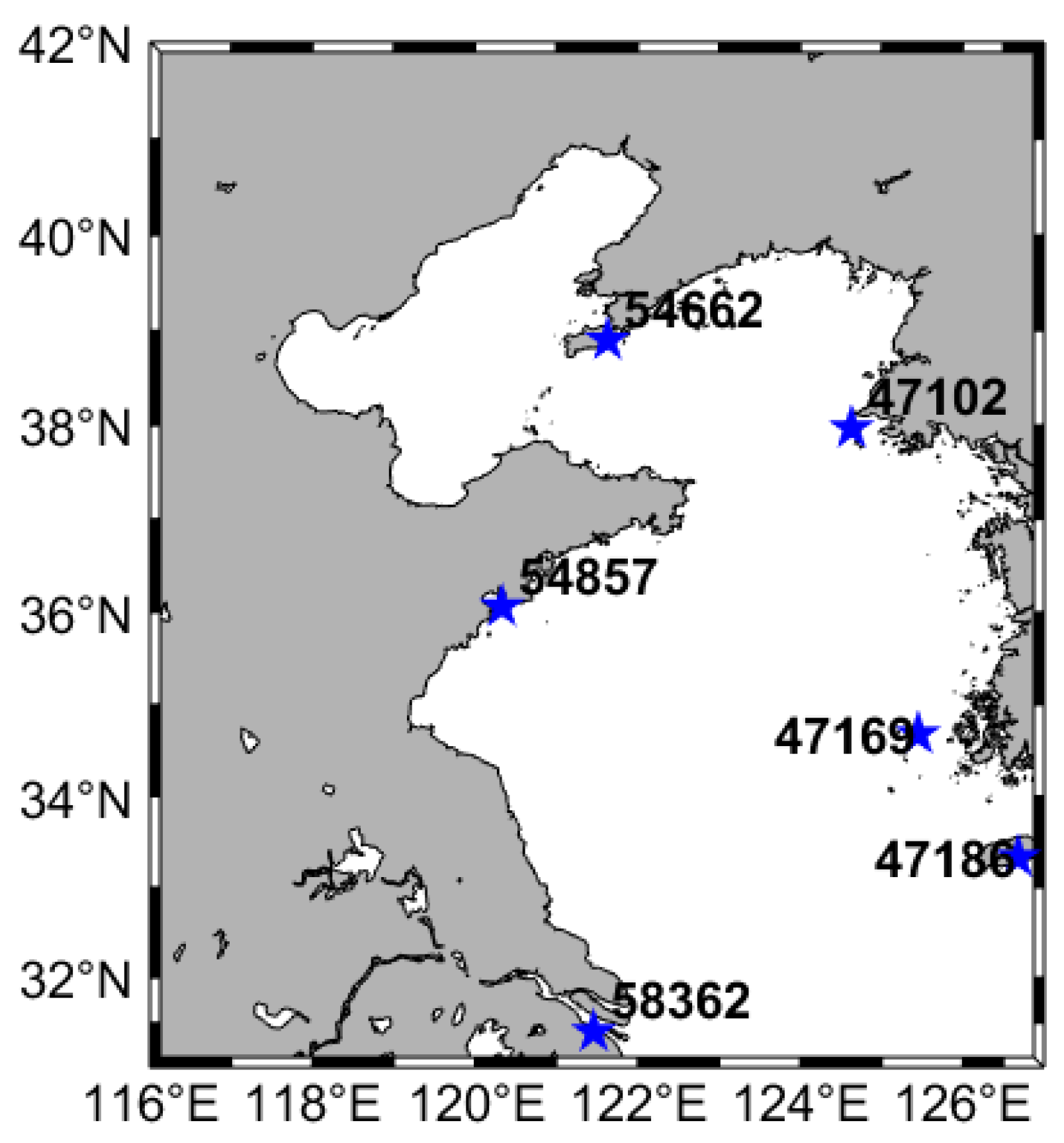




| Station Number | Latitude | Longtitude | Elevation | Parameter |
|---|---|---|---|---|
| 47,102 | 37.97 | 124.63 | 158 (m) | |
| 47,169 | 34.68 | 125.45 | 69 (m) | Atmospheric Pressure (PRES, hPa) |
| 47,186 | 33.33 | 126.68 | 235 (m) | Geopotential Height (HGHT, m) |
| 54,662 | 38.90 | 121.63 | 97 (m) | Temperature (TEMP, °C) |
| 54,857 | 36.06 | 120.33 | 77 (m) | Relative Humidity (RELH, %) |
| 58,362 | 31.40 | 121.46 | 4 (m) |
| Reanalysis Variables | Level | Horizontal Resolution |
|---|---|---|
| Air temperature (K) | 2 m | 0.25° × 0.25° |
| Sea-surface temperature (K) | Sea surface | |
| Sea-level pressure (Pa) | Sea surface | |
| Dewpoint temperature (K) | 2 m | |
| U component of wind (m/s) | 10 m | |
| V component of wind (m/s) | 10 m |
| Station | Surface Duct Base Height | Surface Duct Thickness | Surface Duct Strength | Elevated Duct Base Height | Elevated Duct Thickness | Elevated Duct Strength |
|---|---|---|---|---|---|---|
| 47,102 | 167.1 | 52.8 | 8.8 | 1171.8 | 87.9 | 8.3 |
| 47,169 | 98.7 | 55.8 | 9.3 | 1218.9 | 88.2 | 8.8 |
| 47,186 | 237.9 | 45.1 | 6.1 | 1390.7 | 86.7 | 9.8 |
| 54,662 | 104.7 | 113.4 | 7.9 | 1228.8 | 133.1 | 7.8 |
| 54,857 | 80.6 | 121.4 | 9.5 | 1152.0 | 129.5 | 8.1 |
| 58,362 | 46.8 | 68.9 | 7.1 | 1264.9 | 97.9 | 10.9 |
| Parameter | Value |
|---|---|
| Transmitting antenna height | 5 m |
| Transmitting frequency | 15 GHz |
| Antenna type | Gaussian antenna |
| Polarization type | Horizontal |
| Height | 0–100 m or 0–300 m |
| Range | 0–222 km |
| Modified refractivity profile | Surface duct/evaporation duct/hybrid duct |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Li, L.; Lin, L.; Zhang, R.; Liang, S.; Zhao, Z. Statistical Analysis of Atmospheric Ducts in the Yellow and Bohai Seas of China and Study of Their Electromagnetic Wave Propagation Characteristics. Atmosphere 2024, 15, 1041. https://doi.org/10.3390/atmos15091041
Yang X, Li L, Lin L, Zhang R, Liang S, Zhao Z. Statistical Analysis of Atmospheric Ducts in the Yellow and Bohai Seas of China and Study of Their Electromagnetic Wave Propagation Characteristics. Atmosphere. 2024; 15(9):1041. https://doi.org/10.3390/atmos15091041
Chicago/Turabian StyleYang, Xiao, Lei Li, Leke Lin, Rui Zhang, Shuaishuai Liang, and Zhenwei Zhao. 2024. "Statistical Analysis of Atmospheric Ducts in the Yellow and Bohai Seas of China and Study of Their Electromagnetic Wave Propagation Characteristics" Atmosphere 15, no. 9: 1041. https://doi.org/10.3390/atmos15091041
APA StyleYang, X., Li, L., Lin, L., Zhang, R., Liang, S., & Zhao, Z. (2024). Statistical Analysis of Atmospheric Ducts in the Yellow and Bohai Seas of China and Study of Their Electromagnetic Wave Propagation Characteristics. Atmosphere, 15(9), 1041. https://doi.org/10.3390/atmos15091041





