Next Article in Journal
Influence of Field Sampling Methods on Measuring Volatile Organic Compounds in a Swine Facility Using SUMMA Canisters
Previous Article in Journal
Warm and Dry Compound Events in Poland
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 15
Issue 9
10.3390/atmos15091020
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Deep Forest Algorithm Based on TropOMI Satellite Data to Estimate Near-Ground Ozone Concentration

by
Mao Zong
1,
Tianhong Song
2,3,
Yan Zhang
2,3,*,
Yu Feng
2 and
Shurui Fan
2,3
1
The 54th Research Institute of China Electronics Technology Group Corporation, Shijiazhuang 050081, China
2
School of Electronic and Information Engineering, Hebei University of Technology, Tianjin 300401, China
3
Innovation and Research Institute, Hebei University of Technology, Shijiazhuang 050299, China
*
Author to whom correspondence should be addressed.
Atmosphere 2024, 15(9), 1020; https://doi.org/10.3390/atmos15091020
Submission received: 23 July 2024 / Revised: 15 August 2024 / Accepted: 20 August 2024 / Published: 23 August 2024
(This article belongs to the Section Atmospheric Techniques, Instruments, and Modeling)
Browse Figures
Versions Notes

Abstract

:
The accurate estimation of near-ground ozone (O3) concentration is of great significance to human health and the ecological environment. In order to improve the accuracy of estimating ground-level O3 concentration, this study adopted a deep forest algorithm to construct a model for estimating near-ground O3 concentration. It is pointed out whether input data on particulate matter (PM2.5) and nitrogen dioxide (NO2) concentrations also affect the estimation accuracy. The model first uses the multi-granularity scanning technique to learn the features of the training set, and then it adopts the cascade forest structure to train the processed data, and at the same time, it adaptively adjusts the number of layers in order to achieve a better performance. Daily near-ground O3 concentrations in Shijiazhuang were estimated using satellite O3 column concentrations, ground-based PM2.5 and NO2 concentration data, meteorological element data, and elevation data. The deep forest model was compared with six models, namely, random forest, CatBoost, XGBoost, LightGBM, Decision Tree, and GBDT. The R-squared (R2), Root Mean Square Error (RMSE), and Mean Absolute Error (MAE) of the proposed deep forest model were 0.9560, 13.2542, and 9.0250, respectively, which had significant advantages over other tree-based regression models. Meanwhile, the model performance was improved by adding NO2 and PM2.5 features to the model estimations, indicating the necessity of synergistic observations of NO2, PM2.5, and O3. Finally, the seasonal distribution of O3 concentrations in the Shijiazhuang area was plotted, with the highest O3 concentrations in the summer, the lowest in the winter, and the O3 concentration is in the middle of spring and autumn.

1. Introduction

In 2018, the Chinese government continued to implement blue sky protection actions, mainly focusing on controlling ground-level ozone [1,2]. Compared with PM2.5, the concentration of ground-level O3 is on the rise [1,3,4]. O3 has become the primary pollutant after PM2.5 in many places in China, especially in spring and summer. The synergistic control of PM2.5 and O3 is a landmark event in the understanding and mitigation of air pollution in China [5,6]. In recent years, the concentration of PM2.5 has shown a decreasing trend, while the concentration of O3 has shown an increasing trend (3.4 μg/m3 yearly) [7,8]. Due to the late discovery of the large-scale threat of O3 to public health, the research on O3 is obviously insufficient compared with that on PM2.5. Near-surface O3 is a secondary pollutant, which is mainly generated by a series of photochemical reactions between nitrogen oxides (NOx = NO + NO2) and volatile organic compounds (VOCs) under solar UV irradiation [9]. Meanwhile, VOCs are not only an important precursor for the formation of near-ground O3, but also a major component of secondary organic aerosol (SOA), an important component of PM2.5 [10,11]. Therefore, the collaborative control of O3 and PM2.5 pollutants is of great significance for the large-scale spatial and temporal monitoring of O3 [12]. A new model, RF-CEEMDAN-Attention-LSTM [13], has been proposed to improve the estimation accuracy of PM2.5 and O3. The relationship between O3 and NO2 is very close [14], and when the reduction ratio of VOCs/NOx is in a certain range, the ozone concentration will also be greatly reduced [15]. O3 is generated by the reactions NO + HO2 and NO + RO2 and destructed by the reactions NO2 + RO2 and NO2 + OH [16]. RO2 is a peroxide radical of hydrocarbon molecules, typically formed after the reaction between organic compounds and hydroxyl radicals (OH); HO2 is a radical of hydrogen peroxide, mainly generated by the reaction between OH and oxygen; OH is a highly reactive free radical that can react with various pollutants, exerting significant influence on air quality and ozone levels. These reaction processes are part of the interaction between nitrogen oxides and organic matter in the atmosphere and ozone. There is already a deep learning-based Res-GCN-BiLSTM hybrid model [17] for predicting short-term regional NO2 and O3 concentrations. Ozone concentration is also affected by meteorological conditions and atmospheric pollutants [18]; for example, O3 concentration is higher on sunny days than on cloudy days [19]. On the other hand, meteorological parameters can affect the concentration of NO2 and O3 by affecting the production process and diffusion of NO2 and O3 [20], so meteorological conditions are also very important in the study. He et al. [14] pointed out that the driving mechanism of O3 and NO2 has important guiding significance for NO2 and O3 emission reduction in sub-counties of China’s Yangtze River Delta.
The main models used to estimate large-scale near-ground O3 pollution include atmospheric chemistry models [21,22] and empirical statistical models [23,24]. Atmospheric chemistry models are complex to apply and require expertise and high-end equipment support. In contrast, empirical statistical models are simple and easy to implement, providing high accuracy and practicality. For example, Jiang Yun et al. [25] used greenhouse gas monitor data from the Gaofen-5 satellite combined with cloud detection in the O2-A band to deduce CO2. O2-A refers to the remote sensing monitoring and analysis of atmospheric composition using the absorption characteristics of oxygen within a specific wavelength range. However, the traditional mathematical statistical model makes it difficult to explain the concentration and distribution of ground-level O3 over complex terrains, and there are some limitations for the estimation of ground-level O3 concentration with nonlinear change characteristics. To solve this problem, researchers have carried out a series of studies. Mak, H.W.L et al. [26] used OMI satellite data from some regions in southern China to study and test the accuracy of satellite remote sensing algorithms and chemical transport models in retrieving tropospheric NO2 vertical column density under high spatial resolution conditions. Shu et al. [27] explored the three-dimensional distribution of PM2.5 and studied the impact of basin and plateau topography on PM2.5 concentration.
Deep neural networks (DNNs) can improve the estimation accuracy of near-ground O3, but the estimation results of many DNN models can only be verified in a small-scale region [28]. The decision tree-based machine learning models show superior performance with a simpler model structure and less dependence on high-performance computers, which mainly include decision trees, random forests, XGBoost, LightGBM, GBDT, and CatBoost models, with random forests being one of the most widely used models. Based on the random forest, Zhou et al. [29] proposed a deep forest algorithm, which integrates random forests according to the principle of deep neural networks. This algorithm not only operates efficiently but is also suitable for datasets of various sizes. In addition, Zhou et al. [30] applied the deep forest algorithm to the occupancy estimation model, and the experimental results showed that it was superior to the support vector machine, classification regression tree, and non-homogeneous hidden Markov algorithm. The deep forest algorithm has the advantages of a few hyperparameters, resistance to overfitting, and the ability to adapt to the model structure, and it has performed well in many experimental studies. Liu et al. [31] established a NO2 concentration estimation model based on an LSTM to study the influence of different input indexes on the model accuracy. With the development of smart cities, the framework of Data Openness for Air Quality has been proposed to assess the level of openness of global smart city air quality data [32], and it is necessary to incorporate citizen science into the expansion of O3 and NO2 measurement space coverage [33].
Therefore, in this study, an O3 concentration estimation model was constructed based on the deep forest algorithm by taking in data such as O3 column concentration from the satellite Tropospheric Monitoring Instrument (TropOMI). The present model was compared with six models, including random forest, CatBoost, XGBoost, LightGBM, Decision Tree, and GBDT, to estimate the daily near-ground O3 concentration in the Shijiazhuang using satellite O3 column concentration, ground-based PM2.5 and NO2 concentration data, meteorological element data, and elevation data. And whether the input ground data (PM2.5 and NO2) have any influence on the accuracy of the model was studied. And it was investigated whether inputting ground data (PM2.5 and NO2) or not had any effect on the model accuracy. By constructing the O3 concentration estimation model, the distribution of urban air pollutants can be more accurately monitored and predicted, which is not only helpful to formulate effective environmental protection policies and measures, but also to improve urban air quality. It can also help city residents understand the state of air quality and remind them to take necessary health protection measures.

2. Materials and Methods

2.1. Study Design

The data used in this study are shown in Table 1. In this study, the daily O3 concentration in Shijiazhuang is estimated based on the deep forest algorithm using ground-based NO2 and PM2.5 concentration data, satellite tropospheric O3 column concentration data, meteorological element data, and elevation data, which mainly includes the following four steps:
Step 1: The ground data are matched with TropOMI O3 column concentration data, meteorological element data, and elevation data in space and time. Invalid data are checked for and removed. The data are processed into a two-dimensional matrix of sample data × feature quantity, and they are divided into training and testing sets.
Step 2: Firstly, multi-granularity scanning is used to learn the features of the training set, and then the cascading forest structure is used to learn the processed data. The number of cascade layers of the deep forest is adaptively adjusted to dynamically decide the optimal number of layers based on the training situation to achieve better performance.
Step 3: The model performance is assessed using MAE, RMSE, and R2 as the evaluation metrics of the model.
Step 4: The constructed deep forest model is used to predict the O3 concentration in Shijiazhuang area, and the spatial and temporal distribution map of O3 concentration in the Shijiazhuang area is drawn.

2.2. Research Area

In recent years, with the accelerating industrialization and urbanization in the Shijiazhuang area, air pollution has become an increasingly prominent problem [34]. This poses a great threat to public health [35], visibility [36], and the ecological environment. The research area is Shijiazhuang. The climate of the Shijiazhuang area is a north temperate sub-humid continental monsoon climate, showing the following characteristics: semi-humid and semi-arid, hot and rainy in summer, and cold and dry in winter. Figure 1 shows the elevation map of Shijiazhuang area. Shijiazhuang is located in the hinterland of the North China Plain, north of Beijing–Tianjin, east of the Bohai Sea, west of the Taihang Mountain Range, and has a prevailing north temperate sub-humid continental monsoon climate. Due to the presence of mountain ranges, pollutant diffusion is limited [37].

2.3. Modeling Method Based on Deep Forest Algorithm

In the O3 concentration estimation study, the overall technology roadmap is shown in Figure 2. The concentration data of ground-level PM2.5 and NO2 are used as one of the features, along with other meteorological-related features, as input data to train the machine learning model. The dataset is divided into training and testing sets. During the model training process, the model learns the relationship between these features and the target variable in order to be trained. Data spatiotemporal matching is the process of matching and integrating data from different time and space scales for subsequent analysis. The first step is to ensure that the datasets to be matched have a consistent format. For spatial data, geographic information system tools are used for spatial matching. For time series data, it is necessary to perform time matching to ensure that data from different time points can be aligned, and conduct interpolation operations. When performing spatiotemporal matching, there may be cases where some data are missing, requiring the identification of invalid data for removal. The matched spatiotemporal data should then be merged to create a unified dataset. During the model training process, the Mean Squared Error (MSE) may decrease rapidly in the initial stages, but as training progresses, the model gradually converges to a stable state. At this point, the MSE may no longer continue to decrease because the model has fitted the training data as much as possible.
Deep forest is based on the idea of random forest, and after cascading, a multi-layer random forest is constructed according to the principle of deep neural network, also known as multi-granularity cascade forest. This model was proposed by Professor Zhou [29] and has the advantages of few hyperparameters, strong overfitting resistance, and network depth adaptivity. The deep forest algorithm consists of two phases: the multi-granularity scanning phase and the cascade forest phase.

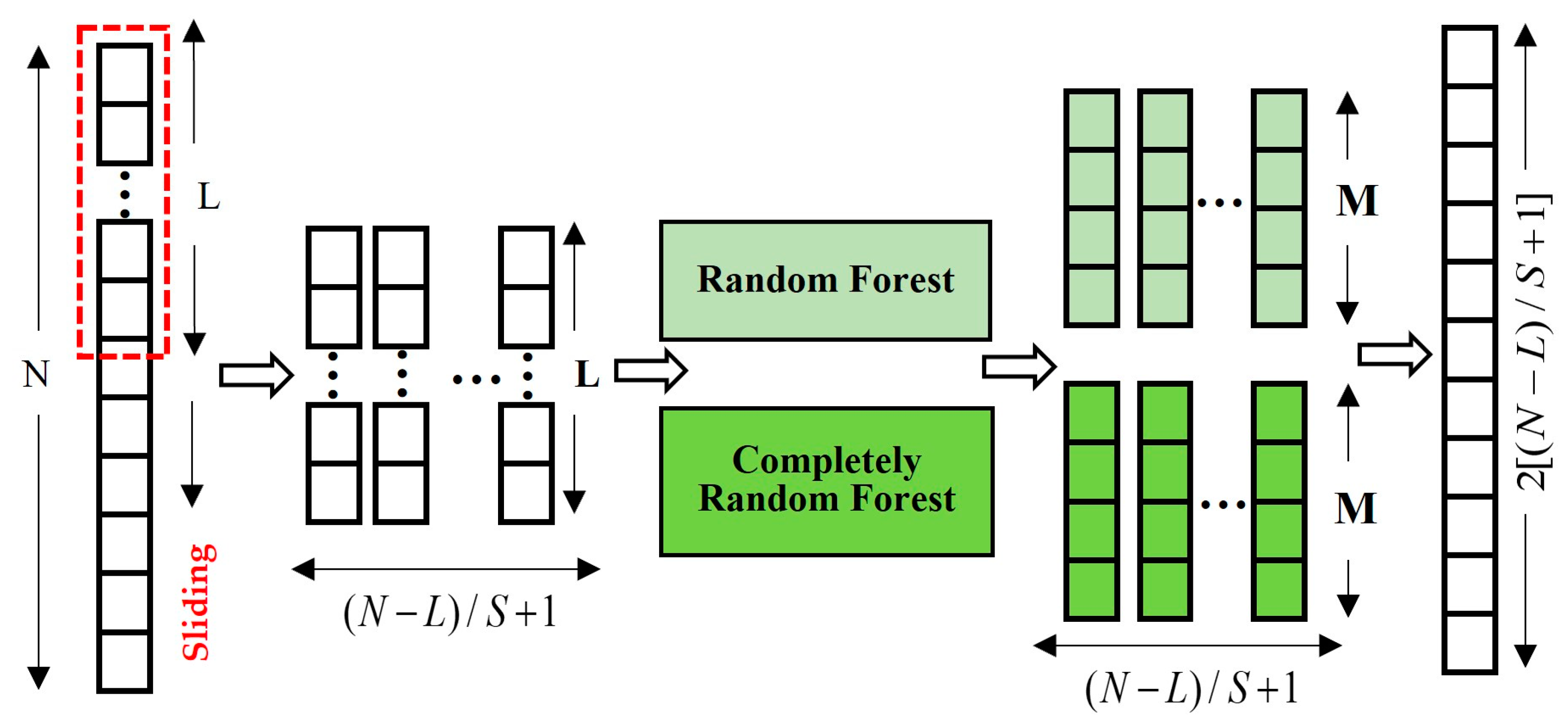
2.3.1. Multi-Granularity Scanning

Multi-granularity scanning uses a window to scan the data. As shown in Figure 3, for sequential data, features can be extracted using multi-granularity scanning. Specifically, for a dataset containing N sequence data, the data are sampled using a sliding window of length L and step size of S , and then D = N − L S + 1 feature vectors are obtained. The reason for separate training between random forest and completely random forest is that they have different properties and workings. The main difference between completely random forests and ordinary random forests is the way they select the candidate feature space. The completely random forest is to randomly select features from the whole feature space to split the decision tree, while the ordinary random forest is to select the best splitting node by Gini coefficient [38] in a random feature subspace. Random forests and completely random forests are trained using these feature vectors, and class vectors of length M are obtained. Each forest generates D × M class vectors, and finally, all the class vectors generated by the random forests are spliced together to obtain the final transformed vectors.
The above scanning process for sequences uses only one window, and in actual model training, in order to improve estimation accuracy, the deep forest algorithm uses multiple windows of different sizes to sample the dataset, which makes the data input into the cascade forest be combined by multiple feature data of different granularities. The deep forest algorithm processes the original feature data through a multi-granularity scanning process that expands the dimensionality of the feature data and can handle the sequential relationships between the sample features, thus enhancing the ability of the subsequent cascade forest stage.

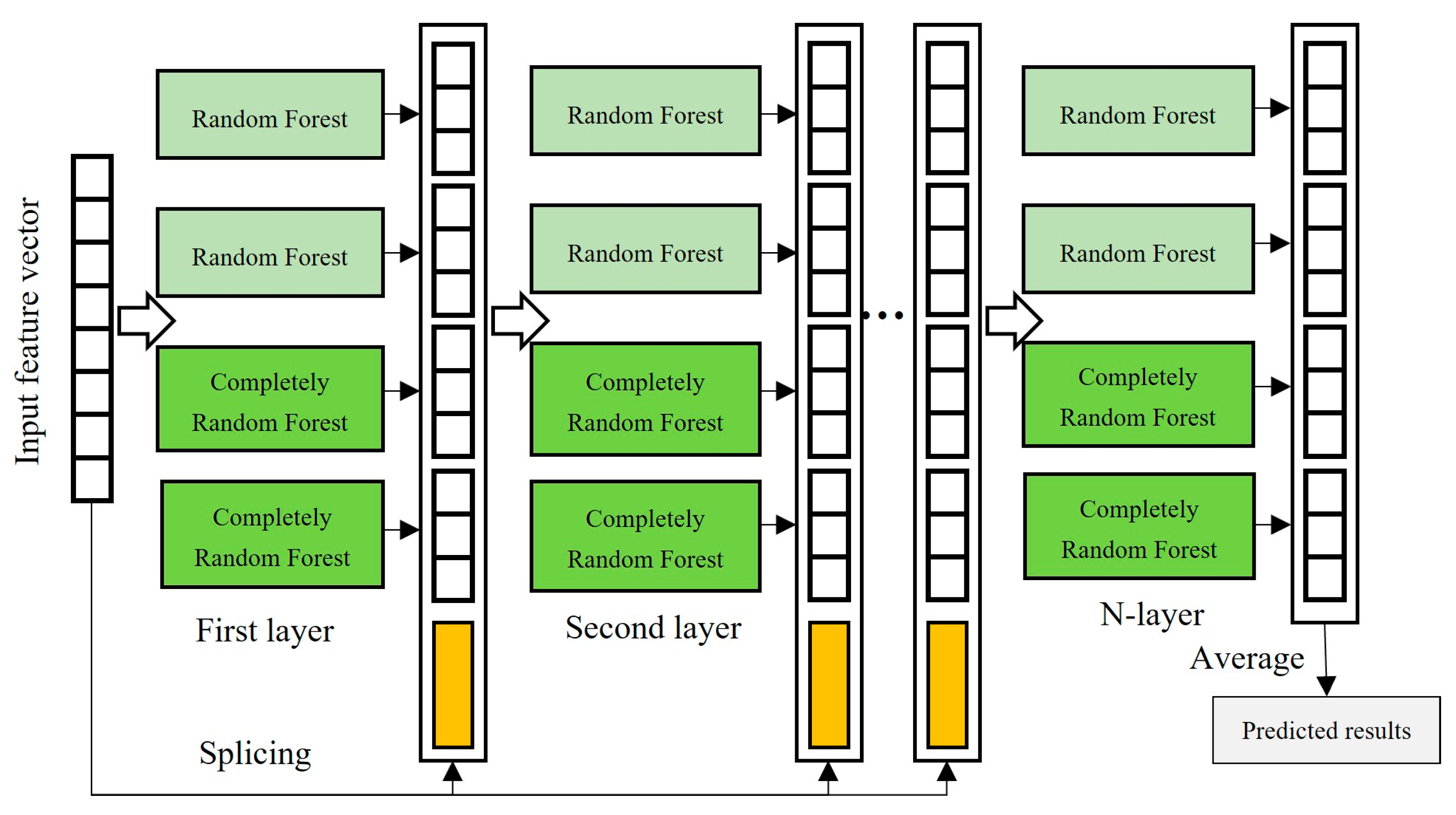
2.3.2. Cascade Forest

The core idea of the deep forest algorithm is cascade forest, which implements the deep learning process by introducing multiple cascade forest stages. Each cascade forest stage contains multiple forest models of different types, which enhances the algorithm‘s representation learning ability and improves estimation accuracy by processing data features layer-by-layer. After the multi-granularity scanning process, the generated feature vectors are input to the cascade forest for training, similar to the layer-by-layer structure in deep neural networks, where each layer of the cascade forest derives its inputs from the processed features of the previous layer and outputs the processed features of the current layer to the next layer. Each layer of the cascade forest is a further integration of the decision tree forest, i.e., “an ensemble of ensembles”. Starting with the generation of the second layer, each generation layer is evaluated against a test set to determine if the performance of the current cascade forest has improved. If the performance does not improve, the algorithm stops generating more layers to automatically determine the optimal number of layers, and thus automatically determining the depth based on the data itself. In addition, the errors in training each layer also determine whether a new layer is generated. The structure of the cascade forest is shown in Figure 4.
For ensemble learning, maintaining diversity in model structures is crucial. Therefore, when building multiple models, different structures and parameter settings should be used to increase the diversity among models, thus enhancing the performance and stability of the ensemble model. In deep forests, this is reflected in the presence of paired random forests and completely random forests. Two completely random forests can provide more randomness, reduce the risk of overfitting, and help capture more relationships between features in the data. Each layer of the deep forest contains two random forests and two completely random forests.

2.4. Data Collection

The data used in this study mainly include ground station monitoring data, satellite remote sensing data, and meteorological data and elevation data.

2.4.1. Near-Ground O3 Monitoring Data

The ground station monitoring data are available on the website https://data.epmap.org/product (accessed on 18 February 2024). The environmental center can provide air, dual carbon, water, and ecology field monitoring data elements. Near-ground O3 monitoring data were adopted from 12 state-controlled monitoring stations in the Shijiazhuang area in 2020, and the locations of the state-controlled monitoring stations in Shijiazhuang are shown in Figure 1, with a daily temporal resolution. Among them, invalid data (concentration value ≤ 0 μg/m3) and missing data (None) generated due to factors such as cloud cover, atmospheric interference, or disruptions in the transmission process were removed before the data integration. The proportion was about 12.57%.

2.4.2. Satellite Data

The estimation of O3 utilizes tropospheric O3 column concentration data from the TropOMI sensor on satellites, which can be downloaded at https://scihub.copernicus.eu/ (accessed on 18 February 2024). The TropOMI sensor observes the troposphere that was launched by the European Space Agency in 2017 on board the “Sentinel-5P” satellite [39,40,41]. The TropOMI sensor has a spatial resolution of 5.5 km × 3.5 km [42,43] and a vertical resolution of 0.5 km per layer, which can effectively monitor various trace gases in the global atmosphere and enhance the monitoring of clouds and aerosols.

2.4.3. Meteorological and Elevation Data

Meteorological elements are derived from the ERA-5 reanalysis data published by the European Mesoscale Prediction Center (EMPC), which provides access to hourly data on atmospheric variables. Meteorological variables included in the meteorological elements are as follows: boundary layer height (BLH, unit: m), surface pressure (SP, unit: hPa), total-column water content (TCW, unit: kg/m−2), total-column ozone (TCO, unit: kg/m−2), temperature of 2 m (T2M, unit: K), and wind speed of U/V at 10 m (U10M, V10M, unit: ms−1). Download meteorological data from the website https://cds.climate.copernicus.eu/cdsapp#!/home (accessed on 20 July 2024). The elevation data were obtained from the Geospatial Data Cloud (https://www.gscloud.cn/ (accessed on 20 July 2024)).

2.5. Experimental Environment

The experimental environment was a PC with the following configuration: Windows 11 64 bit, Intel (R) Core (TM) Ultra 7 155H 3.80 GHz, Anaconda Navigator 3 (Jupyter notebook); Python 3.7 was the experimental platform for the simulation.

2.6. Evaluation Indexes

Three evaluation indexes [44,45], R-squared ( R 2 ), Root Mean Square Error ( R M S E ), and Mean Absolute Error ( M A E ), were used to assess the model performance. M A E can show the real situation of the estimation value error, while R M S E can be used to measure the deviation between the estimation value and the real value, and it is more sensitive to the outliers: the closer the value of both of them is to 0, the more accurate the estimate; R 2 is a statistic measuring the goodness-of-fit, and the closer the value of its value is to 1, the better the model‘s fit is, and they are expressed in Equations (1)–(3), respectively.
M A E = 1 n ∑ i = 1 n y t r u e − y e s t i m a t e ,
R M S E = 1 n ∑ i = 1 n y t r u e − y e s t i m a t e 2 ,
R 2 = 1 − ∑ i = 1 n y t r u e − y e s t i m a t e 2 ∑ i = 1 n y t r u e − y a v e r a g e 2 ,
Among them, y t r u e is the true value, y e s t i m a t e is the estimated value of the model, y a v e r a g e is the average value, and n is the overall length of the data.
During result validation, the time period used for validation is the same as the time period when training the model. The data used for model training include ground-based data, TropOMI O3 column concentration data, meteorological element data, elevation data, etc., to obtain estimated values of ozone concentration. The validation data consist of actual ozone concentrations.

3. Results

3.1. Analysis of the Coordinated Changes in O3, PM2.5, and NO2

Photochemical reactions and convection activities create an inverse relationship between the NO2, PM2.5, and O3 concentrations [46]. Therefore, the correlations between O3 and PM2.5, O3, and NO2 in Shijiazhuang City are analyzed respectively.
Figure 5 shows the correlation matrix between O3 and PM2.5 and NO2 in Shijiazhuang in 2020, and it can be seen that the correlation between O3 and PM2.5 and NO2 is −0.31 and −0.4, respectively, both of which have an obvious negative correlation. From the four graphs on the right side of Figure 5, it can be seen that in the spring and summer seasons, there is a positive correlation between ozone and PM2.5 as well as NO2, while in the autumn and winter seasons, there is a negative correlation.
Figure 6 shows the changes in daily O3 and PM2.5 concentrations at monitoring sites in Shijiazhuang during 2020–2021, in which the South Campus of Shijiazhuang No. 22 Middle School (station code: 2862A) is selected for amplified observation. By observing the data distribution, it can be found that the seasonal variations of O3 and PM2.5 are opposite, and the concentration distribution of O3 is highest in summer, while PM2.5 has the highest concentration in winter.
NO2 is the main precursor for O3 production, which is inhibited by influencing the photochemical reaction process. Figure 7 shows the variation of daily O3 and NO2 concentrations at each monitoring site. It can be clearly seen that O3 has an “M” distribution and NO2 has a “W” distribution. In summer, the high temperature and strong solar radiation increase the photochemical reaction rate, causing the consumption of volatile organic compounds (VOCs) and nitrogen oxide (NOₓ) precursors to speed up, leading to an accelerated rate of ground-level O3 formation. In this process, more NO2 is consumed, so NO2 reaches its lowest value in summer, while O3 reaches its highest value in summer. Therefore, the control of O3 concentration as the second largest pollutant should be combined with the generation and change in a variety of precursors to solve the problem of O3 pollution from the root.

3.2. Estimation and Comparative Analysis of Near-Ground Ozone Concentration

To further demonstrate the reliability of the deep forest model and the necessity of synergistic observation of NO2, PM2.5, and O3, a comparison was made between the deep forest model and various regression models applied to estimate ground-level O3 concentrations. These models include random forest, CatBoost, XGBoost, LightGBM, Decision Tree, and GBDT. Figure 8a–d,e–j show the scatter plots of the estimations obtained from the deep forest and the six comparison models against the measured values of O3.
As shown in Figure 8a–d, the performance of the model before and after adding NO2 and PM2.5 was compared, respectively. PM2.5 and NO2 are added to the estimation of ground O3 in Figure 8a, which has R 2 , R M S E , and M A E of 0.9560, 13.2542, and 9.0250, respectively. However, PM2.5 and NO2 are not added to Figure 8d, and the R 2 , R M S E and M A E of the model are 0.9463, 14.6358, and 9.5159, respectively, indicating that the addition of PM2.5 and NO2 can effectively improve the estimation accuracy of near-surface O3. Figure 8b shows that R 2 is 0.9499 when only PM2.5 is added without NO2 data. Figure 8c shows that the R 2 is 0.9487 when only NO2 is added on the basis of no PM2.5 data, both of which are better than the results of Figure 8d without PM2.5 and NO2. This is because the emission of NO2 affects the concentration of NO in the atmosphere, and NO2 can also react with volatile organic compounds (VOCs), which, in turn, affects the formation of O3. The chemical composition of PM2.5 has a strong extinction effect, and the particles in the atmosphere can attenuate the ultraviolet radiation from the upper atmosphere through absorption and scattering. Thus, the radiant energy reaching the ground and the formation of O3 are affected. High concentrations of PM2.5 have a significant inhibitory effect on O3 generation, so comprehensive measures should be taken to control their emissions and concentrations in order to reduce their impact on human health and the environment. Therefore, the analysis shows that adding PM2.5 is effective in improving the estimation accuracy of O3.
Table 2 demonstrates the specific performance of each model, and it can be seen that the deep forest model has the best performance. The deep forest synthesizes the depth and breadth characteristics of traditional forest models. In order to improve the model‘s representation learning ability, multi-grain scanning is used to enhance the original features, and cascading forest is used to increase the complexity of the model. In addition, to ensure the generalization ability of the model, deep forest uses two different types of forests to construct the cascade layer. Figure 9 is the line chart between the simulated results and the actual measured values after NO2 and PM2.5 data are added to the deep forest model. The time resolution is 1 day. The data here are randomly selected, and the relationship between the actual measured data and the simulated values of the model can be visually seen.

3.3. Spatiotemporal Distribution of Near-Ground-Level Ozone Concentrations

Figure 10 shows the seasonal spatial distribution of near-ground O3 concentrations in the Shijiazhuang area in 2020. The O3 concentration is higher south of the Taihang Mountains compared to the northern mountainous region when analyzed spatially. From the temporal analysis, it can be seen that the concentration ranges of O3 in the four seasons are quite different, with the highest concentration in summer and the lowest concentration in winter. Spring and autumn concentrations are in between. At the same time, it can be seen that there are significant differences in O3 concentration in Shijiazhuang area in different seasons, and the maximum difference between seasons can reach 80 μg/m3. This phenomenon is closely related to the temperature, and the O3 concentration is less affected by the low temperature [47], but when the temperature reaches about 35 °C, the O3 concentration can reach about 200 μg/m3, and the value of the concentration reaches the peak when the highest temperature is reached. The high temperatures and strong ultraviolet radiation in summer are conducive to accelerating photochemical reactions in the atmosphere, especially the photochemical reactions of nitrogen oxides (NOx) and volatile organic compounds (VOCs) [48], thereby promoting the formation of O3. One of the main reaction pathways is as follows: NO2 first undergoes photolysis to produce free NO, which then reacts with O2 to generate O3 [49]. In winter, although coal consumption is high and the concentrations of NOx and VOCs in the atmosphere may be relatively high, the lack of sunlight and lower temperatures inhibit photochemical reactions, resulting in lower O3 concentrations instead.

4. Discussion

With the rapid development of artificial intelligence technology, the integration of satellite remote sensing technology and machine learning models has been widely applied to estimate particulate matter and pollution gas concentrations. This method can provide extensive and dynamic atmospheric information, as well as observe the sources, transport paths, and distribution of pollutants at different time and spatial scales. It provides an effective means for a comprehensive observation of air quality. García, R.D. et al. [50] evaluated different models to predict ozone concentrations. Chen et al. [51] pointed out that the support vector regression (SVR) model has the best estimation performance for annual O3, with R 2 reaching 0.86. Jia et al. [52] proposed a hybrid deep learning model in which a random forest algorithm was used to select input variables for predicting the next day‘s average daily NO2 concentration. For the proposed method of ozone concentration estimation based on the combination of Landsat 8 infrared band and a deep forest [53], the experimental results show that the accuracy of the deep forest is significantly better than some machine learning methods.
While the control of PM2.5 has achieved results, in some cities, ozone has quietly replaced PM2.5 as the primary pollutant. Li et al. [54] established a near-ground ozone concentration inversion model based on feedforward neural network in order to explore the characteristics and spatiotemporal variation trend of near-ground ozone pollution in Beijing, Tianjin, and Tangshan regions, and the R2 of the model was only 0.888. Zhang et al. [55] estimated the near-ground ozone concentration in a satellite observation area by a deep learning model, but its accuracy only reached 0.841. In [56], an inversion method of near-ground ozone concentration based on the combination of machine learning and deep learning is proposed, and the R 2 is 0.90. In this study, in response to the issue that existing studies have used traditional regression algorithms to estimate O3 concentrations and the estimation accuracy needs improvement, a near-surface O3 concentration estimation model based on the deep forest algorithm was proposed. This model integrates ground data, TropOMI O3 column concentration data, meteorological element data, elevation data, etc. In the process of near-surface O3 concentration estimation, NO2 and PM2.5 concentrations were included to achieve a higher prediction accuracy, effectively addressing the issue of coordinated pollution control.
The deep forest model was compared with six other models, and the performance of the deep forest model was the best. As shown in Figure 8a,d, R 2 , R M S E , and M A E indicate that by adding NO2 and PM2.5, a synergistic analysis can effectively improve the estimation accuracy of O3. From Figure 8b–d, it can be seen that PM2.5 has a stronger synergistic observational effect on O3. By analyzing the seasonal distribution map of O3 concentration in Shijiazhuang, the O3 concentration south of Taihang Mountain was higher than that in the northern part of the mountainous region; temporally, the O3 concentration was highest in summer, which also reflected in [57], and it was lowest in winter; the values for spring and autumn are between those of summer and winter. Therefore, comprehensive measures should be taken to control their emissions and concentrations in order to reduce their impact on human health and the environment.
In the process of O3 concentration estimation in this study, the ground monitoring data were adopted from the state-controlled stations, which are mainly distributed in the urban center or more seriously polluted areas, so the model validation was also based on the urban center stations. In the subsequent study, the provincial control stations and the state-controlled stations will be used as the research data to improve the regional representativeness of the samples and the generalization ability of the model. Current research may only reflect the situation in specific regions, lacking diversity and universality. It is also necessary to consider using multiple model validation methods to improve the adaptability of models under different environmental conditions, thereby enhancing the reliability of air quality predictions.

5. Conclusions

In this paper, we propose a method to estimate near-ground O3 concentration using the deep forest algorithm of a satellite tropospheric monitor. Ground data (PM2.5, NO2 concentration data, etc.), TropOMI O3 column concentration data, meteorological element data, and elevation data were used to predict the daily O3 concentration in the Shijiazhuang area. After experimental verification, we concluded the following.
(1) The deep forest algorithm proposed in this paper has a high estimation accuracy and universality to construct the O3 concentration inversion model, which is suitable for the estimation of near-ground O3 concentration. The model uses multi-granularity scanning technology to learn the features of the training set, and then adopts a cascade forest structure to train the processed data; then, it adaptively adjusts the number of layers to achieve better performance.
(2) By adding the ground-level NO2 and PM2.5 concentrations into the inversion process of near-ground O3 concentration, a higher estimation accuracy can be obtained, which indicates that PM2.5, NO2, and O3 have a synergistic effect.
In conclusion, using the deep forest algorithm to construct an O3 concentration inversion model improves the estimation accuracy of O3. Compared to other tree-based regression models, it has significant advantages. By incorporating the PM2.5 feature into the model estimations, the performance of the model is improved, indicating the necessity of the collaborative observation of NO2, PM2.5, and O3. In future studies, more parameters closely associated with O3 will be considered, and both provincial monitoring stations and national monitoring stations will be used to obtain research data to further enhance the performance of the model. This has a positive impact on the prevention and control of air pollution. In addition, improving the time resolution of this type of research is also a direction that this study will consider in the future. It can analyze the daily variation of ozone based on other parameters considered.

Author Contributions

Conceptualization, M.Z. and Y.Z.; methodology, Y.F. and S.F.; software, M.Z. and Y.F.; resources, Y.F.; writing—original draft preparation, Y.Z. and Y.F.; writing—review and editing, T.S.; funding acquisition, S.F. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Science and Technology Cooperation Special Project of Shijiazhuang (SJZZXB23004).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.

Conflicts of Interest

Author Mao Zong was employed by The 54th Research Institute of China Electronics Technology Group Corporation. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

  1. Guo, Y.; Li, K.W.; Zhao, B.; Shen, J.D.; Bloss, W.J.; Azzi, M.; Zhang, Y.P. Evaluating the real changes of air quality due to clean air actions using a machine learning technique: Results from 12 Chinese megacities during 2013–2020. Chemosphere 2022, 300, 10. [Google Scholar] [CrossRef] [PubMed]
  2. Visser, C.; Gonzalez, C. Transportation Air Pollution in China: The Ongoing Challenge to Achieve a ‘Blue Sky’. In Transportation Air Pollutants; Springer: Cham, Switzerland, 2021; pp. 27–41. [Google Scholar]
  3. Wei, J.; Li, Z.Q.; Li, K.; Dickerson, R.R.; Pinker, R.T.; Wang, J.; Liu, X.; Sun, L.; Xue, W.H.; Cribb, M. Full-coverage mapping and spatiotemporal variations of ground-level ozone (O3) pollution from 2013 to 2020 across China. Remote Sens. Environ. 2022, 270, 17. [Google Scholar] [CrossRef]
  4. Mousavinezhad, S.; Choi, Y.; Pouyaei, A.; Ghahremanloo, M.; Nelson, D.L. A comprehensive investigation of surface ozone pollution in China, 2015–2019: Separating the contributions from meteorology and precursor emissions. Atmos. Res. 2021, 257, 13. [Google Scholar] [CrossRef]
  5. Dai, H.B.; Zhu, J.; Liao, H.; Li, J.D.; Liang, M.X.; Yang, Y.; Yue, X. Co-occurrence of ozone and PM2.5 pollution in the Yangtze River Delta over 2013–2019: Spatiotemporal distribution and meteorological conditions. Atmos. Res. 2021, 249, 9. [Google Scholar] [CrossRef]
  6. Xiang, S.L.; Liu, J.F.; Tao, W.; Yi, K.; Xu, J.Y.; Hu, X.R.; Liu, H.Z.; Wang, Y.Q.; Zhang, Y.Z.; Yang, H.Z.; et al. Control of both PM2.5 and O3 in Beijing-Tianjin-Hebei and the surrounding areas. Atmos. Environ. 2020, 224, 10. [Google Scholar] [CrossRef]
  7. Zhao, H.; Chen, K.Y.; Liu, Z.; Zhang, Y.X.; Shao, T.; Zhang, H.L. Coordinated control of PM2.5 and O3 is urgently needed in China after implementation of the “Air pollution prevention and control action plan”. Chemosphere 2021, 270, 12. [Google Scholar] [CrossRef] [PubMed]
  8. Wang, Y.H.; Gao, W.K.; Wang, S.; Song, T.; Gong, Z.Y.; Ji, D.S.; Wang, L.L.; Liu, Z.R.; Tang, G.Q.; Huo, Y.F.; et al. Contrasting trends of PM2.5 and surface-ozone concentrations in China from 2013 to 2017. Natl. Sci. Rev. 2020, 7, 1331–1339. [Google Scholar] [CrossRef]
  9. Li, R.; Cui, L.L.; Fu, H.B.; Li, J.L.; Zhao, Y.L.; Chen, J.M. Satellite-based estimation of full-coverage ozone (O3) concentration and health effect assessment across Hainan Island. J. Clean Prod. 2020, 244, 11. [Google Scholar] [CrossRef]
  10. He, Z.R.; Wang, X.M.; Ling, Z.H.; Zhao, J.; Guo, H.; Shao, M.; Wang, Z. Contributions of different anthropogenic volatile organic compound sources to ozone formation at a receptor site in the Pearl River Delta region and its policy implications. Atmos. Chem. Phys. 2019, 19, 8801–8816. [Google Scholar] [CrossRef]
  11. Lu, K.D.; Rohrer, F.; Holland, F.; Fuchs, H.; Bohn, B.; Brauers, T.; Chang, C.C.; Häseler, R.; Hu, M.; Kita, K.; et al. Observation and modelling of OH and HO2 concentrations in the Pearl River Delta 2006: A missing OH source in a VOC rich atmosphere. Atmos. Chem. Phys. 2012, 12, 1541–1569. [Google Scholar] [CrossRef]
  12. Qu, Y.W.; Wang, T.J.; Yuan, C.; Wu, H.; Gao, L.B.; Huang, C.W.; Li, Y.S.; Li, M.M.; Xie, M. The underlying mechanisms of PM2.5 and O3 synergistic pollution in East China: Photochemical and heterogeneous interactions. Sci. Total Environ. 2023, 873, 12. [Google Scholar] [CrossRef] [PubMed]
  13. Chu, Y.Y.; Yao, J.; Qiao, D.W.; Zhang, Z.Y.; Zhong, C.Y.; Tang, L.J. Three-hourly PM2.5 and O3 concentrations prediction based on time series decomposition and LSTM model with attention mechanism. Atmos. Pollut. Res. 2023, 14, 101879. [Google Scholar] [CrossRef]
  14. He, Z.; He, Y.; Fan, G.; Li, Z.; Liang, Z.; Fang, H.; Zeng, Z.C. Ozone Pollution and Its Response to Nitrogen Dioxide Change from a Dense Ground-Based Network in the Yangtze River Delta: Implications for Ozone Abatement in Urban Agglomeration. Atmosphere 2022, 13, 1450. [Google Scholar] [CrossRef]
  15. Ren, J.; Guo, F.; Xie, S. Diagnosing ozone–NOx–VOC sensitivity and revealing causes of ozone increases in China based on 2013–2021 satellite retrievals. Atmos. Chem. Phys. 2022, 22, 15035–15047. [Google Scholar] [CrossRef]
  16. Yang, X.; Cheng, X.; Yan, H.Z.; Sun, Y.M.; Zhang, G.Q. Ground-Level Ozone Production over an Industrial Cluster of China: A Box Model Analysis of a Severe Photochemical Pollution Episode. Pol. J. Environ. Stud. 2022, 31, 1885–1899. [Google Scholar] [CrossRef]
  17. Wu, C.L.; Song, R.F.; Zhu, X.H.; Peng, Z.R.; Fu, Q.Y.; Pan, J. A hybrid deep learning model for regional O3 and NO2 concentrations prediction based on spatiotemporal dependencies in air quality monitoring network. Environ. Pollut. 2023, 320, 121075. [Google Scholar] [CrossRef]
  18. Latif, S.D.; Lai, V.; Hahzaman, F.H.; Ahmed, A.N.; Huang, Y.F.; Birima, A.H.; Shafie, A.E. Ozone concentration forecasting utilizing leveraging of regression machine learnings: A case study at Klang Valley, Malaysia. Results Eng. 2024, 21, 101872. [Google Scholar] [CrossRef]
  19. Liu, T.; Sun, J.; Liu, B.; Li, M.; Deng, Y.; Jing, W.; Yang, J. Factors Influencing O3 Concentration in Traffic and Urban Environments: A Case Study of Guangzhou City. Int. J. Environ. Res. Public Health 2022, 19, 12961. [Google Scholar] [CrossRef] [PubMed]
  20. Li, Y.; Shi, G.; Chen, Z. Spatial and temporal distribution characteristics of ground-level nitrogen dioxide and ozone across China during 2015–2020. Environ. Res. Lett. 2021, 16, 124031. [Google Scholar] [CrossRef]
  21. Li, K.; Jacob, D.J.; Liao, H.; Qiu, Y.L.; Shen, L.; Zhai, S.X.; Bates, K.H.; Sulprizio, M.P.; Song, S.J.; Lu, X.; et al. Ozone pollution in the North China Plain spreading into the late-winter haze season. Proc. Natl. Acad. Sci. USA 2021, 118, 7. [Google Scholar] [CrossRef]
  22. Gao, M.; Gao, J.H.; Zhu, B.; Kumar, R.; Lu, X.; Song, S.J.; Zhang, Y.Z.; Jia, B.X.; Wang, P.; Beig, G.R.; et al. Ozone pollution over China and India: Seasonality and sources. Atmos. Chem. Phys. 2020, 20, 4399–4414. [Google Scholar] [CrossRef]
  23. Biancofiore, F.; Verdecchia, M.; Di Carlo, P.; Tomassetti, B.; Aruffo, E.; Busilacchio, M.; Bianco, S.; Di Tommaso, S.; Colangeli, C. Analysis of surface ozone using a recurrent neural network. Sci. Total Environ. 2015, 514, 379–387. [Google Scholar] [CrossRef]
  24. Luna, A.S.; Paredes, M.L.L.; de Oliveira, G.C.G.; Corrêa, S.M. Prediction of ozone concentration in tropospheric levels using artificial neural networks and support vector machine at Rio de Janeiro, Brazil. Atmos. Environ. 2014, 98, 98–104. [Google Scholar] [CrossRef]
  25. Jiang, Y.; Wang, X.; Ye, H.; Shi, H.; Pan, Y.; Wang, G. CO2 retrieval method based on GaoFen-5 satellite data. In Proceedings of the First International Conference on Spatial Atmospheric Marine Environmental Optics (SAME 2023), Qingdao, China, 23–26 October 2023. [Google Scholar]
  26. Mak, H.W.L.; Laughner, J.L.; Fung, J.C.H.; Zhu, Q.D.; Cohen, R.C. Improved Satellite Retrieval of Tropospheric NO2 Column Density via Updating of Air Mass Factor (AMF): Case Study of Southern China. Remote Sens. 2018, 10, 23. [Google Scholar] [CrossRef]
  27. Shu, Z.Z.; Liu, Y.B.; Zhao, T.L.; Xia, J.R.; Wang, C.G.; Cao, L.; Wang, H.L.; Zhang, L.; Zheng, Y.; Shen, L.J.; et al. Elevated 3D structures of PM2.5 and impact of complex terrain-forcing circulations on heavy haze pollution over Sichuan Basin, China. Atmos. Chem. Phys. 2021, 21, 9253–9268. [Google Scholar] [CrossRef]
  28. Li, T.W.; Cheng, X. Estimating daily full-coverage surface ozone concentration using satellite observations and a spatiotemporally embedded deep learning approach. Int. J. Appl. Earth Obs. Geoinf. 2021, 101, 13. [Google Scholar] [CrossRef]
  29. Zhou, Z.H.; Feng, J. Deep Forest: Towards an Alternative to Deep Neural Networks. In Proceedings of the 26th International Joint Conference on Artificial Intelligence (IJCAI), Melbourne, Australia, 19–25 August 2017; pp. 3553–3559. [Google Scholar]
  30. Zhou, Y.P.; Chen, J.Y.; Yu, Z.J.; Li, J.; Huang, G.S.; Haghighat, F.; Zhang, G.Q. A novel model based on multi-grained cascade forests with wavelet denoising for indoor occupancy estimation. Build. Environ. 2020, 167, 11. [Google Scholar] [CrossRef]
  31. Liu, B.; Yu, X.; Wang, Q.; Zhao, S.; Zhang, L. A Long Short-Term Memory Neural Network for Daily NO2 Concentration Forecasting. Int. J. Inf. Technol. Web Eng. 2021, 16, 35–51. [Google Scholar] [CrossRef]
  32. Mak, H.W.; Lam, Y.F. Comparative assessments and insights of data openness of 50 smart cities in air quality aspects. Sustain. Cities Soc. 2021, 69, 102868. [Google Scholar] [CrossRef]
  33. Duvall, R.M.; Long, R.W.; Beaver, M.R.; Kronmiller, K.G.; Wheeler, M.L.; Szykman, J.J. Performance Evaluation and Community Application of Low-Cost Sensors for Ozone and Nitrogen Dioxide. Sensors 2016, 16, 1698. [Google Scholar] [CrossRef]
  34. Zhang, T.X.; Zang, L.; Wan, Y.C.; Wang, W.; Zhang, Y. Ground-level PM2.5 estimation over urban agglomerations in China with high spatiotemporal resolution based on Himawari-8. Sci. Total Environ. 2019, 676, 535–544. [Google Scholar] [CrossRef]
  35. Bu, X.; Xie, Z.L.; Liu, J.; Wei, L.Y.; Wang, X.Q.; Chen, M.W.; Ren, H. Global PM2.5-attributable health burden from 1990 to 2017: Estimates from the Global Burden of disease study 2017. Environ. Res. 2021, 197, 9. [Google Scholar] [CrossRef] [PubMed]
  36. Wang, X.Y.; Zhang, R.H.; Yu, W. The Effects of PM2.5 Concentrations and Relative Humidity on Atmospheric Visibility in Beijing. J. Geophys. Res. Atmos. 2019, 124, 2235–2259. [Google Scholar] [CrossRef]
  37. Zhao, N.; Wang, G.; Li, G.H.; Lang, J.L.; Zhang, H.Y. Air pollution episodes during the COVID-19 outbreak in the Beijing-Tianjin-Hebei region of China: An insight into the transport pathways and source distribution. Environ. Pollut. 2020, 267, 11. [Google Scholar] [CrossRef]
  38. Zheng, C.; Baosheng, L.; Xianglin, S. Calculation of Gini Efficient and Gini Efficient of Distribution. J. Ocean Univ. Qingdao 2002, 32, 663–666. [Google Scholar]
  39. Tamiminia, H.; Salehi, B.; Mahdianpari, M.; Quackenbush, L.; Adeli, S.; Brisco, B. Google Earth Engine for geo-big data applications: A meta-analysis and systematic review. ISPRS-J. Photogramm. Remote Sens. 2020, 164, 152–170. [Google Scholar] [CrossRef]
  40. Veefkind, J.P.; Aben, I.; McMullan, K.; Förster, H.; de Vries, J.; Otter, G.; Claas, J.; Eskes, H.J.; de Haan, J.F.; Kleipool, Q.; et al. TROPOMI on the ESA Sentinel-5 Precursor: A GMES mission for global observations of the atmospheric composition for climate, air quality and ozone layer applications. Remote Sens. Environ. 2012, 120, 70–83. [Google Scholar] [CrossRef]
  41. Ingmann, P.; Veihelmann, B.; Langen, J.; Lamarre, D.; Stark, H.; Courrèges-Lacoste, G.B. Requirements for the GMES Atmosphere Service and ESA’s implementation concept: Sentinels-4/-5 and-5p. Remote Sens. Environ. 2012, 120, 58–69. [Google Scholar] [CrossRef]
  42. Spurr, R.; Loyola, D.; Roozendael, M.V.; Lerot, C. S5P/TROPOMI Total Ozone ATBD. Dtsch. Zent. Für Luft Und Raumfahrt 2021, 67, 535. [Google Scholar]
  43. Landgraf, J.; de Brugh, J.; Scheepmaker, R.; Borsdorff, T.; Houweling, S.; Hasekamp, O. Algorithm Theoretical Baseline Document for Sentinel-5 Precursor: Carbon Monoxide Total Column Retrieval; SRON-S5P-LEV2-RP-002; Netherlands Institute for Space Research: Leiden, The Netherlands, 2018. [Google Scholar]
  44. Willmott, C.J. Some comments on the evaluation of model performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef]
  45. Feng, Y.; Fan, S.R.; Xia, K.W.; Wang, L. Estimation of Regional Ground-Level PM2.5 Concentrations Directly from Satellite Top-of-Atmosphere Reflectance Using A Hybrid Learning Model. Remote Sens. 2022, 14, 20. [Google Scholar] [CrossRef]
  46. Chen, L.; Pang, X.B.; Li, J.J.; Xing, B.; An, T.C.; Yuan, K.B.; Dai, S.; Wu, Z.T.; Wang, S.Q.; Wang, Q.; et al. Vertical profiles of O3, NO2 and PM in a major fine chemical industry park in the Yangtze River Delta of China detected by a sensor package on an unmanned aerial vehicle. Sci. Total Environ. 2022, 845, 11. [Google Scholar] [CrossRef] [PubMed]
  47. Wang, T.; Xue, L.K.; Brimblecombe, P.; Lam, Y.F.; Li, L.; Zhang, L. Ozone pollution in China: A review of concentrations, meteorological influences, chemical precursors, and effects. Sci. Total Environ. 2017, 575, 1582–1596. [Google Scholar] [CrossRef] [PubMed]
  48. Kornilova, A.; Saccon, M.; O’Brien, J.M.; Huang, L.; Rudolph, J. Stable Carbon Isotope Ratios and the Photochemical Age of Atmospheric Volatile Organic Compounds. Atmos. Ocean 2015, 53, 7–13. [Google Scholar] [CrossRef]
  49. Han, S.Q.; Bian, H.; Feng, Y.C.; Liu, A.X.; Li, X.J.; Zeng, F.; Zhang, X.L. Analysis of the Relationship between O3, NO and NO2 in Tianjin, China. Aerosol Air Qual. Res. 2011, 11, 128–139. [Google Scholar] [CrossRef]
  50. García, R.D.; Vázquez, M.A. Evaluation of Machine Learning Models for Ozone Concentration Forecasting in the Metropolitan Valley of Mexico. Appl. Sci. 2024, 14, 1408. [Google Scholar] [CrossRef]
  51. Chen, Z.; Liu, R.; Luo, Z.; Xue, X.; Wang, Y.; Zhao, Z.-J. Prediction of Autumn Ozone Concentration in the Pearl River Delta Based on Machine Learning. Huan Jing Ke Xue = Huanjing Kexue 2024, 45, 1–7. [Google Scholar] [CrossRef]
  52. Jia, X.; Gong, X.; Liu, X.; Zhao, X.; Meng, H.; Dong, Q.; Liu, G.; Gao, H. Deep Sequence Learning for Prediction of Daily NO2 Concentration in Coastal Cities of Northern China. Atmosphere 2023, 14, 467. [Google Scholar] [CrossRef]
  53. Li, M.; Yang, Q.; Yuan, Q.; Zhu, L. Estimation of high spatial resolution ground-level ozone concentrations based on Landsat 8 TIR bands with deep forest model. Chemosphere 2022, 301, 134817. [Google Scholar] [CrossRef] [PubMed]
  54. Ziwei, L.I.; Qingxun, M.A.; Jie, L. BP neural network for near-surface ozone estimation and spatial and temporal characteristics analysis. Bull. Surv. Mapp. 2021, 6, 28–36. [Google Scholar]
  55. Zhang, M.; Yang, J.; Song, G.; Li, S. Method for Realizing Near-Ground Ozone Inversion Based on Near-Ground UV Radiation for Use in Ozone Research, Involves Training the Deep Learning Model Based on Satellite Observation, and Estimating near Ground Ozone Concentration in Satellite Observation Area by Deep Learning Model. US2023131036-A1 27 Apr 2023 G06N-003/04 202336 English. 2022. Available online: https://webofscience.clarivate.cn/wos/alldb/full-record/DIIDW:202228283Y (accessed on 17 August 2024).
  56. Zhu, H.; Wang, Z.; Zhao, S.; Li, W.; Zhang, D.; Zhang, L.; Wang, Y.; Zhang, J.; Zhou, C.; Zhang, Y.; et al. Method for Performing Near-Ground Ozone Concentration Inversion Based on Combination of Machine Learning and Deep Learning for Ground Observation and Atmospheric Simulation in Rural and Remote Areas Involves Inputting Satellite Remote Sensing Information of Monitoring Area into Inversion Model. CN113657023-A Chinese. 2022. Available online: https://webofscience.clarivate.cn/wos/alldb/full-record/DIIDW:2021D60319 (accessed on 17 August 2024).
  57. Zhao, L.; Liu, X.; Fan, L.; Liu, C.; Wang, S.; Ma, X. Pollution Characteristic and Source Apportionment of VOCs During Summer Typical Periods in Shijiazhuang. Environ. Monit. China 2019, 35, 78–84. [Google Scholar]
Atmosphere 15 01020 g001
Figure 1. Shijiazhuang elevation and monitoring station distribution map.
Figure 1. Shijiazhuang elevation and monitoring station distribution map.
Atmosphere 15 01020 g001
Atmosphere 15 01020 g002
Figure 2. Deep forest model technology roadmap.
Figure 2. Deep forest model technology roadmap.
Atmosphere 15 01020 g002
Atmosphere 15 01020 g003
Figure 3. Flow chart of multi-granularity scanning.
Figure 3. Flow chart of multi-granularity scanning.
Atmosphere 15 01020 g003
Atmosphere 15 01020 g004
Figure 4. Cascade forest structure diagram.
Figure 4. Cascade forest structure diagram.
Atmosphere 15 01020 g004
Atmosphere 15 01020 g005
Figure 5. Correlation of air pollutants in Shijiazhuang.
Figure 5. Correlation of air pollutants in Shijiazhuang.
Atmosphere 15 01020 g005
Atmosphere 15 01020 g006
Figure 6. Daily variation of O3 and PM2.5 concentrations in Shijiazhuang during 2020–2021.
Figure 6. Daily variation of O3 and PM2.5 concentrations in Shijiazhuang during 2020–2021.
Atmosphere 15 01020 g006
Atmosphere 15 01020 g007
Figure 7. Daily variation of O3 and NO2 concentrations in Shijiazhuang during 2020–2021.
Figure 7. Daily variation of O3 and NO2 concentrations in Shijiazhuang during 2020–2021.
Atmosphere 15 01020 g007
Atmosphere 15 01020 g008aAtmosphere 15 01020 g008b
Figure 8. Scatter plot of the predicted results of different models against the measured values of O3: (a) Deep forest with NO2 and PM2.5; (b) Deep forest with PM2.5; (c) Deep forest with NO2; (d) Deep forest without NO2 and PM2.5; (e) LightGBM; (f) Random forest; (g) GBDT; (h) Catboost; (i) XGBoost; (j) Decision Tree.
Figure 8. Scatter plot of the predicted results of different models against the measured values of O3: (a) Deep forest with NO2 and PM2.5; (b) Deep forest with PM2.5; (c) Deep forest with NO2; (d) Deep forest without NO2 and PM2.5; (e) LightGBM; (f) Random forest; (g) GBDT; (h) Catboost; (i) XGBoost; (j) Decision Tree.
Atmosphere 15 01020 g008aAtmosphere 15 01020 g008b
Atmosphere 15 01020 g009
Figure 9. The line graph of the simulated results and the actual measurements after the addition of the NO2 and PM2.5 data in the deep forest model.
Figure 9. The line graph of the simulated results and the actual measurements after the addition of the NO2 and PM2.5 data in the deep forest model.
Atmosphere 15 01020 g009
Atmosphere 15 01020 g010
Figure 10. Seasonal average distribution of O3 concentration in Shijiazhuang in 2020: (a) Spring; (b) Summer; (c) Autumn; (d) Winter.
Figure 10. Seasonal average distribution of O3 concentration in Shijiazhuang in 2020: (a) Spring; (b) Summer; (c) Autumn; (d) Winter.
Atmosphere 15 01020 g010
Table 1. Descriptive statistics of the inverse O3 dataset.
Table 1. Descriptive statistics of the inverse O3 dataset.
CategoryVariableSpatial ResolutionTemporal Resolution
Ground dataO3
PM2.5—Daily
NO2
Remote sensing dataTropOMI O31 kmDaily
Meteorological element dataBoundary Layer Height, Surface Pressure, 2 m temperature, total-column water content, total-column ozone, 10 m u-component of wind, 10 m v-component of wind0.25° × 0.25°Hourly
Auxiliary dataDigital Elevation Model1 kmYearly
Table 2. Comparing the model performance of different models.
Table 2. Comparing the model performance of different models.
Model R 2 R M S E (μg/m3) M A E (μg/m3)
(a)Deep forest with NO2 and PM2.50.956013.25429.0250
(b)Deep forest with PM2.50.949914.14099.4926
(c)Deep forest with NO20.948714.31469.5011
(d)Deep forest without NO2 and PM2.50.946314.63589.5159
(e)LightGBM0.906619.048512.2511
(f)Random forest0.895620.145211.7856
(g)GBDT0.887720.895012.2659
(h)Catboost0.886920.963513.2224
(i)XGBoost0.886121.042813.1755
(j)Decision Tree0.814626.841116.5232
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Zong, M.; Song, T.; Zhang, Y.; Feng, Y.; Fan, S. A Deep Forest Algorithm Based on TropOMI Satellite Data to Estimate Near-Ground Ozone Concentration. Atmosphere 2024, 15, 1020. https://doi.org/10.3390/atmos15091020

AMA Style

Zong M, Song T, Zhang Y, Feng Y, Fan S. A Deep Forest Algorithm Based on TropOMI Satellite Data to Estimate Near-Ground Ozone Concentration. Atmosphere. 2024; 15(9):1020. https://doi.org/10.3390/atmos15091020

Chicago/Turabian Style

Zong, Mao, Tianhong Song, Yan Zhang, Yu Feng, and Shurui Fan. 2024. "A Deep Forest Algorithm Based on TropOMI Satellite Data to Estimate Near-Ground Ozone Concentration" Atmosphere 15, no. 9: 1020. https://doi.org/10.3390/atmos15091020

APA Style

Zong, M., Song, T., Zhang, Y., Feng, Y., & Fan, S. (2024). A Deep Forest Algorithm Based on TropOMI Satellite Data to Estimate Near-Ground Ozone Concentration. Atmosphere, 15(9), 1020. https://doi.org/10.3390/atmos15091020

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop