Investigating Different Interpolation Methods for High-Accuracy VTEC Analysis in Ionospheric Research
Abstract
1. Introduction
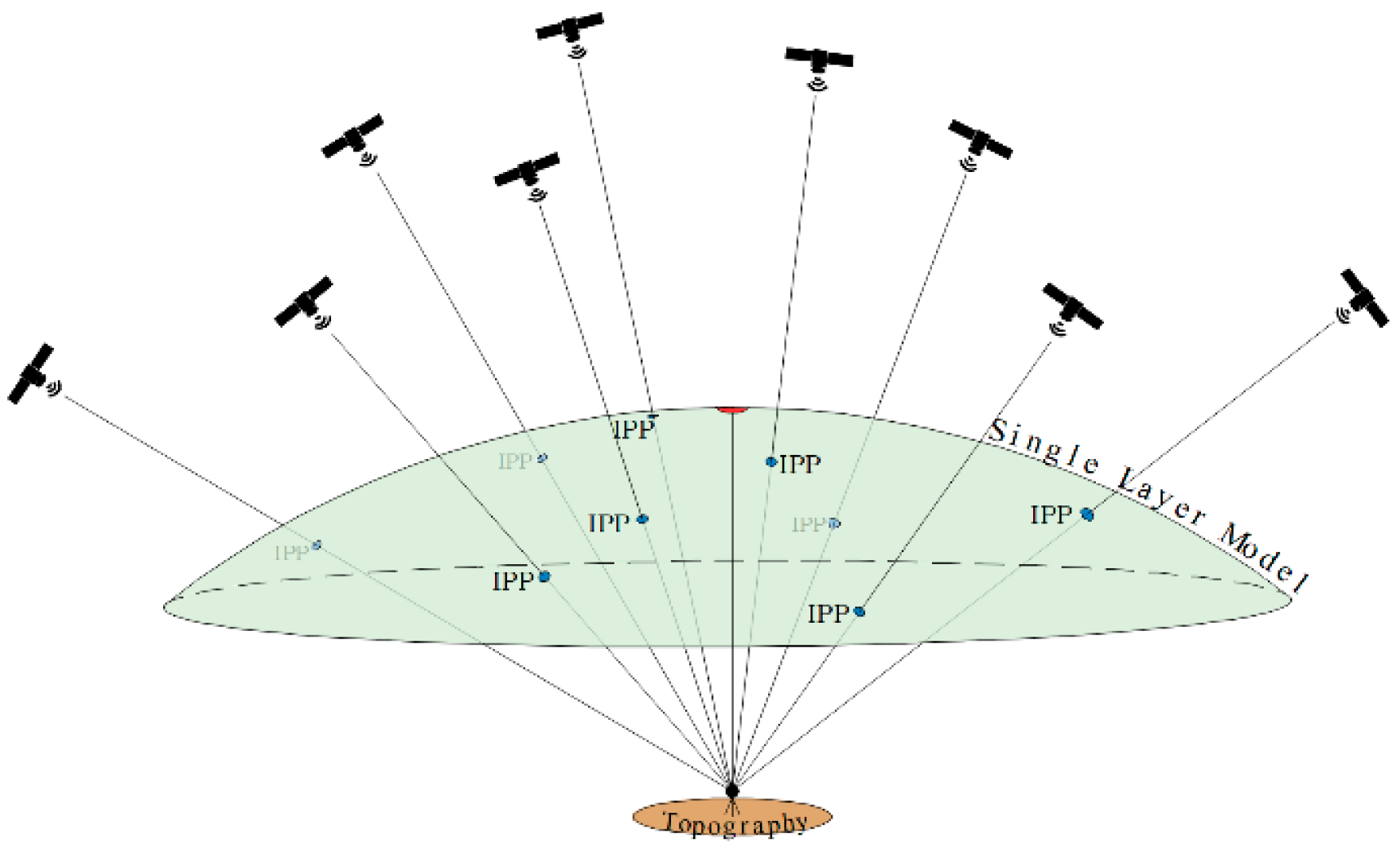
2. Materials and Methods
2.1. Interpolation Methods
- Polynomial Interpolation Method
- Kriging Interpolation Method
- Radial Basis Function
2.2. Evaluation Parameters
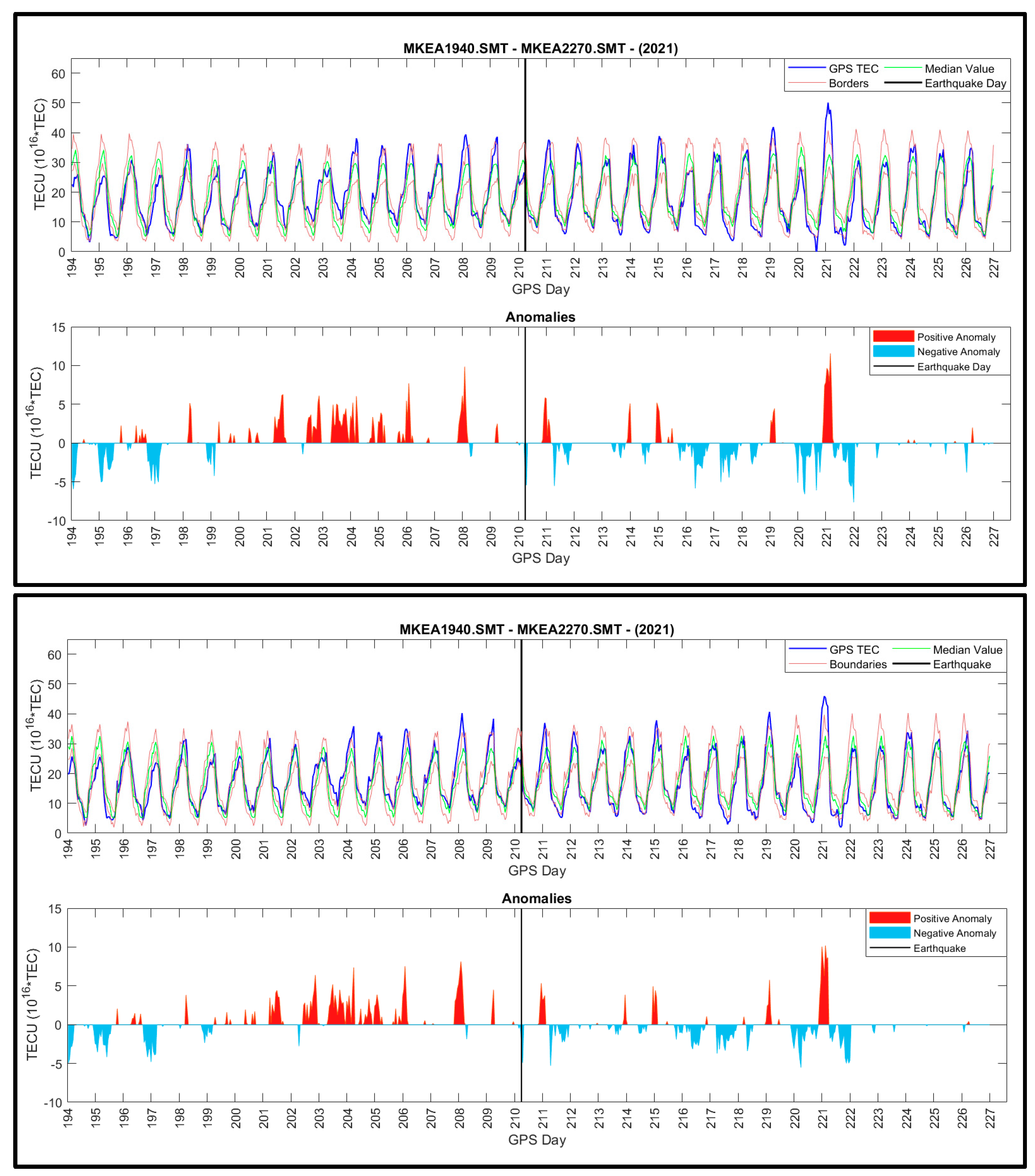
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, C.; Xin, S.; Liu, X.; Shi, C.; Fan, L. Prediction of global ionospheric VTEC maps using an adaptive autoregressive model. Earth Planets Space 2018, 70, 18. [Google Scholar] [CrossRef]
- Yildiz, S.K.; Arikan, F. Estimation of planar trend model parameters for midlatitude ionosphere. J. Geophys. Res. Space Phys. 2020, 125, e2019JA027223. [Google Scholar] [CrossRef]
- Pikridas, C.; Bitharis, S.; Katsougiannopoulos, S.; Spanakaki, K. Study of TEC variations using permanent stations GNSS data in relation with seismic events. Application on Samothrace earthquake of 24 May 2014. Geod. Cartogr. 2019, 45, 137–146. [Google Scholar] [CrossRef]
- Orus, R.; Hernandez-Pajares, M.; Juan, J.M.; Sanz, J. Improvement of global ionospheric VTEC maps by using kriging interpolation technique. J. Atmos. Sol. Terr. Phys. 2005, 67, 1598–1609. [Google Scholar] [CrossRef]
- Krypiak-Gregorczyk, A.; Wielgosz, P.; Borkowski, A. Ionospheric model for European region based on multi-GNSS data and TPS interpolation. Remote Sens. 2017, 9, 1221. [Google Scholar] [CrossRef]
- Şentürk, E.; Çepni, M.S. Performance of different weighting and surface fitting techniques on station-wise TEC calculation and modified sine weighting supported by the sun effect. J. Spatial Sci. 2019, 64, 209–220. [Google Scholar] [CrossRef]
- Ogryzek, M.; Krypiak-Gregorczyk, A.; Wielgosz, P. Optimal geostatistical methods for interpolation of the ionosphere: A case study on the St Patrick’s Day storm of 2015. Sensors 2020, 2, 2840. [Google Scholar] [CrossRef]
- Nayak, K.; López-Urías, C.; Romero-Andrade, R.; Sharma, G.; Guzmán-Acevedo, G.M.; Trejo-Soto, M.E. Ionospheric Total Electron Content (TEC) Anomalies as Earthquake Precursors: Unveiling the Geophysical Connection Leading to the 2023 Moroccan 6.8 Mw Earthquake. Geosciences 2023, 13, 319. [Google Scholar] [CrossRef]
- Sharma, G.; Nayak, K.; Romero-Andrade, R.; Aslam, M.M.; Sarma, K.K.; Aggarwal, S.P. Low Ionosphere Density Above the Earthquake Epicentre Region of Mw 7.2, El Mayor–Cucapah Earthquake Evident from Dense CORS Data. J. Indian Soc. Remote Sens. 2024, 52, 543–555. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, X.; Du, X. Analysis of Ionospheric Perturbations Possibly Related to Yangbi Ms6.4 and Maduo Ms7.4 Earthquakes on 21 May 2021 in China Using GPS TEC and GIM TEC Data. Atmosphere 2022, 13, 1725. [Google Scholar] [CrossRef]
- Nayak, K.; Romero-Andrade, R.; Sharma, G.; Zavala, J.L.C.; Urias, C.L. A combined approach using b-value and ionospheric GPS-TEC for large earthquake precursor detection: A case study for the Colima earthquake of 7.7 Mw, Mexico. Acta Geod. Geophys. 2023, 58, 515–538. [Google Scholar] [CrossRef]
- Seemala, G.P.; GPS-TEC Analysis Application. Technical Document. 2017. Available online: https://seemala.blogspot.com/ (accessed on 8 August 2024).
- Köz, İ.; Doğanalp, S. Investigation of ionospheric anomalies in relation to earthquakes during high and low solar activity periods in years 2002 and 2021. Geomag. Aeron. 2023, 63, 93–104. [Google Scholar] [CrossRef]
- Dobrovolsky, I.P.; Zubkov, S.I.; Miachkin, V.I. Estimation of the size of earthquake preparation zones. Pure Appl. Geophys. 1979, 117, 1025–1044. [Google Scholar] [CrossRef]
- NASA’s Archive of Space Geodesy Data. Available online: https://cddis.nasa.gov/index.html (accessed on 1 May 2022).
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. (Eds.) Bernese GNSS Software Version 5.2; Astronomical Institute, University of Bern: Bern, Switzerland, 2015; pp. 129–132. [Google Scholar] [CrossRef]
- Schaer, S.; Gurtner, W. IONEX: The Ionosphere Map Exchange Format Version 1.1; Astronomical Institute, University of Bern: Bern, Switzerland, 2015; pp. 2–5. [Google Scholar]
- Liu, J.Y.; Chen, Y.I.; Chen, C.H.; Liu, C.Y.; Chen, C.Y.; Nishihashi, M.; Li, J.Z.; Xia, Y.Q.; Oyama, K.I.; Hattori, K.; et al. Seismoionospheric GPS total electron content anomalies observed before the 12 May 2008 Mw 7.9 Wenchuan earthquake. J. Geophy. Res. 2009, 114, 1–10. [Google Scholar] [CrossRef]
- Khampuengson, T.; Wang, W. Novel Methods for Imputing Missing Values in Water Level Monitoring Data. Water Resour. Manag. 2023, 37, 851–878. [Google Scholar] [CrossRef]
- Amoroso, P.P.; Aguilar, F.J.; Parente, C.; Aguilar, M.A. Statistical Assessment of Some Interpolation Methods for Building Grid Format Digital Bathymetric Models. Remote Sens. 2023, 15, 2072. [Google Scholar] [CrossRef]
- Surfer Help. Available online: https://surferhelp.goldensoftware.com/griddata/idd_grid_data_kriging.htm (accessed on 21 December 2023).
- Huang, L.; Zhang, H.; Xu, P.; Geng, J.; Wang, C.; Liu, J. Kriging with Unknown Variance Components for Regional Ionospheric Reconstruction. Sensors 2017, 17, 468. [Google Scholar] [CrossRef]
- Dehvari, A. DEM Application and Qualification with Regard to Terrain Analysis, Land Use Classification and Watershed Modeling. Ph.D. Thesis, The Faculty of Graduate Studies of The University of Guelph, Guelph, Canada, 2010. [Google Scholar]
- Arseni, M.; Voiculescu, M.; Georgescu, L.P.; Iticescu, C.; Rosu, A. Testing Different Interpolation Methods Based on Single Beam Echosounder River Surveying. Case Study: Siret River. ISPRS Int. J. Geo-Inf. 2019, 8, 507. [Google Scholar] [CrossRef]
- Alsharif, F. Quasi-Interpolation on Chebyshev Grids with Boundary Corrections. Computation 2024, 12, 100. [Google Scholar] [CrossRef]
- Sun, J.; Wang, L.; Gong, D. An Adaptive Selection Method for Shape Parameters in MQ-RBF Interpolation for Two-Dimensional Scattered Data and Its Application to Integral Equation Solving. Fractal Fract. 2023, 7, 448. [Google Scholar] [CrossRef]
- Özkaya Yılmaz, Ö.; Kayran, A. A Comparative Study on the Efficiencies of Aerodynamic Reduced Order Models of Rigid and Aeroelastic Sweptback Wings. Aerospace 2024, 11, 616. [Google Scholar] [CrossRef]
- Foster, M.P.; Evans, A.N. An Evaluation of Interpolation Techniques for Reconstructing Ionospheric TEC Maps. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2153–2164. [Google Scholar] [CrossRef]
- Tang, S.; Huang, Z.; Yuan, H. Improving regional ionospheric TEC mapping based on RBF interpolation. Adv. Space Res. 2021, 67, 722–730. [Google Scholar] [CrossRef]
- Jasek, K.; Pasternak, M.; Miluski, W.; Bugaj, J.; Grabka, M. Application of Gaussian Radial Basis Functions for Fast Spatial Imaging of Ground Penetration Radar Data Obtained on an Irregular Grid. Electronics 2021, 10, 2965. [Google Scholar] [CrossRef]
- Rocha, H. On the selection of the most adequate radial basis function. Appl. Math. Model. 2009, 33, 1573–1583. [Google Scholar] [CrossRef]
- Doganalp, S.; Selvi, H.Z. Local geoid determination in strip area projects by using polynomials, least-squares collocation and radial basis functions. Measurement 2015, 73, 429–438. [Google Scholar] [CrossRef]
- Carlson, R.E.; Foley, T.A. The parameter R2 in multiquadric interpolation. Computers Math. Applic. 1991, 21, 29–42. [Google Scholar] [CrossRef]
- Hardy, R.L. Theory of applications of the multiquadratic–biharmonic method: 20 years of discovery 1968–1988. Comput. Math. Appl. 1990, 19, 163–208. [Google Scholar] [CrossRef]
- Rippa, S. An algorithm for selecting a good parameter c in radial basis function interpolation. Adv. Comput. Math. 1999, 11, 193–210. [Google Scholar] [CrossRef]
- Fasshauer, G.E. Newton iteration with multiquadrics for the solution of nonlinear PDEs. Comput. Math. Appl. 2002, 43, 423–438. [Google Scholar] [CrossRef]
- Bildirici, I.O. Numerical inverse transformation for map projections. Comput. Geosci. 2003, 29, 1003–1011. [Google Scholar] [CrossRef]
- Ferdowsi, M.; Gan, M.-H.; Kwan, B.-H.; Tan, M.P.; Goh, C.-H. Anticipating Fainting: Real-Time Prediction of Vasovagal Syncope During Head-Up Tilt Table Testing. In Proceedings of the TENCON 2023—2023 IEEE Region 10 Conference (TENCON), Chiang Mai, Thailand, 31 October–3 November 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Gizachew, S.; Sitotaw, B.; Mengistu, G. Annual Mean and Correlation of Global Vertical Total Electron Content from Various Global Data Centers. Am. J. Astron. Astrophysic. 2020, 8, 1–7. [Google Scholar] [CrossRef]
- Willmott, C.J. On the Validation of Models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Onyutha, C. A hydrological model skill score and revised R-squared. Hydrol. Res. 2022, 53, 51–64. [Google Scholar] [CrossRef]
- Ruezzene, C.B.; Miranda, R.B.; Bolleli, T.M.; Mauad, F.F. Filling and validating rainfall data based on statistical techniques and artificial intelligence. Rev. Ambient. Água 2021, 16, e2767. [Google Scholar] [CrossRef]
- Hafizi, H.; Sorman, A.A. Integrating Meteorological Forcing from Ground Observations and MSWX Dataset for Streamflow Prediction under Multiple Parameterization Scenarios. Water 2022, 14, 2721. [Google Scholar] [CrossRef]
- Pham, L.T.; Luo, L.; Finley, A. Evaluation of random forests for short-term daily streamflow forecasting in rainfall-and snowmelt-driven watersheds. Hydrol. Earth. Syst. Sc. 2021, 25, 2997–3015. [Google Scholar] [CrossRef]

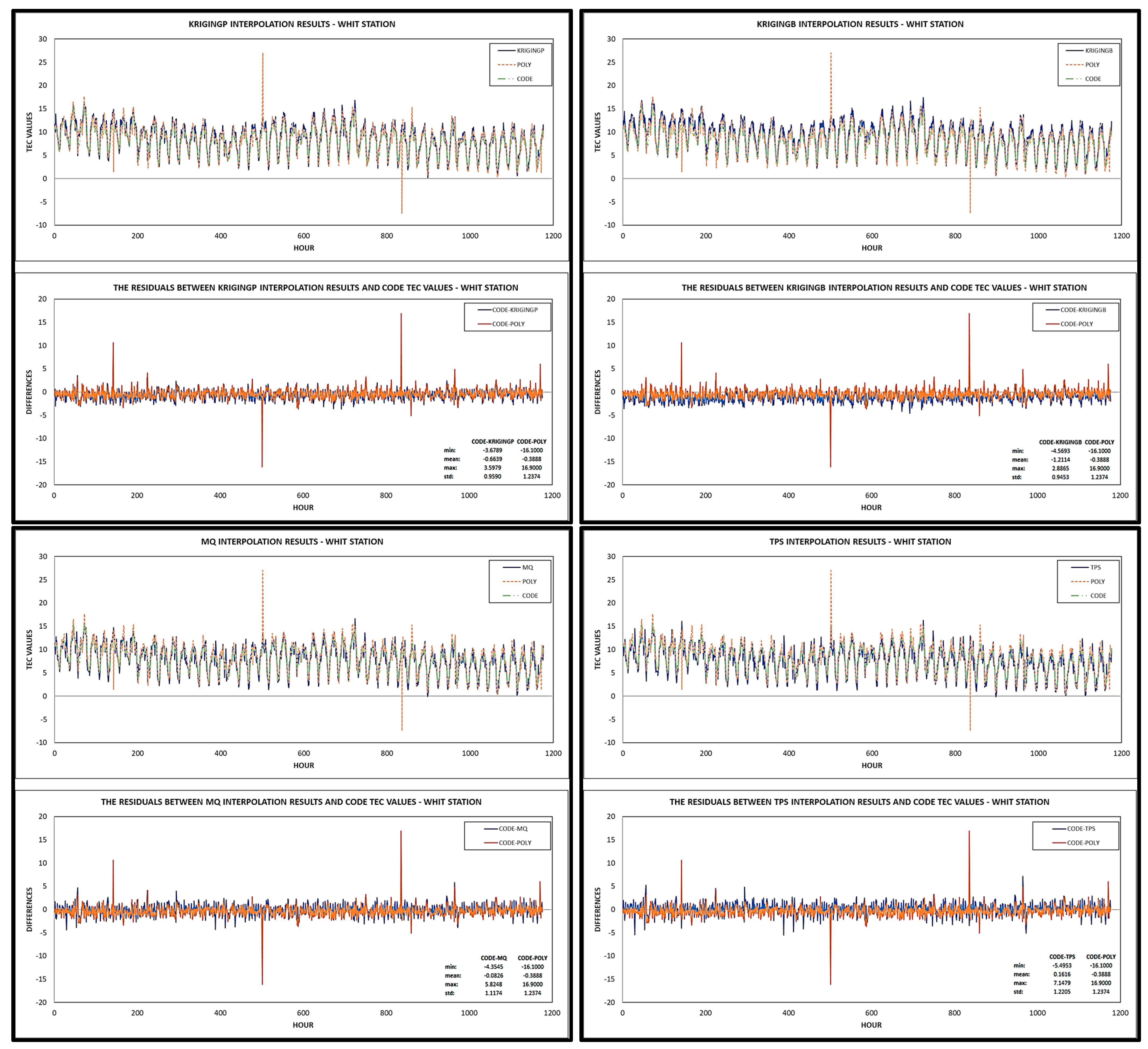
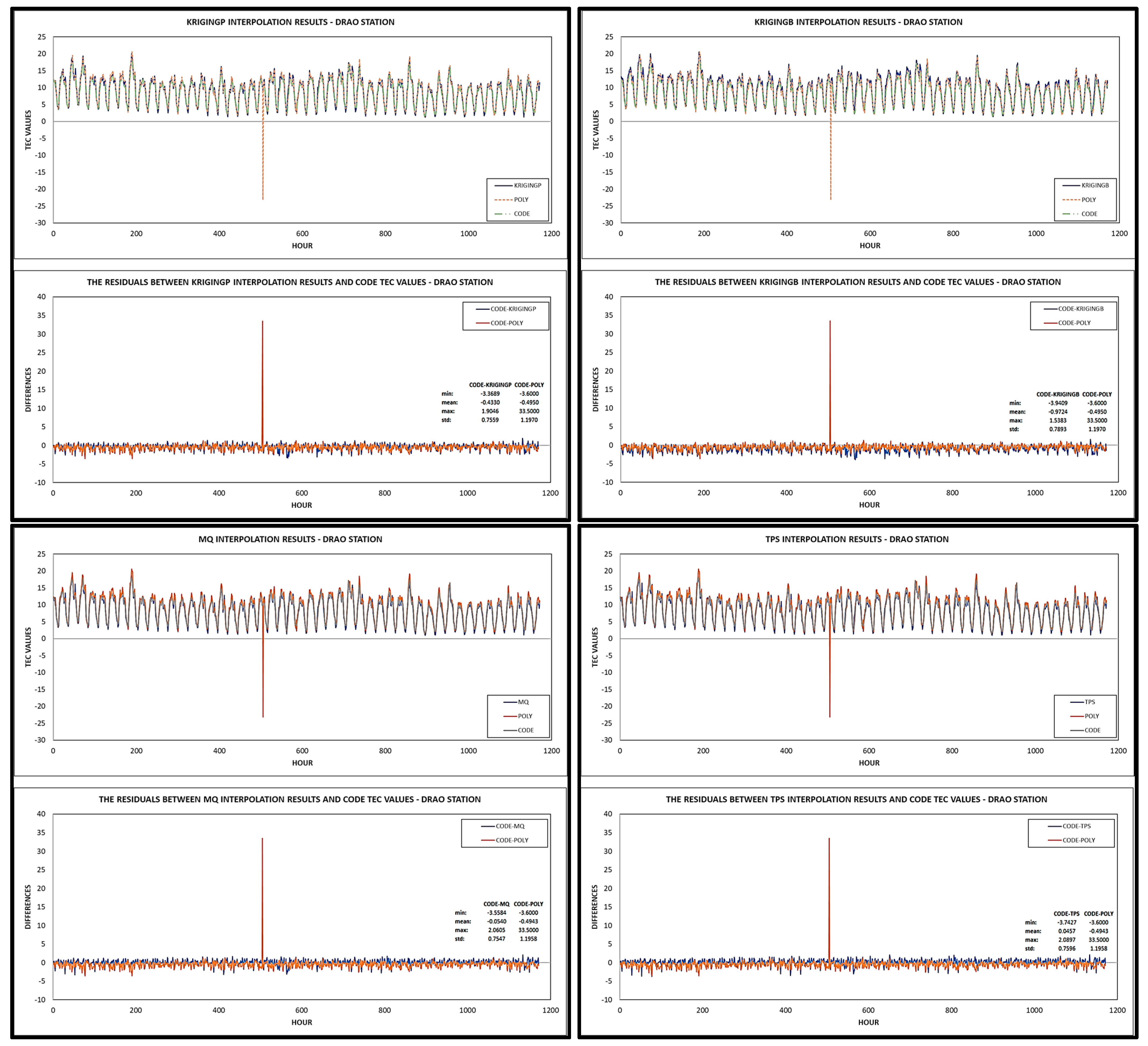
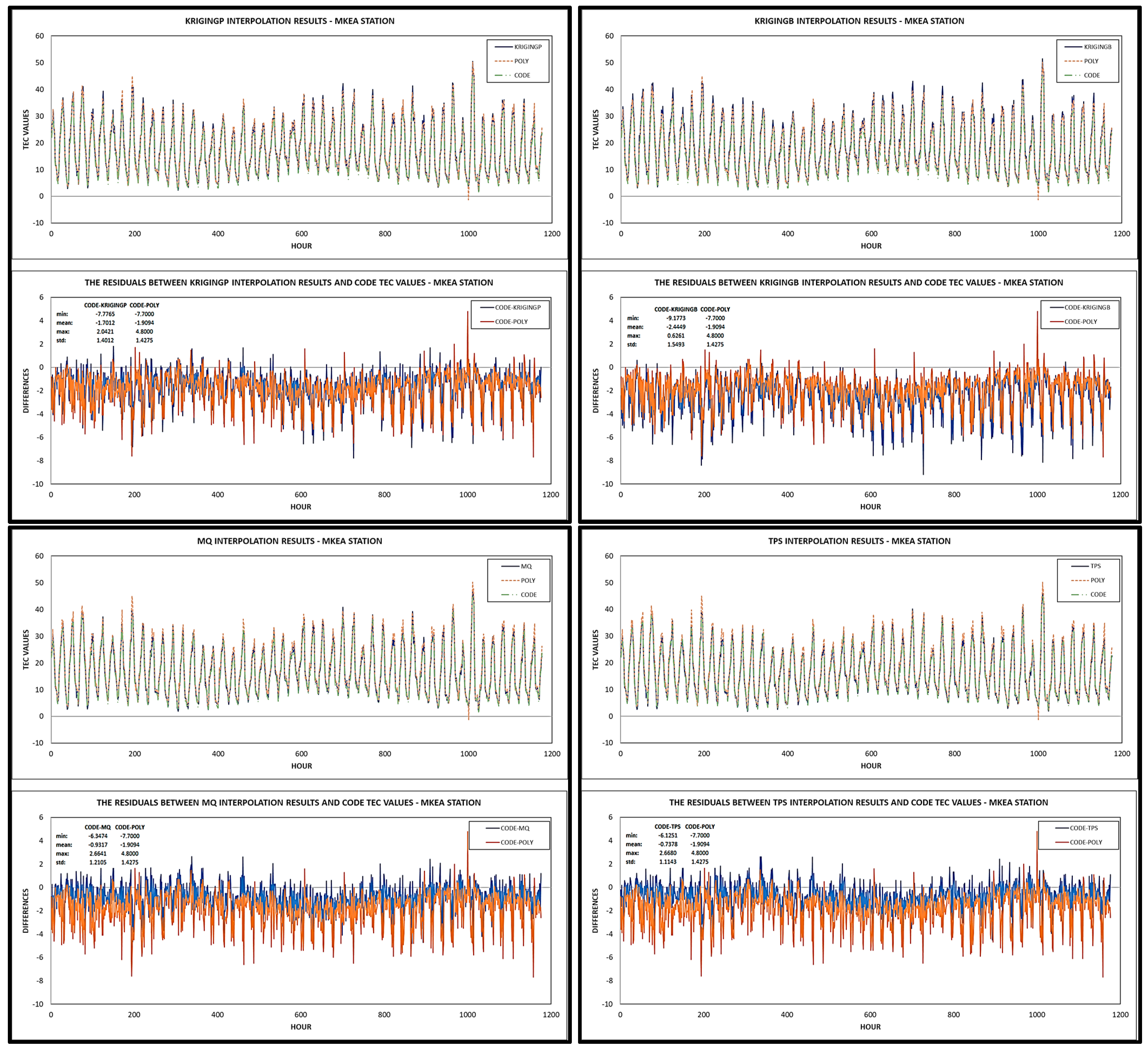
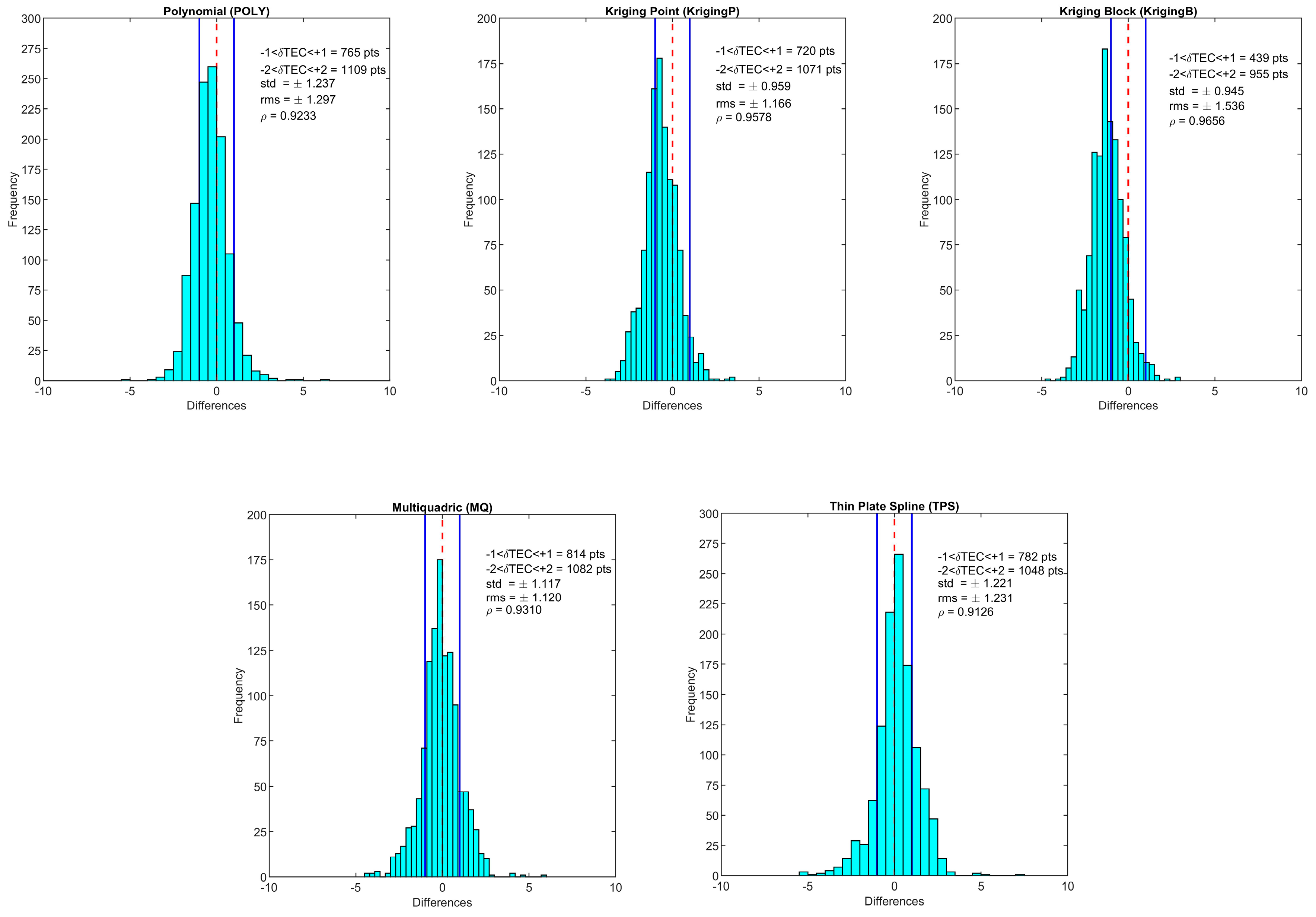

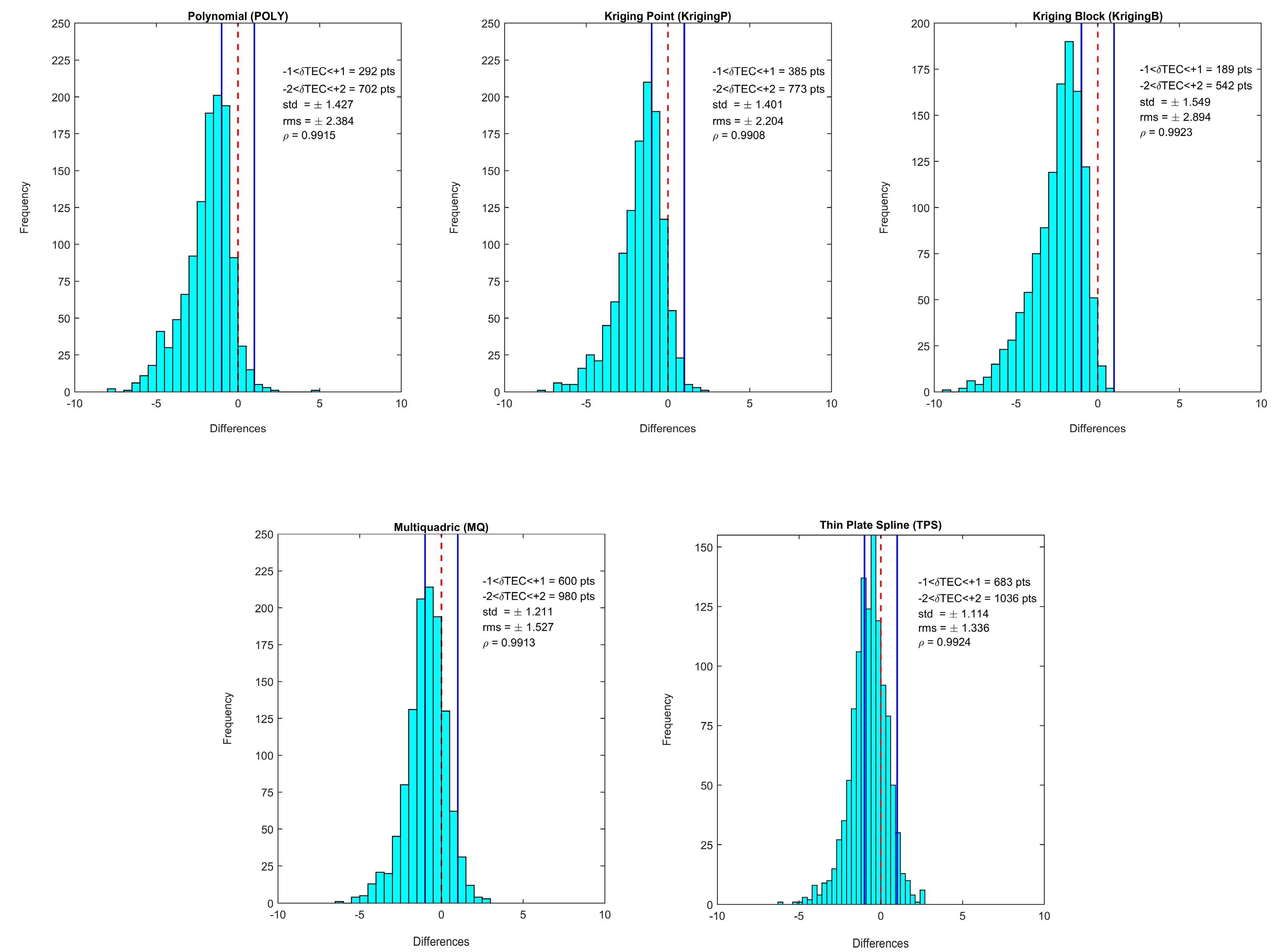
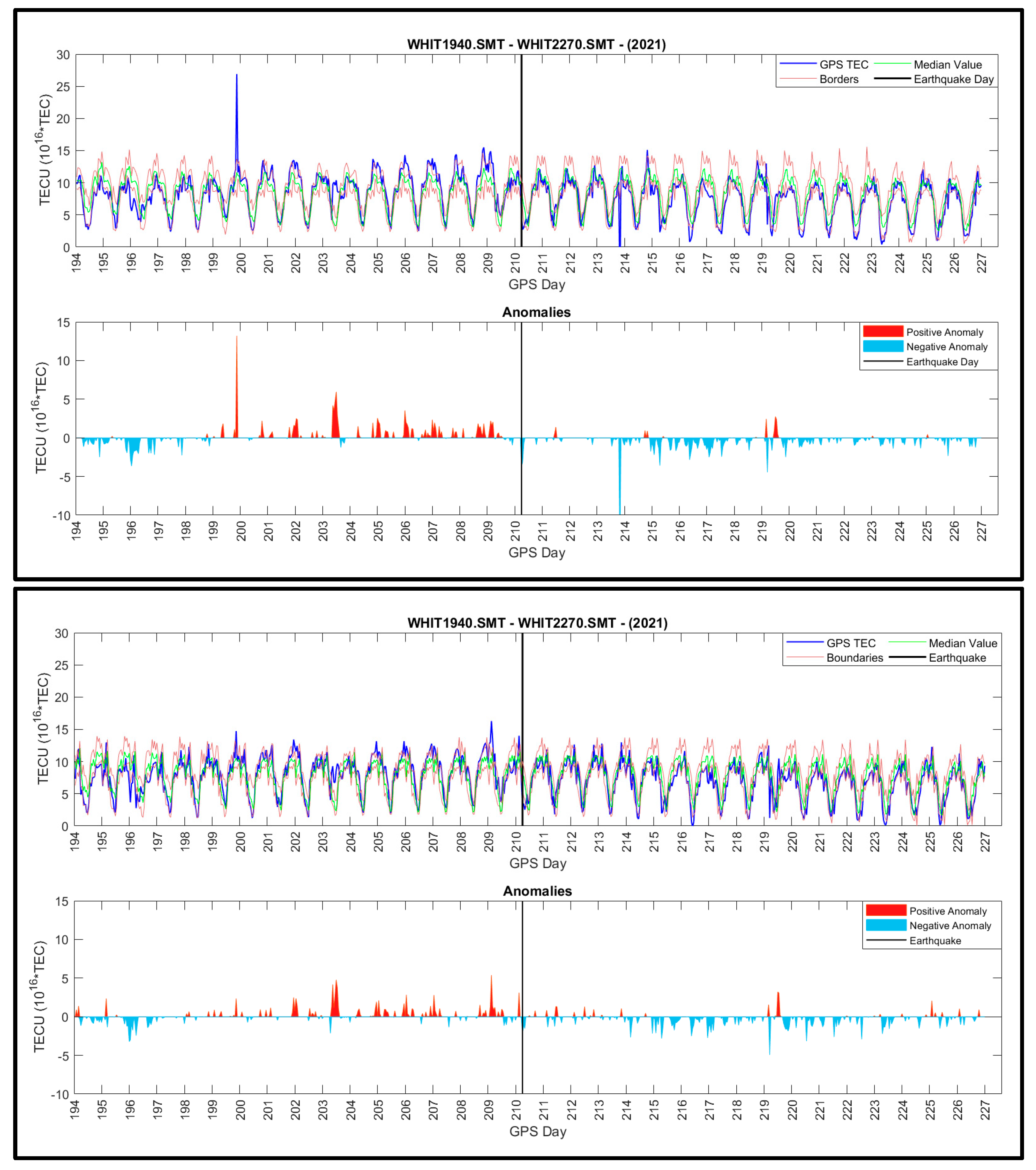
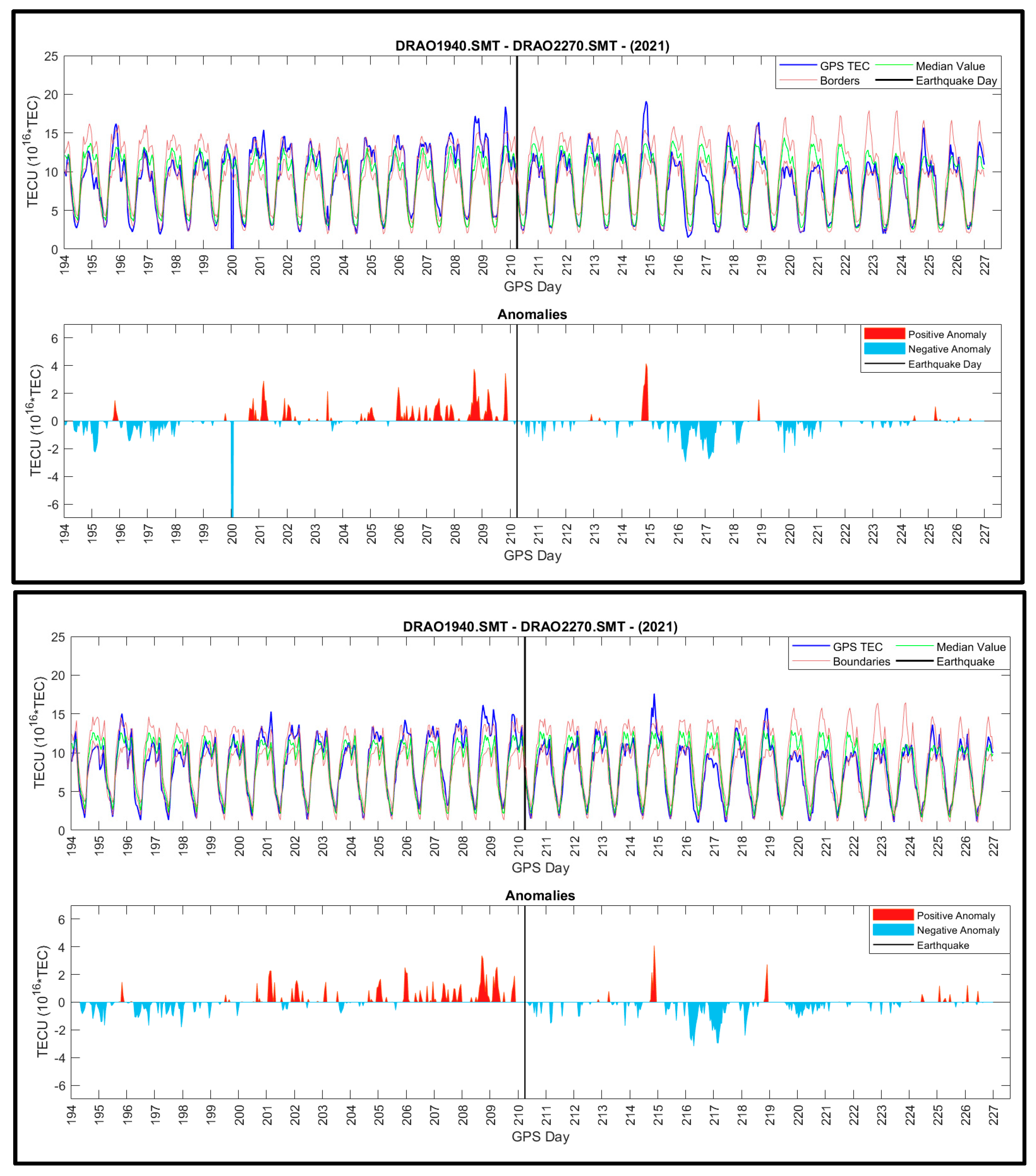
| Station | Criteria | CODE-Poly | CODE-KrigingP | CODE-KrigingB | CODE-MQ | CODE-TPS |
| WHIT | min | −16.100 | −3.679 | −4.569 | −4.355 | −5.495 |
| mean | −0.389 | −0.664 | −1.211 | −0.083 | 0.162 | |
| max | 16.900 | 3.598 | 2.886 | 5.825 | 7.148 | |
| std | 1.237 | 0.959 | 0.945 | 1.117 | 1.221 | |
| RMSE | 1.297 | 1.166 | 1.536 | 1.120 | 1.231 | |
| R2 | 0.852 | 0.917 | 0.932 | 0.867 | 0.833 | |
| IA | 0.949 | 0.959 | 0.933 | 0.960 | 0.950 | |
| Pearson | 0.923 | 0.958 | 0.966 | 0.931 | 0.913 | |
| c | 0.876 | 0.918 | 0.901 | 0.894 | 0.867 | |
| KGE | 0.817 | 0.825 | 0.779 | 0.856 | 0.856 | |
| Station | Criteria | CODE-Poly | CODE-KrigingP | CODE-KrigingB | CODE-MQ | CODE-TPS |
| DRAO | min | −3.600 | −3.369 | −3.941 | −3.558 | −3.743 |
| mean | −0.495 | −0.433 | −0.972 | −0.056 | 0.044 | |
| max | 33.500 | 1.905 | 1.538 | 2.061 | 2.090 | |
| std | 1.197 | 0.756 | 0.789 | 0.754 | 0.760 | |
| RMSE | 1.295 | 0.871 | 1.252 | 0.756 | 0.760 | |
| R2 | 0.916 | 0.966 | 0.972 | 0.960 | 0.958 | |
| IA | 0.970 | 0.986 | 0.973 | 0.989 | 0.989 | |
| Pearson | 0.957 | 0.983 | 0.986 | 0.980 | 0.979 | |
| c | 0.929 | 0.969 | 0.960 | 0.969 | 0.968 | |
| KGE | 0.869 | 0.907 | 0.844 | 0.951 | 0.961 | |
| Station | Criteria | CODE-Poly | CODE-KrigingP | CODE-KrigingB | CODE-MQ | CODE-TPS |
| MKEA | min | −7.700 | −7.776 | −9.177 | −6.347 | −6.125 |
| mean | −1.909 | −1.701 | −2.445 | −0.932 | −0.738 | |
| max | 4.800 | 2.042 | 0.626 | 2.664 | 2.668 | |
| std | 1.427 | 1.401 | 1.549 | 1.211 | 1.114 | |
| RMSE | 2.384 | 2.204 | 2.894 | 1.527 | 1.336 | |
| R2 | 0.983 | 0.982 | 0.985 | 0.983 | 0.985 | |
| IA | 0.983 | 0.985 | 0.976 | 0.993 | 0.994 | |
| Pearson | 0.992 | 0.991 | 0.992 | 0.991 | 0.992 | |
| c | 0.975 | 0.976 | 0.968 | 0.984 | 0.987 | |
| KGE | 0.867 | 0.882 | 0.832 | 0.937 | 0.951 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doğanalp, S.; Köz, İ. Investigating Different Interpolation Methods for High-Accuracy VTEC Analysis in Ionospheric Research. Atmosphere 2024, 15, 986. https://doi.org/10.3390/atmos15080986
Doğanalp S, Köz İ. Investigating Different Interpolation Methods for High-Accuracy VTEC Analysis in Ionospheric Research. Atmosphere. 2024; 15(8):986. https://doi.org/10.3390/atmos15080986
Chicago/Turabian StyleDoğanalp, Serkan, and İrem Köz. 2024. "Investigating Different Interpolation Methods for High-Accuracy VTEC Analysis in Ionospheric Research" Atmosphere 15, no. 8: 986. https://doi.org/10.3390/atmos15080986
APA StyleDoğanalp, S., & Köz, İ. (2024). Investigating Different Interpolation Methods for High-Accuracy VTEC Analysis in Ionospheric Research. Atmosphere, 15(8), 986. https://doi.org/10.3390/atmos15080986






