Analysis of Ionospheric Anomalies before Earthquakes of Mw6.5 and above in Japan from 2011 to 2022
Abstract
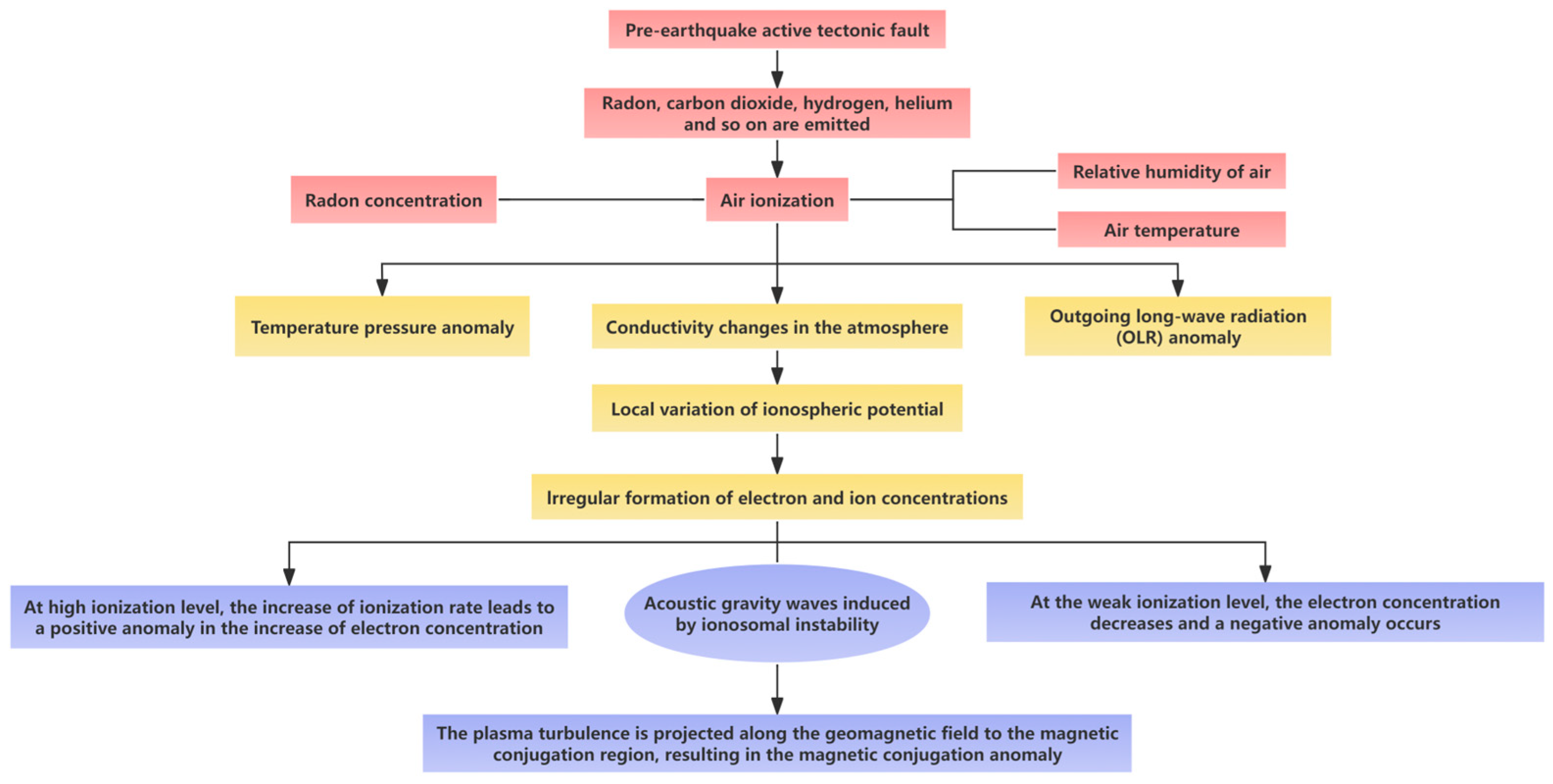
1. Introduction
2. Data and Methodology
2.1. Data Selection
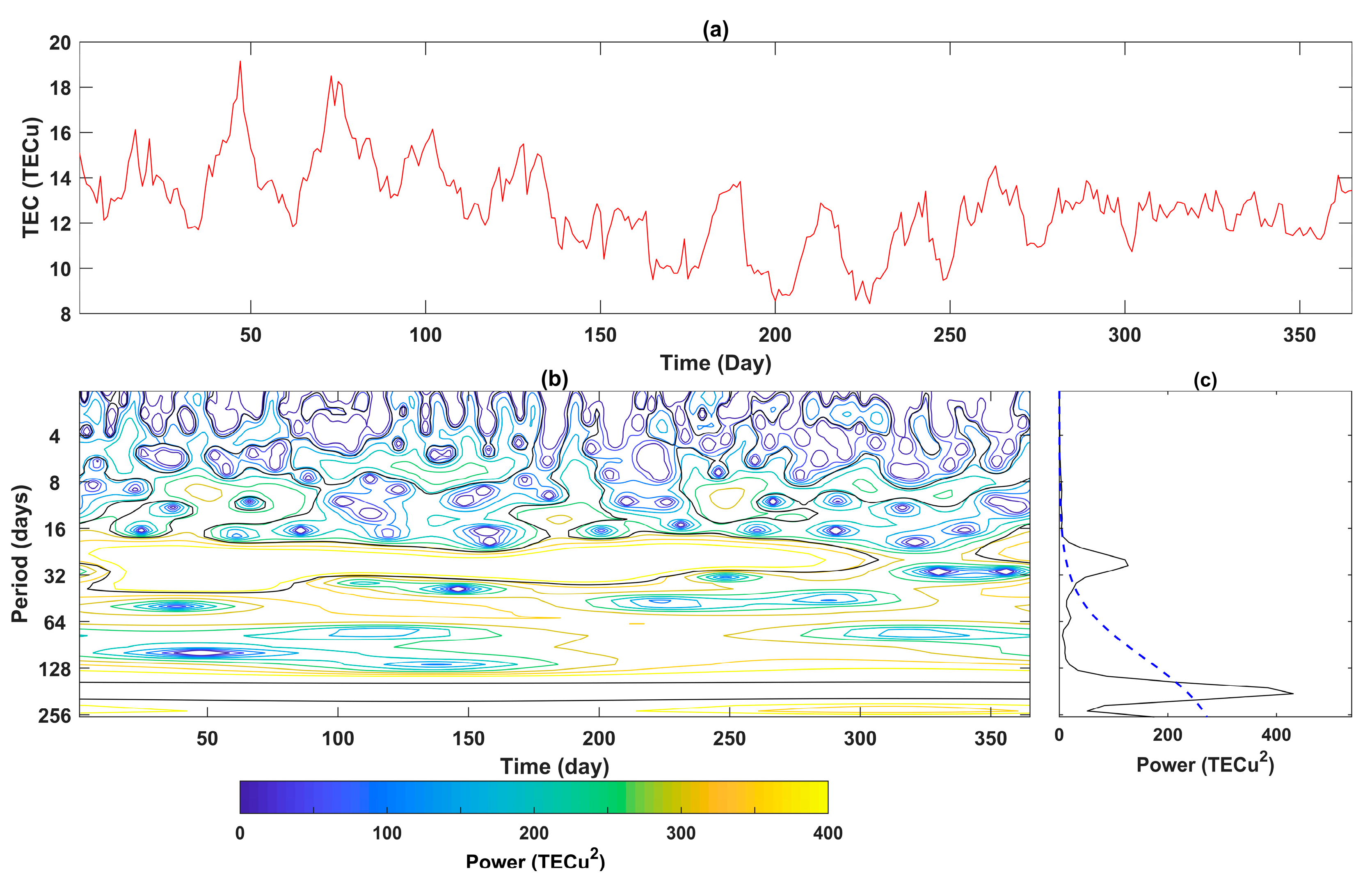
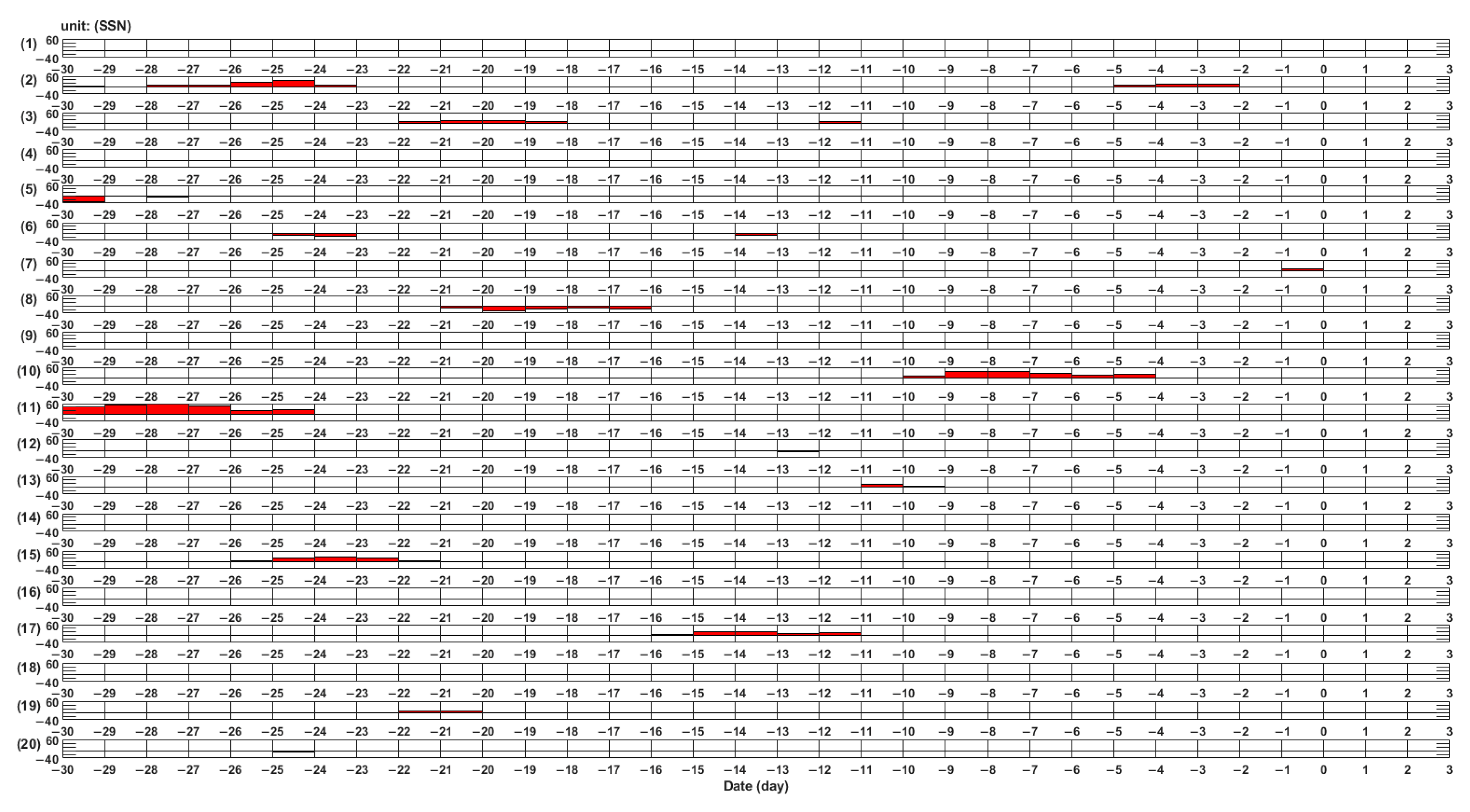
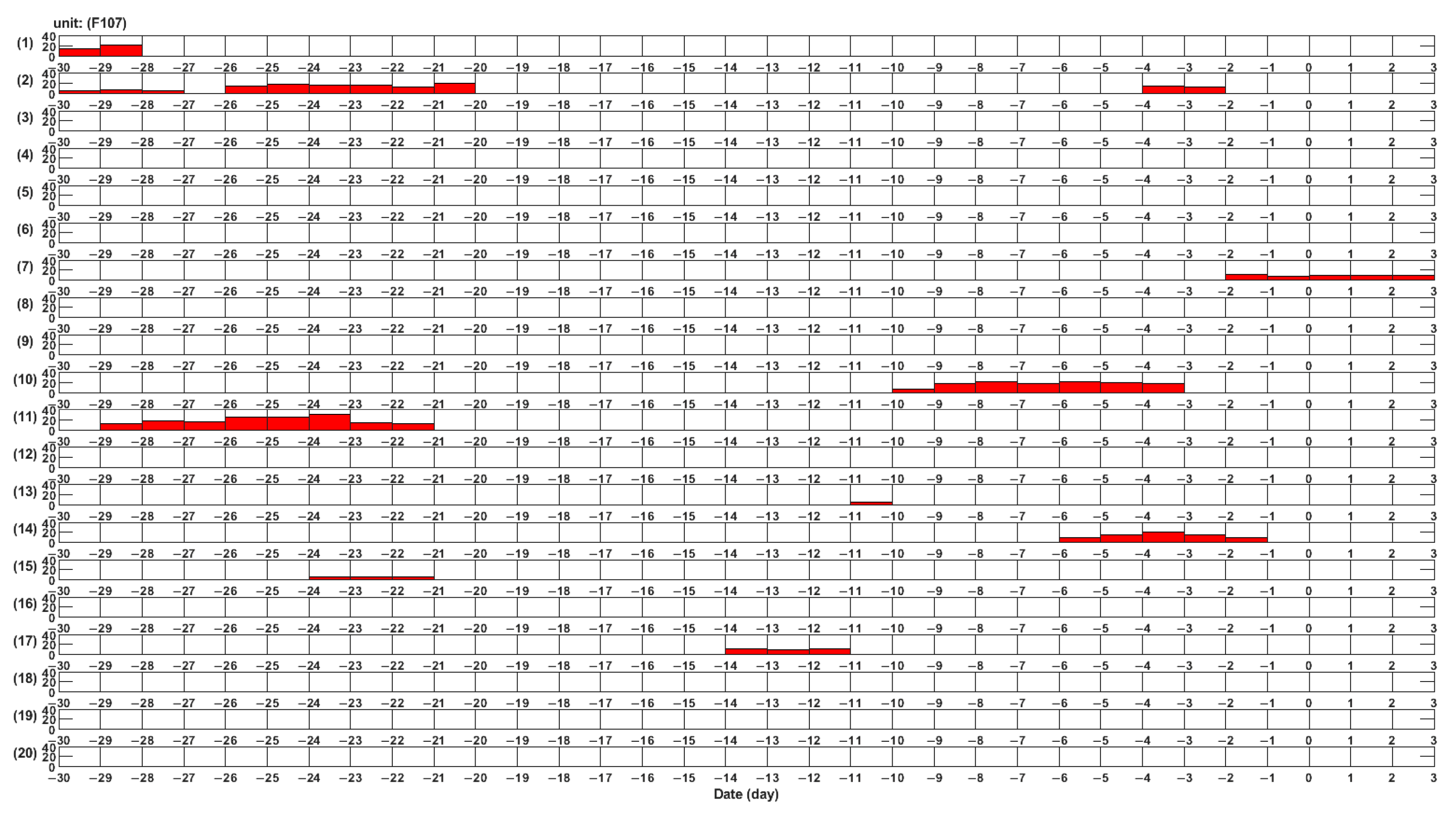
2.2. Methods
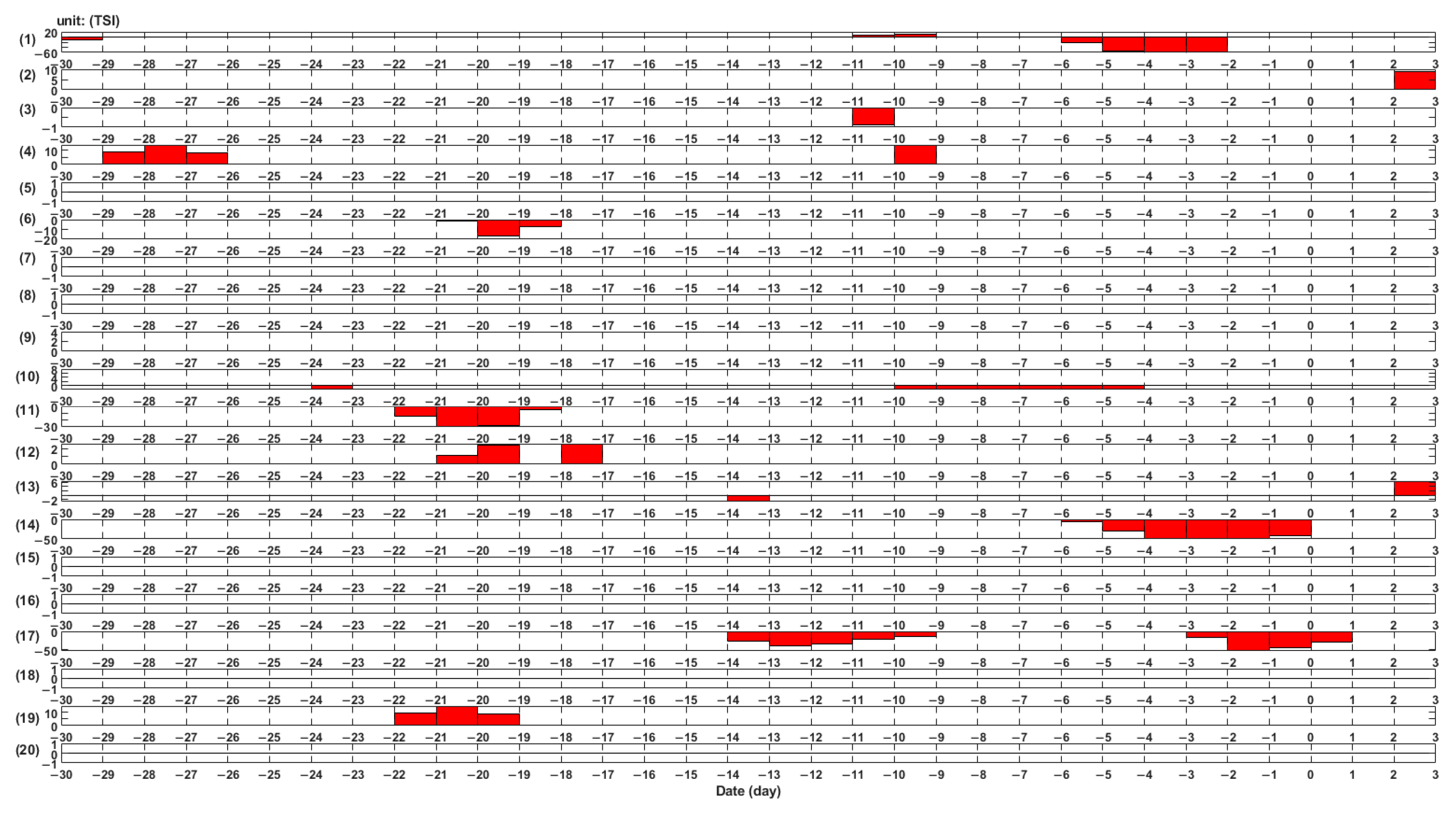
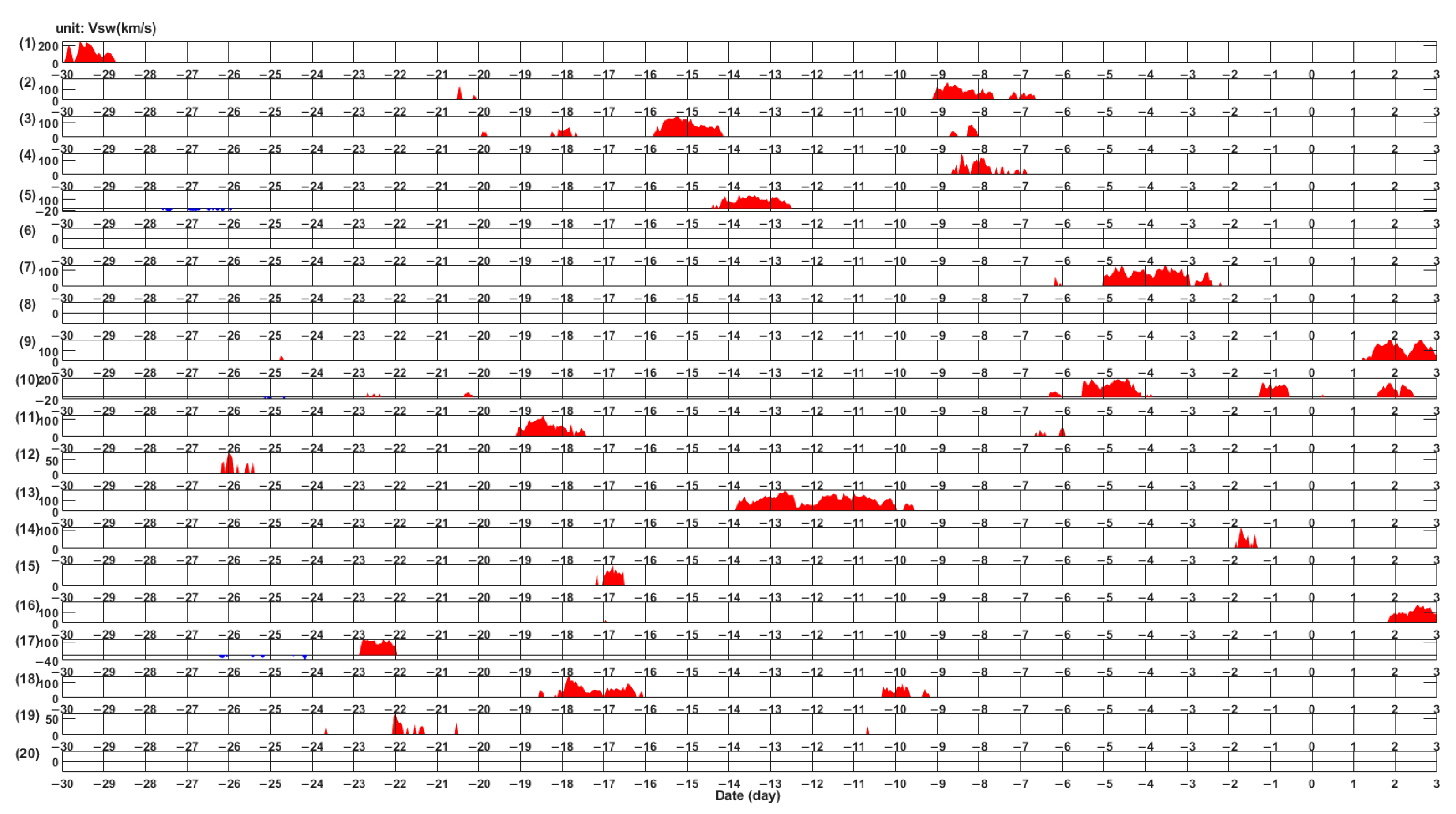
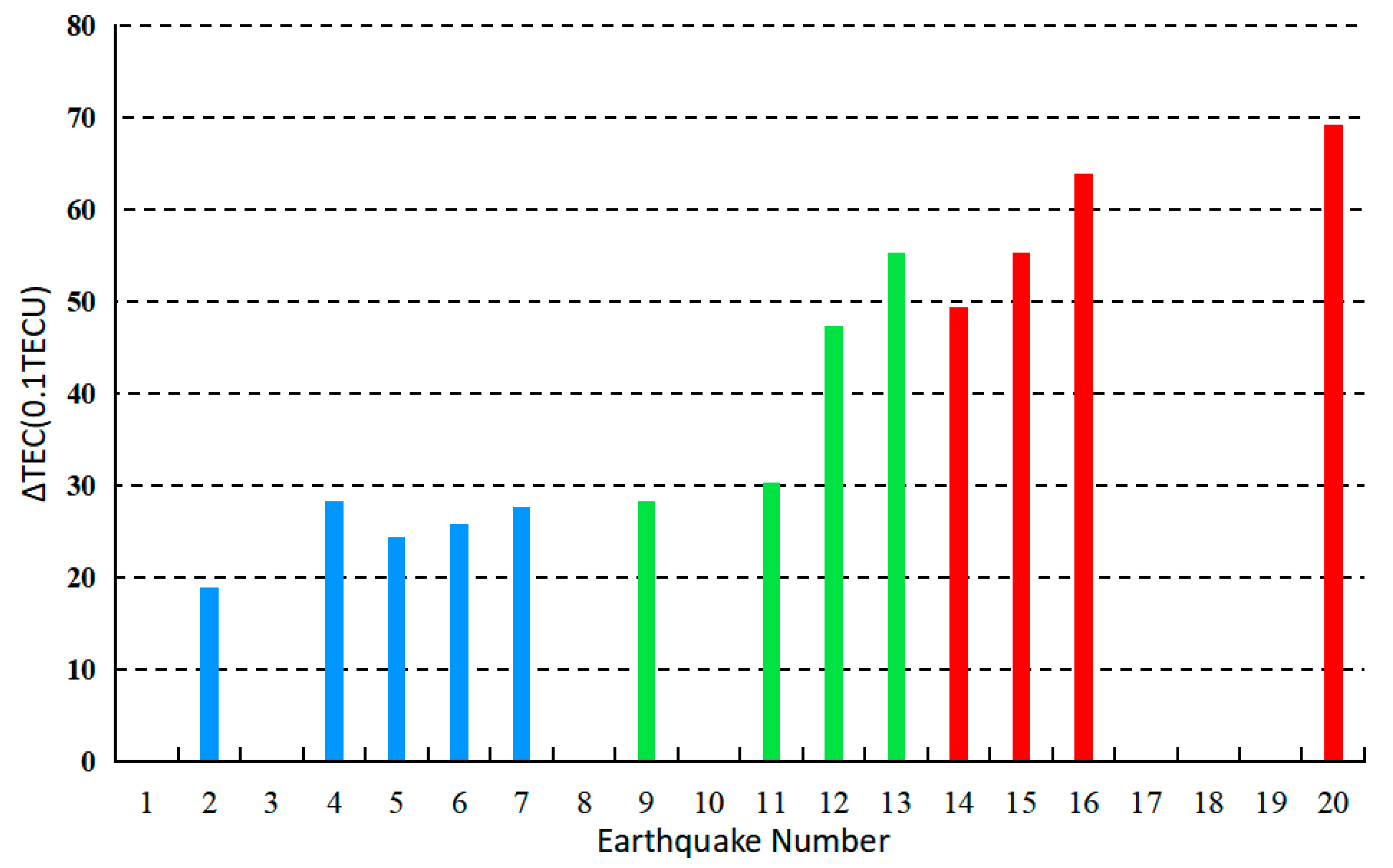
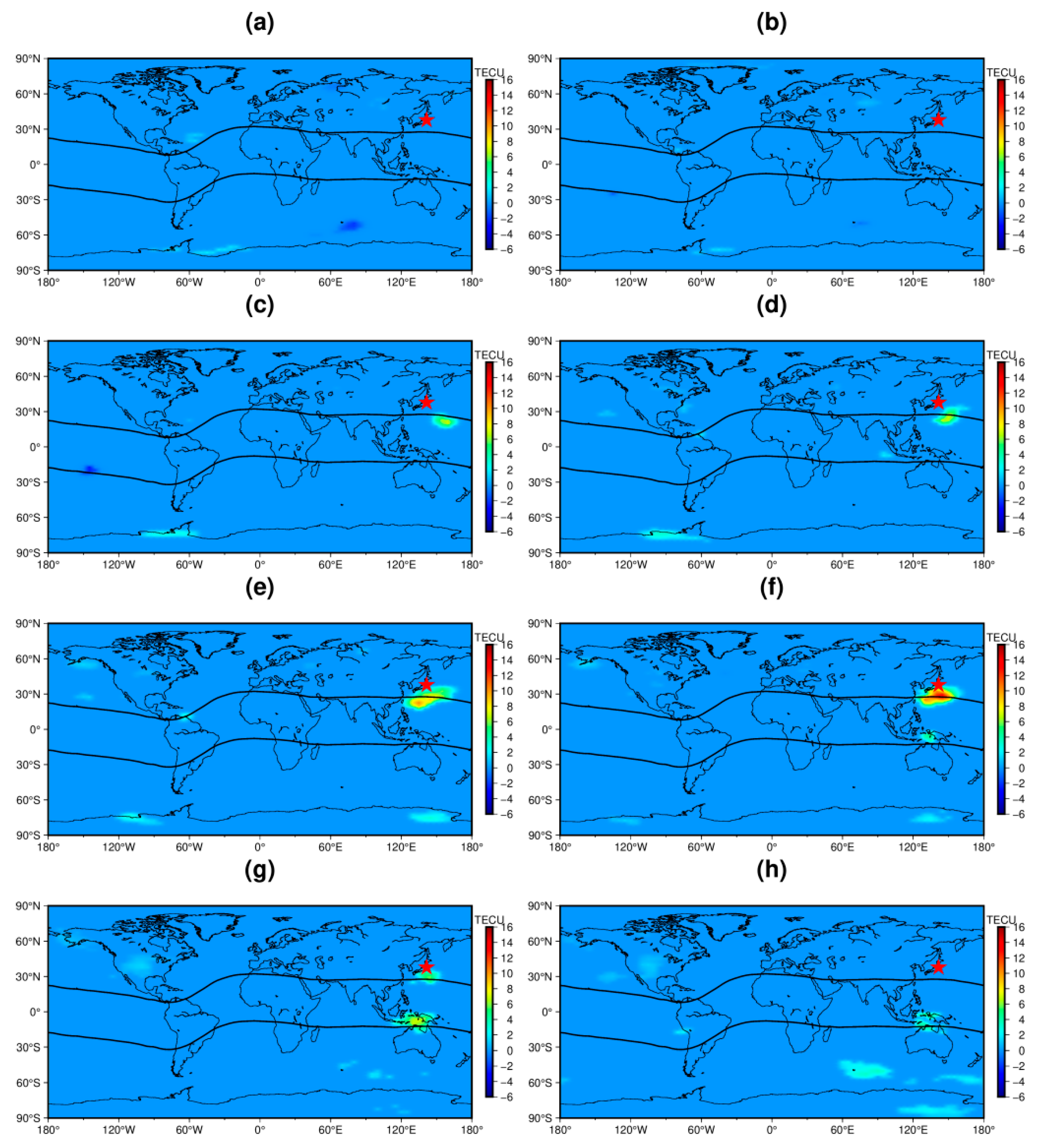
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Davies, K.; Baker, D.M. Ionospheric effects observed around the time of the Alaskan earthquake of 28 March 1964. J. Geophys. Res. 1965, 70, 2251–2253. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, M.; Yu, T.; Wan, W.; Lei, J.; Liu, L.; Ning, B. Is an unusual large enhancement of ionospheric electron density linked with the 2008 great wenchuan earthquake? J. Geophys. Res. Space Phys. 2008, 113, 148–227. [Google Scholar] [CrossRef]
- Li, J.; Meng, G.; You, X.; Zhang, R.; Shi, H.; Han, Y. Ionospheric total electron content disturbance associated with 12 May 2008, Wenchuan earthquake. Geod. Geodyn. 2015, 6, 126–134. [Google Scholar] [CrossRef]
- Liu, J.Y.; Tsai, Y.B.; Chen, S.W.; Lee, C.P.; Chen, Y.C.; Yen, H.Y.; Chang, W.Y.; Liu, C. Giant ionospheric disturbances excited by the M9.3 Sumatra earthquake of 26 December 2004. Geophys. Res. Lett. 2006, 33, 356–360. [Google Scholar] [CrossRef]
- Shah, M.; Jin, S. Pre-seismic ionospheric anomalies of the 2013 Mw = 7.7 Pakistan earthquake from GPS and COSMIC observations. J. Geod. Geodyn. 2018, 9, 378–387. [Google Scholar] [CrossRef]
- Li, Z.; Yang, B.; Huang, J.; Yin, H.; Yang, X.; Liu, H.; Zhang, H.; Lu, H. Analysis of Pre-Earthquake Space Electric Field Disturbance Observed by CSES. Atmosphere 2022, 13, 934. [Google Scholar] [CrossRef]
- Xu, T.; Hu, Y.L.; Wu, J.; Li, C.B.; Wu, Z.S.; Suo, Y.C.; Feng, J. Statistical analysis of seismo-ionospheric perturbation before 14 Ms ≥ 7.0 strong earthquakes in Chinese subcontinent. Chin. J. Radio Sci. 2012, 27, 507–512. [Google Scholar]
- Heki, K. Ionospheric disturbances related to earthquakes. Ionos. Dyn. App. 2021, 511–526. [Google Scholar] [CrossRef]
- Ulukavak, M.; Yalçınkaya, M.; Kayıkçı, E.T.; Öztürk, S.; Kandemir, R.; Karslı, H. Analysis of ionospheric TEC anomalies for global earthquakes during 2000–2019 with respect to earthquake magnitude (Mw ≥ 6.0). J. Geodyn. 2020, 135, 101721. [Google Scholar] [CrossRef]
- Saqib, M.; Şentürk, E.; Sahu, S.A.; Adil, M.A. Ionospheric anomalies detection using autoregressive integrated moving average (ARIMA) model as an earthquake precursor. Acta Geophys. 2021, 69, 1493–1507. [Google Scholar] [CrossRef]
- Pulinets, S.; Ouzounov, D. Lithosphere–Atmosphere–Ionosphere Coupling (LAIC) model—An unified concept for earthquake precursors validation. J. Asian Earth Sci. 2011, 41, 371–382. [Google Scholar] [CrossRef]
- Freund, F. Pre-earthquake signals: Underlying physical processes. J. Asian Earth Sci. 2011, 41, 383–400. [Google Scholar] [CrossRef]
- Freund, F. Earthquake forewarning—A multidisciplinary challenge from the ground up to space. Acta Geophys. 2013, 61, 775–807. [Google Scholar] [CrossRef]
- Freund, F. Toward a unified solid state theory for pre-earthquake signals. Acta Geophys. 2010, 58, 719–766. [Google Scholar] [CrossRef]
- Ouzounov, D.; Pulinets, S.; Romanov, A.; Romanov, A.; Tsybulya, K.; Davidenko, D.; Kafatos, M.; Taylor, P. Atmosphere-ionosphere response to the M 9 Tohoku earthquake revealed by multi-instrument space-borne and ground observations: Preliminary results. Earthq. Sci. 2011, 24, 557–564. [Google Scholar] [CrossRef]
- Ouzounov, D.; Pulinets, S.; Davidenko, D.; Rozhnoi, A.; Solovieva, M.; Fedun, V.; Dwivedi, B.N.; Rybin, A.; Kafatos, M.; Taylor, P. Transient effects in atmosphere and ionosphere preceding the 2015 M7.8 and M7.3 Gorkha–Nepal earthquakes. Front. Earth Sci. 2021, 9, 757358. [Google Scholar] [CrossRef]
- Pulinets, S.A. Physical mechanism of the vertical electric field generation over active tectonic faults. Adv. Space Res. 2009, 44, 767–773. [Google Scholar] [CrossRef]
- Pulinets, S.; Khachikyan, G. The Global electric circuit and global seismicity. Geosciences 2021, 11, 491. [Google Scholar] [CrossRef]
- Parrot, M.; Tramutoli, V.; Liu, T.J.; Pulinets, S.; Ouzounov, D.; Genzano, N.; Lisi, M.; Namgaladze, A. Atmospheric and ionospheric coupling phenomena associated with large earthquakes. Eur. Phys. J. Spec. Top. 2021, 230, 197–225. [Google Scholar] [CrossRef]
- Thomas, E.G.; Baker, J.B.H.; Ruohoniemi, J.M.; Coster, A.J.; Zhang, S.R. The geomagnetic storm time response of GPS total electron content in the North American sector. J. Geophys. Res. Space Phys. 2016, 121, 1744–1759. [Google Scholar] [CrossRef]
- Afraimovich, E.L.; Astafyeva, E.I.; Oinats, A.V.; Yasukevich, Y.V.; Zhivetiev, I.V. Global electron content: A new conception to track solar activity. In Annales Geophysicae; Copernicus Publications: Göttingen, Germany, 2008; Volume 26, pp. 335–344. [Google Scholar]
- Liu, J.Y.; Chen, Y.I.; Chen, C.H.; Liu, C.Y.; Chen, C.Y.; Nishihashi, M.; Li, J.Z.; Xia, Y.Q.; Oyama, K.; Hattori, K.; et al. Seismoionospheric GPS total electron content anomalies observed before the 12 May 2008 Mw7.9 Wenchuan earthquake. J. Geophys. Res. Space Phys. 2009, 114, 023–033. [Google Scholar] [CrossRef]
- Chen, H.; Han, P.; Hattori, K. Recent advances and challenges in the seismo-electromagnetic study: A brief review. Remote Sens. 2002, 14, 5893. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, X.; Liu, J.; Yang, M.; Yang, X.; Du, X.; Lu, J.; Xiao, J. Seismo-Ionospheric Effects Prior to Two Earthquakes in Taiwan Detected by the China Seismo-Electromagnetic Satellite. Atmosphere 2022, 13, 1523. [Google Scholar] [CrossRef]
- Chang, H.; Kil, H.; Sun, A.K.; Zhang, S.R.; Lee, J. Ionospheric disturbances in low-and midlatitudes during the geomagnetic storm on 26 August 2018. J. Geophys. Res. Space Phys. 2022, 127, 2. [Google Scholar] [CrossRef]
- Akahashi, H.; Wrasse, C.M.; Figueiredo, C.A.O.B.; Barros, D.; Abdu, M.A.; Otsuka, Y.; Shiokawa, K. Equatorial plasma bubble seeding by MSTIDs in the ionosphere. Prog. Earth Planet. Sci. 2018, 5, 32. [Google Scholar] [CrossRef]
- Pimenta, A.A.; Sahai, Y.; Bittencourt, J.A.; Abdu, M.A.; Takahashi, H.; Taylor, M.J. Plasma blobs observed by ground-based optical and radio techniques in the Brazilian tropical sector. Geophys. Res. Lett. 2004, 31, 12. [Google Scholar] [CrossRef]
- Pimenta, A.A.; Sahai, Y.; Bittencourt, J.A.; Rich, F.J. Ionospheric plasma blobs observed by OI 630 nm all-sky imaging in the Brazilian tropical sector during the major geomagnetic storm of 6–7 April 2000. Geophys. Res. Lett. 2007, 34, 1–5. [Google Scholar] [CrossRef]
- Miller, E.S.; Kil, H.; Makela, J.J.; Heelis, R.A.; Talaat, E.R.; Gross, A. Topside signature of medium-scale traveling ionospheric disturbances. Ann. Geophys. 2014, 32, 959–965. [Google Scholar] [CrossRef]
- Kil, H.; Paxton, L.J.; Jee, G.; Nikoukar, R. Plasma Blobs Associated with Medium-Scale Traveling Ionospheric Disturbances. Geophys. Res. Lett. 2019, 46, 3575–3581. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, H.; Shi, J.; Wang, G.; Wang, X. Plasma Blobs Concurrently Observed with Bubbles in the Asian-Oceanian Sector During Solar Maximum. J. Geophys. Res. Space Phys. 2019, 124, 7062–7071. [Google Scholar] [CrossRef]
- Kil, H.; Lee, W.K.; Paxton, L.J. Origin and distribution of daytime electron density irregularities in the low-latitude Fregion. J. Geophys. Res. Space Phys. 2020, 125, 9. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.K.; Kil, H.; Paxton, L.J. Global distribution of nighttime MSTIDs and its association with E region irregularities seen by CHAMP satellite. J. Geophys. Res. Space Phys. 2021, 126, 5. [Google Scholar] [CrossRef]
- Aa, E.; Zou, S.; Liu, S. Statistical analysis of equatorial plasma irregularities retrieved from Swarm 2013–2019 observations. J. Geophys. Res. Space Phys. 2020, 125, 4. [Google Scholar] [CrossRef]
- Huang, C.S. Continuous penetration of the interplanetary electric field to the equatorial ionosphere over eight hours during intense geomagnetic storms. J. Geophys. Res. Space Phys. 2008, 113, A11. [Google Scholar] [CrossRef]
- Cowling, D.H.; Webb, D.; Yeh, K.C. Group Rays of Internal Gravity Waves in a Wind-Stratified Atmosphere. J. Geophys. Res. 1971, 76, 213–220. [Google Scholar] [CrossRef]
- Vasseur, G. Dynamics of the F-region observed with Thomson scatter. J. Atmos. Terr. Phys. 1969, 31, 397–420. [Google Scholar] [CrossRef]
- Jonah, O.F.; Zhang, S.; Coster, A.J.; Goncharenko, L.P.; Erickson, P.J.; Rideout, W.; Eurico, R.; de Jesus, R. Understanding inter-hemispheric traveling ionospheric disturbances and their mechanisms. Remote Sens. 2020, 12, 228. [Google Scholar] [CrossRef]
- Frissell, N.A.; Baker, J.B.H.; Ruohoniemi, J.M.; Gerrard, A.J.; Miller, E.S.; Marini, J.P.; West, M.L.; Bristow, W.A. Climatology of medium-scale traveling ionospheric disturbances observed by the midlatitude Blackstone SuperDARN radar. J. Geophys. Res. Space Phys. 2014, 119, 7679–7697. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Wu, J.; Guo, L.X.; Hu, Y.L.; Zhao, H.S.; Xu, T. Influence of solar and geomagnetic activity on sporadic-E layer over low, mid and high latitude stations. Adv. Space Res. 2015, 55, 1366–1371. [Google Scholar] [CrossRef]
- Zhou, C.; Tang, Q.; Song, X.X.; Qing, H.Y.; Liu, Y.; Wang, X.; Gu, X.D.; Ni, B.B.; Zhao, Z.Y. A statistical analysis of sporadic E layer occurrence in the midlatitude China region. J. Geophys. Res. 2017, 122, 3617–3631. [Google Scholar] [CrossRef]
- Zhou, C.; Tang, Q.; Huang, F.Q.; Liu, Y.; Gu, X.D.; Lei, J.H.; Ni, B.B.; Zhao, Z.Y. The simultaneous observations of nighttime ionospheric E region irregularities and F region medium-scale traveling ionospheric disturbances in midlatitude China. J. Geophys. Res. 2018, 123, 5195–5209. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, C.; Xu, T.; Wang, Z.K.; Tang, Q.; Deng, Z.X.; Chen, G.Y. Investigation of midlatitude nighttime ionospheric E-F coupling and interhemispheric coupling by using COSMIC GPS radio occultation measurements. J. Geophys. Res. 2020, 125, 3. [Google Scholar] [CrossRef]
- Mošna, Z.; Edemskiy, I.; Laštovička, J.; Kozubek, M.; Koucká; Knížová, P.; Kouba, D.; Siddiqui, T.A. Observation of the ionosphere in middle latitudes during 2009, 2018 and 2018/2019 sudden stratospheric warming events. Atmosphere 2021, 12, 602. [Google Scholar] [CrossRef]
- Pedatella, N.M. Impact of the lower atmosphere on the ionosphere response to a geomagnetic superstorm. Geophys. Res. Lett. 2016, 43, 9383–9389. [Google Scholar] [CrossRef]
- Zhu, F.; Zhou, Y.; Lin, J.; Su, F. A statistical study on the temporal distribution of ionospheric TEC anomalies prior to M7.0+ earthquakes during 2003–2012. Astrophys. Space Sci. 2014, 350, 449–457. [Google Scholar] [CrossRef]
- Zhu, F.; Wu, Y.; Zhou, Y.; Gao, Y. Temporal and spatial distribution of GPS-TEC anomalies prior to the strong earthquakes. Astrophys. Space Sci. 2013, 345, 239–246. [Google Scholar] [CrossRef]
- Poniatowski, M.; Nykiel, G.; Borries, C.; Szmytkowski, J. Patio-temporal validation of GNSS-derived global ionosphere maps using 16 years of jason satellites observations. Remote Sens. 2023, 15, 5053. [Google Scholar] [CrossRef]
- Collado-Villaverde, A.; Muñoz, P.; Cid, C. Classifying and bounding geomagnetic storms based on the SYM-H and ASY-H indices. Nat. Hazard. 2023, 120, 1141–1162. [Google Scholar] [CrossRef]
- Li, W.; Guo, J.; Yu, X.; Yu, H.; Chang, X.J. Analysis of spatiotemporal variations in the ionosphere detected by gps. Geomat. Sci. Technol. 2014, 31, 561–565. [Google Scholar]
- Shama, A. Spectrum compatible earthquake ground motions by morlet wavelet. In Proceedings of the 20th Analysis and Computation Specialty Conference, Chicago, IL, USA, 29–31 March 2012; Volume 2012, pp. 163–172. [Google Scholar]
- Kamogawa, M. Preseismic lithosphere-atmosphere-ionosphere coupling. Eos Trans. Am. Geophys. 2006, 87, 417–424. [Google Scholar] [CrossRef]
- Harrison, R.G.; Aplin, K.L.; Rycroft, M.J. Atmospheric electricity coupling between earthquake regions and the ionosphere. J. Atmos. Sol. Terr. Phys. 2010, 72, 376–381. [Google Scholar] [CrossRef]
- Rapoport, Y.; Grimalsky, V.; Hayakawa, M.; Ivchenko, V.; Juarez-R, D.; Koshevaya, S.; Gotynyan, O. Change of ionospheric plasma parameters under the influence of electric field which has lithospheric origin and due to radon emanation. Phys. Chem. Earth 2004, 29, 579–587. [Google Scholar] [CrossRef]
- Surkov, V.V.; Pilipenko, V.A. Estimate of ULF electromagnetic noise caused by a fluid flow during seismic or volcano activity. Ann. Geophys. 2014, 58, S0655. [Google Scholar]
- Scoville, J.; Sornette, J.; Freund, F.T. Paradox of Peroxy Defects and Positive Holes in Rocks Part II: Outflow of Electric Currents from Stressed Rocks. J. Asian Earth Sci. 2015, 114, 338–351. [Google Scholar] [CrossRef]
- Roger, F.; Jolivet, M.; Malavieille, J. The tectonic evolution of the Songpan-Garzê (North Tibet) and adjacent areas from Proterozoic to Present: A synthesis. J. Asian Earth Sci. 2010, 39, 254–269. [Google Scholar] [CrossRef]
- Liu, J.Y.; Chi-Kuang, C. An observing system simulation experiment for FORMOSAT-5/AIP detecting seismo-ionospheric precursors. Tao Terr. Atmos. Ocean. Sci. 2007, 28, 117–127. [Google Scholar] [CrossRef]
- Pulinets, S. Low-latitude atmosphere-ionosphere effects initiated by strong earthquakes preparation process. Geophys. J. Int. 2012, 2012, 131842. [Google Scholar] [CrossRef]
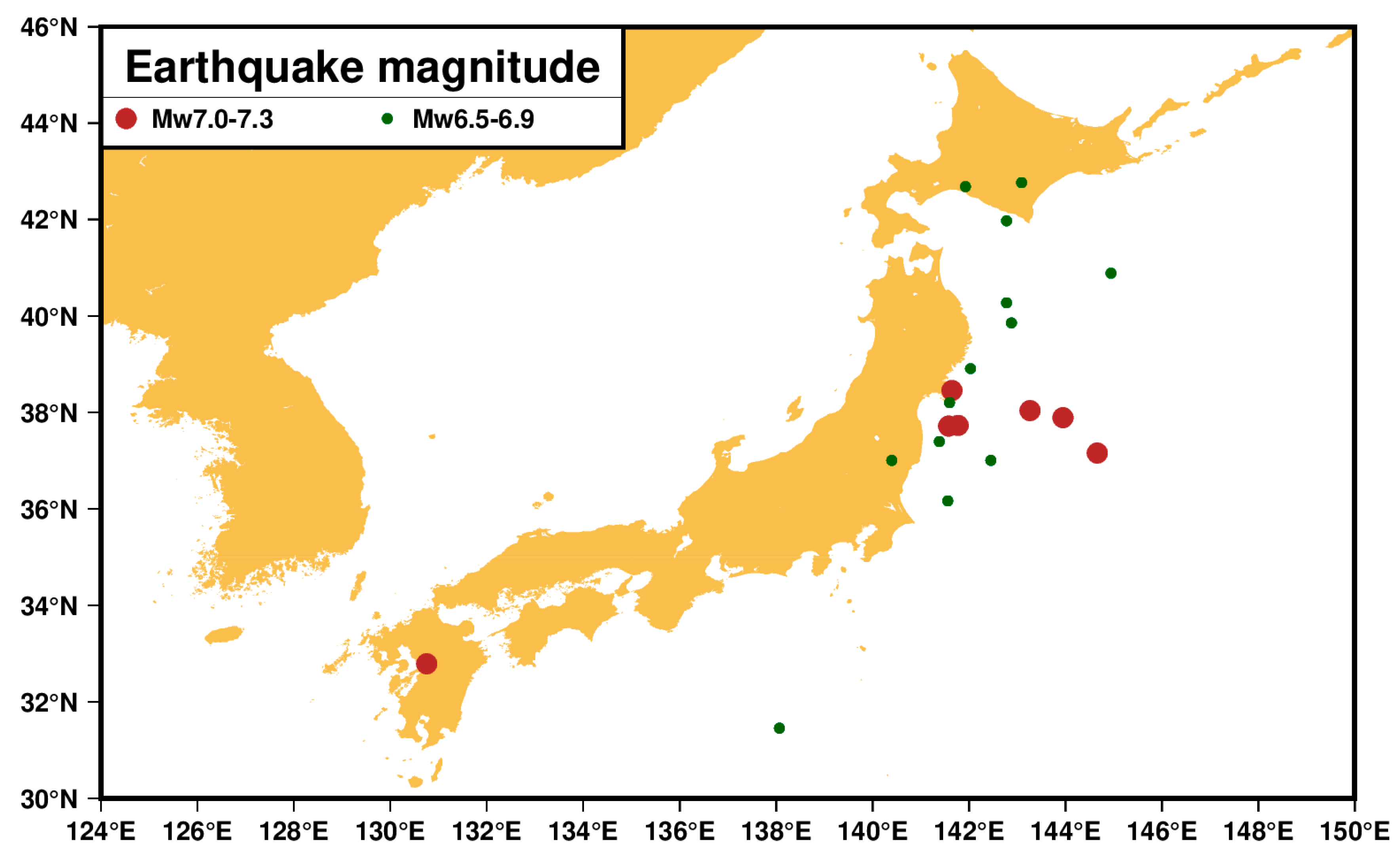





| Time of Earthquake Occurrence | Earthquake Location | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| No. | Year | Month | Day | Hour | Minute | Latitude | Longitude | Hypocenter Depth/km | Mw |
| 1 | 2014 | 07 | 11 | 19 | 22 | 37.01 | 142.45 | 20 | 6.5 |
| 2 | 2011 | 03 | 11 | 08 | 19 | 36.17 | 141.56 | 7 | 6.5 |
| 3 | 2018 | 09 | 05 | 18 | 08 | 42.69 | 141.93 | 35 | 6.6 |
| 4 | 2011 | 04 | 11 | 08 | 16 | 37.00 | 140.40 | 11 | 6.6 |
| 5 | 2015 | 02 | 16 | 23 | 06 | 39.86 | 142.88 | 23 | 6.7 |
| 6 | 2016 | 01 | 14 | 03 | 25 | 41.97 | 142.78 | 46 | 6.7 |
| 7 | 2011 | 09 | 16 | 19 | 26 | 40.27 | 142.78 | 30 | 6.7 |
| 8 | 2012 | 01 | 01 | 05 | 27 | 31.46 | 138.07 | 365 | 6.8 |
| 9 | 2015 | 05 | 12 | 21 | 12 | 38.91 | 142.03 | 35 | 6.8 |
| 10 | 2012 | 03 | 14 | 09 | 08 | 40.89 | 144.94 | 12 | 6.9 |
| 11 | 2013 | 02 | 02 | 14 | 17 | 42.77 | 143.09 | 107 | 6.9 |
| 12 | 2016 | 11 | 21 | 20 | 59 | 37.39 | 141.39 | 9 | 6.9 |
| 13 | 2021 | 05 | 01 | 0 | 27 | 38.20 | 141.60 | 43 | 6.9 |
| 14 | 2016 | 04 | 15 | 16 | 25 | 32.79 | 130.75 | 10 | 7 |
| 15 | 2021 | 03 | 20 | 09 | 09 | 38.45 | 141.65 | 43 | 7 |
| 16 | 2011 | 07 | 10 | 07 | 57 | 38.03 | 143.26 | 23 | 7 |
| 17 | 2013 | 10 | 25 | 17 | 10 | 37.16 | 144.66 | 35 | 7.1 |
| 18 | 2021 | 02 | 13 | 14 | 07 | 37.73 | 141.78 | 44 | 7.1 |
| 19 | 2012 | 12 | 07 | 08 | 18 | 37.89 | 143.95 | 31 | 7.3 |
| 20 | 2022 | 03 | 16 | 14 | 36 | 37.71 | 141.58 | 41 | 7.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Tao, Z.; Cao, L. Analysis of Ionospheric Anomalies before Earthquakes of Mw6.5 and above in Japan from 2011 to 2022. Atmosphere 2024, 15, 887. https://doi.org/10.3390/atmos15080887
Li Z, Tao Z, Cao L. Analysis of Ionospheric Anomalies before Earthquakes of Mw6.5 and above in Japan from 2011 to 2022. Atmosphere. 2024; 15(8):887. https://doi.org/10.3390/atmos15080887
Chicago/Turabian StyleLi, Zhen, Zhen Tao, and Lianhai Cao. 2024. "Analysis of Ionospheric Anomalies before Earthquakes of Mw6.5 and above in Japan from 2011 to 2022" Atmosphere 15, no. 8: 887. https://doi.org/10.3390/atmos15080887
APA StyleLi, Z., Tao, Z., & Cao, L. (2024). Analysis of Ionospheric Anomalies before Earthquakes of Mw6.5 and above in Japan from 2011 to 2022. Atmosphere, 15(8), 887. https://doi.org/10.3390/atmos15080887





