Theory and Modelling of Isotropic Turbulence: From Incompressible through Increasingly Compressible Flows

Abstract

Homogeneous isotropic turbulence (HIT) has been a useful theoretical concept for more than fifty years of theory, modelling, and calculations. Some exact results are revisited in incompressible HIT, with special emphasis on the 4/5 Kolmogorov law. The finite Reynolds number effect (FRN), which yields corrections to that law, is investigated, using both Kármán–Howarth-type equations and a statistical spectral closure of the Eddy-Damped Quasi-Normal Markovian (EDQNM)-type. This discussion offers an opportunity to give an extended review of such spectral closures, from weak turbulence, as in wave turbulence theory, to a strong one. Extensions of the 4/5 or 4/3 Kolmogorov/Monin laws to anisotropic cases, such as stably stratified and MHD turbulence, are briefly touched on. Before addressing more recent work on compressible isotropic turbulence, the simplest case of quasi-incompressible turbulence subjected to externally imposed isotropic compression or dilatation is presented. Rapid distortion theory is found to be a poor model in this isotropic case, in contrast with its relevance in strongly anisotropic flow cases. Accordingly, a fully nonlinear approach based on a rescaling of all fluctuating variables is used, in order to show its interplay with the linear operator. This opens the discussion on the cases of homogeneous incompressible turbulence, where RDT and nonlinear models are relevant, provided that anisotropy is accounted for. Finally, isotropic compressible flows of increasing complexity are considered. Recent studies using weak turbulence theory, modelling, and DNS are discussed. A final unpublished study involves interactions between the solenoidal mode, inherited from incompressible turbulence, and the acoustic and entropic modes, which are specific to the compressible problem. An approach to acoustic wave turbulence, with resonant triads, is revisited on this occasion.

1. Introduction

Homogeneous, isotropic turbulence (HIT) is frequently considered an over-simplified approach, since real turbulent flows are often far from statistical homogeneity and isotropy. However, this idealised case is the subject of a considerable literature, notably the book byMcComb (2014) [1] (whose internet blogs concerning turbulence provide a clear and passionate contribution to the subject) and the review article by Moffatt (2002) [2] (which gives a fascinating insider view of the development of the theory of homogeneous turbulence). It is my belief that HIT still has some important things to say, hence this review article, which focuses on areas in which I think additional work is needed. One such area is compressible turbulence, of which there have been rather few studies. Here, we begin with incompressible flow, then move on through results which approach the fully compressible case.

In the canonical case of incompressible HIT, however, it is worthwhile to compare the very different approaches, when the formalism is developed either in physical space or in 3D Fourier space. From the Navier–Stokes equations, exact laws from the legacy of Kolmogorov are derived using equations for two-point second-order statistical moments, in line with Kármán–Howarth (K-H hereinafter). The asymptotic character of the $4/5$ Kolmogorov law has been recognised for three decades, with a finite Reynolds number effect (FRN) altering it. A recent comprehensive review is given by Tang, Antonia, and Danaila (2024) [3]. Quantification of the FRN effect is naturally supported by an analysis of the K-H equations, when unsteady and viscous terms are displayed in the dynamics of the second-order structure function. For the same purpose, it is also possible to use a classical spectral closure, one of the simplest being the Eddy-Damped Quasi-Normal Markovian (EDQNM) from Orszag (1970) [4]. At this stage, it is crucial to understand that the approach based on the K-H equation is very different from the one using the spectral closure. There is a formal analogy between the equation for the second-order structure function $S_2(r,t)$ in HIT and the Lin equation for the energy spectrum $E(k,t)$, but this is not the main point: the sole Lin equation gives no direct information on the energy spectrum or on the transfer term $T(k,t)$, except in a particular steady limit at a very high Reynolds number. Consequently, the time evolution of the energy spectrum is obtained by a closure of the transfer term, i.e., a non-local relationship of T and E. From the analysis of the FRN effect, perhaps a marginal application of spectral closures, we propose a survey of these closures. The case of weak turbulence, with wave turbulence theory and beyond, is included. When the turbulent motion is dominated by dispersive waves, with quadratic nonlinearity, the weak nonlinearity can reduce to resonant triads, which dominate the transfer term. All these closure theories or models can be gathered into a class of triadic closures and can be considered as exact in some asymptotic cases of weak turbulence.

In the presence of linear wave regimes, the incompressible turbulence is generally anisotropic, at least in the simple examples where resonant triads are allowed. Isotropic WT exists, but resonant quartets are called into play, instead of resonant triads (see Galtier, 2024 [5], and the references therein). Are there other cases in HIT in which a linear operator can interact with the intrinsic nonlinearity? Quasi-incompressible turbulence subjected to externally imposed isotropic compression or dilatation is presented and revisited for this purpose. This case is addressed in Section 3. Rapid distortion theory appears as a poor model and is complemented by a fully nonlinear approach based on a rescaling of all fluctuating variables.

The specificity of an explicit description of anisotropy is discussed in Section 4, for incompressible turbulence subjected to body forces.

In Section 5, compressible flows are considered with an increasing complexity. Recent (unpublished) studies address weak turbulence theory, modelling, and DNSs for turbulent flows, in which the solenoidal mode, inherited from incompressible turbulence, coexists and interacts with the entropic mode and the acoustic mode.

Lastly, Section 6 is devoted to the conclusions and perspectives.

2. Exact Laws, Using Equations for Correlation Tensors Both in Physical Space and the Spectral One

In HIT, the starting point for modelling is given by the scaling laws for n-order velocity structure functions, from the legacy of Kolmogorov.

$$S_n\left(r\right)=C_n{\left(r\epsilon \right)}^{n/3},$$

(1)

where $S_n\left(r\right)=\langle {\left(\delta \mathit{u}·\mathit{r}/r\right)}^n\rangle$ (bold is used for vectors throughout the whole text), $\delta \mathit{u}=\mathit{u}(\mathit{x}+\mathit{r})-\mathit{u}\left(\mathit{x}\right)$, $r=\mid \mathit{r}\mid$, and $\epsilon$ is the dissipation rate. The case of $n=3$ was considered as very specific, since the prefactor $C_3$ can be evaluated theoretically, leading to a so-called exact law. Accordingly, the well-known $4/5$ Kolmogorov law corresponds to $C_3=-4/5$ in Equation (1).

2.1. Incompressible Homogeneous Turbulence

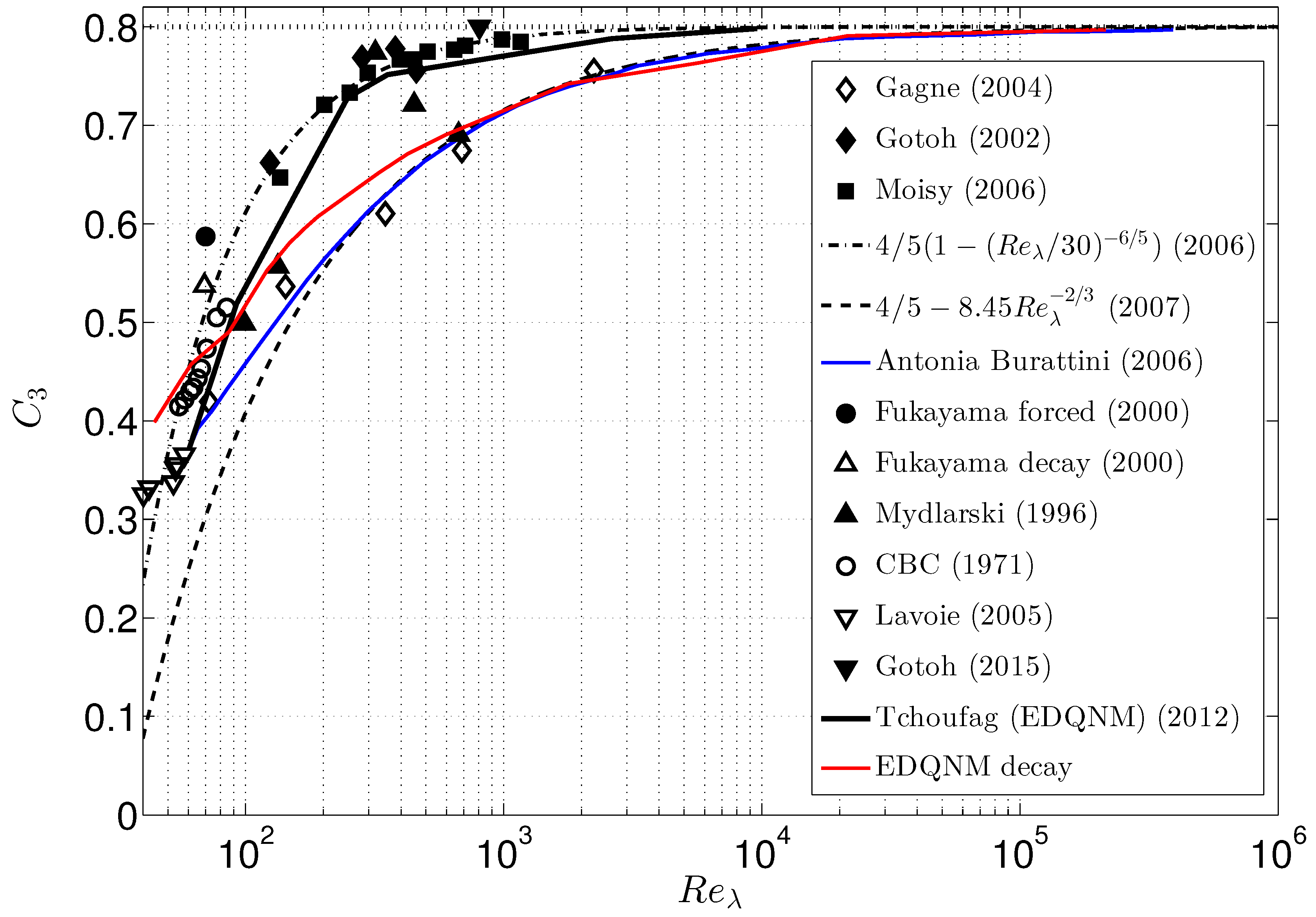
From Antonia and Burratini (2006) [6], the asymptotic character of the $4/5$ Kolmogorov law and the related finite Reynolds number (FRN) effect, was quantified, as illustrated in Figure 1, later completed by Antoine Briard and published in [7].

The notation $C_3$ in the figure holds for

$$C_3=-\underset{r}{max}{\displaystyle \frac{S_3\left(r\right)}{\epsilon r}}$$

(2)

In addition to semi-empirical scalings derived from the Kármán–Howarth (K-H hereinafter) equation, a spectral calculation by the Eddy Damped Quasi-Normal Markovian (EDQNM) was carried out by Tchoufag et al. (2012) [8], with a final improvement by Antoine Briard.

We propose to discuss the analyses using the K-H equation in two-point physical space and the closure of the Lin equation in 3D Fourier space, in order to show the limitations, drawbacks, and advantages of both approaches. A review of the FRN effect can be found in the same issue, by Tang, Antonia, and Danaila [3], with more emphasis on scaling laws in physical space. See also the relevant study by McComb et al. (2014) [10].

The analysis in physical space, avoiding any unuseful assumption, was carried out by Frédéric Moisy (private), and is reported below (in agreement with Monin and Yaglom (1975) [11] and Mathieu & Scott (2000) [12]).

In the simplest case of incompressible homogeneous turbulence, one has to consider the two-point velocity correlation tensor:

$$R_{ij}(\mathit{r},t)=\langle u_i(\mathit{x},t)u_j(\mathit{x}+\mathit{r},t)\rangle$$

(3)

From incompressible Navier–Stokes equations without forcing, it is found that

$$\left({\displaystyle \frac{\partial }{\partial t}}-\nu {\partial }_{kk}^2\right)R_{ij}(\mathit{r},t)={\displaystyle \frac{\partial }{\partial r_k}}\left(R_{ik,j}-R_{i,jk}\right)+{\displaystyle \frac{1}{\rho }}\left({\displaystyle \frac{\partial }{\partial r_i}}\langle p{u}_j^{\prime }\rangle -{\displaystyle \frac{\partial }{\partial r_j}}\langle p^{\prime }{u}_i\rangle \right),$$

(4)

where $p(\mathit{x},t)$ ($p^{\prime }$ at point $\mathit{x}+\mathit{r}$) is the pressure fluctuation, $\nu$ is the kinematic viscosity, and $R_{ik,j}$, $R_{i,kj}$ hold for two-point third-order velocity correlations. The pressure–velocity correlations are no longer accounted for in physical space, provided that only the trace of the previous equation is used.

In isotropic turbulence, only longitudinal and transverse velocity correlation functions are considered, or

$$R_{LL}(\mathit{r},t)=\langle u_L{u}_L^{\prime }\rangle ,R_{NN}(\mathit{r},t)=\langle u_N{u}_N^{\prime }\rangle ,$$

(5)

with $u_L=\mathit{u}·{\displaystyle \frac{\mathit{r}}{r}}$.

Finally, the K-H correlation equation in HIT reduces to

$${\displaystyle \frac{1}{r^4}}{\int }_0^r{r}^4{\displaystyle \frac{\partial }{\partial t}}{R}_{LL}dr=R_{LL,L}+2\nu {\displaystyle \frac{\partial }{\partial r}}{R}_{LL}.$$

(6)

Going back to structure functions, $S_2$ and $S_3$, the exact equation for THI from K-H is

$$S_3(r,t)=-{\displaystyle \frac{4}{5}}\epsilon \left(t\right)r-{\displaystyle \frac{3}{r^4}}{\int }_0^r{r}^4{\displaystyle \frac{\partial }{\partial t}}{S}_2(r,t)dr+6\nu {\displaystyle \frac{\partial }{\partial r}}{S}_2(r,t).$$

(7)

Of course, this equation differs from the so-called exact $4/5$ Kolmogorov equation by the last two terms in the right-hand side, unsteady and viscous.

2.2. Related Discussion of Triadic Models and Theories

In incompressible HIT, the 3D Fourier transform of $R_{ij}(\mathit{r},t)$ displays the single energy spectrum $E(k,t)$, according to

$${\widehat{R}}_{ij}(\mathit{k},t)={\displaystyle \frac{E(k,t)}{4\pi k^2}}\left({\delta }_{ij}-{\displaystyle \frac{k_i{k}_j}{k^2}}\right),$$

(8)

and the energy spectrum is governed by the Lin equation

$$\left({\displaystyle \frac{\partial }{\partial t}}+2\nu k^2\right)E(k,t)=T(k,t).$$

(9)

In this equation, from Lin (1947) [13], the contribution from two-point third-order correlations is encapsulated in the transfer term $T(k,t)$ and not explicitly given as in the left-hand side of Equation (4). In this sense, the Lin equation gives an accurate definition of the transfer term, but it gives no actual result on E before introducing closure assumptions for T (see, for instance, [14]). Leaving aside local (in Fourier space) models, the classical closure theories and/or models use the infinite hierarchy of equations for statistical moments. Accordingly, because of the quadratic nonlinearity, the equations for third-order moments involve fourth-order ones, and so on.

The use of the 3D Fourier space renders most of the linear operators algebraic, so that the effect of fluctuating pressure, which ensures a divergence-free velocity field, can be accounted for, and eventually removed from consideration, provided that n-order correlations are written at n points. Second-order correlations are thereby analysed at two points, separated by r in physical space, resulting in a spectral tensor by Fourier synthesis ${\widehat{R}}_{ij}(\mathit{k},t)$. Similarly triple correlations ought to be analysed at three points in physical space, resulting in a spectral tensor depending on all triads $(\mathit{k},\mathit{p},\mathit{q})$, or ${\widehat{R}}_{inj}(\mathit{k},\mathit{p},t)$, with $\mathit{p}+\mathit{q}=\mathit{k}$.

The infinite hierarchy of moment equations is usually truncated at third-order, where the fourth-order moments appear. The assumption for triadic closures relies on weak fourth-order cumulants, as for a normal law, but with no a priori assumption about triple cumulants. The zero value of fourth-order cumulants can give an exact closure, for instance in weak wave turbulence theory (e.g., AQNM in [15] for rotating turbulence), but this is generally wrong in strong turbulence, as in HIT. One of the simplest triadic closure is the EDQNM, in which fourth-order cumulants act as a nonlinear relaxation of the third-order ones, via an Eddy-Damping (ED) semi-empirical term. In HIT, the transfer term can be expressed as a non-local integral on all triads of the energy spectrum, and the integral is restricted to the domain of p and q (moduli) at a fixed k, so that the vectors k, p, and q form a triangle, as shown in Figure 2.

In line with the comparison of the EDQNM to the experiment of Comte-Bellot and Corrsin [9,16], it was interesting to add the Comte-Bellot and Corrsin (CBC) points to Figure 1. The experimental data in [9] are very comprehensive, with access to $E(k,t)$ at different sections downstream the grid (the downstream distance $x-x_0$ divided by the mean advection velocity U is equivalent to an elapsed time), and the energy spectrum is calculated from its one-dimensional counterpart assuming isotropy. In addition, the dissipation spectrum is derived, and even the transfer term $T(k,t)$ is captured, comparing measures at two close sections for estimating ${\displaystyle \frac{\partial E}{\partial t}}$. Finally, the structure function $S_3(r,t)$ itself is calculated from $T(k,t)$, using the integral relationship in HIT.

It appears that the strategies (theory, modelling, closure) are very different when statistical equations are investigated either in physical space or in spectral space. On the one hand, Fourier space is the best tool for homogeneous, not only isotropic, turbulence. In contrast with the simple local algebraic form of all linear operators in Fourier space, which are almost intractable with their integro-differential form in physical space, nonlinearity amounts to a convolution product, and thereby concentrates only on the nonlocal relationship. When the nonlinearity is quadratic, we have to focus on a spectral transfer term that involves all triads. In this sense, classical spectral closures may be called triadic closures, whereas the old nomenclature ‘two-point closures’ is misleading. Isotropic wave turbulence (WT) theory can offer an extended approach, in which resonant quartets are called into play, even with quadratic nonlinearity, if triple resonances are not permitted (e.g., the case of surface gravity waves). If a quartic nonlinearity is considered, resonant quartets give the first step in wave turbulence theory, and so on. The last case is well known for WT in vibrating plates or quantum turbulence from the Gross–Pitaevskii equations. Of course, the description in spectral space, from basic deterministic equations to those for statistical moments, is needed even more in WT in order to treat the specific dispersion laws of linear wave regimes. On the other hand, the ultimate degree for closure is only the second-order two-point level in physical space, for instance using K-H-type equations, and often only its trace. The related strategy, however, recovers its interest when inhomogeneity cannot be neglected. In search of exact laws, or corrections of them for the FRN effect, the form of two-point third-order correlations, say $S_3\left(r\right)$, results from assumptions made on the linear terms, say on the right-hand side of Equation (7).

A final remark on the FRN effect in HIT using EDQNM can be found from Meldi and Vassilicos (2021, and references therein) [17] as follows. In decaying homogeneous turbulence, non-stationarity has an increasing effect on increasingly large scales and viscous diffusion has an effect on small scales, increasingly so for increasingly small scales. The length scale where both effects are together minimal is the Taylor length $\lambda$, and it is therefore only around $\lambda$ that the Kolmogorov scaling predictions on second and third order structure functions are achieved as Reynolds number Re tends to infinity (Lundgren 2002, 2003, Obligado & Vassilicos 2019) [17]. At all other length-scales, even if a significantly small fraction of the integral scale or a significantly large multiple of the Kolmogorov length, the Kolmogorov predictions are never exactly achieved asymptotically as $Re\to \infty$.

2.3. Stably Stratified Turbulence

In stably stratified turbulence, the velocity field and the scalar field, density or temperature, are coupled by the buoyancy force. In the presence of a uniform gradient of mean density, which results in a constant Brunt–Väisälä frequency N, parallel with the gravity, the turbulent flow can be considered as statistically homogeneous, but anisotropic. Second-order correlations include a kinetic energy, a potential energy, and cross-correlations as the vertical buoyancy flux.

Considering the two-point counterpart of total energy, or the sum of kinetic energy and the potential one, the buoyancy flux terms cancel out, so that the equation for total energy resembles the one for the trace of (4). This is due to the fact that the buoyancy force is a restoring force, whose contributions to kinetic energy and to potential energy are exactly balanced.

From the two-point counterpart of total, kinetic + potential, energy, or the K-H equation, is derived

$$\nabla ·\langle \left[{\left|\delta \mathit{u}\right|}^2+{(\delta b/N)}^2\right]\delta \mathit{u}\rangle =-4\epsilon ,$$

(10)

ignoring viscous and unsteady terms, where b is the buoyancy scalar. This law is valid without assuming isotropy.

A version with ‘isotropisation’ was found by Augier et al. (2012) [18], under a classical $4/3$ law, or

$$\langle \left[{\left|\delta \mathit{u}\right|}^2+{(\delta b/N)}^2\right]\delta u_L\rangle ={\displaystyle \frac{4}{3}}\epsilon r.$$

(11)

The actual axisymmetric case was investigated in this article [18].

2.4. MHD Turbulence

In MHD turbulence, we have to consider both the velocity field u and the magnetic field b. Their equations are coupled by the Lorentz force. As in the previous case of stably stratified turbulence, the contribution of the restoring force cancels out when considering the two-point counterpart of total, kinetic + magnetic, energy.

From the equations of incompressible ideal MHD, it is possible to derive a K-H equation for the two-point counterpart of total (kinetic + magnetic) energy as

$${\displaystyle \frac{1}{2}}{\displaystyle \frac{\partial }{\partial t}}\underset{R_{ii}(\mathit{r},t)+R_{ii}^M(\mathit{r},t)}{\underbrace{\langle u_i(\mathit{x},t)u_i(\mathit{x}+\mathit{r},t)+b_i(\mathit{x},t)b_i(\mathit{x}+\mathit{r},t)\rangle }}=$$

$$={\displaystyle \frac{1}{4}}{\nabla }_r·\langle \left(\delta \mathit{u}·\delta \mathit{u}+\delta \mathit{b}·\delta \mathit{b}\right)\delta \mathit{u}\rangle -{\displaystyle \frac{1}{2}}{\nabla }_r·\langle \left(\delta \mathit{u}·\delta \mathit{b}\right)\delta \mathit{b}\rangle$$

$$+{\displaystyle \frac{\partial }{\partial r_k\partial r_k}}\langle \nu u_i(\mathit{x},t)u_i(\mathit{x}+\mathit{r},t)+\eta b_i(\mathit{x},t)b_i(\mathit{x}+\mathit{r},t)\rangle ,$$

(12)

Accordingly, a Kolmogorov $4/3$ law was derived by Politano et al. (1998) [19] as:

$$-{\displaystyle \frac{4}{3}}{\epsilon }^{T}r=\langle \left(\delta \mathit{u}·\delta \mathit{u}+\delta \mathit{b}·\delta \mathit{b}\right)\delta u_L\rangle -2\langle \left(\delta \mathit{u}·\delta \mathit{b}\right)\delta b_L\rangle ,$$

(13)

in which $\delta u_L$ and $\delta b_L$ denote the longitudinal increments, i.e., projected along the direction of the r-vector. Due to the symmetry of Elsaesser variables ${\mathit{z}}^{\pm }=\mathit{u}\pm \mathit{b}$, a more compact form is found as

$$-{\displaystyle \frac{4}{3}}{\epsilon }^{\pm }r=\langle \left(\delta {\mathit{z}}^{\pm }·\delta {\mathit{z}}^{\pm }\right)\delta z_L^{\pm }\rangle .$$

(14)

We consider that the role of external forcing together with the introduction of ${\epsilon }^T$ may be somewhat misleading. One recovers the same duality as for $\epsilon$ in ‘hydro’, that is both the injection rate of kinetic energy and the ‘true’ dissipation rate. As for the ‘hydro’ case, we recommend avoiding external forcing and the external injection rate, and to derive from Equation (12) an isotropic equation with both an instationary term and the dissipation rate. As shown in in the hydro case, it is possible to recover such a law without forcing, and to evaluate the conditions for which the unsteady term in the K-H equation or in the Lin equation becomes negligible: the Reynolds number is really huge, as $R_{\lambda }\sim 5.{10}^4$. In astrophysics, we are sure that these conditions are fulfilled. An interesting application is to evaluate ${\epsilon }^T$ in the solar wind: there is no possible direct evaluation, but third-order structure functions can be estimated.

3. Isotropic Compression/Dilatation

As considered in the next section, turbulence in the presence of body forces (Coriolis, buoyancy, Lorentz) and/or mean gradients (rotation, shear, strain) becomes anisotropic. Capital letters will be used for the mean variables, as $U_i$ for the mean velocity. In homogeneous, arbitrary, anisotropic turbulence, the mean flow is generated by space-uniform gradients $A_{ij}$, with the Cauchy matrix $F_{ij}$, or:

$$A_{ij}\left(t\right)={\displaystyle \frac{\partial U_i}{\partial x_j}},F_{ij}(t,t_0)={\displaystyle \frac{\partial x_i}{\partial X_j}},$$

(15)

where $X_i$ hold for the Lagrangian coordinates for mean flow trajectories, or positions at the initial time $t_0$.

In this section, it is possible to study a canonical case, in which a quasi-incompressible fluctuating turbulent flow is subjected to an external, mean, compression or dilatation. An interesting class of solenoidal (i.e., with divergence-free velocity fluctuations) homogeneous turbulent flows can be considered in the presence of a mean flow with space-uniform gradients, which takes into account a variation in the mean volume. Provided that the Mach number is small enough, this set of assumptions is self-consistent, and it is possible to extend solenoidal rapid distortion theory (RDT) to compressed turbulence, i.e., to a divergence-free fluctuating velocity field in the presence of a mean dilatational flow, neglecting acoustics and thermal effects.

The mean flow is characterised by the volumetric ratio $J=det\mathsf{F}$, which differs from 1 when the constraint $A_{ii}=0$ is relaxed in Equation (15). For the sake of brevity, we chose $t_0=0$, so that abridged notations $\mathsf{F}\left(t\right)$, $J\left(t\right)$ will now be used in this section, ignoring $t_0$. Among different compressing mean flows, the case of isotropic compression deserves particular attention. In this case, the matrices $\mathsf{A}$ and $\mathsf{F}$ and the trajectory equations are written as

$$A_{ij}\left(t\right)=S\left(t\right){\delta }_{ij},F_{ij}\left(t\right)=J^{1/3}\left(t\right){\delta }_{ij},x_i=J^{1/3}\left(t\right)X_j$$

(16)

in which $S={\displaystyle \frac{1}{3}}{\displaystyle \frac{1}{J}}{\displaystyle \frac{dJ}{dt}}$. The fluctuating velocity field is governed by

$${\displaystyle \frac{\partial u_i}{\partial t}}+S{x}_j{\displaystyle \frac{\partial u_i}{\partial x_j}}+S{u}_i+{\displaystyle \frac{1}{\overline{\rho }}}{\displaystyle \frac{\partial p}{\partial x_i}}=-u_j{\displaystyle \frac{\partial u_i}{\partial x_j}}+\nu {\nabla }^2{u}_i$$

(17)

in which explicit nonlinear terms and viscous terms are gathered in the right-hand side. Setting the right-hand side to zero, the RDT solution is directly found in physical space, without the non-local integral term coming from the fluctuating pressure:

$$\mathit{u}(\mathit{x},t)=J^{-1/3}\left(t\right)\mathit{u}(\mathit{X},0)$$

More interesting is the possibility to derive a rescaling for the full nonlinear Equation (17), in terms of spatial coordinates, velocity, and time. This is expressed as follows:

$${\mathit{x}}^{\ast }=J^{-1/3}\mathit{x},{\mathit{u}}^{\ast }({\mathit{x}}^{\ast },t^{\ast })=J^{1/3}\mathit{u}(\mathit{x},t)d{t}^{\ast }=J^{-2/3}\left(t\right)dt.$$

(18)

Such a dynamical rescaling can also be used in the Boltzmann equations, and applied to the cosmological gas in order to account for the expansion of the universe. When substituting it in Equation (17), which governs the primitive unscaled variables, the rescaled quantities are shown to satisfy the Navier–Stokes equations without the additional mean terms, which depend on S in the left-hand side. For consistency reason, the pressure is rescaled as $p^{\ast }=J^{5/3}p$, and the only difference from uncompressed freely decaying isotropic turbulence for the velocity field ${\mathit{u}}^{\ast }({\mathit{x}}^{\ast },t^{\ast })$ is the possible influence of time variations of the viscosity ${\nu }^{\ast }\left(t\right)$. The variation in the Reynolds number follows directly since $uL=u^{\ast }{L}^{\ast }$. If the Reynolds number is high enough, however, it is reasonable to expect that all classical results dealing with the spatio-temporal dynamics and statistics of isotropic freely decaying turbulence are still valid for (${\mathit{u}}^{\ast }$, ${\mathit{x}}^{\ast }$, $t^{\ast }$), so that the corresponding laws for primitive variables (u, x, t) can be readily derived using Equation (18). The reader is referred to Cambon et al. (1992) [20] for the seminal approach and preliminary applications.

This scaling deserves attention for two reasons. First, it illustrates a particular ‘dynamical’ version of the general scale invariance (see, e.g., [21]):

$${\mathit{x}}^{\ast }=\lambda \mathit{x},{\mathit{u}}^{\ast }={\lambda }^h\mathit{u},t^{\ast }=t{\lambda }^{1-h},{\nu }^{\ast }={\lambda }^{1+h}\nu ,$$

(19)

so that $\lambda$ corresponds to the time-dependent mean density ratio $J^{-1/3}$, with $h=-1$. In the latter invariance group, the viscosity would be left unchanged if $h=-1$, but it should be borne in mind that the dynamical rescaling deals with a continuously time-varying parameter $J^{-1/3}\left(t\right)$ in contrast to $\lambda$.

Second, it can be used to check the consistency of any model or theory, ranging from $\mathcal{K}-\epsilon$ to the elaborated EDQNM, DIA, or LRA versions.

As a simple example, let us start with a classical decay law such as

$$\mathcal{K}\left(t\right)=\mathcal{K}\left(0\right){\left(1+{\displaystyle \frac{t}{n\tau }}\right)}^{-n},L\left(t\right)=L\left(0\right){\left(1+{\displaystyle \frac{t}{n\tau }}\right)}^{1-n/2},$$

consistently obtained for the turbulent kinetic energy $\mathcal{K}$, its dissipation rate $\epsilon =-{\displaystyle \frac{d\mathcal{K}}{dt}}$, and the single relevant integral length scale L, with $1/\tau =-(1/\mathcal{K})d\mathcal{K}/dt$ at the initial time $t=0$. As is well known and documented in decaying HIT, the exponent n is a bit larger than 1, e.g., $n=6/5$ for an initial Saffman energy spectrum and $n=10/7$ for a Batchelor one. Applying the rescaling, which amounts to rewriting the same equations in terms of ‘starred’ variables, the following equations are derived for the ‘compressed’ decay:

$$\mathcal{K}\left(t\right)=\mathcal{K}\left(0\right)e^{2Ct}{\left(1+{\displaystyle \frac{e^{2Ct}-1}{2nC\tau }}\right)}^{-n},L\left(t\right)=L\left(0\right)e^{-Ct}{\left(1+{\displaystyle \frac{e^{2Ct}-1}{2nC\tau }}\right)}^{1-n/2},$$

for a mean compression or dilatation at constant rate $S\left(t\right)=-C$. These equations show immediately that the domain of relevance of RDT in terms of elapsed time is more restricted than usually conjectured, with a dominant nonlinearity having an effect opposite the linear one. Choosing a spherical compression, i.e., $C>0$, the RDT growth rate factor for $\mathcal{K}$, $e^{2Ct}$, is always balanced and rapidly dominated by a nonlinear term given by $e^{-2nCt}$. This reflects the fact that, when the velocity $u^{\prime }$ is affected by a linear ‘RDT’ factor $e^{Ct}$, the nonlinear term of dimension $u^2/l$ is affected by a factor $e^{-3Ct}$, the full nonlinear effect being finally accounted for by the time rescaling $dt=d{t}^{\ast }{e}^{2Ct}$.

This flow is particular in the sense that turbulence is not really compressible, but it offers a very simple way to exactly evaluate the impact of nonlinearity; this is a unique instance of comparing linear RDT with the full nonlinear theory. In contrast, a depletion of nonlinearity is rather expected in true compressible turbulence, with respect to the incompressible flow case, but in the anisotropic case, as discussed in [7]. It is also possible to study the spherical (isotropic) compression or dilatation applied to really compressible homogeneous turbulence. Very consistent results were found by [22,23], using full DNS and isentropic RDT. A recent study useful for inertial fusion [24] is inspired by the approach of this section.

4. To What Extent Is Anisotropy Unavoidable in Theory/Modelling?

Turbulent flows subject to body forces (Coriolis, buoyancy, Lorentz) and/or strong mean gradients, as in Equation (15), are dominated by linear effects, which render them strongly anisotropic. This anisotropy, especially at larger scales, can be described using rapid distortion theory (RDT). Only in some cases where the body force is a restoring force is isotropisation possibly relevant, as shown in the case of stable stratification in search of the $4/3$ law. In other strongly anisotropic flow patterns, re-isotropisation may be recovered at scales smaller than a typical scale such that $\sqrt{\epsilon /S^3}$ (Corrsin, with S the shear rate), $\sqrt{\epsilon /N^3}$ (Ozmidov), or $\sqrt{\epsilon /{\mathrm{\Omega }}^3}$ (Zeman).

Homogeneous RDT for incompressible turbulent flows gathers enough features for solving two problems:

(i)

A deterministic problem, which consists of solving the initial-value linear system of equations for the 3D Fourier transform of the fluctuating variables (velocity, pressure, buoyancy, magnetic field), in the most general way. This is accomplished by determining the spectral Green’s function, which is also the key quantity requested in linear stability analysis.

(ii)

A statistical problem that is useful for the prognostics of the statistical moments of the above-mentioned fluctuating variables. Interpreting the initial amplitude, e.g., $\widehat{\mathit{u}}(\mathit{k},t_0)$, as a random variable with a given dense $\mathit{k}\left(t_0\right)$-spectrum and statistical moments can be predicted though products of the basic Green’s function.

The linear spectral theory, that underlies RDT, is now almost forgotten in the Engineering community, which used it for calibrating some constants in statistical models for Reynolds-Averaged Navier–Stokes equations, e.g., in modelling ‘rapid’ pressure–strain rate tensors. In turn, it is increasingly used in geophysics and astrophysics, taking advantage of the possibility of recovering non-modal stability analysis and, thereby, predicting explosive transient growth and bypass transition to turbulence.

In the largest sense, RDT includes a deterministic aspect, close to linear stability analysis, but it says more in connection with statistical theory. Instead of assuming that the disturbance velocity field, say u, is very small with respect to the base one, say U, as in linear stability, the ‘rapid’ argument assumes that the time scale of the linear term, say $S^{-1}$ for a shear rate, is very small with respect to a nonlinear time scale, say ${\tau }^{-1}=\epsilon /\mathcal{K}$. Accordingly, the RDT (linear) statistical solution is valid for moderate values of the ‘linear’ nondimensional time $St$. Note that this works satisfactorily for parallel mean flows, as a pure plane shear, with several applications, but is questionable for non-parallel (elliptic, hyperbolic mean flows). We think that all cases are different, so that the relevance of RDT cannot be a priori predicted from the initial ratios of the time scales. The case of isotropic compression/dilatation provides a very good example of the poor relevance of RDT. To finish with RDT, let us mention some recent applications, far from its seminal use in Cambridge. In Goldstein (2019, and the references herein) [25], it is applied to non-homogeneous compressible flows. In Candelier et al. [26], it is a part of a complex study of lift and drag, where the ‘linear flow’ is the mean whose gradients are given by Equation (15).

RDT solutions can result from a forcing, with an impulsional linear response, and not only the response to the initial data. The forcing can mimic an implicit nonlinear source term, as in the resolvent analysis, in progress for complex flows.

Strong anisotropy can also result from nonlinearity. This is found in rotating turbulence, in stably stratified turbulence, and in the combination of both, from weak [15,27] to strong nonlinearity. For instance, the anisotropy results from the dispersion law of inertia–gravity waves in rotating and stratified turbulence, or

$$\sigma \left(\mathit{k}\right)=\sqrt{{\left(f{\displaystyle \frac{k_{\Vert }}{k}}\right)}^2+{\left(N{\displaystyle \frac{k_{\perp }}{k}}\right)}^2},$$

(20)

as well as the definition of normal modes. The existence of a non-propagating mode, connected to the quasi-geostrophic (QG) motion, with potential vorticity, precludes the use of conventional WT, so that the weak turbulence is investigated in an original way in [27].

5. Progress in Weakly Compressible Isotropic Turbulence

5.1. Limitations of the Use of Potential Vorticity

Potential vorticity, mentioned at the end of the previous section, is a crucial quantity in geophysics. It is involved in the quasi-geostrophic approach, with plenty of studies. Why is it not used in other domains of turbulence, with compressibility?

The notations for the background equations are from [7]. It is safer to use tensor notations, with Ricci formulae, for intermediate calculations, for instance ${\omega }_i={ϵ}_{inj}{\displaystyle \frac{\partial u_j}{\partial x_n}}$ instead of $\mathit{\omega }=\nabla \times \mathit{u}$.

From the momentum conservation law, the equation for vorticity is found, without any incompressibility condition, as follows:

$${\dot{\omega }}_i+{\displaystyle \frac{\partial u_j}{\partial x_j}}{\omega }_i-{\displaystyle \frac{\partial u_i}{\partial x_j}}{\omega }_j={ϵ}_{ijn}{\displaystyle \frac{\partial }{\partial x_j}}\left[{\displaystyle \frac{1}{\rho }}{\displaystyle \frac{\partial {\sigma }_{nm}}{\partial x_m}}+f_n\right].$$

The right-hand side is exactly the $Curl$ of the acceleration $\dot{u}$, where the overdot denotes the substantial derivative, or convection by the velocity field. Ignoring the viscous and body force terms, this equation can be rewritten as

$$\dot{\left({\displaystyle \frac{{\omega }_i}{\rho }}\right)}={\displaystyle \frac{\partial u_i}{\partial x_j}}{\displaystyle \frac{{\omega }_j}{\rho }}+{\displaystyle \frac{1}{{\rho }^3}}{ϵ}_{ijn}{\displaystyle \frac{\partial \rho }{\partial x_j}}{\displaystyle \frac{\partial p}{\partial x_n}},$$

(21)

in which the baroclinic torque appears as the second term in the right-hand side.

This term vanishes in the barotropic case $p=p\left(\rho \right)$, and not only in the pure incompressible case. More interestingly, it can be cancelled by projecting the equation on the gradient of density. This suggests forming the scalar product ${\displaystyle \frac{1}{\rho }}{\displaystyle \frac{\partial \rho }{\partial x_i}}{\omega }_i$.

The convective derivative of this quantity involves the derivative of the gradient of density, or $\dot{\left({\displaystyle \frac{\partial \rho }{\partial x_i}}\right)}$, which can be expressed as

$$\dot{\left({\displaystyle \frac{\partial \rho }{\partial x_i}}\right)}={\displaystyle \frac{\partial }{\partial x_i}}\left(\dot{\rho }\right)-{\displaystyle \frac{\partial u_j}{\partial x_i}}{\displaystyle \frac{\partial \rho }{\partial x_j}}.$$

(22)

Combining Equations (21) and (22), several terms cancel each other, and one finds

$$\dot{\left({\displaystyle \frac{1}{\rho }}{\displaystyle \frac{\partial \rho }{\partial x_i}}{\omega }_i\right)}={\displaystyle \frac{{\omega }_i}{\rho }}{\displaystyle \frac{\partial }{\partial x_i}}\left(\dot{\rho }\right)$$

(23)

This equation suggests, from the very beginning, before splitting the variables into the mean (or base) and fluctuating (or disturbance) parts, and before adding body forces, that

$${\mathrm{\Pi }}_{\omega }={\displaystyle \frac{1}{\rho }}{\displaystyle \frac{\partial \rho }{\partial x_i}}{\omega }_i={\displaystyle \frac{1}{\rho }}\nabla \rho ·\mathit{\omega },$$

(24)

or the potential vorticity, is an invariant, but not in an arbitrarily compressible case. The Boussinesq approximation, whose starting point is $\dot{\rho }=0$ and $\nabla ·\mathit{u}=0$, from the mass conservation law $\dot{\rho }=-\rho \nabla ·\mathit{u}$, is a necessary condition.

5.2. Towards Weak, Isotropic Turbulence with Increasing Compressibility

The Boussinesq approximation, touched upon in the previous subsection, allows moderate fluctuations of density, but the velocity field remains solenoidal (divergence-free) as in classical incompressible flows. Is there a way to allow both density fluctuations and divergent velocity field, without a drastic change in the strategy used in the incompressible case? A first step in extending the domain of incompressible isotropic turbulence is to consider the decomposition of the (velocity, pressure, density) fluctuating field into three modes, vortical, acoustic, and entropic. In this decomposition, initiated by Kovasznay [7,28,29], only the first mode, vortical, or solenoidal, part of the velocity field, is inherited from the incompressible case.

A very important jump in the complexity is to consider the non-quadratic nonlinearity in the general Navier–Stokes equations, such as $\rho u\otimes u$ terms. Accordingly, a quadratic approximation merits interest.

As a second point, wave turbulence theory can be applied to the acoustic waves, but this is not valid in the presence of the other, non-propagating, modes, say vortical and entropic ones. Note that this problem is similar to the one of stably stratified turbulence, and rotating stably stratified turbulence, which was recently revisited by Scott and Cambon (2024) [27]. The coexistence of a non-propagating (NP) mode with inertia–gravity wave modes is addressed in an original way, which can go beyond wave turbulence theory. On the other hand, the flow in the latter case is strongly anisotropic, but the velocity field remains solenoidal, according to the Boussinesq approximation.

5.3. A Brief Review of Some Existing Spectral Models with Acoustics

Figure 3 presents qualitative features that are both interesting … and very puzzling. These were obtained by Gauthier Fauchet after three Ph.D. studies supervised by Jean-Pierre Bertoglio (reports and articles can be obtained from the author upon request, and a review is available in [7], Chapter 13).

On the one hand, it is shown that the spectral domain is much larger than in the incompressible case, and this is illustrated by the gap between the acoustic bump at a low wavenumber and the maximum of the solenoidal energy spectrum. Such a domain cannot be covered by existing DNSs only, so that a combination of DNSs and statistical models/theories, ranging from the EDQNM to DIA, was involved. The approach is quasi-isentropic and at a low Mach number, so that the turbulent flow is assumed to be a combination of the solenoidal (or vortical) non-propagating (NP) mode, a dilatational mode, and a pressure mode, the latter two being possibly coupled by acoustic modes. Accordingly, four kinds of energy spectra are plotted in the figure: the solenoidal energy spectrum $E^{ss}$, its dilatational counterpart $E^{cc}$, the pressure spectrum $E^{pp}$, and its counterpart in purely incompressible turbulence $E_{inc}^{pp}$. Only at a low wavenumber, $E^{dd}$ and $E^{pp}$ coincide, in agreement with the so-called ‘acoustic equilibrium’ around a maximum, or the above-mentioned acoustic bump. In contrast, $E^{cc}$ is much lower than $E^{pp}$ at larger wavenumbers, with slopes around $k^{-3}$ and $k^{-7/3}$, respectively. It is expected that the apparent inertial zones for $E^{dd}$ and $E^{pp}$ characterise a pseudo-sound, which ought to be distinguished from the true acoustic regime (see also Ristorcelli (1997) [30]). Moreover, $E^{pp}$ coincides with its incompressible counterpart $E_{inc}^{pp}$ in this region. The $-7/3$ slope is a well-known result in incompressible turbulence (Batchelor), where the spectrum of pressure is slaved to the kinetic energy spectrum, here fixed with a $-5/3$ Kolmogorov slope.

5.4. A Recent Approach of Weak Isotropic Turbulence in a Compressible Fluid

The problem illustrated by Figure 3 is revisited by Julian Scott (private) starting from a more complete set of equations, including the entropic mode. Regarding the nonlinearity of the compressible Navier–Stokes equations, being non-quadratic, the turbulence is supposed weak, allowing a quadratic approximation using Taylor’s expansion. Modes, which are solutions of the governing equations without nonlinearity, viscosity, or thermal conduction, form a complete set, which is used to express the flow, hence a modal decomposition into three components: acoustic, vortical (or solenoidal), and entropic. See also [28,29] for a seminal analysis.

The set of basic equations involves the Navier–Stokes equations:

$${\dot{u}}_i=-{\displaystyle \frac{1}{\rho }}{\displaystyle \frac{\partial p}{\partial x_i}}+{\displaystyle \frac{1}{\rho }}{\displaystyle \frac{\partial {\tau }_{ij}}{\partial x_j}},$$

(25)

the mass conservation equation:

$$\dot{\rho }=-\rho {\displaystyle \frac{\partial u_i}{\partial x_i}},$$

(26)

and the equation for entropy:

$$\dot{s}=S$$

(27)

in which the overdot denotes the substantial derivative, as in Equation (21), whereas ${\tau }_{ij}$ and S hold for the viscous and heat conduction terms, as follows:

$${\tau }_{ij}=\lambda {\displaystyle \frac{\partial u_k}{\partial x_k}}{\delta }_{ij}+2\mu D_{ij},D_{ij}={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{\partial u_i}{\partial x_j}}+{\displaystyle \frac{\partial u_j}{\partial x_i}}\right),$$

and

$$S={\displaystyle \frac{1}{\rho T}}\left({\tau }_{ij}{D}_{ij}+{\displaystyle \frac{\partial }{\partial x_i}}\left(\kappa {\displaystyle \frac{\partial T}{\partial x_i}}\right)\right).$$

(28)

To complete the above system, the equations of state are needed, chosen here as $p=p(\rho ,s)$. This implies:

$$\dot{p}=-\rho c^2{\displaystyle \frac{\partial u_i}{\partial x_i}}+\alpha S,$$

(29)

where

$$c^2={\displaystyle \frac{\partial p}{\partial \rho }}{\mid }_s,\alpha ={\displaystyle \frac{\partial p}{\partial s}}{\mid }_{\rho }.$$

(30)

c is the sonic speed.

Perturbation to the obvious uniform state $p=p_0$ (and so on constant variables with zero index) without motion is then considered.

5.4.1. NP Modes

It is shown that the vortical (or solenoidal) and entropic components, respectively, give a classical incompressible flow and a scalar field, which is advected by the vortical velocity. Thus, these two components are expected to decay via turbulent cascades. It is also shown that, for weak turbulence, the time scale for the evolution of the acoustic component is much longer. Thus, following an initial phase, the acoustic component is dominant. For this reason, the main elements of this paper concern the spectral evolution of the acoustic component alone and can be considered as descriptive of a nonlinear acoustics problem with an infinite, random wave field.

5.4.2. Wave Turbulence Theory for Acoustic Waves

Wave turbulence theory, of a rather untraditional type, owing to the specific properties of acoustic waves, is used to derive evolution equations for the distribution of acoustic energy in spectral space. These equations are integrated numerically, and the results show power laws with respect to both time and the wavenumber. The dispersion law of acoustic waves is isotropic in an infinite medium, with

$$\sigma \left(\mathit{k}\right)=c_{0}k.$$

(31)

This is in contrast with the anisotropic dispersion frequency of, e.g., inertia–gravity waves in Equation (20).

Resonant triads are found for

$${\sigma }_k\pm {\sigma }_p\pm {\sigma }_q=0,\mathrm{or}k\pm p\pm q=0,$$

(32)

which correspond to the limits $q=k-p$, $q=p-k$, and $q=p+k$ of the domain for the triadic integration of triple correlations (as for T in Equation (9), shown in Figure 2. In incompressible turbulence, nonlinear interactions exactly vanish on these curves. The acoustic amplitude equation is established. It is shown that an acoustic spectrum can persist after the eventual dissipation of both non-propagating vortical and entropic modes. Numerical solutions of the acoustic equation show transient ranges with different slopes. After a slow evolution, a power law of exponent close to $-7/2$ is apparent in the inertial range. Note that the detailed and comprehensive study by Julian Scott was not published before, because we found that this slope in $k^{-7/2}$ was derived by Zakharov and Sagdeev [31] in 1970 (translation in English by E. Falcon).

6. Conclusions and Perspectives

Astrophysics can give applications to isotropic turbulence at very high Reynolds numbers, as illustrated by [19], and by [32], with very high compressibility.

Considering finite Reynolds numbers, the discussion and comparisons of models and theories carried out in the physical space, from K-H-type equations, and in the spectral space, with triadic closures, are given in Section 2. It was also an opportunity to include wave turbulence theory, as an exact asymptotic approach to weak turbulence, with its obvious connection with conventional spectral closures for strong turbulence. Especially when quadratic nonlinearity is addressed, and triple resonances are permitted, it is not necessary to distinguish a Wave Kinetic Energy (WKE) approach from an Asymptotic Quasi-Normal Markovian (AQNM) one [15]. The term kinetic in WKE is even misleading, with reference to Boltzmann, if only the Lin equation is concerned, its transfer term being affected (weak case, e.g., inertial wave turbulence) or not (strong case, HIT) by interacting dispersive waves.

According to Annick Pouquet (private), the relevance of triple resonances was a conflicting topic in the past. Several studies appeared with resonant quartets before the publication by Galtier et al. [33] (2001) of WT for basic MHD, with evidence of triple resonances. In a large community, it was expected that Alfvén waves were not eligible for WT, being non-dispersive. Older articles with rotating turbulence, as [34], were simply ignored. A very large Russian community made scholarly contributions to WT with resonant quartets, but ignored the MHD turbulence and the rotating turbulence, where triple resonances are relevant. Surprisingly, the topic of triple resonances was addressed by them, but for acoustic wave turbulence, as shown by [31].

From incompressible to increasingly compressible isotropic turbulence, Section 3 revisits a simple model of compressed turbulence, in which linear and nonlinear effects can be compared in an exact way. This introduces the discussion of RDT and nonlinear closures for anisotropic turbulence in Section 4. Incidentally, in Section 5.1, it is shown, or recalled, why potential vorticity is not useful in arbitrary compressible turbulence. The role of the Boussinesq hypothesis is emphasised.

Finally, we can say a few words about internal intermittency. The occurrence of the FRN effect and the need for achieving the complete inertial range renders some results on anomalous exponents for incompressible HIT very questionable, since they are Reynolds-dependent at moderate Reynolds numbers. Results from extended self-similarity, in which Equation (1) is considered as unconditionally valid at $n=3$, and altered for any $n\ne 3$, are simply wrong. On the other hand, anomalous exponents significantly smaller than $n/3$ are evidenced in strongly compressible HIT [32,35].

Some key strands are picked out below:

• The study of the FRN effect, which alters the ‘exact’ equations, can be carried out either in physical space, using K-H-type equations, or in Fourier space, using the Lin equation. But, the Lin equation opens the problem of the infinite hierarchy of equations for statistical moments. Spectral closures that truncate the infinite hierarchy of statistical equations give access to a transfer term mediated by all triads (spectral counterpart of two-point third-order moments), whereas K-H gives only access to two-point second-order correlations. The EDQNM is particularly relevant for quantitative comparisons with the spectral measures in the Comte-Bellot and Corrsin experiment [9] (e.g., CBC points in Figure 1). At higher Reynolds numbers, FRN corrections can be given by much simpler models.
• Rapid distortion theory, or the linear approach in the largest sense, has more applications than generally agreed upon. From homogeneous turbulence, however, it is a useful tool, except for the isotropic case (Section 4). Only in that case, a general rescaling allows us to a priori compare linear and nonlinear effects.
• Weak turbulence, as WT, shares an important background with spectral theories and models for strong turbulence. This is particularly true when the nonlinearity is quadratic, with transfer terms mediated by triads, with resonant triads only in WT. But, anisotropy is essential, as in the rotating, stratified, and MHD cases.
• WT can be applied to incompressible isotropic turbulence, even with quadratic nonlinearity, but resonant quartets are called into play, in contrast with the triads in strong turbulence.
• When weak compressibility is addressed in isotropic turbulence, acoustic WT is relevant with resonant triads.
• More generally, increasing compressibility remains a timely topic for HIT, with theory, modelling, DNSs, and their combination.