Connection between Winter East Asia Flow Patterns and Stratospheric Polar Vortex Anomalies
Abstract
1. Introduction
2. Data and Analyses
2.1. Data
2.2. Analyses
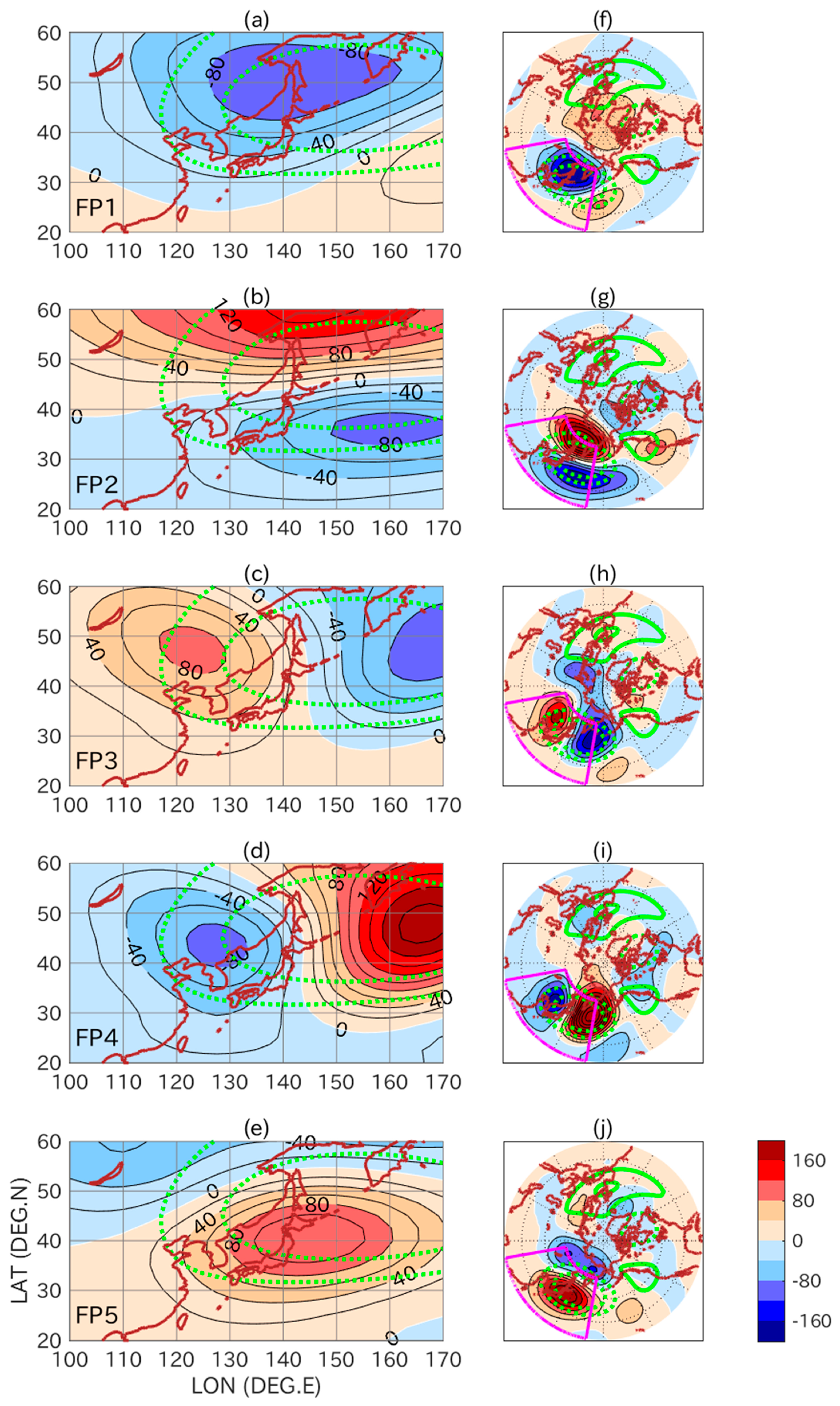
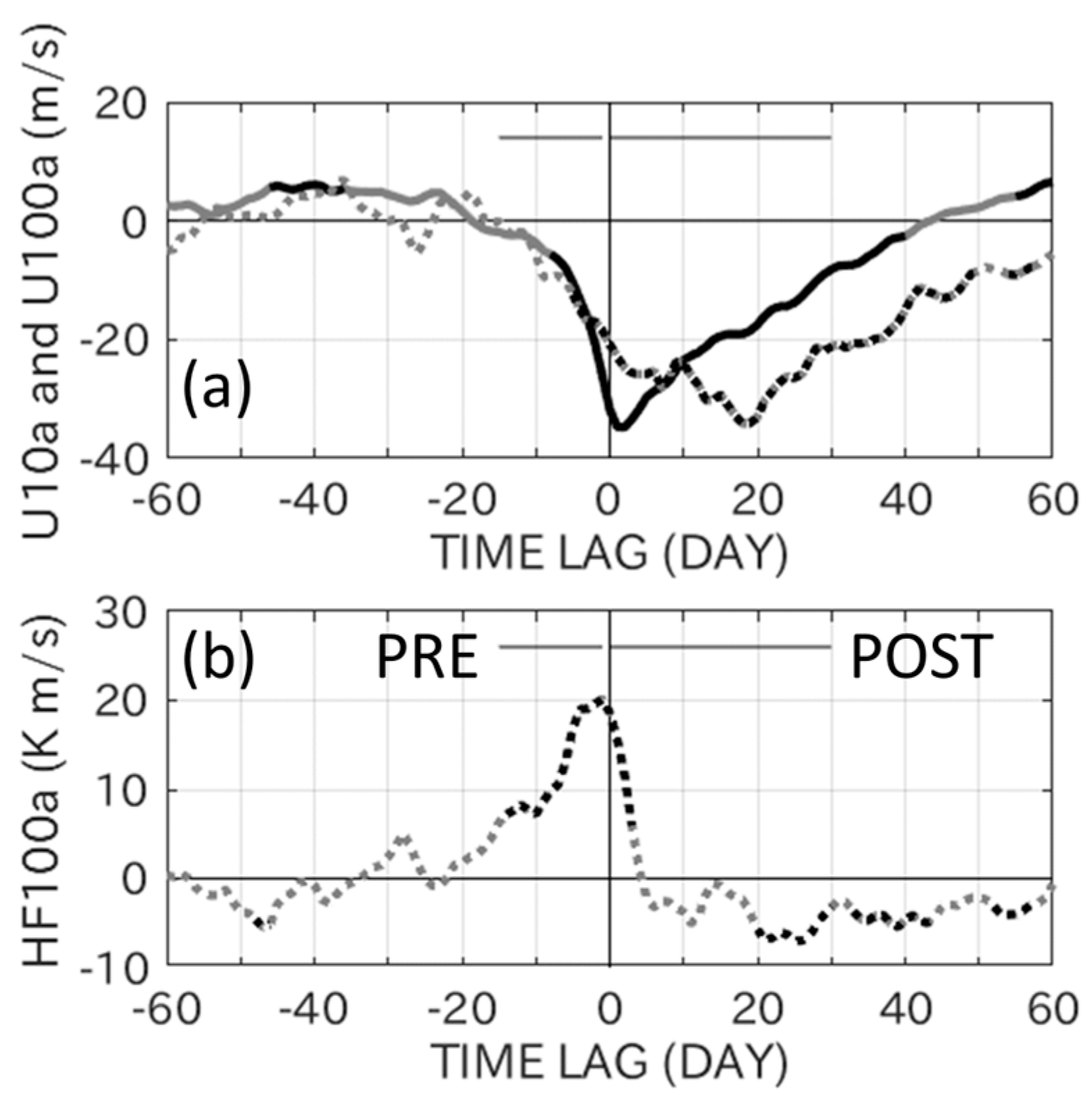
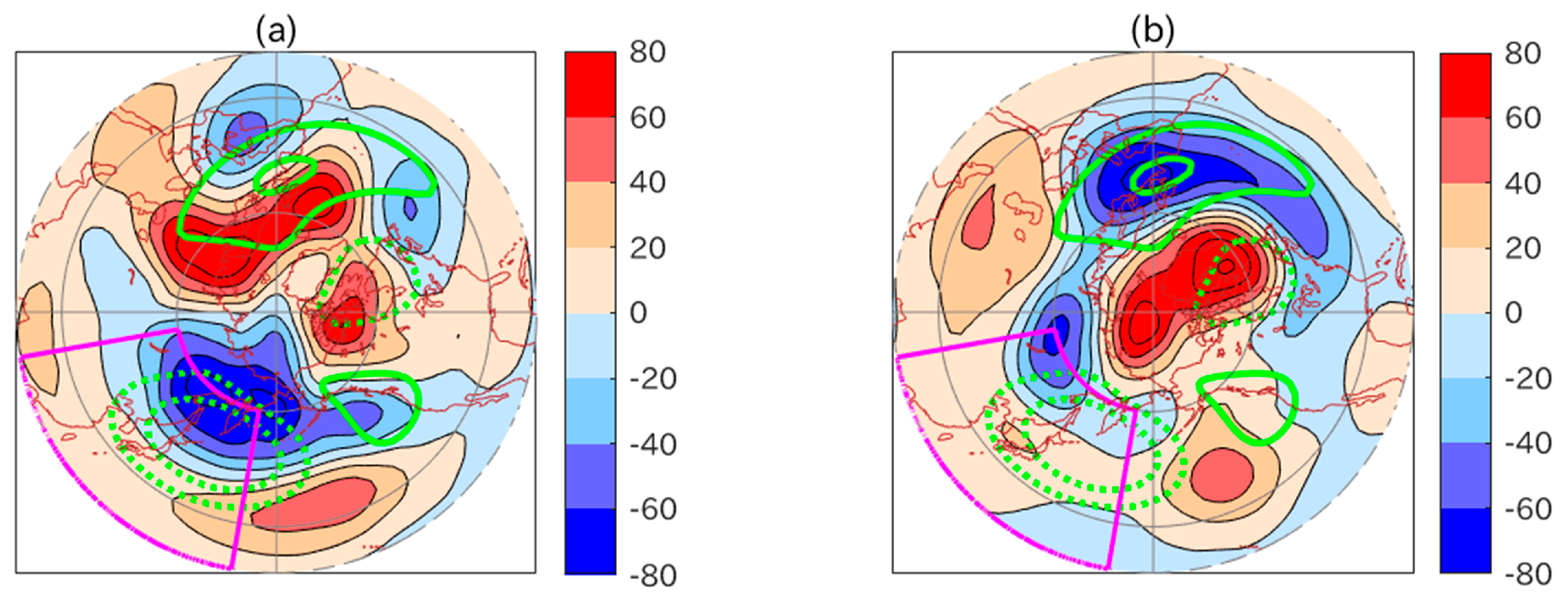
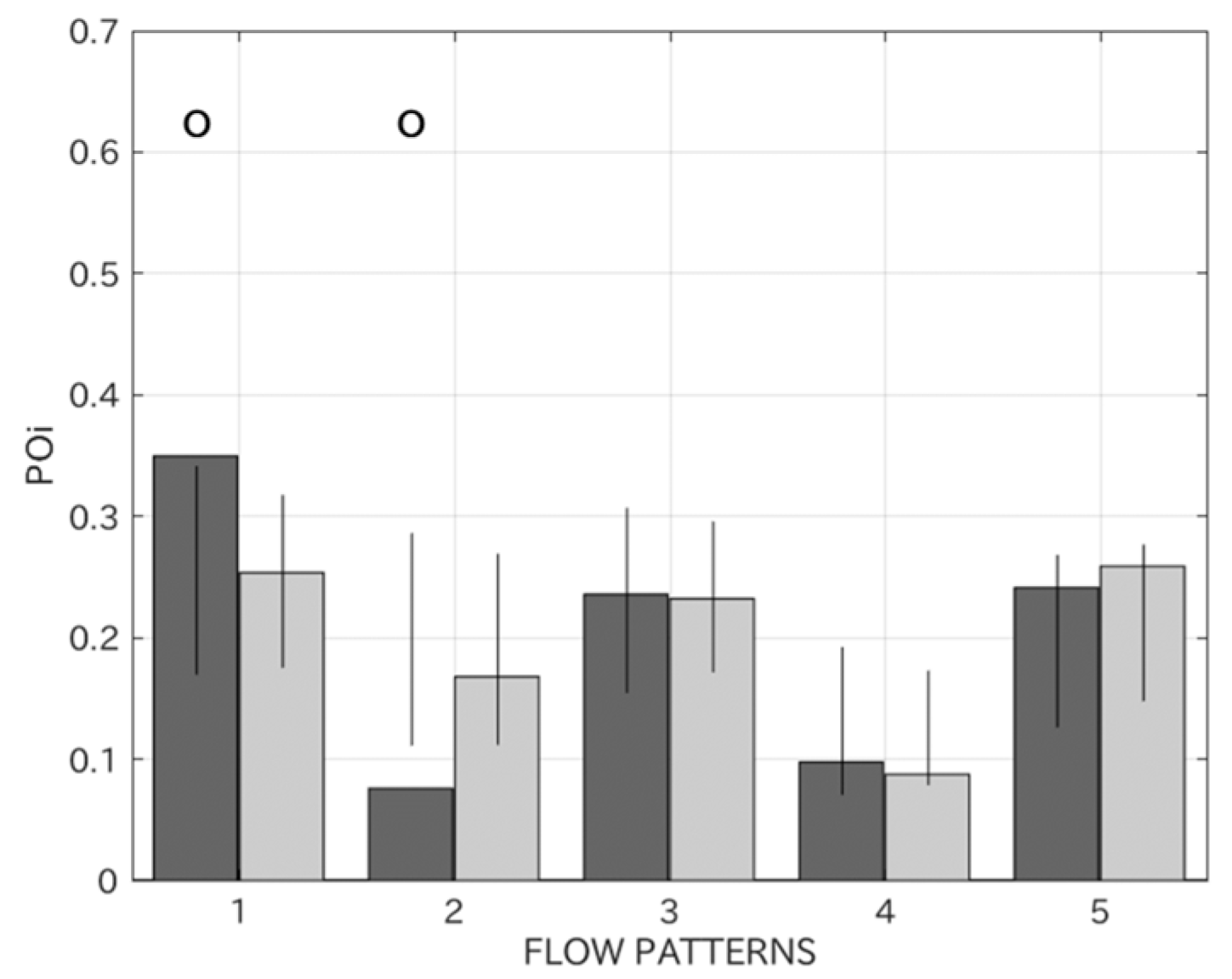
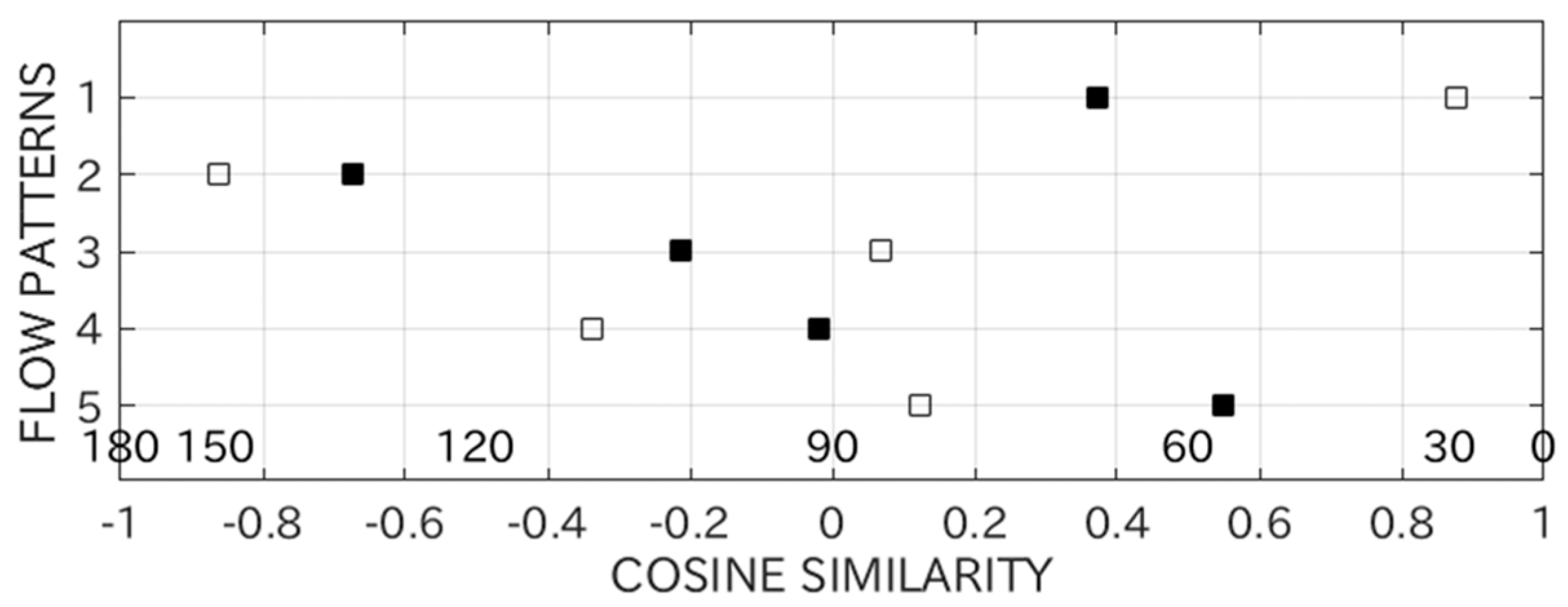
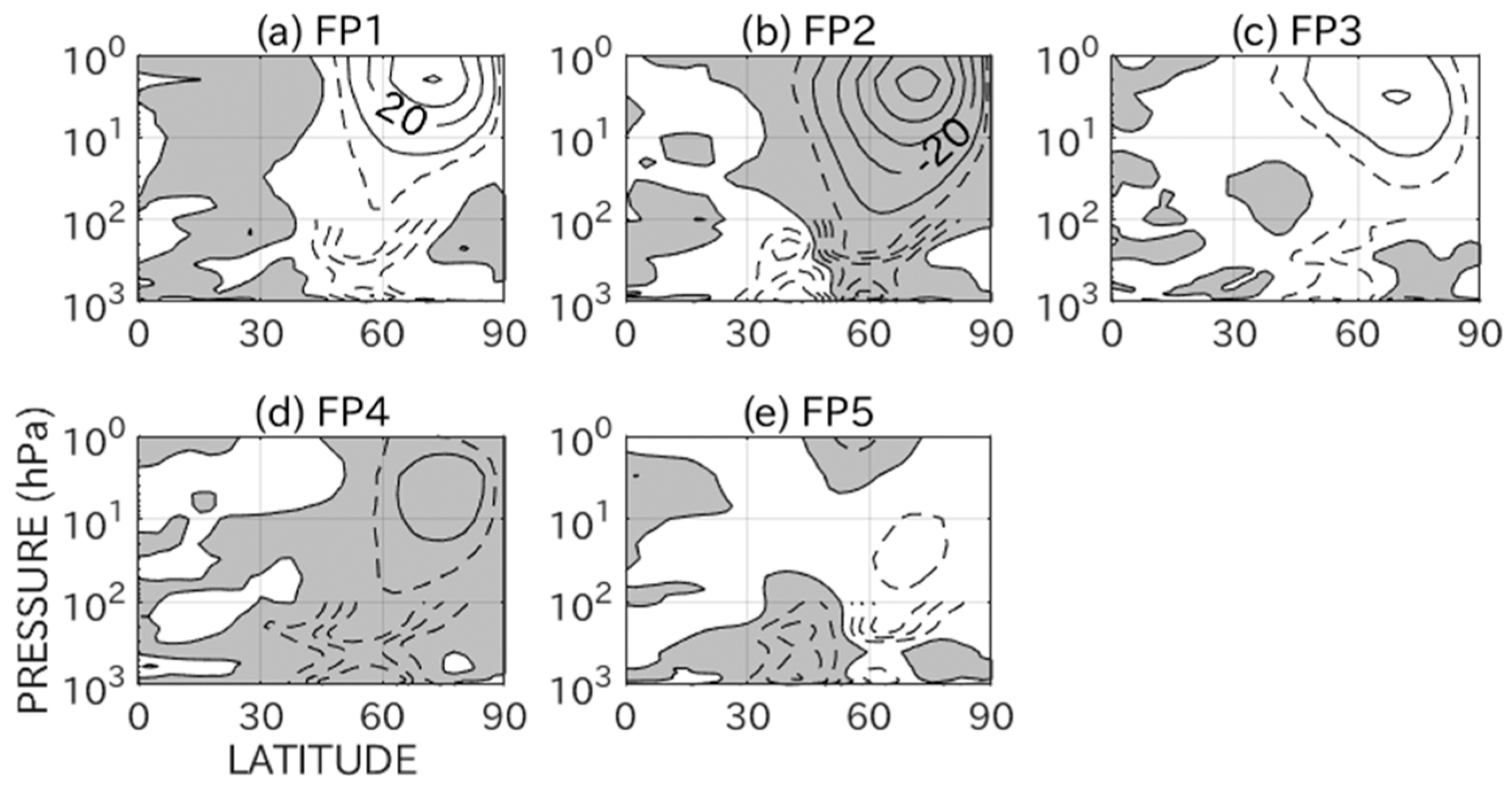
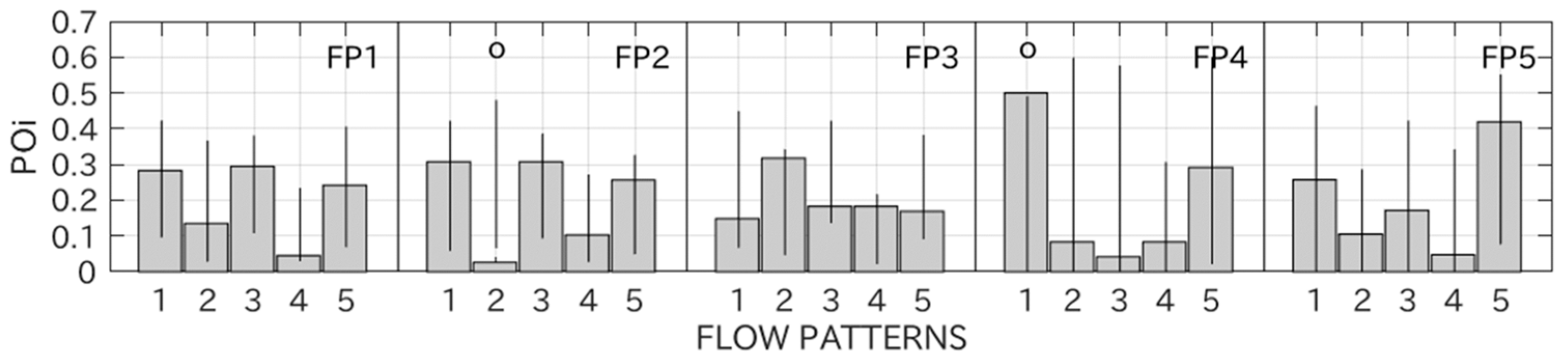
3. Results
4. Summary and Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Butchart, N. The Stratosphere: A Review of the Dynamics and Variability. Weather. Clim. Dyn. 2022, 3, 1237–1272. [Google Scholar] [CrossRef]
- Kidston, J.; Scaife, A.A.; Hardiman, S.C.; Mitchell, D.M.; Butchart, N.; Baldwin, M.P.; Gray, L.J. Stratospheric Influence on Tropospheric Jet Streams, Storm Tracks and Surface Weather. Nat. Geosci. 2015, 8, 433–440. [Google Scholar] [CrossRef]
- Baldwin, M.P.; Ayarzagüena, B.; Birner, T.; Butchart, N.; Butler, A.H.; Charlton-Perez, A.J.; Domeisen, D.I.V.; Garfinkel, C.I.; Garny, H.; Gerber, E.P.; et al. Sudden Stratospheric Warmings. Rev. Geophys. 2021, 59, e2020RG000708. [Google Scholar] [CrossRef]
- Matsuno, T. Vertical Propagation of Stationary Planetary Waves in the Winter Northern Hemisphere. J. Atmos. Sci. 1970, 27, 871–883. [Google Scholar] [CrossRef]
- Matsuno, T. A Dynamical Model of the Stratospheric Sudden Warming. J. Atmos. Sci. 1971, 28, 1479–1494. [Google Scholar] [CrossRef]
- Limpasuvan, V.; Thompson, D.W.J.; Hartmann, D.L. The Life Cycle of the Northern Hemisphere Sudden Stratospheric Warmings. J. Clim. 2004, 17, 2584–2596. [Google Scholar] [CrossRef]
- Polvani, L.M.; Waugh, D.W. Upward Wave Activity Flux as a Precursor to Extreme Stratospheric Events and Subsequent Anomalous Surface Weather Regimes. J. Clim. 2004, 17, 3548–3554. [Google Scholar] [CrossRef]
- Martius, O.; Polvani, L.M.; Davies, H.C. Blocking Precursors to Stratospheric Sudden Warming Events. Geophys. Res. Lett. 2009, 36, L14806. [Google Scholar] [CrossRef]
- Garfinkel, C.I.; Hartmann, D.L.; Sassi, F. Tropospheric Precursors of Anomalous Northern Hemisphere Stratospheric Polar Vortices. J. Clim. 2010, 23, 3282–3299. [Google Scholar] [CrossRef]
- Nishii, K.; Nakamura, H.; Orsolini, Y.J. Geographical Dependence Observed in Blocking High Influence on the Stratospheric Variability through Enhancement and Suppression of Upward Planetary-Wave Propagation. J. Clim. 2011, 24, 6408–6423. [Google Scholar] [CrossRef]
- Bao, M.; Tan, X.; Hartmann, D.L.; Ceppi, P. Classifying the Tropospheric Precursor Patterns of Sudden Stratospheric Warmings. Geophys. Res. Lett. 2017, 44, 8011–8016. [Google Scholar] [CrossRef]
- Scaife, A.A.; Folland, C.K.; Alexander, L.V.; Moberg, A.; Knight, J.R. European Climate Extremes and the North Atlantic Oscillation. J. Clim. 2008, 21, 72–83. [Google Scholar] [CrossRef]
- Kolstad, E.W.; Breiteig, T.; Scaife, A.A. The Association between Stratospheric Weak Polar Vortex Events and Cold Air Outbreaks in the Northern Hemisphere. Q. J. R. Meteorol. Soc. 2010, 136, 886–893. [Google Scholar] [CrossRef]
- King, A.D.; Butler, A.H.; Jucker, M.; Earl, N.O.; Rudeva, I. Observed Relationships Between Sudden Stratospheric Warmings and European Climate Extremes. J. Geophys. Res. Atmos. 2019, 124, 13943–13961. [Google Scholar] [CrossRef]
- Domeisen, D.I.V.; Butler, A.H. Stratospheric Drivers of Extreme Events at the Earth’s Surface. Commun. Earth Environ. 2020, 1, 59. [Google Scholar] [CrossRef]
- Kolstad, E.W. Higher Ocean Wind Speeds during Marine Cold Air Outbreaks. Q. J. R. Meteorol. Soc. 2017, 143, 2084–2092. [Google Scholar] [CrossRef]
- Baldwin, M.P.; Dunkerton, T.J. Propagation of the Arctic Oscillation from the Stratosphere to the Troposphere. J. Geophys. Res. Atmos. 1999, 104, 30937–30946. [Google Scholar] [CrossRef]
- Hitchcock, P.; Shepherd, T.G.; Taguchi, M.; Yoden, S.; Noguchi, S. Lower-Stratospheric Radiative Damping and Polar-Night Jet Oscillation Events. J. Atmos. Sci. 2013, 70, 1391–1408. [Google Scholar] [CrossRef]
- Runde, T.; Dameris, M.; Garny, H.; Kinnison, D.E. Classification of Stratospheric Extreme Events According to Their Downward Propagation to the Troposphere. Geophys. Res. Lett. 2016, 43, 6665–6672. [Google Scholar] [CrossRef]
- Nakagawa, K.I.; Yamazaki, K. What Kind of Stratospheric Sudden Warming Propagates to the Troposphere? Geophys. Res. Lett. 2006, 33, L04801. [Google Scholar] [CrossRef]
- Karpechko, A.Y.; Hitchcock, P.; Peters, D.H.W.; Schneidereit, A. Predictability of Downward Propagation of Major Sudden Stratospheric Warmings. Q. J. R. Meteorol. Soc. 2017, 143, 1459–1470. [Google Scholar] [CrossRef]
- Dai, Y.; Hitchcock, P. Understanding the Basin Asymmetry in Surface Response to Sudden Stratospheric Warmings from an Ocean–Atmosphere Coupled Perspective. J. Clim. 2021, 34, 8683–8698. [Google Scholar] [CrossRef]
- Scaife, A.A.; Baldwin, M.P.; Butler, A.H.; Charlton-Perez, A.J.; Domeisen, D.I.V.; Garfinkel, C.I.; Hardiman, S.C.; Haynes, P.; Karpechko, A.Y.; Lim, E.P.; et al. Long-Range Prediction and the Stratosphere. Atmos. Chem. Phys. 2022, 22, 2601–2623. [Google Scholar] [CrossRef]
- Hannachi, A.; Straus, D.M.; Franzke, C.L.E.; Corti, S.; Woollings, T. Low-Frequency Nonlinearity and Regime Behavior in the Northern Hemisphere Extratropical Atmosphere. Rev. Geophys. 2017, 55, 199–234. [Google Scholar] [CrossRef]
- Charlton-Perez, A.J.; Ferranti, L.; Lee, R.W. The Influence of the Stratospheric State on North Atlantic Weather Regimes. Q. J. R. Meteorol. Soc. 2018, 144, 1140–1151. [Google Scholar] [CrossRef]
- Domeisen, D.I.V.; Grams, C.M.; Papritz, L. The Role of North Atlantic-European Weather Regimes in the Surface Impact of Sudden Stratospheric Warming Events. Weather. Clim. Dyn. 2020, 1, 373–388. [Google Scholar] [CrossRef]
- Lee, S.H.; Furtado, J.C.; Charlton-Perez, A.J. Wintertime North American Weather Regimes and the Arctic Stratospheric Polar Vortex. Geophys. Res. Lett. 2019, 46, 14892–14900. [Google Scholar] [CrossRef]
- Greatbatch, R.J.; Gollan, G.; Jung, T.; Kunz, T. Factors Influencing Northern Hemisphere Winter Mean Atmospheric Circulation Anomalies during the Period 1960/61 to 2001/02. Q. J. R. Meteorol. Soc. 2012, 138, 1970–1982. [Google Scholar] [CrossRef]
- Butler, A.H.; Sjoberg, J.P.; Seidel, D.J.; Rosenlof, K.H. A Sudden Stratospheric Warming Compendium. Earth Syst. Sci. Data 2017, 9, 63–76. [Google Scholar] [CrossRef]
- Nishii, K.; Nakamura, H.; Orsolini, Y.J. Cooling of the Wintertime Arctic Stratosphere Induced by the Western Pacific Teleconnection Pattern. Geophys. Res. Lett. 2010, 37, L13805. [Google Scholar] [CrossRef]
- Jeong, J.H.; Kim, B.M.; Ho, C.H.; Chen, D.; Lim, G.H. Stratospheric Origin of Cold Surge Occurrence in East Asia. Geophys. Res. Lett. 2006, 33, L14710. [Google Scholar] [CrossRef]
- Zhang, Y.; Si, D.; Ding, Y.; Jiang, D.; Li, Q.; Wang, G. Influence of Major Stratospheric Sudden Warming on the Unprecedented Cold Wave in East Asia in January 2021. Adv. Atmos. Sci. 2022, 39, 576–590. [Google Scholar] [CrossRef]
- Matsueda, M.; Kyouda, M. Wintertime East Asian Flow Patterns and Their Predictability on Medium-Range Timescales. Sci. Online Lett. Atmos. 2016, 12, 121–126. [Google Scholar] [CrossRef]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H.; et al. The JRA-55 Reanalysis: General Specifications and Basic Characteristics. J. Meteorol. Soc. Japan Ser. II 2015, 93, 5–48. [Google Scholar] [CrossRef]
- Charlton, A.J.; Polvani, L.M. A New Look at Stratospheric Sudden Warmings. Part I: Climatology and Modeling Benchmarks. J. Clim. 2007, 20, 449–469. [Google Scholar] [CrossRef]
- Baldwin, M.P.; Dunkerton, T.J. Stratospheric Harbingers of Anomalous Weather Regimes. Science (1979) 2001, 294, 581–584. [Google Scholar] [CrossRef] [PubMed]
- Ineson, S.; Scaife, A.A. The Role of the Stratosphere in the European Climate Response to El Nĩo. Nat. Geosci. 2009, 2, 32–36. [Google Scholar] [CrossRef]
- Polvani, L.M.; Sun, L.; Butler, A.H.; Richter, J.H.; Deser, C. Distinguishing Stratospheric Sudden Warmings from ENSO as Key Drivers of Wintertime Climate Variability over the North Atlantic and Eurasia. J. Clim. 2017, 30, 1959–1969. [Google Scholar] [CrossRef]
- Domeisen, D.I.V.; Garfinkel, C.I.; Butler, A.H. The Teleconnection of El Niño Southern Oscillation to the Stratosphere. Rev. Geophys. 2019, 57, 5–47. [Google Scholar] [CrossRef]
- Kretschmer, M.; Cohen, J.; Matthias, V.; Runge, J.; Coumou, D. The Different Stratospheric Influence on Cold-Extremes in Eurasia and North America. NPJ Clim. Atmos. Sci. 2018, 1, 44. [Google Scholar] [CrossRef]
- Spaeth, J.; Birner, T. Stratospheric Modulation of Arctic Oscillation Extremes as Represented by Extended-Range Ensemble Forecasts. Weather. Clim. Dyn. 2022, 3, 883–903. [Google Scholar] [CrossRef]
- Bett, P.E.; Scaife, A.A.; Hardiman, S.C.; Thornton, H.E.; Shen, X.; Wang, L.; Pang, B. Using Large Ensembles to Quantify the Impact of Sudden Stratospheric Warmings and Their Precursors on the North Atlantic Oscillation. Weather. Clim. Dyn. 2023, 4, 213–228. [Google Scholar] [CrossRef]
- Hitchcock, P.; Butler, A.; Charlton-Perez, A.; Garfinkel, C.I.; Stockdale, T.; Anstey, J.; Mitchell, D.; Domeisen, D.I.V.; Wu, T.; Lu, Y.; et al. Stratospheric Nudging And Predictable Surface Impacts (SNAPSI): A Protocol for Investigating the Role of Stratospheric Polar Vortex Disturbances in Subseasonal to Seasonal Forecasts. Geosci. Model. Dev. 2022, 15, 5073–5092. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taguchi, M. Connection between Winter East Asia Flow Patterns and Stratospheric Polar Vortex Anomalies. Atmosphere 2024, 15, 844. https://doi.org/10.3390/atmos15070844
Taguchi M. Connection between Winter East Asia Flow Patterns and Stratospheric Polar Vortex Anomalies. Atmosphere. 2024; 15(7):844. https://doi.org/10.3390/atmos15070844
Chicago/Turabian StyleTaguchi, Masakazu. 2024. "Connection between Winter East Asia Flow Patterns and Stratospheric Polar Vortex Anomalies" Atmosphere 15, no. 7: 844. https://doi.org/10.3390/atmos15070844
APA StyleTaguchi, M. (2024). Connection between Winter East Asia Flow Patterns and Stratospheric Polar Vortex Anomalies. Atmosphere, 15(7), 844. https://doi.org/10.3390/atmos15070844





